IRINELY.ART – схемы и описания вязания амигуруми крючком. Бесплатные мастер-классы по вязанию игрушек

• Мини Маус

• Лисёнок Филипп

• Черепашки Ниндзя

• Анкилозавр

• Голубой динозавр

• Монстрики

• Цыплёнок в корзинке

• Пасхальный декор Зайка

• Улитка Сьюзи

• Молочная корова

• Паучок

• Кролик

• Кукла-валентинка

• Мишка-комфортер

• Пирамидка

• Кавайный котик

• Магнит Солнышко к 8 марта

• Крокодил

• Зайка Дейзи

• Единорожка

• Дракон Дрейк

• Волшебный слон

• Плюшевая Русалка

• Цветы крокусы

IRINELY.

ART — лучшие схемы амигуруми

• Бесплатные схемы амигуруми

  Описания вязания игрушек крючком от разных авторов

• Интересные статьи о рукоделии

  Полезная информация о вязании амигуруми для начинающих

• Регулярный контент
  Вязаные мишки, зайки, котики, тигры, куклы и другие игрушки крючком

• Возможность заявить о себе

  Напишите нам — обязательно опубликуем ваш мастер-класс

для начинающих легкие и маленькие, красиво и быстро, для детей просто картинки

Содержание

1. Наборы для вышивания: основные преимущества
2. Схемы простых вышивок крестом
3. Схемы вышивки крестом для начинающих: легкие и маленькие
4. Учимся правильно: как быстро вышивать крестиком
5. Как быстро вышивать крестиком (видео)
6. Простые схемы вышивки крестиком (фото примеров)

Простые схемы вышивать крестом можно довольно быстро, и справится с этим занятием может каждый, даже новичокСегодня вышивание приобретает широкую популярность.

Особенно модный такой вид вышивания, как крест. Рукодельницы используют разные техники наложения стежков, что позволяет сделать работу уникальной и неповторимой. Однако есть общие правила, которые объединяют все виды техник. Вышивка крестом простая схемы сделают работу намного проще и быстрее. При выборе схем важно учитывать личный опыт, навыки, размеры вышивки и ее цветовые характеристики.

Наборы для вышивания: основные преимущества

В наше время начинающие и опытные рукодельницы могут приобрести набор для вышивания, которые помогают сделать процесс вышивания более простым и приятным. Такие наборы уже содержат все необходимое. В каждом наборе есть инструкция, которая подробно расскажет о действиях, которые нужно совершить.

Наборы подразделяются на несколько видов. Одни предназначены для любителей, другие – для профессионалов.

Выбрать подходящий набор помогут опытные сотрудники магазинов. Наборы для вышивания можно выбрать онлайн. Каталоги интернет-магазинов пестрят самыми разнообразными рисунками и цветовыми решениями.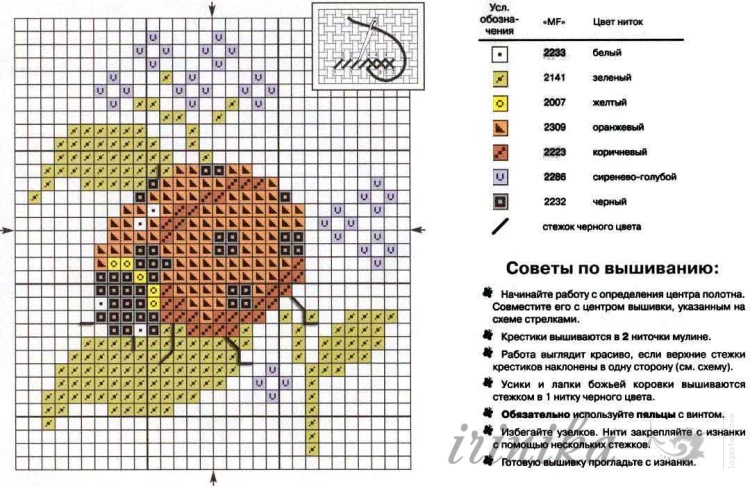

В наборах для вышивания есть все необходимое: канва, нитки, иглы и схема

Содержание набора:

• Канва;
• Мулине;
• Иглы;
• Схема.

Схемы могут быть цветными и монохромными. Начинающие рукодельницы могут приобрести схему небольшого размера. Монохромные схемы помогают наловчиться в накладывании стежков.

Схемы простых вышивок крестом

Очень часто вышивальщицы выбирают любимый вид схем, которыми пользуются впоследствии. Это помогает приобрести определенные профессиональные навыки и опыт. Простые схемы среднего размера подойдут для начинающих рукодельниц.

Существует несколько видов схем, которые различаются по цветовым характеристикам и символичным обозначениям.

Простые схемы предполагают минимальный набор цветов. Это дает возможность неопытным вышивальщицам лучше разобраться в методе переноса определенного цвета при помощи нити на канву. Для начала хватит трех основных цветов.

Схемы простых вышивок крестом могут быть цветные, монохромные и смешанные

Разновидности схем:

• Цветные;
• Монохромные;
• Смешанные.

Перед тем как приступить к работе, важно подготовить все необходимые материалы. Ножницы и нити всегда должны быть под рукой. Маленькие схемы помогут «набить руку» перед исполнением более сложных схем.

Схемы вышивки крестом для начинающих: легкие и маленькие

Те, кто только желает первые шаги на пути к профессиональному вышиванию, часто не знают, с чего начать. Начинать нужно всегда с простых вышивок в несколько цветов. Важно определиться с видом стежков.

Главное правило наложения стежков: все нити должны лежать в одном направлении. Поэтому так важно выбрать определенную технику исполнения.

Легкие схемы подойдут для тех, кто впервые взялся за нитку с иголкой. Важно запастись терпением. Ничто не дается легко с первого раза. Вышивка должна приводить к гармонии, приносить радость и умиротворение.

Даже если вы только начинаете вышивать, следите за тем, чтобы все нити стежков лежали в одном направлении

Виды стежков:

• Английский;
• Датский.

Виды различаются по технике выполнения стежков. В первом варианте выполняется сразу весь крест. Во втором – делается ряд из полустежков, затем этот ряд закрывается стежками в другом направлении.

Учимся правильно: как быстро вышивать крестиком

Чтобы научиться вышивать с большой скоростью, необходимо время. Сперва следует научиться правильно вышивать отельные квадраты на канве. Затем перейти к изучении разных техник.

Каждая вышивальщица решает для себя сама: какая техника ей близка больше всего.

Следует обратить внимание на то, что выполнять стежки можно, следуя разным схемам. Одни наносятся сразу на канву, другие – на бумагу. Второй вариант предполагает подсчет стежков, что затрудняет процесс вышивания.

Существует несколько техник нанесения стежков на канву

Варианты нанесения стежков:

• Счетный;
• Несчетный;
• Машинный.

Каждую из техник можно выполнить быстро, но для этого нужны навыки и опыт. Важно помнить, что быстрое вышивание не означает – качественное. Стежки необходимо накладывать правильно, чтобы не пришлось распарывать вышивку. Для начала можно потренироваться, купив несложные картинки для детей.

Как быстро вышивать крестиком (видео)

Выбор картинок для вышивания очень прост. Схемы можно бесплатно скачать на специализированных сайтах. Самая большая коллекция «Hachette» поможет выполнить вышивку красиво и быстро. Мастер класс и видео из Интернета помогут разобраться в видах техник и нюансах их исполнения. Начинающим рукодельницам лучше выбрать милые детские работы с изображением лесных зверей: белочек, зайчиков, птичек. Простые работы помогут набраться опыта и перейти к более сложным работам.

Простые схемы вышивки крестиком (фото примеров)

Диаграмма

в nLab

Пропустить навигационные ссылки | Домашняя страница | Все страницы | Последние версии | Обсудить эту страницу |

Содержание

Контекст

Теория категорий

Теория категорий

Концепции

• категория

• функтор

• естественная трансформация

• Кот

Универсальные конструкции

• универсальная конструкция

  • представимый функтор

  • сопряженный функтор

  • лимит/колимит

  • взвешенный предел

  • конец/конец

  • Расширение Кан

Теоремы

• Лемма Йонеды

• Двойственность Исбелла

• Гротендик строительство

• Теорема о сопряженном функторе

• теорема монадичности

• теорема о присоединенном подъеме

• Двойственность таннака

• Двойственность Габриэля-Ульмера

• аргумент маленького объекта

• Теорема вложения Фрейда-Митчелла

• связь между теорией типов и теорией категорий

Удлинители

• сноп и теория топоса

• теория обогащенных категорий

• теория высшей категории

Приложения

• приложения теории (высших) категорий

Изменить эту боковую панель

• Идея
• Определения
• Диаграммы в форме категорий
• Функториальное определение
• Определение компонента
• Диаграммы в виде ориентированных графов 9к\\ C& \underset{g}{\to} & D}

  путем рисования некоторых объектов (или точек, помеченных объектами), соединенных стрелками, помеченными морфизмами.

  Эта терминология часто используется, когда речь идет о пределах и копределах; то есть мы говорим о «пределе или копределе диаграммы».

  Есть два естественных способа дать понятию «диаграмма» формальное определение. Во-первых, можно сказать, что диаграмма — это функтор, обычно тот, областью определения которого является (очень) маленькая категория. Этот уровень общности иногда удобен.

  С другой стороны, более прямое представление того, что мы рисуем на странице, когда мы «рисуем диаграмму», предполагает только маркировку вершин и ребер ориентированного графа (или колчана) объектами и морфизмами категории. Диаграмму такого рода можно отождествить с функтором, областью определения которого является свободная категория, и это наиболее распространенный контекст, когда мы говорим о «коммутирующих» диаграммах.

  Определения

  Диаграммы в форме категорий

  Здесь мы обсуждаем диаграммы «формы малой категории», а также понятие конусов/коконусов над ними и ограничивающих/сопредельных (ко-)конусов. Существует быстрое абстрактное функториальное определение

  • функториальное определение

  и есть более длинное, но более подробное определение с точки зрения компонентов

  • определение компонента .

  Функториальное определение

  Приведем краткое функториальное определение диаграмм формы категорий.

  Определение

  (функторное определение)

  Пусть 𝒞\mathcal{C} будет категорией и пусть ℐ\mathcal{I}малая категория,

  Затем

  1. диаграмма XX формы ℐ\mathcal{I} в 𝒞\mathcal{C} является функтором формы

     Х:ℐ⟶𝒞, Х \;\двоеточие\; \mathcal{I} \longrightarrow \mathcal{C} \,

  2. категория ℐ\mathcal{I}-образных диаграмм в 𝒞\mathcal{C} категория функторов Funct(ℐ,𝒞)Funct(\mathcal{I}, \mathcal{C});

  3. диаграмма X:ℐ→𝒞X \двоеточие \mathcal{I} \to \mathcal{C} является константой , если это константный функтор

     constX˜:ℐ⟶∃!*⟶X˜𝒞 const _ {\ тильда X} \;\двоеточие\; \mathcal{I} \overset{\ существует!} {\ longrightarrow} \аст \overset{\тильда X}{\longrightarrow} \mathcal{С}

     , и в этом случае он задается данными одного объекта X˜\tilde X;

  4. конус CC над диаграммой X:ℐ→𝒞X \colon \mathcal{I} \to \mathcal{C} с вершиной объект X˜∈𝒞\tilde X \in \mathcal{C} является естественное преобразование постоянной диаграммы constX˜:ℐ→*→𝒞const_{\tilde X} \colon \mathcal{I} \to \ast \to \mathcal{C} в XX:

     C:constX˜⇒X С \;\двоеточие\; const _ {\ тильда X} \ Rightarrow X

  5. a cocone CC под диаграммой X:ℐ→𝒞X \colon \mathcal{I} \to \mathcal{C} является естественным преобразованием к постоянной диаграмме constX˜:ℐ→*→𝒞const_{\tilde X} \ двоеточие \mathcal{I} \to \ast \to \mathcal{C} от XX:

     C:X⇒constX˜ С \;\двоеточие\; X \ Стрелка вправо const _ {\ тильда X}

  6. предельный конус (или предельный , для краткости) над диаграммой XX является, если он существует, конечным объектом в категории конусов над XX, что означает, что это конус ClimC_{lim} с вершиной, обозначенной lim⟵iXi\underset{\longleftarrow}{\lim}_i X_i такое, что для любого другого конуса CC с вершиной X˜\tilde X существует единственное естественное преобразование ϕ:constX˜⇒constlim⟵iXi\phi \colon const_{\ тильда X} \Rightarrow const _{\underset{\longleftarrow}{\lim}_i X_i} такая, что

     C=Clim∘ϕ C = C_{lim} \circ \phi

  7. копредельный конус (или копредельный , для краткости) по диаграмме XX является, если он существует, исходным объектом в категории коконусов по диаграмме XX, а значит, это коконус ClimC_{lim} с вершина обозначается lim⟶iXi\underset{\longrightarrow}{\lim}_i X_i такая, что для любого другого коконуса CC с вершиной X˜\тильда X существует единственное естественное преобразование ϕ:constlim⟶iXi⇒constX˜\phi \colon const_ {\ underset{\longrightarrow}{\lim}_i X_i} \Rightarrow const _{\tilde X} такой, что

     C=ϕ∘Клим. C = \phi \circ C_{lim} \,.

  Определение компонента

  Мы приводим явное основанное на компонентах определение диаграмм формы категорий.

  Определение

  (диаграмма в категории)

  Диаграмма X•X_\маркер в категории

  1. множество {Xi}i∈I\{ X_i \}_{i \in I} объектов категории;

  2. для каждой пары (i,j)∈I×I(i,j) \in I \times I меток объектов множество {Xi⟶fαXj}α∈Ii,j\{ X_i \overset{ f_\alpha } {\longrightarrow} X_j\}_{\alpha \in I_{i,j}} морфизмов между этими объектами;

  3. для каждой метки i∈Ii \in I выбор элемента ϵi∈Ii,i\epsilon_i \in I_{i,i};

  4. для каждой тройки i,j,k∈Ii,j,k \in I функция

     compi,j,k:Ii,j×Ij,k⟶Ii,k comp_{i,j,k} \;\двоеточие\; I_{i,j} \times I_{j,k} \longrightarrow I_{i,k}

  такой, что

  1. спаривание compcomp ассоциативно и унитально с fϵif_{\epsilon_i}-s нейтральными элементами;

  2. для каждого i∈Ii \in I, тогда fϵi=idXif_{\epsilon_i} = id_{X_i} — тождественный морфизм на ii-м объекте;

  3. для каждой составной пары морфизмов

  Xi⟶fαXj⟶fβXk X_i \ overset {f _ {\ alpha} {\ longrightarrow} X_j \overset{f_{\beta}}{\longrightarrow} X_k

  , то композиция этих двух морфизмов равна морфизму диаграммы, который помечен значением compi,j,kcomp_{i,j,k} на их метках:

  fβ∘fα=fcompi,j,k( а, в). f _ {\ beta} \ circ f_ \ alpha «=» f_{comp_{i,j,k}(\альфа,\бета)} \,. 9{\ mathrlap {е _ {\ бета}}} \\ X_i && \underset{ comp_{i,j,k}(\alpha,\beta) }{\longrightarrow} && X_k } \,.

  Определение

  (конус над диаграммой)

  Рассмотрим диаграмму

  X•=({Xi⟶fαXj}i,j∈I,α∈Ii,j,comp) X_\пуля «=» \левый( \левый\{ X_i \overset{f_\alpha}{\longrightarrow} X_j \right\}_{i,j \in I, \alpha \in I_{i,j}} \,\, \mathrm{комп} \верно)

  в какой-либо категории (по умолчанию). Затем

  1. а конус по этой диаграмме

     1. объект X˜\тильда X в категории;

     2. для каждого i∈Ii \in I морфизм X˜⟶piXi\tilde X \overset{p_i}{\longrightarrow} X_i в категории

     такой, что

     • для всех (i,j)∈I×I(i,j) \in I \times I и всех α∈Ii,j\alpha \in I_{i,j}, то условие

       fα∘pi=pj f_{\alpha} \circ p_i = p_j

       , что мы изобразим следующим образом: 9{\ mathrlap {p’_j}} \\ X_i && \underset{f_\alpha}{\longrightarrow} && X_j }

  2. a co-cone на этой диаграмме

     1. объект X˜\тильда X в категории;

     2. для каждого i∈Ii \in I морфизм qi:Xi⟶X˜q_i \colon X_i \longrightarrow \tilde X в категории

     такой, что

     • для всех (i,j)∈I×I(i,j) \in I \times I и всех α∈Ii,j\alpha \in I_{i,j}, то условие

       qj∘fα=qi q_j \ circ f _ {\ alpha} = q_i

       держится, что изобразим следующим образом:

       Xi⟶fαXjqi↘↙qjX˜. \множество{ X_i && \overset{f_\alpha}{\longrightarrow} && X_j \\ & {}_{\mathllap{q_i}}\searrow && \swarrow_{\mathrlap{q_j}} \\ && \тильда X } \,.

  Определение

  Рассмотрим диаграмму

  X•=({Xi⟶fαXj}i,j∈I,α∈Ii,j,comp) X_\пуля «=» \левый( \левый\{ X_i \overset{f_\alpha}{\longrightarrow} X_j \right\}_{i,j \in I, \alpha \in I_{i,j}} \,\, \mathrm{комп} \верно) 9{\ mathrlap {p’_j}} \\ X_i && \underset{f_\alpha}{\longrightarrow} && X_j } \верно\}

  любой другой конус, то существует единственный морфизм

  ϕ:X˜⟶lim⟶iXi \фи \;\двоеточие\; \тильда X \overset{}{\longrightarrow} \underset{\longrightarrow}{\lim}_i X_i

  , который факторизует данный конус через предельный конус, в котором для всех i∈Ii \in I тогда

  p′i=pi∘ϕ p’_i = p_i \circ \phi

  , который мы изображаем следующим образом:

  9{\ mathllap {q’_i}} \ searrow && \ Swarrow _ {\ mathrlap {q’_j}} \\ && \тильда X } \верно\}

  любой другой кокон, то существует единственный морфизм

  ϕ:lim⟶iXi⟶X˜ \фи \;\двоеточие\; \underset{\longrightarrow}{\lim}_i X_i \overset{}{\longrightarrow} \тильда X

  , который факторизует данный коконус через коограничивающий коконус, в котором для всех i∈Ii \in I тогда

  q’i=ϕ∘qi q’_i = \phi \circ q_i

  , который мы изображаем следующим образом:

  9{\ mathrlap {q’_i}} \\ \тильда X }

Диаграммы в виде ориентированных графов

Определение

(свободная диаграмма)

функтор D: F (J) → CD \ двоеточие F (J) \ в C или, что то же самое, морфизм графов D¯: J → U (C) \ bar {D} \ двоеточие J \ в U (C).

Здесь F:Quiv→CatF\colon Quiv \to Cat обозначает свободную категорию в колчане, а U:Cat→QuivU\colon Cat \to Quiv — базовый колчан категории, которые образуют пару сопряженных функторов. Это виды диаграмм, которые мы «рисуем на странице» — мы рисуем колчан, а затем помечаем его вершины объектами из CC, а его ребра — морфизмами из CC, образуя таким образом морфизм графа J→U(C)J\ к U(С).

• Для любого вида диаграммы JJ может называться формой , схемой или индексом категорией или графиком.

• Обратите внимание, что для данной диаграммы D:J→CD:J\to C образ формы JJ не обязательно является подкатегорией CC, даже если JJ сама считается категорией. Это связано с тем, что функтор DD может идентифицировать объекты JJ, тем самым создавая новые потенциальные композиты, которых нет в JJ. (Иногда говорят об «образе» функтора как о подкатегории, но на самом деле это означает, что подкатегория генерирует изображением в буквальном смысле объектов и морфизмов. )

• CC должен быть строгой категорией, чтобы иметь смысл U(C)U(C); однако F(J)F(J) всегда имеет смысл.

Коммутативные диаграммы

Если JJ является категорией, то диаграмма J→CJ\to C является коммутативной , если она факторизуется через тонкую категорию. Эквивалентно, диаграмма формы JJ коммутирует тогда и только тогда, когда любые два морфизма в CC, сопоставляемые любой паре параллельных морфизмов в JJ (т. е. с одним и тем же источником и целью в JJ), равны.

Если JJ — колчан, что чаще встречается, когда мы говорим о «коммутативных» диаграммах, то диаграмма формы JJ коммутирует, если функтор F(J)→CF(J) \to C пропускается через тонкую категорию. Эквивалентно, это означает, что для любых двух параллельных путей произвольной конечной длины (включая нулевую) в JJ их образы в CC имеют равные композиции.

Примеры

• Форма пустой диаграммы является исходной категорией без объекта и без морфизма.

  Каждая категория CC допускает единственную диаграмму, формой которой является пустая (начальная) категория, называемая пустой диаграммой в CC.

• Форма терминальной диаграммы представляет собой терминальную категорию J={*}J = \{*\}, состоящую из одного объекта и одного морфизма (тождественного морфизма на этом объекте).

  Указание диаграммы в CC, форма которой имеет вид {*}\{*\}, равнозначно указанию одного объекта CC, изображения уникального объекта 11. (См. глобальный элемент)

• Диаграмма формы {a→b}\{a \to b\} в CC есть выбор любого одного морфизма Dab:Xa→XbD_{a b} : X_a \to X_b в CC.

  Заметьте, что, строго говоря, это считается коммутирующей диаграммой , но является вырожденным случаем коммутирующей диаграммы, поскольку задействован только один морфизм, который обязательно равен самому себе.

• Если JJ — колчан с одним объектом aa и одним эндо-ребром a→aa\to a, то диаграмма формы JJ в CC состоит из одного эндоморфизма в CC. Поскольку a→aa\to a и путь нулевой длины параллельны в JJ, такая диаграмма коммутирует только в том случае, если эндоморфизм является тождеством. Обратите внимание, в частности, что отдельный эндоморфизм можно рассматривать как диаграмму с более чем одной формой (этой и предыдущей), и что «коммутативность» этой диаграммы зависит от выбранной формы.

• Диаграмма формы набора, обозначенного

  {а→б↓↓б′→в} \левый\{ \множество{ а &\к& б \\ \вниз && \вниз \\ б’ &\к& с } \верно\}

  — это коммутирующих квадратов в CC: это выбор из четырех (не обязательно различных!) объектов Xa,Xb,Xb′,XcX_a, X_b, X_{b’}, X_c в C вместе с выбором ( не обязательно различные) четыре морфизма Dab:Xa→XbD_{a b} : X_a \to X_b, Dbc:Xb→XcD_{b c} : X_b \to X_c и Dab′:Xa→Xb′D_{a b’} : X_a \ в X_{b’}, Db′c:Xb′→XcD_{b’ c} : X_{b’} \to X_c в CC, такой, что составной морфизм Dbc∘DabD_{b c}\circ D_{a b} равен композит Db′c∘Dab′D_{b’ c}\circ D_{a b’}. 9{\ mathrlap {D_ {b c}}} \\ X_{b’} &\stackrel{D_{b’c}}{\to}& X_{c} }

  в CC и говорит, что диаграмма коммутирует , если имеет место указанное выше равенство составных морфизмов.

  Обратите внимание, что исходное частичное множество обязательно имело морфизм a→ca \to c и могло быть эквивалентно изображено как

  {а→б↓↘↓б’→в} \левый\{ \множество{ а &\к& б \\ \downarrow &\searrow& \downarrow \\ б’ &\к& с } \верно\} 9{\ mathrlap {D_ {b c}}} \\ X_{b’} &\stackrel{D_{b’c}}{\to}& X_{c} }

• Напротив, диаграмма, форма которой колчан

  {а→б↓↓б′→в} \левый\{ \множество{ а &\к& б \\ \вниз && \вниз \\ б’ &\к& с } \верно\}

  — это необязательно коммутирующий квадрат. Свободная категория этого колчана отличается от посета в предыдущем примере наличием двух морфизмы a→ca\to c, один задается композицией a→b→ca\to b\to c, а другой композицией a→b′→ca\to b’\to c. Но ч.у.м. в предыдущей категории является ч.у.м. отражением этого F(J)F(J), поэтому диаграмма этой формы коммутирует в смысле, определенном выше, тогда и только тогда, когда она является коммутирующим квадратом в обычном смысле.

• Пара объектов — это диаграмма, форма которой представляет собой дискретную категорию с двумя объектами.

• Парой параллельных морфизмов называется диаграмма, формой которой является категория J={a→→b}J = \{a \stackrel{\to}{\to}b\} с двумя объектами и двумя морфизмами из одного в другой. другой.

  Обратите внимание, что если бы мы потребовали, чтобы {a→→b}\{a \stackrel{\to}{\to}b\} было частично-упорядоченным множеством, это обязательно сделало бы эти два морфизма равными и, следовательно, свело бы этот пример к тому, где J={a→b}J = \{a \to b\}. Другими словами, диаграмма этой формы только 90 188 коммутирует 90 189, если два морфизма равны.

• Промежуток — это диаграмма, форма которой представляет собой категорию всего с тремя объектами и одиночными морфизмами от одного из объектов к двум другим;

  Дж={а↙↘bc} J = \слева\{ \множество{ && а \\ & \ ворона && \ ворона \\ До нашей эры } \верно\}

  двойственно, коспан — это диаграмма, форма которой противоположна форме пролета.

  Дж={бк↘↙а} J = \слева\{ \множество{ До нашей эры \\ & \сеарроу && \вороу \\ && а } \верно\}

• Трансфинитная композиционная диаграмма имеет форму множества, обозначенного

  .

  Дж={а0→а1→⋯↘↓↙⋯b}, Дж = \левый\{ \множество{ a_0 &\to& a_1 &\to& \cdots \\ & \searrow & \downarrow & \swarrow & \cdots \\ && б } \верно\} \,

  , где индексы могут варьироваться от натуральных чисел или даже от некоторого более общего порядкового числа.

  Это неконечная коммутирующая диаграмма.

• схема башни

• коммутирующая схема

• внутренняя схема

• бесплатная схема

Последняя редакция: 13 июня 2020 г., 10:57:52. См. историю этой страницы для получения списка всех вкладов в нее.

теория категорий. Являются ли диаграммы колчана такими же, как маленькие диаграммы

Задавать вопрос

спросил 3 года 11 месяцев назад

Изменено 1 год, 1 месяц назад

Просмотрено 135 раз

$\begingroup$

Я только начал изучать теорию категорий и наткнулся на два (с моей точки зрения, явно не эквивалентные) определения (маленькой) диаграммы в категории $\mathcal{C}$:

Определение 1 (Бранденбург, определение 2. 4.3):
Определим колчан $\Gamma$ как пару множеств $(V,E)$ с двумя функциями $s,t: E \rightarrow V$. Диаграмма $D$ в категории $\mathcal{C}$ состоит из следующих данных:

• для каждого $v \in V$ объекта $D(v) \in \mathcal{C}$.
• для каждого $e \in E$ морфизм $D(e): D(s(v)) \rightarrow D(t(v))$.

Определение 2 (почти везде, например, здесь):
Диаграмма $D$ в категории $\mathcal{C}$ — это просто функтор из небольшой категории $I$ в $\mathcal{ С}$.

---

Я знаю, что колчан несколько более общий, чем малая категория, в том смысле, что это «маленькие категории с забытыми тождественными морфизмами и композицией». С этой целью Определение 1 можно рассматривать как обобщение определения 2 .
С другой стороны, можно определить свободную диаграмму колчана, превратив сначала $\Gamma$ в свободную категорию, а затем затем . Определение 1 .

---

Вопрос

Является ли диаграмма колчана ( Определение 1 ) действительно эквивалентной диаграмме малой категории ( Определение 2 ) или это истинное обобщение?

Если да, что я получу от этого обобщения? Является ли это обобщением ради обобщения или действительно существуют ситуации, когда требуется Определение 2 ?

• теория категорий
• определение
• функторы
• ориентированные графы
• колчан

$\endgroup$

$\begingroup$

Как вы заметили, эти определения более или менее совпадают, учитывая базовый колчан и сгенерированную свободную категорию.
Однако, условия коммутативности не могут быть поставлены как часть «диаграммы» с определением 1, тогда как если, например. $fg=uv$ в малой категории $I$, оно должно выполняться и для их образов при произвольном функторе.
В этом смысле определение 2 является более сильным определением, и оно стало стандартом.

Тем не менее, у Бранденбурга могла быть причина отделить понятия диаграмм и функторов (из небольшой категории). Одной из таких причин может быть необходимость различать синтаксику и семантику языка категорий.

Рассмотрим это третье, смешанное определение:
Определение 3 Абстрактная диаграмма — это колчан $\Gamma$ с набором $P$ «условий коммутативности», т. е. пар путей с общими начальной и конечной точками.
Диаграмма формы $(\Gamma,P)$ в категории $\mathcal C$ является тогда морфизмом колчанов $D:\Gamma\to\mathcal C$ таким, что $D(p)=D(q )$ для каждого $(p, q)\in P$.

Так, например, «квадрат» и «коммутативный квадрат» — две разные абстрактные диаграммы над одним и тем же колчаном.

Хотя опр. 3 могло бы быть в определенном смысле более точным, на практике оно столь же эффективно, как и определение 2, с которым гораздо проще работать.

$\endgroup$

$\begingroup$

Это правда, что термин «диаграмма» в математике многозначен. Оба определения, которые вы упомянули, действительны (и есть много других). Все эти определения связаны, но я бы не сказал, что одно из них является строгим обобщением другого.

Определение 1 — это просто морфизм колчанов, т. е. отображение, сохраняющее структуру колчана. Колчаны с такими морфизмами составляют категорию, которую мы можем обозначить через $\mathbf{Quiv}$. Определение 1 актуально, когда мы говорим о колчанах.

Определение 2 — это просто функтор. Малость категории предметной области требуется, чтобы избежать теоретико-множественных проблем (а именно, мы хотим, чтобы категория всех таких диаграмм «была категорией»). Определение 2 актуально, когда мы говорим о категориях и категоричных конструкциях, особенно используя функторные категории (или «категории диаграмм») и универсальные конструкции.