Комбинационные логические схемы — Мегаобучалка
Рисунок 1. Функциональная схема цифрового комбинационного устройства
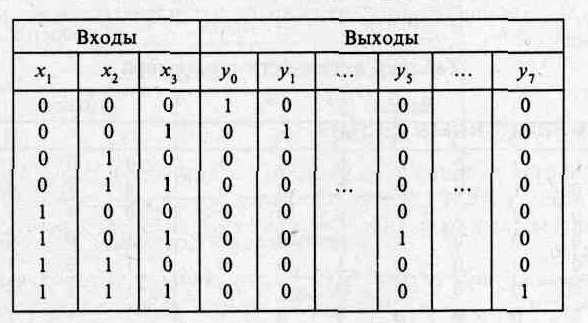
Комбинационная логическая схема – это преобразователь совокупности входных логических уровней (входного слова или входного кода) в выходное слово (выходной код) без запоминания. При изменении входных сигналов практически мгновенно изменяется код на выходе устройства. Небольшая временная задержка, вносимая комбинационной схемой, обусловливается в основном инерционностью транзисторов. Наиболее часто встречающимися комбинационными логическими схемами являются шифраторы, дешифраторы, мультиплексоры.
Дешифратор
Дешифратор- это логическая схема, которая каждую комбинацию сигналов на ее входе, в результате логической обработки, выдает в виде сигнала на одном из ее выходов (при нулевых сигналах на всех остальных выходах). Такая операция широко используется при автоматическом управлении. Дешифраторы также используются при переходе из одной системы исчисления в другую. В качестве отдельных микросхем сейчас дешифраторы практически не применяются. В настоящее время двоичные дешифраторы вместе с мультиплексорами используются в составе микросхем памяти (ОЗУ и ПЗУ) для обращения к конкретной ячейке памяти.
Шифратор
В дополнение к дешифраторам в вычислительной технике используется шифратор- цифровое устройство, выполняющее логические операции, обратные функциям дешифратора. Шифратор преобразует одну или несколько логических единиц, поступивших на входы в двоичный код на выходе. Шифраторы используются, например, в устройствах ввода цифровой информации для преобразования десятичных чисел в двоичный код.
Мультиплексор
Мультиплексор — устройство, имеющее несколько сигнальных входов, один или более управляющих входов и один выход. Мультиплексор позволяет передавать сигнал с одного из входов на выход; при этом выбор желаемого входа осуществляется подачей соответствующей комбинации управляющих сигналов.
Числовые коды
Числовым кодом называют форму представления числа, удобную для различных дискретных устройств.
Каждый числовой код состоит из отдельных элементов или сигналов.
Рассмотрим следующие типы кодов: Двоично-десятичный код 8421, Код с избытком 3, Код Грея.
Двоично-десятичный код 8421
Наиболее естественным и популярным считается упоминавшийся код прямого замещения, в котором каждая цифра десятичного числа заменяется соответствующим четырехразрядным двоичным числом. Его другое название код 8421 отражает значение весовых множителей, приписываемых соответствующим битам в кодирующей группе, в связи с чем называется также взвешенным кодом. Удобства этого кода проявляются при машинном переводе из десятичной системы в двоичную и обратно, а также при суммировании на обычных двоичных сумматорах благодаря его аддитивности (сумма кодов двух цифр представляет код суммы).
Двоично-десятичный код (англ. binary-coded decimal), BCD, 8421-BCD — форма записи рациональных чисел, когда каждый десятичный разряд числа записывается в виде его четырёхбитного двоичного кода. Этот код широко применяется в цифровых системах.
Пример: 926 ► 1001 0010 0110
Код с избытком 3
Код с избытком 3 – самодополняющийся код. Реализация: прибавляем число 3 к каждой цифре десятичного числа и затем заменяем полученные цифры соответствующими четырёхзначными двоичными числами. Для предотвращения потерь информации в канале были придуманы избыточные коды (коды с избыточностью). Преимущество избыточного кода в том, что при приеме его с искажением (количество искаженных символов зависит от степени избыточности и структуры кода) информация может быть восстановлена на приемнике.
Код Грея
Среди невзвешенных двоичных кодов специальные применения находят такие, у которых переход к соседнему числу сопровождается изменениями только в одном разряде (коды с обменной единицей). Так, в технике аналого-цифрового преобразования и пересчетных устройствах широко используется код Грея, называемый также циклическим или рефлексно-двоичным кодом.
Код Грея — система счисления, в которой два соседних значения различаются только в одном разряде. Важной особенностью кода Грея является то, что при переходе к следующему, ниже расположенному числу достаточно в предыдущем числе изменить только одну цифру. Он позволяет существенно сократить время преобразования, упростить кодирующую логику, а также повысить эффективность защиты от нежелательных сбоев при переходах выходного кода. Недостатком кода Грея является то, что в нем затруднено выполнение арифметических операций и цифроаналоговое преобразование. Поэтому при необходимости код Грея преобразуется в обычный двоичный код. Этот код применяется во входных и выходных устройствах цифровых систем.
Преобразователи кодов
Преобразователем кода называется комбинационное устройство, предназначенное для изменения вида кодирования информации. Для реализации комбинационных схем используются логические элементы, выпускаемые в виде интегральных схем. В этот класс входят интегральные схемы дешифраторов, шифраторов, мультиплексоров, демультиплексоров и сумматоров.
Дешифраторы
Дешифратором (декодером) называется логическая комбинационная схема, которая имеет n информационных входов и 2n выходов. Каждой комбинации логических уровней на входах будет соответствовать активный уровень на одном из 2n выходов. Для интегральных микросхем n обычно равно 2, 3 или 4 и соответственно число выходов 4, 8 или 16. Если требуется большее число выходов, дешифраторы наращиваются в систему (каскадируются). На рис. 3.1 изображен дешифратор с n = 2, реализованный на схемах 2И-НЕ.
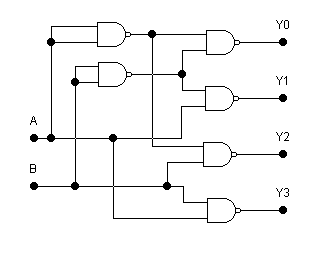
Рисунок 3.1 — Схема дешифратора на элементах 2И-НЕ
Таблица истинности дешифратора приведена в таблице 3.1
В соответствии с таблицей истинности для каждого выхода дешифратора, приведённого на рисунке 3.1 можно записать следующие логические выражения:
 ,
,
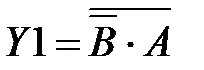 ,
,
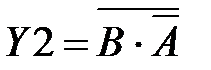 ,
,

Таблица 3.1 — Таблица истинности дешифратора
Входы | Выходы | ||||
| B | A | Y3 | Y2 | Y1 | Y0 |
| 0 | 0 | 1 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 |
Помимо информационных входов А, В дешифраторы могут иметь дополнительные входы управления G. Сигналы на этих входах либо разрешают функционирование дешифратора, либо переводят его в пассивное состояние, при котором, независимо от состояния информационных входов, на всех выходах устанавливается уровень логической единицы. Управляющий вход дешифратора может быть прямым или инверсным.
У дешифратора с несколькими входами управления функция разрешения, как правило, представляет собой логическое произведение всех разрешающих сигналов управления.
Обычно входы управления используются для каскадирования (увеличения разрядности) дешифраторов или при параллельной работе нескольких дешифраторов на общие выходные линии.
Дешифратор может быть использован в качестве демультиплексора — логического коммутатора, подключающего входной сигнал к одному из выходов. В этом случае функцию информационного входа выполняет один из входов разрешения, а состояние входов В и А задает номер выхода, на который передается сигнал со входа разрешения.
Шифраторы (кодеры)
Двоичные шифраторы преобразуют код «1 из N» в двоичный код. Если дешифратор реализует логическую функцию преобразования двоичного кода в единичный, то шифратор реализует обратную функцию, то есть преобразует единичный код в двоичный. Наиболее часто используются шифраторы с приоритетом, на выходах которого формируется двоичное число, соответствующее наивысшему из входов, на который подана логическая единица. Такие шифраторы чаще всего используются в аналого-цифровых преобразователях. Одно из основных применений шифраторов – это ввод данных с клавиатуры, при котором нажатие клавиши с десятичной цифрой должно приводить к передаче в устройство двоичного кода данной цифры. На рисунке 3.2 приведена схема двухразрядного приоритетного шифратора. Таблица истинности приоритетного шифратора приведена в таблице 3.2
Таблица 3.2 — Таблица истинности приоритетного кодера
Входы | Выходы | |||
| X3 | X2 | X1 | Y1 | Y0 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | × | 1 | 0 |
| 1 | × | × | 1 | 1 |
Примечание: Знаком × обозначается произвольное значение (либо 0, либо 1)
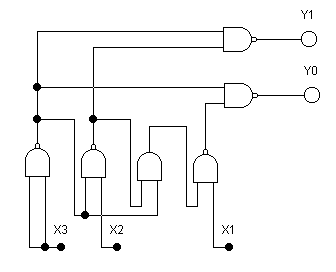
Рисунок 3.2 — Двухразрядный приоритетный шифратор на элементах 2И-НЕ
Мультиплексоры
Мультиплексором называется комбинационная логическая схема, представляющая собой управляемый переключатель. Назначение мультиплексоров (от английского multiplex — многократный) — коммутировать в заданном порядке сигналы, поступающие с нескольких входных шин на одну выходную. В качестве примера рассмотрим мультиплексор, у которого 16 входов и 1 выход. Это означает, что если к этим входам присоединены 16 источников цифровых сигналов — генераторов последовательных цифровых слов, то байты от любого из них можно передавать на единственный выход. Для выбора любого из 16 каналов необходимо иметь 4 управляющих входа (24 = 16), на которые подается двоичный адрес канала. Кроме информационных и управляющих входов, схемы мультиплексоров содержат вход разрешения, при подаче на который активного уровня мультиплексор переходит в активное состояние. При подаче на вход разрешения пассивного уровня мультиплексор переходит в пассивное состояние, в котором его выходной сигнал остаётся постоянным независимо от состояний информационных и управляющих входов.
Мультиплексоры применяются в микропроцессорах (МП) для выдачи на одни и те же выводы МП адреса и данных, что позволяет существенно сократить общее количество выводов микросхемы. В микропроцессорных системах управления мультиплексоры применяются для передачи информации по одной линии от нескольких датчиков.
Схема двухканального мультиплексора на элементах 2И, 2ИЛИ и инверторе приведена на рисунке 3.3.
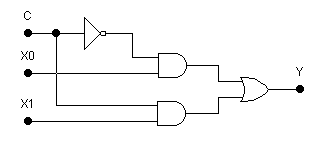
Рисунок 3.3 — Схема двухканального мультиплексора
Схема двухканального мультиплексора реализует функцию:
 .
.
Демультиплексоры
Иногда возникает задача распределения одного входного сигнала по нескольким различным адресам. С помощью демультиплексоров сигналы с одного информационного входа распределяются в требуемой последовательности по нескольким выходам. Выбор нужной выходной шины, как и в мультиплексоре, обеспечивается установкой соответствующего кода на адресных управляющих входах. При n адресных входах демультиплексор может иметь до 2n выходов. Промышленностью демультиплексоры не выпускаются, потому что они могут быть реализованы на основе дешифраторов. На рисунке 3.4 приведена схема демультиплексора, реализованная на двух логических элементах 2И и инверторе.

Рисунок 3.4 — схема демультиплексора
Демультиплексор реализует следующие логические функции:
 ,
,
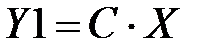 .
.
Сумматоры — это цифровые функциональные устройства, предназначенные для выполнения операции сложения чисел, представленных в различных кодах.
По характеру действия сумматоры подразделяются на комбинационные, не имеющие элементов памяти, и накапливающие – запоминающие результаты вычислений при снятии входных сигналов.
В дальнейшем будут рассматриваться только комбинационные сумматоры, на основе которых выполняется большинство суммирующих ИС.
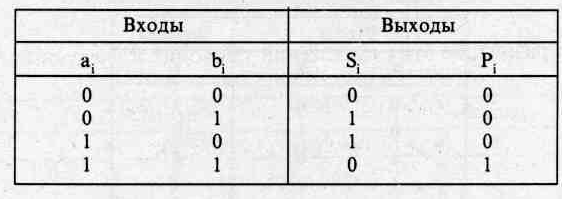
Сумматор по модулю два — Это устройство с двумя входами (а и b), на выходе у которого сигнал «1» появляется только в том случае, когда на входах действуют противоположные сигналы, т. е. «0» и «1». Сумматор не обладает памятью.
Eго таблица истинности и логическое уравнение имеют вид:

Название “по модулю два” этот сумматор получил потому, что y соответствует значению младшего разряда при суммировании одноразрядных двоичных чисел A и B. Построим в базисе И–НЕ схему сумматора по модулю два (рис. 21)
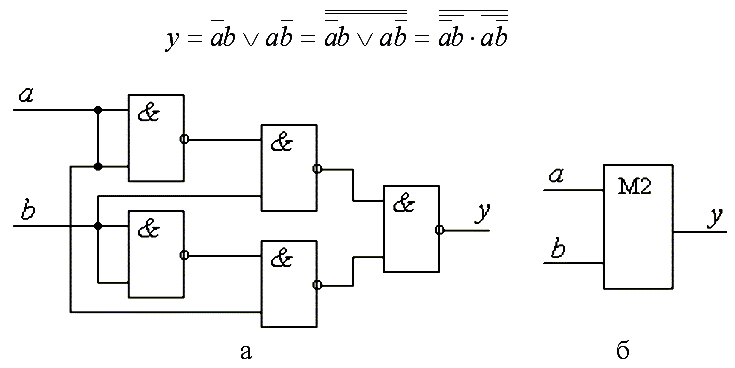
Рис. 21. Реализация сумматора по модулю два:
а – принципиальная схема; б – функциональная схема
Полусумматор — Обеспечивает операцию сложения двух одноразрядных двоичных чисел a и b. Так как при a = 1 и b = 1 получается перенос единицы в следующий разряд, полусумматор должен иметь два выхода: с одного снимается сигнал суммы по модулю два, а с другого — сигнал переноса.
Таблица истинности полусумматора и его логические уравнения имеют вид:

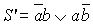
P’ = ab
Реализация полусумматора в базисе И–НЕ представлена на рис. 22

а б
Рис. 22. Схема полусумматора:
а – реализация в базисе И–НЕ; б – условное обозначение
Условное обозначение полусумматора на схемах – HS (halfsum – полусумма), а полного сумматора – SM.
Полный сумматор — Это устройство для сложения трех одноразрядных двоичных чисел a, b, c, где c — сигнал переноса из предыдущего младшего разряда. Имеет два выхода S (сумма) и Р (перенос).
Полный сумматор можно построить из двух полусумматоров (рис. 23), отсюда и название – полусумматор, используя следующие логические уравнения

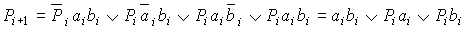

Рис. 23. Полный сумматор
На основе полного сумматора можно построить суммирующие устройства параллельного или последовательного действия для сложения многоразрядных двоичных чисел.
Дешифратор
Дешифратором (декодером) называется логическая комбинационная схема, которая имеет n информационных входов и 2n выходов. Каждой комбинации логических уровней на входах будет соответствовать активный уровень на одном из 2n выходов. Для интегральных микросхем n обычно равно 2, 3 или 4 и соответственно число выходов 4, 8 или 16. Если требуется большее число выходов, дешифраторы наращиваются в систему (каскадируются). На рис. 3.1 изображен дешифратор с n = 2, реализованный на схемах 2И-НЕ.

Рисунок 3.1 — Схема дешифратора на элементах 2И-НЕ
Таблица истинности дешифратора приведена в таблице 3.1
В соответствии с таблицей истинности для каждого выхода дешифратора, приведённого на рисунке 3.1 можно записать следующие логические выражения:
 ,
,
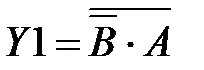 ,
,
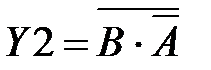 ,
,
 .
.
Таблица 3.1 — Таблица истинности дешифратора
Входы | Выходы | ||||
| B | A | Y3 | Y2 | Y1 | Y0 |
| 0 | 0 | 1 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 |
Помимо информационных входов А, В дешифраторы могут иметь дополнительные входы управления G. Сигналы на этих входах либо разрешают функционирование дешифратора, либо переводят его в пассивное состояние, при котором, независимо от состояния информационных входов, на всех выходах устанавливается уровень логической единицы. Управляющий вход дешифратора может быть прямым или инверсным.
У дешифратора с несколькими входами управления функция разрешения, как правило, представляет собой логическое произведение всех разрешающих сигналов управления.
Обычно входы управления используются для каскадирования (увеличения разрядности) дешифраторов или при параллельной работе нескольких дешифраторов на общие выходные линии.
Дешифратор может быть использован в качестве демультиплексора — логического коммутатора, подключающего входной сигнал к одному из выходов. В этом случае функцию информационного входа выполняет один из входов разрешения, а состояние входов В и А задает номер выхода, на который передается сигнал со входа разрешения.
Шифратор
Шифратор преобразует единичный код в двоичный. Наиболее часто используются шифраторы с приоритетом, на выходах которого формируется двоичное число, соответствующее наивысшему из входов, на который подана логическая единица. Такие шифраторы чаще всего используются в аналого-цифровых преобразователях. Одно из основных применений шифраторов – это ввод данных с клавиатуры, при котором нажатие клавиши с десятичной цифрой должно приводить к передаче в устройство двоичного кода данной цифры. На рисунке 3.2 приведена схема двухразрядного приоритетного шифратора. Таблица истинности приоритетного шифратора приведена в таблице 3.2
Таблица 3.2 — Таблица истинности приоритетного кодера
Входы | Выходы | |||
| X3 | X2 | X1 | Y1 | Y0 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | × | 1 | 0 |
| 1 | × | × | 1 | 1 |
Примечание: Знаком × обозначается произвольное значение (либо 0, либо 1)

Рисунок 3.2 — Двухразрядный приоритетный шифратор на элементах 2И
Комбинационные логические схемы
Л а б о р а т о р н а я р а б о т а № 7
Цель работы: ознакомление с принципом действия и схемотехникой дешифраторов, мультиплексоров и сумматоров; изучение ра-боты этих комбинационных логических схем; реализация на их ос-нове простейших устройств автоматики.
Общие сведения
Комбинационными называются логические устройства, выходные сигналы которых однозначно определяются комбинацией входных сигналов в тот же момент времени. Они используются в информационно-измерительных системах и ЭВМ, системах автоматического управления, устройствах промышленной автоматики и т.п.
Построение комбинационного логического устройства осуществляется следующим образом. По требуемому алгоритму работы со-ставляются таблица истинности и соответствующее ей логическое уравнение. Это уравнение минимизируется по правилам алгебры логики с целью упрощения, и затем строится логическая схема на базе логических элементов (ЛЭ) И-НЕ, ИЛИ-НЕ. Наряду с построением устройств промышленность изготавливает наиболее часто встречающиеся комбинационные логические схемы (КЛС) в виде интегральных микросхем. Примерами КЛС являются шифраторы, дешифраторы, кодопреобразователи, устройства сравнения (компараторы), мультиплексоры, демультиплексоры, сумматоры, арифметико-логические устройства и др.
Дешифратор (декодер) представляет собой комбинационное устройство, в котором при каждой комбинации входных переменных формируется сигнал высокого или низкого уровня только на одном выходе. Дешифратор называется полным, если число выходов n равно числу возможных наборов сигналов на m входах, т.е. n = 2m. Неполный дешифратор имеет меньшее число выходов. Дешифратор может иметь стробирующий (управляющий) вход. Сигнал на этом входе разрешает или запрещает выполнение операции дешифрования.
Исследуемая ИМС К155ИД3 (рис. 7.1) предс-тавляет собой дешифратор-демультиплексор с 4 на 16. Основу этой микросхемы со-ставляют 16 ЛЭ 5И-НЕ и 8 инверторов. Работа дешифратора определяется табли-цей истинности (табл. 7.1). Дешифратор реализует ло-гические функции:
 ;
;
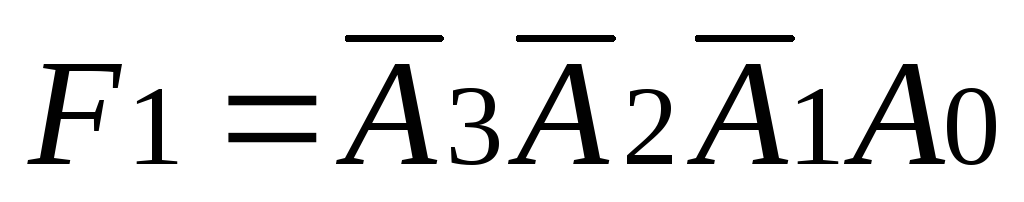 ;
;
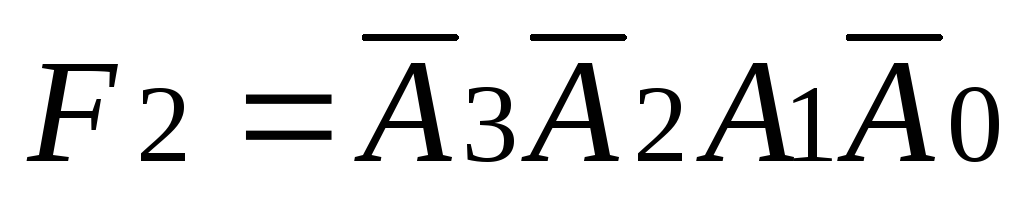 ;
;
…;
.
Т а б л и ц а 7.1
Входы | Выходы | |||||||||||
| | А3 | А2 | А1 | А0 | | | | … | | | |
0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | … | 1 | 1 | 1 |
0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | … | 1 | 1 | 1 |
0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | … | 1 | 1 | 1 |
… | ||||||||||||
0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | … | 0 | 1 | 1 |
0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | … | 1 | 0 | 1 |
0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | … | 1 | 1 | 0 |
0 | 1 | x | x | x | x | 1 | 1 | 1 | … | 1 | 1 | 1 |
1 | 0 | x | x | x | x | 1 | 1 | 1 | … | 1 | 1 | 1 |
1 | 1 | x | x | x | x | 1 | 1 | 1 | … | 1 | 1 | 1 |
Примечание: здесь и далее x – любое значение сигнала.
Он
позволяет преобразовать четырехразрядный
двоичный код, поступивший на входы А0…А3,
в напряжение низкого уровня, появляющееся
на одном из шестнадцати выходов  .
Если входные переменные представить
как двоичную запись чисел, то логический
нуль формируется на том выходе, номер
которого соответствует десятичной
записи того же числа (см. табл. 7.1). Кроме
четырех входов А0…А3
устройство имеет еще два входа
.
Если входные переменные представить
как двоичную запись чисел, то логический
нуль формируется на том выходе, номер
которого соответствует десятичной
записи того же числа (см. табл. 7.1). Кроме
четырех входов А0…А3
устройство имеет еще два входа  и
и 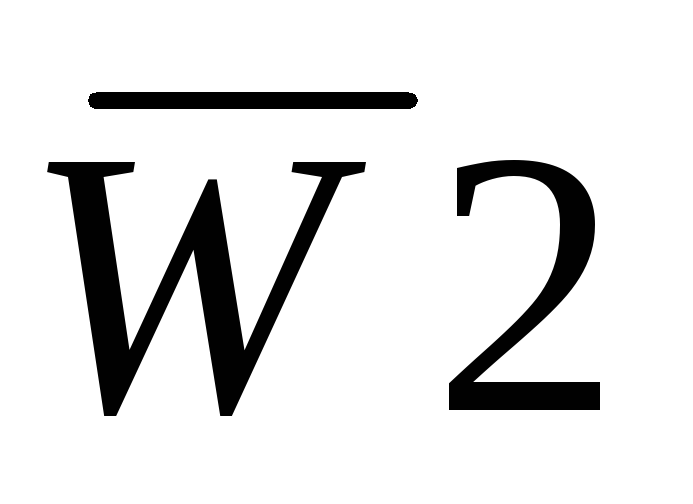 разрешения дешифрации.
Они
играют роль стробирующих входов, если
на них подан низкий уровень напряжения.
Если хотя бы на одном из входов
разрешения дешифрации.
Они
играют роль стробирующих входов, если
на них подан низкий уровень напряжения.
Если хотя бы на одном из входов  и
и 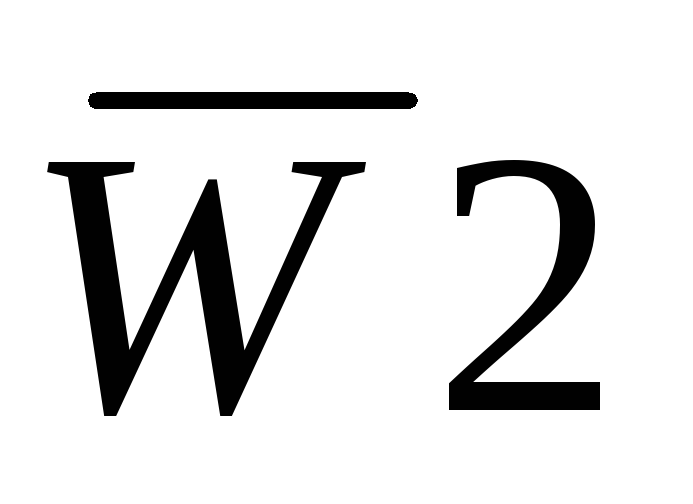 установить высокий уровень, то на всех
выходах
установить высокий уровень, то на всех
выходах 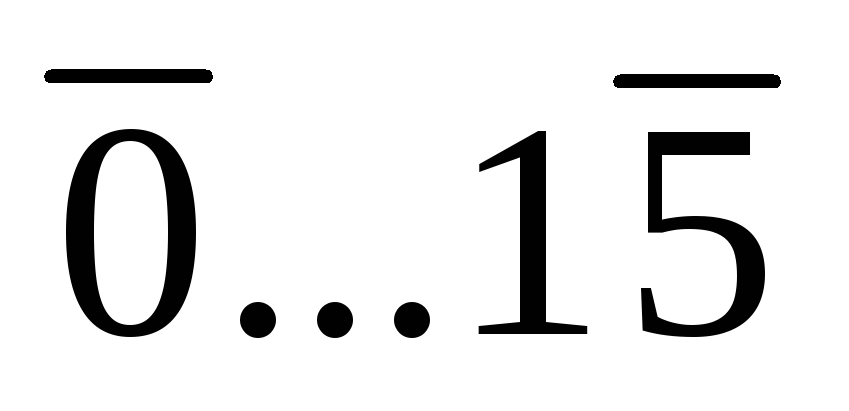 будет высокий уровень напряжения. Такой
режим используется при наращивании
числа разрядов дешифрируемого кода.
будет высокий уровень напряжения. Такой
режим используется при наращивании
числа разрядов дешифрируемого кода.
Входы  и
и  можно использовать как логические,
тогда микросхема ИД3 служит демультиплексором
данных. Входы А0…А3
в этом случае используются как адресные,
чтобы направить поток данных, принимаемых
входами
можно использовать как логические,
тогда микросхема ИД3 служит демультиплексором
данных. Входы А0…А3
в этом случае используются как адресные,
чтобы направить поток данных, принимаемых
входами 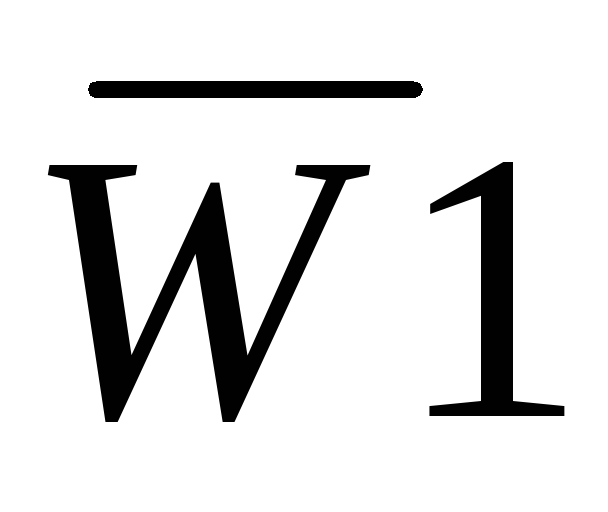 или
или 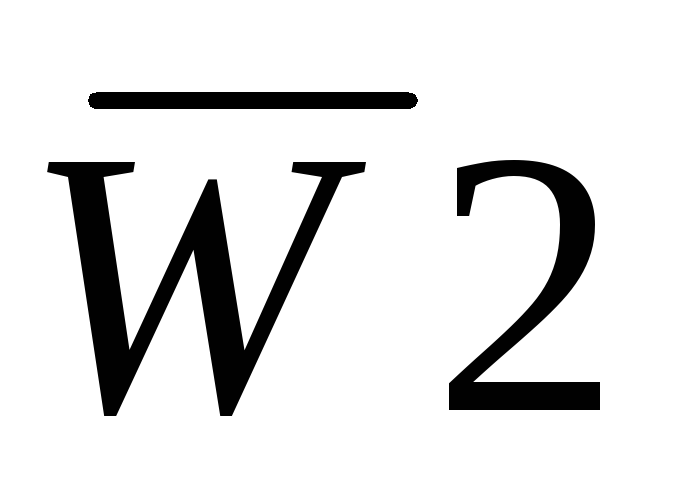 ,
на один из выходов
,
на один из выходов .
Подобные задачи возникают при дистанционном
управлении, в преобразователях
последовательного кода в параллельный
и т.п.
.
Подобные задачи возникают при дистанционном
управлении, в преобразователях
последовательного кода в параллельный
и т.п.
Принцип выбора «1 из n» используется для управления индикаторами в устройствах отображения информации, в различных схемах распределителей импульсов по нескольким каналам (в данном случае – до 16). Как видно из рис. 7.1, на выходе 1 высокий логический уровень появится только при кодовом наборе 0000, на выходе 2 – при наборах 1000 или 1010.
Е сли
в системах управления применяются
генератор тактовых импульсов и
четырехразрядный счетчик, то дешифратор
можно использовать в качестве делителя
частоты (см.
рис. 7.1) или формирователя им-пульсов
(рис. 7.2), благодаря цикличности
«перемещения» логи-ческих
уровней по выходам. Фор-мирование
конечной последовательности импульсов
может осу-ществляться различными
способами (см. рис.
7.2). Например, на
выходе 1 длительность сформированного
импульса равна половине цикла, т.к.
переключение
сли
в системах управления применяются
генератор тактовых импульсов и
четырехразрядный счетчик, то дешифратор
можно использовать в качестве делителя
частоты (см.
рис. 7.1) или формирователя им-пульсов
(рис. 7.2), благодаря цикличности
«перемещения» логи-ческих
уровней по выходам. Фор-мирование
конечной последовательности импульсов
может осу-ществляться различными
способами (см. рис.
7.2). Например, на
выходе 1 длительность сформированного
импульса равна половине цикла, т.к.
переключение 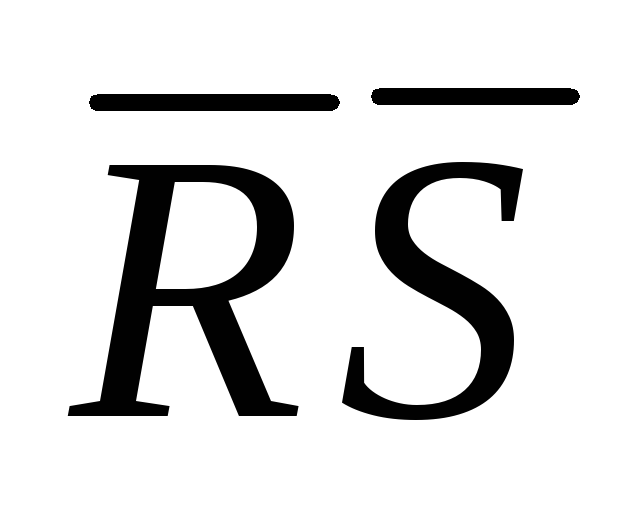 -триггера
происходит при прохождении нулевого
сигнала на выходах 0 и 8 дешифратора. При
выборе других точек подключения входа
2 скважность (q = Tцикла/tимп)
можно изменять в широких пределах (от
1,1 до 16). В другом примере на рис. 7.2 показан
простой способ получения пакета из двух
импульсов на выходе одного ЛЭ. Аналогичная
схемотехника используется и для
формирования последовательности
импульсов различной длительности.
-триггера
происходит при прохождении нулевого
сигнала на выходах 0 и 8 дешифратора. При
выборе других точек подключения входа
2 скважность (q = Tцикла/tимп)
можно изменять в широких пределах (от
1,1 до 16). В другом примере на рис. 7.2 показан
простой способ получения пакета из двух
импульсов на выходе одного ЛЭ. Аналогичная
схемотехника используется и для
формирования последовательности
импульсов различной длительности.
Мультиплексор (управляемый кодом переключатель) предназначен для коммутации одного из m входов на выход. Входы мультиплексора (m – информационных и k – управляющих) находятся в следующем соответствии: m = 2k. Выход обычно один, он может быть прямым или инверсным.
М икросхема
К155КП5 представляет собой восьмиканальный
мультиплексор без стробирования (рис.
7.3). Основу его схемы составляет один ЛЭ
4И-8ИЛИ-НЕ и 6 простых инверторов. Он имеет
8 информационных входов D0…D7,
3 адресных входа V0…V2
и выход
икросхема
К155КП5 представляет собой восьмиканальный
мультиплексор без стробирования (рис.
7.3). Основу его схемы составляет один ЛЭ
4И-8ИЛИ-НЕ и 6 простых инверторов. Он имеет
8 информационных входов D0…D7,
3 адресных входа V0…V2
и выход  .
.
Логическое уравнение имеет вид

Состояние мультиплексора определяется таблицей истинности (табл. 7.2). Как видно из таблицы, мультиплексор выполняет функции простого инвертора только по тому каналу, номер которого соответствует двоичному коду адресных входов. Поэтому мультиплексор нашел широкое применение в качестве преобразователя параллельного кода в последовательный, для передачи информации по линиям связи и для последовательного опроса (контроля) при большом числе каналов или устройств.
Т а б л и ц а 7.2
Адресные входы | Информационные входы | Выход | |||||||||
V2 | V1 | V0 | D0 | D1 | D2 | D3 | D4 | D5 | D6 | D7 | |
0 | 0 | 0 | 0 | x | x | x | x | x | x | x | 1 |
0 | 0 | 0 | 1 | x | x | x | x | x | x | x | 0 |
0 | 0 | 1 | x | 0 | x | x | x | x | x | x | 1 |
0 | 0 | 1 | x | 1 | x | x | x | x | x | x | 0 |
… | … | … | … | … | … | … | … | … | … | … | … |
1 | 1 | 1 | x | x | x | x | x | x | x | 0 | 1 |
1 | 1 | 1 | x | x | x | x | x | x | x | 1 | 0 |
Сумматор предназначен для сложения двух чисел, заданных в двоичном коде. Число входов и выходов сумматора определяется разрядностью слагаемых. Одноразрядный двоичный сумматор характеризуется таблицей истинности (табл. 7.3). Такой сумматор называется полным, т.к. обрабатывает сигнал переноса с предыдущего разряда Pi и выдает сигнал переноса на последующий разряд Pi+1. Схемотехника сумматоров строится на ЛЭ «Исключающее ИЛИ» (функция «неравнозначность») для суммирования и ЛЭ И-НЕ для переноса:
Pi+1 =
AiBi + (Ai B)Pi; Si = (Ai
B)Pi; Si = (Ai Bi)
Bi) Pi.
Pi.
Т а б л и ц а 7.3
Входы | Выходы | |||
Ai | Bi | Pi | Si | Pi+1 |
0 | 0 | 0 | 0 | 0 |
0 | 0 | 1 | 1 | 0 |
0 | 1 | 0 | 1 | 0 |
0 | 1 | 1 | 0 | 1 |
1 | 0 | 0 | 1 | 0 |
1 | 0 | 1 | 0 | 1 |
1 | 1 | 0 | 0 | 1 |
1 | 1 | 1 | 1 | 1 |
М икросхема
К155ИМ3 (рис. 7.4) представляет собой
четырехразрядный сумматор с параллельным
поразрядным сложением и последовательным
формированием сигнала переноса. Он
имеет два четырехразрядных числа по
входам данных А0…А3
и В0…В3,
а по входу Р0
– сигнал переноса с предыдущего разряда.
Сумма разрядов входных чисел появляется
на выходах S0…S3. На выходе Р4
выделяется сигнал переноса на последующий
разряд.
икросхема
К155ИМ3 (рис. 7.4) представляет собой
четырехразрядный сумматор с параллельным
поразрядным сложением и последовательным
формированием сигнала переноса. Он
имеет два четырехразрядных числа по
входам данных А0…А3
и В0…В3,
а по входу Р0
– сигнал переноса с предыдущего разряда.
Сумма разрядов входных чисел появляется
на выходах S0…S3. На выходе Р4
выделяется сигнал переноса на последующий
разряд.
Суммирование происходит по уравнению:
P0 + 20(A0 + B0) + 21(A1 + B1) + 22(A2 + B2) + 23(A3 + B3) =
= 20S0 + 21S1 + 22S2 + 23S3 + 24P4.
Сумматор
можно использовать для вычитания чисел.
Для этого вычитаемое представляют в
дополнительном коде, который образуется
из обратного (инверсного) кода добавлением
к нему единицы. Так, четырехразрядное
число В,
записанное в прямом коде Впр =
В3В2В1В0,
может быть представлено в обратном коде  и в дополнительном коде Вдоп = Вобр + 1.
и в дополнительном коде Вдоп = Вобр + 1.
Комбинационные схемы и цифровые автоматы логические элементы
КОМБИНАЦИОННЫЕ СХЕМЫ И ЦИФРОВЫЕ АВТОМАТЫ: ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
Различают комбинационные схемы и цифровые автоматы. В комбинационных схемах состояние на выходе в данный момент времени однозначно определяется состояниями на входах в тот же момент времени. Комбинационными схемами, например, являются логические элементы И, ИЛИ, НЕ и их комбинации. В цифровом автомате состояние на выходе определяется не только состояниями на входах в данный момент времени, но и предыдущим состоянием системы. К цифровым автоматам относятся триггеры.
Логическими элементами называются элементы, выполняющие логические операции И, ИЛИ, НЕ и комбинации этих операций. Указанные логические операции можно реализовать с помощью контактно-релейных схем и с помощью электронных схем. В настоящее время в подавляющем большинстве применяется электронные логические элементы, причем электронные логические элементы входят в состав микросхем.

Имея в распоряжении логические элементы И, ИЛИ, НЕ, можно сконструировать цифровое электронное устройство любой сложности. Электронная часть любого компьютера состоит из логических элементов.
Система простых логических функций, на основе которой можно получить любую логическую функцию, называется функционально полной.
Отсюда следует, что для построения логического устройства любой сложности достаточно иметь однотипные логические элементы, например, И-НЕ или ИЛИ-НЕ.
Логические элементы могут работать в режимах положительной и отрицательной логики. Для электронных логических элементов в режиме положительной логики логической единице соответствует высокий уровень напряжения, а логическому нулю – низкий уровень напряжения. В режиме отрицательной логики логической единице соответствует низкий уровень напряжения, а логическому нулю – высокий.
Для контактно-релейных схем в режиме положительной логики логической единице соответствует замкнутый контакт ключа или реле, а логическому нулю – разомкнутый. Светящийся индикатор (лампочка, светодиод) соответствует логической единице, а несветящийся – логическому нулю.
Логические элементы, реализующие для режима положительной логики операцию И, для режима отрицательной логики выполняют операцию ИЛИ, и наоборот. Так, например, микросхема, реализующая для положительной логики функции элемента 2И-НЕ, будет выполнять для отрицательной логики функции элемента 2ИЛИ-НЕ.
Как правило, паспортное обозначение логического элемента соответствует функции, реализуемой «положительной логикой». Логические элементы И, ИЛИ, НЕ имеют один выход, число входов логических элементов И, ИЛИ может быть любым начиная с двух. Логические элементы И и ИЛИ, выпускаемые в составе микросхем, обычно имеют 2, 3, 4, 8 входов. В названии элемента первая цифра указывает число входов.
Прежде всего, рассмотрим реализацию логических элементов с помощью контактно-релейных схем. Рассмотрим логический элемент 2И. Он выполняет операцию логического умножения. На рисунке 1.1,а приведена контактно-релейная схема логического элемента 2И для режима положительной логики.
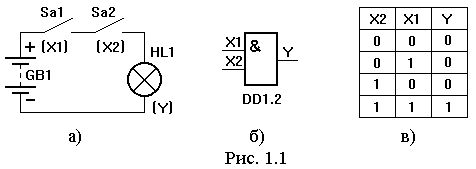
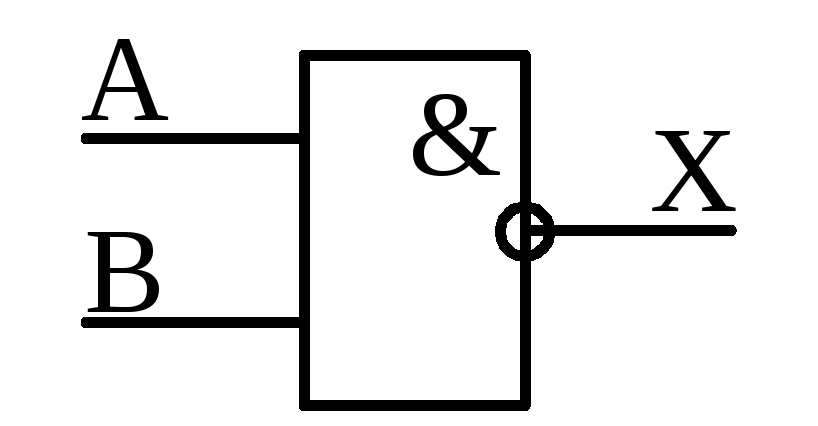
Обозначение логического элемента 2И на принципиальных схемах показано на рисунке 1.1,б. Знак & (амперсант) в левом верхнем углу прямоугольника указывает, что это логический элемент И.
Первые две буквы обозначения DD1.2 указывают на то, что это цифровая микросхема, цифра слева от точки указывает номер микросхемы на принципиальной схеме, а цифра справа от точки – номер логического элемента в составе данной микросхемы.
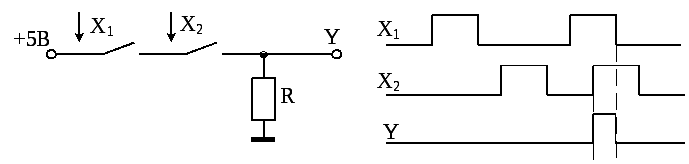
Функционирование логического элемента обычно задают таблицей истинности. Контактно-релейная схема логического элемента 2И (режим положительной логики) позволяет легко составить таблицу истинности этого элемента. Так как микросхема имеет для подачи входных сигналов два входа, то возможны 22=4 различных комбинации входных сигналов. Необходимо проанализировать состояние лампочки при различных положениях тумблеров Sa1, Sa2, т.е. рассмотреть 4 различных комбинации состояний тумблеров (рис. 1.1,в).
Введение понятия активного логического уровня существенно облегчает анализ функционирования сложных цифровых устройств. Активным логическим уровнем на входе элемента (логический нуль, логическая единица) называется такой уровень, который однозначно задает состояние на выходе элемента независимо от логических уровней на остальных входах элемента. Активный логический уровень на одном из входов элемента определяет уровень на его выходе. Уровни, обратные активным, называются пассивными логическими уровнями.
Активным логическим уровнем для элементов И является логический нуль. Пусть, например, имеем логический элемент 8И. Необходимо проанализировать 28=256 различных состояний для составления таблицы истинности этого элемента. Воспользуемся понятием активного логического уровня. Если хотя бы на одном из входов этого элемента будет активный логический уровень, то состояние на выходе элемента определено однозначно и нет необходимости анализировать состояния на остальных входах элемента.
Таким образом, таблицу истинности логического элемента 8И можно свести к двум строчкам: на выходе этого элемента будет логическая единица, если на всех входах будут сигналы логической единицы и на выходе будет логический нуль, если хотя бы на одном из входов элемента будет сигнал логического нуля.
Логический элемент 2ИЛИ выполняет логическую операцию логического сложения у=х 1+х 2. Контактно-релейная схема элемента приведена на рисунке 1.2,а, а его условное обозначение – на рисунке 1.2,б. Знание контактно-релейной схемы элемента позволяет составить таблицу истинности (рис. 1.2,в). Лампочка будет гореть, если замкнуты контакты хотя бы одного тумблера, т.е. активным логическим уровнем для элементов ИЛИ является уровень логической единицы.
Логический элемент НЕ выполняет операцию отрицания, и для этого элемента проще составить сразу таблицу истинности, а не вычерчивать сначала контактно-релейную схему, а затем по ней составлять таблицу истинности. Для логических элементов И и ИЛИ проще сначала вычертить контактно-релейную схему, а уже потом составлять таблицу истинности.
Напомним алгоритм работы электромагнитного реле с нормально замкнутыми контактами: при отсутствии электрического тока через обмотку реле контакты реле замкнуты, а при протекании достаточного тока через обмотку реле контакты реле разомкнуты.

Контактно релейная схема элемента НЕ приведена на рисунке 1.3а, а его условное обозначение – на рисунке 1.3б.

Проанализируем работу контактно-релейной схемы логического элемента НЕ (рис. 1.3а). Если контакты ключа Sa1 разомкнуты, то через обмотку К электромагнитного реле ток протекать не будет. Контакты К 1.1 (цифра слева от точки указывает номер реле на принципиальной схеме, а цифра справа – номер контактной группы данного реле) будут замкнуты (электромагнитное реле с нормально замкнутыми контактами). Электрическая лампочка HL1 в этом случае будет гореть, что для режима положительной логики будет означать логическую единицу. При замкнутых контактах ключа Sa1 (на входе элемента логическая единица) через обмотку реле протекает ток, достаточный для размыкания контактов К 1.1, поэтому лампочка перестает гореть (логический нуль). В результате анализа мы получили, что сигнал на выходе элемента противоположен сигналу на входе, т.е. если на входе элемента сигнал логической единицы, то на выходе элемента сигнал логического нуля и наоборот (рис. 1.3,в).
При анализе работы логических элементов следует помнить о режиме их работы (режим положительной или отрицательной логики). Логические элементы, реализующие для режима положительной логики операцию И, для режима отрицательной логики выполняют операцию ИЛИ и наоборот. Решим следующую задачу.
Задача. Какую логическую операцию выполняет контактно-релейная схема, приведенная на рисунке 1.4.

Правильным ответом в этой задаче будет следующий. Указанная контактно-релейная схема выполняет операцию 3И для режима положительной логики и 3ИЛИ для режима отрицательной логики (решение обосновать самостоятельно).
В практической работе широко используются комбинации логических элементов и особенно элементы И-НЕ и ИЛИ-НЕ.
Рассмотрим подробнее контактно-релейную схему элемента 2ИЛИ-НЕ, приведенную на рисунке 1.5,а.
Условное обозначение элемента на принципиальных схемах показано на рисунке 1.5,б.
Заполним таблицу истинности, приведенную на рисунке 1.5в. Если оба ключа разомкнуты (Х 1=0, Х 2=0), то лампочка HL1 горит, что соответствует логической единице на выходе элемента (Y=1). Замкнем контакты ключа Sa1 (Х 1=1), оставляя ключ Sa2 разомкнутым (Х 2=0). ЛампочкаHL1 в этом случае не горит (Y=0). Если замкнут хотя бы один ключ, то лампочка не горит. Следовательно, активным логическим уровнем на входе элемента ИЛИ-НЕ является уровень логической единицы.

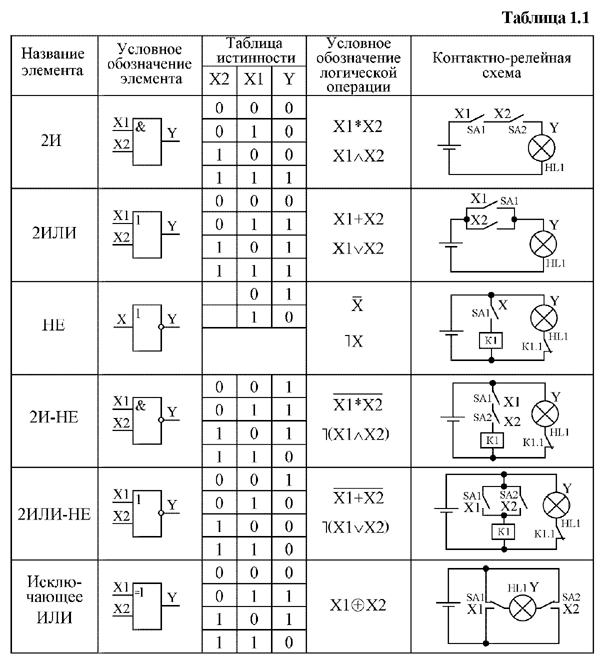
Для двух аргументов логического элемента возможны 16 логических функций. В данном пособии рассматриваются логические функции: логическое И, логическое ИЛИ, логическое НЕ, логическое И-НЕ, логическое ИЛИ-НЕ, сумма по модулю 2.
В таблице 1.1 приведены условные обозначения элементов 2И, 2ИЛИ, НЕ, 2И-НЕ, 2ИЛИ-НЕ, исключающее ИЛИ (сумма по модулю 2), условные обозначения выполняемых этими элементами логических операций, таблицы их истинности и контактно-релейные схемы. При анализе контактно-релейной схемы элемента исключающее ИЛИ необходимо учитывать, что положения переключателей SA1 и SA2 в таблице 1.1 соответствуют логическим единицам (верхнее положение подвижного контакта переключателя соответствует логической единице), т.е. Х 1=1 и Х 2=1. Лампочка HL1 горит лишь в том случае, когда подвижный контакт одного из переключателей находится в верхнем положении, а подвижный контакт второго переключателя в нижнем положении. Из анализа работы данной контактно-релейной схемы получаем таблицу истинности элемента исключающей ИЛИ.
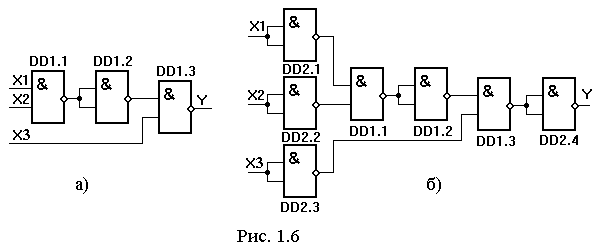
Рассмотрим решение следующей задачи: имея в распоряжении логические элементы 2И-НЕ, сконструировать устройство, реализующее операцию 3ИЛИ-НЕ для режима положительной логики. Эту задачу решим в два этапа. Сначала сконструируем устройство, выполняющее операцию 3И-НЕ для режима положительной логики (рис. 1.6,а), а потом на входах и выходе элемента 3И-НЕ установим логические элементы НЕ (рис. 1.6,б).
По мере развития вычислительной техники электронные логические элементы совершенствовались. Рассмотрим принципиальную схему логического элемента 2И (рис. 1.7,а), построенного на диодах и резисторах. Для простоты рассмотрения будем считать, что напряжение логического «0» на входе элемента равно 0 В, а напряжение логической «1» – 5 В. Внутреннее сопротивление вольтметра значительно больше сопротивления резистора R1.

Вспомним особенности вольтамперной характеристики полупроводникового кремниевого диода небольшой мощности. При обратном напряжении ток, протекающий через диод, составляет десятые доли микроампера.
Напряжение на диоде при протекании через него в прямом направлении тока в десятки миллиампер равно приблизительно 0,7-0,8 В. Определим примерно параметры логических уровней на выходах данного элемента, если на входе действуют логические уровни с указанными ранее параметрами. Если на оба входа поданы напряжения логических «1», то токи через диоды VD1 иVD2 не протекают, и напряжение на выходе элемента при условии, что сопротивление нагрузки значительно больше сопротивления резистора R1, будет примерно равно напряжению питания. Если хотя бы один из входов элемента соединить с минусовым проводом источника питания, то на выходе элемента в случае кремниевых диодов будет напряжение 0,7-0,8 В (зависит от сопротивления резистора R1 и напряжения источника питания).
Примечание: для рассмотренного логического элемента логическая «1» на входе будет, если вход никуда не подключен или подключен к плюсовому выводу источника питания.
На рисунке 1.7,б приведена схема простого и удобного в работе стенда для исследования диодно-резистивного логического элемента 2И. Светодиоды VD3 – VD5 являются индикаторами логических сигналов на входах и выходе логического элемента. Вольтметр V позволяет определить напряжения логической единицы и логического нуля. Для диодно-резистивного логического элемента 2И напряжение логического нуля на выходе примерно 0,7-0,8 В, а напряжение логической единицы чуть меньше напряжения на зажимах источника питания (определяется соотношением сопротивлений резистора R1 и нагрузки).
На рисунках 1.8,а и 1.8,б приведены схемы для исследования диодно-резистивного логического элемента 2ИЛИ. Для этого элемента напряжение логического нуля на выходе равно 0 В, а напряжение логической единицы равно напряжению питания минус 0,7-0,8 В.

Следующим этапом совершенствования элементной базы цифровой техники было создание логических элементов диодно-транзисторной логики.
Рассмотрим принципиальную схему логического элемента 2И-НЕ диодно-транзисторной логики (рис. 1.9,а).

Для понимания принципа работы логического элемента 2И-НЕ диодно-транзисторной логики необходимо знать, какой вид имеет зависимость тока коллектора транзистора от напряжения база-эмиттер при постоянном напряжении эмиттер- коллектор. Эта характеристика имеет примерно такой же вид, как и прямая ветвь вольтамперной характеристики полупроводникового диода. Для кремниевых транзисторов при напряжении база-эмиттер (в прямом направлении) менее 0,5 В ток в цепи коллектор-эмиттер практически равен нулю при любых допустимых напряжениях коллектор-эмиттер (транзистор закрыт, сопротивление между коллектором и эмиттером закрытого транзистора VТ 1 может достигать единиц МОм). При незначительном увеличении напряжения база-эмиттер (в прямом направлении) более 0,5 В ток коллектора значительно увеличивается, говорят, что транзистор открывается.
Диоды VD1, VD2 и резистор R1 (рис. 1.9,а) образуют логический элемент 2И. Роль инвертора выполняет транзистор VT1. Если транзистор закрыт, то ток в цепи: плюс источника питания, резистор R2, коллектор-эмиттер транзистора VT1, минус источника питания не протекает и напряжение между эмиттером и коллектором транзистора будет равно напряжению на зажимах источника питания. Диоды VД 3, VД 4 необходимы для надежного закрытия транзистора VТ 1, когда хотя бы на одном из входов элемента было напряжение логического нуля.
Если на обоих входах Х 1, Х 2 присутствуют сигналы логических единиц, транзистор VT1 открывается током базы, протекающим по цепи: плюс источника питания, резистор R1, диоды VD3, VD4, переход база-эмиттер транзистора VT1, минус источника. На выходе элемента будет напряжение 0,1-0,2 В, что соответствует логическому нулю.
На рисунке 1.9,б приведен вариант логического элемента 2И-НЕ на транзисторах. Инвертор на транзисторе VT1 не обеспечивает большую нагрузочную способность, поэтому в качестве инверторов применяют более сложные схемы. Сложный инвертор в микросхемах транзисторно-транзисторной логики будет рассмотрен чуть позже. Сейчас остановимся на принципе работы инверторов, схемы которых приведены на рисунке 1.10.
Рассмотрим делитель напряжения (делитель напряжения источника питания) образованного резистором R3 и цепью коллектор-эмиттер транзистора VТ 1 (рис. 1.10,а).
Если на входе элемента логическая единица (подвижный контакт переключателя SA1 в верхнем положении), то транзистор VT1 открыт и в его коллекторной цепи протекает ток. Напряжение между коллектором и эмиттером транзистора составляет десятые доли вольта (не более 0,4 В).

При логическом нуле на входе элемента транзистор закрыт и напряжение на выходе элемента равно напряжению питания, что соответствует логической единице.
На рисунках 1.10,б и 1.10,в приведены схемы инверторов с использованием полевых транзисторов. Напомним устройство и принцип действия полевых транзисторов. Существуют следующие виды полевых транзисторов: полевые транзисторы с управляющим p-n переходом, полевые транзисторы с изолированным затвором со встроенным каналом, полевые транзисторы с изолированным затвором с индуцированным каналом.
Полевые транзисторы называются также униполярными, одноканальными. Полевой транзистор в отличие от биполярного имеет большое входное сопротивление по цепи управления. Ток в выходной цепи полевого транзистора управляется напряжением, в то время как в биполярном транзисторе ток в выходной цепи транзистора управляется током во входной цепи транзистора. Таким образом, мощность управления в полевом транзисторе значительно меньше, чем в биполярном.
Полевой транзистор имеет 3 вывода: исток, сток, затвор. Исток – это вывод полевого транзистора, от которого основные носители заряда идут в канал. Сток – это вывод полевого транзистора, к которому идут основные носители заряда из канала. Затвор – это вывод полевого транзистора, на который подается управляющее напряжение относительно истока или относительно стока.
Наибольшее распространение имеют схемы включения транзистора с общим истоком, когда управляющее напряжение подается на затвор относительно истока.
В вычислительной технике в качестве электронных ключей широко используются полевые транзисторы с изолированным затвором с индуцированным каналом. Рассмотрим устройство и принцип действия полевого транзистора с изолированным затвором с индуцированным каналом n-типа (рис. 1.11). В полупроводнике p-типа сделаны два кармана с проводимостью n-типа. Знак n+ указывает на большую концентрацию электронов, что делается для уменьшения сопротивлений выводов стока и истока. Металлический затвор изолирован от кристалла полупроводника.
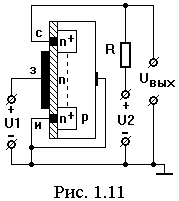
При напряжении затвор-исток, равном нулю, в цепи сток-исток ток не протекает при любых допустимых напряжениях сток-исток, так как образуются два p-n перехода, причем верхний подключен в обратном направлении. логический элемент истинность цифровая
Подадим на затвор относительно истока положительный потенциал. В полупроводниках p-типа имеются неосновные носители заряда (электроны). Рассмотрим движение электронов и дырок в слое полупроводника p-типа, прилежащем к затвору. Для упрощения рассмотрения соединим область p-типа с выводом истока. Под действием электрического поля, обусловленного наличием напряжения затвор – исток, дырки будут двигаться вправо, а электроны влево, т.е. в полупроводнике в приграничной к затвору области концентрация дырок уменьшается, а концентрация электронов увеличивается. При определенном напряжении затвор-исток в указанной области концентрация электронов станет больше концентрации дырок, наступит инверсия проводимости, т.е. в приграничной к затвору области появится слой полупроводника n-типа. В этом случае в цепи сток-исток протекает ток, т.к. между выводами стока и истока появился канал n-типа. Этот канал называется индуцированным (наведенным).
Для понимания принципа работы логических элементов на полевых транзисторах необходимо знать, что собой представляет стоко-затворная характеристика полевого транзистора. Стоко-затворная характеристика полевого транзистора в схеме включения с общим истоком (исток является общим для входной и выходной цепи) – это зависимость тока стока от напряжения затвор-исток при постоянном напряжении сток-исток. Эта характеристика полевого транзистора с изолированным затвором с индуцированным каналом n-типа приведена на рисунке 1.12. Особенности стоко-затворных характеристик полевых транзисторов с изолированным затвором с индуцированным каналом позволяют использовать эти транзисторы в качестве электронных ключей. Сравним основные характеристики электронного ключа на полевом транзисторе с характеристиками механического ключа. Сопротивление разомкнутого механического ключа можно считать бесконечно большим (пока не наступит электрический пробой),сопротивление ключа на полевом транзисторе порядка 10 МОм. Когда контакты механического ключа замкнуты сопротивление между контактами составляет сотые доли ома, для такого же состояния полевого транзистора сопротивление между стоком и истоком сотни Ом.
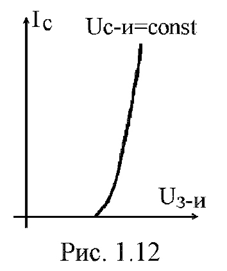
Если на входе инвертора, схема которого приведена на рисунке 1.10,б, напряжение логической единицы, то сопротивление между выводами сток и исток транзистора мало. Сопротивление резистораR1 выбирают значительно больше сопротивления между стоком и истоком открытого полевого транзистора и, следовательно, напряжение на выходе элемента будет близко к нулю вольт. При логическом нуле на входе логического элемента НЕ полевой транзистор будет закрыт, и на выходе элемента будет напряжение, примерно равное напряжению источника питания. Это обусловлено тем, что сопротивление резистора R1 выбирают во много раз меньше сопротивления между стоком и истоком закрытого транзистора.
Рассмотрим принцип работы инвертора (логического элемента НЕ) КМОП (комплементарный, металл, окисел, полупроводник) структуры (рис. 1.10,в). Комплементарный означает дополняющий друг друга по типу проводимости. Микросхемы КМОП имеют транзисторы как с каналом p-типа, так и с каналом n-типа. Учтем, что сопротивление между выводами сток-исток открытого транзистора – 200-300 Ом, а сопротивление между выводами сток-исток закрытого транзистора более 10 МОм.
Выберем напряжение питания 9 В. Пусть на вход Х подано напряжение логического «0», тогда транзистор VТ 2 будет закрыт, а транзистор VТ 1 открыт, так как потенциал затвора транзистора VТ 1 относительно истока этого же транзистора равен минус 9В. На выходе элемента логическая единица.
Подадим на вход Х напряжение, соответствующее логической единице. Для рассмотренного случая это + 9 В относительно общего провода. В этом случае транзистор VТ 2 будет открыт, а транзистор VТ 1 – закрыт и на выходе элемента будет напряжение логического нуля.
Рассмотрим основные параметры, которыми характеризуются цифровые микросхемы.
Помехоустойчивость Uп, макс – наибольшее значение напряжения помехи на входе микросхемы, при котором еще не происходит изменения уровней ее выходного напряжения.
Напряжение логической единицы U1 – значение высокого уровня напряжения для «положительной» логики и значение низкого уровня напряжения для «отрицательной» логики.
Напряжение логического нуля U0 – значение низкого уровня напряжения для «положительной» логики и значение высокого уровня напряжения для «отрицательной» логики.
Пороговое напряжение логической единицы U1пор – наименьшее значение высокого уровня напряжения для «положительной» логики или наибольшее значение низкого уровня напряжения для «отрицательной» логики на входе микросхемы, при котором она переходит из одного устойчивого состояния в другое.
Пороговое напряжение логического нуля U0пор – наибольшее значение низкого уровня напряжения для «положительной» логики или наименьшее значение высокого уровня напряжения для «отрицательной» логики на входе микросхемы, при котором она переходит из одного устойчивого состояния в другое.
Входной ток логической единицы I1вх – измеряется при заданном значении напряжения логической единицы.
Входной ток логического нуля I0вх – измеряется при заданном значении напряжения логического нуля.
Выходной ток логической единицы I1вых – измеряется при заданном значении напряжения логической единицы.
Выходной ток логического нуля I0вых – измеряется при заданном значении напряжения логического нуля.
Ток потребления в состоянии логической единицы I1пот – значение тока, потребляемого микросхемой от источников питания при логических единицах на выходах всех элементов.
Ток потребления в состоянии логического нуля I0пот – значение тока, потребляемого микросхемой от источников питания при логических нулях на выходах всех элементов.
Средний ток потребления Iпот. ср. – значение тока, равное полусумме токов, потребляемых цифровой микросхемой от источников питания в двух устойчивых различных состояниях.
Потребляемая мощность в состоянии логической единицы Р 1пот – значение мощности, потребляемой микросхемой от источника питания при логических единицах на выходах всех элементов.
Потребляемая мощность в состоянии логического нуля Р 0пот – значение мощности, потребляемой микросхемой от источника питания при логических нулях на выходах всех элементов.
Средняя потребляемая мощность Рпот. ср. – полусумма мощностей, потребляемых микросхемой от источников питания в двух устойчивых различных состояниях.
Время перехода интегральной микросхемы из состояния логической единицы в состояние логического нуля t1,0 – интервал времени, в течение которого напряжение на выходе микросхемы переходит от напряжения логической единицы к напряжению логического нуля, измеренный на уровнях напряжения 0,1 и 0,9 от амплитуды импульса.
Время перехода интегральной микросхемы из состояния логического нуля в состояние логической единицы t0,1 – интервал времени, в течение которого напряжение на выходе микросхемы переходит от напряжения логического нуля к напряжению логической единицы, измеренный на уровнях напряжения 0,1 и 0,9 от амплитуды импульса.
Комбинационные логические схемы
Цель работы: ознакомление с принципом действия и схемотехникой дешифраторов, мультиплексоров и сумматоров; изучение работы этих комбинационных логических схем; реализация на их основе простейших устройств автоматики.
Общие сведения
Комбинационными называются логические устройства, выходные сигналы которых однозначно определяются комбинацией входных сигналов в тот же момент времени. Они используются в информационно-измерительных системах и ЭВМ, в системах автоматического управления, в устройствах промышленной автоматики и т.п.
Построение комбинационного логического устройства осуществляется следующим образом. По требуемому алгоритму работы составляются таблица истинности и соответствующее ей логическое уравнение. Это уравнение минимизируется по правилам алгебры логики с целью упрощения и затем строится логическая схема на базе логических элементов (ЛЭ) И-НЕ, ИЛИ-НЕ. Наряду с построением устройств промышленность изготавливает наиболее часто встречающиеся комбинационные логические схемы (КЛС) в виде интегральных микросхем. Примерами КЛС являются шифраторы, дешифраторы, кодопреобразователи, устройства сравнения (компараторы), мультиплексоры, демультиплексоры, сумматоры, арифметико-логические устройства и др.
Дешифратор(декодер) представляет собой комбинационное устройство, в котором при каждой комбинации входных переменных формируется сигнал высокого или низкого уровня только на одном выходе. Дешифратор называется полным, если число выходов n равно числу возможных наборов сигналов на m входах, т.е. n=2m. Неполный дешифратор имеет меньшее число выходов. Дешифратор может иметь стробирующий (управляющий) вход. Сигнал на этом входе разрешает или запрещает выполнение операции дешифрования.
Исследуемая ИМС К155ИД3 (рис.7.1) представляет собой дешифратор-демультиплексор с 4 на 16. Основу этой микросхемы составляют 16 ЛЭ 5И-НЕ и 8 инверторов. Работа дешифратора определяется таблицей истинности (табл. 7.1). Дешифратор реализует логические функции:
 ;
; 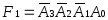 ;
;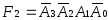 ;
…;
;
…;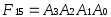 .
.
Он
позволяет преобразовать четырехразрядный
двоичный код, поступивший на входы А0…А3,
в напряжение низкого уровня, появляющееся
на одном из шестнадцати выходов  .
Если входные переменные представить
как двоичную запись чисел, то логический
нуль формируется на том выходе, номер
которого соответствует десятичной
записи того же числа (см.табл.7.1). Кроме
четырех входовА0…А3
устройство имеет еще два входа
.
Если входные переменные представить
как двоичную запись чисел, то логический
нуль формируется на том выходе, номер
которого соответствует десятичной
записи того же числа (см.табл.7.1). Кроме
четырех входовА0…А3
устройство имеет еще два входа 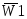 и
и 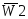 разрешения дешифрации.
Они играют
роль стробирующих входов, если на них
подан низкий уровень напряжения. Если
хотя бы на одном из входов
разрешения дешифрации.
Они играют
роль стробирующих входов, если на них
подан низкий уровень напряжения. Если
хотя бы на одном из входов 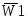 и
и установить высокий уровень, то на всех
выходах
установить высокий уровень, то на всех
выходах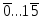 будет
высокий уровень напряжения. Такой режим
используется при наращивании числа
разрядов дешифрируемого кода.
будет
высокий уровень напряжения. Такой режим
используется при наращивании числа
разрядов дешифрируемого кода.
Таблица7.1
Входы | Выходы | |||||||||||
| | А3 | А2 | А1 | А0 | | | | … | | | |
0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | … | 1 | 1 | 1 |
0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | … | 1 | 1 | 1 |
0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | … | 1 | 1 | 1 |
… | ||||||||||||
0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | … | 0 | 1 | 1 |
0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | … | 1 | 0 | 1 |
0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | … | 1 | 1 | 0 |
0 | 1 | x | x | x | x | 1 | 1 | 1 | … | 1 | 1 | 1 |
1 | 0 | x | x | x | x | 1 | 1 | 1 | … | 1 | 1 | 1 |
1 | 1 | x | x | x | x | 1 | 1 | 1 | … | 1 | 1 | 1 |
Примечание: здесь и далее x — любое значение сигнала.
В
 ходы
ходы и
и можно использовать как логические,
тогда микросхема ИД3 служит демультиплексором
данных. ВходыА0…А3
в этом случае используются как адресные,
чтобы направить поток данных, принимаемых
входами
можно использовать как логические,
тогда микросхема ИД3 служит демультиплексором
данных. ВходыА0…А3
в этом случае используются как адресные,
чтобы направить поток данных, принимаемых
входами 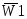 или
или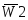 ,
на один из выходов
,
на один из выходов .
Подобные задачи возникают при дистанционном
управлении, в преобразователях
последовательного кода в параллельный
и т.п.
.
Подобные задачи возникают при дистанционном
управлении, в преобразователях
последовательного кода в параллельный
и т.п.
Принцип выбора “1 из n” используется для управления индикаторами в устройствах отображения информации, в различных схемах распределителей импульсов по нескольким каналам (в данном случае — до 16). Как видно из рис.7.1, на выходе 1 высокий логический уровень появится только при кодовом наборе 0000, на выходе 2 — при наборах 1000 или 1010.
Если
в системах управления применяется
генератор тактовых импульсов и
четырехразрядный счетчик, то дешифратор
можно использовать в качестве делителя
частоты (см. рис.7.1) или формирователя
импульсов (рис.7.2), благодаря цикличности
«перемещения» логических уровней
по выходам. Формирование конечной
последовательности импульсов может
осуществляться различными способами
(см. рис.7.2). Например, на выходе 1
длительность сформированного импульса
равна половине цикла, т.к. переключение 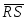 -триггера
происходит при прохождении нулевого
сигнала на выходах 0 и 8 дешифратора. При
выборе других точек подключения входа
2 скважность (q=Tцикла/tимп)
можно изменять в широких пределах (от
1,1 до 16). В другом примере на рис.7.2 показан
простой способ получения пакета из двух
импульсов на выходе одного ЛЭ. Аналогичная
схемотехника используется и для
формирования последовательности
импульсов различной длительности.
-триггера
происходит при прохождении нулевого
сигнала на выходах 0 и 8 дешифратора. При
выборе других точек подключения входа
2 скважность (q=Tцикла/tимп)
можно изменять в широких пределах (от
1,1 до 16). В другом примере на рис.7.2 показан
простой способ получения пакета из двух
импульсов на выходе одного ЛЭ. Аналогичная
схемотехника используется и для
формирования последовательности
импульсов различной длительности.
М ультиплексор(управляемый
кодом переключатель)
предназначен для коммутации одного из m входов на выход. Входы мультиплексора
(m — информационных и k — управляющих) находятся в следующем
соответствии: m=2k.
Выход обычно один, он может быть прямым
или инверсным.
ультиплексор(управляемый
кодом переключатель)
предназначен для коммутации одного из m входов на выход. Входы мультиплексора
(m — информационных и k — управляющих) находятся в следующем
соответствии: m=2k.
Выход обычно один, он может быть прямым
или инверсным.
Микросхема
К155КП5 представляет собой восьмиканальный
мультиплексор без стробирования
(рис.7.3). Основу его схемы составляет
один ЛЭ 4И-8ИЛИ-НЕ и 6 простых инверторов.
Он имеет 8 информационных входов D0…
D7, 3 адресных
входа V0…V2
и выход 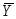 .
.
Логическое уравнение имеет вид:

Состояние мультиплексора определяется таблицей истинности (табл. 7.2). Как видно из таблицы, мультиплексор выполняет функции простого инвертора только по тому каналу, номер которого соответствует двоичному коду адресных входов. Поэтому мультиплексор нашел широкое применение в качестве преобразователя параллельного кода в последовательный, для передачи информации по линиям связи и для последовательного опроса (контроля) при большом числе каналов или устройств.
Таблица7.2
Адресные входы | Информационные входы | Выход | |||||||||
V2 | V1 | V0 | D0 | D1 | D2 | D3 | D4 | D5 | D6 | D7 | |
0 | 0 | 0 | 0 | x | x | x | x | x | x | x | 1 |
0 | 0 | 0 | 1 | x | x | x | x | x | x | x | 0 |
0 | 0 | 1 | x | 0 | x | x | x | x | x | x | 1 |
0 | 0 | 1 | x | 1 | x | x | x | x | x | x | 0 |
… | … | … | … | … | … | … | … | … | … | … | … |
1 | 1 | 1 | x | x | x | x | x | x | x | 0 | 1 |
1 | 1 | 1 | x | x | x | x | x | x | x | 1 | 0 |
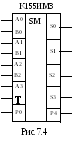 Таблица7.3
Таблица7.3
Входы
Выходы
Ai
Bi
Pi
Si
Pi+1
0
0
0
0
0
0
0
1
1
0
0
1
0
1
0
0
1
1
0
1
1
0
0
1
0
1
0
1
0
1
1
1
0
0
1
1
1
1
1
1
Сумматор предназначен для сложения двух чисел, заданных в двоичном коде. Число входов и выходов сумматора определяется разрядностью слагаемых. Одноразрядный двоичный сумматор характеризуется таблицей истинности (табл.7.3). Такой сумматор называется полным, т.к. обрабатывает сигнал переноса с предыдущего разряда Pi и выдает сигнал переноса на последующий разряд Pi+1. Схемотехника сумматоров строится на ЛЭ «Исключающее ИЛИ» (функция «неравнозначность») для суммирования и ЛЭ И-НЕ для переноса:
Pi+1=AiBi+(Ai B)Pi;
Si=(Ai
B)Pi;
Si=(Ai Bi)
Bi) Pi.
Pi.
Микросхема К155ИМ3 (рис.7.4) представляет собой четырехразрядный сумматор с параллельным поразрядным сложением и последовательным формированием сигнала переноса. Он имеет два четырехразрядных числа по входам данныхА0…А3 иВ0…В3, а по входуР0 — сигнал переноса с предыдущего разряда. Сумма разрядов входных чисел появляется на выходахS0…S3.На выходеР4 выделяется сигнал переноса на последующий разряд.
Суммирование происходит по уравнению:
P0+20(A0+B0)+21(A1+B1)+22(A2+B2)+23(A3+B3)=20S0+21S1+22S2+23S3+24P4.
Сумматор можно использовать для вычитания чисел. Для этого вычитаемое представляют в дополнительном коде, который образуется из обратного (инверсного) кода добавлением к нему единицы. Так, четырехразрядное число В, записанное в прямом коде Впр=В3В2В1В0, может быть представлено в обратном коде и в дополнительном коде Вдоп =Вобр+1.
3.2. Комбинационные схемы
Обработка входной информации X в выходную У (см. рис. 2.1) в любых схемах ЭВМ обеспечивается преобразователями или цифровыми автоматами двух видов: комбинационными схемами и схемами с памятью.
Комбинационные схемы (КС) — это схемы, у которых выходные сигналы Y = (у1, у2,…, ут) в любой момент дискретного времени однозначно определяются совокупностью входных сигналов X=(x1, х2,…, хn), поступающих в тот же момент времени t. Реализуемый в КС способ обработки информации называется комбинационным потому, что результат обработки зависит только от комбинации входных сигналов и формируется сразу же при поступлении входных сигналов. Поэтому одним из достоинств комбинационных схем является их высокое быстродействие. Преобразование информации однозначно описывается логическими функциями вида Y = f(X).
Логические функции и соответствующие им комбинационные схемы подразделяют на регулярные и нерегулярные структуры. Регулярные структуры предполагают построение схемы таким образом, что каждый из ее выходов строится по аналогии с предыдущими. В нерегулярных структурах такая аналогия отсутствует. Примером построения нерегулярной структуры может служить разработка схемы в примере 2.16.
В практике проектирования ЭВМ накоплен огромный опыт по синтезу различных схем. Многие регулярные структуры положены в основу построения отдельных ИС малой и средней степени интеграции или отдельных функциональных частей БИС и СБИС. Из регулярных комбинационных схем наиболее распространены дешифраторы,
шифраторы, схемы сравнения, комбинационные сумматоры, коммутаторы и др. •
Рассмотрим принципы построения подобных регулярных структур.
Дешифраторы (ДШ) — это комбинационные схемы с п входами и т = 2n выходами. Единичный сигнал, формирующийся на одном из т выходов, однозначно соответствует комбинации входных сигналов. Например, разработка структуры ДШ для n=3 согласно методике, изложенной в п. 2.4, позволяет получить таблицу истинности (табл. 3.1) и логические зависимости.
Таблица 3.1 Таблица истинности дешифратора
Дешифраторы широко используются в ЭВМ для выбора информации по определенному адресу, для расшифровки кода операции и др. Логические зависимости дешифратора:

На рис. 3.2 представлены структурная схема ДШ, построенная в базисе (И, НЕ), и условное ее обозначение на принципиальных электрических схемах ЭВМ. Кружочки у линий, выходящих из логических элементов, указывают на инверсию функций, реализуемых элементами.
Шифратор (ШР) решает задачу, обратную схемам ДШ, т. е. по номеру входного сигнала формирует однозначную комбинацию выходных сигналов. Пример по-строения ШР иллюстрируется таблицей истинности (табл. 3.2) и схемами на рис. 3.3.

Рис. 3.2. Структурная схема дешифратора (а) и обозначение дешифратора на принципиальных электрических схемах (б)
Таблица 3.2 Таблица истинности шифратора

Логические зависимости шифратора:


Рис. 3.3. Структурная схема шифратора (а) и обозначение шифратора на принципиальных электрических схемах (б)
Обратим внимание, что табл. 3.1 и 3.2 во многом похожи, входы и выходы в них поменялись местами. Состояния входов табл. 3.2 содержат только по одному единичному элементу. Другие произвольные комбинации входов недопустимы.
Схемы сравнения, или компаратор, обычно строятся как поразрядные. Они широко используются и автономно, и в составе более сложных схем, например при построении сумматоров.
Таблица истинности (табл. 3.3) отражает логику работы i-го разряда схемы сравнения при сравнении двух векторов — А и В. На рис. 3.4 показана структурная схема компаратора.
Таблица 3.3 Таблица истинности компаратора

Логическая зависимость компаратора:

На схеме 3.4, помимо выхода Y2, фиксирующего равенство значений разрядов, показаны выходы Yl и Y3 соответствующие сигналам «больше» и «меньше».

Рис. 3.4. Структурная схема компаратора (а) и обозначение компаратора на принципиальных электрических схемах (б)
Комбинационный сумматор. Принципы построения и работы сумматора вытекают из правил сложения двоичных цифр (см. п. 2.3). Схема сумматора также является регулярной и широко используется в ЭВМ. При сложении одноразрядных двоичных цифр можно выявить закономерности в построении и многоразрядных сумматоров.
Сначала рассмотрим сумматор, обеспечивающий сложение двух двоичных цифр а1 и b1 считая, что переносы из предыдущего разряда не поступают. Этой логике отвечает сложение младших разрядов двоичных чисел. Процесс сложения описывается таблицей истинности (табл. 3.4) и логическими зависимостями (3.2), где Si — функция одноразрядной суммы и Рi — функция формирования переноса. Перенос формируется в том случае, когда а1=1 и bl=1.
Таблица 3.4 Таблица истинности комбинационного полусумматора
Логические зависимости:

Зависимости (3.2) соответствуют логике работы самого младшего разряда любого сумматора. Структурная схема одноразрядного сумматора (полусумматора) представлена на рис. 3.5.

Рис. 3.5. Структурная схема полусумматора (а) и обозначение полусумматора(б)
Логические зависимости полусумматора Si и компаратора (3.1) очень похожи, так как они инверсны по отношению друг к другу.
Уравнения, положенные в основу одноразрядного сумматора, используются и при построении многоразрядных сумматоров. Логика работы каждого разряда сумматора описывается табл. 2.2, которую можно считать его таблицей истинности.
Таблица истинности сумматора, учитывающего сигналы переноса, отличается от таблицы полусумматора (см. табл. 3.4) дополнительным входом р — переносом из предыдущих разрядов.
Исходные логические зависимости, формируемые по табл. 2.2, имеют следующие совершенные ДНФ:

Преобразование этих выражений приводит к следующим зависимостям:
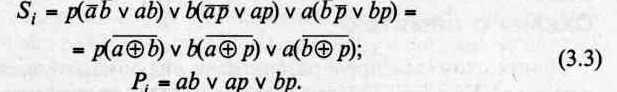
В приведенных выражениях индексы у переменных в правых частях уравнений опущены.

Рис. 3.6. Структурная схема одного разряда комбинационного сумматора: а — структурная схема одного разряда; 6 — условное изображение
Из анализа логических зависимостей видно, что структурная схема i-го разряда сумматора требует включения в свой состав трех схем сравнения для формирования разрядной суммы и шести схем совпадения (рис. 3.6).
Структурная схема многоразрядного комбинационного сумматора на электрических схемах изображена на рис. 3.7.

Рис. 3.7. Структурная схема многоразрядного комбинационного сумматора
Комбинационные схемы
Если рассматривать микросхему при сильном увеличении, можно увидеть её стройную архитектуру. Чтобы понять, как она работает, вспомним, что компьютер работает на электричестве, то есть любая информация представлена в компьютере в виде электрических импульсов.
Преобразование информации в ЭВМ производится электронными устройствами (логическими схемами) двух классов: комбинационными схемами и цифровыми автоматами.
Комбинационной схемой (КС) называется логическая схема, комбинация сигналов на выходе которой в любой момент времени однозначно определяется комбинацией сигналов на её входе.
Реализуемый в этих схемах способ обработки информации называется комбинационным, так как результат обработки информации зависит от комбинации входных сигналов и вырабатывается сразу при подаче входной информации.
Закон функционирования комбинационной схемы определен, если задано соответствие между ее входными и выходными сигналами (например, в виде таблицы истинности), при этом охватываются все сочетания входных сигналов, а их очередность следования не имеет значения.
Примером КС могут служить разнообразные шифраторы, дешифраторы, преобразователи кодов, сумматоры и целый ряд других схем, не содержащих элементов памяти.
Цифровые автоматы – это логические устройства, в которых помимо логических элементов имеются элементы памяти. Значение выходных сигналов такого устройства зависит не только от аргументов на входе в данный момент времени, но и от предыдущего состояния автомата, которое фиксируется элементами памяти. В качестве элементов памяти могут использоваться триггеры.
Комбинационную схему реализуют при помощи т. н. базовых логических элементов, которые также еще называют вентилями.
Логический вентиль – базовый элемент комбинационной схемы, выполняющий элементарную логическую операцию, преобразуя таким образом множество входных логических сигналов в выходной логический сигнал. Логика работы вентиля основана на битовых операциях с входными цифровыми сигналами в качестве операндов. При создании комбинационной схемы вентили соединяют между собой, при этом, если вентиль не выходной, то его выход должен быть подключён к одному или к нескольким входам других вентилей. В настоящее время в созданных человеком цифровых устройствах доминируют электронные логические вентили на базе полевых транзисторов, однако в прошлом для создания вентилей использовались и другие устройства, например, электромагнитные реле, гидравлические устройства, а также механические устройства. В поисках более совершенных логических вентилей исследуются квантовые устройства, биологические молекулы, фононные тепловые системы.
В цифровой электронике логический уровень сигнала представлен в виде уровня напряжения (попадающего в один из двух диапазонов) или в виде значения тока. Это зависит от типа используемой технологии построения электронной логики. Поэтому любой тип электронного вентиля требует наличия питания для приведения выходного сигнала к необходимым уровням сигнала.
Название элемента | Обозначение |
И (конъюнктор) | |
И-НЕ (штрих Шеффера) | |
ИЛИ (дизъюнктор) | |
ИЛИ-НЕ (стрелка Пирса) | |
ИСКЛЮЧАЮЩЕЕ ИЛИ (xor) | |
ИСКЛЮЧАЮЩЕЕ ИЛИ-НЕ (эквиваленция) | |
НЕ (инвертор) | |
Любой сколь угодно сложный элемент компьютера может быть сконструирован из элементарных вентилей.
Пример 3 (задача синтеза комбинационной схемы). Приёмная комиссия в составе трех членов комиссии и одного председателя решает судьбу абитуриента большинством голосов. В случае равного распределения голосов большинство определяется той группой, в которой оказался председатель приемной комиссии. Построить комбинационную схему, обеспечивающую определение большинства голосов.
►
А | B | C | D (председатель) | F(А, B, C, D) |
0 | 0 | 0 | 0 | 0 |
0 | 0 | 0 | 1 | 0 |
0 | 0 | 1 | 0 | 0 |
0 | 0 | 1 | 1 | 1 |
0 | 1 | 0 | 0 | 0 |
0 | 1 | 0 | 1 | 1 |
0 | 1 | 1 | 0 | 0 |
0 | 1 | 1 | 1 | 1 |
1 | 0 | 0 | 0 | 0 |
1 | 0 | 0 | 1 | 1 |
1 | 0 | 1 | 0 | 0 |
1 | 0 | 1 | 1 | 1 |
1 | 1 | 0 | 0 | 0 |
1 | 1 | 0 | 1 | 1 |
1 | 1 | 1 | 0 | 1 |
1 | 1 | 1 | 1 | 1 |
СДНФ и её упрощение:

Комбинационная схема:

Построим минимальную ДНФ:  .
Комбинационная схема:
.
Комбинационная схема:

(Минимальная КНФ:  )
)
Применим к минимальной ДНФ дистрибутивный закон, вынеся D за скобки:
 .
В результате получим ещё более простую
комбинационную схему:
.
В результате получим ещё более простую
комбинационную схему:

◄
~ 9 ~ © LKN
1.2. Комбинационные логические схемы.
Все устройства в МП состоят из элементарных логических схем. Работа этих схем основана на законах и правилах алгебры логики, которая оперирует двумя понятиями: истинности и ложности высказывания. В соответствии с такой двоичной природой высказываний условились называть их логическими двоичными переменными и обозначать 1 в случае истинности и 0 в случае ложности. Преобразование связей между логическими переменными осуществляется в соответствии с правилами алгебры логики, называемой алгеброй Буля или Булевой алгеброй (в честь её автора — английского математика Буля Джоржа).
Две логические переменные А и В, принимающие значение 0 или 1, могут образовывать логические функции. Всего существует 16 возможных функций.
1) Логическое отрицание НЕ переменной А есть логическая функция Х, которая истина только тогда, когда ложно А и наоборот.
В алгебре логики любые функции удобно изображать в виде таблицы соответствия всех возможных комбинаций входных логических переменных и выходной логической функции, называемой таблицей истинности. Для функции логического отрицания НЕ таблица истинности имеет вид:
где А — входная переменная, Х — выходная функция.
Функция НЕ в
символах алгебры логики записывают
следующим образом: 
Графически эта функция обозначается кружком на входе или выходе логического символа:
Практически эта функция реализуется переключателем, у которого замкнутое состояние соответствует «1», а разомкнутое — «0».

Временная диаграмма функции НЕ имеет вид:

2) Логическое умножение И или конъюнкция двух переменных А и В есть логическая функция Х, которая истинна только тогда, когда одновременно истинны входные переменные.
Для функции логического умножения таблица истинности имеет вид:
А
0 0 1 1
В
0 1 0 1
Х
0 0 0 1
и записывается
как 

Графически функция И обозначается в виде прямоугольника

Практический размер реализации функции И и её временные диаграммы имеет вид:
3) Логическая сумма ИЛИ или дизъюнкция переменных А и В есть логическая функция Х, которая истинна, когда хотя бы одна из входных функций истинна. Для логической суммы таблица истинности имеет вид:
А | 0 0 1 1 |
В | 0 1 0 1 |
Х | 0 1 1 1 |
и записывается
так: 
Пример функции логической суммы двух переменных и диаграммы входных и выходных сигналов представлены на рис:

Широкое распрстранение получили в реализации современных логических схем функции ИЛИ-НЕ, И-НЕ, исключающее ИЛИ. Таблицы истинности этих схем имеют вид:
4) Функция И-НЕ (Отрицание коньюнкции или стрелка Пирса)
А | 0 0 1 1 |
В | 0 1 0 1 |
Х | 1 1 1 0 |

5) Функция ИЛИ-НЕ (Отрицание дизъюнкции или Штрих Шеффера)
А | 0 0 1 1 |
В | 0 1 0 1 |
Х | 1 0 0 0 |


6) Функция исключающая ИЛИ (Неравнозначность или сложении по модулю 2)

А | 0 0 1 1 |
В | 0 1 0 1 |
Х | 0 1 1 0 |

Кроме перечисленных функций в алгебре логики имеются следующие теоремы:









а)
 Переместительный
Переместительный
б)  закон
закон
а)
 Сочетательный
Сочетательный
б) 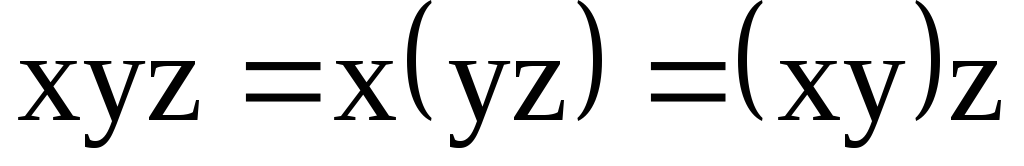 закон
закон
 Распределительный
закон
Распределительный
закон



Теоремы де-Моргана
Технический аналог булевой функции – комбинационная схема, выполняющая соответствующее этой функции преобразование информации.
Комбинационные логические схемы: функции и классификация
Сигналы обычно представлены дискретными полосами аналоговых уровней в цифровых электронных схемах или цифровой электронике вместо непрерывных диапазонов, представленных в аналоговой электронике. Простые электронные представления функций булевой логики, большие сборки логических вентилей обычно используются для создания цифровых электронных схем. В теории цифровых схем схемы, образованные таким образом из логических вентилей, используются для генерации выходных сигналов на основе входной логики.Следовательно, эти схемы называются логическими схемами и подразделяются на два типа, такие как последовательные логические и комбинационные логические схемы.
 Логические схемы
Логические схемыЛогические вентили можно определить как простые физические устройства, используемые для реализации логической функции. Логические вентили используются для выполнения логической операции с одним или несколькими входами и генерируют логический выход. Эти логические схемы формируются путем соединения одного или нескольких логических вентилей вместе. Эти логические схемы подразделяются на два типа: последовательные логические схемы и комбинационные логические схемы.
Комбинационные логические схемы
В этой статье мы обсудим введение в логические схемы, комбинационные логические схемы, определение схем комбинационной логики, дизайн схем комбинационной логики, функции комбинационной логики.
Определение комбинационной логической схемы
Комбинационные логические схемы или не зависящие от времени логические схемы в теории цифровых схем могут быть определены как тип цифровой логической схемы, реализованной с использованием булевых схем, где выход логической схемы является чистой функцией настоящего только входы.Комбинационная логическая схема работает мгновенно, и эти схемы не имеют памяти или контуров обратной связи.
Эта комбинационная логика отличается от последовательной логической схемы, в которой выход зависит как от имеющихся входов, так и от предыдущих входов. Таким образом, мы можем сказать, что комбинационная логика не имеет памяти, тогда как последовательная логика хранит предыдущий ввод в своей памяти. Следовательно, если изменяется вход комбинационной логической схемы, то изменяется и выход.
Конструкция комбинационной логической схемы
 Комбинационная логическая схема
Комбинационная логическая схемаЭти комбинационные логические схемы предназначены для получения определенных выходных сигналов с определенных входов. Комбинационный логический дизайн может быть выполнен с использованием двух методов, таких как сумма произведений и произведение сумм. Комбинационные логические схемы обычно разрабатываются путем соединения или комбинирования основных логических элементов, таких как И-НЕ, ИЛИ-ИЛИ и НЕ. Следовательно, эти логические вентили называются строительными блоками.Эти логические схемы могут быть очень простой схемой, очень сложной схемой или огромной комбинационной схемой, которые могут быть спроектированы с использованием только универсальных логических вентилей, таких как вентили И-НЕ и ИЛИ-ИЛИ.


Функции комбинационной логической схемы
Функцию комбинационной логической схемы можно определить тремя основными способами, например:
- Таблица истинности
- Логическая алгебра
- Логическая диаграмма
Таблица истинности

 Комбинационная Таблица истинности логической функции
Комбинационная Таблица истинности логической функцииФункцию логического элемента можно определить с помощью ее таблицы истинности, которая состоит из выходов для всех возможных комбинаций входов логического элемента.Пример таблицы истинности функции комбинационной логики показан на рисунке выше.
Boolean Algebra
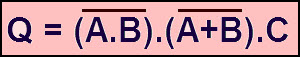
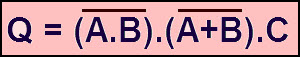 Комбинационная логическая функция Boolean Expression
Комбинационная логическая функция Boolean ExpressionВыходные данные функции комбинационной логики могут быть выражены в виде выражения с использованием булевой алгебры и, например, логическое выражение для приведенной выше таблицы истинности показано на рисунке выше.
Логическая схема

 Комбинационная логическая схема с использованием логических вентилей
Комбинационная логическая схема с использованием логических вентилейГрафическое представление функций комбинационной логики с использованием логических вентилей называется логической схемой.Логическая схема для обсуждаемой выше таблицы истинности логической функции и логического выражения может быть реализована, как показано на рисунке выше.
Комбинационные логические схемы можно также называть схемами принятия решений, поскольку они разработаны с использованием индивидуальных логических вентилей. Комбинационная логика — это процесс объединения логических вентилей для обработки данных двух или более входных данных, чтобы генерировать по крайней мере один выходной сигнал на основе логической функции каждого логического элемента.
Классификация комбинационной логики
 Классификация комбинационной логики
Классификация комбинационной логикиКомбинационные логические схемы можно разделить на различные типы в зависимости от цели использования, например, арифметические и логические функции, передача данных и преобразователи кода.Для решения арифметических и логических функций мы обычно используем сумматоры, вычитатели и компараторы, которые обычно реализуются путем объединения различных логических элементов, называемых комбинационными логическими схемами. Точно так же для передачи данных мы используем мультиплексоры, демультиплексоры, кодеры и декодеры, которые также реализованы с использованием комбинационной логики. Преобразователи кода, такие как двоичные, BCD и 7-сегментные, разработаны с использованием различных логических схем.
Фактически, комбинационная логика наиболее часто используется в схемах типа мультиплексора и демультиплексора.Если несколько входов или выходов подключены к общей сигнальной линии, то логические элементы используются для декодирования адреса, чтобы выбрать один вход данных или переключатель выхода.
Хотите подробнее узнать о схемах комбинационной логики?
Если вы заинтересованы в разработке проектов в области электроники, вы можете использовать нашу бесплатную электронную книгу, чтобы создавать проекты «сделай сам» или делать это самостоятельно. Для получения дополнительной технической помощи размещайте свои комментарии, предложения, идеи и запросы в разделе комментариев ниже.
.Комбинационные логические схемы — вопросы и ответы по цифровой электронике
Почему в цифровой электронике используются комбинационные логические схемы?
В этом разделе вы можете выучить и попрактиковаться в вопросах по цифровой электронике, основанных на «Комбинированных логических схемах», и улучшить свои навыки, чтобы пройти собеседование, конкурсный экзамен и различные вступительные испытания (CAT, GATE, GRE, MAT, банковский экзамен, железнодорожный экзамен). и т.п.) с полной уверенностью.
Где я могу получить вопросы и ответы по комбинированным логическим схемам цифровой электроники с пояснениями?
IndiaBIX предоставляет вам множество полностью решенных вопросов и ответов по цифровой электронике (комбинационные логические схемы) с пояснениями. Решенные примеры с подробным описанием ответов, даны пояснения, которые легко понять. Все студенты и первокурсники могут загрузить вопросы викторины по комбинационным логическим схемам цифровой электроники с ответами в виде файлов PDF и электронных книг.
Где я могу получить вопросы и ответы на собеседование по комбинационным логическим схемам цифровой электроники (тип цели, множественный выбор)?
Здесь вы можете найти вопросы и ответы для собеседований и вступительных экзаменов, касающиеся комбинированных логических схем цифровой электроники. Также предусмотрены вопросы с множественным выбором, а также вопросы истинного или ложного типа.
Как решить проблемы с комбинационными логическими схемами цифровой электроники?
Вы можете легко решить все виды вопросов цифровой электроники, основанные на комбинационных логических схемах, выполнив упражнения объективного типа, приведенные ниже, а также получите быстрые методы для решения задач комбинационных логических схем цифровой электроники.
Упражнение :: Комбинированные логические схемы — общие вопросы
.
Разница между комбинационной и последовательной логической схемой (со сравнительной таблицей)
Основное различие между комбинационной логической схемой и последовательной логической схемой заключается в том, что комбинационная логическая схема состоит только из логических вентилей, а последовательные логические схемы состоят из логических вентилей и элементов памяти.
Еще одним важным фактором, который отличает комбинационную и последовательную логические схемы, является состояние выходных элементов. Состояние выходных элементов комбинационной схемы зависит только от текущего состояния входных элементов.Напротив, выход, полученный из последовательной схемы, зависит от текущего состояния входа, а также от прошлого состояния выхода.
Мы обсудим другое важное различие между комбинационной и последовательной логическими схемами с помощью сравнительной таблицы, но перед этим давайте взглянем на темы, затронутые в этой статье.
Содержимое: комбинационная и последовательная логическая схема
- Таблица сравнения
- Определение
- Ключевые отличия
- Заключение
Сравнительная таблица
| Параметры | Комбинированная логическая схема | Последовательная логическая схема |
|---|---|---|
| Определение | Это логическая схема, которая генерирует вывод на основе имеющихся вводов. | Это логическая схема, которая генерирует вывод на основе текущего ввода, а также на основе прошлого вывода. |
| Элемент памяти | Элемент памяти отсутствует в комбинационной логической схеме. | Элемент памяти присутствует в последовательной логической схеме. |
| Петля обратной связи | Петля обратной связи отсутствует. | Петля обратной связи присутствует. |
| Получен выход | Необязательная комбинация операндов в одной и той же последовательности. | Последовательность операндов необходима в последовательной схеме. |
| Примеры | Полусумматор, Полный сумматор, Кодер, декодер, мультиплексор, демультиплексор и т. Д. | Конечный автомат |
Определение
Комбинационная логическая схема
Комбинационная логическая схема состоит из логических вентилей, и, таким образом, полученный выход напрямую связан с входом. В случае Комбинационной логической схемы элементы обратной связи отсутствуют.Слово комбинация происходит от слова комбинация , что означает два или более элементов, объединенных вместе посредством одной операции.
Комбинационная логическая схема состоит из логических элементов, таких как И-НЕ, ИЛИ-ИЛИ и НЕ. Это строительные блоки цифровой схемы. Комбинационная схема обеспечивает множество операций, таких как арифметические операции над двумя операндами, передача данных, преобразование кода и т. Д.
С помощью логических элементов комбинационная схема выполняет такую операцию, как сложение, вычитание или преобразование кода из двоичного в двоично-десятичный, двоично-десятичный в двоичный и т. Д.Выход схемы комбинационной логики может быть описан различными способами, такими как логическая алгебра, таблица истинности и логические вентили.
Комбинационная схема может принимать любое количество входов, а выходной сигнал, генерируемый схемой, зависит от состояния входа. Любое изменение на входе также будет отражено на выходных клеммах.
Существуют различные типы комбинационных схем, среди которых мультиплексор и демультиплексор являются наиболее важными, которые используются в различных приложениях.Другими комбинационными схемами являются кодер, декодер, полусумматор, полный сумматор, преобразователь двоичного кода в двоично-десятичный и т. Д.
Схема последовательной логики
Последовательная логическая схема также включает элементы памяти вместе с логическими вентилями. Таким образом, выходной сигнал, генерируемый последовательной схемой, зависит не только от текущего состояния входа, но и от предыдущих выходов.
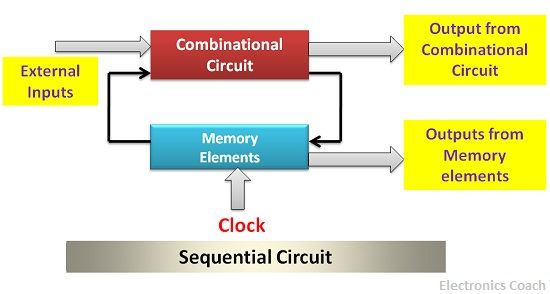
Последовательная схема предполагает использование контуров обратной связи, с помощью которых записывается состояние предыдущего выхода.Таким образом, следующий выход контролируется состоянием предыдущего выхода. Память, присутствующая в последовательной схеме, отслеживает вывод и, таким образом, вывод производится.
Слово последовательное происходит от слова последовательность , что означает в определенном порядке. Чтобы понять работу последовательной схемы, возьмем пример телевизионной схемы. Телевидение также является разновидностью последовательной цепи. Клавиши, доступные на пульте дистанционного управления, для переключения канала или клавиши вверх и вниз для регулировки громкости, весь этот процесс является последовательным.
Когда вы выбираете конкретный канал, телевизионный приемник отслеживает предыдущий выбранный канал и в соответствии с этим выбирается следующий канал.
Последовательные схемы являются основной единицей цифровых схем. Самый популярный пример последовательной схемы — конечный автомат . В основном существует два типа последовательной цепи: один — , синхронный, , а другой — , асинхронный, — последовательный.
Синхронная последовательная логическая схема — это схема, в которой выходной сигнал генерируется с входным и тактовым сигналами. Тактовый сигнал подается в определенном временном интервале. Напротив, асинхронная последовательная логическая схема генерирует ответ в любое время, когда происходит изменение на входных клеммах.
Ключевые различия между комбинационной и последовательной логической схемой
- Комбинационная и последовательная логические схемы являются строительными блоками цифровых схем, но наличие элементов памяти создает основное различие.Схема комбинационной логики не имеет какого-либо элемента памяти, тогда как схема последовательной логики состоит из элементов памяти.
- Выходные данные, полученные от комбинационной и последовательной логических схем, также отличаются друг от друга. Выходной сигнал, генерируемый комбинационной схемой, является функцией только имеющихся входов. Но выход, полученный из последовательной схемы, зависит как от текущего входа, так и от прошлого выхода.
- Цепь обратной связи отсутствует в схемах комбинационной логики.Но последовательная логическая схема должна состоять из этого, чтобы отслеживать прошлые выходные данные.
- Тактовый сигнал не используется в комбинационной схеме, но последовательный использует тактовый сигнал для обеспечения синхронизации.
- Процесс проектирования комбинационной схемы намного проще по сравнению с последовательной схемой.
Заключение
Комбинированная и последовательная логическая схема предназначена для различных приложений. Но на практике большинство схем используют комбинацию как комбинационных, так и последовательных схем для удовлетворения своих потребностей.Комбинационная схема будет обеспечивать выходной сигнал в зависимости от функции входа. Напротив, последовательная схема будет генерировать выходные данные на основе состояния элемента памяти. Он отслеживает прошлый ввод и предыдущие выводы.
.Комбинационных логических схем
Комбинационная логическая схема реализует логические функции, выходы которых зависят только от текущей комбинации входных значений. С другой стороны, последовательные схемы, в отличие от комбинационной логики, имеют состояние или память.
Основное различие между последовательными схемами и комбинационными схемами состоит в том, что последовательные схемы вычисляют свой вывод на основе ввода и состояния, и что состояние обновляется на основе часов. Комбинационные логические схемы реализуют булевы функции и являются функциями только своих входов.
Представление комбинационных логических функций
Есть 3 способа представления функций комбинационной логики
- Логические вентили — Логические вентили используются в качестве строительных блоков при проектировании комбинационных логических схем. Эти ворота являются воротами И, ИЛИ, НЕ, ИЛИ, ИЛИ.
- Boolean Algebra — Boolean Algebra определяет отношения между логическими переменными, которые используются для разработки цифровых схем с использованием логических вентилей. Каждую логическую схему можно полностью описать с помощью логических операций, поскольку элементы ИЛИ, И и НЕ являются основными строительными блоками цифровых систем.
- Таблица истинности — Таблица истинности используется в логике для вычисления функциональных значений логических выражений для каждой комбинации значений, принимаемых их логическими переменными. Если блок комбинированной логики имеет более одного битового выхода, каждый однобитовый выход получает свою собственную таблицу истинности. Часто они объединяются в одну таблицу с несколькими выходными столбцами, по одному для каждого однобитового вывода.
Анализ комбинационных логических схем
Чтобы получить булевы выражения и таблицы истинности из схемы комбинационной логики, нам необходимо проанализировать схему.Сначала убедитесь, что схема является комбинационной, т. Е. Нет обратной связи между выходом и входом, от которого он зависит.
Логические выражения
- пометить все входы — входные переменные
- маркировка всех выходов — функции выходов
- маркировать все промежуточные сигналы (выходы, которые питают входы)
Для каждой выходной функции запишите ее в терминах ее входных переменных и промежуточных сигналов, а затем расширяйте промежуточные сигналы, пока выходы не будут выражены только в терминах входов.
Таблицы истинности
Таблица истинности может быть получена из булевых выражений или путем непосредственной обработки из схемы выходов для каждой возможной комбинации входов.
Если есть n входных переменных
- есть 2 n возможных комбинаций двоичных входов
- есть 2 n записей в таблице истинности для каждого вывода
Из приведенных ниже примеров измените входы для наблюдения за выходами.
Примеры схем
Цепь сигнализации
- C: Датчик открытия двери
- B: Датчик движения
- A: Тревога постановки на охрану
- Z: Тревога
Полусумматор
- A, B: 1-битные входы
- S: Сумма
- C: переносить
Разработка комбинационных логических схем
Вы узнали, как получить логические выражения и таблицы истинности из логических схем. Далее вы узнаете, используя рабочие примеры с инструкциями, как проектировать схемы комбинационной логики за считанные минуты.
Разработка комбинационных логических схем включает следующие шаги
- Из проектной спецификации найдите таблицу истинности
- Из таблицы истинности выведите логическое выражение «Сумма произведений».
- Используйте карту Карно, чтобы минимизировать логическое выражение. Чем проще логическое выражение, тем меньше логических элементов будет использоваться.
- Используйте логические элементы для реализации упрощенного логического выражения.
Поскольку доходы от рекламы падают, несмотря на рост числа посетителей, нам нужна ваша помощь в поддержании и улучшении этого сайта, что требует времени, денег и тяжелого труда.Благодаря щедрости наших посетителей, которые давали ранее, вы можете пользоваться этим сайтом бесплатно.
Если вы получили пользу от этого сайта и можете, пожалуйста, отдать 10 долларов через Paypal . Это позволит нам продолжаем в будущее. Это займет всего минуту. Спасибо!
Я хочу дать!
© 2020 Emant Pte Ltd Co., рег. № 200210155R | Условия использования | Конфиденциальность | О нас
.


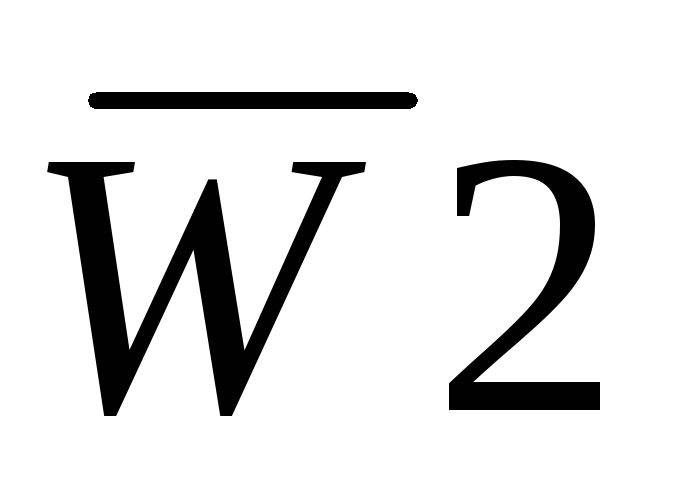
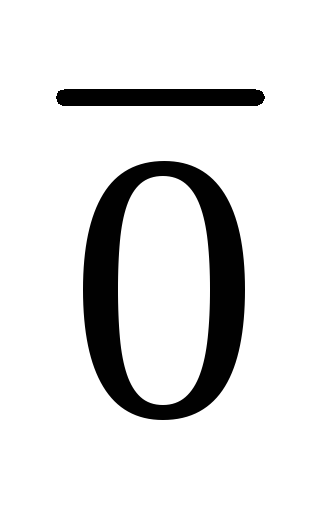







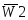
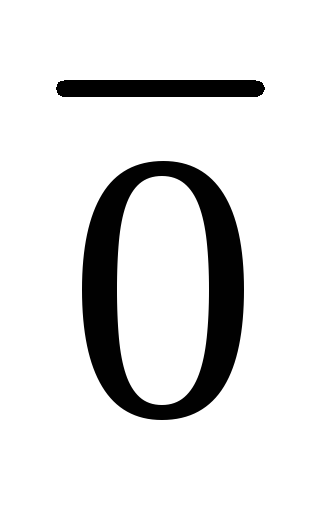

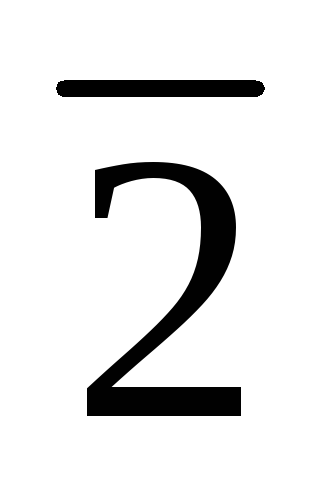


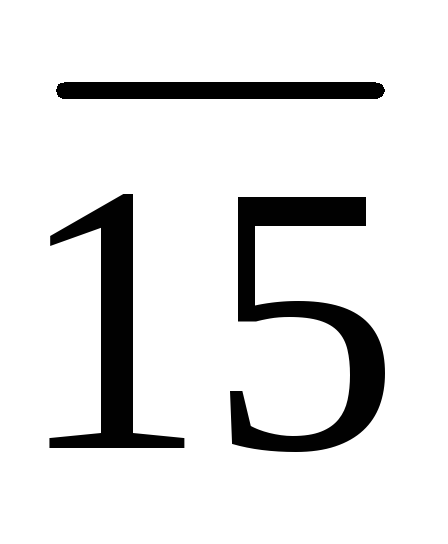




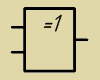





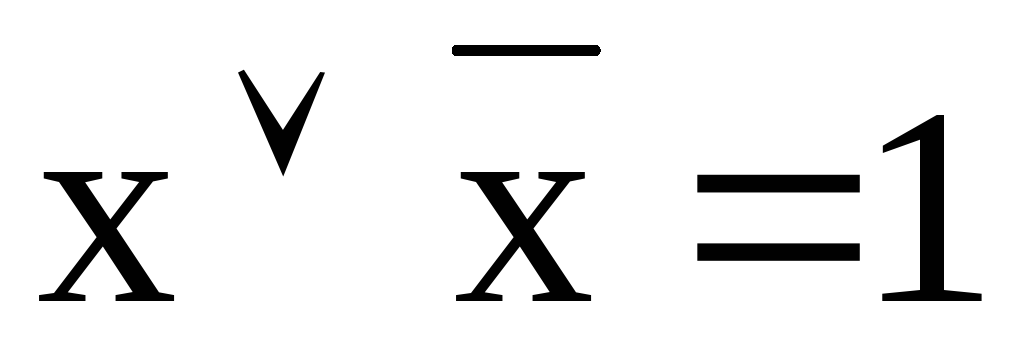
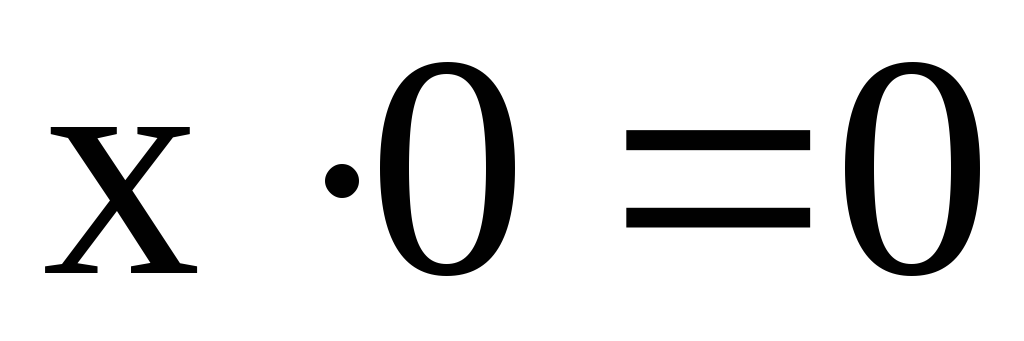




 Переместительный
Переместительный Сочетательный
Сочетательный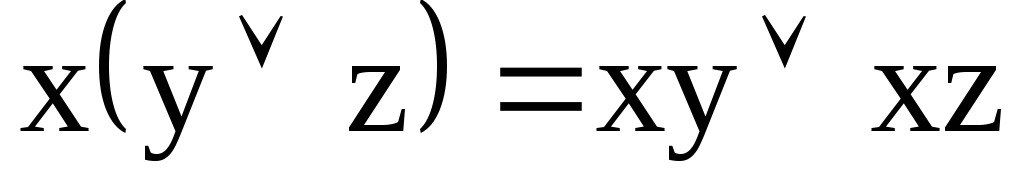 Распределительный
закон
Распределительный
закон
