Катушка индуктивности на схеме — Весёлый Карандашик
2013, Апрель 3 , Среда
Домашняя старницаНемного электричестваКатушка индуктивности на схеме
Автор: Игорь Александрович Немного электричества 0 Комментариев
Самая простая электрическая цепь, состоящая из электрического проводника в виде обычного изолированного провода, и источника переменного тока, представляющего собой понижающий трансформатор, подключённый к бытовой электрической сети, будет примером для описания в этом материале.
В электрической цепи, в которой протекает переменный ток, на величину этого проходящего электрического тока влияет и сопротивление проводника, включённого в цепь, и магнитное поле вокруг проводника, создаваемого при прохождении тока через этот проводник. Получается, что электрическая цепь с переменным током обладает ещё и своими магнитными свойствами, характеризующими величиной, какой является индуктивность. В данном случае — это индуктивность проводника или всей электрической цепи.
Доступными словами будет сказано, чем больше по величине проходящий через проводник переменный ток, тем больше по величине будет создаваемое вокруг этого же проводника переменное магнитное поле.
Но не все проводники обладают одинаковой электрической проводимостью. Каждый материал, используемый для изготовления проводника, обладает своими свойствами, от которых зависит и величина сопротивления электрическому току, называемая активным сопротивлением проводника, и величина индуктивного сопротивления, определяемое индуктивностью проводника, то есть своими магнитными свойствами.
У прямого проводника сопротивление переменному току, создаваемое магнитным полем проводника, индуктивность небольшая. А если этот же проводник свернуть в катушку, то его индуктивность сразу и на много увеличится. Увеличится его индуктивное сопротивление переменному току и электрический ток в такой цепи уменьшится. Для переменного тока индуктивность полученной катушки является преградой и вокруг катушки образуется электромагнитное поле, величина которого будет зависеть от силы проходящего через катушку переменного тока.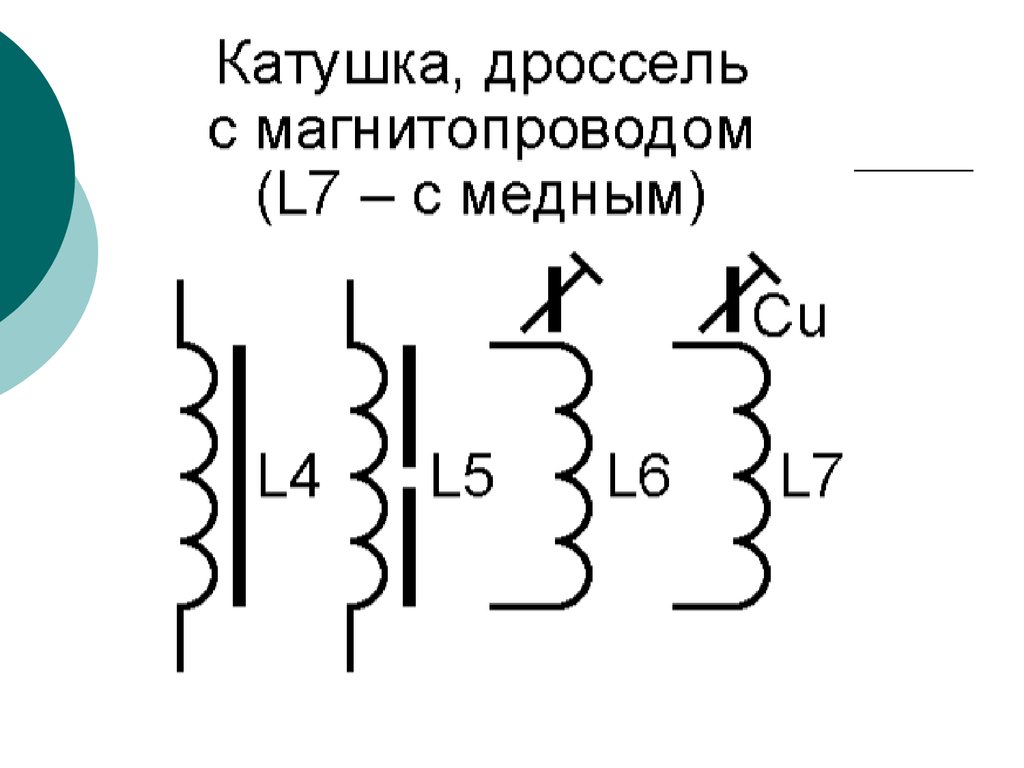
Любой электрический проводник, свёрнутый в катушку, в действующей электрической цепи с переменным током будет представлять собой катушку индуктивности, выполняющую роль дросселя, вариометра(изменяющего индуктивность) или реактора и зависеть от величины и частоты проходящего через катушку тока.
Единицой индуктивности является генри(Гн).
Графическое изображение индуктивных элементов на схеме.
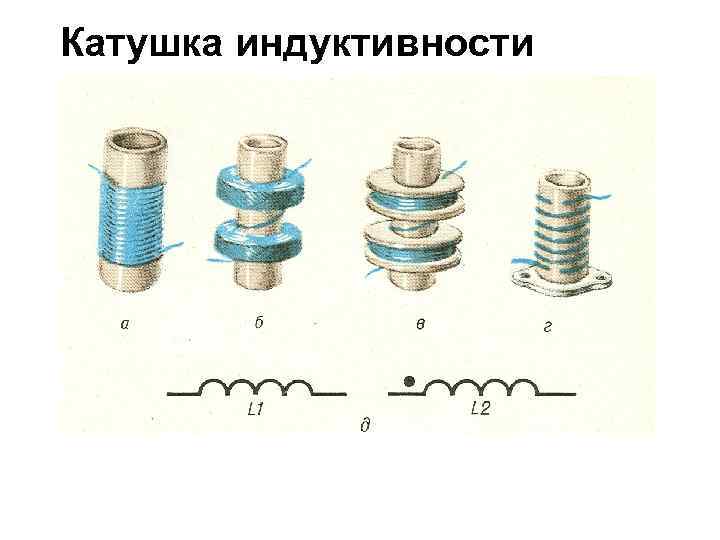
Катушки индуктивности могут иметь винтовую, спиральную или винтоспиральную намотку из изолированного проводника и иметь значительную индуктивность и малое активное сопротивление и малую электрическую ёмкость. Катушки наматываются на каркас с использованием сердечников или без них.
Волнообразная линия, нарисованная параллельно рисунку сердечника или без него и есть наш катушка индуктивности. Напоминает изображение части электрического трансформатора.
Так же как у трансформатора указывается начало обмотки толстой жирной точкой и указывается сердечник, если имеется, а вот обозначается на схеме буквой (L). Рядом устанавливается дополнительный буквенный символ, в зависимости от типа дросселя : L — LL(дроссель ламп люминесцентного освещения), G — LG(реактор), R — LR(обмотка возбуждения генератора).
Катушка индуктивности сама по себе является конструктивной составляющей единицей устройства, а дроссель, вариометр, реактор — это уже целая функционирующая единица устройства, конструкция которого определяется его назначением. То есть, используемая в электросхеме индуктивная катушка в действующей цепи будет являться или дросселем или реактором или вариометром. В неработающей системе катушка индуктивности будет только катушкой и не больше.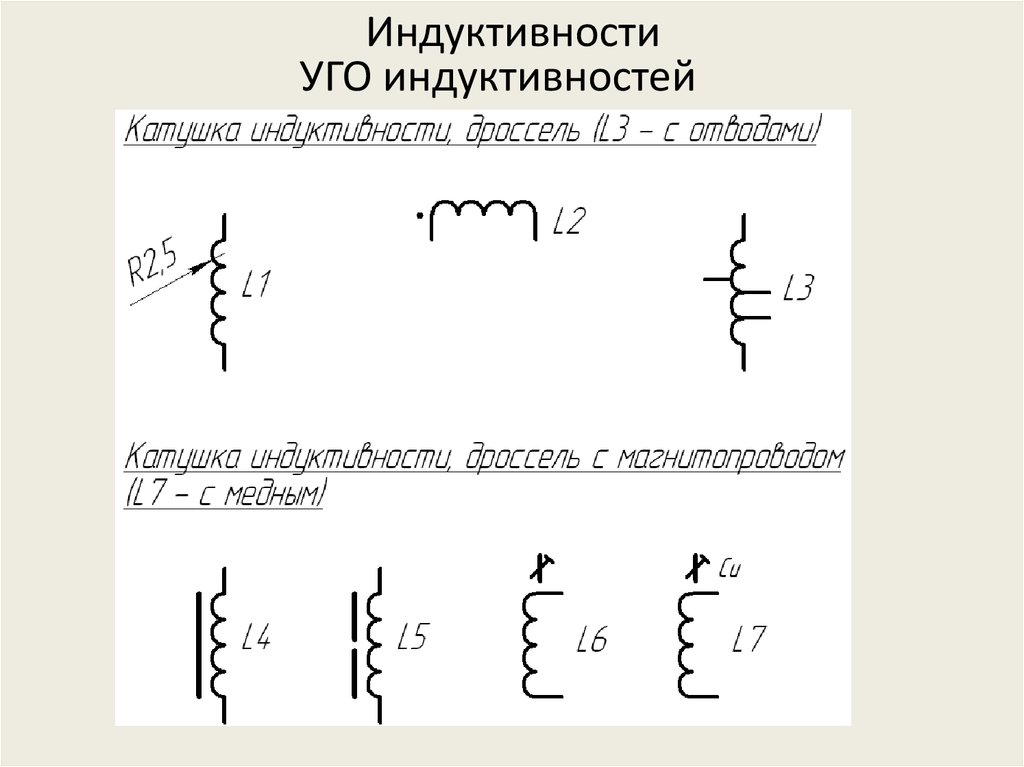 Это моё мнение и его никому не навязываю, только лишь делюсь.
Это моё мнение и его никому не навязываю, только лишь делюсь.
Click to rate this post!
[Total: 1 Average: 5]
◀ Трансформаторы на электросхемах
Громкоговоритель в действии и на схемах ▶
Об Авторе
Игорь Александрович
Возможно, предоставляемые мною сведения не будут достаточно удовлетворять заинтересовавшегося гостя в поиске нужной для него информации. Не оставлю без внимания ни один комментарий, даже компрометирующий меня, но только по соответствующей теме. Обратиться ко мне лично по некоторым вопросам можно на странице Связь с администратором «Весёлый Карандашик» .
Схемы на все случаи жизни » Индуктивность. Катушки индуктивности
Индуктивностью (применительно к компонентам электрической цепи) называется идеализированный элемент электрической цепи, приближающийся по свойствам к катушке индуктивности, в которой накапливается энергия магнитного поля.
Катушка индуктивности представляет собой
проводник, намотанный на сердечник.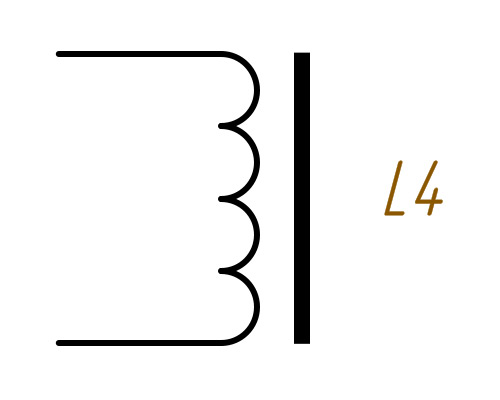 Сердечник может быть магнитным, либо
немагнитным. Схематическое изображение катушки индуктивности показано
на рис 1. При работе в электрической цепи катушка индуктивности
препятствует изменению протекающего через нее тока. Иными словами, если
ток, подаваемый в схему, которая содержит катушку, резко увеличить, то
ток в схеме будет нарастать плавно до достижения своего максимального
значения.
Сердечник может быть магнитным, либо
немагнитным. Схематическое изображение катушки индуктивности показано
на рис 1. При работе в электрической цепи катушка индуктивности
препятствует изменению протекающего через нее тока. Иными словами, если
ток, подаваемый в схему, которая содержит катушку, резко увеличить, то
ток в схеме будет нарастать плавно до достижения своего максимального
значения.
На рисунке 1 показаны условно-графические изображения катушек индуктивности различных типов [3].
Способность катушки индуктивности препятствовать изменению силы тока, протекающего через нее, носит название индуктивности этой катушки. Индуктивность обозначается буквой L, единицей ее измерения является Генри (Гн). Генри — большая единица индуктивности, значительно чаще используются миллигенри (мГн) = 10-3 Гн и микрогенри (мкГн) = 10-6 Гн.
Катушки могут иметь как постоянную, так и изменяемую индуктивность. На рисунке 1 показано схематическое изображение катушки с переменной
индуктивностью (рисунки 1в и 1г). Катушки с переменной индуктивностью
содержат подстроечный сердечник. Сердечник может изготавливаться из
материала, который при введении внутрь катушки как увеличивает
индуктивность (например, феррит), так и уменьшает (например, латунь).
На рисунке 1 показано схематическое изображение катушки с переменной
индуктивностью (рисунки 1в и 1г). Катушки с переменной индуктивностью
содержат подстроечный сердечник. Сердечник может изготавливаться из
материала, который при введении внутрь катушки как увеличивает
индуктивность (например, феррит), так и уменьшает (например, латунь).
Катушки индуктивности с воздушным сердечником, или катушки без сердечника, используются в тех случаях, когда индуктивность не превышает 5 мГн. Они наматываются на керамические или композитные сердечники. Сердечники из феррита или порошкообразного железа обычно используются для индуктивности до 200 мГн.
Тороидальные сердечники имеют кольцеобразную форму и позволяют получить высокую индуктивность при малых размерах. Их магнитное поле сосредоточено внутри сердечника.
Многослойные катушки индуктивности с железным сердечником используются для получения большой индуктивности от 0,1 до 100 Гн. Эта индуктивность зависит от величины тока, протекающего через катушку. Эти катушки иногда называют дросселями. Они используются в цепях фильтрации источников питания для удаления переменных составляющих выпрямленного постоянного тока.
Эти катушки иногда называют дросселями. Они используются в цепях фильтрации источников питания для удаления переменных составляющих выпрямленного постоянного тока.
Если постоянное напряжение приложено к катушке индуктивности L через резистор (рис.2) то, для того чтобы в цепи установился максимальный ток требуется время, прямо пропорциональное величине сопротивления и индуктивности. Постоянная времени цепи определяет время, требуемое для увеличения тока в проводнике от нуля до 63,2% или уменьшения до 36,8% от максимального значения. Постоянная времени определяется следующей формулой: t= L/R, где t — время в секундах, R — сопротивление в омах, L — индуктивность в Генри.
Для того, чтобы создать максимальное магнитное поле в катушке индуктивности требуется примерно пять постоянных времени цепи L/R. Такое же время требуется для того, чтобы магнитное поле исчезло.
Катушка индуктивности в цепи постоянного тока имеет очень малое
сопротивление (с учетом сопротивления проводника) и не препятствует
прохождению постоянного тока.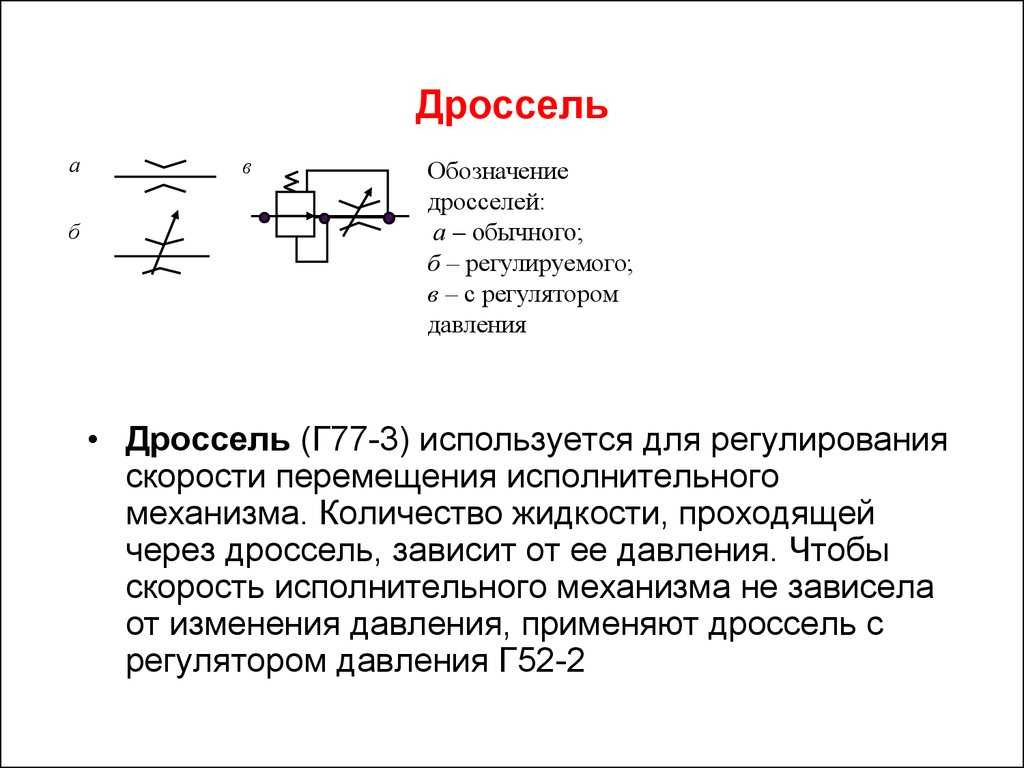
Реактивное сопротивление катушки индуктивности вычисляется по формуле: XL = j*2*π*f*L, где j — означает поворот вектора по часовой стрелке на 90
Индуктивное сопротивление является функцией частоты приложенного переменного напряжения и индуктивности. Рост частоты увеличивает индуктивное сопротивление и вызывает увеличение противодействия току. Уменьшение частоты уменьшает индуктивное сопротивление и снижает противодействие току. Данное свойство катушек индуктивности используетя при построении различных электрических фильтров.
Список использованной литературы
1. Атабеков Г. И. Основы теории цепей: Учебник. 2-е изд.,испр.–СПб.: Издательство «Лань», 2006.–432 с.
Атабеков Г. И. Основы теории цепей: Учебник. 2-е изд.,испр.–СПб.: Издательство «Лань», 2006.–432 с.
2. Эрл Д.Гейтс. Введение в электронику: Учебник. — Ростов-на-Дону.: Издательство «Феникс», 1998 год, 640 стр.
3. ГОСТ 2.723-68. Единая система конструкторской документации. Обозначения условные графические в схемах. Катушки индуктивности, дроссели, трансформаторы, автотрансформаторы и магнитные усилители.
Катушки индуктивности и резисторы в цепях постоянного тока
Google Ads
- Изучив этот раздел, вы сможете описать:
- • Переходные процессы в цепях постоянного тока.
- • Соотношение переходного напряжения и тока в простой цепи LR.
Рис. 4.4.1 Цепь LR
В цепи, которая содержит индуктивность (L), а также сопротивление (R), как показано на рис. 4.4.1, когда переключатель замкнут, ток не не сразу поднимается до своего устойчивого значения, а растет экспоненциально. Это связано с тем, что при изменении тока, протекающего через индуктор, создается ПРОТИВОЭДС. Эта обратная ЭДС имеет амплитуду, пропорциональную СКОРОСТИ ИЗМЕНЕНИЯ тока (чем выше скорость изменения, тем больше противоЭДС) и полярность, которая противодействует изменению тока в катушке индуктивности, вызвавшему его изначально.
Это связано с тем, что при изменении тока, протекающего через индуктор, создается ПРОТИВОЭДС. Эта обратная ЭДС имеет амплитуду, пропорциональную СКОРОСТИ ИЗМЕНЕНИЯ тока (чем выше скорость изменения, тем больше противоЭДС) и полярность, которая противодействует изменению тока в катушке индуктивности, вызвавшему его изначально.
Обратная ЭДС возникает из-за того, что изменяющийся ток в индукторе вызывает изменение магнитного поля вокруг него, а изменяющееся магнитное поле, в свою очередь, вызывает обратное наведение ЭДС в индукторе. Этот процесс называется САМОИНДУКЦИЕЙ.
Ток через индуктор
Рис. 4.4.2 Ток через индуктор
Поскольку обратная ЭДС противодействует быстрому изменению тока, происходящему в индукторе, скорость изменения тока уменьшается, и появляется вертикальная линия. на графике (рис. 4.4.2) становится наклонной. Скорость изменения тока через индуктор теперь меньше, поэтому возникает меньшая обратная ЭДС. Это позволяет увеличить ток. Взаимосвязь между изменяющимся током и противо-ЭДС создает кривую, которая всегда следует математическому закону, чтобы получить определенную форму кривой, т. е. экспоненциальную кривую. Когда переключатель разомкнут, ток спадает аналогичным экспоненциальным образом до нуля.
е. экспоненциальную кривую. Когда переключатель разомкнут, ток спадает аналогичным экспоненциальным образом до нуля.
Напряжение на индукторе
Рис. 4.4.3 Напряжение на индукторе
Глядя на рис. 4.4.3, на котором показано напряжение (V L ) на индукторе (L), мы видим, что при включении, напряжение сразу возрастает до максимального значения. Это связано с тем, что к цепи приложено напряжение, а ток протекает мало или не течет совсем, потому что L фактически (в течение очень короткого времени) является очень высоким сопротивлением из-за эффекта обратной ЭДС, вызванного быстро меняющимся (расширяющимся) магнитным полем вокруг индуктор индуцирует напряжение (обратную ЭДС) обратно в индуктор, которое имеет противоположную полярность по отношению к приложенному напряжению от источника питания и, таким образом, изначально препятствует увеличению тока через индуктор. Из-за этого противодействия, вызванного обратной ЭДС, сначала кажется, что индуктор имеет очень высокое сопротивление.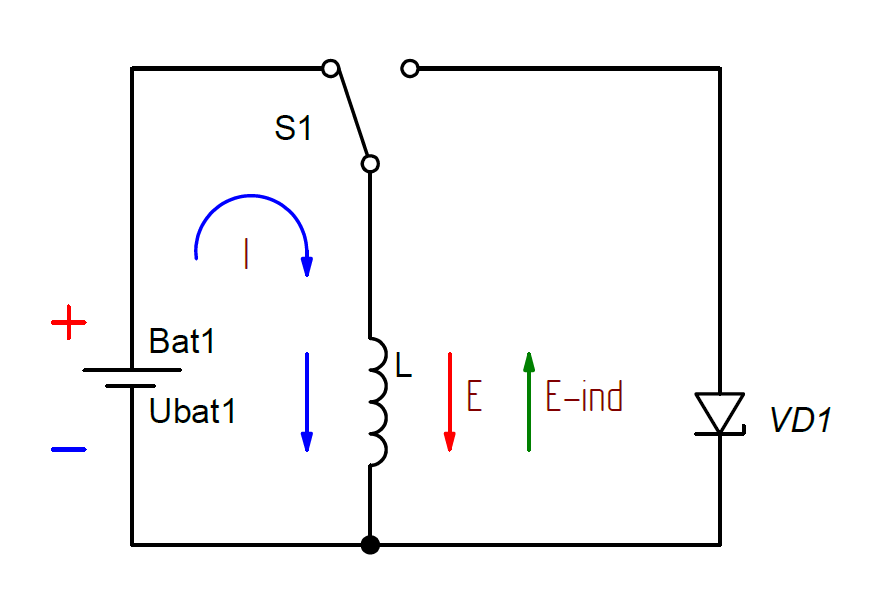 и поэтому полное напряжение питания развивается на катушке индуктивности. Однако по мере того, как ток через L начинает нарастать, скорость изменения магнитного поля уменьшается, сопротивление из-за обратной ЭДС уменьшается, и кажущееся «сопротивление» индуктора падает до низкого значения (реальное сопротивление проволочной катушки). и напряжение В L уменьшается до тех пор, пока не будет достигнута точка, в которой все напряжение батареи вырабатывается на резисторе R; напряжение или разность потенциалов (pd) на L практически равна нулю, и теперь энергия накапливается в магнитном поле вокруг индуктора.
и поэтому полное напряжение питания развивается на катушке индуктивности. Однако по мере того, как ток через L начинает нарастать, скорость изменения магнитного поля уменьшается, сопротивление из-за обратной ЭДС уменьшается, и кажущееся «сопротивление» индуктора падает до низкого значения (реальное сопротивление проволочной катушки). и напряжение В L уменьшается до тех пор, пока не будет достигнута точка, в которой все напряжение батареи вырабатывается на резисторе R; напряжение или разность потенциалов (pd) на L практически равна нулю, и теперь энергия накапливается в магнитном поле вокруг индуктора.
При отключении тока магнитное поле теперь схлопывается, а не растет, как при включении. Это разрушающееся магнитное поле теперь возвращает свою энергию в катушку индуктора и индуцирует напряжение (противоЭДС) в индукторе, но поскольку изменение напряженности магнитного поля происходит в направлении, противоположном направлению расширения поля при включении, индуцируемое напряжение равно теперь в противоположной полярности, как показано на рис.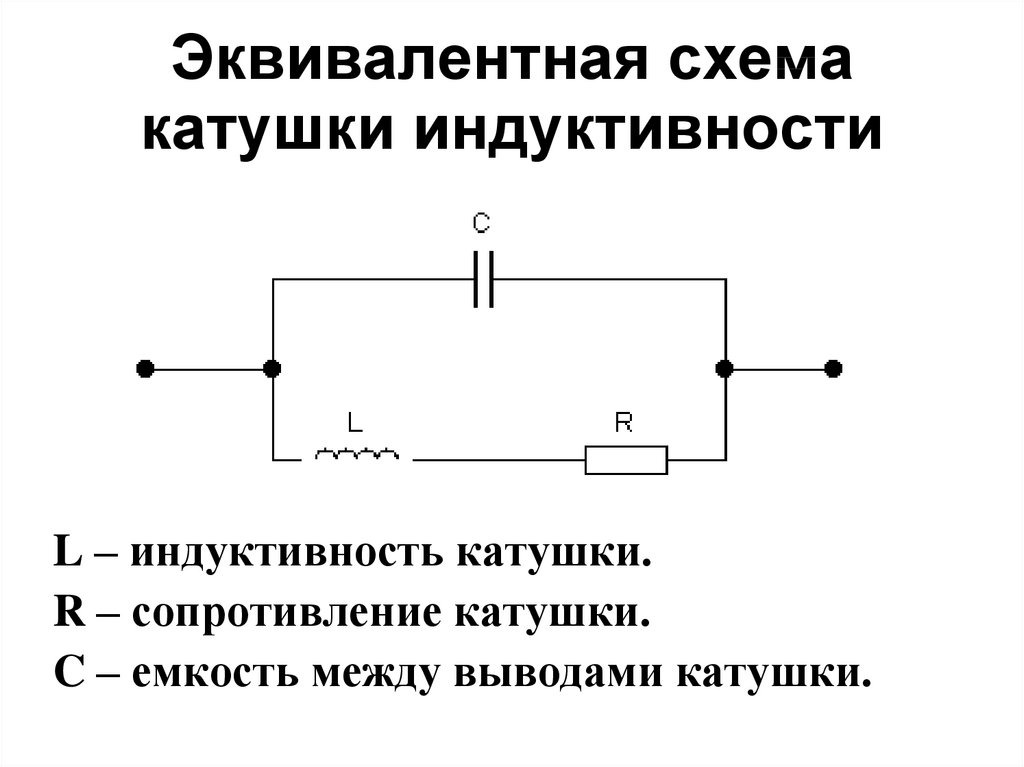 4.4.3. Наведенная обратная ЭДС теперь противостоит уменьшению тока, вызванному выключением, замедляя затухание тока, как показано на рис. 4.4.2.
4.4.3. Наведенная обратная ЭДС теперь противостоит уменьшению тока, вызванному выключением, замедляя затухание тока, как показано на рис. 4.4.2.
Быстрое исчезновение магнитного поля при размыкании переключателя может вызвать очень большие всплески напряжения, поскольку величина индуцируемого напряжения зависит от скорости изменения магнитного поля. Возникающие высокие напряжения могут привести к искрению на контактах переключателя, так как напряжение прыгает через зазор между контактами. Эти большие всплески напряжения могут также повредить другие компоненты в цепи, особенно полупроводники, поэтому необходимо соблюдать осторожность при проектировании цепей, содержащих катушки индуктивности или управляющих индуктивными нагрузками, чтобы предотвратить эти всплески. Однако в некоторых схемах, где требуются высокие напряжения, этот эффект также можно использовать с пользой, подавая прямоугольную волну на катушку индуктивности. Возникающие очень большие всплески напряжения могут затем выпрямляться специальными высоковольтными диодами для получения постоянного напряжения в тысячи вольт.
Отдача индуктора | Spinning Numbers
Катушка индуктивности — один из идеальных элементов схемы. Мы рассмотрим катушку индуктивности, подключенную к переключателю. Нам помогают две формы уравнения индуктора $i$-$v$.
Автор Вилли Макаллистер.
Содержимое
- Катушка индуктивности и переключатель
- Дать место для тока катушки индуктивности
- Имитационные модели
Куда мы направляемся
Катушка индуктивности, подключенная к переключателю, генерирует высокое неконтролируемое напряжение. Мы защищаем близлежащие компоненты от повреждения высоким напряжением, ставя диод параллельно катушке индуктивности.
Катушка индуктивности и переключатель
Мы анализируем эту цепь, используя как производную, так и интегральную форму уравнения катушки индуктивности,
Цепь представляет собой последовательное соединение источника напряжения $3\,\text V$, $10\ ,\text{mH}$ индуктор и кнопочный переключатель $(\text{pb})$.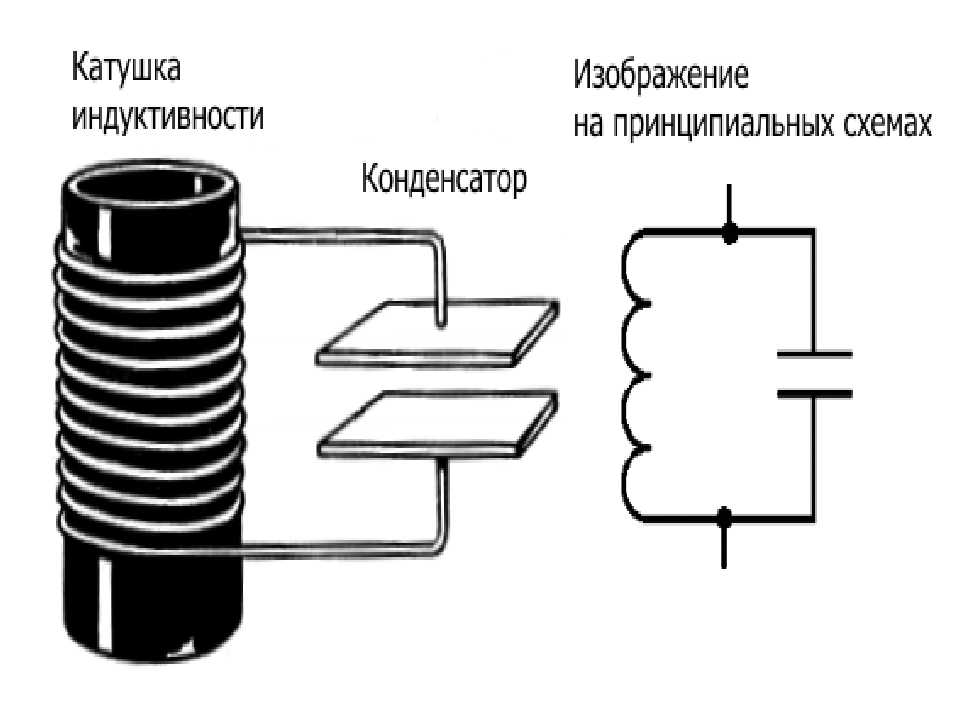 Опорный узел (земля) является отрицательным выводом источника напряжения. Напряжение на катушке индуктивности равно $v_\text L$, а напряжение на ключе равно $v_\text{pb}$.
Опорный узел (земля) является отрицательным выводом источника напряжения. Напряжение на катушке индуктивности равно $v_\text L$, а напряжение на ключе равно $v_\text{pb}$.
Нажимаем кнопку в точке $t = 0$, чтобы замкнуть цепь.
Определим ток $i$ через катушку индуктивности. Мы внимательно смотрим на каждый маленький момент в жизни автодрома. Это может показаться очень подробным — это то, что нужно, чтобы полностью понять, что происходит.
До нажатия переключателя
Перед нажатием переключателя цепь разомкнута. Мы знаем, что ток равен нулю,
$i(t < 0) = 0$
Ток постоянен, что означает, что скорость изменения тока также равна нулю,
$di/dt = 0$
Найдем напряжение на индукторе с помощью производной формы уравнения индуктора $i$-$v$,
$v_\text L = \text L \,\dfrac{ di}{dt}$
$v_\text L = \text L \cdot 0 = 0\,\text V$
На катушке индуктивности $0$ вольт. Это означает, что на клеммах разомкнутого переключателя должно быть $3$ вольт,
$v_{\text{PB}} = 3\,\text V$
Нажимаем переключатель
Нажимаем кнопочный переключатель в точке $t =0$,
9{\,t} v(x)\,dx + i(0)$ Ток катушки индуктивности является функцией переменной $t$, где $t$ — общее время удержания переключателя нажатым.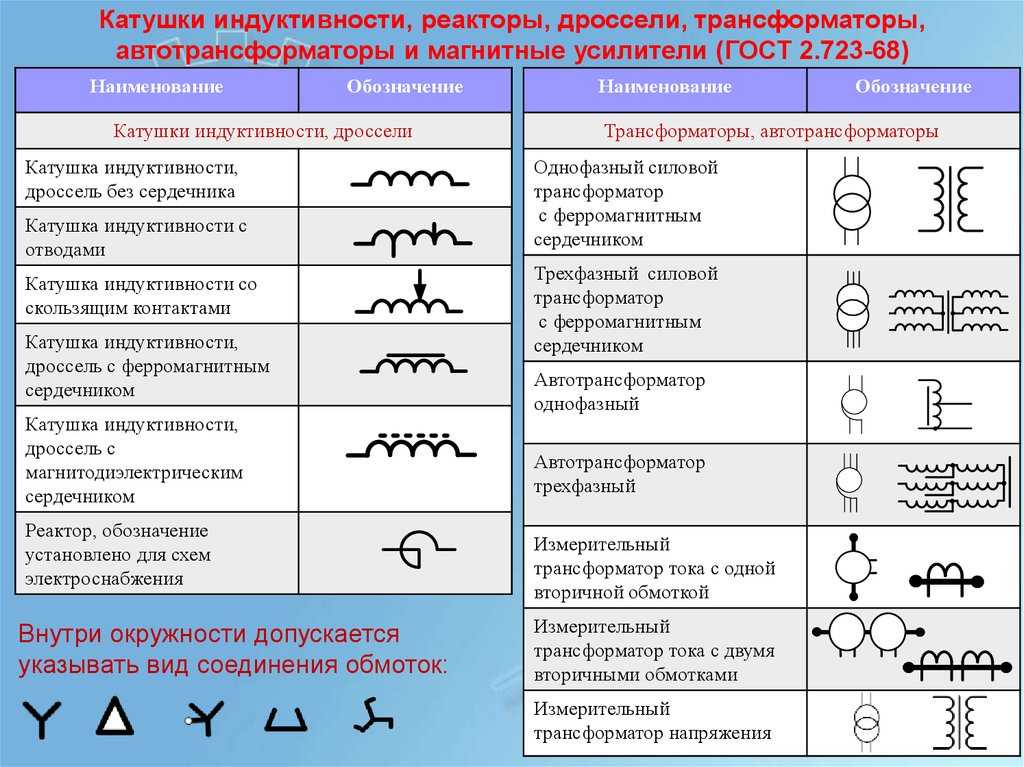 Обратите внимание, что $t$ появляется как верхний предел определенного интеграла.
Обратите внимание, что $t$ появляется как верхний предел определенного интеграла.
Этот интеграл обычно записывается в виде $\displaystyle \int v(t)\,dt$. Однако я хочу использовать $t$ как общее время удержания переключателя. Переменная $x$ играет роль мгновенного времени внутри интеграла. $x$ называется
Если это обозначение вызывает недоумение, обратитесь к тому, как это было сделано для импульса напряжения на конденсаторе.
Давайте посмотрим на момент замыкания переключателя. Существующий ток в индукторе равен $i(0) = 0$, и кнопка удерживалась нажатой в течение $t = 0$ времени.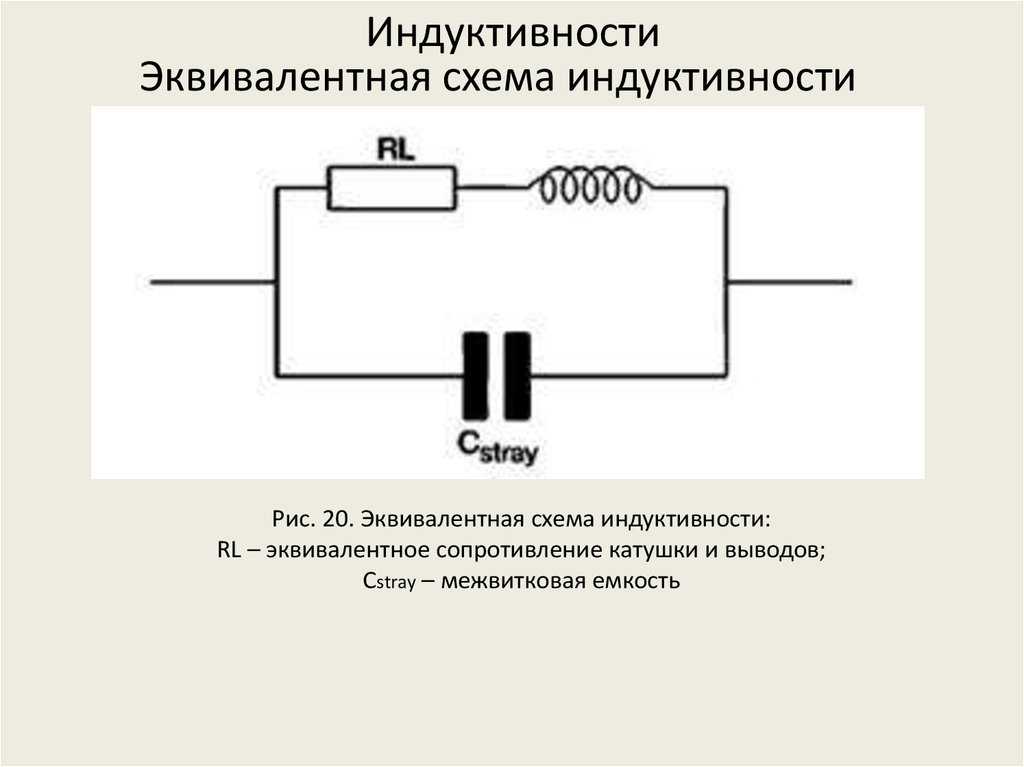
$\displaystyle i(t) = \dfrac{3\text V}{10\,\text{mH}}\,\, [ \,t — 0\,]$
$i(t) = \dfrac{3\text V}{10\,\text{mH}}\,\,t$
Это уравнение линии, когда переключатель нажат. Наклон линии:
$\dfrac{3\,\text V}{0,010\,\text H} = 300\,\text{ампер/сек}$
Пока переключатель удерживается нажатым ток в катушке индуктивности увеличивается на $300$ ампер каждую секунду. Этот ток исходит от идеального источника напряжения.
По мере увеличения тока энергия накапливается в магнитном поле индуктора. (Энергия не рассеивается в виде тепла, как это происходит с резистором.)
Вот имитационная модель, которая делает то же самое. Щелкните TRAN , чтобы выполнить анализ переходных процессов. Кнопочный переключатель моделируется как часть источника напряжения. Источник переходит от $0$ к $3\,\text V$ при $t = 0$.
В качестве конкретного примера,
Найдите ток через $t=0,002$ секунд $(2\,\text{мс})$ после нажатия переключателя.
Используйте уравнение, которое мы вывели для $i(t)$.
$i(t) = 300\,t$
Ток увеличится до $i(0,002) = 300\cdot 0,002 = 0,6\,\text{ампер} = 600 \,\text{мА}$.
В имитационной модели вернитесь назад и измените время перехода с $3$ секунд на $0,002$ секунд и выполните еще одно моделирование TRAN .
Теперь мы знаем, что происходит при нажатии на переключатель. Мы, вероятно, должны отпустить его в какой-то момент.
Отпустить переключатель
Убираем палец с кнопки $t=2\,\text{ms}$. Ток достиг $600\,\text{мА}$. Что происходит с напряжением на катушке индуктивности? Используйте производную форму уравнения индуктора,
$v_\text L = \text L\,\dfrac{di}{dt}$
Когда мы отпускаем кнопку, контакты переключателя физически разъединяются, и мы ожидаем, что ток мгновенно измениться с $600 \,\text{мА}$ на $0\,\text{мА}$ за время $0$. Что об этом говорит уравнение индуктора $i$-$v$?
$di = -600\,\text{мА}$ и $dt = 0$.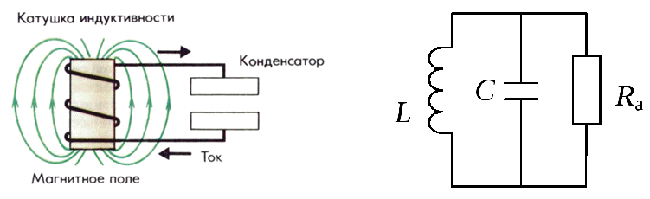
$v_\text L = \text L\,\dfrac{-600\,\text{mA}}{0}= -\infty !$
Уравнение индуктора предсказывает, что $v_\text L$ будет бесконечно ! Это может случиться?
В идеальном математическом мире да — просто запишите бесконечность в качестве ответа. В реальном мире нет, не может. Мгновенное изменение тока в катушке индуктивности требует бесконечного напряжения, которое недоступно в реальной жизни. Катушки индуктивности в реальном мире делают что-то другое.
Этот отказ мгновенно изменяться происходит из-за магнитной энергии, хранящейся в поле, окружающем индуктор. Это приводит нас к основному свойству индукторов,
Ток в катушке индуктивности не изменяется (не будет) мгновенно.
индуктивность аналогична массе Индуктивность в электрической системе аналогична массе или инерции в механической системе. Масса автомобиля имеет тенденцию сопротивляться изменению скорости. Автомобиль не может остановиться или завестись за время $0$. Катушка индуктивности представляет собой электрическую версию первого закона движения Ньютона (также называемого законом инерции): движущееся тело имеет тенденцию оставаться в движении.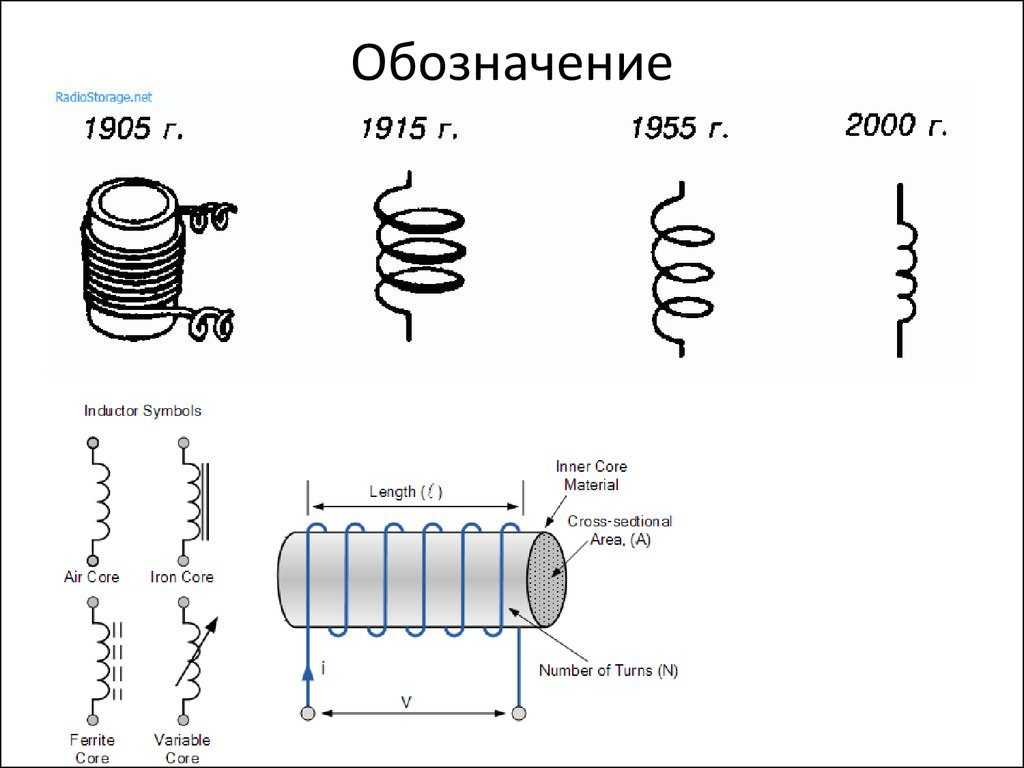
У нас в руках головоломка. Мы размыкали ключ, когда в катушке индуктивности протекал ток. Когда ключ размыкается, что происходит с током индуктора?
Что происходит в идеальной цепи?
Какой беспорядок. В идеальных моделях у нас есть все необходимые ток и напряжение. Но в этой ситуации что-то ломает идеальные модели. Мы создали невозможную борьбу: переключатель говорит, что ток должен быть равен нулю, а индуктор говорит, что ток должен быть таким, каким он был до того, как переключатель разомкнулся. Ноль и не ноль одновременно? Хм? Не разрешима. Мы достигли пределов наших идеальных моделей. Все это происходит из-за операции деления на ноль. Моя голова болит.
Что происходит в реальной цепи?
Когда переключатель размыкается при $t=2\,\text{мс}$, мы ожидаем, что ток изменится с $600\,\text{мА}$ до $0\,\text{мА}$ за время, равное $0$ . Не будем жадничать. Допустим, коммутатору нужно $1\,\mu\text{sec}$, чтобы перейти из закрытого состояния в открытое. {-6}}$
{-6}}$
$v_\text L = -6{,}000 \,\text{вольт} \,!$
Напряжение катушки индуктивности по-прежнему велико. Клемма $+$ катушки индуктивности зафиксирована на уровне $3$ вольт над землей. Знак $-$ на $v_{\text L}$ означает, что отрицательный вывод катушки индуктивности на 6000$ вольт на 90 110 больше, чем положительный вывод на 90 111.
Получается, что $v_{\text{pb}} = 3 + 6000 = +6003\,\text{вольт}$.
Это называется отдачей индуктора или обратного хода . Это действительно происходит? Да, это так.
На самом деле происходит следующее: когда переключатель размыкается, искровые разряды пересекают воздушный зазор между контактами переключателя. Энергия магнитного поля высвобождается в виде короткой яркой вспышки света.
На самом деле, если вы хотите создать искру, это один из лучших способов сделать это. Так работает свеча зажигания в автомобиле. Это также происходит каждый раз, когда вы щелкаете механическим выключателем света в своем доме.
Хотя воздух обычно является очень хорошим изолятором, высокое напряжение может привести к разрушению воздуха. Когда электрическое поле (вольт на метр) составляет около $3000$ вольт при воздушном зазоре в $1$ миллиметр, воздух становится частично проводящим. Если напряжение выше, воздух полностью разрушается и становится проводящим. Электрическое поле настолько сильное, что отрывает электроны от молекул кислорода и азота, а электрическая искра или дуга перекрывает этот промежуток.
Википедия Электрическая поломка
В реальной версии нашей схемы искра начинается при напряжении около 3000$ вольт. Искра длится до тех пор, пока ток индуктора не упадет до нуля. Если у вас есть физически прочный переключатель, он может выдержать физическое насилие искры. Но если переключатель хрупкий (например, транзистор, используемый в качестве переключателя), есть большая вероятность, что высокое напряжение разрушит его.
Рассмотрение парадокса: как может быть ток катушки индуктивности одновременно с открытым ключом? В реальной жизни этот парадокс разрешается следующим образом: катушка индуктивности выигрывает, а открытый переключатель проигрывает. Индуктор заставляет ток течь через искру. Открытый переключатель фактически не открыт во время искры.
Индуктор заставляет ток течь через искру. Открытый переключатель фактически не открыт во время искры.
Стоит ли бояться индукторов? Вам не нужно бояться индукторов, но вы должны относиться к ним с уважением. Катушки индуктивности — это накопители энергии, такие же, как конденсаторы и аккумуляторы. Если вы выпустите всю энергию сразу, может быть бум!
Дайте индуктору место для протекания
Странно думать, что разомкнутая цепь может вызвать проблемы, но когда задействованы индукторы, это может случиться. Катушка индуктивности и переключатель представляют собой общую схему, и об этом нужно беспокоиться. В этом разделе описывается, как спроектировать высоковольтный всплеск катушки индуктивности.
Хорошо, если вы знакомы с принципом работы диода. Диод проводит ток в одном направлении, но не в противоположном.
Как избежать разрушения нашей схемы из-за высокого напряжения, создаваемого отдачей индуктора? Когда мы разрабатываем схему с переключаемой катушкой индуктивности, мы думаем наперед и следим за тем, чтобы ток всегда имел место для протекания.
Если мы поместим диод параллельно катушке индуктивности, он аккуратно уберет всплеск напряжения.
Обратите внимание на направление диода, его стрелка прямого тока указывает вверх. Ток будет течь только до через диод.
Когда ключ замкнут, диод смещен в обратном направлении и не проводит ток.
Когда переключатель размыкается, диод смещается в прямом направлении и обеспечивает путь для тока дросселя.
Давайте рассмотрим это шаг за шагом. Начните с разомкнутого переключателя. Затем нажмите его. Тогда отпусти.
Пуск с разомкнутым переключателем
Когда переключатель находится в исходном разомкнутом положении, ток равен $0$, а на катушке индуктивности (и диоде) $0$ вольт. $\goldD{v_{\text{pb}}}$ равно $3\,\text V$.
Замкните переключатель
Когда переключатель замкнут, ток течет через катушку индуктивности и переключатель, как и раньше, когда у нас не было диода,
Когда переключатель замкнут, каково напряжение на диод?
$v_{\text{L}} = \,$ ______ $\,\text V$
показать ответ Напряжение на диоде такое же, как и на катушке индуктивности, $v_{\text L} = 3\ ,\текст V$.
Диод смещен в прямом или обратном направлении?
показать ответДиод смещен в обратном направлении, поскольку катод находится под более высоким напряжением, чем анод.
Каков приблизительный ток диода?
$i_{\text{диод}}\приблизительно$ ______$\,\text A$
показать ответКогда диод смещен в обратном направлении, его ток очень близок к $0$. Поскольку в диоде нет тока, его как будто и нет.
Отпустите переключатель
Теперь мы отпускаем кнопочный переключатель, и контакты размыкаются. Раньше, когда не было диода, размыкание ключа вызывало скачок $v_{\text{pb}}$ до огромного положительного напряжения. Теперь — с диодом — происходит нечто лучшее.
Коммутатор все еще пытается создать большую $di/dt$ при размыкании. Так же, как когда диода не было, $v_{\text{pb}}$ начинается с $0\,\text V$ и начинает увеличиваться до большого положительного значения. Но на этот раз
Что произойдет, когда $v_{\text{pb}}$ поднимется с $0$ до $3,7$ вольт?
(Выберите все подходящие варианты.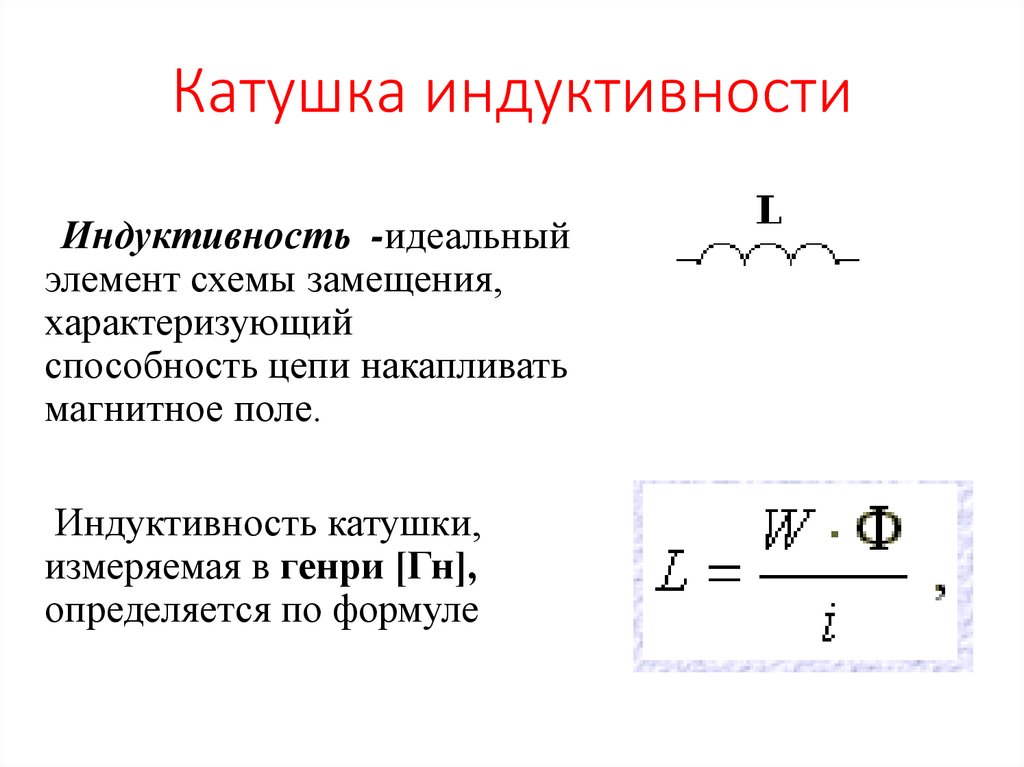 )
)
- Диод смещается в прямом направлении.
- Диод начинает работать.
Оба. Верхняя часть диода зафиксирована на $3\,\text V$. Когда нижняя часть диода поднимается до $3,7\,\text V$, он смещается в прямом направлении — анод на $0,7\text V$ выше катода.
Это один из тех странных случаев, когда напряжение ниже на странице выше, чем напряжение вверху страницы.
Когда напряжение на аноде становится равным напряжению питания — $3$ вольта — плюс дополнительные $\sim0,7$ вольта , диод смещается в прямом направлении и начинает проводить!
Диод с прямым смещением обеспечивает путь для тока катушки индуктивности. Когда диод включается, ток дросселя поворачивается вправо и течет вверх через диод. Когда он проходит через диод, ток поворачивает влево и течет обратно через катушку индуктивности, двигаясь по кругу.
Диод обеспечивает путь для тока катушки индуктивности при размыкании ключа.
Что происходит с напряжением? Напряжение на диоде «зажимает» $v_{\text{pb}}$, не позволяя ему стать намного выше напряжения питания плюс $0,7$ вольт. У $v_{\text{pb}}$ никогда не будет шанса подняться до опасного высокого уровня. Это зажимное действие обеспечивает путь для тока и предотвращает опасную дугу. Все счастливы.
Ток проходит через диод и катушку индуктивности до тех пор, пока реальное сопротивление катушки индуктивности и диода не рассеет запасенную энергию катушки индуктивности в виде тепла. Диод предотвращает значительный индуктивный скачок напряжения и защищает окружающие компоненты.
Имитационные модели
Этот эффект отдачи действительно имеет место. Потратьте некоторое время, чтобы изучить эту имитационную модель с катушкой индуктивности и диодом. МОП-транзистор N-типа QPB и источник напряжения VPB играют роль кнопочного переключателя.
Попробуйте эти эксперименты,
- Нажмите на TRAN , чтобы увидеть, как работает переключатель.

- Обратите внимание на схему включения/выключения источника напряжения VPB. Это управляет переключателем NMOS.
Когда VPB низкий, переключатель разомкнут. Когда VPB высокий, переключатель замкнут.
- Обратите внимание на схему включения/выключения источника напряжения VPB. Это управляет переключателем NMOS.
- Добавьте пробник напряжения к узлу $v_{\text{pb}}$. Установите его цвет на оранжевый. Запустите TRAN еще раз.
- $v_\text{pb}$ — напряжение на дне диода.
- Удалите голубой зонд на VPB, чтобы получить более четкое представление о $v_{\text{pb}}$.
- Что такое $v_\text{pb}$, когда переключатель замкнут?
- Какое напряжение достигает $v_\text{pb}$ при размыкании переключателя?
- Обратите внимание, что напряжение какое-то время остается неизменным, а затем возвращается к $3\,\text V$. В это время ток циркулирует через индуктор и диод, поскольку энергия индуктора иссякает.
- Добавьте датчик тока (стрелка чуть ниже датчика напряжения в корзине инструментов).
 Поверните щуп так, чтобы он был направлен вверх, и вставьте его под диод. Выполнить TRAN еще раз, чтобы увидеть текущую форму сигнала. Вот имитационная модель со всеми тремя датчиками.
Поверните щуп так, чтобы он был направлен вверх, и вставьте его под диод. Выполнить TRAN еще раз, чтобы увидеть текущую форму сигнала. Вот имитационная модель со всеми тремя датчиками. - Имитационная модель с тремя датчиками включает резистор, включенный последовательно с катушкой индуктивности. Поэкспериментируйте с его значением и посмотрите, как оно изменит время, необходимое току, чтобы израсходовать всю накопленную энергию.
- Вот имитационная модель без диода. Запустите TRAN и удивитесь пиковому напряжению, генерируемому катушкой индуктивности. Это сложная схема для симулятора — запуск на ноутбуке может занять порядочную часть минуты.
Резюме
Ток в катушке индуктивности не изменяется мгновенно.
Будьте осторожны при включении катушек индуктивности. Внезапное изменение тока, например размыкание выключателя, означает, что производная тока $di/dt$ может стать очень большой. Уравнение катушки индуктивности говорит нам о том, что на катушке индуктивности может возникать большое обратное напряжение.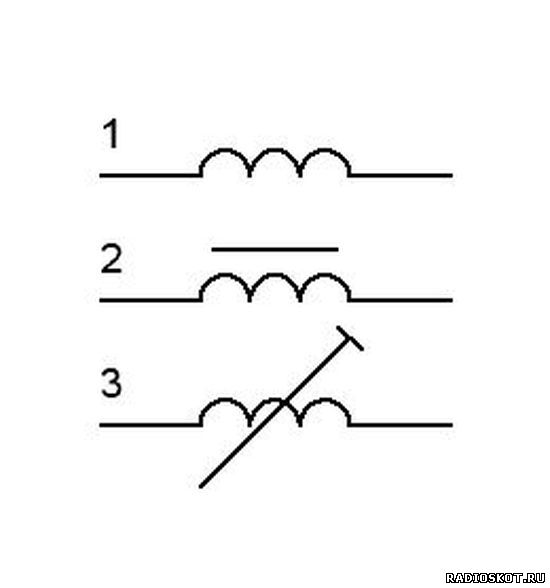



 Поверните щуп так, чтобы он был направлен вверх, и вставьте его под диод. Выполнить TRAN еще раз, чтобы увидеть текущую форму сигнала. Вот имитационная модель со всеми тремя датчиками.
Поверните щуп так, чтобы он был направлен вверх, и вставьте его под диод. Выполнить TRAN еще раз, чтобы увидеть текущую форму сигнала. Вот имитационная модель со всеми тремя датчиками.