Электротехника. Методы расчёта электрических цепей. (лекция 4)
Похожие презентации:
Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов
Газовая хроматография
Геофизические исследования скважин
Искусственные алмазы
Трансформаторы тока и напряжения
Транзисторы
Воздушные и кабельные линии электропередач
Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса
Магнитные аномалии
Нанотехнологии
1. Конспект лекций по электротехнике Подготовлен: Степановым К.С., Беловой Л.В., Кралиным А.А., Панковой Н.Г. Кафедра теоретической и общей элект
Конспект лекций поэлектротехнике
Подготовлен:
Степановым К.С., Беловой Л.В.,
Кралиным А.А., Панковой Н.Г.
Кафедра теоретической и общей
электротехники.
Лекция 4
2. Методы расчёта электрических цепей
• 1. По закону Ома.
По закону Ома.• 2. По методу суперпозиции.
• 3. По уравнениям Кирхгофа.
• 4. По методу контурных токов.
• 5. По методу узловых потенциалов.
• 6. По методу эквивалентного
двухполюсника.
• 7. По методу компенсации.
• 8. Топологический метод расчёта.
4. Расчёт простых цепей
• Простая цепь – это цепь,содержащая один и только один
источник энергии.
• Простые цепи рассчитываются при
помощи метода свертывания и
развертывания. Расчёт идёт по
закону Ома.
5. Пусть требуется определить все токи в такой цепи.
1R4
R6
R2
R7
R1
R5
R3
E
2
R8
6. Для этого будем упрощать схему в следующей последовательности.
1R4
R678
R2
R1
E
R5
R3
2
R678=R6(R7+R8)/(R6+R7+R8)
7. R(4-8)= R678(R4+R5)/(R4+R5+R876)
1R2
R4-8
R1
R3
E
2
R(4-8)= R678(R4+R5)/(R4+R5+R876)
1
R2-8
R1
E
2
R2-8= R(4-8)(R2+R3)/(R2+R3+R(4-8))
E
Rэкв
Rэкв=R1+R2-8
• Тогда токи в ветвях определяются по
следующим формулам:
• I1=E/Rэкв ,
U12=I1 R12
• I2=U12/(R2+R3),
• I3=U12/(R4+R5),
• I5=U12/(R7+R8),
I4=U12/R6
11.
 Метод наложения или суперпозиции
Метод наложения или суперпозиции12. Метод наложения или суперпозиции
• Применяется, когда цепь содержитнесколько источников питания.
• Разветвленная электрическая цепь
с несколькими источниками
питания и все процессы
происходящие в этой цепи можно
рассматривать как совокупность
нескольких цепей в каждой из
которых содержится один и только
один источник питания.
13. Метод наложения или суперпозиции
• При составлении цепей учитываетсяправило:
• Если есть идеальный ЭДС (E) с Rвн=0,
то ЭДС заменяется голым проводом.
• Если есть источник тока (J) с Rвн= ,
то он заменяется разрывом цепи.
• Число составных частей ровно числу
источников питания.
• Тогда, общий ток определится как
сумма токов в вышеприведенных
цепях.
14. Пусть требуется определить токи в такой цепи
R2J5
R3
R5
R1
R4
R6
E1
E4
15. Преобразуем схему к виду 1 и определим токи в ветвях I’1,I’2,I’3,I’4,I’5.
 R2
R2R3
R5
R1
R4
R6
E1
16. Преобразуем схему к виду 2 и определим токи в ветвях I»1,I»2,I»3,I»4,I»5.
R2R3
R5
R1
R4
R6
E4
17. Преобразуем схему к виду 3 и определим токи в ветвях I»’1,I»’2,I»’3,I»’4,I»’5.
R2J5
R3
R5
R1
R4
R6
Тогда общие токи в ветвях определятся
как суммы вышерасчитанных частных
токов.
• I1 = I’1+I»1+I»’1;
• I2 = I’2+I»2+I»’2;
• I3 = I’3+I»3+I»’3;
• I4 = I’4+I»4+I»’4;
• I5 = I’5+I»5+I»’5.
19. Расчёт разветвлённых цепей с помощью законов Кирхгофа.
20. Алгоритм расчёта
• 1. Упрощение элементарныхцепей.
• 2. Произвольный выбор
направления и обозначение
токов в ветвях.
• 3. Выбор и расставление
направления обхода
независимых контуров.
(Независимый контур – такой, который
содержит хотя бы одну ветвь,
которая не рассмотрена в других
контурах.)
21. Алгоритм расчёта
• 4. Запись уравнений по первому
Запись уравнений по первомузакону Кирхгофа. (Число этих урав-
нений на 1 меньше числа узлов. Использовать
все Y уравнений невозможно, т.к. одно из них
обязательно будет зависимым. Это связано с
тем, что токи ветвей войдут в уравнения,
составленные для всех Y узлов, дважды,
причем с разными знаками, т.к. один и тот же
ток направлен от одного узла к другому. При
сложении всех уравнений левая и правая
части будут равны нулю, а это означает, что
одно из уравнений можно получить
суммированием (Y-1) уравнений и заменой
знаков всех токов на противоположные.
Таким образом Y-е уравнение всегда будет
зависимым).
22. Алгоритм расчёта
• 5. Запись уравнений по 2 законуКирхгофа для независимых
контуров.
(Для определения неизвестных токов в
ветвях необходимо составить
уравнения Кирхгофа, количество
которых должно быть равно
количеству неизвестных токов).
• 6. Решение системы уравнений
относительно токов.

23. Пример. Определить токи в ветвях схемы по законам Кирхгофа.
R2J5
R3
R5
R1
R4
R6
E1
E4
24. 1. Упрощаем элементарные цепи. Для этого преобразуем схему.
R2J5
R3
R5
R1
R4
R6
E1
E4
25. В этой схеме источник тока J5 заменён на источник эквивалентной ЭДС E5экв (см.лек.3)
1I2
R2
2
E5экв
к
кон
R3
R5
R1
I3
I5
кон
I4
R4
R6
E4
E1
I1
3
26. Составим уравнения по первому и второму законам Кирхгофа
• Уравнения по первому законуКирхгофа для независимых узлов:
1) I1 – I2 – I5 = 0
2) I2 – I3 – I4 = 0
Уравнения по второму закону
Кирхгофа для независимых
контуров:
3) I1R1 + I5(R5+R6) = E1 + E5экв
4) I2R2 + I3R3 — I5(R5+R6) = -E5экв
5) -I3R3 -I4R4 = -E4
27. Запишем матрицу коэффициентов и столбец свободных членов
|1 –1 0 0 –1|
|0
|0 1 –1 –1 0
|
|0
|R1 0 0 0 (R5+R6)| =
|E1+E5экв|
|0 R2 R3 0 (R5+R6)| | -E5экв
|0 0 R3 R4 0
| | -E4
Решая эту систему, определим токи
во всех ветвях.

|
|
|
|
28. Благодарю за внимание
English Русский Правила
Расчёт электрических цепей методом структурных чисел для детей и взрослых / Хабр
В нулевые годы, когда, скорее в качестве отдушины, я подрабатывал в Альма-матер, ведя лабораторные работы по радиотехнике, мне попалась на глаза эта книжечка:
С.Беллерт, Г. Возняцки
«Анализ и синтез электрических цепей методом структурных чисел».
Перевод с польского
Под редакцией проф. П.А. Ионкина
ИЗДАТЕЛЬСТВО «МИР»
Москва 1972
После беглого просмотра я испытал странное ощущение, которое, наверное, правильно было бы назвать когнитивным диссонансом. В этой книге предлагался эффективный и очень простой в применении (но не с точки зрения теории) метод расчета электрических цепей, но при этом я никогда даже не слышал об этом подходе. Не могу назвать себя профессионалом, радиотехника была скорее хобби, но я неплохо знал всё, что преподавалось у нас в институте и всё же.
Чем больше я вникал в теорию, тем больше очаровывался. Получив эстетическое удовлетворение, я благополучно забыл об этом небольшом открытии, к тому же через некоторое время я переехал в Европу, и моя преподавательская деятельность, да и вообще любая деятельность, связанная с радиотехникой, закончилась.
Но вот, недавно, приехав погостить в Россию, разбирая старые книжки, я опять наткнулся на этот забытый мною (и возможно миром) труд. Покопавшись в интернете, я обнаружил некоторые статьи на эту тему, но, по-прежнему, всё выглядит так, что этот метод мало кому знаком.
И я подумал, что может быть это будет интересно читателям Хабра.
О простоте
Кажется, что этому алгоритму можно научить даже ребенка, что я и попытался проверить.
Думаю, эксперимент удался. За 10 минут я сумел научить рассчитывать электрические цепи моего сына. На картинке вы видите его расчет передаточной функции по напряжению для двухкаскадного делителя. Поверьте моему опыту преподавателя радиотехники — не каждый студент с этим справится.
Ах, да. Сыну 7 лет!
Черными чернилами я составил «карту», которая должна помочь сыну в расчетах.
Синие чернила — это его расчёт.
Внизу вы видите правильный ответ — коэффициент усиления по напряжению.
Умея получать правильный результат, он, конечно же, абсолютно ничего не понимает — для него это просто картинка. Но, если я нарисую ему другую схему того же уровня сложности, он найдет правильный ответ.
Пояснения к записям:
Я нарисовал граф, соответствующий данной цепи. Ребра графа пронумерованы так же, как и импедансы.
Далее, мне пришлось немного рассказать сыну о графах — я показал, что такое вершины и что такое ребра графа. Потом объяснил ему, что такое элементарные контуры (пустые «кружочки») и обратил внимание на грани, из которых они состоят.
Предварительная стадия на этом была закончена, и мы перешли к расчетам.
Комментарий Далее в статье мы будем называть это структурным числом графа, и это будет главным объектом, вокруг которого всё и крутится. Но нет смысла пытаться объяснить это ребенку — для того, чтобы найти ответ, знание элементов теории структурных чисел не является обязательным.
Но нет смысла пытаться объяснить это ребенку — для того, чтобы найти ответ, знание элементов теории структурных чисел не является обязательным.
В общем случае нужно удалять не только столбцы, в которых есть одинаковые элементы, но и попарно убирать столбцы с одинаковым набором элементов (порядок следование элементов в столбцах и порядок следования самих столбцов неважны).
Затем (это написано мною на листке) я попросил найти все столбцы с единичкой («входное» ребро) и удалить единичку из этих столбцов. Понятно, что столбцы с единичкой это
Отбросив единичку, получаем , что и написано в виде
То же самое нужно сделать для двойки («выходное» ребро):
В теории структурных чисел эта функция называется алгебраической производной по элементу.
КомментарийЭта функция от двух структурных чисел и называется конъюнкцией. Мы будем обозначать её как . В данном случае имеем
В принципе на этом все вычисления закончены.
 Осталось только написать ответ.
Осталось только написать ответ.Я провел черту (деление), и попросил сына над чертой написать (независимо от наших расчетов, выходное сопротивление присутствует всегда в формуле передаточной функции по напряжению) и с индексом, который он получил в предыдущем пункте (конъюнкция) — вы видите мою чёрную стрелочку на картинке, указывающую на этот индекс.
Под чертой интересней. Для каждого столбца структурного числа нужно взять числа в этом столбце и использовать их как индексы для в произведении и сложить все полученные таким образом «столбцевые» произведения. Это тот случай, когда легче показать, чем объяснить. Так, в нашем случае для столбцов, которые мы получили
это будет .
Это отношение и есть искомый коэффициент передачи.
Функция в знаменателе — это детерминант структурного числа по и записывается как . Точное определение будет дано ниже в статье.
Комментарий 2В общем виде для данного вида графов (входное и выходное ребра имеют общую вершину и сонаправлены) коэффициент передачи напряжения может быть выражен следующей формулой
Более общая формула, которая подходит для всех пассивных четырёхполюсников
Функция совпадения будет объяснена позже в этой статье
Теперь давайте по-взрослому.
Основные понятия теории структурных чисел
Мы ограничимся достаточно узкой прикладной областью данной математики — для нашей статьи нам будет интересен только расчет пассивных электрических цепей с одним источником (пассивный четырёхполюсник).
Нас будет интересовать лишь прикладной аспект. Мы не будем ничего доказывать. Также некоторые понятия будут представлены упрощенно, главная цель — научиться получать результат. Нас будет интересовать только вопрос «как», и мы даже не будем пытаться ответить на вопрос «почему». Тем, кому станет интересен математический аспект — обращайтесь к первоисточнику.
Структурное число
Структурное число это неупорядоченный набор столбцов элементов со следующими свойствами:
в общем случае, столбцы могут содержать разное количество элементов, но в рамках нашей задачи структурное число всегда будет иметь вид прямоугольной матрицы, то есть все столбцы в структурном числе будут иметь равную длину
каждый столбец представляет собой неупорядоченный (порядок не важен) набор натуральных чисел
в столбце нет повторяющихся элементов.
 Если в процессе алгебраических операций появляются столбцы с одинаковыми элементами, то эти столбцы удаляются.
Если в процессе алгебраических операций появляются столбцы с одинаковыми элементами, то эти столбцы удаляются.в структурном числе нет повторяющихся столбцов. Если в процессе алгебраических операций появляются такие столбцы, то они попарно удаляются. Это значит, что четное количество одинаковых столбцов аннигилируют, а при нечетном количестве один столбец остаётся.
Дополнительное структурное число
Найдем множество всех элементов в структурном числе. Возьмем произвольный столбец этого числа и составим столбец из элементов, которых не хватает в этом столбце до множества всех элементов. Структурное число, составленное из таких столбцов называется дополнительным.
ПримерРассмотрим структурное число
Множество всех элементов:
Тогда дополнительное число:
Сумма структурных чисел
Комментарий:
Мы нигде не будем использовать сумму структурных чисел в данной статье.
Суммой двух структурных чисел A и B называется структурное число, содержащее все столбцы чисел A и B, за исключением идентичных столбцов.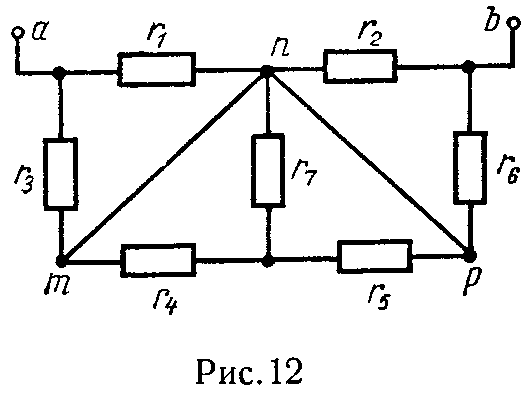
Произведение структурных чисел
Комментарий:
В данной статье мы будем иметь дело только с произведением структурных чисел состоящих из строк (все столбцы имеют лишь один элемент), например,
Произведением двух структурных чисел A и B называется структурное число, столбцы которого представляют собой суммы (согласно понятиям теории множеств) всех возможных комбинаций столбцов A и B, за исключением наибольшего четного числа идентичных столбцов и таких столбцов, в которых какой-либо элемент повторяется.
ПримерСтолбцы 2,3,4,6,7,9 удаляются потому что содержат повторяющиеся элементы.
Столбцы 1 и 5 удаляются в паре потому, что содержат идентичный набор элементов (важно помнить, что если бы одинаковых столбцов было бы нечетное количество, то один столбец остался бы).
Поэтому остается только столбец 8.
Алгебраическая производная
Алгебраическая производная структурного числа по элементу называется структурное число , состоящее только из столбцов , содержащих элементы с исключением этих элементов.
Возьмём структурное число
Алгебраическая обратная производная
Обратная производная структурного числа по элементу называется структурное число состоящее только из столбцов , не содержащих элементы .
ПримерКонъюнкция
Конъюнкцией двух структурных чисел и называется структурное число , состоящее из совпадающих столбцов и . Мы будет обозначать ее как .
ПримерДетерминантная фунция
Давайте возьмем -й столбец структурного числа . Возьмем все индексы в этом столбце и найдем произведение импедансов с этими индексами. Далее, если сложить такие произведения для всех столбцов, то это и будет детерминант. Детерминант от пустого (нет столбцов) структурного числа равен 1.
ПримерСтруктурные числа и электрические схемы
Мы подбираемся к сути, которая заключается в том, что каждому пассивному четырёхполюснику может быть поставлено в соответствие структурное число, и с помощью нововведенной алгебры может быть произведен ее расчет.
Сначала построим граф, соответствующий электрической цепи.
Построение графа
Проще всего это понять на примерах. Начнем с элементарных схем.
Схемы делителя:
Первая схема — элементарный делитель. При этом мы считаем источник напряжения идеальным (сопротивление = 0), и вольтметр (или следующий каскад) имеет входное сопротивление равное бесконечности.
Вторая схема относится к случаю, когда вы подаете напряжение E, на сопротивление , но источник напряжения не идеальный (сопротивление Z1), и вольтметр (или следующий каскад) имеет входное сопротивление Z2.
Третья схема — уже знакомая нам схема двухкаскадного делителя.
То есть, чтобы получить граф, мы просто перерисовываем схему с импедансами со следующими изменениями:
мы «опускаем» идеальный источник напряжения, что выглядит разумно, т.к. его выходное сопротивления равно 0 (его сопротивление мы вынесли в )
мы заменяем импедансы на их индексы
у нас только 2 направленных ребра: входное (мы всегда будем обозначать его индексом 1) и выходное (индекс 2).
 Стрелками обозначено направление тока (которое мы приняли за положительное)
Стрелками обозначено направление тока (которое мы приняли за положительное)
Попробуем применить этот подход для более сложного случая.
Мост Уитстона:
Нахождение структурного числа графа
Теперь давайте построим структурные числа для каждого случая.
Есть два подхода: через произведение структурных чисел, соответствующих вершинам графа, и через произведение структурных чисел, соответствующих элементарным контурам.
Рассмотрим первый метод — через произведение «вершинных» структурных чисел
Метод перемножения «вершинных» структурных чисел
Предположим, что в нашем графе вершин. «Отбрасываем» любую вершину и берем оставшиеся вершины.
Для каждой вершины найдем «вершинное» структурное число. Для этого выписываем все ребра графа, опирающиеся на эту вершину. Предположим, что для i-ой вершины мы имеем ребер. Тогда такое «вершинное» структурное число будет состоять из столбцов, состоящих из одного элемента, равного индексу ребра.
 То есть, не строго говоря, это строка, состоящая из индексов ребер (для данной вершины).
То есть, не строго говоря, это строка, состоящая из индексов ребер (для данной вершины).Перемножаем эти вершинных структурных числа. Получаем некое структурное число .
Находим дополнительное к структурное число . Это и будет наше искомое структурное число.
Для первой схемы (простой делитель) получим:
В графе две вершины, значит, для нашего расчета мы будем использовать одну.
«Вершинное» структурное число (для любой из двух вершин): .
У нас всего одно число, поэтому произведением является то же самое число.
У нас всего два элемента: , поэтому дополнительным элементом опять-таки является тоже самое число.
Итак, для первой схемы нашим структурным числом будет .
В графе две вершины, значит, для нашего расчета мы будем использовать одну.
«Вершинное» структурное число (для любой из двух вершин): .

У нас всего одно число, поэтому произведением является то же самое число.
У нас есть три элемента: , поэтому дополнительным структурным числом будет
В графе три вершины, значит, для нашего расчета мы будем использовать две.
Возьмем верхнюю и нижнюю вершины. Структурные числа для них: и .
Произведение этих двух структурных чисел даёт:
У нас есть 4 элемента: , поэтому дополнительным структурным числом будет
Это совпадает с результатом, который получил мой сын. Там мы использовали метод перемножения «контурных» структурных чисел, который рассматривается ниже.
Пример 4. Мост УитстонаМы видим 4 вершины. Отбросим нижнюю вершину.
Тогда для оставшихся трех вершин мы получим следующие «вершинные» структурные числа:
Перемножим эти 3 числа
Всевозможная комбинация столбцов будет выглядеть следующим образом:
Убираем все столбцы, содержащие одинаковые элементы и попарно равные столбцы.
 Получаем
Получаем
Теперь мы можем выписать структурное число, соответствующее данной схеме — это будет число , являющееся дополнением к
Метод перемножения «контурных» структурных чисел
Найдем наименьшее количество замкнутых контуров, покрывающее все ребра графа.
Для каждого такого контура составим «контурное» структурное число. Предположим, что для -го контура мы имеем рёбер. Тогда такое «контурное» структурное число будет состоять из столбцов, состоящих из одного элемента, равного индексу ребра. То есть, не строго говоря, это строка, состоящая из ребер (для данного контура).
Выполним произведение всех таких контурных чисел — получим искомое структурное число.
Опять-таки проще это понять на примерах.
Очевидно, что у нас только один контур.
Контурное структурное число для него: .

Т.к. это единственное структурное число, то оно и будет ответом, что, как и ожидалось, совпадает с результатом первого метода.
Таких контуров 2.
У нас есть возможность разных комбинаций, но возьмем следующие: , .
Найдем произведение этих двух чисел, что и будет искомым структурным числом:
И опять, конечно же, структурные числа полученные двумя разными методами совпадают.
Пример 3. Двухкаскадный делитель.Структурное число, соответсвующее двухкаскадному делителю, мы нашли в самом начале статьи. Оно равно
Пример 4. Мост УитстонаТаких контуров 3.
Возьмем, например, следующие:
.
Найдем искомое структурное число A через произведение этих трех чисел.
Берем все возможные комбинации столбцов:
Убираем все столбцы, содержащие одинаковые элементы и попарно равные столбцы. Получаем искомое структурное число:
Получаем искомое структурное число:
С учетом того, что порядки следования столбцов и элементов в самих столбцах неважны, легко видеть, что в обоих методах мы получили одинаковые результаты.
Расчет пассивной трёхточки (трёхполюсника)
Комментарий:
Не уверен, что термины «трёхточка» или «трёхполюсник» является общепринятыми, но дальнейшее поясняет, что я имею ввиду.
У нас всё готово для расчета пассивной трёхточки, которую можно представить в виде пассивного четырёхполюсника с общей землей на входе и выходе.
Например, схемы делителей, которые мы рассматривали выше — это трёхточки (в том смысле, в котором мы определили трёхточку).
Передаточные функции напряжения и тока в этой схеме это
а первичный, входной и выходной импедансы:
А теперь самое главное — все эти величины мы легко можем найти, если знаем структурное число A, соответствующее схеме.
Расчет схем трёхточек
Давайте начнем с простейших схем. Хотя, в этом случае данный метод не дает ощутимых преимуществ, но простейшие схемы, как предельный вариант, интересны для оценки адекватности метода.
Хотя, в этом случае данный метод не дает ощутимых преимуществ, но простейшие схемы, как предельный вариант, интересны для оценки адекватности метода.
Схема 1. Простой делитель
Вспомним наше структурное число:
Тогда, помня, что детерминант от пустого (нет столбцов) структурного числа равен 1, легко получить:
Схема 2. Напряжение на сопротивлении.
Что соответствует действительности (расчетам другими известными методами).
Схема 3. Двукаскадный делитель (который мы рассчитывали с сыном)
Рассматриваемые нами трёхточки покрывают довольно большой процент случаев, поэтому уже здесь можно было бы поставить точку.
Но всё же не всегда вход и выход схемы имеют общий контакт (например, мост Уитстона). Метод структурных чисел позволяет найти решение и для общего случая пассивного четырёхполюсника.
Расчет четырехполюсника
Трехполюсник рассмотренный выше является частным случаем четырехполюсника.
Разница лишь в том, что вход и выход в данном случае необязательно имеют общий контакт.
Формулы расчета для четырехполюсника
Как можно видеть, формулы для четырехполюсника такие же, как и для трехполюсника, за исключением коэффициентов передачи по напряжению и току. Здесь в числителе вместо
мы имеем
Это новая функция, которую проще объяснить на примере, и это будет рассмотрено ниже на примере моста Уитстона.
Понятно, что в случае трёхточки, которую мы рассматривали (с правильным выбором направления выходного ребра) мы имеем
Мост Уитстона
Структурное число
Давайте найдем некоторые важные для нашего анализа функции этого структурного числа.
Это рассмотрение позволит нам также ввести последнюю важную функцию — функция совпадения.
Детерминант
Легко видеть что детерминант этого числа это
Алгебраическая производная
Для обратных алгебраических производных соответственно имеем
Конъюнкция
Функция совпадения
Комментарий:
Это и есть та дополнительная функция, которой нам не хватало для расчет четырехполюсника.
Найдем функцию совпадения чисел и . Эта функция вычисляется через конъюнкцию, найденную выше:
где , равны или .
То есть эта функция похожа на детерминант конъюнкции, но со знаками «+» или «-» у каждого слагаемого (в детерминанте все слагаемые имеют знак «+»). Как найти эти коэффициенты? Чтобы найти знак у каждого слагаемого мы должны исключить из графа рёбра, определенные в этом слагаемом. При этом получится цикл, в котором «входное» и «выходное» ребра ориентированы согласно или встречно. В первом случае (согласно) — это даст нам «+», а во втором — «-«. Так, например, в нашем случае для мы должны исключить ребра 5 и 6 из нашего графа, а в случае — ребра 3 и 4. Таким образом получим
В первом случае направления ребер 1 и 2 согласованы, а во втором случае противоположны. Таким образом имеем
Расчет моста Уитстона
Для моста Уитстона, логика и уровень простоты в точности тот же. Но расчет требует внимательности и аккуратности.
В принципе у нас уже все готово.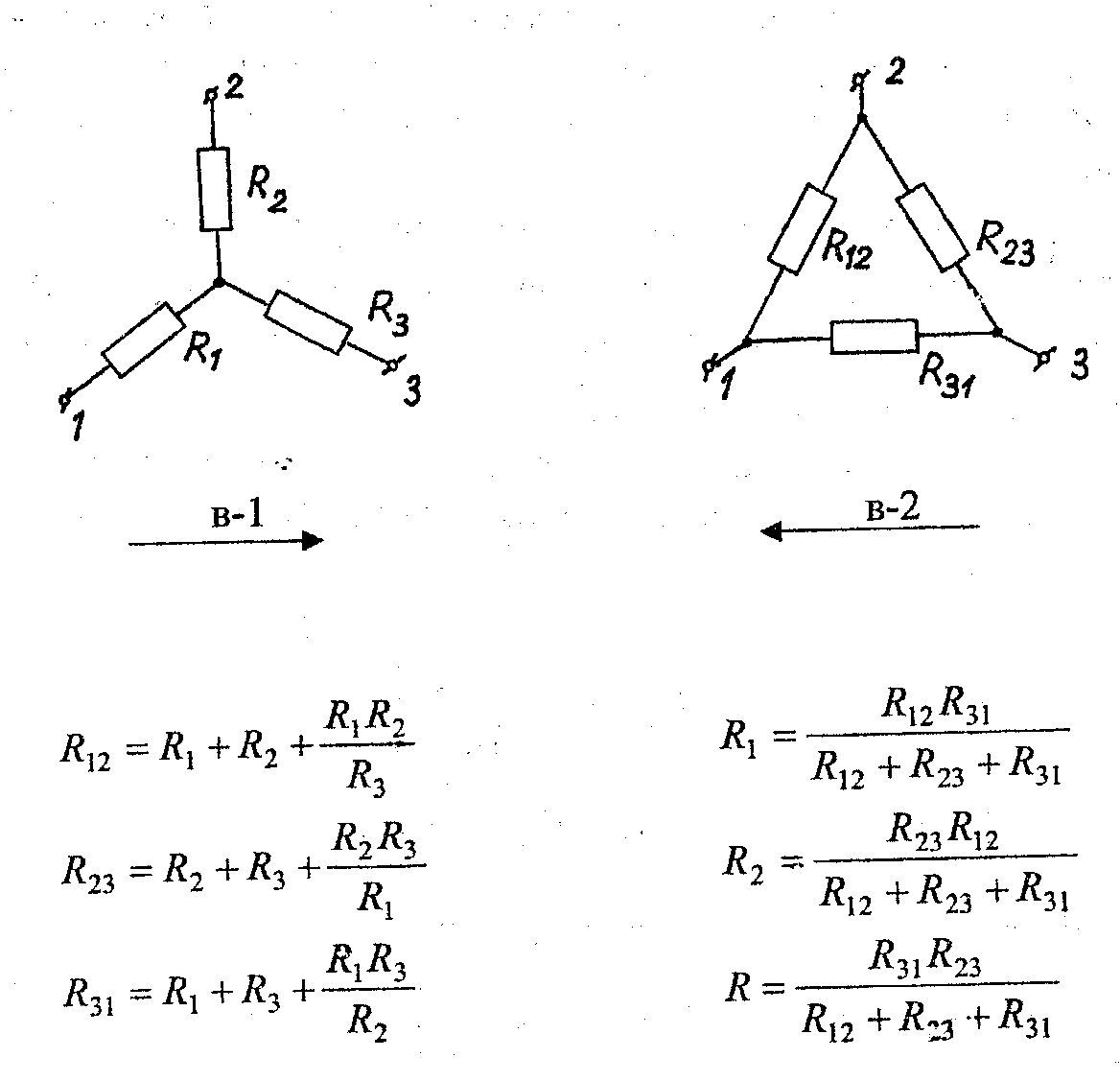
О блеске и нищете
Этот метод создавался в эпоху зарождения компьютеров и предназначался для компьютерного расчёта и синтеза электрических цепей. Поэтому наряду с эффективностью и, не побоюсь этого слова, поразительной простотой в применении этот подход обладает еще и органичной программируемостью. Вы легко можете автоматизировать процесс, описанный выше, и больше не переживать по поводу внимательности и большого количества бумаги.
И, несмотря на все явные достоинства, я не сумел найти этот метод в списке методов расчета электрических цепей в википедии, также я не встречал ни одного учебника или институтского курса, где бы давался этот метод. Думаю профессионалы (коим я никогда не был) знают об этом подходе, но ему не обучают в ВУЗах и, похоже, мало кто им пользуется.
Причина, думаю, понятна. Несмотря на весь блеск, эта тема просто не вписывается в учебную программу. То, что мы можем позволить себе в рамках статьи недопустимо в рамках учебного процесса — невозможно обойтись без теории, представив только манипулятивный подход. А если преподавать с теорией, то это минимум один семестр — и это только для того, чтобы уметь рассчитывать электрические схемы? Скорее этот курс подходит для математиков, но, опять-таки, применение слишком узкое. Поэтому все следуют давно проторенному подходу: стандартные методы линейной алгебры, правила Кирхгофа, различные преобразования схем… И готов согласиться, что с точки зрения образования это позволяет лучше понять суть, а также вписывается в общий курс математики и физики.
А если преподавать с теорией, то это минимум один семестр — и это только для того, чтобы уметь рассчитывать электрические схемы? Скорее этот курс подходит для математиков, но, опять-таки, применение слишком узкое. Поэтому все следуют давно проторенному подходу: стандартные методы линейной алгебры, правила Кирхгофа, различные преобразования схем… И готов согласиться, что с точки зрения образования это позволяет лучше понять суть, а также вписывается в общий курс математики и физики.
И получается, что оригинальность, во многом определяющая изящество и красоту данного подхода, обернулась для него своего рода проклятием.
5.3: Упрощение последовательно-параллельных компонентов — Разработка LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 25121
- Джеймс М.
 Фиоре
Фиоре - Муниципальный колледж Mohawk Valley
Мы можем пойти дальше простых наблюдений, представленных выше. То, как именно мы подходим к этому, будет зависеть от компонентов, представленных блоками (чаще всего это резисторы, но, возможно, источник напряжения или источник тока) и от того, как они соединены вместе. Для начала, если все элементы в подсхеме относятся к одному типу, их можно просто объединить, используя методы, описанные в предыдущих главах. Резисторы добавляются последовательно, так же как и источники напряжения последовательно — будьте осторожны с полярностью. Параллельные резисторы объединяются с использованием проводимости или правила произведения суммы, в то время как добавляются параллельные источники тока, опять же с осторожностью в отношении полярности. Все становится немного сложнее, когда есть смесь, например, два резистора последовательно с источником напряжения или резистор параллельно с парой источников тока. Как именно обрабатываются подобные ситуации, станет ясно в ближайшее время.
Рисунок 5.3.1 : простая последовательно-параллельная резисторная сеть.
Для иллюстрации рассмотрим конфигурацию резистора, представленную на рис. 5.3.1.
. Представьте, что к двум открытым клеммам подключен омметр. Что бы он читал? Омметр будет подавать небольшой ток в цепь, чтобы определить эффективное сопротивление группы. Три резистора, изображенные здесь, не являются простой последовательной конфигурацией, потому что мы можем определить разделение тока на резисторах 40 \(\Omega\) и 80 \(\Omega\). Точно так же это не параллельная сеть, потому что резисторы 40 \(\Omega\) и 160 \(\Omega\) не привязаны к одним и тем же двум узлам. Что мы можем сказать, так это то, что резисторы 40 \(\Omega\) и 160 \(\Omega\) включены последовательно друг с другом, так как каждый из них должен иметь одинаковый ток. Таким образом, мы можем объединить их в одно эквивалентное сопротивление 200 \(\Омега\). Этот эквивалент подключен параллельно резистору 80 \(\Омега\), а 80 \(||\) 200 составляет приблизительно 57,14 \(\Омега\).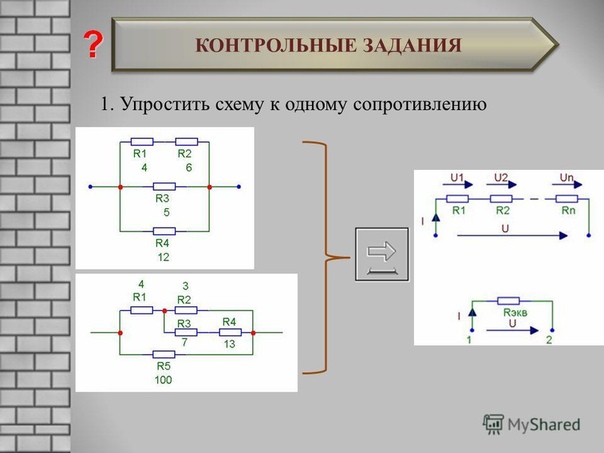
Технику упрощения можно описать следующим образом:
- Определите подгруппы резисторов, которые имеют последовательную или параллельную конфигурацию внутри себя.
- Замените подгруппы одним эквивалентным сопротивлением.
- Повторяйте описанные выше шаги, пока цепь не будет уменьшена до одного сопротивления или, альтернативно, до простой последовательной или только параллельной конфигурации.
В зависимости от сложности сети из-за зацикливания описанного выше метода может потребоваться многократный вызов. В более простых сетях может быть достаточно одного прохода. Первоначально может быть целесообразно перерисовывать схему для каждой итерации цикла. В конце концов, с практикой в этом не будет необходимости, за исключением самых сложных сетей. Давайте рассмотрим несколько более сложный пример.
Пример 5.3.1
Сеть последовательно-параллельных резисторов показана на рис. 5.3.2. . Определите его эквивалентное сопротивление.
Рисунок 5.3.2 : Сеть для примера 5.3.1 .
Первый шаг — распознать те подгруппы, которые идут последовательно или параллельно друг другу. Одним из очевидных кандидатов является то, что два резистора на 100 Ом включены параллельно друг другу. Два резистора равного номинала, включенные параллельно, эквивалентны половине сопротивления, или 50 \(\Омега\) в данном случае.
Другим кандидатом является пара 40 \(\Omega\), 200 \(\Omega\). Эти в серии. Эквивалентным сопротивлением пары является последовательное соединение, или 240 Ом.
Нет других подмножеств резисторов, которые можно уменьшить (пока). Сеть перерисована на рисунке 5.3.3. с эквивалентными сопротивлениями. Теперь процесс повторяется.
Рисунок 5.3.3 : Частично упрощенная сеть.
В новой сокращенной сети сопротивления 50 \(\Омега\) и 30 \(\Омега\) соединены последовательно, что дает 80 \(\Омега\).
Без перерисовки процесс можно повторить снова, на этот раз 240 \(\Omega\) параллельно с новым эквивалентом 80 \(\Omega\). 240 \(||\) 80 равно 60 \(\Омега\). Эта последовательность уменьшила три самых правых сопротивления до одного: новый эквивалент 60 \(\Omega\).
Наконец, резистор 60 \(\Омега\) включен последовательно с резистором 10 \(\Омега\), что дает окончательное эквивалентное сопротивление 70 \(\Омега\).
Лестницы
Лестница представляет собой уникальную последовательно-параллельную конфигурацию. Он организован в виде каскада последовательных и параллельных соединений. Лестницы используются в различных приложениях, одно из которых будет рассмотрено в следующем разделе.
Название очевидно, судя по внешнему виду сети. Пример резистивной лестничной сети показан на рисунке 5.3.4.
. Главное отметить, что лестничная сеть состоит из «секций, загружающих секции» многократно. Под нагрузкой мы подразумеваем, что этот элемент (нагрузка) отбирает ток и мощность от предыдущей секции.
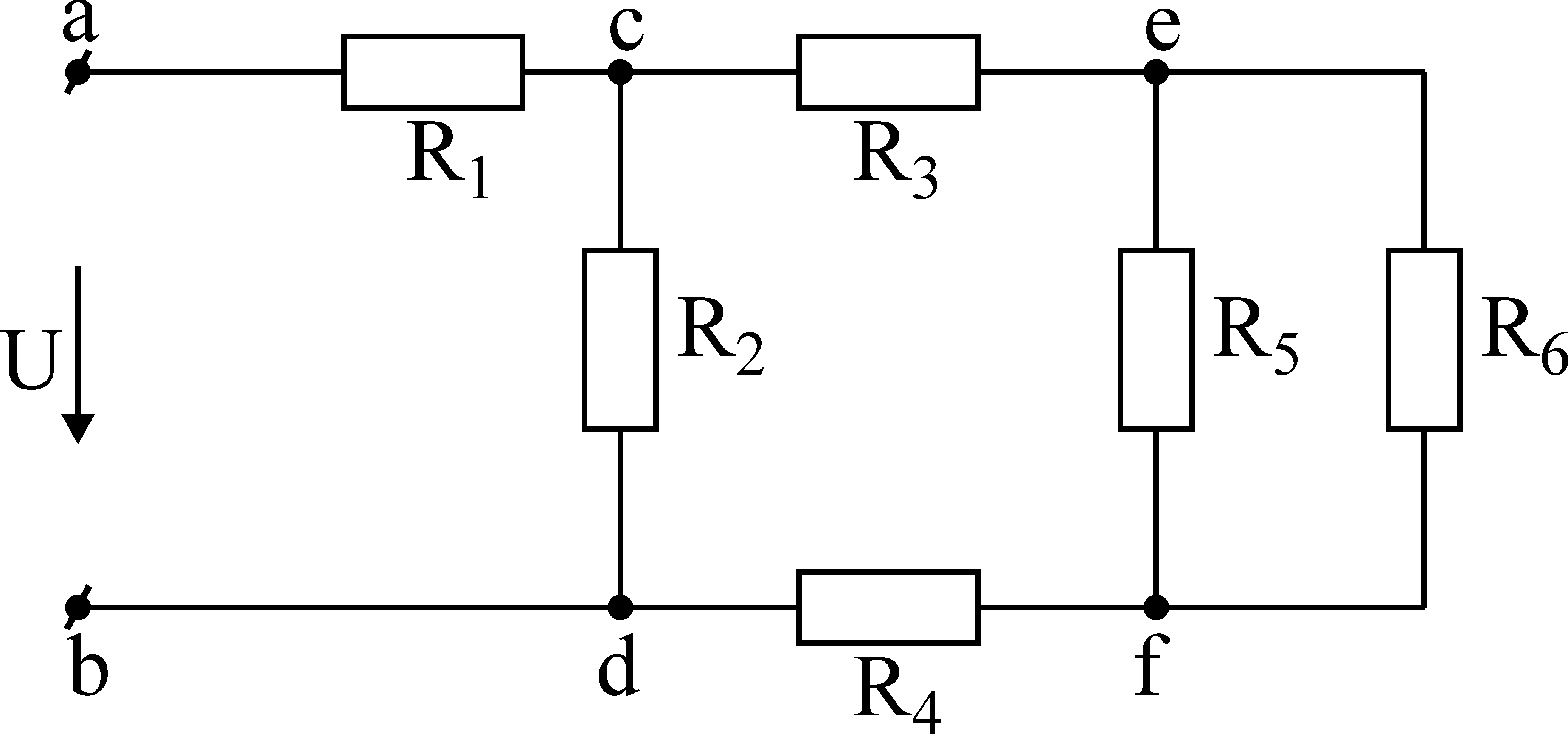
Рисунок 5.3.4 : резистивная лестничная сеть.
Фактически, единственный правильный делитель напряжения в этой конфигурации находится между \(R_7\) и \(R_8\). Причина этого становится очевидной, если мы представим определение эквивалентного сопротивления сети, поместив омметр на клеммы \(a\) и \(f\). Омметр подаст ток на узел \(a\), который проходит через \(R_1\). В узле \(b\) этот ток разделяется, часть идет вниз \(R_2\), а часть продолжается через \(R_3\). Ясно, что \(R_1\) и \(R_2\) не включены последовательно, поскольку они не видят один и тот же ток. Далее ток, протекающий через \(R_3\), входит в узел \(c\), где снова разделяется, часть вниз \(R_4\), а оставшаяся часть течет через \(R_5\).
Как же тогда найти эквивалентное сопротивление этой сети? Начинаем с самого дальнего от открытых терминалов конца. Мы уже отмечали, что \(R_7\) и \(R_8\) идут последовательно. Эта пара, рассматриваемая как одно сопротивление, параллельна \(R_6\) или \(R_6||(R_7+R_8)\). Эта группа из трех последовательно с \(R_5\), что дает \(R_5+R_6||(R_7+R_8)\) 1 . Эта новая группа из четырех параллельна \(R_4\), что дает \(R_4||(R_5+R_6||(R_7+R+8))\). Эта группа находится последовательно с \(R_3\), а эта новая группа, в свою очередь, параллельна \(R_2\). Наконец, эта предпоследняя группа идет последовательно с \(R_1\). Следовательно, эквивалентное сопротивление сети равно \(R_1+R_2||(R_3+ R_4||(R_5+R_6||(R_7+R_8)))\).
Пример 5.3.2
Резистивная лестничная сеть показана на рис. 5.3.5. . Определите его эквивалентное сопротивление.
Рисунок 5.3.5 : Сеть для примера 5.3.2 .
Начиная с дальнего конца от открытых клемм, мы видим, что резисторы 7 кОм\(\Омега\) и 5 кОм\(\Омега\) соединены последовательно, что дает 12 кОм\(\Омега\). Это параллельно с 8к\(\Омега\). 12 k \(||\) 8 k равно 4,8 k\(\Omega\). Это последовательно с 1,2 к\(\Омега\), что дает 6 к\(\Омега\). Эквивалент 6 к\(\Омега\) параллелен 1,5 к\(\Омега\), что дает 1,2 к\(\Омега\).
Наконец, эквивалент 1,2 кОм\(\Омега\) включен последовательно с 3 кОм\(\Омега\), что дает окончательное эквивалентное сопротивление 4,2 кОм\(\Омега\).
Помните, всегда начинайте с дальнего конца и двигайтесь к разомкнутым клеммам, т. е. клеммам, в которых вы пытаетесь найти эквивалентное сопротивление.
Пример 5.3.3
Резистивная лестничная сеть показана на рис. 5.3.6. . Определите его эквивалентное сопротивление.
Рисунок 5.3.6 : Сеть для примера 5.3.3 .
Дальний конец от открытых терминалов — крайний левый. Во-первых, резисторы 6 кОм(\Омега\) и 4 кОм(\Омега\) соединены последовательно, что дает 10 кОм\(\Омега\). Это происходит параллельно с 8k\(\Omega\), достигая примерно 4,444k\(\Omega\). В свою очередь, это последовательно с 2 k\(\Omega\), что дает 6,444 k\(\Omega\). Этот результат соответствует 12 k\(\Omega\), что дает 4,193 k\(\Omega\). Если поставить его последовательно с резистором 10 кОм (\Омега), то получится 14,193 кОм (\Омега). Это параллельно с 20 k\(\Omega\), дающими 8,302 k\(\Omega\).
Наконец, эквивалент 8,302 кОм\(\Омега\) включен последовательно с 5 кОм\(\Омега\), что дает окончательное эквивалентное сопротивление примерно 13,3 кОм\(\Омега\).
Ссылки
1 Напомним, что \(||\) имеет более высокий приоритет, чем + или –, поэтому \(||\) выполняется первым, как умножение, смешанное со сложением и вычитанием.
Эта страница под названием 5.3: Упрощение последовательно-параллельных компонентов распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Джеймсом М. Фиоре с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами. платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Джеймс М.
 Фиоре
Фиоре
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4,0
- Показать оглавление
- нет
- Теги
- источник@http://www.dissidents.com/resources/DCElectricalCircuitAnalysis.pdf
Упрощение резисторных цепей | Spinning Numbers
Сложные цепи резисторов можно упростить, найдя последовательные и параллельные комбинации резисторов в контексте более крупной схемы.
Содержание
- Стратегия
- Пошаговое решение примера
- Исключения
Вот пример схемы, над которой мы будем работать вместе,
Мы видим источник напряжения, подключенный к сети резисторов. Два маленьких кружочка возле левого конца представляют порт сети резисторов.
Два маленьких кружочка возле левого конца представляют порт сети резисторов.
Выясните, какой ток $(i)$ требуется источнику напряжения для подачи в сеть резисторов.
Ответ очевиден не сразу. Но в нашем распоряжении есть некоторые инструменты: мы знаем, как вычислить эквивалентное сопротивление последовательных резисторов и параллельных резисторов. С помощью этих инструментов мы можем упростить схему резисторов до тех пор, пока проблема не станет легко решаемой.
На этом этапе попробуйте решить задачу самостоятельно. Попробовав, продолжайте читать, чтобы увидеть решение.
Освежите свои знания о резисторах последовательного и параллельного подключения.
Стратегия
Вот общая стратегия упрощения любой сети резисторов,
- Начните как можно дальше от рассматриваемой схемы.
- Определите и замените комбинации последовательных или параллельных резисторов эквивалентными резисторами.
- Продолжайте, продвигаясь вперед, пока один эквивалентный резистор не будет представлять всю сеть резисторов.

Пошаговое решение примера
Исходный вопрос задавался про ток от источника напряжения. Таким образом, «рассматриваемое место» находится рядом с источником напряжения на дальнем левом конце цепи. Поэтому мы начинаем процесс упрощения с крайнего правого края и возвращаемся к исходному коду.
Упрощение схемы — это процесс, состоящий из множества маленьких шагов. Рассмотрим небольшой фрагмент схемы, упростите его, а затем перейдите к следующему фрагменту. Совет: перерисовывайте схему после каждого шага, чтобы не упустить возможности упростить.
Шаг 1. Заштрихованные резисторы $2\,\Omega$ и $8\,\Omega$ включены последовательно.
Глядя на заштрихованную область с точки зрения стрелок, два последовательных резистора эквивалентны одному резистору с сопротивлением ______ $\Omega$.
подсказка Эти два резистора соединены последовательно, поэтому мы добавляем их два сопротивления, чтобы получить эквивалентное последовательное сопротивление.
$2\,\Omega + 8\,\Omega = 10 \,\Omega$
Два резистора можно заменить их эквивалентным сопротивлением. Точно такие же ток и напряжение существуют в обеих версиях.
Шаг 2. Теперь мы находим два резистора $10\,\Omega$, подключенных параллельно в новом крайнем правом углу схемы.
Эти два резистора можно заменить их параллельной комбинацией.
Результирующий эквивалентный резистор: ______ $\Omega$.
показать ответ$10\,\Omega \parallel 10\,\Omega = \dfrac{10\cdot 10}{10 + 10}=5\,\Omega$
Обозначение $\parallel$ означает «параллельно с».
Опять же, глядя в заштрихованную рамку слева, ток и напряжение с эквивалентным резистором $5\,\Omega$ по-прежнему неотличимы от всего оригинала.
Шаг 3. Видите ли вы закономерность? Мы прорабатываем схему справа налево, упрощая и перерисовывая по мере продвижения. Далее мы находим два последовательных резистора, $1\,\Omega$ и $5\,\Omega$.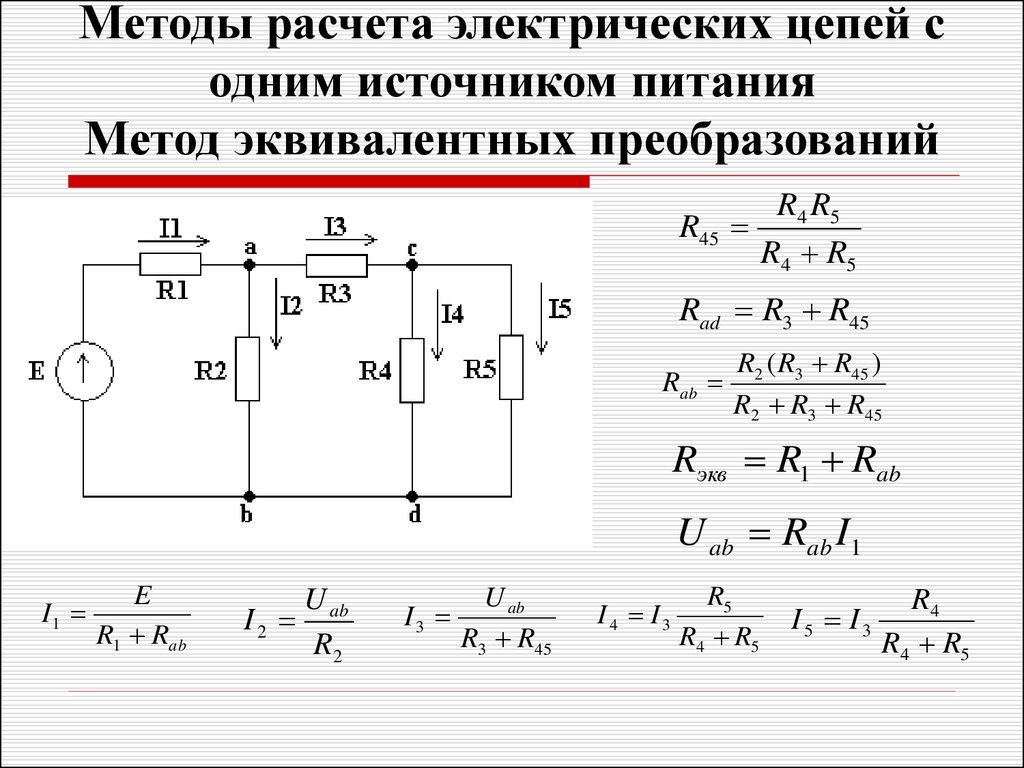
Эти последовательные резисторы можно заменить эквивалентным сопротивлением: ______ $\Omega$.
показать ответ$1\,\Omega + 5\,\Omega = 6\,\Omega$
Шаг 4. Этот шаг немного сложнее. У нас есть три резистора параллельно.
Эти три резистора можно заменить их параллельной комбинацией.
Результирующий эквивалентный резистор: ______ $\Omega$.
подсказкаПоскольку у нас есть три резистора, подключенных параллельно, используйте уравнение полного параллельного резистора,
$\dfrac{1}{\text R_{\text{параллельно}}} = \dfrac{1}{\text{R1}} +\dfrac{1}{\text{R2}} + \dfrac{1 }{\text{R3}}$
покажи ответ$\dfrac{1}{\text R_{\text{parallel}}} = \left (\dfrac{1}{12\,\Omega} +\dfrac{1}{4\,\Omega} + \ dfrac{1}{6\,\Omega}\right ) = \left (\dfrac{1}{12} +\dfrac{3}{12} + \dfrac{2}{12} \right )= \dfrac {1}{2}$
Таким образом, эквивалентное сопротивление является величиной, обратной величине $\dfrac{1}{2}$ или $2\,\Omega$.
Шаг 5. Остались два резистора последней серии,
Вы можете сделать это в уме,
У нас остался один резистор $3\,\Omega$. Насколько может судить источник напряжения, этот один резистор эквивалентен всей сети резисторов.
Для ответа на вопрос: Источник напряжения необходим для подачи тока 9,
$i = \dfrac{\text V}{3\,\Omega}$
Вы начали с резисторов по 7$ и упростили до 1$, что значительно уменьшило сложность. Отличная работа.
Не все упрощения сводятся к одному резистору в конце. (Схема может состоять не только из резисторов.) Но всегда используйте возможность упростить, если представится такая возможность.
Просто для удовольствия, вот анимация процесса упрощения,
Исключения
Определенные конфигурации резисторов нельзя упростить с помощью стратегии, описанной выше.


 Осталось только написать ответ.
Осталось только написать ответ. Если в процессе алгебраических операций появляются столбцы с одинаковыми элементами, то эти столбцы удаляются.
Если в процессе алгебраических операций появляются столбцы с одинаковыми элементами, то эти столбцы удаляются. Стрелками обозначено направление тока (которое мы приняли за положительное)
Стрелками обозначено направление тока (которое мы приняли за положительное) То есть, не строго говоря, это строка, состоящая из индексов ребер (для данной вершины).
То есть, не строго говоря, это строка, состоящая из индексов ребер (для данной вершины).
 Получаем
Получаем
 Фиоре
Фиоре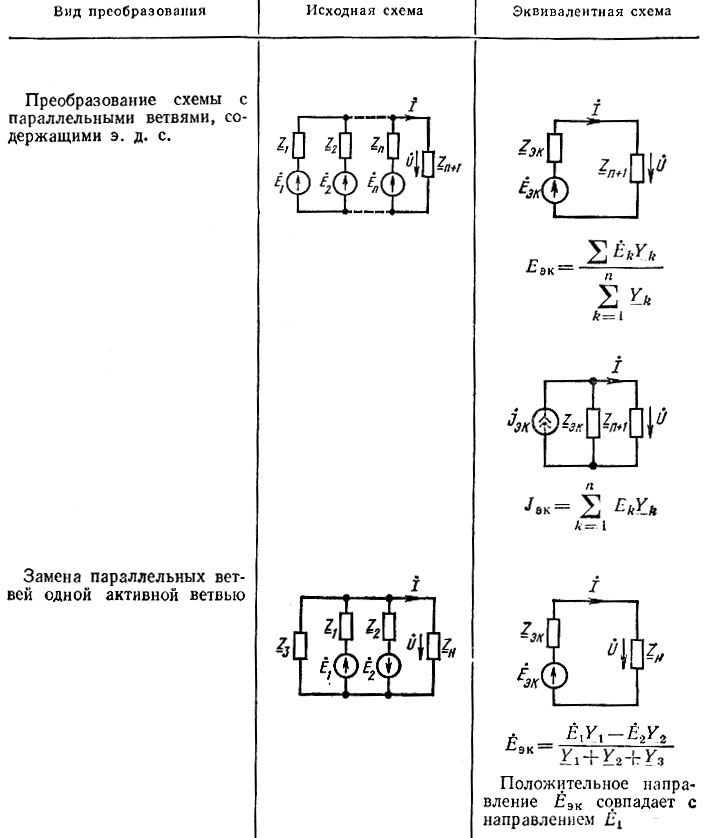 Фиоре
Фиоре