эквивалентная схема конденсатора, реальной катушки индуктивности, постоянного резистора
В элементах различных реально существующих электротехнических устройств происходят сложные процессы, связанные с протеканием токов смещения, токов проводимости, наведения ЭДС, выделения тепла, перераспределения и накопления энергии магнитного поля и электрического поля и прочее. Чтобы описать математически все эти процессы, используют схемы замещения электротехнических устройств, добавляя в них ёмкостные, индуктивные и резистивные элементы.
С помощью ёмкостного элемента в эквивалентной схеме замещения учитывают накопление в электрическом поле энергии и протекание токов смещения в реальном элементе цепи. С помощью индуктивного элемента учитывают накопление в магнитном поле энергии и наведение ЭДС. При помощи резистивного элемента в эквивалентной схеме учитывают выделение тепла.
Любой элемент реально существующей электрической цепи может быть представлен на эквивалентной схеме в виде нескольких идеальных элементов.
Эквивалентная схема замещения резистора
Постоянный резистор, используемый в схеме с низкими частотами может быть представлен в виде одного резистивного элемента R.
Эквивалентная схема того же самого резистора, работающего в схеме на высоких частотах, кроме резистивного элемента включает также индуктивность и ёмкость. С помощью паразитной ёмкости Cп учитывается ток смещения на зажимах элемента. С помощью паразитной индуктивности Lп учитывается сцепленный с резистором магнитный поток.
Эквивалентная схема замещения конденсатора
Конденсатор, который работает в схеме на низких частотах представляют, как один ёмкостной элемент C.
Конденсатор, который работает на высоких частотах в эквивалентной схеме представляется ёмкостным элементом, резистором и индуктивностью. С помощью резистора Rп учитывают потери тепла в диэлектрике конденсатора. Паразитной индуктивность Lп учитывается магнитный поток в подводящих контактах.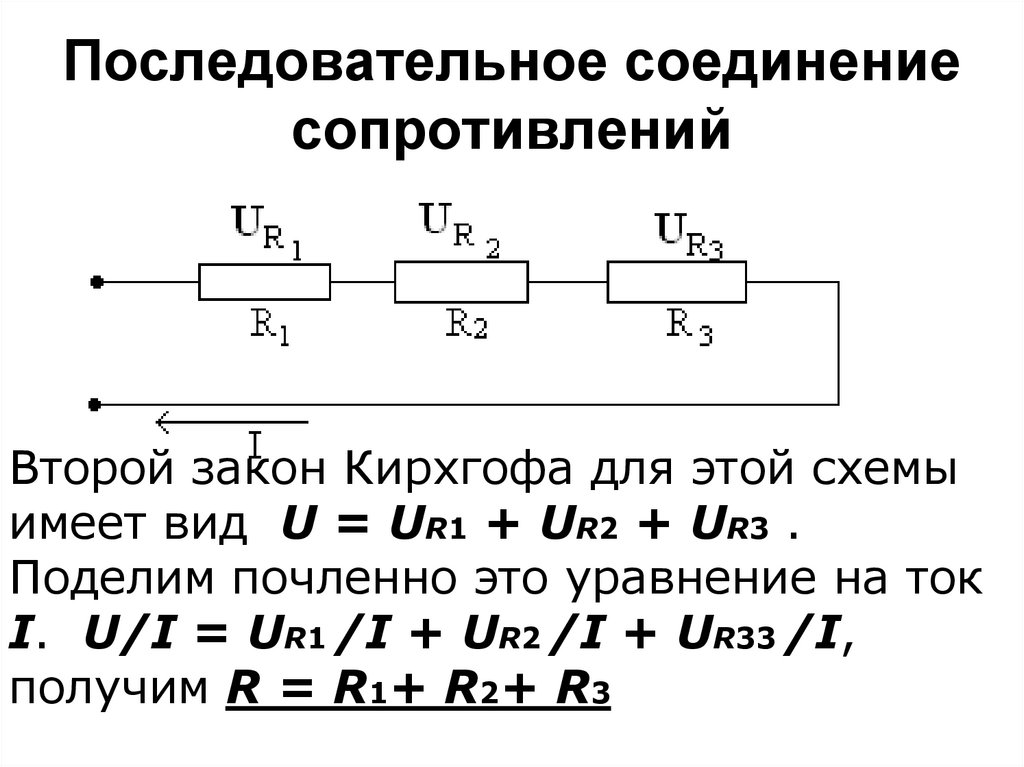
Эквивалентная схема замещения катушки индуктивности
Катушку индуктивности, работающую на низких частотах, представляют в виде индуктивного элемента L.
Схема замещения катушки индуктивности, кроме индуктивного элемента, включает также резистор и ёмкость. Резистивный элемент Rп учитывает потери на выделение тепла в сердечнике и сопротивлении обмотки. При помощи паразитной ёмкости Cп учитываются токи смещения, существующие между витками катушки.
В случае составления эквивалентной схемы для реальных элементов цепи в неё включают такие идеальные элементы, которые могут описать основные процессы, протекающие в этих реальных элементах. При этом второстепенными процессами, как правило, пренебрегают.
Представленную как совокупность идеализированных элементов схемы реальную электрическую цепь называют схемой замещения, эквивалентной схемой или эквивалентной схемой замещения.
Если ток и напряжение на всех элементах в реальной электрической цепи никак не зависят от координат в пространстве, то такую цепь называют цепью с сосредоточенными параметрами. Если же ток и напряжение зависят от координат в пространстве, то это цепь с распределёнными параметрами.
Если же ток и напряжение зависят от координат в пространстве, то это цепь с распределёнными параметрами.
Процессы, которые происходят в цепи с сосредоточенными параметрами описывают при помощи дифференциальных или алгебраических уравнений. Процессы, происходящие в цепях с распределёнными параметрами, описывают с помощью уравнений в частных производных.
Расчётную модель реальной электрической цепи сопоставляют с экспериментальными данными. В случае больших расхождений модель необходимо будет уточнить.
Основы теории цепей
Основы теории цепей
ОглавлениеПРЕДИСЛОВИЕ К ЧЕТВЕРТОМУ ИЗДАНИЮВВЕДЕНИЕ Раздел первый. ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ 1-1. Элементы электрических цепей и электрических схем 1-2. Эквивалентные схемы для источников энергии 1-3. Закон Ома для участка цепи с э. д. с. 1-4. Распределение потенциала вдоль неразветвленной электрической цепи 1-5. Баланс мощностей для простейшей неразветвленной цепи 1-6. Применение законов Кирхгофа для расчета разветвленных цепей 1-7. Метод узловых потенциалов 1-8. Метод контурных токов 1-9. Уравнения состояния цепи в матричной форме Глава вторая. ОСНОВНЫЕ СВОЙСТВА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПРИ ПОСТОЯННЫХ ТОКАХ И НАПРЯЖЕНИЯХ 2-2. Свойство взаимности 2-3.  Входные и взаимные проводимости и сопротивления ветвей; коэффициенты передачи напряжений и токов Входные и взаимные проводимости и сопротивления ветвей; коэффициенты передачи напряжений и токов2-4. Применение топологических методов для расчета цепей 2-5. Топологические формулы и правила для определения передачи электрической цепи 2-6. Теорема о компенсации 2-7. Линейные соотношения между напряжениями и токами 2-8. Теорема о взаимных приращениях токов и напряжений 2-9. Общие замечания о двухполюсниках 2-11. Передача энергии от активного двухполюсника к пассивному Глава третья. ОСНОВНЫЕ ПОНЯТИЯ О ЦЕПЯХ СИНУСОИДАЛЬНОГО ТОКА 3-2. Понятие о генераторах переменного тока 3-3. Синусоидальный ток 3-4. Действующие ток, э. д. с. и напряжение 3-5. Изображение синусоидальных функций времени векторами и комплексными числами 3-6. Сложение синусоидальных функций времени 3-7. Электрическая цепь и ее схема 3-8. Ток и напряжения при последовательном соединении сопротивления, Индуктивности и емкости 3-9.  3-10. Разность фаз напряжения и тока 3-11. Напряжение и токи при параллельном соединении сопротивления, индуктивности и емкости 3-12. Проводимости 3-13. Пассивный двухполюсник 3-14. Мощности 3-15. Мощности в сопротивлении, индуктивности и емкости 3-16. Баланс мощностей 3-17. Знаки мощностей и направление передачи энергии 3-18. Определение параметров пассивного двухполюсника при помощи амперметра, вольтметра и ваттметра 3-19. Условия передачи максимальной мощности от источника энергии к приемнику 3-20. Понятие о поверхностном эффекте и эффекте близости 3-21. Параметры и эквивалентные схемы конденсаторов Глава четвертая. РАСЧЕТ ЦЕПЕЙ ПРИ СИНУСОИДАЛЬНЫХ ТОКАХ 4-1. О применимости методов расчета цепей постоянного тока к расчетам цепей синусоидального тока 4-2. Последовательное соединение приемников 4-3. Параллельное соединение приемников 4-4.  Смешанное соединение приемников Смешанное соединение приемников4-5. Сложные разветвленные цепи 4-6. Топографические диаграммы 4-7. Дуальность электрических цепей 4-8. Сигнальные графы и их применение для расчета цепей Глава пятая. РЕЗОНАНС В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ 5-3. Резонанс в цепи с двумя параллельными ветвями 5-4. Частотные характеристики параллельного контура 5-5. Понятие о резонансе в сложных цепях Глава шестая. ЦЕПИ С ВЗАИМНОЙ ИНДУКТИВНОСТЬЮ 6-2. Электродвижущая сила взаимной индукции 6-3. Последовательное соединение индуктивно связанных элементов цепи 6-4. Параллельное соединение индуктивно связанных элементов цепи 6-5. Расчеты разветвленных цепей при наличии взаимной индуктивности 6-6. Эквивалентная замена индуктивных связей 6-7. Передача энергии между индуктивно связанными элементами цепи 6-8. Трансформатор без стального сердечника (воздушный трансформатор) Глава седьмая. КРУГОВЫЕ ДИАГРАММЫ 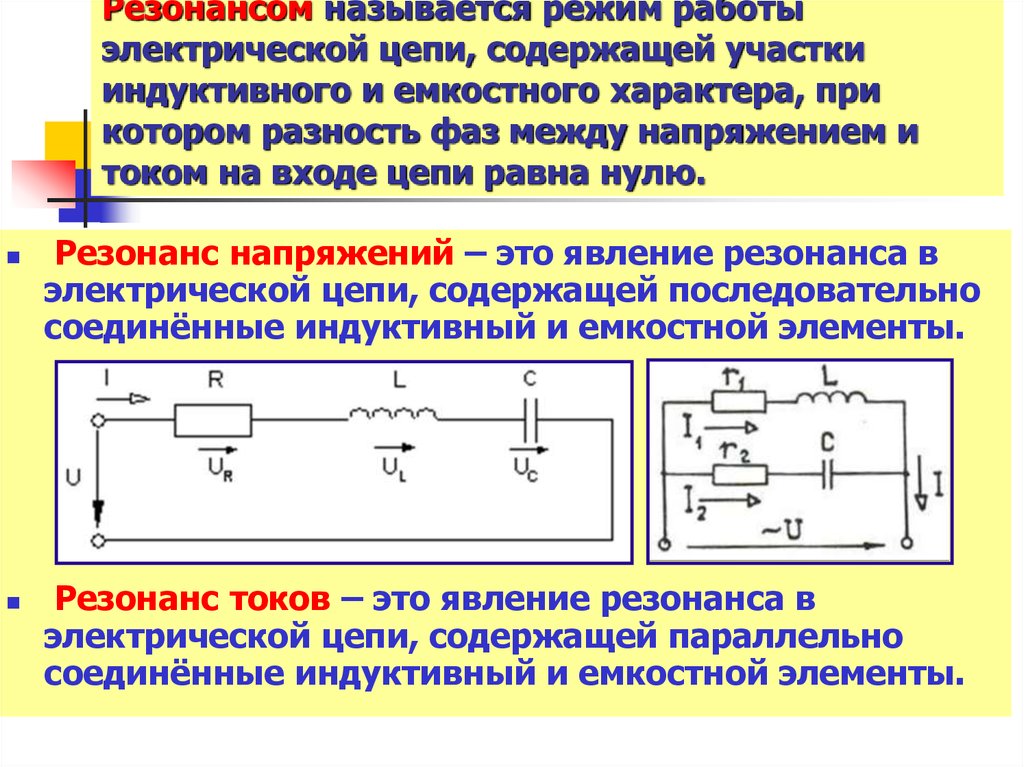 Комплексные уравнения прямой и окружности Комплексные уравнения прямой и окружности7-2. Круговые диаграммы для неразветвленной цепи и для активного двухполюсника 7-3. Круговые диаграммы для любой разветвленной цепи Глава восьмая. МНОГОПОЛЮСНИКИ И ЧЕТЫРЕХПОЛЮСНИКИ ПРИ СИНУСОИДАЛЬНЫХ ТОКАХ И НАПРЯЖЕНИЯХ 8-1. Четырехполюсники и их основные уравнения 8-2. Определение коэффициентов четырехполюсников 8-3. Режим четырехполюсника при нагрузке 8-4. Эквивалентные схемы четырехполюсников 8-5. Основные уравнения и эквивалентные схемы для активного четырехполюсника 8-6. Идеальный трансформатор как четырехполюсник 8-8. Эквивалентные схемы трансформатора со стальным магнитопроводом 8-9. Расчеты электрических цепей с трансформаторами 8-10. Графы пассивных четырехполюсников и их простейшие соединения Глава девятая. ЦЕПИ С ЭЛЕКТРОННЫМИ И ПОЛУПРОВОДНИКОВЫМИ ПРИБОРАМИ В ЛИНЕЙНОМ РЕЖИМЕ 9-2. Эквивалентные схемы лампового триода 9-3. 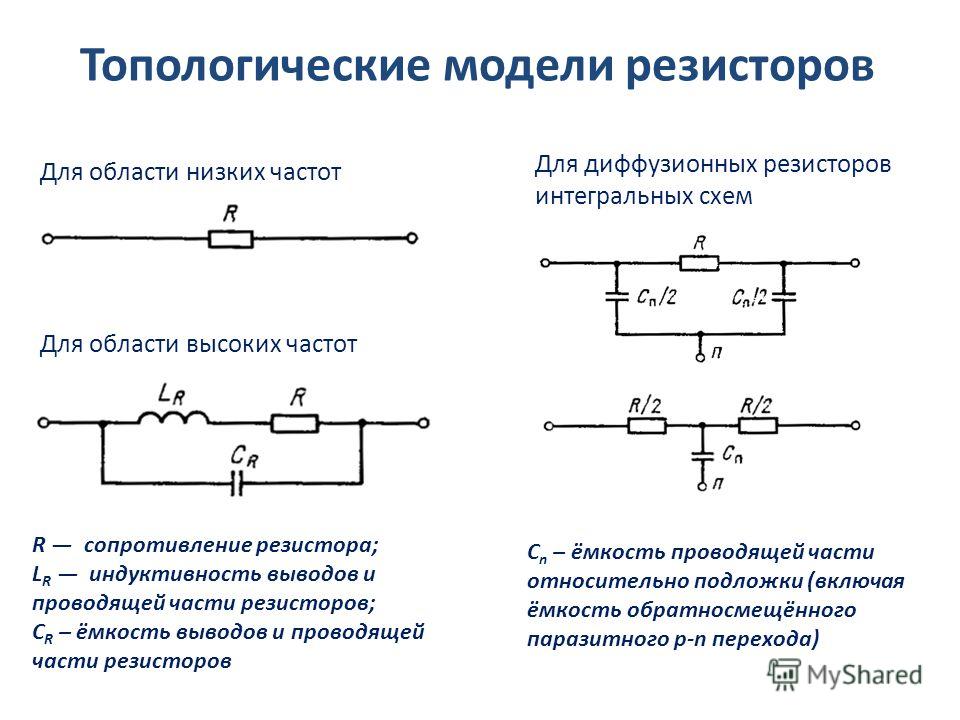 Транзисторы (полупроводниковые триоды) Транзисторы (полупроводниковые триоды)9-4. Эквивалентные схемы транзисторов 9-5. Простейшие электрические цепи с невзаимными элементами и их направленные графы 10-2. Соединения звездой и многоугольником 10-3. Симметричный режим трехфазной цепи 10-4. Некоторые свойства трехфазных цепей с различными схемами соединений 10-5. Расчет симметричных режимов трехфазных цепей 10-6. Расчет несимметричных режимов трехфазных цепей со статической нагрузкой 10-7. Напряжения на фазах приемника в некоторых частных случаях 10-8. Эквивалентные схемы трехфазных линий 10-9. Измерение мощности в трехфазных цепях 10-10. Вращающееся магнитное поле 10-11. Принципы действия асинхронного и синхронного двигателей Глава одиннадцатая. МЕТОД СИММЕТРИЧНЫХ СОСТАВЛЯЮЩИХ 11-2. Некоторые свойства трехфазных цепей в отношении симметричных составляющих токов и напряжений 11-4.  Определение токов в симметричной цепи Определение токов в симметричной цепи11-5. Симметричные составляющие напряжений и токов в несимметричной трехфазной цепи 11-6. Расчет цепи с несимметричной нагрузкой 11-7. Расчет цепи с несимметричным участком в линии Глава двенадцатая. НЕСИНУСОИДАЛЬНЫЕ ТОКИ 12-2. Разложение периодической несинусоидальной кривой в тригонометрический ряд 12-3. Максимальные, действующие и средние значения несинусоидальных периодических э. д. с., напряжений и токов 12-4. Коэффициенты, характеризующие форму несинусоидальных периодических кривых 12-6. Действующие значения э. д. с., напряжений и токов с периодическими огибающими 12-7. Расчет цепей с несинусоидальными периодическими э. д. с. и токами 12-8. Резонанс при несинусоидальных э. д. с. и токах 12-9. Мощность периодических несинусоидальных токов 12-10. Высшие гармоники в трехфазных цепях Глава тринадцатая. КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ 13-2. 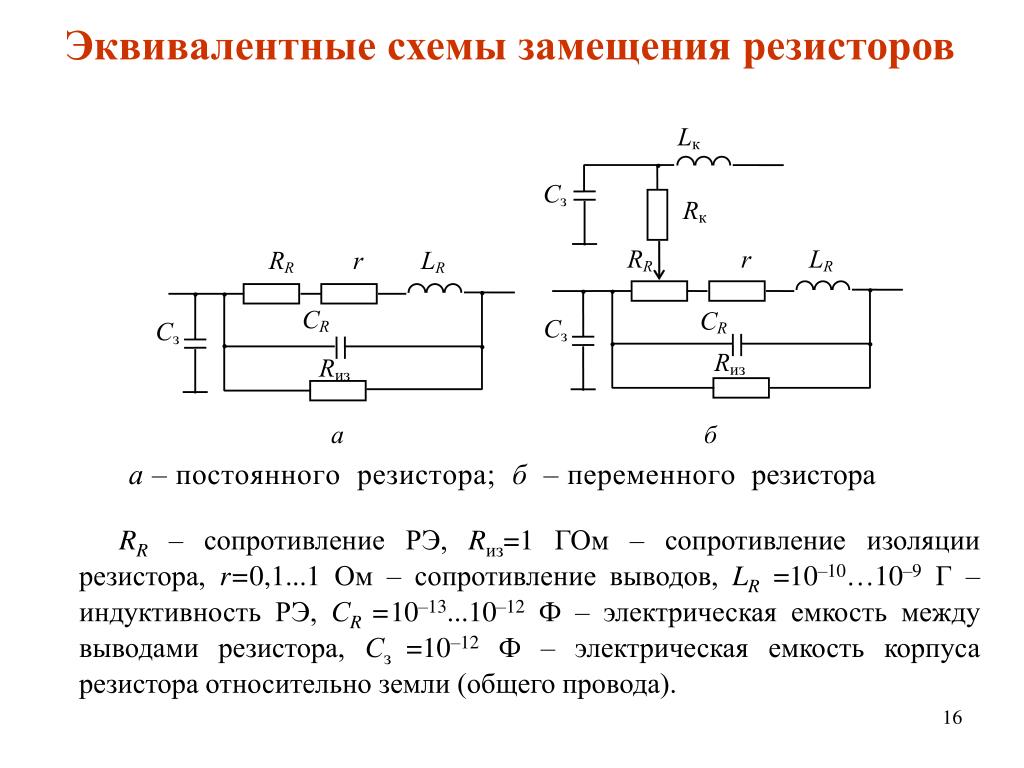 Переходный, принужденный и свободный процессы Переходный, принужденный и свободный процессы13-3. Короткое замыкание цепи r, L 13-4. Включение цепи r, L на постоянное напряжение 13-6. Короткое замыкание цепи r, С 13-7. Включение цепи r, С на постоянное напряжение 13-8. Включение цепи r, С на синусоидальное напряжение 13-9. Переходные процессы в неразветвленной цепи r, С 13-10. Апериодический разряд конденсатора 13-11. Предельный случай апериодического разряда конденсатора 13-12. Периодический (колебательный) разряд конденсатора 13-13. Включение цепи r, С на постоянное напряжение 13-14. Общий случай расчета переходных процессов классическим методом 13-15. Включение пассивного двухполюсника на непрерывно изменяющееся напряжение (формула или интеграл Дюамеля) 13-17. Временная и импульсная переходные характеристики 13-18. Запись теоремы свертки при помощи импульсной переходной характеристики 13-19.  Переходные процессы при скачках токов в индуктивностях и напряжений на конденсаторах Переходные процессы при скачках токов в индуктивностях и напряжений на конденсаторах13-20. Определение переходного процесса и установившегося режима при воздействии периодических импульсов напряжения или тока Глава четырнадцатая. ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ 14-2. Законы Ома и Кирхгофа в операторной форме 14-3. Эквивалентные операторные схемы 14-4. Переходные процессы в цепях с взаимной индуктивностью 14-5. Сведение расчетов переходных процессов к нулевым начальным условиям 14-6. Определение свободных токов по их изображениям 14-7. Формулы включения 14-8. Расчет переходных процессов методом переменных состояния 14-9. Определение принужденного режима цепи при воздействии на нее периодического несинусоидального напряжения Глава пятнадцатая. ЧАСТОТНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ 15-2. Законы Ома и Кирхгофа и эквивалентные схемы для частотных спектров 15-3. Приближенный метод определения оригинала по вещественной частотной характеристике (метод трапеций) 15-4.  О переходе от преобразований Фурье к преобразованиям Лапласа О переходе от преобразований Фурье к преобразованиям Лапласа15-5. Сравнение различных методов расчета переходных процессов в линейных электрических цепях Глава шестнадцатая. ЦЕПНЫЕ СХЕМЫ И ЧАСТОТНЫЕ ЭЛЕКТРИЧЕСКИЕ ФИЛЬТРЫ 16-2. Характеристическое сопротивление и постоянная передачи симметричного четырехполюсника 16-3. Вносимая и рабочая постоянные передачи 16-4. Цепные схемы 16-5. Частотные электрические фильтры 16-6. Низкочастотные фильтры 16-8. Полосные фильтры 16-11. Г-образный фильтр как пример несимметричного фильтра 16-12. Безындукционные (или r, C) фильтры Глава семнадцатая. СИНТЕЗ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ 17-2. Передаточная функция четырехполюсника. Цепи минимальной фазы 17-3. Входные функции цепей. Положительные вещественные функции 17-4. Реактивные двухполюсники 17-5. Частотные характеристики реактивных двухполюсников 17-6. Синтез реактивных двухполюсников. Метод Фостера 17-7. Синтез реактивных двухполюсников. Метод Кауэра 17-8.  Синтез двухполюсников с потерями. Метод Фостера Синтез двухполюсников с потерями. Метод Фостера17-9. Синтез двухполюсников с потерями. Метод Кауэра 17-10. Понятие о синтезе четырехполюсников Раздел второй. ЛИНЕЙНЫЕ ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ Глава восемнадцатая. ГАРМОНИЧЕСКИЕ ПРОЦЕССЫ В ЦЕПЯХ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ 18-2. Уравнения однородной линии 18-3. Установившийся режим в однородной линии 18-4. Уравнения однородной линии с гиперболическими функциями 18-5. Характеристики однородной линии 18-6. Входное сопротивление линии 18-7. Коэффициент отражения волны 18-8. Согласованная нагрузка линии 18-9. Линия без искажений 18-10. Холостой ход, короткое замыкание и нагрузочный режим линии с потерями 18-11. Линии без потерь 18-12. Стоячие волны 18-13. Линия как четырехполюсник Глава девятнадцатая. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПЯХ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ 19-2. Общее решение уравнений однородной линии 19-3. Возникновение волн с прямоугольным фронтом 19-4.  Общие случаи нахождения волн, возникающих при переключениях Общие случаи нахождения волн, возникающих при переключениях19-5. Отражение волны с прямоугольным фронтом от конца линии 19-6. Общий метод определения отраженных волн 19-7. Качественное рассмотрение переходных процессов в линиях, содержащих сосредоточенные емкости и индуктивности 19-8. Многократные отражения волн с прямоугольным фронтом от активного сопротивления 19-9. Блуждающие волны Раздел III. НЕЛИНЕЙНЫЕ ЦЕПИ Глава двадцатая. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПРИ ПОСТОЯННЫХ ТОКАХ И НАПРЯЖЕНИЯХ 20-2. Графический метод расчета неразветвленных цепей с нелинейными элементами 20-3. Графический метод расчета цепей с параллельным соединением нелинейных элементов 20-4. Графический метод расчета цепей со смешанным соединением нелинейных и линейных элементов 20-5. Применение эквивалентных схем с источниками э. д. с. для исследования режима нелинейных цепей 20-6. Вольт-амперные характеристики нелинейных активных двухполюсников 20-7. Примеры расчета разветвленных электрических цепей с нелинейными элементами 20-8. 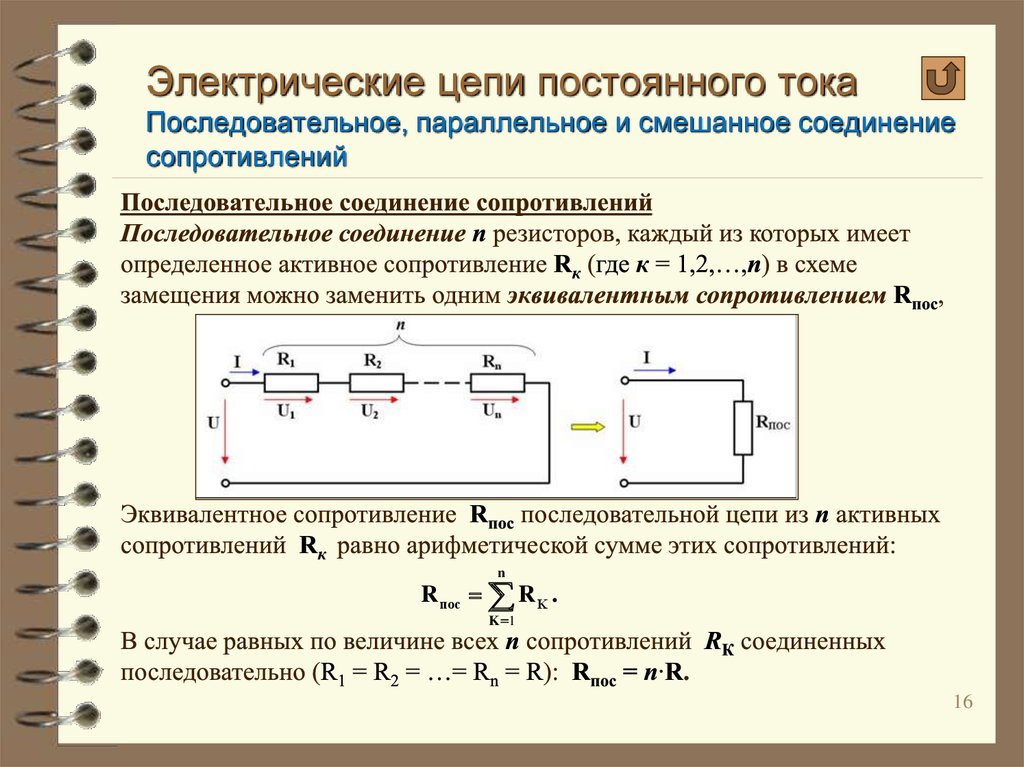 Применение теории активных двухполюсника, четырехполюсника и шестиполюсника для расчета цепей с линейными и нелинейными элементами Применение теории активных двухполюсника, четырехполюсника и шестиполюсника для расчета цепей с линейными и нелинейными элементами20-9. Расчет разветвленных нелинейных цепей итерационным методом (методом последовательных приближений) Глава двадцать первая. МАГНИТНЫЕ ЦЕПИ ПРИ ПОСТОЯННЫХ ТОКАХ 21-2. Расчет неразветвленных магнитных цепей 21-3. Расчет разветвленных магнитных цепей 21-4. Расчет магнитной цепи кольцевого постоянного магнита с воздушным зазором 21-5. Расчет неразветвленной неоднородной магнитной цепи с постоянным магнитом Глава двадцать вторая. ОБЩАЯ ХАРАКТЕРИСТИКА НЕЛИНЕЙНЫХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА И МЕТОДОВ ИХ РАСЧЕТА 22-1. Нелинейные двухполюсники и четырехполюсники при переменных токах 22-2. Определение рабочих точек на характеристиках нелинейных двухполюсников и четырехполюсников 22-3. Явления в нелинейных цепях переменного тока 22-4. Методы расчета нелинейных цепей переменного тока Глава двадцать третья. НЕЛИНЕЙНЫЕ ЦЕПИ С ИСТОЧНИКАМИ Э.  Д. С. И ТОКА ОДИНАКОВОЙ ЧАСТОТЫ Д. С. И ТОКА ОДИНАКОВОЙ ЧАСТОТЫ23-2. Форма кривой тока в цепи с вентилями 23-3. Простейшие выпрямители 23-4. Формы кривых тока и напряжения в цепях с нелинейными реактивными сопротивлениями 23-5. Утроители частоты 23-6. Формы кривых тока и напряжения в цепях с терморезисторами 23-7. Замена реальных нелинейных элементов условно-нелинейными 23-8. Учет реальных свойств стальных магнитопроводов 23-9. Расчет тока в катушке со стальным магнитопроводом 23-10. Понятие о расчете условно-нелинейных магнитных цепей 23-11. Явление феррорезонанса 23-12. Стабилизаторы напряжения Глава двадцать четвертая. НЕЛИНЕЙНЫЕ ЦЕПИ С ИСТОЧНИКАМИ Э. Д. С. И ТОКА РАЗЛИЧНЫХ ЧАСТОТ 24-1. Общая характеристика нелинейных цепей с источниками э. д. с. различных частот 24-2. Вентили в цепях с постоянными и переменными э. д. с. 24-3. Управляемые вентили в простейших выпрямителях и преобразователях постоянного тока в переменный 24-4. Катушки со стальными магнитопроводами в цепях с постоянными и переменными э. 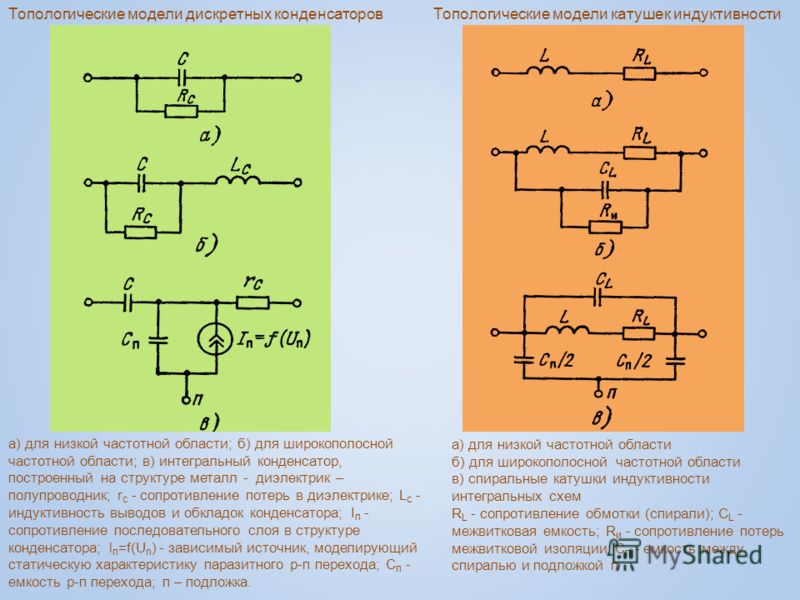 д. с. д. с.24-5. Удвоитель частоты 24-6. Метод гармонического баланса 24-7. Влияние постоянной э. д. с. на переменную составляющую тока в цепях с нелинейными безынерционными сопротивлениядли 24-8. Принцип получения модулированных колебаний 24-9. Влияние постоянной составляющей на переменную в цепях с нелинейными индуктивностями 24-10. Магнитные усилители мощности Глава двадцать пятая. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В НЕЛИНЕЙНЫХ ЦЕПЯХ 25-2. Включение катушки со стальным магнитопроводом на постоянное напряжение 25-3. Включение катушки со стальным магнитопроводом на синусоидальное напряжение 25-4. Импульсное воздействие в цепях с неоднозначными нелинейностями 25-5. Понятие о простейших запоминающих устройствах 25-6. Изображение переходных процессов на фазовой плоскости 25-7. Колебательный разряд емкости через нелинейную индуктивность Глава двадцать шестая. АВТОКОЛЕБАНИЯ 26-1. Нелинейные резисторы со спадающим участком характеристики 26-2. Понятие об устойчивости режима в цепи с нелинейными резисторами 26-3.  Релаксационные колебания в цепи с отрицательным сопротивлением Релаксационные колебания в цепи с отрицательным сопротивлением26-4. Близкие к синусоидальным колебания в цепи с отрицательным сопротивлением 26-5. Фазовые траектории процессов в цепи с отрицательным сопротивлением 26-6. Фазовые траектории процессов в генераторе синусоидальных колебаний 26-7. Определение амплитуды автоколебаний методом гармонического баланса Приложение 1. Разложение периодических функций в тригонометрический ряд Приложение 2. Таблица оригиналов и изображений (по Лапласу) Приложение 3. Таблица функций и их частных спектров Приложение 4. Таблица функций для трапеций СПИСОК ЛИТЕРАТУРЫ |
Эквивалентные цепи и типы цепей катушек индуктивности
ABC of CLR, EEE Components, PASSIVES
Современное измерительное оборудование, такое как анализатор импеданса HP4195A и аналогичные приборы, позволяет компьютеризировать создание эквивалентных схем и их оптимизацию.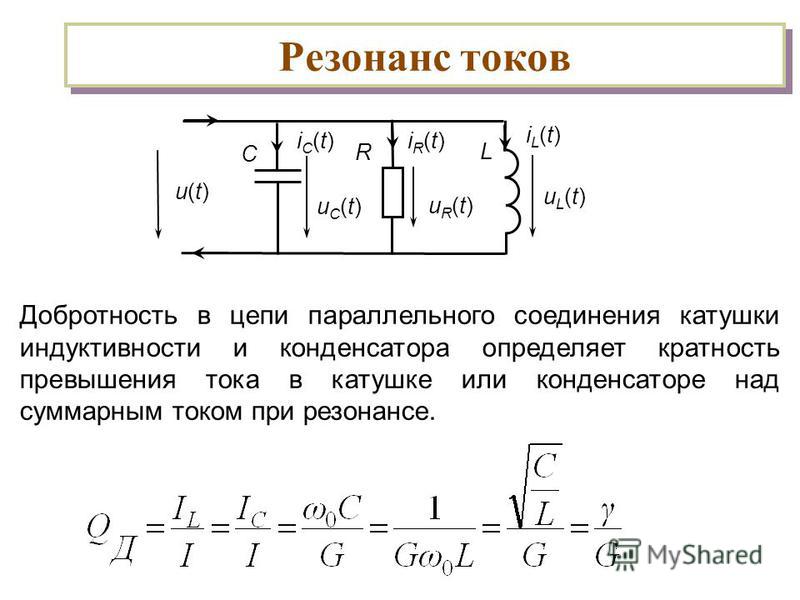 Постоянные параметры индуктивности L, емкости C и сопротивления R необходимы для моделирования электронных схем. Неправильный подход к определению схемы замещения приводит к ошибочным или некорректным результатам моделирования.
Постоянные параметры индуктивности L, емкости C и сопротивления R необходимы для моделирования электронных схем. Неправильный подход к определению схемы замещения приводит к ошибочным или некорректным результатам моделирования.
Нажмите здесь и узнайте, как doEEEt помогает вам выбрать наиболее подходящие катушки индуктивности для включения в ваши списки деталей/DCL/спецификации.
Эквивалентные параметры схемы никоим образом не являются юридически обязывающими, точными наблюдаемыми характеристиками, но показывают пользователю примерное положение основных допусков. Тот факт, что эти данные ранее были недоступны, во многом связан с традициями тестирования и маркетинга, которые в будущем должны быть заменены усилиями по обеспечению удобства для пользователя.
Электронные компоненты, резисторы, конденсаторы, катушки индуктивности, проводники, приближенные к ферритовым материалам и изоляционным материалам могут быть адекватно охарактеризованы параметрами переменного тока. Условием является то, что их свойства не изменяются заметно при различных уровнях высокого напряжения и тока или чтобы они работали в малом диапазоне сигналов. Затем говорят о линейных компонентах в отличие от нелинейных компонентов, таких как варисторы, диоды, транзисторы и т. д.
Условием является то, что их свойства не изменяются заметно при различных уровнях высокого напряжения и тока или чтобы они работали в малом диапазоне сигналов. Затем говорят о линейных компонентах в отличие от нелинейных компонентов, таких как варисторы, диоды, транзисторы и т. д.
Вследствие пространственного размера конструкции компонентов между каждой точкой на поверхности проводника и каждый второй. Проводники генерируют магнитные поля за счет протекания тока и обладают частичной индуктивностью благодаря энергии, запасенной в этих магнитных полях. Конечная проводимость меди, серебра и т. д. или проводимость многослойных резисторов
, генерируемые локально, приводят к частичному сопротивлению. Параллельные проводники также можно рассматривать как участки высокочастотных линий на высоких частотах, обладающие волновым сопротивлением, временем прохождения сигнала и, возможно, затуханием сигнала.
Реальность вообще чрезвычайно сложна. Если бы кто-то захотел нарисовать или даже рассчитать микроскопически тонкую схему со всеми парциальными сопротивлениями, емкостями или индуктивностями, он был бы обречен на неудачу.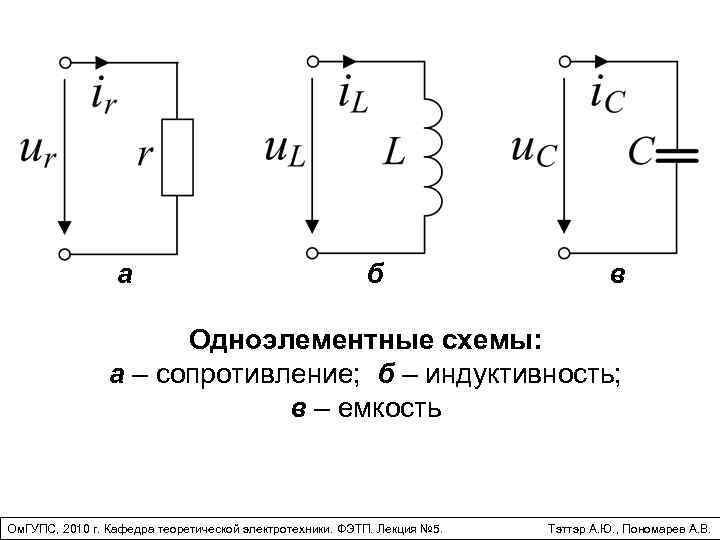 К счастью для пользователя, можно легко найти точные эквивалентные схемы для конденсаторов и катушек индуктивности без железных или ферритовых сердечников. Также хорошо описываются аппроксимации других индуктивных составляющих, усредненные параметры которых намного лучше неизвестных характеристик. Реальные значения измерений в виде кривых сравниваются с моделями эквивалентных схем, чтобы продемонстрировать пользователю получение этих значений. Это особенно относится к ферритам ЭМС, с которыми подавляются помехи, но не формируется точная схема.
К счастью для пользователя, можно легко найти точные эквивалентные схемы для конденсаторов и катушек индуктивности без железных или ферритовых сердечников. Также хорошо описываются аппроксимации других индуктивных составляющих, усредненные параметры которых намного лучше неизвестных характеристик. Реальные значения измерений в виде кривых сравниваются с моделями эквивалентных схем, чтобы продемонстрировать пользователю получение этих значений. Это особенно относится к ферритам ЭМС, с которыми подавляются помехи, но не формируется точная схема.
Конденсаторы → последовательный резонанс
s (порядка нескольких нГн) и сопротивление дорожки R s (тип. порядка 20 мОм … 100 мОм, для конденсаторов с холодным электролитом до 1 Ом). На низких частотах преобладает емкостная составляющая, на собственной резонансной частоте сопротивление дорожки измеримо. Выше последовательного резонанса преобладает индуктивная составляющая, на которую в некоторой степени может влиять наличие коротких соединительных длин.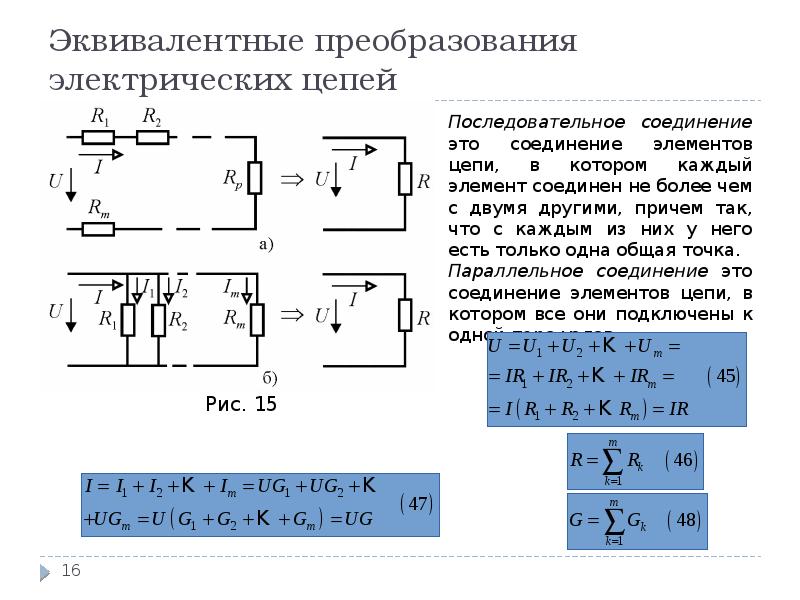 Фазовая кривая изменяется от ≈ –9от 0° до ≈ +90° в области резонанса. Таким образом, фазовая точка 0° точно определяет точку резонансной частоты, часто гораздо точнее, чем это возможно с помощью измерения амплитуды. Фазовая кривая также служит для компьютерного определения схемы замещения (1-е приближение).
Фазовая кривая изменяется от ≈ –9от 0° до ≈ +90° в области резонанса. Таким образом, фазовая точка 0° точно определяет точку резонансной частоты, часто гораздо точнее, чем это возможно с помощью измерения амплитуды. Фазовая кривая также служит для компьютерного определения схемы замещения (1-е приближение).
Индуктивность → параллельный резонанс
Рис. 2: Параллельная цепь и импеданс в зависимости от частоты
На идеальную индуктивность L p влияет неизбежная емкость обмотки C п и ассимилированные потери Р п (материал сердечника, потери в обмотке). Для катушек индуктивности желательно бесконечно большое параллельное сопротивление R p , для ферритов ЭМС, напротив, очень низкое и широкополосное сопротивление R p является желательным параметром. Индуктивность L p играет меньшую роль и является ключом к преобразованию резистивных потерь в линию.
Это означает, что в модели на месте феррита ЭМС разрезана линия и вставлена эквивалентная схема.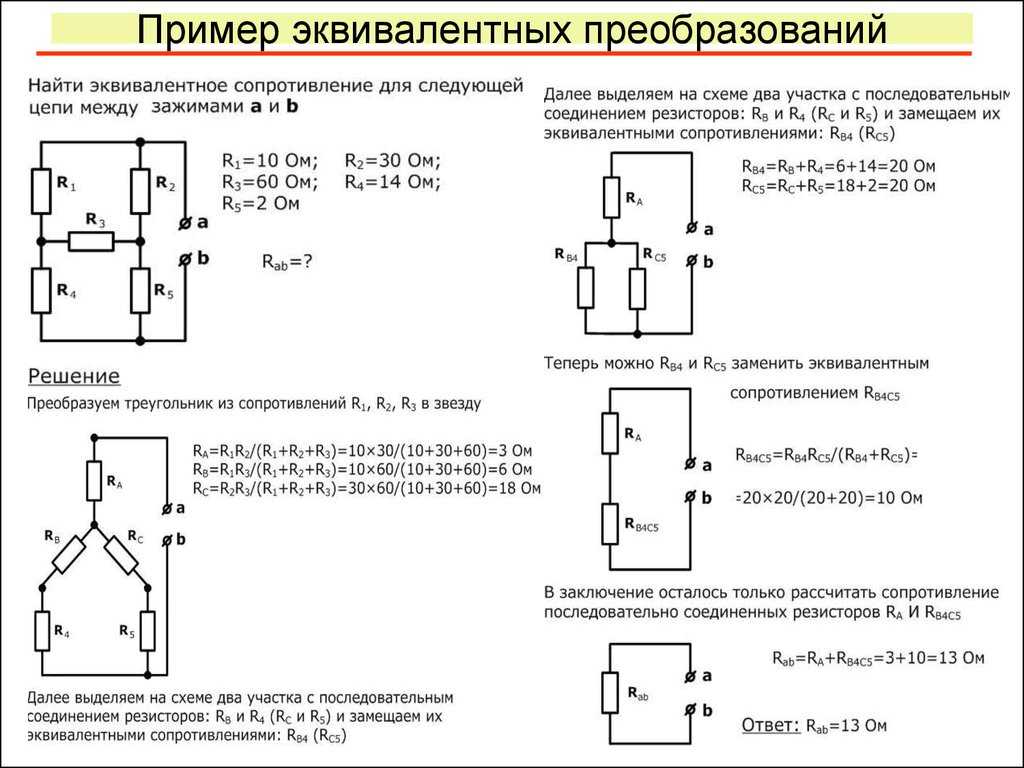 Компонент точно описывается только всеми тремя параметрами L, C и R. Одного параметра недостаточно, хотя для известных конфигураций можно предсказать другие свойства.
Компонент точно описывается только всеми тремя параметрами L, C и R. Одного параметра недостаточно, хотя для известных конфигураций можно предсказать другие свойства.
Представьте трехмерную систему координат с осями R p , L p , C p ; компонент представляет собой точку в этом пространстве, а его поле допуска представляет собой прямоугольное тело. Различные компоненты расположены в этом пространстве допусков как разные точки.
Последовательные резонансные контуры:
Рис. 4: 1 + jΩ (модуль и фаза) как функция Ω Рис. резонанс можно резюмировать следующим образом:Включены унифицированные (нормализованные) резонансные кривые для последовательных и параллельных резонансных контуров в зависимости от нормированного дисбаланса Ω при всех значениях L, C и R. Стандартизированная расстройка унифицирует параметры добротности и резонансной частоты f RES . Это упрощает описание поведения резонансных систем в их диапазоне частот
(Δf … отклонение частоты от резонансной частоты)Параллельные резонансные контуры:
Рис. 5: 1/1 + Jω (величина и фаза) в зависимости от ω
5: 1/1 + Jω (величина и фаза) в зависимости от ω Серия Резонанс
Параллельный резонанс
Условие резонанса:
для серии:
. для параллельного резонанса:
Нормализованный внерезонанс:
для последовательного резонанса:
для параллельного резонанса:
Расстройка v обозначает, насколько расстроен резонансный контур по сравнению с наложенным колебанием. Вкратце: Мера отклонения частоты (контура) от резонансной частоты (контура).
Нормализованные кривые представлены на рисунках 4 и 5 для R = 1 (верхняя амплитуда, нижняя фаза).
Выбрав подходящие операнды (нормализация), можно изобразить все характеристики в виде двух стандартных кривых. Они служат для обеспечения общего понимания, тогда как в приложениях оцениваются измеренные резонансные кривые или в компьютерном моделировании числовые значения L, R и C.
Получение простых эквивалентных схем
, кривые измерения, полученные с помощью HP 4195 анализируются.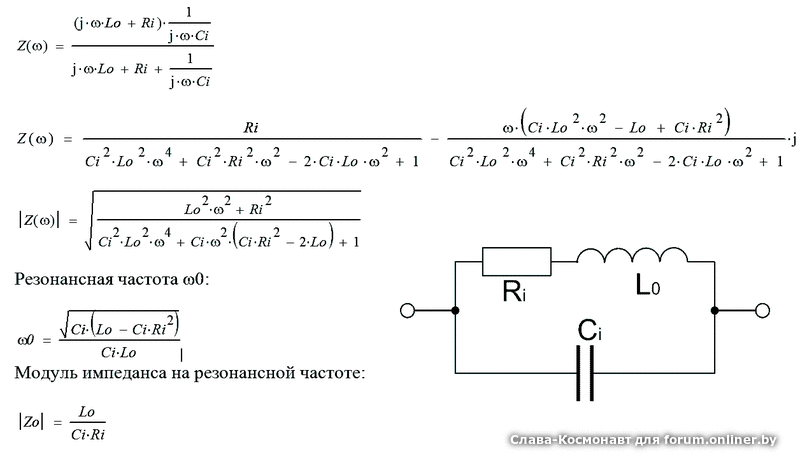 Однако в принципе не имеет значения, с помощью какого измерительного прибора или конфигурации получаются кривые.
Однако в принципе не имеет значения, с помощью какого измерительного прибора или конфигурации получаются кривые.
Анализ основан на фундаментальных концепциях теоретического моделирования.
Рис. 6: Кривая импеданса катушки с 6 витками обмотки на керамическом каркасе ∅ 6 мм витки обмотки. Простая оценка индуктивности по значениям на частотах 10 МГц и 100 МГц дала L 63,7 нГн. Поскольку фаза Θ находится в пределах 85°–90°, можно принять чистую индуктивность и получить из |Z| = 4 Ом на частоте 10 МГц и |Z| = 40 Ом на частоте 100 МГц.
Анализатор измеряет L = 58 нГн благодаря более точно сохраненным значениям, чем отображаемые. На рис. 6 различимы только две кривые: толстая кривая измерения и кривая, построенная анализатором в результате измерения эквивалентной схемы. На самом деле он включает калькулятор эквивалентной схемы. Он вычисляет эквивалентную схему, показанную на рис. 6, и записывает рассчитанные значения |Z| и Θ рядом с кривой измерения. Без компьютера пришлось бы довольствоваться лишь грубым расчетом.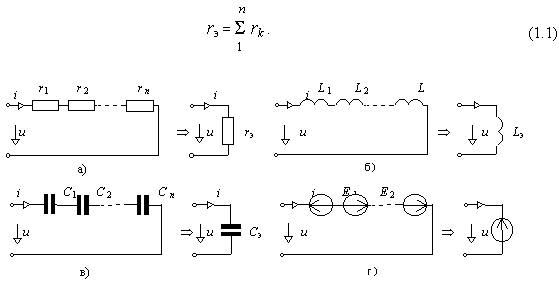
В вопросах ЭМС требуются многомерные меры; точность не имеет первостепенного значения.
Рис. 7: Кривая полного сопротивления керамического конденсатора емкостью 10 нФ прибл. Соединительные ножки длиной 5 ммНа рис. 7 показана кривая импеданса керамического дискового конденсатора с номинальной емкостью 10 нФ и прибл. Соединительные ножки длиной 5 мм. Читая кривые измерения и вычисляя, можно найти C = 11,37 нФ и L = 9,55 нГн. Из |Z| кривая при Θ = –90° можно рассчитать емкость
, а при Θ = + 90° можно рассчитать индуктивную составляющую
.
|З| 200 кГц = 70 Ом, |Z| 4 МГц ≈ 3,5 Ом, C = 11,37 нФ, |Z| 40 МГц ≈ 2 Ом,
|Z| 200 МГц = 12 Ом и L = 9,55 нГн.
Последовательное сопротивление согласно измерениям составило 33,8 мОм. При правильно выбранной схеме замещения (рис. 1.45) анализатор измерил R = 33,7 мОм, C = 11,2 нФ и L = 9 нГн, и ее совпадающая кривая показала, что никаких других паразитных параметров схемы замещения, имеющих какое-либо значение, не было. В то время как катушка на рис. 1.45 по-прежнему полезна на частоте 200 МГц, конденсатор
В то время как катушка на рис. 1.45 по-прежнему полезна на частоте 200 МГц, конденсатор
применим только до 30 МГц.
Отсюда видно, насколько важно учитывать линейные индуктивности в связи с блокирующими процессами. Это иллюстрирует пример на рис. 1.46. без индуктивности падение напряжения на 25 мВ происходит за 10 нс со скругленным задним фронтом. Индуктивность линии 9Только nH добавляет биполярный импульс с крутым фронтом ±90 мВ, эффект, который наблюдал каждый, кто смотрел на свою линию питания с помощью осциллографа. Мало толку заменить 10 нФ на 1 мкФ; если индуктивность остается, шумовое напряжение остается. Чистое изменение заряда конденсатора емкостью 10 нФ за счет треугольного импульса приводит к изменению напряжения ΔU на конденсаторе.
Края тока ΔI/Δt всего при 9 нГн создают биполярный сдвиг напряжения на
Рис. 9: Кривая импеданса и эквивалентная схема резонансного контура В качестве примера на Рисунке 9 показан резонансный контур, состоящий из катушки и конденсатора, соединенных параллельно с резистором 1 кОм. Анализатор с выбранной структурой A побеждает в эквивалентной схеме. Другие структуры приводят к плохим или бесполезным приближениям. Анализатор в первую очередь пытается приблизиться к фазовой кривой. Можно вручную улучшить параметры и получить новые приближения.
Анализатор с выбранной структурой A побеждает в эквивалентной схеме. Другие структуры приводят к плохим или бесполезным приближениям. Анализатор в первую очередь пытается приблизиться к фазовой кривой. Можно вручную улучшить параметры и получить новые приближения.
В этом случае индуктивность можно определить по кривой измерения. Емкость может быть найдена только в ограниченной степени. |З| 3 МГц = 4 Ом, |Z| 57,6 МГц = 969 Ом, |Z| 200 МГц = 24 Ом, L p = 207 нГн, R p = 989 Ом, C p = 36,4 пФ.
Тогда помогает условие резонанса:
Результаты анализатора подтверждают расчетные значения.
Рис. 10: Эквивалентные типы цепей от HP4195A
Рис. 11: Кривые импеданса при параллельном соединении двух разнородных конденсаторов (Обозначение эффективной блокировки по ВЧ)
На Рис. 11 показана кривая импеданса при параллельном соединении 2 разнородных конденсаторов.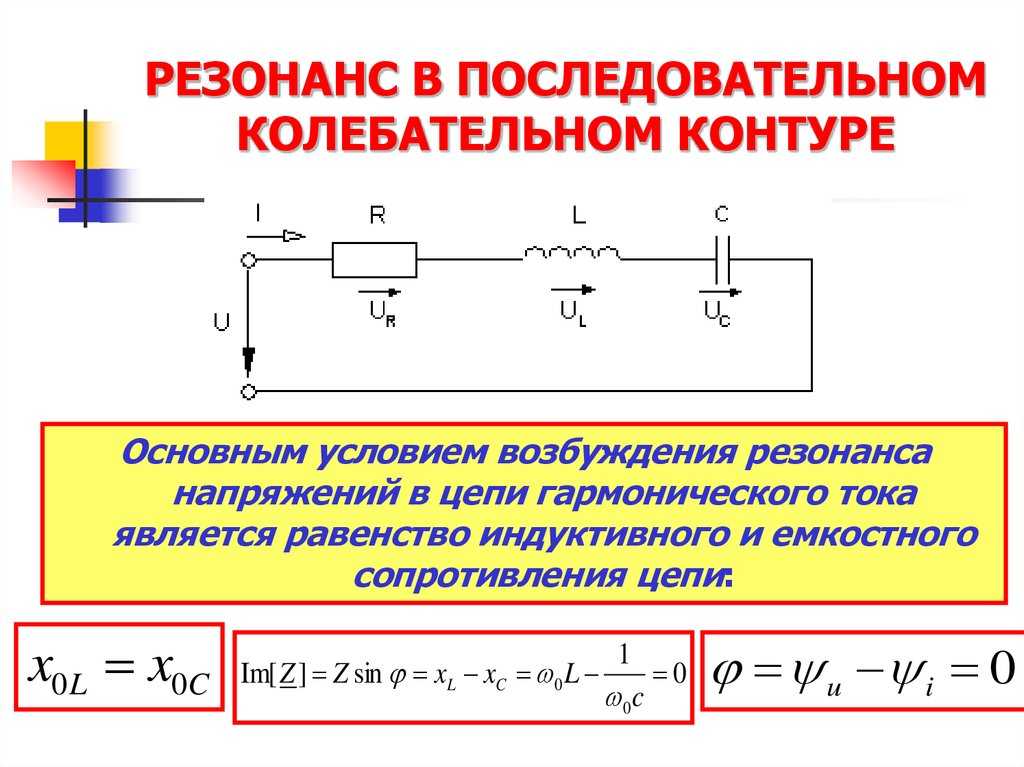 Большой конденсатор емкостью 150 нФ был дополнен небольшим конденсатором емкостью 150 пФ для улучшения блокировки по ВЧ. Он должен «сбалансировать» недостаток более длинной линии конденсатора с нагрузкой. Результатом является резонансный пик на частоте 61,57 МГц с Z 590 Ом (без нагрузки). Каждый крутой фронт импульса обязательно вызовет длительные затухающие колебания и значительно снизит полезность блокировки.
Большой конденсатор емкостью 150 нФ был дополнен небольшим конденсатором емкостью 150 пФ для улучшения блокировки по ВЧ. Он должен «сбалансировать» недостаток более длинной линии конденсатора с нагрузкой. Результатом является резонансный пик на частоте 61,57 МГц с Z 590 Ом (без нагрузки). Каждый крутой фронт импульса обязательно вызовет длительные затухающие колебания и значительно снизит полезность блокировки.
Получение эквивалентной схемы из |Z| кривых происходит в несколько этапов. Фазовая кривая Q сигнализирует о емкости до 2 МГц (зона I). Последовательный резонанс на частоте 2 МГц является следствием прибл. Ножки подключения конденсатора 150 пФ длиной 4 см. Схема индуктивная в зоне II для создания параллельного резонанса с 590 Ом на частоте 60 МГц, где уже нельзя говорить о блокировке. В диапазоне от 30 МГц до 100 МГц (зона III) импеданс превышает 100 Ом и крайне вреден для внутренней связи сигнала. Конденсатор емкостью 150 пФ начинает играть роль за пределами параллельного резонанса и влияет на последовательный резонанс на частоте 154 МГц.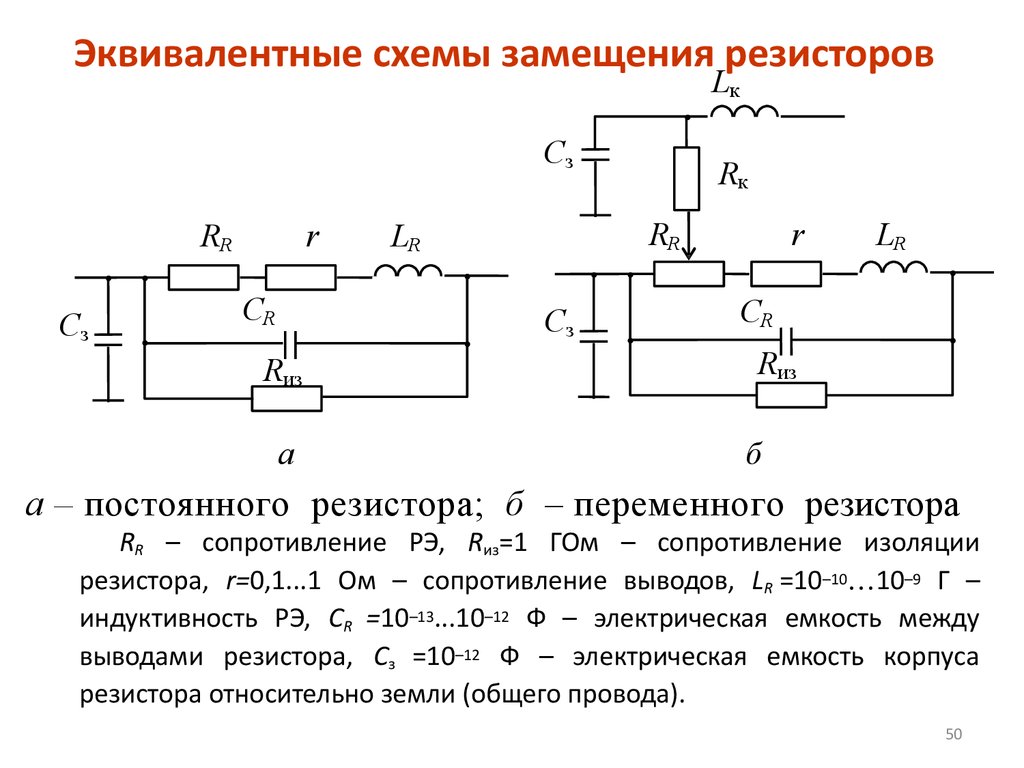 Фазовая кривая Q наблюдается в зоне IV.
Фазовая кривая Q наблюдается в зоне IV.
Расчетные значения
в зоне I |Z| 600 кГц = 2 Ом ∩ 133 нФ,
в зоне II |Z| 20 МГц = 6,5 Ом ∩ 52 нГн,
в зоне III резонанса 61,6 МГц C b = 1/ω 2 · L = 128,6 пФ,
в зоне IV резонанса 5 2 90,6 МГц L – 0 1 · C b = 8,25 нГн
Получена эквивалентная схема
Рис. 12: Эквивалентная схема двух параллельно соединенных конденсаторов
- Автор
- Последние сообщения
Томаш Зедничек
Основатель и президент ЕВРОПЕЙСКОГО ИНСТИТУТА ПАССИВНЫХ КОМПОНЕНТОВ ( EPCI)
EPCI | Объединение пассивных профессионалов
Степень в области электротехники Технического университета Брно, Чехия, 1993 г.
Доктор философии. в танталовых конденсаторах в 2000 г.
> 21 год работы в компании-производителе танталовых конденсаторов
> 15 лет на должности менеджера по техническому маркетингу по всему миру
более 60 технических статей и 1 американский/международный патент
4 выдающиеся/лучшие технические статьи на конференции по пассивным компонентам CARTS
2005 Награда доктора Зандмана за большой вклад в индустрию пассивных компонентов межкультурная коммуникация
Июль 2015 г. – Основатель Европейского института пассивных компонентов
– Основатель Европейского института пассивных компонентов
Последние сообщения Томаша Зедничка (см. все)
0 0 голосов
Артикул Рейтинг
Предыдущий пост
Renesas Electronics America/Intersil RH Информация о продукции
Следующий пост
Конструкция демпфера RC для защиты SMPS (Часть I)
Свиток
3.
 7: Эквивалентные цепи — резисторы и источники
7: Эквивалентные цепи — резисторы и источники- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 1748
- Дон Х. Джонсон
- Университет Райса через Connections
Цели обучения
- Знакомство с эквивалентными схемами, включая функцию в отношении v-i.
Мы обнаружили, что способ думать о цепях состоит в том, чтобы найти и сгруппировать параллельные и последовательные комбинации резисторов. Те резисторы, которые не связаны с интересующими переменными, могут быть объединены в одно сопротивление. Этот результат известен как эквивалентная схема : с точки зрения пары клемм группа резисторов работает как один резистор, сопротивление которого обычно можно найти, применяя правила параллельной и последовательной проводки.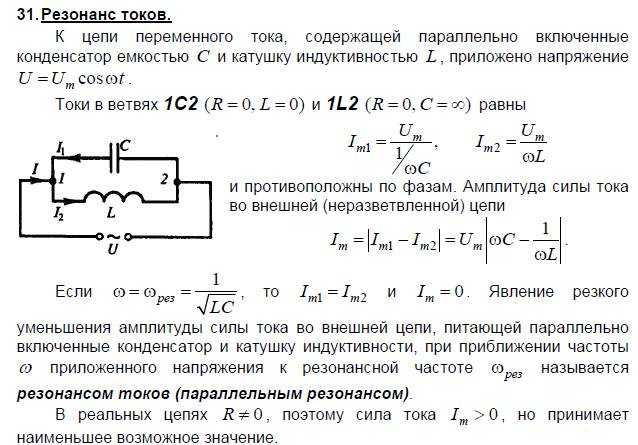
Этот результат обобщается, чтобы включить источники очень интересным и полезным способом. Давайте рассмотрим нашу простую схему аттенюатора (показанную на рис. 3.7.1) с точки зрения выходных клемм. Мы хотим найти соотношение v-i для пары выходных клемм, а затем найти эквивалентную схему для схемы в штучной упаковке. Чтобы выполнить этот расчет, используйте законы схемы и соотношения элементов, но ничего не присоединяйте к выходным клеммам. Мы ищем отношение между
\[v=(R_{1}\parallel R_{2})i+\frac{R_{2}}{R_{1}+R_{2}}v_{in} \nonumber \]
Если бы источник был нулевым, его можно было бы заменить коротким замыканием, что подтвердило бы, что цепь действительно функционирует как параллельная комбинация резисторов. Однако наличие источника означает, что схема , а не , хорошо смоделирована как резистор.
Эквивалентная схема Тевенина
Рисунок 3.7.2 Эквивалентная схема Тевенина Если мы рассмотрим простую схему на рис. 3.7.2, мы обнаружим, что она имеет отношение v-i на своих выводах
3.7.2, мы обнаружим, что она имеет отношение v-i на своих выводах
\[v=R_{eq}i +v_{eq} \номер\]
Сравнивая два отношения v-i , мы обнаруживаем, что они имеют одинаковую форму. В этом случае эквивалентное сопротивление Тевенина равно:
\[R_{eq}=R_{1}\parallel R_{2} \nonumber \]
, а эквивалентный источник Тевенина имеет напряжение:
\[ v_{eq}=\frac{R_{2}}{R_{1}+R_{2}}v_{in} \nonumber \]
Таким образом, с точки зрения терминалов, вы не можете различить две цепи. Поскольку в эквивалентной схеме меньше элементов, ее легче анализировать и понимать, чем любую другую альтернативу.
Для любой цепи , содержащей резисторы и источники, соотношение v-i будет иметь вид: цепь для любой такой цепи показана на рис. 3.7.2. Эта эквивалентность применяется независимо от того, сколько источников или резисторов может присутствовать в цепи. В приведенном ниже примере мы знаем конструкцию схемы и значения элементов и получаем эквивалентный источник и сопротивление. Поскольку теорема Тевенена применима в целом, мы должны иметь возможность проводить измерения или расчеты только с клемм для определения схемы замещения.
В приведенном ниже примере мы знаем конструкцию схемы и значения элементов и получаем эквивалентный источник и сопротивление. Поскольку теорема Тевенена применима в целом, мы должны иметь возможность проводить измерения или расчеты только с клемм для определения схемы замещения.
Чтобы быть более конкретным, рассмотрим эквивалентную схему на рис. 3.7.2. Пусть клеммы разомкнуты, что приведет к установке тока i в ноль. Поскольку ток через резистор не течет, напряжение на нем равно нулю (помните, закон Ома гласит, что ( v = i R ). Следовательно, применяя КВЛ, мы получаем, что так называемое напряжение холостого хода v oc соответствует эквивалентному напряжению Тевенена. Теперь рассмотрим ситуацию, когда мы устанавливаем напряжение на клеммах равным нулю (замыкаем их накоротко) и измеряем результирующий ток. Ссылаясь на эквивалентную схему, напряжение источника теперь появляется полностью на резисторе, оставляя ток короткого замыкания равным:
\[i_{sc}=-\frac{v_{eq}}{R_{eq}} \ nonumber \]
Из этого свойства мы можем определить эквивалентное сопротивление.
\[v_{eq}=v_{oc}\\ R_{eq}=-\frac{v_{oc}}{i_{sc}} \nonumber \]
Упражнение \(\PageIndex{1}\)
Используйте метод разомкнутого/короткого замыкания для получения эквивалента Тевенина схемы, показанной на рисунке ниже.
Решение
\[v_{oc}=\frac{R_{2}}{R_{1}+R_{2}}v_{in}\\ i_{sc}=-\frac{ v_{in}}{R_{1}} \nonumber \]
Резистор R 2 в этом случае закорочен. Таким образом,
\[v_{eq}=\frac{R_{2}}{R_{1}+R_{2}}v_{in}\\ R_{eq}=\frac{R_{1}R_{2 }}{R_{1}+R_{2}} \номер\]
Пример \(\PageIndex{1}\):
Для схемы, изображенной на рисунке выше, давайте получим эквивалент Тевенина двумя разными способами. Начав с подхода обрыва/короткого замыкания, давайте сначала найдем напряжение разомкнутой цепи v oc . У нас есть отношение делителя тока, поскольку R 1 параллельно последовательной комбинации R 2 и R 3 .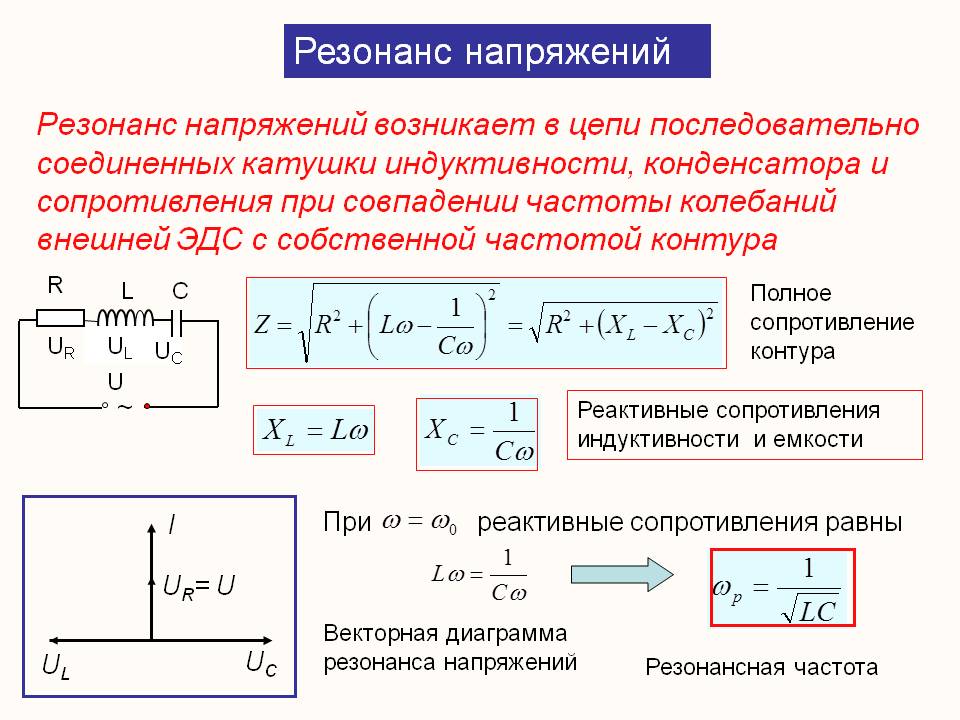 Таким образом,
Таким образом,
\[v_{oc}=\frac{i_{in}R_{3}R_{1}}{R_{1}+R_{2}+R_{3}} \nonumber \]
Когда мы замыкаем клеммы накоротко, на R 3 не появляется напряжение, и, следовательно, через него не протекает ток. Короче говоря, R 3 не влияет на ток короткого замыкания и может быть устранен. У нас снова есть текущее отношение делителя:
\[i_{sc}=-\frac{i_{in}R_{1}}{R_{1}+R_{2}} \nonumber \]
Таким образом, Эквивалентное сопротивление Тевенина составляет
\[\frac{R_{3}(R_{1}+R_{2})}{R_{1}+R_{2}+R_{3}} \nonumber \]
Чтобы проверить, давайте найдем эквивалентное сопротивление, проникнув внутрь цепи и установив источник тока на ноль. Поскольку ток теперь равен нулю, мы можем заменить источник тока разомкнутой цепью. С точки зрения выводов резистор R 3 теперь подключен параллельно последовательной комбинации R 1 и R 2 .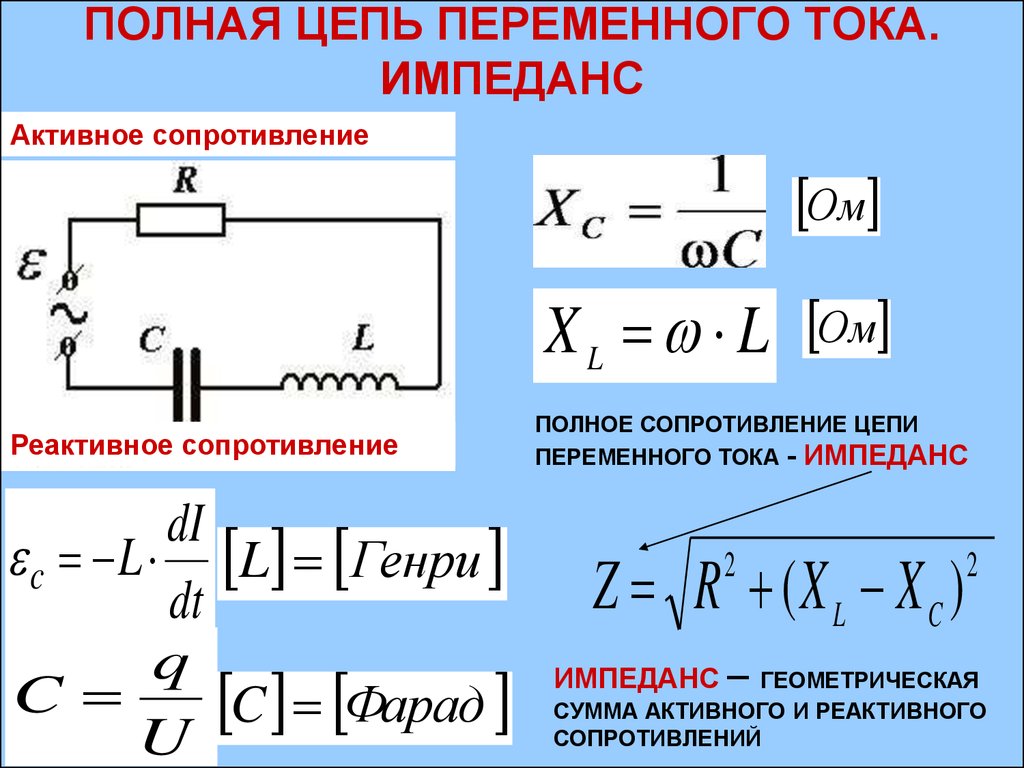 Таким образом,
Таким образом,
\[R_{eq}=R_{3}\parallel R_{1}+R_{2} \nonumber \]
и мы получаем тот же результат.
Эквивалентные схемы
Рисунок 3.7.3 Все схемы , содержащие источники и резисторы, могут быть описаны более простыми эквивалентными схемами. Выбор того, который следует использовать, зависит от приложения, а не от того, что на самом деле находится внутри схемы.Как и следовало ожидать, эквивалентные схемы бывают двух видов: , ориентированная на источник напряжения, эквивалентная Тевенина, и , ориентированная на источник тока, эквивалентная Майера-Нортона (см. рис. 3.7.3). Чтобы получить последнее, v-i соотношение для эквивалента Тевенина может быть записано как:
\[v=R_{eq}i+v_{eq} \nonumber \]
или
\[i=\frac{v}{R_{ eq}}-i_{eq} \nonumber \]
, где
\[i_{eq}=\frac{v_{eq}}{R_{eq}} \nonumber \] — эквивалент Майера-Нортона источник. Можно легко показать, что эквивалент Майера-Нортона, показанный на рис. 3.7.3, имеет отношение v-i . Обратите внимание, что оба варианта имеют одинаковое эквивалентное сопротивление. Ток короткого замыкания равен отрицательному значению эквивалентного источника Mayer-Norton.
3.7.3, имеет отношение v-i . Обратите внимание, что оба варианта имеют одинаковое эквивалентное сопротивление. Ток короткого замыкания равен отрицательному значению эквивалентного источника Mayer-Norton.
Упражнение \(\PageIndex{1}\)
Найдите эквивалентную схему Майера-Нортона для приведенной ниже схемы.
Решение
\[i_{eq}=\frac{R_{1}}{R_{1}+R_{2}}i_{in} \nonumber \]
\[R_{eq }=R_{3}\parallel R_{1}+R_{2} \nonumber \]
Эквивалентные схемы можно использовать двумя основными способами. Во-первых, упростить анализ сложной схемы, поняв, что любая часть схемы может быть описана либо эквивалентом Тевенина, либо эквивалентом Майера-Нортона. Какой из них используется, зависит от того, является ли то, что подключено к терминалам, последовательной конфигурацией (что делает эквивалент Thévenin лучшим) или параллельной конфигурацией (что делает Mayer-Norton лучшим).
Другое приложение для моделирования. Когда мы покупаем аккумулятор для фонарика, любая эквивалентная схема может точно его описать. Эти модели помогают нам понять ограничения батареи. Поскольку батареи имеют маркировку со спецификацией напряжения, они должны служить источниками напряжения, и эквивалент Thévenin служит естественным выбором. Если на его клеммы поместить сопротивление нагрузки R L , выходное напряжение можно найти с помощью делителя напряжения:
Когда мы покупаем аккумулятор для фонарика, любая эквивалентная схема может точно его описать. Эти модели помогают нам понять ограничения батареи. Поскольку батареи имеют маркировку со спецификацией напряжения, они должны служить источниками напряжения, и эквивалент Thévenin служит естественным выбором. Если на его клеммы поместить сопротивление нагрузки R L , выходное напряжение можно найти с помощью делителя напряжения:
\[v=\frac{v_{eq}R_{L}}{R_{L}+ R_{экв}} \номер \]
Если у нас есть сопротивление нагрузки, намного превышающее эквивалентное сопротивление батареи, то, в хорошем приближении, батарея действительно служит источником напряжения. Если сопротивление нагрузки намного меньше, то у нас точно нет источника напряжения (выходное напряжение напрямую зависит от сопротивления нагрузки). Рассмотрим теперь эквивалент Майера-Нортона; ток через сопротивление нагрузки определяется делителем тока и равен:
\[i=\frac{i_{eq}R_{eq}}{R_{L}+R_{eq}} \nonumber \]
Для тока, который не зависит от сопротивления нагрузки, это сопротивление должно быть намного меньше эквивалентного сопротивления. Если сопротивление нагрузки сравнимо с эквивалентным сопротивлением, батарея служит ни , ни как источник напряжения или ток. Таким образом, когда вы покупаете аккумулятор, вы получаете источник напряжения, если его эквивалентное сопротивление на меньше на , чем эквивалентное сопротивление цепи, к которой вы его подключаете. С другой стороны, если вы подключили его к цепи, имеющей небольшое эквивалентное сопротивление, вы купили источник тока.
Если сопротивление нагрузки сравнимо с эквивалентным сопротивлением, батарея служит ни , ни как источник напряжения или ток. Таким образом, когда вы покупаете аккумулятор, вы получаете источник напряжения, если его эквивалентное сопротивление на меньше на , чем эквивалентное сопротивление цепи, к которой вы его подключаете. С другой стороны, если вы подключили его к цепи, имеющей небольшое эквивалентное сопротивление, вы купили источник тока.
Леон Шарль Тевенен
Он был инженером французской компании Postes, Télégraphe et Téléphone. В 1883 году он опубликовал (дважды!) доказательство того, что сейчас называется эквивалентом Тевенена, разрабатывая способы преподавания концепций электротехники в Политехнической школе. Он не знал, что тот же самый результат был опубликован Германом Гельмгольцем, известным физиком девятнадцатого века, три года назад.
Ханс Фердинанд Майер
После получения докторской степени по физике в 19В 20 лет он обратился к технике связи, когда присоединился к Siemens & Halske в 1922 году. В 1926 году он опубликовал в немецком техническом журнале эквивалент Майера-Нортона. За время своей интересной карьеры он дослужился до руководителя Центральной лаборатории Симена в 1936 году, тайно слил британцам все, что знал о военных возможностях Германии, через месяц после вторжения нацистов в Польшу, был арестован гестапо в 1943 году за прослушивание радиопередач Би-би-си, потратил два года в нацистских концентрационных лагерях и уехал в Соединенные Штаты на четыре года, работая в ВВС и Корнельском университете, прежде чем вернуться в Сименс в 1919 году.50. Перед уходом на пенсию он поднялся до должности в совете директоров Siemens.
В 1926 году он опубликовал в немецком техническом журнале эквивалент Майера-Нортона. За время своей интересной карьеры он дослужился до руководителя Центральной лаборатории Симена в 1936 году, тайно слил британцам все, что знал о военных возможностях Германии, через месяц после вторжения нацистов в Польшу, был арестован гестапо в 1943 году за прослушивание радиопередач Би-би-си, потратил два года в нацистских концентрационных лагерях и уехал в Соединенные Штаты на четыре года, работая в ВВС и Корнельском университете, прежде чем вернуться в Сименс в 1919 году.50. Перед уходом на пенсию он поднялся до должности в совете директоров Siemens.
Эдвард Л. Нортон
Эдвард Нортон был инженером-электриком, который работал в лаборатории Белла с момента ее основания в 1922 году. эквивалент. Нет никаких доказательств того, что Нортон знал о публикации Майера.
Эта страница под названием 3.7: Эквивалентные схемы — резисторы и источники распространяется под лицензией CC BY 1.