Программное обеспечение «1-2-3 схема» для комплектации распределительных щитов от компании HAGER | Публикации
Программное обеспечение «1-2-3 схема» («1-2-3 Schema») позволяет подобрать распределительный щит по степени защиты, закомплектовать его автоматическими выключателями, УЗО, АВДТ, контакторами и другими модульными аппаратами, задать иерархию расключения аппаратов, автоматически сформировать однолинейную схему щита и создать спецификацию.
Программа позволяет правильно выбрать тип корпуса и его размер, исходя из количества модулей, нужным образом промаркировать модульные аппараты.
Элементная база «1-2-3-схемы» содержит актуальные артикулы продукции, которые поставляются на российский рынок и сертифицированы по российским и европейским стандартам. С помощью «1-2-3-схемы» можно грамотно составить спецификацию, создать однолинейную схему электрощита и отрисовать его внешний вид. Однолинейную схему щита можно сохранить в формате Autocad (*.
dwg) и изменить ее в соответствии с пожеланиями.
Программа «1-2-3 схема» распространяется бесплатно и доступна для скачивания с сайта ООО «Электросистемы и технологии», официального представительства HAGER в России и Казахстане.
Шаг 1. Выбор серии корпуса щита по техническим требованиям.
Подбор осуществляется на основе требуемого типа монтажа (навесной или встраиваемый), степени защиты (IP30, IP44, IP65), материала оболочки (пластик или сталь), количества модулей (по 17,5 мм).
Шаг 2. Выбор корпуса по количеству модулей (4-10, 12 или кратно 12, 18 или 22).
Результат выбора отображается в новом окне.
Шаг 3. Выбран корпус щита, необходимо выбрать аппараты из элементной базы.
Аппараты выбираются из элементной базы, расположенной справа. При наведении мышки на иконку аппарата подсвечивается его наименование, например, так:
При клике на иконку аппарата в элементной базе он «захватывается» отверткой и «устанавливается» на дин-рейку.
Если аппарат можно установить на дин-рейке, то отвертка подсвечивается красным цветом. Если установка аппарата невозможна (например, если аппарат не помещается на дин-рейке), то отвертка окрашена серым цветом.
В результате перенесения аппарата на дин-рейку, выскакивает меню уточнения характеристик аппарата:
В меню уточнения характеристик автоматического выключателя можно выбрать номинал автомата, увидеть его артикул, задать вручную или из списка тип помещения и тип нагрузки,задать обозначение автоматического выключателя на однолинейной схеме.
Результат выбора и расстановки аппаратов (вид корпуса щита)
Верхнее меню позволяет сохранить файл проекта, распечатать его, отобразить спецификацию, однолинейную схему, сформировать лист маркировок и др.
Результат выбора и расстановки аппаратов (вид однолинейной схемы)
Результат выбора и расстановки аппаратов (вид спецификации)
К сформированной спецификации можно добавить продукты из каталога:
Формирование листа маркировок
Пример 1.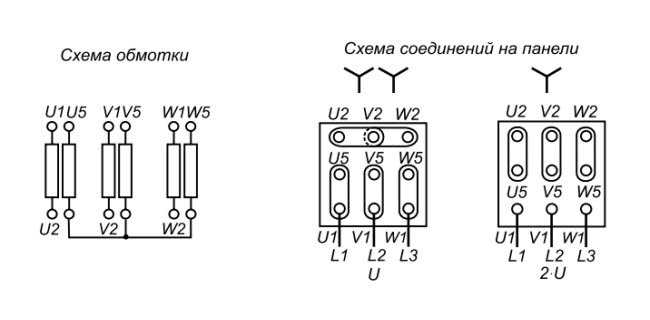
Маркировка аппаратов с помощью шильдиков, расположенных на автоматических выключателях, УЗО, диф. автоматах и др. (серии MCN, ADA, CDA и др.)
Пример 2. Маркировка квартирного щита, скомплектованного на основе «1-2-3 схемы» (проект и сборка щита от компании «Маниэль», www.maniel.ru, партнера HAGER)
Программа «1-2-3 схема» облегчает комплектацию небольших распределительных щитов, надеемся, она будет вам полезной!
По материалам ООО «Электросистемы и технологии»
Переключатель кулачковый схема 56, GN20-56-U, 4G16-56-U Монтажные системы
Поиск по каталогу
Каталог
Мониторинг и контроль работы КРУ
Арматура светосигнальная
- Лампы
- Индикаторы и указатели положения
Кнопки
- LAY4
- SB7
Заземлители РВЗ и аксессуары к ним
- Заземлители, РВЗ (без опорных изоляторов)
- Заземлители, РВЗ-И/ИС (с опорными изоляторами)
- Заземлители, РВЗ-М (мотор.
привод сбоку) - Заземлитель, РВЗ-М.1 (мотор. привод между фаз)
- Приводы заземлителя
- Комплектующие привода заземлителя
Тележки для вакуумного выключателя
- Тележка аппаратная, тип: DPC-4 (ручной привод)
- Тележка аппаратная, тип: DPC-4М (моторизованный привод)
- Комплектующие аппаратной тележки
Шторочные механизмы
Коммутационные аппараты
Эпоксидные изоляторы 6-10 кВ
- Проходные изоляторы
- Опорные изоляторы
Эпоксидные изоляторы 20-35 кВ
- Проходные изоляторы
- Опорные изоляторы
- Изоляция магистральной шины
Контактная система вакуумного выключателя
- Контакт подвижный, тип: КП
- Контакт, тип: КЛ/КР
- Контакт неподвижный, тип: КН
- Изоляция контактной системы
Освещение кабельного отсека и блока релейной защиты
Терморегуляторы
Фурнитура для электротехнических шкафов
Нагревательные элементы
Вентиляторы и фильтры
Кулачковые переключатели
Зажимы кабельные
Полезные мелочи
привод сбоку)Отзывы
Оставить отзыв
Все отзывы (0)
org/BreadcrumbList»>Переключатель кулачковый LW126-20 1-2, 20А, 2 пол. (схема 56)
Заказать
Переключатель кулачковый LW126-20 1-2, 20А, (схема 56)
Номинальное напряжение, Ui: 660V.
Номинальный ток, Ith: 20A.
Заказать
Переключатель кулачковый LW126-20 Y… →
SI413: Основы схемы
SI413: Основы схемыРазжигание доктора Рэкета
В командной строке просто введите « drracket & » и
вы должны увидеть открытое разделенное окно интерпретатора/ввода кода
вверх.
В меню: Lanugagues → Выбрать
Язык выбираем R5RS . ] Нижняя панель — интерпретатор. Вы можете ввести схему
выражение как (+ 3 4) по подсказке и
Клавиша return заставит интерпретатор
оценить выражение — при условии, что курсор находится в
конец строки . Вы можете довести курсор до конца
линии мгновенно с комбинацией ctrl-e (управление и
клавиши e нажаты одновременно).Примечание: в этот момент мы продолжим и сохраним ваш определения (верхнее окно), даже если оно пустое. Сначала добавьте строку
; <вашеимя> <ваша альфа>
в окно определений. ‘;’ является символом комментария в
схема и каждый файл исходного кода, который вы отправляете в рамках курса
должно быть ваше имя и альфа наверху!
Затем сохраните определения с помощью
имя файла схема01.scm .
Если он спросит, хотите ли вы сохранить его как открытый текст, вы говорите да !
Это файл, который вы в конечном итоге отправите в систему отправки.
Арифметические выражения
Выражение в Scheme является либо атомарным объектом (числом,
символ, строка) или это список выражений внутри
круглые скобки — элементы, разделенные пробелом.
Когда список оценивается интерпретатором, первый элемент
рассматривается как функция, а остальные элементы рассматриваются
в качестве аргументов функции. Итак, вместо sqrt(2.4) , на схеме мы говорим (sqrt
2.4) . Конечно, выражения могут быть вложенными.
(композиция функций), поэтому кв.(3,4*2,9) выражается на схеме как (sqrt (* 3,4 2,9)) .
Числовые типы
Раздел
6.2
определения языка схемы R5 описывает числа в
Схема. Вот некоторые важные моменты.
Целые числа в Scheme могут быть произвольно большими (BigInts, вы
слышно, как люди говорят), и число, записанное без десятичной точки
точка задана целочисленным типом. Числа с плавающей запятой (тип
«настоящие») являются
по существу удваивается, и если вы пишете число с
десятичная точка будет рассматриваться как действительная.
Целочисленные функции
Все перечисленные ниже функции возвращают целочисленные значения.
+ - * остаток по модулю макс мин абс числитель знаменатель НОД лкм пол потолок урезать раунд рационализировать эксп
Обратите внимание, что деления здесь нет. Деление возвращает рациональное значение (то есть дробь).
Функции с плавающей запятой Вышеупомянутые функции, которые имеют смысл для вещественных чисел, определены для реалов, кроме того, у вас есть другие, такие как:
грех, потому что загар кв
что должно быть понятно. Функции точно->неточно и неточно-> точно преобразовать из рационального туда и обратно
числа с плавающей запятой.
упражнений:
- Напишите 4,7*(34,453 — 47,728) + 3,7 как схему
выражение и найти его значение. (-58.6925)
- Такие функции, как +,-*,max и min, которые имеют смысл для
работает более двух аргументов (и меньше двух!)
просто отлично для более чем двух аргументов. Например:
(+ 1 2 3) равно 6, как и следовало ожидать.
Напишите выражение, результатом которого является наибольшее значение
sqrt(5), sin(1) + sin(2) + sin(3) и 17/8. Примечание:
Помните, что целочисленное деление дает рациональные числа.
Функция 92 + 3*x — 5, а затем просто вызовите функцию с помощью
аргумент 2.451.
Так как же написать функцию? Ну, выше было бы:
> (определить (f x) (+ (* 2 x x x) (* -1 x x) (* 3 x) -5)) > (f 2,451) 25.793878702
На самом деле это что-то вроде ярлыка для определения функции, как мы обсудим позже. Ясно, что вы определяете новая функция с именем
fи параметром имена — это все остальное, указанное в скобках (простоxв данном случае), и далее следует выражение, являющееся значением функции. Для более простой пример, функция с именемmy-aveможет быть определено так:( определить (мой-ср x y) (/ (+ x y) 2.
Надеюсь, три компонента понятны.
Упражнения
- Функции записи
по Цельсиюивградусов по Фаренгейту, которые конвертируются туда и обратно от Цельсия до Фаренгейта. Напомним: T_C = 5/92 + x*cos(x) и для а для его производной cos(x) — x sin(x) + 2 cos(x) sin(x).
Управление: if и cond
В C++ if являются операторами. Это означает, что у них нет тип и они не имеют значения. Вместо этого они описывают процесс, побочные эффекты которого (выход, изменения переменных значения и т. д.) воплощают фактические вычисления. В схеме все является выражением, и это включает в себя if’s. Выражение if состоит из трех частей: тестовое условие, выражение «тогда» и выражение «иначе». Значение если выражение является либо выражением «тогда» (когда тест оценивается как true) или выражение «else». Например, следующее выражение оценивается как абсолютное значение x:
( если (< х 0) (* -1 х) х )
Видите ли, в зависимости от результата теста мы либо получаем значение -1*x или просто сам x.
Мы можем, конечно, использовать
это, чтобы определить функцию абсолютного значения:(определить (my-abs x) (если (< x 0) (* -1 x) x))
хотя, конечно, схема уже есть. Мы можем вкладывать эти выражения по мере необходимости.
упражнений:
- Определите функцию с именем
signed-inc, который возвращает 1 плюс аргумент, если аргумент неотрицательное, и -1 плюс его аргумент, если аргумент отрицательный. - Переопределить
signed-incтак, чтобы он возвращал аргумент не изменяется, если аргумент равен 0, но в противном случае действует как прежде. - Определите функцию
в середине, которая занимает три числа в качестве аргумента и возвращает среднее из трех. Например.(средний 4 2 3)должен оцениваться как 3.
В схеме присутствуют логические операторы и, или и не как вы и предполагали. Истинной в схеме является константа #t а false — константа #f.
Например:> (и (> 1 0) (< 2 -3)) #ф > (или (> 1 0) (< 2 -3)) #т
Числа можно сравнивать с обычными: т.е. <, >, ≤, ≥, =. Примечание: для нечисловых объектов
равно?- это то, что вы хотите использовать (также работает с числами).Также есть приятная функция
condэто полезно когда у вас есть куча различных случаев для рассмотрения. За например, если вы хотите определить функцию whats-your-sign который возвращает 1,0,-1 в соответствии со знаком числа, вы может использоватьусловиеследующим образом:(определить (какой-ваш-знак x) (конд (( х 0) 1) ((= х 0) 0) ) )Таким образом, аргументы cond образуют список пар условие/результат. Интерпретатор находит первое условие, которое выполняется, и значением выражения cond является результат, связанный с таким условием.
упражнений:
- Переопределить
среднийсверху с условными обозначениями и и х.
Рекурсия!
Чтобы сделать что-нибудь интересное в Scheme, нам нужна рекурсия. Причина в том, что у нас нет петель! Предположим, например, что мы хотел определить функцию
sum-range, которая бы суммировать все целые числа в заданном диапазоне. Обычно мы думаем использования циклов для этого, но Scheme не делает циклы! Они вопреки идее ссылочной прозрачности - т.е. побочные эффекты. Циклы созданы для создания побочных эффектов. снова и снова и снова. В любом случае нам нужно использовать рекурсию:(определить (сумма-диапазон i j) (if (= i j) i (+ i (сумма-диапазон (+ i 1) j))))
В рекурсии нет ничего нового для вас, ребята, вы просто будете использовать много больше об этом в Схеме.
упражнений:
- Определите функцию
факториала. Попробуйте взять факториал числа 111. Что вы заметили в результат. Считаете ли вы, что прямолинейный C++ реализация могла бы дать вам этот результат? - Я хочу вычислить сложные проценты. Написать функцию
начисляемчто занимает остаток, годовой процентная ставка и количество лет и возвращает остаток на конец периода, если предположить, что проценты начисляются ежемесячно. Напомним: если годовой процентная ставка равна r%, а остаток равен B, тогда начисление процентов дает новый баланс B*(1 + r/100/12). Подсказка: Хорошее восходящее решение вероятно, потребуется написать(составной месяц B r)функция, которая делает только один месяц состав, тестирование, а затем двигаться дальше. Далее напишитеначислений-месяцевчто бы взять остаток, а ставки и количество месяцев, и вычислить баланс в конец этого месяца - проверьте это! Тогда должно быть легко написать вашинакапливают функцию. - Напишите функцию
fibдля вычисления чисел Фибоноччи. Напомним, что fib(0) и fib(1) равны 1. Все остальные определенный по правилу fib(n) = fib(n-1) + fib(n-2).
пусть
9Конструкция 0005 let на схеме позволяет дать имя общего подвыражения.
Например, рассмотрим
выражение(33 * (501 - 33)) / ( 1 - (33 * (501 - 33)))
Естественный способ закодировать это на схеме, вероятно,
(/ (- (* 33 501) 33) (- 1 (- (* 33 501) 33)))
Но вы могли бы сказать: "пусть а = 33 * (501 - 33) и вернуть / (1 - а)". По сути, это то, что позволяет вам делать
let.(пусть ((а (- (*32 501) 33))) (/ а (- 1 а)))
По сути,
пусть- это способ схемы получить локальный изменяемый функционал. То, что у вас есть, этоключевое слово let, за которым следует список пары имя-переменная/значение, за которыми следует выражение (предположительно с использованием новых имен), который обеспечивает значение весьпустьвыражение. Например:> ( лет ((а 2) (б 4) (в 6)) (+ а б в) ) 12
Использование
пустьв функциях 92. Пример: , если x=5,1, вышеприведенное значение равно -1,54771. - Функции записи
- Напишите функцию
diff, которая вычисляет разница (в дюймах) между двумя длинами (в футах) и дюймы). Пример:> (diff 3 7 2 11) ← разница между 3' 7'' и 2' 11'' 8
Напишите эту функцию, используя выражениеlet. для создания значенийL1иL2для длины в дюймах входных длин в футах и дюймах.
(-58.6925)
Мы можем, конечно, использовать
это, чтобы определить функцию абсолютного значения:
Например:
Написать функцию 
Например, рассмотрим
выражение
Пример: , если x=5,1, вышеприведенное значение равно -1,54771.Отправить
Вы отправляете файл схема01.scm в
подать систему. Убедитесь, что все, что не является функцией
определение закомментировано, так что нет вывода, когда
скрипт выполняется. Вы будете представлять как:
отправить -c=si413 -p=scheme01 схема01.scm
Кристофер В. Браун
Введение в информатику, глава 9: Лямбда
изобретатель лямбда-исчисления
Простая схема: Введение в информатику 2/e Copyright (C) 1999 MIT
Глава 9
|
Допустим, мы хотим добавить по три к каждому числу в предложении.
С использованием
инструменты из главы 8, мы бы сделали это так:
(определить (добавить три числа) (+ цифра 3)) (определить (добавить три к каждому отправленному) (каждая добавленная тройка отправлена)) > (прибавить три к каждому '(1 99 2)) (4 12 12 5)
Немного раздражает необходимость определять вспомогательную процедуру add-three только для того, чтобы мы могли использовать ее в качестве аргумента для каждые . Были
никогда не будем использовать эту процедуру снова, но нам все еще нужно придумать
имя для него. Нам нужен общий способ сказать: «Вот функция, которую я хочу
вам использовать" без необходимости называть процедуру. Другими словами,
нам нужна процедура генерации процедур общего назначения!
Лямбда — это имя специальной формы, которая генерирует процедуры. Это
принимает некоторую информацию о функции, которую вы хотите создать, в качестве аргументов
и он возвращает процедуру. Объяснить детали будет легче после
вы видите пример.
(определить (добавить три к каждому отправленному) (каждые (лямбда (число) (+ число 3)) отправлено )) > (прибавить три к каждому '(1 9 9 2)) (4 12 12 5)
Первый аргумент каждые , по сути, одна и та же процедура
как тот, который мы называли add-three ранее, но теперь мы можем использовать его без
дать ему имя. (Не делайте ошибку, думая, что лямбда аргумент каждые . Аргумент процедура вернула
к лямбда .)
Возможно, вам интересно, пишется ли слово «лямбда» в обратном порядке.
На самом деле это название греческой буквы Л, которая выглядит как
это: λ. Вероятно, было бы разумнее, если бы лямбда были названы
что-то вроде make-procedure , но имя lambda традиционный.[1]
Создание процедуры с использованием лямбды очень похоже на ее создание.
с определите , как мы делали до этого момента, за исключением того, что мы не
указать имя.
Когда мы создаем процедуру с определить , мы должны
указать имя процедуры, имена ее аргументов (т. е. формальный
параметры) и выражение, которое он вычисляет (его тело). С lambda мы по-прежнему предоставляем последние два из этих трех компонентов.
Как мы уже говорили, лямбда — это особая форма. Это значит, как вы
помните, что его аргументы не оцениваются, когда вы его вызываете.
первый аргумент — это предложение, содержащее формальные параметры; секунда
аргумент - это тело. Что lambda возвращает безымянная процедура.
Вы можете вызвать эту процедуру:
> ((лямбда (a b) (+ (* 2 a) b)) 5 6) 16 > ((лямбда (wd) (слово (последнее wd) (первое wd))) 'озорной) ЗДРАВСТВУЙ
Однако в реальной жизни вы вряд ли создадите процедуру с лямбдой просто для того, чтобы вызвать ее один раз. Чаще мы используем лямбда как в
первый пример в этой главе, чтобы предоставить процедуру в качестве аргумента
функция высшего порядка.
Вот еще несколько примеров:
> (каждый (лямбда (wd) (se (первый wd) wd (последний wd)))
'(только северная песня))
(О ТОЛЬКО Я А А Н СЕВЕРНАЯ Н С ПЕСНЯ Г)
> (держать (лямбда (н) (член? 9 н)) '(4 81 909 781 1969 1776))
(909 1969)
> (накопить (лямбда (это то)
(если (> (считай это) (считай то)) это то))
'(дикий медовый пирог))
МЕДОВЫЙ
> (держать (лямбда (человек) (член? человек '(джон пол джордж ринго)))
'(Мик Смоки Пол Диана Билл Гедди Джон Йоко Кит Репарата))
(ПОЛ ДЖОН)
> (держать (лямбда (человек) (член?'е человек))
'(Мик Смоки Пол Диана Билл Гедди Джон Йоко Кит Репарата))
(СМОКИ ГЕДДИ КИТ РЕПАРАТА)
Процедуры, возвращающие процедуры
Еще более мощное использование лямбда заключается в предоставлении возвращаемого значения.
по какой-то процедуре, которую вы пишете. Вот классический пример:
(определить (сделать-добавочный номер) (лямбда (х) (+ х число))) > ((составить сумматор 4) 7) 11 > (каждый (составить сумматор 6) '(2 4 8)) (8 10 14)
Значение выражения (составить-сумматор 4) - это процедура, не число.
Эта безымянная процедура добавляет 4 к
его аргумент. Мы можем понять это, применив модель замещения к сделать сумматор . Подставляем 4 вместо num в теле make-adder ; мы заканчиваем с
(лямбда (х) (+ х 4))
, а затем мы оцениваем это выражение, чтобы получить желаемую процедуру.
Вот процедура, аргументом которой является процедура:
(определить (один и тот же аргумент дважды fn) (лямбда (аргумент) (фн аргумент аргумент))) > ((один и тот же аргумент-дважды слово) 'привет) ПРИВЕТ ПРИВЕТ > ((один и тот же аргумент-дважды *) 4) 16
Когда мы оцениваем (один и тот же аргумент-дважды слово) подставляем процедуру слово для формального параметра fn , и результат
(лямбда (аргумент) (аргумент слова аргумент))
Еще один пример:
(определить (перевернуть fn) (лямбда (a b) (fn b a))) > ((перевернуть -) 5 8) 3 > ((flip se) 'до свидания' привет) (ПРИВЕТ ПОКА)
Правда о
Определение Помните, как мы говорили, что создать процедуру с лямбдой было много?
как создать процедуру с определить ? Это потому, что обозначение
мы использовали с определить это аббревиатура, которая объединяет два
действия: создание процедуры и присвоение имени чему-либо.
Как вы видели в главе 7, определяет, что настоящая задача — дать имя
к некоторому значению:
> (определить пи 3,141592654) > (* пи 10) 31.41592654 > (определить барабанщика '(Ринго Старр)) > (первый барабанщик) Ринго
Когда мы говорим
(определить (квадрат x) (* x x))
на самом деле это сокращение от
(определить квадрат (лямбда (х) (* х х)))
В этом примере задание лямбда состоит в создании процедуры
что умножает свой аргумент сам на себя; задание определить имя
та процедура квадрат .
В прошлом, даже не говоря об этом, мы говорили так, как будто имя процедура понималась иначе, чем другие имена в программе. В думать о таком выражении, как
(* х х)
мы говорили о замене x некоторым фактическим значением.
но принял * как должное как значение функции умножения.
Правда в том, что мы должны заменить значение * так же, как мы
сделать для х .
Просто так получилось, что * было предопределено для
иметь в качестве значения процедуру умножения. Это определение * глобальный, как определение пи выше. «Глобальный» означает
что это не формальный параметр процедуры, вроде x в квадрате ,
но имеет постоянную стоимость, установленную определением .
При вычислении выражения каждое имя в выражении должно иметь некоторые подставленное вместо него значение. Если имя является формальным параметром, то подставляется соответствующее фактическое значение аргумента. В противном случае имя имело лучше иметь глобальное определение, и заменяет значение . Это просто так получилось, что схема предопределила миллион имен, прежде чем вы начнете работают, и большинство из них являются именами примитивных процедур.
(Кстати, это объясняет, почему, когда вы делаете ошибку в имени
процедуры вы можете увидеть сообщение об ошибке, которое ссылается на переменные, такие как
"переменная сначала не привязана.
" Вы могли бы ожидать, что он скажет " frist не процедура», но проблема ничем не отличается от любой другой
имя, которое не имеет связанного значения.)
Теперь, когда мы знаем всю правду о , определяем , мы можем использовать его в
в сочетании с функциями создания функций в последних двух главах.
> (определить квадрат (один и тот же аргумент дважды *)) > (квадрат 7) 49 > (определить четвертую степень (повторяющийся квадрат 2)) > (четвертая степень 5) 625
Правда о
Пусть В Главе 7 мы ввели пусть как аббревиатуру для
ситуация, в которой мы иначе определили бы вспомогательную процедуру, чтобы
давать имена часто используемым значениям в расчетах. Мы начали с
(определить (корни a b c)
(корни1 a b c (sqrt (- (* b b) (* 4 a c)))))
(определить (корень1 a b c дискриминант)
(se(/(+(-b)дискриминант)(* 2 а))
(/ (- (- b) дискриминант) (* 2 a))))
и ввел новое обозначение
(определить (корни a b c)
(пусть((дискриминант(sqrt(-(*bb)(*4ac)))))
(se(/(+(-b)дискриминант)(* 2 а))
(/ (- (- b) дискриминант) (* 2 а)))))
, чтобы избежать создания бесполезной именованной процедуры.
Но сейчас
что мы знаем о безымянных процедурах, мы можем видеть, что пусть просто
сокращение для создания и вызова анонимной процедуры:
(определить (корни a b c)
( (лямбда (дискриминант)
(se(/(+(-b)дискриминант)(* 2 а))
(/ (- (- b) дискриминант) (* 2 a))))
(квт(- (*б б) (*4 а в)))) )
То, что выделено жирным шрифтом выше, — это часть, которая вызывает процедура, созданная лямбдой, включая фактическое выражение аргумента.
Так же, как обозначение для определения процедуры с круглыми скобками вокруг ее имени
является аббревиатурой для , определяющей и лямбда , пусть обозначение является аббревиатурой лямбда и вызовом.
Конфликты имен
Когда процедура создается внутри другой процедуры, что произойдет, если вы использовать одно и то же имя формального параметра в обоих?
(определить (ф х) (лямбда (х) (+ х 3)))
Ответ: Не делайте этого.
На самом деле происходит то, что внутренний размер x побеждает; это тот, который есть
подставляется в тело. Но если вы окажетесь в такой ситуации, вы
почти наверняка делают что-то не так, например, используют неописательные
имена, такие как x для ваших переменных.
Именованные и безымянные функции
Хотя вы сталкивались с идеей функционирования еще со школы
алгебра, вы, вероятно, никогда не видели безымянная функция до сих пор.
Обозначение функции средней школы, g ( x )=3 x +8, требует от вас
дайте функции имя (в данном случае g ) при ее создании. Большинство из
функции, которые вы знаете, как в математике, так и в программировании, имеют имена, такие как
логарифм или сначала .[2]
Когда вы хотите назвать функцию, а когда нет? Это может помочь подумать
про аналогию с числами. Представьте, если бы каждый номер схемы должен был иметь
имя, прежде чем вы могли его использовать.
Вы должны сказать
> (определить три 3) > (определить четыре 4) > (+ три четыре) 7
Это аналогично тому, как мы имели дело с процедурами до сих пор, давая каждому имя. Иногда гораздо проще использовать номер напрямую, и глупо давать ему имя.
Но иногда это не глупо. Типичный пример, который мы видели ранее, это
(определить пи 3.141592654) (определить (радиус круга) (* радиус пи радиус)) (определить (радиус окружности) (* радиус 2 Пи)) (определить (радиус площади поверхности сферы) (* Радиус радиуса 4 Пи)) (определить (радиус сферы-объема) (* (/ 4 3) пи радиус радиус радиус))
Если бы мы не могли назвать число 3.141592654, мы бы приходится вводить снова и снова. Помимо дополнительного набора текста, наш программы будет труднее читать и понимать. Присвоение π имени делает процедуры более самодокументируемы. (То есть кто-то еще, кто читает нашу процедурам будет легче понять, что мы имели в виду.)
То же самое и с процедурами.
Если мы собираемся использовать процедуру более
один раз, и если для него есть значимое имя, которое поможет прояснить
программы, то мы определяем процедуру с помощью определите и дайте ему имя.
(определить (квадрат x) (* x x))
Квадрат заслуживает такого названия, потому что мы его часто используем и
потому что для него есть хорошее традиционное название, понятное всем.
Что еще более важно, давая квадратных имя, мы переключаем внимание
из процесса, с помощью которого он работает (вызов процедуры умножения)
для своей цели , вычисления квадрата числа. Отныне мы
можно думать о возведении в квадрат, как если бы это был примитив Схемы. Эта идея о
назвать что-то и забыть детали его реализации - вот что
мы называли «абстракция».
С другой стороны, если у нас есть неважная процедура, которую мы используем только
однажды мы могли бы также создать его с лямбдой и без имени.
> (каждый (лямбда (x) (последний (bl x))) '(теперь все вместе)) (ЛЕО)
Мы могли бы определить эту процедуру с именем next-to-last , но если мы больше никогда не будем ее использовать, зачем беспокоиться?
Вот пример, в котором мы используем непонятную безымянную функцию, чтобы помочь мы определим тот, который стоит назвать:
(определить (назад wd) (накопить (лямбда (a b) (слово b a)) wd)) > (назад «вчера») ЯДРЕЦЕЙ > (каждый задом наперед (я видел, как она там стоит)) (Я БЫЛ РЭХ ГНИДНАЦ ЭРЭХТ)
Ловушки
Очень удобно, что определяет в сокращенной форме
определить процедуру, используя скрытую лямбду , но поскольку есть два
обозначения, отличающиеся лишь незначительно — у каждого есть дополнительный набор
круглые скобки — вы можете по ошибке использовать не ту.
Если вы скажете
(определить (пи) 3.141592654)
вы не определяете переменную, значение которой является числом. Вместо
значение pi будет процедурой . Тогда это будет ошибка
сказать
(* 2 шт.)
Когда тело вашей процедуры должно быть выражением lambda ?
Легко переусердствовать и сказать: «Я пишу процедуру, поэтому, наверное,
нужно лямбда ", даже если процедура должна вернуть слово.
Секрет в том, чтобы помнить идеи домен и диапазон что
мы говорили в главе 2. Каков диапазон функции
ты пишешь? Должен ли он возвращать процедуру? Если это так, его тело может быть лямбда выражение. (Вместо этого это может быть вызов
процедура более высокого порядка, такая как , повторенная , которая возвращает процедуру.)
Если ваша процедура не возвращает процедуру, ее тело не будет выражением lambda . (Конечно, ваша процедура может по-прежнему использовать лямбда выражение в качестве аргумента некоторой другой процедуры, например, каждые .
)
Например, вот процедура сохранения слов предложения, содержащих
письмо ч . Домен функции — предложения, а ее диапазон
также предложения. (То есть он принимает предложение в качестве аргумента и возвращает
предложение как его значение.)
(определить (оставить-h отправлено) (держать (лямбда (wd) (член?'h wd)) отправлено))
Напротив, вот функция буквы, которая возвращает процедура для сохранения слов, содержащих эту букву.
(определить (буква хранителя)
(лямбда (отправлено)
(держать(лямбда(вд)(член? буква вд)) отправлено)))
Хранитель процедуры имеет буквы в качестве своего домена и процедуры
как его диапазон. Процедура , возвращенная хранителем , имеет предложения
как его домен и как его диапазон, как это делает keep-h . На самом деле, мы можем
используйте keeper для определения keep-h :
(определить keep-h (хранитель 'h))
Не путайте создание процедуры с вызовом одной.
Lambda создает процедуру. Процедура
вызывается в ответ на выражение, первое подвыражение которого представляет
та процедура. То есть первым подвыражением может быть имя .
процедуры, или это может быть выражение лямбда , если вы хотите
создайте процедуру и сразу же вызовите ее:
((лямбда (х) (+ х 3)) 6)
В частности, когда вы создаете процедуру, вы указываете ее формальную
параметры — именует для своих аргументов. Когда вы вызываете
процедура, вы указываете значений для этих аргументов. (В этом примере
выражение lambda включает формальный параметр x , но
вызов предоставляет фактический аргумент 6 .)
Сверлильные упражнения
9.1 Что напечатает Scheme? Выясните это сами, прежде чем пытаться на компьютере.
> (лямбда (х) (+ (* х 3) 4))
> ((лямбда (х) (+ (* х 3) 4)) 10)
> (каждое (лямбда (wd) (слово (последнее wd) (bl wd)))
'(в любое время))
> ((лямбда (х) (+ х 3)) 10 15)
9.
2 Перепишите следующие определения так, чтобы неявная лямбда явный.
(определить (второй материал) (первый (бф материал))) (определить (сделать число сумматора) (лямбда (х) (+ число х)))
9.3 Что делает эта процедура?
(определить (разрешить отправку) (накопить (лямбда (x y) y) отправлено))
Реальные упражнения
9.4 Следующая программа не работает. Почему бы и нет? Почини это.
(определить (кто отправил) (каждое описание '(пит роджер джон кит))) (определить (описать человека) (сей человек прислал))
Это должно работать так:
> (кто '(продается)) (Пит продает, Роджер продает, Джон продает, Кит продает)
В каждом из следующих упражнений запишите процедуру в терминах лямбда и функции более высокого порядка. Не используйте именованные вспомогательные процедуры.
Если вы читали часть IV, тоже не используйте рекурсию.
9.
5 Напишите перед каждым :
> (добавлять к каждому '(он помогает, он помогает)) (Она сказала, что сказала) > (прибавьте к каждому «анти» (тело ушло из пасты)) (АНТИДОТ АНТИПАСТО АНТИГОН АНТИТЕЛО)
9.6 Напишите процедуру предложение-версия , которая принимает функцию f как
его аргумент и возвращает функцию г . f должен принимать одно слово как
аргумент. g должен принять предложение в качестве аргумента и вернуть предложение
формируется путем применения f к каждому слову этого аргумента.
> ((предложение-версия сначала) '(если бы я упал)) (Я И Ф) > ((квадрат версии предложения) '(8 2 4 6)) (64 4 16 36)
9.7 Напишите процедуру с именем letterwords , которая использует
аргументы письмо и предложение. Он возвращает предложение, содержащее только
те слова из предложения-аргумента, которые содержат букву-аргумент:
> (буквы 'о' (должны ввести тебя в мою жизнь)) (ДОСТАЛИ ВАС В)
9.
8 Предположим, мы пишем программу для игры в палача. В этой игре один игрок
должен угадать секретное слово, выбранное другим игроком, по одной букве за раз.
Вы собираетесь написать только одну маленькую часть этой программы: процедуру, которая
принимает в качестве аргументов секретное слово и угаданные до сих пор буквы,
возвращая слово, в котором отображается ход угадывания, включая
все угаданные буквы вместе с символами подчеркивания для еще не угаданных:
> (повесить 'potsticker' etaoi) _OT_TI__E_
Совет: Вам будет полезно использовать следующую процедуру, которая определяет как отобразить одну букву:
(определить (повесить-догадаться по букве)
(если (участник? буква угадывает)
письмо
'_))
9.9 Напишите процедуру common-words , которая принимает два предложения как
аргументы и возвращает предложение, содержащее только те слова, которые появляются
и в первом предложении и во втором предложении.
9.10 В главе 2 мы использовали функцию с именем вхождений , которая возвращает
сколько раз его первый аргумент появляется в качестве члена его второго
аргумент. Реализовать представлений .
9.11 Напишите процедуру без аббревиатуры , которая принимает два предложения в виде
аргументы. Он должен вернуть предложение, такое же, как и первое
предложение, за исключением того, что любые числа в исходном предложении должны быть
заменить словами из второго предложения. Число 2 в первом
предложение следует заменить вторым словом второго предложения, 6 с шестым словом и так далее.
> (без сокращений '(john 1 wayne fred 4) '(bill hank kermit joey)) (ДЖОН БИЛЛ УЭЙН ФРЕД ДЖОУИ) > (без сокращений '(i 3 4 tell 2) '(хотите узнать секрет?)) (Я ХОЧУ ТЕБЕ СКАЗАТЬ)
9.12 Напишите процедуру first-last , аргументом которой будет предложение. Это
должен вернуть предложение, содержащее только те слова в аргументе
предложение, первая и последняя буквы которого совпадают:
> (первый-последний '(Калифорния, Огайо, Небраска, Алабама, Аляска, Массачусетс)) (Огайо, Алабама, Аляска)
9.
13 Написать процедуру составить , которая принимает две функции f и g в качестве аргументов. Он должен возвращать новую функцию, состав ее входных данных
функции, которые вычисляют f ( g ( x )) при передаче аргумента x .
> ((составить sqrt абс) -25) 5 > (определить второй (составить первый bf)) > (вторая '(функция высшего порядка)) ЗАКАЗ
9.14 Напишите процедуру , заменяющую , которая принимает три аргумента, два
слова и предложение. Он должен вернуть версию предложения, но с
каждый экземпляр второго слова заменяется первым словом:
> (замените «может быть» «да» (она любит тебя, да, да, да)) (ОНА ЛЮБИТ ТЕБЯ, МОЖЕТ БЫТЬ, МОЖЕТ БЫТЬ)
9.15 Многие функции применимы только к аргументам в определенной области и
привести к сообщениям об ошибках, если заданы аргументы за пределами этого домена. За
например, sqrt может потребовать неотрицательный аргумент в версии
Схема, которая не включает комплексные числа.
(В любая версия Scheme, sqrt будет жаловаться, если его аргумент вообще не является числом!)
Как только программа получает сообщение об ошибке, эта программа не может
продолжить расчет.
Напишите процедуру проверки типов , которая принимает в качестве аргументов
процедура с одним аргументом f и процедура предиката с одним аргументом pred . Проверка типа должна возвращать процедуру с одним аргументом, которая сначала
применяет до к своему аргументу; если этот результат верен, процедура
должен вернуть значение, вычисленное путем применения к аргументу f ; если pre возвращает false, новая процедура также должна возвращать #f :
> (определить safe-sqrt (проверить номер sqrt?)) > (безопасная площадь 16) 4 > (safe-sqrt 'сарсапарилья) #F
9.16 В языке APL большинство арифметических функций можно применять либо к
число, с обычным результатом, или до вектор — имя APL для
числовое предложение — в этом случае результатом является новый вектор, в котором каждый
элемент является результатом применения функции к соответствующему элементу
аргумента.
