Умножение и деление чисел в Excel
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 for Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Еще…Меньше
Умножение и деление в Excel не представляют никаких сложностей: достаточно создать простую формулу. Не забывайте, что все формулы в Excel начинаются со знака равенства (=), а для их создания можно использовать строку формул.
Умножение чисел
Предположим, требуется определить количество бутылок воды, необходимое для конференции заказчиков (общее число участников × 4 дня × 3 бутылки в день) или сумму возмещения транспортных расходов по командировке (общее расстояние × 0,46). Существует несколько способов умножения чисел.
Умножение чисел в ячейке
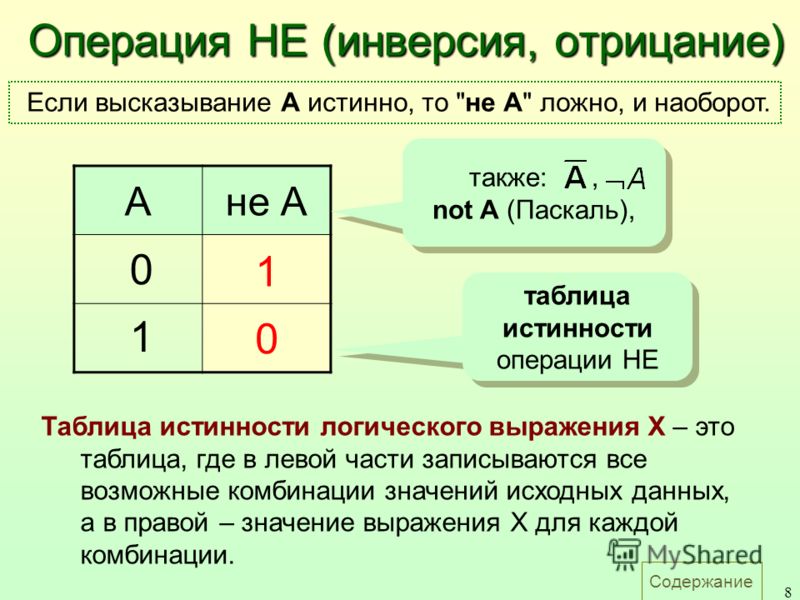
Для выполнения этой задачи используйте арифметический оператор

Например, при вводе в ячейку формулы =5*10 в ячейке будет отображен результат 50.
Умножение столбца чисел на константу
Предположим, необходимо умножить число в каждой из семи ячеек в столбце на число, которое содержится в другой ячейке. В данном примере множитель — число 3, расположенное в ячейке C2.
-
Введите =A2*$B$2 в новом столбце таблицы (в примере выше используется столбец D). Не забудьте ввести символ $ в формуле перед символами B и 2, а затем нажмите ввод.
Примечание: Использование символов $ указывает Excel, что ссылка на ячейку B2 является абсолютной, то есть при копировании формулы в другую ячейку ссылка всегда будет на ячейку B2.
 Если вы не использовали символы $ в формуле и перетащили формулу вниз на ячейку B3, Excel изменит формулу на =A3*C3, которая не будет работать, так как в ячейке B3 нет значения.
Если вы не использовали символы $ в формуле и перетащили формулу вниз на ячейку B3, Excel изменит формулу на =A3*C3, которая не будет работать, так как в ячейке B3 нет значения. -
Перетащите формулу вниз в другие ячейки столбца.
Примечание: В Excel 2016 для Windows ячейки заполняются автоматически.
Перемножение чисел в разных ячейках с использованием формулы
Функцию PRODUCT можно использовать для умножения чисел, ячеек и диапазонов.
Функция ПРОИЗВЕД может содержать до 255 чисел или ссылок на ячейки в любых сочетаниях. Например, формула =ПРОИЗВЕДЕНИЕ(A2;A4:A15;12;E3:E5;150;G4;h5:J6) перемножает две отдельные ячейки (A2 и G4), два числа (12 и 150) и три диапазона (A4:A15, E3:E5 и h5:J6).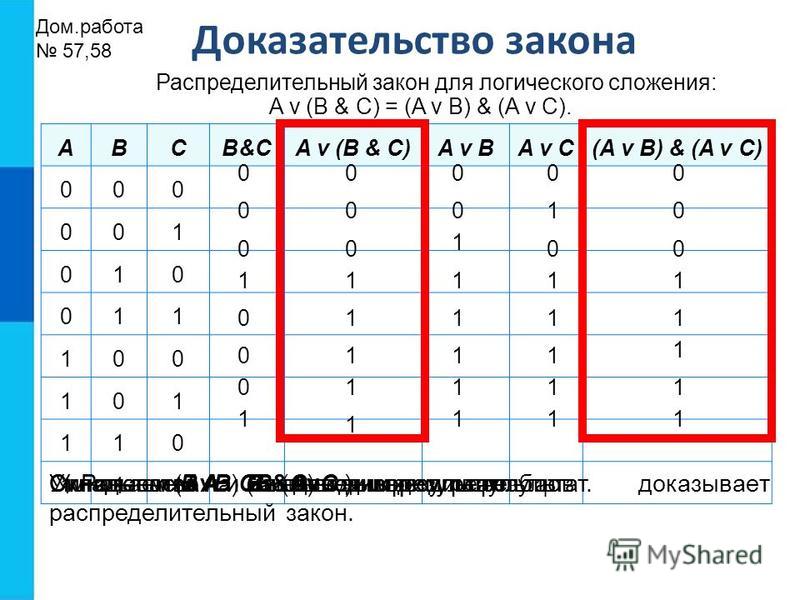
Деление чисел
Предположим, что вы хотите узнать, сколько человеко-часов потребовалось для завершения проекта (общее время проекта ÷ всего людей в проекте) или фактический километр на лилон для вашего последнего меж страны(общее количество километров ÷ лилонов). Деление чисел можно разделить несколькими способами.
Деление чисел в ячейке
Для этого воспользуйтесь арифметическим оператором / (косая черта).
Например, если ввести =10/5 в ячейке, в ячейке отобразится 2.
Важно:
 12.1936 и отобразит в ячейке значение «1-дек».
12.1936 и отобразит в ячейке значение «1-дек».
Примечание: В Excel нет функции DIVIDE.
Деление чисел с помощью ссылок на ячейки
Вместо того чтобы вводить числа непосредственно в формулу, можно использовать ссылки на ячейки, такие как A2 и A3, для обозначения чисел, на которые нужно разделить или разделить числа.
Пример:
Чтобы этот пример проще было понять, скопируйте его на пустой лист.
Копирование примера
-
Создайте пустую книгу или лист.
-
Нажмите клавиши CTRL+C.
-
Выделите на листе ячейку A1 и нажмите клавиши CTRL+V.
-
Чтобы переключиться между просмотром результатов и просмотром формул, которые возвращают эти результаты, нажмите клавиши CTRL+’ (ударение) или на вкладке «Формулы» нажмите кнопку «Показать формулы».

Выделите пример в разделе справки.
Примечание: Не выделяйте заголовки строк или столбцов.
Выделение примера в справке
|
A |
B |
C |
|
|
1 |
Данные |
Формула |
Описание (результат) |
|
2 |
15000 |
=A2/A3 |

|
|
3 |
12 |
Деление столбца чисел на константу
Предположим, вам нужно разделить каждую ячейку в столбце из семи чисел на число, которое содержится в другой ячейке. В этом примере число, на которые нужно разделить, составляет 3, содержалось в ячейке C2.
|
A |
B |
C |
|
|
|
Данные |
Формула |
Константа |
|
2 |
15000 |
=A2/$C$2 |
3 |
|
3 |
12 |
=A3/$C$2 |
|
|
4 |
48 |
=A4/$C$2 |
|
|
5 |
729 |
=A5/$C$2 |
|
|
6 |
1534 |
=A6/$C$2 |
|
|
7 |
288 |
=A7/$C$2 |
|
|
8 |
4306 |
=A8/$C$2 |
В ячейке B2 введите =A2/$C$2. Не забудьте в формуле включить символ $ перед символами C и 2.
Перетащите формулу в ячейке B2 вниз в другие ячейки в столбце B.
Примечание: Символ $ указывает Excel, что ссылка на ячейку C2 является абсолютной, то есть при копировании формулы в другую ячейку ссылка всегда будет на ячейку C2. Если вы не использовали в формуле символы $ и перетащили формулу вниз на ячейку B3, Excel изменит формулу на =A3/C3, которая не будет работать, так как в ячейке C3 нет значения.
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
См. также
Умножение столбца чисел на одно и то же число
Умножение на процентное значение
Создание таблицы умножения
Операторы вычислений и порядок операций
2.2. Арифметические операции над числами, представленными в различных системах счисления. Информатика: аппаратные средства персонального компьютера
2.2. Арифметические операции над числами, представленными в различных системах счисления. Информатика: аппаратные средства персонального компьютераВикиЧтение
Информатика: аппаратные средства персонального компьютера
Яшин Владимир Николаевич
Содержание
2. 2. Арифметические операции над числами, представленными в различных системах счисления
2. Арифметические операции над числами, представленными в различных системах счисления
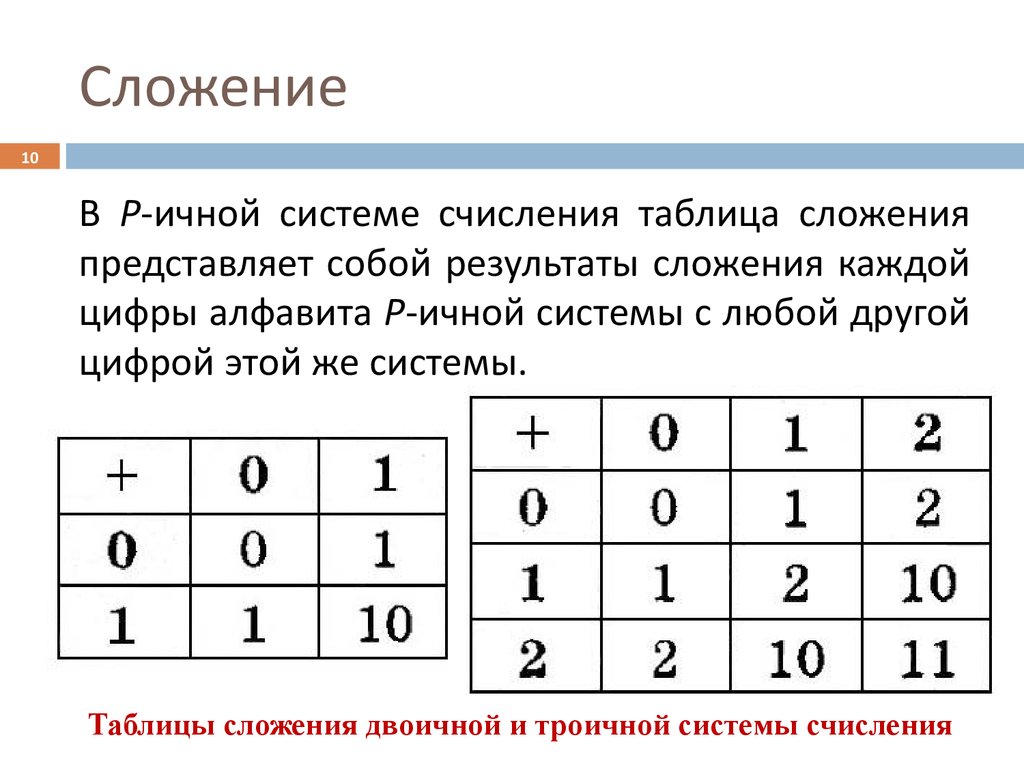
Арифметические операции во всех позиционных системах счисления выполняются по одним и тем же правилам. Для проведения арифметических операций над числами, представленными в различных системах счисления, необходимо предварительно преобразовать их в одну систему счисления и учесть то, что перенос в следующий разряд при операции сложения и заем из старшего разряда при операции вычитания определяется величиной основания системы счисления.
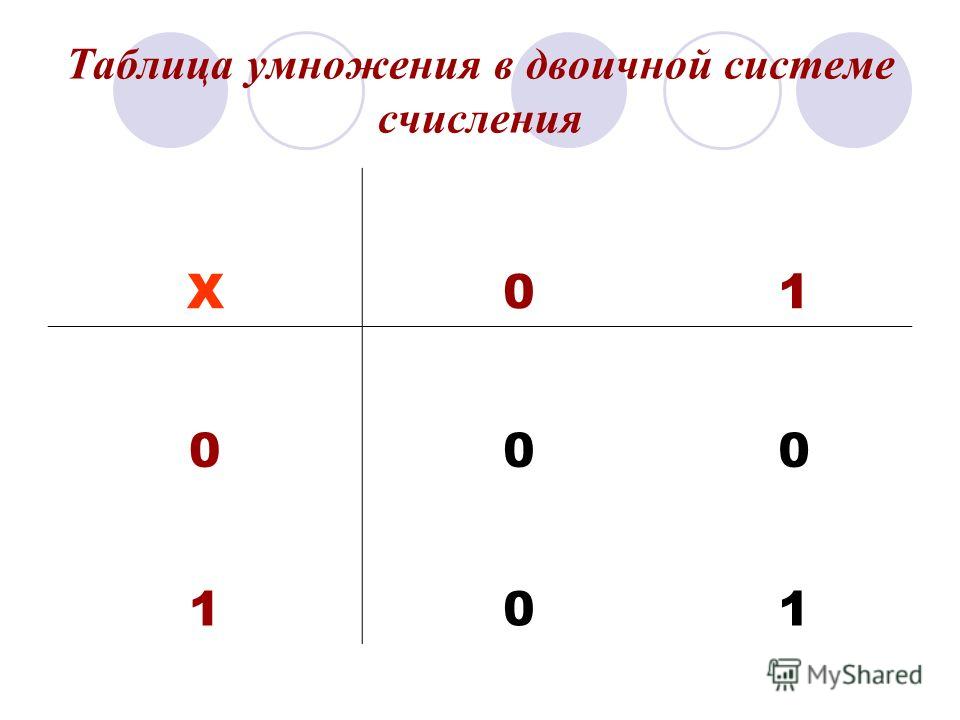
Арифметические операции в двоичной системе счисления основаны на таблицах сложения, вычитания и умножения одноразрядных двоичных чисел.
При сложении двух единиц происходит переполнение разряда и производится перенос единицы в старший разряд, при вычитании 0–1 производится заем из старшего разряда, в таблице «Вычитание» этот заем обозначен 1 с чертой над цифрой.
Ниже приведены примеры выполнения арифметических операций над числами, представленными в различных системах счисления:
Арифметические операции над целыми числами, представленными в различных системах счисления, достаточно просто реализуются с помощью программ Калькулятор и MS Excel..png)
Данный текст является ознакомительным фрагментом.
Арифметические операции
Арифметические операции Для работы с числами используют арифметические операции.• Сложение – знак плюс (+). Например, 5 + 7 = 12.• Вычитание – знак минус (-). Например, 67 – 43 = 24.• Умножение – звездочка (*). Например, 2 * 2 = 4.• Деление – косая черта (/). Например, 45 / 5 = 9.• Остаток от
Арифметические операции
Арифметические операции + – сложение— – вычитание* – умножение/ – делениеDIV – деление нацелоMOD – остаток от деления
Арифметические операции
Арифметические операции
Унарные операции – применяются к одной переменной.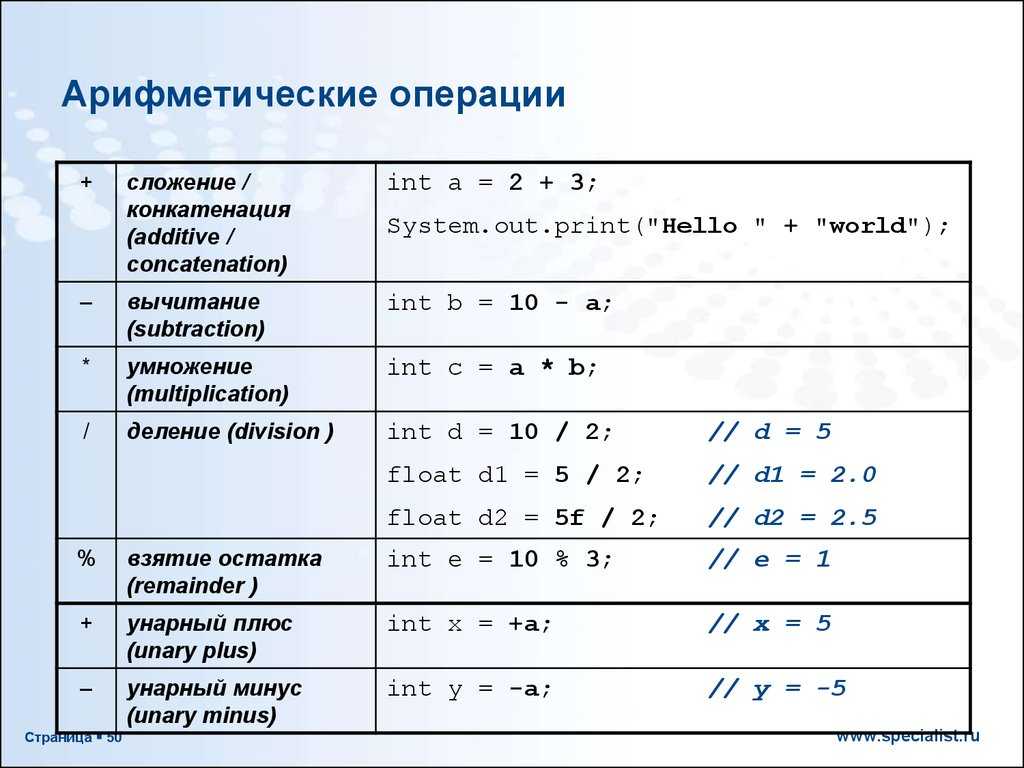 ++ – увеличение на единицу (x++ выдаёт старое значение, ++x – новое значение).– – – уменьшение на единицу, аналогично операции ++.Бинарные операции – стоят между двумя переменными или
++ – увеличение на единицу (x++ выдаёт старое значение, ++x – новое значение).– – – уменьшение на единицу, аналогично операции ++.Бинарные операции – стоят между двумя переменными или
5.2. Основные операции над числами
5.2. Основные операции над числами Обычные операции сложения, вычитания, умножения и деления в Ruby, как и во всех распространенных языках программирования, обозначаются операторами +, -, *, /. Операторы в большинстве своем реализованы в виде методов (и потому могут быть
5.17. Поразрядные операции над числами
5.17. Поразрядные операции над числами Иногда требуется работать с двоичным представлением объекта Fixnum. На прикладном уровне такая необходимость возникает нечасто, но все-таки возникает.Ruby обладает всеми средствами для таких операций. Для удобства числовые константы
I.
 Арифметические операции
Арифметические операцииI. Арифметические операции + Прибавляет величину, находящуюся справа, к величине, стоящей слева — Вычитает величину, стоящую справа, из величины, указанной слева — Будучи унарной операцией, изменяет знак величины, стоящей справа * Умножает величину справа на величину,
Арифметические операции (Arithmetic operations)
Арифметические операции (Arithmetic operations) Библиотека обеспечивает базовые классы функциональных объектов для всех арифметических операторов языка.template ‹class T›struct plus: binary_function‹T, T, T› { Т operator()(const T& x, const T& y) const {return x + y;}};template ‹class T›struct minus: binary_function‹T, T, T› { Т operator()(const T&
Глава 2. Обработка сканированных изображений для использования в различных системах САПР и ГИС
Глава 2. Обработка сканированных изображений для использования в различных системах САПР и ГИС
Векторизация есть процесс, требующий обязательного участия человека, поскольку только человек, глядя на черные и белые точки на экране (а результат сканирования — это черные и
Обработка сканированных изображений для использования в различных системах САПР и ГИС
Векторизация есть процесс, требующий обязательного участия человека, поскольку только человек, глядя на черные и белые точки на экране (а результат сканирования — это черные и
4.2. Арифметические операции
4.2. Арифметические операции Таблица 4.1. Арифметические операции Символ операции Значение Использование * Умножение expr*expr / Деление expr / expr % Остаток от деления expr % expr + Сложение expr + expr — Вычитание expr – expr Деление целых чисел дает в результате целое
4.6. Операции с комплексными числами
4.6. Операции с комплексными числами Класс комплексных чисел стандартной библиотеки С++ представляет собой хороший пример использования объектной модели. Благодаря перегруженным арифметическим операциям объекты этого класса используются так, как будто они
Арифметические операции
Арифметические операции
Арифметические выражения вычисляются слева направо за исключением случаев, когда возникает двусмысленность.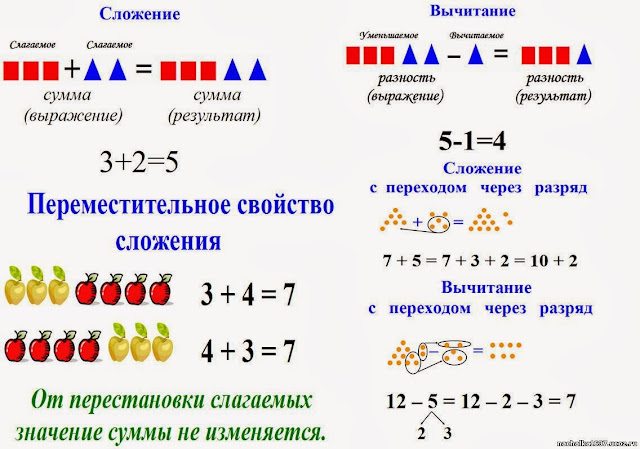 В этих случаях арифметические операции вычисляются в соответствии с приоритетами, описанными в табл. 21.3. Например, умножение
В этих случаях арифметические операции вычисляются в соответствии с приоритетами, описанными в табл. 21.3. Например, умножение
Пример 8-2. Арифметические операции
Пример 8-2. Арифметические операции #!/bin/bash# От 1 до 6 пятью различными способами.n=1; echo -n «$n «let «n = $n + 1» # let «n = n + 1» тоже допустимоecho -n «$n «: $((n = $n + 1))# оператор «:» обязателен, поскольку в противном случае, Bash будет#+ интерпретировать выражение «$((n = $n + 1))» как команду.echo -n «$n «n=$(($n + 1))echo
Операции с числами
Операции с числами Перечень арифметических операций в XPath довольно ограничен. К ним относится сложение, вычитание, умножение, деление и унарная операция отрицания, которая меняет значение операнда на противоположное. Кроме того, числа можно сравнивать при помощи
Арифметические операции
Арифметические операции
К арифметическим относятся бинарные операции +, -, *, / для вещественных и целых чисел, бинарные операции div и mod для целых чисел и унарные операции + и — для вещественных и целых чисел. Тип выражения x op y, где op — знак бинарной операции +, — или *,
Тип выражения x op y, где op — знак бинарной операции +, — или *,
Системы счисления — Сайт по информатике Хорошилова Льва
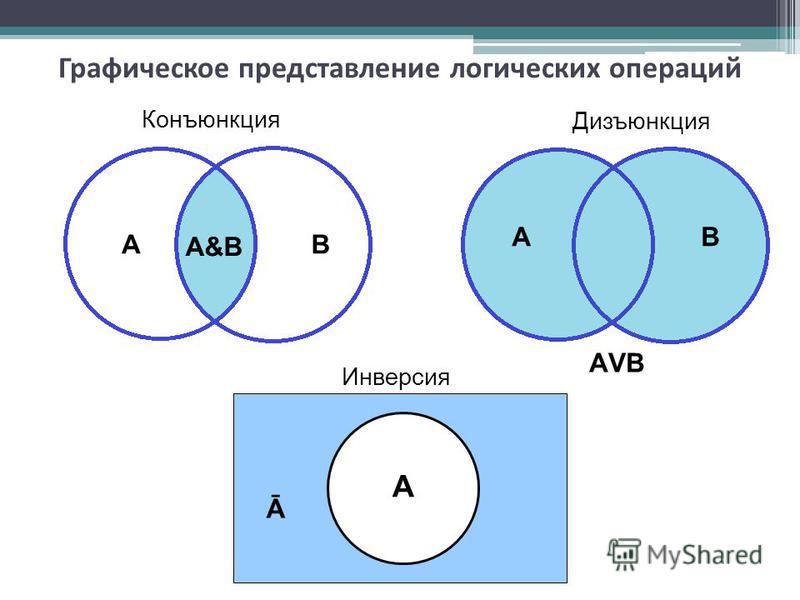
Система счисления — символический метод записи чисел, представление чисел с помощью письменных знаков. Знаки, используемые при записи чисел, называются цифрами. В зависимости от способов изображения чисел цифрами, системы счисления делятся на непозиционные и позиционные. Непозиционной системой называется такая, в которой количественное значение каждой цифры не зависит от занимаемой ей позиции в изображении числа (римская или унарная системы счисления). Позиционная система счисления — система, в которой количественное значение каждой цифры зависит от её позиции в числе (арабская система счисления). Позиционные системы счисления имеют ряд преимуществ перед непозиционными: удобство выполнения арифметических и логических операций, а также представление больших чисел, поэтому в цифровой технике применяются позиционные системы счисления.
Пусть Aq — число в системе с основанием q, аi — цифры данной системы счисления, присутствующие в записи числа A, n + 1 — число разрядов целой части числа, m — число разрядов дробной части числа: Развернутой формой числа А называется запись в виде: Например, для десятичного числа: В следующих примерах приводится развернутая форма шестнадцатеричного и двоичного чисел: В любой системе счисления ее основание записывается как 10. Перевод десятичных чисел в другие системы счисленияПеревод целых чисел Целое десятичное число X требуется перевести в систему с основаниемq:X= (anan-1 …a1a0)q. Нужно найти значащие цифры числа:. Отсюда видно, что a0 есть остаток от деления числаXна числоq. Выражение в скобках — целое частное от этого деления. Обозначим его заX1. Выполняя аналогичные преобразования, получим: Следовательно, a1есть остаток от деленияX1 наq. Продолжая деление с остатком, будем получать последовательность цифр искомого числа. Цифраanв этой цепочке делений будет последним частным, меньшимq. Сформулируем полученное правило: для того чтобы перевести целое десятичное число в систему счисления с другим основанием, нужно: 1) основание новой системы счисления выразить в десятичной системе счисления и все последующие действия производить по правилам десятичной арифметики; 2) последовательно выполнять деление данного числа и получаемых неполных частных на основание новой системы счисления до тех пор, пока не получим неполное частное, меньшее делителя; 3) полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления; 4) составить число в новой системе счисления, записывая его, начиная с последнего частного. Пример 1. Перевести число 3710 в двоичную систему. Для обозначения цифр в записи числа используем символику: a5a4a3a2a1a0 Отсюда: 3710 = l00l0l2 Пример 2.Перевести десятичное число 315 в восьмеричную и в шестнадцатеричную системы: Отсюда следует: 31510= 4738= 13B16. Напомним, что 1110= B16. Десятичную дробь X< 1 требуется перевести в систему с основаниемq:X= (0,a–1a–2…a–m+1a–m)q. Нужно найти значащие цифры числа:a–1, a–2, …,a–m. Представим число в развернутой форме и умножим его наq: Отсюда видно, что a–1 есть целая часть произведенияXна числоq. Следовательно, a–2 есть целая часть произведенияX1 на числоq. Продолжая умножения, будем получать последовательность цифр. Теперь сформулируем правило:для того чтобы перевести десятичную дробь в систему счисления с другим основанием, нужно: 1) последовательно умножать данное число и получаемые дробные части произведений на основание новой системы до тех пор, пока дробная часть произведения не станет равной нулю или не будет достигнута требуемая точность представления числа в новой системе счисления; 2) полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления; 3) составить дробную часть числа в новой системе счисления, начиная с целой части первого произведения. Пример 3. Перевести десятичную дробь 0,1875 в двоичную, восьмеричную и шестнадцатеричную системы. Здесь в левом столбце находится целая часть чисел, а в правом — дробная. Отсюда: 0,187510 = 0,00112 = 0,148 = 0,316 Перевод смешанных чисел, содержащих целую и дробную части, осуществляется в два этапа. Целая и дробная части исходного числа переводятся отдельно по соответствующим алгоритмам. В итоговой записи числа в новой системе счисления целая часть отделяется от дробной запятой (точкой). Двоичные вычисленияСогласно принципу Джона фон Неймана, компьютер производит вычисления в двоичной системе счисления. В рамках базового курса достаточно ограничиться рассмотрением вычислений с целыми двоичными числами. Для выполнения вычислений с многозначными числами необходимо знать правила сложения и правила умножения однозначных чисел. Вот эти правила: Принцип перестановочности сложения и умножения работает во всех системах счисления. Приемы выполнения вычислений с многозначными числами в двоичной системе аналогичны десятичной. Рассмотрим правила вычитания и деления двоичных чисел. Операция вычитания является обратной по отношению к сложению. Из приведенной выше таблицы сложения следуют правила вычитания: 0 — 0 = 0; 1 — 0 = 1; 10 — 1 = 1. Вот пример вычитания многозначных чисел: Полученный результат можно проверить сложением разности с вычитаемым. Должно получиться уменьшаемое число. Деление — операция обратная умножению. В любой системе счисления делить на 0 нельзя. Результат деления на 1 равен делимому. Деление двоичного числа на 102 ведет к перемещению запятой на один разряд влево, подобно десятичному делению на десять. Например: |
Сложение двоичных чисел онлайн
Назначение сервиса. Онлайн-калькулятор предназначен для сложения двоичных чисел в прямом, обратном и дополнительном кодах.
- Решение онлайн
- Видеоинструкция
- Также решают
Число №1
Число №2
Числа представлены в 102 системе счисления.Операция с числами СложениеВычитание Для дробных чисел использовать 2345678 знака после запятой.
Действие производить в: Прямом кодеОбратном кодеДополнительном кодеПодробнее.
Вместе с этим калькулятором также используют следующие:
Перевод чисел в двоичную, шестнадцатеричную, десятичную, восьмеричную системы счисления
Умножение двоичных чисел
Формат представления чисел с плавающей запятой
Пример №1. Представить число 133,54 в форме числа с плавающей точкой.
Решение. Представим число 133.54 в нормализованном экспоненциальном виде:
1.3354*102 = 1. 3354*exp102
3354*exp102
Число 1.3354*exp102 состоит из двух частей: мантиссы M=1.3354 и экспоненты exp10=2
Если мантисса находится в диапазоне 1 ≤ M Представление числа в денормализованном экспоненциальном виде.
Если мантисса находится в диапазоне 0,1 ≤ M Представим число в денормализованном экспоненциальном виде: 0.13354*exp103
Пример №2. Представить двоичное число 101.102 в нормализованном виде, записать в 32-битом стандарте IEEE754.
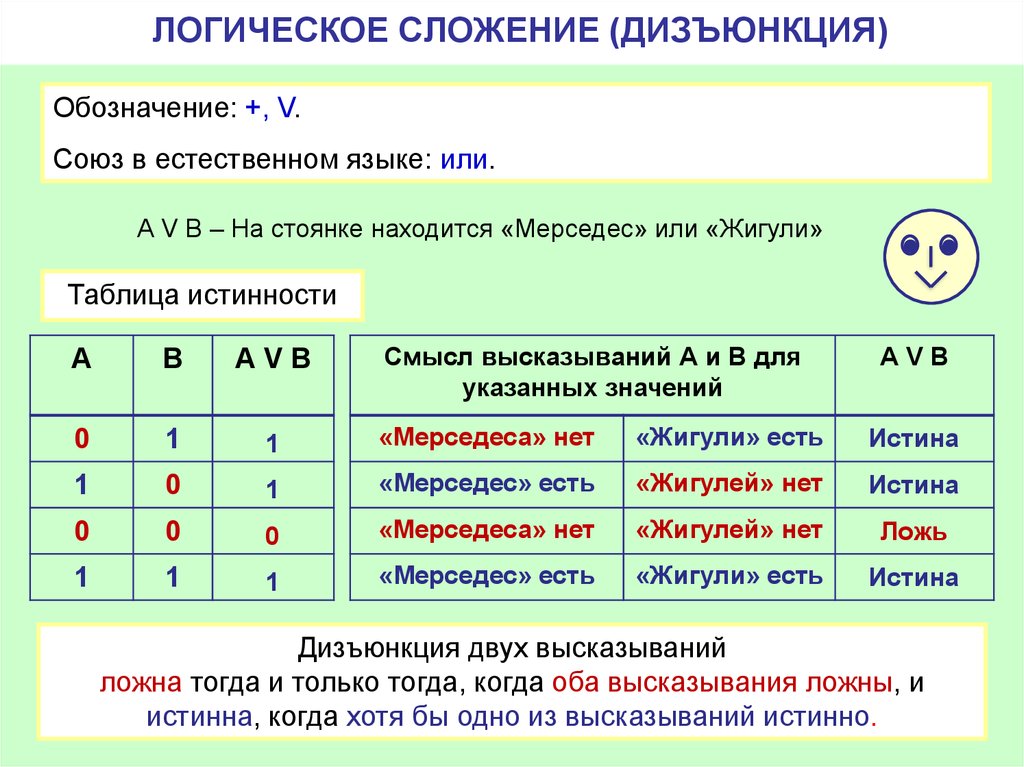
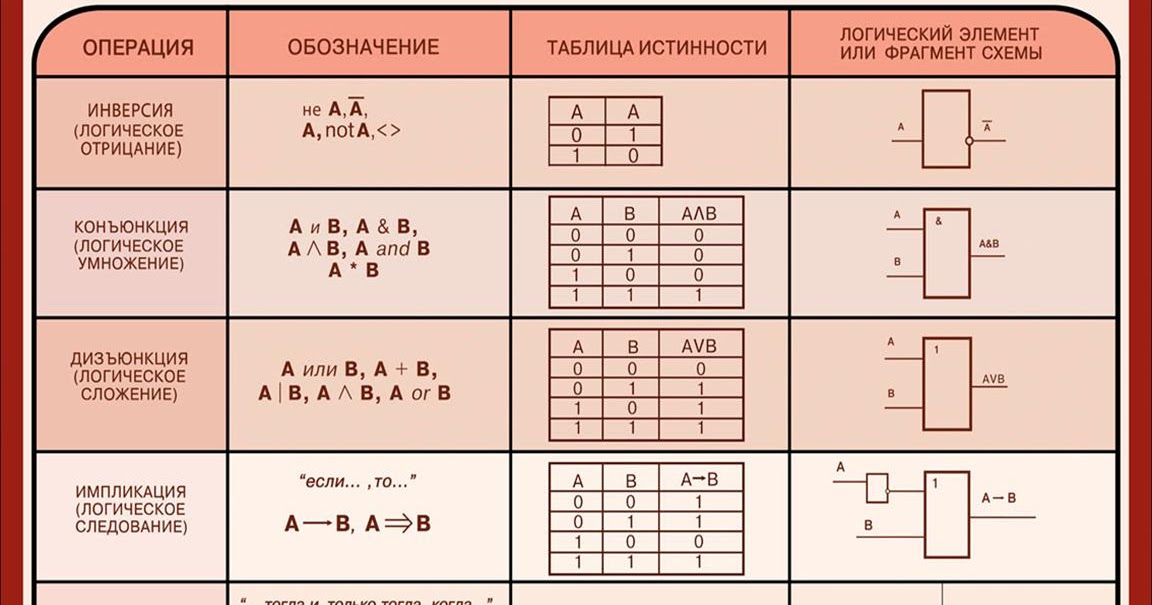
Таблица истинности
Вычисление пределов
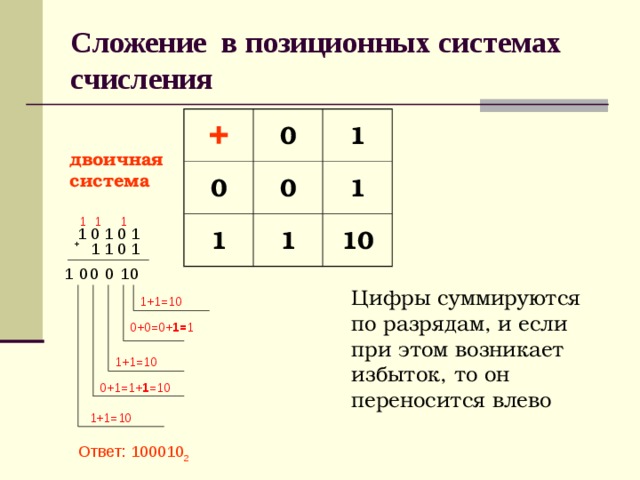
Арифметика в двоичной системе счисления
Арифметические действия в двоичной системе выполняются так же, как и в десятичной. Но, если в десятичной системе счисления перенос и заём осуществляется по десять единиц, то в двоичной — по две единицы. В таблице представлены правила сложения и вычитания в двоичной системе счисления.- При сложении в двоичной системе системе счисления двух единиц в данном разряде будет 0 и появится перенос единицы в старший разряд.

- При вычитании из нуля единицы производится заём единицы из старшего разряда, где есть 1. Единица, занятая в этом разряде, даёт две единицы в разряде, где вычисляется действие, а также по единице, во всех промежуточных разрядах.
| Сложение
0 + 0 = 0 1 + 0 = 1 0 + 1 = 1 1 + 1 = 10 |
Вычитание
0 – 0 = 0 1 – 0 = 1 1 – 1 = 0 10 – 1 = 1 |
Сложение чисел с учетом их знаков на машине представляет собой последовательность следующих действий:
- преобразование исходных чисел в указанный код;
- поразрядное сложение кодов;
- анализ полученного результата.

При выполнении операции в дополнительном (модифицированном дополнительном) коде если в результате сложения в знаковом разряде возникает единица переноса, она отбрасывается.
Операция вычитания в ЭВМ выполняется через сложение по правилу: Х-У=Х+(-У). Дальнейшие действия выполняются также как и для операции сложения.
Пример №1.
Дано: х=0,110001; y= -0,001001, сложить в обратном модифицированном коде.
Дано: х=0,101001; y= -0,001101, сложить в дополнительном модифицированном коде.
Пример №2. Решить примеры на вычитание двоичных чисел, используя метод дополнения до 1 и циклического переноса.
а) 11 — 10.
Решение.
Представим числа 112 и -102 в обратном коде.
Обратный код для положительного числа совпадает с прямым кодом. Для отрицательного числа все цифры числа заменяются на противоположные (1 на 0, 0 на 1), а в знаковый разряд заносится единица.
Двоичное число 0000011 имеет обратный код 0,0000011
Двоичное число 0000010 имеет обратный код 1,1111101
Сложим числа 00000011 и 11111101
В 0-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 1-й разряд.
Поэтому записываем 0, а 1 переносим на 1-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | |||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 |
В 1-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 2-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | ||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 |
В 2-ом разряде возникло переполнение (1 + 1 = 10).
 Поэтому записываем 0, а 1 переносим на 3-й разряд.
Поэтому записываем 0, а 1 переносим на 3-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | |||||
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 |
В 3-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 4-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | ||||
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 |
В 4-ом разряде возникло переполнение (1 + 1 = 10).
 Поэтому записываем 0, а 1 переносим на 5-й разряд.
Поэтому записываем 0, а 1 переносим на 5-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 |
В 5-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 6-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 |
В 6-ом разряде возникло переполнение (1 + 1 = 10).
 Поэтому записываем 0, а 1 переносим на 7-й разряд.
Поэтому записываем 0, а 1 переносим на 7-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
В 7-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 8-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
В итоге получаем:
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Возник перенос из знакового разряда.
 Добавим его (т.е. 1) к полученному числу (тем самым осуществляя процедуру циклического переноса).
Добавим его (т.е. 1) к полученному числу (тем самым осуществляя процедуру циклического переноса).В итоге получаем:
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
Результат сложения: 00000001. Переведем в десятичное представление. Для перевода целой части необходимо умножить разряд числа на соответствующую ему степень разряда.
00000001 = 27*0 + 26*0 + 25*0 + 24*0 + 23*0 + 22*0 + 21*0 + 20*1 = 0 + 0 + 0 + 0 + 0 + 0 + 0 + 1 = 1
Результат сложения (в десятичном представлении): 1
б) 111-010
Представим числа 1112 и -0102 в обратном коде.
Обратный код для положительного числа совпадает с прямым кодом. Для отрицательного числа все цифры числа заменяются на противоположные (1 на 0, 0 на 1), а в знаковый разряд заносится единица.
Двоичное число 0000111 имеет обратный код 0,0000111
Двоичное число 0000010 имеет обратный код 1,1111101
Сложим числа 00000111 и 11111101
В 0-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 1-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | |||||||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 |
В 1-ом разряде возникло переполнение (1 + 1 = 10).
 Поэтому записываем 0, а 1 переносим на 2-й разряд.
Поэтому записываем 0, а 1 переносим на 2-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | ||||||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 |
В 2-ом разряде возникло переполнение (1 + 1 + 1 = 11). Поэтому записываем 1, а 1 переносим на 3-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | |||||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 |
В 3-ом разряде возникло переполнение (1 + 1 = 10).
 Поэтому записываем 0, а 1 переносим на 4-й разряд.
Поэтому записываем 0, а 1 переносим на 4-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | ||||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 |
В 4-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 5-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | |||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 1 | 0 | 0 |
В 5-ом разряде возникло переполнение (1 + 1 = 10).
 Поэтому записываем 0, а 1 переносим на 6-й разряд.
Поэтому записываем 0, а 1 переносим на 6-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | ||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 |
В 6-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 7-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 |
В 7-ом разряде возникло переполнение (1 + 1 = 10).
 Поэтому записываем 0, а 1 переносим на 8-й разряд.
Поэтому записываем 0, а 1 переносим на 8-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
В итоге получаем:
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
Возник перенос из знакового разряда.
 Добавим его (т.е. 1) к полученному числу (тем самым осуществляя процедуру циклического переноса).
Добавим его (т.е. 1) к полученному числу (тем самым осуществляя процедуру циклического переноса).
В итоге получаем:
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
Результат сложения: 00000101
Получили число 00000101. Для перевода целой части необходимо умножить разряд числа на соответствующую ему степень разряда.
00000101 = 27*0 + 26*0 + 25*0 + 24*0 + 23*0 + 22*1 + 21*0 + 20*1 = 0 + 0 + 0 + 0 + 0 + 4 + 0 + 1 = 5
Результат сложения (в десятичном представлении): 5
Сложение двоичных вещественных чисел с плавающей запятой
В компьютере любое число может быть представлено в формате с плавающей точкой. Формат с плавающей точкой показан на рисунке:
Например, число 10101 в формате с плавающей точкой можно записать так:
В компьютерах используется нормализованная форма записи числа, в которой положение запятой всегда задается перед значащей цифрой мантиссы, т.е. выполняется условие:
Формат с плавающей точкой показан на рисунке:
Например, число 10101 в формате с плавающей точкой можно записать так:
В компьютерах используется нормализованная форма записи числа, в которой положение запятой всегда задается перед значащей цифрой мантиссы, т.е. выполняется условие:
b-1≤|M|<b0=1
Нормализованное число — это число, у которого после запятой идет значащая цифра (т.е. 1 в двоичной системе счисления). Пример нормализации:
0,00101*2100=0,101*210
111,1001*210=0,111001*2101
0,01101*2-11=0,1101*2-100
11,1011*2-101=0,11011*2-11
При сложении чисел с плавающей точкой выравнивание порядков выполняют в сторону большего порядка:
Алгоритм сложения чисел с плавающей точкой:
- Выравнивание порядков;
- Сложение мантисс в дополнительном модифицированном коде;
- Нормализация результата.

Пример №4.
A=0,1011*210, B=0,0001*211
1. Выравнивание порядков;
A=0,01011*211, B=0,0001*211
2. Сложение мантисс в дополнительном модифицированном коде;
MAдоп.мод.=00,01011
MBдоп.мод.=00,0001
00,01011
+ 00,00010
=
00,01101
A+B=0,01101*211
3. Нормализация результата.
A+B=0,1101*210
Пример №3. Записать десятичное число в двоично-десятичной системе счисления и сложить два числа в двоичной системе счисления.
Урок математики по теме «Сумма и произведение. Знак умножения». 2-й класс
Ключевые слова: математика, начальная школа, презентация, знак умножения, замена суммы умножением, произведение
Цели:
- Провести исследовательскую работу с целью
знакомства с новым арифметическим действием,
выяснить приемы краткой рациональной записи
действия, отрабатывать умения делать выводы,
обобщения, раскрыть конкретный смысл действия
умножения, использовать соответствующую
терминологию, учить решать задачи при помощи
данных действий, самостоятельно выделять и
формулировать познавательную цель.

- Создать условия для овладения соответствующим вычислительным навыком; использовать фантазию, воображение при выполнении учебных действий, а также творческую самостоятельность, соединяя игровую и обучающую форму деятельности, Обеспечить выбор наиболее эффективных способов решения задач в зависимости от конкретных условий.
- Формировать умение объяснять свой выбор, строить фразы, отвечать на поставленный вопрос, аргументировать.
- Формировать желание выполнять учебные действия; уверенность в своих возможностях, аккуратность при выполнении заданий, ответственность, любознательность, интерес к предмету.
Планируемые результаты:
- Иметь представления о действии умножения как сложении одинаковых слагаемых.
- Знать смысл действий (операций) умножения над
целыми неотрицательными числами.

- Понимать и использовать сочетания слов «по … в каждом…», «… раз по …», составлять числовые выражения. Давать ответы в виде развернутых предложений на вопросы учителя или сказочного персонажа, уметь выполнять инструкции учителя.
- Уметь в процессе учебной деятельности контактировать с товарищами и вести диалоги. Понимать и выполнять учебные требования, предъявляемые со стороны учителя и мультимедиа-персонажей.
Оборудование: смайлики для осуществления обратной связи с учащимися, конспект, презентация, мультимедийный проектор, учебник, рабочая тетрадь, ТПО, черный фломастер, карточки.
План урока:
I. Оргмомент.
II. Устный счет.
1. Карточки.
2. Задание «Бусы».
3. Группировка чисел.
4. Геометрический материал.
5. Итог устного счета.
6. Проверка индивидуальной работы.
III. Формулировка целей и задач урока.
IV. Создание проблемной ситуации.
V. Изучение нового.
VI. Закрепление.
Игра «Помоги приземлиться летчику».
VII. Физминутка.
VIII. Закрепление.
1. Работа в тетрадях (с. 92, 3).
2. Самопроверка.
3. Игра «Ёжики».
4. Задача.
5. Самопроверка.
6. Веселые задачи (устная работа).
7. Кроссворд.
IX. Итог.
X. Эмоциональный отклик.
ХОД УРОКА
Слайд 1
I. Оргмомент
Учитель.
Прозвенел, друзья, звонок.
Начинается урок.
Слайд 2
Учитель. Сегодня наш урок проводится в
необычном месте. Это кабинет информатики.
Информатика близка к математике. Она изучает не
только работу вычислительных систем, и в
частности компьютера, но и сведения из
окружающего мира.
А нам информатика поможет разобраться с
очередным секретом математики. И с нами вместе
будут проводники из мира информатики:
Слайд 3
Мышка и её друг Смайлик, который, несомненно,
вам знаком. Они помогут вам легко и быстро
познакомиться с новым материалом.
У вас на столах тоже есть Смайлик, посмотрите на
него, но он нам понадобится позже, поэтому
отложите пока его в сторону.
II. Устный счет
Учитель. Перед тем, как приступить к изучению новой темы, нужно настроиться на математический лад.
Отдохнуть вы все успели?
А теперь вперед – за дело.
Математика нас ждет.
Начинаем устный счет.
– Пока мы будем выполнять устный счет,
некоторые ребята будут работать по карточкам
самостоятельно. Они расшифруют тему нашего
урока. Посмотрите, у кого на столах есть красные
конвертики, поднимите руку. Откройте конверт,
достаньте карточку. Вам нужно найти значение
выражений, а затем мы вместе откроем шифровку.
Задание понятно? Приступайте к выполнению.
Откройте конверт,
достаньте карточку. Вам нужно найти значение
выражений, а затем мы вместе откроем шифровку.
Задание понятно? Приступайте к выполнению.
1. Карточки.
| Ананьев | Несмашная | Стеблев | |||
40 – 30 |
С Е П З |
44 – 40 |
А У И Р |
66 – 6 |
Н М B О Д |
2. Задание «Бусы»
Задание «Бусы»
Учитель. Первое задание устного счета вам предлагает Мышка, а Смайлик будет ей помогать.
Слайд 4
Из разных цифр собрали бусы
А в тех кружках, где чисел нет,
Поставьте минусы и плюсы,
Чтоб верный получить ответ.
– Дополняем первую ленточку бус.
Дети устно называют пример с вычислением.
– Кто не согласен с ответом, поднимите вверх
Смайлика, который лежит у вас на столах.
Дополняем вторую ленточку бус. Дополняем третью
ленточку бус. Дополняем четвертую ленточку бус.
(Проверка осуществляется с помощью презентации)
3. Группировка чисел
Учитель. Мы посчитали, а теперь вспомним, что мы знаем о числах.
Слайд 5
– Раздели числа на группы. Назовите группы.
– Как называются числа первой группы? (Двузначные
некруглые).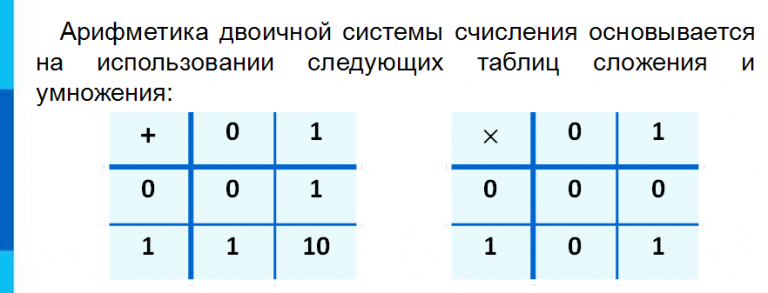
– Как называются числа второй группы? (Двузначные
круглые).
– В каком порядке стоят двузначные некруглые? (Возрастания).
– В каком порядке стоят двузначные круглые? (Убывания).
– Назовите число в котором цифра разряда
десятков на единицу больше цифры разряда единиц. (76).
– Что вы можете рассказать об этом числе? (Двузначное,
некруглое, сумма цифр 13, единиц – 6, десятков – 7,
предшествует число 75, последующее число 77).
4. Геометрический материал
Учитель. Хорошо. А теперь геометрический материал.
Слайд 6
– Разделите все геометрические фигуры на две
группы. Фигуры с какими номерами входят в первую
группу? Во вторую группу?
– Что общего между фигурами каждой группы? (Есть
углы, нет углов).
– Назовите фигуры первой группы.
– Что вы помните о квадрате?
– Что вы помните о прямоугольнике?
5. Итог устного счета
Итог устного счета
Учитель.Мышка довольна тем, как вы быстро и правильно умеете считать и как много знаете о числах и геометрических фигурах.
Слайд 7
6. Проверка индивидуальной работы
Учитель. А сейчас мы проверим ребят, которые выполняли работу по карточкам.
Дети по очереди называют число и соответствующую букву.
Слайд 8
III. Формулировка темы и целей урока
Учитель. Прочитайте тему нашего урока. Какое слово вам знакомо? С помощью какого арифметического действия находится сумма? Значение какого вы еще не знаете? Сегодня мы узнаем значение этого слова.
Слайд 9
– Посмотрите на доску. Что записано на ней? (Суммы).
– Какую сумму вычислить легче? (5 + 5) Чему равно
значение суммы?
– Можем ли мы сразу найти значение второй суммы? (Нет)
– Сегодня на уроке мы познакомимся с новым
действием, которое поможет нам легко и быстро
находить значение подобных выражений. Это
действие умножение и с результатом этого
действия – произведением. Мы познакомимся с
математическим знаком, который используется при
записи данного действия, попробуем решать задачи
с помощью умножения. Будем развивать
вычислительные навыки, память. Вы должны быть
внимательны и аккуратны.
Это
действие умножение и с результатом этого
действия – произведением. Мы познакомимся с
математическим знаком, который используется при
записи данного действия, попробуем решать задачи
с помощью умножения. Будем развивать
вычислительные навыки, память. Вы должны быть
внимательны и аккуратны.
IV. Создание проблемной ситуации
Учитель. Смайлик приготовил для вас следующее задание.
Слайд 10
– Из следующих сумм назови только ту, в которой все слагаемые одинаковые.
1 + 1 + 1 + 2
5 + 5 + 5 + 5 + 5 + 5
3 + 2 + 3 + 2
1 + 2 + 3 + 4 + 5
– Чему равно каждое слагаемое в сумме?
– Сколько раз повторяется слагаемое?
– Можем ли мы данное выражение записать
по-другому? (Пока не можем.)
Учитель. Мышка поможет нам в этом.
V. Изучение нового
Учитель. Сумму, состоящую из
одинаковых слагаемых можно записать по-другому
– в виде ПРОИЗВЕДЕНИЯ.
Сумму, состоящую из
одинаковых слагаемых можно записать по-другому
– в виде ПРОИЗВЕДЕНИЯ.
5 + 5 + 5 + 5 + 5 + 5 = 5 • 6
– Для обозначения произведения используется
специальный знак в виде точки. Данное действие
называется действием умножения.
– Запись читается так: ПРОИЗВЕДЕНИЕ ЧИСЕЛ 5 И
6. (Повторить хором).
– Число 5 в произведении показывает, какое
слагаемое повторяется, и записывается на первом
месте. Число 6 показывает сколько раз оно
повторяется, записывается на втором месте.
– Откройте учебники на странице 91. Прочитайте
правило самостоятельно, постарайтесь запомнить
чтобы потом ответить на мои вопросы.
– Как можно записать сумму, состоящую из
одинаковых слагаемых?
– Скажите, что показывает число 5 в произведении?
На каком месте пишется?
– Что показывает число 6 в произведении? На каком
месте пишется?
Учитель. Мышка предлагает проверить
правильность своих ответов.
Мышка предлагает проверить
правильность своих ответов.
Слайд 11
– Кто ответил так же, поднимите Смайлик.
– Вы были абсолютно правы.
VI. Закрепление
Игра «Помоги приземлиться летчику»
Учитель. Смайлик нашел ответ на свой вопрос и предлагает вам игру.
Слайд 12
– Помоги приземлиться летчику.
– Найди для каждой суммы своё произведение,
прочитай правильно.
– Называем устно, проверяем на компьютере (2 + 2 +
2 произведение чисел 2 и 3)
– Я показываю сумму, вы находите произведение.
9 + 9 …
7 + 7 …
12 + 12 …
3 + 3 …
– Молодцы, вы хорошо справились с заданием. Смайлик очень доволен. Кому было сложно, поднимите Смайлика.
VII. Физминутка (Приложение 3)
Учитель. Вы хорошо потрудились, а
теперь отдохнём. Встали, вышли из-за парт.
Попробуйте повторить движения за утенком.
Встали, вышли из-за парт.
Попробуйте повторить движения за утенком.
Слайд 13
VIII. Закрепление
Учитель. Мы продолжаем свою работу.
Слайд 14
– Прочитайте произведения. Что обозначают
числа, образующие каждое произведение? (Первое
число показывает какое слагаемое использовали,
второе – сколько раз). Попробуйте заменить
суммой первое произведение.
– Мышка хочет проверить усвоение вами материала
и приготовила вам свое задание…
1. Работа в тетрадях
Учитель. Откройте тетради, запишите число, классная работа. Прочитайте задание мышки. Выполните его в тетрадях. Образец выполнения перед вами. Выполните задание по образцу.
2. Самопроверка
Учитель. А теперь проверим выполнение данной работы.
Слайд 15
– Кто выполнил задание безошибочно, поднимите
Смайлик.
– Кто сделал одну ошибку?
– Кто сделал 2 и более ошибок.
– Мышка говорит вам…
Слайд 16
4. Игра «Ёжики»
Учитель. Следующую игру вам
предлагает Смайлик.
Нужно подобрать к произведению сумму, вычислить
значение сумм. А потом мы сделаем вывод о том, как
связано значение суммы и соответствующего
произведения. (Произведение чисел 10 и 4 можно
заменить суммой 10 + 10 + 10 + 10, значение суммы равно
40)
– Кто не согласен, поднимите Смайлик.
Слайд 17
Вывод: Что вы можете сказать о значении сумм и соответствующих произведений? Значение сумм и соответствующих произведений равны.
5. Задача
Учитель. Мышка любит решать разные задачи. Одну из них она предлагает вам.
Слайд 18
– Прочитайте условие задачи.
– О чем говорится в задаче?
– Что известно?
– Что нужно найти?
– Какое действие будем использовать для
нахождения ответа задачи?
– Как сложение заменить умножением?
– Как будет звучать ответ задачи?
– Выполните задание мышки.
– Открыли тетради, записали слово задача. Не
записывая условия, пишем только решение и ответ.
В решении указываем, как найти ответ задачи при
помощи сложения, затем при помощи умножения, а
также находим значение выражения. И записываем
ответ задачи.
Слайд 19
6. Самопроверка
Учитель. Проверьте запись в тетрадях.
– Кто выполнил задание безошибочно, поднимите Смайлик.
Слайд 20
– Мышка снова довольна вашей работой.
7. Веселые задачи
Учитель. Смайлик и Мышка довольны вашей работой и у них есть для вас веселые задачи. Сейчас мы решим некоторые из них.
Слайды 21-29
– Мы выбираем картинку. Слушаем задачу. Решаем её сложением, а затем выполняем дополнительное задание. Будьте внимательны.
Наша Маша рано встала,
Кукол всех она считала:
2 матрешки на окошке,
2 Аринки на перинке,
2 Танюшки на подушке.
Помоги нашей подружке
Посчитать её игрушки.
– Сколько кукол у Маши? Как нашли? Как сумму заменить произведением?
Сбежала от Федоры посуда:
3 стакана, 3 чашки, 3 блюда.
Кто сосчитать готов,
Сколько всего беглецов?
У этого цветка 4 лепестка.
А сколько лепестков
У двух таких цветков?
Как-то раз в лесу густом,
Под березовым кустом,
Собрались грибы лесные,
Все красавцы удалые,
Ученик, ты не зевай
И грибы скорей считай.
5 груздей и 5 волнушек,
5 лисичек, 5 горькушек.
Кто ответить нам готов,
Сколько же всего грибов?
Насушила грибов
Белочка-хозяйка.
Справа – 6, слева – 6
Все пересчитай-ка.
3 зайчонка в час обеда
Захотели пообедать.
В огороде зайцы сели
И по семь морковок съели.
Кто считать, ребята, ловок
Сколько съедено морковок?
Какой шум и гам в лесу!
То кричат ребята.
И с испуга в 2 дупла
Спрятались бельчата.
Сколько маленьких бельчат
В дуплах проживает?
Там по 9 хвостиков
В темноте мелькают.
8. Кроссворд
– А теперь выполним задание Смайлика. Он стал очень умным, многое узнал и хочет проверить вас. Он предлагает вам решить кроссворд.
Каждый вопрос читает учитель. Дети отвечают. Затем следует ответ – заполнение клеток.
- Как можно записать сумму одинаковых слагаемых? (В виде произведения.)
- Назовите арифметическое действие, результатом
которого является произведение? (Умножение.
 )
) - Как выглядит знак, использующийся при записи произведения? (Точка.)
- В виде какого арифметического действия можно представить произведение? (Сложения.)
– Посмотрите, в нашем кроссворде появилось еще одно незнакомое слово. Прочитайте его. А вот что обозначает это слово, мы узнаем на следующем уроке математики.
– Подошел к завершению наш урок. Мышка и Смайлик хотят проверить, что вы запомнили на уроке.
Слайд 30
Учитель. А теперь мы проверим, как вы усвоили материал урока. Откройте тетради на печатной основе с. 39 найдите 2. Прочитайте задание, выполните его самостоятельно в рабочих тетрадях. Проверим устно.
– Кто согласен с ответом, поднимите Смайлик.
IX. Итог
– С какими новыми математическими терминами
познакомились на уроке? (Произведение,
умножение.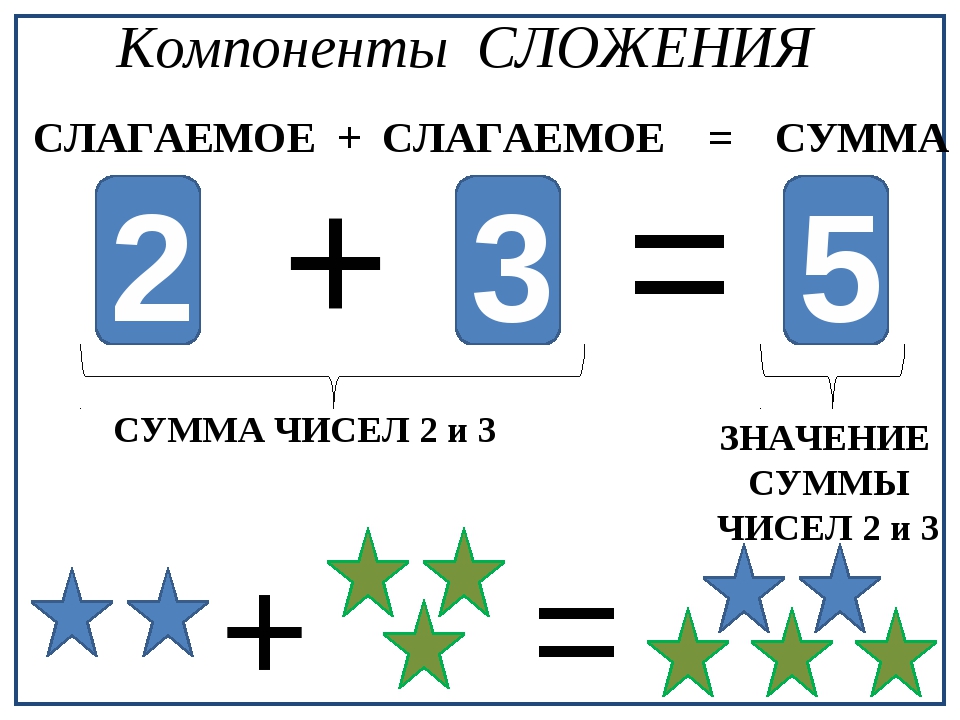 )
)
– Какие слагаемые можно заменить произведением? (Одинаковые.)
– Как называется действие, результатом которого
является произведение? (Умножение.)
– Что вы можете сказать о значении произведения? (Равно
значению соответствующей суммы.)
X. Эмоциональный отклик
Учитель. А теперь я хочу узнать. Понравился ли вам урок. На столах у вас есть Смайлик, который помогал вам на уроке. Но у него чего-то не хватает. Чего? Возьмите черный фломастер или карандаш и нарисуйте Смайлику ротик.
Слайд 31
– Если урок вам понравился, то улыбающийся.
Если нет, то грустный, как на экране.
– Покажите Смайликов. Я вижу, что урок вам
понравился. Вы тоже очень хорошо работали.
– Молодцы! Смайлик и Мышка считают, что за урок вы
заслужили оценку 5!
Слайд 32
– Урок окончен! Спасибо за урок!
Приложение 1
Приложение 2
НПК на тему «Тайны математических символов»
Муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа № 19»
города Новочебоксарска Чувашской Республики
Научно-исследовательская работа
Тайны математических символов
Выполнила: ученица 5-в класса Баряева Дарья
Руководитель: учитель математики Филиппова Лариса Николаевна
Новочебоксарск-2015год
Содержание:
1. Введение
Введение
2.Математическте символы
1)Знаки сложения и вычитания
2)Знак равенства
3)Знаки умножения и деления
4)Знак процента
5)Знак бесконечности
6)Знаки угла и перпендикулярности
7)Знак параллельности
8) Число пи
9)Краткая запись «Что и требовалось доказать»
3.Заключение
4.Литература
5.Приложение
1. Введение
Проблема:
Ребята с первого класса знакомятся со многими математическими обозначениями. Становясь старше, они заинтересовываются о происхождении математических знаков, терминов. Наш проект приоткроет завесу некоторых из этих тайн.
Цель: Создать электронное пособие.
Задачи:
• собрать информацию по теме проекта
• систематизировать собранный материал
• создать презентацию
• познакомить учащихся 4-6 классов с познавательными фактами из истории математики
Актуальность проекта
Когда я училась в
начальных классах, у меня даже не появлялось мысли о том, откуда взялся знак
умножения или знак равенства, я просто выполняла задания учителя, не
задумываясь о таких вещах. Так было до недавнего времени, пока я не
познакомилась с обыкновенными дробями и не узнала от учителя о различном
обозначении обыкновенных дробей. Я заинтересовалась этой проблемой, и у меня
появилось множество вопросов. Я думаю, что у ребят помладше возникает их не
меньше. Мой проект раскрывает некоторые тайны происхождения математических
знаков, терминов. Разыскивая информацию, я сама узнала много интересного,
думаю, это будет интересно и другим ребятам, а также их родителям и учителям.
Желаю успеха!
Так было до недавнего времени, пока я не
познакомилась с обыкновенными дробями и не узнала от учителя о различном
обозначении обыкновенных дробей. Я заинтересовалась этой проблемой, и у меня
появилось множество вопросов. Я думаю, что у ребят помладше возникает их не
меньше. Мой проект раскрывает некоторые тайны происхождения математических
знаков, терминов. Разыскивая информацию, я сама узнала много интересного,
думаю, это будет интересно и другим ребятам, а также их родителям и учителям.
Желаю успеха!
Слово математика пришло
к нам из древнегреческого, где μάθημα означало «учиться»,
«приобретать знания». И не прав тот, кто говорит: «Мне не нужна
математика, я ведь не собираюсь стать математиком». Математика нужна всем.
Раскрывая удивительный мир окружающих нас чисел, она учит мыслить яснее и
последовательнее, развивает мысль, внимание, воспитывает настойчивость и волю.
М.В.Ломоносов говорил: «Математика ум в порядок приводит». Одним
словом, математика учит нас учиться приобретать
знания.
Математика – это первая наука, которую смог освоить человек. Самой древней деятельностью был счёт. Некоторые первобытные племена подсчитывали количество предметов с помощью пальцев рук и ног. Наскальный рисунок, сохранившийся, до наших времён от каменного века изображает число 35 в виде нарисованных в ряд 35 палочек. Можно сказать, что 1 палочка – это первый математический символ.
Математическая «письменность», которую мы сейчас используем — от обозначений неизвестных буквами x, y, z до знака интеграла — складывалась постепенно. Развитие символики упрощало работу с математическими операциями и способствовало развитию самой математики.
С древнегреческого «символ» (греч. symbolon – признак, примета, пароль, эмблема) – знак, который связан с обозначаемой им предметностью так, что смысл знака и его предмет представлены только самим знаком и раскрываются лишь через его интерпретацию.
С открытием
математических правил и теорем ученые придумывали новые математические
обозначения, знаки. Математические знаки — это условные обозначения,
предназначенные для записи математических понятий, предложений и выкладок. В
математике употребляются специальные символы, позволяющие сократить запись и
точнее выразить утверждение. Помимо цифр и букв различных алфавитов
(латинского, греческого, еврейского) математический язык используют множество
специальных символов, изобретенных за последние несколько столетий.
Математические знаки — это условные обозначения,
предназначенные для записи математических понятий, предложений и выкладок. В
математике употребляются специальные символы, позволяющие сократить запись и
точнее выразить утверждение. Помимо цифр и букв различных алфавитов
(латинского, греческого, еврейского) математический язык используют множество
специальных символов, изобретенных за последние несколько столетий.
2. Математические символы
1)Знаки сложения, вычитания
История математических обозначений начинается с палеолита. Этим временем датируются камни и кости с насечками, использовавшимися для счета. Наиболее известный пример — кость Ишанго. Знаменитая кость из Ишанго (Конго) датируемая примерно 20 тысяч лет до новой эры, доказывает, что уже в то время человек выполнял достаточно сложные математические операции. Насечки на кости использовались для сложения и наносились группами, символизируя сложения чисел.
В Древнем Египте была
уже намного более продвинутая система обозначений. Например, в папирусе Ахмеса в
качестве символа сложения используется изображение двух ног, идущих вперед по
тексту, а для вычитания — двух ног, идущих назад. Древние греки обозначали
сложение записью рядом, но время от времени использовали для этого символ косой
черты “/’’ и полуэллиптическую кривую для вычитания.
Например, в папирусе Ахмеса в
качестве символа сложения используется изображение двух ног, идущих вперед по
тексту, а для вычитания — двух ног, идущих назад. Древние греки обозначали
сложение записью рядом, но время от времени использовали для этого символ косой
черты “/’’ и полуэллиптическую кривую для вычитания.
Символы для арифметических операций сложения (плюс “+’’) и вычитания (минус “-‘’) встречаются настолько часто, что мы почти никогда не задумываемся о том, что они существовали не всегда. Происхождение этих символов неясно. Одна из версий — они ранее использовались в торговом деле как признаки прибыли и убытка.
Считается, так
же, что наш знак происходит от одной из форм слова
“et’’, которое по-латыни значит “и’’. Выражение a + b писалось на
латыни так: a et b. Постепенно, из-за частого использования, от
знака «et» осталось только » t » ,
которое, со временем превратилось в » + «. Первым
человеком, который, возможно, использовал знак как аббревиатуру для et,
был астроном Николь д’Орем (автор книги “The Book of the Sky and the World’’ —
“Книги неба и мира’’) в середине четырнадцатого века.
В конце пятнадцатого века французский математик Шике (1484 г.) и итальянский Пачоли (1494 г.) использовали “’’ или “’’ (обозначая “плюс’’) для сложения и “’’ или “’’ (обозначая “минус’’) для вычитания.
Обозначения вычитания были более запутанными, так как вместо простого знака “” в немецких, швейцарских и голландских книгах иногда использовали символ “÷’’, которым мы сейчас обозначаем деление. В нескольких книгах семнадцатого века (например, у Декарта и Мерсенна) использованы две точки “∙ ∙’’ или три точки “∙ ∙ ∙’’ для обозначения вычитания.
Первое
использование современного алгебраического знака “” относится к немецкой рукописи по
алгебре 1481 г., которая была найдена в библиотеке Дрездена. В латинской
рукописи того же времени (также из библиотеки Дрездена), есть оба
символа: « » и « — » . Систематическое использование знаков « » и «
— » для сложения и вычитания встречается у Иоганна Видмана.
Немецкий
математик Иоганн Видманн (1462-1498) первым использовал оба знака для пометок
присутствия и отсутствия студентов на своих лекциях. Правда, есть сведения, что
он «позаимствовал» эти знаки у малоизвестного профессора Лейпцигского
университета. В 1489 году он издал в Лейпциге первую печатную книгу (Mercantile
Arithmetic — “Коммерческая арифметика’’), в которой присутствовали оба
знака и , в труде «Быстрый и приятный
счёт для всех торговцев» (ок. 1490)
Правда, есть сведения, что
он «позаимствовал» эти знаки у малоизвестного профессора Лейпцигского
университета. В 1489 году он издал в Лейпциге первую печатную книгу (Mercantile
Arithmetic — “Коммерческая арифметика’’), в которой присутствовали оба
знака и , в труде «Быстрый и приятный
счёт для всех торговцев» (ок. 1490)
Как исторический курьез, стоит отметить, что даже после принятия знака не все использовали этот символ. Видман сам ввел его как греческий крест (знак, который мы используем сегодня), у которого горизонтальная черта иногда немного длиннее вертикальный. Некоторые математики, такие как Рекорд, Харриот и Декарт, использовали такой же знак. Другие (например, Юм, Гюйгенс, и Ферма) использовали латинский крест « † », иногда расположенный горизонтально, с перекладиной на одном конце или на другом. Наконец, некоторые (например, Галлей) использовали более декоративный вид « ».
2)Знак равенства
Знак равенства в
математике и других точных науках пишут между двумя идентичными по своему
размеру выражениями. Первым употребил знак равенства Диофант. Равенство он
обозначил буквой i (от греческого isos – равный). В античной
и средневековой математике равенство обозначалось словесно,
например, est egale, или
использовали аббревиатуру “ae’’ от латинского aequalis — “равны’’. На других языках также использовали первые
буквы слова “равный’’, но это не было общепринятым. Знак равенства
«=» ввел в 1557 году уэльский врач и математик Роберт Рекорд (Recorde
R., 1510-1558). Математическим
символом для обозначения равенства служил в некоторых случаях символ II. Рекорд ввел символ “=’’ с двумя
одинаковыми горизонтальными параллельными отрезками, гораздо более длинными,
чем те, что используются сегодня. Английский математик Роберт Рекорд был
первым, кто начал использовать символ «равенство», аргументируя
словами: «никакие два предмета не могут быть равны между собой более, чем
два параллельных отрезка». Но ещё в XVII веке Рене
Декарт использовал
аббревиатуру “ae’’. Франсуа
Виет знаком равенства обозначал вычитание.
Первым употребил знак равенства Диофант. Равенство он
обозначил буквой i (от греческого isos – равный). В античной
и средневековой математике равенство обозначалось словесно,
например, est egale, или
использовали аббревиатуру “ae’’ от латинского aequalis — “равны’’. На других языках также использовали первые
буквы слова “равный’’, но это не было общепринятым. Знак равенства
«=» ввел в 1557 году уэльский врач и математик Роберт Рекорд (Recorde
R., 1510-1558). Математическим
символом для обозначения равенства служил в некоторых случаях символ II. Рекорд ввел символ “=’’ с двумя
одинаковыми горизонтальными параллельными отрезками, гораздо более длинными,
чем те, что используются сегодня. Английский математик Роберт Рекорд был
первым, кто начал использовать символ «равенство», аргументируя
словами: «никакие два предмета не могут быть равны между собой более, чем
два параллельных отрезка». Но ещё в XVII веке Рене
Декарт использовал
аббревиатуру “ae’’. Франсуа
Виет знаком равенства обозначал вычитание.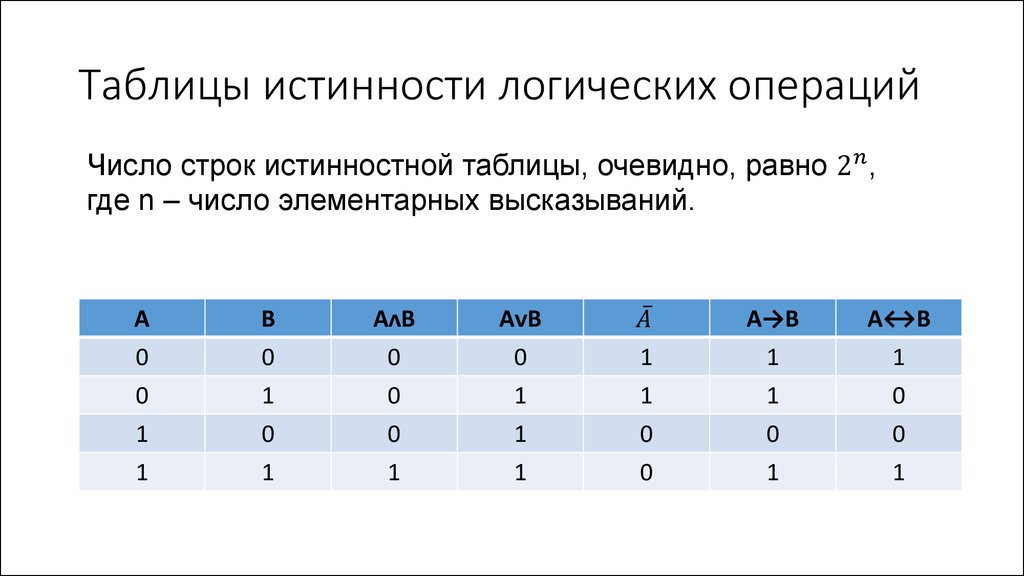 Некоторое время
распространению символа Рекорда мешало то обстоятельство, что такой же символ
использовался для обозначения параллельности прямых; в конце концов было решено
символ параллельности сделать вертикальным. Распространение знак получил только
после работ Лейбница на рубеже XVII—XVIII веков, то есть более чем через 100
лет после смерти впервые использовавшего его для этого Роберта
Рекорда. На его могильной плите нет слов – просто вырезан знак
«равно».
Некоторое время
распространению символа Рекорда мешало то обстоятельство, что такой же символ
использовался для обозначения параллельности прямых; в конце концов было решено
символ параллельности сделать вертикальным. Распространение знак получил только
после работ Лейбница на рубеже XVII—XVIII веков, то есть более чем через 100
лет после смерти впервые использовавшего его для этого Роберта
Рекорда. На его могильной плите нет слов – просто вырезан знак
«равно».
Родственные символы для обозначения приблизительного равенства «≈» и тождества «≡» являются совсем молодыми — первый введен в 1885 году Гюнтером, второй — в 1857 году Риманом
3) Знаки умножения и деления
Знак умножения в виде крестика («х») ввел англиканский священник-математик Уильям Отред в 1631 году. До него для знака умножения использовали букву M, хотя предлагались и другие обозначения: символ прямоугольника (Эригон, 1634), звёздочка (Иоганн Ран, 1659).
Позднее Лейбниц
заменил крестик на точку (конец XVII века), чтобы не
путать его с буквой x; до него такая символика встречалась у Региомонтана
(XV век) и английского
учёного Томаса
Хэрриота (1560—1621).
Для обозначения действия деления Отред предпочитал косую черту. Двоеточием деление стал обозначать Лейбниц. До них часто использовали также букву D. Начиная с Фибоначчи, используется также черта дроби, употреблявшаяся ещё в арабских сочинениях. Деление в виде обелюс («÷») ввел швейцарский математик Иоганн Ран (ок. 1660)
4)Знак процента.
Сотая доля целого, принимаемого за единицу. Само слово «процент» происходит от латинского «pro centum», что означает в переводе «на сто». В 1685 году в Париже была издана книга «Руководство по коммерческой арифметике» Матье де ла Порта (1685). В одном месте речь шла о процентах, которые тогда обозначали «cto» (сокращённо от cento). Однако наборщик принял это «cto» за дробь и напечатал «%». Так из-за опечатки этот знак вошёл в обиход.
5)Знак бесконечности
Нынешний символ
бесконечности «∞» ввел в употребление Джон Уоллис в
1655 году. Джон Уоллис издал большой трактат «Арифметика
бесконечного» (лат. Arithmetica
Infinitorum sive Nova Methodus Inquirendi in Curvilineorum Quadraturam, aliaque
Difficiliora Matheseos Problemata), где ввёл придуманный
им символ бесконечности. До сих пор так и не известно, почему
он остановил свой выбор именно на этом знаке. Одна из наиболее авторитетных
гипотез связывает происхождение этого символа с латинской буквой «М», которую
римляне использовали для обозначения числа 1000. Символ бесконечности назван «lemniscus» (лат. лента)
математиком Бернулли приблизительно сорок лет спустя.
Arithmetica
Infinitorum sive Nova Methodus Inquirendi in Curvilineorum Quadraturam, aliaque
Difficiliora Matheseos Problemata), где ввёл придуманный
им символ бесконечности. До сих пор так и не известно, почему
он остановил свой выбор именно на этом знаке. Одна из наиболее авторитетных
гипотез связывает происхождение этого символа с латинской буквой «М», которую
римляне использовали для обозначения числа 1000. Символ бесконечности назван «lemniscus» (лат. лента)
математиком Бернулли приблизительно сорок лет спустя.
Другая
версия говорит о том, что рисунок «восьмерки» передает главное свойство понятия
«бесконечность»: движение без
конца. По линиям числа 8 можно совершать, как по велотреку,
бесконечное движение. Для того, чтобы не путать введенный знак с числом 8,
математики решили располагать его горизонтально. Получилось .
Такое обозначение cтало стандартным для всей математики, не только алгебры.
Почему бесконечность не обозначают нулем? Ответ очевиден: цифру 0 как не
поворачивай — она не изменится.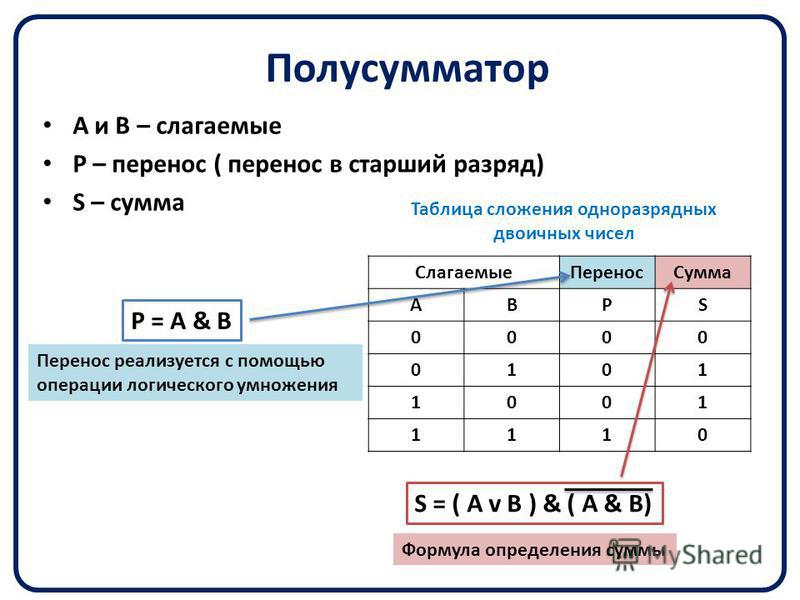 Поэтому выбор и пал именно на 8.
Поэтому выбор и пал именно на 8.
Другой вариант — змей, пожирающий свой хвост, который за полторы тысячи лет до нашей эры в Египте символизировал различные процессы, не имеющие начала и конца.
Многие считают, что лист Мёбиуса является прародителем символа бесконечности, т.к символ бесконечности был запатентован после изобретения устройства «лента Мебиуса» (названный в честь математика девятнадцатого столетия Мебиуса). Лента Мебиуса — полоса бумаги, которая искривлена и соединена концами, формируя две пространственные поверхности. Однако по имеющимся историческим сведениям символ бесконечности стал использоваться для обозначения бесконечности за два столетия до открытия ленты Мёбиуса
6) Знаки угла и перпендикулярности
Символы «угол»
и «перпендикулярно» придумал в 1634 году французский
математик Пьер Эригон. Символ перпендикулярности у него был перевёрнут,
напоминая букву T. Символ угла напоминал значок , современную форму ему
придал Уильям Отред (1657).
7) Знак параллельности
Символ «параллельности» известен с античных времён, его использовали Герон и Папп Александрийский. Сначала символ был похож на нынешний знак равенства, но с появлением последнего, во избежание путаницы, символ был повёрнут вертикально (Отред (1677), Керси (John Kersey) и др. математики XVII века).
8) Число пи
Общепринятое обозначение числа, равного отношению длины окружности к ее диаметру (3,1415926535…), впервые образовал Уильям Джонс в 1706 году, взяв первую букву греческих слов περιφέρεια —окружность и περίμετρος — периметр, то есть длина окружности. Это сокращение понравилось Эйлеру, труды которого закрепили обозначение окончательно.
Синус и косинус
Интересно появление синуса и косинуса.
Sinus с
латинского — пазуха, впадина. Но история у такого названия долгая. Далеко в
тригонометрии продвинулись индийские математики в районе 5 века. Самого слова
«тригонометрия» не было, оно было введено Георгом Клюгелем в 1770
году. ) То, что мы сейчас называем синусом, примерно соответствует тому, что индусы
называли ардха-джия, в переводе — полутетива (т.е. полухорда). Для
краткости называли просто — джия (тетива). Когда арабы переводили
работы индусов с санскрита, они не стали переводить «тетиву» на
арабский, а просто транскрибировали слово арабскими буквами.
Получилась джиба. Но так как в слоговой арабской письменности краткие
гласные не обозначаются, то реально остается дж-б, что похоже на другое
арабское слово — джайб (впадина, пазуха). Когда Герард
Кремонский в 12 веке переводил арабов на латынь, он перевел это слово
как sinus, что по-латыни также означает пазуху, углубление.
) То, что мы сейчас называем синусом, примерно соответствует тому, что индусы
называли ардха-джия, в переводе — полутетива (т.е. полухорда). Для
краткости называли просто — джия (тетива). Когда арабы переводили
работы индусов с санскрита, они не стали переводить «тетиву» на
арабский, а просто транскрибировали слово арабскими буквами.
Получилась джиба. Но так как в слоговой арабской письменности краткие
гласные не обозначаются, то реально остается дж-б, что похоже на другое
арабское слово — джайб (впадина, пазуха). Когда Герард
Кремонский в 12 веке переводил арабов на латынь, он перевел это слово
как sinus, что по-латыни также означает пазуху, углубление.
Косинус появился автоматически, т.к. индусы называли его коти-джия, или сокращено ко-джия. Коти — изогнутый конец лука на санскрите. Современные краткие обозначения и введены Уильямом Отредом и закреплены в трудах Эйлера.
Обозначения тангенса/котангенса имеют
намного более позднее происхождение (английское
слово tangent происходит от латинского tangere — касаться).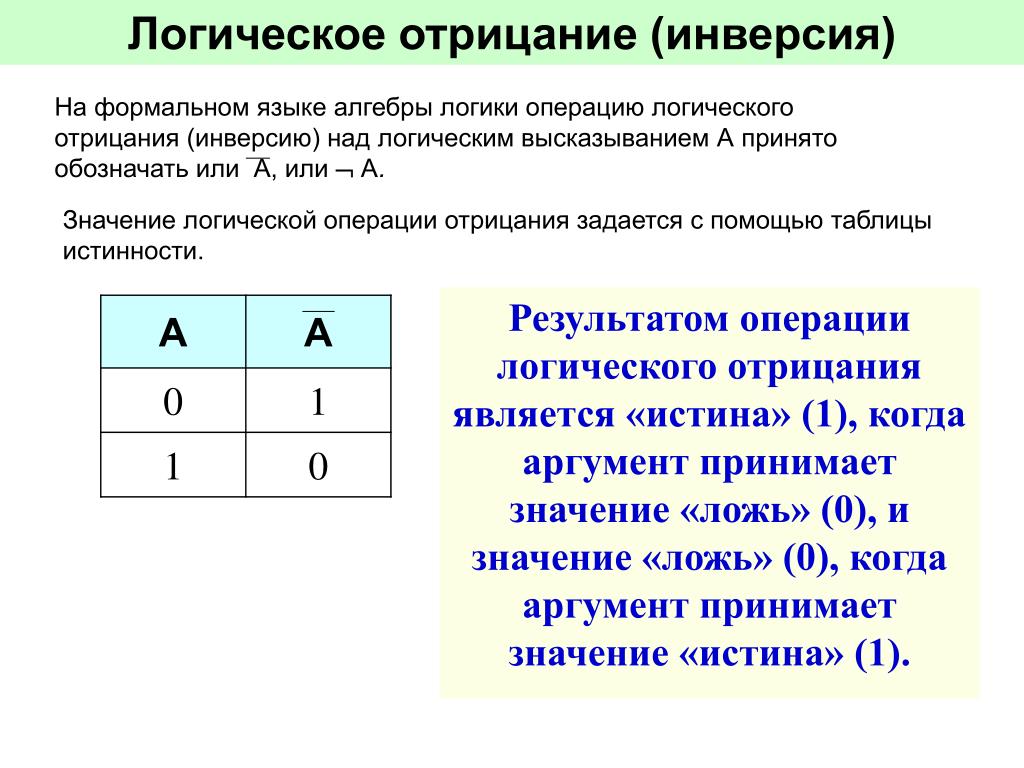 И даже до сих пор нет унифицированного обозначения — в одних странах чаще
используется обозначение tan, в других — tg
И даже до сих пор нет унифицированного обозначения — в одних странах чаще
используется обозначение tan, в других — tg
9) Сокращение «Что и требовалось доказать» (ч.т.д.)
«Quod erat demonstrandum»
(квол эрат лэмонстранлум).
Греческая фраза
имеет значение «что требовалось доказывать», а латинская — «что нужно было
показать». Этой формулой заканчивается каждое математическое рассуждение великого греческого
математика Древней Греции Эвклида (III в. до н. э.). В переводе с
латинского — что и требовалось доказать. В средневековых научных трактатах эту
формулу писали часто в сокращенном виде: QED.
Математические обозначения.
Символы | История символов
|
+ — | Знаки плюса и минуса придумали, по-видимому, в немецкой
математической школе «коссистов» (то есть алгебраистов).
|
× ∙
| Знак умножения ввёл в 1631 году Уильям Отред (Англия) в виде косого крестика. До него использовали букву M. Позднее Лейбниц заменил крестик на точку (конец XVII века), чтобы не путать его с буквой x; до него такая символика встречалась у Региомонтана (XV век) и английского учёного Томаса Хэрриота (1560—1621).
|
/ : ÷
| Отред предпочитал косую черту.
|
=
| Знак равенства предложил Роберт Рекорд (1510—1558) в 1557 году. Он пояснил, что нет в мире ничего более равного, чем два параллельных отрезка одинаковой длины. В континентальной Европе знак равенства был введён Лейбницем.
|
Знаки сравнения ввёл Томас Хэрриот в своём сочинении, изданном посмертно в 1631 году. До него писали словами: больше, меньше.
| |
%
| Символ процента появляется в середине XVII века сразу в нескольких
источниках, его происхождение неясно.
|
√
| Знак корня впервые употребил немецкий математик Кристоф Рудольф, из школы коссистов, в 1525 году. Происходит этот символ от стилизованной первой буквы слова radix (корень). Черта над подкоренным выражением вначале отсутствовала; её позже ввёл Декарт для иной цели (вместо скобок), и эта черта вскоре слилась со знаком корня.
|
an
| Возведение в степень. Современная запись показателя степени введена
Декартом в его «Геометрии» (1637), правда, только для натуральных степеней,
больших 2.
|
( )
| Скобки появились у Тартальи (1556) для подкоренного выражения, но большинство математиков предпочитали вместо скобок надчёркивать выделяемое выражение. В общее употребление скобки ввёл Лейбниц.
|
Σ | Знак суммы ввёл Эйлер в 1755 году |
П | Знак произведения ввёл Гаусс в 1812 году |
i
| Букву i как код мнимой единицы: предложил Эйлер (1777), взявший для этого первую букву слова imaginarius (мнимый).
|
π
| Общепринятое обозначение числа 3.
|
Обозначение интеграла Лейбниц произвёл от первой буквы слова «Сумма» (Summa).
| |
y’
| Краткое обозначение производной штрихом восходит к Лагранжу. |
Символ предела появился в 1787 году у Симона Люилье (1750—1840). | |
Символ бесконечности придумал Валлис, опубликован в 1655 году. |
3. Заключение
Математическая наука необходима для цивилизованного
общества. Математика содержится во всех науках. Математический язык смешивается
с языком химии и физики. Но нам он все равно понятен. Можно сказать, что язык
математики мы начинаем изучать вместе с родной речью. Так неразрывно вошла
математика в нашу жизнь. Благодаря математическим открытиям прошлого, ученые
создают новые технологии. Сохранившиеся открытия дают возможность решать
сложные математически задачи. И древний математический язык нам понятен, а
открытия нам интересны. Благодаря математике Архимед, Платон, Ньютон открыли
физические законы. Мы изучаем их в школе. В физике тоже есть символы термины
присущие физической науке. Но математический язык не теряется среди физических
формул. Наоборот, эти формулы нельзя написать без знания математики. Благодаря
истории сохраняются знания и факты для будущих поколений. Дальнейшее изучение
математики необходимо для новых открытий.
Математика содержится во всех науках. Математический язык смешивается
с языком химии и физики. Но нам он все равно понятен. Можно сказать, что язык
математики мы начинаем изучать вместе с родной речью. Так неразрывно вошла
математика в нашу жизнь. Благодаря математическим открытиям прошлого, ученые
создают новые технологии. Сохранившиеся открытия дают возможность решать
сложные математически задачи. И древний математический язык нам понятен, а
открытия нам интересны. Благодаря математике Архимед, Платон, Ньютон открыли
физические законы. Мы изучаем их в школе. В физике тоже есть символы термины
присущие физической науке. Но математический язык не теряется среди физических
формул. Наоборот, эти формулы нельзя написать без знания математики. Благодаря
истории сохраняются знания и факты для будущих поколений. Дальнейшее изучение
математики необходимо для новых открытий.
Литература
1. Что? Зачем? Почему? Большая книга вопросов и
ответов. Пер.Мишиной К., А Зыковой -М: Издательство ЭКСМО, 2007
Что? Зачем? Почему? Большая книга вопросов и
ответов. Пер.Мишиной К., А Зыковой -М: Издательство ЭКСМО, 2007
2. Глейзер Г.И. История математики в школе VII-VIII кл. Пособие для учителей. М: Просвещение, 1982
3. Рыбников К.А. История математики. Издательство Московского Университета, 1974
4. Интернет. www математические символы.
Приложение.
Копилка стихотворений.
Число пи
Гордый Рим трубил
победу
Над твердыней Сиракуз,
Но трудами Архимеда
Много больше я горжусь.
Надо нынче нам заняться,
Оказать старинке честь.
Чтобы нам не ошибаться,
Чтоб окружность верно счесть.
Надо только постараться
И запомнить все, как есть:
Три-14-15-92 и шесть.
(п= 3,1415926)
Арифметические знаки
Как не на свете
без ножек столов,
Как нет на свете без рожек козлов,
Котов без усов и без панцирей раков,
Так нет в арифметике действий без знаков!
«+»
Я добрый знак соединенья
И в том мое предназначенье
Я для сложения гожусь,
И этим очень я горжусь!
В математике есть
знак.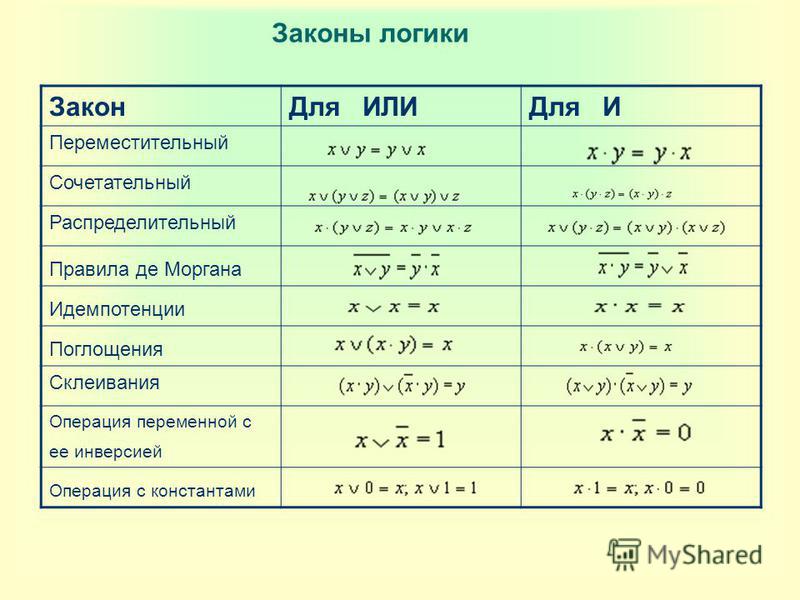
Без него нельзя никак!
Он не жадный, но отнять
Может от восьмёрки пять.
«-»
Я – минус,
Тоже добрый знак.
Ведь не со зла я отнимаю,
Я свою роль лишь выполняю.
Из цифры вычтем мы другую,
Ставим черточку прямую.
Этот знак мы узнаем,
«Минус» мы его зовем.
Перед скобкой “минус” строгий
Загородит нам дорогу.
Чтобы скобки убирать,
Надо знаки поменять.
«*»
Его нам надо пригласить,
Чтоб разных чисел ряд сложить.
Для облегчения сложенья
Есть знак отличный – . . . (умноженье)
«:»
Не все в этом действии гладко:
То целиком, а то – с остатком.
В несколько раз уменьшение
Выполнит знак вам . . . (деление)
Ребусы
Умножить или добавить сначала? Преподавание порядка операций Правила
Назад к ShapedМатематика
Фигурный посох
9 мин Чтение
Когда учащиеся 3-х классов и старше сначала учатся складывать, вычитать, умножать, делить и работать с основными числовыми выражениями, они начинают с выполнения операций над двумя числами. Но что происходит, когда выражение требует нескольких операций? Например, вы сначала складываете или умножаете? А умножить или разделить? В этой статье объясняется, что такое порядок операций, и приводятся примеры, которые вы также можете использовать со студентами. Он также содержит два урока, которые помогут вам представить и развить эту концепцию.
Стандартный ключ:
- Выполнять арифметические операции, включая сложение, вычитание, умножение и деление в обычном порядке, независимо от того, есть скобки или нет. (3 класс)
Порядок операций является примером очень процедурной математики. Легко запутаться, потому что это не столько концепция, которую вы осваиваете, сколько список правил, которые вы должны запомнить. Но не обманывайте себя, думая, что процедурные навыки не могут быть глубокими! В нем могут быть представлены сложные задачи, подходящие для старших школьников и созревшие для обсуждения в классе:
Но не обманывайте себя, думая, что процедурные навыки не могут быть глубокими! В нем могут быть представлены сложные задачи, подходящие для старших школьников и созревшие для обсуждения в классе:
- Изменяется ли правило слева направо, когда умножение подразумевается, а не прописывается? (Например, \(3g\) или \(8(12)\) вместо \(3 \times g\) или \(8 \cdot 12\).)
- Где факториал попадает в порядок операций ?
- Что произойдет, если вы возвели один показатель степени в другой показатель степени, но скобок нет? (Обратите внимание, что этот урок не включает показатели, хотя, если учащиеся готовы, вы можете расширить свой урок, включив их.)
Что важнее в порядке операций?
Со временем математики согласовали набор правил, называемый порядком операций , чтобы определить, какую операцию выполнять первой. Когда выражение включает только четыре основные операции, действуют следующие правила:
- Умножение и деление слева направо.

- Сложение и вычитание слева направо.
При упрощении выражения, такого как \(12 \div 4 + 5 \times 3 — 6\), сначала вычислите \(12 \div 4\), поскольку порядок операций требует сначала вычисления любого умножения и деления (в зависимости от того, что произойдет сначала) слева направо перед оценкой сложения или вычитания. В данном случае это означает, что сначала нужно вычислить \(12 \div 4\), а затем \(5 \times 3\). Как только все умножение и деление завершены, продолжайте складывать или вычитать (в зависимости от того, что наступит раньше) слева направо. Шаги показаны ниже.
| \(12 \дел 4 + 5 \умножить на 3 — 6\) | ||
| \(3 + 5 \умножить на 3 — 6\) | Потому что \(12 \дел 4 = 3\) | |
| \(3 + 15 — 6\) | Потому что \(5 \х3 = 15\) | |
| \(18 — 6\) | Потому что \(3 + 15 = 18\) | |
| \(12\) | Потому что \(18 — 6 = 12\) |
Рассмотрим в качестве примера другое выражение:
| \(6 + 4 \times 7)0048 | ||
| \(6 + 28 — 3\) | Потому что \(4 \times 7 = 28\), что делается первым, потому что умножение и деление вычисляются первыми. | |
| \(34 — 3\) | Потому что \(6 + 28 = 34\) | |
| \(31\) | Потому что \(34 — 3 = 31\) | 90 Иногда |
| \((6 + 4) \times 7 — 3\) | |
| \(10 \times 7 — 3\) | Потому что \(6 + 4 = 10\), что делается первым, потому что оно заключено в круглые скобки. |
| \(70 — 3\) | Потому что \(10 \х7 = 70\), и скобок больше нет.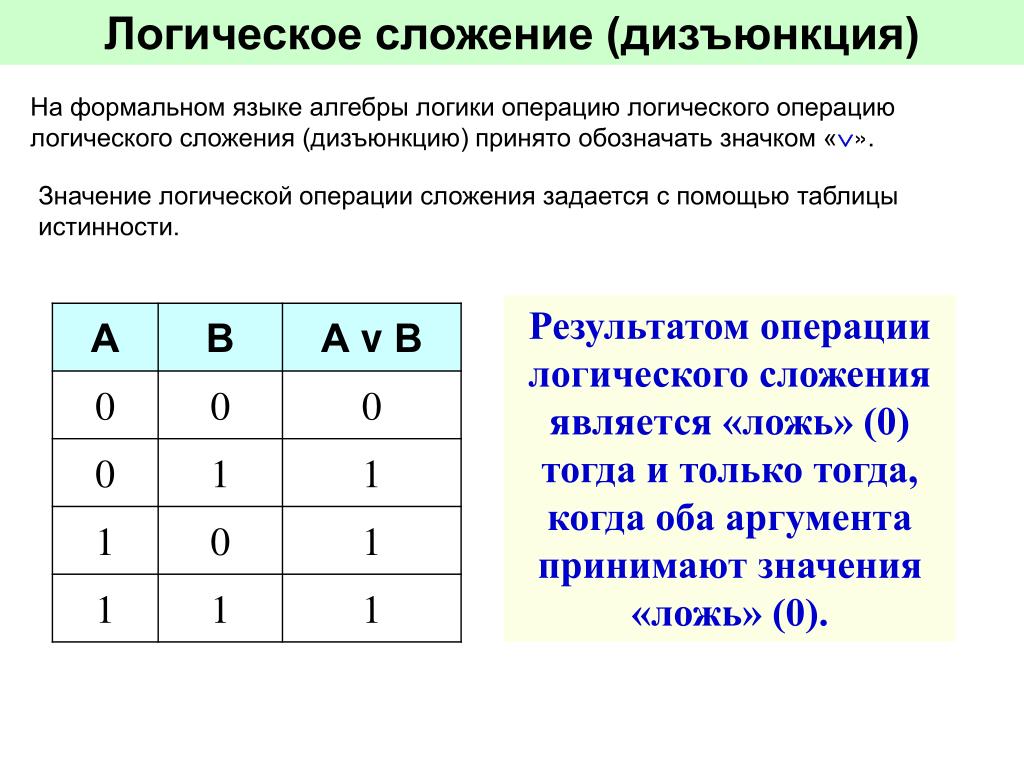 |
| \(67\) | Потому что \(70 — 3 = 67\) |
Обратите внимание, что выражение имеет совершенно другое значение! Что, если вместо этого мы заключим в скобки \(7 — 3\)?
| \(6 + 4 \times (7 — 3)\) | |
| \(6 + 4 \times 4\) | На этот раз \(7 — 3\) в скобках, поэтому мы делаем это в первую очередь. |
| \(6 + 16\) | Поскольку \(4 \times 4 = 16\), и когда не осталось скобок, мы продолжаем умножение перед сложением. |
| \(22\) | Потому что \(6 + 16 = 22\) |
Этот набор скобок дает еще один ответ. Итак, когда задействованы круглые скобки, правила порядка операций следующие:
- Выполнять операции в круглых скобках или группировать символы.
- Умножение и деление слева направо.
- Сложение и вычитание слева направо.
Знакомство с концепцией: порядок операций
Прежде чем ваши учащиеся будут использовать скобки в математике, они должны четко понимать порядок операций без скобок. Начните с повторения правил сложения и умножения в порядке выполнения операций, а затем покажите учащимся, как круглые скобки могут повлиять на этот порядок.
Начните с повторения правил сложения и умножения в порядке выполнения операций, а затем покажите учащимся, как круглые скобки могут повлиять на этот порядок.
Материалы: Белая доска или способ писать для класса публично
Необходимые навыки и понятия: Учащиеся должны уметь оценивать и обсуждать выражения сложения, вычитания, умножения и деления.
- Спросить : Какую операцию выполнить первой в выражении \(5 \times 7 + 3\) ? Почему?
Запишите выражение публично. Если студенты не согласны, попросите их объяснить, не говоря им, правы они или нет. При необходимости напомните им, что по порядку операций умножение и деление предшествуют сложению и вычитанию.
- Спросите : Каково значение этого выражения?
Попросите учащихся оценить выражение. \(5 \times 7 = 35\), поэтому выражение становится \(35 + 3\), что равно \(38\).
- Спросите : Что произойдет, если я поменяю местами символы сложения и умножения? Какое значение я получу?
Перепишите выражение как \(5 + 7 \умножить на 3\) и выполните вычисление.
 \(7 \times 3 = 21\), поэтому выражение становится \(5 + 21\), что равно \(26\).
\(7 \times 3 = 21\), поэтому выражение становится \(5 + 21\), что равно \(26\). - Спросите : Получили ли мы другие значения при изменении операций?
Этот результат, вероятно, не удивит ваших учеников. Скорее всего, они знают, что выполнение разных операций над одними и теми же числами даст разные значения. Если позволяет время и учащиеся готовы, предложите им найти выражение, в котором перестановка символов сложения и умножения, как вы сделали, дает одно и то же значение. Если кто-то из учащихся преуспеет, попросите их показать, как они получили выражения. Обратите внимание, что это возможно только тогда, когда среднее число равно 1 (например, \(5 \times 1 + 3\) или \(5 + 1 \times 3\)) или внешние числа равны (например, \(3 \times 7). + 3\) или \(3 + 7 \умножить на 3\)).
- Спросите : Что делать, если я хочу оставить символы умножения и сложения на одном месте (\(5 \times 7 + 3\)) , но выполнить \(7 + 3\) сначала ? Как вы думаете, как я мог это сделать?
Кратко обсудите вопрос, затем напишите на доске \(5 \times (7 + 3)\).
 Обратите внимание на скобки.
Обратите внимание на скобки. - Скажем : Мы называем эти символы скобками. Если в выражении есть скобки, сначала сделайте то, что внутри скобок.
- Спросите : Что находится в скобках в выражении \(5 \times (7 + 3)\) ?
Убедитесь, что учащиеся правильно понимают, что число \(7 + 3\) находится в скобках и что оно должно оцениваться перед вычислением с помощью \(5\).
- Скажем : Теперь давайте закончим вычисление значения. (Значение равно \(5 \times 10\) или \(50\).) Это то же самое значение, которое мы получили раньше?
Помогите учащимся заметить, что значение не совпадает ни с исходным выражением, ни с выражением с переключенными символами операций.
Это подходящий момент для обсуждения математической практики с учетом точности . В математике очень важно, чтобы мы преднамеренно писали математические выражения и делали математические утверждения.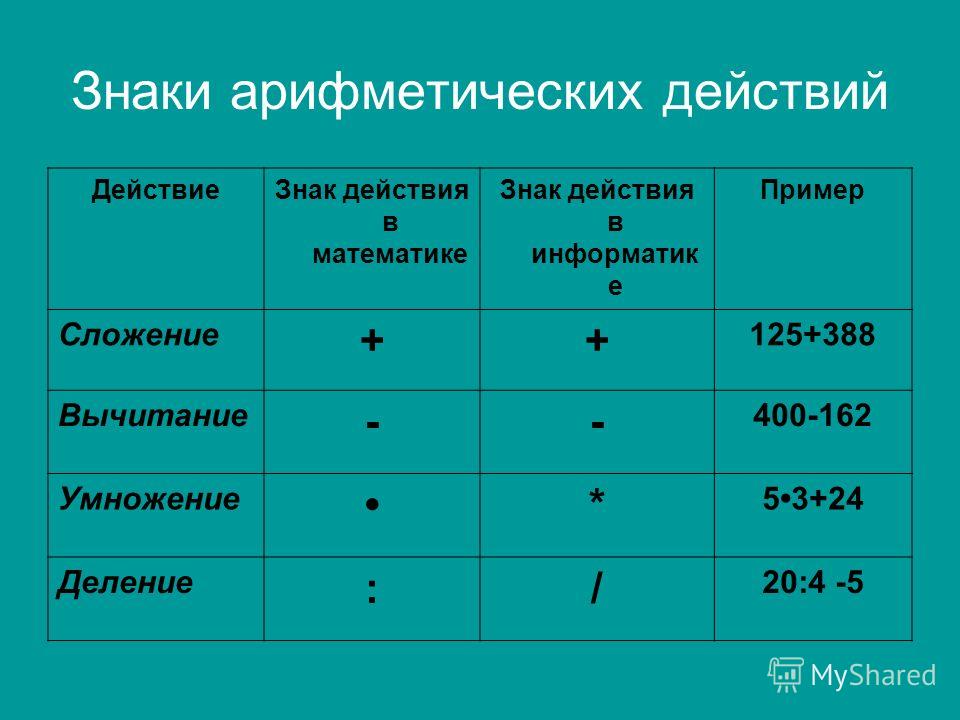 Небольшие перепутывания с математическими правилами операций или скобками могут привести к радикальным изменениям! Представьте себе неправильное вычисление выражения, например, при расчете дозировки или стоимости лекарства.
Небольшие перепутывания с математическими правилами операций или скобками могут привести к радикальным изменениям! Представьте себе неправильное вычисление выражения, например, при расчете дозировки или стоимости лекарства.
Дайте учащимся еще несколько примеров, показывающих выражение со скобками и без них. Попросите студентов-добровольцев оценить выражения и сравнить их значения. Когда учащиеся приходят к разным значениям, не говорите им, правы они или нет. Вместо этого предложите им найти сходства и различия в своих стратегиях и направьте обсуждение так, чтобы учащиеся увидели, какая стратегия соответствует правилам порядка действий.
Разработка концепции: Порядок действий
Материалы: Белая доска или способ записи для класса публично
Необходимые навыки и понятия: Учащиеся должны быть знакомы с порядком действий и чувствовать себя готовыми к его применению.
Продолжая учить своих студентов работе со скобками, не забудьте продемонстрировать, что скобки не всегда изменяют значение выражения, хотя часто изменяют.
- Спросить : Какую операцию выполнить первой в выражении \(3 + 5 \times 8\) и почему?
Запишите выражение публично. Убедитесь, что учащиеся ясно понимают, что порядок операций требует, чтобы они выполняли умножение перед сложением.
- Спросите : Что произойдет, если я хочу добавить 3 и 5 до умножения на 8?
Позвольте учащимся обсудить идеи о том, как изменить порядок операций. Не говорите ученикам, что они правы, а что нет. Вместо этого поощряйте математический дискурс и сравнивайте разные мнения, чтобы исправить неправильные представления. Обратите внимание, что вариантов ответов может быть много! Например, в задаче может быть явно указано «сначала добавьте 3 и 5», или исторически существовали другие способы группировки, такие как использование горизонтальных черт над выражением. Если они не упоминают скобки, напомните им, что вы делали на первом уроке.
- Скажем : Заключив скобки вокруг \(3 + 5\) , мы говорим, что мы должны сначала сложить 3 и 5, а затем умножить на 8.
 Сегодня мы собираемся попрактиковаться в нахождении значения выражений с и без скобок и посмотрите, какое значение имеют скобки.
Сегодня мы собираемся попрактиковаться в нахождении значения выражений с и без скобок и посмотрите, какое значение имеют скобки. - Напишите следующие три выражения публично, чтобы все учащиеся могли их увидеть.
- \(3 + 6 \умножить на 2\)
- \((3 + 6) \умножить на 2\)
- \(3 + (6 \умножить на 2)\)
- Произнесите : Вычислите все три выражения.
Дайте учащимся время закончить вычисления. Затем пусть студенты-добровольцы сообщат о том, что они нашли.
- Спросите : Вы получили одинаковое значение для всех трех выражений? Почему или почему нет?
Учащиеся должны заметить, что выражения 1 и 3 дают одно и то же значение, а выражение 2 отличается. Обсудите, что выражение 2 требует сложения перед умножением, а выражения 1 и 3 требуют умножения перед сложением. Цель состоит в том, чтобы учащиеся увидели, что использование скобок иногда меняет значение выражения, а иногда нет.

- Напишите следующие два выражения публично, чтобы все учащиеся могли их увидеть.
- \((8 \дел 4) — 2\)
- \(8 \дел (4 — 2)\)
- Произнесите: Вычислите оба выражения.
Дайте учащимся время закончить вычисления. Затем пусть студенты-добровольцы сообщат о том, что они нашли.
- Спросите : Значения этих выражений одинаковы? Почему или почему нет?
Еще раз учащиеся должны увидеть значение использования скобок.
- Скажите: Теперь мы попробуем задание со многими возможными решениями. Ваша цель — найти выражение, в котором можно перемещать скобки без изменения значения. Проблема в том, что круглые скобки должны быть около сложения или вычитания .
Пройдите пример. Покажите, как в двух приведенных ниже выражениях скобки окружают выражение сложения, и когда они перемещаются, значение выражения остается прежним: 7.

- \((3 + 4) \умножить на 1\)
- \(3 + (4 \умножить на 1)\)
- Если возможно, попросите учащихся работать в парах, чтобы создать дополнительные примеры. Учащимся, которые застряли, попросите их заменить 3 и/или 4 в приведенных выше выражениях.
- Спросите : Как вы создавали выражения, которые позволяли вам «двигать» скобки? С какими проблемами вы столкнулись?
Организуйте обсуждение различных выражений, сделанных учащимися. Предложите учащимся сравнить сходства и различия как в выражениях, которые они сделали, так и в стратегиях, которые они использовали для их выражения.
Подведение итогов и подсказки для оценивания
Важно, чтобы учащиеся могли запомнить правила порядка операций как со скобками, так и без них. Избегайте давать рабочие листы механического обучения. Вместо этого ищите математические задачи, которые естественным образом приводят к выражениям, которые необходимо вычислить, например, подстановка значений в формулу, и попросите учащихся попрактиковаться в порядке выполнения операций в контексте других задач.
***
Хотите повысить уверенность учащихся в математике, помимо практики математических правил порядка операций? Исследуйте HMH Into Math , наше базовое математическое решение K–8.
Математика 3-5 классы 6-8 классы Занятия и уроки
Дополнительная литератураДженнифер Прескотт
Форма УчастникКристин Кондон
Shaped Главный редакторРичард Бланкман
Фасонный Редактор
Математика 3-5 классы 6-8 классы Занятия и уроки
Подпишитесь на нашу рассылку новостей
Будьте первым, кто прочитает последние новости от Shaped .
Подписаться
1.
 6: Целочисленная арифметика — Инженерные тексты LibreTexts
6: Целочисленная арифметика — Инженерные тексты LibreTexts- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 27020
- Чарльз В. Канн III
- Геттисбергский колледж
1.6.1 Сложение целых чисел
Сложение целых двоичных чисел было рассмотрено в главе 1.4. Сложение целых чисел похоже на сложение целых двоичных чисел, за исключением того, что необходимо учитывать как положительные, так и отрицательные числа. Например, сложите два положительных числа 0010 2 (2 10 ) + 0011 2 (3 10 ) = 0101 2 (5 10 ).
Рисунок 1-2: Сложение двух положительных целых чисел Сложение смешанных положительных и отрицательных чисел и двух отрицательных чисел также работает таким же образом, как показано в следующих двух примерах.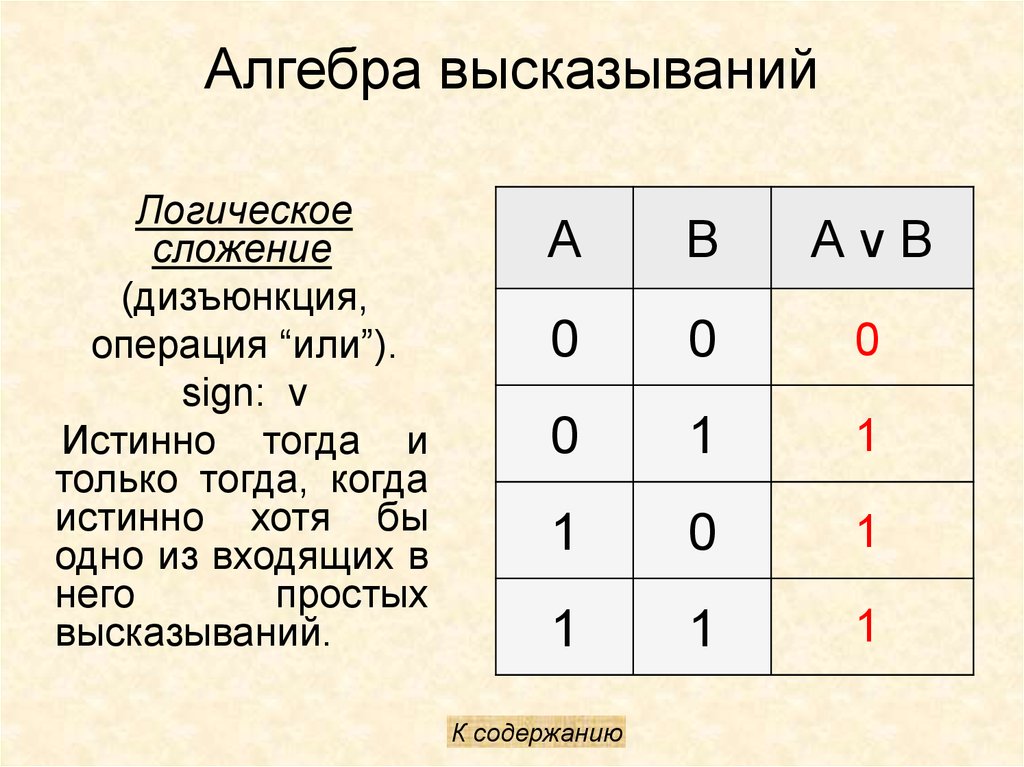 Первый добавляет 0010 2 (2 10 ) + 1101 2 (-3 10 ) = 1111 2 (-1 10 1), а второй добавляет 10 9 10511 2 (-2 10 ) + 1101 2 (-3 10 ) = 1011 2 (-5 10 ).
Первый добавляет 0010 2 (2 10 ) + 1101 2 (-3 10 ) = 1111 2 (-1 10 1), а второй добавляет 10 9 10511 2 (-2 10 ) + 1101 2 (-3 10 ) = 1011 2 (-5 10 ).
Поскольку целые числа имеют фиксированный размер, сложение и вычитание могут вызвать проблему, известную как целочисленное переполнение. Это происходит, когда два добавляемых числа являются большими положительными или отрицательными значениями, а объединение значений приводит к слишком большим числам, чтобы их можно было сохранить в целом числе.
1.6.2 Переполнение при сложении целых чисел
Поскольку целые числа имеют фиксированный размер, сложение и вычитание могут вызвать проблему, известную как переполнение целых чисел. Это происходит, когда два добавляемых числа являются большими положительными или отрицательными значениями, а объединение значений приводит к слишком большим числам, чтобы их можно было сохранить в целочисленном значении.
Например, 4-битное целое число может хранить значения от -8 до 7. Итак, когда 0100 2 (4 10 ) + 0101 2 (5) = 1001 2 (-7) добавляются с использованием 4-битных целых чисел, результат слишком велик для сохранения в целом числе. Когда это происходит, число меняет знак и дает неверный ответ, как показано на следующем рисунке.
Рисунок 1-5: Добавление с переполнениемПопытка алгоритмически выяснить, происходит ли переполнение, затруднена. Во-первых, если одно число положительное, а другое отрицательное, переполнения никогда не происходит. Если оба числа положительные или отрицательные, то если знак суммы отличается от знака любого из входов, произошло переполнение.
Существует гораздо более простой способ выяснить, произошло ли переполнение. Если бит переноса в последнюю цифру совпадает с битом переноса, то переполнения не произошло. Если они разные, то произошло переполнение. На рис. 1.3 перенос и перенос последнего бита равны 0, поэтому переполнения нет. Аналогично, на рис. 1.4 перенос и перенос равны 1, поэтому переполнения не было. На рисунке 1.5 перенос равен 1, а перенос равен 0, поэтому произошло переполнение.
Аналогично, на рис. 1.4 перенос и перенос равны 1, поэтому переполнения не было. На рисунке 1.5 перенос равен 1, а перенос равен 0, поэтому произошло переполнение.
Этот метод также работает для сложения отрицательных чисел. Рассмотрим добавление 1100 2 (-4 10 ) и 1011 2 (-5 10 ) = 0111 2 (7 10 ), как показано на рисунке 1.6. Здесь перенос равен 0, а перенос равен 1, поэтому снова произошло переполнение.
Рисунок 1-6: Вычитание с переполнением1.6.3 Умножение целых чисел с использованием операций сдвига битов
Умножение и деление значений данных или переменных включает аппаратные компоненты в арифметико-логическом устройстве (ALU). В ассемблере эти операции будут обеспечиваться операторами различных форм mul и div, а аппаратное обеспечение для их реализации выходит за рамки этой книги и не будет рассматриваться. Однако, что представляет интерес при написании ассемблера, так это умножение и деление на константу.
Причина, по которой рассматривается умножение и деление на константу, заключается в том, что эти операции могут быть обеспечены операциями сдвига битов, а операции сдвига битов часто выполняются быстрее, чем эквивалентные операции mul или div. Поэтому операции сдвига битов часто используются в ассемблере для выполнения умножения и деления, поэтому программистам на ассемблере важно понимать, как это работает.
Сначала рассмотрим умножение числа на степень 10 по основанию 10. По основанию 10, если число умножить на степень 10 (10 n , где n — степень числа 10), достаточно передвинуть число на n позиций вправо, заполнив его нулями. Например, 15*1000 (или 15*103) = 15 000.
То же самое относится и к двоичному коду. Чтобы умножить двоичное число (например, 15 или 00001111 2 ) на 2, число сдвигается влево на 1 разряд (записывается как 1111<<1), что дает 00011110 2 или 30. Аналогичным образом умножение 00001111 2 на 8 делается путем перемещения цифры 3 пробела влево (00001111 2 <<3), что дает 01111000 2 или 120. Таким образом, любое число, представленное в базе 2, легко умножить на степень 2 (например, 2 n ), выполнив n сдвигов влево и обратное заполнение. с 0-ми.
Таким образом, любое число, представленное в базе 2, легко умножить на степень 2 (например, 2 n ), выполнив n сдвигов влево и обратное заполнение. с 0-ми.
Обратите внимание, что это также работает для умножения отрицательных двойных дополнительных (или целых) чисел. Умножение 11110001 2 (-15) на 2 выполняется путем перемещения битов влево на 1 пробел и повторного добавления 0, что дает 11100010 2 (или -30) (обратите внимание, что в этом случае 0 используется для положительных или отрицательных чисел ). Снова умножить 11110001 2 (-15) на 8 выполняется с использованием 3-битных сдвигов и повторного заполнения числа нулями, что дает 10001000 2 (-120)
Применяя простую арифметику, легко понять, как выполнить умножение на константа 10. Умножение на 10 можно рассматривать как умножение на (8+2), поэтому (n*10) = ((n*8)+(n*2)).
15*10 = 15 * (8+2) = 15 *8 + 15 * 2 = (00001111 2 << 3) + (00001111 2 << 1) = 1111000 2 + 105110 2 = 100100110 2 = 150
Эта процедура факторизации применяется для умножения на любую константу, поскольку любая константа может быть представлена сложением степеней двойки. Таким образом, любое умножение констант может быть закодировано на ассемблере как последовательность сдвигов и сложений. Иногда это быстрее и часто проще, чем выполнение математических операций, и с этим должен быть знаком каждый программист на ассемблере.
Таким образом, любое умножение констант может быть закодировано на ассемблере как последовательность сдвигов и сложений. Иногда это быстрее и часто проще, чем выполнение математических операций, и с этим должен быть знаком каждый программист на ассемблере.
Это объяснение трюка с постоянным умножением работает в ассемблере, что вызывает вопрос, работает ли он также в HLL? Ответ да, и нет. Битовые сдвиги и сложения можно выполнять в большинстве языков программирования, поэтому постоянное умножение может быть реализовано как битовые сдвиги и сложения. Но то, что это можно сделать, не означает, что это нужно делать. В HLL (C/C++, Java, C# и т. д.) этот тип кода является запутанным, его трудно читать и понимать. Кроме того, любой приличный компилятор будет преобразовывать постоянное умножение в правильные базовые битовые сдвиги и добавления, когда это будет более эффективно. И компилятор примет более правильное решение о том, когда использовать этот метод умножения, и реализует его более эффективно и с меньшим количеством ошибок, чем если бы это делал программист.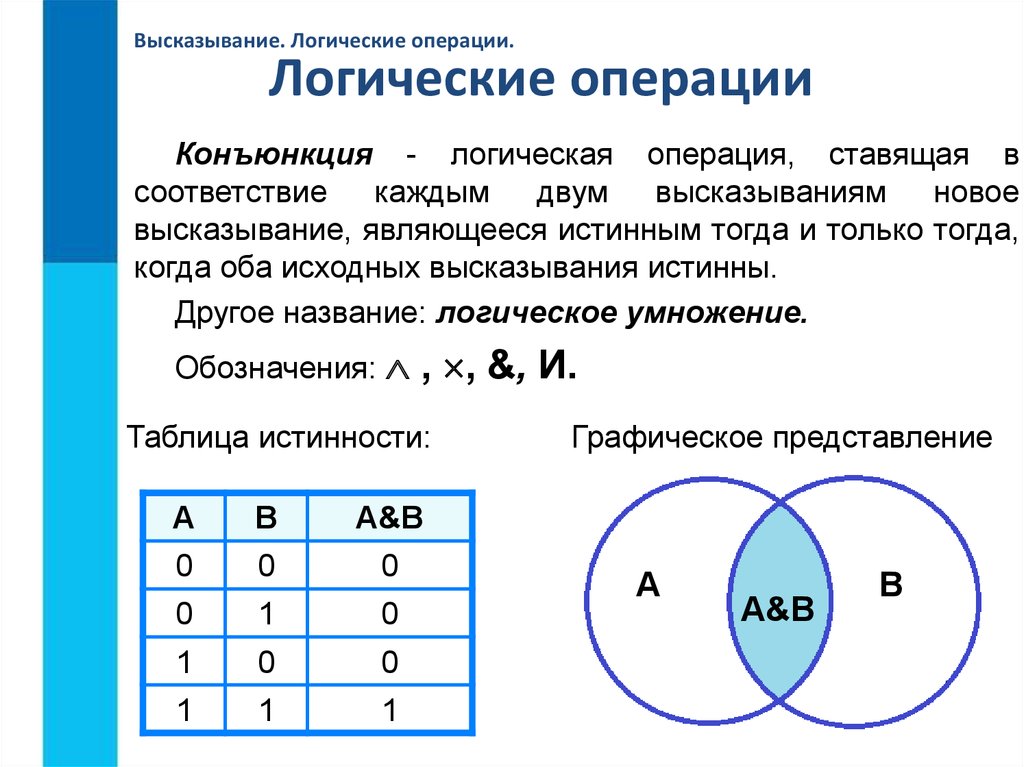 Поэтому, если нет действительно веской причины выполнять умножение с использованием битового сдвига и сложения, его следует избегать в HLL.
Поэтому, если нет действительно веской причины выполнять умножение с использованием битового сдвига и сложения, его следует избегать в HLL.
1.6.4 Целочисленное деление с использованием операций сдвига битов
Поскольку умножение может быть реализовано с использованием операций сдвига битов, возникает очевидный вопрос: применим ли тот же принцип к делению? Ответ заключается в том, что в некоторых полезных случаях деление с использованием операций сдвига битов действительно работает. Но в целом проблем полно.
Случаи, когда работает деление с использованием операций сдвига битов, это когда делимое положительно, а делитель равен степени 2. Например, 00011001 2 (25) разделить на 2 будет сдвигом на 1 бит, или 00001100 2 (12). Ответ 12.5 усечен, так как это легко реализовать, отбрасывая смещенный бит. Аналогичным образом, 00 011001 2 (25) разделить на 2 равно 00000011 2 (3), при этом снова происходит усечение. Обратите также внимание, что в этом случае сдвинутый бит является битом знака, который необходим для сохранения правильного знака числа.
Сдвиг битов для деления полезен в некоторых алгоритмах, таких как бинарный поиск, находящий родителей в полном бинарном дереве. Но опять же, этого следует избегать, если нет веских причин для его использования в HLL.
Остаются две проблемы. Во-первых, почему этот метод не может быть реализован с константами, отличными от степеней двойки. Причина в том, что деление является дистрибутивным только в одном направлении по сравнению с сложением, а в нашем случае это неправильное направление. Рассмотрим уравнение 60/10. Легко показать, что в этом случае деление над сложением не работает.
60/10 = 60/(8+2) ≠ 60/8 + 60/2
Второй вопрос заключается в том, почему дивиденд должен быть положительным. Чтобы понять, почему это так, рассмотрим следующее деление: -15/2. В результате получится следующее:
11111001 2 >> 1 = 11111100 = -8
В этом ответе две вещи. Во-первых, в этом случае бит знака, 1, должен быть сдвинут, чтобы сохранить знак целого числа.
Второй в этом случае самый младший бит, 1, усекается. Это означает, что -7,5 усекается до -8. Однако многие программисты считают, что -7,5 следует урезать до -7. Является ли правильный ответ -7 или -8 спорным, и разные языки программирования реализованы как любое значение (например, Java реализует -15/2 = -7, а Python -15/2 как -8). Та же проблема возникает со многими операциями над отрицательными числами, такими как модуль. И хотя такие дебаты могут быть забавными, и программисты должны осознавать, что такие проблемы могут возникать, цель этой книги не в том, чтобы сделать что-то большее, чем представить проблему.
Эта страница под названием 1.6: Целочисленная арифметика распространяется под лицензией CC BY 4.0, ее автором, ремиксом и/или куратором был Чарльз В. Канн III.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Чарльз В.
 Канн III
Канн III
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Показать оглавление
- нет
- Метки
ПОРЯДОК ДЕЙСТВИЙ
ПОРЯДОК ДЕЙСТВИЙ
ПОРЯДОК ДЕЙСТВИЙ
Бернис Э. Холлоуэй Школьный округ Беллвуд № 88
1801 Н. 36-я авеню
Каменный парк, Иллинойс 60165
1-708-344-9344
ЗАДАЧИ:
-использовать символы группировки и стандартный порядок операций для
упростить числовые выражения.
-использовать порядок операций для вычисления переменных выражений. - пользоваться калькулятором и компьютером для решения числовых выражений.
МАТЕРИАЛЫ:
-компьютеры
-калькуляторы (универсальный бренд)
-бумага
-карандаши
-мел
- классная доска
-ластик
-баннеры(компьютерная распечатка)
-Рекламный проспект
СТРАТЕГИЙ:
А. Выявить сравнение знаков препинания в предложении с
группировка символов в числовом выражении (знаки с выражениями
Робин Ли Трэвис и я любим компьютеры;Медленные дети играют;Сохранить
Тряпки и макулатура), спросите, могут ли учащиеся объяснить, почему баннеры
двусмысленный.
ИНФО
Без запятых предложение Робин Ли Трэвис и я любим компьютеры,
подразумевает, что два человека любят компьютеры. В зависимости от того, где стоят запятые
вставленное предложение может констатировать, что трое или четверо любят
компьютеры.
Примеры деятельности:
1) попросите учащихся упростить 10+2*3-1, чтобы получить как можно больше различных
ответы, как они могут (используйте калькуляторы и компьютеры, чтобы сравнить
ответы).
- пользоваться калькулятором и компьютером для решения числовых выражений.
МАТЕРИАЛЫ:
-компьютеры
-калькуляторы (универсальный бренд)
-бумага
-карандаши
-мел
- классная доска
-ластик
-баннеры(компьютерная распечатка)
-Рекламный проспект
СТРАТЕГИЙ:
А. Выявить сравнение знаков препинания в предложении с
группировка символов в числовом выражении (знаки с выражениями
Робин Ли Трэвис и я любим компьютеры;Медленные дети играют;Сохранить
Тряпки и макулатура), спросите, могут ли учащиеся объяснить, почему баннеры
двусмысленный.
ИНФО
Без запятых предложение Робин Ли Трэвис и я любим компьютеры,
подразумевает, что два человека любят компьютеры. В зависимости от того, где стоят запятые
вставленное предложение может констатировать, что трое или четверо любят
компьютеры.
Примеры деятельности:
1) попросите учащихся упростить 10+2*3-1, чтобы получить как можно больше различных
ответы, как они могут (используйте калькуляторы и компьютеры, чтобы сравнить
ответы). 2) обсудить необходимость типового порядка выполнения операций
чтобы не было двусмысленности в отношении ценности таких
выражения.
3) обсудить этапы стандартного порядка операций и показать
как они будут использоваться для упрощения приведенного выше выражения.
10+2*3-1
10+6-1 умножение
16-1 прибавление (слева направо)
Вычитание 15 (слева направо)
4) показать, как скобки могут быть использованы для придания различных значений
к тому же выражению.
(10+2)х3-1 (10+2)х(3-1)
12 х 3-1 12 х 2
36 -1 24
35
ИНФО
В выражениях с более чем одной операцией символы группировки, такие как
поскольку круглые скобки или разделительные полосы часто используются для обозначения
порядок выполнения операций.
2) обсудить необходимость типового порядка выполнения операций
чтобы не было двусмысленности в отношении ценности таких
выражения.
3) обсудить этапы стандартного порядка операций и показать
как они будут использоваться для упрощения приведенного выше выражения.
10+2*3-1
10+6-1 умножение
16-1 прибавление (слева направо)
Вычитание 15 (слева направо)
4) показать, как скобки могут быть использованы для придания различных значений
к тому же выражению.
(10+2)х3-1 (10+2)х(3-1)
12 х 3-1 12 х 2
36 -1 24
35
ИНФО
В выражениях с более чем одной операцией символы группировки, такие как
поскольку круглые скобки или разделительные полосы часто используются для обозначения
порядок выполнения операций. 2-4
13- 8 -3 2х 9-4
5-3 18-4
2 14
Обратите внимание, что в примерах № 3 и № 4 два выражения имеют
те же числа и те же операции, но результаты
отличаются из-за группировки символов. (Выполняйте операции внутри
круглые скобки, показатели степени, умножение/деление, сложение или
вычитание слева направо.)
№3 (8+5)х3 №4 8+(5х3)
(8+5)х3 8+(5х3)
13х3 8+15
3923
B. Чтобы дать дополнительную практику, используя правильный порядок
операции, у учащихся:
1) замените переменную в каждой строке или столбце, чтобы сделать ее истинной
уравнение в задаче №1 (см. раздаточный материал).
2) напишите знак операции (+,-,x,/) в каждой строке или столбце, чтобы
составьте правильное уравнение в головоломке № 2 (см. раздаточный материал).
2-4
13- 8 -3 2х 9-4
5-3 18-4
2 14
Обратите внимание, что в примерах № 3 и № 4 два выражения имеют
те же числа и те же операции, но результаты
отличаются из-за группировки символов. (Выполняйте операции внутри
круглые скобки, показатели степени, умножение/деление, сложение или
вычитание слева направо.)
№3 (8+5)х3 №4 8+(5х3)
(8+5)х3 8+(5х3)
13х3 8+15
3923
B. Чтобы дать дополнительную практику, используя правильный порядок
операции, у учащихся:
1) замените переменную в каждой строке или столбце, чтобы сделать ее истинной
уравнение в задаче №1 (см. раздаточный материал).
2) напишите знак операции (+,-,x,/) в каждой строке или столбце, чтобы
составьте правильное уравнение в головоломке № 2 (см. раздаточный материал). C. Чтобы проверить успеваемость учащихся, попросите их выполнить групповое задание.
Symbols-Review (см. раздаточный материал и ниже).
IV. КОММЕНТАРИИ/ИНФО.
Использование калькулятора настолько привычно для нас, что мы склонны принимать
некоторые вещи как должное... только при широком использовании личных
компьютеры вынуждают нас переоценивать функцию,
надлежащее использование и правильный метод (ы) обучения студентов
определенные математические концепции с использованием обеих машин.
3
Следует обратить внимание учащихся на то, что люди общаются с
компьютеров с помощью программ. Программы сообщают компьютеру, что делать.
Однако не всегда человеку необходимо уметь писать.
программа для работы с компьютером. Программы можно писать на таких
способ, которым оператор может их использовать, отвечая на ряд вопросов
которые прописаны в программе. Тем не менее, лучший способ научиться
что компьютер может и не может сделать, так это узнать немного о
программирование.
C. Чтобы проверить успеваемость учащихся, попросите их выполнить групповое задание.
Symbols-Review (см. раздаточный материал и ниже).
IV. КОММЕНТАРИИ/ИНФО.
Использование калькулятора настолько привычно для нас, что мы склонны принимать
некоторые вещи как должное... только при широком использовании личных
компьютеры вынуждают нас переоценивать функцию,
надлежащее использование и правильный метод (ы) обучения студентов
определенные математические концепции с использованием обеих машин.
3
Следует обратить внимание учащихся на то, что люди общаются с
компьютеров с помощью программ. Программы сообщают компьютеру, что делать.
Однако не всегда человеку необходимо уметь писать.
программа для работы с компьютером. Программы можно писать на таких
способ, которым оператор может их использовать, отвечая на ряд вопросов
которые прописаны в программе. Тем не менее, лучший способ научиться
что компьютер может и не может сделать, так это узнать немного о
программирование. возведен в степень (показатель степени)
BASIC следует порядку операций. Пример программы на БЕЙСИКЕ:
10 ПЕЧАТЬ 21*34+35/7
20 КОНЕЦ
БЕЖАТЬ
719(отвечать)
Группировка символов-обзор
Выберите каждый ответ из вариантов в скобках. Напишите ответ в
пустой.
1) аб означает а______________б. (плюс, разделить на, раз)
а
2) _ означает а______________б. (плюс, разделить на, раз)
б
3) a____________b означает, что a не равно b. знак равно
4) Круглые скобки являются примером ______________.(символ группировки, значение,
переменная)
Упростите каждое выражение с помощью калькулятора. Переведите каждое выражение в
БАЗОВЫЙ. Используйте компьютер для проверки ответов. (Не забудьте ввести PRINT перед
числовое выражение.)
5) 7+(12-3)_____________________ 6) (18-3) ____________
-----
(3+2)
7) (7х3)-(5х4)__________________ 8) 10-(3+4)___________
9) 24- (63/(6+3))_______________ 10) 36/12+6____________
-------
8-5
11) 15-5х2+8/4__________________ 12) 20(12-8)-30/(10+5)___________
Упростите выражение с каждой стороны ----?----.
возведен в степень (показатель степени)
BASIC следует порядку операций. Пример программы на БЕЙСИКЕ:
10 ПЕЧАТЬ 21*34+35/7
20 КОНЕЦ
БЕЖАТЬ
719(отвечать)
Группировка символов-обзор
Выберите каждый ответ из вариантов в скобках. Напишите ответ в
пустой.
1) аб означает а______________б. (плюс, разделить на, раз)
а
2) _ означает а______________б. (плюс, разделить на, раз)
б
3) a____________b означает, что a не равно b. знак равно
4) Круглые скобки являются примером ______________.(символ группировки, значение,
переменная)
Упростите каждое выражение с помощью калькулятора. Переведите каждое выражение в
БАЗОВЫЙ. Используйте компьютер для проверки ответов. (Не забудьте ввести PRINT перед
числовое выражение.)
5) 7+(12-3)_____________________ 6) (18-3) ____________
-----
(3+2)
7) (7х3)-(5х4)__________________ 8) 10-(3+4)___________
9) 24- (63/(6+3))_______________ 10) 36/12+6____________
-------
8-5
11) 15-5х2+8/4__________________ 12) 20(12-8)-30/(10+5)___________
Упростите выражение с каждой стороны ----?----. Сделайте истинное утверждение, заменив ? с символом = или . Проверьте свои
ответы с помощью компьютера. (Если компьютер напечатает 1, ваш ответ верен; если ваш
ответ неверный, компьютер напечатает 0.) Запомните числовые выражения
должен быть в БЕЙСИКЕ.
13) 16+3 ? 9+3 _______ 14) (8-3x2) ? (8-3)x2_________
---- ---- --- -------
8+4 4-1
4
15) 3(5+2) ? 3x5+2 ______ 16+4 ? 8+4х3____________
----- 16) 1+ ---- ----- ----
3+2 8-2-2
Сделайте истинное утверждение, заменив ? с символом = или . Проверьте свои
ответы с помощью компьютера. (Если компьютер напечатает 1, ваш ответ верен; если ваш
ответ неверный, компьютер напечатает 0.) Запомните числовые выражения
должен быть в БЕЙСИКЕ.
13) 16+3 ? 9+3 _______ 14) (8-3x2) ? (8-3)x2_________
---- ---- --- -------
8+4 4-1
4
15) 3(5+2) ? 3x5+2 ______ 16+4 ? 8+4х3____________
----- 16) 1+ ---- ----- ----
3+2 8-2-2
Вернуться к математическому указателюарифметика — Числа со знаком и без знака
Вопрос
Изменено 3 года, 6 месяцев назад
Просмотрено 5к раз
$\begingroup$
Как АЛУ в микропроцессоре отличит число со знаком -7, которое обозначается 1111, и число 15 без знака, также обозначаемое 1111?
- арифметический
- двоичный
$\endgroup$
9
$\begingroup$
Короткий и простой ответ: нет. Ни один современный процессор ISA не работает так, как вы думаете.
Ни один современный процессор ISA не работает так, как вы думаете.
Для процессора это просто битовый шаблон. Вам, программисту, решать, что означает этот битовый шаблон.
В общем, ISA не делают различий между разными типами данных, когда дело доходит до хранения. (Игнорируя регистры специального назначения, такие как регистры с плавающей запятой в FPU.) Это просто бессмысленный набор битов для ЦП. Однако ISA и имеют разные типы инструкций, которые могут по-разному интерпретировать битовую комбинацию. Например, арифметические команды, такие как MUL , DIV , ADD , SUB интерпретируют битовый шаблон как некоторое число, тогда как логические инструкции, такие как AND , OR , XOR интерпретируют его как массив логических значений. Таким образом, программист (или автор интерпретатора или компилятора, если вы используете язык более высокого уровня) должен выбрать правильные инструкции.
Например, вполне могут быть отдельные инструкции для чисел со знаком и без знака. Некоторые ISA также имеют инструкции для арифметики с двоично-десятичным кодом.
Однако обратите внимание, что выше я написал «современная основная ISA». На самом деле существуют неосновные или исторические ISA, которые работают по-другому. Например, как исходная 48-битная CISC ISA для IBM AS/400, так и текущая 64-битная RISC ISA на базе POWER для системы, которая теперь называется IBM i, различают указатели и другие значения. Указатели всегда помечены, и они включают информацию о типе и управлении правами. ЦП знает, является ли значение указателем или нет, и только привилегированное ядро i/OS может свободно манипулировать указателями. Пользовательские приложения могут манипулировать указателями, которыми они владеют, только для указания на принадлежащую им память, используя небольшое количество безопасных инструкций.
Были также некоторые исторические проекты ISA, которые включали, по крайней мере, некоторую ограниченную форму распознавания типов.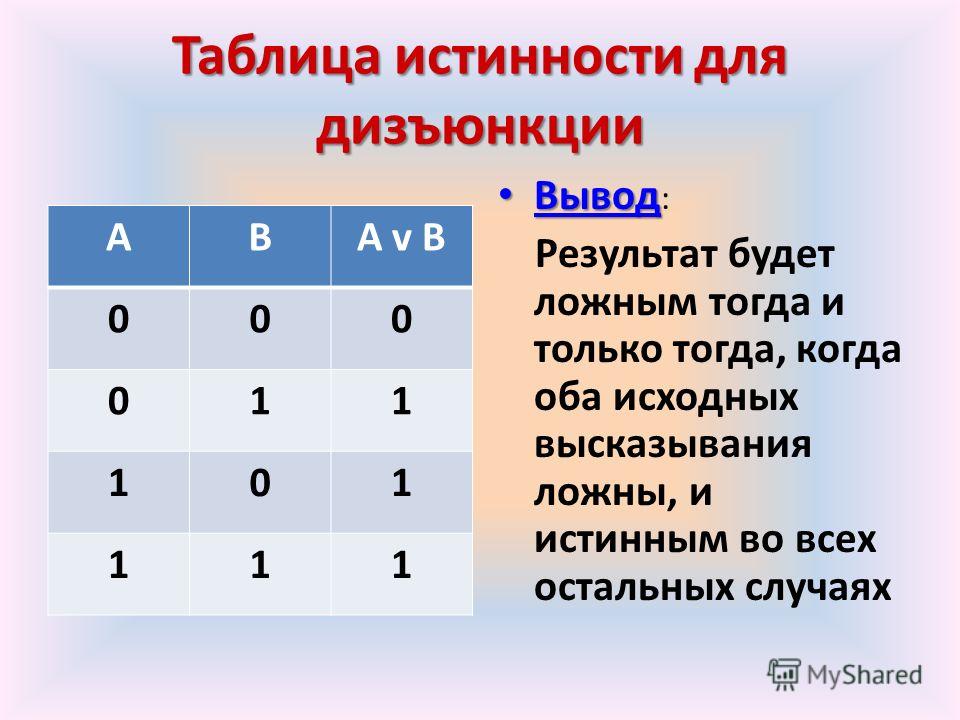
$\endgroup$
3
$\begingroup$
Короткая версия: не знает. Невозможно сказать.
Если 1111 представляет -7, то у вас есть представление величины знака , где первый бит является знаком, а остальные биты являются величиной. В этом случае арифметика несколько усложняется, так как добавление без знака и добавление со знаком используют разную логику. Так что у вас, вероятно, будет SADD и код операции UADD , и если вы выберете неправильный, вы получите бессмысленные результаты.
Однако чаще 1111 представляет -1 в так называемом представлении с дополнением до двух . В этом случае ALU просто не заботится о том, знаковые числа или беззнаковые! Например, возьмем операцию 1110 + 0001 . В арифметике со знаком это означает «-2 + 1», и результат должен быть -1 ( 1111 ). В беззнаковой арифметике это означает «14 + 1», и результат должен быть 15 (
В беззнаковой арифметике это означает «14 + 1», и результат должен быть 15 ( 1111 ). Таким образом, ALU не знает, хотите ли вы результат со знаком или без знака, и ему все равно. Он просто делает сложение, как если бы оно было беззнаковым, и если вы хотите впоследствии рассматривать это как целое число со знаком, это зависит от вас.
РЕДАКТИРОВАТЬ: Как совершенно справедливо отмечают Руслан и Даниэль Шеплер в комментариях, некоторые операнды по-прежнему нуждаются в отдельных версиях со знаком и без знака, даже на машине с дополнением до двух. Сложение, вычитание, умножение, равенство и тому подобное работают нормально, даже не зная, подписаны числа или нет. Но деление и любые сравнения больше/меньше должны иметь отдельные версии.
РЕДАКТИРОВАТЬ РЕДАКТИРОВАТЬ: Есть и другие представления, такие как one’s-complement , но они больше никогда не используются, так что вам не о чем беспокоиться.
$\endgroup$
4
$\begingroup$
Одно из больших преимуществ математики с дополнением до двух, которая используется во всех современных архитектурах, заключается в том, что инструкции сложения и вычитания абсолютно одинаковы как для знаковых, так и для беззнаковых операндов.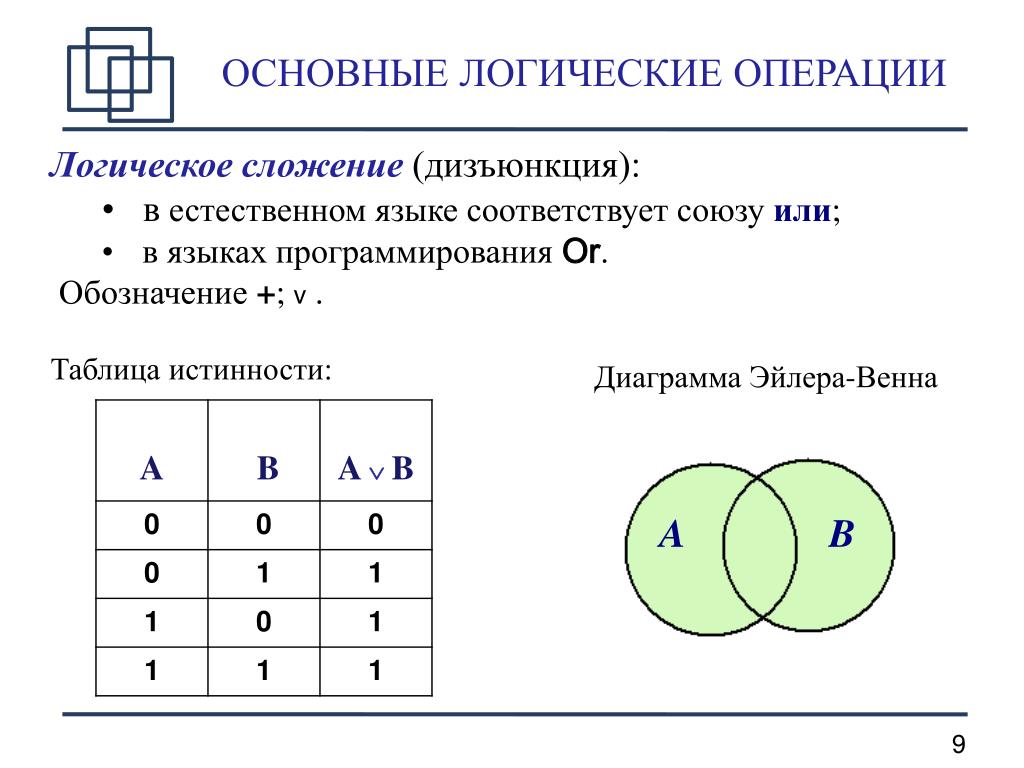
Многие процессоры даже не имеют инструкций умножения, деления или модуля. Если да, то у них должны быть отдельные подписанные и неподписанные формы инструкций, и компилятор (или программист на ассемблере) выбирает подходящую.
Процессоры также обычно имеют разные инструкции для сравнения со знаком и без знака. Например, x86 может следовать за CMP с JL (Перейти, если меньше), если сравнение должно быть со знаком, или JB (Перейти, если ниже), если сравнение должно быть беззнаковым. Опять же, компилятор или программист выберет правильную инструкцию для типа данных.
Некоторые другие инструкции часто бывают со знаком и без знака, например сдвиг вправо или загрузка значения в более широкий регистр, с расширением знака или без него.
$\endgroup$
2
$\begingroup$
Нет. Процессор полагается на набор инструкций, чтобы сообщить ему, какой тип данных он просматривает и куда его отправить.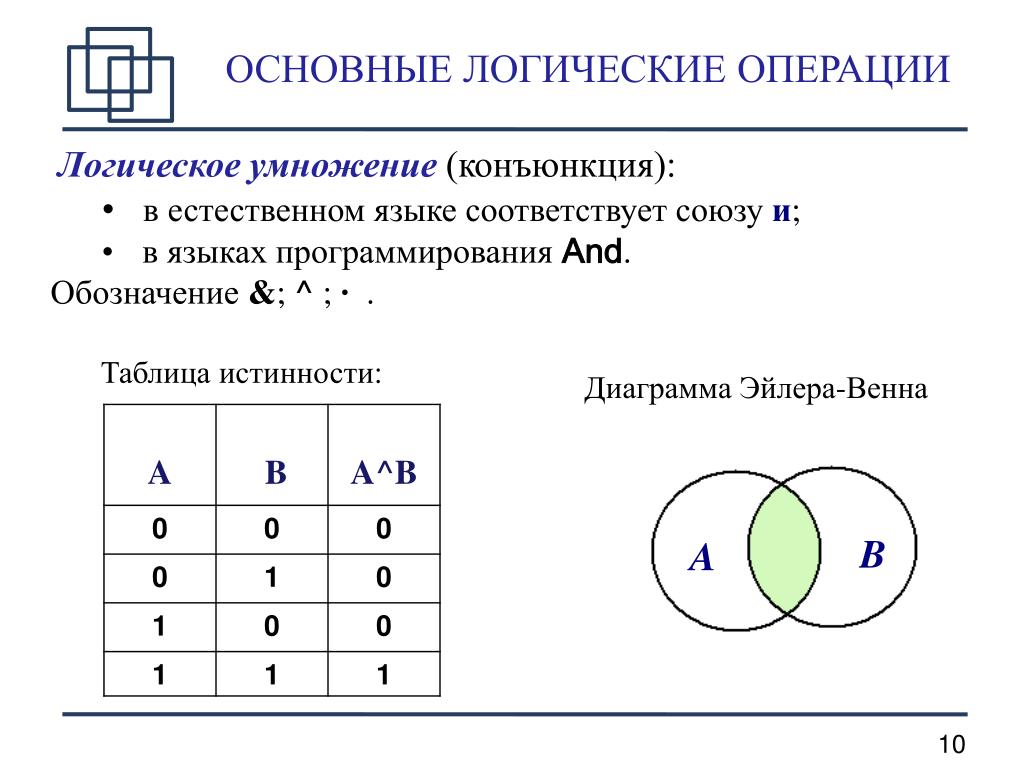 В самом операнде нет ничего о единицах и нулях, что могло бы по своей сути сигнализировать АЛУ, являются ли данные символами, числами с плавающей запятой, целым числом, подписанным целым числом и т. д. интерпретируется как дополнение 2s.
В самом операнде нет ничего о единицах и нулях, что могло бы по своей сути сигнализировать АЛУ, являются ли данные символами, числами с плавающей запятой, целым числом, подписанным целым числом и т. д. интерпретируется как дополнение 2s.
$\endgroup$
1
$\begingroup$
Я хотел бы дать дополнение к уже сделанным ответам:
В большинстве других ответов отмечается, что в арифметике с дополнением до двух результат одинаков для чисел со знаком и без знака:
-2 + 1 = - 1 1110 + 0001 = 1111 14 + 1 = 15 1110 + 0001 = 1111
Однако есть исключения:
Подразделение: -2 / 2 = -1 1110 / 0010 = 1111 14 / 2 = 7 1110 / 0010 = 0111 Сравнение: -2 < 2 = ИСТИНА 1110 < 0010 = ИСТИНА 14 < 2 = ЛОЖЬ 1110 < 0010 = ЛОЖЬ "Типовое" (*) умножение: -2 * 2 = -4 1110 * 0010 = 11111100 14 * 2 = 28 1110 * 0010 = 00011100
(*) На многих процессорах результат умножения двух n-битных чисел имеет ширину (2*n) бит.
Для таких операций процессоры имеют разные инструкции для знаковой и беззнаковой арифметики.
Это означает, что программист (или компилятор) должен использовать другие инструкции для знаковой и беззнаковой арифметики.
ЦП x86, например, имеет инструкцию с именем div для выполнения беззнакового деления и инструкцию с именем idiv для выполнения знакового деления.
Существуют также различные «условные» инструкции (условные переходы, установка бита по условию), а также инструкции умножения для знаковой и беззнаковой арифметики.
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
Введение в теоретическую информатику: Введение
Нашли какие-либо ошибки/опечатки/запутанные объяснения? Откройте вопрос GitHub. Вы также можете прокомментировать ниже.
Вы также можете прокомментировать ниже.
«Информатика связана с компьютерами не больше, чем астрономия с телескопами» , приписывается Эдсгеру Дейкстре. 1
«Хакеры должны понимать теорию вычислений примерно так же, как художники должны понимать химию красок». , Пол Грэм 2003. 2
«Тема моего выступления, пожалуй, наиболее прямо обозначена простыми двумя вопросами: во-первых, труднее ли умножать, чем складывать? и, во-вторых, почему?… Я (хотел бы) показать, что не существует алгоритма умножения, столь же простого в вычислительном отношении, как алгоритм сложения, и это доказывает что-то вроде камня преткновения».
, Алан Кобэм, 1964 г.
Одним из величайших изобретений древних вавилонян является число 9.0200 разрядная система счисления . Система позиционных значений представляет числа как последовательности цифр, где позиция каждой цифры определяет ее значение.
Это противоположно системе римских цифр, где каждая цифра имеет фиксированное значение независимо от положения. Например, среднее расстояние до Луны составляет примерно 259 956 римских миль. Стандартными римскими цифрами это будет
МММММММММММММММММММММММММ. ММММММММММММММММММММММММ ММММММММММММММММММММММММ ММММММММММММММММММММММММ ММММММММММММММММММММММММ ММММММММММММММММММММММММ ММММММММММММММММММММММММ ММММММММММММММММММММММММ
Для записи расстояния до солнца римскими цифрами потребуется около 100 000 символов; потребовалась бы книга на 50 страниц, чтобы содержать это единственное число!
Для того, кто думает о числах в аддитивной системе, такой как римские цифры, такие величины, как расстояние до луны или солнца, не просто велики — они невыразимы : их нельзя выразить или даже постичь. Неудивительно, что Эратосфен, первый вычисливший диаметр Земли (ошибка до десяти процентов), и Гиппарх, первый вычисливший расстояние до Луны, пользовались не римской системой счисления, а вавилонской шестидесятеричной (основание 60). ) позиционная система.
Неудивительно, что Эратосфен, первый вычисливший диаметр Земли (ошибка до десяти процентов), и Гиппарх, первый вычисливший расстояние до Луны, пользовались не римской системой счисления, а вавилонской шестидесятеричной (основание 60). ) позиционная система.
Целочисленное умножение: пример алгоритма
На языке компьютерных наук система разрядных значений для представления чисел известна как структура данных : набор инструкций или «рецепт» для представления объектов в виде символы. Алгоритм представляет собой набор инструкций или «рецепт» для выполнения операций над такими представлениями. Структуры данных и алгоритмы позволили создать удивительные приложения, которые изменили человеческое общество, но их значение выходит за рамки их практической полезности. Структуры из информатики, такие как биты, строки, графы и даже понятие самой программы, а также такие понятия, как универсальность и репликация, не только нашли (многие) практические применения, но и внесли свой вклад в новый язык и новый способ. смотреть на мир.
смотреть на мир.
Вавилоняне не только придумали систему разрядов, но и изобрели «стандартные алгоритмы», которым нас всех учили в начальной школе, для сложения и умножения чисел. Эти алгоритмы были важны на протяжении веков для людей, использующих абаки, папирус или карандаш и бумагу, но в наш компьютерный век они все еще служат какой-либо цели, кроме как мучить третьеклассников? Чтобы понять, почему эти алгоритмы все еще очень актуальны, давайте сравним вавилонский алгоритм умножения цифр за цифрами («умножение в начальной школе») с наивным алгоритмом, который умножает числа путем многократного сложения. Начнем с формального описания обоих алгоритмов, см. Алгоритм 0.1 и Алгоритм 0.2.
Алгоритм 0.1 Умножение повторным сложением
Вход: Неотрицательные целые числа \(x,y\)
Выход: Произведение \(x\cdot y\)
Пусть \(результат \leftarrow 0\).
for{\(i=1,\ldots,y\)}
\(result \leftarrow result + x\)
endfor
return \(result\)
Алгоритм 0.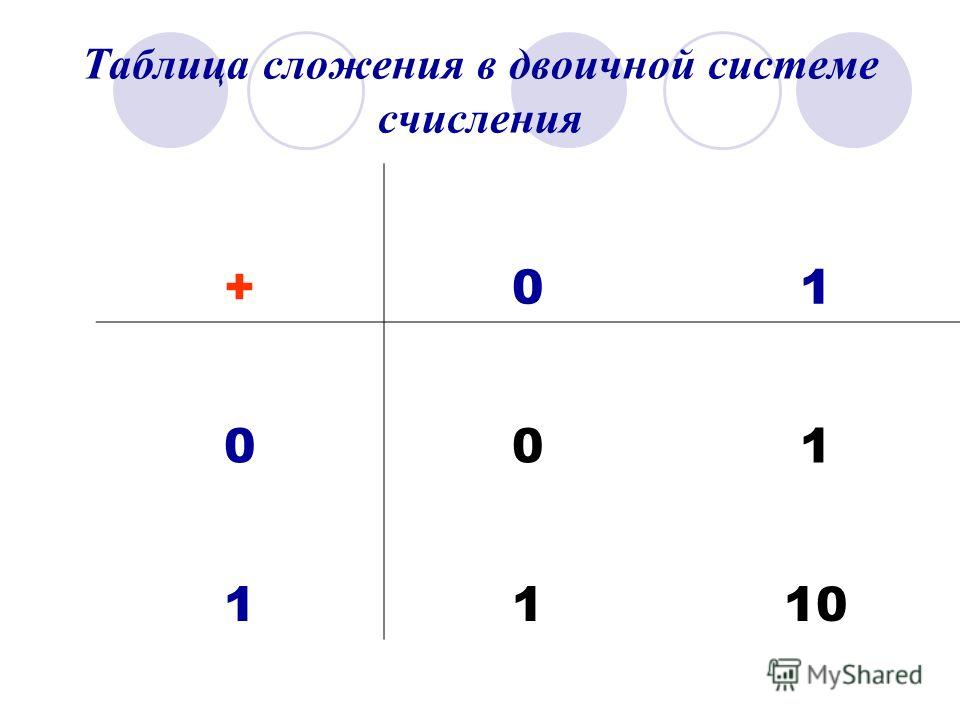 {19{11}\) секунд (что составляет более трех тысячелетий!), чтобы вычислить тот же результат.
{19{11}\) секунд (что составляет более трех тысячелетий!), чтобы вычислить тот же результат.
Компьютеры не сделали алгоритмы устаревшими. Наоборот, значительное увеличение наших возможностей по измерению, хранению и передаче данных привело к гораздо более высокому спросу на разработку более совершенных и сложных алгоритмов, которые позволяют нам принимать более обоснованные решения на основе этих данных. Мы также видим, что в немалой степени понятие алгоритма не зависит от фактического вычислительного устройства, которое его выполняет. Алгоритм поразрядного умножения намного лучше, чем итерируемое сложение, независимо от того, используем ли мы для его реализации технологию кремниевого чипа или третьеклассника с ручкой и бумагой.
Теоретическая информатика занимается неотъемлемыми свойствами алгоритмов и вычислений; а именно те свойства, которые независимы от современной технологии. Мы задаем некоторые вопросы, над которыми уже размышляли вавилоняне, такие как «как лучше всего умножать два числа?», а также вопросы, которые опираются на передовую науку, такие как «можем ли мы использовать эффекты квантовой запутанности для факторизации? цифры быстрее?».
Расширенный пример: более быстрый способ умножения (необязательно) 92)\) алгоритм иногда может иметь решающее значение на практике (см. раздел 0.3 ниже), в этой книге мы в основном будем игнорировать такие различия. Однако ниже мы опишем алгоритм Карацубы, так как это хороший пример того, как алгоритмы часто могут удивлять, а также демонстрация
анализа алгоритмов , который занимает центральное место в этой книге и в теоретической информатике в целом. Алгоритм Карацубы основан на более быстром способе умножения двузначных чисел . Предположим, что \(x,y \in [100]=\{0,\ldots, 99 \}\) — пара двузначных чисел. Давайте напишем \(\overline{x}\) для цифры «десятки» в \(x\) и \(\underline{x}\) для цифры «единицы», так что \(x = 10\overline {x} + \underline{x}\) и напишите аналогично \(y = 10\overline{y} + \underline{y}\) для \(\overline{x},\underline{x},\overline {y},\underline{y} \in [10]\). Алгоритм начальной школы для умножения \(x\) и \(y\) показан на рисунке 1.
Алгоритм начальной школы можно рассматривать как преобразование задачи умножения пары двузначных чисел на четыре однозначных умножения по формуле
\[ (10\overline{x}+\underline{x}) \times (10\overline{y}+\underline{y}) = 100\overline{x}\overline{y}+10(\overline{x} \underline{y} + \underline{x}\overline{y}) + \underline{x}\underline{y} \;\;(1) \]
Как правило, в алгоритме начальной школы удвоение количества цифр во входных данных дает 92)\) раз алгоритм. Напротив, алгоритм Карацубы основан на наблюдении, что мы можем выразить уравнение 1 также как
\[ (10\overline{x}+\underline{x}) \times (10\overline{y}+\underline{y}) = (100-10)\overline{x}\overline{y}+10\left [(\overline{x}+\underline{x})(\overline{y}+\underline{y})\right] -(10-1)\underline{x}\underline{y} \;\; (2) \]
, который сводит умножение двузначных чисел \(x\) и \(y\) к вычислению следующих трех более простых произведений: \(\overline{x}\overline{y}\), \(\underline {x}\underline{y}\) и \((\overline{x}+\underline{x})(\overline{y}+\underline{y})\). Повторяя ту же стратегию рекурсивно, мы можем свести задачу умножения двух \(n\)-значных чисел к задаче умножения 9{1.585}\) операций.
Повторяя ту же стратегию рекурсивно, мы можем свести задачу умножения двух \(n\)-значных чисел к задаче умножения 9{1.585}\) операций.
Вышеизложенное является интуитивной идеей, лежащей в основе алгоритма Карацубы, но этого недостаточно, чтобы полностью описать его. Полное описание алгоритма влечет за собой точную спецификацию его операций вместе с его анализом : доказательство того, что алгоритм действительно делает то, что он должен делать. Операции алгоритма Карацубы подробно описаны в алгоритме 0.4, а анализ дан в лемме 0.5 и лемме 0.6.
2: алгоритм умножения Карацубы для умножения \(x=10\overline{x}+\underline{x}\) и \(y=10\overline{y}+\underline{y}\). Мы вычисляем три оранжевых, зеленых и фиолетовых произведения \(\underline{x}\underline{y}\), \(\overline{x}\overline{y}\) и \((\overline{x}+\ underline{x})(\overline{y}+\underline{y})\), а затем сложите и вычтите их, чтобы получить результат.3: Время выполнения алгоритма Карацубы по сравнению с алгоритмом начальной школы. m) \cdot C\), вычисленный по алгоритму 0.4.
9{\log_2 3})\) операций над входом \(x,y\).
m) \cdot C\), вычисленный по алгоритму 0.4.
9{\log_2 3})\) операций над входом \(x,y\).Рисунок 2 иллюстрирует идею доказательства, которое мы здесь только набросаем, оставив детализацию как в упражнении 0.4. Доказательство проводится снова по индукции. Мы определяем \(T(n)\) как максимальное количество шагов, которое алгоритм 0.4 выполняет на входных данных длины не более \(n\). Поскольку в базовом случае \(n\leq 4\) в упражнении 0.4 выполняется постоянное число вычислений, мы знаем, что \(T(4) \leq c\) для некоторой константы \(c\) и для \(n >4\), он удовлетворяет рекуррентному уравнению 9{\log_2 3})\). Интуиция, стоящая за этим, представлена на рисунке 2, и это также является следствием так называемой «главной теоремы» о рекуррентных соотношениях. Как упоминалось выше, мы оставляем завершение доказательства читателю в качестве упражнения 0.4.
4: Алгоритм Карацубы сводит \(n\)-битное умножение к трем \(n/2\)-битным умножениям, которые, в свою очередь, сводятся к девяти \(n/4\)-битным умножениям и так далее. {\log_2 3}\) по формуле суммирования геометрического ряда. 9{\log_k (2k-1)})\) алгоритм умножения времени для каждой константы \(k\). В 1971 году Шенхаге и Штрассен получили еще более совершенные алгоритмы, используя быстрое преобразование Фурье ; их идея заключалась в том, чтобы каким-то образом рассматривать целые числа как «сигналы» и выполнять умножение более эффективно, перейдя в область Фурье. (Преобразование Фурье является центральным инструментом в математике и инженерии, используемым во многих приложениях; если вы еще не видели его, вы, вероятно, столкнетесь с ним в какой-то момент в своих исследованиях.) В годы, последовавшие за исследователями продолжал улучшать алгоритм, и только совсем недавно Харви и Ван Дер Хувену удалось получить алгоритм времени \(O(n \log n)\) для умножения (хотя он только начинает превосходить алгоритм Шёнхаге-Штрассена для действительно астрономических чисел). Тем не менее, несмотря на весь этот прогресс, мы до сих пор не знаем, существует ли алгоритм \(O(n)\) времени для умножения двух \(n\) цифр!
{\log_2 3}\) по формуле суммирования геометрического ряда. 9{\log_k (2k-1)})\) алгоритм умножения времени для каждой константы \(k\). В 1971 году Шенхаге и Штрассен получили еще более совершенные алгоритмы, используя быстрое преобразование Фурье ; их идея заключалась в том, чтобы каким-то образом рассматривать целые числа как «сигналы» и выполнять умножение более эффективно, перейдя в область Фурье. (Преобразование Фурье является центральным инструментом в математике и инженерии, используемым во многих приложениях; если вы еще не видели его, вы, вероятно, столкнетесь с ним в какой-то момент в своих исследованиях.) В годы, последовавшие за исследователями продолжал улучшать алгоритм, и только совсем недавно Харви и Ван Дер Хувену удалось получить алгоритм времени \(O(n \log n)\) для умножения (хотя он только начинает превосходить алгоритм Шёнхаге-Штрассена для действительно астрономических чисел). Тем не менее, несмотря на весь этот прогресс, мы до сих пор не знаем, существует ли алгоритм \(O(n)\) времени для умножения двух \(n\) цифр! 3"> Алгоритмы за пределами арифметики
3"> Алгоритмы за пределами арифметики
Поиск лучших алгоритмов никоим образом не ограничивается арифметическими задачами, такими как сложение, умножение или решение уравнений. Многие графовые алгоритмы , включая алгоритмы поиска путей, сопоставлений, остовных деревьев, разрезов и потоков, были открыты за последние несколько десятилетий, и это все еще является областью интенсивных исследований. (Например, за последние несколько лет алгоритмы решения задачи о максимальном потоке значительно усовершенствовались благодаря неожиданным связям с электрическими цепями и решателям линейных уравнений.) Эти алгоритмы используются не только для «естественных» приложений маршрутизации. сетевой трафик или навигация на основе GPS, но также и для таких разнообразных приложений, как поиск лекарств путем поиска структур в графах взаимодействия генов для расчета рисков, связанных с корреляциями в финансовых инвестициях.
Компания Google была основана на основе алгоритма PageRank , который является эффективным алгоритмом для аппроксимации «главного собственного вектора» (демпфированной версии) матрицы смежности веб-графа.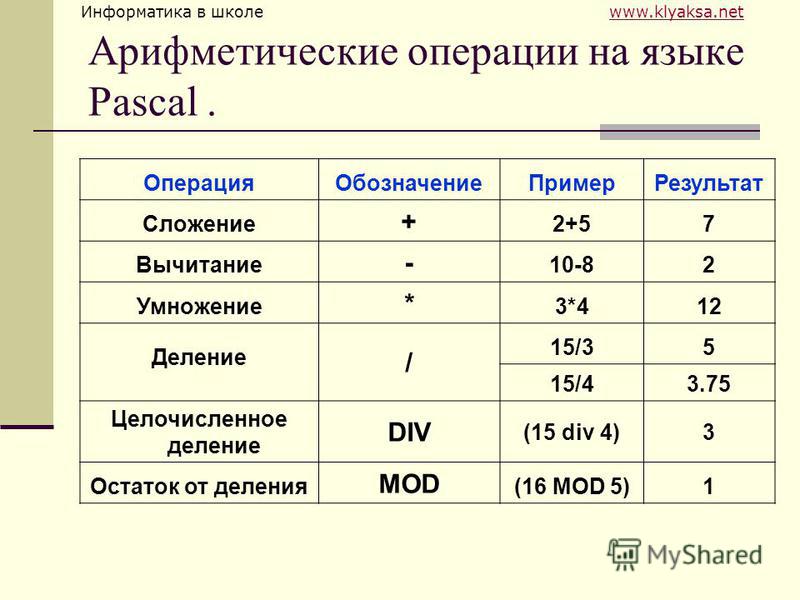 2)\) времени, лежит в основе многих недавних феноменальных успехов в обучении глубоких нейронных сетей. Алгоритмы решения линейных уравнений с ограничениями разреженности, концепция, известная как , сжатое считывание , использовались для резкого уменьшения количества и качества данных, необходимых для анализа МРТ-изображений. Это имело решающее значение для МРТ-визуализации раковых опухолей у детей, где раньше врачам приходилось использовать анестезию, чтобы приостановить дыхание во время МРТ-исследования, что иногда приводило к ужасным последствиям.
2)\) времени, лежит в основе многих недавних феноменальных успехов в обучении глубоких нейронных сетей. Алгоритмы решения линейных уравнений с ограничениями разреженности, концепция, известная как , сжатое считывание , использовались для резкого уменьшения количества и качества данных, необходимых для анализа МРТ-изображений. Это имело решающее значение для МРТ-визуализации раковых опухолей у детей, где раньше врачам приходилось использовать анестезию, чтобы приостановить дыхание во время МРТ-исследования, что иногда приводило к ужасным последствиям.
Даже для классических вопросов, изученных веками, все еще делаются новые открытия. Например, для вопроса о том, является ли заданное целое число простым или составным, который изучается со времен Пифагора, эффективные вероятностные алгоритмы были открыты только в 19 веке.70-х годов, в то время как первый детерминированный полиномиальный алгоритм был найден только в 2002 году. Для родственной проблемы фактического нахождения множителей составного числа новые алгоритмы были найдены в 1980-х годах, и (как мы увидим позже в этом курсе) Открытия 1990-х породили заманчивую перспективу получения более быстрых алгоритмов за счет использования квантово-механических эффектов.
Несмотря на весь этот прогресс, вопросов в мире алгоритмов по-прежнему намного больше, чем ответов. Почти для всех естественных задач мы не знаем, является ли текущий алгоритм «лучшим» или еще ждет своего открытия значительно лучший алгоритм. Как упоминалось во вступительной цитате Кобэма к этой главе, даже для базовой задачи умножения чисел мы еще не ответили на вопрос, существует ли алгоритм умножения, столь же эффективный, как наши алгоритмы сложения. Но, по крайней мере, теперь мы знаем правильный путь к спросите это.
О важности отрицательных результатов
Поиск лучших алгоритмов для таких задач, как умножение, решение уравнений, графические задачи или подгонка нейронных сетей к данным, несомненно, стоит усилий. Но почему важно доказывать, что таких алгоритмов не существует? Одним из мотивов является чистое интеллектуальное любопытство. Еще одна причина для изучения результатов невозможности заключается в том, что они соответствуют фундаментальным ограничениям нашего мира.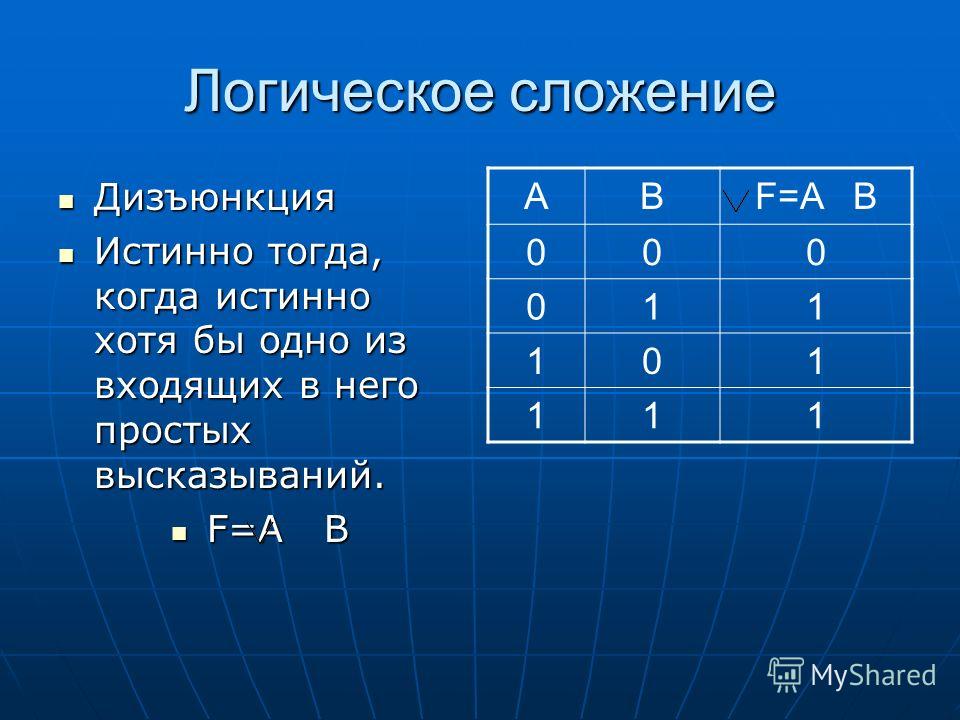 Другими словами, результаты невозможности равны 9.0200 законы природы .
Другими словами, результаты невозможности равны 9.0200 законы природы .
Вот несколько примеров невозможных результатов за пределами информатики (подробнее об этом см. Раздел 0.7). В физике невозможность построить вечный двигатель соответствует закону сохранения энергии . Невозможность построить тепловую машину, превосходящую границу Карно, соответствует второму закону термодинамики, а невозможность передачи информации со скоростью, превышающей скорость света, является краеугольным камнем специальной теории относительности. В математике, хотя мы все учили формулу решения квадратных уравнений в средней школе, невозможность обобщить эту формулу на уравнения пятой и более степени породила теория групп . Невозможность доказать пятую аксиому Евклида из первых четырех породила неевклидовы геометрии, которые оказались решающими для общей теории относительности.
Аналогичным образом результаты невозможности вычислений соответствуют «вычислительным законам природы», которые говорят нам о фундаментальных ограничениях любого устройства обработки информации, будь то на основе кремния, нейронов или квантовых частиц.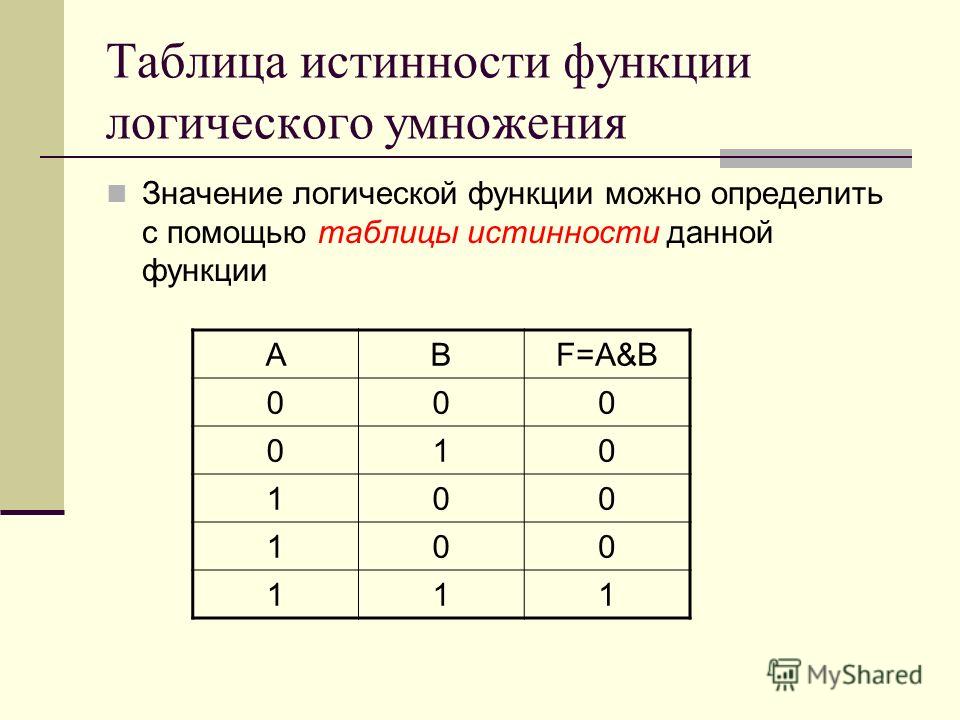 Более того, компьютерщики нашли творческие подходы к применяет вычислительные ограничения для выполнения определенных полезных задач. Например, большая часть современного интернет-трафика шифруется с использованием схемы шифрования RSA, безопасность которой основана на (предполагаемой) невозможности эффективного разложения больших целых чисел на множители. Совсем недавно в системе Биткойн используется цифровой аналог «золотого стандарта», где вместо использования драгоценного металла новая валюта получается путем «добычи» решений вычислительно сложных задач.
Более того, компьютерщики нашли творческие подходы к применяет вычислительные ограничения для выполнения определенных полезных задач. Например, большая часть современного интернет-трафика шифруется с использованием схемы шифрования RSA, безопасность которой основана на (предполагаемой) невозможности эффективного разложения больших целых чисел на множители. Совсем недавно в системе Биткойн используется цифровой аналог «золотого стандарта», где вместо использования драгоценного металла новая валюта получается путем «добычи» решений вычислительно сложных задач.
- История алгоритмов насчитывает тысячи лет; они были необходимы для большей части человеческого прогресса и в наши дни составляют основу многомиллиардных отраслей промышленности, а также спасающих жизнь технологий.
- Часто для решения одной и той же вычислительной задачи существует более одного алгоритма. Поиск более быстрого алгоритма часто может иметь гораздо большее значение, чем улучшение вычислительного оборудования.

- Более совершенные алгоритмы и структуры данных не только ускоряют вычисления, но и могут дать новые качественные результаты.
- Один из вопросов, который мы будем изучать, состоит в том, чтобы выяснить, какой алгоритм является наиболее эффективным для данной задачи.
- Чтобы показать, что алгоритм является наиболее эффективным для данной задачи, нам нужно уметь доказать что невозможно решить задачу с использованием меньшего количества вычислительных ресурсов.
Путь к остальной части этой книги
Часто, когда мы пытаемся решить вычислительную задачу, будь то решение системы линейных уравнений, поиск верхнего собственного вектора матрицы или попытка ранжировать результаты поиска в Интернете, это достаточно, чтобы использовать стандарт «я узнаю это, когда увижу это» для описания алгоритмов. Пока мы находим какой-то способ решения проблемы, мы счастливы и можем не слишком заботиться о точной математической модели для нашего алгоритма.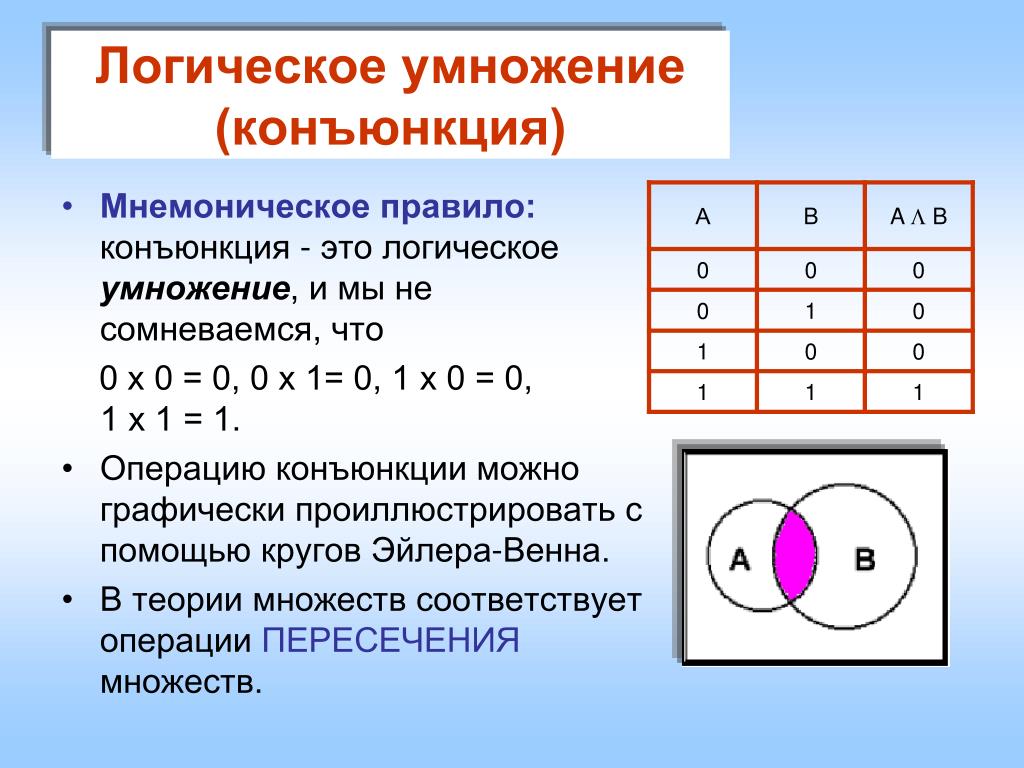 Но когда мы хотим ответить на такой вопрос, как «есть ли существует алгоритм решения задачи \(P\)?» нам нужно быть гораздо более точными.
Но когда мы хотим ответить на такой вопрос, как «есть ли существует алгоритм решения задачи \(P\)?» нам нужно быть гораздо более точными.
В частности, нам потребуется (1) точно определить, что значит решить \(P\), и (2) точно определить, что такое алгоритм. Даже (1) иногда может быть нетривиальным, но (2) особенно сложен; совершенно не ясно, как (и даже если) мы можем охватить все возможные способы разработки алгоритмов. Мы рассмотрим несколько простых моделей вычислений , и утверждают, что, несмотря на их простоту, они охватывают все «разумные» подходы к достижению вычислений, включая все те, которые в настоящее время используются в современных вычислительных устройствах.
Когда у нас есть эти формальные модели вычислений, мы можем попытаться получить результаты невозможности для вычислительных задач, показывающие, что некоторые проблемы не могут быть решены (или, возможно, не могут быть решены в рамках ресурсов нашей вселенной). Архимед однажды сказал, что если бы у него была точка опоры и достаточно длинный рычаг, он мог бы перевернуть мир. посмотрим как сокращений позволяют нам использовать один результат твердости для множества других, освещая границы между вычислимыми и невычислимыми (или разрешимыми и неразрешимыми) проблемами.
Архимед однажды сказал, что если бы у него была точка опоры и достаточно длинный рычаг, он мог бы перевернуть мир. посмотрим как сокращений позволяют нам использовать один результат твердости для множества других, освещая границы между вычислимыми и невычислимыми (или разрешимыми и неразрешимыми) проблемами.
Позже в этой книге мы вернемся к изучению наших моделей вычислений и посмотрим, как такие ресурсы, как случайность или квантовая запутанность, потенциально могут изменить мощность нашей модели. В контексте вероятностных алгоритмов мы увидим, как случайность стала незаменимым инструментом для понимания вычислений, информации и коммуникации. Мы также увидим, как вычислительная сложность может быть преимуществом, а не помехой, и использоваться для «дерандомизации» вероятностных алгоритмов. Те же идеи появляются и в криптография , которая за последние несколько десятилетий претерпела не только технологическую, но и интеллектуальную революцию, большая часть которой основана на основах, которые мы изучаем в этом курсе.
Теоретическая информатика — обширная тема, затрагивающая многие научные и инженерные дисциплины. Эта книга представляет собой очень частичный (и предвзятый) образец этой области. Больше всего на свете я надеюсь, что мне удастся «заразить» вас хотя бы частью своей любви к этой области, которая вдохновляется и обогащается связью с практикой, но также глубока и прекрасна независимо от приложений.
Зависимости между главами
Эта книга разделена на следующие части, см. рис. 5.
Предварительные сведения: Введение, математические основы и представление объектов в виде строк.
Часть I: Конечные вычисления (булевы схемы): Эквивалентность схем и прямолинейных программ. Универсальные ворота. Существование схемы для каждой функции, представление схем в виде строк, универсальная схема, нижняя граница размера схемы с использованием аргумента подсчета.
Часть II: Равномерное вычисление (машины Тьюринга): Эквивалентность машин Тьюринга и программ с циклами.
 Эквивалентность моделей (включая RAM-машины, \(\lambda\) исчисление и клеточные автоматы), конфигурации машин Тьюринга, существование универсальной машины Тьюринга, невычислимые функции (включая проблему остановки и теорему Райса), теорему Гёделя о неполноте, ограничения вычислительные модели (регулярные и контекстно-свободные языки).
Эквивалентность моделей (включая RAM-машины, \(\lambda\) исчисление и клеточные автоматы), конфигурации машин Тьюринга, существование универсальной машины Тьюринга, невычислимые функции (включая проблему остановки и теорему Райса), теорему Гёделя о неполноте, ограничения вычислительные модели (регулярные и контекстно-свободные языки).Часть III: Эффективные вычисления: Определение времени выполнения, теорема об иерархии времени, \(\mathbf{P}\) и \(\mathbf{NP}\), \(\mathbf{P_{/poly}} \), \(\mathbf{NP}\) полнота и теорема Кука-Левина, вычисления, ограниченные пространством.
Часть IV: Рандомизированные вычисления: Вероятность, рандомизированные алгоритмы, \(\mathbf{BPP}\), усиление, \(\mathbf{BPP} \subseteq \mathbf{P}_{/poly}\), псевдослучайное генераторы и дерандомизация.
Часть V: Дополнительные темы: Криптография, доказательства и алгоритмы (интерактивные доказательства и доказательства с нулевым разглашением, соответствие Карри-Ховарда), квантовые вычисления.

Книга в основном развивается в линейном порядке, каждая глава основывается на предыдущих, за следующими исключениями:
Темы \(\лямбда\) исчисления (раздел 8.
 5 и раздел 8.5), теоремы Гёделя о неполноте (глава 11), автоматов/регулярных выражений и контекстно-свободных грамматик (глава 10) и вычислений с ограниченным пространством ( Глава 17), не используются в следующих главах. Следовательно, вы можете выбрать, охватить или пропустить любое их подмножество.
5 и раздел 8.5), теоремы Гёделя о неполноте (глава 11), автоматов/регулярных выражений и контекстно-свободных грамматик (глава 10) и вычислений с ограниченным пространством ( Глава 17), не используются в следующих главах. Следовательно, вы можете выбрать, охватить или пропустить любое их подмножество.Часть II (Единообразные вычисления / Машины Тьюринга) не имеет сильной зависимости от Части I (Конечные вычисления / Булевы схемы), и должна быть возможность обучать их в обратном порядке с небольшими изменениями. Булевы схемы используются в части III (эффективные вычисления) для таких результатов, как \(\mathbf{P} \subseteq \mathbf{P_{/poly}}\) и теоремы Кука-Левина, а также в части IV (для \ (\mathbf{BPP} \subseteq \mathbf{P_{/poly}}\) и дерандомизация) и Часть V (особенно в криптографии и квантовых вычислениях).
Все главы Части V (Расширенные темы) не зависят друг от друга и могут быть рассмотрены в любом порядке.
Курс, основанный на этой книге, может использовать все части I, II и III (возможно, пропуская часть или все \(\лямбда\) исчисление, главу 11, главу 10 или главу 17), а затем охватывать полностью или частично из Части IV (рандомизированные вычисления) и добавить «небольшое количество» продвинутых тем из Части V в зависимости от интереса учащихся или преподавателей.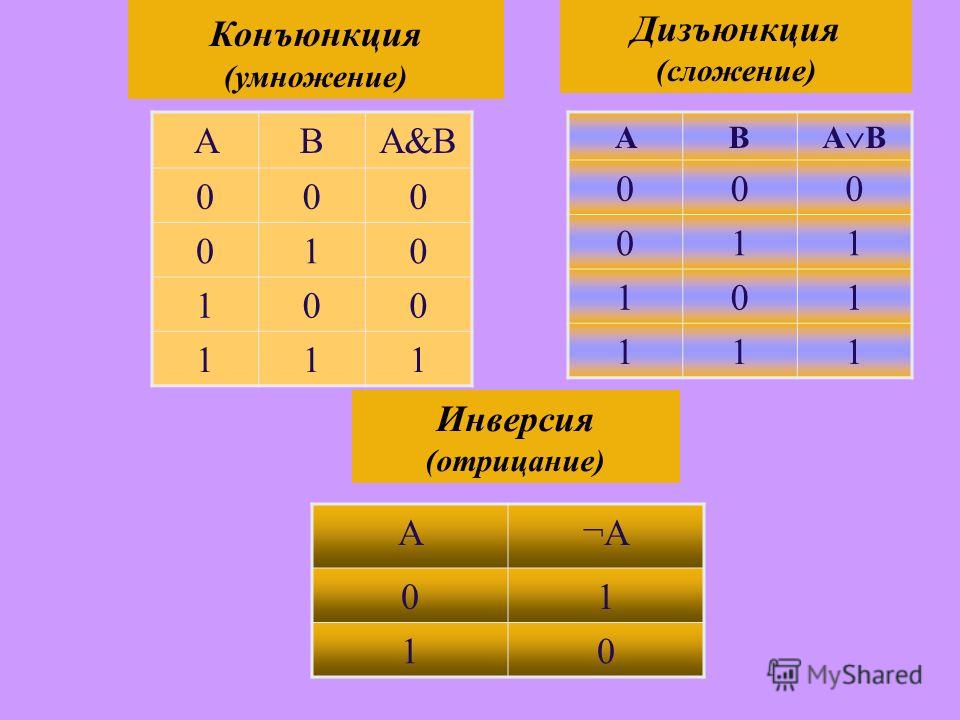
Упражнения
Оцените значимость следующих изобретений для ускорения умножения больших (то есть стозначных и более) чисел. То есть используйте оценки «обратной стороны конверта», чтобы упорядочить их с точки зрения коэффициента ускорения, который они предложили по сравнению с предыдущим положением дел.
Открытие школьного алгоритма «цифра за цифрой» (улучшение при многократном добавлении).
Открытие алгоритма Карацубы (улучшение алгоритма цифра за цифрой). 9п\) операций.
\(n!\) операций.
В этой главе мы упомянули несколько компаний, основанных на открытии новых алгоритмов. Можете ли вы привести пример компании, основанной на несуществовании алгоритма? См. сноску для подсказки. 4
Предположим, что \(T_1,T_2,T_3,\ldots\) — последовательность чисел такая, что \(T_2 \leq 10\) и для любых \(n\), \(T_n \leq 3T_{\lfloor n/2 \rfloor+1} + Cn\) для некоторого \(C \geq 1\).
 {\log_2 3}\) для любого \(n>2\). 9{\log_2 3}\).
{\log_2 3}\) для любого \(n>2\). 9{\log_2 3}\).
Реализуйте на выбранном вами языке программирования функции Gradeschool_multiply(x,y) и Karatsuba_multiply(x,y) , которые принимают два массива цифр x и y и возвращают массив, представляющий произведение x и y (где x идентифицируется с числом x[0]+10*x[1]+100*x[2]+... и т. д.) с использованием алгоритма начальной школы и алгоритм Карацубы соответственно. При каком количестве цифр алгоритм Карацубы превосходит школьный? 9{\omega+\epsilon})\) арифметических операций. См. сноску для подсказки. 6
Библиографические примечания
Для краткого обзора того, что мы увидим в этой книге, вы могли бы сделать гораздо хуже, чем прочитать замечательное эссе Бернара Шазеля «Алгоритм как идиома современной науки». Книга Мура и Мертенса (Moore, Mertens, 2011) дает замечательный и всесторонний обзор теории вычислений, включая большую часть содержания, обсуждаемого в этой главе и в остальной части этой книги. Книга Ааронсона (Aaronson, 2013) — еще одно замечательное произведение, затрагивающее многие из тех же тем.
Книга Ааронсона (Aaronson, 2013) — еще одно замечательное произведение, затрагивающее многие из тех же тем.
Чтобы узнать больше об алгоритмах, которые использовали вавилоняне, см. статью Кнута и классическую книгу Нойгебауэра.
Многие из алгоритмов, которые мы упоминаем в этой главе, описаны в учебниках по алгоритмам, таких как книги Кормена, Лейзерсона, Ривеста и Штейна (Cormen, Leiserson, Rivest, Stein, 2009), Клейнберга и Тардоса (Kleinberg, Tardos, 2006). , и Dasgupta, Papadimitriou and Vazirani (Dasgupta, Papadimitriou, Vazirani, 2008), а также учебник Джеффа Эриксона. Книга Эриксона находится в свободном доступе в Интернете и содержит прекрасное описание рекурсивных алгоритмов в целом и алгоритма Карацубы в частности.
История открытия Карацубой своего алгоритма умножения изложена им в (Karatsuba, 1995). Как упоминалось выше, дальнейшие улучшения были сделаны Тоом и Куком (Toom, 1963) (Cook, 1966), Шёнхаге и Штрассеном (Schönhage, Strassen, 1971), Фюрером (Fürer, 2007), а недавно Харви и Ван Дер Ховеном ( Harvey, Van Der Hoeven, 2019), хороший обзор см.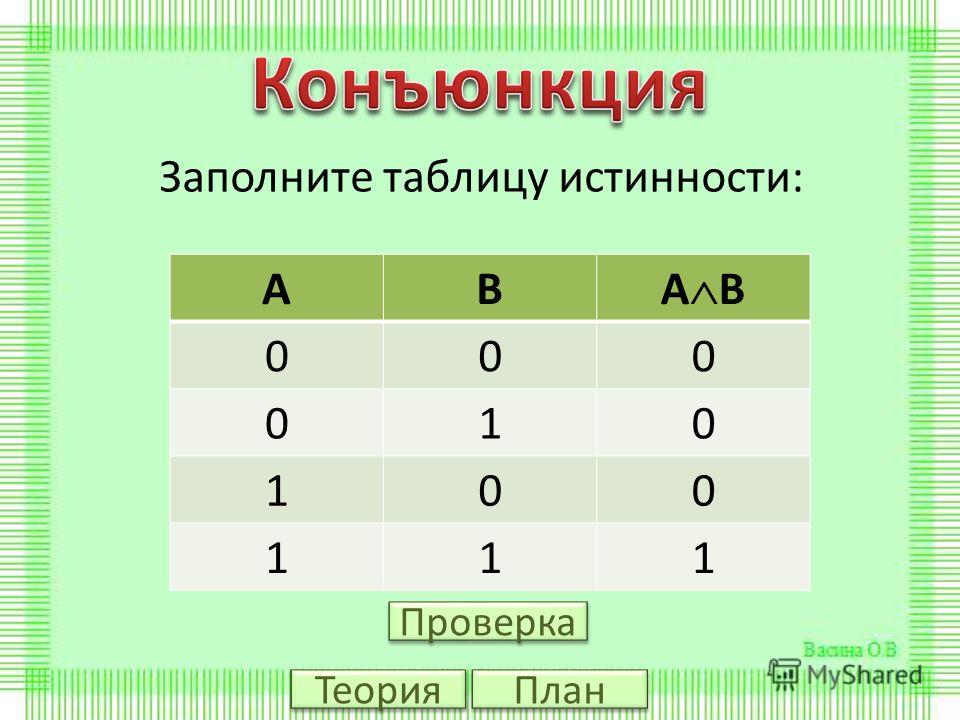 в этой статье. Последние статьи в значительной степени опираются на алгоритм быстрого преобразования Фурье . Захватывающая история (повторного) открытия этого алгоритма Джоном Тьюки в контексте холодной войны изложена в (Cooley, 1987) . (Мы говорим повторное открытие, потому что позже выяснилось, что алгоритм восходит к Гауссу (Heideman, Johnson, Burrus, 1985).) Быстрое преобразование Фурье рассматривается в некоторых книгах, упомянутых ниже, а также в онлайн-лекциях. как у Джеффа Эриксона. См. также эту популярную статью Дэвида Остина. Быстрое умножение матрицы на было открыто Штрассеном (Strassen, 1969), и с тех пор это стало активной областью исследований. (Bläser, 2013) является рекомендуемым самодостаточным исследованием этой области.
в этой статье. Последние статьи в значительной степени опираются на алгоритм быстрого преобразования Фурье . Захватывающая история (повторного) открытия этого алгоритма Джоном Тьюки в контексте холодной войны изложена в (Cooley, 1987) . (Мы говорим повторное открытие, потому что позже выяснилось, что алгоритм восходит к Гауссу (Heideman, Johnson, Burrus, 1985).) Быстрое преобразование Фурье рассматривается в некоторых книгах, упомянутых ниже, а также в онлайн-лекциях. как у Джеффа Эриксона. См. также эту популярную статью Дэвида Остина. Быстрое умножение матрицы на было открыто Штрассеном (Strassen, 1969), и с тех пор это стало активной областью исследований. (Bläser, 2013) является рекомендуемым самодостаточным исследованием этой области.
Алгоритм Backpropagation для быстрой дифференциации нейронных сетей был изобретен Вербосом (Werbos, 1974). Алгоритм Pagerank был изобретен Ларри Пейджем и Сергеем Брином (Page, Brin, Motwani, Winograd, 1999). Он тесно связан с алгоритмом HITS Клейнберга (Kleinberg, 1999). Компания Akamai была основана на основе структуры данных с последовательным хешированием , описанной в (Karger, Lehman, Leighton, Panigrahy, Levine, Lewin, 1997) . Сжатое зондирование имеет долгую историю, но есть два основополагающих документа (Candes, Romberg, Tao, 2006) (Donoho, 2006). (Lustig, Donoho, Santos, Pauly, 2008) дает обзор приложений сжатого зондирования к МРТ; см. также эту популярную статью Элленберга (Ellenberg, 2010). Детерминированный полиномиальный алгоритм проверки простоты был предложен Агравалом, Каялом и Саксеной (Agrawal, Kayal, Saxena, 2004).
Он тесно связан с алгоритмом HITS Клейнберга (Kleinberg, 1999). Компания Akamai была основана на основе структуры данных с последовательным хешированием , описанной в (Karger, Lehman, Leighton, Panigrahy, Levine, Lewin, 1997) . Сжатое зондирование имеет долгую историю, но есть два основополагающих документа (Candes, Romberg, Tao, 2006) (Donoho, 2006). (Lustig, Donoho, Santos, Pauly, 2008) дает обзор приложений сжатого зондирования к МРТ; см. также эту популярную статью Элленберга (Ellenberg, 2010). Детерминированный полиномиальный алгоритм проверки простоты был предложен Агравалом, Каялом и Саксеной (Agrawal, Kayal, Saxena, 2004).
Мы кратко упомянули о классических математических результатах невозможности, включая невозможность доказательства пятого постулата Евклида из четырех других, невозможность разделить угол на три части с помощью линейки и циркуля и невозможность решения уравнения пятой степени с помощью радикалов. Геометрическое доказательство невозможности трисекции угла (одна из трех геометрических задач древности, восходящая к древним грекам) дано в этом блоге Тао.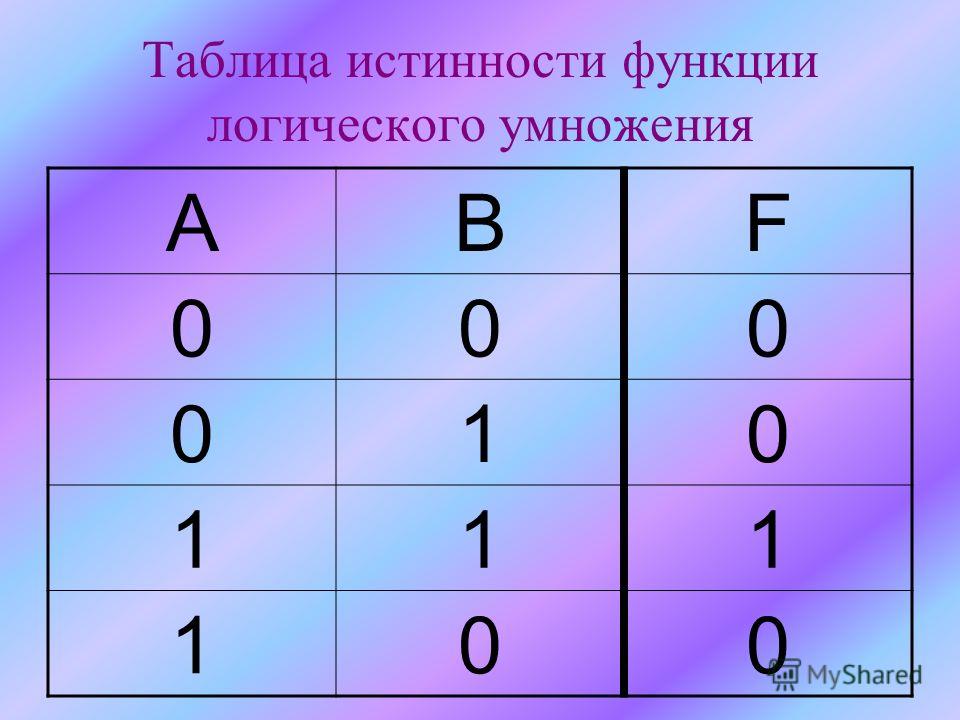 Книга Марио Ливио (Livio, 2005) освещает некоторые предпосылки и идеи, лежащие в основе этих невозможных результатов. Некоторые захватывающие недавние исследования сосредоточены на попытке использовать вычислительную сложность, чтобы пролить свет на фундаментальные вопросы физики, такие как понимание черных дыр и согласование общей теории относительности с квантовой механикой 9.0003
Книга Марио Ливио (Livio, 2005) освещает некоторые предпосылки и идеи, лежащие в основе этих невозможных результатов. Некоторые захватывающие недавние исследования сосредоточены на попытке использовать вычислительную сложность, чтобы пролить свет на фундаментальные вопросы физики, такие как понимание черных дыр и согласование общей теории относительности с квантовой механикой 9.0003
Эта цитата обычно читается как умаляющая важность реальных физических компьютеров в информатике, но обратите внимание, что телескопы абсолютно необходимы для астрономии, поскольку они предоставляют нам средства для соединения теоретических предсказаний с реальными экспериментальными наблюдениями.
↩Справедливости ради, в следующем предложении Грэм говорит: «вам нужно знать, как вычислять временную и пространственную сложность, а также о полноте по Тьюрингу». Эта книга включает в себя эти темы, а также другие, такие как NP-трудность, рандомизация, криптография, квантовые вычисления и многое другое.
↩
Если \(x\) — число, то \(\floor{x}\) — это целое число, полученное округлением в меньшую сторону, см. раздел 1.7.
↩Как мы увидим в главе 21, почти любая компания, полагающаяся на криптографию, вынуждена допускать несуществование определенных алгоритмов. В частности, RSA Security была основана на безопасности криптосистемы RSA, которая предполагает отсутствие эффективного алгоритма для вычисления простой факторизации больших целых чисел. 9t\) для некоторого натурального числа \(t\), и в этом случае вы можете сделать это рекурсивно, разбив матрицы на \(k\k\) блоков.
↩
Комментарии публикуются в репозитории GitHub с помощью приложения utteranc.es. Чтобы комментировать, требуется авторизация на GitHub. Если вы не хотите разрешать приложению публиковать сообщения от вашего имени, вы также можете комментировать непосредственно Ошибка GitHub для этой страницы.
Составлено 27.09.2022 14:58:04
Copyright 2022, Боаз Барак.
Эта работа
под лицензией Creative Commons
Attribution-NonCommercial-NoDerivatives 4.0 Международная лицензия.
Создано с использованием pandoc и panflute с шаблонами, полученными из gitbook и bookdown.
математическая оптимизация - Как компьютер умножает 2 числа?
Спросил
Изменено 5 лет, 8 месяцев назад
Просмотрено 23k раз
Как компьютер выполняет умножение 2 чисел, скажем, 100 * 55.
Я предположил, что компьютер выполнял многократное сложение для достижения умножения. Конечно, это может иметь место для целых чисел. Однако для чисел с плавающей запятой должна быть какая-то другая логика.
Примечание: этот вопрос был задан в интервью.
- информатика
- математическая оптимизация
2
Повторное сложение было бы очень неэффективным способом умножения чисел, представьте себе умножение 1298654825 на 85324154. Гораздо быстрее просто использовать длинное умножение с использованием двоичного кода.
Гораздо быстрее просто использовать длинное умножение с использованием двоичного кода.
1100100 0110111 ======= 0000000 -1100100 --1100100 ---0000000 ----1100100 -----1100100 ------1100100 ============== 10101011111009(6+5)
Обычно используемый метод называется частичных произведений , как это делают люди, поэтому, например, имея 100*55 , он будет делать что-то вроде
100 X 55 ---- 500 + 500 ----
В основном старые подходы использовали алгоритм сдвига и накопления, в котором вы сохраняете сумму, сдвигая частичные произведения для каждой цифры второго числа. Единственная проблема этого подхода заключается в том, что числа хранятся в дополнении до 2, поэтому вы не можете выполнять простое умножение бит на бит при сдвиге.
В настоящее время большинство оптимизаций способны суммировать все частичные вычисления всего за 1 цикл, что позволяет ускорить вычисления и упростить распараллеливание.
Взгляните сюда: http://en. wikipedia.org/wiki/Binary_multiplier
wikipedia.org/wiki/Binary_multiplier
В конце концов, вы можете найти некоторые реализации, такие как
- Дерево Уоллеса
- Множитель Дадда
- Кодировка стенда
3
Одним из способов является использование длинного умножения в двоичном формате:
01100100 <- 100
*00110111 <- 55
----------
01100100
01100100
01100100
01100100
01100100
---------------
1010101111100 <- 5500
Этот метод иногда называют методом сдвига и добавления.
Ладно, поехали. Я написал это некоторое время назад (1987!), так что некоторые вещи изменились, а другие остались прежними...
http://moneybender.com/transactor_article.pdf
3
Компьютеры используют алгоритм Бута или другие алгоритмы, выполняющие сдвиг и сложение для арифметических операций. Если вы изучали компьютерную архитектуру, книги по компьютерной архитектуре должны стать хорошим местом для изучения этих алгоритмов.
0
Для умножения двух чисел с плавающей запятой используется следующая процедура:
- Умножение мантиссы
- Добавить показатели степени
- Нормализация результата (десятичная точка ставится после первой цифры, отличной от нуля)
Таким образом, в системе счисления 10 умножить 5.1E3 и 2.6E-2
Умножить мантиссы => 5,1 * 2,6 = 13,26 (Обратите внимание, что это можно сделать с помощью целочисленного умножения, если вы отслеживаете, где должна быть десятичная точка)
Сложение показателей степени => 3 + -2 = 1
Дает нам результат 13.26E1
Нормализация 13.26E1 => 1.326E2
Интуитивно можно свести к минимуму повторяющиеся сложения, также используя сдвиг.
С точки зрения поплавков эта статья выглядит довольно актуальной:
http://oopweb.com/Assembly/Documents/ArtOfAssembly/Volume/Chapter_14/Ch24-1.html#HEADING1-19
Ответ: это зависит от обстоятельств.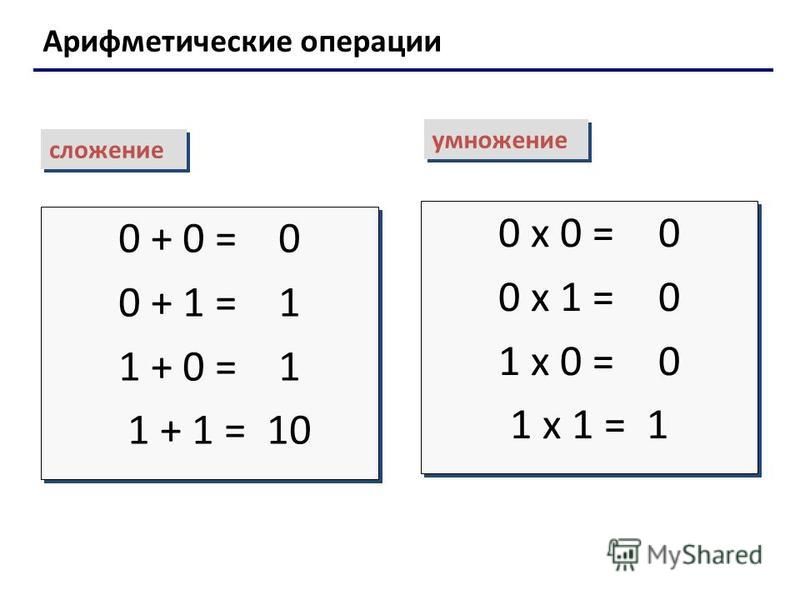 Как указывали другие, вы можете использовать тот же алгоритм, которому нас учили в школе, но вместо этого использовать двоичный код. Но для небольших количеств есть и другие способы.
Как указывали другие, вы можете использовать тот же алгоритм, которому нас учили в школе, но вместо этого использовать двоичный код. Но для небольших количеств есть и другие способы.
Допустим, вы хотите перемножить два 8-битных числа. Это можно сделать с помощью большой таблицы поиска. Вы просто объединяете два 8-битных числа, чтобы сформировать 16-битное число, и используете это число для индексации в таблице со всеми продуктами.
Или вы можете просто иметь большую сеть вентилей, которая напрямую вычисляет функцию. Однако эта сеть ворот становится довольно громоздкой для умножения больших чисел.
Я просто написал простую программу, умножающую два числа, хранящиеся в двух строках файла, используя алгоритм длинного умножения. Он может умножать два числа, которые имеют более 1 миллиарда чисел друг в друге
Пример:
23958233
5830 ×
------------
00000000 (= 23 958 233 × 0)
71874699 (= 23 958 233 × 30)
191665864 (= 23 958 233 × 800)
1197 (= 23 958 233 × 5000)
Исходный код:
Пожалуйста, просмотрите и оставьте свой комментарий
http://code.


 Если вы не использовали символы $ в формуле и перетащили формулу вниз на ячейку B3, Excel изменит формулу на =A3*C3, которая не будет работать, так как в ячейке B3 нет значения.
Если вы не использовали символы $ в формуле и перетащили формулу вниз на ячейку B3, Excel изменит формулу на =A3*C3, которая не будет работать, так как в ячейке B3 нет значения.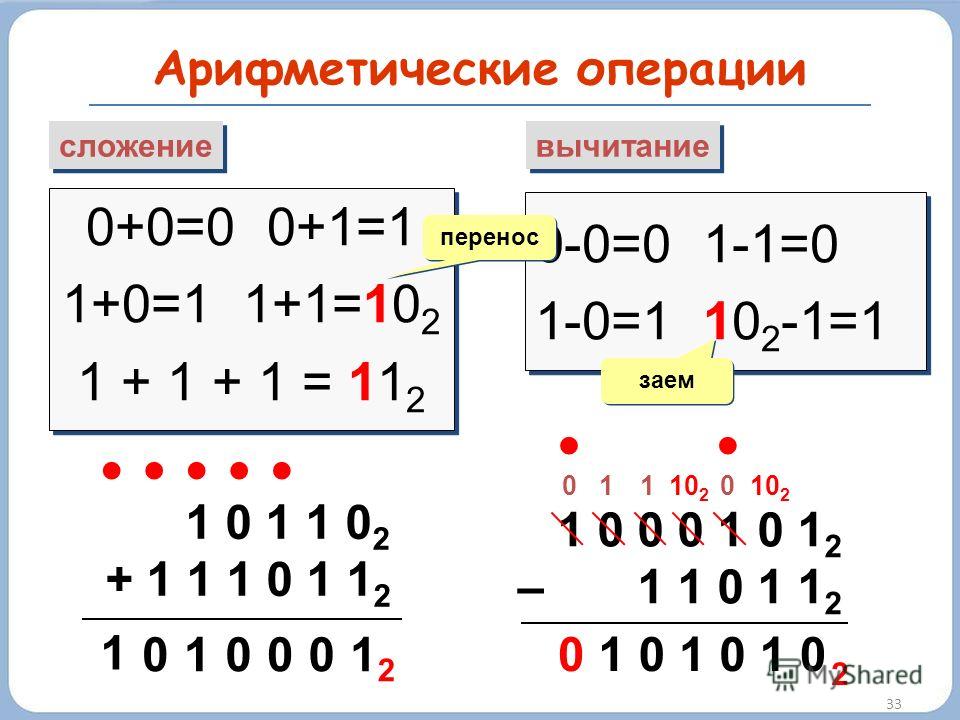
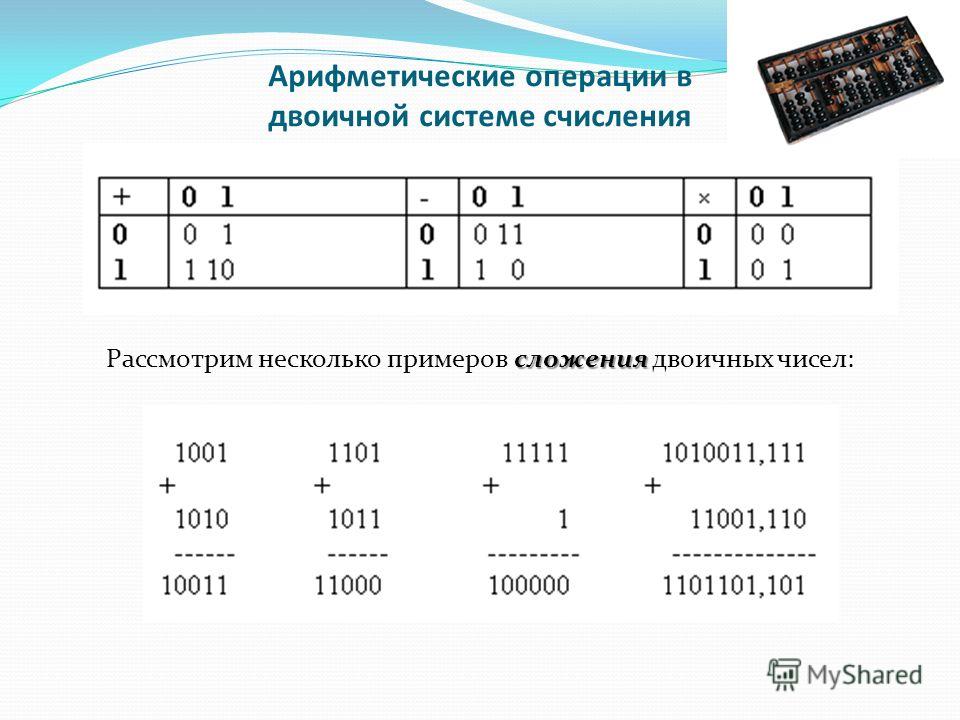 Количество знаков или символов, используемых для изображения числа, называется основанием системы счисления.
Количество знаков или символов, используемых для изображения числа, называется основанием системы счисления.
 Если все слагаемые в развернутой форме недесятичного числа представить в десятичной системе и вычислить полученное выражение по правилам десятичной арифметики, то получится число в десятичной системе, равное данному. По этому принципу производится перевод из недесятичной системы в десятичную. Например, перевод в десятичную систему написанных выше чисел производится так:
Если все слагаемые в развернутой форме недесятичного числа представить в десятичной системе и вычислить полученное выражение по правилам десятичной арифметики, то получится число в десятичной системе, равное данному. По этому принципу производится перевод из недесятичной системы в десятичную. Например, перевод в десятичную систему написанных выше чисел производится так:  Представим число в развернутой форме и выполним тождественное преобразование:
Представим число в развернутой форме и выполним тождественное преобразование:
 Обозначим заX1 дробную часть произведения и умножим ее наq:
Обозначим заX1 дробную часть произведения и умножим ее наq:
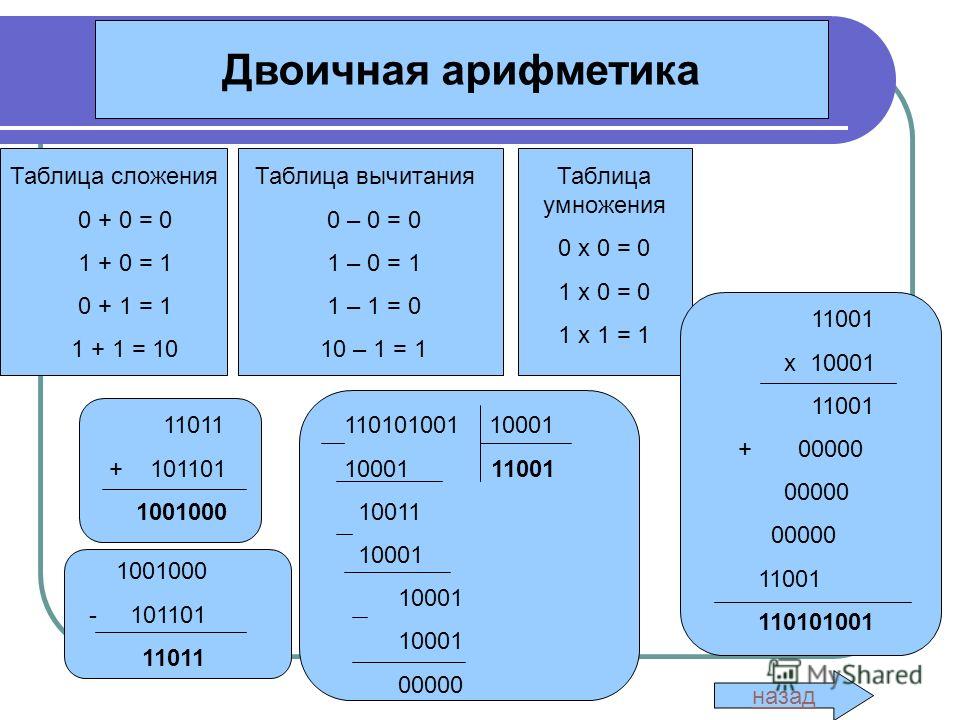 Иначе говоря, процедуры сложения, вычитания и умножения “столбиком” и деления “уголком” в двоичной системе производятся так же, как и в десятичной.
Иначе говоря, процедуры сложения, вычитания и умножения “столбиком” и деления “уголком” в двоичной системе производятся так же, как и в десятичной.




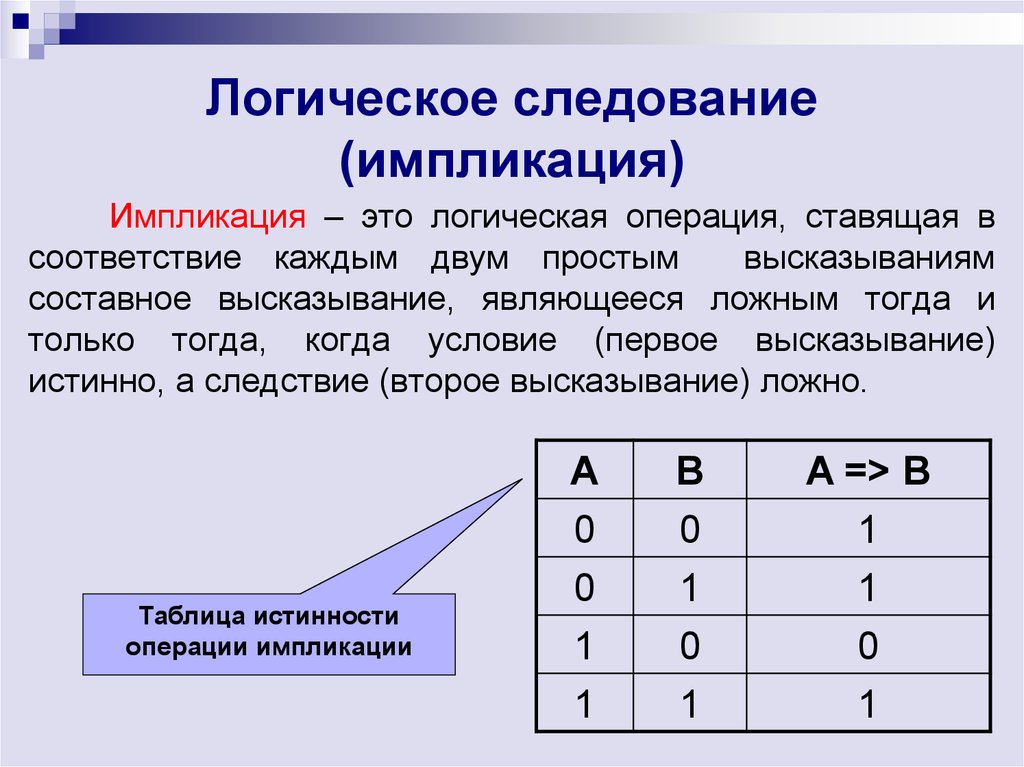
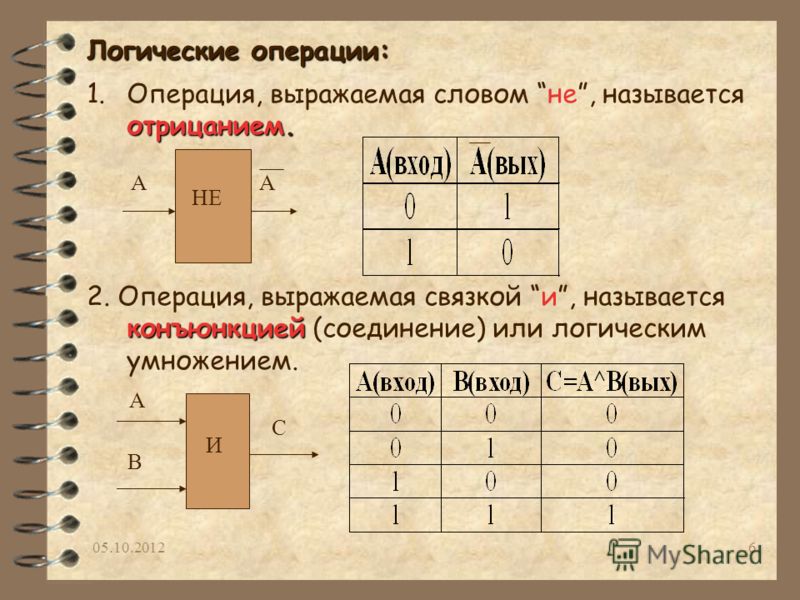 )
) Они используются в
«Арифметике» Иоганна Видмана изданной в 1489 году. До этого сложение
обозначалось буквой p (plus) или латинским словом et (союз «и»), а
вычитание — буквой m (minus). У Видмана символ плюса заменяет не только
сложение, но и союз «и». Происхождение этих символов неясно, но, скорее
всего, они ранее использовались в торговом деле как признаки прибыли и
убытка. Оба символа практически мгновенно получили общее распространение в
Европе — за исключением Италии.
Они используются в
«Арифметике» Иоганна Видмана изданной в 1489 году. До этого сложение
обозначалось буквой p (plus) или латинским словом et (союз «и»), а
вычитание — буквой m (minus). У Видмана символ плюса заменяет не только
сложение, но и союз «и». Происхождение этих символов неясно, но, скорее
всего, они ранее использовались в торговом деле как признаки прибыли и
убытка. Оба символа практически мгновенно получили общее распространение в
Европе — за исключением Италии. Двоеточием деление стал обозначать
Лейбниц. До них часто использовали также букву D. Начиная с Фибоначчи,
используется также черта дроби, употреблявшаяся ещё в арабских сочинениях. В
Англии и США распространение получил символ ÷ (обелюс), который предложили Йоханн
Ран и Джон Пелл в середине XVII века.
Двоеточием деление стал обозначать
Лейбниц. До них часто использовали также букву D. Начиная с Фибоначчи,
используется также черта дроби, употреблявшаяся ещё в арабских сочинениях. В
Англии и США распространение получил символ ÷ (обелюс), который предложили Йоханн
Ран и Джон Пелл в середине XVII века.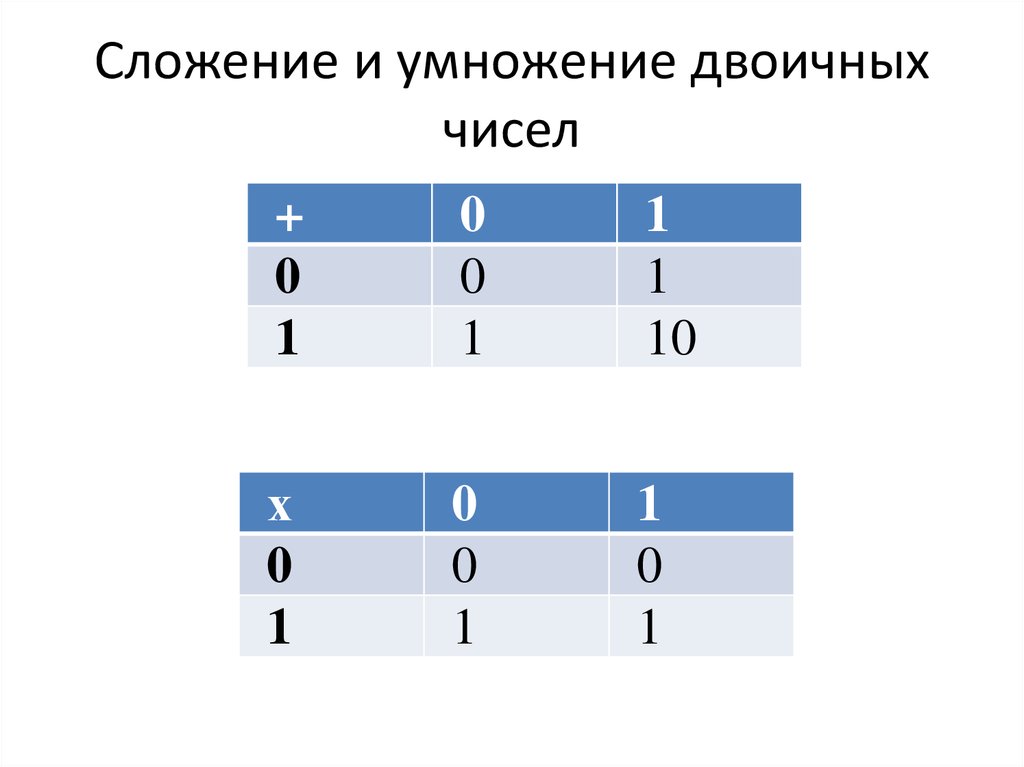 Есть гипотеза, что он возник от ошибки
наборщика, который сокращение cto (cento, сотая доля) набрал как 0/0. Более
вероятно, что это скорописный коммерческий значок, возникший лет на 100
раньше.
Есть гипотеза, что он возник от ошибки
наборщика, который сокращение cto (cento, сотая доля) набрал как 0/0. Более
вероятно, что это скорописный коммерческий значок, возникший лет на 100
раньше. Позднее Ньютон распространил эту форму записи на отрицательные и
дробные показатели (1676).
Позднее Ньютон распространил эту форму записи на отрицательные и
дробные показатели (1676).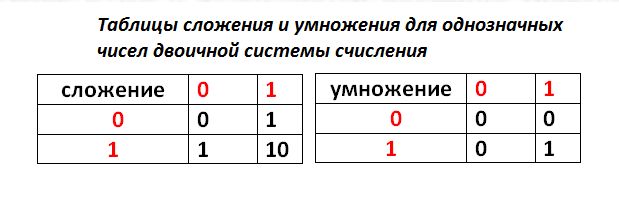 14159… образовал Уильям Джонс в 1706
году, взяв первую букву греческих слов περιφέρεια — окружность и
περίμετρος — периметр, то есть длина окружности.
14159… образовал Уильям Джонс в 1706
году, взяв первую букву греческих слов περιφέρεια — окружность и
περίμετρος — периметр, то есть длина окружности.
 \(7 \times 3 = 21\), поэтому выражение становится \(5 + 21\), что равно \(26\).
\(7 \times 3 = 21\), поэтому выражение становится \(5 + 21\), что равно \(26\).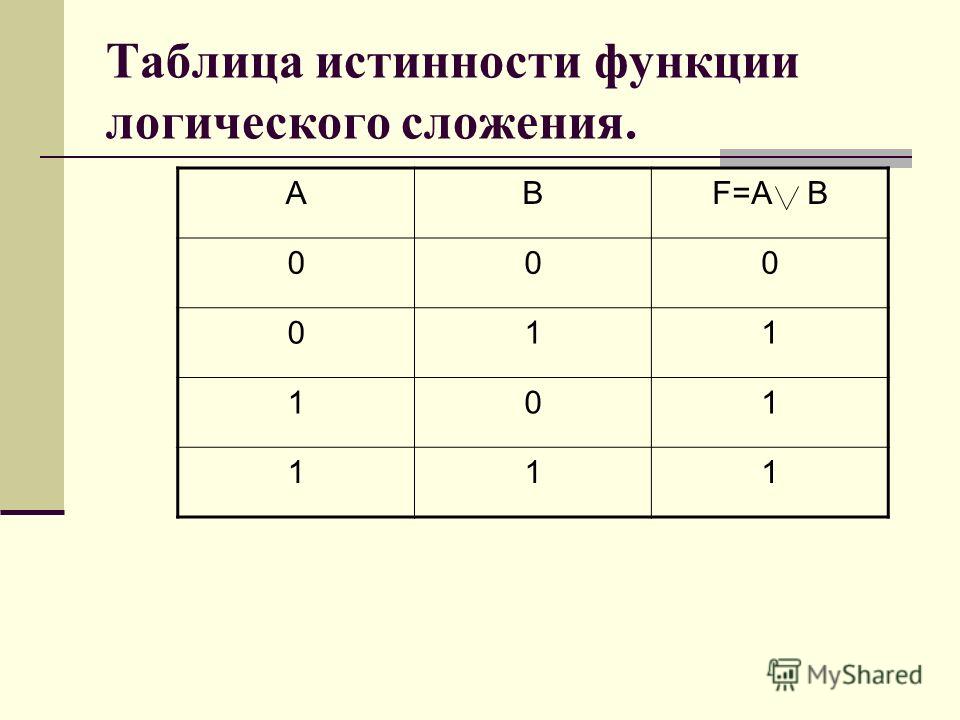 Обратите внимание на скобки.
Обратите внимание на скобки. Сегодня мы собираемся попрактиковаться в нахождении значения выражений с и без скобок и посмотрите, какое значение имеют скобки.
Сегодня мы собираемся попрактиковаться в нахождении значения выражений с и без скобок и посмотрите, какое значение имеют скобки. 

 Канн III
Канн III - пользоваться калькулятором и компьютером для решения числовых выражений.
МАТЕРИАЛЫ:
-компьютеры
-калькуляторы (универсальный бренд)
-бумага
-карандаши
-мел
- классная доска
-ластик
-баннеры(компьютерная распечатка)
-Рекламный проспект
СТРАТЕГИЙ:
А. Выявить сравнение знаков препинания в предложении с
группировка символов в числовом выражении (знаки с выражениями
Робин Ли Трэвис и я любим компьютеры;Медленные дети играют;Сохранить
Тряпки и макулатура), спросите, могут ли учащиеся объяснить, почему баннеры
двусмысленный.
ИНФО
Без запятых предложение Робин Ли Трэвис и я любим компьютеры,
подразумевает, что два человека любят компьютеры. В зависимости от того, где стоят запятые
вставленное предложение может констатировать, что трое или четверо любят
компьютеры.
Примеры деятельности:
1) попросите учащихся упростить 10+2*3-1, чтобы получить как можно больше различных
ответы, как они могут (используйте калькуляторы и компьютеры, чтобы сравнить
ответы).
- пользоваться калькулятором и компьютером для решения числовых выражений.
МАТЕРИАЛЫ:
-компьютеры
-калькуляторы (универсальный бренд)
-бумага
-карандаши
-мел
- классная доска
-ластик
-баннеры(компьютерная распечатка)
-Рекламный проспект
СТРАТЕГИЙ:
А. Выявить сравнение знаков препинания в предложении с
группировка символов в числовом выражении (знаки с выражениями
Робин Ли Трэвис и я любим компьютеры;Медленные дети играют;Сохранить
Тряпки и макулатура), спросите, могут ли учащиеся объяснить, почему баннеры
двусмысленный.
ИНФО
Без запятых предложение Робин Ли Трэвис и я любим компьютеры,
подразумевает, что два человека любят компьютеры. В зависимости от того, где стоят запятые
вставленное предложение может констатировать, что трое или четверо любят
компьютеры.
Примеры деятельности:
1) попросите учащихся упростить 10+2*3-1, чтобы получить как можно больше различных
ответы, как они могут (используйте калькуляторы и компьютеры, чтобы сравнить
ответы). 2) обсудить необходимость типового порядка выполнения операций
чтобы не было двусмысленности в отношении ценности таких
выражения.
3) обсудить этапы стандартного порядка операций и показать
как они будут использоваться для упрощения приведенного выше выражения.
10+2*3-1
10+6-1 умножение
16-1 прибавление (слева направо)
Вычитание 15 (слева направо)
4) показать, как скобки могут быть использованы для придания различных значений
к тому же выражению.
(10+2)х3-1 (10+2)х(3-1)
12 х 3-1 12 х 2
36 -1 24
35
ИНФО
В выражениях с более чем одной операцией символы группировки, такие как
поскольку круглые скобки или разделительные полосы часто используются для обозначения
порядок выполнения операций.
2) обсудить необходимость типового порядка выполнения операций
чтобы не было двусмысленности в отношении ценности таких
выражения.
3) обсудить этапы стандартного порядка операций и показать
как они будут использоваться для упрощения приведенного выше выражения.
10+2*3-1
10+6-1 умножение
16-1 прибавление (слева направо)
Вычитание 15 (слева направо)
4) показать, как скобки могут быть использованы для придания различных значений
к тому же выражению.
(10+2)х3-1 (10+2)х(3-1)
12 х 3-1 12 х 2
36 -1 24
35
ИНФО
В выражениях с более чем одной операцией символы группировки, такие как
поскольку круглые скобки или разделительные полосы часто используются для обозначения
порядок выполнения операций. 2-4
13- 8 -3 2х 9-4
5-3 18-4
2 14
Обратите внимание, что в примерах № 3 и № 4 два выражения имеют
те же числа и те же операции, но результаты
отличаются из-за группировки символов. (Выполняйте операции внутри
круглые скобки, показатели степени, умножение/деление, сложение или
вычитание слева направо.)
№3 (8+5)х3 №4 8+(5х3)
(8+5)х3 8+(5х3)
13х3 8+15
3923
B. Чтобы дать дополнительную практику, используя правильный порядок
операции, у учащихся:
1) замените переменную в каждой строке или столбце, чтобы сделать ее истинной
уравнение в задаче №1 (см. раздаточный материал).
2) напишите знак операции (+,-,x,/) в каждой строке или столбце, чтобы
составьте правильное уравнение в головоломке № 2 (см. раздаточный материал).
2-4
13- 8 -3 2х 9-4
5-3 18-4
2 14
Обратите внимание, что в примерах № 3 и № 4 два выражения имеют
те же числа и те же операции, но результаты
отличаются из-за группировки символов. (Выполняйте операции внутри
круглые скобки, показатели степени, умножение/деление, сложение или
вычитание слева направо.)
№3 (8+5)х3 №4 8+(5х3)
(8+5)х3 8+(5х3)
13х3 8+15
3923
B. Чтобы дать дополнительную практику, используя правильный порядок
операции, у учащихся:
1) замените переменную в каждой строке или столбце, чтобы сделать ее истинной
уравнение в задаче №1 (см. раздаточный материал).
2) напишите знак операции (+,-,x,/) в каждой строке или столбце, чтобы
составьте правильное уравнение в головоломке № 2 (см. раздаточный материал).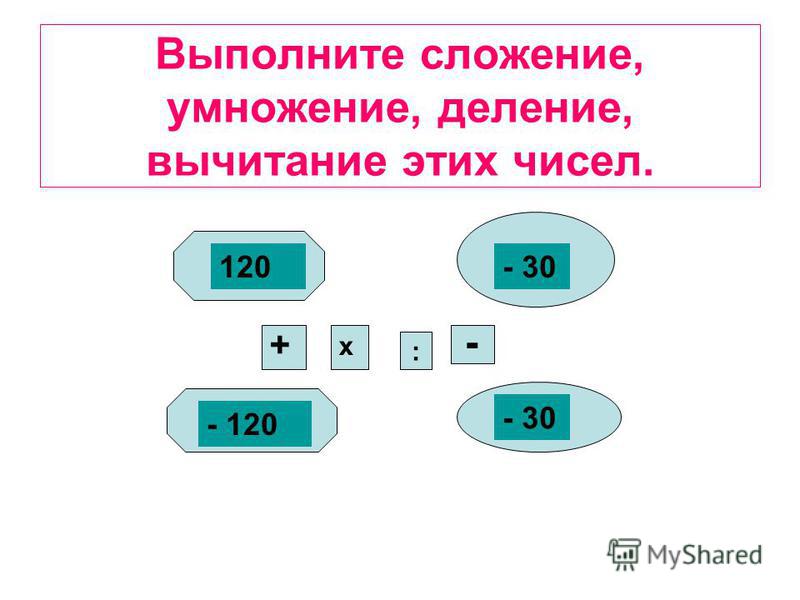 C. Чтобы проверить успеваемость учащихся, попросите их выполнить групповое задание.
Symbols-Review (см. раздаточный материал и ниже).
IV. КОММЕНТАРИИ/ИНФО.
Использование калькулятора настолько привычно для нас, что мы склонны принимать
некоторые вещи как должное... только при широком использовании личных
компьютеры вынуждают нас переоценивать функцию,
надлежащее использование и правильный метод (ы) обучения студентов
определенные математические концепции с использованием обеих машин.
3
Следует обратить внимание учащихся на то, что люди общаются с
компьютеров с помощью программ. Программы сообщают компьютеру, что делать.
Однако не всегда человеку необходимо уметь писать.
программа для работы с компьютером. Программы можно писать на таких
способ, которым оператор может их использовать, отвечая на ряд вопросов
которые прописаны в программе. Тем не менее, лучший способ научиться
что компьютер может и не может сделать, так это узнать немного о
программирование.
C. Чтобы проверить успеваемость учащихся, попросите их выполнить групповое задание.
Symbols-Review (см. раздаточный материал и ниже).
IV. КОММЕНТАРИИ/ИНФО.
Использование калькулятора настолько привычно для нас, что мы склонны принимать
некоторые вещи как должное... только при широком использовании личных
компьютеры вынуждают нас переоценивать функцию,
надлежащее использование и правильный метод (ы) обучения студентов
определенные математические концепции с использованием обеих машин.
3
Следует обратить внимание учащихся на то, что люди общаются с
компьютеров с помощью программ. Программы сообщают компьютеру, что делать.
Однако не всегда человеку необходимо уметь писать.
программа для работы с компьютером. Программы можно писать на таких
способ, которым оператор может их использовать, отвечая на ряд вопросов
которые прописаны в программе. Тем не менее, лучший способ научиться
что компьютер может и не может сделать, так это узнать немного о
программирование.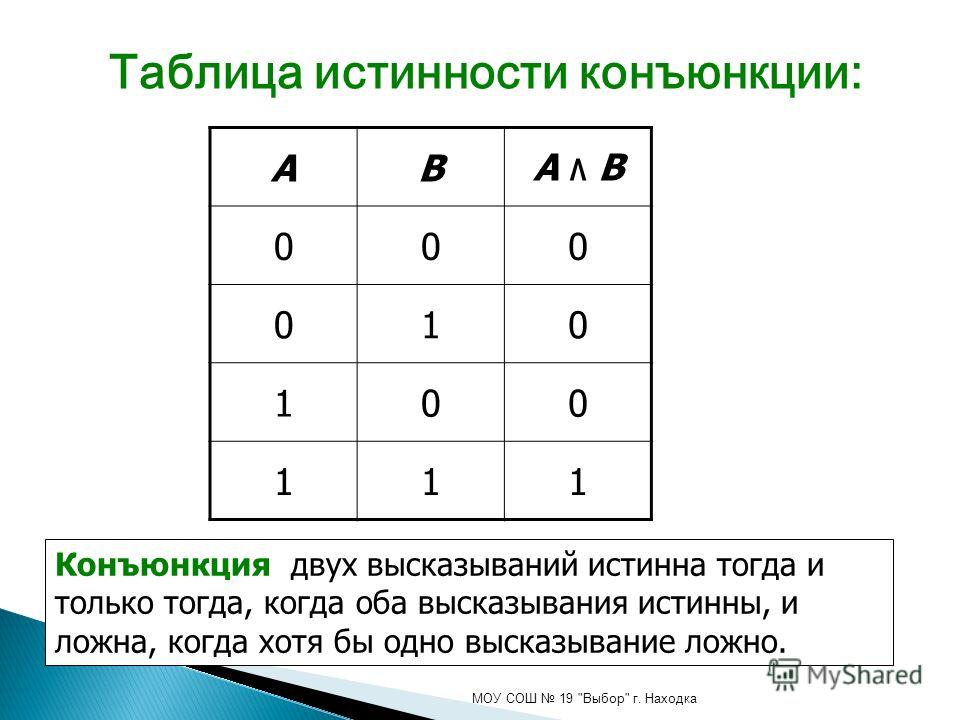 возведен в степень (показатель степени)
BASIC следует порядку операций. Пример программы на БЕЙСИКЕ:
10 ПЕЧАТЬ 21*34+35/7
20 КОНЕЦ
БЕЖАТЬ
719(отвечать)
Группировка символов-обзор
Выберите каждый ответ из вариантов в скобках. Напишите ответ в
пустой.
1) аб означает а______________б. (плюс, разделить на, раз)
а
2) _ означает а______________б. (плюс, разделить на, раз)
б
3) a____________b означает, что a не равно b. знак равно
4) Круглые скобки являются примером ______________.(символ группировки, значение,
переменная)
Упростите каждое выражение с помощью калькулятора. Переведите каждое выражение в
БАЗОВЫЙ. Используйте компьютер для проверки ответов. (Не забудьте ввести PRINT перед
числовое выражение.)
5) 7+(12-3)_____________________ 6) (18-3) ____________
-----
(3+2)
7) (7х3)-(5х4)__________________ 8) 10-(3+4)___________
9) 24- (63/(6+3))_______________ 10) 36/12+6____________
-------
8-5
11) 15-5х2+8/4__________________ 12) 20(12-8)-30/(10+5)___________
Упростите выражение с каждой стороны ----?----.
возведен в степень (показатель степени)
BASIC следует порядку операций. Пример программы на БЕЙСИКЕ:
10 ПЕЧАТЬ 21*34+35/7
20 КОНЕЦ
БЕЖАТЬ
719(отвечать)
Группировка символов-обзор
Выберите каждый ответ из вариантов в скобках. Напишите ответ в
пустой.
1) аб означает а______________б. (плюс, разделить на, раз)
а
2) _ означает а______________б. (плюс, разделить на, раз)
б
3) a____________b означает, что a не равно b. знак равно
4) Круглые скобки являются примером ______________.(символ группировки, значение,
переменная)
Упростите каждое выражение с помощью калькулятора. Переведите каждое выражение в
БАЗОВЫЙ. Используйте компьютер для проверки ответов. (Не забудьте ввести PRINT перед
числовое выражение.)
5) 7+(12-3)_____________________ 6) (18-3) ____________
-----
(3+2)
7) (7х3)-(5х4)__________________ 8) 10-(3+4)___________
9) 24- (63/(6+3))_______________ 10) 36/12+6____________
-------
8-5
11) 15-5х2+8/4__________________ 12) 20(12-8)-30/(10+5)___________
Упростите выражение с каждой стороны ----?----. Сделайте истинное утверждение, заменив ? с символом = или . Проверьте свои
ответы с помощью компьютера. (Если компьютер напечатает 1, ваш ответ верен; если ваш
ответ неверный, компьютер напечатает 0.) Запомните числовые выражения
должен быть в БЕЙСИКЕ.
13) 16+3 ? 9+3 _______ 14) (8-3x2) ? (8-3)x2_________
---- ---- --- -------
8+4 4-1
4
15) 3(5+2) ? 3x5+2 ______ 16+4 ? 8+4х3____________
----- 16) 1+ ---- ----- ----
3+2 8-2-2
Сделайте истинное утверждение, заменив ? с символом = или . Проверьте свои
ответы с помощью компьютера. (Если компьютер напечатает 1, ваш ответ верен; если ваш
ответ неверный, компьютер напечатает 0.) Запомните числовые выражения
должен быть в БЕЙСИКЕ.
13) 16+3 ? 9+3 _______ 14) (8-3x2) ? (8-3)x2_________
---- ---- --- -------
8+4 4-1
4
15) 3(5+2) ? 3x5+2 ______ 16+4 ? 8+4х3____________
----- 16) 1+ ---- ----- ----
3+2 8-2-2
 , Алан Кобэм, 1964 г.
, Алан Кобэм, 1964 г. 3"> Алгоритмы за пределами арифметики
3"> Алгоритмы за пределами арифметики 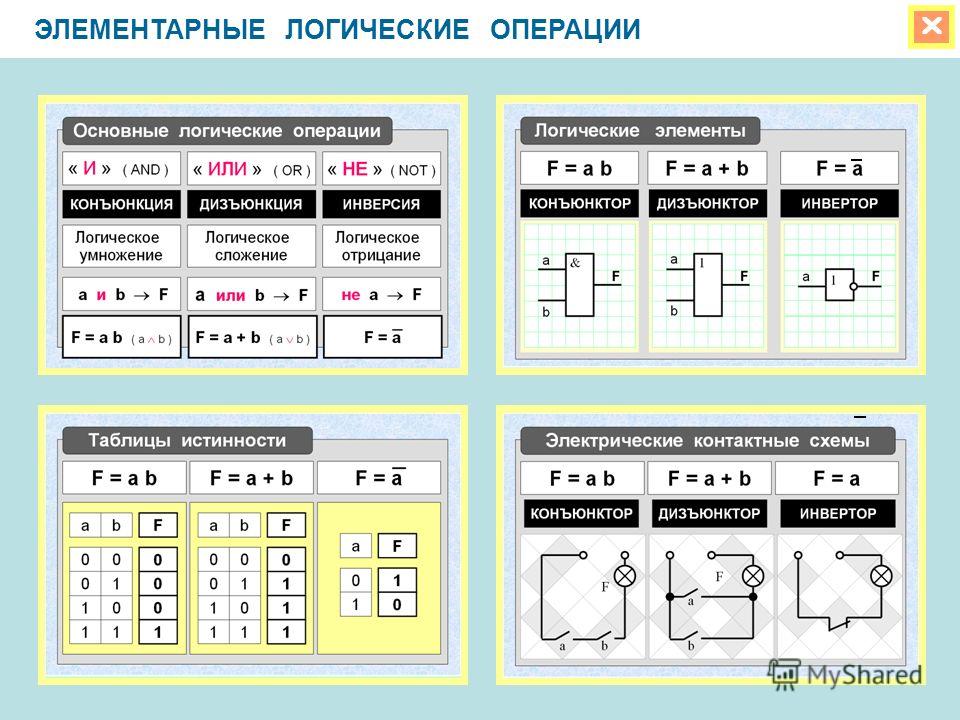
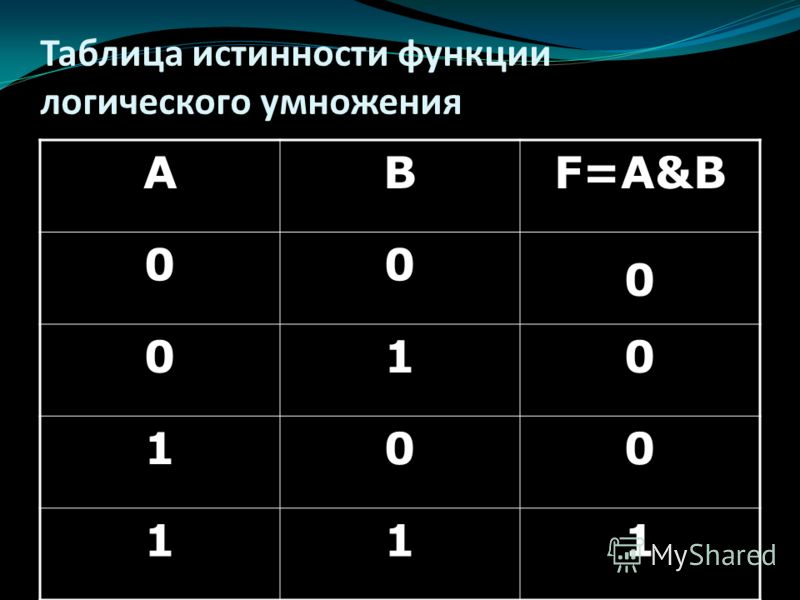 Эквивалентность моделей (включая RAM-машины, \(\lambda\) исчисление и клеточные автоматы), конфигурации машин Тьюринга, существование универсальной машины Тьюринга, невычислимые функции (включая проблему остановки и теорему Райса), теорему Гёделя о неполноте, ограничения вычислительные модели (регулярные и контекстно-свободные языки).
Эквивалентность моделей (включая RAM-машины, \(\lambda\) исчисление и клеточные автоматы), конфигурации машин Тьюринга, существование универсальной машины Тьюринга, невычислимые функции (включая проблему остановки и теорему Райса), теорему Гёделя о неполноте, ограничения вычислительные модели (регулярные и контекстно-свободные языки).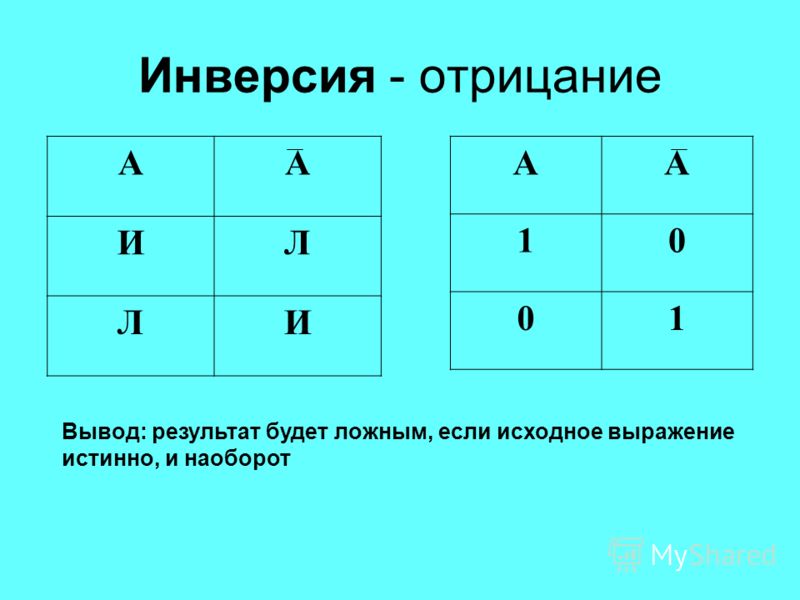
 5 и раздел 8.5), теоремы Гёделя о неполноте (глава 11), автоматов/регулярных выражений и контекстно-свободных грамматик (глава 10) и вычислений с ограниченным пространством ( Глава 17), не используются в следующих главах. Следовательно, вы можете выбрать, охватить или пропустить любое их подмножество.
5 и раздел 8.5), теоремы Гёделя о неполноте (глава 11), автоматов/регулярных выражений и контекстно-свободных грамматик (глава 10) и вычислений с ограниченным пространством ( Глава 17), не используются в следующих главах. Следовательно, вы можете выбрать, охватить или пропустить любое их подмножество. {\log_2 3}\) для любого \(n>2\). 9{\log_2 3}\).
{\log_2 3}\) для любого \(n>2\). 9{\log_2 3}\).