Список логических символов — frwiki.wiki
В логике для выражения логического представления обычно используется набор символов . В следующей таблице перечислены многие символы с их именами, возможные способы их чтения и связанные области математики . Кроме того, третий столбец содержит неформальное определение, четвертый столбец дает краткий пример, пятый дает их код Unicode, а шестой и седьмой — числовые или текстовые ссылки, используемые в документах HTML (см. Сущность HTML ). Последний столбец содержит символ LaTeX .
Резюме
- 1 Основные логические символы
- 2 Продвинутые и редко используемые логические символы
- 3 Статьи по теме
- 4 Примечания и ссылки
- 4.1 Примечания
- 4.2 Ссылки
Основные логические символы
| Символ | Фамилия | Объяснение | Примеры | Юникод (шестнадцатеричный) | (десятичный) | HTML (текст) | Латекс |
|---|---|---|---|---|---|---|---|
| Чтение | |||||||
| Категория | |||||||
| Участие | A ⇒ B истинно, только если либо A ложно, либо B истинно. → означает то же, что и ⇒ Означает то же, что и ⇒ | Пусть x будет действительным числом: | U + 21D2 U + 2192 U + 2283 | & # 8658; & # 8594; & # 8835; | & rArr; & rarr; & Как дела; | ⇒{\ displaystyle \ Rightarrow} \ Правая стрелка →{\ displaystyle \ to} \ к ⊃{\ displaystyle \ supset} \ supset ⟹{\ displaystyle \ implies} \ подразумевает | |
| вовлеченный если так является достаточным условием для | |||||||
| Логическая эквивалентность | A ⇔ B истинно, если A и B ложны или если A и B истинны.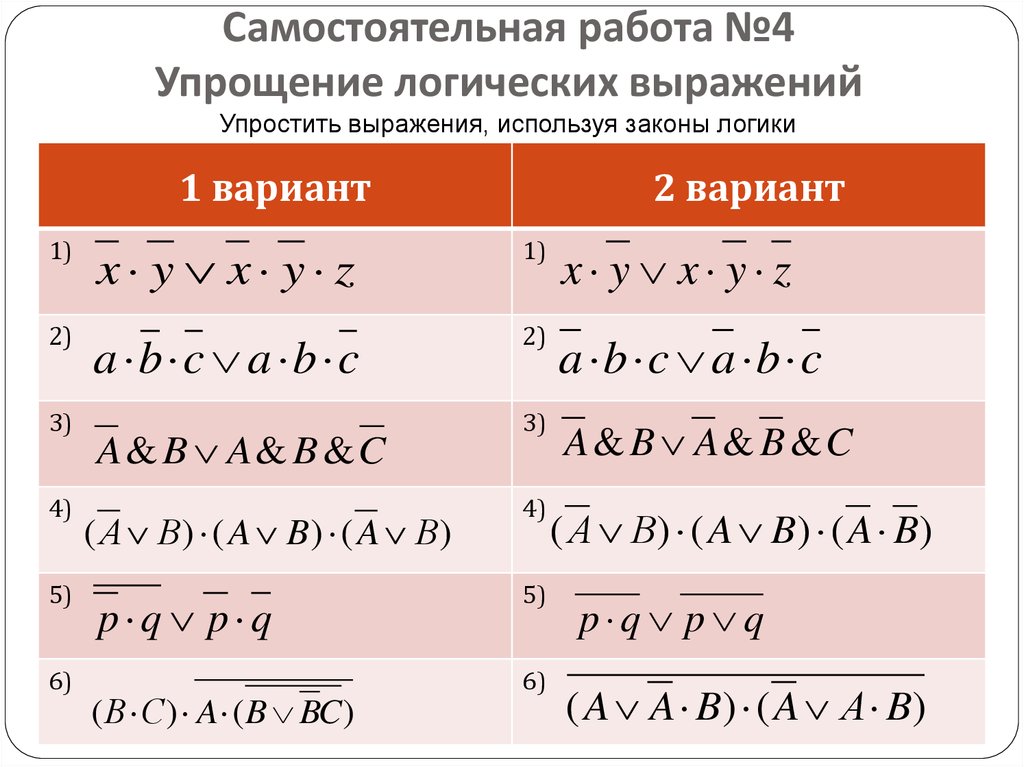 | х + 5 знак равно у + 2 ⇔ х + 3 = у | U + 21D4 U + 2261 U + 2194 | & # 8660; & # 8801; & # 8596; | & hArr; & Equiv; & harr; | ⇔{\ displaystyle \ Leftrightarrow} \ Leftrightarrow ≡{\ Displaystyle \ Equiv} \ Equiv ↔{\ displaystyle \ leftrightarrow} \ leftrightarrow ⟺{\ Displaystyle \ iff} \ iff | |
| если и только если равно означает то же, что и | |||||||
| Логика высказываний | |||||||
| Отрицание | Утверждение ¬ A истинно тогда и только тогда, когда A ложно. | ¬ (¬ А ) ⇔ А х ≠ у ⇔ ¬ ( х = у ) | U + 00AC U + 0021 | & # 172; & # 732; & # 33; | & нет; & тильда; & искл; | ¬{\ displaystyle \ neg}\ lnot или \ neg ∼{\ displaystyle \ sim} \ sim | |
| Не Нет | |||||||
| Логика высказываний | |||||||
| Соединение | Утверждение A ∧ B истинно, если истинны A и B ; в противном случае это ложь.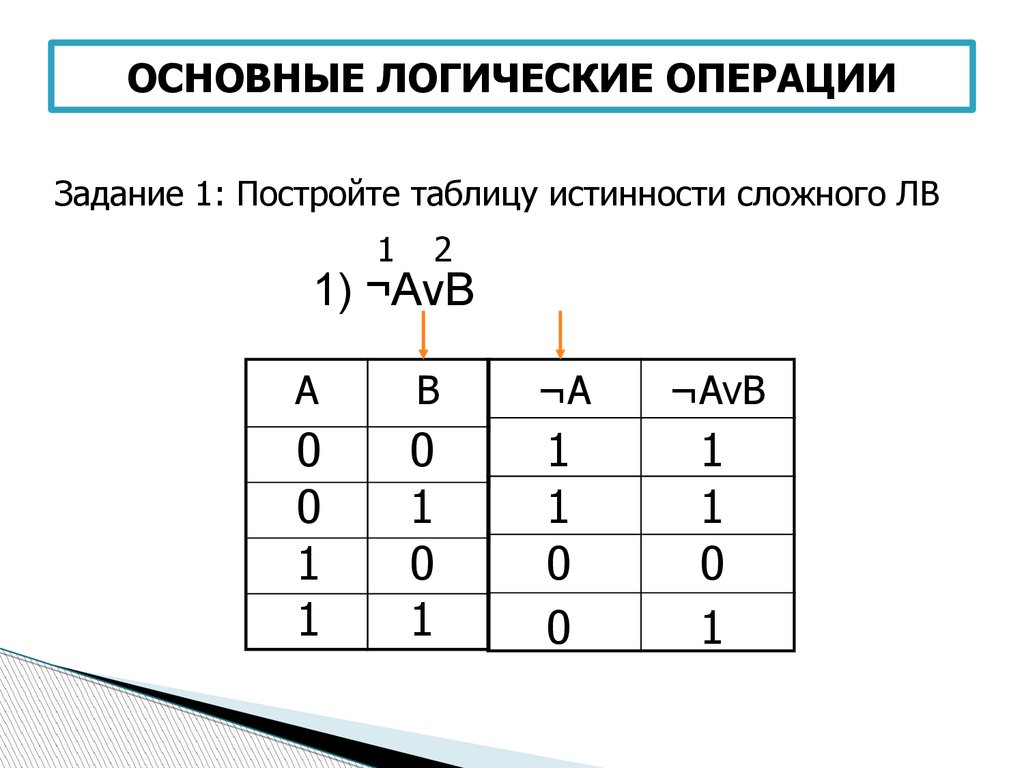 | n <4 ∧ n > 2 ⇔ n = 3, когда n — целое число . | U + 2227 U + 00B7 U + 0026 | & # 8743; & # 183; & # 38; | & а также; & middot; & amp; | ∧{\ Displaystyle \ клин}\ клин или \ земля &{\ Displaystyle \ &} \ & | |
| а также | |||||||
| Логика высказываний , булева алгебра | |||||||
| Инклюзивная дизъюнкция | Утверждение A ∨ B истинно, если истинны A | n ≥ 4 ∨ n ≤ 2 ⇔ n ≠ 3, когда n — целое число . | U + 2228 U + 002B U + 2225 | & # 8744; & # 43; & # 8741; | &золото; | ∨{\ displaystyle \ lor}\ lor или \ vee | |
| или же | |||||||
| Логика высказываний , булева алгебра | |||||||
⊕ | Исключительная дизъюнкция | Утверждение A ⊕ B истинно, когда истинно либо A, либо B, только одно или другое.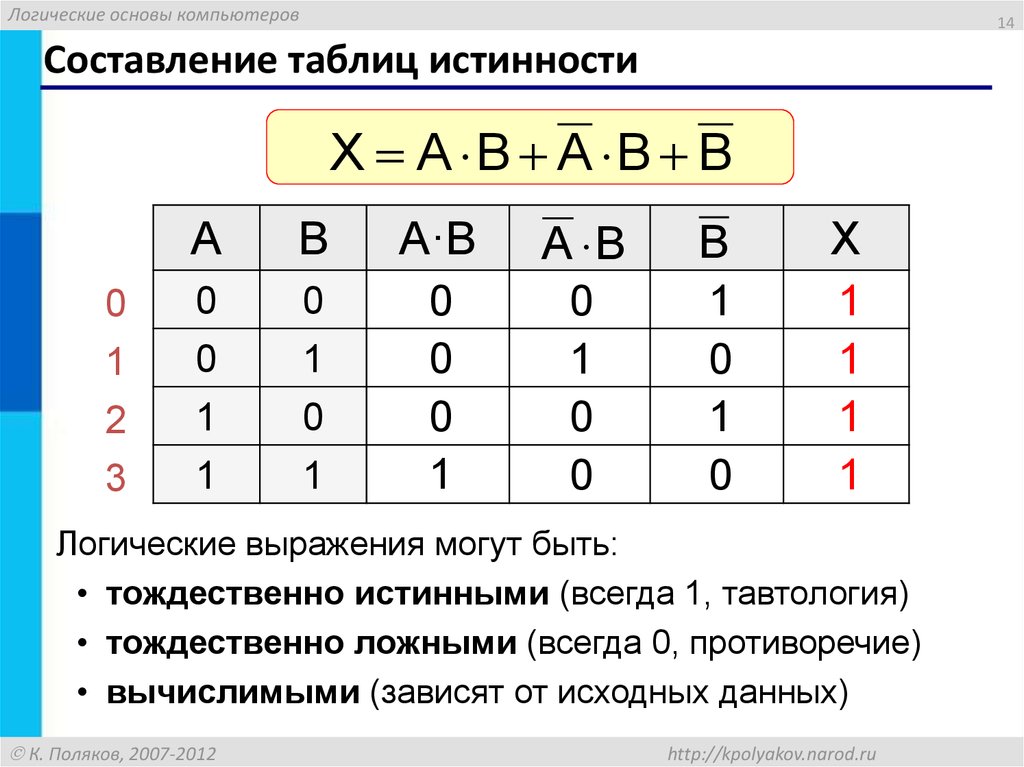 | (¬ A ) ⊕ A всегда верно, A ⊕ A всегда ложно. | U + 2295 U + 22BB | & # 8853; & # 8891; | & oplus; | ⊕{\ displaystyle \ oplus} \ oplus ⊻{\ displaystyle \ veebar} \ veebar |
| xor | |||||||
| Логика высказываний , булева алгебра | |||||||
| Тавтология | Утверждение ⊤ безусловно верно. | A ⇒ ⊤ всегда верно. | U + 22A4 | & # 8868; | ⊤{\ displaystyle \ top} \вершина | ||
| Высокая Правда | |||||||
| Логика высказываний , булева алгебра | |||||||
| Противоречие | Утверждение ⊥ безусловно ложно.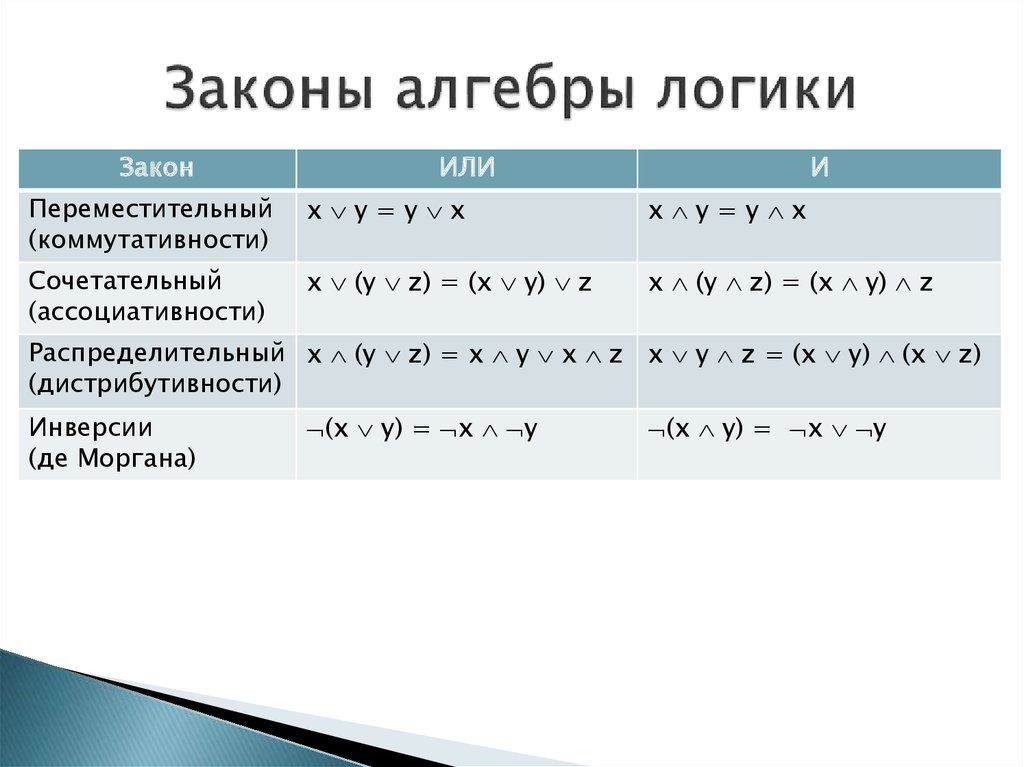 (Символ ⊥ также может относиться к перпендикулярным линиям .) | ⊥ ⇒ A всегда верно. | U + 22A5 | & # 8869; | & perp; | ⊥{\ displaystyle \ bot} \ бот | |
| Низкий Ложь | |||||||
| Логика высказываний , булева алгебра | |||||||
| Универсальный квантификатор | ∀ x : P ( x ) или ( x ) P ( x ) означает, что P ( x ) истинно для всех x . | ∀ | U + 2200 | & # 8704; | & для всех; | ∀{\ displaystyle \ forall} \ для всех | |
| За все Для всех Для каждого | |||||||
| вычисление предикатов | |||||||
∃ | Экзистенциальный квантификатор | ∃ x : P ( x ) означает, что существует хотя бы один x такой, что P ( x ) истинно.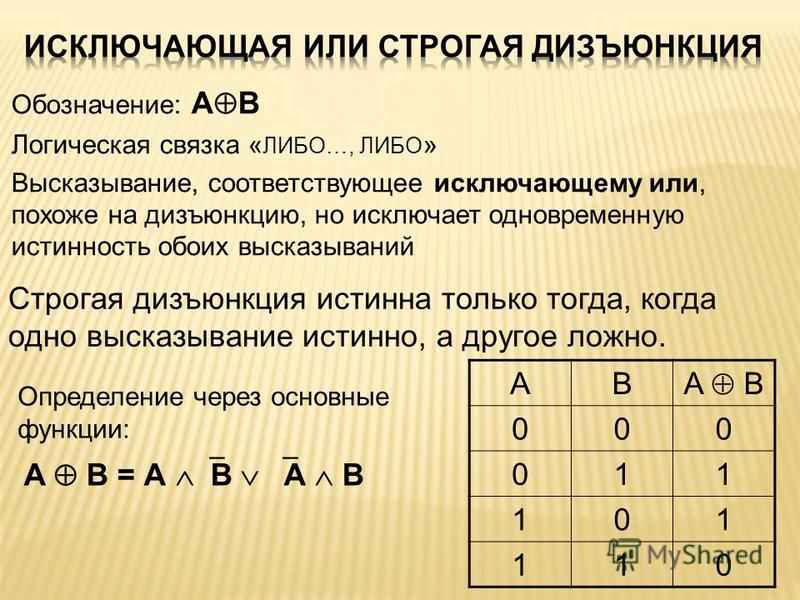 | ∃ n ∈ ℕ: | U + 2203 | & # 8707; | &существовать; | ∃{\ Displaystyle \ существует} \ существуют |
| Это существует | |||||||
| вычисление предикатов | |||||||
∃! | Уникальный экзистенциальный квантификатор | ∃! x : P ( x ) означает, что существует ровно один x такой, что P ( x ) истинно. | ∃! n ∈ ℕ: n + 5 = 2 n . | U + 2203 U + 0021 | & # 8707; & # 33; | ∃!{\ displaystyle \ существует!} \ существуют! | |
| Есть ровно один | |||||||
| вычисление предикатов | |||||||
≔ ≡ : ⇔ | Определение | x ≔ y или x ≡ y означает, что x определяется как другое имя для y, но обратите внимание, что ≡ также может означать что-то еще, например конгруэнтность . Р : ⇔ Q означает , что Р определяется как логически эквивалентны с Q . | cosh x ≔ (ехр х + ехр (- х )) / 2 Исключающее ИЛИ Б : ⇔ ( ∨ B ) ∧ ¬ ( ∧ B ) | U + 2254 (U + 003A; U + 003D) U + 2261 U + 003A; U + 229C | & # 8788; (& # 58; & # 61;) & # 8801; & # 8860; | & Equiv; & hArr; | знак равно{\ displaystyle: =} знак равно ≡{\ Displaystyle \ Equiv} \ Equiv : ⇔{\ displaystyle: \ Leftrightarrow} : \ Leftrightarrow |
| определяется как | |||||||
| Всюду | |||||||
() | Порядок операций | Операции в круглых скобках имеют приоритет.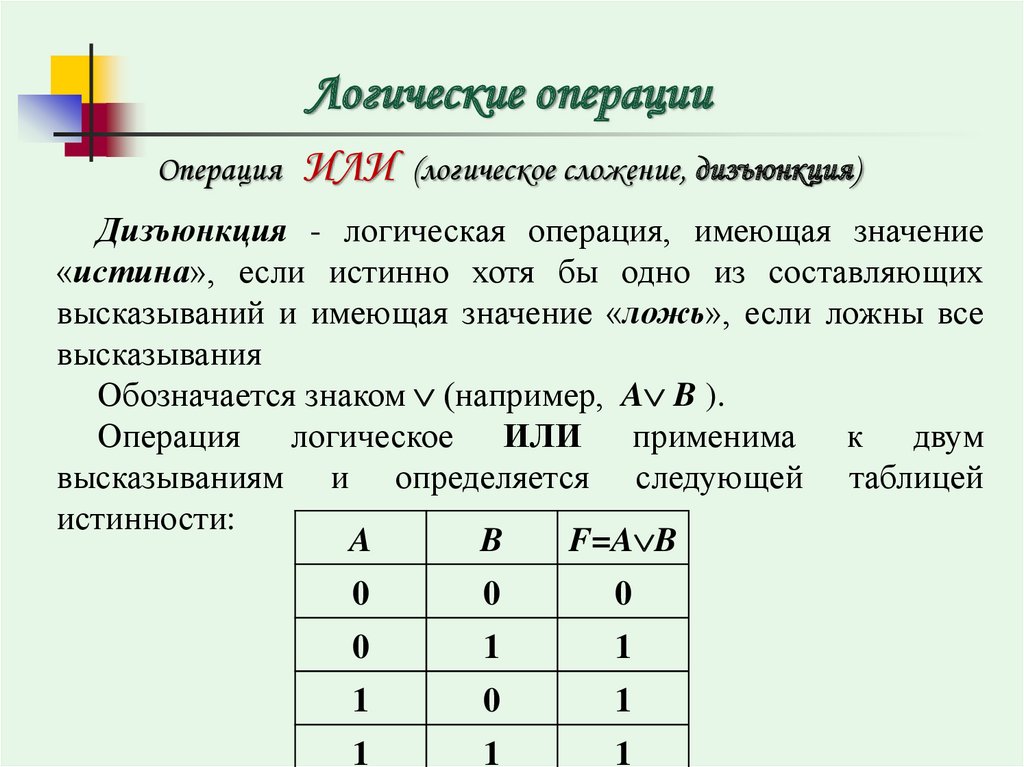 | (8 ÷ 4) ÷ 2 = 2 ÷ 2 = 1, но 8 ÷ (4 ÷ 2) = 8 ÷ 2 = 4. | U + 0028 U + 0029 | & # 40; & # 41; | ( ){\ Displaystyle (~)} () | |
| круглые скобки, скобки | |||||||
| Всюду | |||||||
⊢ | Удержание | x ⊢ y означает, что y доказуемо относительно x (в определенной формальной системе ). | A → B ⊢ ¬ B → ¬ A | U + 22A2 | & # 8866; | ⊢{\ displaystyle \ vdash} \ vdash | |
| доказуемо ( стопор ) | |||||||
| Логика высказываний , исчисление предикатов | |||||||
⊨ | Моделирование | x ⊨ y означает, что x семантически влечет y .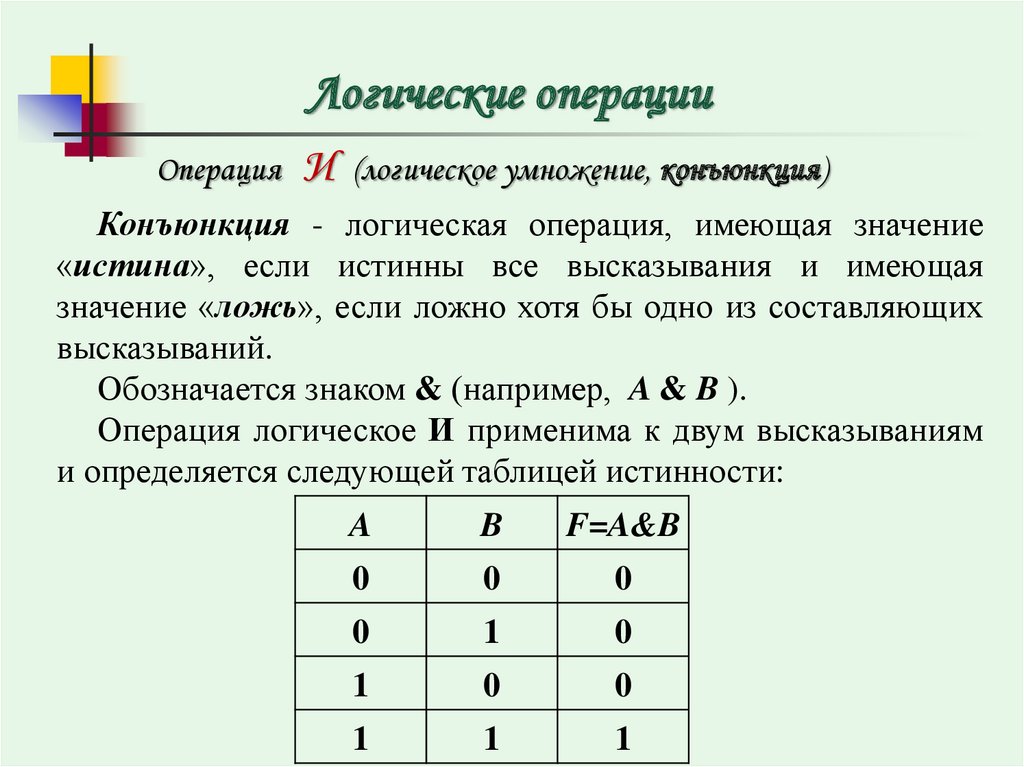 | A → B ⊨ ¬ B → ¬ A | U + 22A8 | & # 8872; | ⊨{\ displaystyle \ vDash} \ vDash | |
| Включает | |||||||
| Логика высказываний , исчисление предикатов |
Продвинутые и редко используемые логические символы
- Монеты Куайна
Статьи по Теме
- Юзеф Мария Бохенский
- Таблица математических символов
- Логический разъем
- Инфиксные, префиксные, польские и постфиксные обозначения
- Таблица истинности
- Логический квадрат
- Логический шестиугольник
Примечания и ссылки
Заметки
- (ru) Эта статья частично или полностью взята из статьи в англоязычной Википедии под названием « Список логических символов » ( см.
 список авторов ) .
список авторов ) .
Рекомендации
- ↑ (in) « Ссылки на именованные символы » в HTML 5.1 Nightly , W3C (по состоянию на 9 сентября 2015 г. )
- ↑ Этот персонаж доступен в LaTeX, но не в системе TeX от MediaWiki .
Типографские символы | |
|---|---|
| Пунктуация | Скобы ({}) · Круглые скобки (()) · шевроны (<> или <> или ⟨⟩) · Крючки ([]) · Половина крючки (⸢ ⸣ ⸤ ⸥) · кавычки ( «» или «» или » или «» или » или » » или ») · Апостроф (‘ или ‘) · запятая (,) · косая черта (/) · обратная косая черта (\) · косое пропускание (⸍ ⸌) · Пробел () · Точка () . · многоточие (… или …) · запятой (;) · двоеточие (:) · восклицательный знак ! () · восклицательный знак переворачивается (¡) · Точка Вопросительный знак ? () · Выброс знак вопроса (¿ ) · Восклицательный знак (‽) · Знак иронии (moins) · Коммерческий знак минус (⁒) · Дефис (- или -) · Дефис (- или — или -) · Другая пунктуация |
| Диакритический знак (от латинского алфавита ) | Акут (◌) · Двойной ударения (◌̋) · апостроф (◌) · Двойной апостроф (◌̏) · Каре (◌) · Caret подписался (◌̭) · Бар включен (◌̶) · Краткая (◌ ̆) · Обратный бриф (◌̑) · Подписанный бриф (◌̮) · Подписанный обратный бриф (◌̯) · Caron (◌̌) · Cédille (◌̧) · Рог (◌ ̛) · Крючок в голове (◌̉) · вертикальная линия (◌̍) · вертикальная линия , на которые подписан (◌̩) · Macron (◌̄) · Macron подписался (◌) · Огонек (◌̨) · Огонек suscrit (◌᷎) · Точка подписки (◌̣) · Точка suscrit (◌̇) · Главный раунд (◌̊) · Круглый подписался (◌̥) · Тильда (◌) · Тильда подписался (◌̰) · линия suscrit (◌̅) · Двойной Overline (◌̿) · черта подписываемый (◌) · Двойной функция подписываемый (◌̳) · Умляут (◌̈) · Умляут подписался (◌̤) · Умляут (◌̈) · разделенные по подписчикам (◌̦) · запятой верхний индекс (◌̓) |
| Типографский символ | Ampersand (&) · В знаке (@) · Звездочка (*) · Астеризм (⁂) · Вертикальная черта (| или |) · Пунктирного круг (◌) · Copyright (©) · Фонографические авторские права (℗) · Товарный знак (® или ?) · Товарный знак (™ или ?) · знак обслуживания (℠) · Флажок (✓) · Паук (#) · Пунктирные крест (⁜) · Референтная метка (※) · Степень (°) · Цельсия (° C) · Фаренгейта (° F) · Количество ( Et ) · и Tironian (icule) · Manicule (☞) · Obele († и ‡) · Prime: минута, второй и третий ( » » ‘) · Пункт (§) · Поэтому (∴ ) · из (∵) · пестрой-де-Муш (¶) · Midpoint (·) · Чип (•) · Подчеркивание (_) · Ведущий дефис (~) · Конец знак статьи (◼) · х бюллетеней для голосования (✘ ) · Пояснительный символ (ɔ 🙂 |
| Математический символ | Больше (+) · Меньше (-) · Плюс или минус (±) · Крест (x) или точка (⋅) умножения · Двоеточие (:) или Obelus (÷) деления · Равно (=) · Отличается от (≠ ) · Меньше или больше (<, ≤,>, ≥, ≮ и ≯) · приближение (≈) · дробная черта (/ или /) · процент (%) · до тысячи (‰) · Через десять миль (‱ ) · Квадрат , куб и экспонирование ( 2 3 . .. n ) · Радикал (√) · Интеграл (∫) · Сумма (Σ) · индексированный продукт (Π) · Микро (μ) · Вся партия (⌊ ⌋ ⌈ ⌉) .. n ) · Радикал (√) · Интеграл (∫) · Сумма (Σ) · индексированный продукт (Π) · Микро (μ) · Вся партия (⌊ ⌋ ⌈ ⌉) |
| Логический символ | И и или логическое (∧ ∨) · Экзистенциальные и универсальные кванторы (∃ ∀) · Отрицание (¬) · Пустое множество (∅) · Пересечение и объединение (∩ ∪) · Подмножество и надмножество (⊆ ⊇) · Принадлежность (∈ ∋) · Дополнительные (∁) · Монеты Куайн (⌜ ⌝ ⌞ ⌟) |
| Символ валюты | Валюта (¤) · Бат (฿) · Биткойн (₿) · Седи (₵) · Цент (¢) · Двоеточие (₡) · Доллар ($) · Донг (₫) · Драм (֏) · Евро (€) · Гуарани (₲) · гривна (₴) · Кип (₭) · Фунт стерлингов (£) · Турецкая лира (₺) · Азербайджанский манат (₼) · Найра (₦) · Филиппинское песо (₱) · Риель (៛) · Рубль Русский (₽) · Индийская рупия (₹) · Шекель (₪) · тенге (₸) · Тугрик (₮) · Вон (₩) · Йена или юань (¥) |
<img src=»https://fr. wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
Основы алгебры логики
8
3.2. Основы алгебры логики
В цифровых устройствах (сокращённо ЦУ) используются только два символа 0 и 1, поэтому алгебра логики использует логические переменные и функции от них, которые также принимают только два значения — 0 и 1. В логике символы 0 и 1 не цифры. Единица обозначает истину, символ 0 — ложь. Основы алгебры логики придумал в середине XIX века ирландский математик Джон Буль, поэтому алгебра логики иногда называется булева алгебра.
В
алгебре логики операции сложения и
умножения заменяют операцией логического
умножения,
которую называют конъюнкция,
и операцией логического
сложения (дизъюнкция).
Для обозначения операций сложения и
умножения используют специальные
символы: \/ — логическое сложение, /\ — логическое умножение, но для простоты
можно обозначать привычными «+» и
«х», «х» — это знак умножения.
Операция логического сложения обозначается союзом «ИЛИ«.
Выражение a + b означает «или a или b«. т. е. если и a, и b равно нулю, то и результат равен нулю. Результат равен единице, если хотя бы одна из переменных равна единице. Результат также будет единицей, если обе переменных равны единице.
Логическое умножение обозначается союзом «И».
Выражение a x b означает «a и b», т. е. если a и b равны нулю, то и результат равен нулю. Если одна из переменных равна единице, другая нулю, то результат все равно равен нулю. Результат равен единице, если обе переменных равны единице.
В двух словах: для логического сложения результат равен нулю только при совпадении нулей, для логического умножения результат равен единице только при совпадении единиц.
Есть
еще операция отрицания,
обозначаемое «НЕ«.
Обозначается отрицание чертой над
обозначением переменной или символом ¬,
стоящим перед переменной. Например, ā означает отрицание a.
По-другому это отрицание называется инверсией.
То есть, если a
= 1, то ā = 0 и наоборот. Отрицание может быть не
только одной переменной, но и целого
выражения.
Например, ā означает отрицание a.
По-другому это отрицание называется инверсией.
То есть, если a
= 1, то ā = 0 и наоборот. Отрицание может быть не
только одной переменной, но и целого
выражения.
Понятие двоичной переменной, логических операций И, ИЛИ, НЕ образуют систему аксиом алгебры логики.
Аналогично обычной алгебре, в булевой действительны свойства перестановки, сочетательности и распределительности:
a + b = b + a |
a x b = b x a |
a + (b + c) = (a + b) + c |
a x (b x c) = (a x b) x c |
a x (b + c) = a x b + a x c |
Помимо этих есть и другие, свойственные только алгебре логики, законы:
Законы одинарных элементов |
a x 1 = a |
a + 1 = 1 |
a x 0 = 0 |
a + 0 = a |
Законы отрицания (правила де Моргана) |
a x ā = 0 |
a + ā = 0 |
= ā + |
= ā + |
Распределительность дизъюнкции |
a + (b x c) = (a x b) + (a x c) |
Правила поглощения |
a + (a x b) = a |
a x (a + b) = a |
Эти
правила и законы позволяют упростить
логические уравнения и функции. Рассмотрим
логические элементы, реализующие
логические функции.
Рассмотрим
логические элементы, реализующие
логические функции.
Схема «И»
Изображение логического элемента «И» на схемах ЦУ:
Таблица истинности:
x2 | x1 | y |
0 | 0 | 0 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 1 |
Таблица
поясняет, как работает логический
элемент, т.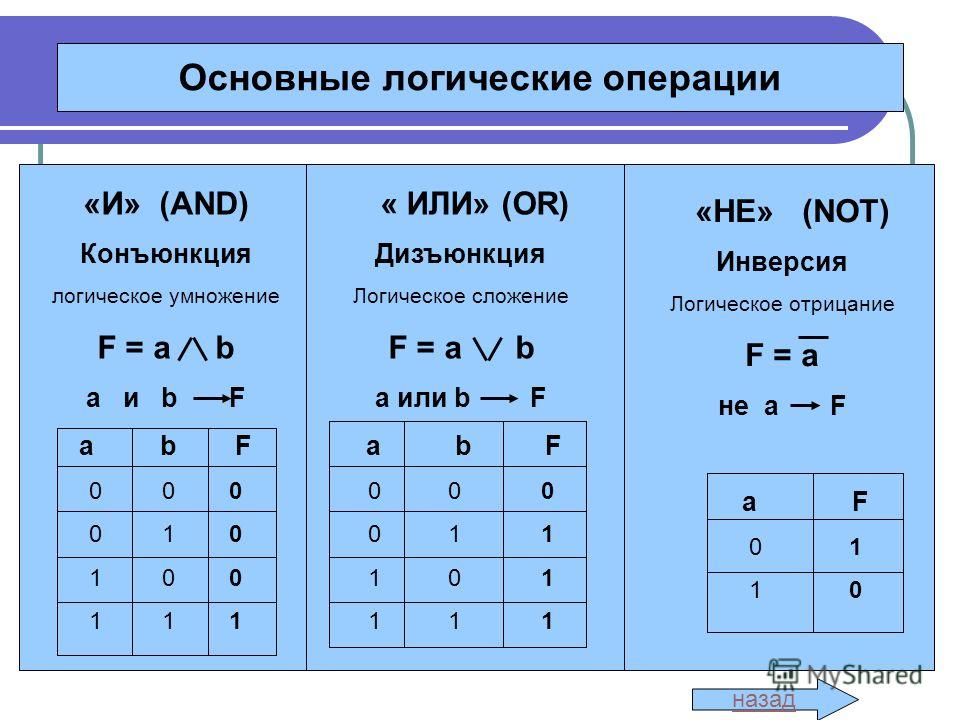 е. какой сигнал есть на его
выходе при определенных сигналах на
входе. Таблицы истинности присущи всем ЦУ.
В этой таблице символы x1 и
x2означают
входные сигналы, y —
выходные. Причем входы принято обозначать
слева (это касается любых устройств),
выходы — справа. Переменная х1 обозначает младший разряд, x2 —
старший. Судя по таблице, единица будет
на выходе только тогда, когда на обоих
входах будут единицы. Символ & говорит
о том, что это элемент «И».
е. какой сигнал есть на его
выходе при определенных сигналах на
входе. Таблицы истинности присущи всем ЦУ.
В этой таблице символы x1 и
x2означают
входные сигналы, y —
выходные. Причем входы принято обозначать
слева (это касается любых устройств),
выходы — справа. Переменная х1 обозначает младший разряд, x2 —
старший. Судя по таблице, единица будет
на выходе только тогда, когда на обоих
входах будут единицы. Символ & говорит
о том, что это элемент «И».
Схема «ИЛИ»
Изображение логического элемента «ИЛИ» на схемах ЦУ:
Таблица истинности:
x2
x1
y
0
0
0
0
1
1
1
0
1
1
1
1
То
есть, единица на выходе тогда, когда
хотя бы на одном из входов присутствует
единица. Символ 1 говорит
о том, что это элемент «ИЛИ«.
Символ 1 говорит
о том, что это элемент «ИЛИ«.
2курс Схема «НЕ»
Изображение логического элемента «НЕ», иначе инвертора:
Таблица истинности:
x | y |
0 | 1 |
1 | 0 |
Видно,
этот элемент проще всех. О том, что это
инвертор, говорит кружок на выходе
элемента. В электронике принято кружком
обозначать инверсию сигнала, т. е.
переворот фазы на 180 градусов. Вспомните
операционный усилитель (ОУ),
неинвертирующий вход как обычно,
инвертирующий с кружком, т. к. на выходе ОУ при
подаче сигнала на инвертирующий вход
сигнал переворачивается по фазе на 180
градусов, т. е. инвертируется.
е. инвертируется.
Теперь рассмотрим еще пару элементов, имеющих некоторые особенности.
Базисные элементы
Базисом называется совокупность элементов, с помощью которых схемотехнически можно реализовать устройство любой сложности. Простым языком базис — это те элементы, при помощи которых можно сделать любое устройство цифровой техники. Интересно, что этих базисных элементов всего 2.
Базис «И-НЕ»
И-НЕ — это схема И и схема НЕ, сложенные вместе. Операция, которую производит такой элемент называется инверсией логического умножения или отрицанием логического умножения, или инверсией конъюнкции и еще штрих Шеффера. Штрихом она называется потому, что в виде формулы операция И-НЕ записывается так: y = x1 | x2. Вертикальная черта между иксами и есть штрих.
Логический элемент И-НЕ на схемах ЦУ изображается так:
Таблица истинности:
x2 | x1 | y |
0 | 0 | 1 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 0 |
Сначала
как бы умножаем (логически), а потом все
это отрицаем (логически).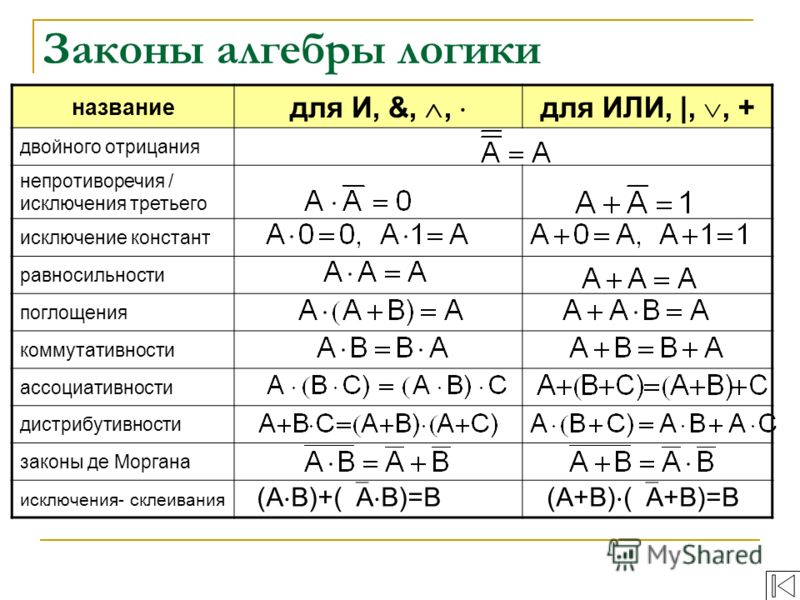 Если к элементу И (см.
выше) прицепить на выход инвертор, то
получим такой вот элемент И-НЕ.
Ну и если к элементу И-НЕ прицепить на выход инвертор, то получим
элемент И.
Если у элемента И-НЕ замкнуть входы, то получится тот самый
инвертор.
Если к элементу И (см.
выше) прицепить на выход инвертор, то
получим такой вот элемент И-НЕ.
Ну и если к элементу И-НЕ прицепить на выход инвертор, то получим
элемент И.
Если у элемента И-НЕ замкнуть входы, то получится тот самый
инвертор.
Базис ИЛИ-НЕ
Здесь все по аналогии с элементом И-НЕ. Операция, выполняемая элементом ИЛИ-НЕ, называется инверсией логического сложения или инверсией дизъюнкции и еще стрелка Пирса. Стрелка потому, что в виде формулы функция записывается так: y = x 1↓ x2. Символ между иксами и есть стрелка Пирса.
Логический элемент ИЛИ-НЕ на схемах ЦУ изображается так:
Таблица истинности:
x2 | x1 | y |
0 | 0 | 1 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 0 |
Аналогично,
если к выходу элемента ИЛИ-НЕ прицепить инвертор, то получится элемент ИЛИ.
Существуют и другие элементы. Они представляют собой комбинацию перечисленных.
Рассмотрим Элемент “ИСКЛЮЧАЮЩЕЕ-ИЛИ”
Операция, выполняемая таким элементом, называется сложение по модулю два и обозначается плюсом в кружочке, т. е. символом . В виде уравнения функция записывается так: X1X2. Читается это, как «либо икс один, либо икс два».
Изображение элемента ИСКЛЮЧАЮЩЕЕ-ИЛИ на схемах ЦУ:
Таблица истинности:
x2 | x1 | y |
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 0 |
Этот элемент можно заменить логическими элементами И, ИЛИ, НЕ, так как
Для
иллюстрации составим схему этой функции
из базисных элементов.
Таким образом, зная свойства цифровых устройств и основы булевой алгебры, любой логический элемент можно заменить другими логическими элементами. Этот метод имеет и обратное направление. Если в какой-то схеме стоит изображенная на нашем рисунке её часть, в виде подсхемы, она легко заменяется на один элемент ИСКЛЮЧАЮЩЕЕ-ИЛИ. Следуя этому принципу можно менять элементную базу проектируемого цифрового устройства. Главное, чтобы в этом был смысл, чтобы улучшались характеристики устройства – функциональные или конструктивные, производственные или экономические.
Булева алгебра (булевы выражения, правила, теоремы и примеры)
Булева алгебра — это категория алгебры, в которой значения переменных являются значениями истинности, истинными и ложными, обычно обозначаются 1 и 0 соответственно. Он используется для анализа и упрощения цифровых схем или цифровых вентилей. Его также называют Bi nary Algebra или логической алгеброй . Он был основополагающим при разработке цифровой электроники и предусмотрен во всех современных языках программирования. Он также используется в теории множеств и статистике.
Он был основополагающим при разработке цифровой электроники и предусмотрен во всех современных языках программирования. Он также используется в теории множеств и статистике.
Важными операциями, выполняемыми в булевой алгебре, являются – конъюнкция (∧), дизъюнкция (∨) и отрицание (¬) . Следовательно, эта алгебра сильно отличается от элементарной алгебры, где значения переменных являются числовыми, а над ними выполняются арифметические операции, такие как сложение, вычитание.
Содержание:
- Операции
- Терминология
- Таблица истинности
- Правила
- Законы
- Теоремы
- Пример
- Часто задаваемые вопросы
Булевы алгебраические операции
Основные операции булевой алгебры следующие:
- Соединение или операция И
- Дизъюнкция или операция ИЛИ
- Отрицание или не операция
Ниже приведена таблица, определяющая символы для всех трех основных операций.
| Оператор | Символ | Приоритет |
| НЕ | ‘ (или) ¬ | Самый высокий |
| И | . (или) ∧ | Средний |
| ИЛИ | + (или) ∨ | Самый низкий |
Предположим, что A и B — две логические переменные, тогда мы можем определить три операции как;
- Соединение B или A AND B удовлетворяет условию A ∧ B = True, если A = B = True или в противном случае A ∧ B = False.
- Дизъюнкция B или A OR B удовлетворяет условию A ∨ B = False, если A = B = False, иначе A ∨ B = True.
- Отрицание A или ¬A удовлетворяет ¬A = False, если A = True, и ¬A = True, если A = False
Логическое выражение
Логический оператор, результатом которого является логическое значение, будь то True или False, является логическим выражением. Иногда для выражения утверждения используются синонимы, такие как «да» для «верно» и «нет» для «ложно». Кроме того, 1 и 0 используются для цифровых цепей для True и False соответственно.
Иногда для выражения утверждения используются синонимы, такие как «да» для «верно» и «нет» для «ложно». Кроме того, 1 и 0 используются для цифровых цепей для True и False соответственно.
Логические выражения — это операторы, в которых используются логические операторы, т. е. AND, OR, XOR и NOT. Таким образом, если мы напишем X AND Y = True, то это логическое выражение.
Терминология булевой алгебры
Теперь давайте обсудим важные термины, используемые в булевой алгебре.
Булева алгебра : Булева алгебра — это раздел алгебры, который имеет дело с логическими операциями и бинарными переменными.
Логические переменные: Булева переменная определяется как переменная или символ, определяемый как переменная или символ, как правило, алфавит, представляющий логические величины, такие как 0 или 1.
Булева функция: Булева функция состоит из двоичных переменных, логических операторов, констант, таких как 0 и 1, равных оператору, и символов скобок.
Литерал: Литерал может быть переменной или дополнением переменной.
Дополнение : Дополнение определяется как инверсия переменной, которая представлена чертой над переменной.
Таблица истинности: Таблица истинности — это таблица, которая дает все возможные значения логических переменных и комбинации переменных. Можно преобразовать логическое уравнение в таблицу истинности. Количество строк в таблице истинности должно быть равно 2 n , где «n» — количество переменных в уравнении. Например, если логическое уравнение состоит из 3 переменных, то число строк в таблице истинности равно 8. (т.е.) 2 3 = 8.
Таблица истинности булевой алгебры
Теперь, если мы представим вышеуказанные операции в виде таблицы истинности, мы получим;
| А | Б | А ∧ В | А ∨ В |
| Правда | Правда | Правда | Правда |
| Правда | Ложь | Ложь | Правда |
| Ложь | Правда | Ложь | Правда |
| Ложь | Ложь | Ложь | Ложь |
| А | ¬А |
| Правда | Ложь |
| Ложь | Правда |
Правила булевой алгебры
Ниже приведены важные правила, используемые в булевой алгебре.
- Используемая переменная может иметь только два значения. Двоичный 1 для HIGH и двоичный 0 для LOW.
- Дополнение переменной представлено чертой сверху.
\(\begin{array}{l} Таким образом,\ дополнение\ к\ переменной\ B\ представляется\ в виде\ \bar{B}.\ Таким образом\ если\ B = 0\ then\ \bar{B} =1\ и\ B\ = 1\ тогда\ \bar{B}= 0.\end{массив} \)
- Операция ИЛИ над переменными представлена знаком плюс (+) между ними. Например, ИЛИ-соединение A, B и C представлено как A + B + C.
- Логическая операция И двух или более переменных представлена точкой между ними, например, A.B.C. Иногда точка может быть опущена, как ABC.
Законы булевой алгебры
Существует шесть типов законов булевой алгебры. Они:
- Коммунативное право
- Ассоциативный закон
- Распределительный закон
- И закон
- ИЛИ закон
- Закон инверсии
Эти шесть законов подробно объясняются здесь.
Коммунативное право
Любая бинарная операция, удовлетворяющая следующему выражению, называется коммутативной операцией. Коммутативный закон гласит, что изменение последовательности переменных не влияет на выход логической схемы.
- А. В = В. А
- А + В = В + А
Ассоциативный закон
Указывает, что порядок, в котором выполняются логические операции, не имеет значения, поскольку их эффект одинаков.
- (А. Б). С = А . ( Б . В )
- (А + В) + С = А + (В + С)
Распределительное право
Распределительный закон устанавливает следующие условия:
- А. (В + С) = (А. В) + (А. С)
- А + (В. С) = (А + В) . (А+С)
И Закон
В этих законах используется операция И. Поэтому они называются законами И.
ИЛИ Закон
В этих законах используется операция ИЛИ. Поэтому они называются законами ИЛИ.
Закон об инверсии
В булевой алгебре закон обращения гласит, что двойное обращение переменной приводит к самой исходной переменной.
Теоремы булевой алгебры
Две важные теоремы, которые широко используются в булевой алгебре, — это первый закон де Моргана и второй закон де Моргана. Эти две теоремы используются для изменения логического выражения. Эта теорема в основном помогает привести данное логическое выражение к упрощенной форме. Эти два закона Де Моргана используются для преобразования выражения из одной формы в другую. Теперь давайте подробно обсудим эти две теоремы.
Первый закон Де Моргана:
Первый закон Де Моргана гласит, что (A.B)’ = A’+B’.
Первый закон гласит, что дополнение произведения переменных равно сумме их индивидуальных дополнений переменной.
Таблица истинности, показывающая проверку Первого закона Де Моргана, имеет следующий вид:
А | Б | А’ | Б’ | (А.Б)’ | А’+В’ |
0 | 0 | 1 | 1 | 1 | 1 |
0 | 1 | 1 | 0 | 1 | 1 |
1 | 0 | 0 | 1 | 1 | 1 |
1 | 1 | 0 | 0 | 0 | 0 |
Последние два столбца показывают, что (A. B)’ = A’+B’.
B)’ = A’+B’.
Таким образом, Первый закон Де Моргана доказан.
Второй закон Де Моргана:
Второй закон Де Моргана гласит, что (А+В)’ = А’. Б’.
Второй закон гласит, что дополнение суммы переменных равно произведению их индивидуальных дополнений переменной.
Следующая таблица истинности показывает доказательство второго закона Де Моргана.
| А | Б | А’ | Б’ | (А+В)’ | А’. Б’ |
| 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 |
Последние два столбца показывают, что (A+B)’ = A’. Б’.
Б’.
Таким образом, второй закон Де Моргана доказан.
Другими теоремами булевой алгебры являются дополнительная теорема, теорема двойственности, теорема о перестановке, теорема об избыточности и так далее. Все эти теоремы используются для упрощения данного булева выражения. Сокращенное логическое выражение должно быть эквивалентно заданному логическому выражению.
Решенные примеры
Вопрос: Упростите следующее выражение:
\(\begin{array}{l}c+\bar{BC}\end{array} \)
Решение:
Дано:
\(\begin{array}{l}C+\bar{BC}\end{array} \)
Согласно закону Деморгана, мы можем записать приведенные выше выражения как
\(\begin{array}{l}C+(\bar{B}+ \bar{C})\end{array} \)
Из коммуникативного права:
\(\begin{массив}{l}(C+\bar{C})+ \bar{B}\end{массив} \)
Из дополнения к закону
\(\begin{array}{l}1+ \bar{B} = 1\end{array} \)
Следовательно,
\(\begin{array}{l}C+\bar{BC} = 1\end{array} \)
Вопрос 2: Нарисуйте таблицу истинности для A(B+D).
Решение: задано выражение A(B+D).
| А | Б | Д | Б+Д | А(Б+Г) |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Следите за новостями с BYJU’S — обучающим приложением, а также смотрите другие видео.
Часто задаваемые вопросы по булевой алгебре
Что понимается под булевой алгеброй?
Булева алгебра в математике называется логической алгеброй, состоящей из двоичных переменных, принимающих значения 0 или 1, и логических операций.
Каковы некоторые приложения булевой алгебры?
В электрических и электронных схемах булева алгебра используется для упрощения и анализа логических или цифровых схем.
Каковы три основных логических оператора?
Три важных логических оператора:
И (соединение)
ИЛИ (дизъюнкция)
НЕ (отрицание)
Является ли значение 0 истинным или ложным?
В булевой логике ноль (0) представляет ложь, а единица (1) — истину. Во многих приложениях ноль интерпретируется как ложь, а ненулевое значение интерпретируется как истина.
Назовите шесть важных законов булевой алгебры.
Шесть важных законов булевой алгебры:
Коммутативный закон
Ассоциативный закон
Распределительный закон
Закон обращения
И закон
ИЛИ закон
Логические символы — Citizendium
- Содержание этой страницы создано в Википедии и еще не было значительно улучшено.
 Авторам предлагается заменить и добавить материал, чтобы сделать эту статью оригинальной.
Авторам предлагается заменить и добавить материал, чтобы сделать эту статью оригинальной.
В логике базовый набор из логических символов используется как сокращение для логических конструкций. Поскольку эти символы часто считаются знакомыми, они не всегда объясняются. Для удобства в следующей таблице перечислены некоторые распространенные символы вместе с их названиями, произношением и соответствующими областями математики. Кроме того, в третьем столбце содержится неформальное определение, а в четвертом столбце приведен краткий пример.
Имейте в виду, что вне логики разные символы имеют одно и то же значение, а один и тот же символ имеет, в зависимости от контекста, разные значения.
| Примечание : Эта статья содержит логические символы. Без надлежащей поддержки рендеринга вы можете увидеть вопросительные знаки, прямоугольники или другие символы вместо логических символов. |
Символ | Имя | Пояснение | Примеры | Юникод Значение | HTML Сущность | LaTeX символ |
|---|---|---|---|---|---|---|
| Следует читать как | ||||||
| Категория | ||||||
| материальное значение | А ⇒ В означает, что если А верно, то В также верно; если A ложно, то о B ничего не говорится. → может означать то же, что и ⇒ (символ может также указывать домен и домен функции; см. таблицу математических символов). ⊃ может означать то же, что и ⇒ (символ может также означать надмножество). | x = 2 ⇒ x 2 = 4 верно, но x 2 = 4 ⇒ x = 2 в общем случае может быть 6 x 9072 ложно (поскольку 6 x 9072 может быть -1). | U+21D2 U+2192 U+2283 | ⇒ → &up; | ⇒ {\ displaystyle \ Rightarrow} \ Rightarrow | |
| подразумевает; если .. то | ||||||
| логика высказываний, алгебра Гейтинга | ||||||
| эквивалент материала | A ⇔ B означает, что A истинно тогда и только тогда, когда B истинно. | x + 5 = y +2 ⇔ x + 3 = y | U+21D4 U+2261 U+2194 | ⇔ &эквивалент; ↔ | ⇔ {\ displaystyle \ Leftrightarrow} \ Leftrightarrow | |
| тогда и только тогда, когда; если | ||||||
| пропозициональная логика | ||||||
| отрицание | Утверждение ¬ A истинно тогда и только тогда, когда A ложно. Косая черта, помещенная через другой оператор, аналогична «¬», помещенной впереди. | ¬(¬ А ) ⇔ А x ≠ y ⇔ ¬( x = y ) | U+00AC U+02DC | &нет; &тильда; ~ | ¬{\ displaystyle \ lnot} \ lnot | |
| нет | ||||||
| пропозициональная логика | ||||||
| логическое соединение | Утверждение A ∧ B истинно, если A и B оба истинны; иначе это ложь. | n < 4 ∧ n >2 ⇔ n = 3, когда n — натуральное число. | и+2227 и+0026 | &и; &ампер; | ∧ {\ Displaystyle \ клин} \ клин или \ земля \ & [1] | |
| и | ||||||
| пропозициональная логика | ||||||
| логическая дизъюнкция | Утверждение A ∨ B верно, если A или B (или оба) верны; если оба ложны, утверждение ложно. | n ≥ 4 ∨ n ≤ 2 ⇔ n ≠ 3, когда n — натуральное число. | U+2228 | &или; | ∨{\ Displaystyle \ лор} \ лор | |
| или | ||||||
| пропозициональная логика | ||||||
| | исключительная дизъюнкция | Выписка A ⊕ B истинно, когда истинны либо A, либо B, но не оба. A ⊻ B означает то же самое. A ⊻ B означает то же самое. | (¬ A ) ⊕ A всегда верно, A ⊕ A всегда ложно. | U+2295 U+22BB | + | ⊕ {\ displaystyle \ oplus} \ oplus ⊻ {\ displaystyle \ veebar} \ veebar |
| хор | ||||||
| логика высказываний, булева алгебра | ||||||
| | Тавтология | Утверждение ⊤ безусловно истинно. | A ⇒ ⊤ всегда верно. | У+22А4 | Т | ⊤ {\ displaystyle \ top} \ top |
| верх | ||||||
| логика высказываний, булева алгебра | ||||||
| | Противоречие | Утверждение ⊥ безусловно ложно. | ⊥ ⇒ Число всегда верно. | У+22А5 | % Ф | ⊥{\ Displaystyle \ бот} \ бот |
| снизу | ||||||
| логика высказываний, булева алгебра | ||||||
∀ | универсальный количественный анализ | ∀ x : P ( x ) означает P ( x ) верно для всех x . | ∀ n ∈ N : n 2 ≥ н . | U+2200 | ∀ | ∀{\ displaystyle \ forall} \ forall |
| для всех; для любого; для каждого | ||||||
| логика предикатов | ||||||
∃ | экзистенциальная квантификация | ∃ x : P ( x ) означает, что существует хотя бы одно x такое, что P ( x ) истинно. | ∃ n ∈ N : n четно. | U+2203 | &существует; | ∃ {\ Displaystyle \ существует} \ существует |
| существует | ||||||
| логика первого порядка | ||||||
∃! | количественная оценка уникальности | ∃! x : P ( x ) означает, что существует ровно одно x такое, что P ( x ) истинно. | ∃! n ∈ N : n + 5 = 2 n . | U+2203 U+0021 | &существует; ! | ∃! {\ Displaystyle \ существует!} \ существует! |
| существует ровно один | ||||||
| логика первого порядка | ||||||
| определение | x := y или x ≡ y означает, что x определяется как другое имя для y (но обратите внимание, что ≡ может также означать и другие вещи, например конгруэнтность). P :⇔ Q означает, что P определен как логически эквивалентный Q . | COSH x : = (1/2) (exp x + exp ( — x )) A XOR B : ⇔ A a B ). ∧ Б ) | U+2254 (U+003A U+003D) U+2261 U+003A U+229C | := : &эквивалент; ⇔ | : = {\ Displaystyle: =}: = | |
| определяется как | ||||||
| везде | ||||||
( ) | приоритет группировки | Сначала выполните операции внутри скобок. | (8/4)/2 = 2/2 = 1, но 8/(4/2) = 8/2 = 4. | U+0028 U+0029 | ( ) | ( ) {\ Displaystyle (~)} ( ) |
| везде | ||||||
⊢ | вывод | x ⊢ y означает, что y получено из x . |


 список авторов ) .
список авторов ) .