Физика. Механика
Рассмотрим абсолютно неупругий удар двух шаров одинаковой массы, сделанных из пластилина. Если эти шары летят друг на друга с одной и той же скоростью, то при соударении они прилипнут друг к другу и остановятся. В этом случае суммарный импульс обоих шаров остался равным нулю, хотя состояние системы изменилось. Шары при этом нагрелись. Этот пример показывает, что импульс не всегда может служить мерой движения. Такой мерой является энергия. В данном случае механическая энергия при ударе перешла в другой вид энергии (тепловую).
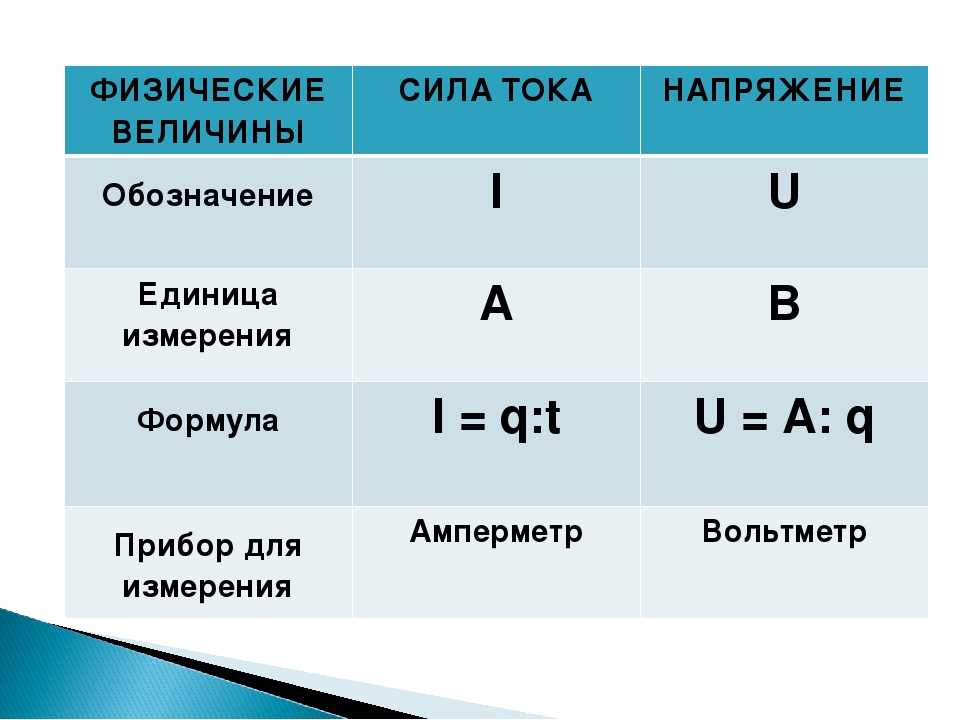
Сначала рассмотрим важную характеристику — работу. Пусть материальная точка движется по траектории AB (рис. 1). На точку во время движения действует в общем случае переменная сила F. На участке ds (настолько малом, что модуль перемещения равен пройденному пути) силу F можно считать постоянной.
Рис 4.1. Элементарная работа
Элементарная работа силы равна скалярному произведению вектора силы на вектор перемещения её точки приложения
Работа — скалярная величина, ее знак зависит от знака . Положительная работа совершается силой, если ее направление составляет острый угол с направлением движения тела. Отрицательная работа совершается силой, направление которой составляет тупой угол с направлением движения, при этом сила тормозит это движение. Величина
Положительная работа совершается силой, если ее направление составляет острый угол с направлением движения тела. Отрицательная работа совершается силой, направление которой составляет тупой угол с направлением движения, при этом сила тормозит это движение. Величина
— это проекция силы F на направление перемещения. Следовательно,
Полная работа силы находится как сумма (интеграл) элементарных работ по всей траектории L точки:
При перемещении вдоль оси x работу графически можно представить как площадь под кривой Fx(x) (рис. 4.2), причем площади под осью абсцисс следует приписывать отрицательное значение.
Рис. 2. Графическая интерпретация работы силы. Здесь для краткости положено F = Fx(x)
Если перемещение ортогонально силе, то = 0 и работа равна нулю:
Последнее показывает, что понятие работы в механике отлично от обыденного представления о работе. Так, при перемещении груза с постоянной скоростью в горизонтальном направлении сила тяжести не совершает работы. Работа не совершается также и тогда, когда тело покоится, так как точка приложения силы не перемещается и = 0. Здесь и ниже и означают одно и то же — бесконечно малое перемещение, а ||=||= — соответствующий бесконечно малый путь.
Так, при перемещении груза с постоянной скоростью в горизонтальном направлении сила тяжести не совершает работы. Работа не совершается также и тогда, когда тело покоится, так как точка приложения силы не перемещается и = 0. Здесь и ниже и означают одно и то же — бесконечно малое перемещение, а ||=||= — соответствующий бесконечно малый путь.
Если на тело действует несколько сил, то
то есть работа результирующей нескольких сил равна алгебраической сумме работ, совершаемых каждой из сил в отдельности.
Рассмотрим для примера работу, совершаемую внешней силой по сжатию и растяжению пружины с жесткостью . Направим ось 0x вдоль пружины, причем за начало координат 0 выберем положение свободного конца пружины, находящейся в ненагруженном состоянии. Процесс сжатия/растяжения представляем как последовательность равновесных состояний: в каждый момент времени прилагаем внешнюю силу, равную по величине силе упругости со стороны пружины. Тогда согласно закону Гука
где x — удлинение пружины.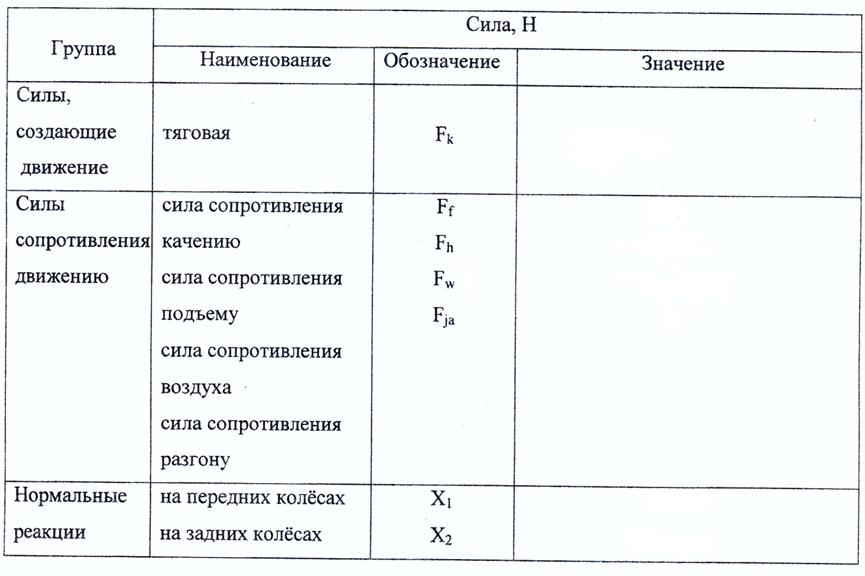 При положительных x (растяжение пружины) внешняя cила направлена направо, при отрицательных (сжатие) — налево (рис. 4.3).
При положительных x (растяжение пружины) внешняя cила направлена направо, при отрицательных (сжатие) — налево (рис. 4.3).
Рис. 4.3. Работа, совершаемая при сжатии/растяжении пружины
Скалярное произведение для элементарной работы внешней силы имеет в этом случае вид
так что для полной работы упругой деформации пружины получаем
Заметим, что A не зависит от знака x: и при растяжении, и при сжатии пружины внешняя сила совершает одну и ту же положительную работу.
Дополнительная информация
http://www.plib.ru/library/book/17833.html – Хайкин С.Э. Физические основы механики, Наука, 1971 г.– стр. 476–479 (§ 111): выведено выражение для потенциальной энергии упруго деформированного тела.
Статика — Физика — Теория, тесты, формулы и задачи
Оглавление:
- Основные теоретические сведения
- Основы статики
- Момент силы. Правило моментов
- Рычаги и блоки
- Центр тяжести тела
Основы статики
К оглавлению. ..
..
Статикой называется раздел механики, изучающий условия равновесия тел. Равновесием называют такое состояние тела или системы тел, в котором оно не движется в данной системе отсчета. Различают три вида равновесия:
- Устойчивое равновесие. Если систему вывести из состояния устойчивого равновесия, то она самопроизвольно в него вернется, то есть при выведении из положения равновесия возникает сила, возвращающая систему к равновесию. Для этого необходимо, чтобы потенциальная энергия системы в состоянии устойчивого равновесия имела минимальное значение. Любая физическая система стремится к состоянию устойчивого равновесия. Это значит, что любой самопроизвольный процесс всегда проходит с уменьшением потенциальной энергии.
- Неустойчивое равновесие. В данном случае при выведении из состояния равновесия возникают силы, уводящие систему от равновесия, и система самопроизвольно не может в него вернуться.
 В состоянии неустойчивого равновесия потенциальная энергия системы имеет максимальное значение.
В состоянии неустойчивого равновесия потенциальная энергия системы имеет максимальное значение. - Безразличное равновесие. При выведении из состояния равновесия в системе не возникает ни возвращающих, ни уводящих в сторону сил.
Из второго закона Ньютона следует, что если геометрическая сумма всех внешних сил, приложенных к невращающемуся телу, равна нулю, то тело находится в состоянии покоя или совершает равномерное прямолинейное движение (действительно, ведь ускорение тела при этом равно нулю). В этом случае принято говорить, что силы, приложенные к телу, уравновешивают друг друга. При вычислении равнодействующей силы все силы, действующие на тело, можно прикладывать к центру масс. Центр масс (или центр тяжести) – точка к которой приложена сила тяжести, действующая на тело.
Чтобы невращающееся тело находилось в равновесии, необходимо, чтобы равнодействующая всех сил, приложенных к телу, была равна нулю.
Момент силы.
 Правило моментов
Правило моментовК оглавлению…
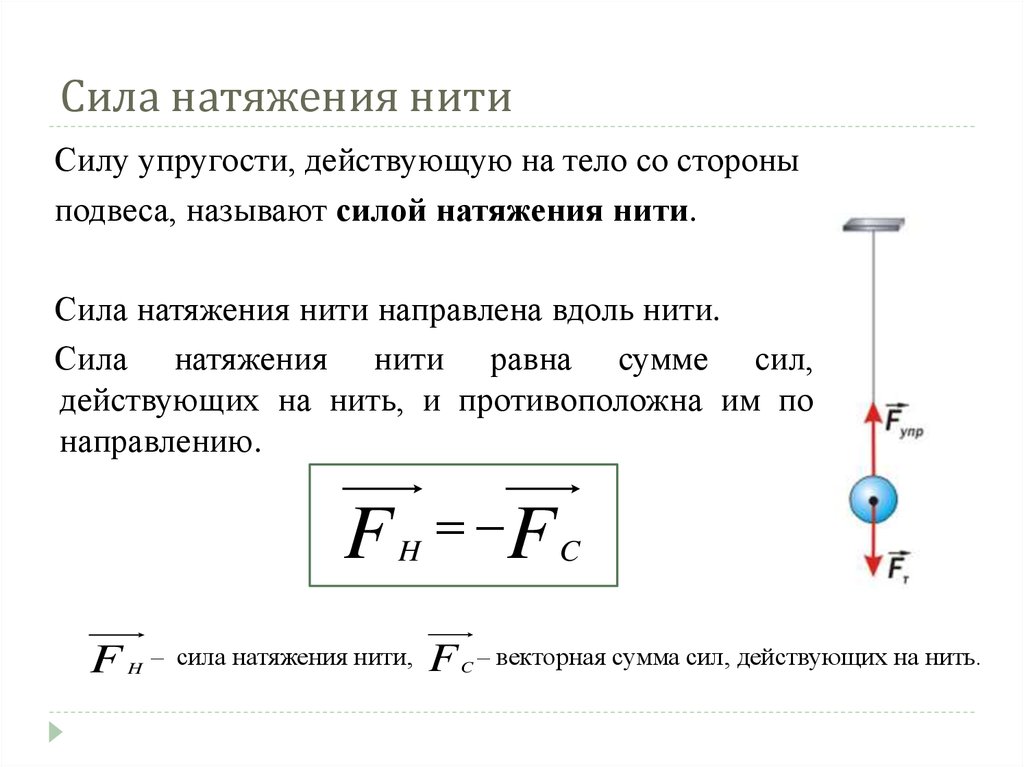
Если тело может вращаться относительно некоторой оси, то для его равновесия недостаточно равенства нулю равнодействующей всех сил. Вращающее действие силы зависит не только от ее величины, но и от расстояния между линией действия силы и осью вращения. Длина перпендикуляра, проведенного от оси вращения до линии действия силы, называется плечом силы.
Для описания причин вызывающих вращения и условия равновесия тела в статике вводится новое понятие — момент силы. Произведение модуля силы
Обычно в физике используется следующее правило знаков: если сила поворачивает тело по часовой стрелке, то ее момент считается положительным, а если против – то отрицательным. Момент силы может и равняться нулю, если сила проходит (сама или продолжением) через ось. Обратите внимание: если Вы перепутаете, и возьмете знаки моментов наоборот (по часовой стрелке со знаком минус, а против часовой со знаком плюс), то ничего страшного не произойдет.
Обратите внимание, что момент силы зависит не только от величины силы, но и от ее плеча. Следовательно, одно и то же значение момента можно получить двумя способами: взять большую силу и малое плечо или взять малую силу и большое плечо. Вывод: чем больше плечо, тем меньшую силу необходимо прилагать для получения одного и того же результата.
Правило моментов: тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю:
При записи этого условия в ходе решения конкретной задачи по статике моменты сил необходимо записывать с учётом их знаков. В Международной системе единиц (СИ) моменты сил измеряются в ньютоно-метрах (Н∙м).
Обратите внимание: в общем случае, когда тело может двигаться поступательно и вращаться, для равновесия необходимо выполнение обоих условий: равенство нулю равнодействующей силы и равенство нулю суммы всех моментов.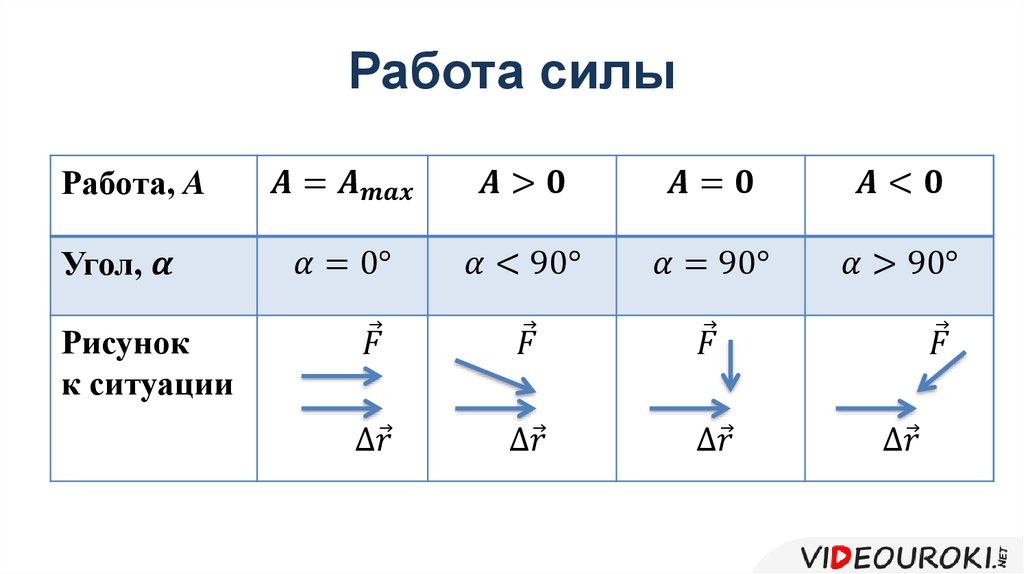
Алгоритм решения задач на правило моментов (задач по статике):
- Нарисовать рисунок. Следует помнить, что сила тяжести, действующая на тело изображается один раз. Если же в задаче идет речь об изломанной палочке, то удобнее рисовать отдельно силы тяжести, действующие на каждую часть палочки, считая массы частей пропорциональными их длинам. В отличие от динамики, где силы изображаются из одной точки, в статике важно точно указать точку приложения силы.
- Выбрать ось вращения в точке приложения самой ненужной в задаче силы или сил (той силы, которую определять не надо и не хочется из-за природного чувства лени). При этом плечо (и, следовательно, момент) этой силы обратится в нуль независимо от ее величины, и в дальнейших вычислениях эту силу можно не учитывать совсем.
- Записать правило моментов относительно данной оси, на забывая про правило знаков.
- При необходимости записать также условие согласно которому равнодействующая сила равна нолю.

- Выразить искомую силу.
Рычаги и блоки
К оглавлению…
Как вы знаете из практики, иногда необходимо изменить направление силы, увеличить или уменьшить ее величину. Этой цели служат простые механизмы: устройства, преобразующие величину или направление силы с помощью механических явлений. Для всех простых механизмов справедливо золотое правило механики: выиграл в силе – проиграл в перемещении (или наоборот)
- Равноплечий рычаг (весы). Рычаг, ось вращения которого проходит через его геометрический центр.
- Неравноплечий рычаг. Рычаг ось вращения которого проходит через произвольную точку.
- Неподвижный блок. Это диск с закрепленной осью, через который переброшена нить.
 Неподвижный блок используется для изменения направления приложения силы. Если трение в блоке отсутствует, нить невесома, то сила ее натяжения до и после блока не изменяется. Таким образом, неподвижный блок не дает ни выигрыша в силе, ни проигрыша в перемещении.
Неподвижный блок используется для изменения направления приложения силы. Если трение в блоке отсутствует, нить невесома, то сила ее натяжения до и после блока не изменяется. Таким образом, неподвижный блок не дает ни выигрыша в силе, ни проигрыша в перемещении. - Подвижный блок. Это диск, ось которого может двигаться поступательно. Подвижный блок позволяет уменьшить силу в два раза, одновременно с этим вдвое увеличивая перемещение.
- Наклонная плоскость. Это устройство применяется для поднятия тяжестей. При достаточно малых значениях угла наклона и небольшом коэффициенте трения сила, которую необходимо приложить чтобы поднимать некоторое тело вдоль наклонной плоскости может быть значительно меньше веса тела. Таким образом, подъем становится легче. Естественно, при этом в полном соответствии с «золотым правилом» увеличивается перемещение тела.
Центр тяжести тела
К оглавлению…
Центр масс (или центр тяжести) – точка к которой приложена сила тяжести, действующая на тело. В общем случае центр тяжести может и не лежать внутри тела, а выходить за его пределы (например, различные изогнутые длинные предметы, кольца, полукольца и так далее).
В общем случае центр тяжести может и не лежать внутри тела, а выходить за его пределы (например, различные изогнутые длинные предметы, кольца, полукольца и так далее).
Рассмотрим основные методы определения положения центра масс тел для некоторых конкретных случаев, возникающих при решении задач по статике:
1. У однородных тел правильной формы (шары, прямоугольники, стержни) центр тяжести совпадает с геометрическим центром. Следует запомнить, что центр тяжести однородной треугольной пластины лежит в точке пересечения ее медиан. Для однородных симметричных тел центр тяжести всегда расположен на оси симметрии.
2. Определение положения центра тяжести системы из двух тел с известными центрами тяжести. Здесь можно использовать замечательное свойство центра тяжести. Подперев центр тяжести, мы обеспечим равновесие тела. Таким образом, центр тяжести системы из двух тел лежит на отрезке, соединяющем их центры тяжести, и делит его в отношении, обратном отношению масс тел:
где: l1 – расстояние от центра масс до тела с массой m1, а l2 – до тела с массой m2.
3. Определение положения центра тяжести любой системы тел с известными положениями центров тяжести. Необходимо ввести систему координат (естественно, начало координат выбрать в точке, относительно которой необходимо рассчитать положение центра тяжести), определить в ней координаты центров тяжести всех тел и найти координаты центра тяжести системы по формуле:
Аналогичные уравнения получаются для остальных координатных осей, если таковые необходимо рассматривать в задаче (просто переменная x меняется на y или z соответственно).
4. Однородное тело правильной формы с вырезом правильной формы. Проще всего свести задачу к обратной: мысленно вставить вырез обратно и получить тело правильной формы с известным положением центра тяжести. Далее представить его в виде двух тел: страшного с вырезом и самого выреза. А теперь все просто. У одного из тел (выреза) мы знаем положения центра тяжести. У другого – нет. Зато знаем положение центра тяжести системы двух тел. Составив уравнение для определения общего центра тяжести получим выражение с одной неизвестной – центром тяжести тела с вырезом. Решив уравнение получим искомый ответ.
Составив уравнение для определения общего центра тяжести получим выражение с одной неизвестной – центром тяжести тела с вырезом. Решив уравнение получим искомый ответ.
5. Теорема Паппа. Применяется для определения положения центра тяжести плоской пластины, которая при вращении вокруг некоторой оси образует тело с легко вычисляемым объемом. Необходимо мысленно повернуть пластину на один оборот, нарисовать рисунок и применить теорему:
Формулировка теоремы: объем тела, полученного при вращении пластины, равен произведению ее площади на путь, пройденный центром тяжести при вращении:
Прочность материалов. Основы и уравнения
В механике материалов прочность материала — это его способность выдерживать приложенную нагрузку без разрушения или пластической деформации. Прочность материалов учитывает взаимосвязь между внешними нагрузками , приложенными к материалу, и результирующей деформацией или изменением размеров материала. При проектировании конструкций и машин важно учитывать эти факторы, чтобы выбранный материал имел достаточную прочность, чтобы противостоять приложенным нагрузкам или силам и сохранять свою первоначальную форму. Прочность материала – это его способность выдерживать приложенную нагрузку без разрушения или пластической деформации.
При проектировании конструкций и машин важно учитывать эти факторы, чтобы выбранный материал имел достаточную прочность, чтобы противостоять приложенным нагрузкам или силам и сохранять свою первоначальную форму. Прочность материала – это его способность выдерживать приложенную нагрузку без разрушения или пластической деформации.
Однако следует отметить, что нагрузка, которая деформирует небольшой компонент, будет меньше, чем нагрузка, деформирующая более крупный компонент из того же материала. Поэтому нагрузка (усилие) не является подходящим термином для силы . Вместо этого мы можем использовать силу (нагрузку) на единицу площади (σ = F/A), называемую напряжением , которая постоянна (пока не произойдет деформация) для данного материала независимо от размера составной части. В этой концепции 9Деформация 0003 также является очень важной переменной, поскольку она определяет деформацию объекта. Таким образом, механическое поведение твердых тел обычно определяется определяющими соотношениями напряжения и деформации. Деформация называется упругой деформацией, если напряжение является линейной функцией деформации. Другими словами, напряжение и напряжение подчиняются закону Гука . За пределами линейной области напряжение и деформация демонстрируют нелинейное поведение. Это неупругое поведение называется пластической деформацией.
Таким образом, механическое поведение твердых тел обычно определяется определяющими соотношениями напряжения и деформации. Деформация называется упругой деформацией, если напряжение является линейной функцией деформации. Другими словами, напряжение и напряжение подчиняются закону Гука . За пределами линейной области напряжение и деформация демонстрируют нелинейное поведение. Это неупругое поведение называется пластической деформацией.
Напряжение
В механике и материаловедении напряжение (обозначается строчной греческой буквой сигма – σ ) является физической величиной, выражающей внутренние силы, которые соседние частицы сплошного материала действуют друг на друга. В то же время деформация является мерой деформации материала, которая не является физической величиной.
Хотя невозможно измерить интенсивность этого напряжения, можно измерить внешнюю нагрузку и площадь, к которой она приложена. Напряжение (σ) можно приравнять к нагрузке на единицу площади или силе (F), приложенной к площади поперечного сечения (A) перпендикулярно силе, как:
Когда металл подвергается нагрузке (силе ), он искажается или деформируется, независимо от того, насколько прочный металл или легкая нагрузка.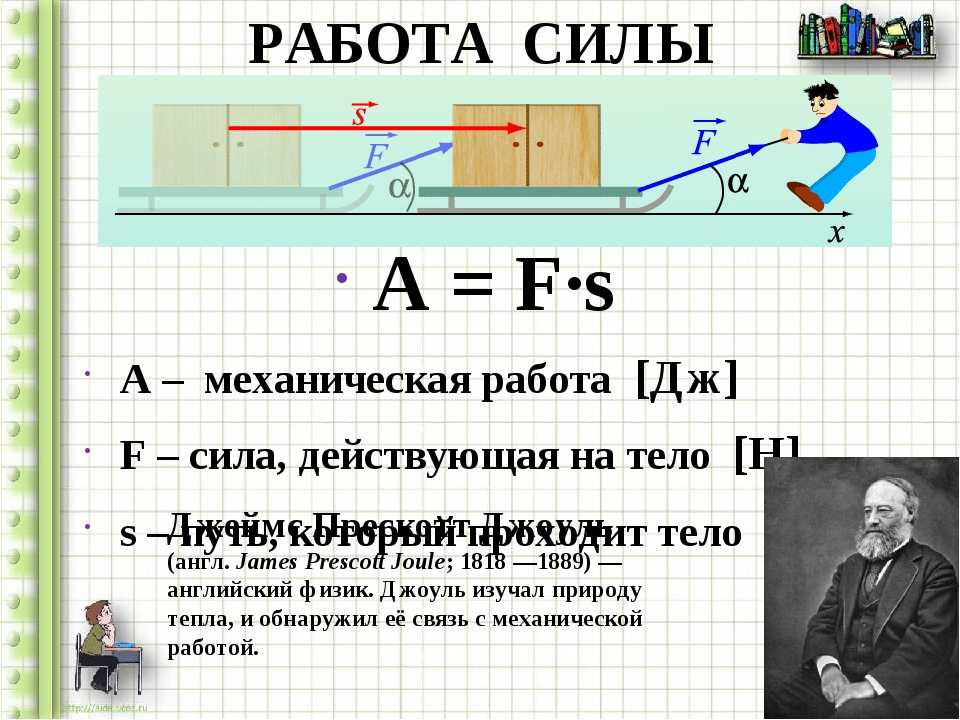 Если нагрузка мала, искажение, вероятно, исчезнет при снятии нагрузки. Интенсивность или степень искажения известна как деформация . Деформация называется упругая деформация , если напряжение является линейной функцией деформации. Другими словами, напряжение и напряжение подчиняются закону Гука . За пределами линейной области напряжение и деформация демонстрируют нелинейное поведение. Это неупругое поведение называется пластической деформацией .
Если нагрузка мала, искажение, вероятно, исчезнет при снятии нагрузки. Интенсивность или степень искажения известна как деформация . Деформация называется упругая деформация , если напряжение является линейной функцией деформации. Другими словами, напряжение и напряжение подчиняются закону Гука . За пределами линейной области напряжение и деформация демонстрируют нелинейное поведение. Это неупругое поведение называется пластической деформацией .
Напряжение – это внутреннее сопротивление или противодействующая сила материала искажающему воздействию внешней силы или нагрузки. Эти противодействующие силы стремятся вернуть атомы в их нормальное положение. Полное развиваемое сопротивление равно внешней нагрузке.
Типы напряжений
Напряжения возникают в любом материале, подверженном нагрузке или приложенной силе. Существует много видов напряжения , но все они могут быть в целом классифицированы в одну из шести категорий:
- Структурные напряжения — это напряжения, возникающие в элементах конструкции из-за веса, который они поддерживают.
 Веса обеспечивают нагрузки. Эти напряжения возникают в фундаментах и каркасах зданий, а также в деталях машин.
Веса обеспечивают нагрузки. Эти напряжения возникают в фундаментах и каркасах зданий, а также в деталях машин. - Остаточные напряжения – это напряжения, вызванные производственными процессами. Этот тип напряжения остается в твердом материале после устранения первоначальной причины напряжения. Например, сварка оставляет остаточные напряжения в свариваемых металлах. Тепло от сварки может вызвать локальное расширение, которое во время сварки поглощается либо расплавленным металлом, либо размещением свариваемых деталей.
- Напряжения давления представляют собой напряжения, возникающие в сосудах, содержащих материалы под давлением, и нагрузка создается той же силой, что и давление. Корпус реактора является ярким примером корпуса высокого давления в реакторной установке. Одной из проблем безопасности, которая является долгосрочной проблемой, вызванной старением ядерных установок, является тепловой удар под давлением (PTS) . PTS — это удар, испытываемый толстостенным сосудом из-за комбинированных напряжений от быстрого изменения температуры и/или давления.

- Термические напряжения существуют всякий раз, когда в материале присутствуют температурные градиенты, а разные температуры вызывают разные расширения и подвергают материалы внутренним напряжениям. Этот вид напряжения особенно заметен в механизмах, работающих при высоких температурах, охлаждаемых холодной жидкостью. Одной из проблем безопасности, которая является долгосрочной проблемой, вызванной старением ядерных установок, является тепловой удар под давлением (PTS). PTS — это удар, испытываемый толстостенным сосудом из-за комбинированных напряжений от быстрого изменения температуры и/или давления.
- Напряжения течения возникают, когда масса текущей жидкости создает динамическое давление на стенку трубопровода. Сила удара жидкости о стенку действует как нагрузка. Этот тип напряжения может применяться нестационарным образом, когда скорость потока колеблется. Гидравлический удар является примером переходного напряжения потока. Гидравлический удар в трубе или трубе — это скачок давления, вызванный внезапным изменением скорости потока.
 И энергия скорости преобразуется в энергию давления.
И энергия скорости преобразуется в энергию давления. - Усталостные напряжения. Усталость — это ослабление материала, вызванное циклическим нагружением, которое приводит к прогрессирующему и локальному структурному повреждению и росту трещин. Как только трещина образовалась, каждый цикл нагрузки будет увеличивать трещину на небольшую величину. Напряжения могут быть вызваны вибрацией или термоциклированием.
Приложенное напряжение
С внутренней точки зрения интенсивность напряжения в теле компонента выражается одним из трех основных типов внутренней нагрузки: растяжение, сжатие и сдвиг . В инженерной практике многие нагрузки являются скручивающими, а не чисто сдвиговыми. Математически существует только два типа внутренней нагрузки, потому что растягивающее и сжимающее напряжение можно рассматривать как положительную и отрицательную версии одного и того же типа нормальной нагрузки.
- Напряжение растяжения .
 Одно из наиболее распространенных механических испытаний на растяжение проводится на растяжение. Растягивающее напряжение — это такой тип напряжения, при котором два участка материала по обе стороны от плоскости напряжения стремятся разойтись или удлиниться. Способность материала или конструкции выдерживать нагрузки, имеющие тенденцию к удлинению, известна как 9.0003 предел прочности при растяжении (UTS) . Предел прочности на растяжение измеряется максимальным напряжением, которое материал может выдержать при растяжении или растяжении до разрыва. При изучении прочности материалов прочность на растяжение, прочность на сжатие и прочность на сдвиг можно анализировать независимо друг от друга. Поскольку растягивающие и сжимающие нагрузки создают напряжения, действующие поперек плоскости в направлении, перпендикулярном (нормальном) к плоскости, растягивающие и сжимающие напряжения называются нормальными напряжениями .
Одно из наиболее распространенных механических испытаний на растяжение проводится на растяжение. Растягивающее напряжение — это такой тип напряжения, при котором два участка материала по обе стороны от плоскости напряжения стремятся разойтись или удлиниться. Способность материала или конструкции выдерживать нагрузки, имеющие тенденцию к удлинению, известна как 9.0003 предел прочности при растяжении (UTS) . Предел прочности на растяжение измеряется максимальным напряжением, которое материал может выдержать при растяжении или растяжении до разрыва. При изучении прочности материалов прочность на растяжение, прочность на сжатие и прочность на сдвиг можно анализировать независимо друг от друга. Поскольку растягивающие и сжимающие нагрузки создают напряжения, действующие поперек плоскости в направлении, перпендикулярном (нормальном) к плоскости, растягивающие и сжимающие напряжения называются нормальными напряжениями . - Напряжение сжатия . Напряжение сжатия является противоположностью напряжения растяжения.
 Соседние части материала имеют тенденцию прижиматься друг к другу через типичную плоскость напряжения. Напряжение сжатия стержней, колонн и т. д. приводит к их укорочению. Напряжение сжатия определяется аналогично напряжению растяжения, но имеет отрицательные значения для выражения сжатия, поскольку дельта L имеет противоположное направление. Можно увеличивать сжимающее напряжение до тех пор, пока не будет достигнута прочность на сжатие. Тогда материалы будут реагировать с пластичным поведением или с разрушением в случае хрупких материалов. Поскольку растягивающие и сжимающие нагрузки создают напряжения, действующие поперек плоскости в направлении, перпендикулярном (нормальном) к плоскости, растягивающие и сжимающие напряжения называются 9.0019 нормальные напряжения . Способность материала реагировать на сжимающее напряжение или давление называется сжимаемостью.
Соседние части материала имеют тенденцию прижиматься друг к другу через типичную плоскость напряжения. Напряжение сжатия стержней, колонн и т. д. приводит к их укорочению. Напряжение сжатия определяется аналогично напряжению растяжения, но имеет отрицательные значения для выражения сжатия, поскольку дельта L имеет противоположное направление. Можно увеличивать сжимающее напряжение до тех пор, пока не будет достигнута прочность на сжатие. Тогда материалы будут реагировать с пластичным поведением или с разрушением в случае хрупких материалов. Поскольку растягивающие и сжимающие нагрузки создают напряжения, действующие поперек плоскости в направлении, перпендикулярном (нормальном) к плоскости, растягивающие и сжимающие напряжения называются 9.0019 нормальные напряжения . Способность материала реагировать на сжимающее напряжение или давление называется сжимаемостью. - Напряжение сдвига . Напряжение сдвига возникает, когда две части материала стремятся скользить друг по другу в любой типичной плоскости сдвига при приложении силы, параллельной этой плоскости.
 Кручение — это разновидность чистого сдвига, при котором элемент конструкции скручивается. Силы кручения производят вращательное движение вокруг продольной оси одного конца элемента относительно другого. Напряжение сдвига также имеет большое значение в природе, тесно связанное с движением земных материалов вниз по склону (как в случае лавин).
Кручение — это разновидность чистого сдвига, при котором элемент конструкции скручивается. Силы кручения производят вращательное движение вокруг продольной оси одного конца элемента относительно другого. Напряжение сдвига также имеет большое значение в природе, тесно связанное с движением земных материалов вниз по склону (как в случае лавин).
Деформация
В материаловедении деформация также является очень важной переменной, поскольку она определяет деформацию объекта. В отличие от напряжения в объекте, которое вы не можете увидеть, деформация является видимой и измеримой величиной. Когда вы тянете натяжной стержень, вы можете видеть, что стержень физически увеличивается в длину (или удлиняется). Когда вы сгибаете балку, вы видите, что она изгибается. Деформации являются прямым показателем напряжения. Механическое поведение твердых тел обычно определяется определяющими отношения напряжение-деформация. Когда металл подвергается нагрузке (силе), он искажается или деформируется, независимо от того, насколько прочный металл или легкая нагрузка. Если нагрузка мала, искажение, вероятно, исчезнет при снятии нагрузки. Такое пропорциональное размерное изменение (интенсивность или степень искажения) называется деформацией . Из-за приложенного напряжения оно измеряется как общая деформация (удлинение) материала на опорную длину.
Если нагрузка мала, искажение, вероятно, исчезнет при снятии нагрузки. Такое пропорциональное размерное изменение (интенсивность или степень искажения) называется деформацией . Из-за приложенного напряжения оно измеряется как общая деформация (удлинение) материала на опорную длину.
В механике материалов мы можем определить два основных типа деформации:
- Нормальные штаммы . Нормальная деформация является результатом растягивающего напряжения и представляет собой деформацию, вычисленную по относительным смещениям, измеренным перпендикулярно двум опорным плоскостям. Нормальные деформации измеряют относительное перпендикулярное перемещение одной базовой плоскости относительно другой. Символом нормальной деформации обычно является строчный греческий символ эпсилон (ε).
- Деформации сдвига. Деформация сдвига является результатом напряжения сдвига и представляет собой деформацию, вычисленную по относительным смещениям, измеренным параллельно двум опорным плоскостям.
 Деформации сдвига измеряют относительное параллельное движение одной базовой плоскости относительно другой. Символ деформации сдвига обычно представляет собой строчную греческую букву гамма (γ).
Деформации сдвига измеряют относительное параллельное движение одной базовой плоскости относительно другой. Символ деформации сдвига обычно представляет собой строчную греческую букву гамма (γ).
Деформация
Деформация измеряет, насколько объект деформируется по сравнению с его первоначальными размерами или размером в заданном направлении. В зависимости от того, какую деформацию вы измеряете, вы можете рассчитать различные типы деформации.
Деформация называется упругой деформацией, если напряжение является линейной функцией деформации. Другими словами, напряжение и напряжение подчиняются закону Гука . За пределами линейной области напряжение и деформация проявляют нелинейное поведение, и это неупругое поведение называется пластической деформацией.
- Упругая деформация . Упругая деформация и Упругая деформация представляет собой временное изменение размеров, которое существует только во время приложения начального напряжения и исчезает сразу после снятия напряжения.
 Когда металл подвергается нагрузке (силе), он искажается или деформируется, независимо от того, насколько прочный металл или легкая нагрузка. Эта деформация может быть, а может и не быть постоянной. До предельного напряжения тело сможет восстановить свои размеры при снятии нагрузки. Приложенные напряжения заставляют атомы в кристалле перемещаться из своего равновесного положения, и все атомы смещаются на одинаковую величину и по-прежнему сохраняют свою относительную геометрию. Когда напряжения снимаются, все атомы возвращаются в исходное положение, и никакой остаточной деформации не происходит.
Когда металл подвергается нагрузке (силе), он искажается или деформируется, независимо от того, насколько прочный металл или легкая нагрузка. Эта деформация может быть, а может и не быть постоянной. До предельного напряжения тело сможет восстановить свои размеры при снятии нагрузки. Приложенные напряжения заставляют атомы в кристалле перемещаться из своего равновесного положения, и все атомы смещаются на одинаковую величину и по-прежнему сохраняют свою относительную геометрию. Когда напряжения снимаются, все атомы возвращаются в исходное положение, и никакой остаточной деформации не происходит. - Пластическая деформация. Пластическая деформация и Пластическая деформация представляет собой изменение размеров, которое не исчезает при снятии исходного напряжения. Если предельная нагрузка превышена, тело будет испытывать остаточные деформации при снятии нагрузки. Пластическая деформация возникает в материальных телах после того, как напряжения достигают порогового значения, известного как предел упругости или предел текучести , и является результатом скольжения или механизмов дислокации на атомном уровне.

Кривая напряжения-деформации
Прочность материалов рассматривает взаимосвязь между внешними нагрузками , приложенными к материалу, и результирующей деформацией или изменением размеров материала. При проектировании конструкций и машин важно учитывать эти факторы, чтобы выбранный материал имел достаточную прочность, чтобы противостоять приложенным нагрузкам или силам и сохранять свою первоначальную форму. Прочность материала – это его способность выдерживать приложенную нагрузку без разрушения или пластической деформации.
Однако следует отметить, что нагрузка, которая деформирует небольшой компонент, будет меньше, чем нагрузка, деформирующая более крупный компонент из того же материала. Поэтому нагрузка (усилие) не является подходящим термином для силы . Вместо этого мы можем использовать силу (нагрузку) на единицу площади (σ = F/A), называемую напряжением , которая постоянна (пока не произойдет деформация) для данного материала независимо от размера составной части.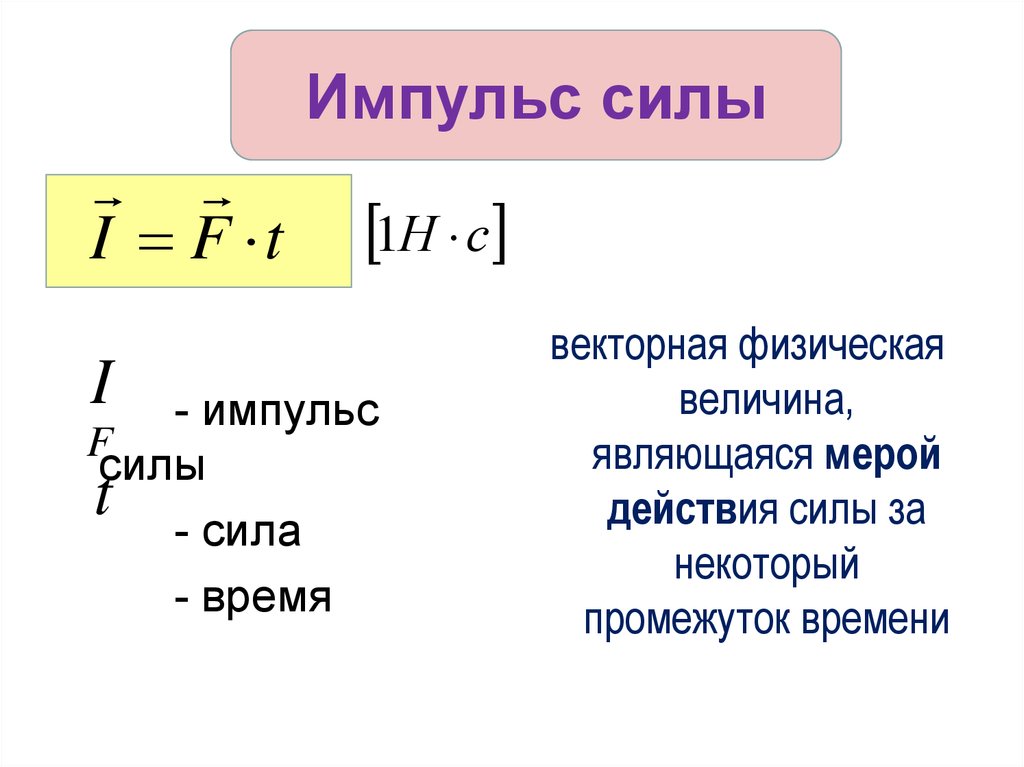 В этой концепции 9Деформация 0003 также является очень важной переменной, поскольку она определяет деформацию объекта. Таким образом, механическое поведение твердых тел обычно определяется определяющими соотношениями напряжения и деформации. Деформация называется упругой деформацией, если напряжение является линейной функцией деформации. Другими словами, напряжение и напряжение подчиняются закону Гука . За пределами линейной области напряжение и деформация демонстрируют нелинейное поведение. Это неупругое поведение называется пластической деформацией.
В этой концепции 9Деформация 0003 также является очень важной переменной, поскольку она определяет деформацию объекта. Таким образом, механическое поведение твердых тел обычно определяется определяющими соотношениями напряжения и деформации. Деформация называется упругой деформацией, если напряжение является линейной функцией деформации. Другими словами, напряжение и напряжение подчиняются закону Гука . За пределами линейной области напряжение и деформация демонстрируют нелинейное поведение. Это неупругое поведение называется пластической деформацией.
Схематическая диаграмма кривой напряжения-деформации для низкоуглеродистой стали при комнатной температуре показана на рисунке. Несколько стадий демонстрируют разное поведение, что предполагает разные механические свойства. Материалы могут пропускать одну или несколько стадий, показанных на рисунке, или иметь разные стадии, которые необходимо уточнить. В этом случае приходится различать напряженно-деформированные характеристики пластичных и хрупких материалов.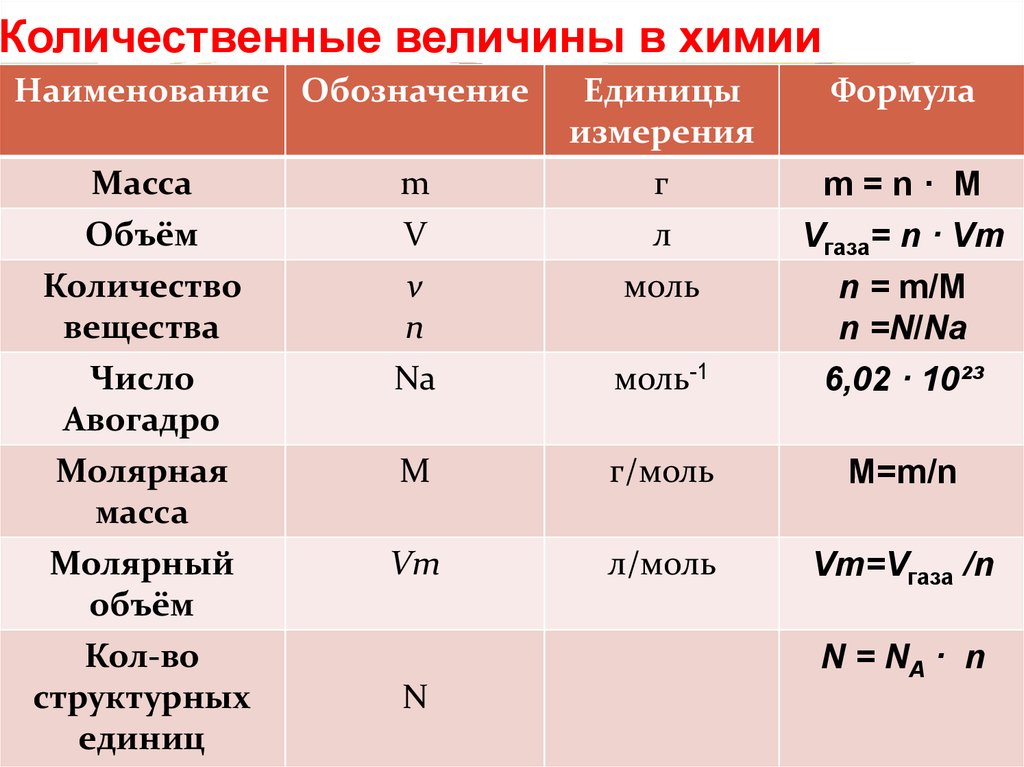 Следующие пункты описывают различные области кривой напряжения-деформации и важность нескольких конкретных мест.
Следующие пункты описывают различные области кривой напряжения-деформации и важность нескольких конкретных мест.
- Пропорциональный предел . Пропорциональный предел соответствует расположению напряжения в конце линейного участка , поэтому график напряжения-деформации представляет собой прямую линию, а градиент будет равен модулю упругости материала. Для напряжения растяжения и сжатия наклон части кривой, где напряжение пропорционально деформации, называется модулем Юнга , и применяется закон Гука . Между пропорциональным пределом и пределом текучести закон Гука становится сомнительным, и деформация возрастает быстрее.
- Предел текучести . Предел текучести — это точка на кривой напряжения-деформации, которая указывает предел упругого поведения и начало пластического поведения. Предел текучести или предел текучести — это свойство материала, определяемое как напряжение, при котором материал начинает пластически деформироваться.
 Напротив, предел текучести — это место, где начинается нелинейная (упругая + пластическая) деформация. Перед пределом текучести материал упруго деформируется и возвращается к своей первоначальной форме после снятия приложенного напряжения. Как только предел текучести пройден, некоторая часть деформации будет постоянной и необратимой. Некоторые стали и другие материалы демонстрируют явление, называемое явлением предела текучести. Пределы текучести варьируются от 35 МПа для низкопрочного алюминия до более 1400 МПа для высокопрочной стали.
Напротив, предел текучести — это место, где начинается нелинейная (упругая + пластическая) деформация. Перед пределом текучести материал упруго деформируется и возвращается к своей первоначальной форме после снятия приложенного напряжения. Как только предел текучести пройден, некоторая часть деформации будет постоянной и необратимой. Некоторые стали и другие материалы демонстрируют явление, называемое явлением предела текучести. Пределы текучести варьируются от 35 МПа для низкопрочного алюминия до более 1400 МПа для высокопрочной стали. - Предел прочности при растяжении . Предел прочности при растяжении является максимальным на инженерной кривой напряжения-деформации. Это соответствует максимальному напряжению , выдерживаемому растянутой конструкцией. Предельная прочность на растяжение часто сокращается до «предельной прочности» или «предела прочности». Если это напряжение применяется и поддерживается, в результате произойдет перелом.
 Часто это значение значительно превышает предел текучести (на 50–60 % превышает предел текучести для некоторых типов металлов). Когда пластичный материал достигает предела прочности, он испытывает сужение, когда площадь поперечного сечения локально уменьшается. Кривая напряжение-деформация не содержит более высокого напряжения, чем предел прочности. Несмотря на то, что деформации могут продолжать увеличиваться, напряжение обычно уменьшается после достижения предела прочности. Это интенсивное свойство; поэтому его значение не зависит от размера испытуемого образца. Однако это зависит от других факторов, таких как подготовка образца, наличие или отсутствие поверхностных дефектов, температура тестовой среды и материала. Предел прочности при растяжении варьируется от 50 МПа для алюминия до 3000 МПа для очень высокопрочной стали.
Часто это значение значительно превышает предел текучести (на 50–60 % превышает предел текучести для некоторых типов металлов). Когда пластичный материал достигает предела прочности, он испытывает сужение, когда площадь поперечного сечения локально уменьшается. Кривая напряжение-деформация не содержит более высокого напряжения, чем предел прочности. Несмотря на то, что деформации могут продолжать увеличиваться, напряжение обычно уменьшается после достижения предела прочности. Это интенсивное свойство; поэтому его значение не зависит от размера испытуемого образца. Однако это зависит от других факторов, таких как подготовка образца, наличие или отсутствие поверхностных дефектов, температура тестовой среды и материала. Предел прочности при растяжении варьируется от 50 МПа для алюминия до 3000 МПа для очень высокопрочной стали. - Точка излома : Точка излома — это точка деформации, в которой материал физически разделяется.
 В этот момент деформация достигает своего максимального значения, и материал разрушается, хотя соответствующее напряжение может быть меньше предела прочности в этот момент. Пластичные материалы имеют предел прочности на излом ниже, чем предел прочности при растяжении (UTS), тогда как в хрупких материалах предел прочности при изломе эквивалентен пределу прочности при растяжении (UTS). Если пластичный материал достигает своего предела прочности при растяжении в ситуации с регулируемой нагрузкой, он будет продолжать деформироваться без приложения дополнительной нагрузки, пока не разорвется. Однако, если нагрузка контролируется по смещению, деформация материала может уменьшить нагрузку, предотвращая разрыв.
В этот момент деформация достигает своего максимального значения, и материал разрушается, хотя соответствующее напряжение может быть меньше предела прочности в этот момент. Пластичные материалы имеют предел прочности на излом ниже, чем предел прочности при растяжении (UTS), тогда как в хрупких материалах предел прочности при изломе эквивалентен пределу прочности при растяжении (UTS). Если пластичный материал достигает своего предела прочности при растяжении в ситуации с регулируемой нагрузкой, он будет продолжать деформироваться без приложения дополнительной нагрузки, пока не разорвется. Однако, если нагрузка контролируется по смещению, деформация материала может уменьшить нагрузку, предотвращая разрыв.
Во многих случаях предел текучести используется для определения допустимого напряжения, которому может подвергаться материал. Этот критерий не подходит для компонентов, которые должны выдерживать высокие давления, например, используемые в водо-водяных реакторах (PWR). Теория максимального напряжения сдвига отказа была включена в Кодекс ASME (Американское общество инженеров-механиков) по котлам и сосудам под давлением, раздел III, Правила строительства ядерных сосудов под давлением, чтобы охватить эти ситуации. Эта теория утверждает, что отказ компонента трубопровода происходит, когда максимальное напряжение сдвига превышает напряжение сдвига в пределе текучести при испытании на растяжение.
Эта теория утверждает, что отказ компонента трубопровода происходит, когда максимальное напряжение сдвига превышает напряжение сдвига в пределе текучести при испытании на растяжение.
Вязкость и хрупкость – Кривые напряжения-деформации
Некоторые материалы ломаются очень резко, без пластической деформации, при хрупком разрушении. Другие, более пластичные, включая большинство металлов, испытывают некоторую пластическую деформацию и, возможно, образование шейки перед разрушением. Среди кривых растяжения различных групп материалов можно выделить некоторые общие характеристики. На этом основании можно разделить материалы на две широкие категории; а именно:
- Пластичные материалы . Пластичность — это способность материала удлиняться при растяжении. Пластичный материал будет деформироваться (удлиняться) больше, чем хрупкий материал. Пластичные материалы демонстрируют большую деформацию перед разрушением. При вязком разрушении перед разрушением происходит обширная пластическая деформация (образование шейки).
 Вязкое разрушение (разрушение при сдвиге) лучше, чем хрупкое разрушение, потому что перед разрушением происходит медленное распространение и поглощение большого количества энергии. Пластичность желательна при высоких температурах и высоких давлениях в реакторных установках из-за дополнительных нагрузок на металлы. Высокая пластичность в этих применениях помогает предотвратить хрупкое разрушение.
Вязкое разрушение (разрушение при сдвиге) лучше, чем хрупкое разрушение, потому что перед разрушением происходит медленное распространение и поглощение большого количества энергии. Пластичность желательна при высоких температурах и высоких давлениях в реакторных установках из-за дополнительных нагрузок на металлы. Высокая пластичность в этих применениях помогает предотвратить хрупкое разрушение. - Хрупкие материалы . Под действием напряжения хрупкие материалы разрушаются с небольшой упругой деформацией и без значительной пластической деформации. Хрупкие материалы поглощают относительно мало энергии перед разрушением, даже высокопрочные материалы. При хрупком разрушении (транскристаллитный скол) перед разрушением не происходит видимой пластической деформации, и трещины быстро распространяются.
На следующем рисунке показана типичная кривая напряжения-деформации пластичных и хрупких материалов. Пластичный материал — это материал с небольшой прочностью, а область пластичности велика. Материал будет выдерживать большую нагрузку (деформацию) перед разрушением. Хрупкий материал — это материал, в котором пластическая область мала, а прочность материала высока. Испытание на растяжение дает три описательных факта о материале. Это напряжение, при котором начинается наблюдаемая пластическая деформация или «податливость»; предел прочности при растяжении или максимальная интенсивность нагрузки, которую можно выдержать при растяжении; и процентное удлинение или деформация (насколько материал будет растягиваться) и сопутствующее процентное уменьшение площади поперечного сечения, вызванное растяжением. Также можно определить место разрыва или перелома.
Материал будет выдерживать большую нагрузку (деформацию) перед разрушением. Хрупкий материал — это материал, в котором пластическая область мала, а прочность материала высока. Испытание на растяжение дает три описательных факта о материале. Это напряжение, при котором начинается наблюдаемая пластическая деформация или «податливость»; предел прочности при растяжении или максимальная интенсивность нагрузки, которую можно выдержать при растяжении; и процентное удлинение или деформация (насколько материал будет растягиваться) и сопутствующее процентное уменьшение площади поперечного сечения, вызванное растяжением. Также можно определить место разрыва или перелома.
Деформационное упрочнение
Одним из этапов кривой напряжение-деформация является область деформационного упрочнения . Эта область начинается, когда деформация выходит на за точку текучести , и заканчивается в точке предела прочности, максимальное напряжение, показанное на кривой напряжение-деформация. В этой области напряжение в основном увеличивается по мере удлинения материала, за исключением того, что в начале имеется почти плоская область. Деформационное упрочнение также называется деформационное упрочнение или холодная обработка . Он называется холодной обработкой, потому что пластическая деформация должна происходить при достаточно низкой температуре, чтобы атомы не могли перестроиться. Это процесс, при котором металл становится более твердым и прочным за счет пластической деформации. При пластической деформации металла дислокации перемещаются и генерируются дополнительные дислокации. Дислокации могут двигаться, если атомы из одной из окружающих плоскостей разрывают свои связи и снова соединяются с атомами на концевой кромке. Плотность дислокаций в металле увеличивается при деформации или наклепе из-за размножения дислокаций или образования новых дислокаций. Чем больше дислокаций в материале, тем больше они взаимодействуют между собой и становятся зажатыми или запутанными.
В этой области напряжение в основном увеличивается по мере удлинения материала, за исключением того, что в начале имеется почти плоская область. Деформационное упрочнение также называется деформационное упрочнение или холодная обработка . Он называется холодной обработкой, потому что пластическая деформация должна происходить при достаточно низкой температуре, чтобы атомы не могли перестроиться. Это процесс, при котором металл становится более твердым и прочным за счет пластической деформации. При пластической деформации металла дислокации перемещаются и генерируются дополнительные дислокации. Дислокации могут двигаться, если атомы из одной из окружающих плоскостей разрывают свои связи и снова соединяются с атомами на концевой кромке. Плотность дислокаций в металле увеличивается при деформации или наклепе из-за размножения дислокаций или образования новых дислокаций. Чем больше дислокаций в материале, тем больше они взаимодействуют между собой и становятся зажатыми или запутанными. Это приведет к уменьшению подвижности дислокаций и упрочнению материала.
Это приведет к уменьшению подвижности дислокаций и упрочнению материала.
Закон Гука
Большинство поликристаллических материалов имеют почти постоянную зависимость между напряжением и деформацией в пределах своего диапазона упругости. В 1678 году английский ученый по имени Роберт Гук провел эксперименты, которые предоставили данные, показывающие, что деформация пропорциональна напряжению в области упругости материала. Роберт Гук пришел к выводу, что сила F любой пружины пропорциональна растяжению (деформации из расслабленного состояния) x следующим образом:
F = k · x
где член k представляет собой жесткость пружины, а x мало по сравнению с общей возможной деформацией пружины. В конечном итоге он должен выйти из строя, как только силы превысят некоторый предел, поскольку ни один материал не может быть сжат до определенного минимального размера или растянут до максимального размера без какой-либо остаточной деформации или изменения состояния.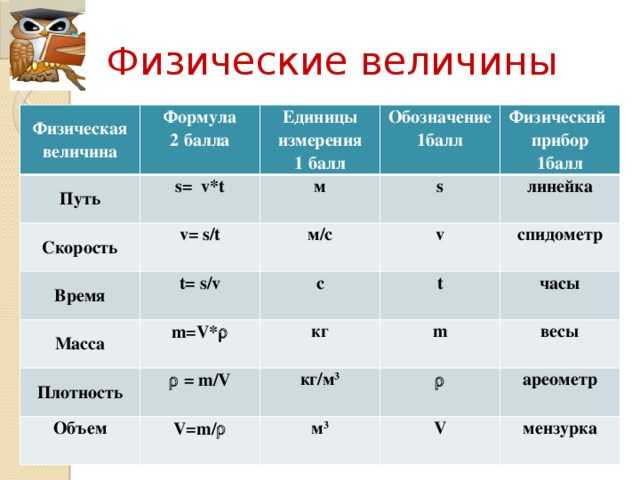
В случае напряжения растяжения однородного стержня (кривая напряжения-деформации), Закон Гука описывает поведение стержня в упругой области. В этой области удлинение стержня прямо пропорционально силе растяжения и длине стержня и обратно пропорционально площади поперечного сечения и модулю упругости . Вплоть до предельного напряжения тело сможет восстановить свои размеры при снятии нагрузки. Приложенные напряжения заставляют атомы в кристалле перемещаться из своего равновесного положения, и все атомы смещаются на одинаковую величину и по-прежнему сохраняют свою относительную геометрию. Когда напряжения снимаются, все атомы возвращаются в исходное положение, и никакой остаточной деформации не происходит. Согласно Закон Гука, напряжение пропорционально деформации (в области упругости), а наклон равен модулю Юнга .
Мы можем расширить ту же идею связи напряжения с деформацией с приложениями сдвига в линейной области, связать напряжение сдвига с деформацией сдвига, чтобы создать Закон Гука для напряжения сдвига :
Для изотропных материалов в области упругости вы можно связать коэффициент Пуассона (ν), модуль упругости Юнга (E) и модуль упругости сдвига (G):
Модули упругости, относящиеся к поликристаллическим материалам:
- Модуль упругости Юнга.
 Модуль упругости Юнга представляет собой модуль упругости при растяжении и сжатии в режиме линейной упругости при одноосной деформации и обычно оценивается испытаниями на растяжение.
Модуль упругости Юнга представляет собой модуль упругости при растяжении и сжатии в режиме линейной упругости при одноосной деформации и обычно оценивается испытаниями на растяжение. - Модуль упругости при сдвиге. Модуль сдвига или модуль жесткости получают из кручения цилиндрического образца для испытаний, описывая реакцию материала на напряжение сдвига. Его символ — G. Модуль сдвига — одна из нескольких величин для измерения жесткости материалов, и он возникает в обобщенном законе Гука.
- Объемный модуль упругости. Объемный модуль упругости описывает объемную упругость или тенденцию объекта деформироваться во всех направлениях при равномерной нагрузке во всех направлениях. Например, он описывает упругую реакцию на гидростатическое давление и равностороннее растяжение (как давление на дне океана или в глубоком бассейне). Это также свойство материала, определяющее упругую реакцию на прилагаемое напряжение. Для жидкости имеет значение только объемный модуль.

7.1: Прочность человеческих костей
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 17758
- Лоуренс Дэвис
- Общественный колледж Ампкуа via OpenOregon
Бедренная кость
«В анатомии человека бедренная кость (бедренная кость) является самой длинной и большой костью. Наряду с височной костью черепа это одна из двух самых прочных костей в организме. Средняя бедренная кость взрослого мужчины составляет 48
Бедренная кость человека. Изображение предоставлено: Анатомография через Wikimedia Commons
Изображение предоставлено: Анатомография через Wikimedia Commons
[2]
Сжатие
Когда вы кладете объект на верхнюю часть конструкции, вес объекта имеет тенденцию сжимать конструкцию. Любой толчок, стремящийся сжать конструкцию, называется сжимающей силой. Средний вес взрослых мужчин в США составляет 196 фунтов (872 N ) [3] . Согласно утверждению, что бедренная кость может выдержать в 30 раз больше веса тела, бедренная кость взрослого мужчины может выдержать примерно 6000 фунта силы сжатия! Такие большие силы редко создаются телом собственными силами, поэтому автомобильные столкновения являются причиной номер один переломов бедренной кости [4] .
Натяжение
Когда вы подвешиваете объект к конструкции, вес объекта будет растягивать конструкцию. Структура реагирует, создавая силу натяжения, чтобы удерживать объект. Силы растяжения — это восстанавливающие силы, возникающие в ответ на растяжение материалов.
Локтевой сустав сгибается, образуя угол 60 ° между плечом и предплечьем, в то время как рука держит мяч весом 50 фунтов . Изображение предоставлено: Openstax University Physics
[5]
Напряжение
Максимальная сила сжатия или растяжения, которую может выдержать кость, зависит от размера кости. В частности, чем больше площадь, на которую может быть распределена сила, тем большую силу может выдержать кость. Это означает, что максимальные силы, которые могут выдержать кости (и другие объекты), пропорциональны площади поперечного сечения кости, которая перпендикулярна (90 ° ) к направлению действия силы. Например, сила, которую бедренная кость может поддерживать вертикально по всей своей длине, зависит от площади ее горизонтального поперечного сечения, которое имеет примерно круглую форму и несколько полое (костный мозг заполняет центральное пространство).
Например, сила, которую бедренная кость может поддерживать вертикально по всей своей длине, зависит от площади ее горизонтального поперечного сечения, которое имеет примерно круглую форму и несколько полое (костный мозг заполняет центральное пространство).
На этих поперечных сечениях показана средняя часть бедренной кости 84-летней женщины с выраженным остеопорозом (справа) по сравнению со здоровой бедренной костью 17-летней женщины (слева). Изображение предоставлено: Смитсоновский национальный музей естественной истории
[6]
Более крупные кости могут выдерживать большую силу, поэтому для анализа поведения самого костного материала нам необходимо разделить силу, приложенную к кости, на минимальную площадь поперечного сечения (). Эта величина известна как напряжение (σ) в материале. Стресс имеет единицу силы на единицу площади, поэтому единицы СИ составляют ( Н/м 2 ), которые также известны как Паскали. Единицы измерения фунтов на квадратный дюйм ( PSI , фунтов/дюйм 2 ) распространены в США
Единицы измерения фунтов на квадратный дюйм ( PSI , фунтов/дюйм 2 ) распространены в США
(1)
Упражнения на укрепление
Оценка напряжения сжатия в пределах 1,0 см x 2,0 см Блок Lego, когда вы наступаете на него полным весом тела, в единицах pb_glossary id=”3977″]Паскалей[/pb_glossary]. [Подсказка: нам нужен результат в единицах СИ, поэтому перед расчетом площади поперечного сечения преобразуйте длину и ширину в метры и используйте единицы СИ для веса.]
Предельная прочность бедренной кости
Максимальное напряжение, которое может испытать кость или любой другой материал до того, как материал начнет разрушаться или разорваться, называется пределом прочности. Обратите внимание, что прочность материала определяется с точки зрения напряжения, а не силы, поэтому мы анализируем сам материал, не включая влияние того, сколько материала присутствует. Для некоторых материалов предел прочности отличается, когда напряжение действует на раздавливание материала (сжатие) и когда силы действуют на растяжение материала при растяжении, поэтому мы часто ссылаемся на предел прочности при растяжении или предел прочности при сжатии. Например, предел прочности на сжатие бедренной кости человека составляет 205 9 .0003 МПа (205 млн паскалей) при сжатии по всей длине. Предел прочности бедренной кости при растяжении по ее длине составляет 135 МПа . [7] Наряду с костью, бетон и мел являются другими примерами материалов с различным пределом прочности при сжатии и растяжении.
Для некоторых материалов предел прочности отличается, когда напряжение действует на раздавливание материала (сжатие) и когда силы действуют на растяжение материала при растяжении, поэтому мы часто ссылаемся на предел прочности при растяжении или предел прочности при сжатии. Например, предел прочности на сжатие бедренной кости человека составляет 205 9 .0003 МПа (205 млн паскалей) при сжатии по всей длине. Предел прочности бедренной кости при растяжении по ее длине составляет 135 МПа . [7] Наряду с костью, бетон и мел являются другими примерами материалов с различным пределом прочности при сжатии и растяжении.
Задание по армированию
Попробуйте растолочь кусок мела, надавив пальцами на концы и сжав его вдоль длинной оси, изгибать нельзя. При удаче?
Теперь используйте свои пальцы, чтобы разбить мел, потянув его в стороны, прямо вдоль длинной оси, снова не допуская изгибов. При удаче?
Запишите свои результаты и объясните, что они говорят вам о пределе прочности при сжатии и пределе прочности при растяжении мела.
Сравните наблюдаемое вами поведение мела с известным поведением кости и бетона. Укажите ваши источники.
Повседневный пример
Давайте проверим, согласуются ли измеренные значения предела прочности при сжатии с утверждением, что бедренная кость человека может выдержать в 30 раз больше веса взрослого человека, или примерно в 6000 lbs
Сначала давайте переведем заявленные 6000 lbs силы в ньютоны и будем работать в единицах СИ.
Приблизительная минимальная площадь поперечного сечения бедренной кости составляет . ( * См. нижнюю часть этого примера, если вам интересно узнать, как мы аппроксимировали это значение ). Делим сжимающую силу на площадь поперечного сечения, чтобы найти сжимающую нагрузку на кость.
Наше приблизительное значение предельной прочности кости, необходимой для поддержки 30-кратного веса тела, составило 80 МПа , что на самом деле меньше, чем измеренное значение 205 МПа , поэтому утверждение, что бедренная кость может выдержать 30-кратный вес тела кажется разумным.
*Вот как мы аппроксимировали площадь поперечного сечения бедренной кости, пропустите это, если вам это не интересно:
Сначала мы делим диаметр бедренной кости 2,34 см , указанный ранее, на два, чтобы найти радиус бедренной кости, затем мы переводим его в стандартные единицы измерения – метры.
Используя уравнение для площади круга, мы вычисляем общую площадь бедренной кости:
Наконец, мы должны вычесть площадь полой средней части, чтобы получить чистую площадь кости. Мы использовали линейку на приведенном выше изображении поперечных сечений бедренной кости, чтобы увидеть, что внутренний радиус составляет примерно половину внешнего радиуса, или поэтому мы вычисляем недостающую внутреннюю площадь:
И вычесть внутреннюю площадь из общей суммы:
Предел прочности в поперечном направлении
До сих пор мы обсуждали предел прочности вдоль длинной оси бедренной кости, известной как продольное направление. Некоторые материалы, такие как кость и дерево, имеют разную предельную прочность по разным осям. Предел прочности на сжатие кости по короткой оси (в поперечном направлении) составляет 131 МПа , что примерно на 36 % меньше, чем у 205 МПа продольное значение. Материалы, которые имеют разные свойства по разным осям, известны как анизотропные. Материалы, которые ведут себя одинаково во всех направлениях, называются изотропными.
Некоторые материалы, такие как кость и дерево, имеют разную предельную прочность по разным осям. Предел прочности на сжатие кости по короткой оси (в поперечном направлении) составляет 131 МПа , что примерно на 36 % меньше, чем у 205 МПа продольное значение. Материалы, которые имеют разные свойства по разным осям, известны как анизотропные. Материалы, которые ведут себя одинаково во всех направлениях, называются изотропными.
Интересный факт в завершение этой главы: когда человек стоит, бедренная кость действительно испытывает сжимающие и растягивающие напряжения с разных сторон кости. Это происходит из-за того, что структура тазобедренного сустава переносит вес тела в сторону, а не прямо вдоль длинной оси кости.
В положении стоя на бедренную кость воздействуют как растягивающие, так и сжимающие напряжения. Изображение предоставлено: Blausen Medical через Wikimedia Commons
[8]
- «Бедро» от Orthapaedics One↵
- By Anatomography [CC BY-SA 2.
 1 jp (https://creativecommons.org/licenses/by-sa/2.1/jp/deed.en)], через Wikimedia Commons↵
1 jp (https://creativecommons.org/licenses/by-sa/2.1/jp/deed.en)], через Wikimedia Commons↵ - «Измерение тела» от FastStats, Центров по контролю за заболеваниями США, находится в открытом доступе ↵
- «Переломы диафиза бедренной кости», OrthoInfo, Американская академия хирургов-ортопедов↵
- Университетская физика OpenStax, Университетская физика, том 1. OpenStax CNX. 11 июля 2018 г. [1] http://cnx.org/contents/[email protected]. ↵
- «Последствия хронического состояния: остеопороз», автор: Written in Bone, Smithsonian National Museum of Natural History ↵
- «Анизотропия упругости кости», Род Лейкс, Инженерный колледж, Университет Висконсона ↵
- Сотрудники Blausen.com (2014 г.). «Медицинская галерея Blausen Medical 2014». ВикиЖурнал медицины 1 (2). DOI: 10.15347/wjm/2014.010. ISSN 2002-4436. [CC BY 3.0 (https://creativecommons.org/licenses/by/3.
 0)], с Викисклада ↵
0)], с Викисклада ↵
Эта страница под названием 7.1: Сила человеческих костей распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Лоуренсом Дэвисом (OpenOregon) с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами. платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Лоуренс Дэвис
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4,0
- Программа OER или Publisher
- Открытый Орегон
- Показать оглавление
- нет
- Теги
- источник@https://openoregon.

- источник@https://openoregon.


 В состоянии неустойчивого равновесия потенциальная энергия системы имеет максимальное значение.
В состоянии неустойчивого равновесия потенциальная энергия системы имеет максимальное значение.
 Неподвижный блок используется для изменения направления приложения силы. Если трение в блоке отсутствует, нить невесома, то сила ее натяжения до и после блока не изменяется. Таким образом, неподвижный блок не дает ни выигрыша в силе, ни проигрыша в перемещении.
Неподвижный блок используется для изменения направления приложения силы. Если трение в блоке отсутствует, нить невесома, то сила ее натяжения до и после блока не изменяется. Таким образом, неподвижный блок не дает ни выигрыша в силе, ни проигрыша в перемещении.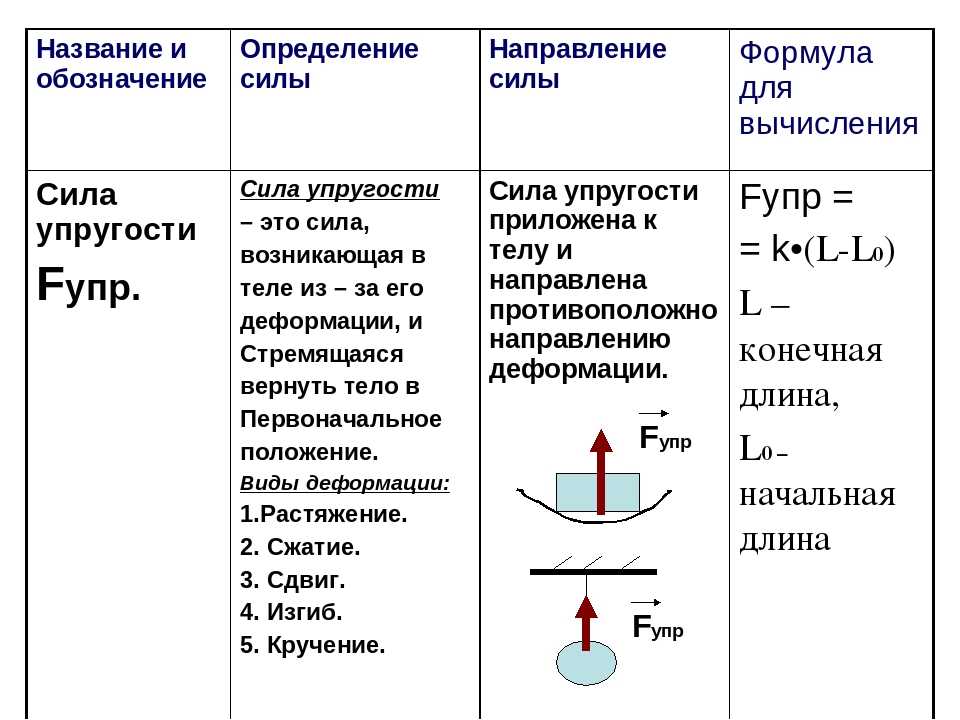 Веса обеспечивают нагрузки. Эти напряжения возникают в фундаментах и каркасах зданий, а также в деталях машин.
Веса обеспечивают нагрузки. Эти напряжения возникают в фундаментах и каркасах зданий, а также в деталях машин.
 И энергия скорости преобразуется в энергию давления.
И энергия скорости преобразуется в энергию давления. Одно из наиболее распространенных механических испытаний на растяжение проводится на растяжение. Растягивающее напряжение — это такой тип напряжения, при котором два участка материала по обе стороны от плоскости напряжения стремятся разойтись или удлиниться. Способность материала или конструкции выдерживать нагрузки, имеющие тенденцию к удлинению, известна как 9.0003 предел прочности при растяжении (UTS) . Предел прочности на растяжение измеряется максимальным напряжением, которое материал может выдержать при растяжении или растяжении до разрыва. При изучении прочности материалов прочность на растяжение, прочность на сжатие и прочность на сдвиг можно анализировать независимо друг от друга. Поскольку растягивающие и сжимающие нагрузки создают напряжения, действующие поперек плоскости в направлении, перпендикулярном (нормальном) к плоскости, растягивающие и сжимающие напряжения называются нормальными напряжениями .
Одно из наиболее распространенных механических испытаний на растяжение проводится на растяжение. Растягивающее напряжение — это такой тип напряжения, при котором два участка материала по обе стороны от плоскости напряжения стремятся разойтись или удлиниться. Способность материала или конструкции выдерживать нагрузки, имеющие тенденцию к удлинению, известна как 9.0003 предел прочности при растяжении (UTS) . Предел прочности на растяжение измеряется максимальным напряжением, которое материал может выдержать при растяжении или растяжении до разрыва. При изучении прочности материалов прочность на растяжение, прочность на сжатие и прочность на сдвиг можно анализировать независимо друг от друга. Поскольку растягивающие и сжимающие нагрузки создают напряжения, действующие поперек плоскости в направлении, перпендикулярном (нормальном) к плоскости, растягивающие и сжимающие напряжения называются нормальными напряжениями . Соседние части материала имеют тенденцию прижиматься друг к другу через типичную плоскость напряжения. Напряжение сжатия стержней, колонн и т. д. приводит к их укорочению. Напряжение сжатия определяется аналогично напряжению растяжения, но имеет отрицательные значения для выражения сжатия, поскольку дельта L имеет противоположное направление. Можно увеличивать сжимающее напряжение до тех пор, пока не будет достигнута прочность на сжатие. Тогда материалы будут реагировать с пластичным поведением или с разрушением в случае хрупких материалов. Поскольку растягивающие и сжимающие нагрузки создают напряжения, действующие поперек плоскости в направлении, перпендикулярном (нормальном) к плоскости, растягивающие и сжимающие напряжения называются 9.0019 нормальные напряжения . Способность материала реагировать на сжимающее напряжение или давление называется сжимаемостью.
Соседние части материала имеют тенденцию прижиматься друг к другу через типичную плоскость напряжения. Напряжение сжатия стержней, колонн и т. д. приводит к их укорочению. Напряжение сжатия определяется аналогично напряжению растяжения, но имеет отрицательные значения для выражения сжатия, поскольку дельта L имеет противоположное направление. Можно увеличивать сжимающее напряжение до тех пор, пока не будет достигнута прочность на сжатие. Тогда материалы будут реагировать с пластичным поведением или с разрушением в случае хрупких материалов. Поскольку растягивающие и сжимающие нагрузки создают напряжения, действующие поперек плоскости в направлении, перпендикулярном (нормальном) к плоскости, растягивающие и сжимающие напряжения называются 9.0019 нормальные напряжения . Способность материала реагировать на сжимающее напряжение или давление называется сжимаемостью. Кручение — это разновидность чистого сдвига, при котором элемент конструкции скручивается. Силы кручения производят вращательное движение вокруг продольной оси одного конца элемента относительно другого. Напряжение сдвига также имеет большое значение в природе, тесно связанное с движением земных материалов вниз по склону (как в случае лавин).
Кручение — это разновидность чистого сдвига, при котором элемент конструкции скручивается. Силы кручения производят вращательное движение вокруг продольной оси одного конца элемента относительно другого. Напряжение сдвига также имеет большое значение в природе, тесно связанное с движением земных материалов вниз по склону (как в случае лавин). Деформации сдвига измеряют относительное параллельное движение одной базовой плоскости относительно другой. Символ деформации сдвига обычно представляет собой строчную греческую букву гамма (γ).
Деформации сдвига измеряют относительное параллельное движение одной базовой плоскости относительно другой. Символ деформации сдвига обычно представляет собой строчную греческую букву гамма (γ). Когда металл подвергается нагрузке (силе), он искажается или деформируется, независимо от того, насколько прочный металл или легкая нагрузка. Эта деформация может быть, а может и не быть постоянной. До предельного напряжения тело сможет восстановить свои размеры при снятии нагрузки. Приложенные напряжения заставляют атомы в кристалле перемещаться из своего равновесного положения, и все атомы смещаются на одинаковую величину и по-прежнему сохраняют свою относительную геометрию. Когда напряжения снимаются, все атомы возвращаются в исходное положение, и никакой остаточной деформации не происходит.
Когда металл подвергается нагрузке (силе), он искажается или деформируется, независимо от того, насколько прочный металл или легкая нагрузка. Эта деформация может быть, а может и не быть постоянной. До предельного напряжения тело сможет восстановить свои размеры при снятии нагрузки. Приложенные напряжения заставляют атомы в кристалле перемещаться из своего равновесного положения, и все атомы смещаются на одинаковую величину и по-прежнему сохраняют свою относительную геометрию. Когда напряжения снимаются, все атомы возвращаются в исходное положение, и никакой остаточной деформации не происходит.
 Напротив, предел текучести — это место, где начинается нелинейная (упругая + пластическая) деформация. Перед пределом текучести материал упруго деформируется и возвращается к своей первоначальной форме после снятия приложенного напряжения. Как только предел текучести пройден, некоторая часть деформации будет постоянной и необратимой. Некоторые стали и другие материалы демонстрируют явление, называемое явлением предела текучести. Пределы текучести варьируются от 35 МПа для низкопрочного алюминия до более 1400 МПа для высокопрочной стали.
Напротив, предел текучести — это место, где начинается нелинейная (упругая + пластическая) деформация. Перед пределом текучести материал упруго деформируется и возвращается к своей первоначальной форме после снятия приложенного напряжения. Как только предел текучести пройден, некоторая часть деформации будет постоянной и необратимой. Некоторые стали и другие материалы демонстрируют явление, называемое явлением предела текучести. Пределы текучести варьируются от 35 МПа для низкопрочного алюминия до более 1400 МПа для высокопрочной стали. Часто это значение значительно превышает предел текучести (на 50–60 % превышает предел текучести для некоторых типов металлов). Когда пластичный материал достигает предела прочности, он испытывает сужение, когда площадь поперечного сечения локально уменьшается. Кривая напряжение-деформация не содержит более высокого напряжения, чем предел прочности. Несмотря на то, что деформации могут продолжать увеличиваться, напряжение обычно уменьшается после достижения предела прочности. Это интенсивное свойство; поэтому его значение не зависит от размера испытуемого образца. Однако это зависит от других факторов, таких как подготовка образца, наличие или отсутствие поверхностных дефектов, температура тестовой среды и материала. Предел прочности при растяжении варьируется от 50 МПа для алюминия до 3000 МПа для очень высокопрочной стали.
Часто это значение значительно превышает предел текучести (на 50–60 % превышает предел текучести для некоторых типов металлов). Когда пластичный материал достигает предела прочности, он испытывает сужение, когда площадь поперечного сечения локально уменьшается. Кривая напряжение-деформация не содержит более высокого напряжения, чем предел прочности. Несмотря на то, что деформации могут продолжать увеличиваться, напряжение обычно уменьшается после достижения предела прочности. Это интенсивное свойство; поэтому его значение не зависит от размера испытуемого образца. Однако это зависит от других факторов, таких как подготовка образца, наличие или отсутствие поверхностных дефектов, температура тестовой среды и материала. Предел прочности при растяжении варьируется от 50 МПа для алюминия до 3000 МПа для очень высокопрочной стали. В этот момент деформация достигает своего максимального значения, и материал разрушается, хотя соответствующее напряжение может быть меньше предела прочности в этот момент. Пластичные материалы имеют предел прочности на излом ниже, чем предел прочности при растяжении (UTS), тогда как в хрупких материалах предел прочности при изломе эквивалентен пределу прочности при растяжении (UTS). Если пластичный материал достигает своего предела прочности при растяжении в ситуации с регулируемой нагрузкой, он будет продолжать деформироваться без приложения дополнительной нагрузки, пока не разорвется. Однако, если нагрузка контролируется по смещению, деформация материала может уменьшить нагрузку, предотвращая разрыв.
В этот момент деформация достигает своего максимального значения, и материал разрушается, хотя соответствующее напряжение может быть меньше предела прочности в этот момент. Пластичные материалы имеют предел прочности на излом ниже, чем предел прочности при растяжении (UTS), тогда как в хрупких материалах предел прочности при изломе эквивалентен пределу прочности при растяжении (UTS). Если пластичный материал достигает своего предела прочности при растяжении в ситуации с регулируемой нагрузкой, он будет продолжать деформироваться без приложения дополнительной нагрузки, пока не разорвется. Однако, если нагрузка контролируется по смещению, деформация материала может уменьшить нагрузку, предотвращая разрыв. Вязкое разрушение (разрушение при сдвиге) лучше, чем хрупкое разрушение, потому что перед разрушением происходит медленное распространение и поглощение большого количества энергии. Пластичность желательна при высоких температурах и высоких давлениях в реакторных установках из-за дополнительных нагрузок на металлы. Высокая пластичность в этих применениях помогает предотвратить хрупкое разрушение.
Вязкое разрушение (разрушение при сдвиге) лучше, чем хрупкое разрушение, потому что перед разрушением происходит медленное распространение и поглощение большого количества энергии. Пластичность желательна при высоких температурах и высоких давлениях в реакторных установках из-за дополнительных нагрузок на металлы. Высокая пластичность в этих применениях помогает предотвратить хрупкое разрушение. Модуль упругости Юнга представляет собой модуль упругости при растяжении и сжатии в режиме линейной упругости при одноосной деформации и обычно оценивается испытаниями на растяжение.
Модуль упругости Юнга представляет собой модуль упругости при растяжении и сжатии в режиме линейной упругости при одноосной деформации и обычно оценивается испытаниями на растяжение.
 1 jp (https://creativecommons.org/licenses/by-sa/2.1/jp/deed.en)], через Wikimedia Commons↵
1 jp (https://creativecommons.org/licenses/by-sa/2.1/jp/deed.en)], через Wikimedia Commons↵  0)], с Викисклада ↵
0)], с Викисклада ↵