Сферическое зеркало — Википедия
Материал из Википедии — свободной энциклопедии
 Мнимое изображение фотокамеры и окружающего пространства в выпуклом сферическом зеркале — ёлочном шаре.
Мнимое изображение фотокамеры и окружающего пространства в выпуклом сферическом зеркале — ёлочном шаре.Сферическое зеркало — зеркало, отражающая поверхность которого имеет вид сегмента сферы.
Сферическое зеркало может быть выпуклым или вогнутым — в зависимости от того, какая сторона сегмента сферы — выпуклая или вогнутая — является отражающей. Центр соответствующей сферическому зеркалу сферы называется его центром или оптическим центром, середина сегмента — полюсом зеркала, прямая, проходящая через центр и полюс — главной оптической осью зеркала. Другие прямые, проходящие через центр зеркала и точку, отличную от полюса, называются его побочными оптическими осями.
Параксиальные лучи, параллельные главной оптической оси выпуклого сферического зеркала, так же как и продолжения параксиальных лучей, параллельных главной оптической оси вогнутого сферического зеркала, пересекаются в одной точке, называемой его фокусом. Он расположен посередине между центром и полюсом зеркала, то есть расстояние (f) его до зеркала равно половине радиуса (R):
f=R2{\displaystyle f={\frac {R}{2}}}
У сферического зеркала, как вообще у любого зеркала, отсутствует хроматическая аберрация, но выражена сферическая аберрация. Сферическая аберрация выражена потому, что в отличие от параболического зеркала (то есть сегмента параболоида вращения), сферическое зеркало может собирать в одной точке лишь параксиальные лучи, то есть те из лучей, параллельных главной оптической оси, которые близки к этой оси. Сферическая аберрация в одном из примеров применения сферического вогнутого зеркала, зеркально-линзовом телескопе системы Дмитрия Максутова, устраняется компенсированием специально подобранной линзой — мениском.
Известным примером выпуклого сферического зеркала является ёлочный шар.
Построение изображения в сферическом зеркале[править | править код]
Проще всего построить изображение отрезка, перпендикулярного главной оптической оси зеркала и настолько небольшого по высоте, что луч, исходящий из его верхней точки и параллельный главной оптической оси зеркала — параксиальный. Его изображение будет также перпендикулярным главной оптической оси зеркала, расстояние его от зеркала при известном расстоянии от зеркала до предмета и фокусного расстояния зеркала можно вычислить по формуле зеркала. Высота изображения (y’) будет равна произведению высоты предмета (y) на отношение расстояния от изображения до зеркала (v) к расстоянию от зеркала до предмета (u):
y′=y⋅vu{\displaystyle y’=y\cdot {\frac {v}{u}}}
Для вогнутого сферического зеркала[править | править код]
Видеоурок: вогнутое зеркалоЕсли сферическое зеркало вогнутое, возможны различные случаи расположения изображения относительно зеркала при различных расстояниях до предмета. Буквой C обозначен центр зеркала, а буквой F — его фокус. При u>f формула зеркала имеет вид:
1u+1v=2R,{\displaystyle {\frac {1}{u}}+{\frac {1}{v}}={\frac {2}{R}},}
а при u<f:
1u−1v=2R.{\displaystyle {\frac {1}{u}}-{\frac {1}{v}}={\frac {2}{R}}.}
Для построения взято три луча (хотя достаточно и двух):
- луч, параллельный главной оптической оси после отражения от зеркала пройдёт через его фокус;
- луч, проходящий через фокус после отражения пойдёт параллельно главной оптической оси;
- луч, падающий на полюс зеркала после отражения пойдёт под углом, равным углу падения (по закону отражения света).
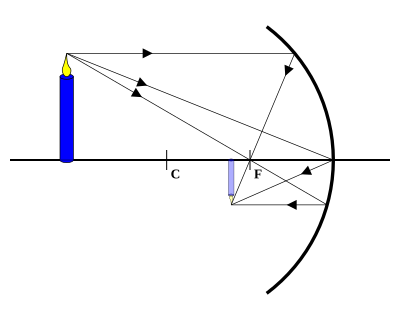 Если предмет приближён к зеркалу и находится на расстоянии, превышающем расстояние от зеркала до его центра, то изображение его будет Если предмет приближён к зеркалу и находится на расстоянии, превышающем расстояние от зеркала до его центра, то изображение его будет | 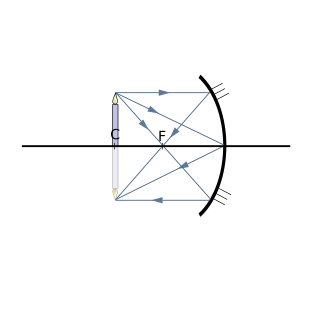 Если предмет помещён в центре зеркала, то его изображение также будет расположено в центре зеркала. Изображение получается действительным, перевёрнутым и равным по величине предмету. Если предмет помещён в центре зеркала, то его изображение также будет расположено в центре зеркала. Изображение получается действительным, перевёрнутым и равным по величине предмету. |
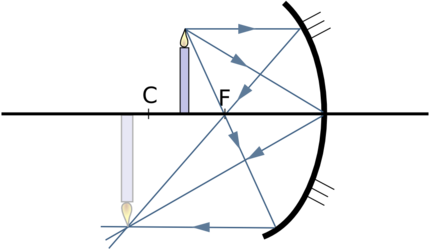 | 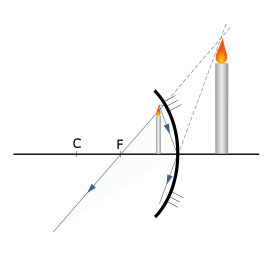 Если предмет ближе фокуса к зеркалу, то изображение — мнимое, прямое, увеличенное, по другую сторону зеркала от предмета. Если предмет ближе фокуса к зеркалу, то изображение — мнимое, прямое, увеличенное, по другую сторону зеркала от предмета. |
Для выпуклого сферического зеркала[править | править код]
Построение изображения в выпуклом сферическом зеркале проще, чем в вогнутом: здесь при любом расстоянии предмета до зеркала его изображение будет расположено за зеркалом. На рисунке ниже буквой
1u−1v=−2R{\displaystyle {\frac {1}{u}}-{\frac {1}{v}}=-{\frac {2}{R}}}
Для построения взято два луча:
- луч от верхней точки предмета, параллельный главной оптической оси, отразится от зеркала, и продолжение этого отражённого луча пройдёт через фокус и через верхнюю точку изображения;
- луч от верхней точки предмета, продолжение которого проходит через фокус, после отражения пойдёт параллельно главной оптической оси, а продолжение этого отражённого луча также пройдёт через верхнюю точку изображения.
Таким образом, верхней точкой изображения будет точка пересечения продолжения первого отражённого луча и продолжения второго отражённого луча.

Изображение в выпуклом зеркале — мнимое, прямое, уменьшенное, находится по другую сторону зеркала от предмета.
- Ландсберг Г.С.
Плоское и сферическое зеркало. Построение. Основные элементы. Фокус. Оптический центр. Формула
Любые отражающие поверхности в курсе школьной физики принято называть зеркалами. Рассматривают две геометрические формы зеркал:
- плоское
- сферическое
Плоское зеркало — отражающая поверхность, формой которой является плоскость. Построение изображения в плоском зеркале основывается на законах отражения, которые, в общем случае, даже можно упростить (рис. 1).
Рис. 1. Плоское зеркало
Пусть источником в нашем примере будет точка А (точечный источник света). Лучи от источника распространяются во все стороны. Чтобы найти положение изображения, достаточно проанализировать ход двух любых лучей и найти построением точку их пересечения. Первый луч (1) пустим под любым углом к плоскости зеркала, и, по законам отражения, его дальнейшее движение будет под углом отражения, равным углу падения. Второй луч (2) также можно пускать под любым углом, но проще нарисовать его перпендикулярно поверхности, т.к., в этом случае, он не испытает преломления. Продолжения лучей 1 и 2 сходятся в точке B, в нашем случае, данная точка и есть изображение точки А (мнимое) (рис. 1.1).
Однако получившиеся на рисунке 1.1 треугольники одинаковы (по двум углам и общей стороне), тогда в качестве правила построения изображения в плоском зеркале можно принять: при построении изображения в плоском зеркале достаточно из источника А опустить перпендикуляр на плоскость зеркала, а затем продолжить данный перпендикуляр на ту же длину по другую сторону от зеркала (рис. 1.2).
Воспользуемся этой логикой (рис. 2).
Рис. 2. Примеры построения в плоском зеркале
В случае не точечного предмета важно помнить, что форма предмета в плоском зеркале не меняется. Если учесть, что любой предмет фактически состоит из точек, то, в общем случае, надо отразить каждую точку. В упрощённом варианте (например, отрезок или простая фигура) можно отразить крайние точки, а потом соединить их прямыми (рис. 3). При этом АВ — предмет, А’В’ — изображение.
Рис. 3. Построение предмета в плоском зеркале
Также нами было введено новое понятие — точечный источник света — источник, размерами которого можно пренебречь в нашей задаче.
Сферическое зеркало — отражающая поверхность, формой которой является часть сферы. Логика поиска изображения та же — найти два луча, идущих от источника, пересечение которых (или их продолжений) и даст искомое изображение. На самом деле, для сферического тела есть три достаточно простых луча, преломление которых можно легко предсказать (рис. 4). Пусть
— точечный источник света.Рис. 4. Сферическое зеркало
Для начала введём характерную линию и точки сферического зеркала. Точка 4 называется оптическим центром сферического зеркала. Эта точка является геометрическим центром системы. Линия 5 — главная оптическая ось сферического зеркала — линия, проходящая через оптический центр сферического зеркала и перпендикулярно касательной к зеркалу в этой точке. Точка F — фокус сферического зеркала, обладающая особыми свойствами (об этом позже).
Тогда существует три хода лучей, достаточно простых для рассмотрения:
- синий. Луч, проходящий через фокус, отражаясь от зеркала, проходит параллельно главной оптической оси (свойство фокуса),
- зелёный. Луч, падающий на главный оптический центр сферического зеркала, отражается под тем же углом (законы отражения),
- красный. Луч, идущий параллельно главной оптической оси, после преломления проходит через фокус (свойство фокуса).
Выбираем любые два луча и их пересечение даёт изображение нашего предмета (
).Фокус — условная точка на главной оптической оси, в которую сходятся лучи, отражённые от сферического зеркала шедшие параллельно главной оптический оси.
Для сферического зеркала фокусное расстояние (расстояние от оптического центра зеркала до фокуса) чисто геометрическое понятие, и данный параметр может быть найден через соотношение:
(1)- где
- — фокусное расстояние,
- — радиус кривизны зеркала.
Вывод: для зеркал используются самые общие законы отражения. Для плоского зеркала существует упрощение для построения изображений (рис. 1.2). Для сферических зеркал существуют три хода луча, два любых из которых дают изображение (рис. 4).
Поделиться ссылкой:
Понравилось это:
Нравится Загрузка…
Плоское зеркало. Видеоурок. Физика 8 Класс
На сегодняшнем уроке речь пойдет о зеркалах, а точнее – о плоском зеркале.
Зеркало – это гладкая поверхность, которая отражает излучение (рис. 1). Оптические зеркала – это обычно полированные металлы или стекла, которые отражают почти весь видимый свет (рис. 2).

Рис. 1. Зеркало

Рис. 2. Оптическое зеркало
Зеркала бывают трех видов – плоские, вогнутые и выпуклые.
Плоские зеркала отражают излучения без искажений и дают изображение, близкое к оригиналу (рис. 3).

Рис. 3. Отражение в плоском зеркале
Вогнутые – концентрируют энергию излучения (рис. 4).

Рис. 4. Отражение в вогнутом зеркале
Выпуклые – рассеивают (рис. 5).

Рис. 5. Отражение в выпуклом зеркале
На сегодняшнем уроке мы подробнее поговорим о плоском зеркале.
Плоское зеркало – это плоская поверхность, зеркально отражающая свет (рис. 6).

Рис. 6. Плоское зеркало
Рассмотрим, как образуется изображение в плоском зеркале.
Пусть из точечного источника света 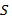 на поверхность плоского зеркала падает расходящийся пучок света. Из множества падающих лучей выделим лучи
на поверхность плоского зеркала падает расходящийся пучок света. Из множества падающих лучей выделим лучи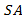
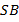 и
и 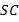 . Пользуясь законами отражения света, построим отраженные лучи
. Пользуясь законами отражения света, построим отраженные лучи  ,
, 
 .
.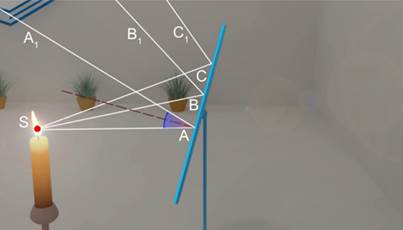
Рис.  . Построение отраженных лучей
. Построение отраженных лучей
Эти лучи пойдут также расходящимся пучком. Если продолжить их в противоположном направлении, все они пересекутся в одной точке 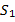 , расположенной за зеркалом. Нам будет казаться, что эти лучи выходят из точки
, расположенной за зеркалом. Нам будет казаться, что эти лучи выходят из точки 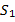 , хотя в действительности никакого источника света в этой точке не существует. Поэтому точку
, хотя в действительности никакого источника света в этой точке не существует. Поэтому точку 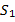 называют мнимым изображением точки
называют мнимым изображением точки 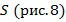 .
.
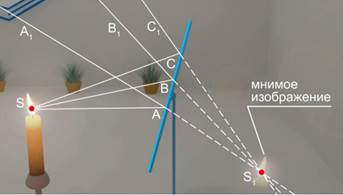
Рис. 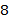 . Построение мнимого изображения в зеркале
. Построение мнимого изображения в зеркале
Зеркальное и рассеянное отражение света. Поглощение света
Вечером, когда в комнате горит свет, мы можем видеть свое отражение в оконном стекле, однако стоит нам задернуть шторы, и изображение пропадает. Мы не видим своего отражения в ткани.
Это связано с двумя физическими явлениями. Одно из них – отражение света.
Чтобы появилось изображение, свет должен отразиться от зеркальной поверхности. Если свет отражается от неровной и шероховатой поверхности, то такое отражение называется рассеянным, или диффузным (рис. 9).

Рис. 9. Отражение света от зеркальной и от шероховатой поверхностей
На такой поверхности нельзя получить изображение. Даже некоторые гладкие на ощупь поверхности, такие как кусок пластика или обложка книги, для света являются недостаточно гладкими, свет отражается от таких поверхностей рассеянно.
Другое физическое явление, влияющее на возможность видеть изображение, – это поглощение света. Физические тела могут не только отражать свет, но и поглощать его. Наилучший отражатель света – зеркало, оно отражает более 90 % света, падающего на него. Хорошими отражателями являются также тела белого цвета, именно поэтому в солнечный зимний день, когда все бело от снега, мы жмуримся, защищая глаза от яркого света. А вот черная поверхность поглощает практически весь свет, например, на черный бархат можно смотреть, не жмурясь, даже при самом ярком освещении.
Поговорим о том, какие виды оптических изображений существуют и что такое оптическое изображение.
Оптическое изображение – это картина, получаемая в результате прохождения через оптическую систему световых лучей, распространяющихся от объекта, и воспроизводящая его контуры и детали.
Различают два случая: действительное изображение и мнимое изображение.
Действительное изображение создается, когда после всех отражений и преломлений лучи, вышедшие из одной точки предмета, собираются в одну точку (рис. 10).

Рис. 10. Действительное изображение
Действительное изображение нельзя видеть непосредственно, можно увидеть его проекцию, поставив рассеивающие экраны. Действительное изображение создается такими оптическими системами, как объектив кинопроектора или фотоаппарата или собирающая линза (рис.11).

Рис.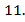 Оптические системы
Оптические системы
Мнимое изображение – такое изображение, которое можно видеть глазом.
При этом каждой точке предмета соответствует выходящий из оптической системы пучок лучей, которые, если продолжить их обратно прямыми линиями, сошлись бы в одной точке. Возникает видимость, что пучок выходит именно оттуда.
Мнимое изображение создается такими системами, как бинокль, микроскоп, отрицательная или положительная линза, лупа, а также плоское зеркало. Плоское зеркало дает именно мнимое изображение.
Интересные факты
Существуют так называемые полупрозрачные зеркала, или, как их иногда называют, зеркальные, или односторонние, стекла.
Такие стекла применяются для скрытого наблюдения за людьми в целях контроля за поведение или шпионажа. При этом шпион находится в темном помещении, а объект наблюдения – в светлом (рис. 12). Принцип действия зеркального стекла в том, что тусклый шпион не виден на фоне яркого зеркального отражения. Полупрозрачных зеркал, которые пропускали бы свет в одну сторону и не пропускали в другую, не существует.

Рис. 12 Помещение с полупрозрачным зеркалом
Не так давно в новых американских аттракционах ужаса появились зеркальные лабиринты. В России первые зеркальные лабиринты появились в Санкт-Петербурге и приобрели большую популярность в развлекательной индустрии.
Проведем демонстрацию, с помощью которой выясним, как расположены предмет и его изображение относительно плоского зеркала.
Возьмем плоское стекло, закрепленное вертикально. С одной стороны стекла установим горящую свечу, с другой стороны – точно такую же, но не зажженную. Передвигая незажженную свечу, найдем такое ее расположение, когда эта свеча будет казаться горящей. В этом случае незажженная свеча окажется в месте, где наблюдается в стекле изображение горящей свечи.
Схематично изобразим местоположение стекла – прямая линия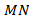 , зажженной свечи
, зажженной свечи 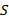 и незажженной свечи
и незажженной свечи 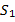 .
.
Эта точка также показывает местоположение изображения зажженной свечи (рис.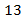 ). Если теперь соединить точки
). Если теперь соединить точки 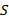 и
и 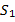 и провести необходимые измерения, то мы убедимся, что прямая
и провести необходимые измерения, то мы убедимся, что прямая 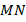 перпендикулярна отрезку
перпендикулярна отрезку 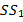 , а длина отрезка
, а длина отрезка 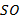 равна длине отрезка
равна длине отрезка  .
.
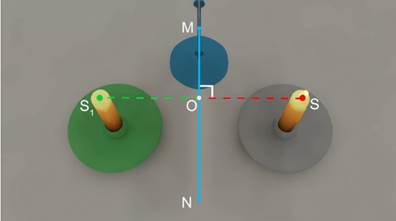
Рис.  . Местоположение изображения горящей свечи
. Местоположение изображения горящей свечи
Проведем еще ряд демонстраций, которые позволят нам охарактеризовать изображения в плоских зеркалах.
Возьмем плоское зеркало, линейку и ластик. Сначала линейку расположим так, чтобы ее ноль располагался около зеркала (рис.  ).
).

Рис.  . Расстояние от зеркала до предмета и его изображения
. Расстояние от зеркала до предмета и его изображения
В результате мы увидим, что расстояние от зеркала до предмета равно расстоянию от зеркала до изображения предмета в зеркале. Сделаем на ластике отметку. Мы увидим, что изображение в зеркале симметрично самому предмету, однако не является тождественным (рис.  ).
).

Рис.  . Симметричность предмета и его изображения в зеркале
. Симметричность предмета и его изображения в зеркале
Благодаря проведенным демонстрациям можно установить общие характеристики изображений в плоских зеркалах:
- Плоское зеркало дает мнимое изображение предмета.
- Изображение предмета в плоском зеркале равно по размеру самому предмету и расположено на том же расстоянии от зеркала, что и предмет.
- Прямая, которая совмещает точку на предмете с соответствующей ей точкой на изображении предмета в зеркале, перпендикулярна поверхности зеркала.
Решение задач
Задача № 1
Почему на машинах скорой помощи надписи пишутся «перевернутыми»?
Решение
Водители других автомобилей должны быстро и безошибочно определить машину скорой помощи в потоке других машин, чтобы уступить ей дорогу. Такая ситуация возникает тогда, когда скорой помощи необходимо обогнать автомобиль и водитель может увидеть ее только в зеркало заднего вида.
Как мы уже знаем, изображение в зеркале не является тождественным, а является симметричным. Поэтому на машине скорой помощи пишут текст «перевернутым», чтобы водитель в зеркале заднего вида видел правильную надпись и мог своевременно совершить необходимые маневры.
Задача № 2
Какая минимальная высота должна быть у плоского зеркала, чтобы вы могли увидеть себя в нем в полный рост?
Решение
Изображение в зеркале равно предмету, расположенному перед зеркалом, и находится на том же расстоянии от зеркала, что и предмет. Нарисуем рисунок с изображением человека, стоящего перед зеркалом (рис. 16).

Рис. 16. Изображение человека, стоящего перед зеркалом
Закон отражения света. Плоское зеркало. Видеоурок. Физика 11 Класс
Как мы видим подавляющее большинство предметов вокруг нас, ведь они не являются источниками света? Ответ вам хорошо знаком, вы его получили еще в курсе физики 8 класса. Мы видим окружающий нас мир за счет отражения света.
Для начала вспомним определение.
Когда световой луч падает на границу раздела двух сред, он испытывает отражение, то есть возвращается в исходную среду.
Обратите внимание на следующее: отражение света – это далеко не единственный возможный исход дальнейшего поведения падающего луча, частично он проникает в другую среду, то есть поглощается.
Поглощение света (абсорбция) – явление потери энергии световой волной, проходящей через вещество.
Построим падающий луч 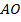 , отраженный луч
, отраженный луч 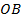 и перпендикуляр
и перпендикуляр 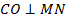 в точку падения
в точку падения 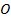 (рис. 1.).
(рис. 1.).
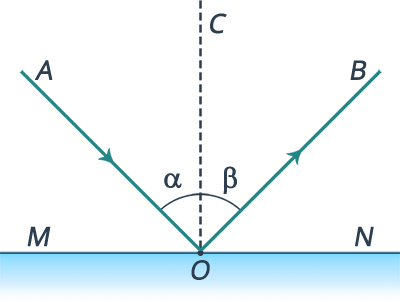
Рис. 1. Падающий луч
Углом падения называется угол между падающим лучом и перпендикуляром (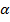 ),
),
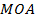 – угол скольжения.
– угол скольжения.
Эти законы впервые были сформулированы Евклидом в его труде «Катоптрика». И с ними мы уже ознакомились в рамках программы физики 8 класса.
Законы отражения света
1. Падающий луч, отраженный луч и перпендикуляр в точку падения лежат в одной плоскости.
2. Угол падения равен углу отражения.
Из закона отражения света следует обратимость световых лучей. То есть если мы поменяем местами падающий луч и отраженный, то ничего не изменится с точки зрения траектории распространения светового потока.
Спектр применения закона отражения света весьма широк. Это и тот факт, с которого мы начали урок, что большинство предметов вокруг нас мы видим именно в отраженном свете (луну, дерево, стол). Еще одним хорошим примером использования отражения света являются зеркала и светоотражатели (катафоты).
Катафоты
Разберемся в принципе работы простого световозвращателя.
Катафот (от древнегреческого kata – приставка со значением усилия, fos – «свет»), световозвращатель, фликер (от англ. flick – «мигать») – устройство, предназначенное для отражения луча света в сторону источника с минимальным рассеиванием.
Каждый велосипедист знает, что передвижение в темное время суток без наличия катафотов может быть опасным.
Также фликеры используются в униформах дорожных рабочих, сотрудников ГИБДД.
Как ни удивительно, свойство катафота основано на простейших геометрических фактах, в частности на законе отражения.
Отражение луча от зеркальной поверхности происходит по закону: угол падения равен углу отражения. Рассмотрим плоский случай: два зеркала, образующих угол в 90 градусов. Луч, идущий в плоскости и попадающий на одно из зеркал, после отражения от второго зеркала уйдет ровно в том направлении, в котором пришел (см. рис. 2).
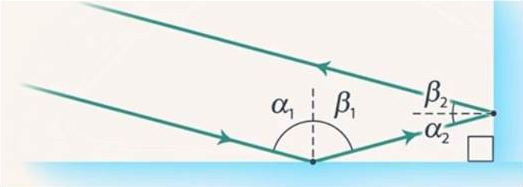
Рис. 2. Принцип действия углового катафота
Для получения такого эффекта в обычном трехмерном пространстве необходимо расположить три зеркала во взаимно перпендикулярных плоскостях. Возьмем уголок куба с краем в виде правильного треугольника. Луч, попавший на такую систему зеркал, после отражения от трех плоскостей уйдет параллельно пришедшему лучу в обратном направлении (см. рис. 3.).
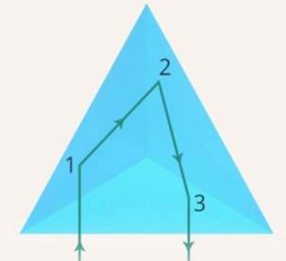
Рис. 3. Уголковый отражатель
Произойдет световозвращение. Именно это простое устройство с его свойствами и называют уголковым отражателем.
Рассмотрим отражение плоской волны (волна называется плоской, если поверхности равной фазы представляют собой плоскости) (рис. 1.)
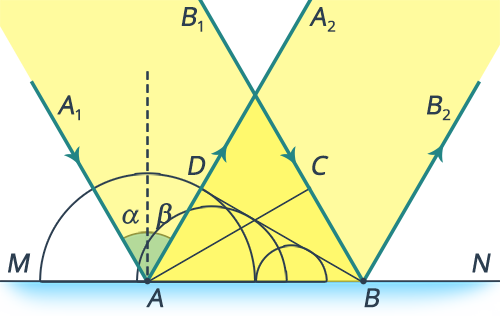
Рис. 4. Отражение плоской волны
На рисунке 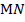 – поверхность,
– поверхность, 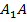 и
и 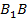 – два луча падающей плоской волны, они параллельны друг другу, а плоскость
– два луча падающей плоской волны, они параллельны друг другу, а плоскость  – волновая поверхность. Волновую поверхность отраженной волны можно получить, если провести огибающую вторичных волн, центры которых лежат на границе раздела сред.
– волновая поверхность. Волновую поверхность отраженной волны можно получить, если провести огибающую вторичных волн, центры которых лежат на границе раздела сред.
Различные участки волновой поверхности  достигают отражающей границы не одновременно. Возбуждение колебаний в точке
достигают отражающей границы не одновременно. Возбуждение колебаний в точке 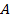 начнется раньше, чем в точке
начнется раньше, чем в точке 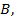 на промежуток времени
на промежуток времени 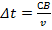 . В момент когда волна достигнет точки
. В момент когда волна достигнет точки 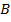 и в этой точке начнется возбуждение колебаний, вторичная волна с центром в точке
и в этой точке начнется возбуждение колебаний, вторичная волна с центром в точке 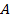 (отраженный луч
(отраженный луч 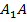 ) уже будет представлять собой полусферу радиусом
) уже будет представлять собой полусферу радиусом 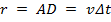 . Исходя из того, что мы только что записали, этот радиус так же будет равен отрезку
. Исходя из того, что мы только что записали, этот радиус так же будет равен отрезку 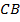 .
.
Теперь мы видим: 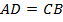 , треугольники
, треугольники 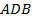 и
и 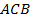 – прямоугольные, а значит,
– прямоугольные, а значит, 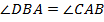 . А в свою очередь,
. А в свою очередь, 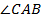 и есть угол падения
и есть угол падения 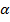 . А
. А  – угол отражения
– угол отражения 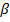 . Следовательно, мы получаем, что угол падения
. Следовательно, мы получаем, что угол падения 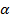 равен углу отражения
равен углу отражения 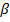 .
.
Итак, при помощи принципа Гюйгенса ми доказали закон отражения света. Получить это же доказательство можно, пользуясь принципом Ферма.
В качестве примера (рис. 5.) изображено отражение от волнообразной, шероховатой поверхности.
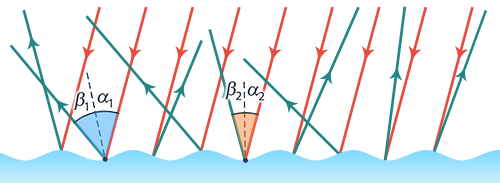
Рис. 5. Отражение от шероховатой, волнообразной поверхности
На рисунке видно, что отраженные лучи идут в самых различных направлениях, Ведь направление перпендикуляра к точке падения для разного луча будет разным, соответственно, и угол падения, и угол отражения тоже будут разными.
Но что считать неровной поверхностью и какие из поверхностей можно назвать ровными?
Поверхность считается неровной, если размеры ее неровностей не меньше длины световых волн.
Поверхность, которая будет отражать лучи во все стороны равномерно, называется матовой. Таким образом, матовая поверхность гарантирует нам рассеянное или диффузное отражение, которое возникает вследствие неровностей, шероховатостей, царапин.
Поверхность, которая равномерно рассевает свет во все стороны, называется абсолютно матовой. В природе абсолютно матовую поверхность вы не встретите, тем не менее к ним очень близки поверхность снега, бумаги и фарфора.
Если же размер неровностей поверхности меньше длинны световой волны, то такая поверхность будет называться зеркальной.
При отражении от зеркальной поверхности параллельность пучка сохраняется (рис. 6.).
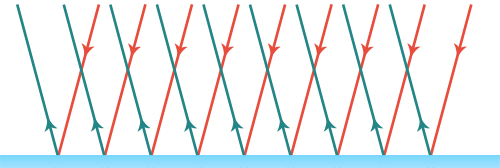
Рис. 6. Отражение от зеркальной поверхности
Приблизительно зеркальной является гладкая поверхность воды, стекла и полированного металла. Даже матовая поверхность может оказаться зеркальной, если изменить угол падения лучей.
В начале урока мы говорили о том, что часть падающего луча отражается, а часть поглощается. В физике есть величина, которая характеризует, какая доля энергии падающего луча отразилась, а какая поглотилась.
Альбедо
Альбедо – коэффициент, который показывает, какая доля энергии падающего луча отражается от поверхности, (от латинского albedo – «белизна») – характеристика диффузной отражательной способности поверхности.
Или иначе – это доля, выраженная в процентах отраженной радиации энергии от поступающей на поверхность.
Чем ближе альбедо к ста, тем больше энергия отражается от поверхности. Несложно догадаться, что коэффициент альбедо зависит от цвета поверхности, в частности, от белой поверхности энергия будет значительно лучше отражаться, чем от черной.
Самое большое альбедо для веществ у снега. Оно составляет порядка 70–90 %, в зависимости от его новизны и сорта. Именно поэтому снег медленно тает, пока он свежий, а точнее белый. Значения альбедо для других веществ, поверхностей указаны на рисунке 7.


Рис. 7. Значение альбедо для некоторых поверхностей
Очень важным примером применения закона отражения света являются плоские зеркала – плоская поверхность, которая зеркально отражает свет. Такие зеркала есть у вас в доме.
Разберемся, как строить изображение предметов в плоском зеркале (рис. 8.).

Рис. 8. Построение изображения предмета в плоском зеркале
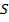 – точечный источник света, испускающий лучи в разные направления, возьмем два близких луча, падающих на плоское зеркало. Отраженные лучи пойдут так, будто они исходят из точки
– точечный источник света, испускающий лучи в разные направления, возьмем два близких луча, падающих на плоское зеркало. Отраженные лучи пойдут так, будто они исходят из точки 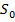 , которая симметрична точке
, которая симметрична точке 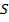 относительно плоскости зеркала. Самое интересное начнется, когда отраженные лучи попадут нам в глаз: наш мозг сам достраивает расходящийся пучок, продолжая его за зеркало до точки
относительно плоскости зеркала. Самое интересное начнется, когда отраженные лучи попадут нам в глаз: наш мозг сам достраивает расходящийся пучок, продолжая его за зеркало до точки 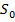
Нам кажется, что отраженные лучи исходят из точки 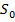 .
.
Эта точка и служит изображением источника света 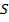 . Конечно же, в реальности за зеркалом ничего не светится, это всего лишь иллюзия, поэтому эту точку называют мнимым изображением.
. Конечно же, в реальности за зеркалом ничего не светится, это всего лишь иллюзия, поэтому эту точку называют мнимым изображением.
От расположения источника и размеров зеркала зависит область видения – область пространства, из которой видно изображение источника. Область видения задается краями зеркала 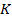 и
и 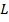 .
.
Например, в зеркало в ванной можно смотреться под определенным углом, если отойти от него вбок, то вы себя или предмет, который хотите рассмотреть, не увидите.
Для того чтобы построить изображение произвольного предмета в плоском зеркале, необходимо построить изображение каждой его точки. Но если мы знаем, что изображение точки симметрично относительно плоскости зеркала, то и изображение предмета будет симметричным относительно плоскости зеркала (рис. 9.)
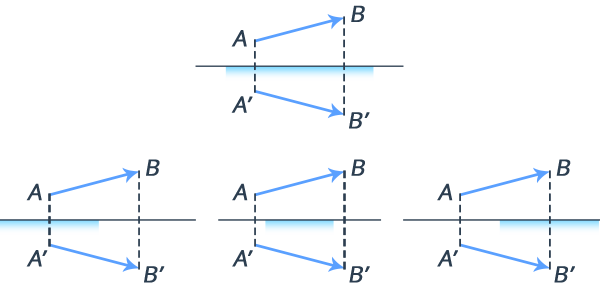
Рис. 9. Симметричное отражение объекта относительно плоскости зеркала
Еще одним применением зеркалу является создание перископа, который является прибором для наблюдений из укрытия.
На этом уроке мы не только ознакомились с законом отражения, но и доказали его с помощью уже известного нам принципа Гюйгенса. Кроме того, мы научились строить изображения предметов в плоском зеркале и характеризовать их.
Разбор задачи на закон отражения света
Задача № 1
Ученики исследовали соотношение между скоростями автомобильчика и его изображения в плоском зеркале в системе отсчета, связанной с зеркалом.Проекция на ось 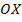 вектора скорости, с которой движется изображение, в этой системе отсчета равна:
вектора скорости, с которой движется изображение, в этой системе отсчета равна:
1.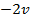 ; 2.
; 2. 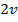 ; 3.
; 3. 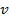 ; 4.
; 4.  (см. рис. 10.)
(см. рис. 10.)
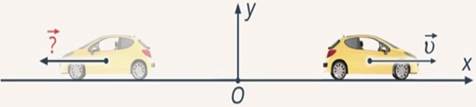
Рис. 10. Иллюстрация к задаче
Решение
Вспомним, что изображение в плоском зеркале расположено симметрично объекту относительно зеркальной плоскости. Это значит, что если за время 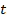 автомобиль совершит перемещение
автомобиль совершит перемещение 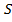 , то изображение, которое расположено симметрично, за то же время совершит перемещение
, то изображение, которое расположено симметрично, за то же время совершит перемещение 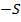 и, следовательно, изображение отдаляется от зеркала со скоростью
и, следовательно, изображение отдаляется от зеркала со скоростью 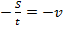 . Проекция на ось
. Проекция на ось 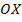 будет равна
будет равна  .
.
Ответ: 4. 
Список литературы
1. Жилко В.В., Маркович Я.Г. Физика. 11 класс. – 2011.
2. Мякишев Г.Я., Буховцев Б.Б., Чаругин В.М. Физика. 11 класс. Учебник.
3. Касьянов В.А. Физика, 11 класс. – 2004.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Интернет портал «Физика для всех» (Источник)
2. Интернет портал Единой коллекции цифровых образовательных ресурсов (Источник)
3. Интернет портал «diplomivanov.narod.ru» (Источник)
Домашнее задание
1. Постройте изображения АВ в плоском зеркале
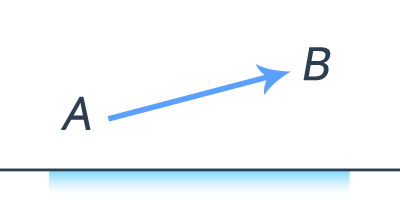
2. Постройте изображение в плоском зеркале
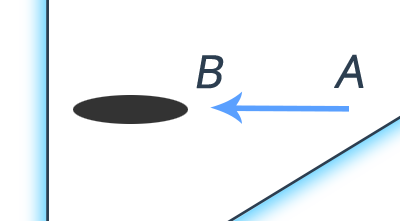
Геометрическая оптика: зеркала
В этой статье собраны задачи на плоское зеркало. Угол падения равен углу отражения – это все, что нужно помнить для их решения.
Задача 1. Почему мы не видим лица фехтовальщика, если оно закрыто частой сеткой, но она не мешает самому фехтовальщику хорошо видеть окружающие предметы?
Снаружи свет проникает сквозь сетку, и фехтовальщику хватает этих лучей, чтобы хорошо видеть. Чтобы мы могли увидеть его лицо, нужно, чтобы отраженный луч попал в глаза наблюдателя, а так как сквозь сетку попадает мало лучей на пути туда, и не все отраженные лучи проникают обратно (мешает сетка), и тем более далеко не все из вышедших лучей попадут в глаза наблюдателя, – мы не видим лица фехтовальщика.
Задача 2. Почему в свете фар автомобиля лужа на асфальте кажется водителю темным пятном?
Свет, отраженный от лужи, не попадает в глаза водителя.
Задача 3. С помощью плоского зеркала надо осветить дно глубокого колодца. Солнечные лучи составляют с поверхностью земли угол 30°. Под каким углом к вертикали надо расположить плоское зеркало, чтобы выполнить задуманное?

К задаче 3
Для развернутого угла плоскости зеркала, глядя на рисунок, запишем:
![Rendered by QuickLaTeX.com \[2\beta+90^{\circ}+30^{\circ}=180^{\circ}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-c2baf9683a589828f0439258f23b9aa5_l3.png)
![Rendered by QuickLaTeX.com \[2\beta=60^{\circ}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a87094d119752db258de2dd68896426a_l3.png)
![Rendered by QuickLaTeX.com \[\beta=30^{\circ}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-bbf170306158cbc97784fda63b6348db_l3.png)
Таким образом, с горизонталью зеркало составляет  , а с вертикалью тогда –
, а с вертикалью тогда –  .
.
Ответ:  .
.
Задача 4. Человек, идущий по шоссе, увидел в лобовом стекле встречного автомобиля Солнце. Под каким углом наклонено к горизонту это стекло, если высота Солнца над горизонтом равна  , а отраженный от стекла луч попадает в глаза наблюдателя по горизонтальному направлению? Считайте, что Солнце, человек и автомобиль находятся в одной плоскости.
, а отраженный от стекла луч попадает в глаза наблюдателя по горизонтальному направлению? Считайте, что Солнце, человек и автомобиль находятся в одной плоскости.

К задаче 4
Так как угол падения равен углу отражения, то  – это сумма этих двух углов, откуда следует, что угол падения лучей на стекло автомобиля равен
– это сумма этих двух углов, откуда следует, что угол падения лучей на стекло автомобиля равен  .
.
Искомый угол обозначен на рисунке  , он равен
, он равен
![Rendered by QuickLaTeX.com \[\delta=90^{\circ}-9^{\circ}=81^{\circ}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-21530c11e9c6b38af6394ba42886ec90_l3.png)
Ответ:  .
.
Задача 5. Человек, стоящий на берегу озера, видит в гладкой поверхности воды изображение Солнца. Как будет перемещаться это изображение при удалении человека от озера? Солнечные лучи считать параллельными.

К задаче 5
Из рисунка видно, что изображение будет передвигаться по направлению к берегу, пока не исчезнет.
Задача 6. В комнате вертикально висит зеркало, верхний край которого расположен на уровне волос верхней части головы человека ростом 182 см. Какой наименьшей длины должно быть зеркало, чтобы этот человек видел себя во весь рост?

К задаче 6
Так как изображение располагается на таком же расстоянии, какое отделяет человека от зеркала, то треугольники  и
и  подобны с коэффициентом подобия
подобны с коэффициентом подобия  . Поэтому зеркало должно быть вдвое меньше по размеру, чем рост человека, то есть 91 см.
. Поэтому зеркало должно быть вдвое меньше по размеру, чем рост человека, то есть 91 см.
Ответ: 91 см.
Задача 7. Сбоку от зеркала в точке А стоит один человек. Второй человек из точки В идет по направлению к плоскому зеркалу по прямой, проходящей перпендикулярно через середину зеркала. На каком расстоянии от зеркала будет точка В в момент, когда оба человека увидят друг друга в зеркале?

К задаче 7
Из рисунка видно, что угол падения луча из точки  на зеркало равен
на зеркало равен  . Отражаться луч будет под таким же углом. Следовательно, человек из точки
. Отражаться луч будет под таким же углом. Следовательно, человек из точки  должен переместиться в точку
должен переместиться в точку  , чтобы он мог увидеть человека
, чтобы он мог увидеть человека  . Из подобия треугольников, образованных лучами и стенами видно, что расстояние от зеркала до
. Из подобия треугольников, образованных лучами и стенами видно, что расстояние от зеркала до  будет равно половине ширины зеркала – 0,5 м.
будет равно половине ширины зеркала – 0,5 м.
Ответ: 0,5 м.
Плоские и сферические зеркала
С зеркалом мы сталкиваемся очень часто. Даже оконное стекло или поверхность воды пруда тоже вполне могут служить плоскими зеркалами. Рассмотрим изображения, получающиеся при этом.
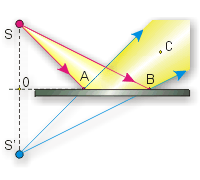
Пусть свет источника S падает на зеркало. Отразившись от него, лучи SA и SB пойдут так, как показано на чертеже синими стрелками. Если глаз расположить в точке С, то наблюдатель увидит, что источник света находится позади зеркала, в точке S’. Заметим, что из построения видно: отрезки OS и OS’ равны, а отрезок SS’ перпендикулярен плоскости зеркала.
Итак, изображения предметов в плоском зеркале являются мнимыми, так как кажутся расположенными там, где свет отсутствует. Кроме того, изображения находятся позади зеркала на таком же расстоянии от него, как и сами предметы, и равны им по размерам. Эти выводы мы получили геометрическим построением, теперь проверим их опытом.
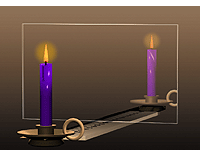
Положим на стол линейку, поверх неё поставим стекло. Оно будет служить полупрозрачным зеркалом. Поместив перед ним свечу, мы увидим её отражение. Оно будет казаться расположенным позади стекла. Однако, заглянув за стекло, мы не увидим изображения. То есть изображение в плоском зеркале является мнимым.
Чтобы убедиться в правильности второго вывода, измерим линейкой расстояния от стекла до свечи и от стекла до изображения, а также размеры свечи и её изображения. Они окажутся попарно равны. Следовательно, опыт подтверждает и второй вывод. Примечание: вместо зеркала мы использовали стекло, чтобы одновременно видеть изображение свечи и деления линейки.
Кроме плоских зеркал, существуют сферические, параболические, эллиптические и другие зеркала. Они применяются в прожекторах и телескопах. Сферические зеркала представляют собой часть шарообразной поверхности и могут быть выпуклыми или вогнутыми (см. рисунок-чертёж).
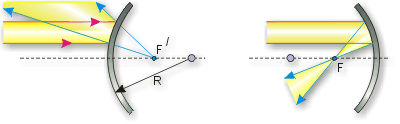
Направим параллельные лучи на выпуклое зеркало (левый чертёж). После отражения лучи станут расходящимися. Поэтому выпуклое зеркало называют рассеивающим зеркалом. Направим теперь лучи на вогнутое зеркало (правый чертёж). Сразу же после отражения лучи станут сходящимися. Поэтому вогнутое зеркало называют собирающим зеркалом.
Точки F и F’ называют главными фокусами зеркала. Фокус выпуклого (рассеивающего) зеркала является мнимым, так как световые лучи через него не проходят. Фокус вогнутого (собирающего) зеркала является действительным, так как через него лучи проходят.

Изображения предметов в выпуклом зеркале всегда уменьшенные. Например, на левом рисунке видно, что размеры изображений чашек значительно меньше размеров самих чашек. При помощи вогнутого зеркала можно получить увеличенные изображения предметов. Взгляните на правый рисунок. Размеры всех изображений больше размеров самих предметов. Наряду с изменением размеров изображений аналогичным образом изменяются расстояния между ними. На среднем рисунке для сравнения показано отражение в плоском зеркале.
Формула зеркала
Найдем связь между оптической характеристикой и расстояниями, определяющими положение предмета и его изображения.
Пусть предметом служит некоторая точка А, располагающаяся на оптической оси. Используя законы отражения света, построим изображение этой точки (рис. 2.13).
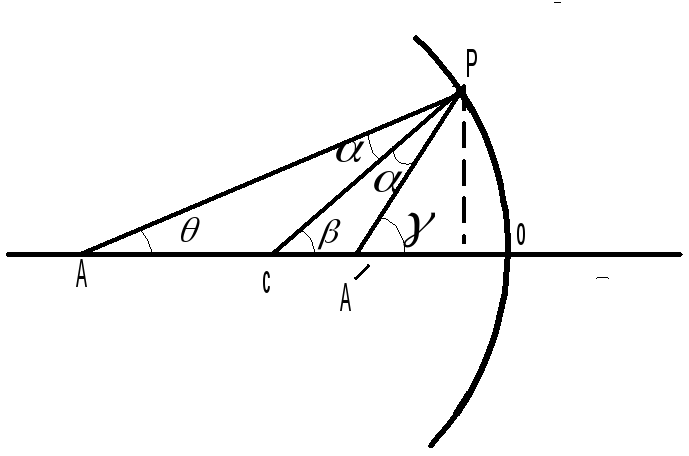
Рис.2.13
Обозначим
расстояние от предмета до полюса зеркала 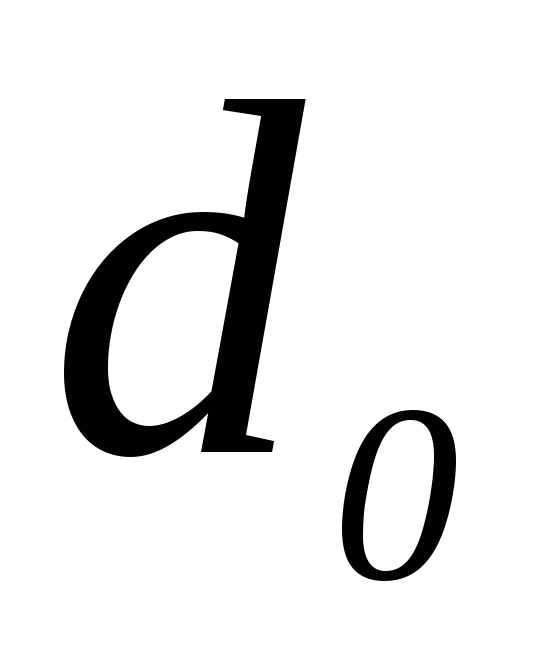 (АО),
а от полюса до изображения
(АО),
а от полюса до изображения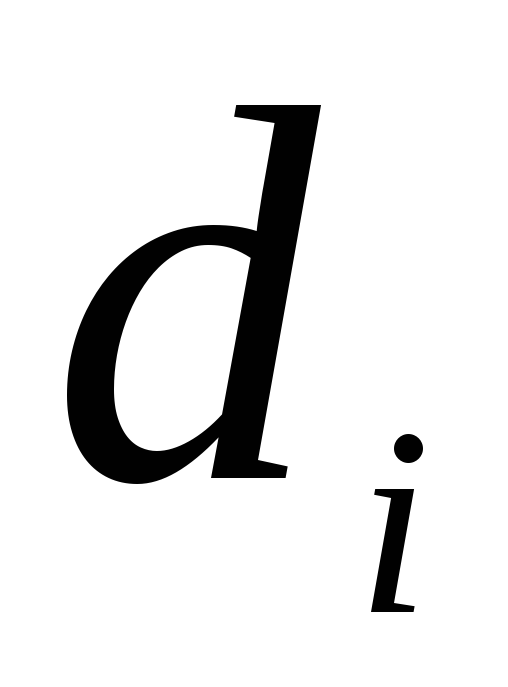 (ОА).
(ОА).
Рассмотрим
треугольник АРС, получаем, что 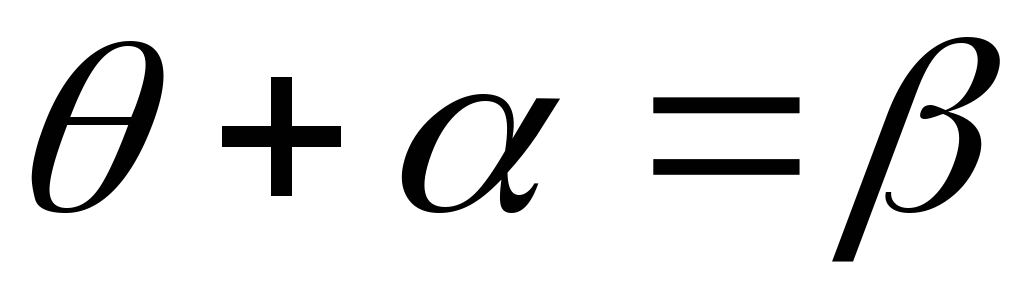
Из треугольника
АРА, получаем, что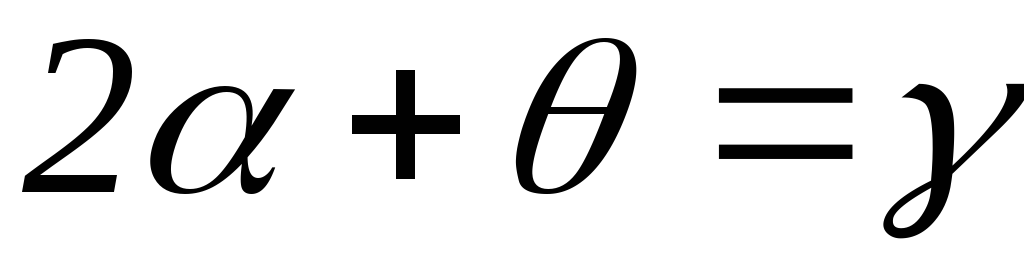 .
Исключим из этих выражений угол
.
Исключим из этих выражений угол ,
так как единственный который не опирается
на ОР.
,
так как единственный который не опирается
на ОР.
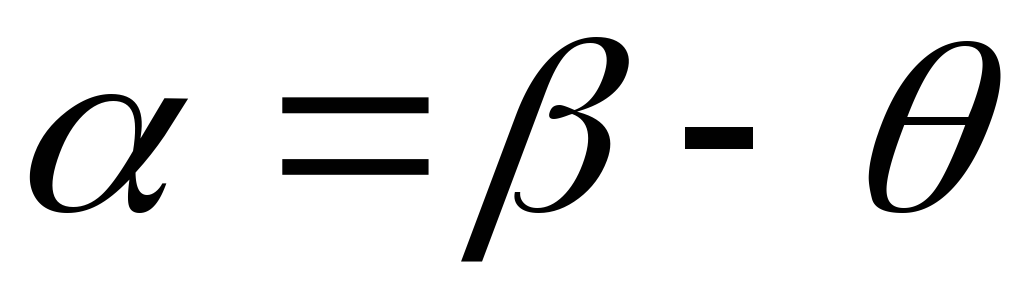 ,
,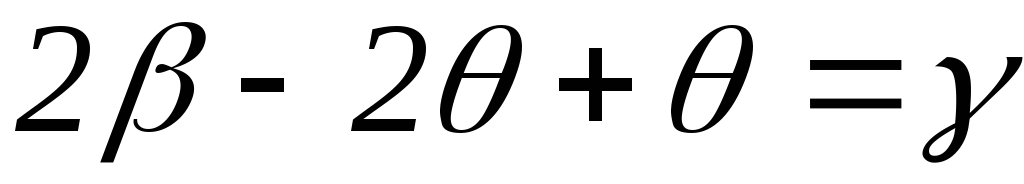 или
или
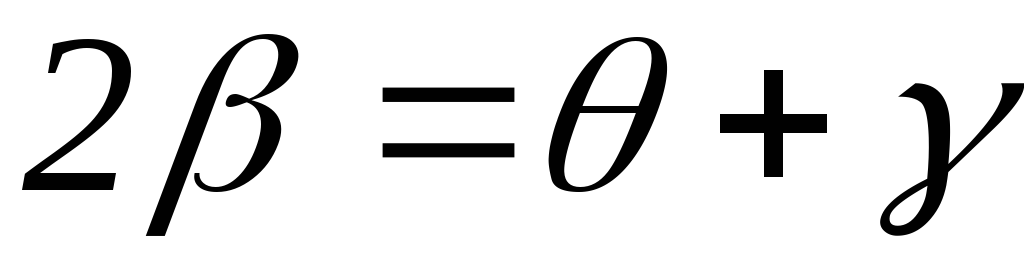 (2.3)
(2.3)
Углы ,,опираются на ОР. Пусть рассматриваемые пучки параксиальны, тогда эти углы малы и, следовательно, их значения в радианной мере равно тангенсу этих углов:
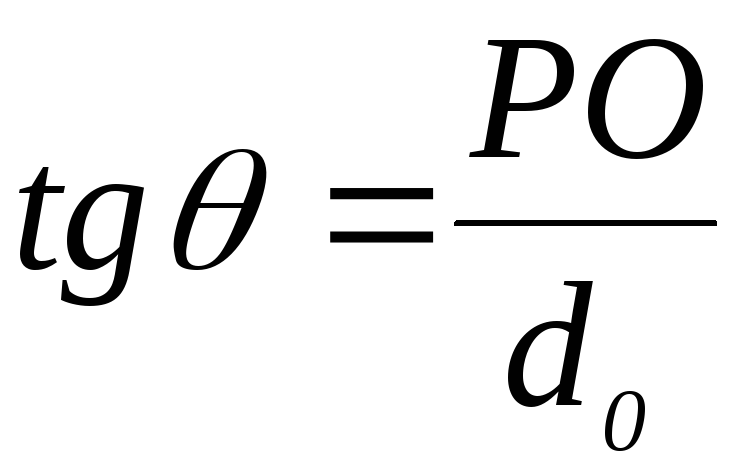 ;
;
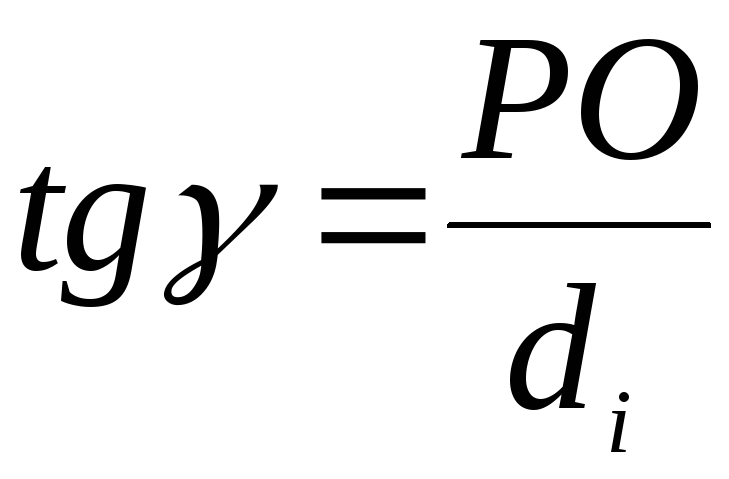 ;
;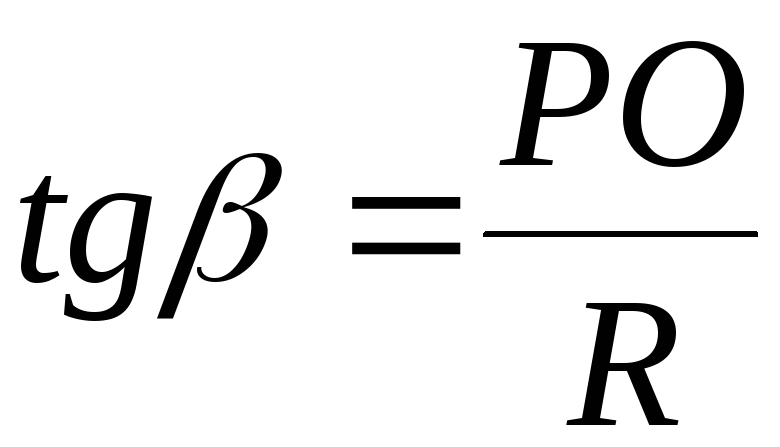 ,
гдеR=OC,
является радиусом кривизны зеркала.
,
гдеR=OC,
является радиусом кривизны зеркала.
Подставим полученные выражения в уравнение (2.3)
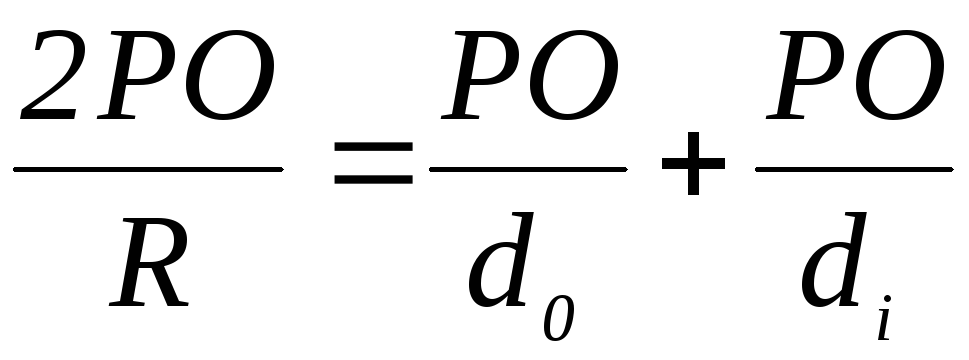
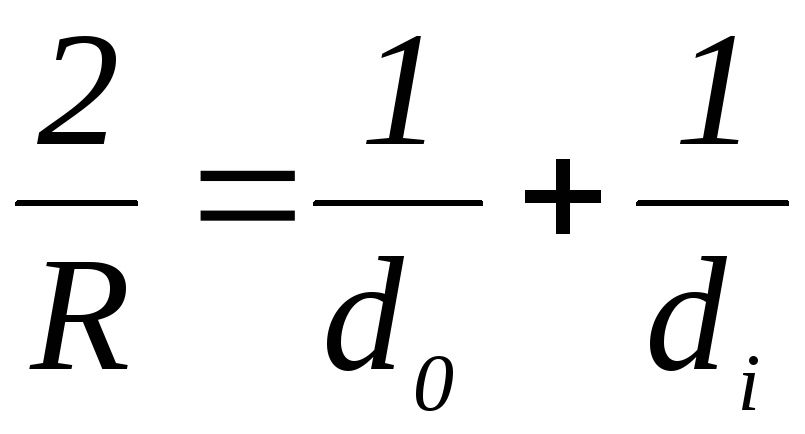
Так как мы ранее выяснили, что фокусное расстояние связано с радиусом кривизны зеркала, то
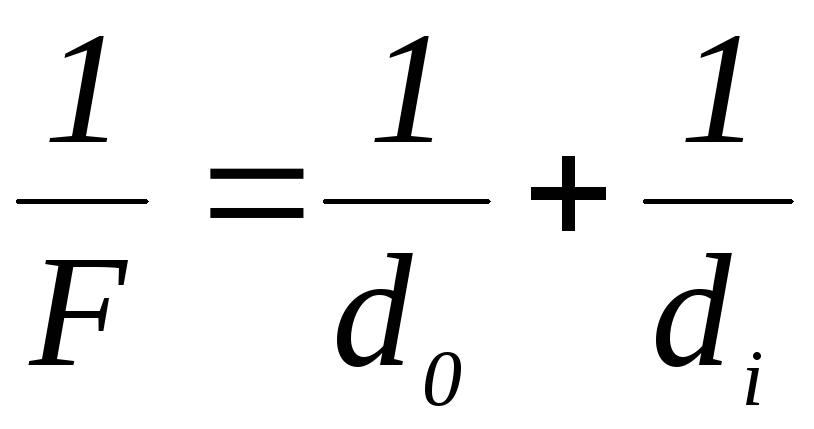 (2.4)
(2.4)
Выражение (2.4) называется формулой зеркала, которая используется лишь с правилом знаков:
Расстояния 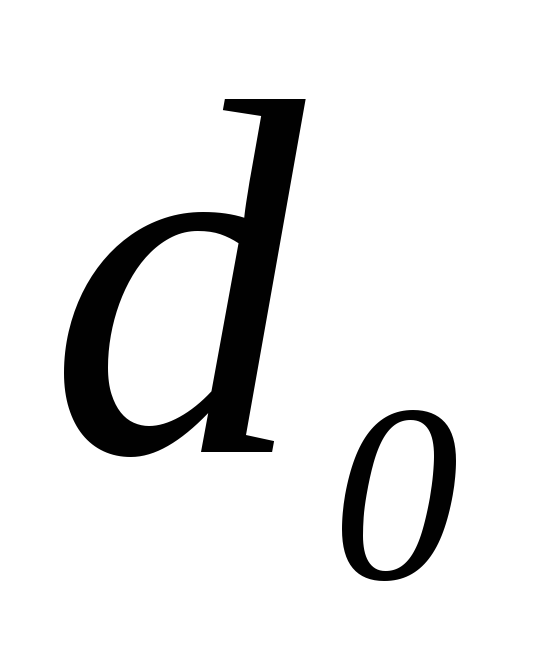 ,
,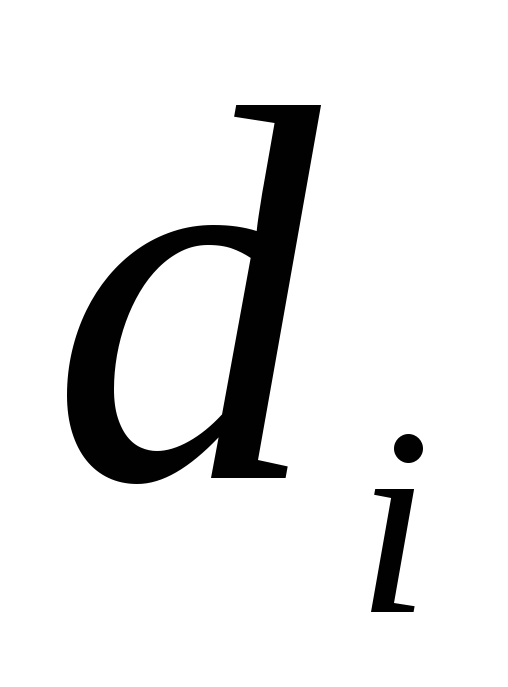 ,
,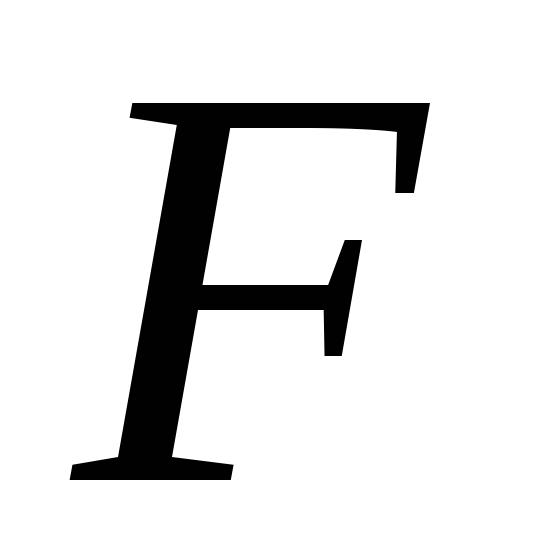 считаются положительными, если они
отсчитываются по ходу луча, и отрицательными
– в противном случае.
считаются положительными, если они
отсчитываются по ходу луча, и отрицательными
– в противном случае.
Выпуклое зеркало.
Рассмотрим несколько примеров на построение изображений в выпуклых зеркалах.
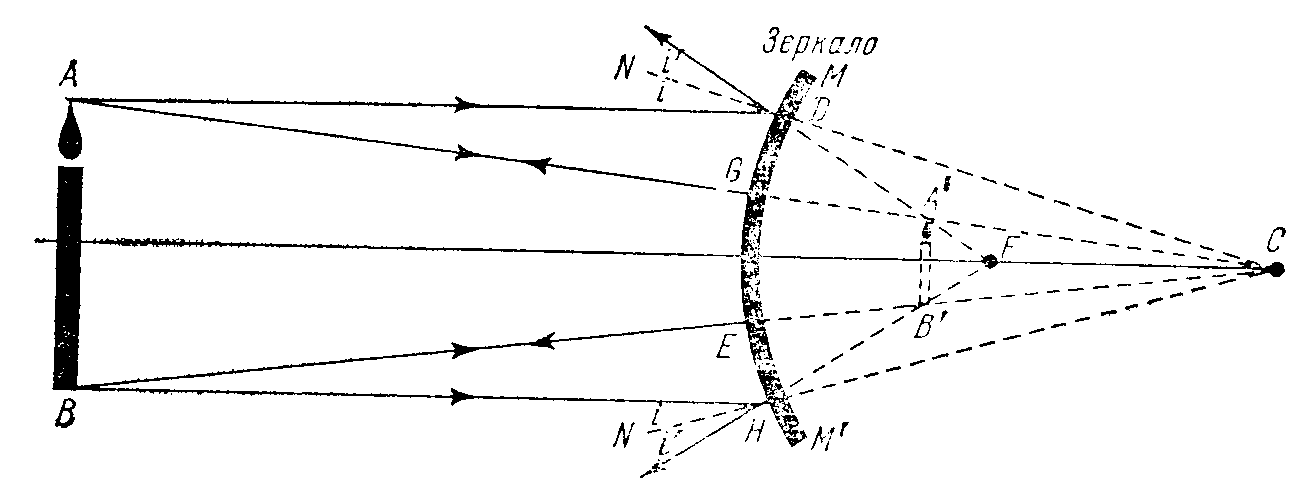
Рис. 2.14
1) Предмет расположен на расстоянии большем радиуса кривизны. Строим изображение концевых точек предмета А и В. Используем лучи: 1) параллельный главной оптической оси; 2) луч, проходящий через оптический центр зеркала. Получим изображение мнимое, уменьшенное, прямое.(рис.2.14)
Рис. 2.15.
2) Предмет расположен на расстоянии равном радиусу кривизны. Изображение мнимое, уменьшенное, прямое (рис.2.15)Фокус выпуклого зеркала мнимый. Формула выпуклого зеркала
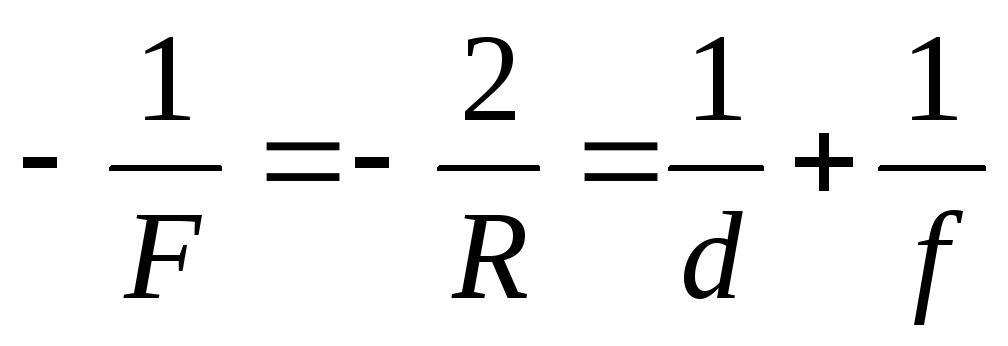 .
.
Правило знаков для d и f остается таким же, как и для вогнутого зеркала.
Линейное увеличение предмета определяется отношением высоты изображения к высоте самого предмета
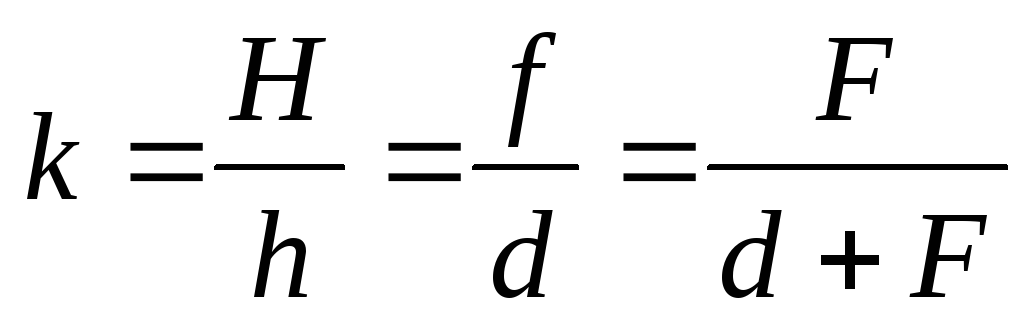 . (2.5)
. (2.5)
Таким образом, независимо от расположения предмета относительно выпуклого зеркала изображение оказывается всегда мнимым, прямым, уменьшенным и расположенным за зеркалом. В то время как изображения в вогнутом зеркале более разнообразны, зависят от расположения предмета относительно зеркала. Поэтому вогнутые зеркала применяются чаще.
Рассмотрев принципы построения изображений в различных зеркалах, мы подошли к пониманию действия столь различных приборов, как астрономические телескопы и увеличивающие зеркала в косметических приборах и медицинской практике, мы способны сами спроектировать некоторые приборы.
Зеркальное отражение, диффузное отражение
Плоское зеркало.
Простейшей оптической системой является плоское зеркало. Если параллельный пучок лучей, падающий на плоскую поверхность раздела двух сред, после отражения остается параллельным, то отражение называется зеркальным, а сама поверхность называется плоским зеркалом (рис. 2.16).
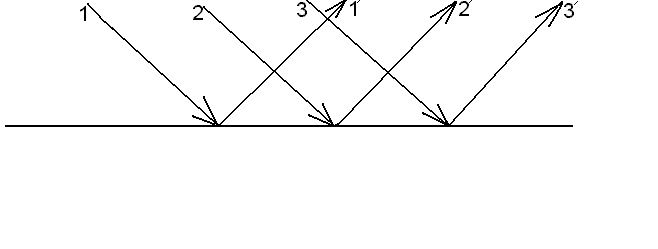
Рис.2.16
Изображения в плоских зеркалах строятся на основании закона отражения света. Точечный источник S (рис.2.17) дает расходящийся пучок света, построим отраженный пучок. Восстановим перпендикуляр в каждую точку падения и отраженный луч изображаем из условияÐa=Ðb(Ða1=Ðb1, Ða2=b2и т.д.) Получаем расходящийся пучок отраженных лучей, продолжаем эти лучи до пересечения, точка их пересечения S¢является изображением точки S, это изображение будет мнимым. 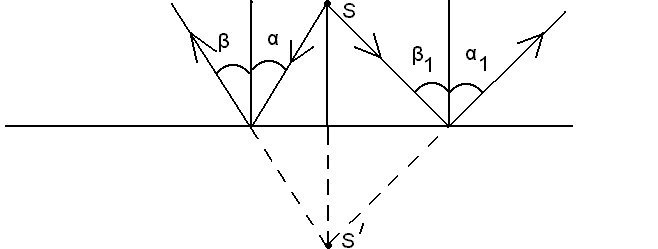
Рис. 2.17
Изображение прямой линии AB можно построить, соединяя прямой изображения двух концевых точек А¢и В¢. Измерения показывают, что это изображение находится на таком же расстоянии за зеркалом, на каком предмет находится перед зеркалом, и, что размеры его изображения такие же, как и размеры предмета. Изображение, образующееся в плоском зеркале, обращенное и мнимое (см. рис.2.18). 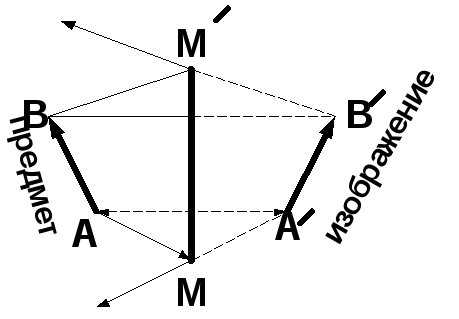
Рис.2.18
Если отражающая поверхность шероховата, то отражение неправильное и свет рассеивается, или диффузно отражается (рис.2.19)
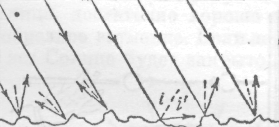
Рис. 2.19
Диффузное отражение гораздо более приятно для глаза, чем отражение гладкими поверхностями, называемое правильным отражением.
Линзы.
Линзы, также как и зеркала являются оптическими системами, т.е. способны изменять ход светового луча. Линзы по форме могут быть различными: сферическими, цилиндрическими. Мы остановимся только на сферических линзах.
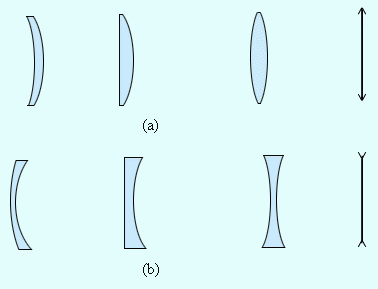
Прозрачное тело, ограниченное двумя сферическими поверхностями, называется линзой.
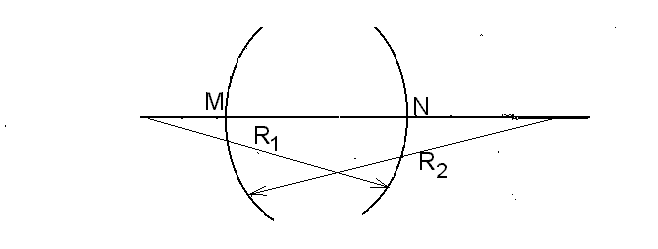
Рис.2.20
Прямую линию, на которой лежат центры сферических поверхностей, называют главной оптической осью линзы. Главная оптическая ось линзы пересекает сферические поверхности в точках М и N – это вершины линзы. Если расстоянием MN можно пренебречь по сравнению с R1 и R2, то линза называется тонкой. В этом случае (×)М совпадает с (×)N и тогда (×)М будет называться оптическим центром линзы. Все прямые, проходящие через оптический центр линзы, кроме главной оптической оси называются побочными оптическими осями (рис.2.20).Собирающие линзы. Фокусомсобирающей линзы называется точка, в которой пересекаются параллельные оптической оси лучи после преломления в линзе. Фокус собирающей линзы – действительный. Фокус, лежащий на главной оптической оси, называется главным фокусом. Любая линза имеет два главных фокуса: передний (со стороны падающих лучей) и задний (со стороны преломленных лучей). Плоскость, в которой лежат фокусы, называется фокальной плоскостью. Фокальная плоскость всегда перпендикулярна главной оптической оси и проходит через главный фокус. Расстояние от центра линзы до главного фокуса называется главным фокусным расстоянием F (рис.2.21).
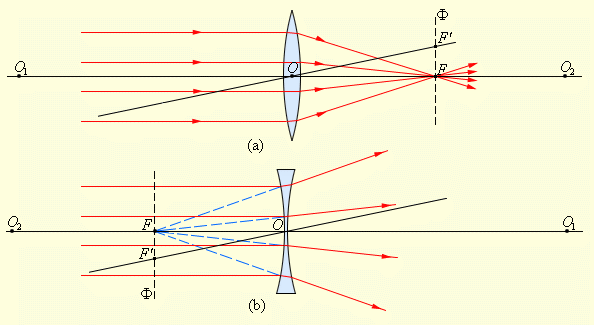
Рис.2.21
Для построения изображений какой- либо светящейся точки следует проследить ход любых двух лучей, падающих на линзу и преломленных в ней до их пересечения (или пересечения их продолжения). Изображение протяженных светящихся предметов представляет собой совокупность изображений отдельных его точек. Наиболее удобными лучами, используемыми при построении изображений в линзах, являются следующие характерные лучи:
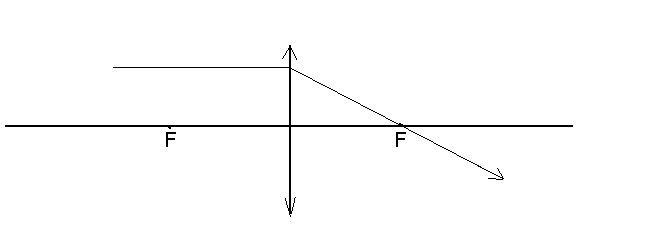
Рис.2.22
1) луч, падающий на линзу параллельно какой-либо оптической оси, после преломления пройдет через фокус, лежащий на этой оптической оси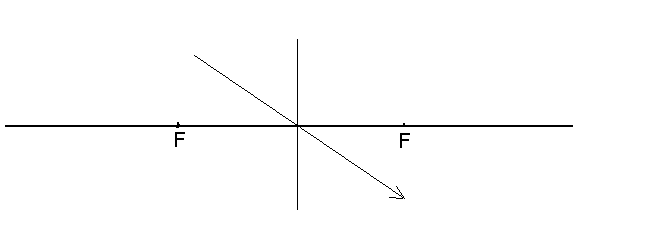
Рис.2.23
Рис.6
2) луч, идущий вдоль оптической оси, не меняет своего направления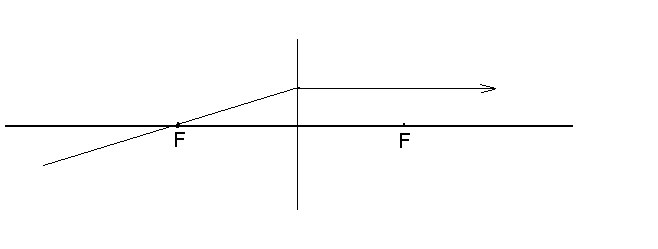
Рис. 2.24
3) луч, проходящий через передний фокус, после преломления в линзе пойдет параллельно главной оптической оси;На рисунке 2.25 продемонстрировано построение изображения точки А предмета АВ.
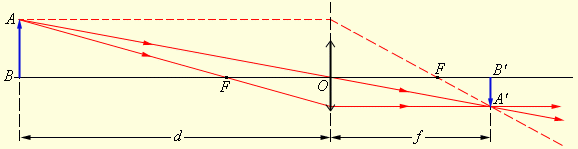
Рис.2.25
Кроме перечисленных лучей при построении изображений в тонких линзах используют лучи, параллельные какой-либо побочной оптической оси. Следует иметь в виду, что лучи, падающие на собирающую линзу пучком, параллельным побочной оптической оси, пересекают заднюю фокальную поверхность в той же точке, что и побочная ось.
Формула тонкой линзы:
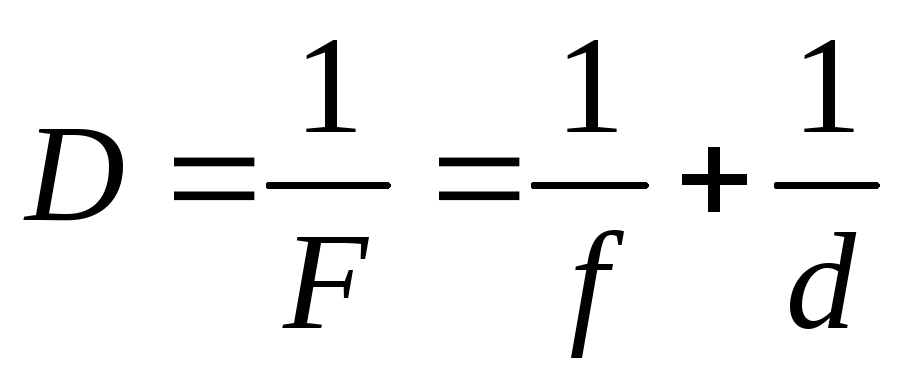 , (2.6)
, (2.6)
где F — фокусное расстояние линзы; D — оптическая сила линзы; d — расстояние от предмета до центра линзы; f — расстояние от центра линзы до изображения. Правило знаков будет таким же, как и для зеркала: все расстояния до действительных точек считаются положительными, все расстояния до мнимых точек считаются отрицательными.
Линейное увеличение, даваемое линзой,
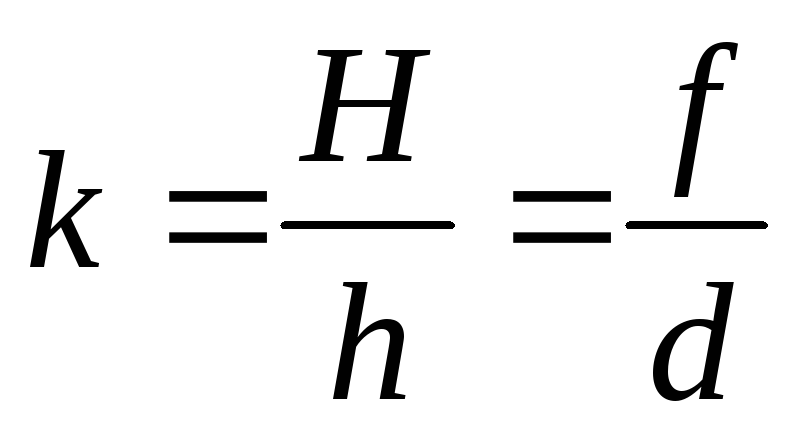 , (2.7)
, (2.7)
где H — высота изображения; h — высота предмета.
Рассеивающие линзы. Лучи, падающие на рассеивающую линзу параллельным пучком, расходятся так, что их продолжения пересекаются в точке, называемоймнимым фокусом.
Правила хода лучей в рассеивающей линзе:
Рис.2.26
1) лучи, падающие на линзу параллельно какой-нибудь оптической оси, после преломления пойдут так, что их продолжения пройдут через фокус, лежащий на оптической оси (рис. 2.26):2)луч, идущий вдоль оптической оси, не меняет своего направления.
Формула рассеивающей линзы:
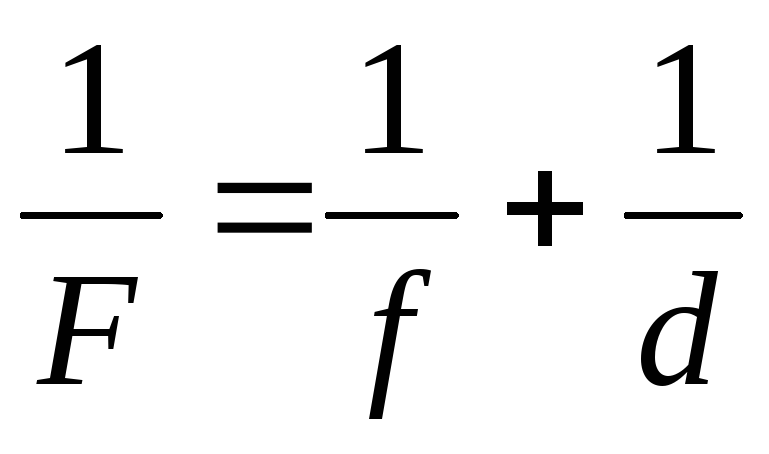
(правило знаков остается прежним).
На рисунке 2.27 приведен пример построения изображений в рассеивающих линзах.

Рис.2.27

