Существует ли зависимость напряжения от частоты?
Казалось бы, раскрыть зависимость напряжения от частоты просто. Стоит только обратиться с соответствующим запросом ко всезнающим поисковым системам и… убедиться, что ответа на этот вопрос попросту нет. Что же предпринять? Давайте разбираться вместе в этом непростом вопросе.
Напряжение или разность потенциалов?
Надо заметить, что напряжение и разность потенциалов — это одно и то же. По сути, это сила, которая способна заставить электрические заряды двигаться потоком. Не имеет значения, куда будет направлено это движение.
Разность потенциалов — просто другое выражение для напряжения. Оно нагляднее и, может быть, понятнее, но сути дела не меняет. Поэтому главный вопрос состоит в том, откуда берется напряжение, и от чего оно зависит.
В том, что касается домашней сети 220 Вольт, ответ простой. На гидростанции поток воды вращает ротор генератора. Энергия вращения трансформируется в силу напряжения. Атомная электростанция вначале превращает воду в пар. Он и крутит турбину. В бензоэлектростанции ротор вращает сила сгорающего бензина. Есть и другие источники, но суть всегда одна и та же: энергия превращается в напряжение.
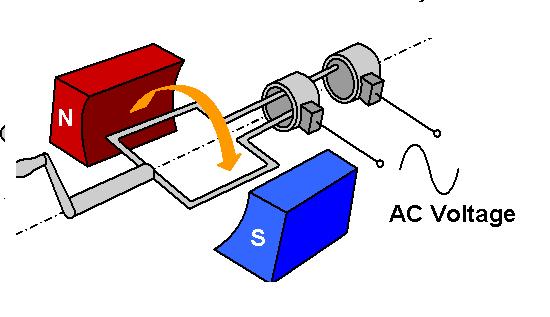
Самое время задаться вопросом о зависимости напряжения от частоты. Но мы еще не знаем, откуда берется частота.
Что является источником частоты
Тот же самый генератор. Частота его вращения превращается в одноименное свойство напряжения. Вращайте генератор быстрее — частота будет больше. И наоборот.
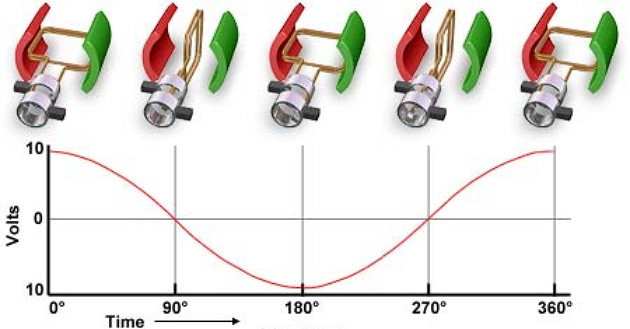
Хвост не может «вилять» собакой. По той же причине частота не может изменить напряжение. Следовательно, выражение «зависимость напряжения от частоты тока» не имеет смысла?
Чтобы найти ответ, надо правильно сформулировать вопрос. Есть такая присказка про глупца и 10 ученых мужей. Он задавал неправильные вопросы, а они не могли ответить.
Если назвать напряжение другим определением, все встанет на свои места. Оно применяется для цепей, состоящих из множества разных сопротивлений. «Падение напряжения». Оба выражения часто считаются синонимами, что почти всегда неправильно. Потому что падение напряжения действительно может зависеть от частоты.
С чего бы напряжению падать?
Да просто потому, что не может не падать. Итак. Если на одном полюсе источника потенциал равен 220 Вольт, а на другом — ноль, то это падение могло произойти только в цепи. Закон Ома говорит о том, что, если в сети имеется одно сопротивление, то все напряжение на нем и упадет. Если два и больше — каждое падение будет пропорционально его величине, а их сумма равна исходной разности потенциалов.
Ну и что? Где здесь указание на зависимость напряжения от частоты тока? Пока что все зависит от величины сопротивления. Вот, если бы найти такой резистор, который меняет свои параметры при изменении частоты! Тогда и падение напряжения на нем менялось бы автоматически.
Есть такие резисторы
Их еще называют реактивными, в отличие от активных собратьев. На что же они реагируют, изменяя свою величину? На частоту! Существует 2 вида реактивных сопротивлений:
- индуктивное;
- емкостное.
Каждый вид связан со своим полем. Индуктивное — с магнитным, емкостное — с электрическим. На практике они представлены в первую очередь, соленоидами.

Они представлены на фото выше. И конденсаторами (ниже).

Их можно считать антиподами, потому что реакция на изменение частоты прямопротивоположная. Индуктивное сопротивление растет с частотой. Емкостное, наоборот, падает.
Теперь, учитывая особенности реактивных сопротивлений, в соответствии с законом Ома, можно утверждать, что зависимость напряжения от частоты переменного тока существует. Она может быть рассчитана с учетом величин реактивных сопротивлений в цепи. Только для ясности надо помнить, что речь идет именно о падении напряжения на элементе цепи.
И все-таки она существует!
Вопросительный знак в заголовке статьи превратился в восклицательный. «Яндекс» реабилитирован. Осталось только привести формулы зависимости напряжения от частоты для разных видов реактивных сопротивлений.
Емкостное: XC = 1/(w · C). Здесь w — угловая частота, C — емкость конденсатора.
Индуктивное: XL = w · L, где w — то же, что и в предыдущей формуле, L — индуктивность.
Как видно, частота влияет на величину сопротивления, изменяя его, следовательно, изменяет и падение напряжения. Если в сети имеется активное сопротивление R, емкостное XC и индуктивное XL, то сумма падений напряжений на каждом элементе будет равна разности потенциалов источника: U = Ur + Uxc+ Uxl.
Конспект урока «Зависимость силы тока от частоты колебаний в цепи переменного тока»
Конспект урока физики в 11 классе
Учитель Васильчуковской СОШ филиала МБОУ «Ключевская СОШ №1»
Попов Андрей Геннадьевич
Тема урока:
«Зависимость силы тока от частоты колебаний в цепи переменного тока»
Тип урока: изучение нового материала.
Цели урока:
Образовательная: установить зависимость силы тока от частоты, используя математическую и физическую модели.
Развивающая: развивать у учащихся умение применять полученные знания о переменном токе в практическом применении в быту и технике; способность анализировать, обобщать, выделять главное.
Воспитательная: формирование познавательного интереса к физике.
Ход урока
1.Организационный момент: объявление темы и целей урока.
2.Актуализация опорных знаний
1) Проверка домашнего задания.
К сегодняшнему уроку было задано:
— выяснить значение оптимальной частоты переменного тока в бытовых сетях;
— привести примеры бытовых приборов, в которых мощность может регулироваться.
Предполагаемые ответы: 50 Гц; холодильник, телевизор, микроволновка, мобильный телефон, радиоприемник и т.п.
2) Вопросы для фронтального опроса:
Какие колебания называются электромагнитными?
В каком устройстве создаются электромагнитные колебания?
Из каких частей состоит колебательный контур?
От каких величин зависит частота и период колебаний в контуре?
Как будут меняться колебания в реальном контуре с течением времени?
Что приводит к затуханию колебаний?
3) Тест:
А1. Если сопротивлением колебательного контура можно пренебречь, то при увеличении ёмкости конденсатора в 4 раза период свободных колебаний…
1) увеличится в 2 раза 3) увеличится в 4 раза
2) уменьшится в 2 раза 4) уменьшится в 4 раза
А2. Как изменится частота свободных электромагнитных колебаний в контуре, если расстояние между пластинами конденсатора увеличить в 4 раза?
1) увеличится в 2 раза 3) увеличится в 4 раза
2) уменьшится в 2 раза 4) уменьшится в 4 раза
А3. Заряд q на пластинах конденсатора колебательного контура с течением времени меняется в соответствии с уравнением
1) I = 0,1π∙ sin 104πt 2) I = 0,1∙ cos(104πt + 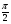 ) 3) I = 0,1∙ sin(104πt +
) 3) I = 0,1∙ sin(104πt + 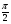
А4. Согласно предыдущего условия задачи определить собственную частоту колебаний ω.
1) 0,5·10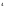 Гц 2) 0,5·10
Гц 2) 0,5·10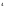 π рад/с 3) 10
π рад/с 3) 10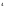 π рад/с 4) 10-5 рад/с
π рад/с 4) 10-5 рад/с
А5. Последовательно соединены конденсатор, катушка индуктивности и резистор. Если при неизменной частоте и амплитуде напряжения на концах цепи увеличивать емкость конденсатора от 0 до ∞, то амплитуда тока в цепи будет
1) монотонно убывать 3) монотонно возрастать
2) сначала возрастать, затем убывать 4) сначала убывать, затем возрастать
3.Объяснение нового материала
1) Рассмотрим действие осциллографа. С помощью регуляторов мы наблюдаем изменения частоты, амплитуды переменного тока.
2) Обратимся к математической модели: формула Томсона
 Зная, что период и частота обратно пропорциональны, видим, что при уменьшении ёмкости увеличивается частота. По-другому формулу Томсона можно записать так:
Зная, что период и частота обратно пропорциональны, видим, что при уменьшении ёмкости увеличивается частота. По-другому формулу Томсона можно записать так: 
3) Теперь вопрос: а где сила тока? Математическое выражение зависимости будет иметь следующий вид: I = UCω; здесь показана прямая зависимость силы тока от напряжения, ёмкостного сопротивления и частоты.
Можно сделать вывод: при повышении частоты снижается ёмкостное сопротивление, и повышается ток, протекающий по цепи.
4) Проделаем опыт по данному рисунку.

Вывод: чем быстрее поворачивается рамка в магнитном поле, тем больше отклонение стрелки гальванометра (силы тока)
.
5) Рассмотрим видеоэксперимент (на диске). Вывод:
4.Закрепление и обобщение нового материала.
1) Итак, что же сегодня мы с вами выяснили, как связаны сила тока и частота колебаний контура?
2) Вопрос: что произойдет, если частота свободных колебаний контура совпадет с частотой вынужденных колебаний?
3) Решим задачу: В цепь переменного тока с частотой 500 Гц включена катушка индуктивностью 10 мГн. Какой емкости конденсатор надо включить в эту цепь, чтобы наступил резонанс?
Подсказка: формула Томсона.
5.Подведение итогов урока. Выставление оценок и их комментарии.
6.Задание на дом: § 17-19 а1 – а3 с. 76
Самоанализ урока физики в 11 классе
Проведенный мною урок по теме: «Зависимость силы тока от частоты
колебаний в цепи переменного тока» стал ответом на ежегодные вопросы школьников: можно ли увеличить силу тока без потерь энергии? Как увеличить (уменьшить) силу тока в цепи, меняя частоту электромагнитных колебаний? И т. п.
При построении урока были учтены следующие требования к теме: знать физическую сущность постоянного и переменного тока, электродинамических параметров.
В ходе урока опытный факт получает теоретическое обоснование, а теоретическое положение подтверждается опытом.
Чтобы проверить прочность полученных знаний, учащимся был предложен небольшой тест (по форме ЕГЭ).
В 11 классе 5 девочек. В ходе урока используются такие формы самостоятельной работы как: фронтальный опрос, тестирование, самопроверка, работа в парах при сборке моделей генераторов переменного тока, привлечение ученика как лаборанта при работе с осциллографом и генератором.
На уроке были использованы источники:
http://pue8.ru/elektrotekhnik/413-elektricheskoe-soprotivlenie.html
http://school.mephi.ru/content/file/elibrary/phy/lekciya_18.pdf
(формулы, рисунок)
CD «Школьный физический эксперимент»
интенсивность колебания зарядов в электрической сети, способы измерения
 Направленное движение заряжённых частиц под действием электрической движущей силы (ЭДС) называют электротоком, он бывает переменным и постоянным. В последнем случае перемещение нуклонов происходит во времени стабильно, а в первом — периодически обращает направление и величину. Один из основных параметров переменного тока — частота. Зависит характеристика от периодичности колебаний электронов, может измеряться несколькими способами и приборами.
Направленное движение заряжённых частиц под действием электрической движущей силы (ЭДС) называют электротоком, он бывает переменным и постоянным. В последнем случае перемещение нуклонов происходит во времени стабильно, а в первом — периодически обращает направление и величину. Один из основных параметров переменного тока — частота. Зависит характеристика от периодичности колебаний электронов, может измеряться несколькими способами и приборами.
Переменный электрический ток
В английском языке этому термину соответствует выражение alternating current — аббревиатура AC, в энерготехнике как буквенное обозначение используют знак тильда (~). Переменный ток изменяется в периоде по синусоиде. Источниками служат генераторы, вырабатывающие ЭДС посредством электромагнитной индукции. Характеризуется АС следующими параметрами:
- напряжение сети U в вольтах;
- сила тока I=Q/Δt, [A] — количество зарядов, прошедших через поперечник проводника в единицу времени;
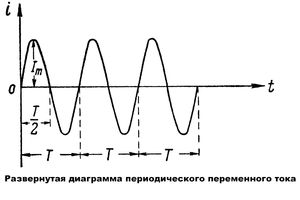
 период Т — отрезок времени полного цикла изменений;
период Т — отрезок времени полного цикла изменений;- плотность тока j=I/S, [A/мм2] — векторная величина, где S площадь сечения проводника, направление j совпадает с курсом движения электронов;
- фаза — состояние АС, может быть одно- и многофазным;
- амплитуда I max — высота синусоиды, максимальная величина мгновенно достигаемого за период значения тока.
В энергетике преимущественно используются трёхфазные сети: 3 отдельных электроцепи с одинаковыми напряжением и частотой при сдвиге φ=120°. От стабильности колебательных движений нуклонов в системе зависит устойчивость и надёжность работы всей энергосети.
Период пульсаций и частота
Физическая сущность переменного тока заключается в перемещении электронов в проводнике сначала в одном направлении, затем в другую сторону. Полный цикл движений туда и обратно совершается за определённый период, определяемый по частоте колебаний: Т=1/ f.
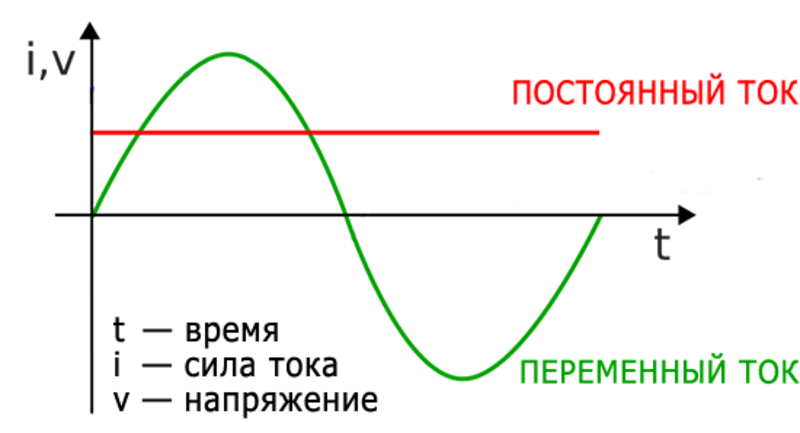
Интенсивность циклов
Для условий электросетей России показатель f =50 Гц, а время одной пульсации составляет Т=1/50=0,02 секунды. Обратная связь двух параметров позволяет определить частоту ~ тока по длительности сигнала: f =1/0,02=50 Гц.
Один герц означает 1 колебание за секунду. Чем быстрее изменяется электродвижущая сила, тем скорее обращается радиус-вектор и сокращается период. Соответственно, при форсировании оборотов возрастает частота: величины Т и f обратно пропорциональны, чем больше одна, тем меньше вторая. Значения характеристики f изменяются в широких пределах, что предопределяет использование расширенной терминологии:
| Количество нулей после единицы | Приставка к размерности герц |
| 3 (тысяча) | Кило (кГц) |
| 6 (миллион) | Мега (мГц) |
| 9 (миллиард) | Гига (ГГц) |
В зависимости от величины частота переменного тока подразделяется на следующие подгруппы:
- промышленные: 16―25 Гц на железнодорожных сетях некоторых стран, 25 и 75 Гц в схемах блокировки рельсовых цепей, в автономных системах авиационной и военной энергетики — 400 Гц, на некоторых производственных и сельскохозяйственных установках 200―400 Гц;
 звуковые находятся в интервале 20―20000 Гц (20 кГц), в передающих антеннах — до 1,5 ГГц;
звуковые находятся в интервале 20―20000 Гц (20 кГц), в передающих антеннах — до 1,5 ГГц;- технические: автоматика — используется диапазон от 1 кГц до 1 ГГц, металлургия и машиностроение: плавка, сварка и термообработка металлов;
- радиолокационные станции спутниковой связи, спецсистемы ГЛОНАСС, GPS — до 40 ГГц и выше.
Токи высокой частоты (ТВЧ) начинаются с уровня десятков кГц, когда значимо проявляются излучения электромагнитных волн и скин-эффект: заряд, перемещающийся в проводнике, распределяется не по сечению, а в поверхностном слое.
Для выработки ТВЧ используют энергомашинные генераторы и колебательные контуры. В последнем случае устройство представляет собой цепь с включением в состав ёмкости и индуктивности.
Опасность разночастотных зарядов
Эквивалентные по воздействию на организм человека напряжения переменного и постоянного тока, равны соответственно 42 В и 120 В. Неравенство опасности исчезает при достижении ЭДС 500 В, а при больших значениях опаснее становится константный. Проявления неблагоприятного действия последнего — термическое и электролитическое, а переменного — преимущественно выражается в сокращении сосудов, мышц, голосовых связок. При этом определяющее значение на опасность оказывает частота тока:
 40―60 Гц — наибольшая угроза поражения, возможность фибрилляции сердца; дальнейшее повышение интенсивности колебаний зарядов приводит к снижению риска, но вероятность гибельности сохраняется в пределах всего диапазона промышленных частот — до 500 Гц;
40―60 Гц — наибольшая угроза поражения, возможность фибрилляции сердца; дальнейшее повышение интенсивности колебаний зарядов приводит к снижению риска, но вероятность гибельности сохраняется в пределах всего диапазона промышленных частот — до 500 Гц;- свыше 10 кГц начинаются ТВЧ — они безопасны до уровня 1 мГц относительно внутренних поражений, что обусловлено скин-эффектом, но вызывают ожог и угроза от них не меньше, чем от постоянных или переменных предшествующей группы;
- токи высокой частоты сопровождаются электромагнитными излучениями — с этой стороны существует возможность негативного воздействия на живые организмы.
На относительной безопасности ТВЧ основано их применение в медицине для физиотерапевтических процедур. Тяжесть поражения электротоком зависит не только от физических параметров заряда, но и от состояния организма человека.
Измерительные приборы
Для определения интенсивности колебаний используют осциллограф, на котором можно увидеть частоту и форму сигнала. Существуют также специальные приборы — частотомеры. В них применяют следующие способы определения параметра:
 перезаряд конденсатора — среднее значение силы тока пропорционально соотносится с его интенсивностью и измеряется магнитоэлектрическим амперметром со шкалой в герцах;
перезаряд конденсатора — среднее значение силы тока пропорционально соотносится с его интенсивностью и измеряется магнитоэлектрическим амперметром со шкалой в герцах;- дискретный счёт — фиксирование импульсов нужной частоты за определённый период, получают данные достаточной точности: погрешность в пределах 2%, этого хороший показатель для бытового применения прибора;
- резонансный метод основан на одноимённом электрическом явлении, возникающем в цепи с настраиваемыми элементами; частота — больше 50 Гц, определяется по шкале регулировочного механизма.
Ещё один известный способ применяется в осциллографах, основан на смешивании и сравнении эталонного параметра с измеряемой частотой. Вследствие наложения возникают биения, а при выравнивании на экране устанавливается определённая фигура. Рассчитывают искомую характеристику по зафиксированному графику посредством математических формул.
Определение зависимости силы тока в колебательном контуре от частоты вынуждающей ЭДС
ЦЕЛЬ РАБОТЫ: определение зависимости силы тока в колебательном контуре от частоты вынуждающей ЭДС. Построение резонансных кривых.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ.
Рассмотрим процессы, протекающие в колебательном контуре (рис. 1), присоединенном к внешнему источнику, ЭДС которого изменяется по гармоническому закону
e(t) = e0coswt
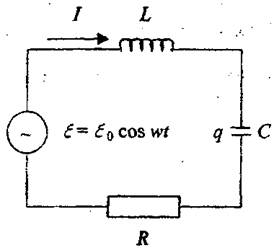 Обозначим через U напряжение на конденсаторе, а
через I – ток в контуре. Согласно второму правилу Кирхгофа
сумма напряжений на элементах цепи равна алгебраической сумме ЭДС в контуре:
Обозначим через U напряжение на конденсаторе, а
через I – ток в контуре. Согласно второму правилу Кирхгофа
сумма напряжений на элементах цепи равна алгебраической сумме ЭДС в контуре:
IR + U = e0coswt + eS (2.1)
где eS = —LdI/dt – ЭДС самоиндукции, возникающей в катушке с индуктивностью L при прохождении в ней переменного тока.
Уравнение (2.1) можно записать в виде
IR + U + LdI/dt = e0coswt (2.2)
 Выразим
напряжение в конденсаторе через ток:
Выразим
напряжение в конденсаторе через ток:
U = q/C = (1/C) ∫Idt
Здесь q – заряд на конденсаторе.
Подставляя в (2.2) найденное значение напряжения, получим:
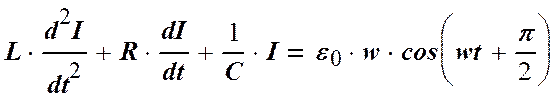 IR + (1/C) ∫Idt + LdI/dt = e0coswt
IR + (1/C) ∫Idt + LdI/dt = e0coswt
Продифференцируем это выражение по t:
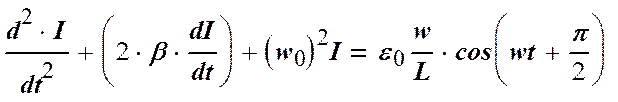 Далее будем использовать обозначения, введенные в лабораторной
работе №24. Тогда (2.3) примет вид:
Далее будем использовать обозначения, введенные в лабораторной
работе №24. Тогда (2.3) примет вид:
Полученное уравнение является линейным неоднородным (b = const, w0 = const) дифференциальным уравнением второго порядка.
Уравнения типа (2.4) описывают поведение широкого класса колебательных систем (электрических, механических и т.п.) под влиянием внешнего гармонического воздействия.
Через некоторое время после включения гармонически изменяющейся ЭДС (t >> 1/b), которое потребуется для полного затухания собственных колебаний, в колебательном контуре устанавливается переменный ток с частотой, равной частоте вынуждающей ЭДС.
Установившиеся колебаний в контуре, независимые от начальных условий, определяются частным решением уравнения (2.4), которое имеет вид
I = I0*cos(wt — j) (2.5)
Здесь I0 – амплитудное значение силы тока,
j — угол сдвига фаз между внешней ЭДС и током в цепи.
Подставив (2.5) в (2.4) найдем значения I0 и j:
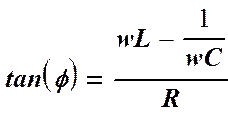
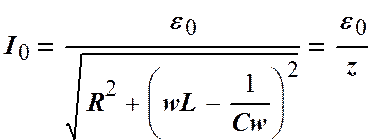
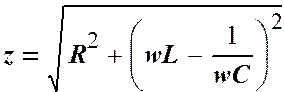 где
где
Формула (2.6), показывающая зависимость амплитуды I0 переменного тока в колебательном контуре от амплитуды e0 вынуждающей ЭДС, аналогична закону Ома для замкнутой цепи постоянного тока. Поэтому величина z называется полным сопротивлением электрической цепи переменного тока (колебательного контура). Оно складывается из активного (омического) сопротивления R, индуктивного сопротивления wL и емкостного сопротивления 1/wC. Как видно из (2.6) амплитуда силы тока в контуре достигает максимального значения при минимальном значении z, т.е. при [wL – 1/wC]2 = 0. При этом полное сопротивление контура минимально и равно его активному сопротивлению. В этом случае j = 0, т.е. сила тока совпадает по фазе с вынуждающей ЭДС и равна
Imax = e0/R (2.9)
При постоянных значениях L, С независимо от величины активного сопротивления контура, амплитуда силы тока достигает максимального значения при одном и том же значении w — циклической частоты вынуждающей ЭДС, называемой резонансной, равной
wрез = 1/ÖLC = w0 (2.10)
где w0 — собственная циклическая частота колебательного контура (см. лабораторную работу № 6).
Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей ЭДС к частоте, равной или близкой собственной частоте колебательного контура называется резонансом.
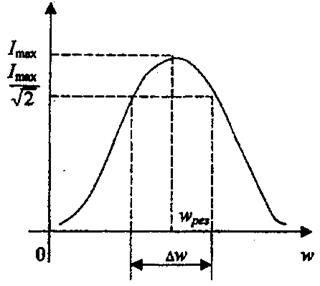 Графическая зависимость амплитуды тока от частоты
вынуждающей ЭДС называется резонансной кривой. Чем меньше активное
сопротивление контура, тем больше амплитуда силы тока при резонансе и ярче
выражена резонансная кривая.
Графическая зависимость амплитуды тока от частоты
вынуждающей ЭДС называется резонансной кривой. Чем меньше активное
сопротивление контура, тем больше амплитуда силы тока при резонансе и ярче
выражена резонансная кривая.
Добротностью контура Q при wрез >> b называют соотношение
Частота переменного тока зависит от его напряжения?
нет. . скорее даже наоборот.. . но объяснять долго
От вращнгтя турбины на электростанции.
Частота не зависит .Для определенных параметров сети, она величина постоянная. Переменная зависимость только между током, наряжением и сопротивлением сети. (Изучи закон Ома и всё будет ясно).
никак не зависит
Нет, не зависит. Частота тока напрямую зависит от частоты вращения ротора генератора и числа его полюсов. Частота измеряется в Герцах и находится по формуле f=np/60, где n — частота вращения ротора, р — число пар полюсов. В энергосистеме частота колеблется от того, что изменяется нагрузка, т. е. мощность потребителей. Это происходит из-за того, что на ротор действуют две противоположно направленные силы. Одна, обусловленная вращением турбины под действием пара или потока воды, разгоняет его, другая, обусловленная мощностью потребителей энергии, тормозит. Для поддержания частоты увеличивается подача пара или воды при росте нагрузок, и уменьшается при снижении.
Частота тока, как правило, ровна частоте приложенного напряжения, меняется частота напряжения меняется частота тока. Таким образом частота тока зависит только от частоты напряжения, но не зависит от его величины.
Частота f = (p x n) / 60, где р- число пар полюсов, n — обороты.
Пожалуйста объясните! Как мощность зависит от частоты электрического тока?
мощность определятся не частотой
Если имеется в виду, что при частоте N Гц цепь подключенная к генератору потребляет 320 кВА, то при увеличении частоты до 2*N Гц цепь будет потреблять полную мощность иную чем 320 кВА. Почему? — Полная мощность S (кВА) является векторной суммой активной мощности Р (кВт) и реактивной мощности Q (кВАр) и если Р не зависит от частоты тока (т. к. R — активное сопротивление цепи определяется только характеристиками материала, а если точнее — то сколько тепловой энергии рассеивает тот или иной материал при данной силе тока), то Q весьма зависит от частоты (т. к. Х — реактивное сопротивление цепи находится в прямой зависимости от частоты для индуктивной цепи Х=2*пи*f*L, для емкостной цепи X=1/(2*пи*f*C). Физический смысл реактивного сопротивления — это энергия затрачиваемая на перемагничивание либо изменение заряда цепи) — соотв. при росте частоты в 2 раза индуктивное сопротивление цепи возрастет в эти 2 раза и в эти же 2 раза возрастет потребляемая реактивная мощность, емкостное же сопротивление цепи упадет в 2 раза => 2 раза упадет потребляемая реактивная мощность.
Зависимость амплитуды силы тока в колебательном контуре от частоты

Ширина резонансной линии при R =______ Ом:
Δν1 = _______________
Ширина резонансной линии при R =______ Ом:
Δν2 = _______________
Добротность колебательного контура при R = ________ Ом:
Q1 = ________________
Добротность колебательного контура при R =_________ Ом:
Q2 = ________________
Вывод:____________________________________________
__________________________________________________
Оглавление
1. | Изучение электростатического поля………………………. | 3 |
2. | Определение заряда электрона…………………………….. | 7 |
3. | Измерение электроемкости конденсаторов……………….. | 10 |
4. | Изучение электрических свойств сегнетоэлектрика……… | 13 |
5. | Шунты и дополнительные сопротивления………………… | 17 |
6. | Измерение сопротивления проводников………………….. | 19 |
7. | Изучение процессов заряда и разряда конденсатора……… | 21 |
8. | Изучение зависимости мощности источника тока от сопротивления нагрузки……………………………………. | 25 |
9. | Изучение температурной зависимости электропровод-ности полупроводников.……………………………………. | 28 |
10. | Определение работы выхода электронов из металла с помощью вакуумного диода……………………………… | 34 |
11. | Изучение эффекта Зеебека…………………………………. | 38 |
12. | Изучение свойств полупроводникового диода……………. | 41 |
13. | Определение горизонтальной составляющей вектора напряженности магнитного поля Земли…………………… | 45 |
14. | Изучение магнитного гистерезиса…………………………. | 47 |
15. | Определение удельного заряда электрона методом магнетрона…………………………………………………… | 51 |
16. | Эффект Холла в полупроводниках и его применение при исследовании магнитных полей…………………………… | 54 |
17. | Изучение затухающих электромагнитных колебаний……. | 57 |
18. | Изучение вынужденных колебаний и резонанса в цепи переменного тока……………………………………………. | 60 |
Оценка учебной деятельности студента _____________________________________ группы________
Наименование учебной деятельности | Кол. баллов | Подпись препод. | |
Лабораторные работы (макс. — 5 баллов/раб.) | |||
1. | Изучение электростатического поля | ||
2. | Определение заряда электрона | ||
3. | Измерение электроемкости конденсаторов | ||
4. | Изучение электрических свойств сегнетоэлектрика | ||
5. | Шунты и дополнительные сопротивления | ||
6. | Измерение сопротивления проводников | ||
7. | Изучение процессов заряда и разряда конденсатора | ||
8. | Изучение зависимости мощности источника тока от сопротивления нагрузки | ||
9. | Изучение температурной зависимости электропроводности полупроводников | ||
10. | Определение работы выхода электронов из металла с помощью вакуумного диода | ||
11. | Изучение эффекта Зеебека | ||
12. | Изучение свойств полупроводникового диода | ||
13. | Определение горизонтальной составляющей вектора напряженности магнитного поля Земли | ||
14. | Изучение магнитного гистерезиса | ||
15. | Определение удельного заряда электрона методом магнетрона | ||
16. | Эффект Холла в полупроводниках и его применение при исследовании магнитных полей | ||
17. | Изучение затухающих электромагнитных колебаний | ||
18. | Изучение вынужденных колебаний и резонанса в цепи переменного тока | ||
Всего баллов за лабораторный практикум | |||
Контрольная работа | |||
Экзаменационное тестирование | |||
Общая сумма баллов | |||
Итоговая оценка | |||


 период Т — отрезок времени полного цикла изменений;
период Т — отрезок времени полного цикла изменений;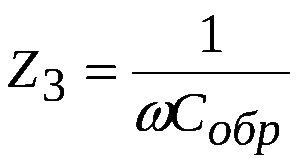 звуковые находятся в интервале 20―20000 Гц (20 кГц), в передающих антеннах — до 1,5 ГГц;
звуковые находятся в интервале 20―20000 Гц (20 кГц), в передающих антеннах — до 1,5 ГГц;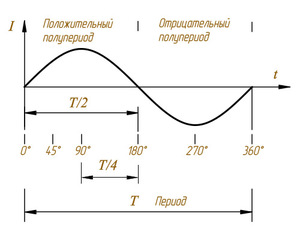 40―60 Гц — наибольшая угроза поражения, возможность фибрилляции сердца; дальнейшее повышение интенсивности колебаний зарядов приводит к снижению риска, но вероятность гибельности сохраняется в пределах всего диапазона промышленных частот — до 500 Гц;
40―60 Гц — наибольшая угроза поражения, возможность фибрилляции сердца; дальнейшее повышение интенсивности колебаний зарядов приводит к снижению риска, но вероятность гибельности сохраняется в пределах всего диапазона промышленных частот — до 500 Гц; перезаряд конденсатора — среднее значение силы тока пропорционально соотносится с его интенсивностью и измеряется магнитоэлектрическим амперметром со шкалой в герцах;
перезаряд конденсатора — среднее значение силы тока пропорционально соотносится с его интенсивностью и измеряется магнитоэлектрическим амперметром со шкалой в герцах;