Влияние температуры на обратный ток p-n перехода

⇐ ПредыдущаяСтр 3 из 24Следующая ⇒

Для маломощных германиевых диодов ток утечки (или обрат­ный ток) находится в пределах от 1 до 200 мкА. У кремниевых диодов ток утечки значительно меньше. Но в обоих случаях ток утечки сильно зависит от температуры.

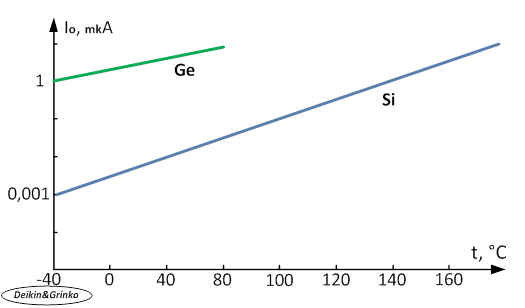
Рис.2.7. Зависимость от температуры обратного тока насыщения для германиевого и кремниевого диодов (рисунок выполнен авторами)

Эта зависимость показана на рис. 2.7, где приведены графики температурного изменения обратного тока германиевого и кремниевого диодов. Основные причины возникновения тока утечки следующие:

а) Образование неосновных носителей при нагревании, воздействии радиации и нарушениях структуры кристаллической решетки. В этих случаях образуются электронно-дырочные пары и носители заряда, которые являются неосновными, свободно проходят через р-п переход, смещенный в обратном направлении для основных носителей. Образование электронно-дырочных пар при нагревании является наиболее существенной причиной возрастания тока утечки. В общем случае возрастание обратного тока составляет примерно 10% на 1°С (ток увеличивается приблизительно в 2 раза при нагревании на 8°С). По этой причине применение германиевых полупроводниковых приборов ограничивается диапазоном температур не выше 70°С. Кремниевые приборы могут применяться вплоть до 150°С.

б) Поверхностные токи утечки являются существенным фактором только для кремниевых приборов, в которых тепловой ток утечки весьма незначителен. Поверхностный ток утечки часто обусловлен загрязнением поверхности и в конечном итоге снижает обратное сопротивление перехода (Фишер Дж.Э., 1980) .

Виды полупроводниковых диодов

Полупроводниковые диоды в зависимости от их свойств и назначения бывают нескольких типов. Рассмотрим некоторые из них.

— Выпрямительные диоды. Предназначены в основном для выпрямления переменных токов. Диоды малой мощности рассчитаны на токи меньше 0,3 ампера. Средней мощности — от 0,3 до 10 А. Большой мощности больше 10 А.

— Универсальные диоды. Применяются в основном для детектирования (выпрямления) модулированных колебаний. Но их можно использовать и как выпрямительные: при малых токах и небольших обратных напряжениях.

— Высокочастотные диоды. Высокочастотные диоды — это приборы универсального назначения, которые могут быть использованы для выпрямления, детектирования и других нелинейных преобразований электрических сигналов в диапазоне до 600 МГц. Они изготовляются, как правило, из германия или кремния и имеют точечную структуру.

— Импульсные диоды. Применяются для работы в импульсных схемах. Они должны обладать способностью сохранять форму импульсов при пропускании их к различным участкам схемы.

— Стабилитроны. Предназначены для стабилизации постоянных напряжений. Их работа основана на явлении пробоя некоторых кремниевых переходов. У таких переходов характеристика пробоя расположена почти параллельно оси токов, то есть при одном и том же напряжении на диоде ток может изменяться в довольно широких пределах (Радиолекторий, 2013).

— Варикапы. Диоды, изменяющие свою ёмкость под действием приложенного обратного напряжения. Могут использоваться в качестве конденсатора переменной ёмкости в различных электронных устройствах.

— Фотодиоды. Диоды, изменяющие своё сопротивление под действием света. Могут применяться в качестве датчика освещённости.

— Светодиоды. При прохождении электрического тока через них способны выделять свет. Находят очень широкое применение, как в качестве индикационных устройств, так и для освещения.

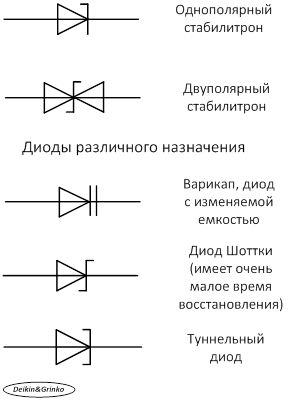
Рис. 2.8. Условные графические обозначения некоторых диодов (рисунок выполнен авторами)

Выпрямители

Для питания электронных устройств используются химические и сетевые источники питания.

К химическим источникам относятся гальванические и аккумуляторные элементы и батареи. Их недостатком является сравнительно малый срок службы и малая мощность. Этих недостатков нет у сетевых источников напряжения постоянного тока.

Источник питания состоит из четырёх основных узлов:

• трансформатора;
• выпрямителя;
• сглаживающего фильтра;
• стабилизатора напряжения или тока.

Рассмотрим процесс выпрямления переменного напряжения. Частота сетевого напряжения 50 Гц, т.е. в 1 секунду имеем 50 периодов. В течение каждого периода имеется полпериода отрицательного напряжения и полпериода положительного напряжения. Для выпрямления надо избавиться от разнополярности. Это можно достигнуть двумя способами:

1. избавиться от напряжения одного из полупериодов;

2. изменить полярность одного из полупериодов на противоположную.

Рекомендуемые страницы:

4.6. Температурная зависимость прямой ветви вах диода.

При обратном смещении температурная зависимость ВАХ идеализированного диода сводится к температурной зависимости теплового тока от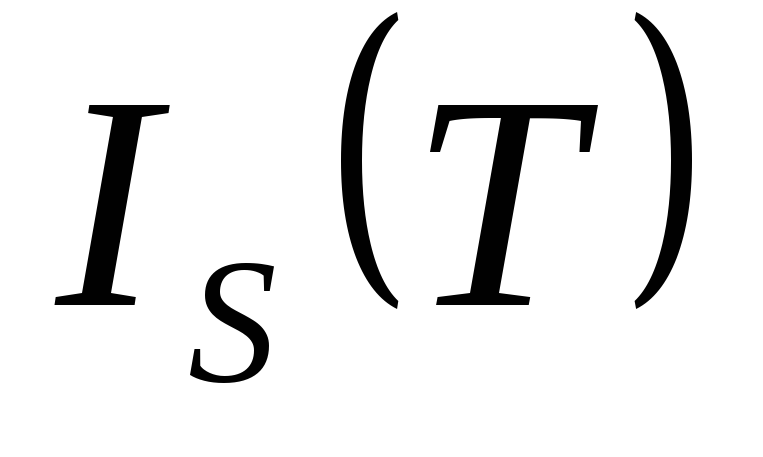

, рассмотренной в предыдущем параграфе.

При прямом смещении температурную зависимость ВАХ удобно характеризовать температурным коэффициентом напряжения (ТКН):

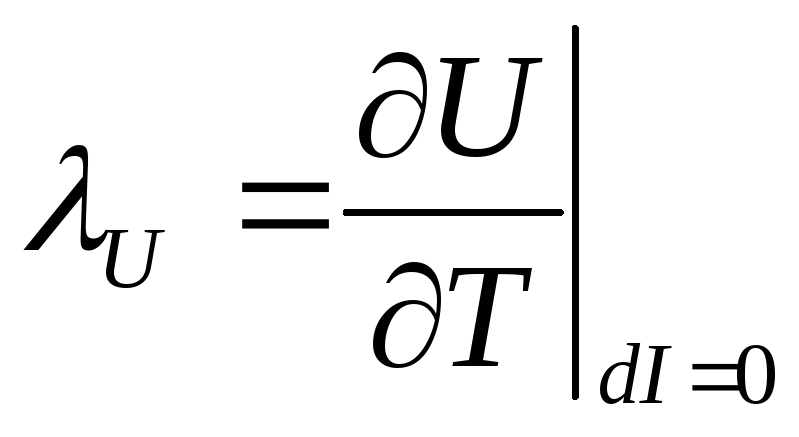. (4.35)

ТКН численно равен изменению прямого напряжения на диоде при изменении температуры на 1 градус и постоянном токе диода.

При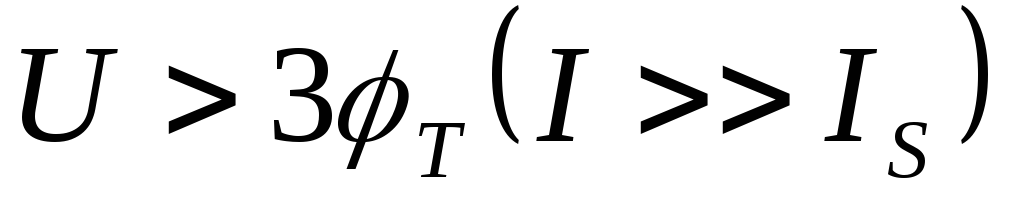

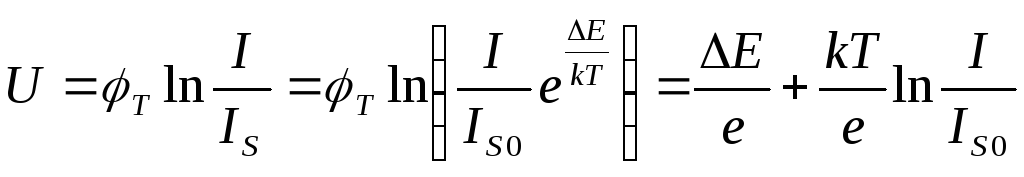соотношение (4.25) с учетом (4.32) дает

.

Дифференцируя по температуре, получим

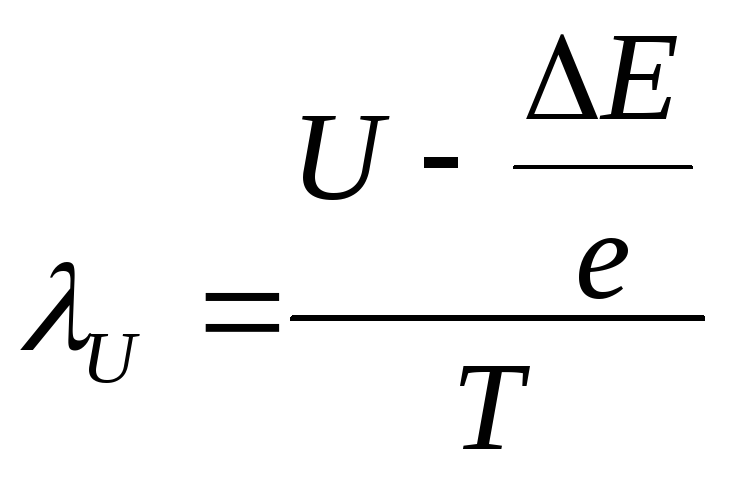. (4.36)

Для невырожденных полупроводников 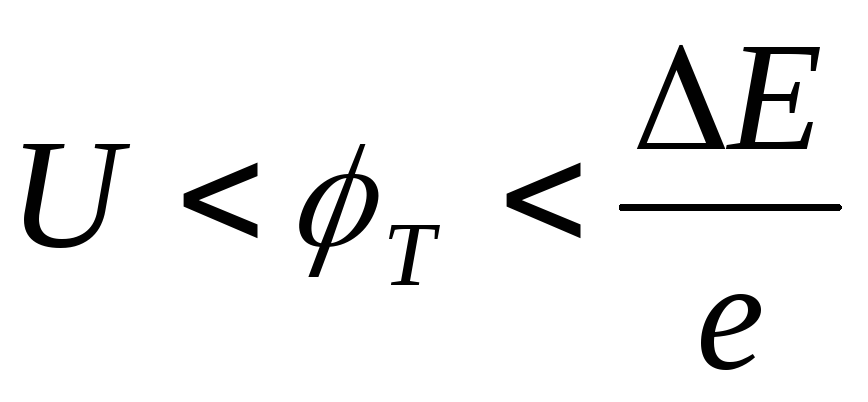, а величина ТКН отрицательна, поэтому при увеличении температуры прямая ветвь ВАХ диода сдвигается в сторону меньших напряжений. При

290 К и:

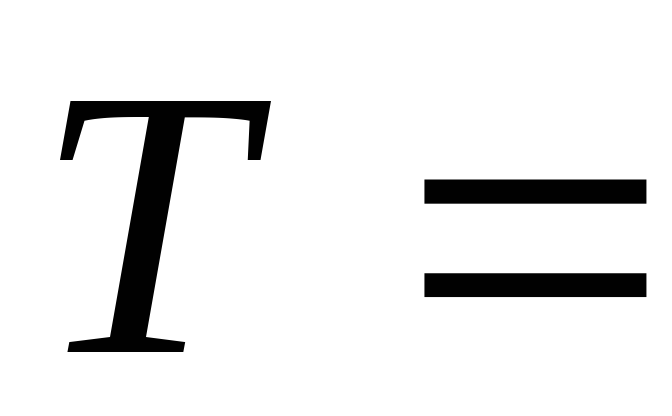
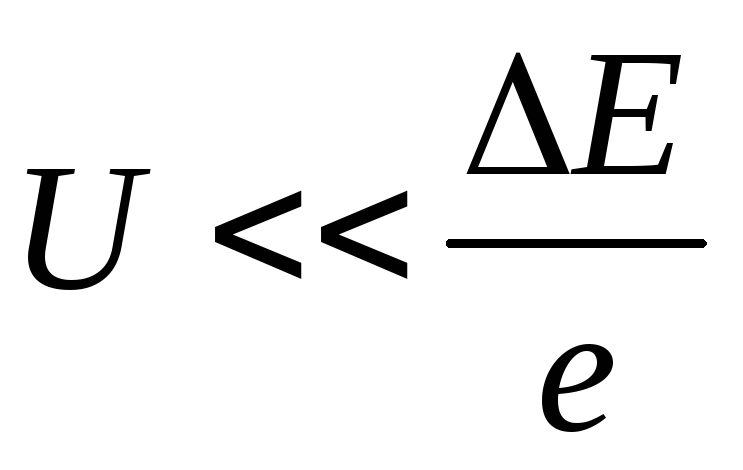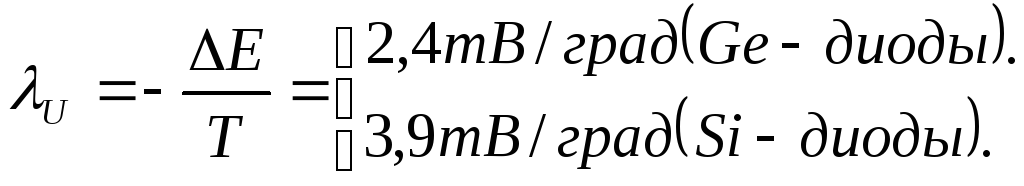
4.7. Характеристические сопротивления диода и коэффициент качества вах диода.

Основным показателем качества ВАХ диода является нелинейность его характеристики, позволяющая осуществлять выпрямление электрических сигналов, ограничение их по амплитуде, преобразования частотного спектра и другие нелинейные операции.

Нелинейность ВАХ проявляется в различии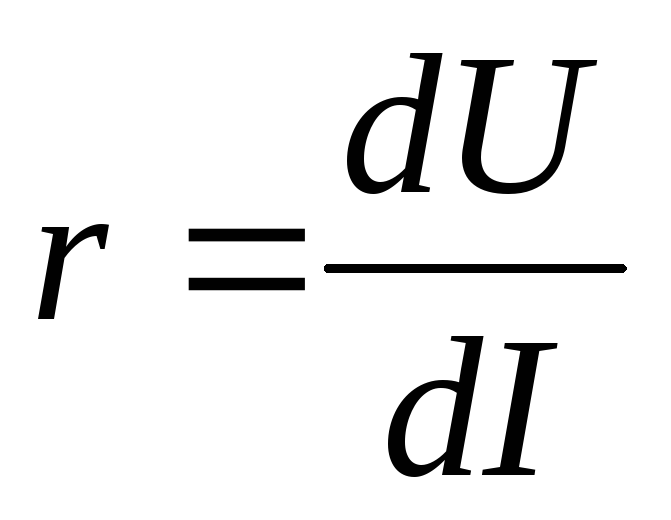

дифференциального сопротивления истатического сопротивления 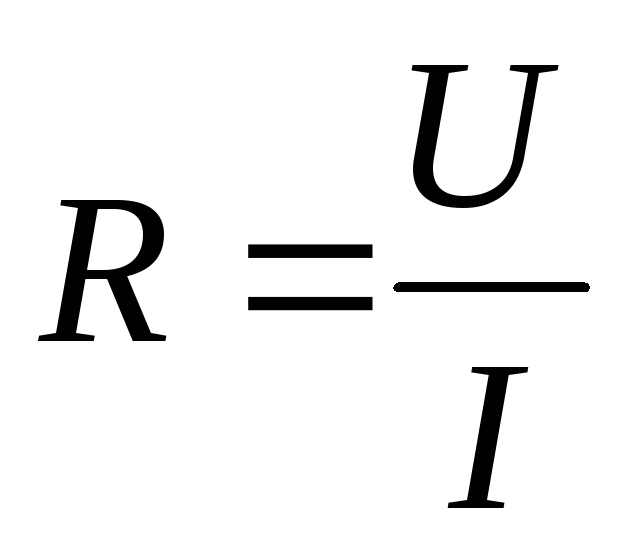. Из ВАХ (4.25) находим

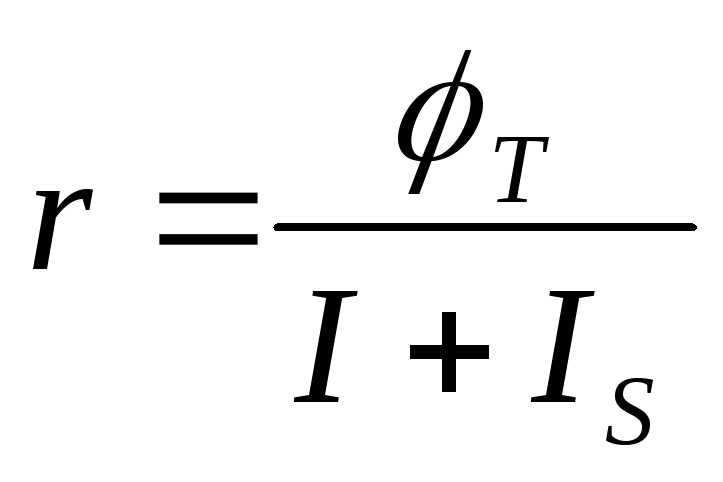, (4.37)

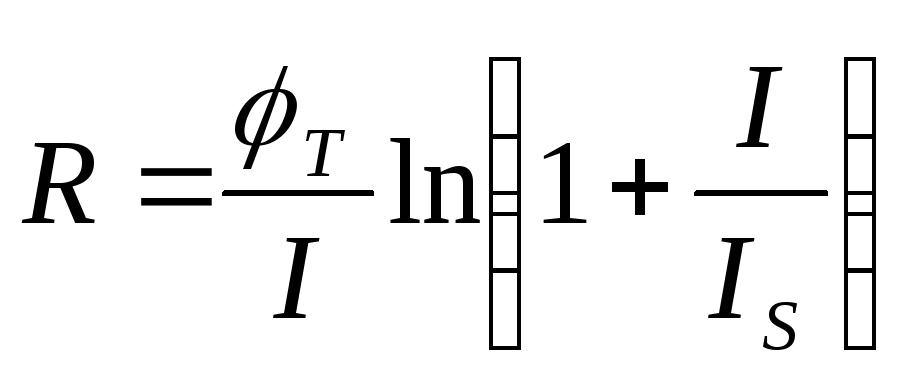(4.38)

Легко видеть, что в состоянии равновесия (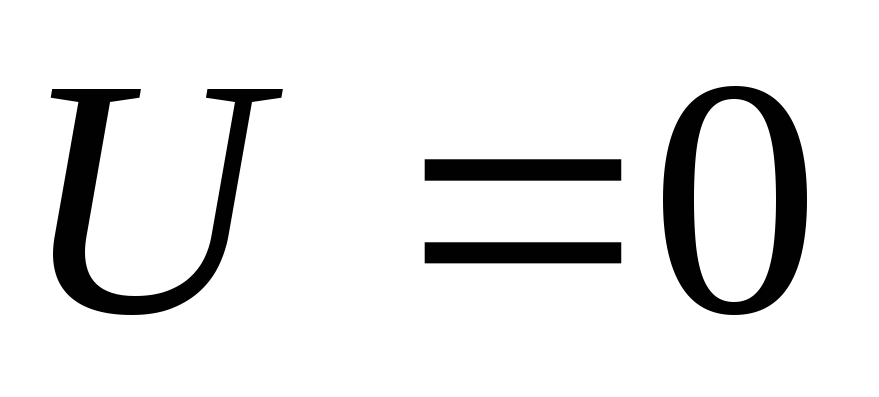

) дифференциальное и статическое сопротивления совпадают.

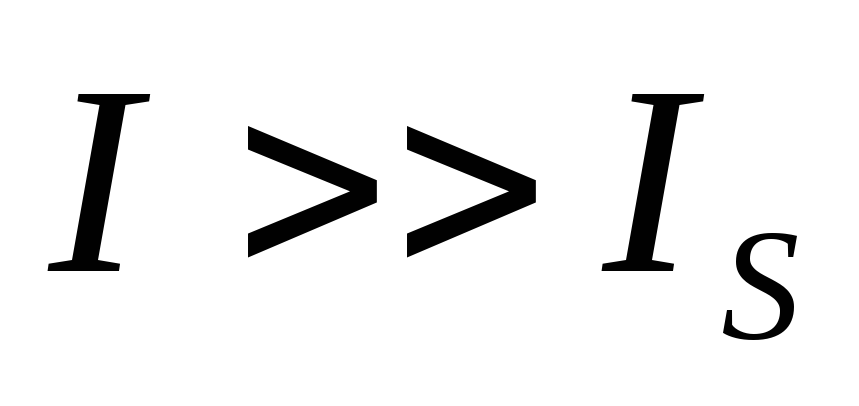На прямой ветви ВАХ () дифференциальное сопротивление меньше статического. Придифференциальное сопротивление зависит только от тока и температуры, причем эта зависимость одинакова для всех диодов:

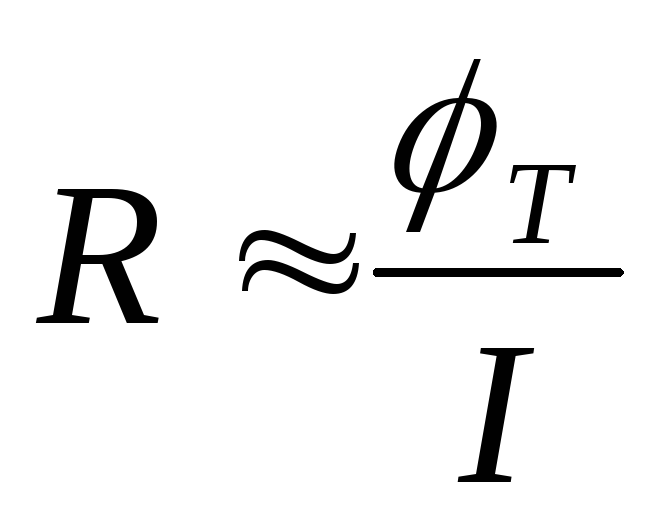. (4.39)

На обратной ветви ВАХ (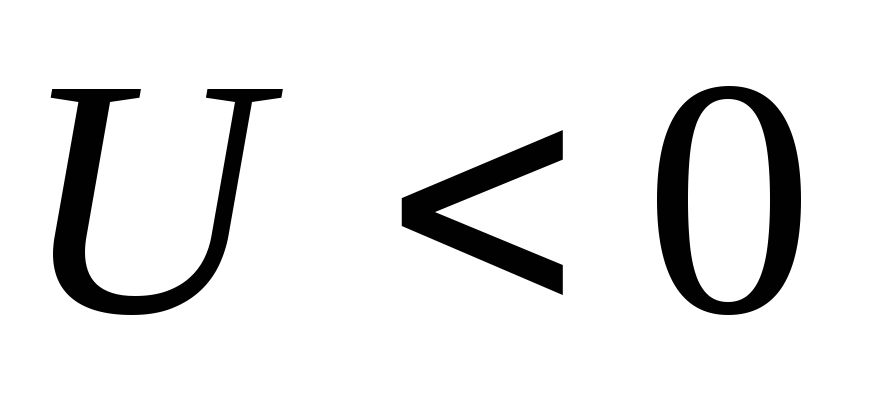

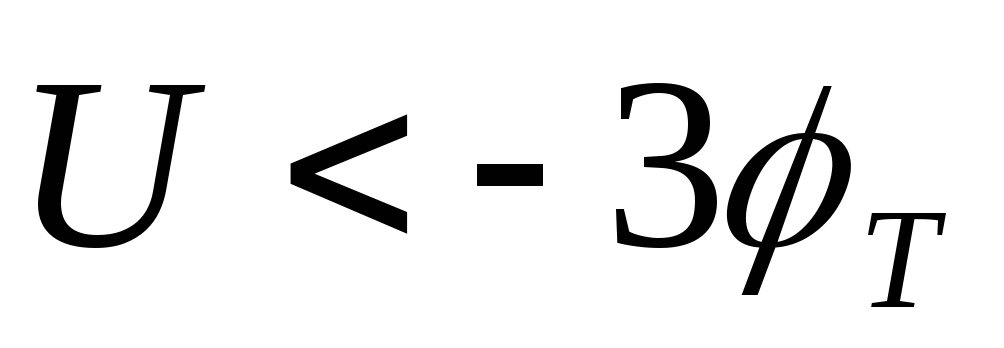) дифференциальное сопротивление больше статического. Привеличина дифференциального сопротивления может считаться бесконечно большой, так как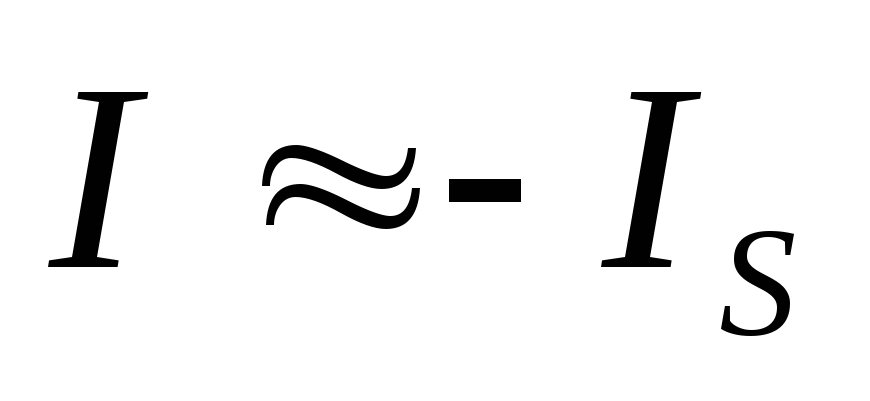. Статическое сопротивление при этом пропорционально обратному напряжению:

. (4.40)

Критерием качества диода может служить коэффициент качества ВАХ, определяемый следующим образом:

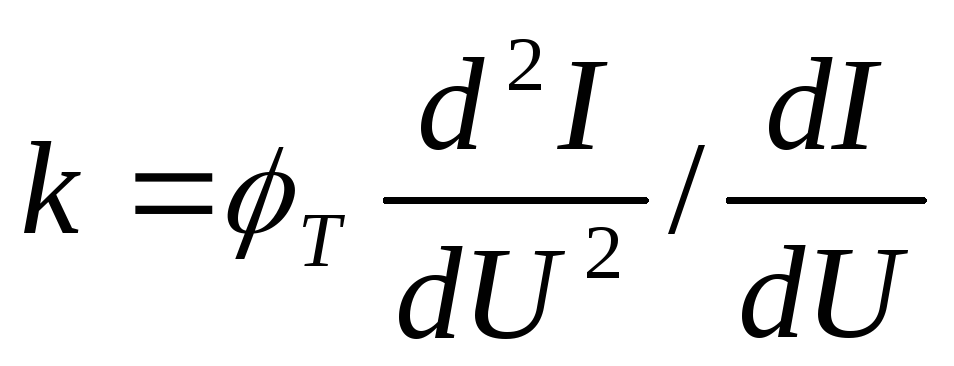(4.41)

Для элемента, обладающего линейной ВАХ вида 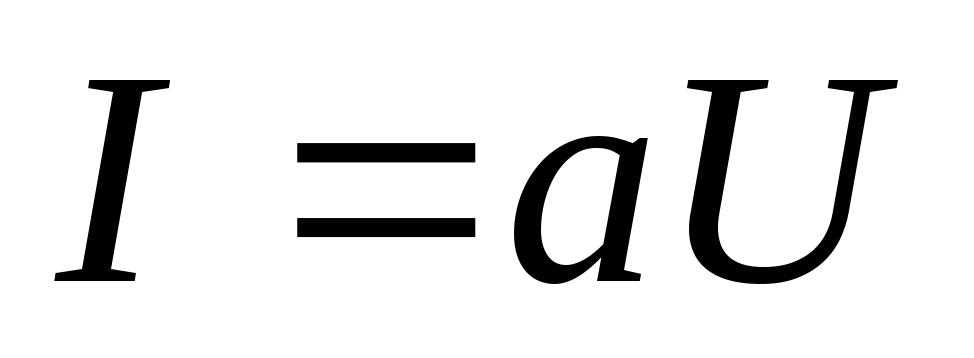, 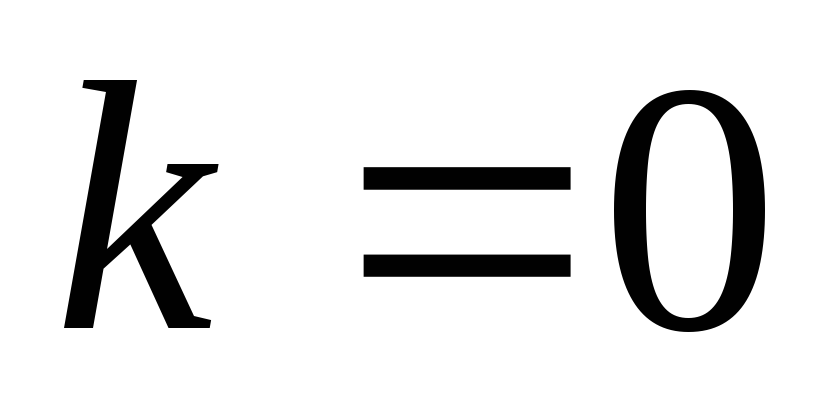. Для идеального диода, имеющего ВАХ вида (4.25), .

4.8. Коэффициент инжекции.

В плоскости перехода (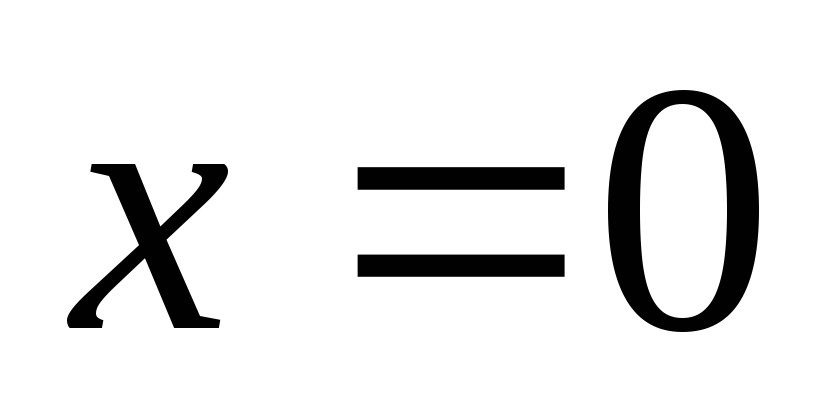) ток диода имеет электронную и дырочную составляющие (4.14).

Отношение

, (4.42а)

показывающее, какая часть тока в плоскости перехода переносится дырками, называется коэффициентом инжекции дырок. Соответственно, величина

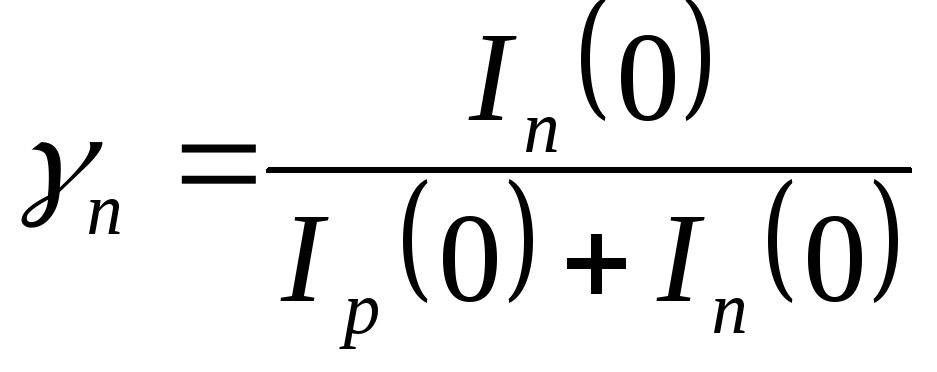— (4.42б)

коэффициент инжекции электронов.

Очевидно, что сумма коэффициентов инжекции электронов и дырок равна 1:

. (4.43)

Коэффициент инжекции носителей, инжектируемых из эмиттера в базу, называется эффективностью эмиттера . В случае эмиттерар-типа эффективность эмиттера равна коэффициенту инжекции дырок:

.

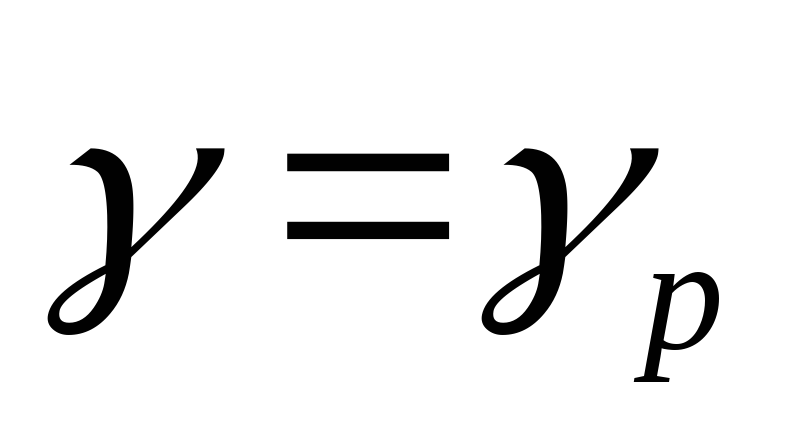Величина эффективности эмиттера не является, как правило, важным параметром полупроводникового диода, однако в транзисторе смеет решающее значение. Коэффициенты инжекции определяются соотношениями (4.25) -(4.27).

Для расчета эффективности эмиттера могут быть использованы соотношения (4.25) — (4.27):

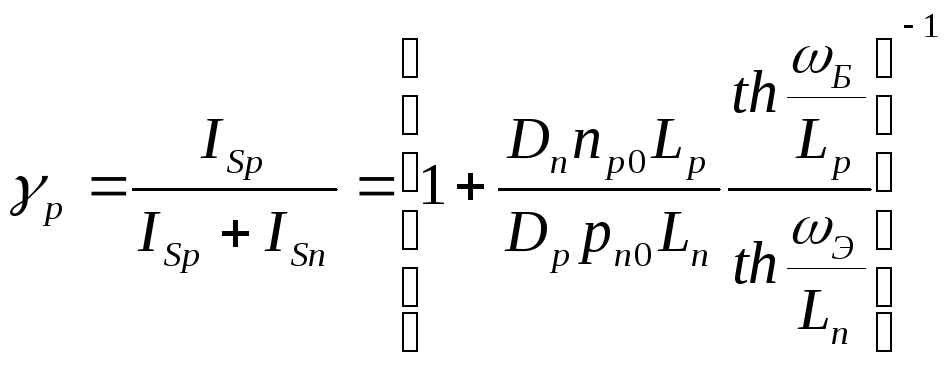. (4.44а)

Учитывая, что для р-эмиттера

, ,

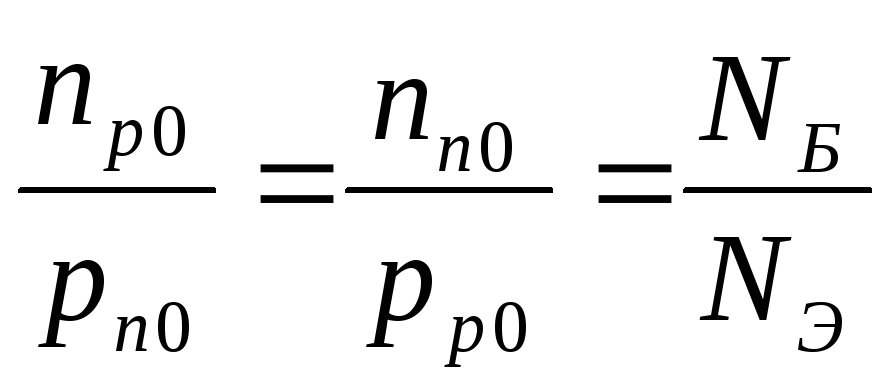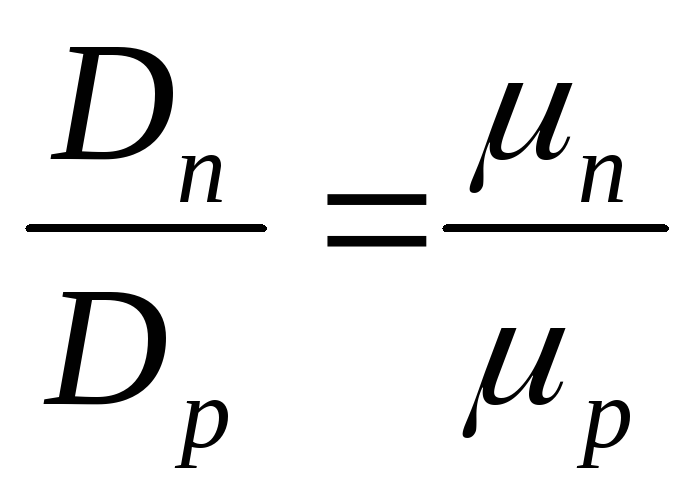получим

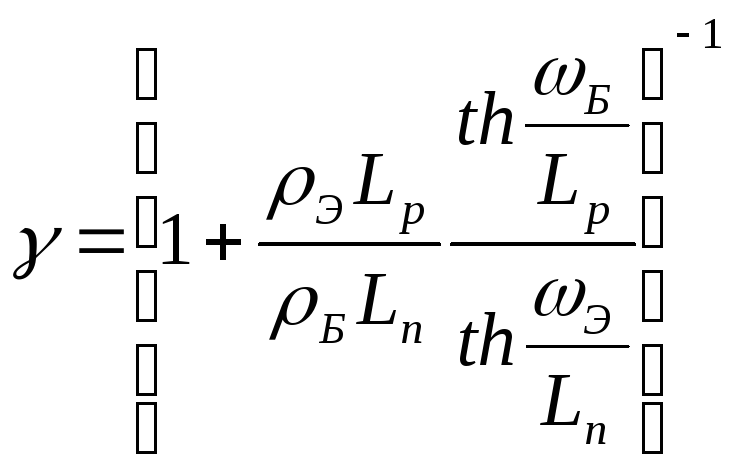
или

,

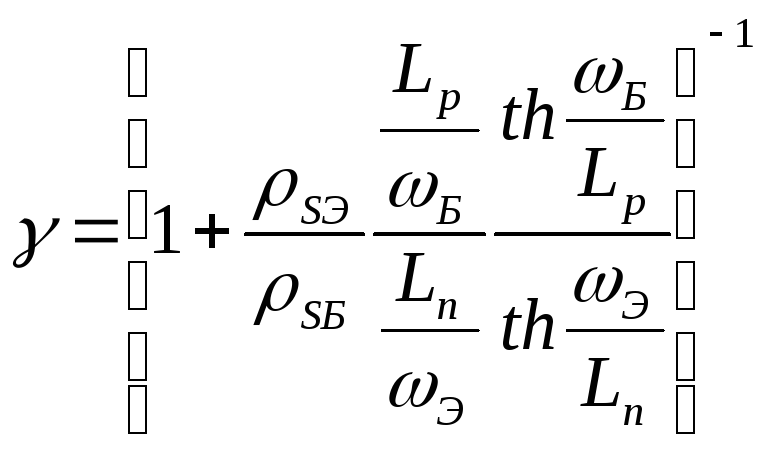где 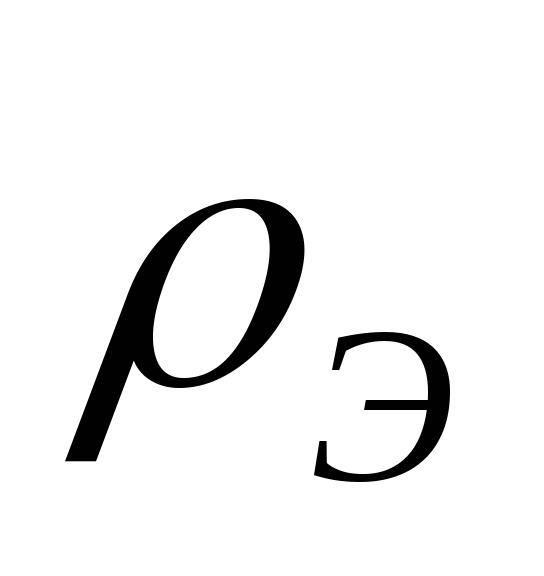,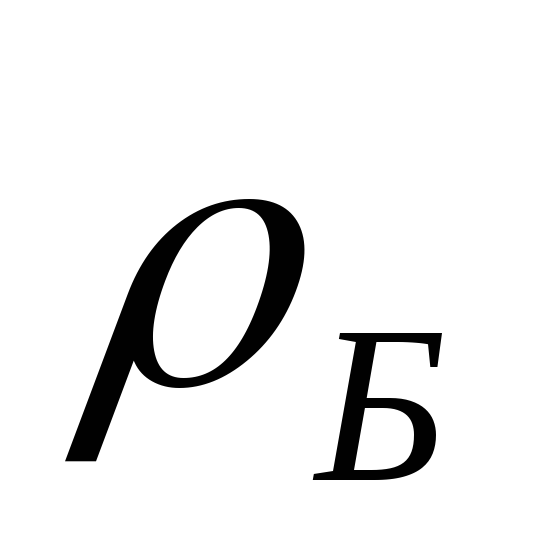— удельное сопротивления материала эмиттера и базы;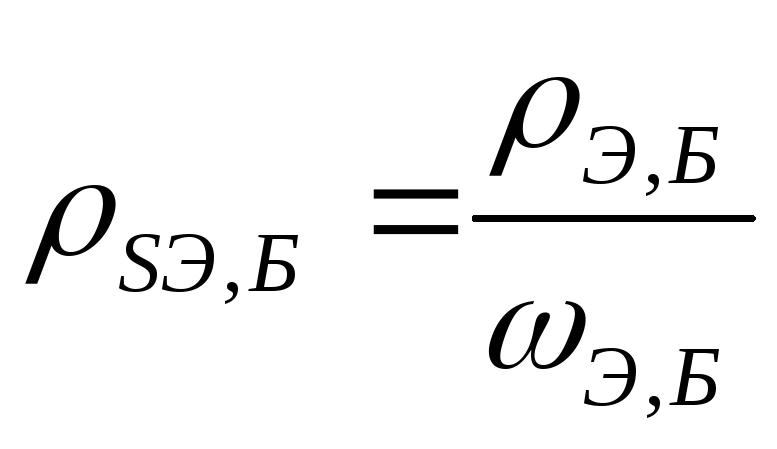— поверхностные сопротивления эмиттерного и базового слоев.

В случае короткой базы и короткого эмиттера (,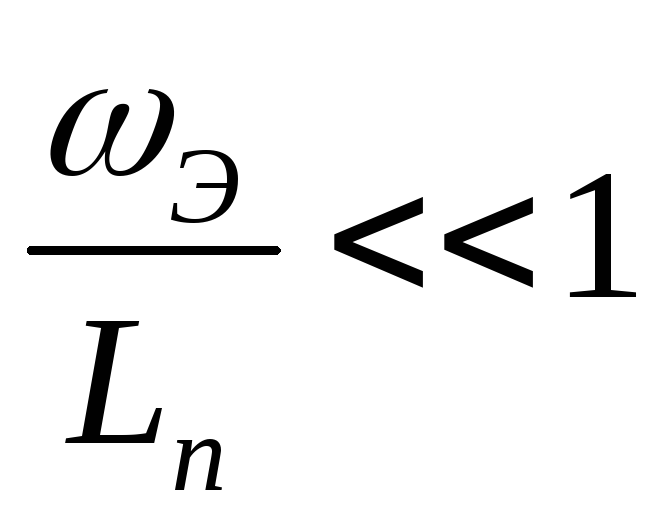) эффективность эмиттера определяется соотношением поверхностных сопротивлений эмиттера и базы:

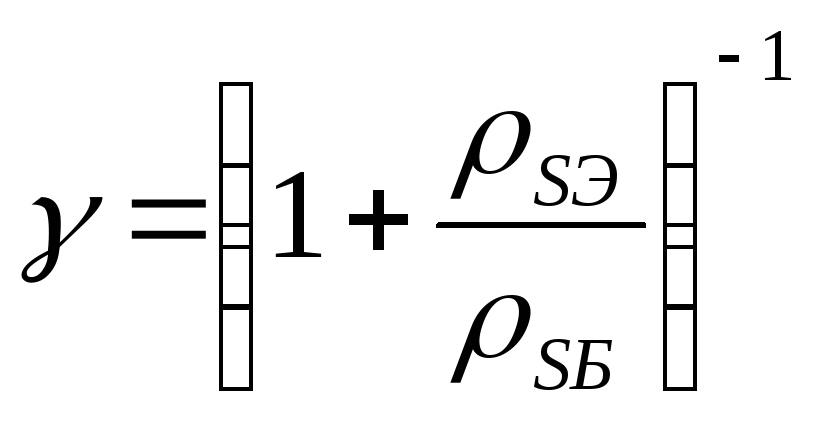. (4.44г)

Эффективность эмиттера приближается к единице при увеличении степени легирования эмиттера и уменьшении степени легирования базы.

Из (4.44а) следует, что эффективность эмиттера зависит от отношения концентраций неосновных носителей в эмиттер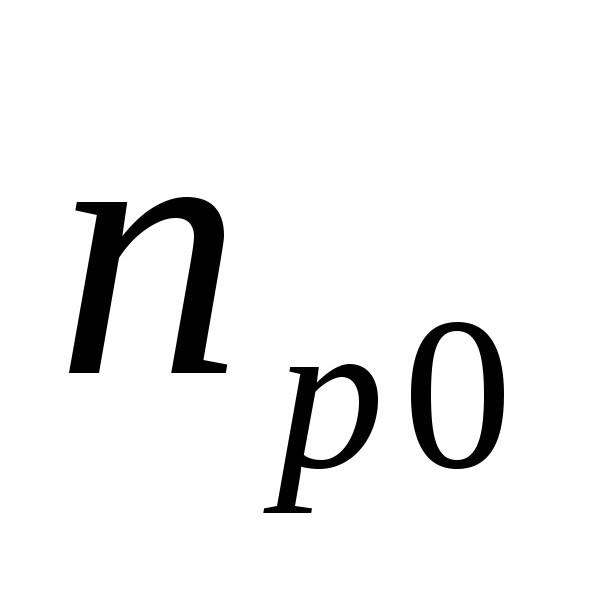е () и базе (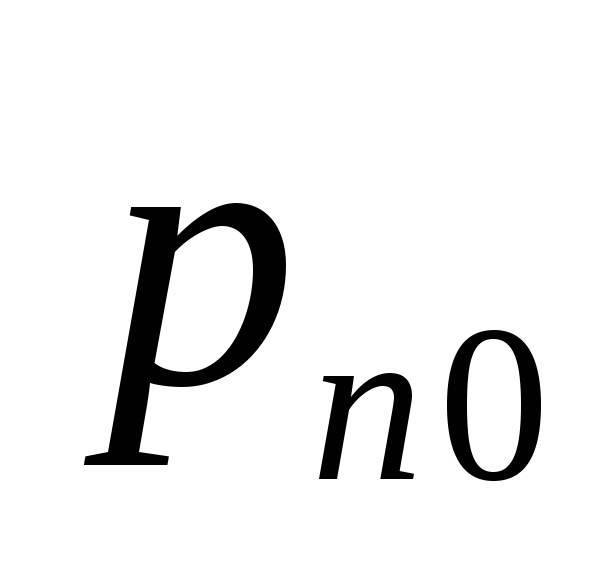). Особенно большим это отношение может быть в гетеропереходах. Если высота потенциального барьера для электронов существенно превышает высоту барьера для дырок, ток через переход практически полностью переносится дырками, и их коэффициент инжекции равен 1.

2.11 Температурная зависимость прямого напряжения.

Вах идеализированной модели (2.44)

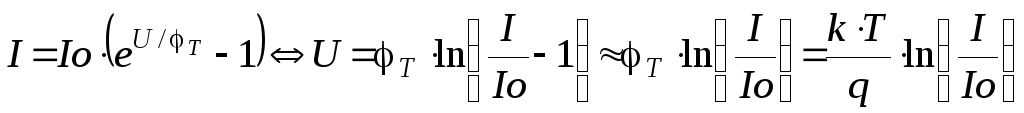
позволяет получить значение температурного коэффициента прямого напряжения на p-n переходе. Применим (2.47) и (1.11).

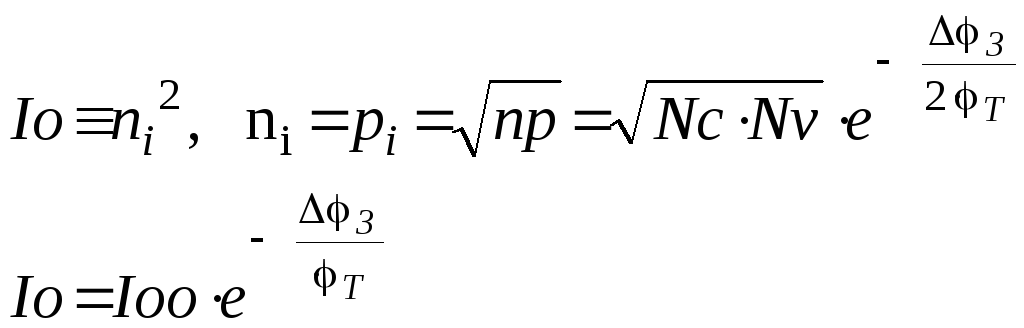
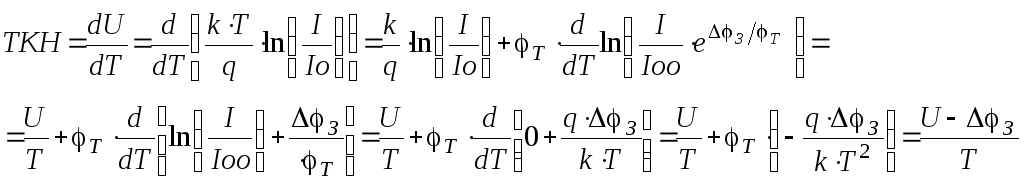
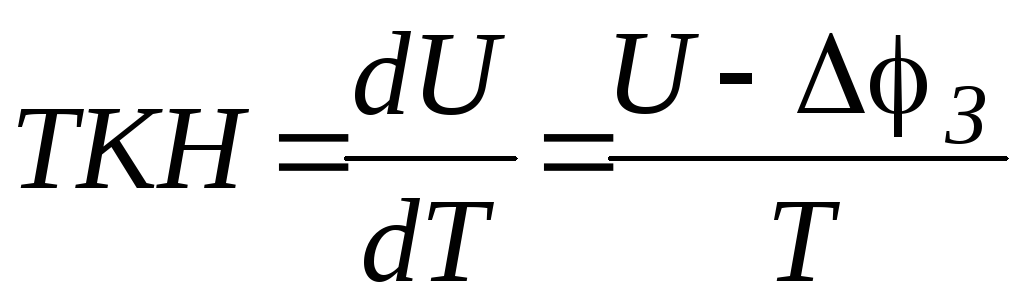
(2.54)

Так как U<_З, то ТКН<0. Для кремния при Т=300К _З=1,1 В и если U=0,6 В ТКН 2мВ/^oC ,

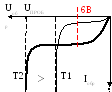
На рис. построены ВАХ диода для трех температур в области малых токов (I<5мА). При увеличении тока растет влияние омического сопротивления (2.50), которое имеет положительный ТК. Поэтому в области больших токов суммарный ТКН диода уменьшается по модулю и может даже изменить знак, графики тока сближаются и пересекаются.

2.12 Обратная ветвь вах реального диода.

Идеализированная модель (2.44) имеет обратный ток

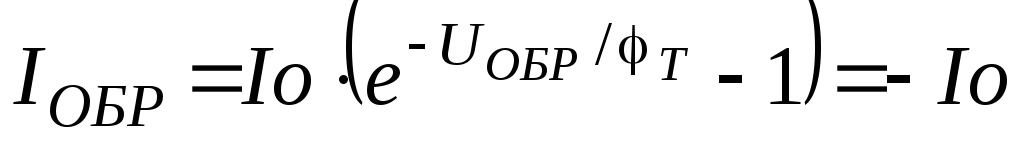
Тепловой ток (2.47)

.

Поскольку SL – объем, а p_n/_p и n_p/_n – скорости термогенерации, то тепловой ток обусловлен генерацией неосновных зарядов в прилегающих к p-n переходу слоях с объемами SL.

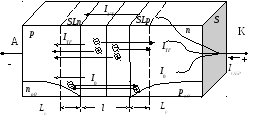
Реальный диод имеет дополнительные составляющие токов, которые могут превышать тепловой ток.

При обратном напряжении благодаря увеличению высоты потенциального барьера ток рекомбинации пренебрежимо мал (он преобладает при Uпр) и не компенсирует ток термогенерации (2.48)

I_Т.Г.+Ij_рек= I_Т.Г  0 (2.55)

По аналогии (2.12.2)

. (2.56)

Ток термогенерации суммируется с тепловым и увеличивает обратный ток. Тепловой ток Io пропорционален квадрату собственной концентрации: Ion_i². Отношение собственных концентраций для Ge и Si составляет примерно 10³, поэтому соотношение тепловых токов для Ge и Si составляет 10⁶. Так как I_Т.Гn_i, то отношение токов термогенерации для Ge и Si составляет 10³.

Вгерманиевых диодахI_Т.Г <<Io, в кремниевых наоборот, ток I_Т.Г >>Io, поэтому Ge: IoбрIo. (2.57)

Si: Ioбр I_Т.Г. (2.58)

По этой причине германиевые диоды имеют обратные токи примерно в 10³ раз больше кремниевых, а не в 10⁶ в соответствии с идеализированной моделью.

В кремниевых диодах ток I_О с ростом температуры увеличивается быстрее, чем ток термогенерации в переходе и при температурах выше +100^оС превышает I_Т.Г.

Кроме теплового тока и тока термогенерации в реальных диодах, особенно кремниевых, наблюдается ток утечки по поверхности I_УТ, обусловленные дефектами кристаллической структуры и наличием различных поверхностных пленок, молекул газов, воды и др. В общем случае

I_ОБР= I₀+I_Т.Г.+I_УТ , I_обр (Ge) ≈ 10³ I_обр (Si) (2.59)

2.13 Аппроксимация обратной ветви.

При наличии экспериментальной (справочной) обратной ветви ВАХ возможна аппроксимация (линейное моделирование) диода.

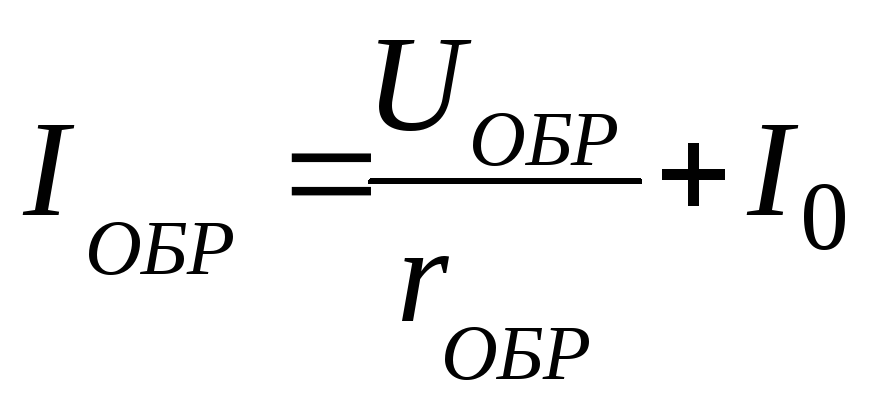(2.60)

2.14 Пробой p-n перехода. Механизмы пробоя. Температурная зависимость напряжения пробоя. ( му 1973)

Пробой – резкое увеличение обратного тока. Существует 2 основных типа первичного пробоя: туннельный и лавинный.

1. Туннельный пробой.Характерен для узких p-n переходов. Образуется между слоями с высокой концентрацией примесей. Туннельный эффект состоит в «просачивании» электронов через потенциальный барьер, когда их энергия недостаточна для преодоления потенциального барьера.

С ростом температуры уменьшается ширина запрещённой зоны, сам p-n переход сужается, энергия электронов увеличивается. Это приводит к уменьшению напряжения туннельного пробоя.

ТКН – температурный коэффициент напряжения пробоя. ТКН<0.

2. Лавинный пробой. Характерен для широких p-n переходов. Образуется между низко легированными слоями с большим удельным сопротивлением.

Д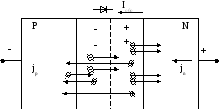вижение электронов вp-n переходе с высокой напряженностью поля сопровождается ударной ионизацией атомов основного материала, в результате чего образуются электронно-дыроч-ные пары. Новые носители также могут набрать скорость (энергию), достаточную для ионизации – развивается лавинообразный процесс увеличения обратного тока.

При увеличении температуры электроны чаще сталкиваются с атомами основного материала, не успевая набрать энергию ионизации и для лавинного пробоя необходимо увеличивать напряжённость, т.е. напряжение пробоя. ТКН>0.

Ток пробоя необходимо ограничивать с помощью внешних резисторов. В противном случае за счёт саморазогрева первичный (туннельный и лавинный) пробой перейдёт во вторичный (тепловой) и диод выйдет из строя. Для выпрямительных диодов пробой является вредным эффектом. Ge -диоды как правило имеют в 100-1000 раз больше обратные токи и соответственно в 10 раз меньше напряжение пробоя.

Пробой – полезный эффект при ограничении токов: используется в стабилитронах.

«Исследование температурных характеристик полупроводниковых диодов»

Цель работы: Исследовать механизмы прохождения носителей заряда в р-n переходе по результатам температурных характеристик Si и Ge диодов. Определить энергию активации обратного тока.

Теоретическая часть

1. Температурная зависимость параметров ВАХ p-n перехода

С увеличением температуры ВАХ p-n перехода претерпевает изменения. Обратный ток j_S0 увеличивается по экспоненте, а прямое падение напряжения при заданном j_пр на малых уровнях инжекции уменьшается линейно.

Основная температурная зависимость j_S0 в температурном диапазоне ниже собственной (Т < Т_i) определяется собственной концентрацией носителей заряда

.

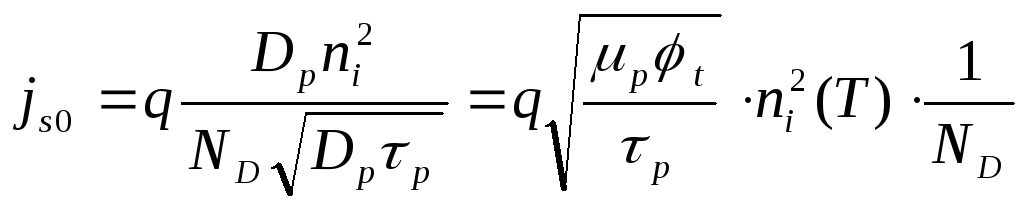Температурная зависимость подвижности определяется рассеянием на фононах и ионах примеси. В первом приближении:

,

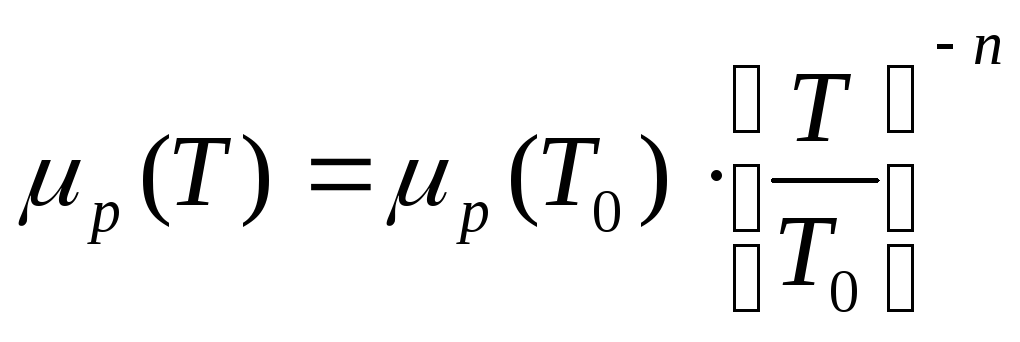где n изменяется от 2,3 до 0,9 для кремния в зависимости от степени легирования n-базы.

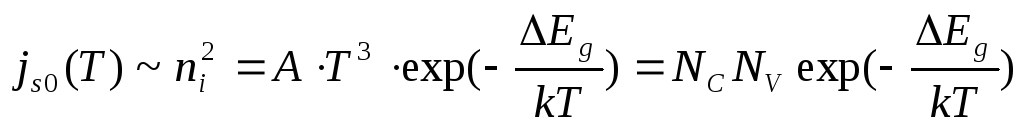
Следовательно, ; .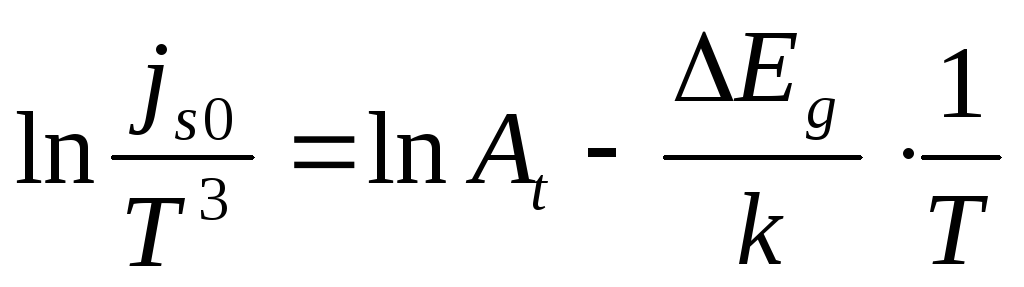

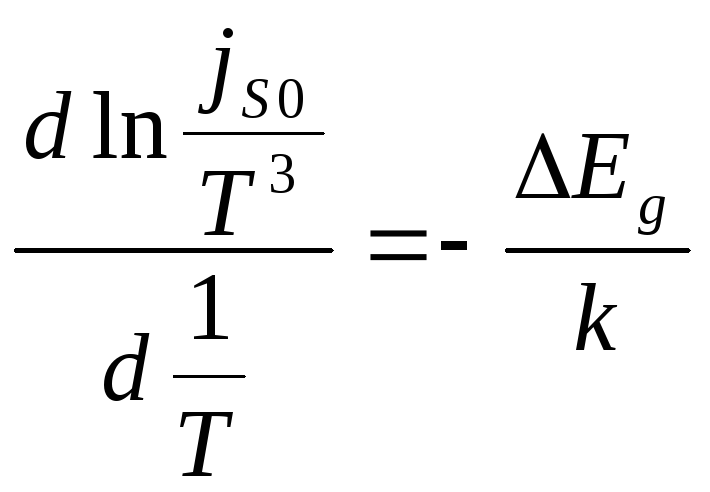По температурной зависимости обратного тока можно определить ширину запрещенной зоны полупроводника (рис. 2.1а).

Прямое падение напряжения на p-n переходе при заданной плотности прямого тока j_пр определяется из зависимости тока от напряжения:

,

.

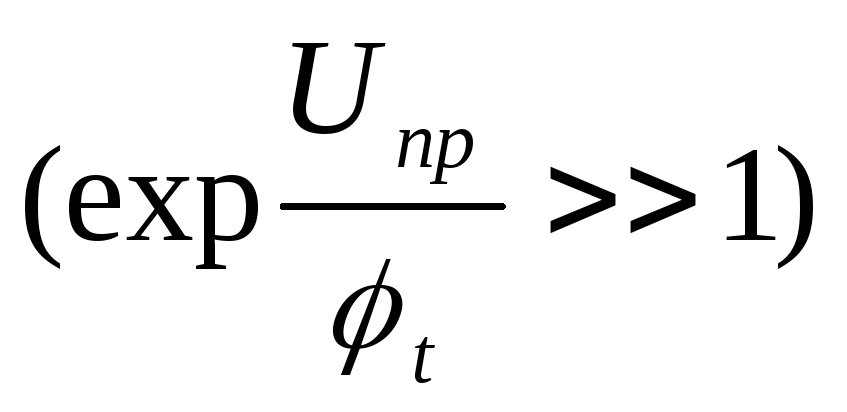Пренебрегая более слабой зависимостью T³ по сравнению с, получим:

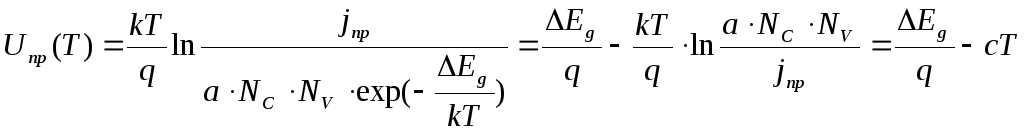При увеличении температуры возрастает энергия носителей заряда и вероятность их перехода через барьер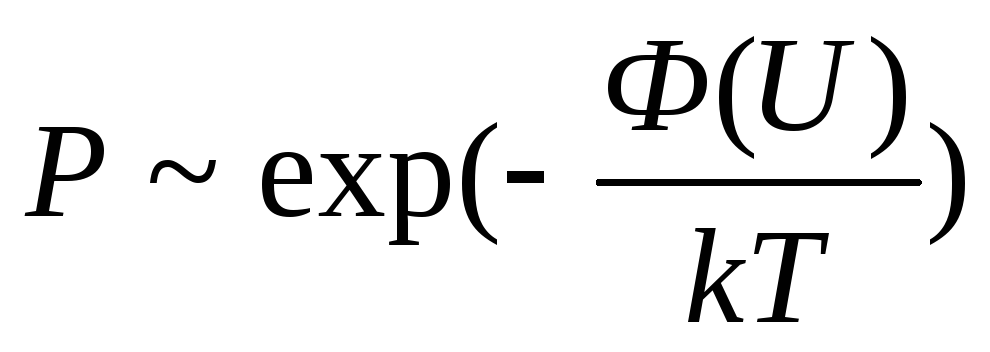, следовательно, необходимо меньшее напряжение (увеличить барьер) для поддержания тока на одном и том же уровне.

Если поток носителей поддерживается постоянным внешним источником (j_пр = const), то это означает, что с увеличением температуры величина потенциального барьера должна возрастать, поэтому Uпр уменьшается (рис. 2.1б).

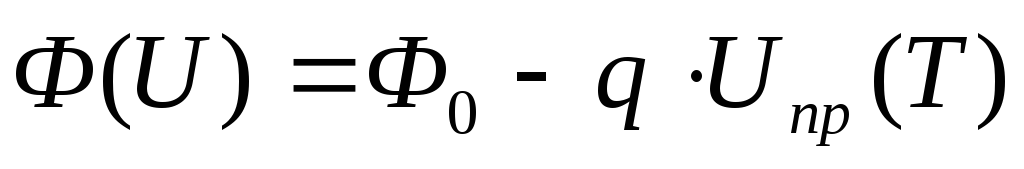
При увеличении плотности тока температурная зависимость Uпр ослабляется, так как a·N_СN_V = j_max, представляет собой максимальную плотность тока при спрямленном барьере, и при больших плотностях тока увеличение энергии носителей существенно не увеличивает вероятность переброса (нет барьера) (рис. 2.1в).

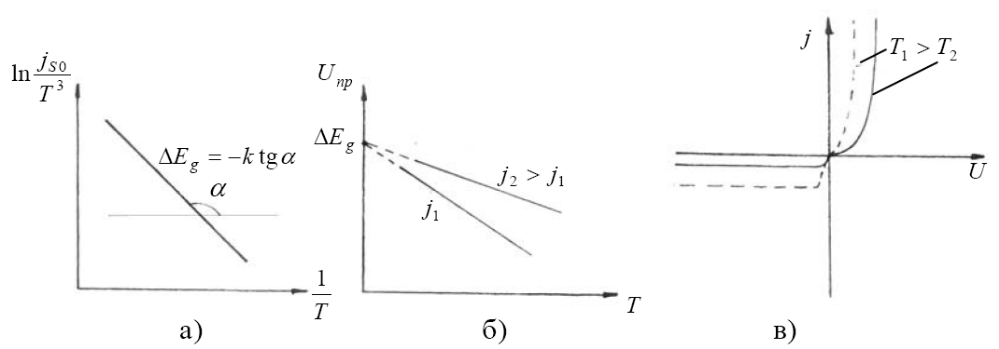
Рисунок 2.1 — Температурная зависимость обратного тока (а), прямого падения напряжения (б), ВАХ p-n перехода (в)

2. Энергия активации обратного тока

Во всех случаях обратный ток р-n перехода связан с генерацией носителей заряда, т.е. является активационным процессом. Активационный процесс характеризуется энергией активации, т.е. тем энергетическим барьером, который должен преодолеть носитель заряда при генерации.

Естественно, что процесс активации очень чувствителен к температуре. Чем больше энергия активации, тем меньше вероятность носителю заряда преодолеть этот барьер. С увеличением температуры и средней энергии носителей эта вероятность возрастает.

Следовательно, если идут одновременно два процесса с различными энергиями активации, то при низких температурах будет преобладать процесс с меньшей энергией активации, а при высоких — с большей. Определяя энергию активации генерационной составляющей тока, можно показать из (1.8), (1.13), что температурная зависимость этих выражений определяется формулой:

, (2.1)

откуда 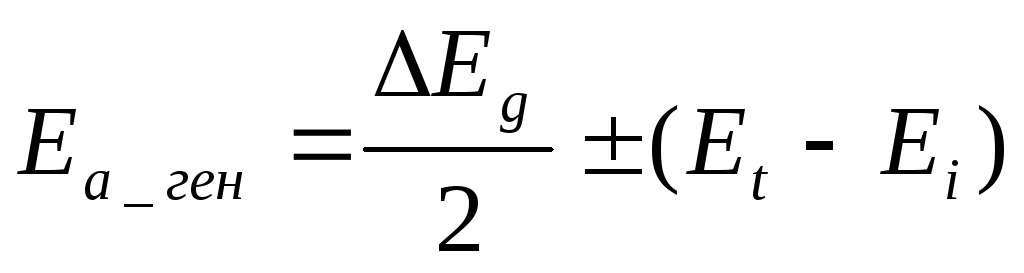, т.е. энергия активации генерационной составляющей тока при Еt=Еi, равна .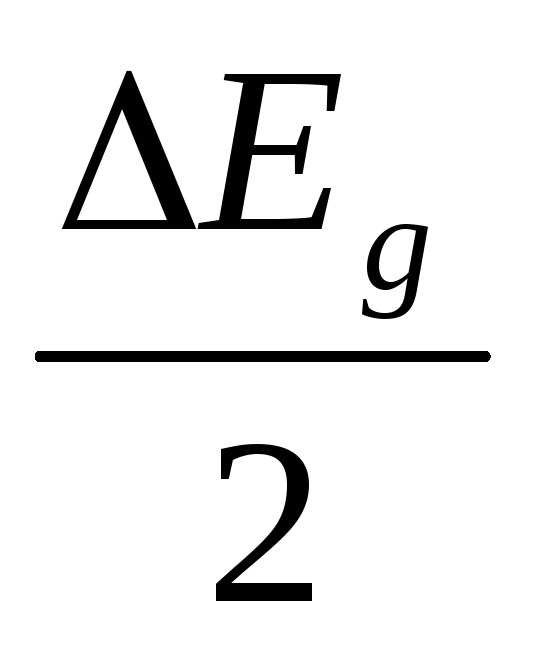

Предэкспоненциальный член T^3/2 слабо зависит от температуры по сравнению с экспонентой, поэтому, используя зависимость ln(Iобр)=f(1/T), можно определить энергию активации данной составляющей тока (рис.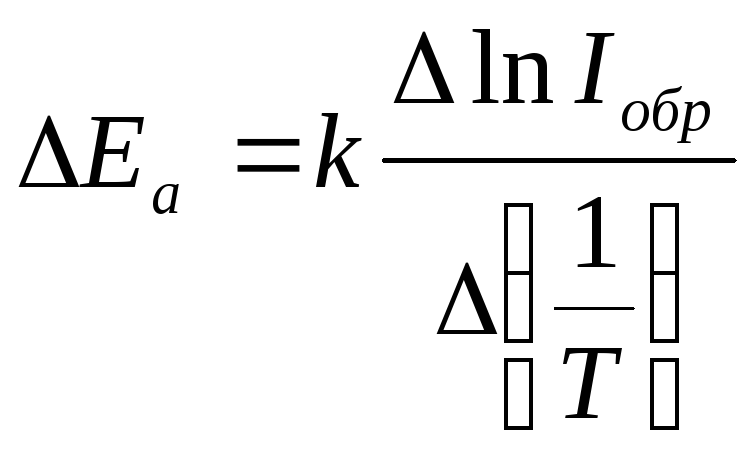2.2).

(2.2)

Рисунок 2.2 – К определению энергии активации температурной зависимости обратного тока диода

Получить этот результат можно из физических соображений. Статистика Шокли—Рида показывает, что эффективная генерация осуществляется ловушками, энергетический уровень которых расположен вблизи середины запрещенной зоны. Ловушки, расположенные выше и ниже, активного участия в генерации не принимают, т.к. при большом энергетическом зазоре резко уменьшается сечение захвата для одного из типов носителей. Действительно, ловушки, расположенные выше середины запрещённой зоны, легко захватывают электроны, но вероятность захвата дырки мала. Поэтому электрон продолжительное время как бы скачет между ловушкой и С—зоной, прежде чем примет участие в генерации или рекомбинации в зависимости от условий.

Электрон из валентной зоны захватывается ловушкой, оставляя в валентной зоне дырку. Так как при отрицательных смещениях в области: ОПЗ р-n перехода существует сильное электрическое поле, то она тут же уносится за пределы р-n перехода. Электрон из ловушки не может попасть в валентную зону, так как дырки там отсутствуют. Поэтому он может быть переброшен только в зону проводимости. Обратно упасть в ловушку он не успевает, так как подобно дырке быстро уносится полем, Из этого рассмотрения видно, что каждый образовавшийся носитель заряда преодолевает барьер Δ Еg/2 , т.е. энергия активации генерационной составляющей тока равна Δ Еg/2. Последовательность процесса генерации в слое объёмного заряда иллюстрируется рис.2.3.

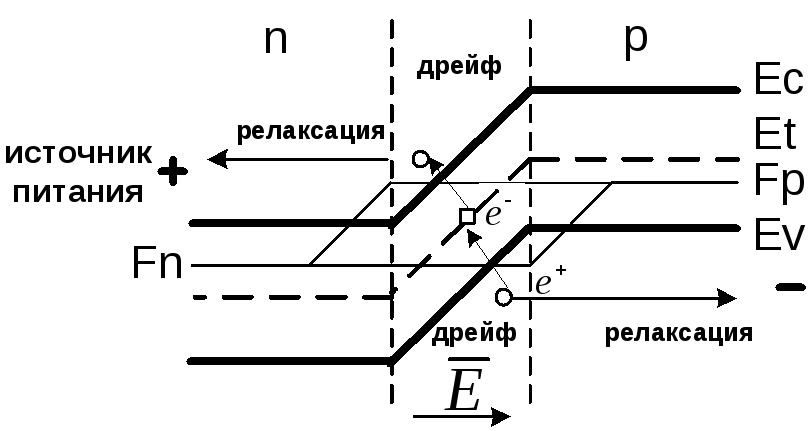
Рисунок 2.3 – Схема процесса генерации в слое объемного заряда p-n перехода

Аналогично определяем энергию активации диффузионной составляющей тока:

.

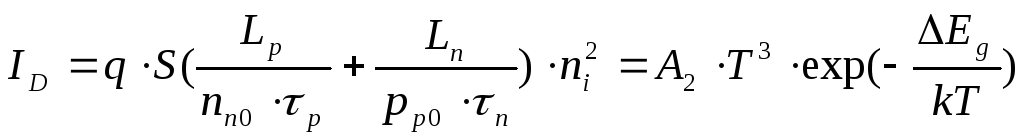Энергия активации диффузионной составляющей тока равна ширине запрещённой зоны. Но это не означает, что генерация происходит по типу зона—зона.

В базе диода соблюдается условие электронейтральности, т.е. в любой точке положительный заряд дырок в точности равен отрицательному заряду электронов и акцепторов. Это условие вытекает в силу слабого влияния поля в базе на диффузию неосновных носителей. Поэтому, когда электрон из V —зоны захватывается ловушкой, оставляя дырку, она не может участвовать в токе, пока электрон из ловушки не перебросится в С—зону.

Захват ловушкой электрона приводит к нарушению электронейтральности в локальной области базы. Сила Кулона будет препятствовать диффузии дырки. Дырка может диффундировать к р-n переходу только в случае, когда электрон с ловушки перебросится в зону проводимости, где он за время релаксации (практически мгновенно) уходит на «+» источника. Диполь: заряженная ловушка — дырка разрушается, и дырка под действием градиента концентрации движется к ОПЗ, где захватывается полем. В результате необходимая энергия для генерации и разделения электронно—дырочной пары составляет ΔEg (рис.2.4). Следует отметить, что коллектирование дырок возможно лишь в пределах 3Lp. Если дырка возникла на расстоянии больше 3Lp, то она не дойдёт до ОПЗ, а прорекомбинирует, поэтому разделения пары в р-n переходе не будет, а, следовательно, и тока.

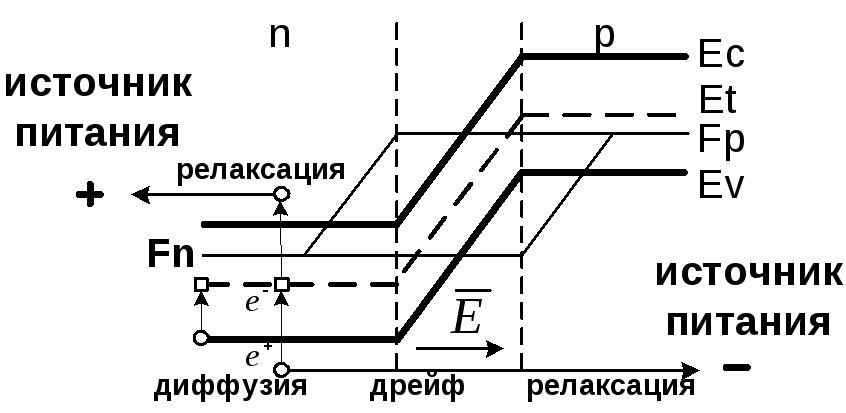
Рисунок 2.4 – Схема процесса генерации в нейтральной области

Энергию активации канального тока удобно определять из выражения (1.15):

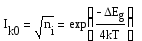. (2.3)

т.е. в случае канальной проводимости генерация и рекомбинация происходит на мелких ловушках. Этот факт можно пояснить из рассмотрения рис.2.5. При канальном токе проводимости генерация происходит на поверхностных уровнях. Т.к. уровень Ферми расположен в этом случае выше середины запрещенной зоны, то ловушки, расположенные вблизи середины запрещенной зоны (рис.2.5б), практически заполнены, а поэтому не могут участвовать в генерации (ловушка не может захватить электрон из валентной зоны, так как занята). Процесс генерации носителей заряда происходит через менее эффективные, на свободные ловушки (рис.2.5а), глубина залегания которых примерно равна Δ Eg/4.

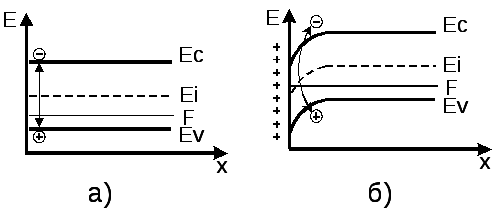
Рисунок 2.5 – Рисунок к пояснению температурной зависимости обратного канального тока

Экспериментально энергию активации, а значит, механизм проводимости обратного тока определяют из зависимости ln(Iобр)=а(1/T) по наклону прямой. Как было показано выше, при низких температурах наклон соответствует энергии активации ΔЕg/4 , при высоких температурах — ΔEg/2 , либо ΔEg, в зависимости от того, какая составляющая тока, диффузионная или генерационная, преобладает.

3. Пробой р-n перехода

С увеличением обратного напряжения, прикладываемого к p-n переходу достигается такая область, в которой происходит резкое возрастание обратного тока (рис. 2.6). Эту область называют областью пробоя перехода, а напряжение (Uв), при котором наступает пробой — напряжением пробоя. Различают тепловой, туннельный и лавинный пробой.

Рисунок 2.6 – ВАХ диода при пробое: кривая 1 – тепловой пробой, кривая 2 – лавинный пробой, кривая 3 – туннельный пробой

3.1.2. Зависимости тока туннельного диода от температуры

Изменение температуры туннельного диода может по-разному влиять на туннельную составляющую тока и на составляющую, связанную с инжекцией.

На температурную зависимость туннельной составляющей тока могут влиять следующие физические факторы:

1.С повышением температуры уменьшается ширина запрещенной зоны арсенида галлия и германия – основных исходных полупроводниковых материалов для туннельных диодов. Уменьшение ширины запрещенной зоны приводит к уменьшению толщины потенциального барьера, сквозь который туннелируют электроны, при этом вероятность туннелирования растет. Туннельная составляющая тока и, в частности, пиковый ток увеличиваются (рисунок 3.5).

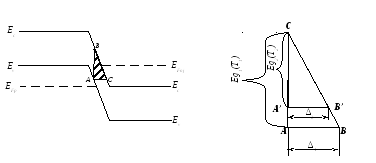
Рисунок 3.5 — Рисунки, поясняющие увеличение пикового

тока туннельного диода при росте температуры

2.При увеличении температуры изменяется распределение электронов по энергетическим уровням – количество электронов под уровнем Ферми в зоне проводимости n-области уменьшается, так как часть свободных электронов переходит на более высокие энергетические уровни, а уровень Ферми смещается вниз. Поэтому уменьшается число электронов, которые могут туннелировать из n-области в р-область. Туннельная составляющая прямого тока уменьшается (рисунок 3.6).

Рисунок 3.6 — Рисунок, поясняющий уменьшение пикового тока туннельного

диода при росте температуры

Так как эти факторы действуют, так сказать, в разные стороны, то суммарное их влияние, во-первых, должно быть малым, а во вторых, оно может привести как к увеличению, так и к уменьшению пикового тока туннельного диода с увеличением температуры.

Инжекционная составляющая тока туннельного диода растет с увеличением температуры по двум причинам, имеющим место и в выпрямительных диодах – уменьшение потенциального барьера и перераспределение носителей заряда по энергетическим уровням. Поэтому у туннельного диода ток впадины растет с увеличением температуры.

3.1.3. Частотные свойства туннельных диодов

Механизм действия туннельных диодов связан с туннелированием электронов сквозь потенциальный барьер. Время, необходимое для завершения этого процесса, составляет 10^-13 – 10^-14с. Эффекта накопления неосновных носителей в базе туннельных диодов практически нет, так как они используются при малых напряжениях, соответствующих падающему участку вольт-амперной характеристики (с отрицательным дифференциальным сопротивлением). Поэтому туннельные диоды способны работать на частотах до сотен гигагерц, что соответствует миллиметровому диапазону радиоволн. Верхний предел частотного диапазона работу туннельных диодов ограничен лишь паразитными реактивностями – собственной емкостью, основу которой составляет барьерная емкость электронно-дырочного перехода, и индуктивностью выводов и корпуса.

Для анализа и расчета параметров, характеризующих частотные свойства туннельных диодов, воспользуемся эквивалентной схемой туннельного диода для малого переменного сигнала при наличии постоянного напряжения которое смещает рабочую точку на падающий участок вольтамперной характеристики. Эквивалентная схема туннельного диода отличается от эквивалентной схемы обычного диода только тем, что здесь вместо активного сопротивления перехода введено отрицательное дифференциальное сопротивление 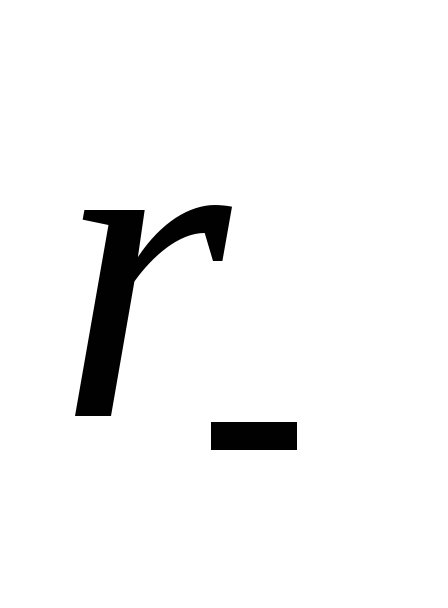и учитывается индуктивность выводов L (рисунок 3.7).

Рисунок 3.7 — Физическая эквивалентная схема туннельного диода

Полное сопротивление туннельного диода при малом синусоидальном напряжении

(3.1)

где g = 1/ 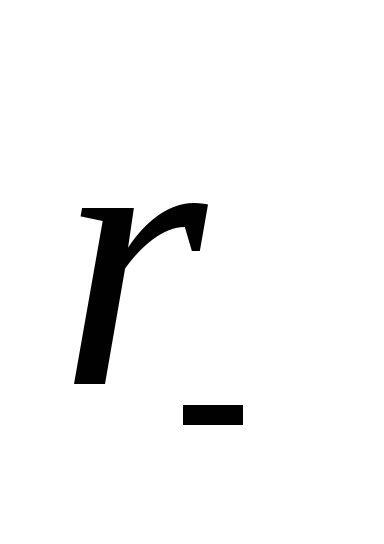– отрицательная дифференциальная проводимость туннельного диода.

Отрицательное дифференциальное сопротивление у туннельного диода будет существовать, если вещественная часть полного сопротивления будет меньше нуля, т.е. при

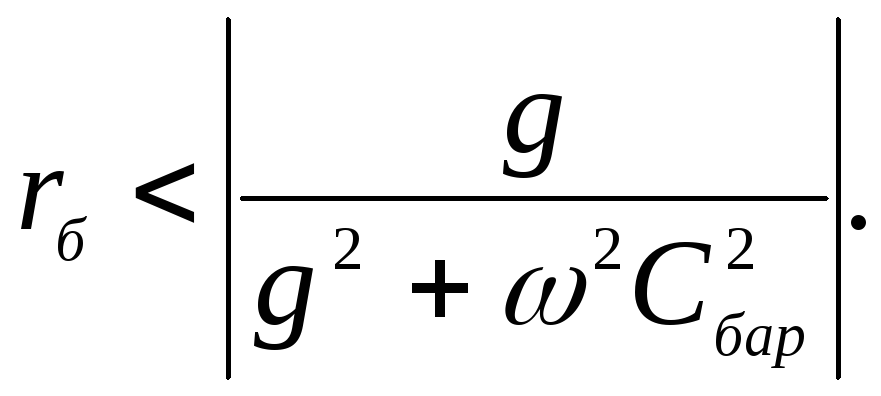(3.2)

При большой частоте второе слагаемое в вещественной части (3.1) окажется меньше (по абсолютному значению) первого слагаемого. Это значит, что туннельный диод при больших частотах не будет обладать отрицательным дифференциальным сопротивлением. Определим предельную резистивную частоту, на которой активная составляющая полного сопротивления туннельного диода обращается в нуль, т.е. неравенство (3.2) обращается в равенство:

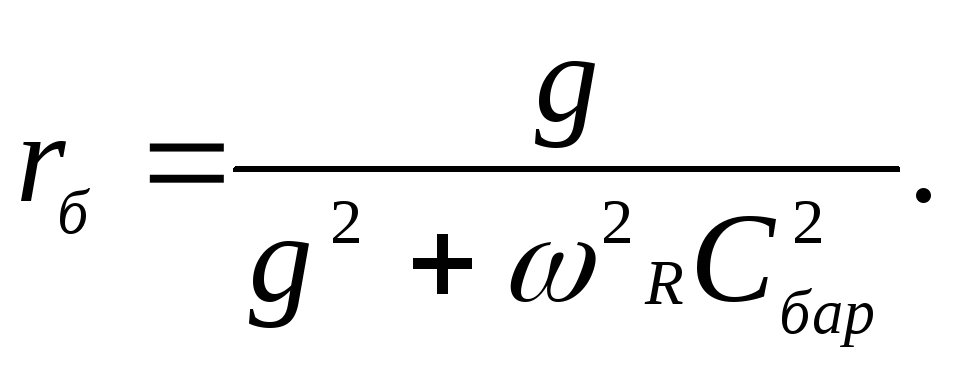
Отсюда

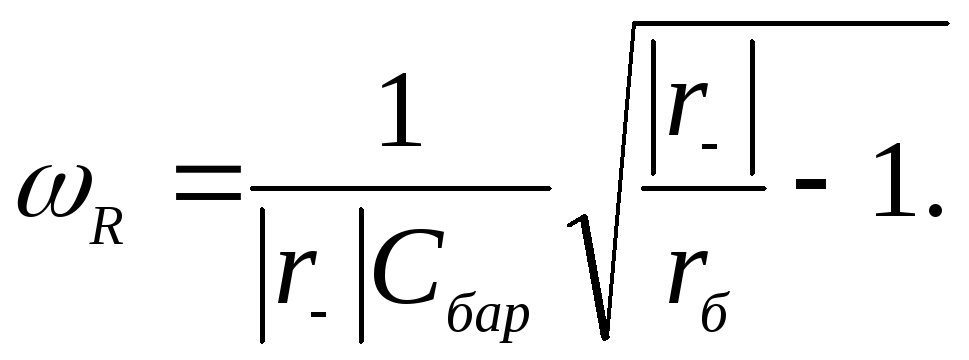(3.3)

Из соотношения (3.3) видно, что предельная резистивная частота туннельного диода зависит от соотношения сопротивления базы диода и абсолютного значения отрицательного дифференциального сопротивления. Для нахождения экстремальных значений предельной резистивной частоты надо продифференцировать (3.3) по 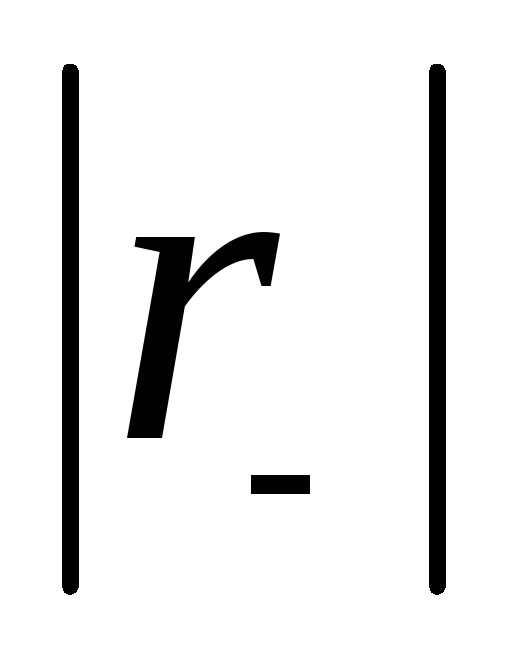и приравнять полученное выражение нулю. Тогда получаем условие

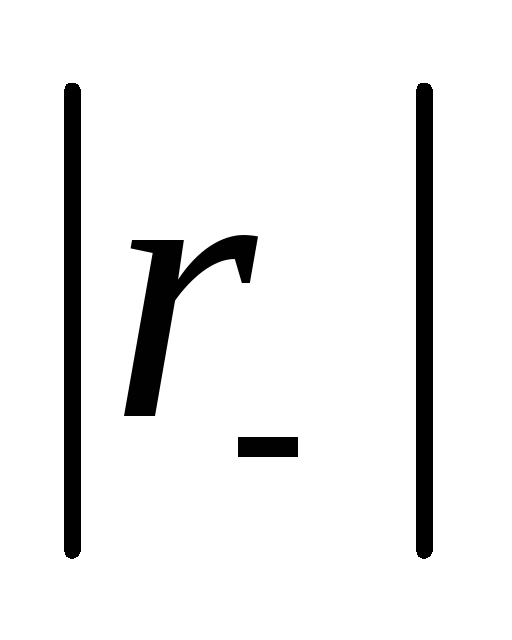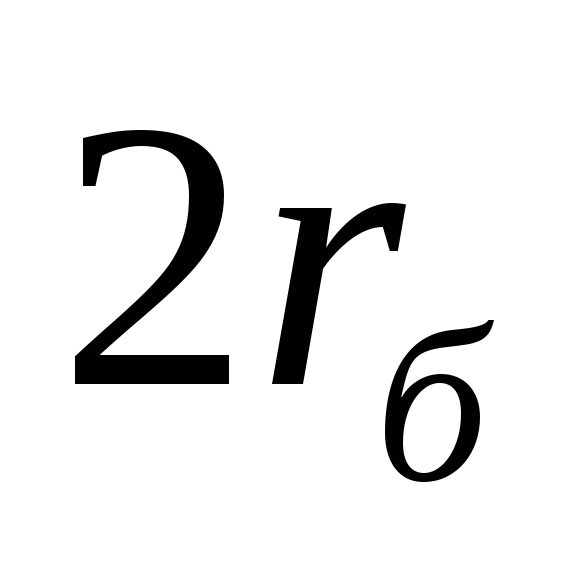=, (3.4)

при выполнении которого предельная резистивная частоту будет максимальной. Связь ее с параметрами эквивалентной схемы можно получить, подставив 3.4 в 3.3. Тогда

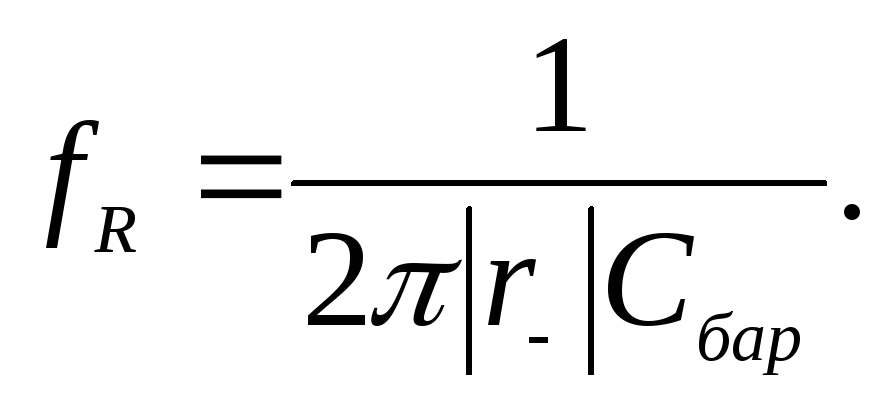(3.5)

Усредненное отрицательное дифференциальное сопротивление можно представить в виде:

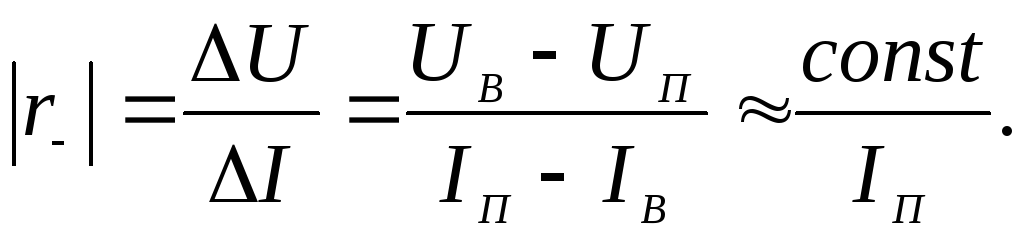
Если полученное соотношение подставить в (3.5), то

~

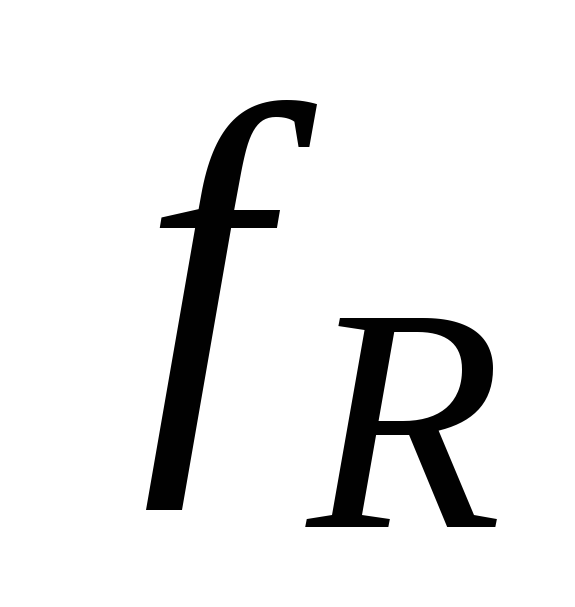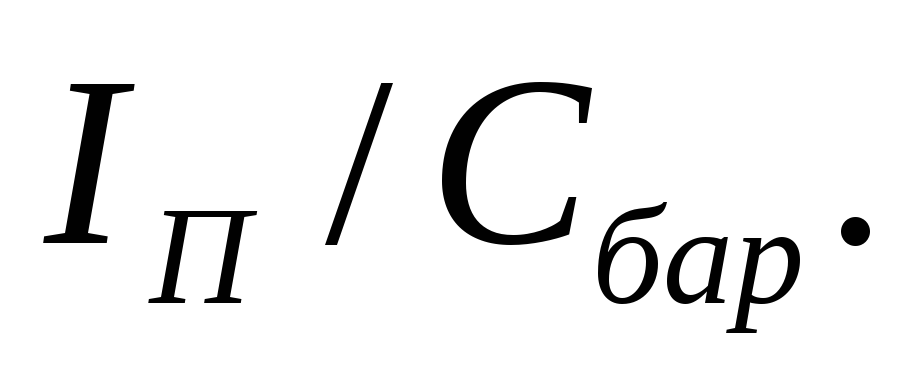
Поэтому отношение емкости туннельного диода к пиковому току является одним из основных параметров туннельного диода, который характеризует его частотные свойства.

В туннельном диоде, имеющем паразитную индуктивность и емкость, при некоторой частоте могут возникнуть условия для резонанса, что нарушит нормальную работу схемы с туннельным диодом. Поэтому резонансная частота туннельного диода является еще одним параметром, характеризующим частотные свойства туннельного диода.

Резонансную частоту туннельного диода можно определить из соотношения (3.1) при условии равенства нулю мнимой части полного сопротивления диода:

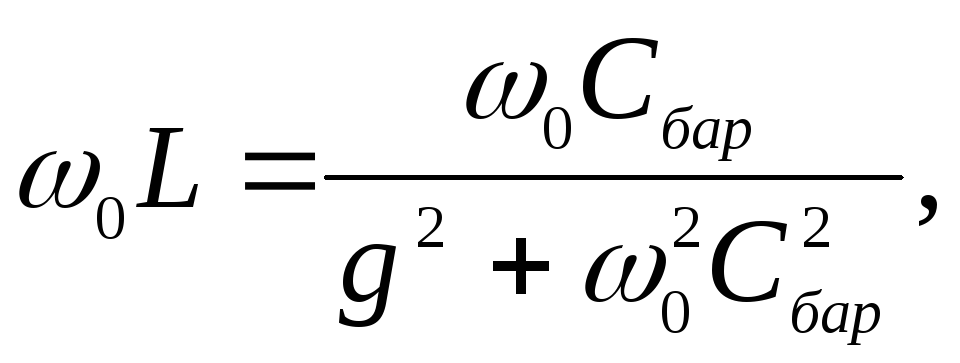
тогда

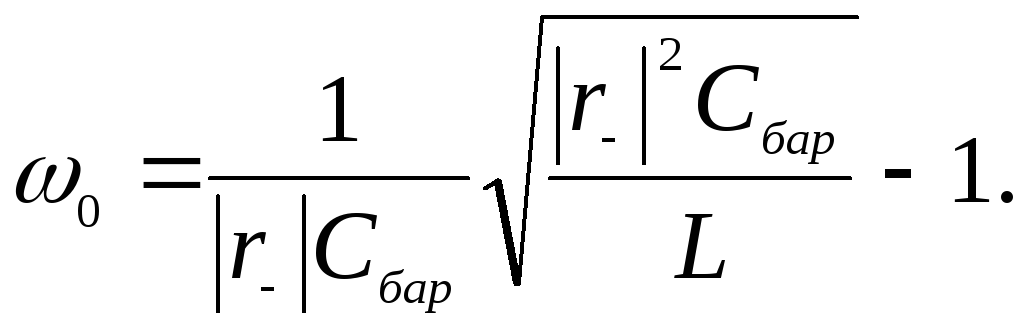(3.6)

Туннельные диоды должны быть сконструированы так, чтобы резонансная частота была выше предельной резистивной частоты 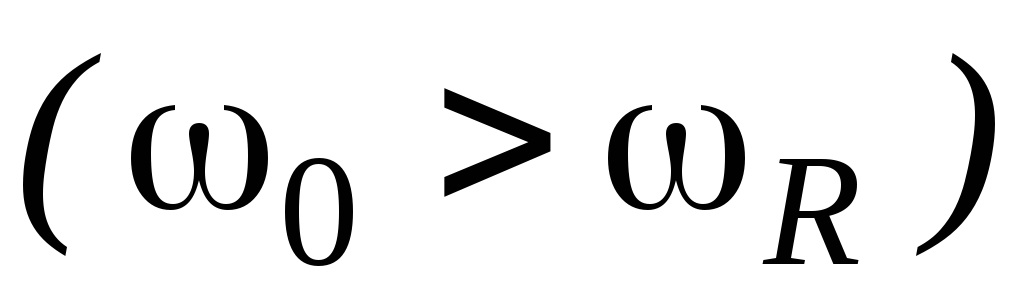, тогда возможные нежелательные резонансные явления возникают только на частотах, на которых туннельный диод уже не будет обладать отрицательным дифференциальным сопротивлением. Неравенство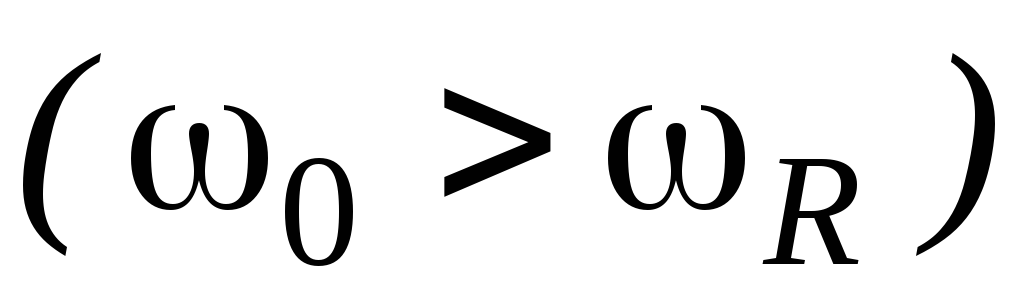с учетом соотношений (3.6) и (3.3) преобразуем следующим образом:

Следовательно, индуктивность эквивалентной схемы туннельного диода, которая определяется в основном индуктивностью внутренних и внешних выводов диода, должна быть по возможности малой. Поэтому внутренние и внешние выводы у туннельных диодов делают не из тонкой проволоки, а из плющенки или в виде мембран, пластин и т.п.

Температурная зависимость обратного тока полупроводникового диода

Соотношение (50), описывающее ВАХ идеального p-n перехода называют формулой Шокли. При приложении к p-n переходу положительного напряжения 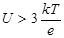 наклон ВАХ в полулогарифмическом масштабе  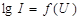постоянен. При T=300 К для увеличения плотности тока в 10 раз требуется увеличить напряжение на p-n переходе на ≈59.2 мВ ( 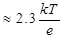). При приложении же к p-n переходу отрицательного напряжения  плотность обратного тока J_R через него становится постоянной и равной по модулю плотности тока насыщения J_R=-J_S (рис.3).

Рассмотрим теперь влияние температуры на плотность обратного тока идеального p-n перехода, то есть тока насыщения. Для простоты ограничимся рассмотрением асимметричного p⁺-n перехода, (N_A>>N_D). При этом

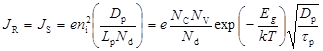,                               (52)

где 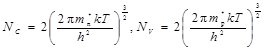 — эффективные плотности состояний соответственно в зоне проводимости и в валентной зоне.

Учитывая, что 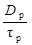~ , выделим зависящую от температуры часть плотности тока насыщения

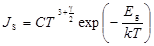,                                                  (53)

где C=const.

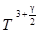Степенной член  по сравнению с экспоненциальным членом  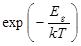слабо зависит от температуры. При обратном смещении, когда 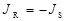, модуль обратного тока  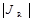будет увеличиваться с температурой примерно по экспоненте.

Прологарифмировав обе части уравнения (53) получим линейную зависимость логарифма плотности обратного тока от обратной температуры.

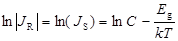.        (54)

Наклон зависимости  будет определяться шириной запрещенной зоны E_g.

Из уравнения (54) можно получить ширину запрещенной зоны полупроводника в Дж:

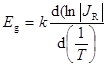.              (55)

Сплошная кривая 1 (Ge) на рис.4 представляет собой зависимость 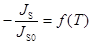 в координатах Аррениуса 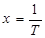,  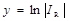для идеального p-n перехода в германии (I_S0 – плотность тока насыщения при температуре 25 °C).

Рассмотрим теперь ток термогенерации при обратном смещении p-n перехода. Так как при обратном смещении будут уменьшаться концентрации носителей заряда в обедненном слое (pn<<n_i²), то скорость термогенерации электронно-дырочных пар согласно теории Шокли-Рида-Холла при условиях p<n_i и n<n_i составит

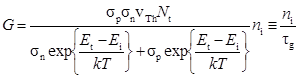,                                     (56)

где E_i – энергия середины запрещенной зоны полупроводника, E_t – энергия уровня генерации-рекомбинации, σ_n – сечение захвата электрона, σ_p – сечение захвата дырки, v_Th – тепловая скорость носителей заряда, N_t – плотность центров генерации-рекомбинации, τ_g – эффективное время жизни.

Плотность тока термогенерации электронно-дырочных пар в области пространственного заряда полупроводникового диода будет равна.

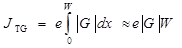,                                           (57)

где W – толщина слоя ОПЗ.

Полный обратный ток в асимметричном p⁺-n переходе (при p_n0>>n_p0 и 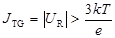) приближенно можно представить суммой диффузионного тока в нейтральной области и тока термогенерации в ОПЗ.

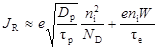.                                                 (58)

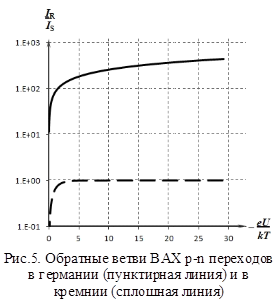При неизменной температуре плотность тока J_TG пропорциональна толщине ОПЗ W, которая зависит от приложенного к p⁺-n переходу обратного напряжения U_R. Для резкого p⁺-n перехода плотность тока термогенерации пропорциональна корню квадратному из суммы контактной разности потенциалов и обратного напряжения.

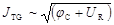.             (59)

В полупроводниках с большим значением собственной концентрации, например, в германии, при комнатной температуре преобладает диффузионный ток, и обратный ток p-n перехода подчиняется уравнению Шокли (рис.3 и рис.5, пунктирная кривая).

При малом значении собственной концентрации n_i, например, в кремнии, может преобладать ток термогенерации (рис.6, сплошная кривая).

Для p-n переходов в полупроводниках с достаточно широкой запрещенной зоной (например, в кремнии), если эффективное время жизни τ_g не зависит или слабо зависит от температуры, то в уравнении (58) можно пренебречь первым членом, и плотность обратного тока такого p⁺-n перехода будет пропорциональна собственной концентрации носителей n_i.

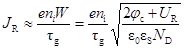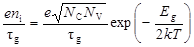~ .               (60)

То есть при обратном смещении 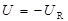, когда  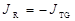модуль плотности обратного тока  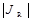будет увеличиваться с температурой примерно по экспоненте.

Поэтому наклон зависимости 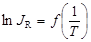 будет определяться половиной ширины запрещенной зоны .

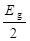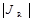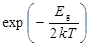~ .                                           (61)

Прологарифмировав обе части уравнения (61) получим линейную зависимость логарифма удельной электропроводности от обратной температуры.

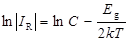,                                           (62)

Из уравнения (62) можно получить ширину запрещенной зоны полупроводника в Дж:

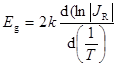.                                               (63)

Пунктирная кривая на рис.4 представляет собой зависимость 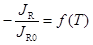 в координатах Аррениуса 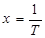,  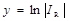для p+-n перехода в кремнии (I_R0 – плотность обратного тока при температуре 25 °C).

Учет температурной зависимости ширины запрещенной зоны

Величина ширины запрещенной зоны, вычисленная по формуле (55) или (63), даёт истинное значение Е_g, лишь в случае, когда Е_g не зависит от температуры. В действительности ширина запрещенной зоны зависит от температуры. Эта зависимость определяется рядом причин, обусловленных статическими и динамическими факторами. К уменьшению ширины запрещенной зоны может приводить рост амплитуды тепловых колебаний атомов кристаллической решетки и увеличение расстояний между атомами при термическом расширении кристалла. Строго учесть эти факторы невозможно, поэтому зависимость ширины запрещенной зоны от температуры E_g(T) находят эмпирически.

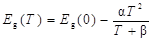,                                                  (64)

где E_g(0) – ширина запрещенной зоны полупроводника при температуре абсолютного нуля, α и β – постоянные.

Для линейного участка при температурах от 280 K до 400 K эту зависимость Е_g(Т)можно представить в линейной функции температуры

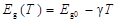,                                                           (65)

 

где Е_g0 — ширина запрещенной зоны, полученная экстраполяцией линейной зависимости к абсолютному нулю; g — температурный коэффициент.

Величины Е_g(0 K), α, β, Е_g(З00 K), Е_g0 и g для кремния и германия приведены в таблице 1.

Таблица 1

Полупроводник	Еg(0), эВ	α∙104, эВ∙K-1	β, K	Еg(300 K), эВ	Еg0, эВ	g , эВ∙град-1
Ge	0.743	4.774	235	0.67	0.785	4.06∙10-4
Si	1.170	4.730	636	1.12	1.209	2.81∙10-4

Графики эмпирических зависимостей E_g(T) и экстраполирующих прямых (линейных линий тренда) в диапазоне температур от 280 K до 400 K представлены на рис.6. На этом же рисунке приведены данные линий тренда и коэффициенты корреляции, показывающие, что совпадение линий тренда с эмпирическими данными достаточно хорошее (R²≥0.99).

Для германиевого p-n перехода подставим зависимость (65) в выражение (55) и получим

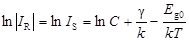.                                         (66)

В координатах Аррениуса 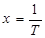,  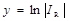это выражение представляет собой прямую линию (рис.4, сплошная кривая). Ширина запрещенной зоны, определенная по представленной на рис.4 сплошной кривой составляет ≈0.66 эВ, что соответствует ширине запрещенной зоны германия при температуре 300 K.

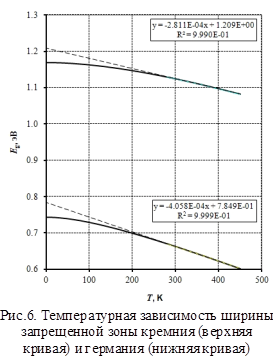Ширина запрещённой зоны определяется из значений производной функции ln(I_R) по .

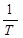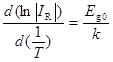.             (67)

Подставив же зависимость (65) в выражение (62) получаем

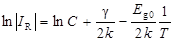.         (68)

В координатах Аррениуса 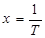,  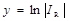выражение (67) представляет собой прямую линию (рис.4, пунктирная кривая).

Ширина запрещенной зоны, определенная по представленной на рис.4 пунктирной кривой 2 E_g≈1.12 эВ, что соответствует ширине запрещенной зоны кремния при температуре 300 K.

Окончательно ширина запрещённой зоны (в эВ), полученная экстраполяцией к абсолютному нулю, равна:

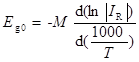,                                                     (69)

где .

Для нахождения ширины запрещённой зоны при комнатной температуре необходимо воспользоваться формулой (65).

Статические параметры диодов

Для п/п диодов важным является ряд статических параметров:

1. Дифференциальное сопротивление

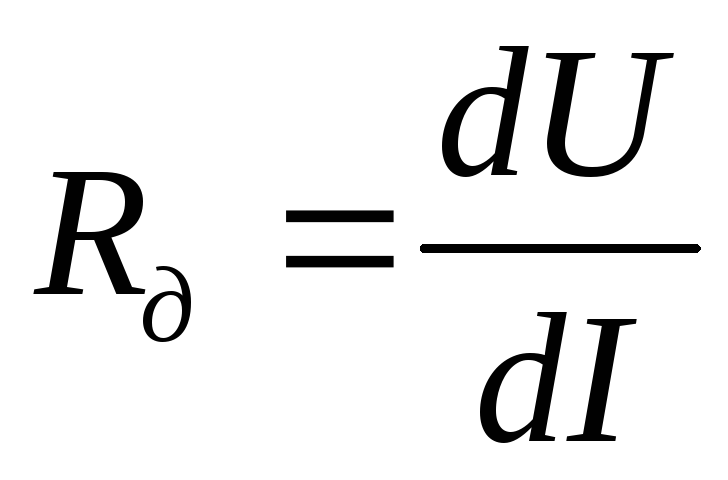
Определяет, как изменяется ток через диод вблизи некоторого значения U, заданного рабочей точкой

I

β A

α U

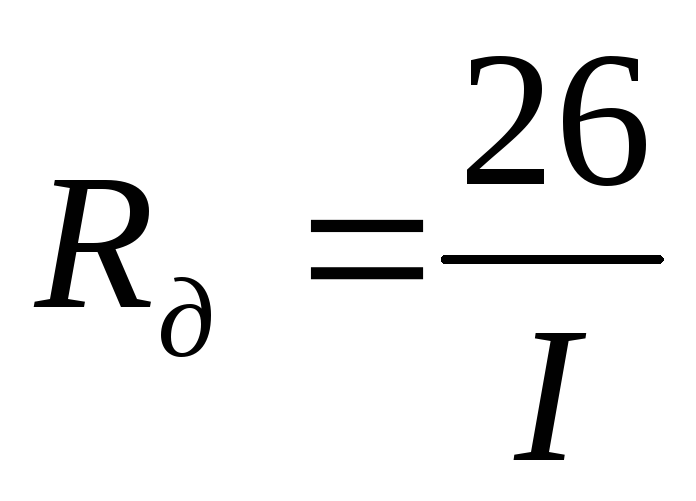
R_дзависит от тока или от напряжения. При обратном напряжении оно велико (сотни МОм).

2. Сопротивление постоянному току

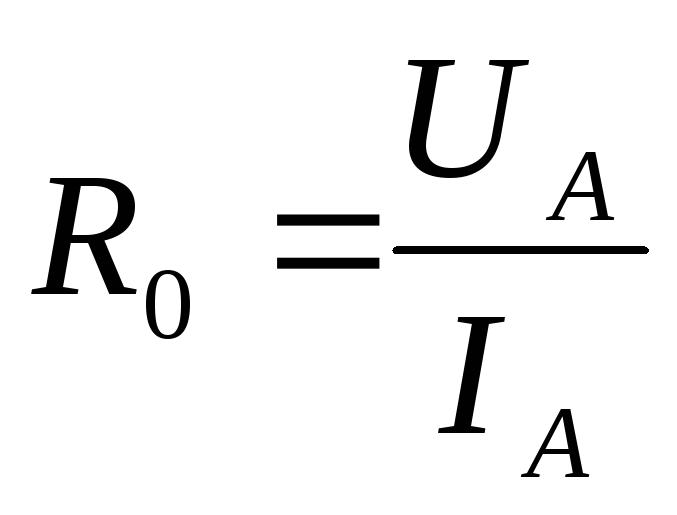
А – рабочая точка

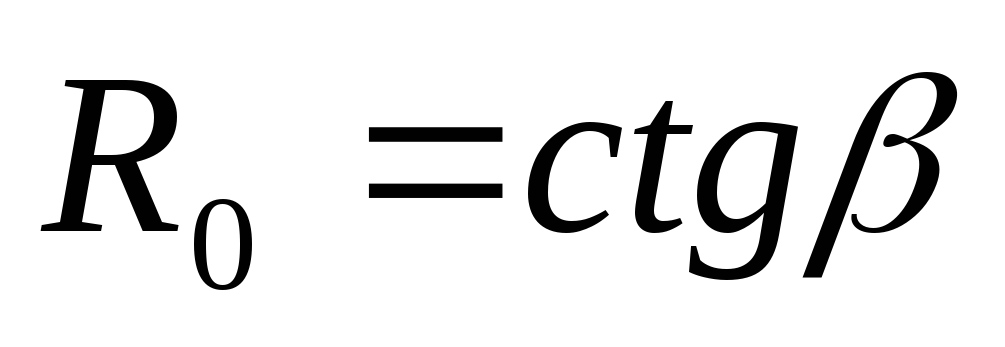
3. RиR– сопротивление диода постоянному току при номинальных значениях тока и напряжения.

Зависимость характеристики и параметров диодов от температуры

С изменением температуры меняется как прямая, так и обратная ветвь ВАХ.

Обратная ветвь ВАХ меняется из-за того, что тепловой ток в германиевом диоде и ток тепловой генерации в кремниевом значительно увеличивается с повышением температуры.

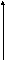
IT=370K

T=300K

U

U₂U₁

Прямой ток меняется, и характеристики сдвигаются влево с увеличением температуры.

Для оценки температурной зависимости прямой ветви ВАХ используется температурный коэффициент напряжения:

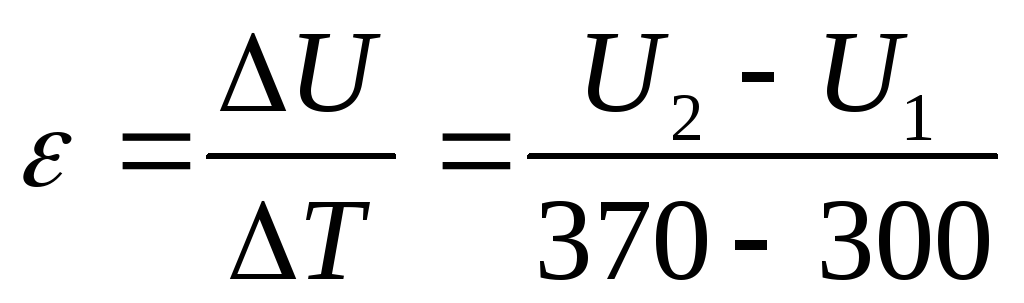
Температурный коэффициент характеризует изменение прямого напряжения при изменении температуры на 1 К.

Температурная зависимость прямого тока объясняется следующими причинами:

1. Процессами в самом переходе (изменение I_пов,I_д,I₀).

2. Изменением сопротивления базового слоя. При увеличении температуры проводимость п/п базы увеличивается. Следовательно, уменьшается напряжение базы и прямой участок ВАХ становится более крутым. Есть диоды, у которых сопротивление базы с увеличением температуры увеличивается. Это возможно при низком легировании базы (все носители участвуют в создании прямого тока). Собственная проводимость п/п такого диода мала.

_Ge=2 мВ/К.

Выпрямительные диоды

ППВД различаются по материалу, используемому для образования p-n-перехода: германиевые, кремниевые, селеновые, медно-закисные, титановые. По характеру контакта они бывают точечные и плоскостные.

Выпрямительными эти диоды называются потому, что при применении в схемах используют свойство односторонней проводимости.

U_вх

А К (-)+

R_нt

(+)-

U_вых

U_вхR_НU_выхt

При «+» U_вхк диоду приложено обратное напряжение и ток протекать не будет. Ток идёт через сопротивление нагрузки.

Если подать «-» U_вх, то диод открыт, через него протекает ток, т.к. сопротивление по постоянному току диода много меньше сопротивления нагрузки, через которое ток проходить не будет.

Параметры вд

Это статические параметры и электрические величины, определяющие работу ВД в выпрямителях.

• I_пр – среднее за период значение прямого тока;

• U_пр – среднее за период падение напряжения на диоде при протекании прямого тока;

• I_обр – среднее за период значение обратного тока;

• U_обр – среднее за период значение обратного напряжения;

• f_max – предельная рабочая частота;

• Величина ёмкости диода;

• Предельное значение рабочей температуры.

Схема простейшего выпрямителя

ТрU_вх

t

U₂=U_вх CR_н U_с

t

t₁ t₂ t₃ t₄

It

0 – t₁ U_с >U_вх i_д= 0

t₁–t₂ U_с <U_вх i_д= 0

t₂–t₃ U_с>U_вх i_д= 0, конденсатор разряжается.

Скорость разряда конденсатора зависит от его ёмкости и сопротивления нагрузки.

Недостатками данной схемы является: низкий КПД, значительная пульсация и значительная потребляемая мощность.

Существуют параметры, характеризующие качество выпрямления:

Коэффициент выпрямления

Крутизна характеристики

Обычно [S]=1мА/В.