Длина звуковых волн — КОРДА
Волновое движение материи под воздействием источника звука, воспринимаемое слухом как ощущение звука называется звуковой волной
Длина звуковой волны λ (в м) прямо пропорциональна скорости звука с (в м/сек) и обратно пропорциональна его частоте f (в Гц) [см. формулу (4)].
(4)
UПример:
Длина звуковой волны с частотой 1000 Гц в воздухе при температуре + 15°С составит:
(м)
Это приводит к уяснению физического свойства звука, имеющего огромное практическое значение.
По сопоставлению с другими волновыми физическими явлениями — светом, теплом — звук характеризуется исключительно большой длиной волн.
Длина самых коротких звуковых воли (см.
UТаблица №2U |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
Средняя длина звуковых волн в воздухе при t =15ºC |
||||||||||
Частота в Гц |
20 |
50 |
100 |
200 |
1000 |
2000 |
4000 |
10000 |
20000 |
|
Длина волны в м |
17 |
7 |
3,4 |
1,7 |
0,34 |
0,17 |
0,085 |
0,034 |
0,017 |
|
Волны изгиба в частях здания, имеющих вид плиты, могут достигать довольно большой длины.
В то время как длина звуковой волны, распространяющейся в воздухе, при частоте 100 Гц составляет 3,4 м, длина продольной звуковой волны в кирпичной стене при той же частоте 100 Гц может достигать 24-х метров. Длина волны изгиба в кирпичной стене толщиной 12 см равна 2,2 м.
длина волн изгиба тем меньше, чем тоньше стена.
Назад к разделам
Нужна консультация специалиста?
Заполните форму и наш специалист позвонит вам в ближайшее время и ответит на все вопросы.
Отправляя данные из данной формы, я даю согласие на обработку персональных данных и соглашаюсь на политику конфиденциальности
Как заказать?
Что такое WiFi? Подробно о свойствах WiFi сигнала
на картинке: графическое отображение WiFi волн в городе.
1. Что такое WiFi?
1.1. Связь частоты и длины волны.
2. Свойства WiFi сигнала.
2.1. Поглощение.
2.2. Огибание препятствий.
2.3. Естественное затухание.
2.4. Отражения сигнала.
2.5. Плотность данных.
2.6. Почему сложно дать однозначный ответ: на какое расстояние будет передавать сигнал WiFi оборудование?
3. Диапазоны и частоты WiFi
3.1. Диапазон 2,4 ГГц.
3.2. Диапазон 5 ГГц.
Что такое WiFi?
WiFi — беспроводной способ связи, основанный на всем нам знакомом электромагнитном излучении. Сигнал WiFi относят к радиоволнам, соответственно, он имеет такие же свойства, характеристики и поведение. Радиоволны, в свою очередь, подчиняются практически тем же физическим законам, что и свет: распространяются в пространстве с такой же скоростью (почти 300 000 километров в секунду), подвержены дифракции, поглощению, затуханию, рассеиванию и т. д.
Основные характеристики радиоволны, а значит и сигнала WiFi — это ее длина и частота (частотный диапазон). Последний параметр означает частоту переменного тока, необходимую для получения волны нужной длины и используется для классификации радиоволн. Другое определение частоты — это количество волн, проходящих через определенную точку пространства в секунду.
Последний параметр означает частоту переменного тока, необходимую для получения волны нужной длины и используется для классификации радиоволн. Другое определение частоты — это количество волн, проходящих через определенную точку пространства в секунду.
Существует распределение радиоволн по диапазонам, в зависимости от частоты, утвержденная Международным союзом электросвязи (МСЭ, английская аббревиатура — ITU).
Буквенные обозначения диапазона | Название волн. Название частот. | Диапазон частот | Диапазон длины волны |
| ОНЧ (VLF) | Мириаметровые. Очень низкие | 3—30 кГц | 100–10 км |
| НЧ (LF) | Километровые. Низкие. | 30—300 кГц | 10–1 км |
| СЧ (MF) | Гектометровые. Средние. | 300—3000 кГц | 1–0.1 км |
| ВЧ (HF) | Декаметровые. Высокие. | 3—30 МГц | 100–10 м |
| ОВЧ (VHF) | Метровые. Очень высокие. Очень высокие. | 30—300 МГц | 10–1 м |
| УВЧ (UHF) | Дециметровые. Ультравысокие. | 300—3000 МГц | 1–0.1 м |
| СВЧ (SHF) | Сантиметровые. Сверхвысокие. | 3—30 ГГц | 10–1 см |
| КВЧ (EHF) | Миллиметровые. Крайне высокие. | 30—300 ГГц | 10–1 мм |
| THF | Дециметровые. Гипервысокие. | 300—3000 ГГц | 1–0.1 мм |
Сфера применения радиоволн зависит от частотного диапазона. Это может быть телевидение, радиосвязь, мобильная связь, радиорелейная связь и т. д. Вообще, радиочастотный эфир занят довольно плотно: использование всех диапазонов буквально расписано:
В том числе это и беспроводная связь WiFi. Для нее используются дециметровые и сантиметровые волны ультравысокой и сверхвысокой частоты (УВЧ и СВЧ) в частотных диапазонах 2,4 ГГц, 5 ГГц и и других редкоиспользуемых: 900 МГц, 3,6 ГГц, 10 ГГц, 24 ГГц.
Главное преимущество WiFi-связи отражено во втором ее названии — беспроводная связь. Именно отсутствие проводов вкупе со все возрастающей скоростью передачи данных является ключевым моментом при выборе этого способа соединения.
Именно отсутствие проводов вкупе со все возрастающей скоростью передачи данных является ключевым моментом при выборе этого способа соединения.
Если речь идет о домашних пользователях — беспроводная связь удобна, она позволяет не привязываться к определенному месту в квартире для входа в интернет.
Если мы говорим о корпоративной связи, о провайдерских услугах, то иногда прокладка кабеля для передачи данных — это дорого, нецелесообразно или вообще невозможно. Например, нужно раздать интернет в частном секторе, прокинуть магистральный канал через ущелье, в удаленный населенный пункт и т. д. В этом случае на выручку приходит WiFi. Проблемная территория преодолевается с помощью беспроводного канала.
Связь частоты сигнала WiFi и длины волны
Характеристики длины волны сравнительно редко используются в параметрах оборудования WiFi. Однако иногда, для понимания физических свойств и поведения сигнала беспроводной связи в различных условиях неплохо разбираться в связи частоты и длины радиоволн.
Общее правило: Чем выше частота, тем короче длина волны. И наоборот.
Формула для расчета длины волны:
Длина волны WiFi сигнала (в метрах)= Скорость света (в м/сек) / Частота сигнала (в герцах).
Скорость света в м/сек = 300 000 000.
После упрощения формулы получаем: Длина волны в метрах = 300/ Частота в МГц.
Свойства WiFi сигнала
Поглощение.
Главное условие для создания беспроводного линка на расстояние большее, чем сотня метров — прямая видимость между точками установки оборудования. Проще говоря, если мы стоим рядом с одной точкой доступа WiFi, то наш взгляд, направленный в сторону второй точки, не должен упираться в стену, лес, многоэтажный дом, холм и т. д. (Это еще не все, нужно также учитывать помехи в Зоне Френеля, но об этом в другой статье.)
Такие объекты просто-напросто отражают и поглощают сигнал WiFi, если не весь, то львиную его часть.
То же самое происходит и в помещении, где сигнал от WiFi роутера или точки доступа проходит через стены в другие комнаты/на другие этажи. Каждая стена или перекрытие «отбирает» у сигнала некоторое количество эффективности.
На небольшом расстоянии, например, от комнатного роутера до ноута, у радиосигнала еще есть шансы, преодолев стену, все-таки добраться до цели. А вот на длинной дистанции в несколько километров любое такое ослабление существенно сказывается на качестве и дальности WiFi связи.
Процент ухудшения сигнала вай-фай при прохождении через препятствия зависит от нескольких факторов:
- Длины волны. В теории, чем больше длина волны (и ниже частота вай-фай), тем больше проникающая способность сигнала. Соответственно, WiFi в диапазоне 2,4 ГГц имеет большую проникающую способность, чем в диапазоне 5 ГГц. В реальных условиях выполнение этого правила очень тесно зависит от того, через препятствие какой структуры и состава проходит сигнал.

- Материала препятствия, точнее, его диэлектрических свойств.
Преграда | Дополнительные потери при прохождении (dB) | Процент эффективного расстояния*, % |
Открытое пространство | 0 | 100 |
Нетонированное окно (отсутствует металлизированное покрытие) | 3 | 70 |
Окно с металлизированным покрытием (тонировкой) | 5-8 | 50 |
Деревянная стена | 10 | 30 |
Стена 15,2 см (межкомнатная) | 15-20 | 15 |
Стена 30,5 см (несущая) | 20-25 | 10 |
Бетонный пол или потолок | 15-25 | 10-15 |
Цельное железобетонное перекрытие | 20-25 | 10 |
* Процент эффективного расстояния — эта величина означает, какой процент от первоначально рассчитанной дальности (на открытой местности) сможет пройти сигнал после преодоления препятствия.
Например, если на открытой местности дальность сигнала Wi-Fi — до 200 метров, то после прохождения через нетонированное окно она уменьшится до 140 метров (200 * 70% = 140). Если следующим препятствием для этого же сигнала станет бетонная стена, то после нее дальность составит уже максимум 21 метр (140*15%).
Отметим, что вода и металл — самые эффективные поглотители WiFi, т. к. являются электрическими проводниками и «забирают» на себя большое количество энергии сигнала. Например, если дома на пути вай-фай от роутера до вашего ноута стоит аквариум, то практически наверняка соединения не будет.
Именно поэтому во время дождя и других «влажных» атмосферных осадков наблюдается небольшое снижение качества беспроводного соединения, поскольку капли воды в атмосфере поглощают сигнал.
Частично этот фактор влияет и на затухание WiFi передачи в листве деревьев, т. к. они содержат большой процент воды.
- Угла падения луча на препятствие.
 Помимо материала преграды, через которую проходит сигнал вай-фай, важен также угол падения луча. Так, если сигнал проходит через препятствие под прямым углом, это обеспечит меньшие потери, чем если бы он падал на него под углом 45 градусов. Еще хуже, если сигнал проходит через преграду под очень острым углом. В этом случае, грубо говоря, можно смело умножать толщину стены на 10 и рассчитывать потери WiFi передачи согласно этой величине.
Помимо материала преграды, через которую проходит сигнал вай-фай, важен также угол падения луча. Так, если сигнал проходит через препятствие под прямым углом, это обеспечит меньшие потери, чем если бы он падал на него под углом 45 градусов. Еще хуже, если сигнал проходит через преграду под очень острым углом. В этом случае, грубо говоря, можно смело умножать толщину стены на 10 и рассчитывать потери WiFi передачи согласно этой величине.
Огибание препятствий.
По-научному это поведение луча WiFi называется дифракцией, хотя на самом деле понятие дифракции гораздо сложнее, чем простое «огибание препятствий».
В общем можно вывести правило — чем короче длина волны (выше частота), тем хуже она огибает препятствия.
Основывается это правило на известном физическом свойстве волны: если размер препятствия меньше, чем длина волны, то она его огибает. В целом отсюда логично проистекает, что чем короче длина волны, тем меньшее остается вариантов препятствий, которые она может в принципе обойти, и поэтому принимается, что ее огибающая способность хуже.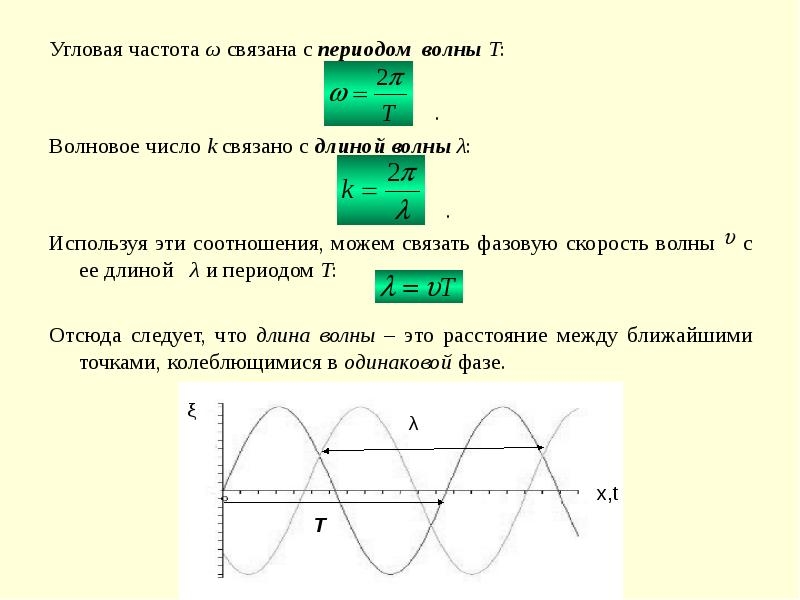
Огибание на практике означает меньшее рассеивание волны как луча энергии вокруг препятствия, меньшее количество потерь сигнала.
Возьмем популярные частоты 2,4 ГГц (длина волны 12,5 см) и 5 ГГц (длина волны 6 см). Мы видим подтверждение правила на примере прохождения лесного массива. Стандартные размеры листьев, стволов, веток деревьев, в среднем будут меньше, чем 12,5 см, но больше, чем 6 см. Поэтому сигнал WiFi 5 ГГц диапазона при прохождении через густую листву “потеряется” практически полностью, в то время как 2,4 ГГц справится лучше.
Поэтому WiFi оборудование, работающее в диапазоне 900 МГц, используется в условиях отсутствия прямой видимости сигнала — его длина волны составляет 33,3 см, что позволяет огибать большее количество преград. Однако надо учитывать размеры предполагаемых препятствий и понимать, что сигнал 900 МГц не сможет “обойти” бетонную стену, расположенную перепендикулярно направлению сигнала. Здесь уже сыграют роль проникающие способности волны, которые, как мы уже говорили у сигналов с низкой частотой довольно неплохие.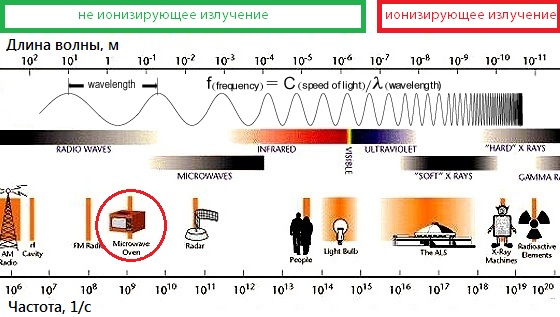
Также именно поэтому для нормальной работы беспроводного оборудования, использующего частоту 24ГГц (длина волны 1,25 см) необходима абсолютно чистая видимость, потому что все препятствия больше сантиметра будут отражать и поглощать сигнал.
Как мы уже упоминали, в отношении прохождении сигнала через лесной массив играет роль также содержание воды в листьях, а также длина волны.
Естественное затухание.
Как далеко мог бы передаваться сигнал WiFi, если создать ему идеальные условия прямой видимости? В любом случае не бесконечно, потому что чем больше дальность беспроводного “пролета”, тем больше сигнал затухает сам по себе. Происходит это по 2 причинам:
Земная поверхность поглощает часть энергии сигнала. Чем выше частота WiFi, тем интенсивнее идет поглощение.
Сигнал WiFi даже из самой узконаправленной антенны распространяется не прямой линией, а лучом.
 Соответственно, чем дальше расстояние, тем шире становится луч, тем меньшая мощность сигнала приходится на единицу площади, и тем меньше энергии сигнала попадает в принимающую антенну.
Соответственно, чем дальше расстояние, тем шире становится луч, тем меньшая мощность сигнала приходится на единицу площади, и тем меньше энергии сигнала попадает в принимающую антенну.
Отражения сигнала.
Сигнал WiFi, как любая радиоволна, как свет, отражается от поверхностей и ведет себя при этом аналогично. Но тут есть нюансы — какие-то поверхности будут поглощать сигнал (полностью или частично), а какие-то — отражать (полностью или частично). Это зависит от материала поверхности, его структуры, наличия неровностей на поверхности и частоты WiFi.
Неконтролируемые отражения сигнала ухудшают его качество. Частично — из-за потери общей энергии сигнала (до принимающей антенны, упрощенно говоря, “долетает не всё” или долетает после переотражений, с задержками). Частично — из-за интерференции с негативным влиянием, когда волны накладываются в противофазе и ослабляют друг друга.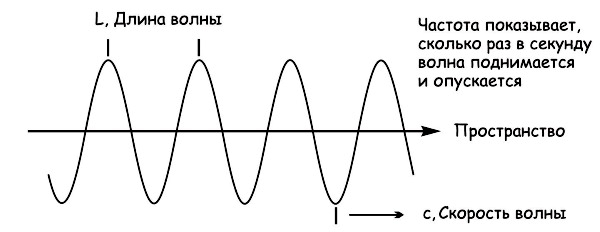
Интерференция может иметь и положительное влияние, если волны WiFi накладываются друг на друга в одинаковых фазах. Это часто используется для усиления мощности сигнала.
Плотность данных.
Частота WiFi влияет также на еще один важный параметр — объем передаваемых данных. Здесь существует прямая связь — чем выше частота, тем больше данных в единицу времени можно передать. Возможно, именно поэтому первая высокопроизводительная РРЛ от Ubiquiti — AirFiber 24, а также ее более мощная модификация — Airfiber 24HD были выпущены на частоте 24 ГГц.
Почему сложно дать однозначный ответ: на какое расстояние будет передавать сигнал WiFi оборудование?
Физические свойства и поведение радиоволны в окружающем мире довольно сложны. Нельзя взять какой-то один параметр и по нему рассчитать дальность беспроводного сигнала.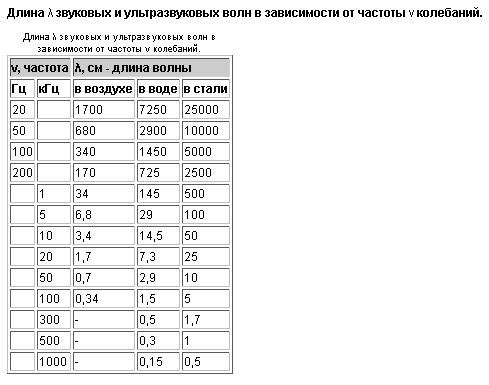 В каждом конкретном случае на дальность будут оказывать влияние различные факторы окружающей среды:
В каждом конкретном случае на дальность будут оказывать влияние различные факторы окружающей среды:
- Поглощение сигнала препятствиями, земной корой, поверхностью водоемов.
- Дифракция и рассеивание сигнала из-за преград на пути.
- Отражения сигнала от препятствий, земли, воды и возникающие в результате этого интерференции волны.
- На больших расстояниях — радиогоризонт, т. е. искривление земной коры.
- Зона Френеля и, соответственно — высота расположения оборудования над поверхностью земли.
Именно поэтому реальная дальность оборудования, как, впрочем, и пропускная способность, может очень сильно отличаться в различных условиях.
Диапазоны и частоты WiFi
Как мы уже сказали, для WiFi связи выделено несколько разных частотных диапазонов: 900 МГц, 2,4 ГГц, 3,65 ГГц, 5 ГГц, 10 ГГц, 24 ГГц.
В Украине на данный момент чаще всего применяются точки доступа WiFi и антенны WiFi 2,4 ГГц и 5ГГц.
Основные отличия 2,4 ГГц и 5ГГц:
2,4 ГГц. Длина волны 12,5 см. Относится к дециметровым волнам ультравысокой частоты (УВЧ).
- В реальных условиях — меньшая дальность сигнала из-за более широкой зоны Френеля, что чаще всего не компенсируется тем, что сигнал на этой частоте меньше подвержен естественному затуханию.
- Лучшее преодоление небольших преград, например, густых лесных массивов, благодаря хорошей проникающей способности и огибанию препятствий.
- Меньше относительно неперекрывающихся каналов (всего 3), а значит, “ пробки на дорогах” — теснота в эфире, и как результат — плохая связь.
- Дополнительная зашумленность эфира другими устройствами, работающими на этой же частоте, в том числе мобильных телефонов, микроволновок и т. п.
5 ГГц. Длина волны 6 см. Относится к сантиметровым волнам сверхвысокой частоты (СВЧ).
- Большее количество относительно неперекрывающихся каналов (19).

- Большая емкость данных.
- Большая дальность сигнала, в связи с тем, что Зона Френеля меньше.
- Такие препятствия, как листва деревьев, стены волны диапазона 5ГГц преодолевают гораздо хуже, чем 2,4.
Диапазоны 900 МГц, 3,6 ГГц, 10 ГГц, 24 ГГц для нас скорее экзотика, однако могут использоваться:
Для работы в условиях, когда стандартные диапазоны плотно заняты.
Если требуется создать беспроводное соединение между двумя точками при отсутствии прямой видимости (лес и другие препятствия). Это касается такой частоты, как 900 МГц (в нашей стране ее нужно использовать с осторожностью, так как на ней работают сотовые операторы).
Если для использования частоты не требуется получать лицензию в контролирующих органах. Такое преимущество часто встречается в презентациях зарубежных производителей, однако для Украины это не совсем актуально, так как условия лицензирования в нашей стране другие.

В IEEE ведутся разработки по принятию новых стандартов и, соответственно, использованию других частот для WiFi. Не исключено, к примеру, что в ближайшее время диапазон 60 ГГц также станет использоваться для беспроводной передачи. Точно также, как и возможна вероятность “отжатия” в будущем некоторых частот, сейчас принадлежащих WiFi, в пользу, например, сотовых операторов.
Разница между частотой и длиной волны
Существенная разница между частотой и длиной волны заключается в том, что частота показывает количество колебаний волны в заданный период времени. Принимая во внимание, что длина волны показывает расстояние между любыми двумя последовательными гребнями и впадинами волны. Таким образом, частота и длина волны являются важными параметрами формы сигнала.
Сравнительная таблица (частота и длина волны)| Основа для сравнения | Частота | Длина волны |
|---|---|---|
| Базовый | Число циклов волны, совершаемых в секунду, называется частотой. | Длина волны — это расстояние между двумя последовательными гребнями или впадинами волны. |
| Меры в | Время | Расстояние |
| Обозначается буквой | f | λ |
| Единица измерения | Герц (Гц) | Метр |
| Формула | f = v / λ, где v — скорость волны | λ = v / f, где v — скорость волны |
| Диапазон — слышимый и видимый слышимый диапазон частот от 20 Гц до 20 кГц. | Длина волны видимого света составляет от 400 до 700 нм. |
Волна совершает колебания или колебания в единицу времени. Волна начинается из точки А, достигает амплитуды В, идет к С, затем к D и, наконец, приходит в начальную точку А. Таким образом, волна совершает один цикл. Если волне требуется одна секунда, чтобы завершить этот один цикл, то частота волны равна 1 циклу/с (C/s) или 1 Гц. Если волна совершает 10 колебаний за 1 секунду, то ее частота равна 10 Гц или 10 Гц.
Если волна совершает 10 колебаний за 1 секунду, то ее частота равна 10 Гц или 10 Гц.
Чем больше колебаний, тем выше частота волны.
Из приведенного выше рисунка очень ясно, что частота увеличивается с увеличением колебаний в волне. Если частота равна 20 кГц, это означает, что волна совершает 20 000 колебаний за одну секунду.
Частота волны может иметь значения в большем диапазоне, например, кГц, МГц или ГГц. Обозначим частоту буквой « f » или « ν ». Продолжительность совершения одного полного колебания называется период времени.
Частота показывает вибрационное или колебательное движение волны любой формы, такой как звуковая волна, световая волна, микроволновая печь, электромагнитная волна, инфракрасная волна, механические колебания и т. д. Существует зависимость между частотой и периодом времени. Частота волны обратно пропорциональна периоду времени.
Например, если период времени волны составляет 20 миллисекунд, то частота волны будет 50 Гц.
Период времени говорит о продолжительности повторения волны. Если период времени волны составляет 20 миллисекунд, и это показывает, что волна завершает свой один цикл за 20 миллисекунд, а затем волна повторяется.
Определение длины волныРасстояние между двумя последовательными гребнями или впадинами называется длиной волны. Точка гребня — это самая высокая точка волны, а впадина — самая низкая точка.
Длина волны измеряется в единицах расстояния, таких как метры, сантиметры, миллиметры, нанометры и т. д. Длина волны измеряется в направлении движения волны и обозначается как « λ » (лямбда) .
Меньшая длина звуковой волны имеет более высокую частоту и производит более высокие тона. Звуковая волна с большей длиной волны имеет низкую частоту и производит звуки более низкого тона. Таким образом, звуковые волны с меньшей длиной волны достигают слушателя быстрее, чем волны с большей длиной волны.
Формула длины волны или уравнение длины волны приведены ниже.
Пример: Если скорость волны 1000 метров в секунду, а частота волн 50 колебаний в секунду, какова ее длина волны?
Длина волны обратно пропорциональна частоте. Следовательно, более длинная длина волны имеет более низкую частоту. Точно так же более короткая длина волны имеет более высокую частоту.
Различные цвета имеют разные длины волн. Длина волны красного цвета самая большая, а длина волны фиолетового цвета самая маленькая.
Основные различия между частотой и длиной волны- Частота — это общее количество колебаний или вибраций в единицу времени. Принимая во внимание, что длина волны — это расстояние между двумя последовательными точками гребней или впадин волны.
- Частота показывает время волны. В то время как длина волны измеряет расстояние.
- Единицей измерения частоты являются циклы в секунду или герцы. Единицей измерения длины волны является метр.
- Частота – это отношение скорости к длине волны.
 Принимая во внимание, что длина волны — это отношение скорости и частоты.
Принимая во внимание, что длина волны — это отношение скорости и частоты. - Диапазон слышимых частот от 20 до 20 кГц. Диапазон длин волн видимого света составляет от 400 до 700 нм.
Читать далее
Похожие посты:
Подписывайтесь и ставьте нам лайки:
Длина волны, скорость и частота — понимание звука
Бегущие волны
Почему важна длина волны?
Рябь на озере Лох-Дуич перед замком Эйлин-Донан.Когда вы создаете импульсы в среде, каждый импульс удаляется от источника с одной и той же постоянной скоростью. Если вы делаете импульсы через равные промежутки времени, результатом будет «последовательность» равномерно расположенных импульсов. С технической точки зрения периодическая вибрация создает волну. Расстояние между одним импульсом и следующим называется длиной волны.
Длина волны объясняет многое о том, как работает звук: почему тубы должны быть большими, почему низкочастотные звуки трудно сдержать, почему гидролокатор может обнаруживать определенные объекты (а не другие), как образуются мертвые зоны в аудиториях, почему инструменты производят обертоны.
Длина волны, скорость и частота
Когда источник с определенной частотой создает волны, каждый гребень проходит определенное расстояние, прежде чем сформируется следующий гребень. Это расстояние и есть длина волны. В результате длина волны определяется всего двумя факторами: частотой источника и скоростью волн.
Если частота звука низкая, между импульсами проходит много времени, и каждый импульс проходит большое расстояние, прежде чем будет создан следующий. Результатом являются импульсы, которые разнесены друг от друга на большую длину волны. Сократите временную задержку между импульсами, и длина волны станет короче. (Помните, что все волны в одной и той же среде распространяются с одинаковой скоростью). Суть в том, что низкочастотные источники создают длинноволновые волны, а высокочастотные источники создают короткие волны.
Длина волны также зависит от среды, поскольку волны распространяются с разной скоростью в разных средах. Если звук распространяется медленно в определенном материале, каждый гребень проходит лишь небольшое расстояние, прежде чем сформируется следующий гребень. Если источник той же частоты создает волны в среде, где звуки распространяются быстрее, каждый гребень распространяется дальше (за то же время), создавая гребни, которые находятся дальше друг от друга (более длинная длина волны).
Анимации особенно полезны для понимания понятий, изложенных в последних двух абзацах. Моделирование Desmos компании Abbott Pulse Train [1] показывает два источника, создающих волны в одной и той же среде. Несмотря на то, что источники имеют разные частоты, вы можете ясно видеть, что оба набора волн распространяются по экрану с одинаковой скоростью. Вы также можете видеть, что высокочастотный источник излучает короткие волны. Видео Майка Ричардсона на YouTube  Если вы хотите попробовать некоторые вещи Ричардсон показывает в видео, что вы можете играть с симуляцией PhET [3] самостоятельно. Вам нужно будет установить флажок в левом верхнем углу моделирования, чтобы избавиться от зажима и заменить его открытым окном, иначе вы будете исследовать стоячие волны, а не бегущие волны.
Если вы хотите попробовать некоторые вещи Ричардсон показывает в видео, что вы можете играть с симуляцией PhET [3] самостоятельно. Вам нужно будет установить флажок в левом верхнем углу моделирования, чтобы избавиться от зажима и заменить его открытым окном, иначе вы будете исследовать стоячие волны, а не бегущие волны.
Вот математическое уравнение, связывающее длину волны со скоростью волны и частотой источника:
[латекс]\лямбда = \dfrac{v} {f}[/латекс]
Скорость ([латекс]v[/латекс]) в уравнении — это скорость волны в среде. Частота ([latex]f[/latex]) — это основная частота источника волны, а [latex]\lambda[/latex] — результирующая длина волны.
Откуда уравнение
Уравнение, приведенное выше, является прямым применением уравнения постоянной скорости к волне. Вот логика. Поскольку все гребни и впадины волны движутся с одной и той же постоянной скоростью, гребни и впадины (и все другие точки волны) движутся в соответствии с уравнением постоянной скорости:
[латекс]d = vt[/латекс]
Следующий шаг является ключевым: вы должны признать, что за время, необходимое источнику для завершения одного полного цикла, каждая рябь в волне проходит расстояние в одну длину волны. Поскольку каждый гребень (или впадина) перемещается ровно на одну длину волны за время, необходимое источнику для завершения одного полного цикла, вы можете заменить [latex]d[/latex] на [latex]\lambda[/latex], при условии, что вы также замените [латекс]т[/латекс] с [латекс]\тау[/латекс]. Результат
Поскольку каждый гребень (или впадина) перемещается ровно на одну длину волны за время, необходимое источнику для завершения одного полного цикла, вы можете заменить [latex]d[/latex] на [latex]\lambda[/latex], при условии, что вы также замените [латекс]т[/латекс] с [латекс]\тау[/латекс]. Результат
[латекс]\лямбда= v\тау[/латекс]
Проще говоря, длина волны равна расстоянию, которое гребень (или впадина) проходит за один период источника.
Несмотря на то, что это уравнение является верным и информативным, большинство людей говорят об источниках с точки зрения частоты, а не периода. Чтобы выразить это уравнение через частоту, замените [латекс]\тау[/латекс] на [латекс]1/f[/латекс]. Когда вы это сделаете, [латекс]\лямбда= v\тау[/латекс] станет
[латекс]\лямбда = \dfrac{v}{f}[/латекс]
Причина и следствие
Во многих учебниках приведенное выше уравнение выражается как [латекс]v=f\лямбда[/латекс]. Я думаю, что это заблуждение.
Вот почему: величины [латекс]\лямбда[/латекс], [латекс]в[/латекс] и [латекс]f[/латекс] не равноправны в уравнении. Причинами являются частота и скорость волны. Длина волны — это ответ. Частота полностью определяется источником — все остальное не имеет значения. Скорость волны полностью определяется свойствами среды — все остальное не имеет значения. Поместите источник, вибрирующий на определенной частоте, в определенную среду, и волна автоматически будет иметь определенную длину волны.
Уравнение как руководство для мышления
Если вы знаете, что делаете, уравнения могут стать мощным руководством для постановки вопросов «что, если»: что произойдет с длиной волны, если частота увеличится? Что происходит с длиной волны, когда звук переходит из воды в воздух?
Ключом к «чтению уравнений» является правильное определение того, какие величины изменяются, а какие нет. Бегло взглянув на уравнение [latex]v=f\lambda[/latex], можно предположить, что увеличение частоты источника увеличивает скорость волны. В конце концов, использование большего числа для звука [latex]f[/latex] приводит к большему числу для [latex]v[/latex]. Тем не менее, мы знаем, что вывод неверен — все звуки, распространяющиеся в одном и том же материале, распространяются с одинаковой скоростью. Что не так с математикой? Проблема в том, что мы предполагали, что [латекс]\лямбда[/латекс] не изменились. Реальность такова, что [латекс]v[/латекс] не может измениться (поскольку среда не изменилась), и [латекс]\лямбда[/латекс] должен измениться, чтобы компенсировать это. Если частота увеличивается, длина волны должна уменьшаться, чтобы скорость волны оставалась неизменной.
В конце концов, использование большего числа для звука [latex]f[/latex] приводит к большему числу для [latex]v[/latex]. Тем не менее, мы знаем, что вывод неверен — все звуки, распространяющиеся в одном и том же материале, распространяются с одинаковой скоростью. Что не так с математикой? Проблема в том, что мы предполагали, что [латекс]\лямбда[/латекс] не изменились. Реальность такова, что [латекс]v[/латекс] не может измениться (поскольку среда не изменилась), и [латекс]\лямбда[/латекс] должен измениться, чтобы компенсировать это. Если частота увеличивается, длина волны должна уменьшаться, чтобы скорость волны оставалась неизменной.
Что происходит с длиной волны звука, распространяющегося из воды в воздух? Ключом к чтению уравнения для ответа является определение того, какая величина меняется, а какая нет. При переходе звука из воды в воздух скорость уменьшается. (Вы можете посмотреть это; ключ в том, чтобы понять, что скорость волны должна меняться, потому что изменяется материал, в котором распространяется волна. ) Это предполагает, что частота остается неизменной, и если вы подумаете под микроскопом, это имеет смысл — вибрации на дальней стороне границы должны совпадать с вибрациями их соседей на ближней стороне границы. Поскольку [латекс]f[/латекс] остается постоянным, а [латекс]v[/латекс] увеличивается, длина волны должна увеличиваться, чтобы уравнение работало.
) Это предполагает, что частота остается неизменной, и если вы подумаете под микроскопом, это имеет смысл — вибрации на дальней стороне границы должны совпадать с вибрациями их соседей на ближней стороне границы. Поскольку [латекс]f[/латекс] остается постоянным, а [латекс]v[/латекс] увеличивается, длина волны должна увеличиваться, чтобы уравнение работало.
Остановись, чтобы подумать
- Рябь, движущаяся по поверхности воды, создается путем покачивания длинной прямой палки вверх и вниз по поверхности воды. Рябь может быть изменена либо 1) изменением того, как часто вы качаете стик вверх и вниз, либо 2) изменением того, насколько далеко вверх и вниз перемещается стик в каждом цикле (без изменения того, как часто вы качаете стик вверх и вниз). Объясните, что вы можете сделать с источником для достижения каждой из следующих целей:
- увеличить амплитуду волн
- сократить длину волны
- увеличить скорость создаваемых волн
- Один звук в воздухе имеет длину волны 10 см.
 Другой звук в воздухе имеет длину волны 20 см. Какой звук имеет более высокую частоту? Какой звук распространяется быстрее?
Другой звук в воздухе имеет длину волны 20 см. Какой звук имеет более высокую частоту? Какой звук распространяется быстрее? - Что происходит со скоростью волны при переходе из холодного воздуха в теплый? Что происходит с частотой? Что происходит с длиной волны звуковой волны?
Слышимые звуки в воздухе
Вы можете рассчитать длину волны слышимого звука в воздухе. Слышимые звуки в воздухе имеют частоту примерно от 20 Гц до 20 кГц. Неудивительно, что длины волн слышимых звуков также сильно различаются. Предполагая скорость звука 340 м/с,
Для звука частотой 20 Гц в воздухе: [латекс]\лямбда = \dfrac{v}{f}= \dfrac{340 м/с}{20 Гц}=17 м[/латекс]
Для звука частотой 20 кГц в воздухе: [латекс]\лямбда = \dfrac{v}{f}= \dfrac{340 м/с}{20 000 Гц}=0,017 м=1,7 см[/латекс]
Этот расчет показывает, что длина звуковой волны в воздухе явно соответствует человеческому размеру. Длины волн варьируются от примерно диаметра десятицентовой монеты (для самых высоких частот) до примерно длины городского автобуса (для самых низких частот). Для сравнения, все длины волн видимого света намного меньше толщины одного человеческого волоса и имеют очень узкий диапазон (примерно от 400 до 700 нм).
Для сравнения, все длины волн видимого света намного меньше толщины одного человеческого волоса и имеют очень узкий диапазон (примерно от 400 до 700 нм).
Остановитесь, чтобы подумать ответы
- Чтобы увеличить амплитуду, увеличьте расстояние, которое проходит палочка за каждый цикл (т. е. увеличьте амплитуду источника). Чтобы сократить длину волны, увеличьте частоту взмахов палочкой (т. е. увеличьте частоту источника). Невозможно изменить скорость путей, изменив то, как вы двигаете палкой. Скорость волн определяется свойствами самой воды.
- Звук с более короткой длиной волны имеет более высокую частоту. Оба звука распространяются с одинаковой скоростью.
- Когда звук переходит от более холодного воздуха к более теплому, его скорость увеличивается (поскольку звук распространяется быстрее в более теплом воздухе). Частота не меняется (если не меняется источник). Поскольку скорость увеличивается, а частота остается неизменной, длина волны должна увеличиваться.
 (Увеличение числа для скорости волны в уравнении [латекс]\лямбда = v/f[/латекс] без изменения числа для частоты приведет к большему значению длины волны).
(Увеличение числа для скорости волны в уравнении [латекс]\лямбда = v/f[/латекс] без изменения числа для частоты приведет к большему значению длины волны).
Интернет-ресурсы
Игра с симуляцией звука PhET (Java-апплет). [4] Отрегулируйте частоту и посмотрите, как изменится длина волны. Нажмите на вкладку «Измерение» вверху, чтобы добавить линейку и секундомер.
Игра с волнами PhET на струнной симуляции (HTML5). [5] . Чтобы создать бегущие волны, выберите «Без конца» в диалоговом окне в правом верхнем углу.
Изображение предоставлено
Рябь на озере Лох-Дуич, перед замком Эйлин-Донан. (автор Гийом Пиоль; взято с Викисклада) [6]
- Эббот Д. (27 июля 2018 г.). Импульсный поезд. Получено с https://www.desmos.com/calculator/h7fy2cpthw ↵
- Richardson, M. (2013, 26 февраля). Частота против длины волны. Получено с https://youtu.be/9UPnWfBYf28 ↵
- Интерактивное моделирование PhET.



 Помимо материала преграды, через которую проходит сигнал вай-фай, важен также угол падения луча. Так, если сигнал проходит через препятствие под прямым углом, это обеспечит меньшие потери, чем если бы он падал на него под углом 45 градусов. Еще хуже, если сигнал проходит через преграду под очень острым углом. В этом случае, грубо говоря, можно смело умножать толщину стены на 10 и рассчитывать потери WiFi передачи согласно этой величине.
Помимо материала преграды, через которую проходит сигнал вай-фай, важен также угол падения луча. Так, если сигнал проходит через препятствие под прямым углом, это обеспечит меньшие потери, чем если бы он падал на него под углом 45 градусов. Еще хуже, если сигнал проходит через преграду под очень острым углом. В этом случае, грубо говоря, можно смело умножать толщину стены на 10 и рассчитывать потери WiFi передачи согласно этой величине. Соответственно, чем дальше расстояние, тем шире становится луч, тем меньшая мощность сигнала приходится на единицу площади, и тем меньше энергии сигнала попадает в принимающую антенну.
Соответственно, чем дальше расстояние, тем шире становится луч, тем меньшая мощность сигнала приходится на единицу площади, и тем меньше энергии сигнала попадает в принимающую антенну.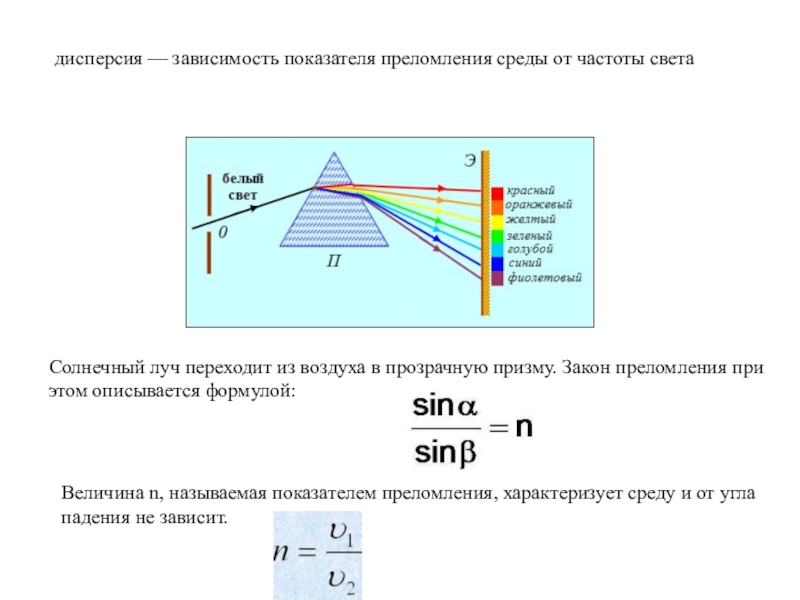

 Принимая во внимание, что длина волны — это отношение скорости и частоты.
Принимая во внимание, что длина волны — это отношение скорости и частоты. Другой звук в воздухе имеет длину волны 20 см. Какой звук имеет более высокую частоту? Какой звук распространяется быстрее?
Другой звук в воздухе имеет длину волны 20 см. Какой звук имеет более высокую частоту? Какой звук распространяется быстрее? (Увеличение числа для скорости волны в уравнении [латекс]\лямбда = v/f[/латекс] без изменения числа для частоты приведет к большему значению длины волны).
(Увеличение числа для скорости волны в уравнении [латекс]\лямбда = v/f[/латекс] без изменения числа для частоты приведет к большему значению длины волны).