Site Loader
Posted on 13.03.1990

Содержание

Частотная зависимость — емкость — Большая Энциклопедия Нефти и Газа, статья, страница 3

Cтраница 3


Влияние частоты переменного тока на сопротивление и емкость окрашенных электродов.  [31]

Покрытия, сохраняющие большую зависимость сопротивления от частоты и меньшую зависимость емкости от частоты, будут обладать и лучшими защитными свойствами. Так, например, из рис. 2, в можно заключить, что покрытие из каменноугольного лака ( трехслойное) должно обладать меньшими защитными свойствами, чем покрытие из этинолевого лака, поскольку частотная зависимость емкости в первом случае появляется уже через 30 суток, тогда как для этинолевого лака зависимости емкости от частоты не наблюдается. Практические наблюдения согласуются с данными электрохимических исследований.  [32]

Следует отметить, что емкость МДП-конденсатора может иметь сложную зависимость от напряжения постоянного смещения и от частоты переменного напряжения.

Связано это с возможностью образования у поверхности полупроводника ( в данном примере у поверхности / г — области) обедненных и инверсных слоев под действием проникающего в полупроводник электрического поля. Частотная зависимость емкости МДП-конденсатора может появиться, если в полупроводнике образуется инверсный слой, в котором накопление и рассасывание неосновных для исходного полупроводника носителей заряда происходят в результате процессов тепловой генерации и рекомбинации, а инерционность этих процессов может быть велика.  [33]

Следует отметить, что емкость МДП-конденсатора может иметь сложную зависимость от напряжения постоянного смещения и от частоты переменного напряжения. Связано это с возможностью образования у поверхности полупроводника ( в данном примере у поверхности я — области) обедненных и инверсных слоев под действием проникающего в полупроводник электрического поля.

Частотная зависимость емкости МДП-конденсатора может появиться, если в полупроводнике образуется инверсный слой, в котором накопление и рассасывание неосновных для исходного полупроводника носителей заряда происходят в результате процессов тепловой генерации и рекомбинации, а инерционность этих процессов может быть велика.  [34]

Формула ( 96) показывает, что увеличение емкости конденсатора при заданном значении г усиливает частотную зависимость. Особенно сильная частотная зависимость емкости наблюдается в случае электролитических конденсаторов, где г велико, так как роль одной из обкладок играет электролит, имеющий резко повышенное удельное сопротивление по сравнению с металлами, а также в связи с большими значениями номинальных емкостей конденсаторов этого типа. В этом случае

частотная зависимость емкости проявляется уже в области низких частот, тогда как в других типах конденсаторов, особенно при малых емкостях, мы замечаем ее только в области радиочастот.  [35]

 Зависимость емкости ( а и сопротивления ( б пленок, образующихся иа алюминии в результате коррозии в воде при различных температурах ( С, от частоты переменного тока.  [36]

Сопротивление электролита в порах слабо зависит от частоты. На рис. 2 приведены частотные зависимости емкости ( а) и сопротивления ( 6) в интервале 200 — 200 000 гц для окисленных при различных температурах в воде электродов из чистого алюминия.  [37]

Дисперсия активного сопротивления и емкости капельного ртутного электрода в 0 1 М КС1, 20 С.  [38]

Однако и применение симметричных систем электродов не всегда обеспечивает отсутствие ложной дисперсии. Так, если в ячейке с плоскопараллельными электродами края электродов не ограничить изоляторами, у этих краев равномерность распределения тока по поверхности нарушается ( рис. 33) и уравнения (18.11) и (18.12) не выполняются. Это ведет к появлению ложной частотной зависимости емкости и сопротивления.  [39]

Как известно, ток заряда геометрической емкости. Известно также, что емкость влажной изоляции в отличие от емкости сухой изоляции содержит за счет неодно-родностей более значительную абсорбционную емкость, ток заряда которой изменяется медленней, чем геометрической емкости.

Это свойство и использовано в методе частотной зависимости емкости, при которой измеряется емкость изоляции на частотах 2 и 50 гц. При измерении емкости изоляции на частоте 50 гц ( С5о) успевает проявиться только геометрическая емкость, одинаковая у сухой и влажной изоляции.  [40]

Оксидно-полупроводниковые конденсаторы по своим свойствам и характеристикам качественно отличаются от жидкостных и сухих электролитических конденсаторов. При этом уменьшается не только сопротивление Rn, но изменяется характер его зависимости от температуры и частоты. В результате этого в области низких температур тангенс угла потерь мало изменяется с температурой, в меньшей степени зависит от температуры емкость,

частотные зависимости емкости и тангенса угла потерь выражены менее резко, а униполярный эффект проявляется слабее, чем в обычных элетролитических конденсаторах. По своим характеристикам оксидно-полупроводниковые конденсаторы приближаются к бумажным и к конденсаторам из полярных пленок. Промышленностью выпускаются оксидно-полупроводниковые конденсаторы алюминиевые, танталовые и ниобиевые.  [41]

Вольт-кулоновая характеристика конденсатора с сегнетоэлектриком.  [42]

Как известно, для конденсаторов с сегнетоэлектриком характерно отсутствие прямой пропорциональности между зарядом и напряжением на его обкладках. Пренебрегая гистерезисом, можно качественно изобразить эту зависимость в виде графика рис. 1.6. Для каждого конкретного случая ее легко получить экспериментально, и она представляет собой характеристику нелинейного элемента колебательной системы. Здесь следует иметь в виду, что свойства конденсатора с сегнетоэлектриком существенно зависят от типа применяемого сег-нетоэлектрика, который обладает определенной инерционностью, связанной со скоростью изменения заряда, что приводит к

частотной зависимости емкости конденсатора. Поэтому нелинейные характеристики таких конденсаторов могут существенно изменяться при значительном уселичении частоты электрических колебаний в контуре, содержащем нелинейный элемент.  [43]

Конденсаторы Кобаяси имеют при комнатной температуре ток утечки порядка 0 2 мка / мкф-в. В интервале температур от — 100 до 200 С емкость этих конденсаторов изменяется линейно с температурой и температурный коэффициент емкости составляет 5 — Юх ХЮ-4 град-1. При — 180 С емкость конденсаторов составляет приблизительно 80 % от значения при комнатной температуре. Тангенс угла потерь мало изменяется в интервале температур от — 180 до 200 С, и его среднее значение равно 3 % при частоте 1000 гц. Конденсаторы отличаются

малой частотной зависимостью емкости и тангенса угла потерь в диапазоне частот от 100 до 10 000 гц.  [44]

Электрокапиллярные кривые, снятые в 1 н. NaCl с добавлением трет — С5Е. Н в следующих концентрациях. 1 0. 2 0 01 М. 3 0 05 М. 4 0 1 М. 5 0 2 М. 6 0 4 М. а — экспериментальные. б — расчетные данные.  [45]

Страницы:      1    2    3    4

Зависимость напряжения от емкости конденсатора

Емкость конденсатора при повышении частоты уменьшается, так как уменьшается диэлектрическая проницаемость диэлектрика, обусловленная ослаблением релаксационных видов поляризации. В случае если же в диэлектрике имеет место только электронная и ионная поляризация, то диэлектрическая проницаемость в широком диапазоне частот не должна зависеть от частоты, а следовательно не должна изменяться и емкость. Но и в данном случае емкость может изменяться за счёт влияния конструктивных элементов конденсатора: его индуктивности и сопротивления обкладок и выводов. Наличие индуктивности в конденсаторе дает увеличение его действующей емкости с ростом частоты рис. Приравняем значения полных сопротивлений:.


Поиск данных по Вашему запросу:

Схемы, справочники, даташиты:

Прайс-листы, цены:

Обсуждения, статьи, мануалы:

Дождитесь окончания поиска во всех базах.

По завершению появится ссылка для доступа к найденным материалам.

Содержание:

  • Конденсатор в цепи переменного тока
  • Электролитические конденсаторы: особенности применения
  • Конденсатор
  • Зависимость силы тока от емкости конденсатора. Емкостное сопротивление
  • Конденсатор в цепи постоянного и переменного тока
  • Почему емкость конденсатора постоянна
  • В помощь изучающему электронику

ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Сдвиг фаз между током и напряжением, электрический конденсатор. Что это такое на примере аналогии.

Конденсатор в цепи переменного тока


Электрический ток в цепи возникает в результате изменения заряда конденсатора, поэтому колебания силы тока в цепи будут происходить по закону:. Произведение w CU m является амплитудой колебаний силы тока:. Аналогично тому, как было сделано с индуктивностью, введем понятие емкостного сопротивления конденсатора:.

Рассмотрим электрическую схему на рис. В этой цепи возникают вынужденные колебания силы тока и напряжения на отдельных её элементах.

Амплитуда колебаний силы тока в цепи будет зависеть от частоты w приложенного постоянного напряжения генератора, так как сопротивления реактивных элементов — конденсатора и катушки индуктивности зависят от частоты.

При низкой частоте w переменного тока емкостное сопротивление конденсатора 24 будет очень большим, поэтому сила тока в цепи будет мала. В обратном предельном случае большой частоты w переменного тока большим будет индуктивное сопротивление катушки 22 , и сила тока в цепи опять будет мала.

Ясно, что максимальная сила тока в цепи будет соответствовать такой частоте w 0 приложенного переменного напряжения, при которой индуктивное и ёмкостное сопротивления будут одинаковы:. Колебания напряжения на катушке и конденсаторе противоположны по фазе, поэтому их сумма при выполнении условия 26 будет равна нулю. Циклическая частота w колебаний силы тока и ЭДС при этом равна.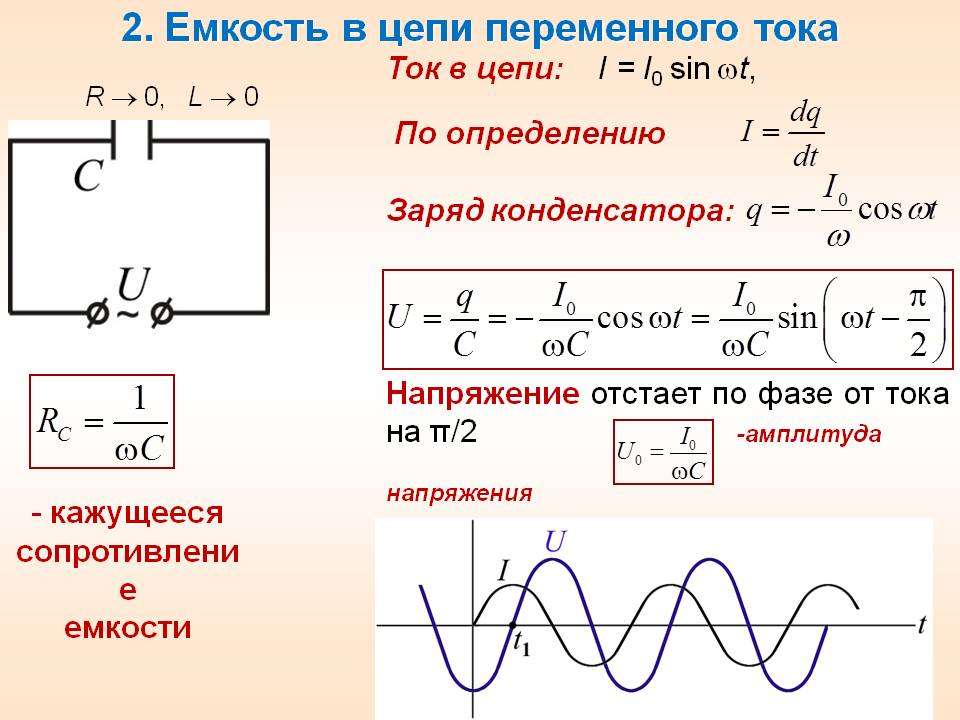

Явление резкого возрастания амплитуды вынужденных колебаний силы тока в колебательном контуре при приближении циклической частоты w внешней переменной Э. Резонансная циклическая частота не зависит от активного сопротивления R. График зависимости I m от w называется резонансной кривой. Резонансные кривые имеют тем более острый максимум, чем меньше активное сопротивление R :. Исследование явления резонанса.

Выберите материал проводника — никель, установите значения длины и площади поперечного сечения:. Для этого необходимо подключить параллельно проводнику мультиметр в режиме измерения постоянного напряжения, соблюдая полярность. Включите мультиметр в режиме измерения постоянного тока последовательно в цепь, соблюдая полярность. Проделайте пункты 3 — 6. Измерьте сопротивление проводника непосредственно с помощью омметра. Сравните полученные результаты, сформулируйте выводы.

Определите экспериментально с помощью мультиметра в режиме измерения сопротивлений сопротивление между точками:. Рассчитайте теоретические значения сопротивлений между указанными точками схемы и сравните их с измеренными. Какие выводы можно сделать из этого опыта? Измерьте с помощью мультиметра в режиме измерения тока токи, текущие через каждое сопротивление.

Запишите показания прибора. Проверьте экспериментально, что в последовательной цепи ток одинаков через все сопротивления, а в параллельной цепи разделяется так, что сумма всех токов через параллельно соединенные элементы, равна полному току через весь участок. Измерьте с помощью мультиметра в режиме измерения постоянного напряжения напряжения на каждом сопротивлении.

Проверьте экспериментально, что в последовательной цепи напряжение на всем участке равно сумме напряжений на каждом элементе, а в параллельной цепи, напряжение одно и то же на каждом элементе. Соберите цепь по схеме, изображенной на рис.

При помощи мультиметра определите напряжение на батарейке при разомкнутом ключе. Это и будет ЭДС источника в соответствии с формулой Повторите измерения силы тока и напряжения для 6 различных положений ползунка реостата и запишите полученные значения в таблицу. Соберите на монтажном столе схему, показанную на рис. Выберите значения сопротивлений одинаковыми и равными 1 кОм. Измерьте с помощью омметра сопротивление между точками А и В при замкнутом и разомкнутом положении выключателя.

Объясните результаты измерений. Измерьте силу тока при разомкнутом и замкнутом ключе. Точки схемы, напряжение между которыми равно нулю, можно соединять и такое соединение не изменит токов, текущих по элементам схемы.

Иногда такое соединение может существенно упростить схему. Исследуйте аналогичным способом сопротивление между противоположными вершинами проволочного куба. Чему равно сопротивление между этими точками? Изменяя положение движка реостата, измеряйте силу тока в цепи и напряжение на реостате нагрузке. Занесите полученные данные сопротивление реостата R , силу тока I и напряжение U в таблицу. Определите из графика значение сопротивления нагрузки, на которой выделяется максимальная мощность.

Использую программу EWB, соберите схему на рис. Изменяя емкость конденсатора от 5 до 50 мкФ через 5 мкФ , запишите показания вольтметров напряжение на конденсаторе и на резисторе.

Рассчитайте эффективное значение токов, текущих в цепи, в зависимости от значения емкости конденсатора для этого надо напряжение на резисторе разделить на его сопротивление. Определите значения емкостных сопротивлений конденсатора для соответствующих значений его емкости и сравните их с рассчитанными по формуле Установите емкость конденсатора 10 мкФ.

Изменяя частоту генератора от 20 до Гц через 10 Гц, повторите измерения и расчеты емкостного сопротивления в зависимости от частоты переменного тока. Используйте конденсаторы из набора с наиболее близкими к указанным параметрами.

Изменяя индуктивность катушки от 50 до мГн через 50 мГн , запишите показания вольтметров напряжение на катушке и на резисторе. Рассчитайте эффективное значение токов, текущих в цепи, в зависимости от значения индуктивности катушки для этого надо напряжение на резисторе разделить на его сопротивление.

Определите индуктивные сопротивления катушки для соответствующих значений ее индуктивности и сравните их с рассчитанными по формуле Установите индуктивность катушки мГн. Изменяя частоту генератора от 20 до Гц через 10 Гц, повторите измерения и расчеты индуктивного сопротивления в зависимости от частоты переменного тока.

Постройте графики зависимостей индуктивного и емкостного сопротивлений от частоты переменного тока. Используйте индуктивности из набора с наиболее близкими к указанным параметрами.

Изменяя частоту генератора от 10 Гц до Гц через 10 Гц, с помощью вольтметров измерьте напряжения на катушке, конденсаторе, резисторе и занесите измеренные значения в таблицу. В наборе конструктора имеется лишь два мультиметра, поэтому придется, изменяя частоту генератора, провести измерения дважды — сначала подключив вольтметры к катушке и конденсатору, а второй раз — подключив вольтметр к резистору.

Постройте графики зависимости напряжений на резисторе, конденсаторе и катушке в зависимости от частоты генератора. Рассчитайте по формуле 27 частоту резонанса и сравните полученное значение с экспериментальным. Попытайтесь объяснить экспериментальные графики зависимости напряжений на элементах от частоты переменного тока в цепи. Отчет по выполненной лабораторной работе выполняется на отдельных листах в рукописном или печатном вариантах и включает следующие разделы:.

Дата добавления: ; Просмотров: ; Нарушение авторских прав? Нам важно ваше мнение! Был ли полезен опубликованный материал? Да Нет. Главная Случайная страница Контакты. Полное сопротивление Z цепи, изображенной на рис. Циклическая частота w колебаний силы тока и ЭДС при этом равна 27 и совпадает с циклической частотой свободных незатухающих электромагнитных колебаний в электрическом контуре.

Отключите adBlock!


Электролитические конденсаторы: особенности применения

Господа, сегодняшнюю статью можно считать в некотором роде продолжением предыдущей. Сначала я даже хотел поместить весь этот материал в одну статью. Но его получилось довольно много, на горизонте были новые проекты, и я в итоге разделил его на две. Итак, сегодня мы поговорим про сопротивление конденсатора переменному току. Мы получим выражение, по которому можно будет рассчитать, чему равно сопротивление любого конденсатора, включенного в цепь с переменным током, а в конце статьи рассмотрим несколько примеров такого расчета. Сразу оговорюсь про одну важную вещь. Вообще говоря, реальный конденсатор обладает помимо емкостного сопротивления еще резистивным и индуктивным.

Использование конденсаторов в цепях переменного тока (шпаргалка для Где С — ёмкость конденсатора, Ф, U — напряжение, В, Хс — ёмкостное конденсатора изменять ёмкостное сопротивление в зависимости от частоты .

Конденсатор

Конденсатор является пассивным электронным компонентом. Ёмкость конденсатора измеряется в фарадах. Первые конденсаторы, состоящие из двух проводников, разделенных непроводником диэлектриком , упоминаемые обычно как конденсатор Эпинуса или электрический лист, были созданы ещё раньше [3]. Конденсатор является пассивным электронным компонентом [4]. В простейшем варианте конструкция состоит из двух электродов в форме пластин называемых обкладками , разделённых диэлектриком , толщина которого мала по сравнению с размерами обкладок см. Практически применяемые конденсаторы имеют много слоёв диэлектрика и многослойные электроды, или ленты чередующихся диэлектрика и электродов, свёрнутые в цилиндр или параллелепипед со скруглёнными четырьмя рёбрами из-за намотки. Конденсатор в цепи постоянного тока может проводить ток в момент включения его в цепь происходит зарядка или перезарядка конденсатора , по окончании переходного процесса ток через конденсатор не течёт, так как его обкладки разделены диэлектриком.

Зависимость силы тока от емкости конденсатора. Емкостное сопротивление

Соберем цепь с конденсатором , в которой генератор переменного тока создает синусоидальное напряжение. Разберем последовательно, что произойдет в цепи, когда мы замкнем ключ. Начальным будем считать тот момент, когда напряжение генератора равно нулю.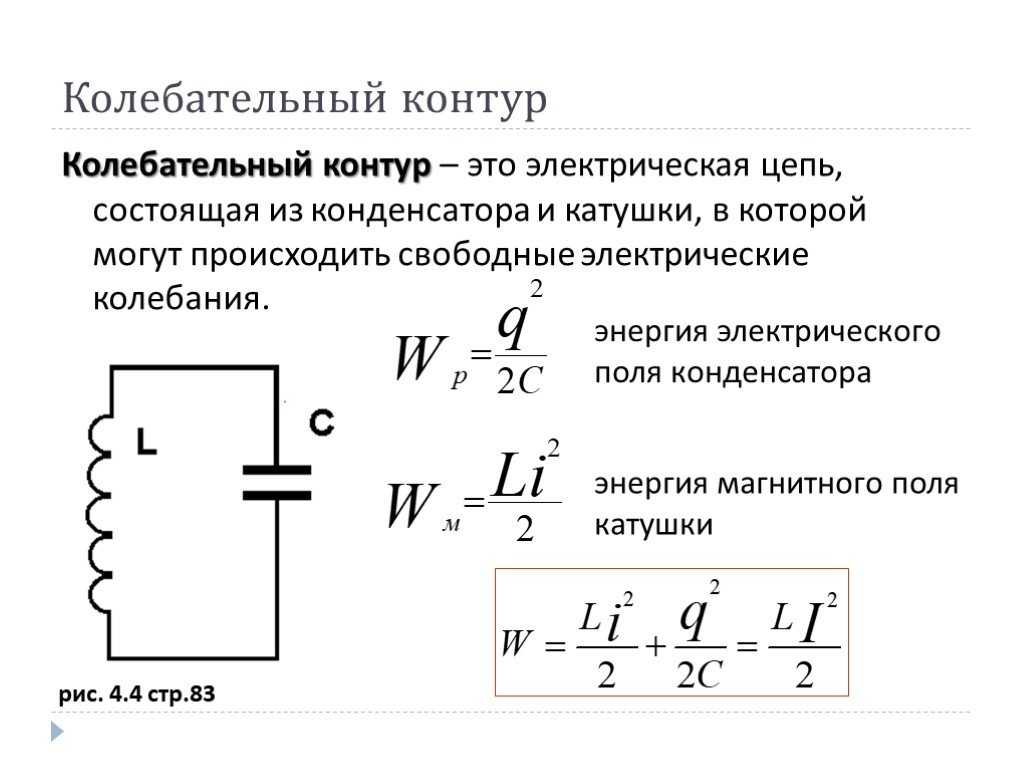 Изменение тока и напряжения в цепи с емкостью.

Много написано про конденсаторы, стоит ли добавлять еще пару тысяч слов к тем миллионам, что уже есть?

Конденсатор в цепи постоянного и переменного тока

Конденсатор — электронный компонент, предназначенный для накопления электрического заряда. Способность конденсатора накапливать электрический заряд зависит от его главной характеристики — емкости. Емкость конденсатора С определяется как соотношение количества электрического заряда Q к напряжению U. Емкость конденсатора измеряется в фарадах F — единицах, названых в честь британского ученого физика Майкла Фарадея. Емкость в один фарад 1F равняется количеству заряда в один кулон 1C , создающему напряжение на конденсаторе в один вольт 1V. Вспомним, что один кулон 1С равняется величине заряда, прошедшего через проводник за одну секунду 1sec при силе тока в один ампер 1A.

Почему емкость конденсатора постоянна

Заряд и разряд конденсатора. Конденсатор представляет собой устройство, способное накапливать электрические заряды. Простейшим конденсатором являются две металлические пластины электроды , разделенные каким-либо диэлектриком. Конденсатор 2 можно зарядить, если соединить его электроды с источником 1 электрической энергии постоянного тока рис. При заряде конденсатора свободные электроны, имеющиеся на одном из его электродов, устремляются к положительному полюсу источника, вследствие чего этот электрод становится положительно заряженным.

Мы знаем, что конденсатор не пропускает через себя постоянного тока. Поэтому ток отставал от напряжения, а в цепи с емкостью ток опережает напряжение. Зависимость емкостного сопротивления конденсатра от частоты.

В помощь изучающему электронику

Войдите , пожалуйста. Хабр Geektimes Тостер Мой круг Фрилансим. Войти Регистрация. Изменение ёмкости керамических конденсаторов от температуры и напряжения, или как ваш конденсатор на 4,7мкФ превращается в 0,33мкФ Автор оригинала: Mark Fortunato.

Изучение процессов заряда и разряда конденсаторов в RC -цепях, ознакомление с работой приборов, используемых в импульсной электронной технике. Р ассмотрим схему, пред-ставленную на рис. Схема включает в себя источник постоянного тока, активное сопротивление и конденсатор, процессы заряда и разряда в котором и будем рассматривать. Эти процессы разберем по-отдельности.

На рис. После включения цепи вольтметр, включенный в цепь, покажет полное напряжение генератора.

Алюминиевые электролитические конденсаторы широко используются в различных электро- и радиотехнических приборах теле-, радио-, аудиоустройствах, стиральных машинах, кондиционерах воздуха и т. Применение на постоянном напряжении с наложенной переменной составляющей пульсирующее напряжение :. Алюминиевый электролитический конденсатор имеет простую конструкцию. Две ленты из конденсаторной бумаги проложены между двумя лентами из специальным образом обработанной алюминиевой фольги и эта комбинация из четырех лент свернута в рулон. Бумага, служащая сепаратором для алюминиевых электродов, пропитана электропроводящим раствором. К электродам присоединены выводы, образуя активный элемент конденсатора.

Лампочку тоже берем на 12 Вольт. Теперь между одним щупом блока питания и лампочки вставляем конденсатор:. Не-а, не горит. Отсюда напрашивается вывод: постоянный ток через конденсатор не течет!


Емкостное сопротивление конденсатора при увеличении частоты

Оборудование: источник электропитания для практикума ИЭПП-1, набор конденсаторов, комплект электроизмерительных приборов «Учебный-2», соединительные проводники.

Задание. Рассчитайте сопротивление конденсатора электроемкостью 6 мкФ в цепи переменного тока с частотой 50 Гц. Выполните измерение силы тока через конденсатор при включении в цепь с переменным напряжением 12 В.

Указание. Два проводника, разделенные слоем диэлектрика, обладают электроемкостью С. При подаче переменного напряжения между такими проводниками не происходит перенос электрических зарядов сквозь диэлектрик, но периодически повторяющиеся процессы зарядки и разрядки конденсатора приводят к возникновению переменного тока в проводах, ведущих к обкладкам конденсатора. Действующее значение силы тока в проводах, ведущих к конденсатору, определяется значением его электроемкости С, частотой вынужденных колебаний силы тока в цепи и действующим значением напряжения на обкладках:

Таким образом, конденсатор в цепи переменного тока эквивалентен элементу цепи с электрическим сопротивлением равным:

Возможный вариант выполнения работы

1. Вычислите емкостное сопротивление этого конденсатора электроемкостью 6 мкФ на частоте 50 Гц.

2. Рассчитайте действующее значение силы тока через конденсатор при подаче на его обкладки переменного напряжения 12 В.

3. Выполните измерение силы тока через конденсатор при напряжении 12 В между его обкладками. Сравните результаты расчета и измерений.

Исследуйте зависимость действующего значения силы тока через конденсатор от действующего значения напряжения, постройте график. Рассчитайте значения силы тока в цепи при последовательном и параллельном включении конденсаторов с электроемкостью 6 и 4 мкФ. Результаты расчета проверьте экспериментально.

1. Объясните, почему через конденсатор не проходит постоянный ток, а переменный ток проходит.

2. Как изменится емкостное сопротивление конденсатора при увеличении частоты переменного тока в 2 раза?

Электросопротивление — это параметр в электротехнике, характеризующий возможность вещества препятствовать прохождению электричества. В зависимости от качеств материала, электросопротивляемость может уменьшаться до крайне маленьких величин (микромилиОмы — у проводников, металлов) или повышаться до огромных значений (ГигаОмы — изоляторов, диэлектриков). Величина противоположная сопротивлению — проводимость.

Что такое

Цепь, по которой протекает непостоянный ток, обладает полным сопротивлением. Вычисляется оно по сумме активного и реактивного сопротивлений, возведенных в квадрат.

Графическое изображение этой формулы представляет собой треугольник. Его катеты представлены активным и реактивным сопротивлениями, а гипотенуза полным электросопротивлением.

Емкостное электросопротивление (Xc) является одним из видов реактивного сопротивления. Этот показатель характеризует противодействие электроемкости в цепи электротоку с переменными параметрами. Преобразование электроэнергии в тепловую в момент протекания электричества сквозь емкость не возникает (свойство реактивного сопротивления). Вместо этого осуществляется передача энергии электрического тока электрическому полю и обратно. Потерь энергии при таком обмене не происходит.

Емкостное сопротивление конденсатора можно сравнить с кастрюлей, наполняемой жидкостью, при полном заполнении ее объема она переворачивается, выливая содержимое, а затем наполняется заново. После достижения максимального заряда конденсатора происходит разрядка, затем он заряжается вновь.

Дополнительная информация: Конденсатор цепи способен накопить лишь ограниченную величину заряда до перемены полярности напряжения. По данной причине непостоянный ток не падает до нуля, важное отличие от постоянного электричества. Низкие значения частоты тока соответствуют низким показателям заряда, накопленного конденсатором, низким значениям противодействия электричеству, что придает реактивные свойства.

По сути, Xc — это противостояние электродвижущей силы конденсатора, уровню его заряда.

От чего зависит сопротивление конденсаторов цепей переменного тока

Показатели его, зависят не только от емкостных характеристик последнего, но и от частотной характеристики электротока, протекающего по цепи. Когда речь идет о сопротивлении резистора, то говорится о параметрах самого резистора, например, материале, форме, но полностью отсутствует взаимосвязь сопротивления его и показателей частоты электричества цепи (речь идет об идеальном резисторе, паразитные параметры которому не характерны). Когда речь идет об устройстве накопления энергии и заряда электрического поля — все иначе. Конденсатор одной и той же емкости при разных частотах тока обладает неодинаковым уровнем сопротивления. Амплитуда протекающего через него электричества при постоянной амплитуде напряжения обладает разной величиной.

Рассматривая эту формулу сопротивления конденсатора в цепи переменного тока, к каким выводам можно прийти? При повышении частотных показателей сигнала, электросопротивляемость конденсатора снижается.

При повышении емкостных характеристик устройства для накопления заряда и энергии электрического поля Xc переменного электричества, проходящего сквозь него, будет стремиться вниз.

Момент приближения значений частоты к нулевым отметкам на оси (когда переменный электроток становится похож своими параметрами на постоянный), сопровождается возрастанием Xc конденсатора до беспредельных величин. Это действительно так: известно, что конденсатор сети постоянного тока является фактически разрывом цепи. Реальная электросопротивляемость, естественно, не бесконечна, ее ограничивает уровень конденсаторной утечки. Но величины его остаются на высоком уровне, который невозможно не учитывать.

При возрастании цифр частоты до уровня бесконечных значений, емкостное сопротивление электроконденсатора стремится к нулевым отметкам. Такое характеризует идеальные модели. В реальных условиях конденсатор имеет неприятные характеристики (такие как индуктивность и сопротивления утечек), поэтому снижение емкостного сопротивления происходит до определенных значений, после которых оно возрастает.

Обратите внимание! При подключении конденсатора к цепочке электричества с переменными параметрами, его мощность не тратится, потому что фазовые характеристики напряжения и силы тока сдвинуты на 90° в отношении друг друга. В одну четверть периода происходит зарядка электроконденсатора (энергия запасается в его электрополе), в следующее время происходит его разрядка, энергия поступает обратно в цепочку. Его электросопротивляемость является безваттной, реактивной.

Причины ёмкостного сопротивления

Причиной возникновения сопротивления емкостного считается уровень напряжения, возникающий на конденсаторе в процессе его заряда. Вектор его действия встречен вектору напряжения источника электричества, потому создает помеху воспроизведению электротока этим источником.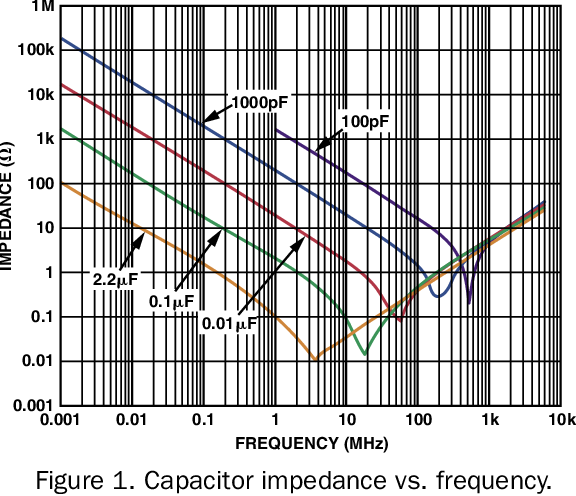

Как рассчитать Xc

Сила тока цепи с постоянными показателями напряжения в момент работы электроконденсатора равно 0. Ее значения в цепи с переменным напряжением после подключения конденсатора I ? 0. В итоге, цепочке с непостоянным напряжением конденсатор придает Xc меньшее, чем цепочке с неизменным показателем напряжения.

Получается, что изменения напряжения отличаются по фазе от изменений тока на π/2.

По закону, сформулированному Омом, показатели силы электротока находятся в прямой пропорциональной зависимости от величины напряжения цепи. Формула вычисления наибольших величин напряженности и силы тока:

f — показатель частоты непостоянного тока, измеряется в герцах;

ω — показатель угловой частоты тока;

С — размер конденсатора в фарадах.

Важно! Xc не выступает параметром проводника, оно находится в зависимости от такой характеристики электроцепи, как частота электротока.

Повышение значений данной величины вызывает рост пропускающей способности конденсатора (предел его сопротивления току непостоянному понижается).

Представим, к цепи подключен конденсатор, емкостью 1 мкФ. Необходимо вычислить, уровень емкостного сопротивления при величине частоты 50 Гц и как изменится емкостное сопротивление цепи переменного тока при частоте 1 кГц. Амплитуда напряжения, подведенного к конденсатору, составляет 50 В.

После введения данных в формулу, определяющую Xc, и получаются значения:

Емкостное сопротивление приравнивается к соотношению отклонений колебаний напряжения зажимов электрической цепочки с емкостными параметрами (с небольшими индуктивным и активным сопротивлениями) к колебаниям электротока цепочки. Она равнозначна электроконденсатору.

В чем измеряется емкостное электросопротивление

R представлено отношением напряжения к силе тока замкнутой электрической цепи, по закону Ома. Единицы измерения — Ом. Xc, как его разновидность, тоже измеряется в Омах.

Конденсаторы применяются при изготовлении фильтров. При параллельном присоединении к цепи, он способен задерживать высокие частоты, при последовательном удаляет низкие. Также они используются с целью отсечения переменной части от постоянной. Он незаменим в радиотехнике, при производстве датчиков приближения, для контроля процессов производства. Технологии, обладающие выше описанными свойствами, используются во всех областях промышленности.

Емкость конденсатора при повышении частоты уменьшается, так как уменьшается диэлектрическая проницаемость диэлектрика, обусловленная ослаблением релаксационных видов поляризации.

Если же в диэлектрике имеет место только электронная и ионная поляризация, то диэлектрическая проницаемость в широком диапазоне частот не должна зависеть от частоты, а следовательно не должна изменяться и емкость. Но и в этом случае емкость может изменяться за счет влияния конструктивных элементов конденсатора: его индуктивности и сопротивления обкладок и выводов.

Наличие индуктивности в конденсаторе дает увеличение его действующей емкости с ростом частоты (рис. 30), так как ток будет возрастать за счет компенсации реактивного емкостного сопротивления индуктивным сопротивлением.

Приравняем значения полных сопротивлений:

конденсатора с индуктивностью, L и емкостью

эквивалентного ему конденсатора с действующей емкостью , без индуктивности.

Пренебрегая наличием активного сопротивления можно написать:

[84]

[85]

[86]

[87]

[88]

Зависимость от частоты увеличивается как при увеличении индуктивности L так и при увеличении емкости при заданной индуктивности.

Наличие активного сопротивления r, включенного последовательно с емкостью С должно ограничивать ток, протекающий через конденсатор, причем этот эффект должен быть заметнее при увеличении частоты, так как с увеличением частоты падает емкостное реактивное сопротивление и влияние активного сопротивления на величину тока возрастает (рис. 31).

Величину можно вычислить по формуле:

[89]

Увеличение емкости С при заданном r усиливает частотную зависимость.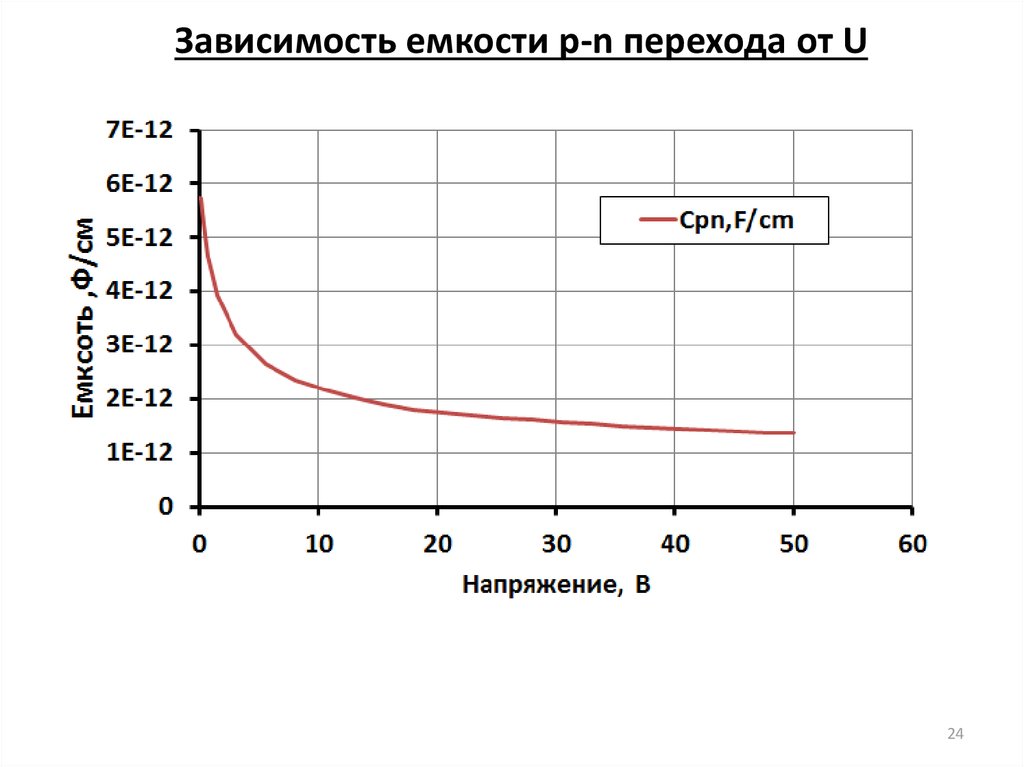

В обычных конденсаторах сопротивление обкладок и выводов, определяющее величину r, мало, а поэтому снижение емкости C с увеличением частоты f можно заметить лишь в области радиочастот, даже при больших емкостях.

Выражения [88] и [89] являются приближенными, хотя и правильно характеризуют качественный характер частотной зависимости емкости.

Как частотная зависимость диэлектрической проницаемости, так и влияние активного сопротивления вызывают уменьшение емкости от частоты; увеличение емкости может быть обусловлено только влиянием индуктивности.

Как для полярных, так и для неполярных диэлектриков величина диэлектрической проницаемости не зависит от напряженности, а поэтому для большинства типов конденсаторов емкость не должна зависеть от величины приложенного напряжения.

Небольшое увеличение емкости при увеличении напряжения выше напряжения ионизации может наблюдаться для конденсаторов, диэлектрик которого содержит значительное число воздушных включений.

В сегнетокерамических конденсаторах диэлектрик обладает спонтанной поляризацией, для которой характерна зависимость диэлектрической проницаемости от напряжения. Для них емкость сильно зависит от напряжения, что используется для изготовления нелинейных конденсаторов – «варикондов».

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 10099 – | 7532 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

импеданс — Частотная зависимость электролитических конденсаторов

Этот эффект обусловлен влиянием паразитных характеристик устройства. Конденсатор имеет четыре основных паразитных параметра:

Эквивалентное последовательное сопротивление — ESR:

Конденсатор на самом деле представляет собой конденсатор, соединенный последовательно с сопротивлениями его выводов, фольги в диэлектрике и другими малыми сопротивлениями. Это означает, что конденсатор не может действительно мгновенно разрядиться, а также что он будет нагреваться при многократной зарядке и разрядке. Это важный параметр при проектировании энергосистем.

Ток утечки:

Диэлектрик не идеален, поэтому вы можете добавить сопротивление параллельно конденсатору. Это важно в системах резервного копирования, и ток утечки электролита может быть намного больше, чем ток, необходимый для поддержания оперативной памяти на микроконтроллере.

Диэлектрическое поглощение — CDA:

Обычно этот параметр представляет меньший интерес, чем другие параметры, особенно для электролитов, для которых ток утечки подавляет эффект. Для крупной керамики можно представить, что параллельно конденсатору имеется RC-цепь. Когда конденсатор заряжается в течение длительного периода времени, воображаемый конденсатор приобретает заряд. Если конденсатор быстро разряжается в течение короткого периода времени, а затем возвращается в разомкнутую цепь, паразитный конденсатор начинает перезаряжать основной конденсатор.

Эквивалентная последовательная индуктивность — ESL:

К настоящему моменту вас не должно слишком удивлять, что если у всего есть емкость, а также ненулевое и небесконечное сопротивление, у всего также есть паразитная индуктивность. Значимы ли они, зависит от частоты, что приводит нас к теме импеданса.

Импеданс обозначается буквой Z. Импеданс можно рассматривать как сопротивление, только в частотной области. Точно так же, как сопротивление сопротивляется протеканию постоянного тока, импеданс препятствует протеканию переменного тока. Точно так же, как сопротивление — это V/R, если мы интегрируем во временную область, импеданс — это V(t)/I(t).

Вам придется либо произвести некоторые расчеты, либо купить следующие утверждения об импедансе компонента с приложенным синусоидальным напряжением с частотой w:

\$ \начать{выравнивать} Z_{резистор} &= R\\ Z_{конденсатор} &= \frac{1}{j \omega C} = \frac{1}{sC}\\ Z_{индуктор} &= j\omega L = sL \end{выравнивание} \$

Да, \$j\$ это то же самое, что и \$i\$ (мнимое число, \$\sqrt{-1}\$), но в электронике \$i\$ обычно обозначает ток, поэтому мы используем \$j\$. Кроме того, \$\omega\$ традиционно представляет собой греческую букву омега (которая выглядит как w). Буква «s» относится к комплексной частоте (не синусоидальной).

Фу, да? Но вы поняли идею: резистор не меняет своего импеданса, когда вы подаете сигнал переменного тока. Конденсатор имеет уменьшенный импеданс с более высокой частотой, и он почти бесконечен при постоянном токе, как мы и ожидали. Катушка индуктивности имеет увеличенный импеданс с более высокой частотой — подумайте о ВЧ-дросселе, предназначенном для устранения пиков.

Мы можем рассчитать импеданс двух последовательно соединенных компонентов путем сложения импедансов. Если у нас есть конденсатор последовательно с катушкой индуктивности, мы имеем:

\$ \начать{выравнивать} Z &= Z_C + Z_L\\ &= \frac{1}{j\omega C + j\omega L} \end{выравнивание} \$

Что происходит, когда мы увеличиваем частоту? Давным-давно нашим компонентом был электролитический конденсатор, поэтому мы будем считать, что \$C\$ намного больше, чем \$L\$. 2 LC — 1) * j)}{\omega C} \конец{выравнивание*} \$

Ну, это было весело, правда? Это то, что вы делаете один раз, запоминаете ответ, а затем не беспокоитесь об этом. Что мы знаем из последнего уравнения? Сначала рассмотрим случай, когда \$\omega\$ мала, \$L\$ мала, а \$C\$ велика. Имеем, примерно,

\$ \начать{выравнивать*} \frac{(маленький * маленький * большой — 1) \times j}{маленький * большой} \конец{выравнивание*} \$

, что является отрицательным числом (предполагается, что \$маленький * маленький * большой <1\$, что для практических компонентов). Это известно как \$Z_C = \frac{-j}{\omega C}\$ - это конденсатор! 92 ЛК = 1\$? Тогда импеданс равен нулю!?!? Да! Это называется резонансной частотой. Это точка внизу кривой, которую вы указали в своем вопросе. Почему на самом деле не ноль? Из-за СОЭ.

TL,DR: Когда вы сильно увеличиваете частоту, происходят странные вещи. Всегда следуйте спецификациям производителей для развязки ваших ИС, и получите хороший учебник или посещайте занятия, если вам нужно делать высокоскоростные вещи.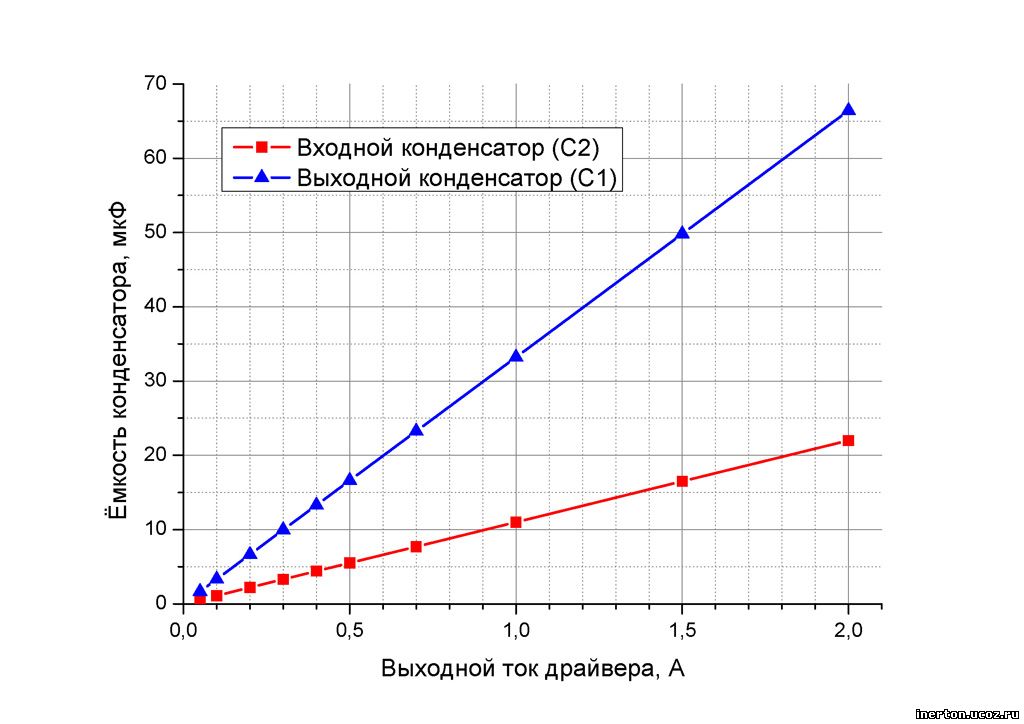

конденсатор — почему емкость зависит от частоты физически независимо от математического факта?

Спросил

Изменено 7 лет, 10 месяцев назад

Просмотрено 1к раз

\$\начало группы\$

Сэр, я знаю, что когда f = 0, емкостное сопротивление будет равно бесконечности в соответствии с математической формулой, и поэтому конденсатор блокирует постоянный ток. Но каково его физическое значение? Я имею в виду, почему конденсатор блокирует постоянный ток, когда частота равна нулю? Я действительно не понимаю его ответ, чтобы четко понять это.Спасибо.

  • конденсатор

\$\конечная группа\$

2

\$\начало группы\$

Конденсаторы блокируют постоянный ток, поскольку существует физический барьер (непроводник), который препятствует протеканию тока. Переменный ток может проходить просто потому, что заряды на одной стороне толкают (отталкивают) и притягивают (притягивают) заряды на другой стороне в течение каждого полупериода формы волны переменного тока.

Это приводит к тому, что заряды кажутся циркулирующими, даже если они на самом деле не в обращении. Эта концепция называется фантомным током , потому что кажется, что ток пересекает непроводник в центре конденсатора, хотя на самом деле его нет. То, что пересекается, это линии электрического поля. Более интуитивный способ понять это состоит в том, что силы, создаваемые концентрацией одинаковых зарядов на одной стороне, действуют через промежуток на заряды противоположного сходства на дальней стороне.

Реактивное сопротивление – это сопротивление элемента цепи изменению напряжения. При постоянном токе сигнал не прилагает усилий для «изменения напряжения» и, следовательно, обладает идеальной способностью конденсатора сопротивляться изменению (следовательно, бесконечное реактивное сопротивление). Физически неспособность статических зарядов генерировать фантомный ток означает, что в идеальном случае конденсатор может полностью сопротивляться передаче энергии.

\$\конечная группа\$

2

\$\начало группы\$

Основная формула для конденсатора: —

Заряд конденсатора = емкость * Напряжение или Q=CV

Скорость изменения Q равна току, и если емкость постоянна, то: —

I = C\$\ dfrac{dV}{dt}\$

Это в основном означает, что ток через конденсатор связан со скоростью изменения напряжения. Статические напряжения постоянного тока не создают тока, медленно меняющиеся напряжения создают небольшой ток, а быстро меняющиеся напряжения создают большой ток.

\$\конечная группа\$

\$\начало группы\$

Конденсатор состоит из двух металлических пластин с изолятором между ними. Электроны не могут перепрыгнуть через этот промежуток (ну, могут, если напряжение слишком высокое, но это не проблема в пределах указанного рабочего диапазона конденсатора). Когда на пластины подается напряжение, электроны будут течь ВХОД к одной пластине и ВЫХОД из другой пластины. По мере движения электронов между пластинами будет создаваться электрическое поле из-за дисбаланса заряда. Ток от смещенных электронов называется током смещения. Как только электронов переместится достаточно, чтобы внутреннее электрическое поле сравнялось с приложенным потенциалом, ток смещения перестанет течь. Изменение приложенного потенциала приведет к смещению большего количества электронов, пока внутреннее поле снова не сравняется с приложенным напряжением. Если приложенное напряжение не меняется, ток не будет течь — следовательно, при постоянном токе конденсатор выглядит как разомкнутая цепь. Что касается реактивного сопротивления, то напряжение и ток связаны законом Ома V = I * R. Если I равно нулю, то R = V/0 и, следовательно, не определено. Поскольку пассивные линейные компоненты всегда имеют положительное сопротивление, сопротивление конденсатора постоянному току считается бесконечным.

\$\конечная группа\$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Изменяется ли емкость с частотой?

Добро пожаловать на EDAboard.com

Добро пожаловать на наш сайт! EDAboard.com — это международный дискуссионный форум по электронике, посвященный программному обеспечению EDA, схемам, схемам, книгам, теории, документам, asic, pld, 8051, DSP, сети, радиочастотам, аналоговому дизайну, печатным платам, руководствам по обслуживанию… и многому другому. более! Для участия необходимо зарегистрироваться. Регистрация бесплатна. Нажмите здесь для регистрации.

Регистрация Авторизоваться

JavaScript отключен. Для лучшего опыта, пожалуйста, включите JavaScript в вашем браузере, прежде чем продолжить.