Максимальный заряд конденсатора формула через силу тока
Конденсатор — электронный компонент, предназначенный для накопления электрического заряда. Способность конденсатора накапливать электрический заряд зависит от его главной характеристики — емкости. Емкость конденсатора С определяется как соотношение количества электрического заряда Q к напряжению U. Емкость конденсатора измеряется в фарадах F — единицах, названых в честь британского ученого физика Майкла Фарадея. Емкость в один фарад 1F равняется количеству заряда в один кулон 1C , создающему напряжение на конденсаторе в один вольт 1V.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Заряд конденсатора
- Все формулы.
Заряд конденсатора формула - Конденсатор
- В помощь изучающему электронику
- Колебательный контур
- Конденсатор в цепи переменного тока. Емкостное сопротивление конденсатора.
- Как найти заряд конденсатора, имеющего емкость, если известны ЭДС каждого из двух источников тока?
- Чему будет равен максимальный заряд конденсатора
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Как рассчитать цепи?
Заряд конденсатора
Мы знаем, что конденсатор не пропускает через себя постоянного тока.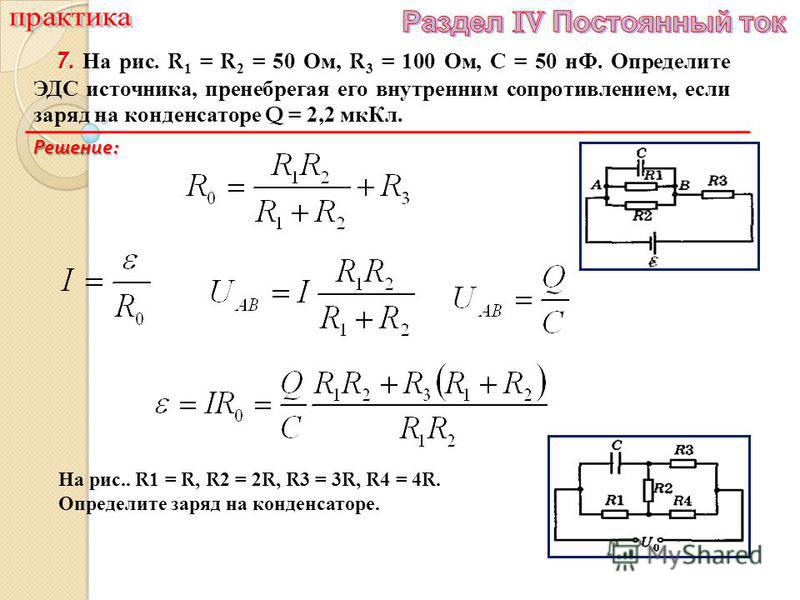 Поэтому в электрической цепи, в которой последовательно с источником тока включен конденсатор, постоянный ток протекать не может. Рисунок 1. Сравнение конденсатора в цепи переменного тока с пружиной, на которую воздействует внешняя сила. В течение первой четверти периода, когда переменная ЭДС нарастает, конденсатор заряжается, и поэтому по цепи проходит зарядный электрический ток i , сила которого будет наибольшей вначале, когда конденсатор не заряжен.
Поэтому в электрической цепи, в которой последовательно с источником тока включен конденсатор, постоянный ток протекать не может. Рисунок 1. Сравнение конденсатора в цепи переменного тока с пружиной, на которую воздействует внешняя сила. В течение первой четверти периода, когда переменная ЭДС нарастает, конденсатор заряжается, и поэтому по цепи проходит зарядный электрический ток i , сила которого будет наибольшей вначале, когда конденсатор не заряжен.
По мере приближения заряда к концу сила зарядного тока будет уменьшаться. Заряд конденсатора заканчивается и зарядный ток прекращается в тот момент, когда переменная ЭДС пе-рестает нарастать, достигнув своего амплитудного значения. Этот момент соответствует концу первой четверти периода.
После этого переменная ЭДС начинает убывать, одновременно с чем конденсатор начинает разряжаться. Следовательно, в течение второй четверти периода по цепи будет протекать разрядный ток. Так как убывание ЭДС происходит вначале медленно, а затем все быстрее и быстрее, то и сила разрядного тока, имея в начале второй четверти периода небольшую величину, будет постепенно возрастать.
Итак, к концу второй четверти периода конденсатор разрядится, ЭДС будет равна нулю, а ток в цепи достигнет наибольшего, амплитудного, значения.
С началом третьей четверти периода ЭДС, переменив свое направление, начнет опять возрастать, а конденсатор — снова заряжаться. Заряд конденсатора будет происходить теперь в обратном направлении, соответственно изменившемуся направлению ЭДС.
Поэтому направление зарядного тока в течение третьей четверти периода будет совпадать с направлением разрядного тока во второй четверти, т. Вначале, пока конденсатор не заряжен, сила зарядного тока имеет наибольшее значение. По мере увеличения заряда конденсатора сила зарядного тока будет убывать.
Заряд конденсатора закончится и зарядный ток прекратится в конце третьей четверти периода, когда ЭДС достигнет своего амплитудного значения и нарастание ее прекратится.
Итак, к концу третьей четверти периода конденсатор окажется опять заряженным, но уже в обратном направлении, т. При этом ЭДС достигнет амплитудного значения противоположного направления , а ток в цепи будет равен нулю.
В течение последней четверти периода ЭДС начинает опять убывать, а конденсатор разряжаться; при этом в цепи появляется постепенно увеличивающийся разрядный ток.
Направление этого тока совпадает с направлением тока в первой четверти периода и противоположно направлению тока во второй и третьей четвертях. Из всего изложенного выше следует, что по цепи с конденсатором проходит переменный ток и что сила этого тока зависит от величины емкости конденсатора и от частоты тока. Кроме того, из рис. Отметим, что в цепи с индуктивностью ток отставал от напряжения , а в цепи с емкостью ток опережает напряжение.
И в том и в другом случае между фазами тока и напряжения имеется сдвиг, но знаки этих сдвигов противоположны. Мы уже заметили, что ток в цепи с конденсатором может протекать лишь при изменении приложенного к ней напряжения, причем сила тока, протекающего по цепи при заряде и разряде конденсатора, будет тем больше, чем больше емкость конденсатора и чем быстрее происходят изменения ЭДС.
Конденсатор, включенный в цепь переменного тока, влияет на силу протекающего по цепи тока, т. Величина емкостного сопротивления тем меньше, чем больше емкость и чем выше частота переменного тока. И наоборот, сопротивление конденсатора переменному току увеличивается с уменьшением его емкости и понижением частоты. Рисунок 2. Зависимость емкостного сопротивления конденсатра от частоты. Для постоянного тока, т. Энергия в течение одной четверти периода— при заряде конденсатора — запасается в электрическом поле конденсатора, а в течение другой четверти периода — при разряде конденсатора — отдается обратно в цепь.
Поэтому емкостное сопротивление, как и индуктивное , является реактивным или безваттным. Нужно, однако, отметить, что практически в каждом конденсаторе при прохождении через него переменного тока затрачивается большая или меньшая активная мощность, обусловленная происходящими изменениями состояния диэлектрика конденсатора. Кроме того, абсолютно совершенной изоляции между пластинами конденсатора никогда не бывает; утечка в изоляции между пластинами приводит к тому, что параллельно конденсатору как бы оказывается включенным некоторое активное сопротивление, по которому течет ток и в котором, следовательно, затрачивается некоторая мощность.
И в первом и во втором случае мощность затрачивается совершенно бесполезно на нагревание диэлектрика, поэтому се называют мощностью потерь. Потери, обусловленные изменениями состояния диэлектрика, называются диэлектрическими, а потери, обусловленные несовершенством изоляции между пластинами, — потерями утечки. Ранее мы сравнивали электрическую емкость с вместимостью герметически наглухо закрытого сосуда или с площадью дна открытого сосуда, имеющего вертикальные стенки.
Конденсатор в цепи переменного тока целесообразно сравнивать с гиб-костью пружины. Представим себе, что мы периодически сжимаем и растягиваем спиральную пружину, прикрепленную одним концом наглухо к стене. Время, в течение которого мы будем производить полный цикл сжатия и растяжения пружины, будет соответствовать периоду переменного тока. Таким образом, мы в течение первой четверти периода будем сжимать пружину, в течение второй четверти периода отпускать ее, в течение третьей четверти периода растягивать и в течение четвертой четверти снова отпускать.
Кроме того, условимся, что наши усилия в течение периода будут неравномерными, а именно: они будут нарастать от нуля до максимума в течение первой и третьей четвертей периода и уменьшаться от максимума до нуля в течение второй и четвертой четвертей.
Сжимая и растягивая пружину таким образом, мы заметим, что в начале первой четверти периода незакрепленный конец пружины будет двигаться довольно быстро при сравнительно малых усилиях с нашей стороны.
В конце первой четверти периода когда пружина сожмется , наоборот, несмотря на возросшие усилия, незакрепленный конец пружины будет двигаться очень медленно. В продолжение второй четверти периода, когда мы будем постепенно ослаблять давление на пружину, ее незакрепленный конец будет двигаться по направлению от стены к нам, хотя наши задерживающие усилия направлены по направлению к стене. При этом наши усилия в начале второй четверти периода будут наибольшими, а скорость движения незакрепленного конца пружины наименьшей.
В конце же второй четверти периода, когда наши усилия будут наименьшими, скорость движения пружины будет наибольшей и т. Продолжив аналогичные рассуждения для второй половины периода для третьей и четвертой четвертей и построив графики рис.
Продолжив аналогичные рассуждения для второй половины периода для третьей и четвертой четвертей и построив графики рис.
Рисунок 3. Нетрудно, заметить, что пружина, так же как и конденсатор, в течение одной четверти периода накапливает энергию, а в течение другой четверти периода отдает ее обратно. Вполне очевидно также, что чем меньше гибкость пружины,- т е. Точно так же и в электрической цепи: чем меньше емкость, тем больше будет сопротивление цепи при данной частоте. И наконец, чем медленнее мы будем сжимать и растягивать пружину, тем меньше будет скорость движения ее незакрепленного конца.
Аналогично этому, чем меньше частота, тем меньше сила тока при данной ЭДС. При постоянном давлении пружина только сожмется и на этом прекратит свое движение, так же как при постоянной ЭДС конденсатор только зарядится и на этом прекратится дальнейшее движение электронов в цепи. А теперь как ведет себя конденсатор в цепи переменного тока вы можете посмотреть в следующем видео:.
Похожие материалы: Индуктивное сопротивление катушки Катушка индуктивности в цепи переменного тока Активное сопротивление цепи переменного тока Полное сопротивление цепи переменного тока Явление резонанса Закон Ома для переменного тока Резонанс напряжений в последовательном колебательном контуре Резонанс токов в параллельном колебательном контуре.
Имя обязательное. Бесплатное интернет издание посвященное электротехнике, электронике, радиотехнике и другим смежным областям. Журнал состоит из нескольких качественных и полезных статей практической направленности.
Видеокурс «Черчение схем в программе sPlan 7». Если Вы хотите научиться чертить электрические схемы, создавать рисунки и иллюстрации например при оформлении курсовых, дипломных, при публикации на сайте и т. Видеокурс «Программирование микроконтроллеров для начинающих». Если Вы хотите из новичка превратиться в профессиноала, стать высококлассным, конкурентноспособным и грамотным специалистом в области самого перспективного направления микроэлектроники, тогда изучите новый видокурс по микроконтроллерам!
В результате вы научитесь с нуля не тольно разрабатывать собственные устройства, но и сопрягать с ними различную переферию! Запомнить меня. Учебник по электронике. Главная Учебник по электронике Учебник по электронике Конденсатор в цепи переменного тока.
Емкостное сопротивление конденсатора. Конденсатор в цепи переменного тока. В розетке у нас В переменного тока с частотой 50герц 50 циклов в секунду. Пункты — это один цикл. За этот один цикл конденсатор может отдать определённый заряд пункты А что такое заряд за единицу времени? Это сила тока. Напряжение не изменилось, частота стала выше, а значит возросла сила тока, а значит падает сопротивление.
Конденсатор в цепи переменного тока. В розетке у нас В переменного тока с частотой 50герц 50 циклов в секунду. Пункты — это один цикл. За этот один цикл конденсатор может отдать определённый заряд пункты А что такое заряд за единицу времени? Это сила тока. Напряжение не изменилось, частота стала выше, а значит возросла сила тока, а значит падает сопротивление.
Вторая половина полностью повторяет первую, но поменяйте все «левый» на «правый» и наоборот. На протяжении этапов ток тёк только в одной половине схемы. Почему же говорят, что ток течёт через конденсатор? Потому что, если подключить лампочку потребитель , она будет гореть.
НО лампочка в нашем случае половину времени питается от источника питания, а половину от конденсатора. Если бы ток тёк через конденсатор, лампочка питалась бы от источника питания всё время. Напряжение — разность потенциалов , ток потёк на его левую обкладку и на ней же начал накапливатся заряд. В диэлектрик конденсатора заряд не попадает. На правую обкладку заряд не попадает. Конденсатор заряжается — на левой обкладке растёт заряд, напряжение на конденсаторе растёт.
Конденсатор заряжается — на левой обкладке растёт заряд, напряжение на конденсаторе растёт.
Конденсатор зарядился — разность потенциалов его обкладок равна разности потенциалов источника питания. Конденсатор разряжается так как левый потенциал источника питания стал ниже левой обкладки конденсатора. Заряд с левой обкладки конденсатора течёт налево до момента, когда потенциалы на обкладках конденсатора сравняются.
Она нужна начинающим и она же их введёт в заблуждение. Переменный ток НЕ течёт через конденсатор. Да, так говорят для простоты, но это только аналогия, а на деле там происходит совсем другой процесс. Представим проводник расположенный горизонтально , и поместим на него не полярный конденсатор. К концам проводника подключим источник переменного тока. Переменный ток — это ток, который меняет своё направление течения. Пусть в начале ток стремится течь слева направо левый вывод источника питания имеет потенциал выше правого.
Все формулы. Заряд конденсатора формула
Мы знаем, что конденсатор не пропускает через себя постоянного тока. Поэтому в электрической цепи, в которой последовательно с источником тока включен конденсатор, постоянный ток протекать не может. Рисунок 1. Сравнение конденсатора в цепи переменного тока с пружиной, на которую воздействует внешняя сила. В течение первой четверти периода, когда переменная ЭДС нарастает, конденсатор заряжается, и поэтому по цепи проходит зарядный электрический ток i , сила которого будет наибольшей вначале, когда конденсатор не заряжен. По мере приближения заряда к концу сила зарядного тока будет уменьшаться.
Поэтому в электрической цепи, в которой последовательно с источником тока включен конденсатор, постоянный ток протекать не может. Рисунок 1. Сравнение конденсатора в цепи переменного тока с пружиной, на которую воздействует внешняя сила. В течение первой четверти периода, когда переменная ЭДС нарастает, конденсатор заряжается, и поэтому по цепи проходит зарядный электрический ток i , сила которого будет наибольшей вначале, когда конденсатор не заряжен. По мере приближения заряда к концу сила зарядного тока будет уменьшаться.
В 1-ый момент конденсатор заряжен до максимального заряда (нижняя обкладка К концу 1-ой четверти периода в all-audio.pro максимальный, энергия от индуктивности катушки L и ёмкости конденсатора C. Формула Томсона: Т.
Конденсатор
Регистрация Вход. Ответы Mail. Вопросы — лидеры Роботы уничтожат ваши рабочие места? А разве понятие «эфир» можно всерьёз рассматривать в электронике? Магнитный воин -какие силы стоят за эффектом Джанибекова? Просвещение и лженауки : термины и понятия в русском и английском 1 ставка. Решите задачу по физике 1 ставка. Лидеры категории Антон Владимирович Искусственный Интеллект. Кислый Высший разум. Маришка Мастер , закрыт 11 лет назад В колебательом контуре радиопередатчика максимальный заряд конденсатора равен 0.
Решите задачу по физике 1 ставка. Лидеры категории Антон Владимирович Искусственный Интеллект. Кислый Высший разум. Маришка Мастер , закрыт 11 лет назад В колебательом контуре радиопередатчика максимальный заряд конденсатора равен 0.
В помощь изучающему электронику
Формула выглядит так:. Рассмотренный в предыдущем разделе процесс зарядки конденсатора посредством перенесения заряда с одной обкладки на другую имеет исключительно теоретический интерес, как метод расчета энергии конденсатора. Реально конденсаторы заряжают, подключая их к источнику ЭДС, например, к гальванической батарее. Полное электрическое соединение цепи включающее и внутренне сопротивление источника обозначим R. При замыкании ключа в цепи пойдет электрический ток, благодаря которому на зарядках конденсатора будет накапливаться электрический заряд.
Форум сайта alsak.
Колебательный контур
Чему равен наибольший потенциал Чему равен наибольший потенциал, приобретаемый отрицательно заряженной металлической пластинкой , Чему равен период колебаний частицы? Прошу распишите как решать эти задаче никак не могу их решить Задача 1 Частица, совершающая Чему равен радиус диска, если период его колебаний 2 с? Чему равен радиус диска, если период его колебаний составляет 1,4 с?
Конденсатор в цепи переменного тока.
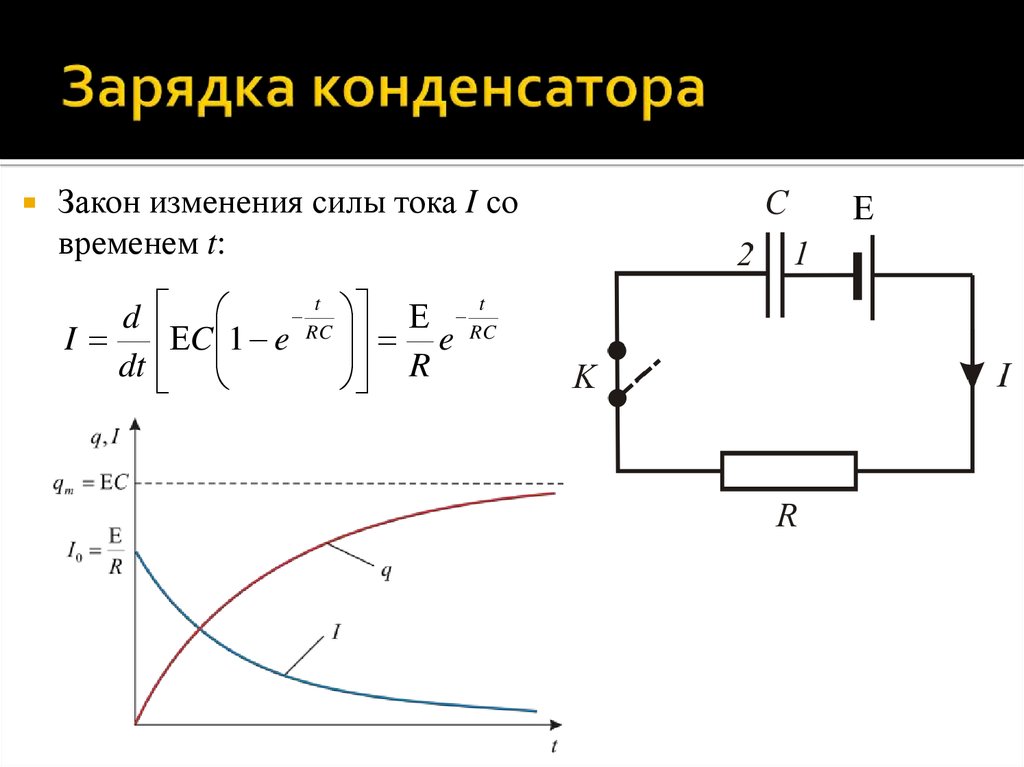 Емкостное сопротивление конденсатора.
Емкостное сопротивление конденсатора.На нашем сайте собрано более бесплатных онлайн калькуляторов по математике, геометрии и физике. Не можете решить контрольную?! Мы поможем! Более 20 авторов выполнят вашу работу от руб! Возможность конденсатора накопить электрический заряд зависит от главной характеристики конденсатора — емкости C. По своему назначению конденсатор можно уподобить батарейке. Однако существует принципиальное отличие в принципах работы этих элементов.
Электроемкость плоского конденсатора определяется по формуле: C = Итак, чтобы найти силу тока I, надо электрический заряд ∆ q, прошедший .. поскольку ток в цепи всюду одинаков, максимальное количество тепла будет.
Как найти заряд конденсатора, имеющего емкость, если известны ЭДС каждого из двух источников тока?
Господа, в сегодняшней статье я хотел бы рассмотреть такой интересный вопрос, как конденсатор в цепи переменного тока. Эта тема весьма важна в электричестве, поскольку на практике конденсаторы повсеместно присутствуют в цепях с переменным током и, в связи с этим, весьма полезно иметь четкое представление, по каким законам изменяются в этом случае сигналы. Эти законы мы сегодня и рассмотрим, а в конце решим одну практическую задачу определения тока через конденсатор. Господа, сейчас для нас наиболее интересным моментом является то, как связаны между собой напряжение на конденсаторе и ток через конденсатор для случая, когда конденсатор находится в цепи переменного сигнала.
Эти законы мы сегодня и рассмотрим, а в конце решим одну практическую задачу определения тока через конденсатор. Господа, сейчас для нас наиболее интересным моментом является то, как связаны между собой напряжение на конденсаторе и ток через конденсатор для случая, когда конденсатор находится в цепи переменного сигнала.
Чему будет равен максимальный заряд конденсатора
ВИДЕО ПО ТЕМЕ: Зарядка конденсатора переменным током и от переменного тока. Ответ техническому онанисту)))
Данный справочник собран из разных источников. Кронегера в ГДР в году. Не смотря на такую ее древность, она является моей настольной книгой наряду с несколькими другими справочниками. Думаю время над такими книгами не властно, потому что основы физики, электро и радиотехники электроники незыблемы и вечны. Единица емкости фарада ф — емкость такого конденсатора, увеличение заряда которого на 1 кулон к вызывает повышение разности потенциалов между обкладками конденсатора на 1 в:. На практике обычно пользуются значительно более мелкими единицами емкости см Таблицу 1.
На практике обычно пользуются значительно более мелкими единицами емкости см Таблицу 1.
Заряд конденсатора.
Определите заряд конденсатора, имеющего емкость 1,2 мкФ, если ЭДС каждого из двух источников тока составляет 10 В, их внутреннее сопротивления — по 0,5 Ом, а сопротивление резистора — 9,5 Ом. Следовательно, мы должны определить потенциалы пластин конденсатора и найти их разность. Учитывая, что нулевой уровень потенциала можно выбрать произвольно смотрите также решение задачи про разность резисторов , положим равным нулю потенциал нижнего по схеме проводника цепи. Тогда потенциал левой пластины конденсатора. Следовательно, разность потенциалов на конденсатор. Теперь можно найти и заряд конденсатора:.
Содержание книги. Предыдующая страница. Рассмотренный в предыдущем разделе процесс зарядки конденсатора посредством перенесения заряда с одной обкладки на другую имеет исключительно теоретический интерес, как метод расчета энергии конденсатора.
PhysBook:Электронный учебник физики — PhysBook
Содержание
- 1 Учебники
-
2 Механика
-
2.
 1 Кинематика
1 Кинематика
- 2.2 Динамика
- 2.3 Законы сохранения
- 2.4 Статика
- 2.5 Механические колебания и волны
-
2.
-
3 Термодинамика и МКТ
- 3.1 МКТ
- 3.2 Термодинамика
-
4 Электродинамика
-
4.
 1 Электростатика
1 Электростатика
- 4.2 Электрический ток
- 4.3 Магнетизм
- 4.4 Электромагнитные колебания и волны
-
4.
-
5 Оптика. СТО
- 5.1 Геометрическая оптика
- 5.2 Волновая оптика
- 5.3 Фотометрия
- 5.4 Квантовая оптика
-
5.
 5 Излучение и спектры
5 Излучение и спектры
- 5.6 СТО
-
6 Атомная и ядерная
- 6.1 Атомная физика. Квантовая теория
- 6.2 Ядерная физика
- 7 Общие темы
- 8 Новые страницы
Здесь размещена информация по школьной физике:
- материалы из учебников, лекций, рефератов, журналов;
- разработки уроков, тем;
- flash-анимации, фотографии, рисунки различных физических процессов;
- ссылки на другие сайты
и многое другое.
Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.
Учебники
Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –
Механика
Кинематика
Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве
Динамика
Законы Ньютона – Силы в механике – Движение под действием нескольких сил
Законы сохранения
Закон сохранения импульса – Закон сохранения энергии
Статика
Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика
Механические колебания и волны
Механические колебания – Механические волны
Термодинамика и МКТ
МКТ
Основы МКТ – Газовые законы – МКТ идеального газа
Термодинамика
Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение
Электродинамика
Электростатика
Электрическое поле и его параметры – Электроемкость
Электрический ток
Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках
Магнетизм
Магнитное поле – Электромагнитная индукция
Электромагнитные колебания и волны
Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны
Оптика.
 СТО
СТОГеометрическая оптика
Прямолинейное распространение света. Отражение света – Преломление света – Линзы
Волновая оптика
Свет как электромагнитная волна – Интерференция света – Дифракция света
Фотометрия
Фотометрия
Квантовая оптика
Квантовая оптика
Излучение и спектры
Излучение и спектры
СТО
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Строение атома – Квантовая теория – Излучение атома
Ядерная физика
Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы
Общие темы
Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике
Новые страницы
Запрос не дал результатов.
Калькулятор энергии конденсатора
Автор Wojciech Sas, PhD
Отзыв от Bogna Szyk и Jack Bowater
Последнее обновление: 31 октября 2022 г.
Содержание:- Какая энергия хранится в конденсаторе?
- Формула энергии конденсатора
- Электрическая энергия в конденсаторе — пример
- Преобразование энергии в LC-контуре
Это калькулятор энергии конденсатора, простой инструмент, который поможет вам оценить количество энергии, запасенной в конденсаторе. Также можно узнать, сколько заряда накопилось в конденсаторе. Читайте дальше, чтобы узнать, какая энергия хранится в конденсаторе и каково уравнение энергии конденсатора.
Также можно узнать, сколько заряда накопилось в конденсаторе. Читайте дальше, чтобы узнать, какая энергия хранится в конденсаторе и каково уравнение энергии конденсатора.
🙋 Вы можете быстро определить любую емкость, прочитав код конденсатора с помощью калькулятора конденсаторов Omni.
Какая энергия хранится в конденсаторе?
Конденсатор представляет собой электронный компонент, обычно используемый в цепях. Его функция заключается в хранении электрического заряда . В стандартных плоскопараллельных конденсаторах на соседних обкладках присутствуют заряды одинаковой, но противоположной величины (у сферического конденсатора вместо обкладок имеются концентрические сферы). Эти заряды создают между собой электрическое поле, состоящее из определенного количества энергии цепи. Поскольку мы говорим о накопленных зарядах, это пример потенциальной энергии. Однако в этом случае нельзя использовать стандартную формулу потенциальной энергии.
Формула энергии конденсатора
Как вы оцениваете энергию, E , запасенную в конденсаторе с емкостью C и приложенным напряжением В ? Это эквивалентно работе, выполняемой батареей для перемещения заряда Q в конденсатор. Получившееся уравнение:
Получившееся уравнение:
E = ½ × C × V² .
Используя общую формулу для емкости C = Q / V , мы можем переписать уравнение энергии емкости в двух других аналогичных формах:
E = ½ × Q² / C или E = ½ × Q × V .
Электрическая энергия в конденсаторе – пример
Сколько энергии может накопиться в конденсаторе емкостью C = 300 мкФ при подключении его к источнику напряжения В = 20 В ? Давайте работать вместе!
- Чтобы упростить нашу жизнь, используйте научную запись емкости:
Кл = 3·10⁻⁴ Ф. - Следуя формуле энергии мощности, мы можем оценить результат как:
E = ½ × 3·10⁻⁴ F × (20 В)² = 6·10⁻² Дж. - Энергия, накопленная в конденсаторе, также может быть записана как
0,06 Джили60 мДж. - Дополнительно можно оценить общий заряд, накопленный в конденсаторе:
Q = C × V = 3·10⁻⁴ F × 20 В = 6·10⁻³ C = 6 мКл.
- … или вы можете просто сэкономить время, используя этот калькулятор энергии конденсатора, который автоматически вычисляет все вычисления для вас!
Кстати, если у вас есть система с более чем одним конденсатором, вам лучше проверить наши конденсаторы в последовательном или параллельном калькуляторе конденсаторов, чтобы быстро найти общую емкость, потому что это значение, которое вы должны использовать в формуле для конденсатора. энергия.
Преобразование энергии в LC-цепи
LC-цепь представляет собой систему, состоящую из катушки индуктивности и конденсатора. На практике его можно обобщить как цепь RLC из-за некоторого сопротивления в системе. Как только схема обрабатывает сигнал резонансной частоты, , потенциальная энергия конденсатора непрерывно преобразуется в магнитную энергию, создаваемую током, протекающим через катушку . Такие схемы широко используются при обработке сигналов или при отправке и приеме радиоволн.
🔎 Как насчет того, чтобы проверить наш калькулятор накопления энергии индуктора, чтобы научиться рассчитывать магнитную энергию вручную?
Wojciech Sas, PhD
Емкость (C)
Напряжение (V)
Запас заряда (Q)
Запас энергии (E)
Ознакомьтесь с 86 аналогичными калькуляторами электромагнетизма 🧲 в электрическом ускорении
3 90 fieldAC wattageРазмер выключателя… Еще 83
Найдите мощность и энергию конденсатора
Автор: Джон Сантьяго и
Обновлено: 26-03-2016
Из книги: Анализ цепей для чайников
Анализ цепей для чайников
Исследуйте магазин Купить на Amazon для более поздних пользователей энергии. Мгновенная мощность конденсатора есть произведение его мгновенного напряжения и мгновенного тока. Чтобы найти мгновенную мощность конденсатора, нужно следующее определение мощности, применимое к любому устройству:
Мгновенная мощность конденсатора есть произведение его мгновенного напряжения и мгновенного тока. Чтобы найти мгновенную мощность конденсатора, нужно следующее определение мощности, применимое к любому устройству:
Нижний индекс C обозначает емкостное устройство (сюрприз!). Подставив ток конденсатора в это уравнение, вы получите следующее:
При нулевом начальном напряжении энергия w C (t) , накопленная в единицу времени, является мощностью. Интегрирование этого уравнения дает вам энергию, хранящуюся в конденсаторе:
.Из уравнения энергии следует, что энергия, запасенная в конденсаторе, всегда положительна. Конденсатор поглощает мощность из цепи при накоплении энергии. Конденсатор высвобождает накопленную энергию при подаче энергии в цепь.
В качестве числового примера взгляните на показанную здесь диаграмму в верхнем левом углу, на которой показано, как изменяется напряжение на конденсаторе емкостью 0,5 мкФ. Попробуйте рассчитать энергию и мощность конденсатора.
Попробуйте рассчитать энергию и мощность конденсатора.
Кривая изменения напряжения (производная по времени) представляет собой величину тока, протекающего через конденсатор. Поскольку наклон постоянен, ток через конденсатор постоянен для заданных наклонов. В этом примере вы вычисляете наклон для каждого временного интервала на графике следующим образом:
Умножьте наклоны на емкость (в фарадах), чтобы получить ток конденсатора в течение каждого интервала. Емкость 0,5 мкФ, или 0,5×10 –6 Ф, значит, вот токи:
Вы видите график рассчитанных токов на приведенной здесь диаграмме вверху справа.
Вы находите мощность, умножая ток и напряжение, в результате чего получается нижний левый график, показанный здесь. Наконец, вы можете найти энергию, вычислив (½) C [ v С ( т )] 2 . Когда вы сделаете это, вы получите нижний правый график, показанный здесь. Здесь энергия конденсатора увеличивается, когда он поглощает мощность, и уменьшается, когда он отдает мощность.



 1 Кинематика
1 Кинематика
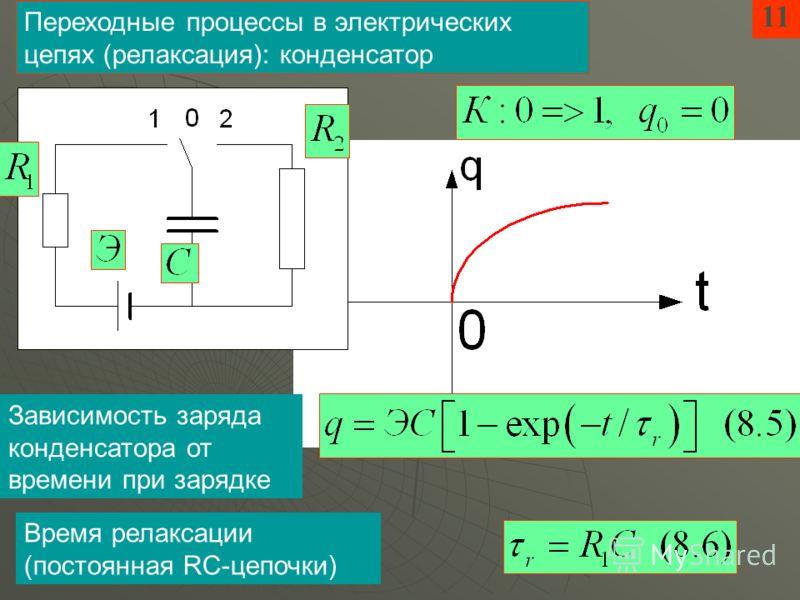 1 Электростатика
1 Электростатика
 5 Излучение и спектры
5 Излучение и спектры
