Квантовая запутанность — Википедия

Ква́нтовая запу́танность^[1][2] — квантовомеханическое явление, при котором квантовые состояния двух или большего числа объектов оказываются взаимозависимыми. Например, можно получить пару фотонов, находящихся в запутанном состоянии, и тогда если при измерении спина первой частицы спиральность оказывается положительной, то спиральность второй всегда оказывается отрицательной, и наоборот.

Такая взаимозависимость сохраняется, даже если эти объекты разнесены в пространстве за пределы любых известных взаимодействий. Измерение параметра одной частицы приводит к мгновенному (выше скорости света) прекращению запутанного состояния другой, что находится в логическом противоречии с принципом локальности (при этом теория относительности не нарушается и информация не передаётся).

Спор Бора и Эйнштейна, ЭПР-Парадокс[править | править код]

На Пятом Сольвеевском конгрессе 1927 года одним из центров дискуссии стал спор Бора и Эйнштейна о принципах Копенгагенской интерпретации квантовой механики

[3], которая, впрочем, ещё не имела этого названия, закрепившегося только в 50-е годы XX века^[4]. Эйнштейн настаивал на сохранении в квантовой физике принципов детерминизма классической физики и на трактовке результатов измерения с точки зрения «несвязанного наблюдателя» (англ. «detached observer»). С другой стороны, Бор настаивал на принципиально недетерминированном (статистическом) характере квантовых явлений и на неустранимости эффекта влияния измерения на само состояние. Как квинтэссенция этих споров часто приводится диалог Эйнштейна с Бором: «— Бог не играет в кости. — Альберт, не указывай Богу, что ему делать.», а также саркастический вопрос Эйнштейна: «Вы действительно считаете, что Луна существует, только когда вы на неё смотрите?»

[5]

В продолжение начавшихся споров в 1935 году Эйнштейн, Подольский и Розен сформулировали ЭПР-парадокс, который должен был показать неполноту предлагаемой модели квантовой механики. Их статья «Можно ли считать квантово-механическое описание физической реальности полным?» была опубликована в № 47 журнала «Physical Review»^[6].

В ЭПР-парадоксе мысленно нарушался принцип неопределённости Гейзенберга: при наличии двух частиц, имеющих общее происхождение, можно измерить состояние одной частицы и по нему предсказать состояние другой, над которой измерение ещё не производилось. Анализируя в том же году подобные теоретически взаимозависимые системы, Шрёдингер назвал их «спутанными» (англ. entangled)

[7]. Позднее англ. entangled и англ. entanglement стали общепринятыми терминами в англоязычных публикациях^[8]. Следует отметить, что сам Шрёдингер считал частицы запутанными, только пока они физически взаимодействовали друг с другом. При удалении за пределы возможных взаимодействий запутанность исчезала^[8] . То есть значение термина у Шрёдингера отличается от того, которое подразумевается в настоящее время.

Эйнштейн не рассматривал ЭПР-парадокс как описание какого-либо действительного физического феномена. Это была именно мысленная конструкция, созданная для демонстрации противоречий принципа неопределённости. В 1947 году в письме Максу Борну он назвал подобную связь между запутанными частицами «жутким дальнодействием» (нем. spukhafte Fernwirkung, англ. spooky action at a distance в переводе Борна)^[9]:

Поэтому я не могу в это поверить, так как (эта) теория непримирима с принципом того, что физика должна отражать реальность во времени и пространстве, без (неких) жутких дальнодействий.

Оригинальный текст (нем.)

Ich kann aber deshalb nicht ernsthaft daran glauben, weil die Theorie mit dem Grundsatz unvereinbar ist, dass die Physik eine Wirklichkeit in Zeit und Raum darstellen soll, ohne spukhafte Fernwirkungen.

— «Entangled systems: new directions in quantum physics»^[10]

Уже в следующем номере «Physical Review» Бор опубликовал свой ответ в статье с таким же заголовком, как и у авторов парадокса^[11]. Сторонники Бора посчитали его ответ удовлетворительным, а сам ЭПР-парадокс — вызванным неправильным пониманием сути «наблюдателя» в квантовой физике Эйнштейном и его сторонниками^[8]. В целом большинство физиков просто устранилось от философских сложностей Копенгагенской интерпретации. Уравнение Шрёдингера работало, предсказания совпадали с результатами, и в рамках позитивизма этого было достаточно. Гриббин пишет по этому поводу

[12]: «чтобы добраться из точки А в точку Б, водителю необязательно знать, что происходит под капотом его машины». Эпиграфом же к своей книге Гриббин поставил слова Фейнмана:

Думаю, я могу ответственно заявить, что никто не понимает квантовую механику. Если есть возможность, прекратите спрашивать себя «Да как же это возможно?» — так как вас занесёт в тупик, из которого ещё никто не выбирался.

Неравенства Белла, экспериментальные проверки неравенств[править | править код]

Предсказываемые теоремой Белла результаты корреляций спина при наличии локального реализма (сплошная линия) и при его отсутствии (точечная синусоида).

Такое состояние дел оказалось не слишком удачным для развития физической теории и практики. «Запутанность» и «жуткие дальнодействия» игнорировались почти 30 лет^[8], пока ими не заинтересовался ирландский физик Джон Белл. Вдохновлённый идеями Бома^[13] (Теория де Бройля — Бома), Белл продолжил анализ ЭПР-парадокса и в 1964 сформулировал свои неравенства^[14][15]. Весьма упрощая математические и физические составляющие, можно сказать, что из работы Белла следовали две однозначно распознаваемые ситуации при статистических измерениях состояний запутанных частиц. Если состояния двух запутанных частиц определённы в момент разделения, то должно выполняться одно неравенство Белла. Если состояния двух запутанных частиц неопределённы до измерения состояния одной из них, то должно выполняться другое неравенство.

Неравенства Белла предоставили теоретическую базу для возможных физических экспериментов, однако по состоянию на 1964 год техническая база не позволяла ещё их поставить. Первые успешные эксперименты по проверке неравенств Белла были осуществлены Клаузером и Фридманом в 1972 году^[16]. Из результатов следовала неопределённость состояния пары запутанных частиц до проведения измерения над одной из них. И всё же вплоть до 1980-х годов большинство физиков рассматривали квантовую сцеплённость «не как новый неклассический ресурс, который можно использовать, а скорее как конфуз, ждущий окончательного разъяснения»

[8].

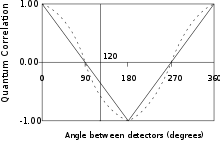
Однако за экспериментами группы Клаузера последовали эксперименты Аспе в 1981 году^[16]. В классическом эксперименте Аспе (см. схему) два потока фотонов с нулевым суммарным спином, вылетавшие из источника S, направлялись на призмы Николя a и b. В них за счёт двойного лучепреломления происходило разделение поляризаций каждого из фотонов на элементарные, после чего пучки направлялись на детекторы

D+ и D-. Сигналы от детекторов через фотоумножители поступали в регистрирующее устройство R, где вычислялось неравенство Белла.

Результаты, полученные как в опытах Фридмана — Клаузера, так и в опытах Аспе, чётко говорили в пользу отсутствия эйнштейновского локального реализма: «жуткое дальнодействие» из мысленного эксперимента окончательно стало физической реальностью. Последний удар по локальности был нанесён в 1989 году многосвязными состояниями Гринбергера — Хорна — Цайлингера (англ.)русск.^[17], заложившими базис квантовой телепортации. В 2010 году Джон Клаузер, Ален Аспе и Антон Цайлингер стали лауреатами премии Вольфа по физике «за фундаментальный концептуальный и экспериментальный вклад в основы квантовой физики, в частности за серию возрастающих по сложности проверок неравенств Белла (или расширенных версий этих неравенств) с использованием запутанных квантовых состояний»

[18].

• Лауреаты премии Вольфа по физике 2010 года
• 

  Джон Клаузер (слева)

• 

• Антон Цайлингер

Современный этап[править | править код]

Современные версии описанного выше эксперимента создают сегменты Sa и Sb такой длины, чтобы регистрация фотонов происходила в заведомо не связанных известными взаимодействиями областях пространства-времени. В 2007 году исследователям из Мичиганского университета удалось разнести запутанные фотоны на рекордное в тот момент расстояние в 1 м^[19][20].

В 2008 году группе швейцарских исследователей из Университета Женевы удалось разнести два потока запутанных фотонов на расстояние 18 километров. Помимо прочего, это позволило произвести временны́е измерения с недостижимой ранее точностью. В результате было установлено, что если некое скрытое взаимодействие и происходит, то скорость его распространения должна как минимум в 100 000 раз превышать скорость света в вакууме. При меньшей скорости временные задержки были бы замечены

[21]^[22].

Летом того же года другой группе исследователей из австрийского Института квантовой оптики и квантовой информации (англ.)русск., включая Цайлингера, удалось поставить ещё более масштабный эксперимент, разнеся потоки запутанных фотонов на 144 километра, между лабораториями на островах Пальма и Тенерифе. Обработка и анализ столь масштабного эксперимента продолжаются, последняя версия отчёта была опубликована в 2010 году^[23][24]. В данном эксперименте удалось исключить возможное влияние недостаточного расстояния между объектами в момент измерения и недостаточной свободы выбора настроек измерения. В результате были ещё раз подтверждены квантовая запутанность и, соответственно, нелокальная природа реальности. Правда, осталось третье возможное влияние — недостаточно полной выборки. Эксперимент, в котором все три потенциальных влияния будут исключены одновременно, на сентябрь 2011 года является вопросом будущего.

В большинстве экспериментов с запутанными частицами используются фотоны. Это объясняется относительной простотой получения запутанных фотонов и их передачи в детекторы, а также бинарной природой измеряемого состояния (положительная или отрицательная спиральность). Однако явление квантовой запутанности существует и для других частиц и их состояний. В 2010 году международный коллектив учёных из Франции, Германии и Испании получил и исследовал^[25][26] запутанные квантовые состояния электронов, то есть частиц с массой, в твёрдом сверхпроводнике из углеродных нанотрубок. В 2011 году исследователям из Института квантовой оптики общества Макса Планка удалось создать состояние квантовой запутанности между отдельным атомом рубидия и конденсатом Бозе-Эйнштейна, разнесёнными на расстояние 30 м^[27][28].

В 2017 г. удалось экспериментально зафиксировать связанные состояния из трёх фотонов внутри облака атомов рубидия, возникающие под действием лазерных импульсов^[29].

Название явления в русскоязычных источниках[править | править код]

При устойчивом английском термине quantum entanglement, достаточно последовательно использующимся в англоязычных публикациях, русскоязычные работы демонстрируют широкое разнообразие узуса. Из встречающихся в источниках по теме терминов можно назвать (в алфавитном порядке):

1. Запутанные квантовые состояния^[30]
2. Квантовая запутанность
3. Квантовая зацепленность^[31]
4. Квантовые корреляции^[32][33] (термин неудачен из-за неоднозначности^[34][35])
5. Квантовая нелокальность^[36]
6. Квантовая перепутанность^[37]
7. Несепарабельность^[38] (как уточнение к «квантовым корреляциям»)
8. Квантовая сцепленность^[1]

В популярной прессе употребляется также выражение «квантовая спутанность»^[39].

Такое разнообразие можно объяснить несколькими причинами, в том числе объективным наличием двух обозначаемых объектов: а) само состояние (англ. quantum entanglement) и б) наблюдаемые эффекты в этом состоянии (англ. spooky action at a distance), которые во многих русскоязычных работах различаются по контексту, а не терминологически.

Получение запутанных квантовых состояний[править | править код]

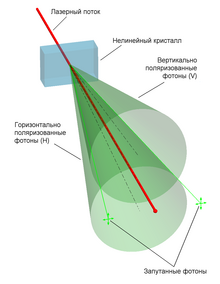
В простейшем случае источником S потоков запутанных фотонов служит определённый нелинейный материал, на который направляется лазерный поток определённой частоты и интенсивности (схема с одним эмиттером)^[40]. В результате спонтанного параметрического рассеяния (СПР) на выходе получаются два конуса поляризации H и V, несущие пары фотонов в запутанном квантовом состоянии (бифотоны)^[41].

подробнее[42]

При СПР типа II под воздействием поляризованного лазерного излучения накачки в кристалле бета-бората бария спонтанно рождаются бифотоны, сумма частот которых равна частоте излучения накачки: ω1 + ω2 = ω а поляризации ортогональны в базисе, определяемом ориентацией кристалла. Благодаря двойному лучепреломлению, при определённых условиях фотоны имеют одну частоту и излучаются вдоль двух конусов, не имеющих общей оси. При этом в одном конусе поляризация вертикальная, а во втором — горизонтальная (по отношению к ориентации кристалла и поляризации излучения накачки). При СПР для волновых векторов также верно k1→+k2→=k→{\displaystyle {\vec {k_{1}}}+{\vec {k_{2}}}={\vec {k}}} поэтому, если забирать один фотон бифотонной пары из одной линии пересечения конусов, то второй фотон можно всегда забрать из второй линии пересечения. В кристалле фотоны разных поляризаций распространяются с разной скоростью, поэтому в реальной экспериментальной установке каждый пучок дополнительно пропускается через такой же кристалл половинной толщины, повёрнутый на 90°. Кроме того, для нивелирования поляризационных эффектов, в одном из пучков вертикальная и горизонтальная поляризации меняются местами при помощи комбинации полуволновой и четвертьволновой пластинок. Создаваемые в результате СПР члены бифотонной пары можно обозначить индексами 1 и 2, при этом: каждый фотон с равной вероятностью может находиться в одном из двух состояний поляризации |x⟩{\displaystyle |x\rangle } или |y⟩{\displaystyle |y\rangle } поляризации фотонов ортогональны, каждый фотон с равной вероятностью может попасть в пучок m или n — это мы назовём пространственным состоянием фотона — мода |m⟩{\displaystyle |m\rangle } и мода |n⟩{\displaystyle |n\rangle } По аналогии с двухщелевым экспериментом два возможных варианта измерений поляризации (после поворота в одном из пучков поляризации одинаковы) можно описать суперпозицией произведений |x⟩1|x⟩2{\displaystyle |x\rangle _{1}|x\rangle _{2}} и |y⟩1|y⟩2{\displaystyle |y\rangle _{1}|y\rangle _{2}}, а возможные варианты измерения пространственных мод |m⟩1|n⟩2{\displaystyle |m\rangle _{1}|n\rangle _{2}} и |n⟩1|m⟩2{\displaystyle |n\rangle _{1}|m\rangle _{2}}. Так как состояние поляризации и пространственные моды независимы друг от друга, то общая волновая функция принимает вид: |Ψ⟩=12(|x⟩1|x⟩2+eiα|y⟩1|y⟩2)⋅12(|m⟩1|n⟩2+eiβ|n⟩1|m⟩2){\displaystyle |\Psi \rangle ={\frac {1}{\sqrt {2}}}(|x\rangle _{1}|x\rangle _{2}+e^{i\alpha }|y\rangle _{1}|y\rangle _{2})\cdot {\frac {1}{\sqrt {2}}}(|m\rangle _{1}|n\rangle _{2}+e^{i\beta }|n\rangle _{1}|m\rangle _{2})} Фотоны являются бозонами, поэтому волновая функция пары фотонов должна быть симметрична относительно перестановки индексов. В результате симметризации получаем: |Ψ⟩=12(|x⟩1|x⟩2+eiϕ|y⟩1|y⟩2)⋅12(|m⟩1|n⟩2+|n⟩1|m⟩2){\displaystyle |\Psi \rangle ={\frac {1}{\sqrt {2}}}(|x\rangle _{1}|x\rangle _{2}+e^{i\phi }|y\rangle _{1}|y\rangle _{2})\cdot {\frac {1}{\sqrt {2}}}(|m\rangle _{1}|n\rangle _{2}+|n\rangle _{1}|m\rangle _{2})} Ориентацией компенсационных кристаллов фазовый множитель eiϕ{\displaystyle e^{i\phi }} можно привести к 1 и мы получаем окончательный вид волновой функции бифотона: |Ψ⟩=12(|x⟩1|x⟩2+|y⟩1|y⟩2)⋅12(|m⟩1|n⟩2+|n⟩1|m⟩2){\displaystyle |\Psi \rangle ={\frac {1}{\sqrt {2}}}(|x\rangle _{1}|x\rangle _{2}+|y\rangle _{1}|y\rangle _{2})\cdot {\frac {1}{\sqrt {2}}}(|m\rangle _{1}|n\rangle _{2}+|n\rangle _{1}|m\rangle _{2})} Множитель, описывающий состояние поляризации, является одним из четырёх белловских максимально запутанных состояний: |Φ+⟩12=12(|x⟩1|x⟩2+|y⟩1|y⟩2){\displaystyle |\Phi ^{+}\rangle _{12}={\frac {1}{\sqrt {2}}}(|x\rangle _{1}|x\rangle _{2}+|y\rangle _{1}|y\rangle _{2})}

Выбор конкретного материала зависит от задач эксперимента, используемой частоты и мощности^[43][44]. В таблице ниже приводятся лишь некоторые часто используемые неорганические нелинейные кристаллы с регулярной доменной структурой (англ.)русск.^[45] (РДС-кристаллы, англ. periodically poled):

Интересным и сравнительно молодым направлением стали нелинейные кристаллы на органической основе^[46][47]. Предполагалось, что органические составляющие живых организмов должны обладать сильными нелинейными свойствами из-за позиций орбиталей в π-связях. Эти предположения подтвердились, и несколькими группами исследователей были получены высококачественные нелинейные кристаллы путём дегидратации насыщенных растворов аминокислот. Некоторые из этих кристаллов:

LMMM из таблицы получается кристаллизацией смеси в пропорции два к одной L-метионина (метаболическое средство) и малеиновой кислоты (пищевая промышленность), то есть из массово производимых веществ. При этом эффективность правильно выращенного кристалла составляет 90 % от более дорогого и труднодоступного неорганического KTP^[47].

«Сверхсветовой коммуникатор» Херберта[править | править код]

Всего через год после эксперимента Аспэ, в 1982 году, американский физик Ник Херберт (англ.)русск. предложил журналу «Foundations of Physics» статью с идеей своего «сверхсветового коммуникатора на основе нового типа квантовых измерений» FLASH (First Laser-Amplified Superluminal Hookup). По позднейшему рассказу Ашера Переса^[48], бывшего в тот момент одним из рецензентов журнала, ошибочность идеи была очевидной, но, к своему удивлению, он не нашёл конкретной физической теоремы, на которую мог бы кратко сослаться. Поэтому он настоял на публикации статьи, так как это «пробудит заметный интерес, а нахождение ошибки приведёт к заметному прогрессу в нашем понимании физики». Статья была напечатана^[49], и в результате развернувшейся дискуссии Вуттерсом, Зуреком (англ.)русск. и Диксом (англ.)русск. была сформулирована и доказана теорема о запрете клонирования. Так излагается история у Переса в его статье, опубликованной 20 лет спустя после описываемых событий.

Теорема о запрете клонирования утверждает невозможность создания идеальной копии произвольного неизвестного квантового состояния. Весьма упрощая ситуацию, можно привести пример с клонированием живых существ. Можно создать идеальную генетическую копию овцы, но нельзя «клонировать» жизнь и судьбу прототипа.

Учёные обычно скептически относятся к проектам со словом «сверхсветовой» в названии. К этому добавился неортодоксальный научный путь самого Херберта. В 1970-х он вместе с приятелем из Xerox PARC сконструировал «метафазовую печатную машинку» для «коммуникации с бесплотными духами»^[50] (результаты интенсивных экспериментов были признаны участниками непоказательными). А в 1985 Херберт написал книгу о метафизическом в физике^[51]. В целом, события 1982 года достаточно сильно скомпрометировали идеи квантовой коммуникации в глазах потенциальных исследователей, и до конца XX века существенного прогресса в этом направлении не наблюдалось.

Квантовая коммуникация[править | править код]

Теория квантовой механики запрещает передачу информации со сверхсветовой скоростью. Это объясняется принципиально вероятностным характером измерений и теоремой о запрете клонирования. Представим разнесённых в пространстве наблюдателей А и Б, у которых имеется по экземпляру квантово-запутанных ящиков с котами Шрёдингера, находящимися в суперпозиции «жив-мёртв». Если в момент t1 наблюдатель А открывает ящик, то его кот равновероятно оказывается либо живым, либо мёртвым. Если живым, то в момент t2 наблюдатель Б открывает свой ящик и находит там мёртвого кота. Проблема в том, что до исходного измерения нет возможности предсказать, у кого именно что окажется, а после один кот жив, другой мёртв, и назад ситуацию не повернуть.

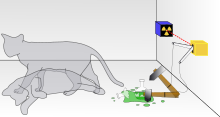
Обход классических ограничений был найден в 2006 году А. Коротковым и Э. Джорданом^[52] из Калифорнийского университета за счёт слабых квантовых измерений (англ. weak quantum measurement). Продолжая аналогию, оказалось, что можно не распахивать ящик, а лишь чуть-чуть приподнять его крышку и подсмотреть в щёлку. Если состояние кота неудовлетворительно, то крышку можно сразу захлопнуть и попробовать ещё раз. В 2008 году другая группа исследователей из Калифорнийского университета объявила об успешной экспериментальной проверке данной теории. «Реинкарнация» кота Шрёдингера стала возможной. Наблюдатель А теперь может приоткрывать и закрывать крышку ящика, пока не убедится, что у наблюдателя Б кот окажется в нужном состоянии.^[53][54][55]

Открытие возможности «обратного коллапса» во многом перевернуло представления о базовых принципах квантовой механики:

Профессор Влатко Ведрал, Оксфордский университет: «Теперь мы даже не можем сказать, что измерения формируют реальность, — ведь можно элиминировать эффекты замеров и начать всё заново»

Профессор Шлоссхауэр, университет Мельбурна: «Квантовый мир стал ещё более хрупким, а реальность ещё более таинственной».

Возникла идея не просто передачи потоков запутанных частиц в разнесённые в пространстве приёмники, но и хранения таких частиц неопределённо долгое время в приёмниках в состоянии суперпозиции для «последующего использования». Ещё из работ Раньяды 1990 года^[56] было известно о таких расслоениях Хопфа, которые могли быть топологическими решениями уравнений Максвелла. В переводе на обычный язык это означало, что теоретически (математически) могут существовать ситуации, при которых пучок фотонов или отдельный фотон будет бесконечно циркулировать по сложной замкнутой траектории, выписывая тор в пространстве. До недавнего времени это оставалось просто ещё одной

Просто о квантовой запутанности / Habr

Квантовая запутанность – одно из самых сложных понятий в науке, но основные её принципы просты. А если понять её, запутанность открывает путь к лучшему пониманию таких понятий, как множественность миров в квантовой теории.

Чарующей аурой загадочности окутано понятие квантовой запутанности, а также (каким-то образом) связанное с ним требование квантовой теории о необходимости наличия «многих миров». И, тем не менее, по сути своей это научные идеи с приземлённым смыслом и конкретными применениями. Я хотел бы объяснить понятия запутанности и множества миров настолько просто и ясно, насколько знаю их сам.

I

Запутанность считается явлением, уникальным для квантовой механики – но это не так. На самом деле, для начала будет более понятным (хотя это и необычный подход) рассмотреть простую, не квантовую (классическую) версию запутанности. Это позволит нам отделить тонкости, связанные с самой запутанностью, от других странностей квантовой теории.

Запутанность появляется в ситуациях, в которых у нас есть частичная информация о состоянии двух систем. К примеру, нашими системами могут стать два объекта – назовём их каоны. «К» будет обозначать «классические» объекты. Но если вам очень хочется представлять себе что-то конкретное и приятное – представьте, что это пирожные.

Наши каоны будут иметь две формы, квадратную или круглую, и эти формы будут обозначать их возможные состояния. Тогда четырьмя возможными совместными состояниями двух каонов будут: (квадрат, квадрат), (квадрат, круг), (круг, квадрат), (круг, круг). В таблице указана вероятность нахождения системы в одном из четырёх перечисленных состояний.

Мы будем говорить, что каоны «независимы», если знание о состоянии одного из них не даёт нам информации о состоянии другого. И у этой таблицы есть такое свойство. Если первый каон (пирожное) квадратный, мы всё ещё не знаем форму второго. И наоборот, форма второго ничего не говорит нам о форме первого.

С другой стороны, мы скажем, что два каона запутаны, если информация об одном из них улучшает наши знания о другом. Вторая табличка покажет нам сильную запутанность. В этом случае, если первый каон будет круглым, мы будем знать, что второй тоже круглый. А если первый каон квадратный, то таким же будет и второй. Зная форму одного, мы однозначно определим форму другого.

Квантовая версия запутанности выглядит, по сути, также – это отсутствие независимости. В квантовой теории состояния описываются математическими объектами под названием волновая функция. Правила, объединяющие волновые функции с физическими возможностями, порождают очень интересные сложности, которые мы обсудим позже, но основное понятие о запутанном знании, которое мы продемонстрировали для классического случая, остаётся тем же.

Хотя пирожные нельзя считать квантовыми системами, запутанность квантовых систем возникает естественным путём – например, после столкновений частиц. На практике незапутанные (независимые) состояния можно считать редкими исключениями, поскольку при взаимодействии систем между ними возникают корреляции.

Рассмотрим, к примеру, молекулы. Они состоят из подсистем – конкретно, электронов и ядер. Минимальное энергетическое состояние молекулы, в котором она обычно и находится, представляет собой сильно запутанное состояние электронов и ядра, поскольку расположение этих составляющих частиц никак не будет независимым. При движении ядра электрон движется с ним.

Вернёмся к нашему примеру. Если мы запишем Φ■, Φ● как волновые функции, описывающие систему 1 в её квадратных или круглых состояниях и ψ■, ψ● для волновых функций, описывающих систему 2 в её квадратных или круглых состояниях, тогда в нашем рабочем примере все состояния можно описать, как:

Независимые: Φ■ ψ■ + Φ■ ψ● + Φ● ψ■ + Φ● ψ●

Запутанные: Φ■ ψ■ + Φ● ψ●

Независимую версию также можно записать, как:

(Φ■ + Φ●)(ψ■ + ψ●)

Отметим, как в последнем случае скобки чётко разделяют первую и вторую системы на независимые части.

Существует множество способов создания запутанных состояний. Один из них – измерить составную систему, дающую вам частичную информацию. Можно узнать, например, что две системы договорились быть одной формы, не зная при этом, какую именно форму они выбрали. Это понятие станет важным чуть позже.

Более характерные последствия квантовой запутанности, такие, как эффекты Эйнштейна-Подольского-Розена (EPR) и Гринберга-Хорна-Зейлингера (GHZ), возникают из-за её взаимодействия ещё с одним свойством квантовой теории под названием «принцип дополнительности». Для обсуждения EPR и GHZ позвольте мне сначала представить вам этот принцип.

До этого момента мы представляли, что каоны бывают двух форм (квадратные и круглые). Теперь представим, что ещё они бывают двух цветов – красного и синего. Рассматривая классические системы, например, пирожные, это дополнительное свойство означало бы, что каон может существовать в одном из четырёх возможных состояний: красный квадрат, красный круг, синий квадрат и синий круг.

Но квантовые пирожные – квантожные… Или квантоны… Ведут себя совсем по-другому. То, что квантон в каких-то ситуациях может обладать разной формой и цветом не обязательно означает, что он одновременно обладает как формой, так и цветом. Фактически, здравый смысл, которого требовал Эйнштейн от физической реальности, не соответствует экспериментальным фактам, что мы скоро увидим.

Мы можем измерить форму квантона, но при этом мы потеряем всю информацию о его цвете. Или мы можем измерить цвет, но потеряем информацию о его форме. Согласно квантовой теории, мы не можем одновременно измерить и форму и цвет. Ничей взгляд на квантовую реальность не обладает полнотой; приходится принимать во внимание множество разных и взаимоисключающих картин, у каждой из которых есть своё неполное представление о происходящем. Это и есть суть принципа дополнительности, такая, как её сформулировал Нильс Бор.

В результате квантовая теория заставляет нас быть осмотрительными в приписывании свойствам физической реальности. Во избежание противоречий приходится признать, что:

Не существует свойства, если его не измерили.
Измерение – активный процесс, изменяющий измеряемую систему

II

Теперь опишем две образцовые, но не классические, иллюстрации странностей квантовой теории. Обе были проверены в строгих экспериментах (в реальных экспериментах люди меряют не формы и цвета пирожных, а угловые моменты электронов).

Альберт Эйнштейн, Борис Подольский и Натан Розен (EPR) описали удивительный эффект, возникающий при запутанности двух квантовых систем. EPR-эффект объединяет особую, экспериментально достижимую форму квантовой запутанности с принципом дополнительности.

EPR-пара состоит из двух квантонов, у каждого из которых можно измерить форму или цвет (но не то и другое сразу). Предположим, что у нас есть множество таких пар, все они одинаковые, и мы можем выбирать, какие измерения мы проводим над их компонентами. Если мы измерим форму одного из членов EPR-пары, мы с одинаковой вероятностью получим квадрат или круг. Если измерим цвет, то с одинаковой вероятностью получим красный или синий.

Интересные эффекты, казавшиеся EPR парадоксальными, возникают, когда мы проводим измерения обоих членов пары. Когда мы меряем цвет обоих членов, или их форму, мы обнаруживаем, что результаты всегда совпадают. То есть, если мы обнаружим, что один из них красный и затем меряем цвет второго, мы также обнаруживаем, что он красный – и т.п. С другой стороны, если мы измеряем форму одного и цвет другого, никакой корреляции не наблюдается. То есть, если первый был квадратом, то второй с одинаковой вероятностью может быть синим или красным.

Согласно квантовой теории, мы получим такие результаты, даже если две системы будет разделять огромное расстояние и измерения будут проведены почти одновременно. Выбор типа измерений в одном месте, судя по всему, влияет на состояние системы в другом месте. Это «пугающее дальнодействие», как называл его Эйнштейн, по-видимому, требует передачу информации – в нашем случае, информации о проведённом измерении – со скоростью, превышающей скорость света.

Но так ли это? Пока я не узнаю, какой результат получили вы, я не знаю, чего ожидать мне. Я получаю полезную информацию, когда я узнаю ваш результат, а не когда вы проводите измерение. И любое сообщение, содержащее полученный вами результат, необходимо передать каким-либо физическим способом, медленнее скорости света.

При дальнейшем изучении парадокс ещё больше разрушается. Давайте рассмотрим состояние второй системы, если измерение первой дало красный цвет. Если мы решим мерить цвет второго квантона, мы получим красный. Но по принципу дополнительности, если мы решим измерить его форму, когда он находится в «красном» состоянии, у нас будут равные шансы на получение квадрата или круга. Поэтому, результат EPR логически предопределён. Это просто пересказ принципа дополнительности.

Нет парадокса и в том, что удалённые события коррелируют. Ведь если мы положим одну из двух перчаток из пары в коробки и отправим их в разные концы планеты, неудивительно, что посмотрев в одну коробку, я могу определить, на какую руку предназначена другая перчатка. Точно так же, во всех случаях корреляция пар EPR должна быть зафиксирована на них, когда они находятся рядом и потому они могут выдержать последующее разделение, будто бы имея память. Странность EPR-парадокса не в самой по себе возможности корреляции, а в возможности её сохранения в виде дополнений.

III

Дэниел Гринбергер, Майкл Хорн и Антон Зейлингер открыли ещё один прекрасный пример квантовой запутанности. ОН включает три наших квантона, находящихся в специально подготовленном запутанном состоянии (GHZ-состоянии). Мы распределяем каждый из них разным удалённым экспериментаторам. Каждый из них выбирает, независимо и случайно, измерять ли цвет или форму и записывает результат. Эксперимент повторяют многократно, но всегда с тремя квантонами в GHZ-состоянии.

Каждый отдельно взятый экспериментатор получает случайные результаты. Измеряя форму квантона, он с равной вероятностью получает квадрат или круг; измеряя цвет квантона, он с равной вероятностью получает красный или синий. Пока всё обыденно.

Но когда экспериментаторы собираются вместе и сравнивают результаты, анализ показывает удивительный результат. Допустим, мы будем называть квадратную форму и красный цвет «добрыми», а круги и синий цвет – «злыми». Экспериментаторы обнаруживают, что если двое из них решили измерить форму, а третий – цвет, тогда либо 0, либо 2 результата измерений получаются «злыми» (т.е. круглыми или синими). Но если все трое решают измерить цвет, то либо 1 либо 3 измерения получаются злыми. Это предсказывает квантовая механика, и именно это и происходит.

Вопрос: количество зла чётное или нечётное? В разных измерениях реализовываются обе возможности. Нам приходится отказаться от этого вопроса. Не имеет смысла рассуждать о количестве зла в системе без связи с тем, как его измеряют. И это приводит к противоречиям.

Эффект GHZ, как описывает его физик Сидни Колман, это «оплеуха от квантовой механики». Он разрушает привычное, полученное из опыта ожидание того, что у физических систем есть предопределённые свойства, независимые от их измерения. Если бы это было так, то баланс доброго и злого не зависел бы от выбора типов измерений. После того, как вы примете существование GHZ-эффекта, вы его не забудете, а ваш кругозор будет расширен.

IV

Пока что мы рассуждаем о том, как запутанность не позволяет назначить уникальные независимые состояния нескольким квантонам. Такие же рассуждения применимы к изменениям одного квантона, происходящим со временем.

Мы говорим об «запутанных историях», когда системе невозможно присвоить определённое состояние в каждый момент времени. Так же, как в традиционной запутанности мы исключаем какие-то возможности, мы можем создать и запутанные истории, проводя измерения, собирающие частичную информацию о прошлых событиях. В простейших запутанных историях у нас есть один квантон, изучаемый нами в два разных момента времени. Мы можем представить ситуацию, когда мы определяем, что форма нашего квантона оба раза была квадратной, или круглой оба раза, но при этом остаются возможными обе ситуации. Это темпоральная квантовая аналогия простейшим вариантам запутанности, описанным ранее.

Используя более сложный протокол, мы можем добавить чуть-чуть дополнительности в эту систему, и описать ситуации, вызывающие «многомировое» свойство квантовой теории. Наш квантон можно подготовить в красном состоянии, а затем измерить и получить голубое. И как в предыдущих примерах, мы не можем на постоянной основе присвоить квантону свойство цвета в промежутке между двумя измерениями; нет у него и определённой формы. Такие истории реализовывают, ограниченным, но полностью контролируемым и точным способом, интуицию, свойственную картинке множественности миров в квантовой механике. Определённое состояние может разделиться на две противоречащие друг другу исторические траектории, которые затем снова соединяются.

Эрвин Шрёдингер, основатель квантовой теории, скептически относившийся к её правильности, подчёркивал, что эволюция квантовых систем естественным образом приводит к состояниям, измерение которых может дать чрезвычайно разные результаты. Его мысленный эксперимент с «котом Шрёдингера» постулирует, как известно, квантовую неопределённость, выведенную на уровень влияния на смертность кошачьих. До измерения коту невозможно присвоить свойство жизни (или смерти). Оба, или ни одно из них, существуют вместе в потустороннем мире возможностей.

Повседневный язык плохо приспособлен для объяснения квантовой дополнительности, в частности потому, что повседневный опыт её не включает. Практические кошки взаимодействуют с окружающими молекулами воздуха, и другими предметами, совершенно по-разному, в зависимости от того, живы они или мертвы, поэтому на практике измерение проходит автоматически, и кот продолжает жить (или не жить). Но истории с запутанностью описывают квантоны, являющиеся котятами Шрёдингера. Их полное описание требует, чтобы мы принимали к рассмотрению две взаимоисключающие траектории свойств.

Контролируемая экспериментальная реализация запутанных историй – вещь деликатная, поскольку требует сбора частичной информации о квантонах. Обычные квантовые измерения обычно собирают всю информацию сразу – к примеру, определяют точную форму или точный цвет – вместо того, чтобы несколько раз получить частичную информацию. Но это можно сделать, хотя и с чрезвычайными техническими трудностями. Этим способом мы можем присвоить определённый математический и экспериментальный смысл распространению концепции «множественности миров» в квантовой теории, и продемонстрировать её реальность.

Квантовая запутанность — королева парадоксов — Naked Science

Мир вокруг велик и разнообразен – разнообразен настолько, что на одних масштабах проявляются законы, совершенно немыслимые для других. Законы политики и битломания никак не следуют из устройства атома – для их описания требуются свои «формулы» и свои принципы. Трудно представить, чтобы яблоко – макроскопический объект, поведение которого обычно следует законам ньютоновской механики, – взяло и исчезло, слилось с другим яблоком, превратившись в ананас. А между тем именно такие парадоксальные феномены проявляются на уровне элементарных частиц. Узнав, что это яблоко красное, вряд ли мы сделаем зеленым другое, находящееся где-нибудь на орбите. А между тем именно так действует явление квантовой запутанности, и именно это продемонстрировали китайские физики, с работы которых мы начали наш разговор. Попробуем разобраться, что же это такое и чем может помочь человечеству.

 

Бор, Эйнштейн и другие

 

Мир вокруг локален – иначе говоря, для того чтобы какой-то далекий объект изменился, он должен провзаимодействовать с другим объектом. При этом никакое взаимодействие не может распространяться со скоростью быстрее световой: это и делает физическую реальность локальной. Яблоко не может шлепнуть Ньютона по голове, не добравшись до нее физически. Вспышка на Солнце не может мгновенно сказаться на работе спутников: заряженным частицам придется преодолеть расстояние до Земли и провзаимодействовать с электроникой и частицами атмосферы. Но вот в квантовом мире локальность нарушается. 

 

 

Самым знаменитым из парадоксов мира элементарных частиц можно назвать принцип неопределенности Гейзенберга, согласно которому невозможно точно определить величину обеих «парных» характеристик квантовой системы. Положение в пространстве (координата) или скорость и направление движения (импульс), ток или напряжение, величина электрической или магнитной компоненты поля – все это «взаимодополняющие» параметры, и чем точнее мы измерим один из них, тем менее определенным станет второй.

 

Когда-то именно принцип неопределенности вызвал непонимание Эйнштейна и его знаменитое скептическое возражение «Бог не играет в кости». Однако, похоже, играет: все известные эксперименты, косвенные и прямые наблюдения и расчеты указывают, что принцип неопределенности является следствием фундаментальной недетерменированности нашего мира. И снова мы приходим к несочетанию масштабов и уровней реальности: там, где существуем мы, все вполне определенно: если разжать пальцы и отпустить яблоко, оно упадет, притянутое гравитацией Земли. Но на уровне более глубинном причин и следствий попросту нет, а существует лишь пляска вероятностей.

 

 

Парадоксальность квантово запутанного состояния частиц в том и состоит, что «удар по голове» может произойти ровно одновременно с отрывом яблока от ветки. Запутанность нелокальна, и изменение объекта в одном месте мгновенно – и без всякого очевидного взаимодействия – меняет другой объект совершенно в другом. Теоретически мы можем отнести одну из запутанных частиц хоть на другой конец Вселенной, но все равно стоит нам «коснуться» ее партнера, оставшегося на Земле, и вторая частица откликнется моментально. Самому Эйнштейну поверить в это было непросто, и спор его с Нильсом Бором и коллегами из «лагеря» квантовой механики стал одним из самых увлекательных сюжетов в современной истории науки. «Реальность определенна, – как бы говорили Эйнштейн и его сторонники, – несовершенны лишь наши модели, уравнения и инструменты». «Модели могут быть какими угодно, но сама реальность в основе нашего мира никогда не определена до конца», – возражали адепты квантовой механики. 

 

 

Выступая против ее парадоксов, в 1935 г. Эйнштейн вместе с Борисом Подольским и Натаном Розеном сформулировал свой парадокс. «Ну хорошо, – рассуждали они, – допустим, узнать одновременно координату и импульс частицы невозможно. Но что, если у нас есть две частицы общего происхождения, состояния которых идентичны? Тогда мы можем измерить импульс одной, что даст нам косвенным образом сведения об импульсе другой, и координату другой, что даст знание координаты первой». Такие частицы были чисто умозрительной конструкцией, мысленным экспериментом – возможно, поэтому достойный ответ Нильсу Бору (а точнее, его последователям) удалось найти только 30 лет спустя.

 

Пожалуй, первый призрак квантово-механических парадоксов наблюдал еще Генрих Герц, заметивший, что если электроды разрядника осветить ультрафиолетом, то прохождение искры заметно облегчается. Эксперименты Столетова, Томсона и других великих физиков позволили понять, что происходит это благодаря тому, что под действием излучения вещество испускает электроны. Однако происходит это совершенно не так, как подсказывает логика; например, энергия высвободившихся электронов не будет выше, если мы увеличим интенсивность излучения, зато возрастет, если мы уменьшим его частоту. Увеличивая же эту частоту, мы придем к границе, за которой никакого фотоэффекта вещество не проявляет – этот уровень у разных веществ разный. 

 

Объяснить эти феномены удалось Эйнштейну, за что он и был удостоен Нобелевской премии. Связаны они с квантованием энергии – с тем, что она может передаваться лишь определенными «микропорциями», квантами. Каждый фотон излучения несет определенную энергию, и если ее достаточно, то электрон поглотившего его атома вылетит на свободу. Энергия фотонов обратно пропорциональна длине волны, и при достижении границы фотоэффекта ее уже недостаточно даже для сообщения электрону минимально нужной для выхода энергии. Сегодня это явление встречается нам повсеместно – в виде солнечных батарей, фотоэлементы которых работают именно на основе этого эффекта.

 

Эксперименты, интерпретации, мистика

 

В середине 1960-х Джон Белл заинтересовался проблемой нелокальности в квантовой механике. Ему удалось предложить математическую основу для вполне осуществимого эксперимента, который должен заканчиваться одним из альтернативных результатов. Первый итог «срабатывал», если принцип локальности действительно нарушается, второй – если все-таки он действует всегда и нам придется искать какую-то другую теорию для описания мира частиц. Уже в начале 1970-х такие эксперименты были поставлены Стюартом Фридманом и Джоном Клаузером, а затем – Аленом Аспэном. Упрощенно говоря, задача состояла в создании пар спутанных фотонов и измерении их спинов, одного за другим. Статистические наблюдения показали, что спины оказываются не свободными, а скоррелированными друг с другом. Такие опыты проводятся с тех пор почти непрерывно, все более точные и совершенные – и результат один и тот же. 

 

 

Стоит добавить, что механизм, объясняющий квантовую запутанность, неясен до сих пор, существует лишь явление – и различные интерпретации дают свои объяснения. Так, в многомировой интерпретации квантовой механики запутанные частицы – это лишь проекции возможных состояний одной-единственной частицы в других параллельных вселенных. В транзакционной интерпретации эти частицы связывают стоячие волны времени. Для «квантовых мистиков» феномен запутанности – еще один повод рассматривать парадоксальный базис мира как способ объяснения всему непонятному, от самих элементарных частиц до человеческого сознания. Мистиков можно понять: если вдуматься, то от последствий кружится голова. 

 

Простой опыт Клаузера–Фридмана указывает на то, что локальность физического мира в масштабе элементарных частиц может нарушаться, и сама основа реальности оказывается – к ужасу Эйнштейна – расплывчатой и неопределенной. Это не значит, что взаимодействие или информация могут передаваться мгновенно, за счет запутанности. Разнесение запутанных частиц в пространстве идет с обычной скоростью, результаты измерения случайны, и пока мы не измерим одну частицу, вторая не будет содержать никакой информации о будущем результате. С точки зрения получателя второй частицы, результат совершенно случаен. Почему же все это нас интересует?

 

Как запутать частицы: возьмите кристалл с нелинейными оптическими свойствами – то есть такой, взаимодействие света с которым зависит от интенсивности этого света. Например, триборат лития, бета-борат бария, ниобат калия. Облучите его лазером подходящей длины волны – и высокоэнергетические фотоны лазерного излучения будут иногда распадаться на пары запутанных фотонов меньшей энергии (это явление называется «спонтанным параметрическим рассеянием») и поляризованных в перпендикулярных плоскостях. Остается удержать запутанные частицы в целости и разнести как можно дальше друг от друга.

 

Кажется, при разговоре о принципе неопределенности мы уронили яблоко? Поднимите его и бросьте об стену – разумеется, оно разобьется, ведь в макромире не работает еще один квантово-механический парадокс – туннелирование. При туннелировании частица способна преодолевать энергетический барьер более высокий, чем ее собственная энергия. Аналогия с яблоком и стеной, конечно, очень приблизительная, зато наглядная: туннельный эффект позволяет фотонам проникать внутрь отражающей среды, а электронам – «не замечать» тонкой пленки оксида алюминия, которая покрывает провода и вообще-то является диэлектриком.

 

Наша бытовая логика и законы классической физики к квантовым парадоксам не слишком-то приложимы, но они все равно работают и широко применяются в технике. Физики как будто (временно) решили: пусть мы пока не знаем до конца, как это работает, но пользу из этого можно извлечь уже сегодня. Туннельный эффект лежит в основе работы некоторых современных микрочипов – в виде туннельных диодов и транзисторов, туннельных переходов и т. д. И, конечно, нельзя забывать о сканирующих туннельных микроскопах, в которых туннелирование частиц обеспечивает наблюдение за отдельными молекулами и атомами – и даже манипуляцию ими.

 

Коммуникация, телепортация и спутник

 

В самом деле, давайте представим, что мы «квантово запутали» два яблока: если первое яблоко окажется красным, то второе обязательно зеленым, и наоборот. Мы можем отправить одно из Петербурга в Москву, сохранив их спутанное состояние, но это, казалось бы, все. Только когда в Петербурге яблоко будет измерено как красное, второе станет зеленым в Москве. До момента измерения возможности предсказать состояние яблока нет, потому что (все те же парадоксы!) самого определенного состояния они не имеют. Какой же в этом запутывании толк?.. А толк нашелся уже в 2000‑х, когда Эндрю Джордан и Александр Коротков, опираясь на идеи советских физиков, нашли способ как бы «не до конца» измерять, а значит, и фиксировать состояния частиц. 

 

 

Используя «слабые квантовые измерения», можно как бы взглянуть на яблоко вполглаза, мельком, стараясь угадать его цвет. Можно проделывать такое снова и снова, фактически не посмотрев на яблоко как следует, но вполне уверенно определиться с тем, что оно, например, красное, а значит, спутанное с ним яблоко в Москве будет зеленым. Это позволяет использовать спутанные частицы снова и снова, а предложенные около 10 лет назад методы позволяют хранить их, запустив бегать по кругу неопределенно долгое время. Остается унести одну из частиц подальше – и получить исключительно полезную систему. 

 

Откровенно говоря, создается ощущение, что пользы в запутанных частицах куда больше, чем принято думать, просто наша скудная фантазия, скованная все тем же макроскопическим масштабом реальности, не позволяет придумать им настоящие применения. Впрочем, и уже существующие предложения вполне фантастичны. Так, на основе спутанных частиц можно организовать канал для квантовой телепортации, полного «считывания» квантового состояния одного объекта и «записи» его в другой, как если бы первый просто перенесся на соответствующее расстояние. Более реалистичны перспективы квантовой криптографии, алгоритмы которой обещают почти «невзламываемые» каналы связи: любое вмешательство в их работу скажется на состоянии запутанных частиц и будет тут же замечено владельцем. Тут-то на сцену и выходит китайский эксперимент QESS (Quantum Experiments at Space Scale – «Квантовые эксперименты в космическом масштабе»).

 

Компьютеры и спутники

 

Проблема в том, что на Земле трудно создать надежную связь для разнесенных на большое расстояние запутанных частиц. Даже в самом совершенном оптоволокне, по которому идет передача фотонов, сигнал постепенно затухает, а требования к нему здесь особенно высокие. Китайские ученые даже подсчитали, что если создавать запутанные фотоны и рассылать их в две стороны с плечами длиной около 600 км – по половине расстояния от центра квантовой науки в Дэлинхе до центров в Шэньчжэне и Лицзяне, – то можно рассчитывать поймать по спутанной паре примерно за 30 тыс. лет. Иное дело космос, в глубоком вакууме которого фотоны пролетают такое расстояние, не встречая каких-либо преград. И тут на сцену выходит экспериментальный спутник Mozi («Мо-Цзы»). 

 

 

На космическом орбитальном аппарате установили источник (лазер и нелинейный кристалл), каждую секунду выдававший несколько миллионов пар запутанных фотонов. С дистанции от 500 до 1700 км одни эти фотоны направлялись в наземную обсерваторию в Дэлинхе на Тибете, а вторые – в Шэньчжэне и Лицзяне на юге Китая. Как и можно было ожидать, основные потери частиц происходили в нижних слоях атмосферы, однако это лишь около 10 км пути каждого пучка фотонов. В результате же канал запутанных частиц покрыл расстояние от Тибета до юга страны – около 1200 км, а в ноябре этого года была открыта новая линия, которая соединяет провинцию Аньхой на востоке с центральной провинцией Хубэй. Пока что каналу не хватает надежности, но это уже дело техники. 

 

В ближайшее время китайцы планируют запуск более совершенных спутников для организации таких каналов и обещают, что уже скоро мы увидим действующую квантовую связь между Пекином и Брюсселем, фактически с одного конца континента до другого. Очередной «невозможный» парадокс квантовой механики обещает очередной скачок в технологиях. 

Нашли опечатку? Выделите фрагмент и нажмите Ctrl + Enter.

Скопировать ссылку

Квантовая запутанность без путаницы — что это такое / Habr

Введение

Появилось много популярных статей, где рассказывается о квантовой запутанности. Опыты с квантовой запутанностью весьма эффектны, но премиями не отмечены. Почему вот такие интересные для обывателя опыты не представляют интереса для учёных? Популярные статьи рассказывают об удивительных свойствах пар запутанных частиц — воздействие на одну приводит к мгновенному изменению состояния второй. И что же такое скрывается за термином «квантовая телепортация», о которой уже начали говорить, что она происходит со сверхсветовой скоростью. Давайте рассмотрим все это с точки зрения нормальной квантовой механики.

Что получается из квантовой механики

Квантовые частицы может находиться в двух типах состояний, согласно классическому учебнику Ландау и Лифшица — чистом и смешанном. Если частица не взаимодействует с другими квантовыми частицами, она описывается волновой функцией, зависящей только от её координат или импульсов — такое состояние называют чистым. В этом случае волновая функция подчиняется уравнению Шредингера. Возможен другой вариант — частица взаимодействует с другими квантовыми частицами. В этом случае волновая функция относится уже ко всей системе взаимодействующих частиц и зависит от всех их динамических переменных. Если мы интересуемся только одной частицей, то её состояние, как показал Ландау ещё 90 лет назад, можно описать матрицей или оператором плотности. Матрица плотности подчиняется уравнению, аналогичному уравнению Шредингера

где — матрица плотности, H — оператор Гамильтона, а скобки обозначают коммутатор.

Его вывел Ландау. Любые физические величины, относящиеся к данной частицы, можно выразить через матрицу плотности. Такое состояние называют смешанным. Если у нас есть система взаимодействующих частиц, то каждая из частиц находится в смешанном состоянии. Если частицы разлетелись на большие расстояния, и взаимодействие исчезло, их состояние все равно останется смешанным. Если же каждая из нескольких частиц находятся в чистом состоянии, то волновая функция такой системы есть произведение волновых функций каждой из частиц (если частицы различны. Для одинаковых частиц, бозонов или фермионов, надо составить симметричную или антисимметричную комбинацию см. [1], но об этом позже. Тождественность частиц, фермионы и бозоны – это уже релятивистская квантовая теория.

Запутанным состоянием пары частиц называется такое состояние, в котором имеется постоянная корреляция между физическими величинами, относящимися к разным частицам. Простой и наиболее часто распространенный пример — сохраняется некая суммарная физическая величина, например, полный спин или момент импульса пары. Пара частиц при этом находится в чистом состоянии, но каждая из частиц — в смешанном. Может показаться, что изменение состояния одной частицы сразу скажется на состоянии другой частицы. Даже если они разлетелись далеко и не взаимодействуют, Именно это высказывается в популярных статьях. Это явление уже окрестили квантовой телепортацией, Некоторые малограмотные журналисты даже утверждают, что изменение происходит мгновенно, то есть распространяется быстрее скорости света.

Рассмотрим это с точки зрения квантовой механики, Во-первых, любое воздействие или измерение, меняющее спин или момент импульса только одной частицы, сразу же нарушает закон сохранения суммарной характеристики. Соответствующий оператор не может коммутировать с полным спином или полным моментом импульса. Таким образом, нарушается первоначальная запутанность состояния пары частиц. Спин или момент второй частицы уже нельзя однозначно связать с таковым для первой. Можно рассмотреть эту проблему с другой стороны. После того, как взаимодействие между частицами исчезло, эволюция матрицы плотности каждый из частиц описывается своим уравнением, в которое динамические переменные другой частицы не входят. Поэтому воздействие на одну частицу не будет менять матрицу плотности другой.

Имеется даже теорема Эберхарда [2], которая утверждает, что взаимное влияние двух частиц невозможно обнаружить измерениями. Пусть имеется квантовая система, которая описывается матрицей плотности. И пусть эта система состоит из двух подсистем A и B. Теорема Эберхарда гласит, что никакое измерение наблюдаемых, связанных только с подсистемой A, не влияет на результат измерения любых наблюдаемых, которые связаны только с подсистемой B. Впрочем, доказательство теоремы использует гипотезу редукции волновой функции, которая не доказана ни теоретически, ни экспериментально. Но все эти рассуждения сделаны в рамках нерелятивистской квантовой механики и относятся к различным, не тождественным частицам.

Эти рассуждения не работают в релятивистской теории в случае пары одинаковых частиц. Еще раз напомню, что тождественность или неразличимость частиц – из релятивистской квантовой механики, где число частиц не сохраняется. Однако для медленных частиц мы можем использовать более простой аппарат нерелятивистской квантовой механики, просто учитывая неразличимость частиц. Тогда волновая функция пары должна быть симметричной (для бозонов) или антисимметричной (для фермионов) по отношению к перестановке частиц. Такое требование возникает в релятивистской теории, независимо от скоростей частиц. Именно это требование приводит к дальнодействующим корреляциям пары одинаковых частиц. В принципе протон с электроном тоже могут находиться в запутанном состоянии. Однако если они разойдутся на несколько десятков ангстрем, то взаимодействие с электромагнитными полями и другими частицами разрушит это состояние. Обменное взаимодействие (так называют это явление) действует на макроскопических расстояниях, как показывают эксперименты. Пара частиц, даже разойдясь на метры, остается неразличимой. Если вы проводите измерение, то вы точно не знаете, к какой частице относится измеряемая величина. Вы проводите измерения с парой частиц одновременно. Поэтому все эффектные эксперименты проводились именно с одинаковыми частицами – электронами и фотонами. Строго говоря, это не совсем то запутанное состояние, которое рассматривают в рамках нерелятивистской квантовой механики, но что-то похожее.

Рассмотрим простейший случай – пара одинаковых невзаимодействующих частиц. Если скорости малы, мы можем пользоваться нерелятивистской квантовой механикой с учетом симметрии волновой функции по отношению к перестановке частиц. Пусть волновая функция первой частицы , второй частицы — , где и — динамические переменные первой и второй частиц, в простейшем случае – просто координаты. Тогда волновая функция пары

Знаки + и – относятся к бозонам и фермионам. Предположим, что частицы находятся далеко друг от друга. Тогда локализованы в удаленных областях 1 и 2 соответственно, то есть вне этих областей они малы. Попробуем вычислить среднее значение какой-нибудь переменной первой частицы, например, координаты. Для простоты можно представить, что в волновые функции входят только координаты. Окажется, что среднее значение координат частицы 1 лежит МЕЖДУ областями 1 и 2, причем оно совпадает со средним значением для частицы 2. Это на самом деле естественно – частицы неразличимы, мы не можем знать, у какой частицы измеряются координаты. Вообще все средние значения у частиц 1 и 2 будут одинаковы. Это значит, что, перемещая область локализации частицы 1 (например, частица локализована внутри дефекта кристаллической решетки, и мы двигаем весь кристалл), мы воздействуем на частицу 2, хотя частицы не взаимодействуют в обычном смысле – через электромагнитное поле, например. Это простой пример релятивистской запутанности.

Никакой мгновенной передачи информации из-за этих корреляций между двумя частицами не происходит. Аппарат релятивистской квантовой теории изначально построен так, что события, находящиеся в пространстве-времени по разные стороны светового конуса, не могут влиять друг на друга. Проще говоря, никакой сигнал, никакое воздействие или возмущение не могут распространяться быстрее света. Обе частицы на самом деле являются состоянием одного поля, например, электрон-позитронного. Воздействуя на поле в одной точке (на частицу 1), мы создаем возмущение, которое распространяется подобно волнам на воде. В нерелятивистской квантовой механике скорость света считается бесконечно большой, оттого возникает иллюзия мгновенного изменения.

Ситуация, когда частицы, разнесенные на большие расстояния, остаются связанными в паре, кажется парадоксальной из-за классических представлений о частицах. Надо помнить, что реально существуют не частицы, а поля. То, что мы представляем, как частицы – просто состояния этих полей. Классическое представление о частицах совершенно непригодно в микромире. Сразу же возникают вопросы о размерах, форме, материале и структуре элементарных частиц. На самом деле ситуации, парадоксальные для классического мышления, возникают и с одной частицей. Например, в опыте Штерна-Герлаха атом водорода пролетает через неоднородное магнитное поле, направленное перпендикулярно скорости. Спином ядра можно пренебречь из-за малости ядерного магнетона, пусть изначально спин электрона направлен вдоль скорости.

Эволюцию волновой функции атома нетрудно рассчитать. Первоначальный локализованный волновой пакет расщепляется на два одинаковых, летящих симметрично под углом к первоначальному направлению. То есть атом, тяжелая частица, обычно рассматриваемая, как классическая с классической траекторией, расщепился на два волновых пакета, которые могут разлететься на вполне макроскопические расстояния. Заодно замечу – из расчета следует, что даже идеальный эксперимент Штерна-Герлаха не в состоянии измерить спин частицы.

Если детектор связывает атом водорода, например, химически, то «половинки» — два разлетевшихся волновых пакета, собираются в один. Как происходит такая локализация размазанной частицы – отдельно существующая теория, в которой я не разбираюсь. Желающие могут найти обширную литературу по этому вопросу.

Заключение

Возникает вопрос – в чем смысл многочисленных опытов по демонстрации корреляций между частицами на больших расстояниях? Кроме подтверждения квантовой механики, в которой давно уже ни один нормальный физик не сомневается, это эффектная демонстрация, производящая впечатление на публику и дилетантов-чиновников, выделяющих средства на науку (например, разработку квантовых линий связи спонсирует Газпромбанк). Для физики эти дорогостоящие демонстрации ничего не дают, хотя позволяют развивать технику эксперимента.

Литература
1. Ландау, Л. Д., Лифшиц, Е. М. Квантовая механика (нерелятивистская теория). — Издание 3-е, переработанное и дополненное. — М.: Наука, 1974. — 752 с. — («Теоретическая физика», том III).
2. Eberhard, P.H., “Bell’s theorem and the different concepts of nonlocality”, Nuovo Cimento 46B, 392-419 (1978)

чего такого пугающего есть в квантовой запутанности? / Habr

Создав два запутанных фотона в существующей системе, а затем разделив их на большое расстояние, мы сможем получить информацию о состоянии одного из них, измерив состояние другого

Квантовая физика полна загадок, печально известных тем, что они противоречат нашей интуиции. Частицы, кажется, знают, смотрите ли вы на них, или нет, и демонстрируют различное поведение, в зависимости от того, наблюдаете вы за ними, или нет, проходя через двойную щель. Измерение одной величины, допустим, положения частицы, создаёт присущую ей неопределённость в дополняющей величине, к примеру, импульсе. А если вы измерите её спин в вертикальном направлении, то уничтожите информацию о спине в горизонтальном направлении. Но самым «пугающим» из всех квантовых явлений будет квантовая запутанность, когда одна частица, кажется, мгновенно «узнаёт», измерили ли спутанного с ней партнёра, даже если это проделают на другом конце Вселенной. На этой неделе мы рассмотрим вопрос читателя, заинтригованного тем, почему это вообще считается загадкой.

С точки зрения фотонов они прошли нулевое расстояние за нулевое время. Так что в этом пугающего? Пока один из них не измерят, они находятся в одном и том же месте и в одно и то же время (если верить им), так что нельзя назвать загадкой то, что они координируют свои состояния.

Разумные рассуждения: замедление времени для быстро двигающихся частиц означает, что они могут координировать свои состояния с любой скоростью. Но эту загадку не так просто решить.


Схема третьего эксперимента Аспе по проверке квантовой нелокальности. Запутанные фотоны из источника отправляются к двум переключателям, направляющим их к поляризующим датчикам. Переключатели очень быстро переключают свои состояния, меняя настройки детектора во время полёта фотонов.

Для начала пройдёмся по вопросу запутанности. Эксперимент обычно проводят с фотонами: вы передаёте один квант света через специальный материал (рассеивающий кристалл), расщепляющий его на два фотона. Эти фотоны будут запутаны в определённом смысле, то есть, если у одного будет спин, внутренний момент импульса, +1, тогда у другого он будет -1. Но у какого какой, нам неизвестно. Можно даже проделать эксперименты, в которых после рассмотрения большого числа фотонов будет видно разницу между
• статистическими результатами в случае, если спин +1,
• статистическими результатами в случае, если спин -1,
• и статистическими результатами в случае, если спин остался неопределённым.

Очень сложно визуализировать эти результаты, но в квантовой механике есть прекрасная аналогия: прохождение частицы через двойную щель.

Если пропускать электроны, фотоны или любые другие частицы через двойную щель, возникает картина интерференции. Но это происходит, только если вы не проверяете, через какую щель они проходят!

Если пропустить частицу через двойную щель – то есть, экран с двумя узкими щелями, находящимися очень близко друг от друга – и она пройдёт сквозь них, вместо того, чтобы быть задержанной экраном, вы легко можете определить, где она окажется с другой стороны. Если вы будете запускать множество частиц по одной через двойную зель, вы обнаружите, что прошедшие через щели частицы формируют интерференционную картину. Иначе говоря, каждая частица ведёт себя не так, будто она прошла через одну или другую щель; она ведёт себя так, будто она прошла через обе щели сразу, проинтерферировала сама с собой на манер волны, и продолжила движение.

Но этот рисунок, демонстрирующий странную квантовомеханическую природу всех частиц Вселенной, появляется, только если вы не определяете, через какую щель проходит частица.

Если вы определяете, через какую щель проходит частица, оставив весь остальной эксперимент без изменений, вы вообще не получаете интерференционную картину.

Если вы вместо этого вы измеряете частицу на проходе через одну из щелей – это можно сделать через установку счётчика – вы не получите интерференционную картину. Вы получите кучу частиц, соответствующую прохождению через щель 1, и кучу для щели 2.

Волновой рисунок электронов, проходящих через двойную щель по одному. Если вы измерите, через какую щель прошёл электрон, вы уничтожаете квантовую интерференционную картину. Отметим, что для создания такой картины требуется больше одного электрона.

Иначе говоря, проводя измерение, определяющее избранный частицей путь, вы меняете результат этого выбора! Для одной частицы вы сможете только определить вероятность прохождения через щель 1, щель 2, или интерференции с самой собой. Для открытия реального состояния вашего эксперимента потребуется больше статистики.

Квантовомеханический тест Белла для частиц с полуцелым спином

Вернёмся к запутанным фотонам. Или вообще к любым запутанным частицам. Вы создаёте две запутанные частицы, у которых вам известна общая сумма их свойств, но не свойства каждой из них. Простейшим примером будет спин – у двух фотонов он получится либо (+1 и -1), либо (-1 и +1), у двух электронов — (+½ и -½) или (-½ и +½) – и вы не знаете, у какого из них будет какой спин, пока не измерите. Вместо щелей можно отправлять их через поляризатор. И как только вы измеряете один, вы определяете другой. Иначе говоря, знаете это мгновенно.

Эксперимент квантового стирания, в котором две запутанных частицы разделяются и измеряются. Никакие действия с одной из частиц в точке назначения не влияют на другую.

«Пугающим» становится тот факт, что в физике ничто другое не происходит мгновенно. Самая большая скорость передачи любого сигнала будет равна с, скорости света в вакууме. Но эти две запутанные частицы можно разделить на метры, километры, астрономические единицы или световые года, и измерение одной из них мгновенно определяет состояние другой. Неважно, двигаются ли запутанные частицы со скоростью света или нет, обладают они массой или нет, много ли у них энергии, и изолируете ли вы их друг от друга, чтобы они не отправляли друг другу фотоны. Нет никаких лазеек, позволяющих скорости взаимодействия в любой системе отсчёта как-то это компенсировать. В конце 1990-х эксперименты с разделением и одновременным измерением этих частиц определили, что если какая-либо информация и передаётся между ними, то она двигается быстрее скорости света в 10000 раз.

Квантовая телепортация, которую часто путают с путешествием быстрее света. В реальности информация быстрее скорости света не передаётся.

Но этого не может быть! В реальности никакой информации не передаётся. Нельзя провести измерение частицы в одном месте и использовать это для передачи чего-либо частице, расположенной очень далеко. Было разработано множество хитроумных схем, задуманных так, чтобы, используя это свойство, передавать информацию быстрее света, но в 1993 году доказали, что этот механизм не допустит передачи информации. Тому есть простое объяснение:

• Если вы измерите «каково состояние имеющейся у меня частицы», вы узнаете состояние другой частицы, но с этой информацией нельзя ничего сделать до тех пор, пока либо вы доберётесь до другой частицы, либо она доберётся до нас, и передача сообщений должна будет идти со скоростью света или медленнее.
• Если же вы заставите имеющуюся у вас частицу принять определённое состояние, это не изменит состояние запутанной частицы. Наоборот, это разрушит запутанность, так что вы не узнаете ничего о второй частице.

[Итан немного не до конца раскрыл суть проблемы. Всё вышеописанное может и не удивить вас, если представить себе аналогию с перчатками. Некто отправил вам одну перчатку из пары, а вашему другу – другую. И вы, открыв свою посылку, мгновенно узнаёте не только то, какую перчатку, левую или правую, вы получили, но и то, какую получил ваш друг. Однако в случае с запутанными частицами состояние «перчаток» изначально не определено. И мы его не просто не знаем или не умеем определять – оно на самом деле определяется случайным образом, и именно в момент измерения одной из «перчаток». Тогда другая «перчатка» мгновенно принимает противоположное состояние. Именно это Эйнштейн и называл «пугающим дальнодействием» / прим. перев.]

Если две частицы запутаны, свойства их волновых функций дополняют друг друга, и измерение одной из них определяет свойства другой. Но является ли волновая функция абстрактным математическим описанием, или же она лежит в основе более глубокой истины Вселенной и детерминистской, фундаментальной реальности – вопрос открытый.

Это философская проблема для реалистов. Это значит, что волновая функция частицы – или запутанная волновая функция нескольких частиц – представляет собой реальный, физический объект, существующий и эволюционирующий во Вселенной, но для этого требуется большое количество неудобных предположений. Нужно предположить, что существует бесконечное число возможных реальностей, и что мы живём только в одной из них, хотя никаких свидетельств о существовании других нет. Если вы инструменталист (как автор; это проще и практичнее), у вас нет этой философской проблемы. Вы просто принимаете, как данность, что волновая функция – это инструмент для расчётов.

Эйнштейн был убеждённым реалистом в вопросах квантовой механики, и это предубеждение он унёс с собой в могилу. Никаких свидетельств в поддержку его интерпретации квантовой механики обнаружено не было, хотя у неё до сих пор есть много приверженцев

Стивен Вайнберг, нобелевский лауреат, сооснователь Стандартной Модели и гениальный во многих областях физик-теоретик, недавно осудил подход инструментализма в журнале Science News, описывая его так:

Это так ужасно, представлять, что у нас нет знаний по поводу всего, что существует – мы можем сказать, что произошло, только проведя измерение.

Но вне зависимости от ваших философских увиливаний, квантовая механика работает, и волновая функция, запутывающая частицы, позволяет разрушать эту запутанность, даже на космических расстояниях. Это единственный мгновенный процесс во Вселенной, известный нам, и поэтому он действительно стоит особняком!

Итан Сигель – астрофизик, популяризатор науки, автор блога Starts With A Bang! Написал книги «За пределами галактики» [Beyond The Galaxy], и «Трекнология: наука Звёздного пути» [Treknology].

Возможна ли мгновенная передача информации? Эксперименты с квантово запутанными частицами

Доброго времени суток всем!
Мы продолжаем рассматривать возможности квантовой механики для передачи информации с использованием корреляции квантово-запутанных частиц. В отличие от классических способов связи, использование квантово запутанных частиц дает потенциальную возможность мгновенно передавать информацию на большие расстояния. Трудность заключается в том, чтобы найти способы кодирования и декодирования передаваемой информации. Данная статья посвящена поиску решений данной задачи и возможности создания экспериментальной установки. Если вас тоже интересует данная задача — добро пожаловать под кат!

Напомню, что в прошлой статье мы рассматривали одну из возможных схем для передачи информации между двумя удаленными объектами. В частности была рассмотрена оптическая схема со светоделителями для получения интерференции, а также схема детектирования и квантового стирания с использованием двух даун-конверторов. В комментариях было множество обсуждений по поводу работоспособности такой схемы, а также критика со стороны хабрапользователей, что применение даун-конверторов приводит к взаимодействию с исходной частицей, сдвигу фаз интерференционного паттерна и прочим неприятным последствиям. Я не исключаю такой возможности, поэтому после детального рассмотрения решил исключить использование даун-конверторов и построить схему с использованием круговых и линейных поляризаторов. Забегая вперед, могу сказать, что у данного решения есть свои трудности, вследствие которых невозможно получить картину интерференции. Для решения этих трудностей мы применим элегантный подход, вытекающий из следствия самой квантовой механики. Я глубоко благодарен всем, кто участвовал в обсуждении прошлой статьи. Ваши доводы и критика помогли мне глубже понять сопутствующие трудности, искать больше информации и находить новые решения.

Для начала рассмотрим реальную экспериментальную установку. Луч лазера попадает на нелинейно-оптическое устройство: кристалл бета-бората бария (BBO), благодаря которому один фотон преобразуется в два запутанных фотона более низкой частоты. Процесс, известен как спонтанное параметрическое рассеяние. Полученная пара фотонов следуют разными путями, один из которых поступает непосредственно на детектор 1, а второй проходит через двойную щель и попадает на детектор 2. Оба детектора подключены к схеме совпадений, гарантируя, что будут учитываться только запутанные пары фотонов. Шаговый двигатель перемещает второй детектор и сканирует целевой область, создавая карту интенсивности, которая формирует знакомую картину интерференции.

Для фотона, проходящего через двойную щель перед каждой щелью помещаются круговые поляризаторы, создающие поляризацию света по часовой стрелке при прохождении одной щели, и поляризацию против часовой стрелки при прохождении другой щели. Фотоны проходящие через поляризатор по часовой стрелке не могут пройти через поляризатор направленный против часовой стрелки. А фотоны проходящие через поляризатор против часовой стрелки, соответственно, не могут пройти через поляризатор направленный по часовой стрелке. Круговые поляризаторы «маркируют» фотоны, разрушая интерференционную картину на втором детекторе (Законы Френеля-Араго).

Далее вводится линейный поляризатор на пути первого фотона, позволяющий получить диагональную поляризацию фотонов. Запутывание обеспечивает также дополнительную диагональную поляризацию в своем партнере, которая проходит через двойную щель. Это меняет эффект круговых поляризаторов — теперь каждый фотон способен пройти через круговые поляризаторы по часовой стрелке и против часовой стрелки. Таким образом, больше невозможно определить по какому пути прошли фотоны, и интерференционные полосы восстанавливаются.

Рассмотрим это подробнее на следующем примере. Представим себе Алису, использующую линейную или круговую поляризацию на первом детекторе мгновенно влияя на результаты измерения Боба на втором детекторе. Предположим, что кристалл BBO производит следующее состояние:

Если Алиса помещает круговой поляризатор перед детектором, который отфильтровывает фотоны с поляризацией по часовой стрелке, то каждый раз, когда Алиса измеряет фотон, соответствующий фотон Боба обязательно имеет поляризацию по часовой стрелки:
Поскольку Боб разместил возле каждой щели противоположные поляризационные фильтры, мы знаем, что эти фотоны могут пройти только (скажем) первую щель. Из этой щели они попадают на экран в соответствии с волновой функцией:
где a — расстояние между прорезями, d — расстояние от щелей до экрана, а x — расстояние до середины экрана. Интенсивность света на экране (количество фотонов) будет пропорциональна квадрату амплитуды этой волны, другими словами
Аналогично, когда Алиса измеряет фотон с поляризацией против часовой стрелки, соответствующий фотон Боба оказывается поляризованным против часовой стрелки, который может проходить только через вторую щель и попадать на экран с волновой функцией
Обратите внимание, что единственным отличием является знак a / 2, потому что фотон испускался из другой щели. На экране мы также увидим пятно, — но это другое пятно, который сдвинут на расстояние a. Здесь есть один важный момент: если Боб никогда не узнает, какую поляризацию применила Алиса, то Боб на самом деле видит на своем экране сумму двух интенсивностей:
поскольку оба они производятся в равных количествах кристаллом. Боб может различать только два пика в своих данных. Только после получения результатов измерения Алисы он сможет увидеть, что для набора фотонов, где Алиса измерила поляризацию по часовой стрелке, подмножество фотонов Боба распределилось согласно а для набора фотонов, где Алиса измеряет поляризацию против часовой стрелки, подмножество фотонов Боба распределилось согласно (два пика и их сумма, когда Алиса измеряет поляризацию фотонов с помощью кругового поляризатора)

Теперь рассмотрим ситуацию, когда Алиса будет использовать линейный поляризатор вместо кругового. Первое, что нужно сделать, это записать волновую функцию системы в терминах состояний линейной поляризации:

При использовании Алисой горизонтального поляризатора, волновая функция фотонов Боба окажется в состоянии суперпозиции поляризации по часовой стрелке и против часовой стрелки. Это означает, что фотон действительно сможет проходить через обе щели! При попадании на экран мы получим амплитуду волны и его интенсивность

где представляет собой разность фаз между двумя волновыми функциями в положении х на экране. Теперь на экране действительно интерференционная картина! Аналогично, если Алиса будет использовать вертикальный поляризатор, то амплитуда волн фотонов Боба равна а интенсивность

И снова на экране возникает интерференционная картина, но она слегка изменилась от предыдущего из-за разности фаз фотонов, пересекающих горизонтальный и вертикальный поляризатор.

Так может ли Алиса послать сообщение Бобу, кодируя свое сообщения с использованием линейных и круговых поляризаторов? К сожалению нет. Так как Бобу не сообщили, какая поляризация была использована Алисой, все, что он видит, является суммой двух интерференций. Следовательно, результат,

снова является пятном.
(два шаблона интерференции и их сумма, когда Алиса измеряет поляризацию фотонов с помощью линейного поляризатора)

Корреляции меняются в зависимости от того, какой эксперимент проводит Алиса. Несмотря на то, что общая картина одинакова, два подмножества в итоге дают радикально разные корреляции: если Алиса использует линейную поляризацию, то полная картина на экране формируется из двух интерференционных картин, а если Алиса использует круговую поляризацию, то картина представляет собой сумму двух пиков.

Чтобы обнаружить интерференцию потребуется изменить данный эксперимент следующим образом: вместо двух щелей с круговыми поляризаторами необходимо будет установить интерферометр Маха Цендера. Рассмотрим подробнее принцип работы данного интерферометра и попробуем узнать, что измениться при его использовании.

ИНТЕРФЕРОМЕТР МАХА ЦЕНДЕРА
На входе интерферометра находится полупрозрачное зеркало, расщепляющее световой поток на два луча. Отражаясь от двух непрозрачных зеркал они сводятся вместе во втором полупрозрачном зеркале. Будь фотон классической частицей то с вероятностью 50% он мог бы пройти через первое полупрозрачное зеркало, и с вероятностью 50% отразится от него.

Допустим, фотон прошел первое полупрозрачное зеркало и двигается по нижней ветке. На втором полупрозрачном зеркале он также может пройти или отразиться с вероятностью 50%. То есть вклад нижней ветки таков: 25% от исходного количества фотонов будут двигаться вверх после второго полупрозрачного зеркала и 25% вниз. Если же фотон отразился на первом полупрозрачном зеркале и пошел по верхней ветке, то на втором полупрозрачном зеркале он тоже может либо пройти либо отразиться. Вклад верхней ветки также будет по 25% вверх и вниз. Общая вероятность есть сумма вкладов от двух веток и составляет 50%, что фотон будет двигаться вверх после прохождения второго полупрозрачного зеркала и 50% что вниз.

Если же провести реальный эксперимент, мы увидим, что все фотоны пройдя прибор будут двигаться вниз. Ни один фотон после второго полупрозрачного зеркала не будет двигаться вверх. Дело в том, что пройдя первое полупрозрачное зеркало фотон будет описываться не классическими вероятностями, а квантовой суперпозицией.

Обозначим базисными кет-векторами со стрелочками два возможных направления движения фотона: вверх и вниз. Тогда изначально фотон будет описываться вектором состояния «вниз». После прохождения первого полупрозрачного зеркала фотон будет в суперпозиции базисных векторов «вверх» и «вниз». Эта суперпозиция является еще одной физической реализацией кубита, наравне со спином электрона и поляризацией фотона.

Квадраты абсолютного значения амплитуд вероятности как раз будут классические вероятности прохождения и отражения фотона. После первого полупрозрачного зеркала они будут совпадать с классическими: 50% что фотон движется вверх и 50% что вниз. После прохождения второго полупрозрачного зеркала амплитуды вероятности изменят свои значения. Причем в рамках квантовой механики можно посчитать, что одна из них будет равна нулю, а другая единице. То есть фотон вернется в состояние, описываемое базисным вектором вниз. Со стопроцентной вероятностью после прохождения второго полупрозрачного зеркала фотон будет двигаться вниз.

На выходе второго полупрозрачного зеркала наблюдается ни что иное как интерференция фотона с самим собой. Если мы попытаемся узнать по какому из плечей интерферометра действительно прошел фотон, то интерференция пропадает.

ЭКСПЕРИМЕНТ
Попробуем разместить круговые поляризаторы в интерферометре Маха Цендера. На одном плече интерферометра установим круговой поляризатор по часовой стрелке. На другом плече установим круговой поляризатор против часовой стрелки. Причем на верхнем плече круговой поляризатор устанавливается непосредственно после полупрозрачного зеркала. На нижнем плече круговой поляризатор устанавливается после отражающего зеркала. Дело в том, что фотон с круговой поляризацией отражаясь от зеркала меняет направление поляризации на противоположный. Поэтому для фотонов, которые не отразились от полупрозрачного зеркала, круговая поляризация устанавливается после отражения от зеркала.

Наличие поляризаторов в интерферометре дает потенциальную возможность определить путь, по которой прошел фотон. Поэтому фотон будет проходит либо по верхнему плечу, либо по нижнему плечу, и никогда не пройдет через оба плеча одновременно. Соответственно мы не наблюдаем интерференцию на выходе. Отсутствие интерференции приводит к тому, что на выходе мы получим 50% фотонов направленных вверх и 50% фотонов направленных вниз.

Ситуация изменится, если использовать квантово-запутанные частицы. Допустим луч лазера попадает на нелинейно-оптическое устройство: кристалл бета-бората бария (BBO), благодаря которому один фотон преобразуется в два запутанных фотона более низкой частоты. Полученная пара фотонов будут следовать разными путями, один из которых проходит поляризатор и попадает непосредственно на детектор 1, а второй проходит через интерферометр с круговыми поляризаторами и попадает на детектор 2 или 3.

Если на пути первого фотона разместить круговой поляризатор мы также не увидим интерференцию. Соответственно, на выходе мы получим 50% фотонов направленных вверх и 50% фотонов направленных вниз.
Но если на пути первого фотона разместить линейный поляризатор расположенный по диагонали, то запутанное состояние обеспечит дополнительную диагональную поляризацию в своем партнере. Наличие дополнительной линейной поляризации позволит фотонам пройти через оба плеча и интерферировать самим собой. При этом интерференция будет иметь разность фаз (фотоны, партнеры которых прошли через линейный поляризатор и партнеры которых не прошли, создадут на экране интерференцию, смещенный друг относительно друга). Несмотря на это, фотон на выходе из второго полупрозрачного зеркала вернется в состояние, описываемое базисным вектором вниз. Поэтому после прохождения второго полупрозрачного зеркала все фотоны будут двигаться вниз.

Такая схема реализации удобна тем, что не требует устанавливать схему совпадений запутанных частиц, выпускать фотоны поодиночке и анализировать положение каждого фотона на экране. Устанавливая или убирая линейный поляризатор на пути запутанных частиц можно моментально влиять на распределение их партнеров между детекторами 2 и 3. Достаточно сравнить интенсивность светового потока в обоих детекторах и определить передаваемый бит информации. Естественно, на выходе кристалла BBO не все фотоны получатся запутанными. Количество запутанных пар будет составлять несколько десятков процентов из общего числа. Но даже небольшое изменение интенсивности света могут быть зафиксированы детекторами, что позволит расшифровать передаваемую информацию. Второй большой плюс состоит в том, что запутанные пары не находятся в состоянии суперпозиции между собой. Это позволяет им взаимодействовать с окружающей средой и при этом не разрушать передаваемую информацию, в отличии от квантовой телепортации, когда взаимодействие с воздухом или оптическим кабелем разрушает волновую функцию фотона.

СОПУТСТВУЮЩИЕ ПРОБЛЕМЫ
Применение такой схем позволит достичь минимальной задержки при передачи информации на большие расстояния. Скорость передачи информации может существенно превосходить скорость света в вакууме. Некоторые утверждают, что СТО/ОТО запрещает передачу информации со скоростью выше скорости света. Идея конечности скорости света была предложена Пуанкаре и получена из формул Максвелла. При этом изначально речь шла об электромагнитном поле, а затем с лёгкой руки Альберта Германовича была распространена на все массивные и безмассовые материальные объекты. Важно подчеркнуть, что об информации речи не было, если открыть любую книжку по СТО/ОТО, информация не присутствует в математическом формализме. Поэтому когда утверждают о том, что СТО/ОТО запрещает передачу информации выше скорости света, делается неявное предположение, что иного способа, кроме как «посадить информацию» на пучок фотонов/электронов и т.д. не существует.

ПРИНЦИП ПРИЧИННОСТИ
Одним из основных проблем мгновенной передачи информации является нарушение принципа причинности. Но можно заметить, что современная физика нигде не требует соблюдения причинности на квантовом уровне, поэтому её среди постулатов физики нет. Существуют квантовые эксперименты, в которых стрела времени вполне может быть повернута вспять. Однако от соблюдения причинности человек пока отказаться не может, т. к. это противоречит нашей логике.

Согласно теории относительности Эйнштейна мгновенная передача информации позволяет получить информацию прежде, чем она будет отправлена. Например, если решим отправить информацию самому себе, то можем провести эксперимент таким образом, чтобы получить информацию до того, как мы его отправим. Допустим, что мы будем передавать информацию с помощью запутанной пары. Тогда один фотон пройдет через интерферометр и попадет на детектор, а второй фотон, например, отправится на Луну, где отразится от зеркала и вернется обратно к нам.

Устанавливая или убирая линейной поляризатор на пути второго фотона, мы можем влиять на результат на выходе интерферометра. Значит, наблюдая за детекторами на выходе интерферометра, мы будем заранее знать, какую информацию решим отправить через 2,5 секунды (время полета фотонов до Луны и обратно). Это может привести к «парадоксу убитой дедушки», когда мы увидели одно значение, а решили отправить противоположное.

Данную проблему позволяет решить теория альтернативных реальностей Хью Эверетта, у которого на сегодняшний день имеется много сторонников. Согласно теории Эверетта, существует бесчисленное множество альтернативных реальностей. При каждой возможности выбора наша реальность делится на несколько альтернативных реальностей, в которых реализуются все возможные варианты выбора. Реальности могут пересекаться и расходится, образуя множество вариантов прошлого и будущего.

По этой теории интерференция на двух щелях – это пересечение двух схожих реальностей без какого либо коллапса волновой функции. В одной реальности фотон проходил через первую щель, в другой реальности фотон проходил через вторую щель. При пересечении двух реальностей получается, что фотон проходил через обе щели. Мы не можем узнать через какую именно щель прошел фотон, потому что прошлое фотона для нас неопределенно. Тоже самое относится к будущему. После излучения фотона мы не можем знать где оно находится. Фотон может находится где угодно, и в каждой версии будущего реализуется один из вероятностей, где траектория фотона точно определена.

Если теория Хью Эверетта верна, то наше решение отправить противоположное значение вместо увиденного не приведет к «парадоксу убитой дедушки». В данном случае мы увидим на экране лишь среднее значение из двух возможных вариантов, по которому уже не сможем определить какую информацию решили отправить себе в будущем. Мы можем отправить любой вариант и это не приведет никаким проблемам.

Проведение реальных экспериментов, возможно, позволят нам получить экспериментальное подтверждение данной теории. Хотя косвенное подтверждение теории уже имеется. Например, существует возможность получить фотографию микроскопических объектов, не возмущая исследуемый объект (т.е. не направляя на объект ни единого фотона). Данное явление активно изучается с целью построения новых типов микроскопов.

ЭНТРОПИЯ
Как мы знаем энтропия – это мера беспорядка. Считается, что течение времени приводит к увеличению энтропии. Значит, прошлое должно иметь меньшую энтропию, чем будущее. И если мы попытаемся вернуться в прошлое, то это приведет к проблеме возросшей энтропией. В действительности энтропия никак не связана с передачей информации, поскольку мы не отправляем в прошлое никакие материальные тела. Поэтому проблему возросшей энтропии термодинамических систем нельзя применять к фотонам.

АНАЛИЗ БУДУЩЕГО
Теория многомировой интерпретации не означает, что нет никакой возможности получить достоверную информацию из будущего. Использование вышеописанной схемы в детерминированных системах позволит получить достоверный прогноз с высокой степенью вероятности. Например, если мы решим узнать «исчезнет ли завтра Луна», то во многих альтернативных вариантах развития событий (расходящихся из нашей сегодняшней реальности) такая вероятность будет минимальна. Соответственно, результаты эксперимента будут указывать преимущественно на один вариант ответа. Можно также получить прогноз погоды с высокой степенью достоверности, минуя огромное количество вычислений в суперкомпьютерах. Возможности применения в области прогнозирования весьма велики. Одним из важных задач для анализа может выступать прогнозирование важнейших решений (например, начало военных действий, и, возможно, ядерный удар по противнику) и анализ их последствий.

Следует отметить, что до реального использования в области прогнозирования будущего еще далеко. Чтобы получить задержку на сутки, потребуется вывести диэлектрическое зеркало на границу Солнечной системы, и изготовить очень качественный лазер с минимальным углом расходимости. Если использовать многократное переотражение луча, то потребуется создание идеально отражающих диэлектрических зеркал. Например, за сутки придется 70000 раз переотразить луч лазера между Землей и Луной. Возможно, решением станет замедление скорости света при помощи сверхохлажденной среды, известной как конденсат Бозе-Эйнштейна. Насколько мне известно, физикам из Роуландовского института научных исследований удалось замедлить скорость света до 17 метров в секунду, а через несколько лет группе ученых из Гарвардского университета удалось даже полностью остановить свет на 10-20 мс.

P.S. К сожалению данная схема оказалась не рабочим, так как при тщательной проверке расчетов выяснилось, что не правильно учитывался фазовый сдвиг при использование квантово-запутанных частиц.

Источники:
Quantum eraser experiment
Интерференция кубита с самим собой
Реально ли многомирие?

Квантовая сцепленность, информация и сигнал / Habr

Издавна мы передаем сигналы при помощи различных носителей информации. Мы использовали сигнальные костры, барабаны, голубей, электричество. И в итоге опять пришли к свету — к передаче информации по оптике. А теперь изучаем сцепленные фотоны. Все мы знаем, что напрямую через квантовую сцепленность передать можно ключ, но не иную информацию. А если не напрямую, но при помощи? Кому интересно, добро пожаловать под кат.

Квантовая сцепленность

Для начала попробую пояснить эффект квантовой сцепленности:

Есть пара носков. Каждый носок из пары сразу после момента создания сцепленности помещен в отдельный ящик и отправлен своему адресату. В момент, когда один из адресатов открывает посылку, он видит правый (или левый) носок и тут же получает информацию о том, какой носок у второго адресата, как бы далеко тот ни находился. Причем заранее точно предсказать, будет ли носок правый или левый, невозможно. А самое главное, что и делает квантовую физику столь отличной от физики классической: пока носки не открыли, они и сами «не знают», какой правый, а какой левый. Но как только один из носков подвергся наблюдению и «определился», второй в тот же момент обретает строго противоположное свойство. Более подробно, с доказательством, можно узнать по запросу «Теорема Белла».

Как видим, передать осмысленную информацию напрямую через это свойство невозможно. Но есть обходной путь.

Принцип передачи носителя информации и сигнала

Итак, квантовому спутнику связи QUESS удалось передать запутанные фотоны между парами обсерваторий, находившихся на расстоянии до 1203 километров. Ученые подтвердили соотношение: одно событие успешной передачи на шесть миллионов отправленных фотонных пар. Соотношение сигнал/шум, казалось бы, не вызывает оптимизма, однако сам факт успешности передачи переводит задачу работы с подобным носителем информации из невозможных в инженерную задачу борьбы избыточности и шума.

Надеюсь, со временем мы придумаем много способов использовать квантовую сцепленность. Опишу один из, по-моему, возможных.

Первый этап: устройство разделяет сцепленные пары и передает на вышки «А» (будущий условно передатчик) и «В» (будущий условно приемник) на хранение запутанные фотоны последовательной цепочкой. Носитель информации передан.

Второй этап: вышка «А» проводит измерение (наблюдение) первого фотона в цепочке, определяя момент начала передачи сообщения, запускает таймер «Т», за время которого проводит измерение тех фотонов в цепочке, которые будут условными единицами и не затрагивает те фотоны, которые будут условным нулем; посредством слабого измерения аппаратура вышки «В» определяет изменение состояния первого фотона и запускает таймер «Т».

Третий этап: по окончании заданного времени «Т» аппаратура вышки «В» фиксирует состояние фотонов в цепочке посредством слабого взаимодействия, где потерявшие сцепленность фотоны — 1, оставшиеся сцепленными — 0.

Так же, например, триггером начала и конца наблюдения цепочки может быть таймер синхронизированного заранее времени.

Таким образом, нас не интересует, каков именно фотон в паре. Нас интересует сам факт: сохранилась сцепленность, или нет. Сигнал передан.

Это концепция из идеального мира, где ни один фотон не потерялся, цепочка была собрана правильно, и так далее. Проблемы реального мира — это проблемы борьбы избыточности и шума, а также сложность в создании систем хранения, воздействия, и контроля частиц.
Но главное — принципиальная возможность передачи сигнала посредством квантовой сцепленности.

Взаимосвязь носителя информации и сигнала

Сама возможность подобного способа работы с сигналом позволяет нам взглянуть на информацию под новым углом. Получается, что в момент передачи носителя информации (цепочки сцепленных частиц) в рамках действующих законов, не быстрее скорости света, мы передаем всю возможную информацию, которую только можно таким образом закодировать.

Приведу аналогию: вы заказали книгу в библиотеке, встречаете курьера, а у него за спиной, невидимые вам, все книги из библиотеки, знаете вы о них, или нет. Вы называете автора и название, забираете свою одну книгу, и остальные тут же уничтожаются.
До следующего курьера из библиотеки.

Еще аналогия: я пишу слово «коса» и у вас в мозгу возникают образы, которые могут быть инициированы этим носителем информации. Однако для передачи сигнала требуется конкретизация: «русая» или «деревянная» или «песчаная». На других языках это сочетание символов «коса» может означать что-то иное, и информация содержится в носителе независимо от того, знаем ли мы ее. Мы просто не имеем уточняющего триггера и памяти для нужного сигнала.

Так и с цепочкой частиц: в момент передачи к вышкам мы передали всю возможную информацию (возможные варианты), оставаясь в рамках знакомой физики, не быстрее скорости света, а фактом измерения лишь произвели уточнение.

В целом, нас ждет увлекательное время в попытках объяснить (и понять), что условный шпион, протащив пару запутанных частиц на объект и нажав в определенное время кнопку (или не нажав, оставив частицы сцепленными) не передал через парные частицы «в штабе» информацию быстрее скорости света. Он пер свою часть информации как улитка на своем горбу. А кнопкой лишь уточнил, выбрал, конкретизировал. Нам еще предстоит разобраться, что он сделал. Но военным понравится. Понравятся шахты, которые невозможно экранировать от команды, и без управляющих проводов. Понравится возможность отдать приказ на любое расстояние, через любые глушилки, на заранее взятый с собой приемник с контейнером частиц. Думаю, именно они, опять, будут двигать технологию.

Или хирург, для которого вышки по всему миру всю ночь накапливали носители информации (запутанные частицы) на разных концах планеты со всем почтением к скорости света, будет делать операцию и видеть мгновенные реакции хирургического робота за десятки тысяч километров от своего кабинета. Он будет потом в интервью говорить, что все происходило мгновенно. А читающий это физик будет ворчать, что вся информация обо всех возможных действиях хирурга была передана еще ночью (с точки зрения физики), с нормальной скоростью. А хирург лишь «уточнил» своими действиями, как именно он прооперировал.

Или взаимодействие информации и, например, свойства локальности мира. Это свойство означает, что событие в одной точке, скажем, планеты не может мгновенно повлиять на физическую действительность в другой точке планеты. Тогда, если условное нажатие кнопки посредством эффекта квантовой запутанности мгновенно зажжет лампочку на другой стороне планеты, значит информация о влияющем событии содержалась в носителе информации до того, как влияющее событие произошло.

Получается, мы находимся на пороге следующего шага эволюции сигнала. При помощи квантового мира мы разделяем скорость прохождения сигнала и скорость распространения носителя информации. Обеспечив запас сцепленных пар с нормальной скоростью, в тот момент, когда критично передать сигнал практически мгновенно, мы можем, пусть пока теоретически, это осуществить.