При прямолинейном равноускоренном движении без начальной скорости
Главная » Компьютеры
На чтение 6 мин Просмотров 250
Содержание
- Случай равномерного движения
- Случай движения без начальной скорости
- Перемещения за последовательные (равные) промежутки времени
- Рассмотренные закономерности на примере задачи
1. По каким формулам рассчитываются проекция и модуль вектора перемещения тела при его равноускоренном движении из состояния покоя?
Исходная расчетная формула проекции вектора перемещения тела, движущегося равноускоренно:
Проекция вектора перемещения тела, движущегося равноускоренно, если его начальная скорость v равна нулю:
Модуль вектора перемещения при прямолинейном равноускоренном движении без начальной скорости прямо пропорционален квадрату промежутка времени, в течение которого это перемещение было совершено:
2. Каковы закономерности равноускоренного движения без начальной скорости ?
Каковы закономерности равноускоренного движения без начальной скорости ?
а)
ОА : ОВ : ОС : OD : 0E = 1 : 4 : 9 : 16 : 25
т. е. при увеличении промежутков времени, отсчитываемых от начала движения, в целое число раз по сравнению с t1, модули соответствующих векторов перемещений возрастают как ряд квадратов последовательных натуральных чисел.
б)
OA : AB : BC : CD : DE = 1 : 3 : 5 : 7 : 9
т. е. модули векторов перемещений, совершаемых телом за последовательные равные промежутки времени (каждый из которых равен t
3. Во сколько раз увеличится модуль вектора перемещения тела при увеличении времени его движения из состояния покоя в n раз?
При увеличении в n раз времени движения, отсчитываемого от момента начала движения, перемещение увеличивается в n 2 раз.
4. Как относятся друг к другу модули векторов перемещений тела, движущегося равноускоренно из состояния покоя, при увеличении времени его движения в целой число раз по сравнению с t1?
При увеличении промежутков времени, отсчитываемых от начала движения, в целое число раз по сравнению с t1, модули соответствующих векторов перемещений возрастают как ряд квадратов последовательных натуральных чисел.
5. Как относятся друг к другу модули векторов перемещений, совершаемых телом за последовательные равные промежутки времени, если это тело движется равноускоренно из состояния покоя?
Модули векторов перемещений, совершаемых телом за последовательные равные промежутки времени, относятся как ряд последовательных нечётных чисел.
6. С какой целью можно использовать эти закономерности?
ОА : ОВ : ОС : OD : ОЕ = 1 : 4 : 9 : 16 : 25
ОА : АВ : ВС : CD : DE = 1 : 3 : 5 : 7 : 9
Вышеуказанные закономерности присущи только равноускоренному движению.
Ими можно пользоваться, если необходимо определить, является движение равноускоренным или нет.
Задача.
Определим, было ли равноускоренным движение улитки, которая:
– за первые 20 с движения переместилась на 0,5 см,
– за вторые 20 с — на 1,5 см,
– за третьи 20 с — на 2,5 см.
Для этого найдём, во сколько раз перемещения, совершённые за второй и третий промежутки времени, больше, чем за первый:
Значит, 0,5 см : 1,5 см : 2,5 см = 1 : 3 : 5.
Поскольку эти отношения представляют собой ряд последовательных нечётных чисел, то движение тела было равноускоренным.
Равноускоренный характер движения был выявлен на основании закономерности:
ОА : АВ : ВС : CD : DE = 1 : 3 : 5 : 7 : 9
- 5 – 9 классы
- Физика
- 8 баллов
При прямолинейном равноускоренном движении без начальной скорости тело тело прошло за первую секунду 3 м.Какой путь пройдет это тело за 2с ?3 с?
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
где – это ускорение.
Примеры равноускоренного движения без начальной скорости
Равноускоренное движение без начальной скорости – важный особый случай равноускоренного движения. Рассмотрим примеры:
1. Свободное падение без начальной скорости. Примером такого движения может быть падение сосульки в конце зимы (рис. 1).
Рис. 1. Падение сосульки
В тот момент, когда сосулька отрывается от крыши, ее начальная скорость равна нулю, после чего она движется равноускоренно, ведь свободное падение – это равноускоренное движение.
2. Старт любого движения. Например, автомобиль трогается с места и разгоняется (рис 2).
Рис. 2. Старт движения
Когда мы говорим, что время набора скорости 100 км/ч у автомобиля той или иной марки, например, 6 с., чаще всего мы говорим о движении равноускоренном без начальной скорости. Аналогично когда мы говорим о старте ракеты и т. д.
3. Особую актуальность равноускоренное движение имеет для разработчиков оружия. Ведь вылет любого снаряда или пули – это движение без начальной скорости, а во время движения в стволе пуля (снаряд) движется равноускоренно. Рассмотрим пример.
Длина автомата Калашникова –
Рис. 3. Иллюстрация к задаче
Для нахождения скорости вылета пули из ствола автомата воспользуемся выражением для перемещения при прямолинейном равноускоренном движении, если неизвестно время:
Движение осуществляется без начальной скорости, а значит,
Читайте также: Как вставить карту памяти в планшет леново
Решение задачи записываем следующим образом с учетом единиц измерения в СИ:
Ответ: .
Равноускоренное движение без начальной скорости часто встречается и в природе, и в технике. Более того, умение работать с таким движением позволяет решать обратные задачи, когда начальная скорость существует, а конечная равна нулю.
Случай равномерного движения
Если , то уравнение, приведенное выше, превратится в уравнение:
Это уравнение дает возможность найти пройденный путь
Случай движения без начальной скорости
Рассмотрим ситуацию, когда – начальная скорость равна нулю. Это значит, что движение начинается из состояния покоя. Тело покоилось, затем начинает приобретать и увеличивать скорость. Движение из состояния покоя будет записываться без начальной скорости:
Если S (проекцию перемещения) обозначить как разность начальной и конечной координаты (), то получится уравнение движения, которое дает возможность определить координату тела для любого момента времени:
Проекция ускорения может быть, как отрицательной, так и положительной, поэтому можно говорить о координате тела, которая может как увеличиваться, так и уменьшаться.
График зависимости скорости от времени
Так как равноускоренное движение без начальной скорости является особым случаем равноускоренного движения, рассмотрим график зависимости проекции скорости от времени для такого движения.
На рис. 4 представлен график зависимости проекции скорости от времени для равноускоренного движения без начальной скорости (график начинается в начале координат).
График устремлен вверх. Это говорит о том, что проекция ускорения положительна
Рис. 4. График зависимости проекции скорости от времени при равноускоренном движении без начальной скорости
Используя график, можно определить проекцию перемещения тела или пройденный путь. Для этого необходимо посчитать площадь фигуры, ограниченной графиком, координатными осями и перпендикуляром, опущенным на ось времени. То есть необходимо найти площадь прямоугольного треугольника (половина произведения катетов)
где – конечная скорость при равноускоренном движении без начальной скорости:
На рис. 5 представлен график зависимости проекции перемещения от времени двух тел для равноускоренного движения без начальной скорости.
5 представлен график зависимости проекции перемещения от времени двух тел для равноускоренного движения без начальной скорости.
Рис. 5 График зависимости проекции перемещения от времени двух тел для равноускоренного движения без начальной скорости
Начальная скорость обоих тел равна нулю, так как вершина параболы совпадает с началом координат:
У первого тела проекция ускорения положительна
Например, если
Читайте также: Почему мясо после варки розовое
Если за единицу времени выбираем некий промежуток, то полные расстояния, пройденные телом за последующие равные промежутки времени, будут относиться как квадраты целых чисел.
Иными словами, перемещения, совершенные телом за каждую последующую секунду, будут относиться как нечетные числа:
Исследованные два очень важных заключения свойственны только прямолинейному равноускоренному движению без начальной скорости.
Задача. Автомобиль начинает двигаться от остановки, т. е. из состояния покоя, и за четвертую секунду своего движения проходит 7 м. Определите ускорение тела и мгновенную скорость через 6 с после начала движения (рис. 8).
е. из состояния покоя, и за четвертую секунду своего движения проходит 7 м. Определите ускорение тела и мгновенную скорость через 6 с после начала движения (рис. 8).
Решение: автомобиль начинает движение из состояния покоя, следовательно, путь, который проходит автомобиль, рассчитывается по формуле: – расстояние, которое автомобиль прошел за четвертую секунду своего движения. Его можно выразить как разность полного пути, пройденного телом за 4 с, и пути, пройденного телом за 3 с (рис. 9).
Рис. 9. Разность полного пути, пройденного телом за 4 с, и пути, пройденного телом за 3 с
Чтобы определить мгновенную скорость, т. е. скорость в конце шестой секунды, следует ускорение умножить на время, т. е. на 6 с, во время которых тело которое продолжало двигаться.
Уравнения, которые сегодня мы использовали в уроке, впервые были исследованы Галилео Галилеем. На следующем уроке мы рассмотрим, как именно были проведены эти опыты.
Белорусский государственный университет транспорта — БелГУТ (БИИЖТ)
Регистрация на конференцию «Проблемы безопасности на транспорте»
Регистрация на конференцию «Тихомировские чтения»
Как поступить в БелГУТ:
дневное, заочное полное,
заочное сокращенное
Как получить место
в общежитии БелГУТа
Как поступить иностранному гражданину
События
Все события
| Пн | Вт | Ср | Чт | Пт | Сб | Вс |
|---|---|---|---|---|---|---|
1 Дата : 2022-09-01 | 2 | 3 | 4 | |||
5 Дата : 2022-09-05 | 6 Дата : 2022-09-06 | 7 Дата : 2022-09-07 | 8 Дата : 2022-09-08 | 9 Дата : 2022-09-09 | 10 Дата : 2022-09-10 | 11 Дата : 2022-09-11 |
12 | 13 | 14 | 15 Дата : 2022-09-15 | 16 Дата : 2022-09-16 | 17 Дата : 2022-09-17 | 18 |
19 | 20 | 21 | 22 | 23 | 24 | 25 |
26 | 27 | 28 | 29 | 30 | ||
Все анонсы
- Матч по мини-футболу между БелГУТом и ГГТУ.
 ..
.. - Велопробег «В единстве — сила»…
- Диалоговая площадка ко Дню народного единства…
- Логистика. Обучение для студентов выпускных курсов…
- ЕДИ «История белорусской государственности – основ…
- Акция «Мы едины» — поем гимн вместе…
- Набор в студию рисунка и живописи…
- Открытая лекция Быченко Олега Владимировича…
- Квиз «Гісторыя майго жыцця»…
- Набор в волонтерский сектор Студсовета…
Анонсы
Университет
Абитуриентам
Студентам
Конференции
Приглашения
Матч по мини-футболу между БелГУТом и ГГТУ…
Велопробег «В единстве — сила»…
Диалоговая площадка ко Дню народного единства…
Логистика. Обучение для студентов выпускных курсов…
Новости
Университет
Международные связи
Спорт
Воспитательная работа
Жизнь студентов
Новости подразделений
- Университет
Проект студента востребован в городе
14 сентября 2022
- Университет
Будущее Беларуси — в единстве
14 сентября 2022
- Университет
Видео-репортаж Дня рождения Гомеля
13 сентября 2022
- Воспитательная работа
Віктарына да Дня народнага адзінства
13 сентября 2022
- Студенческая жизнь
Интервью с участниками открытия фестиваля «Сожскi карагод» и видео-реп.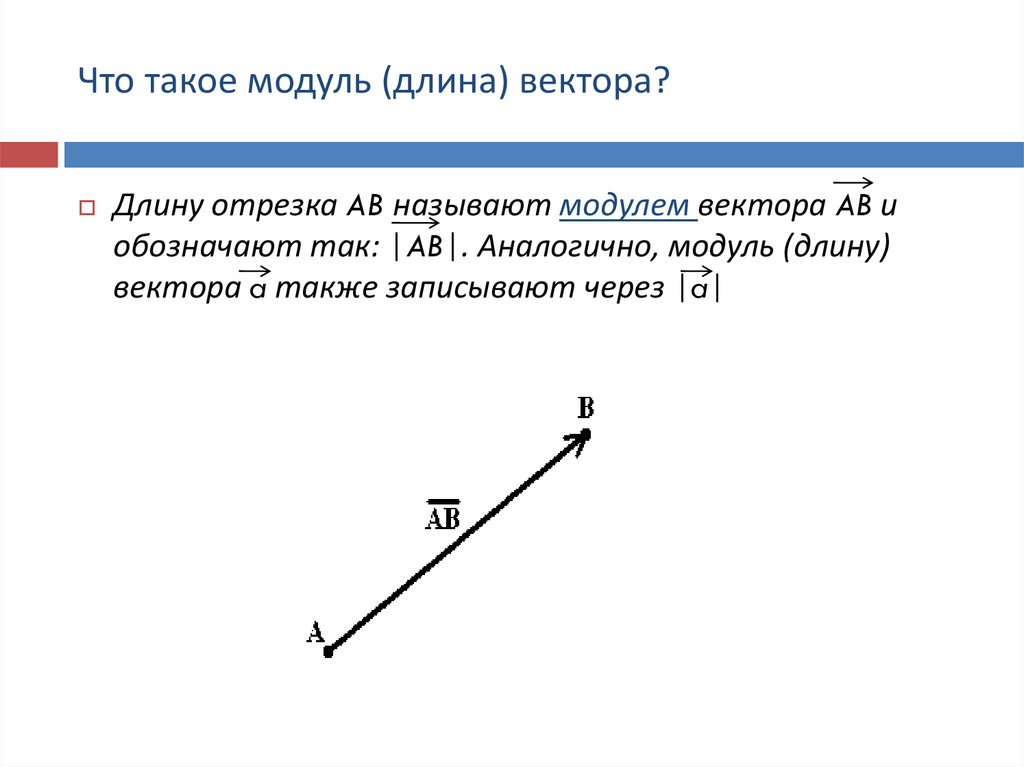 ..
..
13 сентября 2022
- Спорт
Неделя спорта и здоровья
13 сентября 2022
- Университет
Опубликован сборник материалов конференции «Водоснабжение, химия и при…
12 сентября 2022
- Университет
Студент БелГУТа из Марокко рассказывает об учебе в Беларуси…
12 сентября 2022
- Студенческая жизнь
БРСМ — всегда на помощь! День города Гомеля…
12 сентября 2022
Другие новости
- Новый номер газеты «Вести БелГУТа»
- Республиканский легкоатлетический студенческий забег…
- БелГУТ предлагает жилые помещения арендного использования.
 ..
.. - С Днем рождения, Гомель!
- Живой герб Гомеля на открытии «Сожскага карагода» …
- Круглый стол «Вопросы подготовки специалистов в области правовой инфор…
- Встреча первокурсников с инспектором по делам несовершеннолетних желез…
- Атрымай асалоду ад роднай мовы
- Региональный форум «Беларусь адзiная»
- Профилактика правонарушений
- Делегация Самарского государственного университета путей сообщения в Б…
КУДА ПОСТУПАТЬ
Все факультеты
БелГУТ на Доске почета
Достижения университета
Предложения
Все предложения
Видеотека
Все видео
Фотогалерея
Все фото
Урок 2. равномерное прямолинейное движение материальной точки — Физика — 10 класс
Физика, 10 класс
Урок 2. Равномерное прямолинейное движение материальной точки
Перечень вопросов, рассматриваемых в теме: 1) основная задача механики; 2) относительность механического движения; 3) система отсчёта, материальная точка, перемещение, траектория, скорость; 4) кинематическое уравнение.
Глоссарий по теме:
Раздел механики, в котором изучается движение тел без выяснения причин, вызывающих данное движение, называют кинематикой.
Механическим движением тела называется изменение положения тела в пространстве относительно других тел с течением времени.
Материальной точкой называют тело, размерами и формой которого в условиях рассматриваемой задачи можно пренебречь. Тело, относительно которого рассматривается движение, называется телом отсчета. Совокупность тела отсчета, связанной с ним системы координат и часов называют системой отсчета.
Траектория — линия, по которой движется точка в пространстве.
Длину траектории, по которой двигалось тело в течение какого-то промежутка времени, называют путем, пройденным за этот промежуток времени.
Перемещением тела (материальной точки) называется вектор, соединяющий начальное положение тела с его последующим положением.
Равномерное прямолинейное движение – это движение, при котором за любые равные промежутки времени тело совершает равные перемещения.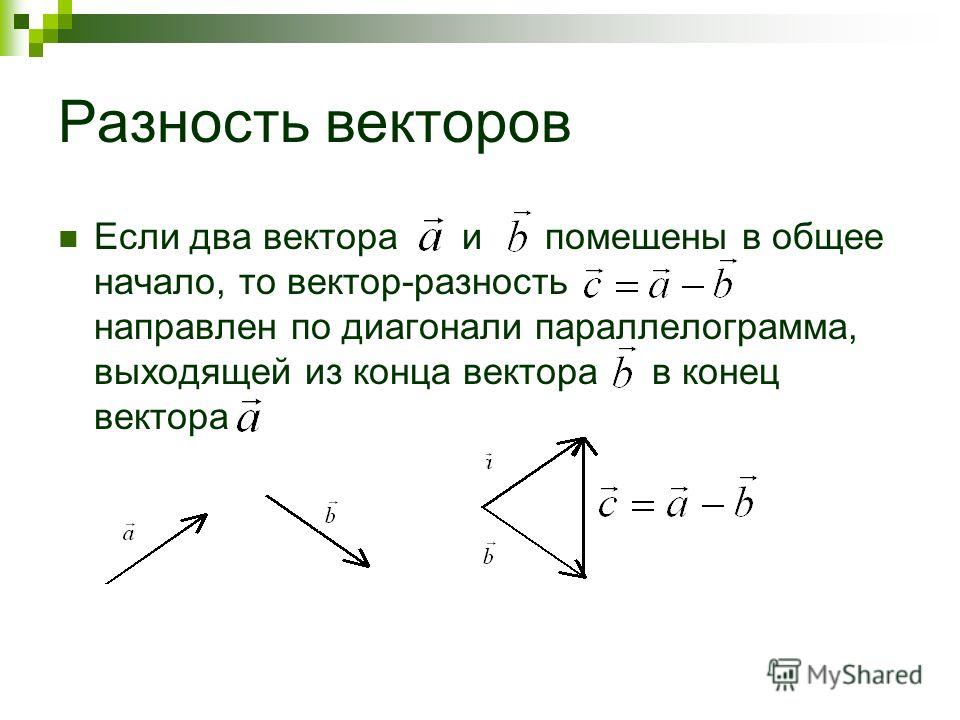
Скорость равномерного прямолинейного движения точки – величина, равная отношению перемещения к промежутку времени, в течение которого это перемещение произошло.
Относительность механического движения – это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта
Основная и дополнительная литература по теме урока:
Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н.. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2016.– С.10-30.
Рымкевич А.П. Сборник задач по физике. 10-11 класс.-М.:Дрофа,2009.
Открытые электронные ресурсы по теме урока:
http://kvant.mccme.ru/1974/12/byvaet_li_ravnomernoe_dvizheni.htm.
Теоретический материал для самостоятельного изучения
Основная задача классической механики — определить положение тела в пространстве в любой момент времени. По характеру решаемых задач классическую механику делят на кинематику, динамику и статику. В кинематике описывают движение тел без выяснения причин, вызывающих данное движение. Раздел механики, в котором изучаются причины движения, называют динамикой. Статика — раздел механики, в котором изучаются условия равновесия абсолютно твердых тел. Законы сохранения импульса и энергии являются следствиями законов Ньютонов.
В кинематике описывают движение тел без выяснения причин, вызывающих данное движение. Раздел механики, в котором изучаются причины движения, называют динамикой. Статика — раздел механики, в котором изучаются условия равновесия абсолютно твердых тел. Законы сохранения импульса и энергии являются следствиями законов Ньютонов.
Механическим движением тела называется изменение положения тела в пространстве относительно других тел с течением времени. Сформулируем закон относительности движения: характер движения тела зависит от того, относительно каких тел мы рассматриваем движение. Нет абсолютно неподвижных тел.
Рассмотрим самое простое движение – прямолинейное равномерное движение. Описать движение тела – это значит, указать способ определения его положения в пространстве в любой момент времени.
Для описания движения нужно ввести некоторые понятия: материальная точка, траектория, путь, перемещение, координата, момент времени, промежуток времени, скорость. Материальной точкой называют тело, размерами которого в условиях рассматриваемой задачи можно пренебречь. Это первая физическая модель реальных тел. Практически всякое тело можно рассматривать как материальную точку в тех случаях, когда расстояния, проходимые точками тела, очень велики по сравнению с его размерами. Например, материальными точками считают Землю и другие планеты при изучении их движения вокруг Солнца. В данном случае различия в движении разных точек любой планеты, вызванные её суточным вращением, не влияют на величины, описывающие годовое движение. Но при решении задач, связанных с суточным вращением планет (например, при определении времени восхода солнца в разных местах поверхности земного шара), считать планету материальной точкой нельзя, так как результат задачи зависит от размеров этой планеты и скорости движения точек её поверхности.
Это первая физическая модель реальных тел. Практически всякое тело можно рассматривать как материальную точку в тех случаях, когда расстояния, проходимые точками тела, очень велики по сравнению с его размерами. Например, материальными точками считают Землю и другие планеты при изучении их движения вокруг Солнца. В данном случае различия в движении разных точек любой планеты, вызванные её суточным вращением, не влияют на величины, описывающие годовое движение. Но при решении задач, связанных с суточным вращением планет (например, при определении времени восхода солнца в разных местах поверхности земного шара), считать планету материальной точкой нельзя, так как результат задачи зависит от размеров этой планеты и скорости движения точек её поверхности.
Тело, движущееся поступательно, можно принимать за материальную точку даже в том случае, если его размеры соизмеримы с проходимыми им расстояниями. Поступательным называется такое движение абсолютно твердого тела, при котором любой отрезок, соединяющий любые две точки тела, остается параллельным самому себе.
Что нужно знать для того, чтобы в любой момент времени указать положение тела? Надо, во-первых, знать, где оно было в начальный момент времени; во-вторых, каков вектор перемещения в любой момент времени. Мы уже знаем, что движение любого тела относительно. Поэтому, изучая движение тела, мы обязательно указываем, относительно какого тела это движение рассматривается. Тело, относительно которого рассматривается движение, называется телом отсчета. Чтобы рассчитать положение материальной точки относительно выбранной точки отсчета, надо связать с ним систему координат и измерить время. Совокупность тела отсчета, связанной с ним системы координат и часов называют системой отсчета.
Рассмотрим два наиболее часто применяемых способа описания движения тел: координатный и векторный. В координатном способе положение тела в пространстве задается координатами, которые с течением времени меняются.
Рассмотрим движение материальной точки М с координатами (х, y, z) в момент времени t.
Математически это принято записывать в виде:
Количество координат зависит от условия задачи: на прямой – одна, в плоскости – две, в пространстве – три.
В векторном способе используется радиус-вектор. Радиус-вектор – это направленный отрезок, проведенный из начала координат в данную точку. Закон (или уравнение) движения в векторной форме — зависимость радиуса-вектора от времени:
Итак, для задания закона движения материальной точки необходимо указать либо вид функциональной зависимости всех трех ее координат от времени, либо зависимость от времени радиус-вектора этой точки.
Три скалярных уравнения или эквивалентное им одно векторное уравнение называются кинематическими уравнениями движения материальной точки.
Двигаясь, материальная точка занимает различные положения в пространстве относительно выбранной системы отсчета. При этом она «описывает» в пространстве какую-то линию. Линия, по которой движется точка в пространстве, называется траекторией. По форме траектории все движения делятся на прямолинейные и криволинейные. Траектория движения указывает все положения, которые занимала точка, но, зная траекторию, ничего нельзя сказать о том, быстро или медленно проходила точка отдельные участки траектории. Длину траектории, по которой двигалось тело в течение какого-то промежутка времени, называют путём, пройденным за этот промежуток времени, его обозначают буквой S. Путь – скалярная величина.
По форме траектории все движения делятся на прямолинейные и криволинейные. Траектория движения указывает все положения, которые занимала точка, но, зная траекторию, ничего нельзя сказать о том, быстро или медленно проходила точка отдельные участки траектории. Длину траектории, по которой двигалось тело в течение какого-то промежутка времени, называют путём, пройденным за этот промежуток времени, его обозначают буквой S. Путь – скалярная величина.
Для описания движения тела нужно указать, как меняется положение точек с течением времени. Если участки криволинейные, то изменение координат тела описывают с помощью такого понятия как перемещение. Перемещением тела (материальной точки) называется вектор, соединяющий начальное положение тела с его последующим положением. Обозначается на чертежах как направленный отрезок, соединяющий начальное и конечное положение тела в пространстве:
Путь и модуль перемещения могут совпадать по значению, только в том случае, если тело движется вдоль одной прямой в одном направлении.
Важной величиной, характеризующей движение тела, является его скорость. Скорость – векторная величина. Она считается заданной, если известен ее модуль и направление. Скорость равномерного прямолинейного движения точки – векторная величина, равная отношению перемещения к промежутку времени, в течение которого это перемещение произошло. Пусть радиус-вектор задает положение точки в начальный момент времени t0, а радиус-вектор- в момент времени t. Тогда промежуток времени:
,
и перемещение:
.
Подставляя выражение для скорости, получим:
Если начальный момент времени t0 принять равным нулю, то скорость равна:
Выразим отсюда радиус-вектор :
Это и есть уравнение равномерного прямолинейного движения точки, записанное в векторной форме. Оно позволяет найти радиус-вектор точки при этом движении в любой момент времени, если известны скорость точки и радиус-вектор, задающий ее положение в начальный момент времени. В проекциях на ось ОХ уравнение можно записать в виде:
В проекциях на ось ОХ уравнение можно записать в виде:
х=х0+vхt.
Это уравнение есть уравнение равномерного прямолинейного движения точки, записанное в координатной форме. Оно позволяет найти координату х тела при этом движении в любой момент времени, если известны проекция его скорости на ось ОX и его начальная координата х0.
Путь S, пройденный точкой при движении вдоль оси ОХ, равен модулю изменения ее координаты:
Его можно найти, зная модуль скорости
Строго говоря, равномерного прямолинейного движения не существует. Но приближенно на протяжении не слишком большого промежутка времени движение автомобиля можно считать равномерным и прямолинейным с достаточной для практических целей точностью. Таково одно из упрощений действительности, позволяющее без больших усилий описывать многие движения.
Полученные результаты можно изобразить наглядно с помощью графиков. Для прямолинейного равномерного движения график зависимости проекции скорости от времени очень прост. Это прямая, параллельная оси времени.
Это прямая, параллельная оси времени.
Как мы уже знаем, зависимость координаты тела от времени описывается формулой х=х0+𝞾хt. График движения представляет собой прямую линию:
Из второго рисунка видим, что углы наклона прямых разные. Угол наклона второй прямой больше угол наклона первой прямой , т.е за одно и тоже время тело, движущееся со скоростью , проходит большее расстояние, чем при движении со скоростью А значит А что же в случае 3, когда угол α < 0? В случае 3 тело движется в сторону, противоположную оси ОХ. Проекция скорости в случае 3 имеет отрицательное значение и график проходит ниже оси ОХ. Проекция скорости определяет угол наклона прямой х(t) к оси t и численно равна тангенсу угла
Относительность механического движения – это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта. В рамках классической механики время есть величина абсолютная, то есть протекающее во всех системах отсчета одинаково.
Примеры и разбор решения заданий
1. Тело движется равномерно и прямолинейно в положительном направлении оси ОХ. Координата тела в начальный момент времени равна xо = -10м. Найдите координату тела через 5с, если модуль её скорости равен ʋ=2 м/с. Какой путь проделало тело за это время?
Дано: xо = — 10 м, t = 5 c, ʋ = 2 м/с. Найти s, х.
Решение: координату точки найдем по формуле:
х = х0 + 𝞾х t
Так как направление вектора скорости совпадает с направлением оси координат, проекция вектора скорости положительна и равна ʋx=ʋ; тогда вычисляем:
х = — 10 + 2· 5 = 0 (м).
Пройденный путь найдем s = ʋ t; s = 2·5 = 10 м.
2. Равномерно друг за другом движутся два поезда. Скорость первого равна 72 км/ч, а скорость второго — 54 км/ч. Определите скорость первого поезда относительно второго.
Дано:
Найти .
Решение: Из условия задачи ясно, что векторы скоростей поездов направлены в одну сторону. По закону сложения скоростей запишем:
По закону сложения скоростей запишем:
,
где — искомая величина.
Находим проекцию скоростей на ось ОХ и записываем, чему равен модуль искомой величины
Ответ: .
абстрактная алгебра — О двух разных определениях модуля
спросил
Изменено 1 год, 7 месяцев назад
Просмотрено 111 раз
$\begingroup$
Я читаю книгу «Симметрия и Стандартная модель: математика и физика элементарных частиц» Мэтью Робинсон. На странице $70$ книги автор дает следующую характеристику модуля множества $M$.
Ранее мы обсуждали, как элементы группы действуют друг на друга, а также говорили о том, как элементы группы действуют на какой-то другой объект или набор объектов (например, на три крашеных яйца).
Теперь мы обобщим это понятие на набор $q$ абстрактных объектов, над которыми может воздействовать группа, обозначаемый $M=\{m_0,m_1,m_2,\dots,m_{q-1}\}$. Как и раньше, мы строим векторное пространство, подобное тому, которое использовалось выше при построении алгебры. Ортонормированных векторов здесь будет 9{q-1}a_i|m_i\rangle\,\right|\,a_i\in\mathbb{R}\,\forall i\right\}\tag{3.49} \end{уравнение}
называется Module из $M$ (здесь мы не используем квадратные скобки, чтобы отличить модули от алгебр).
Но потом я посмотрел определение модуля в Википедии, и оказалось, что это совсем другое.
Кто-нибудь может объяснить разницу/сходство между двумя определениями?
модули абстрактной алгебры
$\endgroup$
4
$\begingroup$
Сначала более общее замечание: модули над кольцами являются естественным обобщением векторных пространств над полями. В частности, $R$-модуль с $R$ полем есть не что иное, как $R$-векторное пространство. Таким образом, можно называть модулями векторных пространств, но я думаю, что это более запутанно, чем все остальное.
В частности, $R$-модуль с $R$ полем есть не что иное, как $R$-векторное пространство. Таким образом, можно называть модулями векторных пространств, но я думаю, что это более запутанно, чем все остальное.
Здесь построен так называемый бесплатный модуль свыше $M$. Это самая общая модульная структура, которую можно построить по заданному множеству $M$ и некоторому базовому кольцу $R$. Формально это можно ввести через универсальные свойства, но я не думаю, что это сейчас выгодно. Интуитивно конструкция понятна: нужно как-то замкнуть наше множество относительно линейных комбинаций, то есть разрешить сложение его элементов и скалярное умножение на элементы нашего основного кольца (совершенно аналогичная конструкция существует для векторных пространств, если задано основное поле, дающее свободное векторное пространство над $M$), как диктуют нам модульные аксиомы.
Чтобы уточнить это (как я видел ваш вопрос в комментариях): модуль $M$ над кольцом $R$ является абелевой группой $M$ с внешним скалярным умножением $\cdot\colon R\times M\to M$, удовлетворяющие некоторой аксиоме совместимости (т.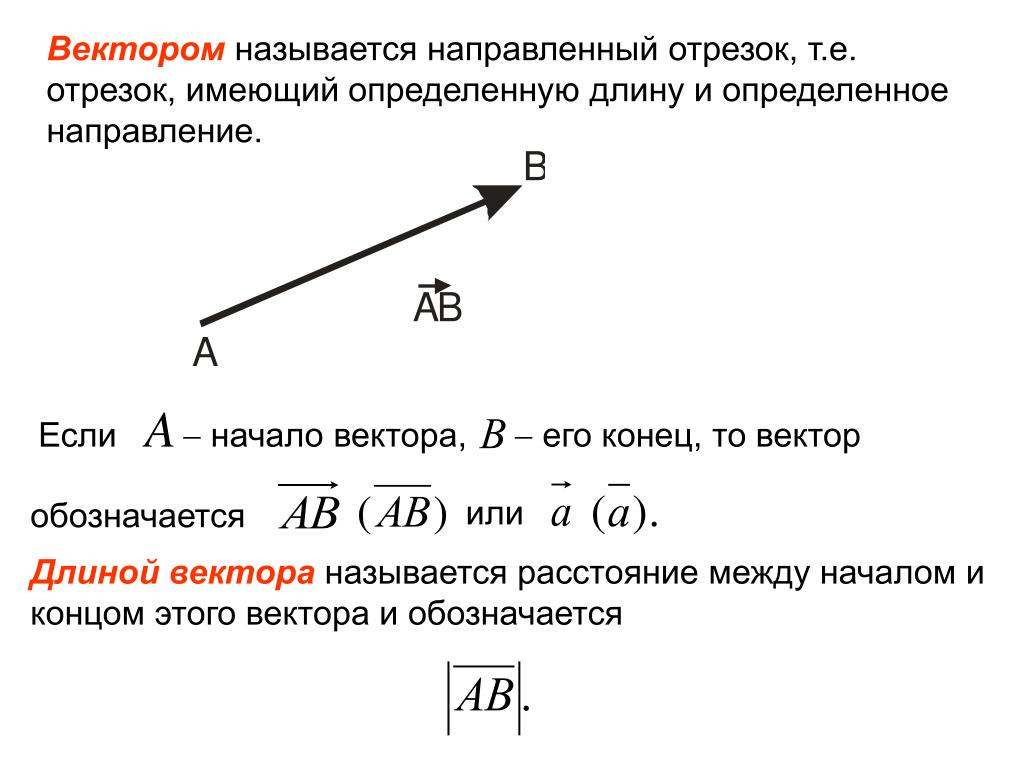 е. обеспечивающие правильное поведение всего объекта). Как оказалось, достаточно ожидать, что каждая (конечная) линейная комбинация элементов из $M$ с коэффициентами из $R$ будет в нем.
е. обеспечивающие правильное поведение всего объекта). Как оказалось, достаточно ожидать, что каждая (конечная) линейная комбинация элементов из $M$ с коэффициентами из $R$ будет в нем.
Действительно, тривиальная линейная комбинация является нашим нейтральным элементом в $M$, и мы имеем $(-1)\cdot m=-m$ как аддитивную обратную. Так что это даст нам абелеву группу. Аксиомы совместимости касаются только скалярного умножения и его взаимодействия со сложением. Ситуация очень похожа на векторные пространства, и все аксиомы следуют сразу, если мы рассмотрим множество (конечных) линейных комбинаций.
В данном случае фактически имеется базис (то, чего модули вообще не имеют и почему их общее определение другое; модули с базисом называются свободными), заданный $|m_i\rangle$, что существенно упрощает обсуждение. На самом деле важно только то, что $M$ конечно в вашем случае, что делает все настолько простым.
Отображение $m_i\mapsto|m_i\rangle$ представляет собой «векторификацию» элементов $M$, позволяющую различать их роль как элементов $M$ и как базовых векторов для $\mathbb R\mathbf M$ . Затем определение модуля $M$ делает именно то, что я упомянул выше: включает все линейные комбинации в $|m_i\rangle$ вручную. Вы можете проверить, что эта конструкция на самом деле дает $\mathbb R$-векторное пространство (т. е. $\mathbb R$-модуль, но $\mathbb R$ оказывается полем; так что вот ваша связь с общим понятием модулей).
Затем определение модуля $M$ делает именно то, что я упомянул выше: включает все линейные комбинации в $|m_i\rangle$ вручную. Вы можете проверить, что эта конструкция на самом деле дает $\mathbb R$-векторное пространство (т. е. $\mathbb R$-модуль, но $\mathbb R$ оказывается полем; так что вот ваша связь с общим понятием модулей).
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
линейная алгебра — разница между модулями и векторными пространствами
спросил
Изменено 1 год, 4 месяца назад
Просмотрено 1к раз
$\begingroup$
У меня любопытный вопрос о принципиальной разнице между векторными пространствами и общими модулями над кольцами.
Некоторые фундаментальные факты линейной алгебры:
(1) Конечное векторное пространство имеет базис.
(2) Минимальные порождающие (остовные) множества векторного пространства линейно независимы и поэтому образуют базис.
Недавно я прошел курс по модулям. Обсуждался один базовый пример: пусть $R = K[x,y]$, где $K$ — поле, и пусть $I = \langle x,y \rangle $. Мы рассматриваем $I$ как модуль над $R$.
Мы рассматриваем $I$ как модуль над $R$.
$I$ конечно порожденный модуль, однако он не свободен (не содержит базы). Это связано с тем, что наименьший порождающий набор имеет размер $2$, и независимо от того, какой порождающий набор вы выберете, вы можете написать нетривиальную $R-$линейную комбинацию элементов этого набора, которая равна $0$.
Если $S = \{ f(x,y), g(x,y) \} $, так что $I = \langle S \rangle $, то $g(x,y)f(x,y) + (-f(x,y))g(x,y) = 0$. Аналогичный аргумент можно сделать для любого конечного набора образующих для $I$.
Этот пример показывает, что эти фундаментальные факты о векторных пространствах не обязательно верны для модулей над общими кольцами.
Мой вопрос: что такого в скалярах, происходящих из поля, что делает эти факты верными, но не так, когда скаляры исходят из общего кольца? У меня никогда не было возможности спросить своего профессора во время занятий. Я пробовал читать доказательства из текстов по линейной алгебре, но я не вижу, в чем разница между лежащим в основе скалярным ПОЛЕМ.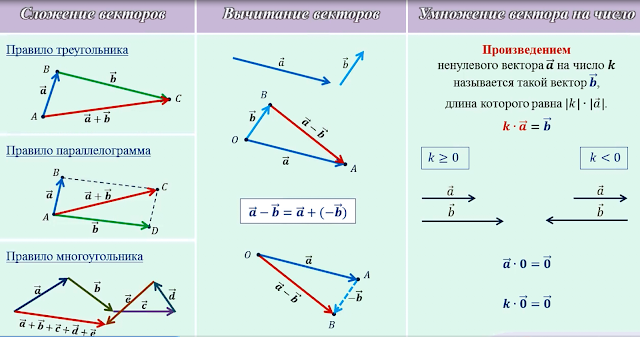
Любое разъяснение было бы очень полезно.
модули линейной алгебры конечно порожденные свободные модули
$\endgroup$
6
$\begingroup$
Поскольку вы спросили о теореме о том, что минимальное остовное множество в векторном пространстве линейно независимо, кажется целесообразным изучить доказательство этой теоремы, чтобы увидеть, как используется деление. Стандартное доказательство начинается с предположения, что у нас есть остовное множество, которое не является независимым, поэтому у нас есть отношение линейной зависимости, включающее некоторые из векторов $v_i$ из этого остовного множества, скажем, $0=c_1v_1+\dots+c_nv_n$, где скалярные коэффициенты $c_i$ не все равны нулю. Затем мы можем показать, что наше остовное множество не является минимальным следующим образом. В нашем отношении линейной зависимости перенесите один из членов с ненулевым коэффициентом, скажем, $c_j$, в левую часть уравнения, получив $-c_jv_j=\dots$, где $\dots$ в правой части равно линейная комбинация векторов , кроме $v_j$ из нашего остовного набора. [Пока что это работает в модулях над любым коммутативным кольцом.] Затем мы разделим обе части уравнения на $-c_j$ [здесь нам нужно поле], чтобы выразить $v_j$ как линейную комбинацию других векторов из нашего остовного множества . Таким образом, мы могли бы удалить $v_j$ из остовного набора, и то, что останется, все равно будет span. Это противоречит предполагаемой минимальности нашего остовного множества.
[Пока что это работает в модулях над любым коммутативным кольцом.] Затем мы разделим обе части уравнения на $-c_j$ [здесь нам нужно поле], чтобы выразить $v_j$ как линейную комбинацию других векторов из нашего остовного множества . Таким образом, мы могли бы удалить $v_j$ из остовного набора, и то, что останется, все равно будет span. Это противоречит предполагаемой минимальности нашего остовного множества.
Если вам не нравится коммутативность, вы можете заменить «модуль», «коммутативное кольцо» и «поле» в предыдущем абзаце на «левый модуль», «кольцо» и «кольцо делений» соответственно.
Возможно, вам стоит вернуться к примеру в вашем вопросе, чтобы увидеть, насколько важна для этого примера необратимость коэффициентов $f$ и $g$.
$\endgroup$
$\begingroup$
В некотором смысле особой разницы нет. На самом деле, вы были бы точны, если бы сказали, что векторное пространство — это модуль, за исключением особого случая, когда кольцо оказывается полем.
Но в другом смысле есть важные отличия. Просто для обозначения я буду повсюду ссылаться на векторное пространство $V$ над полем $F$ и модуль $M$ над кольцом $R$.
Например, возьмем один вектор $v \in V$ . Множество ${v}$ линейно независимо. Но не так (вообще) для элемента $m\in M$ . Например, $\mathbb{Z}_n$ (как аддитивная группа) является $\mathbb{Z}$ -модулем с умножением, определенным естественным образом: умножить, затем уменьшить по модулю $n$ . Таким образом, ни один элемент в $\mathbb{Z}_n$ не является линейно независимым одноэлементным множеством, поскольку $mn=0$ для любого $m \in \mathbb{Z}_n$ .
Соответственно, в векторных пространствах множество $S$ линейно зависимо тогда и только тогда, когда некоторый элемент $S$ является линейной комбинацией других элементов $S$ . Или, в более простом случае, когда $S$ состоит из двух элементов, $S$ линейно зависима тогда и только тогда, когда один элемент является скалярным кратным другого.
Неверно для модулей. В качестве примера возьмем $M=\mathbb{Z}$ в качестве $\mathbb{Z}$ -модуля, и пусть $n$ и $m$ взаимно просты. Поскольку они взаимно просты, ни один из них не является скалярным кратным другого. Но $S={n,m}$ линейно зависим. Если вы хотите решить $an+bm=0$, напишите $a=m$ и $b=−n$.
В качестве примера возьмем $M=\mathbb{Z}$ в качестве $\mathbb{Z}$ -модуля, и пусть $n$ и $m$ взаимно просты. Поскольку они взаимно просты, ни один из них не является скалярным кратным другого. Но $S={n,m}$ линейно зависим. Если вы хотите решить $an+bm=0$, напишите $a=m$ и $b=−n$.
Эти результаты — лишь два из многих, иллюстрирующих, на мой взгляд, основное различие между модулями и векторными пространствами. В векторных пространствах есть понятие размерности. Это просто, и это очень полезно. В модулях есть понятия разных типов измерений, но они далеко не так просты и далеко не так полезны.
$\endgroup$
4
$\begingroup$
Модуль представляет собой структуру абелевой группы в отношении «сложения» над кольцом (не обязательно коммутативным), а векторное пространство одинаково над полем.
Поскольку каждое поле является кольцом, каждое векторное пространство является модулем, но обратное преобразование неверно.
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
направление, ориентация, сложение, умножение, скаляры
Определение вектораПусть $A$ и $B$ — две разные точки плоскости.
Направленный отрезок $\overrightarrow{AB}$ — это отрезок, в котором мы точно знаем, какая точка является начальной, а какая конечной.
Два направленных отрезка эквивалентны, если существует перевод, при котором один переводится в другой.
Вектор является набором всех направленных отрезков, которые эквивалентны друг другу.
Любой направленный отрезок мы будем называть вектором из-за простоты речи. Векторы мы будем обозначать через $\overrightarrow{AB}, \overrightarrow{CD}, \ldots$ или просто как $\overrightarrow{a}, \overrightarrow{b}, \ldots$.
Векторы однозначно определяются их величиной, направлением и ориентацией.
Рисование векторов в двумерных декартовых координатах
Каждый вектор определяется двумя точками. Это делает их рисование в координатной плоскости довольно простым. Например, если нам даны две точки с их координатами $A=(1, 2)$ и $B = (5, 6)$ и наша задача состоит в том, чтобы нарисовать вектор $\overrightarrow{AB}$, мы должны сначала нарисовать отрезок $\overline{AB}$, а затем просто нарисуйте стрелку, обозначающую нашу конечную точку.
Это делает их рисование в координатной плоскости довольно простым. Например, если нам даны две точки с их координатами $A=(1, 2)$ и $B = (5, 6)$ и наша задача состоит в том, чтобы нарисовать вектор $\overrightarrow{AB}$, мы должны сначала нарисовать отрезок $\overline{AB}$, а затем просто нарисуйте стрелку, обозначающую нашу конечную точку.
Каждой точке плоскости может быть поставлен в соответствие уникальный вектор, начальная точка которого находится в начале координат, а конечная точка — в данной точке. Эти векторы очень важны в векторной геометрии и называются позиция или радиус-векторы .
Величина векторов
Величина вектора $\overrightarrow{AB}$ равна длине отрезка $\overline{AB}$.
Некоторые дополнительные имена для величин векторов, такие как: норма вектора, модуль вектора или абсолютное значение вектора.
Величина любого вектора определяется положением его начальной и конечной точки и рассчитывается точно так же, как длина отрезка. Величина вектора всегда либо положительное число, либо ноль. Величина вектора равна нулю тогда и только тогда, когда начальная точка равна конечной точке. 92}.$$
Величина вектора всегда либо положительное число, либо ноль. Величина вектора равна нулю тогда и только тогда, когда начальная точка равна конечной точке. 92}.$$
Нулевой вектор или нулевой вектор — это вектор, длина которого равна $0$. Нулевой вектор обозначается $\overrightarrow{0}$.
Единичный вектор — это вектор, длина которого равна $1$, однако он может двигаться в любом направлении. Для вектора $\overrightarrow{a}$ длины $|\overrightarrow{a}|$ единичный вектор $\overrightarrow{a_0}$ определяется как
$$\overrightarrow{a_0} = \frac{\overrightarrow {а}}{|\overrightarrow{а}|}.$$ 92} = \sqrt{50} = \sqrt{2 \cdot 25} = 5\sqrt{2}$.
3. $\overrightarrow{EF} = 0$, потому что $E=F$.
Направление векторов
Направление вектора — это мера угла, заключенного с осью $y$. Его можно наблюдать как наклон линии, на которой он лежит, потому что его наклон вычисляется так же, как мы вычисляем наклон линии. Мы будем отмечать направление вектора с помощью $\varphi$.
Мы будем отмечать направление вектора с помощью $\varphi$.
Если у нас есть вектор $\overrightarrow{PQ}$, $P = (x_1, y_1)$, $ Q = (x_2, y_2)$, то 9{\circ}$.
Ориентация векторов
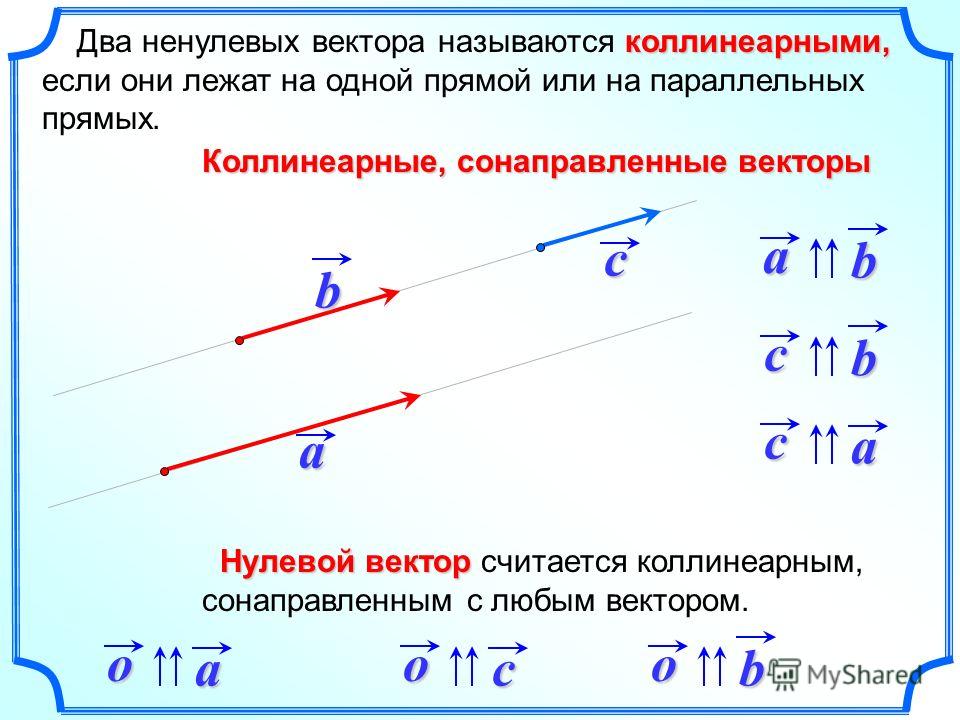
Ориентация вектора относится исключительно к коллинеарным векторам. Коллинеарные векторы – это векторы, лежащие на одной прямой или параллельной одной и той же прямой. Например, если у нас есть два вектора $\overrightarrow{AB}$ и $\overrightarrow{CD}$, то их ориентация может быть только равной или противоположной.
Как мы можем таким образом определить ориентацию, если предположить, что эти два вектора коллинеарны? Сначала мы должны взять один вектор и перевести его так, чтобы его начальная точка попала в начальную точку другого вектора. Это означает, что мы переносим вектор $\overrightarrow{CD}$ так, что $C = A$. Если точки $B$ и $D$ лежат по одну сторону от точки $A$, то они обе имеют одинаковую ориентацию, если же они находятся по разные стороны от точки $A$, то они имеют противоположную ориентацию. .
.
Векторы с одинаковой ориентацией:
Векторы с противоположной ориентацией:
Примечание. Два вектора равны, если они имеют одинаковую величину, направление и ориентацию. Если два коллинеарных вектора имеют одинаковую длину, хотя и разную ориентацию, они называются противоположными векторами . Если $\overrightarrow{a}$ — вектор, который мы наблюдаем, то его противоположный вектор обозначается $\overrightarrow{- a}$.
Сложение векторов
Складывая векторы $\overrightarrow{AB}$ и $\overrightarrow{CD}$, мы получим новый вектор $\overrightarrow{AD}$, начальная точка которого совпадает с первым слагаемым, а конец точка нового вектора совпадает со вторым слагаемым. Применяя это правило, получается треугольник. Вот почему этот метод сложения называется правилом треугольника . Когда у нас есть два вектора, которые мы должны сложить, сначала мы переводим один вектор на другой таким образом, чтобы конечная точка первого была начальной точкой второго. Затем все, что осталось, это завершить треугольник и отметить ориентацию нашего нового вектора.
Затем все, что осталось, это завершить треугольник и отметить ориентацию нашего нового вектора.
Сложение с нулевым вектором:
$\overrightarrow{a}$ + $\overrightarrow{0}$ = $\overrightarrow{a}$
$\overrightarrow{0}$ + $\overrightarrow{ а}$ = $\overrightarrow{а}$.
Закон параллелограмма сложения векторов
Если у нас есть два вектора, имеющих одну и ту же начальную точку, то мы можем использовать закон параллелограмма вектора сложения . Мы просто рассматриваем эти два вектора как смежные стороны параллелограмма, их сумма будет диагональю параллелограмма. Начальная точка суммы этих двух векторов будет их начальной точкой.
Шаг за шагом:
Свойства сложения
Для любых двух векторов $\overrightarrow{a}$ и $\overrightarrow{b}$ верно:
$$\overrightarrow{a}\overrightarrow{a} + \overrightarrow{b} = \overrightarrow{b} + \overrightarrow{a}. $$
$$
Это означает, что сложение векторов коммутативно.
Для любых трех векторов $\overrightarrow{a}$, $\overrightarrow{b}$ и $\overrightarrow{c}$ допустимо:
$$(\overrightarrow{a} + \overrightarrow{b}) + \overrightarrow{c} = \overrightarrow{a} + (\overrightarrow{b} + \overrightarrow{c}).$$
Следовательно, сложение векторов ассоциативно.
Сложение более двух векторов
Сложение $n$ взаимосвязанных векторов $\overrightarrow{A_1 A_2}, \overrightarrow{A_2 A_3}, \overrightarrow{A_3 A_4}, … , \overrightarrow{ A_{n-1}A_n}$ равен вектору $\overrightarrow{A_1 A_n}$
Примечание: Как мы уже знаем, $\overrightarrow{-a}$ — это вектор, ориентация которого противоположна ориентации вектора $\overrightarrow{a}$, однако их величина и направление равны. Используя это утверждение, мы знаем, как вычитать векторы. Если у нас есть два вектора, $\overrightarrow{a}$ и $\overrightarrow{b}$, и нам нужно вычесть $\overrightarrow{b}$ из $\overrightarrow{a}$ $ (\overrightarrow{a} – \overrightarrow{b})$, мы просто меняем ориентацию вектора $\overrightarrow{b}$ и добавляем их как таковые $\overrightarrow{a} + (\overrightarrow{-b})$.
Умножение векторов на действительные числа
Произведение действительного числа $ k \not = 0$ на вектор $\overrightarrow{a}$ представляет собой вектор, который мы обозначаем как $ k \overrightarrow{a}$ , с правилами:
- Векторы $\overrightarrow{a}$ и $k \vec{a}$ являются коллинеарными векторами одной ориентации, если $k > 0$, и противоположной ориентации, если $k < 0$
- Величина вектора $ k \overrightarrow{a}$ равно $\mid k \mid \cdot\mid \overrightarrow{a} \mid$
- Произведение вектора на ноль является нуль-вектором
- Произведение вектора на $1$ является одним и тем же вектором
Например, если у нас есть вектор $\overrightarrow{AB}$, где $ A = (2, 4)$, $ B = (5, 6)$, вычислить $2\overrightarrow{AB}$ и $-2\overrightarrow{AB}$, произведение вектора на действительное число всегда будет расположено на линии, на которой лежит наблюдаемый вектор. Поэтому первое, что мы должны сделать, это провести линию, на которой лежит вектор $\overrightarrow{AB}$.
Теперь нам нужно вычислить $ 2\overrightarrow{AB}$. Его величина будет в два раза больше, чем у вектора $\overrightarrow{AB}$. Вектор будет расположен на той же прямой и будет иметь ту же ориентацию, потому что $2 > 0$. Теперь у нас есть все необходимые данные:
Теперь нам нужно вычислить $-2 \cdot\vec{AB}$. Поскольку $-2 < 0$, этот вектор будет иметь противоположную вектору $\overrightarrow{AB}$ ориентацию, двойную величину и то же направление.
Свойства умножения вектора на вещественное число
Справедливо для любых двух действительных чисел $k$ и $l$ и для любых двух векторов $\overrightarrow{a}$ и $\overrightarrow{b }$:
$ k (\overrightarrow{a} + \overrightarrow{b}) = k \overrightarrow{a} + k \overrightarrow{b}$
$ (k + l) \overrightarrow{a} = k \overrightarrow{a} + l \overrightarrow{a}$
$(kl) \overrightarrow{a} = k (l \overrightarrow{a})$
Линейная комбинация – линейная зависимость и независимость
Если $\overrightarrow{a}$ и $\overrightarrow{b}$ являются векторами и $\alpha$ и $\beta$ действительными числами, то вектор
$\overrightarrow{ c} = \alpha \overrightarrow{a} + \beta \overrightarrow{b}$
называется линейной комбинацией векторов $\overrightarrow{a}$ и $\overrightarrow{b}$ с коэффициентами $\alpha$ и $\бета$.
Если $\overrightarrow{a}$ и $\overrightarrow{b}$ — два коллинеарных, а не нуль-вектора с одинаковой ориентацией, где $\overrightarrow{a}$ в $k$ раз длиннее, чем $\overrightarrow{b }$, то мы можем написать:
Это означает, что один вектор может быть представлен с помощью другого и что $\overrightarrow{a}$ и $\overrightarrow{b}$ линейно зависимы .
Векторы $\overrightarrow{a_1}, \overrightarrow{a_2} … , \overrightarrow{a_n}$ называются линейно зависимыми, если существуют действительные числа $\alpha_1, \alpha_2, … , \alpha_n$ такие, что:
$\overrightarrow{0} = \alpha_1 \overrightarrow{a_1} + \alpha_2 \overrightarrow{a_2}, … , \alpha_n \overrightarrow{a_n}$.
Если линейная комбинация $\alpha_1 \overrightarrow{a_1} + \alpha_2 \overrightarrow{a_2}, … , \alpha_n \overrightarrow{a_n}$ равна $\overrightarrow{0}$ только тогда, когда $\alpha_1, \alpha_2 , … , \alpha_n$ равны нулю, то говорят, что векторы $\overrightarrow{a_1}, \overrightarrow{a_2} … , \overrightarrow{a_n}$ линейно независимы .
Любые два коллинеарных вектора на плоскости линейно зависимы, а каждые два неколлинеарных вектора линейно независимы.
Каждый вектор на плоскости может быть представлен уникальным образом как линейная комбинация двух неколлинеарных векторов.
Векторы в координатной плоскости
Пусть $E$ — единичная точка на оси $x$, $F$ — единичная точка на оси $y$, а точка $O$ — начало координат. Тогда радиус-вектор $\overrightarrow{OE}$ равен единичному вектору $\overrightarrow{i}$, а радиус-вектор $\overrightarrow{OF}$ равен единичному вектору $\overrightarrow{j}$.
Используя эти два вектора, мы можем представить любой вектор на плоскости уникальным образом.
Если точка $P$ имеет координаты $(x, y)$, то радиус-вектор $\overrightarrow{OP}$ имеет представление $\overrightarrow{OP} = x \overrightarrow{i} + y \overrightarrow{j}$ .
Если $A_1 = (x_1, y_1)$ и $A_2 = (x_2, y_2)$ две точки плоскости, то: $\overrightarrow{A_1A_2} = (x_2 – x_1) \overrightarrow{i} + (y_2 – y_1) \overrightarrow{j}$.
Например, если у нас есть две точки $ A = (1, 3)$ и $ B = (2 , 5)$, то вектор $\overrightarrow{AB}$ равен:
$\overrightarrow{AB} = (x_2 – x_1) \vec{i} + (y_2 – y_1) \overrightarrow{j} = (2 – 4) \overrightarrow{i} + (5 – 3) \overrightarrow{ j} = \overrightarrow{i} + 2 \overrightarrow{j}$.
Скалярное или скалярное произведение
Предположим, что на плоскости есть два вектора, оба отличные от $\overrightarrow{0}$. Если они не имеют одной и той же начальной точки, мы просто переводим один вектор в другой таким образом, чтобы у них была одна и та же начальная точка.
Угол между этими двумя векторами — это меньший угол из двух углов, заключенных между полупрямыми, на которых лежат эти два вектора.
Если $\overrightarrow{a}$ и $\overrightarrow{b}$ — два вектора, отличные от $\overrightarrow{0}$, произведение
$$\overrightarrow{a} \cdot \overrightarrow{b } = |\overrightarrow{a}| \cdot |\overrightarrow{b}| cos \angle (\overrightarrow{a}, \overrightarrow{b})$$
называется скалярным произведением или скалярным произведением векторов $\overrightarrow{a}$ и $\overrightarrow{b}$.
Свойства скалярного произведения
1. $ \cdot \overrightarrow{a} \cdot \overrightarrow{b} = \overrightarrow{b} \cdot \overrightarrow{a}$ для любых двух векторов $\overrightarrow{a}$ и $\overrightarrow{b }$
2. $ (\overrightarrow{a} + \overrightarrow{b}) \cdot \overrightarrow{c} = \overrightarrow{a} \cdot \overrightarrow{c} + \overrightarrow{b} \cdot \overrightarrow {c}$, для каждых трех векторов $\overrightarrow{a}$, $\overrightarrow{b}$ и $\overrightarrow{c}$
3. $(\alpha \cdot \overrightarrow{a}) \cdot \overrightarrow{b} = \overrightarrow{a}\cdot (\alpha \cdot \overrightarrow{b}) = \alpha \cdot (\overrightarrow{a} \cdot \overrightarrow{b})$ , для любых двух векторов $ \overrightarrow{a}$ и $\overrightarrow{b}$ и $\forall \alpha \in \mathbb{R}$ 92$, для каждого вектора $\overrightarrow{a}$
5. $\overrightarrow{a} \cdot \overrightarrow{b} = 0$ , если $\cos \angle(\overrightarrow{a}, \overrightarrow{ b}) = 0$
Для единичных векторов $\overrightarrow{i}$ и $\overrightarrow{j}$ справедливо:
$$\overrightarrow{i} \cdot \overrightarrow{j} = \overrightarrow{j } \cdot \overrightarrow{i} = 0. $$
$$
Рабочие листы
Именование вершин и векторов (419,4 КиБ, 717 совпадений)
Векторы измерения углов (490,3 КиБ, 10 158 совпадений)
Модуль 26 — Векторы
На этом уроке вы научитесь определять векторы, использовать различные обозначения для описания векторов и выполнять два типа умножения векторов: скалярное умножение и скалярное произведение. Будут обсуждены единичные векторы и проиллюстрированы векторные проекции.
Определение векторов
Величины, которые имеют как величину, так и направление, называются векторами и часто представляются направленными отрезками, как показано ниже.
Показанный вектор имеет начальную точку в точке O и конечную точку в точке P .
Представление векторов
Любой двумерный вектор можно представить в виде направленного отрезка с начальной точкой в начале координат, а векторы, имеющие начальную точку в начале координат, можно представить с помощью координат кончика стрелки. Например, вектор, идущий от начала координат к точке (3, 2), представляется с помощью обозначения <3, 2>. Для вектора v = < a , b >, a и b называются координатами или компоненты из v , или, более конкретно, x-координата и y-координата из v .
Например, вектор, идущий от начала координат к точке (3, 2), представляется с помощью обозначения <3, 2>. Для вектора v = < a , b >, a и b называются координатами или компоненты из v , или, более конкретно, x-координата и y-координата из v .
Единичные векторы i и j
Вектор i имеет длину в одну единицу и указывает вдоль положительной оси x , а вектор j имеет длину в одну единицу и указывает на положительную ось y . Поскольку векторы i и j имеют длину в одну единицу, они называются единичными векторами . И i , и j показаны ниже вместе с вектором a , который имеет конечную точку (3, 2).
Обратите внимание, что a , i и j выделены жирным шрифтом, чтобы показать, что они являются векторами.
Представление векторов с помощью i и j
Вектор также может быть представлен с использованием единичных векторов i и j . Например, вектор a = <3, 2> можно записать как
Например, вектор a = <3, 2> можно записать как
Длина вектора
Длина или величина любого вектора a =
Длина a = <3, 2> равна единицы.
Скалярное умножение векторов
Пусть c представляет собой
| |||
- вектор, длина которого |c| раз больше длины и и
- вектор, направление которого
- то же, что a , если c положительно и
- противоположное направление от к , если c отрицательно.

Координаты c a находятся путем умножения каждой координаты a по c .
26.1.1 Что такое скаляр, кратный 2 <3, -1>? Щелкните здесь, чтобы получить ответ.
Единичный вектор
Любой вектор, величина которого равна единице, называется единичным вектором . Часто бывает полезно найти единичный вектор, который указывает в том же направлении, что и заданный вектор a . Чтобы найти этот вектор, каждая компонента на делится на величину на .
Чтобы определить единичный вектор, который указывает в том же направлении, что и a = <3,2>, найдите величину a , а затем умножьте вектор на величину, обратную величине.
Величина a равна , поэтому единичный вектор равен
26.1.2 Определите единичный вектор, который указывает в том же направлении, что и a = <-2, 5>.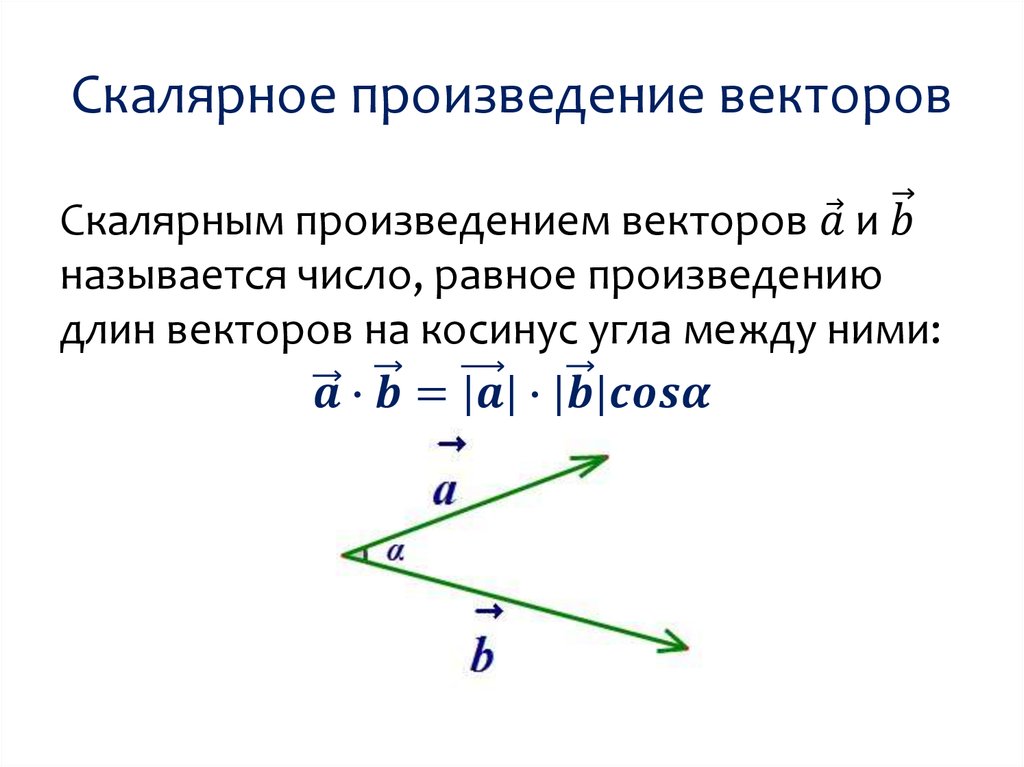 Щелкните здесь, чтобы получить ответ.
Щелкните здесь, чтобы получить ответ.
Скалярные произведения векторов
Существует второй тип умножения с участием векторов, называемый скалярным произведением . Скалярные произведения широко используются в физике. Например, они используются для расчета работы силы, действующей на объект.
Скалярное произведение двух векторов а также определяется как
То есть скалярное произведение двух векторов представляет собой сумму произведений их соответствующих компонентов. Обратите внимание, что результатом скалярного произведения двух векторов является число 9.0237 реальное число , а не вектор.
26.1.3 Пусть а также . Вычислить скалярное произведение a · b . Щелкните здесь, чтобы получить ответ.
Альтернативное определение скалярного произведения
Скалярное произведение также может быть определено как произведение величины a , величины b и косинуса угла между а и б . Если угол между a и b
Проецирование одного вектора на другой вектор
Проекцию можно получить, опустив перпендикуляр из начала одного вектора на линию, содержащую другой. Когда два вектора имеют одну и ту же начальную точку, проекция б на а
- параллелен a и
- имеет длину проекции на b .
Компонент b вдоль a
Величина проекции b на a , |proj a b |, также называется компонентом b вдоль a . Он обозначается как comp a b и равен величине b , умноженной на косинус , угол между a и б . Потому что , comp a b также равно скалярному произведению a и b , деленному на величину a . Символически,
Он обозначается как comp a b и равен величине b , умноженной на косинус , угол между a и б . Потому что , comp a b также равно скалярному произведению a и b , деленному на величину a . Символически,
26.1.4 Найдите комп. a b и комп. b a , если а также . Щелкните здесь, чтобы получить ответ.
Модуль 3: Векторы, матрицы и матрично-векторное уравнение
Цели модуля
К концу этого модуля вы должны уметь
- Объясните, что такое векторы и матрицы и почему они определены так, как они есть.
- Выполнение простых вычислений с векторами и матрицами.
- Решите вручную некоторые матрично-векторные уравнения.
- Описать различные способы интерпретации матрицы-вектора уравнение.
3.0 Набор чисел как математический объект
На самом базовом уровне каждое приложение, которое мы видели, вычисляет с
числа.
\(\rhd\)
Организованная серия операций над числами.
Более пристальный взгляд показывает, что некоторые числа естественным образом делятся на группы:
- Например, рассмотрим приложение №1: линейные уравнения
- Коэффициенты одного уравнения явно связаны.
- Все числа в правой части могут быть группой.
- Приложение №3: Кривые Безье
\(\rhd\) Координаты контрольных точек. - Приложение №6: Поиск изображений
\(\rhd\) Все числа (значения интенсивности) в изображении.
Классное упражнение 1: Выберите три других приложения и предложите естественные группы номеров для этих приложений.
Что мы уже знаем из математики о группах чисел?
- Теория множеств — одна из возможностей.
- Например, \(\{1,4,9,16\}\) — это группа связанных чисел.
- Что можно делать с наборами?
- Обычные бинарные операторы: \(\cup, \cap\)
- Можно ли «сложить» два набора?
- Одна практическая проблема с теорией множеств:
- Реальные приложения фактически работают (складывают, умножают и т.
 д.) на
фактические цифры.
д.) на
фактические цифры. - Операторы теории множеств не приводят к операциям над числами.
- Таким образом, не существует оператора \(+\) для множеств, который приводит к
добавление номера,
\(\rhd\) например, что-то вроде \(\{1,2,3\} + \{2,3,4\} = \{3,5,7\}\)
- Реальные приложения фактически работают (складывают, умножают и т.
- Мы могли бы определить такие операторы, но столкнулись бы с
проблемы с заказом :
- Пример: мы знаем \(\{1,2,3\} = \{3,2,1\}\)
\(\rhd\) Тогда \(\{3,2,1\} + \{2,3,4\} = \{3,5,7\}\)?
- Пример: мы знаем \(\{1,2,3\} = \{3,2,1\}\)
Что мы хотели бы:
- Математический объект для хранения набора чисел.
- Определения таких операторов, как \(+,\times\)
на коллекций таких, что:
- Нет двусмысленности.
- Оператор, применяемый к коллекции, имеет естественный способ перехода к номерам в коллекции.
Ответ: кортеж
- Кортеж представляет собой упорядоченный набор чисел.

- Примеры:
- \((1,2,3)\) — кортеж.
- Кортеж \((1,2,3)\) отличается от \((2,1,3)\) и от \((1,2,3,3)\).
- Мы не ограничены целыми числами: \((1,414, 2,718, 3,141)\) является кортежем.
- Кортеж из \(n\)- — это кортеж из \(n\) элементов.
- Что мы можем делать с кортежами? Определим сложение и
умножение как:
- Добавление двух кортежей:
$$
(u_1,u_2,\ldots,u_n) + (v_1,v_2,\ldots,v_n) =
(u_1+v_1, \; u_2+v_2, \; \ldots, \;u_n+v_n)
$$
9п у_и в_и
$$
\(\rhd\) В результате получается одно число. - Пример: $$ (1,2,3) \cdot (4,5,6) = 1\умножить на 4 + 2\умножить на 5 + 3\умножить на 6 = 4 + 10 + 18 = 32 $$
- Добавление двух кортежей:
$$
(u_1,u_2,\ldots,u_n) + (v_1,v_2,\ldots,v_n) =
(u_1+v_1, \; u_2+v_2, \; \ldots, \;u_n+v_n)
$$
9п у_и в_и
$$
- Примечание:
- Умножение неожиданно отличается от сложения. Это
не ясно (пока), почему мы должны это делать.

- Оба вышеприведенных кортежа кроме сложения или умножения должны иметь одинаковое количество элементов.
- Умножение неожиданно отличается от сложения. Это
не ясно (пока), почему мы должны это делать.
- Вычитание следует из определяющего сложения.
- Мы пока отложим деление, пока не получим к инвертирует .
- Нас также будут интересовать операторы, объединяющие один
номер и коллекция.
- Для действительного числа \(\alpha\) и кортежа \((v_1,v_2,\ldots,v_n)\), определить скалярное умножение как $$ \альфа (v_1,v_2,\ldots,v_n) \;\; знак равно (\альфа v_1, \альфа v_2,\ldots, \альфа v_n) $$
- Можно представить себе эквивалент скалярного сложения но оказывается бесполезно.
Продолжая это исследование, давайте спросим: существует ли полезная геометрическая интерпретация кортежей?
- Мы наверняка видели двойку типа \((1,2)\) раньше.
\(\rhd\) Точка на двумерной плоскости.
- Точно так же можно сказать, что тройка — это трехмерная точка, а скоро.
Две проблемы с кортежами как точками:
- Во-первых, означает добавления точек: каким образом мы видим добавление двух вещей?
- Во-вторых, мы получаем противоречивые результаты, если кадр
изменения привязки (системы координат):
- Выше, чтобы получить «синие» координаты из черных координат,
сдвигаем на \((1,2)\)
\(\rhd\) например, \(\color{blue}{(3,1)} = \color{black}{(4,3) — (2,1)}\) - Но добавленные черным цветом точки дают нам: \((9,10)\),
который становится \(\color{blue}{(8,8)}\) при смещении.
\(\rhd\) Это не равно прямому сложению, которое дает \(\цвет{синий}{(7,6)}\)
- Выше, чтобы получить «синие» координаты из черных координат,
сдвигаем на \((1,2)\)
Чтобы решить эту проблему, вернемся к 1D:
Теперь мы сделаем это для 2D:
- Пусть кортеж \((x,y)\) связан со стрелкой , идущей от
\((0,0)\) в точку \((x,y)\).

- Например:
- Чтобы добавить \((4,3)\) и \((5,7)\), сдвиньте стрелку, соответствующую
в \((4,3)\) так, чтобы его хвост касался стрелки \((5,7)\):
\(\rhd\) Результатом является стрелка к \((9,10)\): - Примечание: мы не меняем ориентацию (направление) стрелки, когда мы перемещаем его.
- При рассмотрении приведенного выше примера необходимо сделать важный вывод:
- Стрелка между \((5,7)\) и \((9,10)\) не действительно существует как кортеж.
- Перемещено туда только до иллюстрируют дополнение .
- Технически правильный рисунок:
- только правильная стрелка — это стрелка, у которой конец \((0,0)\).
- Однако мы будем рисовать «перемещенные» стрелки, потому что они делают это легче визуализировать операции и результаты.
- Стрелки типа выше называются векторов .

- Поскольку кортежи теперь имеют векторы как геометрическую интерпретацию,
нам не нужны два термина для одного и того же.
\(\rhd\) В дальнейшем мы будем использовать термин вектор .
Классное упражнение 2: Объясните следующее:
- Вернитесь к примеру с двумя системами координат и проверьте вручную это сложение дает тот же результат, относительный к новому происхождению.
- Что было бы, если бы второй набор координатных осей имели то же происхождение, но были немного повернуты (скажем, на 60 градусов)?
- Согласно приведенным выше правилам, нам не разрешено менять ориентацию стрелки, когда она перемещается для добавления. Почему это? Что бы ошибетесь с теорией, если мы позволим изменить направление?
3.1 Векторы
Векторное обозначение:
- Существует три типа обозначений для векторов.
- Рассмотрим вектор \((v_1,v_2,\ldots,v_n)\).

- Это часто записывается в краткой форме как одно из следующих:
- \({\bf v} = (v_1,v_2,\ldots,v_n)\) (жирный шрифт)
- \(\vec{v} = (v_1,v_2,\ldots,v_n)\) (стрелка)
- \(\stackrel{\rightharpoonup}{v} = (v_1,v_2,\ldots,v_n)\) (гарпун)
- Обычно мы предпочитаем полужирный шрифт, а иногда и стрелку.
- Когда пишешь домашние задания от руки трудно выделить жирным шрифтом: вместо этого используйте стрелку.
Закон параллелограмма:
Далее, давайте посмотрим на скалярное умножение на .
- Напомним: $$\eqb{ \ альфа {\ бф v} & \;\; знак равно & \альфа (v_1, v_2, \ldots, v_n) \\ & \;\; знак равно & (\альфа v_1, \альфа v_2, \ldots, \альфа v_n) \\ }$$
- Пример: \( 2 (3,2) = (6,4)\)
- Пример: \( 1,5 (1,4) = (1,5,6)\)
- Давайте нарисуем вот это:
- Другой пример: \(-0,5 (3,2)\)
- Таким образом, скалярное умножение «растягивается» или «сжимается»,
а также может изменить направление, если скаляр отрицательный.

- Обычно мы будем использовать слово «растянуть» для обозначения любого из вышеперечисленных.
- Отрицательное растяжение меняет направление.
- Дробное растяжение фактически сжимается.
Классное упражнение 3: Почему верно, что ориентация (угол), кроме флипов, неизменна на скалярное умножение?
Специальный вектор: нулевой вектор- Мы будем использовать обозначение \({\bf 0}\) для обозначения вектор, содержащий все нули: \({\bf 0} = (0,0,\ldots,0)\).
- Очевидно, что для любого вектора \({\bf u}\)
имеем \({\bf u} + {\bf 0} = {\bf u}\)
\(\rhd\) \({\bf 0}\) — аддитивная идентичность для сложения векторов. - Подобно числам, \({\bf u} \cdot {\bf 0} = 0\)
\(\rhd\) Здесь правая сторона — это число 9.0238 \(0\), а не вектор \({\bf 0}\).
3.2 Линейные комбинации
Давайте теперь рассмотрим важнейшую идею: линейную комбинацию
- Линейная комбинация векторов является вектором.

- Каждый вектор в комбинации сначала растянут, и , затем добавляются все растянутые векторы.
- Пример: \(1,5(1,4) + 2(3,2)\)
- Вектор \((1,4)\) растянут до \(1,5(1,4) = (1,5,6)\).
- Вектор \((3,2)\) растянут до \(2(3,2) = (6,4)\).
- Два растянутых вектора складываются: \((1.5,6) + (6,4) = (7.5,10)\).
- Эта простая маленькая «комбинированная» операция, как мы увидите, оказывается сердцем линейной алгебры.
Классное упражнение 4: Скачать LinCombExample.java и DrawTool.java. Затем осмотрите код в LinCombExample, чтобы увидеть, как векторы и стрелки нарисованы. Затем нарисуйте оставшиеся стрелки, чтобы завершить параллелограмм.
Классное упражнение 5: Скачать LinCombExample2.java
(у вас уже есть DrawTool).
Напишите код для реализации векторного сложения и скалярного умножения,
и протестируйте на примере в main().
Давайте продолжим изучение линейных комбинаций:
- Вопрос: если три вектора, всегда ли третий выражается как линейная комбинация первых двух?
- Смежный вопрос: уникальны ли скаляры?
- Пусть \({\bf u, v, z}\) — три вектора.
- Всегда ли можно найти числа \(\alpha, \beta\) такие, что \(\ альфа {\bf u} + \beta {\bf v} = {\bf z}\)?
- Есть ли несколько вариантов для \(\alpha, \beta\)?
Классное упражнение 6: Загрузите LinCombExample3.java. Цикл double-for пытается систематически перебирать все возможные варианты. значения \(\alpha, \beta\), чтобы увидеть, будет ли работать какая-либо комбинация. Напишите код, чтобы увидеть, является ли линейная комбинация \(\ альфа {\bf и} + \бета {\bf v}\) приблизительно равно \({\bf z}\).
Классное упражнение 7: Решите вышеуказанную задачу вручную: существуют ли
значения \(\alpha, \beta\) такие, что
\(\ альфа {\bf u} + \beta {\bf v} = {\bf z}\)
когда \({\bf u}=(1,4)\), \({\bf v}=(3,2)\)
и \({\bf z}=(7. 5,10)\)?
5,10)\)?
Классное упражнение 8: Предположим, \({\bf u}=(1,2), {\bf v}=(3,6)\) и \({\bf z}=(7.5,10)\). Скачать LinCombExample4.java и нарисуйте все три вектора. Затем:
- Используйте рисунок, чтобы объяснить, почему линейная комбинация \({\bf u}\) и \({\bf v}\) будут работать.
- Решите вручную, чтобы подтвердить объяснение алгебраически.
Линейная комбинация может выходить за пределы двух векторов:
- Предположим, \({\bf u}=(1,4), {\bf v}=(3,2), {\bf w}=(-1,1)\).
- Если \(\alpha, \beta, \gamma\) три числа, то
\( \alpha{\bf u} + \beta{\bf v} + \gamma{\bf w}\)
линейная комбинация.
9к \ alpha_i {\ bf v} _i
= \alpha_1{\bf v}_1 + \ldots + \alpha_k{\bf v}_k \)
является линейной комбинацией векторов \(k\).

- Мы использовали \({\bf v} = (v_1,v_2,\ldots,v_n)\) для описания одного вектора .
- Здесь \(v_i\) — число, элемент вектора.
- Но, выше, \({\bf v}_1, {\bf v}_2, \ldots\) равно векторов в коллекции векторов.
- Итак, иногда необходимо тщательно анализировать индексы.
Далее рассмотрим 3D-пример:
- Пусть \({\bf u}=(1,3,1), {\bf v}=(4,1,0), {\bf w}=(3,2,6)\)
и \({\bf z}=(1,7,8)\).

- Мы хотели бы знать, является ли линейная комбинация \({\bf u,v,w}\) продукт \({\bf z}\).
- То есть можем ли мы найти числа \(\alpha, \beta, \gamma\) такой, что \(\alpha{\bf u} + \beta{\bf v} + \gamma{\bf w} = {\bf z}\)?
- В приведенном выше примере это будет означать $$ \альфа(1,3,1) + \бета (4,1,0) + \гамма (3,2,6) = (1,7,8) $$
 Мы ищем
\(\альфа,\бета,\гамма\) такой, что
\(\alpha{\bf u} + \beta{\bf v} + \gamma{\bf w} = {\bf z}\).
Запишите уравнения для \(\alpha,\beta,\gamma\) и
решить вручную.
Код в LinComb3DExample3.java
отображает четыре вектора.
Объясните геометрически, почему это согласуется с вашим решением.
Мы ищем
\(\альфа,\бета,\гамма\) такой, что
\(\alpha{\bf u} + \beta{\bf v} + \gamma{\bf w} = {\bf z}\).
Запишите уравнения для \(\alpha,\beta,\gamma\) и
решить вручную.
Код в LinComb3DExample3.java
отображает четыре вектора.
Объясните геометрически, почему это согласуется с вашим решением.3.3 Векторы в виде столбца
Форма столбца:
- Раньше мы записывали векторы в виде «строки», например, $$ {\ бф и} \; \; знак равно (4,1,0) $$
- В виде столбца это выглядит так: $$ {\ бф и} \; \; знак равно \vecthree{4}{1}{0} $$
- Обычно предпочтительнее столбчатая форма. По крайней мере, для по теоретическим соображениям, вот как вы должны думать об этом.
- Позже мы увидим, что форма строки называется транспонирует формы столбца. 9Т \;\; знак равно \vecthree{4}{1}{0} $$
3.4 Матрицы
Чтобы увидеть, откуда берутся матрицы, давайте посмотрим на некоторые из предыдущих примеры с линейными комбинациями
- Вспомните этот двумерный пример: мы ищем \(\alpha, \beta\) такие, что
$$
\альфа (1,4) + \бета (3,2) \eql (7.
 5,10)
$$
5,10)
$$ - В виде столбца это становится $$ \alpha \vectwo{1}{4} + \beta \vectwo{3}{2} \eql \vectwo{7.5}{10} $$
- В каком-то смысле \(\alpha\) и \(\beta\) — это два интересующие элементы, а остальные числа в качестве «данных».
- Предположим, мы сгруппировали «данные» следующим образом: $$ \мат{ 1 и 3\\ 4 и 2\\} \ раз \rvectwo{\альфа}{\бета} \eql \vectwo{7.5}{10} $$
- На данный момент мы поставили линейный комбинация скаляров \(\alpha\) и \(\beta\) в том, что выглядит как вектор-столбец.
- Аналогичным образом рассмотрим 3D-пример: $$ \альфа (1,3,1) + \бета (4,1,0) + \гамма (3,2,6) \экл (1,7,8) $$
- В виде столбца: $$ \alpha \vecthree{1}{3}{1} + \beta \vecthree{4}{1}{0} + \gamma\vecthree{3}{2}{6} \eql\vecthree{1}{7}{8} $$
- Как и в случае 2D, мы сгруппируем «данные» и множители (скаляры) отдельно: $$ \мат{ 1 и 4 и 3\\ 3 и 1 и 2\\ 1 и 0 и 6\\ } \ раз \rvecthree{\alpha}{\beta}{\gamma} \eql \vecthree{1}{7}{8} $$
- И снова линейная комбинация множители \(\альфа,\бета,\гамма\)
сгруппированы в то, что подозрительно похоже на вектор, но им не является.
 (Пока что.)
(Пока что.) - Более крупные прямоугольные блоки, такие как $$ \мат{ 1 и 3\\ 4 и 2\\} \;\;\; \mbox{ и } \;\;\; \мат{ 1 и 4 и 3\\ 3 и 1 и 2\\ 1 и 0 и 6\\ } $$ называются матриц ( матрица в единственном числе).
- Наблюдайте, как «отклеиваются» столбцов матрицы чтобы соответствовать соответствующему множителю в линейной комбинации.
- Пример: письменно
$$
\мат{
\color{dkgreen}{1} и \color{dkred}{3} \color{black}{}\\
\color{dkgreen}{4} и \color{dkred}{2} \color{black}{}\\
}
\ раз
\rvectwo{\color{dkgreen}{\alpha}}{\color{dkred}{\beta}}
\черный цвет}{}
\eql
\vectwo{7.5}{10}
$$
мы действительно имеем в виду
$$
\color{dkgreen}{\alpha} \color{black}{}
\mat{\color{dkgreen}{1}\\ \color{dkgreen}{4} \color{black}{}}
\; + \;
\color{dkred}{\beta} \color{black}{}
\mat{\color{dkred}{3} \\\color{dkred}{2} \color{black}{}}
\eql\vectwo{7.
 5}{10}
$$
5}{10}
$$ - Аналогично, в письменной форме $$ \мат{ \color{dkgreen}{1} & \color{dkred}{4} & \color{dkblue}{3} \color{black}{}\\ \color{dkgreen}{3} & \color{dkred}{1} & \color{dkblue}{2} \color{black}{}\\ \color{dkgreen}{1} & \color{dkred}{0} & \color{dkblue}{6} \color{black}{}\\ } \ раз \rvecthree{\color{dkgreen}{\alpha}}{\color{dkred}{\beta}}{\color{dkblue}{\gamma}} \color{black}{} \eql \vecthree{1}{7}{8} $$ мы действительно имеем в виду $$ \color{dkgreen}{\alpha} \color{black}{} \mat{\color{dkgreen}{1}\\ \color{dkgreen}{3} \\ \color{dkgreen}{1} \черный цвет}{}} \; + \; \color{dkred}{\beta} \color{black}{} \mat{\color{dkred}{4}\\ \color{dkred}{1} \\ \color{dkred}{0} \черный цвет}{}} \; + \; \color{dkblue}{\gamma} \color{black}{} \mat{\color{dkblue}{3}\\ \color{dkblue}{2} \\ \color{dkblue}{6} \черный цвет}{}} \eql\vecthree{1}{7}{8} $$
- Теперь обратите внимание, как легко «читать» уравнения
для множителей из линейно-комбинационной формы:
\(\rhd\) Просто умножьте строку на множители и приравняйте к соответствующую запись справа.
- Таким образом, для первого уравнения мы читаем, если от $$ \color{dkgreen}{\bf \alpha} \color{black}{} \mat{\color{dkgreen}{\bf 1}\\ \color{dkgreen}{3} \\ \color{dkgreen}{1} \черный цвет}{}} \; + \; \color{dkred}{\bf \beta} \color{black}{} \mat{\color{dkred}{\bf 4}\\ \color{dkred}{1} \\ \color{dkred}{0} \черный цвет}{}} \; + \; \color{dkblue}{\bf \gamma} \color{black}{} \mat{\color{dkblue}{\bf 3}\\ \color{dkblue}{2} \\ \color{dkblue}{6} \черный цвет}{}} \eql\vecthree{\bf 1}{7}{8} $$ получить $$ \color{dkgreen}{\bf \alpha \times 1} \color{black}{} + \color{dkred}{\bf \beta \times 4} \color{black}{} + \color{dkblue}{\bf \gamma \times 3} \color{black}{} \eql {\bf 1} $$
- Это немного сложнее прочитать из матричной формы, но к этому привыкаешь: $$ \мат{ \color{dkgreen}{\bf 1} & \color{dkred}{\bf 4} & \color{dkblue}{\bf 3} \color{black}{}\\ \color{dkgreen}{3} & \color{dkred}{1} & \color{dkblue}{2} \color{black}{}\\ \color{dkgreen}{1} & \color{dkred}{0} & \color{dkblue}{6} \color{black}{}\\ } \ раз \rvecthree{\color{dkgreen}{\alpha}}{\color{dkred}{\beta}}{\color{dkblue}{\gamma}} \color{black}{} \eql \vecthree{\bf 1}{7}{8} $$
- Итак, матрица на самом деле представляет собой набор векторов (столбцов).

3,5 Матрично-векторное уравнение
Вернемся к приведенному выше 3D-примеру: $$ \мат{ 1 и 4 и 3\\ 3 и 1 и 2\\ 1 и 0 и 6\\ } \ раз \rvecthree{\alpha}{\beta}{\gamma} \eql \vecthree{1}{7}{8} $$
- Как уже упоминалось, группировка множителей \(\alpha, \beta, \gamma\) подозрительно похоже на вектор.
- Можно разработать разумную теорию линейной алгебры рассматривая эту группу как «набор множителей» но НЕ как вектор.
- Однако мы совершим прыжок веры прямо сейчас и просто поместите множители в вектор (обратите внимание на квадратные скобки): $$ \мат{ 1 и 4 и 3\\ 3 и 1 и 2\\ 1 и 0 и 6\\ } \ раз \vecthree{\alpha}{\beta}{\gamma} \eql \vecthree{1}{7}{8} $$
- Нам разрешено это делать?
- Три числа — это просто числа.
- Таким образом, группировка представляет собой кортеж.

- Это означает, что мы могли бы рассматривать его как вектор (и получить прочь с ним).
- Конечно, на данный момент мы не знаем, делает ли это геометрический смысл в этом.
- Поскольку теперь это вектор, мы будем использовать один символ с индексами: $$ \мат{ 1 и 4 и 3\\ 3 и 1 и 2\\ 1 и 0 и 6\\ } \ раз \vecthree{x_1}{x_2}{x_3} \eql \vecthree{1}{7}{8} $$
- Таким образом, множители теперь называются \(x_1, x_2\) и \(x_3\).
\(\rhd\) Они являются элементами вектора \({\bf x}=(x_1, x_2, x_3)\). - Мы также назовем вектор справа: $$ {\bf b} = \vecthree{1}{7}{8} $$
- Наконец, мы также будем использовать жирный шрифт для самой матрицы, например: $$ {\bf А} \экл \мат{ 1 и 4 и 3\\ 3 и 1 и 2\\ 1 и 0 и 6\\ } $$
- Наконец, мы можем написать линейную
комбинация в самой компактной форме:
$$
{\bf А х} \eql {\bf b}
$$
- Давайте рассмотрим, как это будет выглядеть для большего размера
матрицы:
- Матрица \(n \times n\) \({\bf A}\) часто записывается следующим образом, где \(a_{ij}\) обозначает запись (число) в строке \(i\) и столбце \(j\): $$ \мат{ а_{11} и а_{12} и \cdots и а_{1n} \\ а_{21} и а_{22} и \cdots и а_{2n} \\ \vdots & \vdots & & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \\ } $$
- Тогда произведение на вектор \({\bf x}\) длины \(n\) похоже: $$ \мат{ а_{11} и а_{12} и \cdots и а_{1n} \\ а_{21} и а_{22} и \cdots и а_{2n} \\ \vdots & \vdots & & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} } \мат{ х_1\\ х_2\\ \vdots\\ х_n } $$
- Результатом является вектор:
$$
\мат{
а_{11} и а_{12} и \cdots и а_{1n} \\
а_{21} и а_{22} и \cdots и а_{2n} \\
\vdots & \vdots & & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn}
}
\мат{
х_1\\
х_2\\
\vdots\\
х_n
}
\eql
\мат{
\sum_{k=1}^n a_{1k} x_k\\
\sum_{k=1}^n a_{2k} x_k\\
\vdots\\
\sum_{k=1}^n a_{nk} x_k
}
$$
Обратите внимание: каждая сумма справа представляет собой одно число.

Два основных толкования матрично-векторное уравнение \({\bf A x} = {\bf b}\):
- Интерпретация как линейная комбинация столбцов \({\bf A}\):
- Здесь элементы \({\bf x}\) являются просто множителями.
- \({\bf x}\) не рассматривается как вектор, за исключением удобство написания.
- Нам обычно дают \({\bf b}\) (и \({\bf A}\)), и хотите найти \({\bf x}\).
- Интерпретация как матрица, «действующая» на вектор (или
трансформируя его):
- Здесь \({\bf x}\) рассматривается как вектор.
- Матрица «что-то с ней делает» посредством умножения, производя вектор \({\bf b}\) справа.
- Таким образом, можно сказать, что матрица \({\bf A}\) преобразует вектор \({\bf x}\) в вектор \({\bf b}\).

- При такой интерпретации \({\bf A x} = {\bf b}\) не столько уравнение, сколько производящая формула: нам даны \({\bf A}\) и \({\bf x}\) для вычисления \({\bf b}\).
Классное упражнение 16: Скачать MatrixVectorExample.java и напишите код для выполнения матрично-векторного произведения. затем подтвердите свои расчеты выше из отображаемых векторов.
Классное упражнение 17: Вычислите вектор, полученный путем умножения \({\bf x}\)
выше матрицей \({\bf C} = \mat{2 & -1\\ 0 & -3}\). Сравните со значением \({\bf z}\), рассчитанным ранее.
Сравните со значением \({\bf z}\), рассчитанным ранее.
Классное упражнение 18: Вычислите вектор, полученный путем умножения \({\bf z}\) выше с помощью матрицы \({\bf C}_2 = \mat{1,0/2 & -1,0/6\\ 0 & -1,0/3}\). Сравните со значением \({\bf x}\), рассчитанным ранее.
Классное упражнение 19: Ранее вы вычислили произведение \({\bf A}=\mat{a_{11} & a_{12}\\ a_{21} & a_{22}}\) с вектором \({\bf x}=\vectwo{x_1}{x_2}\), который создает результирующий вектор. Умножьте этот результирующий вектор на \({\bf B}=\mat{b_{11} & b_{12}\\ b_{21} & b_{22}}\). (Результат, по общему признанию, не очень.)
Наконец, обратите внимание, что матрицы не обязательно должны быть квадратными: $$ \мат{ 1 и 4 и 3 и 0 и 5\\ 3 и 1 и 2 и -1,5 и 5\\ 1 и 0 и 6 и -2 и 1\\ } \ раз \mat{ х_1 \\ х_2 \\ х_3 \\ х_4 \\ х_5} \eql x_1 \vecthree{1}{3}{1} + x_2 \vecthree{4}{1}{0} + x_3 \vecthree{3}{2}{6} + x_4 \vecthree{0}{-1. 5}{-2}
+ x_5 \vecthree{5}{5}{1}
\eql
\мат{б_1\б_2\б_3}
$$
5}{-2}
+ x_5 \vecthree{5}{5}{1}
\eql
\мат{б_1\б_2\б_3}
$$- Здесь 5 столбцов матрицы представляют собой трехкомпонентные векторы.
- Для линейной комбинации из 5 столбцов требуется 5 множителей: \(x_1, x_2, x_3, x_4, x_5\).
- Результатом линейной комбинации является трехкомпонентный вектор, который мы назвали \({\bf b}=(b_1,b_2,b_3)\).
- Таким образом, матрица из \(m\) строк и \(n\) столбцов равна многократно совместимый с вектором, который имеет \(n\) компонентов, в результате чего получается вектор с \(m\) компонентами.
- Мы пишем это как $$ {\bf A}_{m\times n} {\bf x}_{n\times 1} \eql {\bf b}_{m\times 1} $$
3,6 Матрично-матричное умножение
Рассмотрим следующий пример матрицы \({\bf A}\) умножение (и, таким образом, преобразование) вектора \({\bf x}\): $$ {\bf топор} \eql \mat{2 & -3\\ 0 & 1} \vectwo{2}{3} $$ Предположим, что результатом является вектор \({\bf y}\): $$ \mat{2 & -3\\ 0 & 1} \vectwo{2}{3} \eql \vectwo{y_1}{y_2} $$ Теперь предположим, что мы умножаем \({\bf y}\) на матрицу \({\bf B}\) чтобы получить вектор \({\bf z}\): $$ \mat{1 & 2\\ 0 & -3} \vectwo{y_1}{y_2} \eql \vectwo{z_1}{z_2} $$ Но поскольку \({\bf y}\) сам создан из матрицы-вектора произведение \({\bf Ax}\), мы можем заменить \({\bf y}\) на $$ \mat{1 & 2\\ 0 & -3} \left( \mat{2 & -3\\ 0 & 1} \vectwo{2}{3} \right) \eql \vectwo{z_1}{z_2} $$ Очевидно, интересен вопрос, являются ли эти два матрицы могут быть «объединены», чтобы создать единую матрицу для преобразовать \({\bf x}=(2,3)\) в \({\bf z}\): $$ \color{dkgreen}{ \mat{1 & 2\\ 0 & -3} \mat{2 & -3\\ 0 & 1} } \color{черный}{} \vectwo{2}{3} \eql \color{dkgreen}{\mat{? & ?\\ ? & ?}} \цвет{черный}{} \vectwo{2}{3} \eql \vectwo{z_1}{z_2} $$
Как оказалось, есть хороший способ «умножить» матрицы. чтобы полученный продукт производил то же действие, что и
две исходные матрицы применялись последовательно.
чтобы полученный продукт производил то же действие, что и
две исходные матрицы применялись последовательно.
Давайте решим это для случая \(2\times 2\): $$ \eqb{ \mat{b_{11} и b_{12}\\ b_{21} и b_{22}} \мат{а_{11} и а_{12}\\ а_{21} и а_{22}} \vectwo{x_1}{x_2} & \eql & \mat{b_{11} и b_{12}\\ b_{21} и b_{22}} \mat{a_{11}x_1 + a_{12}x_2 \\ a_{21}x_1 + a_{22}x_2}\\ & \eql & \мат{ b_{11}(a_{11}x_1 + a_{12}x_2) + b_{12} (a_{21}x_1 + a_{22}x_2)\\ b_{21}(a_{11}x_1 + a_{12}x_2) + b_{22} (a_{21}x_1 + a_{22}x_2) }\\ & \eql & \мат{ (b_{11}a_{11} + b_{12}a_{21})x_1 + (b_{11}a_{12} + b_{12}a_{22})x_2 \\ (b_{21}a_{11} + b_{22}a_{21})x_1 + (b_{21}a_{12}+ b_{22}a_{22})x_2 }\\ & \eql & \мат{ б_{11}а_{11} + б_{12}а_{21} и б_{11}а_{12} + б_{12}а_{22} \\ б_{21}а_{11} + б_{22}а_{21} и б_{21}а_{12}+ б_{22}а_{22} } \vectwo{x_1}{x_2} } $$
Итак, у нас есть произведение матриц на матрицу $$ \mat{b_{11} и b_{12}\\ b_{21} и b_{22}} \мат{а_{11} и а_{12}\\ а_{21} и а_{22}} \eql \мат{ б_{11}а_{11} + б_{12}а_{21} и б_{11}а_{12} + б_{12}а_{22} \\ б_{21}а_{11} + б_{22}а_{21} и б_{21}а_{12}+ б_{22}а_{22} } $$ Обратите внимание, что каждая запись результата представляет собой строк из \({\bf B}\) умножить на столбец из \({\bf A}\)
И случается обобщать на большие матрицы:
- Предположим, мы перемножаем матрицы \({\bf B}\) и \({\bf A}\) чтобы получить \({\bf C}\): $$ \мат{ b_{11} & b_{12} & \cdots & b_{1n} \\ b_{21} & b_{22} & \cdots & b_{2n} \\ \vdots & \vdots & & \vdots \\ b_{n1} & b_{n2} & \cdots & b_{nn} } \мат{ а_{11} и а_{12} и \cdots и а_{1n} \\ а_{21} и а_{22} и \cdots и а_{2n} \\ \vdots & \vdots & & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} } \eql \мат{ c_{11} & c_{12} & \cdots & c_{1n} \\ c_{21} & c_{22} & \cdots & c_{2n} \\ \vdots & \vdots & & \vdots \\ c_{n1} & c_{n2} & \cdots & c_{nn} } $$ 9n b_{ik} a_{kj} $$
Классное упражнение 20: Скачать MatrixVectorExample2. java
и напишите код умножения матриц, чтобы пример работал.
Убедитесь, что вы получили ту же матрицу в упражнении 17, а
тот же результирующий вектор.
java
и напишите код умножения матриц, чтобы пример работал.
Убедитесь, что вы получили ту же матрицу в упражнении 17, а
тот же результирующий вектор.
Классное упражнение 21: Рассмотрим матрицы $$ {\бф А} \; знак равно \мат{ 3 и 2 и 1\\ -2 и 3 и 5\\ 0 и 0 и 3 } \;\;\;\;\;\;\; \mbox{ и } \;\;\;\;\;\;\; {\ бф В} \; знак равно \мат{ -4 и 1 и 0\\ 1 и 0 и 1\\ 3 и -2 и 1 } $$ Пусть \({\bf x}=(1,-1,2)\) и определим \({\bf y}={\bf Ax}\) и \({\bf z}={\bf By}\). Вычислить каждое из \({\bf y, z}\) и произведение матриц \({\bf C}={\bf BA}\). Подтвердить путем расчета \({\bf Cx}\).
Классное упражнение 22: Загрузите MatrixVector3DExample.java, затем заполните код (из предыдущих упражнений), чтобы выполнить матрицу умножение и умножение матрицы на вектор. Убедитесь, что результаты совпадают с расчетами в предыдущем упражнении.
Классное упражнение 23: Предположим, \({\bf A}\) и \({\bf B}\) две \(n \times n\) матрицы. Докажите или опровергните: \({\bf AB} = {\bf BA}\).
Докажите или опровергните: \({\bf AB} = {\bf BA}\).
3,7 Неквадратные матрицы
Потому что умножение матриц берет строку слева матрица и умножается в столбец правой матрицы, оказывается, мы можем перемножать неквадратные матрицы:
- Пример:
- Предположим $$ {\bf А} \экл \мат{ 1 и 0 и -1 и 2 и 0\\ 0 и 2 и -3 и 1 и 3 } \;\;\;\;\;\;\;\; \mbox{ и } \;\;\;\;\;\;\;\; {\ бф В} \ экл \мат{ -1 и 2 и 0\\ 4 и 0 и -2\\ 0 и -2 и 1\\ -1 и 1 и 3\\ 5 и -2 и -1 } $$
- Тогда \({\bf AB}\) можно вычислить как $$ {\bf AB} \eql \мат{ 1 и 0 и -1 и 2 и 0\\ 0 и 2 и -3 и 1 и 3 } \мат{ -1 и 2 и 0\\ 4 и 0 и -2\\ 0 и -2 и 1\\ -1 и 1 и 3\\ 5 и -2 и -1 } \eql \мат{ -3 и 6 и 5\\ 22 и 1 и -7 } $$
- Они совместимы по множеству, потому что строка \({\bf A}\)
имеет то же количество элементов, что и столбец \({\bf B}\).

- Каждая строка \({\bf A}\) (их 2)
умножает каждый столбец \({\bf B}\) (3 из них)
\(\rhd\) Будет \(2 \times 3\) записей для \(2 \times 3\) матрица.
- Обозначение: мы часто пишем \({\bf A}_{m\times n}\) в явно обратите внимание на количество строк (\(m\)) и столбцов (\(n\)).
- Таким образом, \({\bf C}_{m\times k} = {\bf A}_{m\times n} {\bf
B}_{n\раз k}\)
- Здесь \({\bf A}_{m\times n}\) и \({\bf B}_{n\times k}\) являются многократно совместимыми.
- Результирующая матрица равна \(m \times k\).
- Обозначение: для любой матрицы \({\bf A}\ запись в i-я строка и j-й столбец иногда называются \({\bf A}_{ij}\) или \({\bf A}(i,j)\).
Классное упражнение 24: Что получается в результате умножения \({\bf A} = \mat{0 & 1 & 0 \\ -1 & 2 & 0}\) а также \({\bf B}= \mat{1 & 1\\ 2 & 2\\ 0 & -3}\)? Что такое \({\bf Ax}\), если \({\bf x}=(2,3,4)\)?
3,8 Обзор трех случаев, связанных с уравнениями
Давайте вернемся к трем типам ситуаций, с которыми мы столкнулись, когда решение уравнений:
- Проблема 1: $$ \eqb{ х_1+3х_2&=7,5\ 4x_1+2x_2&=10\ } $$
- Проблема 2 $$ \eqb{ х_1+3х_2&=7,5\ 2х_1+6х_2&=10\ } $$
- Проблема 3 $$ \eqb{ х_1+3х_2&=4\ 2х_1+6х_2&=8\ } $$
Проблема 1:
- Первый набор уравнений:
$$
\eqb{
х_1+3х_2&=7,5\
4x_1+2x_2&=10\
}
$$
Что в матричной форме:
$$
\мат{
1 и 3\\
4 и 2\\}
\vectwo{x_1}{x_2}
\eql
\vectwo{7.
 5}{10}
$$
5}{10}
$$ - Теперь запишем то же самое в форме «векторного растяжения»: $$ x_1 \vectwo{1}{4} + x_2 \vectwo{3}{2} \eql \vectwo{7.5}{10} $$
- Решение: \(x_1=1,5, \;\; x_2=2\).
- На фото:
- Таким образом, мы ясно видим, что существует один линейный комбинация двух векторов \((1,4)\) и \((3,2)\), которая дает \((7.5,10)\).
- Второй набор уравнений $$ \eqb{ х_1+3х_2&=7,5\ 2х_1+6х_2&=10\ } $$ в виде «векторного растяжения»: $$ x_1 \vectwo{1}{2} + x_2 \vectwo{3}{6} \eql \vectwo{7.5}{10} $$
- Решение? Нет решения.
- На фото:
- Ясно, что никакая линейная комбинация \((1,2)\) и \((3,6)\) дает \((7.5,10)\).
- Фактически, все линейных комбинаций \((1,2)\) и \((3,6)\) лежат на прямой, на которую падают оба.
- Это означает, что они не могут линейно комбинироваться для формирования вектора
под любым другим углом.

- Таким образом, без всяких попыток вы можете сказать, что эти уравнения делают не имеют решения: $$ \eqb{ х_1+3х_2&=4\ 2x_1+6x_2&=3\ } $$
- Третий набор $$ \eqb{ х_1+3х_2&=4\ 2х_1+6х_2&=8\ } $$ в виде «векторного растяжения»: $$ x_1 \vectwo{1}{2} + x_2 \vectwo{3}{6} \eql \vectwo{4}{8} $$
- Решение? Существует бесконечно много решений.
- На фото:
- Из картинки видно, что бесконечно много решений?
- Вернемся к картинке в Задаче 1:
- На рисунке показано, почему в данном случае решение единственное.
- Некоторые вопросы, которые возникают в этот момент:
- Это единственные три возможных случая для любой системы уравнений?
- Когда существует несколько решений, всегда ли они бесконечны? их количество?
- Когда есть единственное решение, всегда ли оно соответствует картинка как на картинке выше?
3,9 Советы по учебе
- Этот модуль содержит много важных идей seed .
 Это стоит
тщательно просматривая.
Это стоит
тщательно просматривая. - Когда вы читаете, читайте с ручкой и бумагой и работайте над упражнения, как вы идете, а НЕ в конце чтения всего этого.
- Несмотря на то, что некоторые примеры ручного решения немного утомительно, их стоит сделать хотя бы раз, потому что они помогают привести домой определение или процедуру.
- Запишите резюме или список основных моментов для каждого модуля.
Одной из важных целей обучения в любом курсе должно быть создание внутренний рассказ о том как разные штуки конечно подходят друг-другу.
На этом раннем этапе нам не хватает «кусочков», чтобы сформировать представление о целом.
Поскольку это теоретический курс, рекомендуется чтобы отметить интересные теоретические вопросы по пути.
В этом модуле некоторые вопросы, которые приходят на ум:
- Даны два вектора \({\bf u,v}\), при каких условиях Является ли это возможным выразить любой другой вектор \({\bf w}\) в виде линейной комбинации из двух?
- Зависит ли ответ на этот вопрос от измерения?
- В общем, обобщаются ли наблюдения о 2D и 3D на \(n\) Габаритные размеры?
- Какие свойства обычного (числа на число) умножения также удовлетворяются умножением матриц?
- Если матрица \({\bf A}\) преобразует вектор \({\bf x}\)
в \({\bf b}={\bf Ax}\), можно ли найти
матрица \({\bf A’}\) для обращения преобразования, т.
 е.
\({\bf x}={\bf A’b}\)?
е.
\({\bf x}={\bf A’b}\)?
Документы векторной поисковой системы Weaviate
Добро пожаловать в документацию Weaviate. Здесь вы узнаете, что такое Weaviate, как создать свой экземпляр Weaviate, взаимодействовать с ним и использовать его для выполнения векторного поиска и классификации.
Вкратце о Weaviate :
- Weaviate — это база данных с открытым исходным кодом векторной поисковой системы.
- Weaviate позволяет хранить документы JSON в виде свойств класса, прикрепляя к этим документам векторы машинного обучения для представления их в векторном пространстве.
- Weaviate можно использовать автономно (он же приносит ваши векторы ) с широким спектром модулей, которые могут выполнять векторизацию за вас или расширять основные возможности.
- У Weaviate есть GraphQL-API для простого доступа к вашим данным.

- Мы стремимся довести вашу настройку векторного поиска до производства, чтобы выполнять запросы всего за миллисекунды (проверьте наши тесты с открытым исходным кодом, чтобы увидеть, подходит ли Weaviate для вашего варианта использования).
- Познакомьтесь с Weaviate в руководстве по началу работы менее чем за пять минут.
Weaviate в деталях : Weaviate — векторный поисковик с малой задержкой и встроенной поддержкой различных типов мультимедиа (текст, изображения и т. д.). Он предлагает семантический поиск, извлечение вопросов и ответов, классификацию, настраиваемые модели (PyTorch/TensorFlow/Keras) и т. д. Созданный с нуля на Go, Weaviate хранит как объекты, так и векторы, что позволяет сочетать векторный поиск со структурированной фильтрацией и отказоустойчивостью. облачной базы данных, доступной через клиент GraphQL, REST и различных языков программирования.
- Инженеры-программисты — которые используют Weaviate в качестве базы данных на основе машинного обучения для своих приложений.

- Готовые модули для НЛП/семантического поиска, автоматической классификации и поиска сходства изображений.
- Легко интегрируется с текущей архитектурой, с полной поддержкой CRUD, как и другие базы данных OSS.
- Облачная, распределенная, хорошо работает в Kubernetes и масштабируется в соответствии с рабочими нагрузками.
- Data Engineers — которые используют Weaviate в качестве векторной базы данных, созданной с нуля с использованием ANN в основе и с тем же UX, который им нравится в поисковых системах на основе Lucene.
- Weaviate имеет модульную настройку, которая позволяет вам использовать ваши модели машинного обучения внутри Weaviate. Благодаря его гибкости вы также можете использовать готовые модели машинного обучения (например, SBERT, ResNet, fasttext и т. д.).
- Weaviate позаботится о масштабируемости, чтобы вам не приходилось этого делать.
- Надежно и эффективно развертывайте и обслуживайте модели машинного обучения в производственной среде.

- Специалисты по данным — которые используют Weaviate для беспрепятственной передачи своих моделей машинного обучения в MLOps.
- Надежно и эффективно развертывайте и обслуживайте модели машинного обучения в производственной среде.
- Модульная конструкция Weaviate позволяет легко упаковать любую специально обученную модель.
- Плавная и ускоренная передача моделей машинного обучения инженерам.
Weaviate упрощает использование современных моделей искусственного интеллекта, обеспечивая при этом масштабируемость, простоту использования, безопасность и экономичность специализированной векторной базы данных. В частности:
Быстрые запросы
Weaviate обычно выполняет поиск ближайшего соседа (NN) миллионов объектов значительно менее чем за 100 мс. Вы можете найти больше информации на нашей странице тестов.Загрузка любого типа мультимедиа с помощью модулей Weaviate
Использование современной модели искусственного интеллекта (например, Transformers) для доступа к тексту, изображениям и т. д. данным во время поиска и запроса, чтобы позволить Weaviate управлять процесс векторизации данных для вас или возможность импорта ваших собственных векторов.
д. данным во время поиска и запроса, чтобы позволить Weaviate управлять процесс векторизации данных для вас или возможность импорта ваших собственных векторов.Комбинированный векторный и скалярный поиск
Weaviate позволяет выполнять эффективный комбинированный векторный и скалярный поиск, например, «статьи, связанные с пандемией COVID-19, опубликованные за последние 7 дней». Weaviate хранит как объекты, так и векторы и обеспечивает постоянную эффективность их извлечения. Нет необходимости в стороннем объектном хранилище.Постоянный и постоянный
Weaviate позволяет выполнять поиск по вашим данным, даже если они в настоящее время импортируются или обновляются. Кроме того, каждая запись записывается в журнал опережающей записи (WAL) для немедленной записи, даже если происходит сбой.Горизонтальная масштабируемость
Масштабирование Weaviate для ваших конкретных потребностей, например, максимальное потребление, максимально возможный размер набора данных, максимальное количество запросов в секунду и т. д.
д.Высокая доступность
выпущен позже в этом году.Экономическая эффективность
Очень большие наборы данных не нужно хранить полностью в памяти в Weaviate. В то же время доступную память можно использовать для увеличения скорости запросов. Это позволяет найти компромисс между скоростью и стоимостью для каждого варианта использования.Связи между объектами в виде графиков
Создавайте произвольные связи между объектами в виде графиков, чтобы они напоминали реальные связи между точками данных. Пройдите эти соединения с помощью GraphQL.
В Weaviate все отдельные объекты данных основаны на структуре свойств класса, где каждый объект данных представляет вектор. Вы можете соединять объекты данных (как в традиционном графе) и искать объекты данных в векторном пространстве.
Вы можете добавлять данные в Weaviate через конечные точки RESTful API и получать данные через интерфейс GraphQL.
Механизм индексации векторов Weaviates является модульным, а текущий доступный подключаемый модуль представляет собой многослойный граф Hierarchical Navigable Small World (HNSW).
Модули Weaviate используются для расширения возможностей Weaviate и являются дополнительными. Существуют модули Weaviate, которые автоматически векторизируют ваш контент (например, *2vec ) или расширяют возможности Weaviate (часто связанные с типом векторов, которые у вас есть). Вы также можете создавать свои собственные модули. Нажмите здесь, чтобы начать работу с ними.
Если вы работаете с данными, вы, вероятно, работаете с технологией поисковых систем. Лучшие поисковые системы — это удивительные программы, но из-за их основной архитектуры они имеют ограничения, когда дело доходит до поиска данных, которые вы ищете.
Возьмем, к примеру, объект данных: { "data": "Эйфелева башня — это решетчатая башня из кованого железа на Марсовом поле в Париже." }
Сохранение этого в традиционной поисковой системе может использовать инвертированные индексы для индексации данных. Это означает, что для получения данных; вам нужно искать «Эйфелева башня» или «решетка из кованого железа» и т. д., чтобы найти его. Но что, если у вас есть огромное количество данных и вам нужен документ об Эйфелевой башне, но вы ищете: «достопримечательности Франции»? Традиционные поисковые системы не могут вам помочь, и именно здесь векторные поисковые системы показывают свое превосходство.
Это означает, что для получения данных; вам нужно искать «Эйфелева башня» или «решетка из кованого железа» и т. д., чтобы найти его. Но что, если у вас есть огромное количество данных и вам нужен документ об Эйфелевой башне, но вы ищете: «достопримечательности Франции»? Традиционные поисковые системы не могут вам помочь, и именно здесь векторные поисковые системы показывают свое превосходство.
Weaviate использует в своей основе механизмы векторной индексации для представления данных. Модули векторизации (например, модуль НЛП) векторизуют вышеупомянутый объект данных в векторном пространстве, где объект данных находится рядом с текстом «достопримечательности Франции». Это означает, что Weaviate не может дать 100% совпадение, но очень высокое, чтобы показать вам результаты.
Приведенный выше пример предназначен для текста (т. е. НЛП), но вы можете использовать его для любой модели машинного обучения, которая векторизует, например изображения, аудио, видео, гены и т. д.
д.
И последнее, но не менее важное: использование векторной поисковой системы для машинного обучения — это то, что вы делаете по той же причине, что и традиционную поисковую систему. Он позволяет быстро масштабировать, искать и классифицировать в режиме реального времени и может использоваться в надежной производственной среде.
Существует четыре основные ситуации, в которых следует рассмотреть возможность использования Weaviate.
- Если вам не нравится качество результатов, которые выдает ваша текущая поисковая система. (с помощью Weaviate вы можете осуществлять семантический поиск данных.)
- Если вы хотите выполнять поиск сходства текста и изображений с помощью готовых современных моделей машинного обучения. (Объедините хранение и запрос нескольких типов мультимедиа в одном экземпляре Weaviate.)
- Если вы хотите объединить семантический (векторный) и скалярный поиск с векторной базой данных, занимающей миллисекунды.
 (Weaviate хранит как ваши объекты, так и векторы и гарантирует, что поиск обоих всегда будет эффективным).
(Weaviate хранит как ваши объекты, так и векторы и гарантирует, что поиск обоих всегда будет эффективным). - Если вам нужно масштабировать собственные модели машинного обучения до производственного размера. (алгоритм HNSW и горизонтально масштабируемая поддержка операций с базой данных в режиме, близком к реальному времени)
- Если вам нужно классифицировать большие наборы данных быстро и почти в реальном времени. (kNN, нулевая или контекстная классификация с готовыми или пользовательскими моделями ML).
Люди используют Weaviate для таких задач, как семантический поиск, поиск изображений, поиск по сходству, обнаружение аномалий, системы рекомендаций по мощности, поиск в электронной коммерции, классификация данных в системах ERP, автоматическая гармонизация данных, анализ угроз кибербезопасности и многое-многое другое. случаи.
Хотите начать работу или узнать больше? Эти ресурсы могут помочь вам в дальнейшем:
- Начало работы:
- Обзор руководств Weaviate по началу работы
- Установка
- Дополнительные сведения:
- Страница ресурсов Weaviate
Если вы не можете найти ответ - вопрос здесь, пожалуйста, посмотрите на:
- Часто задаваемые вопросы.

- Часто задаваемые вопросы.


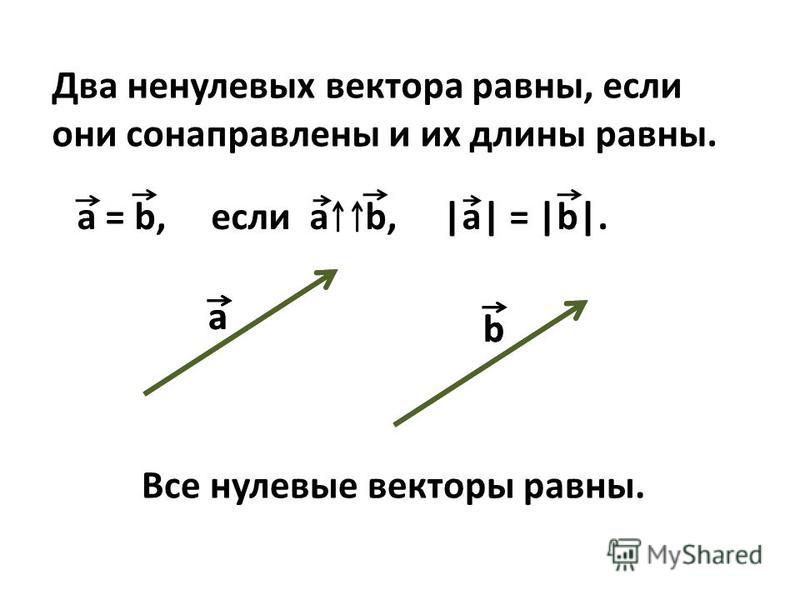 ..
.. ..
.. Теперь мы обобщим это понятие на набор $q$ абстрактных объектов, над которыми может воздействовать группа, обозначаемый $M=\{m_0,m_1,m_2,\dots,m_{q-1}\}$. Как и раньше, мы строим векторное пространство, подобное тому, которое использовалось выше при построении алгебры. Ортонормированных векторов здесь будет 9{q-1}a_i|m_i\rangle\,\right|\,a_i\in\mathbb{R}\,\forall i\right\}\tag{3.49}
\end{уравнение}
Теперь мы обобщим это понятие на набор $q$ абстрактных объектов, над которыми может воздействовать группа, обозначаемый $M=\{m_0,m_1,m_2,\dots,m_{q-1}\}$. Как и раньше, мы строим векторное пространство, подобное тому, которое использовалось выше при построении алгебры. Ортонормированных векторов здесь будет 9{q-1}a_i|m_i\rangle\,\right|\,a_i\in\mathbb{R}\,\forall i\right\}\tag{3.49}
\end{уравнение}
 д.) на
фактические цифры.
д.) на
фактические цифры.



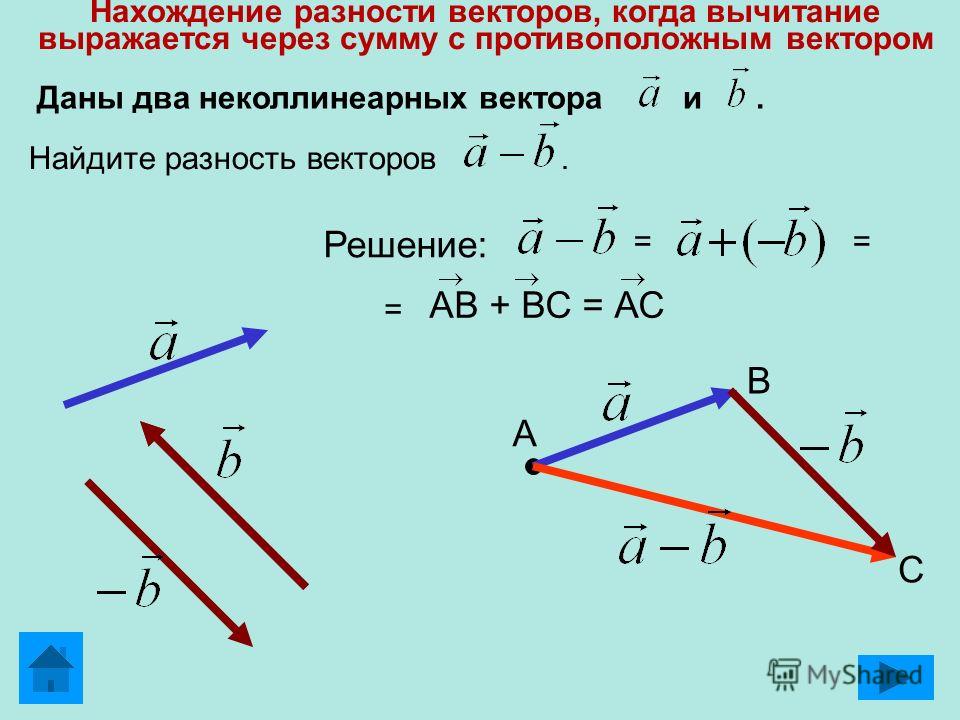

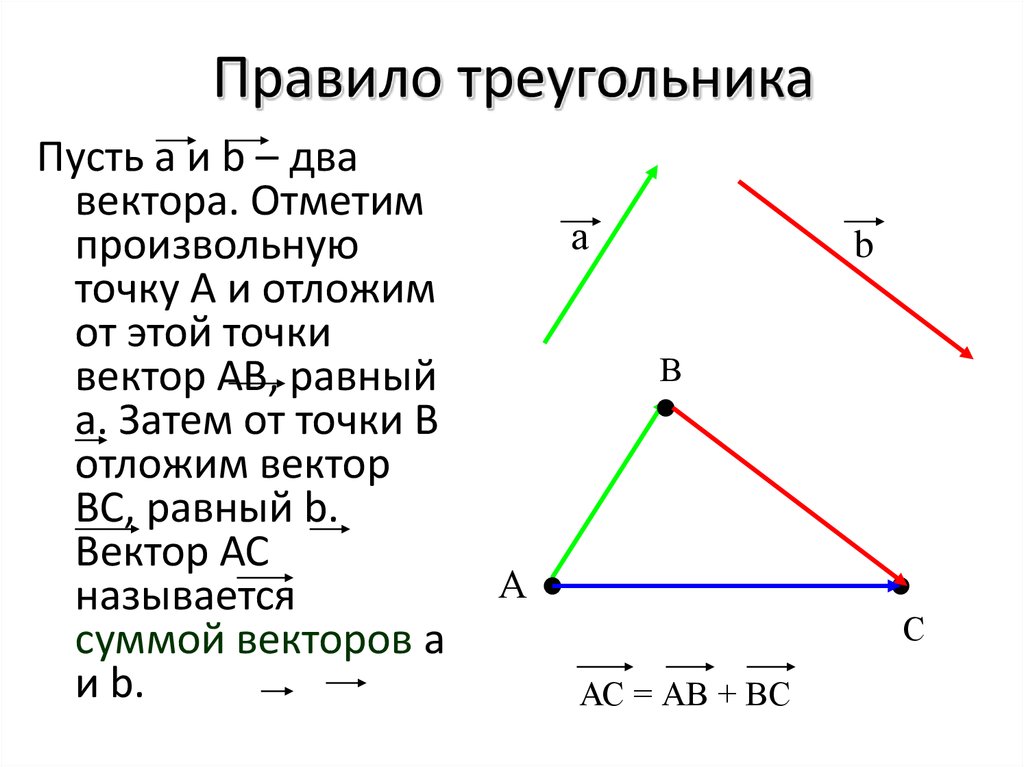


 5,10)
$$
5,10)
$$ (Пока что.)
(Пока что.) 5}{10}
$$
5}{10}
$$