Запись двоичная: Перевод чисел из десятичной системы в двоичную — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

Курс Java Multithreading — Лекция: Запись двоичного числа как 1000100В

— Привет, Амиго!

— Привет, Билаабо!

Хочу рассказать тебе немного про различные системы счисления.

Ты уже слышал, что люди пользуются десятичной системой счисления. Вот главные факты этого подхода:

1) Для записи числа используются 10 цифр: 0,1, 2, 3, 4, 5, 6, 7, 8, 9.

2) Число 543 значит 5 сотен + 4 десятка + 3 единицы.

Эта равносильно записи 5*100 + 4*10 + 3*1, что можно записать как 5*10²+4*10¹+3*10⁰

Обрати внимание – тысячи, сотни, десятки и единицы – это степени числа 10.

1) Единица – это 10 в нулевой степени.

2) Десять – это 10 в первой степени

3) Сто – это 10 во второй степени

4) Тысяча – это 10 в третьей степени и т.д.

— Ага. Понятно.

— А теперь представь, что цифр всего 8. Тогда у нас есть восьмеричная система счисления и вот ее главные факты:

1) Для записи числа используются 8 цифр: 0,1, 2, 3, 4, 5, 6, 7.

2) Число 543₈ значит 5*8²+4*8¹+3*8⁰. Т.е. это 5*64+4*8+3*1 = 320+32+3=355₁₀

Я написал снизу числа знаки 8 и 10, чтобы мы знали, сколько цифр используется для его записи.

— Вроде как и ясно. Я думаю, я бы смог перевести число из восьмеричной системы в десятичную. Но наоборот – вряд ли.

— Все не так уж и сложно. Представь, что тебе нужно перевести кучу песка на нескольких грузовых машинах. У тебя есть карьерные самосвалы, обычные, и совсем маленькие машинки. Но надо, чтобы машины не ехали полупустыми.

Как бы ты возил?

— Сначала я бы насыпал в карьерные самосвалы, они самые большие. Затем, когда понял, что для заполнения машины песка не хватит, то перешел бы на машины поменьше. Затем еще меньше.

— Тут все тоже очень похоже. Давай попробуем перевести число 355₁₀ обратно в восьмеричный формат.

Сначала мы разделим его на 64 (8²), получим 5 целых и 35 в остатке.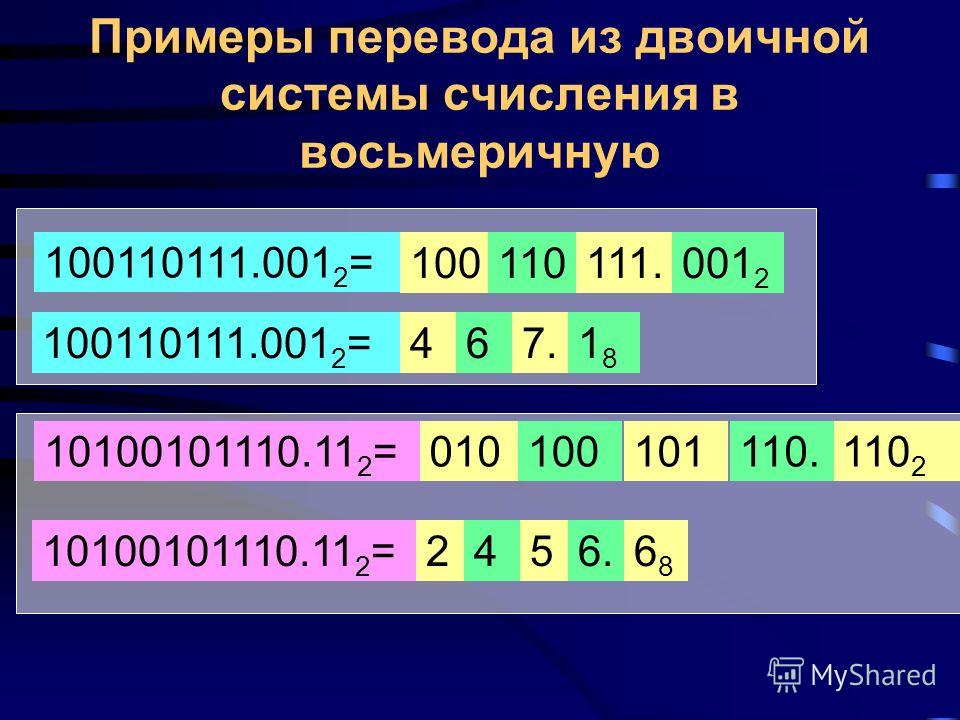 Значит первая цифра нашего числа – 5. Затем разделим остаток на 8(8¹), получим 4 и 3 в остатке. Так и получится число 543₈.

Можно, кстати, пойти и с другой стороны. Ведь 543₈ ==5*64+4*8+3 == ((5)*8+4)*8+3. Наши восьмеричные «десятки» и «сотни» обязательно делятся на 8. Значит, остаток от деления на 8 это и будут наши восьмеричные единицы.

Поделим сначала число 355 на 8. Получим 44 и 3 в остатке. Т.е. 355=44*8+3. А 44 можно представить как 5*8+4. Значит 355= (5*8+4)*8+3; Вот наши цифры: 5,4,3. Искомое число 543₈

— В общем вроде понятно, но надо немного попрактиковаться, чтобы окончательно во всем разобраться.

— В программировании очень часто используются числа с различным основанием (количеством цифр). Самые популярные – это 2, 8, 10, 16, 64.

— А зачем это нужно. Зачем нужны числа, состоящие из 2, 8, 16 и 64 цифр?

— Дело во внутреннем устройстве процессора. Очень упрощенно — если в проводе есть ток, то говорят, что в нем «единица», если тока нет, то в нем «ноль».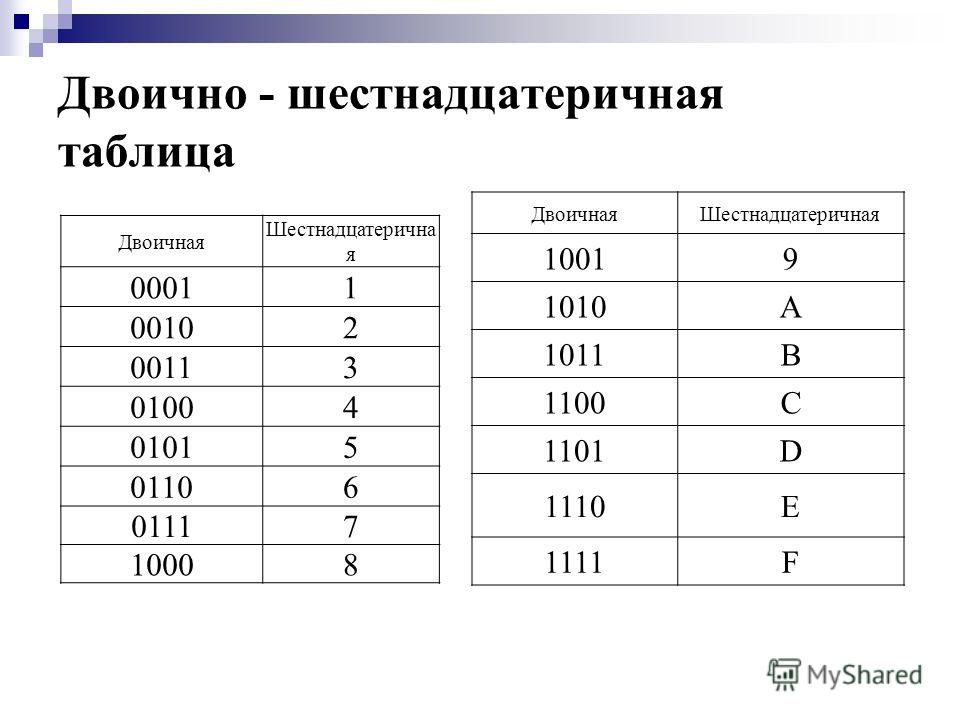

Все числа хранятся в памяти в виде ячеек. Устройство таких ячеек очень примитивно. Они тоже могу хранить только 0 или 1.

Зато такое упрощение всего (только 0 или 1) дало возможность сделать элементы внутри процессора и памяти очень маленькими. Современные процессоры и модули памяти включают миллиарды различных элементов. При том, что их площадь зачастую не превышает квадратного сантиметра.

— Ничего себе. Буду знать.

— Теперь перейдем к двоичным числам. Там то же самое, что и с восьмеричными, только еще проще.

1) Для записи числа используются 2 цифры: 0,1

2) Число 101₂ значит 1*2²+0*2¹+1*2⁰. Т.е. это 1*4+0*2+1*1 =4+1=5₁₀

— Да. Я помню. Одна ячейка, которая принимает значение 0 или 1 называется битом. Но т.к. в ней можно сохранить очень мало информации, то их объединяют в группы по 8. И называют такую группу – байтом.

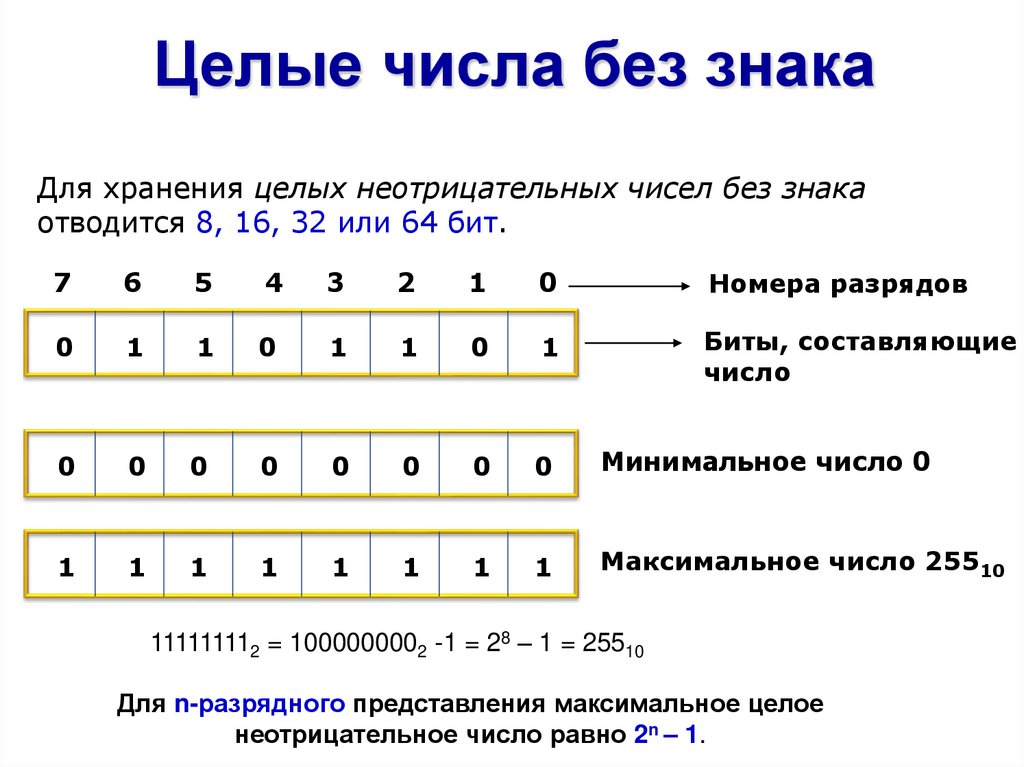
— Именно. Байт – это группа из восьми бит. В нем можно хранить значения: 00000000, 00000001, …, 11111111. Которые соответствуют десятичным 0,1,… 255. Всего 256 значений.

Какое самое большое целое число в Java? Вернее его тип?

— long. long состоит из 8 байт. Т.е. 64 бита и может хранить значения от -2⁶³ до 2⁶³-1

— Ага. Я не буду касаться темы, как переводить числа из десятичной системы в двоичную или наоборот. Иначе лекция слишком затянется.

Давай лучше еще немного расскажу про 16-ричную систему счисления.

— Да, очень интересно. Для двоичной и восьмеричной систем мы просто выкинули цифры начиная с двойки или восьмерки. А тут как? Мы добавим новые цифры?

— Именно! Смотри:

1) Для записи числа используются 16 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

2) Число 543₁₆ значит 5*16²+4*16¹+3*16

0. Т.е. это 5*256+4*16+3*1 =1280+64+3=1347₁₀

— Т.е. мы просто добавили буквы в качестве цифр? О_о

— Ага.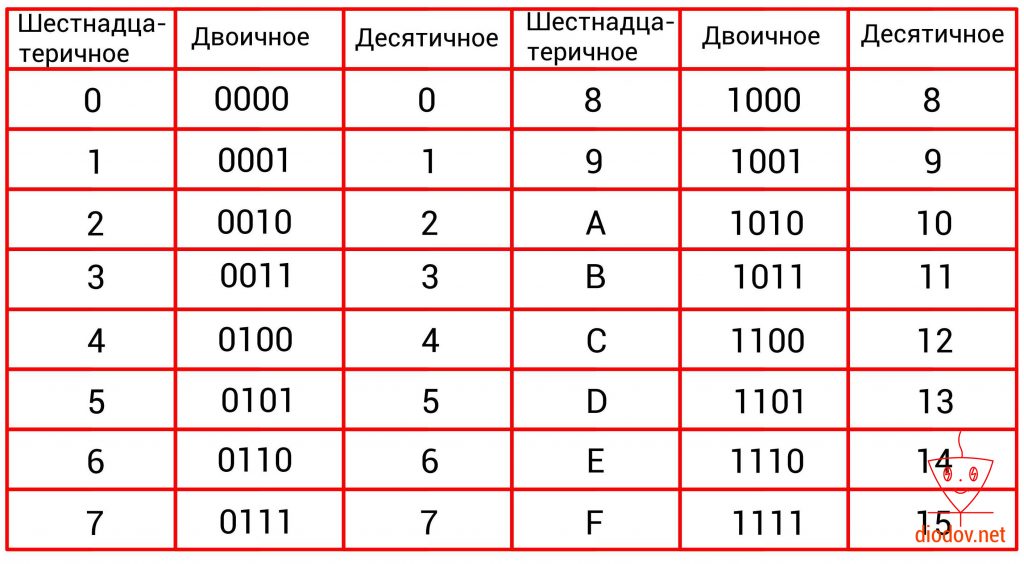 А что в этом такого? Зачем придумывать новые цифры, когда с этой ролью отлично справляются буквы. Вот смотри:

Шестнадцатеричная цифра	Десятичное значение
0	0
1	1
8	8
9	9
A	10
B	11
C	12
D	13
E	14
F	15

Про перевод из десятичной системы в шестнадцатеричную тоже рассказывать не буду. Зато есть один интересный факт. Шестнадцатеричная цифра – это ровно 4 бита со значениями от 0 до 15. Поэтому один байт можно записать восемью двоичными цифрами (0 или 1) или двумя шестнадцатеричными.

Пример:

Десятичное число	Двоичное число	Шестнадцатеричное число
0	0000 0000	00
1	0000 0001	01
15	0000 1111	0f
16	0001 0000	10
31	0001 1111	1f
32	0010 0000	20
128	1000 0000	80
129	1000 0001	81
255	1111 1111	ff

Шестнадцатеричное представление легко приводится к двоичному (и обратно). Поэтому, если где-то в программировании нужно показать именно внутреннее байтовое представление числа, то очень редко прибегают к двоичной записи через 0 и 1. Слишком длинно и не понятно. Шестнадцатеричная запись гораздо читабельней и компактней.

— Согласен. Даже мне понравилось.

— Кстати, в Java можно прямо в коде записывать числа в различных системах счисления:

Основание	Отличительный признак	Примеры	Неправильные числа
2	0b в начале числа	0b00001111	0b1111121
8	0 в начале числа	01234343	0128
10	нет	95459	909a
16	0x в начале числа	0x10ff	0x1cgh

— Отличная лекция. Спасибо, Билаабо.

Запись двоичных чисел

Двоичная система счисления является частным случаем сдвоенных двоичных показательных

позиционных систем счисления с обоими основаниями (a и b) равными 2.

Целые числа записываются в виде:

где:

 n — число цифр (знаков) в числе x_2,2,

 k — порядковый номер цифры,

 a = 2 — основание внутриразрядной системы счисления, * a_k — цифры числа x_2,2 из множества a={0,1},

 b = 2 — основание показательной функции, основание межразрядной системы счисления.

Целые числа являются частными суммами

степенного ряда:

в котором коэффициенты a_n берутся из кольца R=a{0,1}, X=2, n=k, а верхний предел в частных суммах ограничен с до — n-1.

Из комбинаторики известно, что число записываемых кодов не зависит от основания показательной функции — b, которое определяет диапазон представляемых числами x_2,b величин, и равно числу размещений с повторениями:

где a=2 — 2-х элементное множество a={0,1} из которого берутся цифры a

k, n — число элементов (цифр) в числе x_2,b.

Дробные числа записываются в виде:

где:

 m — число цифр дробной части числа,

 a = 2 — основание внутриразрядной системы счисления,

 b = 2 — основание показательной функции, основание межразрядной системы счисления.

Следует отметить, что число может быть записано в двоичном виде, а система счисления при этом может быть не двоичной, с другим основанием. Пример: двоично-десятичное кодирование, в котором десятичные цифры записываются в двоичном виде, а система счисления — десятичная.

Таблица сложения

+	0	1
0	0	1
1	1	10

Пример сложения «столбиком» (14 + 5 = 19):

+		1	1	1	0
+			1	0	1
	1	0	0	1	1

Таблица умножения

х	0	1
0	0	0
1	0	1

Пример умножения «столбиком» (14 × 5 = 70):

Х				1	1	1	0
Х					1	0	1
+				1	1	1	0
+		1	1	1	0
	1	0	0	0	1	1	0

Преобразование чисел

Для преобразования из двоичной системы в десятичную используют следующую таблицу степеней основания 2:

512

256

128

Начиная с цифры 1 все цифры умножаются на два. Точка, которая стоит после 1, называется двоичной точкой.

Преобразование двоичных чисел в десятичные

Допустим, вам дано двоичное число 110001. Для перевода в десятичное просто запишите его справа налево как сумму по разрядам следующим образом:

Можно записать это в виде таблицы следующим образом:

512	256	128	64	32	16	8	4	2	1
				1	1	0	0	0	1
				+32	+16				+1

Точно так же, начиная с двоичной точки, двигайтесь справа налево.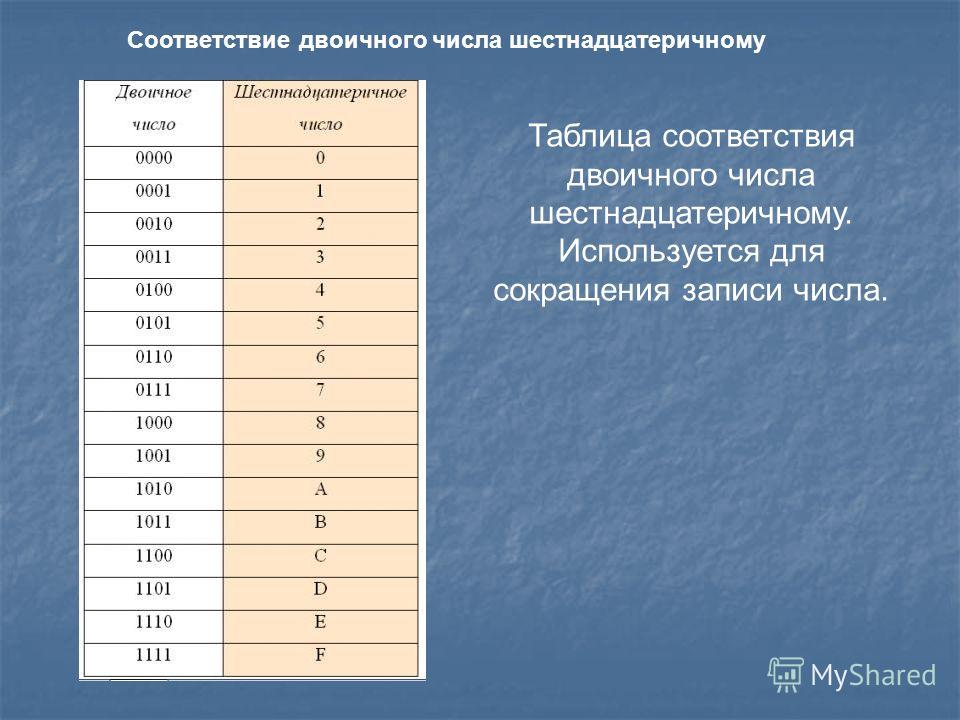 Под каждой двоичной единицей напишите её эквивалент в строчке ниже. Сложите получившиеся десятичные числа.

Таким образом, двоичное число 110001 равнозначно десятичному 49.

Преобразование методом Горнера

Метод Горнера

Для того, чтобы преобразовывать числа из двоичной в десятичную систему данным методом, надо суммировать цифры слева направо, умножая ранее полученный результат на основу системы (в данном случае 2). Например, двоичное число 1011011 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+0=22 >> 22*2+1=45 >> 45*2+1=91 То есть в десятичной системе это число будет записано как 91. Или число 101111 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+1=23 >> 23*2+1=47 То есть в десятичной системе это число будет записано как 47.

Преобразование десятичных чисел в двоичные

Допустим, нам нужно перевести число 19 в двоичное. Вы можете воспользоваться следующей процедурой:

19 /2 = 9 с остатком 1

9 /2 = 4 c остатком 1

4 /2 = 2 с остатком 0

2 /2 = 1 с остатком 0

1 /2 = 0 с остатком 1

Итак, мы делим каждое частное на 2 и записываем остаток в конец двоичной записи. Продолжаем деление до тех пор, пока в делимом не будет 0. В результате получаем число 19 в двоичной записи: 10011.

Преобразование дробных двоичных чисел в десятичные

Нужно перевести число 1011010.101 в десятичную систему. Запишем это число следующим образом:

Преобразование дробных десятичных чисел в двоичные

Перевод дробного числа из десятичной системы счисления в двоичную осуществляется по следующему алгоритму:

 Вначале переводится целая часть десятичной дроби в двоичную систему счисления;

 Затем дробная часть десятичной дроби умножается на основание двоичной системы счисления;

 В полученном произведении выделяется целая часть, которая принимается в качестве значения первого после запятой разряда числа в двоичной системе счисления;

 Алгоритм завершается, если дробная часть полученного произведения равна нулю или если достигнута требуемая точность вычислений. В противном случае вычисления продолжаются с предыдущего шага.

Пример: Требуется перевести дробное десятичное число 206,116 в дробное двоичное число.

Перевод целой части дает 206₁₀=11001110₂ по ранее описанным алгоритмам; дробную часть умножаем на основание 2, занося целые части произведения в разряды после запятой искомого дробного двоичного числа:

.116 • 2 = 0.232

.232 • 2 = 0.464

.464 • 2 = 0.928

.928 • 2 = 1.856

.856 • 2 = 1.712

.712 • 2 = 1.424

.424 • 2 = 0.848

.848 • 2 = 1.696

.696 • 2 = 1.392

.392 • 2 = 0.784

И т. д.

Получим: 206,116₁₀=11001110,0001110110₂

Применения

В цифровых устройствах

Двоичная система используется в цифровых устройствах, поскольку является наиболее простой и соответствует требованиям:

 Чем меньше значений существует в системе, тем проще изготовить отдельные элементы, оперирующие этими значениями.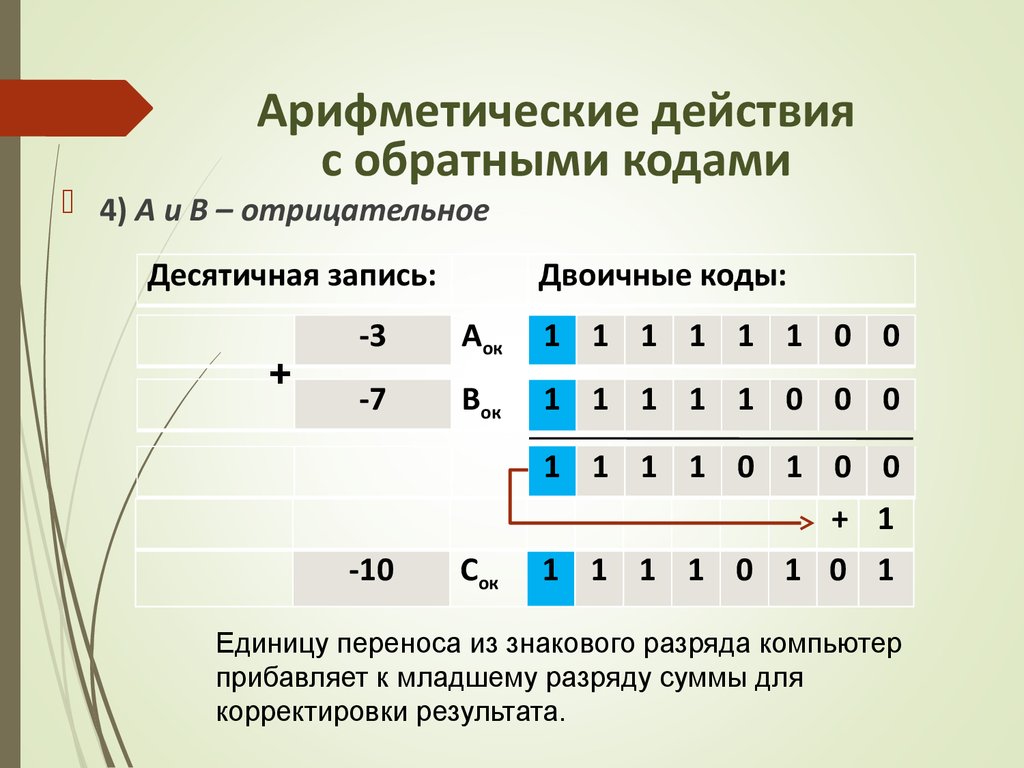 В частности, две цифры двоичной системы счисления могут быть легко представлены многими физическими явлениями: есть ток (ток больше пороговой величины) — нет тока (ток меньше пороговой величины), индукция магнитного поля больше пороговой величины или нет (индукция магнитного поля меньше пороговой величины) и т. д.

 Чем меньше количество состояний у элемента, тем выше помехоустойчивость и тем быстрее он может работать. Например, чтобы закодировать три состояния через величину напряжения, тока или индукции магнитного поля, потребуется ввести два пороговых значения и два компаратора, что не будет способствовать помехоустойчивости и надёжности хранения информации.

 Двоичная арифметика является довольно простой. Простыми являются таблицы сложения и умножения \— основных действий над числами.

В цифровой электронике одному двоичному разряду в двоичной системе счисления соответствует (очевидно) один двоичный разряд двоичного регистра, то есть двоичный триггер с двумя состояниями (0,1).

В английской системе мер

При указании линейных размеров в дюймах по традиции используют двоичные дроби, а не десятичные, например: 5¾″, 7¹⁵/₁₆″, 3¹¹/₃₂″ и т. д.

Логические вентили.

Любой, самый примитивный компьютер – сложнейшее техническое устройство. Но даже такое сложное устройство, как и все в природе и в технике, состоит их простейших элементов. Любой компьютер, точнее, любой его электронный логический блок состоит из десятков и сотен тысяч так называемых вентилей (логических устройств, базовых логических схем), объединяемых по правилам и законам (аксиомам) алгебры вентилей в схемы, модули.

Логический вентиль (далее – просто вентиль) – это своего рода атом, из которого состоят электронные узлы ЭВМ. Он работает по принципу крана (отсюда и название), открывая или закрывая путь сигналам.

Логические схемы предназначены для реализации различных функций алгебры логики и реализуются с помощью трех базовых логических элементов (вентилей, логических схем или так называемых переключательных схем). Они воспроизводят функции полупроводниковых схем.

Работу вентильных, логических схем мы, как и принято, будем рассматривать в двоичной системе и на математическом, логическом уровне, не затрагивая технические аспекты (аспекты микроэлектроники, системотехники, хотя они и очень важны в технической информатике).

Логические функции отрицания, дизъюнкции и конъюнкции реализуют, соответственно, логические схемы, называемые инвертором, дизъюнктором и конъюнктором.

Логическая функция «инверсия», или отрицание, реализуется логической схемой (вентилем), называемой инвертор.

Принцип его работы можно условно описать следующим образом: если, например, «0» или «ложь» отождествить с тем, что на вход этого устройства скачкообразно поступило напряжение в 0 вольт, то на выходе получается 1 или «истина», которую можно также отождествить с тем, что на выходе снимается напряжение в 1 вольт.

Аналогично, если предположить, что на входе инвертора будет напряжение в 1 вольт («истина»), то на выходе инвертора будет сниматься 0 вольт, то есть «ложь» (схемы на рисунках 6.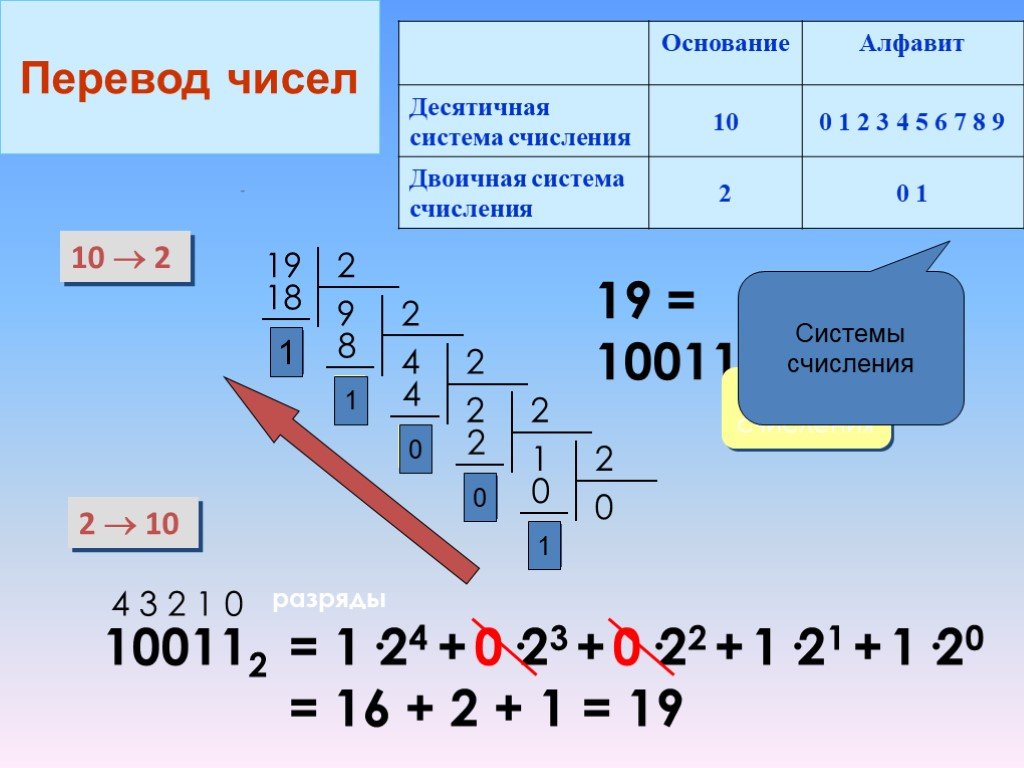 1 а, б).

Рис. 6.1. Принцип работы инвертора

Функцию отрицания можно условно отождествить с электрической схемой соединения в цепи с лампочкой (рис. 6.2), в которой замкнутая цепь соответствует 1 («истина») или х = 1, а размыкание цепи соответствует 0 («ложь») или х = 0.

Рис. 6.2. Электрический аналог схемы инвертора

Дизъюнкцию реализует логическое устройство (вентиль) называемое дизьюнктор (рис. 6.3 а, б, в):

Рис. 6.3a.

Рис. 6.3b.

Рис. 6.3c. Принцип работы дизъюнктора

Дизъюнктор условно изображается схематически электрической цепью вида (рис. 6.4)

Рис. 6.4. Электрический аналог схемы дизъюнктора

Конъюнкцию реализует логическая схема (вентиль), называемая конъюнктором (рис. 6.5 а, б, в):

Рис. 6.5a.

Рис. 6.5b.

Рис. 6.5c. Принцип работы конъюнктора

Конъюнктор можно условно изобразить схематически электрической цепью вида (рис. 6.6)

Рис. 6.6. Электрический аналог схемы конъюнктора

Схематически инвертор, дизъюнктор и конъюнктор на логических схемах различных устройств можно изображать условно следующим образом (рис. 6.7 а, б, в). Есть и другие общепринятые формы условных обозначений.

Рис. 6.7. а, б, в. Условные обозначения вентилей (вариант)

Пример. Транзисторные схемы, соответствующие логическим схемам (инвертор), (дизъюнктор), (конъюнктор) имеют, например, следующий вид (рис. 6.8 а, б, в):

Рис. 6.8a. Инвертор

Рис. 6.8b. Дизъюнктор

Рис. 6.8c. Конъюнктор

Из указанных простейших базовых логических элементов собирают, конструируют сложные логические схемы ЭВМ, например, сумматоры, шифраторы, дешифраторы и др. Большие (БИС) и сверхбольшие (СБИС) интегральные схемы содержат в своем составе (на кристалле кремния площадью в несколько квадратных сантиметров) десятки тысяч вентилей. Это возможно еще и потому, что базовый набор логических схем (инвертор, конъюнктор, дизъюнктор) является функционально полным (любую логическую функцию можно представить через эти базовые вентили), представление логических констант в них одинаково (одинаковы электрические сигналы, представляющие 1 и 0) и различные схемы можно «соединять» и «вкладывать» друг в друга (осуществлять композицию и суперпозицию схем).

Таким способом конструируются более сложные узлы ЭВМ – ячейки памяти, регистры, шифраторы, дешифраторы, а также сложнейшие интегральные схемы.

Пример. В двоичной системе таблицу суммирования цифры x и цифры y и получения цифры z с учетом переноса p в некотором разряде чисел x и y можно изобразить таблицей вида

xyzp

0000

0110

1010

1101

Эту таблицу можно интерпретировать как совместно изображаемую таблицу логических функций (предикатов) вида

Логический элемент, соответствующий этим функциям, называется одноразрядным сумматором и имеет следующую схему (обозначим ее как или – если мы хотим акцентировать именно выбранный, текущий i-й разряд) (рис. 6.9):

Рис. 6.9. Схема одноразрядного сумматора

Пример. «Черным ящиком» называется некоторое закрытое устройство (логическая, электрическая или иная схема), содержимое которого неизвестно и может быть определено (идентифицировано) только по отдельным проявлениям входа/выхода ящика (значениям входных и выходных сигналов). В «черном ящике» находится некоторая логическая схема, которая в ответ на некоторую последовательность входных (для ящика) логических констант выдает последовательность логических констант, получаемых после выполнения логической схемы внутри «черного ящика». Определим логическую функцию внутри «черного ящика» (рис. 6.10), если операции выполняются с логическими константами для входных последовательностей (поразрядно). Например, х = 00011101 соответствует последовательности поступающих значений: «ложь», «ложь», «ложь», «истина», «истина», «истина», «ложь», «истина».

Рис. 6.10. Схема «черного ящика 1»

Из анализа входных значений (входных сигналов) х, у и поразрядного сравнения логических констант в этих сообщениях с константами в значении z – результате выполнения функции в «черном ящике», видно, что подходит, например, функция вида

Действительно, в результате «поразрядного» сравнения сигналов (последовательностей значений «истина», «ложь») получаем следующие выражения (последовательности логических констант):

Пример. Попробуйте самостоятельно выписать функцию для «черного ящика»? указанного на рис. 6.11:

Рис. 6.11. Схема «черного ящика 2»

Важной задачей (технической информатики) является минимизация числа вентилей для реализации той или иной схемы (устройства), что необходимо для более рационального, эффективного воплощения этих схем, для большей производительности и меньшей стоимости ЭВМ.

Эту задачу решают с помощью методов теоретической информатики (методов булевой алгебры).

Пример. Построим схему для логической функции

Схема, построенная для этой логической функции, приведена на рис. 6.12.

Рис. 6.12.Схема для функции 1

Пример. Определим логическую функцию

, реализуемую логической схемой вида (рис. 6.13)

Рис. 6.13. Схема для функции 2

Искомая логическая функция, если выписать ее последовательно, заполняя «верх» каждой стрелки, будет иметь следующий вид:

Введение в нотацию Big O. Начало работы с нотацией Big O… | Эндрю Джеймисон

Начало работы с нотацией Big O с использованием примеров линейного поиска и двоичного поиска

Нотация Big O — это способ измерения эффективности алгоритма. Он измеряет время, необходимое для запуска вашей функции по мере роста входных данных. Или, другими словами, насколько хорошо функция масштабируется.

Измерение эффективности состоит из двух частей — временной сложности и пространственной сложности. Временная сложность — это мера того, сколько времени требуется для выполнения функции с точки зрения ее вычислительных шагов. Сложность пространства связана с объемом памяти, используемой функцией. Этот блог иллюстрирует временную сложность с двумя алгоритмами поиска.

Большой O иногда называют верхней границей алгоритма, что означает, что он имеет дело с наихудшим сценарием. В лучшем случае нам ничего не говорят — это будет нахождение нашего предмета при первом проходе. Мы используем наихудший случай для устранения неопределенности — алгоритм никогда не будет работать хуже, чем мы ожидаем.

Фото Jr Korpa на Unsplash

Давайте рассмотрим простой пример.

Мы будем искать число восемь в диапазоне от 1 до 8.

Наша первая стратегия состоит в том, чтобы начать с первого числа в массиве и двигаться вверх на единицу, пока не найдем целевое число. Шаги нашего алгоритма будут выглядеть примерно так.

Начать с начала
Сравнить текущее значение с нашим целевым
Перейти к следующему значению
Дойти до конца списка

Линейный поиск — изображение автора

В раунде 1 мы выбираем номер один; это неправильно, поэтому мы переходим ко второму раунду и, как вариант, исключаем номер один. Шаг 2 тоже не правильный, и продолжаем до конца, пока не выберем цифру восемь.

В худшем случае это не очень эффективно. Мы должны проверить каждое число в списке, пока не получим ответ. Этот метод называется Линейный поиск . Обозначение Big O для линейного поиска — O(N) . Сложность напрямую связана с размером входных данных — алгоритм делает дополнительный шаг для каждого дополнительного элемента данных.

 def linear_search(arr, x): #входной массив и цель  для i in range(len(arr)): 
 if arr[i] == x: 
 return i 
  return -1 
 # return -1 если цель отсутствует в массиве

Попробуем другую стратегию. Важнейшей частью этой стратегии является то, что список должен быть упорядочен.

На этот раз мы начинаем с середины списка. Мы проверяем, выбрали ли мы целевой номер. Если нет, мы проверяем, меньше или больше число, чем мы выбрали. В любом случае мы удаляем половину списка, в котором нет нашей цели. Затем мы выбираем число в середине оставшихся значений.

Найдите середину списка — середину
Сравните среднюю точку с целью
Если наше значение и цель совпадают, мы останавливаемся — мы нашли нашу цель
Если наше значение меньше целевого, мы создаем новый список от средней точки плюс один до наибольшего значения.
Если наше значение больше целевого, мы создаем новый список в диапазоне от наименьшего значения до средней точки минус один.
Повторять до тех пор, пока мы не найдем цель или не дойдем до последнего элемента, который не соответствует цели.

Бинарный поиск — изображение автора

Средняя точка для нашего первого выбора — четыре. Цель больше четырех, поэтому мы исключаем значения четыре и ниже и создаем новый список от пяти до восьми. Мы выбираем среднее значение, равное шести, и выбираем снова. Продолжаем, пока не останется только цифра восемь.

Эта стратегия называется Двоичный поиск . Он эффективен, поскольку удаляет половину списка при каждом проходе. Если бы мы удвоили наш поиск и искали число 16 в диапазоне от 1 до 16, это заняло бы у нас всего один раунд. Удивительно, но если бы нам нужно было выбрать число от одного до миллиона, в худшем случае было бы 20 попыток.

Когда мы получаем такие большие числа, мы ясно видим, насколько этот метод эффективнее, чем линейный поиск: 20 предположений против 1 000 000 предположений.

Мы можем смоделировать это математически. Число восемь эквивалентно 2 x 2 x 2. Мы также можем выразить это уравнение, используя показатели степени: два в степени трех, или 2³.

Обратное значение показателя степени является логарифмом. Запись по основанию 2 из 8 означает, сколько раз вам нужно умножить два, чтобы получить восемь. Как показано выше, 2 x 2 x 2 = 8, поэтому Log2 8 = 3.

В общем, наихудшим сценарием двоичного поиска является Log of n + 1. Обозначение Big O для двоичного поиска равно 9.0031 О(лог N) . В отличие от O(N), который выполняет дополнительный шаг для каждого элемента данных, O(log N) означает, что алгоритм выполняет дополнительный шаг каждый раз, когда данные удваиваются.

 def binary_search4(arr, target): 
 left = 0 
 right = len(arr) - 1while left <= right: 
 mid_point = (left + right) // 2  if target < arr[mid_point]: 
 right = mid_point - 1 
 elif target > arr[mid_point]: 
 left = mid_point + 1 
 else: 
 return mid_pointreturn -1

Примечание. Несмотря на то, что бинарный поиск намного эффективнее линейного поиска, вы не всегда будете выбирать его в каждом примере. Причиной этому является самая первая квалификация. Двоичный поиск требует, чтобы список был в порядке. Сортировка списка сама по себе сложна, поэтому в некоторых случаях может оказаться более эффективным использовать линейный поиск, чем сначала сортировать список.

Когда мы записываем нотацию Big O, мы ищем самый быстрорастущий термин по мере того, как входные данные становятся все больше и больше. Мы можем упростить уравнение, опустив константы и любые недоминирующие члены. Например, O(2N) становится O(N), а O(N² + N + 1000) становится O(N²).

Двоичный поиск равен O(log N), что менее сложно, чем линейный поиск. Есть и более сложные алгоритмы. Типичным примером квадратичного алгоритма или O(N²) является вложенный цикл for. Во вложенном цикле мы перебираем все данные во внешнем цикле. Затем для каждого элемента мы перебираем данные во внутреннем цикле. Это N x N раз N².

Сложность — изображение автора

Вот как эти среды выполнения Big O выглядят на графике. Примеры в этом блоге — это две наименее сложные нотации.

Big O Chart — изображение автора

Часто существует множество вариантов написания кода для получения решения. Понимание нотации Big O важно при написании алгоритмов. Это поможет вам определить, когда ваш алгоритм становится быстрее или медленнее. Вы также можете сравнить различные методы и выбрать наиболее эффективный.

Treehouse через freeCodeCamp предлагает отличный курс на YouTube, который проведет вас от новичка до понимания нотации Big O. Предупреждаю, что это более пяти часов. (Вот блог с некоторыми советами по эффективному просмотру YouTube)

Учебное пособие по домику на дереве

Шпаргалка по Big O

https://www.bigocheatsheet.com/

Введение в позиционную нотацию. Руководство Тайлера

В вычислительной технике вы столкнетесь с различными системами счисления, такими как двоичная и шестнадцатеричная. Эти системы известны как позиционная нотация, но с разными основаниями. В этом руководстве объясняется позиционная система счисления и показано, как преобразовать одну систему, например шестнадцатеричную, в другую.

Позиционное обозначение

Вы, вероятно, учились этому в начальной школе, но важно понимать, как это работает. Десятичная система — это позиционная система счисления с основанием 10. Основание — это количество цифр (символов, представляющих числа) в системе. Десятичная система имеет 10 цифр, от 0 до 9. Двоичная система имеет основание 2 и имеет две цифры, 0 и 1. Каждая позиция в числе имеет разрядное значение, которое определяется его относительным положением и основанием. Например, число 1 в двоичное и десятичное числа означают одно и то же. Число 10 нет. 10 в двоичном формате равно 2 в десятичном. 100 в двоичном формате равно 4 в десятичном. Обратите внимание, как в двоичном формате каждое значение разряда в два раза превышает значение того, что справа от него. Каждое значение места кратно его основанию. Таблица ниже должна прояснить это. Значения в каждой строке представляют собой десятичное значение числа в верхней строке. Обратите внимание, что каждое место кратно основанию.

Номер:	1000	100	10	1
Основание 2 Значение:	8	4	2	1
Основание 10 Значение:	1000	100	10	1
Основание 16 Значение:	4096	256	16	1

Преобразование в десятичное число

Каждое место в любом основании преобразуется в десятичное путем умножения десятичного значения каждой цифры на цифру, умноженную на ее разрядное значение. Значение места вычисляется путем возведения основания в степень его положения. Начните с крайнего правого положения и показателя степени 0. Прибавляйте единицу к показателю степени по мере продвижения влево. Как только вы закончите умножать все цифры на разрядные значения, сложите их все, чтобы получить десятичную версию. Давайте поработаем с некоторыми примерами.

Двоичное число в десятичное Пример

Преобразуем четырехзначное двоичное число в десятичное:

1011

Шаг 1: Рассчитаем разрядные значения

Четыре цифры, поэтому у нас есть четыре разрядных значения: 2 ^{01 . ¹, 2 ² и 2 ³.}

2 ⁰ = 1 2 ¹ = 2 2 ² = 4 2 ³ = 8

0178

1 x 8 = 8 0 x 4 = 0 1 x 2 = 2 1 x 1 = 1

Шаг 3. Суммируйте результат

8 + 0 + 2 + 1 = 11 отношения между цифрами и разрядными значениями.

1	0	1	1
2 ³ = 8	2 ² = 4	2 ¹ = 2	2 ⁰ = 1
1 х 8 = 8	0 х 4 = 0	1 х 2 = 2	1 х 1 = 1

Гексадецимальный в десятичный пример

Теперь давайте преобразуем шестнадцатеричное число в десятичное значение:

2B40

Шаг 1: Рассчитайте значения места

16 ⁰ = 1 16101010101010101010101010101010101010101010101010 2

010101010101010181 = 1 1610101010101010101010181 =. 256 16 ³ = 4096

Шаг 2. Умножьте каждую цифру на соответствующий разряд

2 x 8192 = 4096 B (11) x 256 = 2816 4 x 16 = 64 0 x 1 = 0

Шаг 3: Складка результата

8192 + 2816 + 64 + 0 = 11072

2	Б	4	0
2 ³ = 4096	2 ² = 256	2 ¹ = 16	2 ⁰ = 1
2 х 4096 = 8192	В (11) х 256 = 2816	4 х 16 = 64	0 х 1 = 0

Преобразование десятичной системы счисления

Метод 1: использование целевой системы нумерации

Приведенные выше примеры могут работать, если вы не возражаете против выполнения операций в системе нумерации, в которую вы конвертируете. Например, я преобразую 123 из десятичного числа в двоичное.

Обратите внимание, что в таблице разрядные значения и показатели степени представлены в двоичном формате.

1	2	3
1010 ¹⁰ = 1100100	1010 ¹ = 1010	1010 ⁰ = 1
1 х 1100100 = 1100100	2 (10) х 1010 = 10100	3 (11) х 1 = 11

1100100 + 10100 + 11 = 1111011

Как и большинство людей, я предпочитаю работать с десятичными числами, поэтому покажу вам другой способ.

Метод 2: Разделение на разрядные значения

Давайте снова преобразуем 123 в двоичное число.

Шаг 1. Расчет стоимости места

Найдите значения места системы нумерации целевого нумерации до тех пор, пока не превышаете значение, которое вы преобразуете:

2 ⁰ = 1 2 ¹ = 2 2 ² = 4 2 ³ = 8 2 ⁴ = 4 2 ³ = 8 2 ⁴ = 4 2 ^{= 16 2 ⁵ = 32 2 ⁶ = 64 2 ⁷ = 128}

Шаг 2: Сбросьте наибольшее значение расчетного места

В этом случае это 2 ⁷ = 128.

: Разделить на разрядные значения

Возьмите десятичное число и разделите его на значение самого большого разряда. Найдите остаток вместо любых дробных значений. Целая часть номера — это старшая значащая цифра вашего номера в целевой системе. Возьмите остаток и разделите его на следующий по величине разряд. Продолжайте делать это, пока у вас не закончатся значения мест.

123 / 64 = 1 остаток 59
59 / 32 = 1 остаток 27
27 / 16 = 1 остаток 11
11 / 8 = 1 остаток 3
3 / 4 = 0 остаток 3
3/2 = 1 Остаток 1
1 /1 = 1 Остаток 0

Результат: 1111011

Метод 2: шестнадцатеричный пример

Давайте преобразуем 123 в шестнадцатеричный метод. 1 = 16 16 ² = 256

123 / 16 = 7 остатка 11
11 / 1 = 11 (B) остатка 0

Результат: 7B

Есть несколько коротких путей, которые делают определенные2 90 системы счисления намного проще.

Шестнадцатеричное в/из Двоичное

Шестнадцатеричная цифра может быть представлена четырьмя двоичными цифрами. Используйте это в своих интересах при преобразовании между шестнадцатеричными и двоичными числами.

Шестнадцатеричный код в двоичный

Преобразуем F70A3021 в двоичный.

Начиная со старшей цифры, преобразовать каждую цифру в четырехзначное двоичное число и объединить результаты. Обычно я конвертирую шестнадцатеричное значение в десятичное, а затем десятичное в двоичное. Я сделал это достаточно там, где я могу сделать это в своей голове, так что это не займет у меня много времени. Вы также можете запомнить двоичные значения для каждой шестнадцатеричной цифры.

F = 1111
7 = 0111
0 = 0000
a = 1010
3 = 0011
0 = 0000
2 = 0010
1 = 0001

Результат: 1111 0111 0000111111110011011

777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777 9017

777777777777777777777777777777777777777777777777777777.

Преобразуем 10110100101 в шестнадцатеричное число.

Этот ярлык почти такой же, как шестнадцатеричный код в двоичный, только обратное преобразование.

Для удобства разбейте десятичное число на группы по четыре, начиная с младшей значащей цифры. Используя ручку и бумагу, я просто провожу линию между группами из четырех цифр.

101 1010 0101

Теперь преобразуйте каждую группу цифр в шестнадцатеричный вид и соедините их.

101 = 5
1010 = A
0101 = 5

Результат: 5A5

Восьмеричное в/из двоичного

Восьмеричное в двоичное

Это работает так же, как шестнадцатеричное в двоичное. Вместо четырех двоичных цифр, представляющих шестнадцатеричную цифру, вы можете представить восьмеричную цифру тремя двоичными цифрами. Преобразуем восьмеричное число 547 в двоичное.

5 = 101
4 = 100
7 = 111

Результат: 101100111

Двоичный в восьмеричный

Как и при преобразовании двоичного кода в шестнадцатеричный, разделите двоичное число на части, начиная с младшей значащей цифры. Вместо четырехразрядных разделов используйте трехразрядные разделы.