4.5. Замена нескольких параллельных ветвей, содержащих источники эдс и тока, одной эквивалентной
Схемы
рис. 4.15а и рис. 4.15б являются эквивалентными,
если при любых значениях тока  напряжение на зажимах
напряжение на зажимах  обеих схем будет одинаковым. Для
определения величин
обеих схем будет одинаковым. Для
определения величин 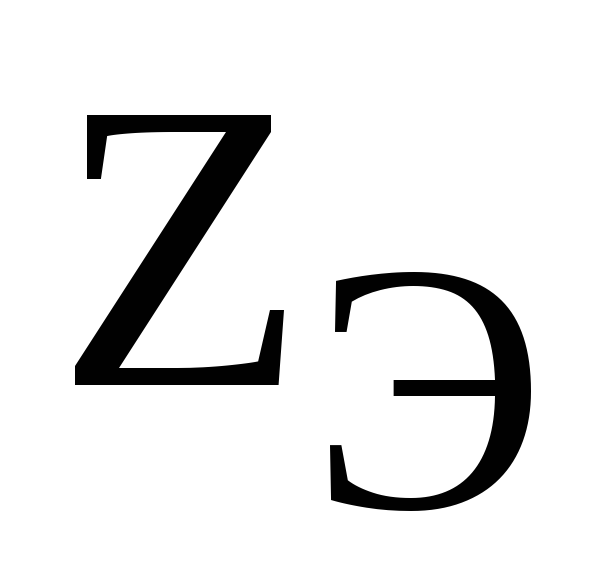 и
и  сопоставим выражения для тока
сопоставим выражения для тока 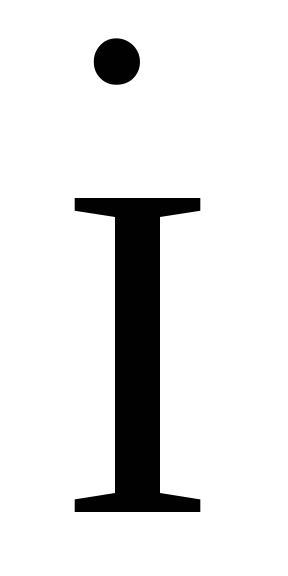 обеих схем.
обеих схем.
Для цепи рис. 4.15а:
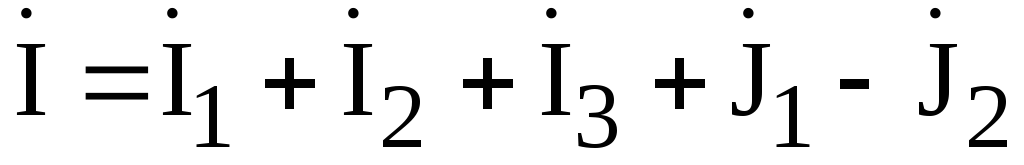 .
(4.17)
.
(4.17)
Выразим
отдельные составляющие (4.17) через
напряжение  с помощью закона Ома:
с помощью закона Ома:
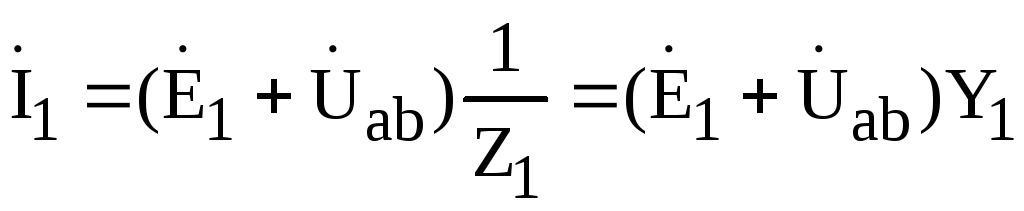 ,
,
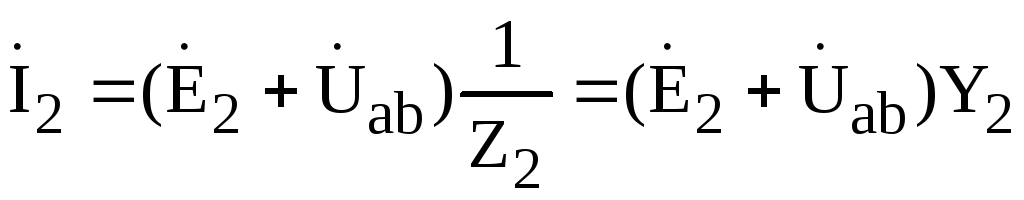 ,
,
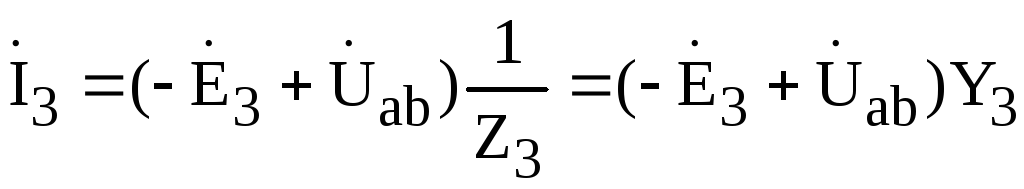 ,
,
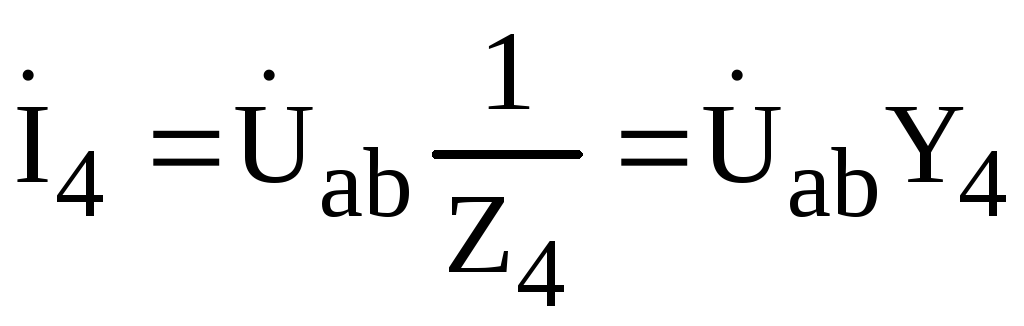 .
.
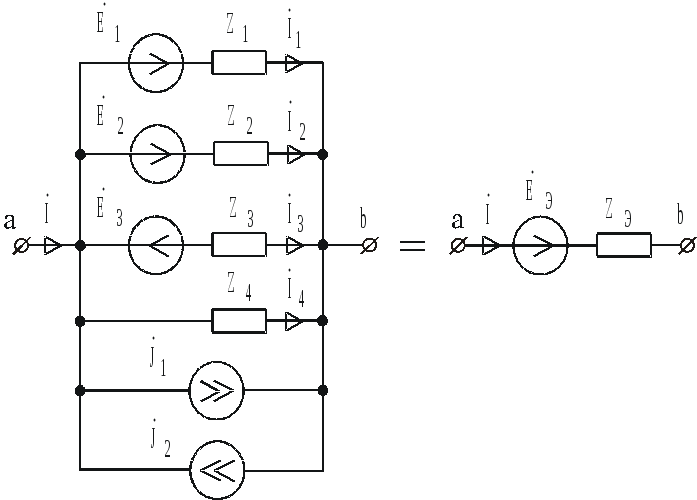
б)
а)
Рис. 4.15
Подставим
полученные выражения для токов  —
— 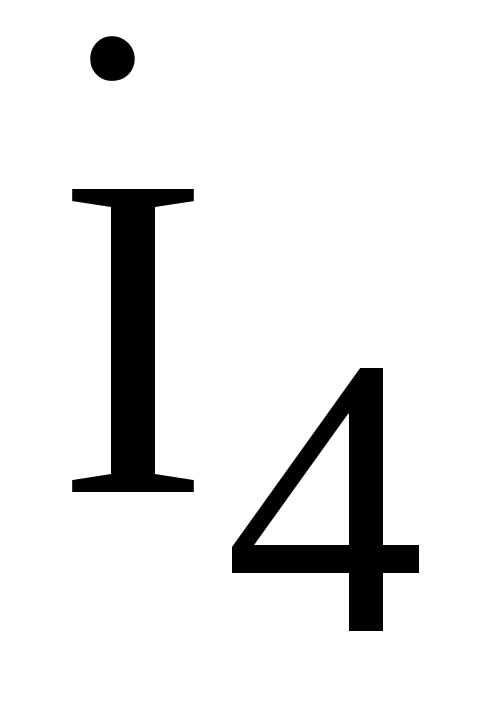 в формулу (4.17):
в формулу (4.17):
 .
(4.18)
.
(4.18)
Для цепи рис. 4.15б справедливо

Равенство
токов 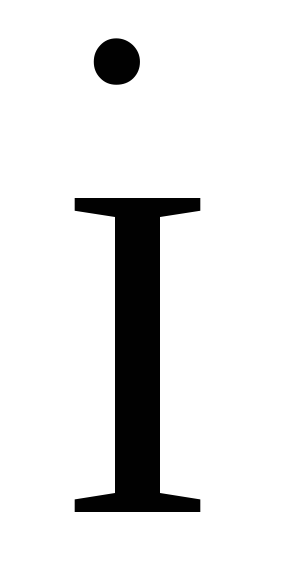 в (4.18) и (4.19) возможно при выполнении двух
условий:
в (4.18) и (4.19) возможно при выполнении двух
условий:
а)  ;
(4.20)
;
(4.20)
б) 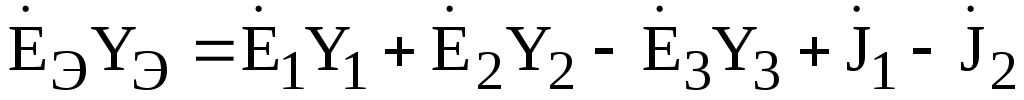 .
(4.21)
.
(4.21)
Из
(4.20) и (4.21) можно определить искомые
величины 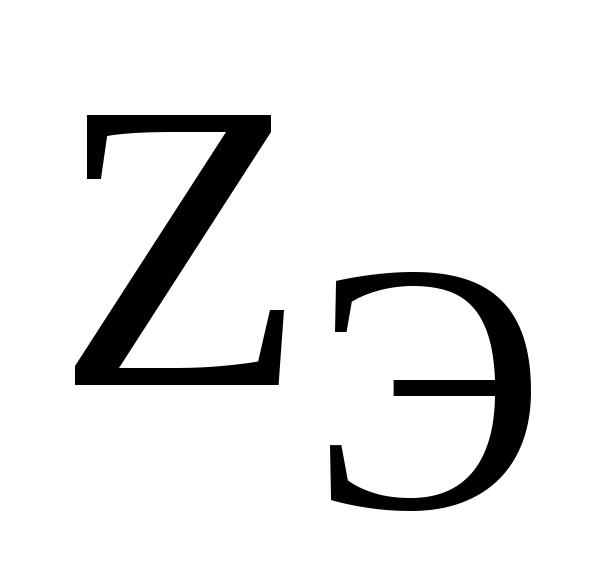 и
и 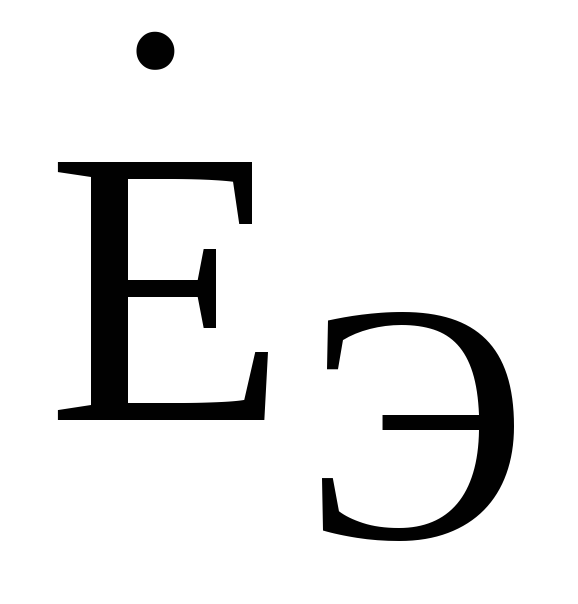
 ,
(4.22)
,
(4.22)
 .
(4.23)
.
(4.23)
Обобщим
вышеизложенное. Пусть требуется заменить
n
ветвей, содержащих источники ЭДС, q
ветвей с источниками тока и p
пассивных ветвей без источников
электрической энергии (все ветви включены
параллельно) одной эквивалентной.
Искомые величины 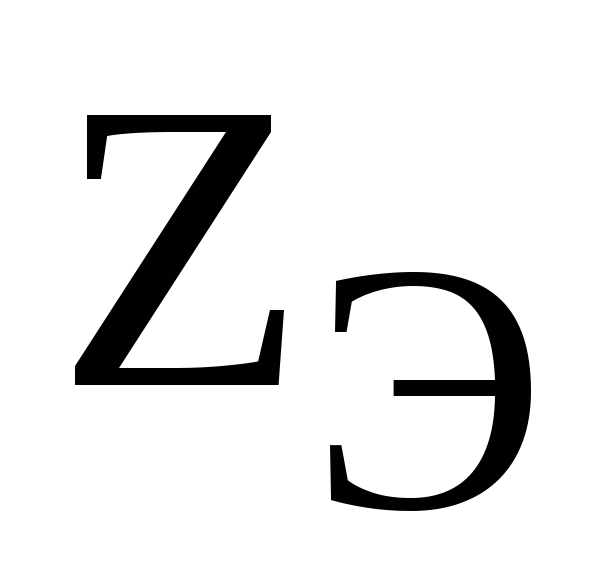 и
и 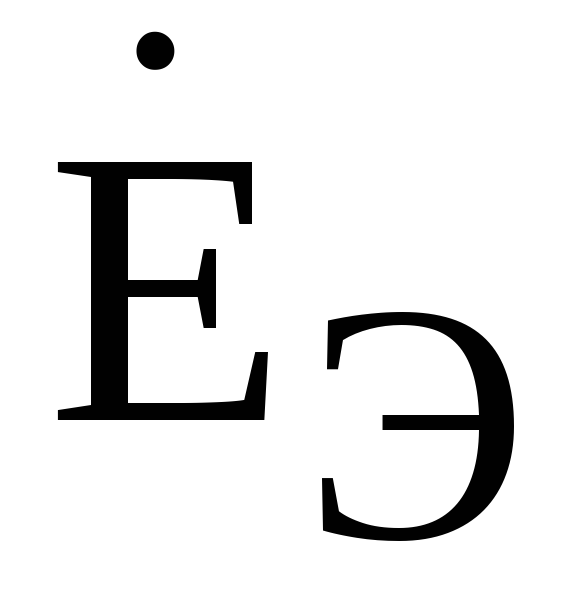

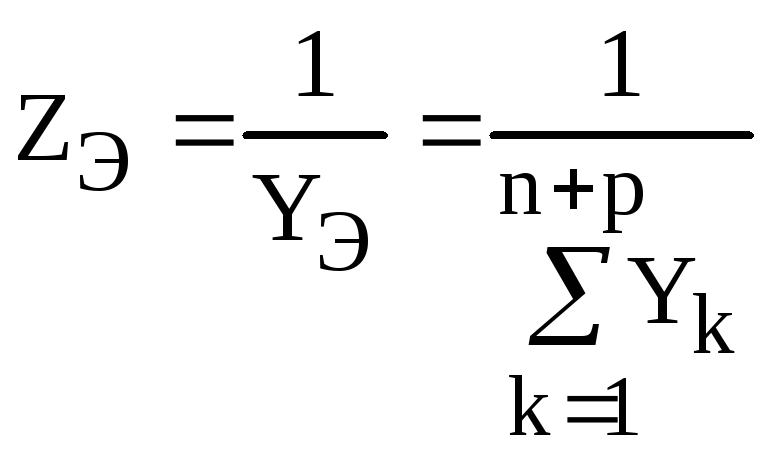 ,
(4.24)
,
(4.24)
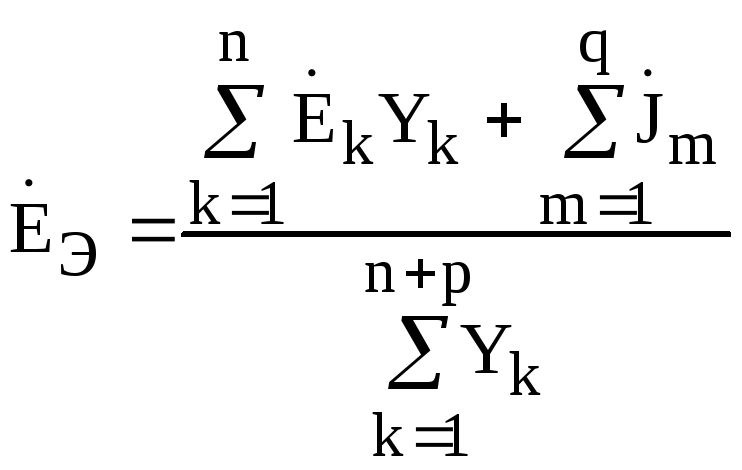 .
(4.25)
.
(4.25)
Если направление источника ЭДС (тока) в исходной ветви совпадает с выбранным направлением эквивалентной ЭДС, то в числителе (4.25) перед соответствующим слагаемым ставится знак “ + ”, в противном случае – “ – ”.
4.6. Принцип наложения и метод наложения
Принцип наложения:
Принцип наложения применяется в методе расчета, получившем название метода наложения. При использовании данного метода поступают следующим образом: поочередно рассчитывают токи, возникающие от действия каждого источника электрической энергии в отдельности, мысленно удаляя остальные источники из схемы. При этом внутренние сопротивления источников должны остаться в цепи. Это означает, что участок ветви, в котором был источник ЭДС, замыкается накоротко (рис. 4.16а), а участок с источником тока размыкается (рис. 4.16б). Затем находят фактические токи в ветвях путем алгебраического сложения частичных токов. Если направление частичного тока совпадает с выбранным направлением фактического тока, то при суммировании частичный ток берется со знаком “ + ”, иначе – “ – ”.

а) б)
Рис. 4.16
Рассмотрим в качестве примера расчет токов в цепи рис. 4.17а методом наложения.
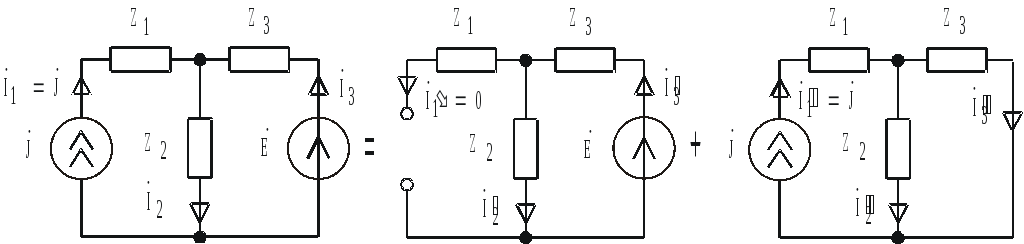
а) б) в)
Рис. 4.17
На
первом этапе удалим из схемы источник
тока  ,
а источник ЭДС
,
а источник ЭДС  оставим (рис. 4.17б). Очевидно, что частичные
токи в этой цепи
оставим (рис. 4.17б). Очевидно, что частичные
токи в этой цепи
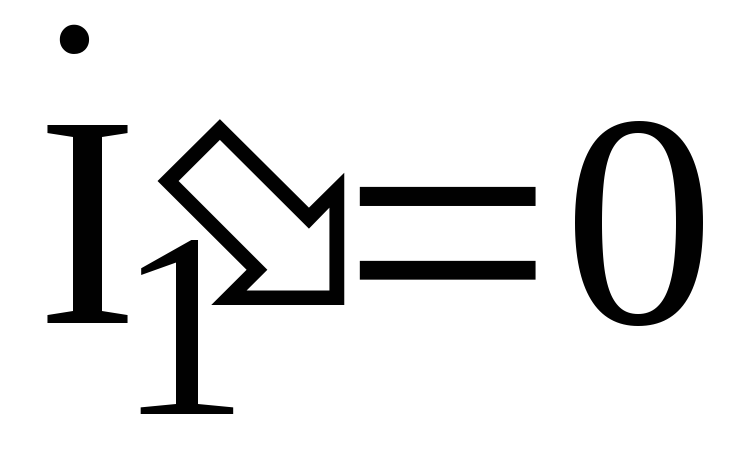 ,
,
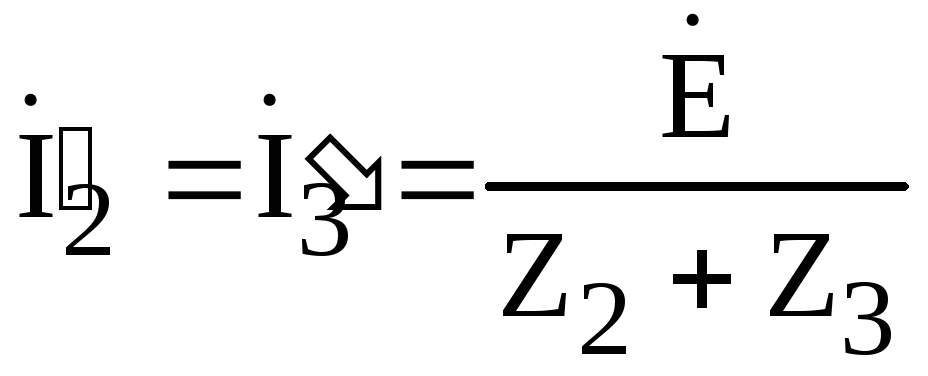 .
.
На
втором этапе удалим из схемы источник
ЭДС
,
а источник тока 
 ,
,
 ,
,
 .
.
На заключительном этапе находим фактические токи в ветвях цепи рис. 4.17а путем сложения частичных токов:

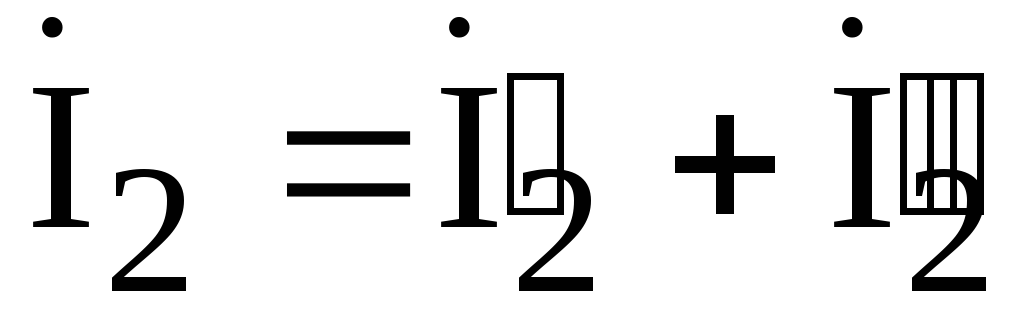 ,
,
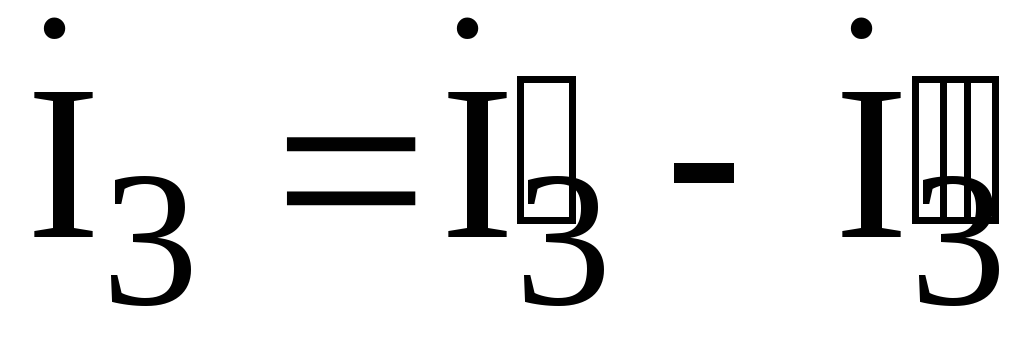 .
.
Источник эдс и источник тока
Процессы, происходящие в источниках электрической энергии, различаются многообразием в зависимости от их вида и описываются сложными уравнениями. Однако с позиций потребителей электрической энергии рассчитанные токи и напряжения получаются очень близкими к реальным, если источники электрической энергии заменить идеальными, а потери мощности и напряжения в них учесть включенными последовательно или параллельно сопротивлениями, индуктивностями или емкостями.

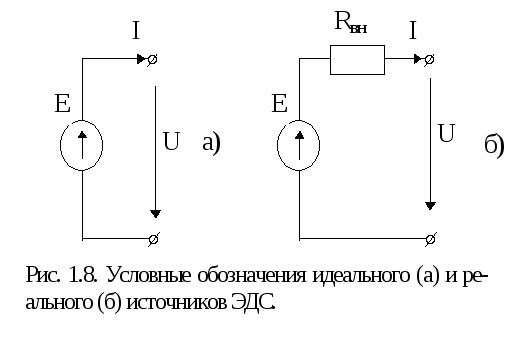
Источник ЭДС конечной мощности изображается идеальным источником ЭДС и последовательно включенным пассивным элементом (рис. 1.8.б), параметры которого подбираются такими, чтобы отобразить реальные процессы на выводах источника. В цепях постоянного тока это, как правило, внутреннее сопротивление (на рис. 1.8б обозначено как Rвн), величина которого много меньше параметров внешней цепи. В некоторых случаях этим сопротивлением можно пренебречь (в зависимости от требуемой точности расчета). Вольтамперные характеристики идеального (1) и реального (2) источников ЭДС постоянного тока изображены на рис. 1.10а.
Источник токапредставляет собой активный элемент, ток которого практически не зависит от напряжения на его выводах. Это может быть, если сопротивление источника тока несоизмеримо больше сопротивления внешней цепи. Целесообразно ввести понятие идеального источника тока. Очевидно, чтоу идеального источника тока внутреннее сопротивление равно бесконечности.
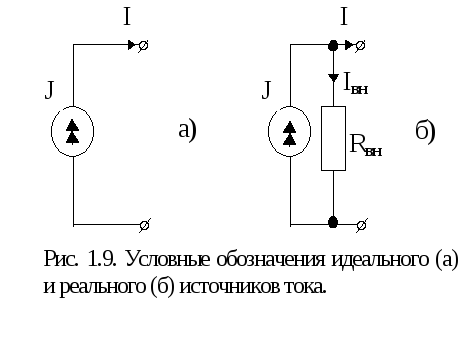
Если к идеальному источнику тока подключить сопротивление и увеличивать его до бесконечности, то напряжение на его выводах и соответственно мощность будут неограниченно возрастать. Поэтому идеальный источник тока, также как и идеальный источник ЭДС, рассматриваются как источники бесконечной мощности.
Источники тока конечной мощности (реальные) изображается в виде идеального с подключенным к нему пассивным элементом (рис. 1.9б), которым ограничивается мощность, выдаваемая во внешнюю цепь, и отражаются внутренние параметры источника. Ток реального источника меньше тока идеального на величину тока Iвн, протекающего по внутреннему сопротивлениюRвн.
В ольтамперные
характеристики идеального 3 и реального
4 источников постоянного тока изображены
на рис. 1.10б.
ольтамперные
характеристики идеального 3 и реального
4 источников постоянного тока изображены
на рис. 1.10б.
14. Замена нескольких параллельных ветвей, содержащих эдс, одной эквивалентной
Рассмотрим схему электрической цепи с двумя узлами (рис. 49). Цепь состоит из mветвей и включает в себя приемник электрической энергии, который расположен в ветви с номеромmи представлен на схеме сопротивлением нагрузкиRm. Через нагрузку протекает токIm. Приемник электрической энергии питается от нескольких параллельно включенных источников. Общее количество источников равно (m– 1). Каждый источник характеризуетсяЭДС E1, E2, E3,…, Em-1 и внутренним сопротивлением источника Ri1, Ri2, Ri3,…, Ri(m-1).

Рис. 49. Схема электрической цепи с параллельным
Включением источников эдс
Схема рис. 49 имеет важное прикладное значение. Она часто встречается на практике, особенно в автономных системах электроснабжения. В частности, параллельное включение генераторов характерно для судовых электроэнергетических систем.
С точки зрения анализа электрических цепей схема рис. 49 является схемой сложной электрической цепи. Для анализа такой цепи можно воспользоваться одним из вышерассмотренных методов, например, методом двух узлов или методом эквивалентного генератора. Однако следует иметь в виду, что нас, как правило, интересует ток в нагрузке при различных значениях сопротивления нагрузки Rm. Поэтому целесообразно сделать эквивалентную замену рассматриваемой схемы на одноконтурную схему, анализ которой строится на основе закона Ома для замкнутой цепи.
Применим правило об эквивалентных источниках напряжения и тока и заменим каждый из источников ЭДС схемы рис. 49 эквивалентным ему источником тока. В результате получим схему замещения с источниками тока, представленную на рис. 50.

Рис. 50. Схема замещения с источниками тока
В схеме замещения рис. 50 ток короткого замыкания и внутренняя проводимость каждого источника тока определяются по формулам (4), (5), представленным выше:
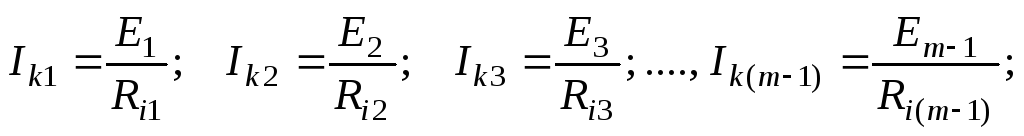
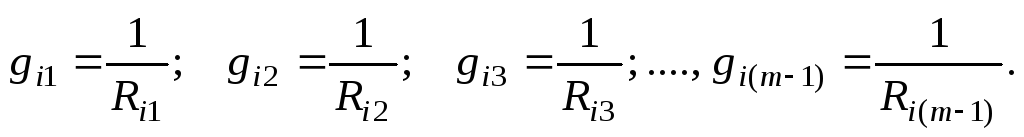
Используя первый закон Кирхгофа, можно найти эквивалентный суммарный ток короткого замыкания, отдаваемый источниками тока схемы рис. 50, как сумму токов короткого замыкания каждого из источников:
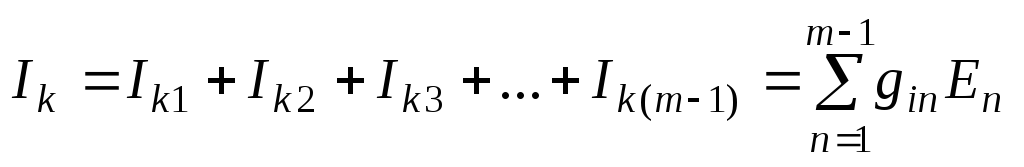 ,
,
где n – текущий номер ветви с источником ЭДС.
Также можно найти эквивалентную проводимость всех внутренних ветвей источников тока как сумму внутренних проводимостей каждого из параллельно включенных источников:

Наличие эквивалентного тока короткого замыкания Ik и эквивалентной проводимостиgi позволяет от схемы рис. 50 перейти к эквивалентной ей схеме замещениярис. 51 с одним источником тока.
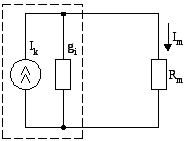
Рис. 51. Схема замещения с эквивалентным источником тока
Вновь применим правило об эквивалентных источниках напряжения и тока и, используя формулы (4), (5), от схемы рис. 51 перейдем к схеме рис. 52, где
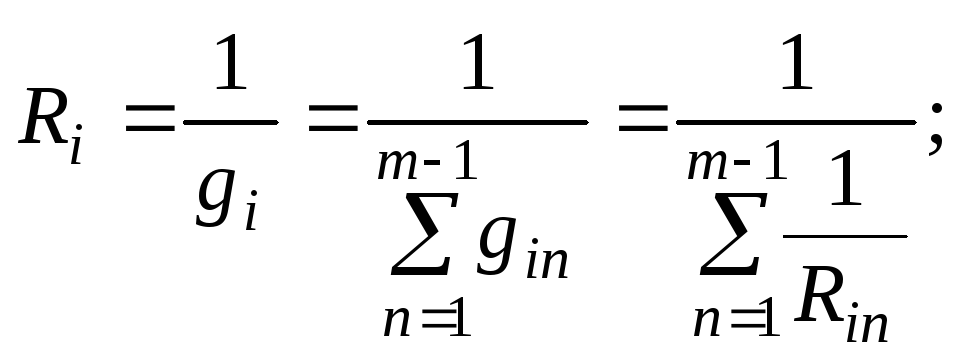


Рис. 52. Схема замещения с эквивалентным источником ЭДС
Для нахождения тока нагрузки в схеме рис. 52 справедлива формула (3) закона Ома для замкнутой цепи:
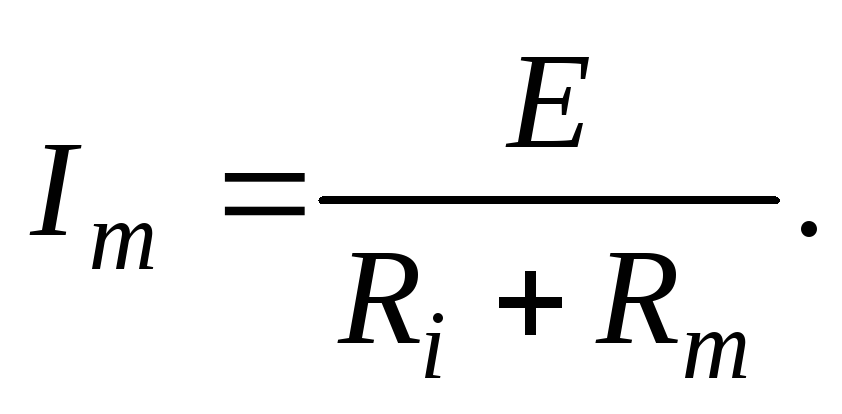
15. Энергетические соотношения в цепях постоянного тока
В настоящем параграфе рассматриваются особенности работы цепи постоянного тока с реальным источником ЭДС в двух режимах. Первый из них иллюстрируется схемой рис. 53.

Рис. 53. Схема работы реального источника ЭДС в режиме
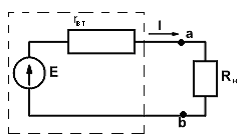
1.3. Источник эдс и источник тока
Источник энергии в схеме рис. 1.5.а), очерченный пунктирной линией, включает источник ЭДС Е и внутреннее сопротивление rвт.
Внешняя характеристика
источника напряжения (или ВАХ) 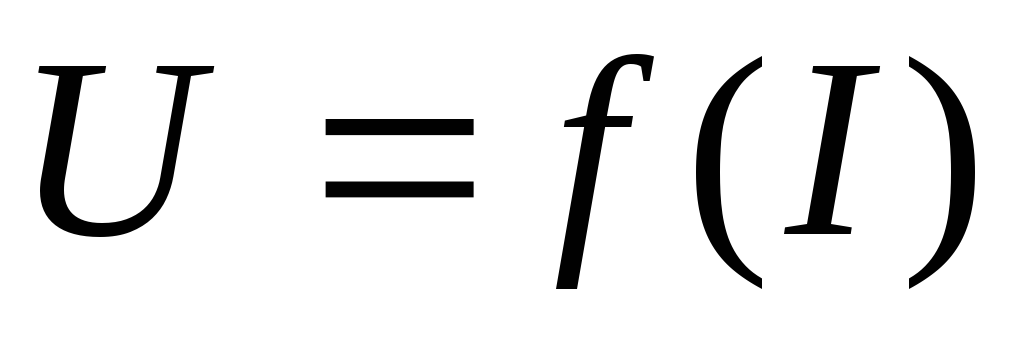 в
общем случае определяется как
в
общем случае определяется как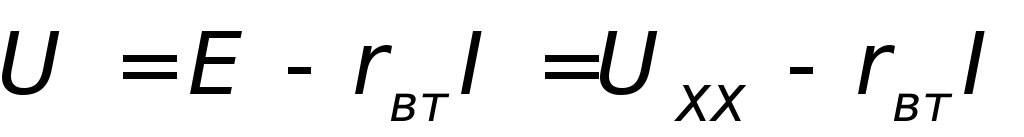 ,
,
где Uxx− напряжение при разомкнутой цепи нагрузки. Этому выражению соответствует прямая наклонная линия на рис. 1.5.а).
а)
б)
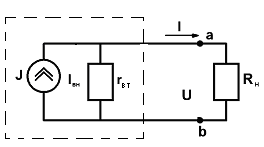
Рис. 1. 5.

а)
б)
в)
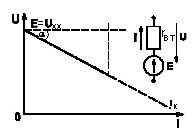
Рис. 1.6.
Рассмотрим два крайних случая.
1) При  и
и ,
получим
,
получим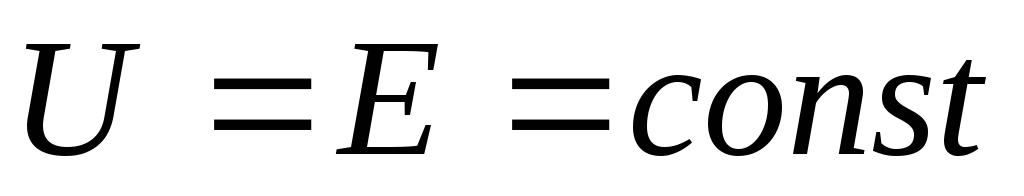 ,
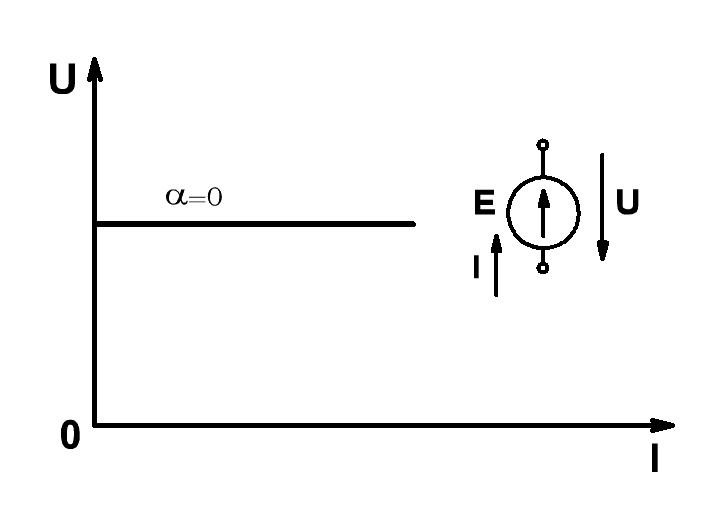
тогда ВАХ − прямая линия, источник ЭДС
(рис. 1.6.б) представляет собой идеализированный
источник питания, напряжение на зажимах
которого не зависит от величины тока.
,
тогда ВАХ − прямая линия, источник ЭДС
(рис. 1.6.б) представляет собой идеализированный
источник питания, напряжение на зажимах
которого не зависит от величины тока.
2) Если у источника
питания повышается ЭДС и внутреннее
сопротивление 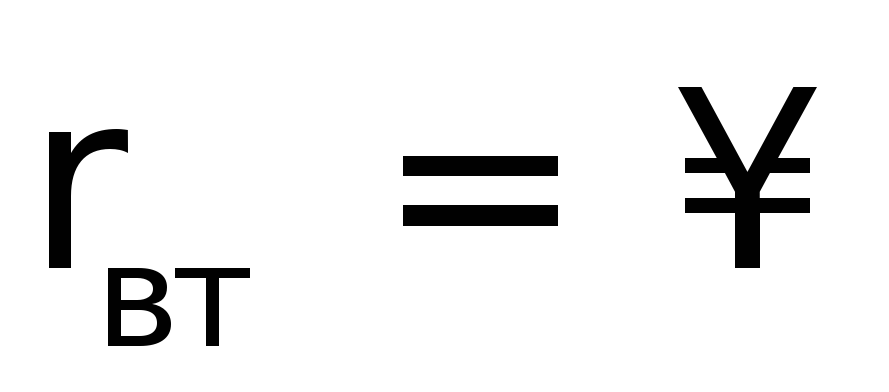 ,
,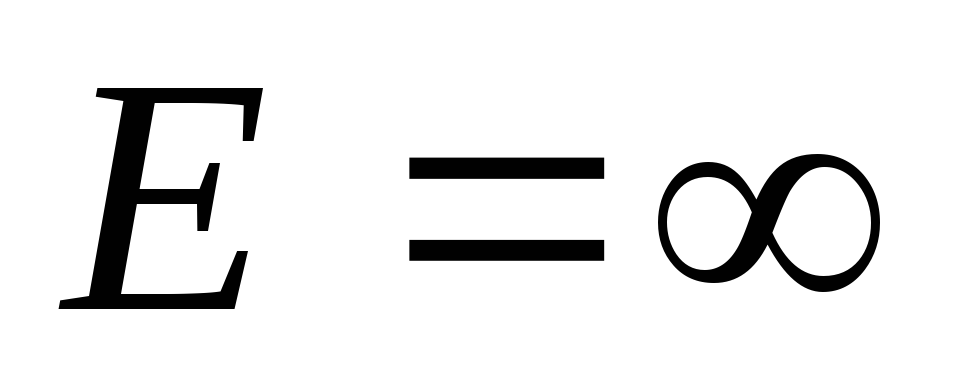 ,
то
,
то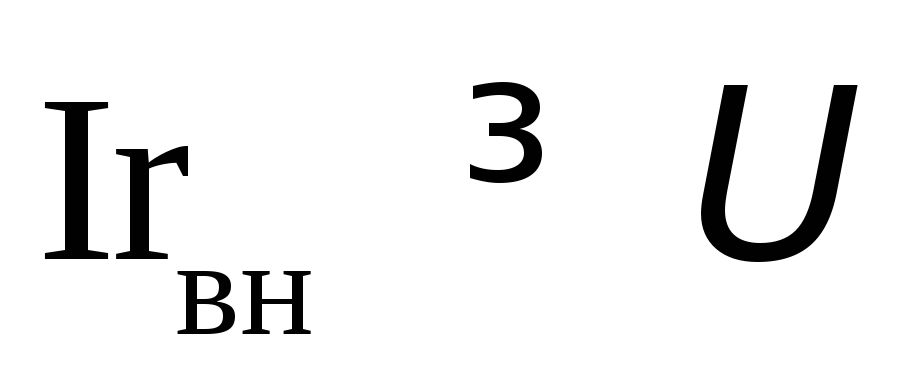 ,
тогда
,
тогда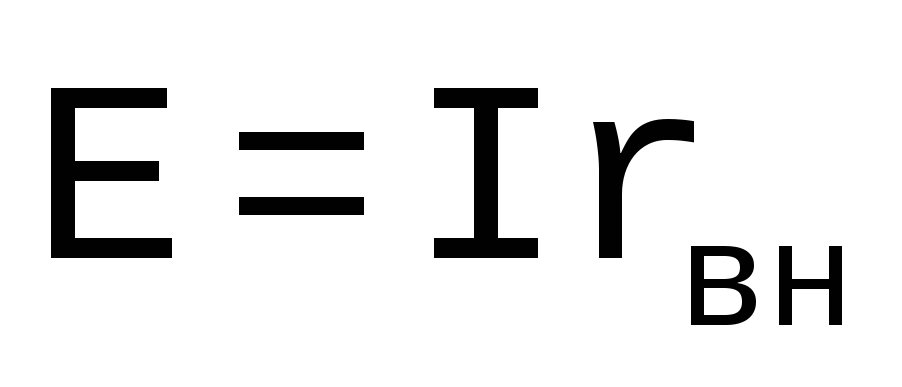 .
Ток источника тока
.
Ток источника тока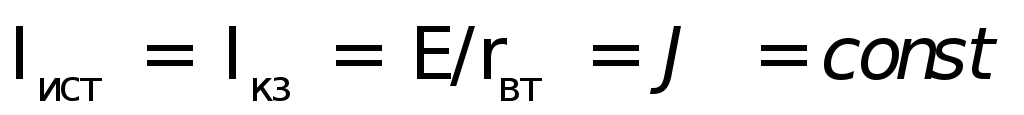 ,
и ВАХ примет вид, показанный на рис.1.6.в).
,
и ВАХ примет вид, показанный на рис.1.6.в).
Следовательно, источник тока представляет собой идеализированный источник питания, в котором ток не зависит от сопротивления нагрузки.
При построении
эквивалентных схем замещения ветви,
содержащие источники напряжения,
замыкают накоротко (rвт=0),
а ветви с источниками тока ликвидируют
(т. к. 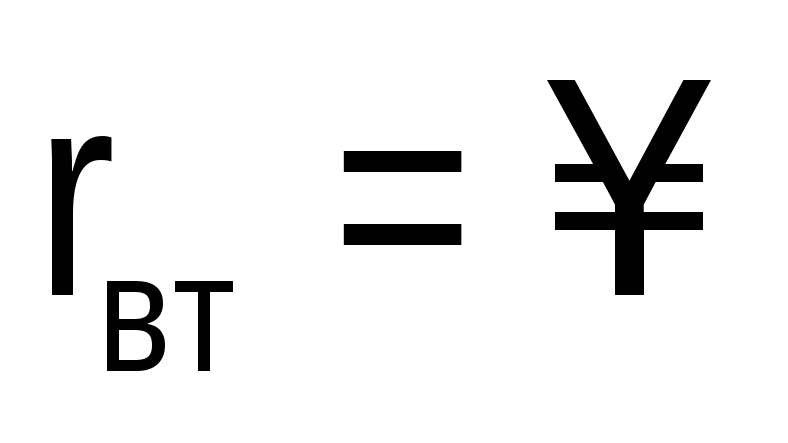 ).
Ток в нагрузке
).
Ток в нагрузке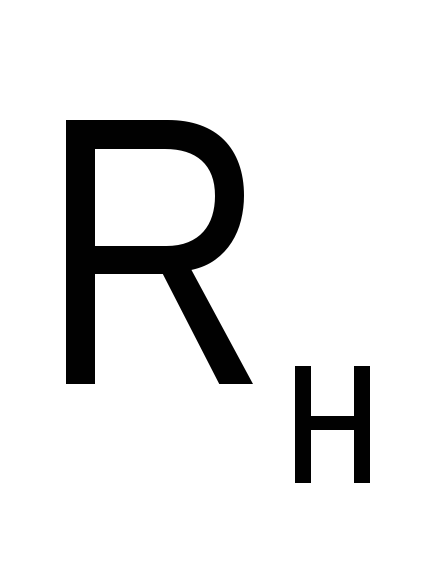 для схем рис. 1.6.б) и в) одинаков;
для схем рис. 1.6.б) и в) одинаков;
для источника ЭДС  ,
для источника тока
,
для источника тока .
.
Осуществим переход
от схемы с источником тока к схеме с
источником ЭДС. Пусть в схеме б)  =50
А,
=50
А, =2
Ом, в схеме а) ЭДС
=2
Ом, в схеме а) ЭДС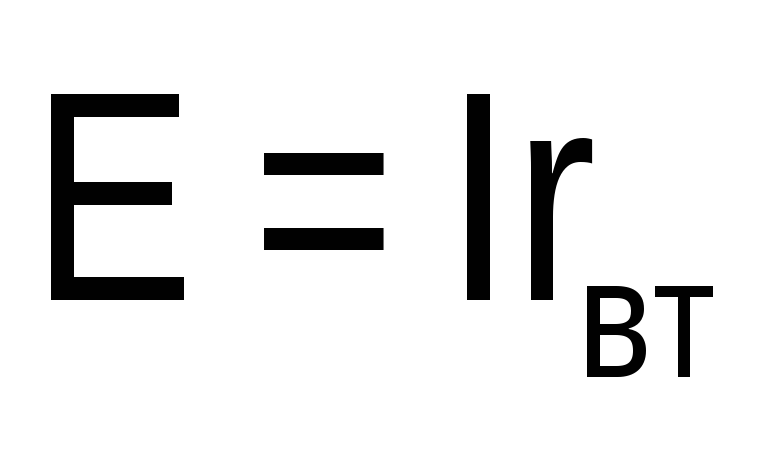 =100
В. Следовательно, параметры эквивалентной
схемы рис.1.5.а) равны
=100
В. Следовательно, параметры эквивалентной
схемы рис.1.5.а) равны = 100 В,
= 100 В, = 2 Ом.
= 2 Ом.
Можно пользоваться любым эквивалентом, но в основном пользуются источником напряжения.
1.4. Методы расчета электрических цепей постоянного тока
1.4.1.Расчет по законам Кирхгофа
Все ЭЦ подчиняются первому и второму законам Кирхгофа.
П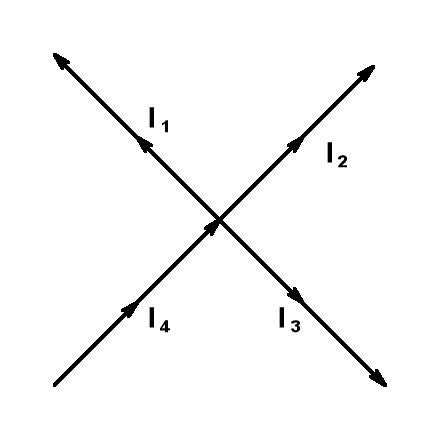 ервый
закон Кирхгофа можно сформулировать двояко. Алгебраическая
сумма токов, приходящих к любому узлу
схемы, равна нулю. Сумма токов, приходящих
к узлу, равна сумме токов, уходящих от
узла. Е
сли токи, приходящие к узлу, на рис.
1.7. считать положительными, а токи,
уходящие от узла, отрицательными, то,
согласно первой формулировке, получим
ервый
закон Кирхгофа можно сформулировать двояко. Алгебраическая
сумма токов, приходящих к любому узлу
схемы, равна нулю. Сумма токов, приходящих
к узлу, равна сумме токов, уходящих от
узла. Е
сли токи, приходящие к узлу, на рис.
1.7. считать положительными, а токи,
уходящие от узла, отрицательными, то,
согласно первой формулировке, получим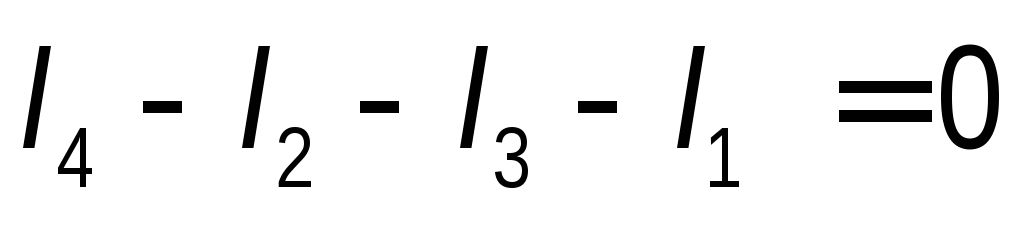 ;
; ,
,
где n – число ветвей, образующих узел.
С
Рис. 1.7.
огласно 2-й формулировке .
.Физически 1-й закон Кирхгофа означает, что при движении электронов по цепи ни в одном из узлов заряды не накапливаются.
Второй закон
Кирхгофа так же можно сформулировать двояко.
Алгебраическая сумма падений напряжений
на резистивных элементах в любом
замкнутом контуре равно алгебраической
сумме ЭДС. 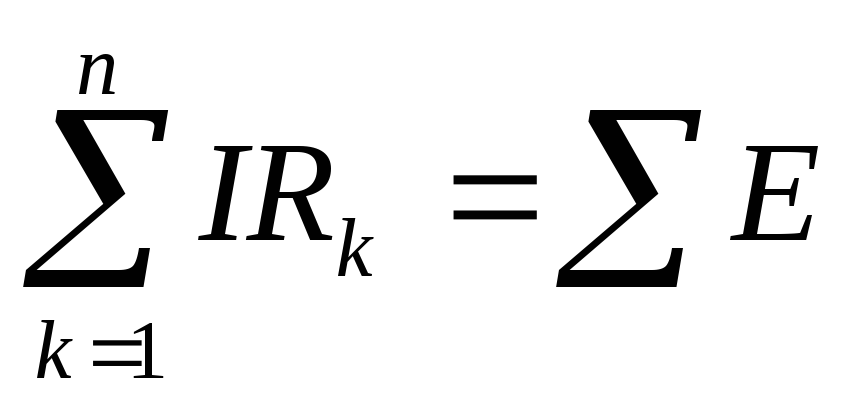 .
.
В каждую из сумм составляющие слагаемые входят со знаком «+», если они совпадают с направлением обхода контура, и со знаком «», если не совпадают.
Алгебраическая
сумма напряжений участков вдоль любого
замкнутого контура равна нулю 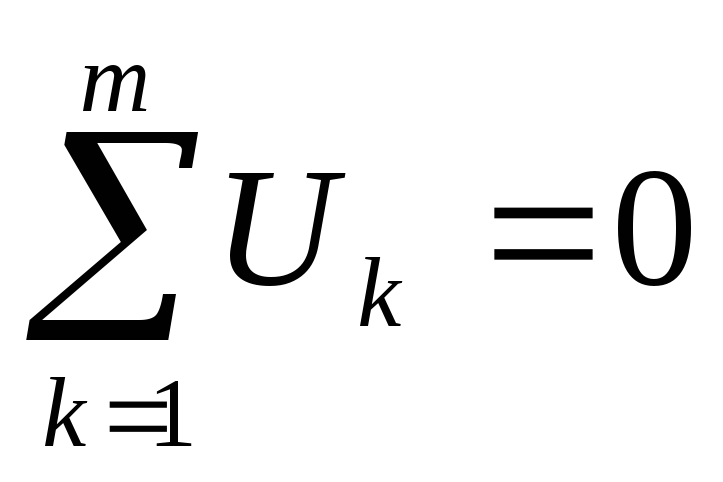 ,
,
где m – число
участков контура, так, для периферийного
контура схемы рис.1.8. имеем  .
.
Законы Кирхгофа справедливы для линейных и нелинейных цепей при любом характере изменений токов и напряжений во времени.
При составлении уравнений для расчетов токов в ветвях схемы с помощью законов Кирхгофа учитываем, что в каждой ветви течет свой ток.
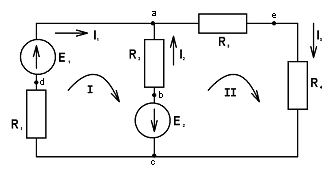
Рис. 1.8.
Обозначим число всех ветвей схемы через «б», число ветвей, содержащих источники тока, через «бист.т», и число узлов – через «у». Так как токи в ветвях с источниками тока неизвестны, то число неизвестных токов запишем как «б» — «бист.т».
Перед тем как составить уравнения, необходимо а) произвольно выбрать положительные направления токов в ветвях и обозначить их на схеме; б) выбрать положительные направления контуров для составления уравнений по 2-ому закону Кирхгофа.
Желательно во всех контурах положительные направления обхода выбирать одинаковыми, например, по часовой стрелке, как показано на рис. 1.9.
Чтобы получить независимые уравнения, по 1-ому закону Кирхгофа составляют число уравнений, равное числу узлов без единицы, т.е. «у-1». По 2-ому закону Кирхгофа составляют число уравнений, равное числу ветвей без источников тока б — бист.т, за вычетом числа уравнений, составленных по 1- му закону Кирхгофа. В рассмотренном (б — бист.т)-(у -1) = 3 – 2 + 1 = 2.
При записи линейно независимых уравнений по второму закону Кирхгофа стремятся, чтобы в каждый новый контур, для которого составляют уравнение, входила хотя бы одна новая ветвь, не вошедшая в контуры, для которых уже записаны уравнения. Такие контуры условно можно назвать независимыми.
По 1- ому закону
Кирхгофа составляем одно уравнение  .
.
По 2-ому закону Кирхгофа надо составить два уравнения. Положительные направления обхода контуров выбираем по часовой стрелке.
Для контура 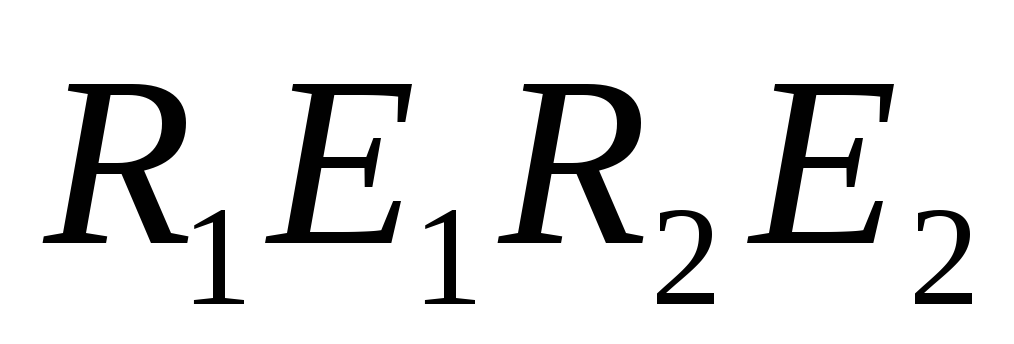
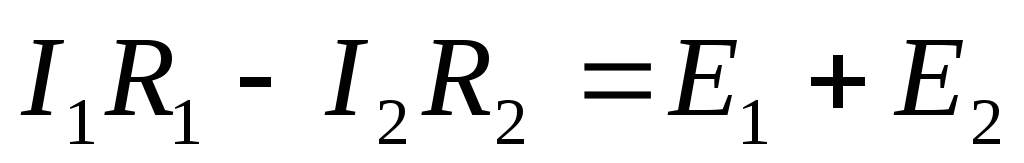 ,
знак«+» взят перед
,
знак«+» взят перед  ,
потому что направление тока
,
потому что направление тока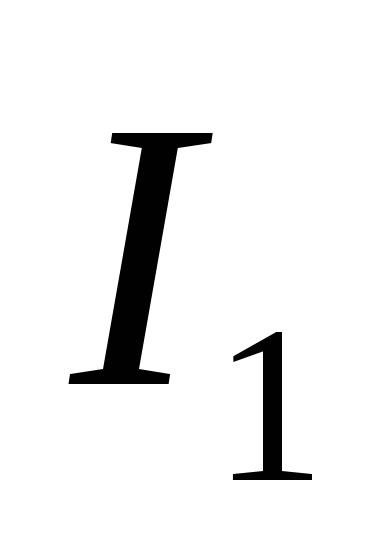 совпадает с направлением обхода контура;
знак «»
перед
совпадает с направлением обхода контура;
знак «»
перед 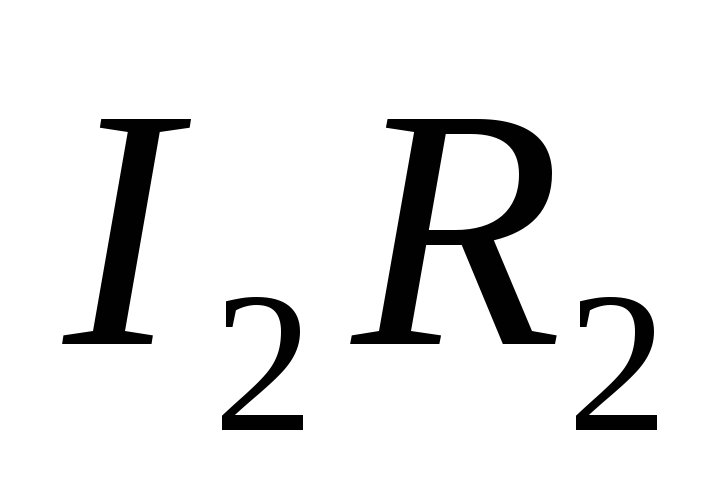 показывает, что направление
показывает, что направление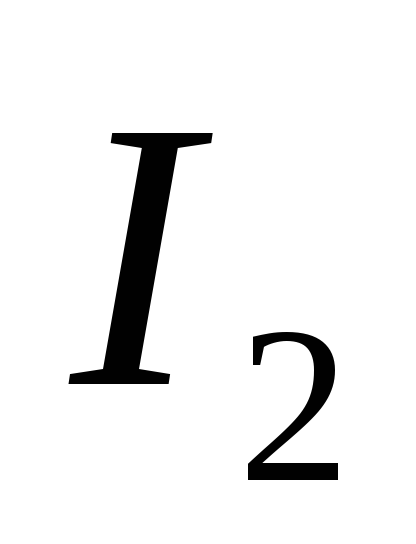 встречно обходу контура.
встречно обходу контура.
Для контура 
 .
.
Используя законы Кирхгофа, можно для любой разветвленной электрической цепи составить необходимое число уравнений, путем совместного решения которых можно найти все определяемые величины (например, токи), а также установить зависимости между ними.
1.4. Источник эдс и источник тока
Представим простейшую электрическую цепь схемой рис.1.3, на которой указан реальный источник ЭДС, например аккумулятор.
Свойства
источника электрической энергии
определяет вольт-амперная характеристика
(рис.1.4) — зависимость напряжения U от
тока 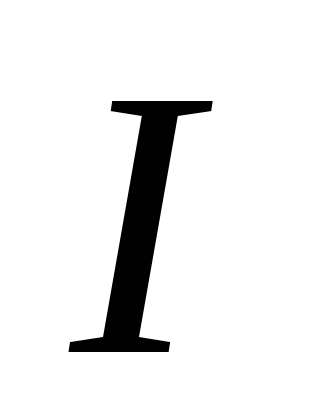 :
:
 .
(1.15)
.
(1.15)
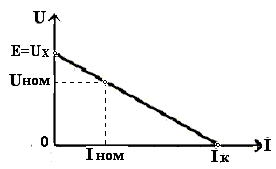
Рис.1.4. Вольт-амперая характеристика источника ЭДС
Точка  =
= 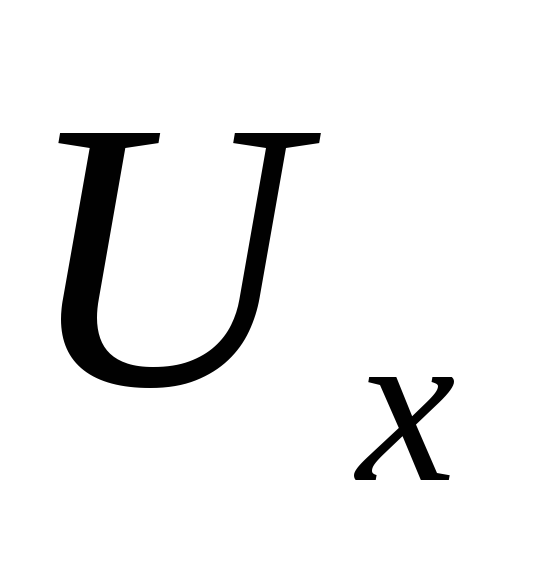 соответствует режиму холостого хода,
точка Iк —
режиму короткого замыкания реального
источника ЭДС. Уменьшение напряжения
источника при увеличении тока связано
с увеличением падения напряжения
соответствует режиму холостого хода,
точка Iк —
режиму короткого замыкания реального
источника ЭДС. Уменьшение напряжения
источника при увеличении тока связано
с увеличением падения напряжения  .
При отрицательных значениях тока,
увеличивается напряжение, что соответствует
зарядке аккумулятора.
.
При отрицательных значениях тока,
увеличивается напряжение, что соответствует
зарядке аккумулятора.
При  = 0 идеализированный источник электрической
энергии называется идеальным источником
ЭДС, а вольт-амперная характеристика
(рис.1.5) определяется выражением:
= 0 идеализированный источник электрической
энергии называется идеальным источником
ЭДС, а вольт-амперная характеристика
(рис.1.5) определяется выражением:
 .
(1.16)
.
(1.16)
Такой источник называется также источником напряжения. На этом же рисунке приведено условное схемное изображение источника напряжения.

Рис.1.5. Идеальный источник ЭДС
В
электрических цепях с полупроводниковыми
приборами и электронными лампами  значительно превышает
значительно превышает 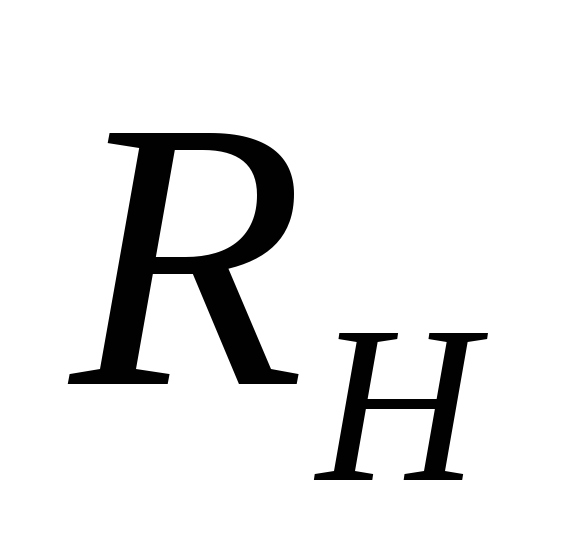 .
Источник электрической энергии, у
которого
.
Источник электрической энергии, у
которого 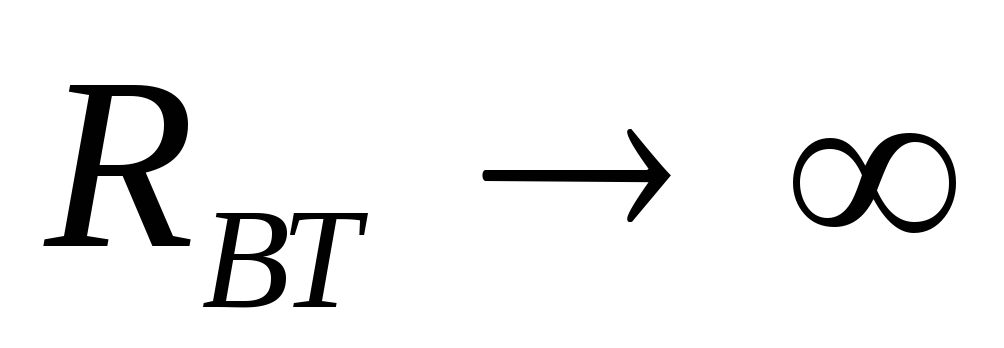 ,
называется идеальным источником тока
с параметром:
,
называется идеальным источником тока
с параметром:
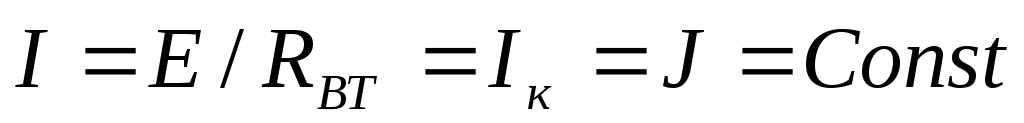 .
(1.17)
.
(1.17)
Такому источнику соответствует характеристика рис.1.6:
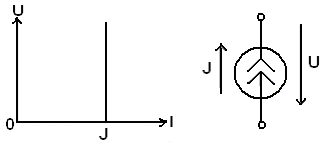
Рис.1.6. Идеальный источник тока
На этом же рисунке приведено условное схемное изображение источника тока.
Если
все слагаемые формулы (1.15) разделить на
внутреннее сопротивление  источника, то получим выражение:
источника, то получим выражение:
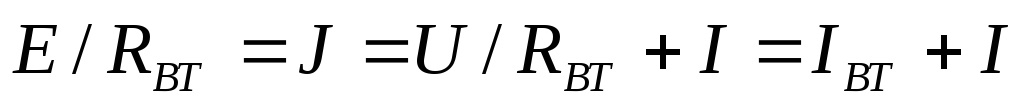 .
(1.18)
.
(1.18)
Откуда
следует, что ток источника тока J складывается из тока I (во внутреннем участке цепи) и тока I (во
внешнем участке цепи). Схема с источником
тока J приведена на рис.1.7:
(во внутреннем участке цепи) и тока I (во
внешнем участке цепи). Схема с источником
тока J приведена на рис.1.7:

Рис.1.7. Электрическая схема цепи с источником тока
1.5. Законы Кирхгофа
Электрические цепи делятся на неразветвленные и разветвленные цепи. Неразветвленные цепи представляют собой последовательно соединенные источники и приёмники электрической энергии. При этом источники электрической энергии могут иметь либо согласное включение (одинаковое направление), либо встречное включение (направление разное).
Разветвленными называются цепи, в которых источники и приемники электрической энергии соединены параллельно или имеют смешанное соединение. Такие цепи являются сложными, и для их расчета используются либо законы Кирхгофа, либо другие методы расчёта цепей постоянного тока.
Первый закон Кирхгофа: алгебраическая сумма токов в любом узле электрической цепи равна нулю:
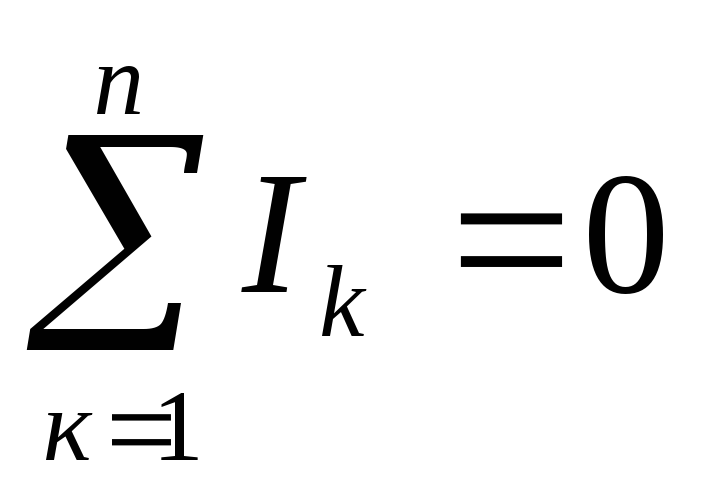 .
(1.19)
.
(1.19)
На схеме рис.1.8 показано параллельное соединение трёх приемников электрической энергии, указано направление токов для узла ‘‘а’’.
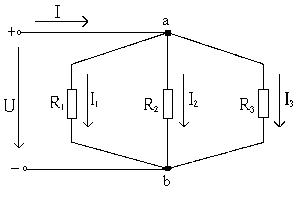
Рис.1.8. Электрическая цепь с параллельным соединением приемников
Будем считать направление тока к узлу положительным, а от узла отрицательным. Тогда, используя выражение (1.19), для узла “а” напишем:
 или
или 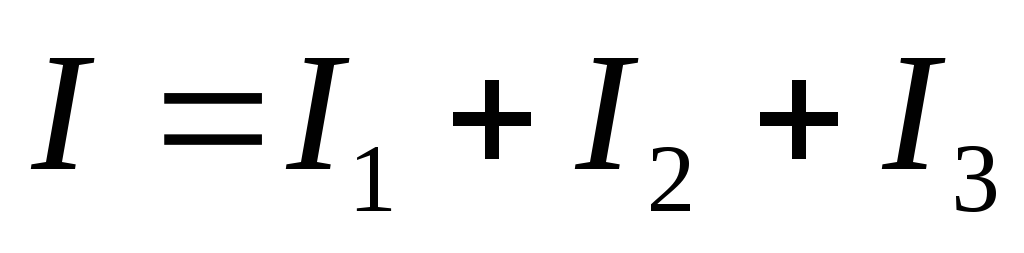 .
.
Второй закон Кирхгофа: во всяком замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме напряжений на резистивных элементах:
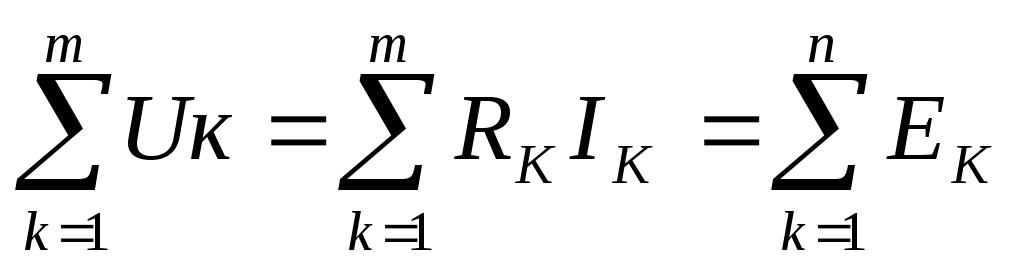 ,
(1.20)
,
(1.20)
где m — число резистивных элементов, n — число ЭДС в контуре.
При этом необходимо задаться направлением обхода контура, а также направлениями токов в ветвях контура и источников ЭДС.
На схеме рис.1.9. рассмотрим один из контуров сложной электрической цепи с указанным направлением обхода контура. По второму закону Кирхгофа запишем:
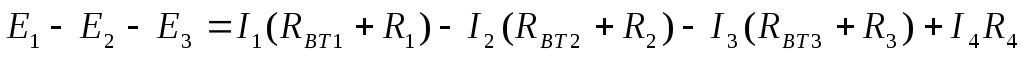
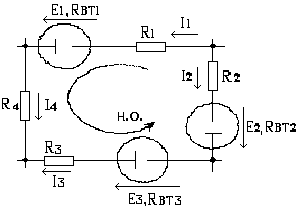
Рис.1.9. Пример схемы расчёта по второму закону Кирхгофа
Работа 217 Определение ЭДС неизвестного источника
ОПРЕДЕЛЕНИЕ ЭДС НЕИЗВЕСТНОГО ИСТОЧНИКА МЕТОДОМ КОМПЕНСАЦИИ
Цель работы: Ознакомление с методом компенсации и его применение для определения электродвижущей силы (ЭДС) неизвестного источника.
Введение
Гальванические элементы, аккумуляторы, электрические генераторы и другие устройства, которые преобразуют различные виды энергий (химическую, механическую, световую и др.) в электрическую энергию, являются источниками ЭДС. Устройство способное поддерживать определённую разность потенциалов и обеспечить поток электрических зарядов во внешней цепи, называются источниками ЭДС.
Разность потенциалов на клеммах гальванического элемента при разомкнутой внешней цепи называется электродвижущей силой (ЭДС) и обозначается E. Когда сила тока во внешней цепи отсутствует, напряжение на клеммах равно ЭДС. Когда к клеммам гальванического элемента подключается внешняя нагрузка (например, сопротивление вольтметра), т.е. во внешней цепи протекает электрический ток, согласно закону Ома для неоднородной электрической цепи этот ток равен:
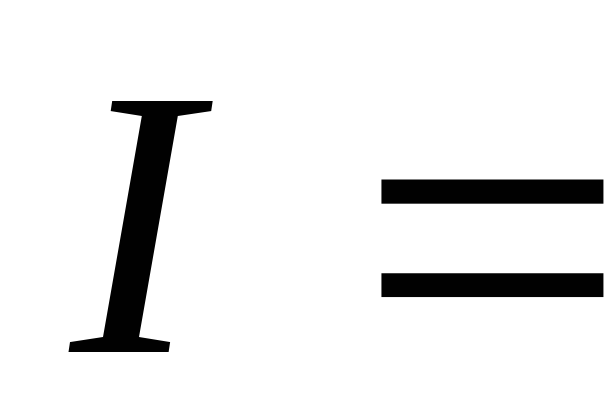
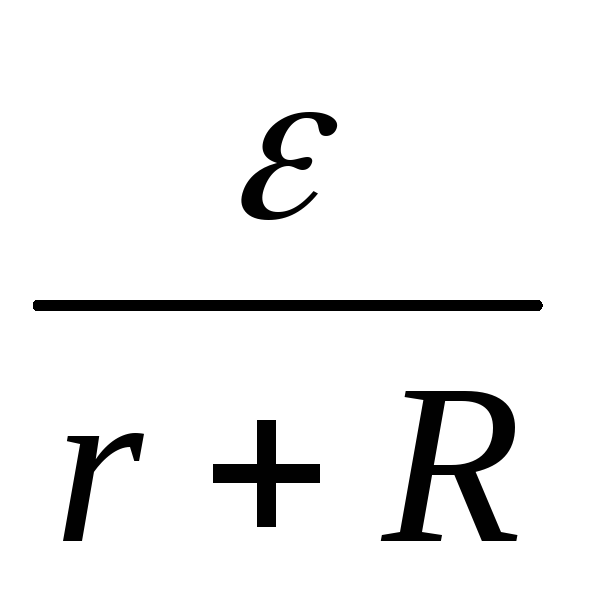 , тогда E
= Ir + IR, (1)
, тогда E
= Ir + IR, (1)
следовательно, напряжение на клеммах гальванического элемента оказывается ниже величины ЭДС из-за падения напряжения на внутреннем сопротивлении источника ЭДС и равно:
IR = E – Ir, (2)
где E — ЭДС источника тока, R – внешнее сопротивление, r – внутреннее сопротивление источника тока, I – сила тока.
Электродвижущая сила численно равна работе, совершаемой сторонними силами по перемещению единичного положительного заряда:
E .
(3)
.
(3)
Эта работа производится за счёт энергии, затрачиваемой в источнике тока.
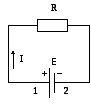
Рис. 1.
Напряжение U на участке 1-2 электрической цепи (см. рис. 1) называется физическая величина, определяемая работой, совершаемой суммарным полем кулоновских и сторонних сил при перемещении единичного положительного заряда на этом участке:
U12 = 1 –2 + E12. (4)
Если на участке цепи не действует ЭДС, напряжение на концах участка цепи равна разности потенциалов на этом участке.
Разность потенциалов численно равна работе, совершаемой силами электростатического поля по перемещению единичного положительного заряда:
1 – 2 = (5)
(5)
Для определения величины электродвижущей силы используется метод компенсации («нулевой метод»). В этом методе ток текущий через источник с неизвестной ЭДС – Eх, компенсируется током от какого-либо внешнего источника ЭДС – E. При этом разность потенциалов на зажимах неизвестного источника будет равна его ЭДС.
Принципиальная схема установки, служащей для измерений ЭДС неизвестного источника изображена на рис. 2.
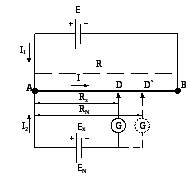
Рис. 2.
В цепи, благодаря разности потенциалов между точками А и В через резистор R со скользящим контактом D создаётся постоянный ток. Резистор R может представлять собой однородный провод (реохорд) по которому скользит контакт D, что позволяет изменять величину сопротивления между А и D. Исследуемый источник ЭДС Eх присоединяется через гальванометр G ( с нулём на середине шкалы) к движку D и концу реохорда АВ таким образом, чтобы внешний источник ЭДС и исследуемый источник были включены навстречу друг другу. Только в этом случае возможна компенсация.
Контакт реохорда перемещают до тех пор, пока стрелка гальванометра не установится на нуле шкалы. В этом положении контакта D ток от источника неизвестной ЭДС равен нулю, а напряжение между точками АD равно Eх:
UАD = Eх
Это равенство справедливо только при условии, что сила тока через гальванометр равна нулю, т.к. в противном случае наблюдалось бы падение напряжения на внутреннем сопротивлении источника неизвестной ЭДС и сопротивлении гальванометра. Сила тока I через резистор R не равна нулю, и если обозначать через Rх сопротивление между точками А и D реохорда R то:
Eх = IRх. (6)
Затем необходимо произвести ещё одно измерение, подключив в установке вместо Eх «стандартный элемент» — источник EN ЭДС которого известна с высокой точностью. Контакт D переводят в новое положение D`, в котором гальванометр вновь не регистрирует тока. В этом положении справедливо равенство:
EN = IRN, (7)
где RN – сопротивление между точками А и D`. Т.к. через R протекает ток той же величины I, то:
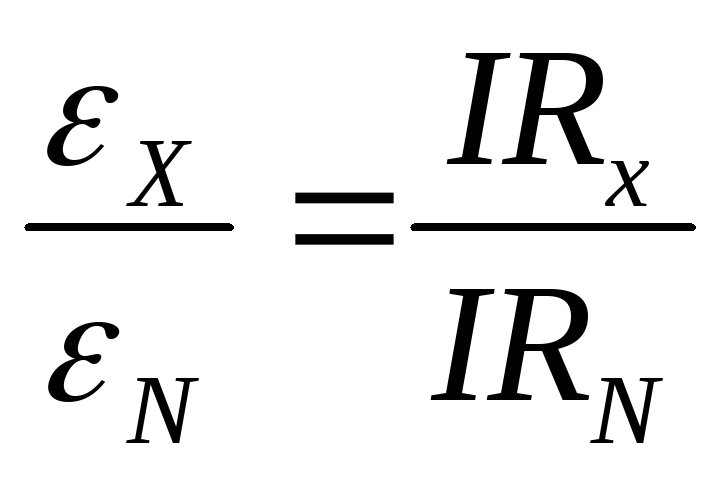 ,
,
или
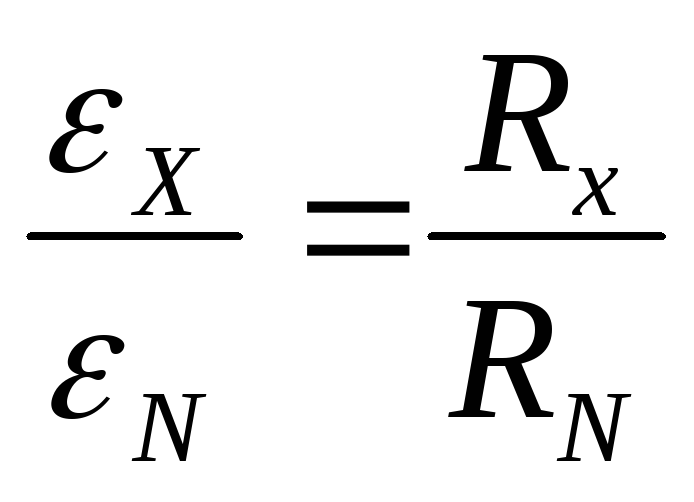 ,
,
отсюда:
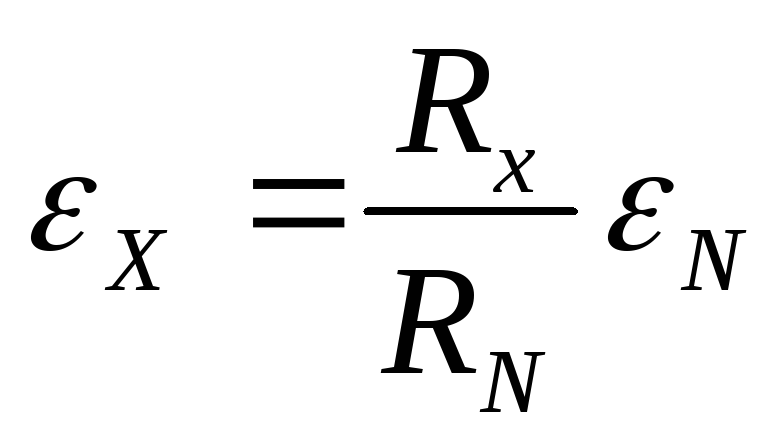 .
(8)
.
(8)
Т.к. резистор R представляет собой однородную проволоку, то сопротивления Rх и RN пропорциональны соответствующим длинам плеч реохорда lx и lN, поэтому окончательно получаем:
 .
(9)
.
(9)
Следовательно, экспериментально определив длины плеч реохорда в двух случаях — в случае включения в компенсационную схему источника с неизвестной ЭДС Eх и в случае включения источника с известной ЭДС EN можно по формуле (9) рассчитать ЭДС неизвестного источника Eх. В компенсационном методе роль измерительного прибора, гальванометра сводится не к измерению тока, а к установлению его отсутствия на участке цени с источником неизвестной ЭДС. Поэтому в компенсационных схемах применяются не точные, но очень чувствительные гальванометры (так называемые ноль-гальванометры).
Приборы и принадлежности: источник питания, нормальный элемент Вестона (или другой эталонный источник), исследуемый источник ЭДС (гальванический элемент или другие источники ЭДС), потенциометр (или реохорд), вольтметр V с нулём посередине шкалы, ключ включения источника питания, переключатель Eх — EN с нейтральным положением.
Порядок выполнения работы
1. Ознакомиться с принципом работы компенсационной схемы и её применением в данной лабораторной работе, т. е. с монтажной компенсационной схемой, представленной на рис. 3. Здесь К1 — ключ включения источника E питания, К2 — переключатель для ввода в цепь попеременно исследуемого и эталонного источников ЭДС. В лабораторной установке реохорд АВ заменен потенциометром АВ с движком D. При этом выводы расчётной формулы (9) остаются справедливыми. Остальные обозначения соответствуют обозначениям схемы, представленной на рис. 2.
2. Ознакомиться с эксплуатационными особенностями схемы (см. последующие пункты).
3. Замкнуть переключатель К2 (двойной ключ) на исследуемый элемент Eх.
4. Замкнуть ключ К1.
Замыкание ключей необходимо производить только в указанном порядке.
Цепь должна замыкаться только на короткое время во избежание неэкономного расходования источника напряжения.
5. Добившись полного отсутствия тока в цепи вольтметра V передвижением подвижного контакта потенциометра, произвести измерение lх с помощью линейки, установленной на потенциометре. Аналогичным образом измерить lN, замкнув элемент EN ключом К2. Измерения проделать 4 (четыре) раза. Найти средние значения lх и lN. Полученные данные занести в таблицу1.
6. По окончании работы переключатель К2 обязательно поставить в среднее (нейтральное) положение!
7. Рассчитать значение Eх по формуле (9), используя средние значения lх ср и lN ср и занести результат в таблицу 1.

Рис. 3.
Таблица 1
Источники ЭДС | Длина плеча потенциометра l, мм | ЭДС источника, В | ||||
1 | 2 | 3 | 4 | Среднее значение, lср | ||
Исследуемый | ||||||
Эталонный | 1,018 | |||||
8. Определить предельную относительную погрешность измерений по формуле:
δE ,
(10)
,
(10)
считая, что в данной работе преобладают приборные ошибки.
Контрольные вопросы
1. В чем суть метода компенсации? Зарисовать схему цепи.
2. Написать уравнения Кирхгофа для контуров цепи компенсационной схемы.
3. Какие преимущества имеет метод компенсации по сравнению с другими методами измерения ЭДС?
4. Сформулировать закон Ома для замкнутой цепи, участка цепи, содержащего ЭДС и участка цепи, не содержащего ЭДС.
5. Как устроен гальванический элемент?
6. Что называется ЭДС?
7. Что называется напряжением?
8. В каких единицах измеряются ЭДС и напряжение в международной системе единиц?
9. Может ли резистор обладать ЭДС?
10. Может ли напряжение на клеммах батареи превышать её ЭДС?
Список литературы
1.Савельев И. В. Курс общей физики. – М., Наука, 2001.-Т.2 .
2. Яворский Б.М., Детлаф А.А. Курс физики. – М. «Высшая школа», 2003.
3. Колотилова В.Г. Определение ЭДС неизвестного источника методом компенсации. – М. МИИТ, 1987.
Учебно-методическое издание
Кули-Заде Тофик Салман-Оглы
Васильев Евгений Васильевич
ОПРЕДЕЛЕНИЕ ЭДС НЕИЗВЕСТНОГО
ИСТОЧНИКА МЕТОДОМ КОМПЕНСАЦИИ
Методические указания к лабораторной работе №217
под редакцией доцента Харитонова Ю.Н.
Подписано к печати Заказ № Формат 60х84х21/16
Усл.-печ. л. Изд. № 192-10 Тираж 300 экз.
127994, Москва, ул. Образцова д. 9, стр. 9.
Типография МИИТа
10

