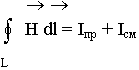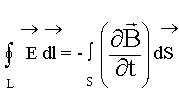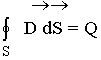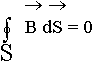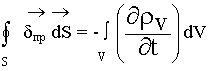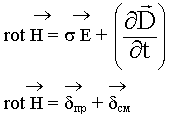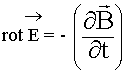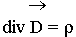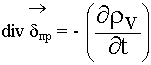Уравнения Максвелла — Википедия
Уравне́ния Ма́ксвелла — система уравнений в дифференциальной или интегральной форме, описывающих электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах. Вместе с выражением для силы Лоренца, задающим меру воздействия электромагнитного поля на заряженные частицы, эти уравнения образуют полную систему уравнений классической электродинамики, называемую иногда уравнениями Максвелла — Лоренца. Уравнения, сформулированные Джеймсом Клерком Максвеллом на основе накопленных к середине XIX века экспериментальных результатов, сыграли ключевую роль в развитии представлений теоретической физики и оказали сильное, зачастую решающее влияние не только на все области физики, непосредственно связанные с электромагнетизмом, но и на многие возникшие впоследствии фундаментальные теории, предмет которых не сводился к электромагнетизму (одним из ярчайших примеров здесь может служить специальная теория относительности).

Уравнения, сформулированные Джеймсом Клерком Максвеллом, возникли на основе ряда важных экспериментальных открытий, которые были сделаны в начале XIX века. В 1820 году Ганс Христиан Эрстед обнаружил[1], что пропускаемый через провод гальванический ток заставляет отклоняться магнитную стрелку компаса. Это открытие привлекло широкое внимание учёных того времени. В том же 1820 году Био и Савар экспериментально нашли выражение[2] для порождаемой током магнитной индукции (закон Био — Савара), а Андре Мари Ампер обнаружил также, что взаимодействие на расстоянии возникает между двумя проводниками, по которым пропускается ток. Ампер ввёл термин «электродинамический» и выдвинул гипотезу, что природный магнетизм связан с существованием в магните круговых токов
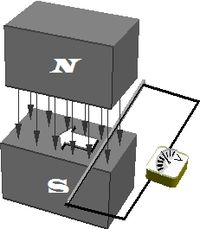
Влияние тока на магнит, обнаруженное Эрстедом, привело Майкла Фарадея к идее о том, что должно существовать обратное влияние магнита на токи. После длительных экспериментов, в 1831 году, Фарадей открыл, что перемещающийся возле проводника магнит порождает в проводнике электрический ток. Это явление было названо электромагнитной индукцией. Фарадей ввёл понятие «поля сил» — некоторой среды, находящейся между зарядами и токами. Его рассуждения носили качественный характер, однако они оказали огромное влияние на исследования Максвелла.
После открытий Фарадея стало ясно, что старые модели электромагнетизма (Ампер, Пуассон и др.) неполны. Вскоре появилась теория Вебера, основанная на дальнодействии. Однако к этому моменту вся физика, кроме теории тяготения, имела дело только с близкодействием (оптика, термодинамика, механика сплошных сред и др.). Гаусс, Риман и ряд других учёных высказывали догадки, что свет имеет электромагнитную природу, так что теория электромагнитных явлений тоже должна быть близкодейственной. Этот принцип стал существенной особенностью теории Максвелла.
В своём знаменитом «Трактате об электричестве и магнетизме» (1873) Максвелл писал[4]:
Приступая к изучению труда Фарадея, я установил, что его метод понимания явлений был так же математическим, хотя и не представленным в форме обычных математических символов. Я также нашёл, что этот метод можно выразить в обычной математической форме и таким образом сравнить с методами профессиональных математиков.
Заменяя фарадеевский термин «поле сил» на понятие «напряжённость поля», Максвелл сделал его ключевым объектом своей теории[5]:
Если мы примем эту среду в качестве гипотезы, я считаю, что она должна занимать выдающееся место в наших исследованиях, и что нам следовало бы попытаться сконструировать рациональное представление о всех деталях её действия, что и было моей постоянной целью в этом трактате.
Подобная электродинамическая среда явилась абсолютно новым понятием для ньютоновской физики. Последняя изучала взаимодействие между собой материальных тел. Максвелл же записал уравнения, которым должна подчиняться среда, определяющая взаимодействие зарядов и токов и существующая даже в их отсутствие.
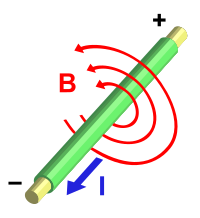 Электрический ток создаёт магнитную индукцию (закон Ампера)
Электрический ток создаёт магнитную индукцию (закон Ампера)Анализируя известные эксперименты, Максвелл получил систему уравнений для электрического и магнитного полей. В 1855 году в своей самой первой статье «О фарадеевых силовых линиях»
Оказалось, что не только ток, но и изменяющееся со временем электрическое поле (ток смещения) порождает магнитное поле. В свою очередь, в силу закона Фарадея, изменяющееся магнитное поле снова порождает электрическое. В результате, в пустом пространстве может распространяться электромагнитная волна. Из уравнений Максвелла следовало, что её скорость равна скорости света, поэтому Максвелл сделал вывод об электромагнитной природе света.
Часть физиков выступила против теории Максвелла (особенно много возражений вызвала концепция тока смещения). Гельмгольц предложил свою теорию, компромиссную по отношению к моделям Вебера и Максвелла, и поручил своему ученику Генриху Герцу провести её экспериментальную проверку. Однако опыты Герца однозначно подтвердили правоту Максвелла.
Максвелл не использовал векторных обозначений и записывал свои уравнения в достаточно громоздком компонентном виде. В своём трактате[13] он, кроме того, частично использовал кватернионную формулировку. Современная форма уравнений Максвелла появилась около 1884 года после работ Хевисайда, Герца и Гиббса. Они не только переписали систему Максвелла в векторном виде, но и симметризовали её, переформулировав в терминах поля, избавившись от электрического и магнитного потенциалов, игравших в теории Максвелла существенную роль, поскольку полагали, что эти функции являются лишь ненужными вспомогательными математическими абстракциями
Система уравнений в формулировке Герца и Хевисайда некоторое время называлась уравнениями Герца — Хевисайда[16]. Эйнштейн в классической статье «К электродинамике движущихся тел»[17] назвал их уравнениями Максвелла — Герца. Иногда в литературе встречается также название уравнения Максвелла — Хевисайда
Уравнения Максвелла сыграли важную роль при возникновении специальной теории относительности (СТО). Джозеф Лармор (1900 год)[19] и независимо от него Хенрик Лоренц (1904 год)[20] нашли преобразования координат, времени и электромагнитных полей, которые оставляют уравнения Максвелла инвариантными при переходе от одной инерциальной системы отсчёта к другой. Эти преобразования отличались от преобразований Галилея классической механики и, с подачи Анри Пуанкаре[21], стали называться преобразованиями Лоренца. Они стали математическим фундаментом специальной теории относительности.
Распространение электромагнитных волн со скоростью света первоначально интерпретировалось как возмущения некоторой среды, так называемого эфира[22]. Были предприняты многочисленные попытки (см.исторический обзор) обнаружить движение Земли относительно эфира, однако они неизменно давали отрицательный результат.[23] Поэтому Анри Пуанкаре высказал гипотезу о принципиальной невозможности обнаружить подобное движение (принцип относительности). Ему же принадлежит постулат о независимости скорости света от скорости его источника и вывод (вместе с Лоренцем), исходя из сформулированного так принципа относительности, точного вида преобразований Лоренца (при этом были показаны и групповые свойства этих преобразований). Эти две гипотезы (постулата) легли и в основу статьи Альберта Эйнштейна (1905 год)
Классическая электродинамика, основанная на уравнениях Максвелла, лежит в основе многочисленных приложений электро- и радиотехники, СВЧ и оптики. До настоящего времени не было обнаружено ни одного эффекта, который потребовал бы видоизменения уравнений. Они оказываются применимы и в квантовой механике, когда рассматривается движение, например, заряженных частиц во внешних электромагнитных полях. Поэтому уравнения Максвелла являются основой микроскопического описания электромагнитных свойств вещества.
Уравнения Максвелла востребованы также в астрофизике и космологии, поскольку многие планеты и звезды обладают магнитным полем. Магнитное поле определяет, в частности, свойства таких объектов, как пульсары и квазары.
На современном уровне понимания все фундаментальные частицы являются квантовыми возбуждениями («квантами») различных полей. Например, фотон — это квант электромагнитного поля, а электрон — квант спинорного поля[24]. Поэтому полевой подход, предложенный Фарадеем и существенно развитый Максвеллом, является основой современной физики фундаментальных частиц, в том числе её стандартной модели.
Исторически несколько раньше он сыграл важную роль в появлении квантовой механики в формулировке Шрёдингера и вообще открытии квантовых уравнений, описывающих движение частиц, в том числе и релятивистских (уравнение Клейна — Гордона, уравнение Дирака), хотя первоначально аналогия с уравнениями Максвелла здесь виделась скорее лишь в общей идее, тогда как впоследствии оказалось, что она может быть понята как более конкретная и детальная (как это описано выше).
Также полевой подход, в целом восходящий к Фарадею и Максвеллу, стал центральным в теории гравитации (включая ОТО).
Запись уравнений Максвелла и системы единиц[править | править код]
Запись большинства уравнений в физике не зависит от выбора системы единиц. Однако в электродинамике это не так. В зависимости от выбора системы единиц в уравнениях Максвелла возникают различные коэффициенты (константы). Международная система единиц (СИ) является стандартом в технике и преподавании, однако споры среди физиков о её достоинствах и недостатках по сравнению с конкурирующей системой единиц СГС не утихают[25]; здесь и всюду далее под СГС подразумевается исключительно симметричная гауссова система СГС. Преимущество системы СГС в электродинамике состоит в том, что все поля в ней имеют одну размерность, а уравнения, по мнению многих учёных, записываются проще и естественней[26]. Поэтому СГС продолжает применяться в научных публикациях по электродинамике и в преподавании теоретической физики, например, в курсе теоретической физики Ландау и Лифшица. Однако для практических применений вводимые в СГС единицы измерений, многие из которых неименованы и неоднозначны, часто неудобны. Система СИ стандартизована и лучше самосогласованна, на этой системе построена вся современная метрология[27]. Кроме того, система СИ обычно используется в курсах общей физики. В связи с этим все соотношения, если они по-разному записываются в системах СИ и СГС, далее приводятся в двух вариантах.
Иногда (например, в «Фейнмановских лекциях по физике», а также в современной квантовой теории поля) применяется система единиц, в которой скорость света, электрическая и магнитная постоянные принимаются за единицу (c=ε0=μ0=1{\displaystyle c=\varepsilon _{0}=\mu _{0}=1}). В такой системе уравнения Максвелла записываются вообще без коэффициентов, все поля имеют единую размерность, а все потенциалы — свою единую. Такая система особенно удобна в ковариантной четырёхмерной формулировке законов электродинамики через 4-потенциал и 4-тензор электромагнитного поля.
Уравнения Максвелла в дифференциальной форме[править | править код]
Уравнения Максвелла представляют собой в векторной записи систему из четырёх уравнений, сводящуюся в компонентном представлении к восьми (два векторных уравнения содержат по три компоненты каждое плюс два скалярных[28]) линейным дифференциальным уравнениям в частных производных первого порядка для 12 компонент четырёх векторных функций (D,E,H,B{\displaystyle \mathbf {D} ,\;\mathbf {E} ,\;\mathbf {H} ,\;\mathbf {B} }):
Жирным шрифтом в дальнейшем обозначаются векторные величины, курсивом — скалярные.
Введённые обозначения:
Приведённые выше уравнения Максвелла не составляют ещё полной системы уравнений электромагнитного поля, поскольку они не содержат свойств среды, в которой возбуждено электромагнитное поле. Соотношения, связывающие величины E{\displaystyle \mathbf {E} }, B{\displaystyle \mathbf {B} }, D{\displaystyle \mathbf {D} }, H{\displaystyle \mathbf {H} } и j{\displaystyle \mathbf {j} } и учитывающие индивидуальные свойства среды, называются материальными уравнениями.
Уравнения Максвелла в интегральной форме[править | править код]
При помощи формулы Остроградского — Гаусса и теоремы Стокса дифференциальным уравнениям Максвелла можно придать форму интегральных уравнений:
Закон Ампера — Максвелла — Википедия
Закон Ампера — Максвелла (синоним: обобщенная теорема Ампера о циркуляции) — закон электромагнетизма, исторически завершивший создание замкнутой и непротиворечивой классической электродинамики.
Открыт Максвеллом, обобщившим теорему Ампера о циркуляции магнитного поля на общий случай, включающий переменные несоленоидальные (незамкнутые) токи и меняющиеся во времени поля.
Формулировка этого закона составляет четвёртое уравнение Максвелла:
- ∮∂SB⋅dl=∫S(j+∂E∂t)⋅dS{\displaystyle \oint \limits _{\partial S}\mathbf {B} \cdot \mathbf {dl} =\int \limits _{S}{\Big (}\mathbf {j} +{\frac {\partial \mathbf {E} }{\partial t}}{\Big )}\cdot \mathbf {dS} }
Единицы и обозначения
Здесь уравнение записано в интегральной форме в наиболее простом и фундаментальном виде: для вакуума, в рационализированной системе единиц с кулоновской константой 1/(4π){\displaystyle 1/(4\pi )} и скоростью света равной единице. S — любая поверхность, интеграл в правой части — сумма обычного тока (первый член) и тока смещения (второй член), введенного в уравнение Максвеллом. ∂S{\displaystyle \partial S} — край этой поверхности, представляющий собой замкнутую кривую, по которой взят контурный интеграл в левой части — циркуляция магнитного поля (вектора магнитной индукции) В; j — плотность тока, Е — напряженность электрического поля, ∂/∂t{\displaystyle \partial /\partial t} — производная по времени.
- Запись для вакуума и среды в разных системах единиц — см. ниже.
Это же уравнение в дифференциальной форме:
- ∇×B=j+∂E∂t{\displaystyle \nabla \times \mathbf {B} =\mathbf {j} +{\frac {\partial \mathbf {E} }{\partial t}}}
(здесь в левой части ротор магнитного поля, ∇{\displaystyle \nabla } — оператор набла, ×{\displaystyle \times } — векторное произведение).
Запись в системе СГСВ обычной гауссовой системе единиц (с кулоновской константой 1, в отличие от единиц, примененных в статье выше) эти уравнения выглядят так:
Для вакуума:
- ∮∂SB⋅dl=4πc∫Sj⋅dS+1c∫S∂E∂t⋅dS{\displaystyle \oint \limits _{\partial S}\mathbf {B} \cdot \mathbf {dl} ={\frac {4\pi }{c}}\int \limits _{S}\mathbf {j} \cdot \mathbf {dS} +{\frac {1}{c}}\int \limits _{S}{\frac {\partial \mathbf {E} }{\partial t}}\cdot \mathbf {dS} }
или
- ∇×B=4πcj+1c∂E∂t.{\displaystyle \nabla \times \mathbf {B} ={\frac {4\pi }{c}}\mathbf {j} +{\frac {1}{c}}{\frac {\partial \mathbf {E} }{\partial t}}.}
Для диэлектрической среды:
- ∮∂SH⋅dl=4πc∫Sj⋅dS+1c∫S∂D∂t⋅dS{\displaystyle \oint \limits _{\partial S}\mathbf {H} \cdot \mathbf {dl} ={\frac {4\pi }{c}}\int \limits _{S}\mathbf {j} \cdot \mathbf {dS} +{\frac {1}{c}}\int \limits _{S}{\frac {\partial \mathbf {D} }{\partial t}}\cdot \mathbf {dS} }
или
- ∇×H=4πcj+1c∂D∂t.{\displaystyle \nabla \times \mathbf {H} ={\frac {4\pi }{c}}\mathbf {j} +{\frac {1}{c}}{\frac {\partial \mathbf {D} }{\partial t}}.}
Для вакуума:
- ∮∂SB⋅dl=μ0∫Sj⋅dS+1c2∫S∂E∂t⋅dS{\displaystyle \oint \limits _{\partial S}\mathbf {B} \cdot \mathbf {dl} =\mu _{0}\int \limits _{S}\mathbf {j} \cdot \mathbf {dS} +{\frac {1}{c^{2}}}\int \limits _{S}{\frac {\partial \mathbf {E} }{\partial t}}\cdot \mathbf {dS} }
или
- ∇×B=μ0j+1c2∂E∂t.{\displaystyle \nabla \times \mathbf {B} =\mu _{0}\mathbf {j} +{\frac {1}{c^{2}}}{\frac {\partial \mathbf {E} }{\partial t}}.}
Для диэлектрической среды:
- ∮∂SH⋅dl=∫Sj⋅dS+∫S∂D∂t⋅dS{\displaystyle \oint \limits _{\partial S}\mathbf {H} \cdot \mathbf {dl} =\int \limits _{S}\mathbf {j} \cdot \mathbf {dS} +\int \limits _{S}{\frac {\partial \mathbf {D} }{\partial t}}\cdot \mathbf {dS} }
или
- ∇×H=j+∂D∂t.{\displaystyle \nabla \times \mathbf {H} =\mathbf {j} +{\frac {\partial \mathbf {D} }{\partial t}}.}
Обобщение теоремы Ампера о циркуляции потребовало[1] ввести в формулу Ампера дополнительный член с током смещения.
Теорема Ампера о циркуляции магнитного поля, сводящаяся к формуле
- ∮∂SB⋅dl=∫Sj⋅dS{\displaystyle \oint \limits _{\partial S}\mathbf {B} \cdot \mathbf {dl} =\int \limits _{S}\mathbf {j} \cdot \mathbf {dS} }
Единицы и обозначения
Здесь снова записываем уравнение в том же виде, как в начале статьи, то есть для вакуума, в рационализированной системе единиц с кулоновской константой 1/(4π){\displaystyle 1/(4\pi )} и скоростью света равной единице.
S — любая поверхность, интеграл в правой части — электрический ток через эту поверхность. ∂S{\displaystyle \partial S} — граница этой поверхности — замкнутая кривая, по которой взят контурный интеграл в левой части — циркуляция магнитного поля (вектора магнитной индукции) В; j — плотность тока.
верная в рамках магнитостатики (и никак не меняющаяся при добавлении электростатики) достаточно хорошо обоснована эмпирически для статических (а также и для медленно меняющихся со временем) полей. Теоретически она прямо связана с законом Био-Савара (аналогом закона Кулона в магнитостатике) и может быть доказана как теорема исходя из него (так же как и обратно закон Био — Савара может быть получен из основных уравнений магнитостатики — формулы Ампера и закона Гаусса для магнитного поля).
Поэтому при поиске варианта этой формулы для общего случая меняющихся полей и токов, то есть аналогичного закона в электродинамике, можно исходить из хорошо обоснованного постулата, что теорема Ампера верна для постоянных токов и постоянных во времени полей (из чего исторически и исходил Максвелл).
Однако при переходе к общему случаю переменных токов (и меняющихся во времени полей), обнаруживается, что мы не можем пользоваться этой формулой, по крайней мере, не можем пользоваться ею в неизменном виде (а это означает, что формула должна быть как-то исправлена, хотя, по-видимому, общую её структуру хотелось бы сохранить, раз уж она хорошо работает в магнитостатическом случае).
Возникающую проблему (состоящую в том, что формула Ампера становится внутренне противоречивой при попытке использовать её вне магнитостатики) мы опишем несколько по-разному в двух параграфах ниже, так же как и несколько по-разному обоснуем в каждом из них необходимую поправку.
Элементарное обоснование на частном примере[править | править код]
Рассмотрим конкретно представленную на схеме электрическую цепь, содержащую конденсатор[2].
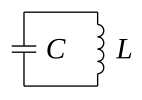
Например, это может быть простой колебательный контур, как на рисунке (конденсатор обозначен на нём как C, а L — катушка индуктивности). (Нас на самом деле будет интересовать только часть цепи вблизи конденсатора, а остальная часть схемы не важна, то есть вместо L может быть просто провод[3], а может содержать и какое угодно устройство, способное (автоматически или вручную) изменять ток, текущий в конденсатор, например, это может быть электрическая батарея с выключателем. Будем считать для простоты, что зазор между пластинами конденсатора не содержит способной поляризоваться среды, то есть это вакуум (или, скажем, воздух, поляризуемостью которого можно с хорошей точностью пренебречь).

Иными словами, мы здесь можем ограничиться рассмотрением только вот этой части цепи:
Теперь можно приступить к анализу работы формулы Ампера в этом нашем конкретном примере.
1. Непротиворечивость исходной теоремы в нашем примере для случая постоянного тока:
В случае наложенного условия постоянности тока в цепи, оказывается, что ток через конденсатор просто не может течь. Действительно, если ток, втекающий на пластины конденсатора не меняется со временем, то заряд на пластинах растет до бесконечности, что, очевидно, физически бессмысленно, и такой вариант можно смело исключить из рассмотрения[4]. Таким образом, теорема Ампера в этом случае очевидно работает, так как нет никаких токов и магнитных полей, т.е. левая и правая часть уравнения
- ∮∂SB⋅dl=∫Sj⋅dS{\displaystyle \oint \limits _{\partial S}\mathbf {B} \cdot \mathbf {dl} =\int \limits _{S}\mathbf {j} \cdot \mathbf {dS} }
просто нулевые[5].
Однако всё коренным образом меняется, когда мы рассматриваем переменные токи (которые, конечно же, возможны в реальности). Эта формула начинает давать противоречивые результаты, если попытаться её использовать.
2. Противоречие исходной формулы в случае переменного тока:
Действительно, выберем конкретную поверхность интегрирования S=S1{\displaystyle S=S_{1}} такой, чтобы она проходила между пластинами конденсатора (то есть на рисунке — почти горизонтальной, чтобы проходить между горизонтальными пластинами, не касаясь их; будем — просто для определенности и удобства — считать, что она почти горизонтальна и за краями пластин конденсатора; можно выбрать её и строго горизонтальной) и выходящей за его края, то есть большей площади, чем пластины. Тогда край этой поверхности ∂S1{\displaystyle \partial S_{1}}, представляющий собой контур для вычисления интеграла (циркуляции B) в левой части, будет некоторой кривой вокруг конденсатора (а если мы выбрали S1{\displaystyle S_{1}} строго горизонтальной, то этот контур будет также лежать в горизонтальной плоскости).
Поверхность S1{\displaystyle S_{1}} нигде не пересекается проводником, через неё нигде не течет ток (j в зазоре конденсатора везде равно нулю, там нет зарядов, способных переносить ток). Значит, правая часть уравнения равна нулю, и, в предположении что само уравнение верно — нулю равна и левая — то есть циркуляция магнитного поля по краю S1{\displaystyle S_{1}}:
- ∮∂S1B⋅dl=∫S1j⋅dS1=0.{\displaystyle \oint \limits _{\partial S_{1}}\mathbf {B} \cdot \mathbf {dl} =\int \limits _{S_{1}}\mathbf {j} \cdot \mathbf {dS_{1}} =0.}
Обозначим C этот край поверхности S1{\displaystyle S_{1}} (контур интегрирования в левой части уравнения): C=∂S1{\displaystyle C=\partial S_{1}}.
Однако S1{\displaystyle S_{1}} — не единственная поверхность, имеющая такой край. На контур C можно «натянуть» и другую, не совпадающую с S, поверхность, и даже бесконечно много различных поверхностей (так что край у всех будет совпадать).
Конкретно выберем («натянем» на C) другую поверхность S2{\displaystyle S_{2}} так, чтобы её край совпадал с C, а сама она проходила не через зазор конденсатора, а чуть выше, пересекая провод, подводящий к конденсатору ток (такую поверхность можно получить из S1{\displaystyle S_{1}} несколько выгнув её вверх).
Очевидно, что интеграл в правой части, представляющий собой электрический ток через поверхность S2{\displaystyle S_{2}} не равен нулю:
- ∮∂S2B⋅dl=∫S2j⋅dS2≠0.{\displaystyle \oint \limits _{\partial S_{2}}\mathbf {B} \cdot \mathbf {dl} =\int \limits _{S_{2}}\mathbf {j} \cdot \mathbf {dS_{2}} \neq 0.}
Получилось противоречие, т.к. в левой части, вследствие
- ∂S1=∂S2=C{\displaystyle \partial S_{1}=\partial S_{2}=C}
стоит один и тот же контурный интеграл по контуру C, а правые части дают разный результат:
- ∮CB⋅dl=∫S1j⋅dS1=0,{\displaystyle \oint \limits _{C}\mathbf {B} \cdot \mathbf {dl} =\int \limits _{S_{1}}\mathbf {j} \cdot \mathbf {dS_{1}} =0,}
- ∮CB⋅dl=∫S2j⋅dS2≠0.{\displaystyle \oint \limits _{C}\mathbf {B} \cdot \mathbf {dl} =\int \limits _{S_{2}}\mathbf {j} \cdot \mathbf {dS_{2}} \neq 0.}
Следовательно, формула Ампера в своем первоначальном виде в случае переменных токов[6].
3. Нахождение поправки, устраняющей противоречие:
Уже чисто качественно довольно очевидно, что в зазоре конденсатора (там, где проходит поверхность S1{\displaystyle S_{1}} и где j = 0), есть, наверное, единственное, что могло бы заменить собой j, чтобы интеграл по S1{\displaystyle S_{1}} дал тот же результат, что по S2{\displaystyle S_{2}}, и этим самым устранилось противоречие. Это меняющееся электрическое поле.
Более того, сразу видно, что быстрота изменения напряженности электрического поля ∂E/∂t{\displaystyle \partial E/\partial t} в конденсаторе пропорциональна току, подходящему к этому конденсатору (а этот ток — и есть интеграл по второй поверхности:
- I=∫S2j⋅dS2.{\displaystyle I=\int \limits _{S_{2}}\mathbf {j} \cdot \mathbf {dS_{2}} .}
Значит, есть шанс, что проинтегрировав ∂E/∂t{\displaystyle \partial E/\partial t} по поверхности S1{\displaystyle S_{1}} мы получим результат, совпадающий с I (может быть, домножив на какой-то коэффициент).
Теперь осталось выяснить, каким должен быть этот коэффициент и убедиться, что все детали вычислений совпадают.
Для этого выразим теперь поле в конденсаторе количественно: E=σ{\displaystyle E=\sigma } (в выбранных нами здесь единицах измерения[7]).
Если законно пренебречь краевыми эффектами (считая площадь пластин конденсатора очень большой, а расстояние между ними маленьким)[8], можем пользоваться формулой для напряженности поля, выписанной выше, по всей площади конденсатора (за исключением самых краев, областями вблизи которых мы пренебрегаем), а направление вектора E всюду (за тем же исключением) перпендикулярно пластинам (на рисунке — вертикально). Плотность заряда σ{\displaystyle \sigma } (в том же приближении) не зависит от положения (постоянна на подавляющей части пластины).
Исходя из всего этого поток
- ΦS1,∂E/∂t=∫S1∂E∂t⋅dS1=∫S1∂E∂tdS1=∫S1∂σ∂tdS1=∂Q∂t=I,{\displaystyle \Phi _{S_{1},\partial \mathbf {E} /\partial t}=\int \limits _{S_{1}}{\frac {\partial \mathbf {E} }{\partial t}}\cdot \mathbf {dS_{1}} =\int \limits _{S_{1}}{\frac {\partial E}{\partial t}}dS_{1}=\int \limits _{S_{1}}{\frac {\partial \sigma }{\partial t}}dS_{1}={\frac {\partial Q}{\partial t}}=I,}
То есть он точно равен I, а значит коэффициент не нужен (он равен единице)[9].
Итак, имеем для поправочного члена (который мы обосновали для интегрирования по S1{\displaystyle S_{1}}, но который, видимо, должен оставаться таким и для произвольной поверхности интегрирования)
- I+=∫S∂E∂t⋅dS{\displaystyle I_{+}=\int \limits _{S}{\frac {\partial \mathbf {E} }{\partial t}}\cdot \mathbf {dS} },
а сама формула Ампера после добавки этого поправочного члена приобретает вид:
- ∮∂SB⋅dl=I+I+{\displaystyle \oint \limits _{\partial S}\mathbf {B} \cdot \mathbf {dl} =I+I_{+}}
или
- ∮∂SB⋅dl=∫Sj⋅dS+∫S∂E∂t⋅dS.{\displaystyle \oint \limits _{\partial S}\mathbf {B} \cdot \mathbf {dl} =\int \limits _{S}\mathbf {j} \cdot \mathbf {dS} +\int \limits _{S}{\frac {\partial \mathbf {E} }{\partial t}}\cdot \mathbf {dS} .}
(В нашем примере когда мы интегрируем по S1{\displaystyle S_{1}} — «работает» член I+{\displaystyle I_{+}} — на этой поверхности I=0{\displaystyle I=0}, а когда по S2{\displaystyle S_{2}} — «работает» член I{\displaystyle I} — на этой поверхности I+{\displaystyle I_{+}} превращается в ноль[10]).
Таким образом, мы нашли поправочный член Максвелла к формуле Ампера и показали, что он устраняет противоречивость формулы в нашем простом примере. На самом деле он устраняет противоречивость формулы не только в этом частном случае, а всегда. Доказательство последнего утверждения содержится в следующем параграфе, оно чуть более формальное.
Стандартное общее обоснование[править | править код]
Здесь мы покажем, что поправка к формуле Ампера необходима и что она может иметь вид, предложенный Максвеллом, а также по возможности проследим, как она может быть точно построена из достаточно естественных и конструктивных соображений.
- 1. Начнем с утверждения о сохранении заряда.[11]
Сохранение заряда выражается уравнением непрерывности:
- ∇⋅j+∂ρ∂t=0,{\displaystyle \nabla \cdot \mathbf {j} +{\frac {\partial \rho }{\partial t}}=0,}
где j{\displaystyle \mathbf {j} } — плотность тока, ρ{\displaystyle \rho } — плотность заряда, ∇⋅j{\displaystyle \nabla \cdot \mathbf {j} } — дивергенция плотности токаj{\displaystyle \mathbf {j} }.
- 2. Проанализируем непротиворечивость формулы Ампера в магнитостатическом случае вот в каком смысле:
В её левой части стоит циркуляция по некоторому контуру, который является краем поверхности интегрирования в правой части. При этом утверждается, что формула верна всегда, то есть для любых поверхностей. Однако две разные поверхности (и вообще сколь угодно много разных поверхностей) могут иметь совпадающий край; иными словами, мы можем натянуть на один и тот же контур две разные поверхности (а если надо, то и больше).
Очевидно, что для двух разных поверхностей, натянутых на один и тот же контур, левая часть уравнения будет одинаковой. В правой же части будет ток (поток j) через две разные поверхности, и если он не окажется одинаковым, то формула Ампера внутренне противоречива уже в магнитостатике. Покажем, что это не так.
В принципе достаточно было бы заметить, что линии тока замкнуты либо уходят на бесконечность. (Это утверждение представляется интуитивно очевидным, если заметить, что токи в магнитостатике по определению постоянны, а заряд сохраняется — и следовательно источников и стоков у плотности тока нет , а значит у линий тока нет начал или концов, и значит все они либо замкнуты, либо уходят на бесконечность). Тогда в любую замкнутую поверхность (или в пару разных поверхностей, натянутых на один и тот же контур, которая и образует вместе одну замкнутую поверхность) входит столько же линий тока, сколько из неё выходит.
Таким образом, в магнитостатике поле j соленоидально.
Сейчас полезно показать это и исходя из уравнения непрерывности.
В магнитостатике ∂ρ∂t=0,{\displaystyle {\frac {\partial \rho }{\partial t}}=0,} поскольку изменение плотности заряда привело бы к изменению порождаемого ею электрического поля, т.е. нарушило бы условие постоянства полей.
Подставив это в уравнение непрерывности, сразу получаем, что для магнитостатики оно имеет вид:
- ∇⋅j=0{\displaystyle \nabla \cdot \mathbf {j} =0}
Это и есть условие соленоидальности поля j (так как проинтегрировав дивергенцию j по любому объёму, получим[12] поток через его поверхность, и он будет равен нулю, так как дивергенция везде ноль.[13]
- 3. Теперь заметим, что в случае перехода к общему (электродинамическому) случаю соленоидальность поля j сразу же теряется.
Действительно, теперь, вообще говоря, ∂ρ∂t≠0,{\displaystyle {\frac {\partial \rho }{\partial t}}\neq 0,} а следовательно и ∇⋅j≠0.{\displaystyle \nabla \cdot \mathbf {j} \neq 0.}
Таким образом мы получаем результат, что первоначальная аналитическое выражение закономерности, выведенной Ампером, содержит в правой части формулы только обозначение силы тока, и может принята, но с условием внутренней противоречивости (по причинам, разобранным выше, а именно, если ∇⋅j≠0{\displaystyle \nabla \cdot \mathbf {j} \neq 0}, то найдётся объём, интеграл по которому от такой дивергенции не равен нулю, и следовательно имеется не нулевой ток из этой поверхности[14], а значит можно найти две поверхности, натянутые на один и тот же контур, через которые течёт ток разных величин, а значит, если первоначальная формула Ампера верна. В этом случае, мы получим два разных взаимоисключающих значения циркуляции по одному и тому же контуру, то есть противоречие. Достаточно условное.
- 4. Теперь осталось найти исправление, которое устранило бы это противоречие.
Исходя из того, что мы хотим оставить общую структуру формулы Ампера, наиболее естественным путём её исправления было бы попытаться восстановить представление поля как соленоид (в правой части), но поскольку поле j в общем случае представленное в виде соленоида теряет наглядность модели, то естественно — было бы представить, какой более полной модели оно потребует для восстановления соленоидальности (после чего формула станет внутренне непротиворечивой, вероятно, в общем случае).
Заметим также, что эта поправка должна исчезать в случае постоянных во времени полей и постоянных токов.
Поскольку, при доказательстве гипотезы о «соленоидальности» поля j в магнитостатике, при несоленоидальных моделях, в электростатике приходится принимать уравнение непрерывности. Тогда, путём естественной логики может быть выведена мысль попытаться использовать именно его для введения поправок. Ведь в магнитостатическом случае одновременно приобретают нулевое значение оба выражения — и ∇⋅j{\displaystyle \nabla \cdot \mathbf {j} }, и ∂ρ/∂t{\displaystyle \partial \rho /\partial t}. А для компенсации ненулевого потока, описываемого первой частью в общем случае, естественно было бы использовать вторую, так как их сумма всегда будет равна нулю.
Поищем, как использовать ρ{\displaystyle \rho }.
Из электростатики известно[15], что[16]
- ∇⋅E=ρ.{\displaystyle \nabla \cdot \mathbf {E} =\rho .}
Постулируя, что это уравнение верно и в электродинамике, сопоставим его с уравнением непрерывности
- ∇⋅j+∂ρ∂t=0.{\displaystyle \nabla \cdot \mathbf {j} +{\frac {\partial \rho }{\partial t}}=0.}
Очевидно, что продифференцировав первое уравнение по времени, мы сразу получим в его правой части интересующий нас член ∂ρ/∂t{\displaystyle \partial \rho /\partial t}:
3. Уравнения Максвелла. Дифференциальные уравнения электромагнитного поля. Электромагнитные поля и волны
3.1. Первое уравнение Максвелла
3.2. Второе уравнение Максвелла
3.3. Третье уравнение Максвелла
3.4. Четвертое уравнение Максвелла
3.5. Закон сохранения заряда в дифференциальной форме
3.6. Таблица уравнений ЭМП
Интегральные уравнения не позволяют получать информацию об электромагнитных процессах в каждой точке пространства. Они дают усредненные решения полей в пространстве.
Хорошо развитый аппарат математических решений позволят переходить от интегральной формы к дифференциальным решениям.
Впервые переход от интегральных уравнений к дифференциальным сделал Максвелл.
3.1. Первое уравнение Максвелла
Первое уравнение Максвелла является дифференциальной формулировкой закона полного тока:
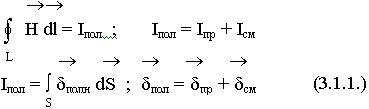
S — опирается на контур L.
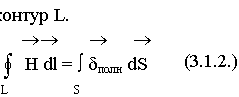
Используем теорему Стокса:
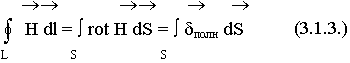
Равенство сохраняет силу по любой поверхности, опирающейся на контур L, отсюда следует, что подинтегральные функции равны.
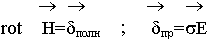 — дифференциальная форма закона Ома.
— дифференциальная форма закона Ома.
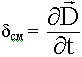
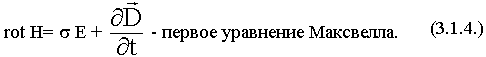
Физический смысл 1-го уравнения Максвелла.
Источниками вихревых магнитных полей являются токи проводимости и токи смещения.
3.2. Второе уравнение Максвелла
Второе уравнение Максвелла является дифференциальной формулировкой закона электромагнитной индукции:
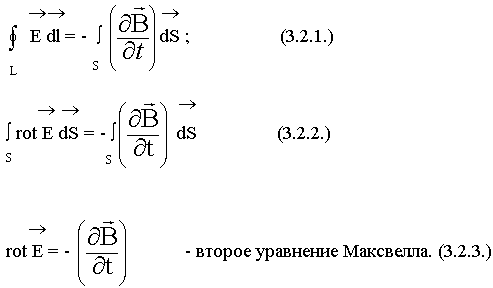
Физический смысл. Вихревое электрическое поле создается переменным магнитным полем.
3.3. Третье уравнение Максвелла
Третье уравнение Максвелла является дифференциальной формулировкой теоремы Гаусса для электрических полей.
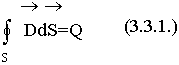
Воспользуемся теоремой Остроградского-Гаусса, которая позволяет осуществить переход от
поверхностного интеграла П ( ) к объемному интегралу от (div D):
) к объемному интегралу от (div D):
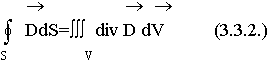
Запишем правую часть уравнения (3.3.1.) для объемного заряда. Объединим два выражения:
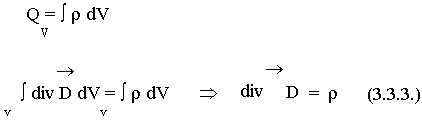
— третье уравнение Максвелла. (3.3.3.)
Физический смысл. Источниками электрического поля (векторов Е и D) являются заряды с плотностью r .
3.4. Четвертое уравнение Максвелла
Четвертое уравнение Максвелла является дифференциальной формулировкой теоремы Гаусса для магнитных полей:

Физический смысл. Дивергенция вектора 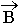 любой точке пространства равняется нулю, т.е. — источников нет (магнитные заряды в природе отсутствуют). Нет ни стоков, ни источников.
любой точке пространства равняется нулю, т.е. — источников нет (магнитные заряды в природе отсутствуют). Нет ни стоков, ни источников.
3.5. Закон сохранения заряда в дифференциальной форме
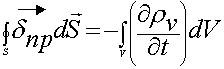
Используем теорему Остроградского-Гаусса:
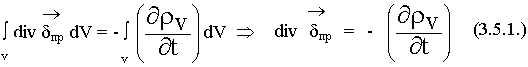
— это уравнение является следствием из предыдущих уравнений
3.6. Таблица интегральных и дифференциальных уравнений электромагнитного поля
Материальные уравнения среды.
 =
= 

Все эти уравнения являются обобщением в математической форме опытов всего человечества об электромагнитных явлениях. Они не доказываются и не выводятся — это результат опытов.
 =
= 

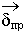 =
= 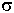

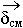 =
= 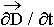
|
Интегральные уравнения электромагнитного поля |
Дифференциальные уравнения электромагнитного поля. Уравнения Максвелла |
|
1. Закон полного тока:
2. Закон электромагнитной индукции:
3. Теорема Гаусса для электрических полей:
4. Теорема Гаусса для магнитных полей:
5. Закон сохранения заряда
|
|
Уравнения Максвелла | Все Формулы
![Rendered by QuickLaTeX.com \[ \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-9b26b31cc88858c6b01bc73f6d36171f_l3.png)
Система уравнений Максвелла является обобщением основных законов об электрических и электромагнитных явлениях. Она описывает абсолютно все электромагнитные явления. Являясь основой теории электромагнитного поля, эта система уравнений позволяет решать задачи, связанные с отысканием электрических и магнитных полей, создаваемых заданным распределением электрических зарядов и токов. Уравнения Максвелла были отправной точкой для создания общей теории относительности Эйнштейна. В теории Максвелла раскрывается электромагнитная природа света. Уравнения сформулированы Дж. Максвеллом в шестидесятых годах 19 века на основе обобщения эмпирических законов и развития идей ученых, исследовавших электромагнитные явления до него (Законы Кулона, Био – Савара, Ампера и, в особенности, исследования Фарадея). Сам Максвелл записал 20 уравнений с 20 неизвестными в дифференциальной форме, которые позднее были преобразованы. Современная форма Максвелла дана немецким физиком Г. Герцем и английским физиком О. Хевисайдом. Запишем уравнения используя систему единиц Гаусса.
В состав системы уравнений Максвелла входят четыре уравнения.
Первое уравнение:
![Rendered by QuickLaTeX.com \[ \[rot\overline{E}=-\frac{1}{c}\frac{\partial \overline{B}}{\partial t}\qquad (1.1)\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-9d63549643d28adf4424ab5d86fdef42_l3.png)
\]
Это Закон Фарадея (Закон электромагнитной индукции).
где
![Rendered by QuickLaTeX.com \[\overline{E}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-feee400f68db6bf5b9add5dac385c317_l3.png)
-напряженность электрического поля,
![Rendered by QuickLaTeX.com \[\overline{B}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-8000563a9026417a8f93a845b7a41990_l3.png)
-вектор магнитной индукции, c – скорость света в вакууме.
Это уравнение говорит, о том, что ротор напряженности электрического поля
![Rendered by QuickLaTeX.com \[\overline{E}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-feee400f68db6bf5b9add5dac385c317_l3.png)
равен потоку (т.е. скорости изменения во времени) вектора магнитной индукции
![Rendered by QuickLaTeX.com \[ \overline{B}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-1460acd8acfd006d69a08084bc3bc885_l3.png)
сквозь этот контур.Уравнение (1.1) представляет собой первое уравнение Максвелла в дифференциальной форме.
Это же уравнение можно записать в интегральной форме, тогда оно примет следующий вид:
![Rendered by QuickLaTeX.com \[ \[\oint_L{\overline{E}\cdot \overline{dl}=-\frac{1}{c}\frac{\partial \Phi_m}{\partial t}}\ (1.2.)\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-a21c928cf72bec3b2bc5d646871b78bb_l3.png)
или
![Rendered by QuickLaTeX.com \[ \[\oint_L{\overline{E}\cdot \overline{dl}=-\frac{1}{c}\int_S{\frac{\partial B_n}{\partial t}}}dS\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-e8f3e66ca0bde69c9818c8b83aa2fc29_l3.png)
где
![Rendered by QuickLaTeX.com \[ B_n\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-93833dc0fb3b69e2324b2fd69c8f2a43_l3.png)
– проекция на нормаль к площадке dS вектора магнитной индукции,
![Rendered by QuickLaTeX.com \[\Phi_m\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-d7308b4bd6348f9e417ddc9989510a0c_l3.png)
– магнитный поток.
Уравнения Максвелла в интегральной формерис. 2.
Циркуляция вектора напряженности электрического поля вдоль замкнутого контура L (ЭДС индукции) определяется скоростью изменения потока вектора магнитной индукции через поверхность, ограниченную данным контуром. Знак минус по правилу Ленца означает направление индукционного тока.
Согласно Максвеллу закон электромагнитной индукции (а это именно он), справедлив для любого замкнутого контура, произвольно выбранного в переменном магнитном поле.
Смысл этого уравнения: Переменное магнитное поле в любой точке пространства создает вихревое электрическое поле.
Второе уравнение Максвелла:
![Rendered by QuickLaTeX.com \[ \[rot\overline{H}=\frac{4\pi}{c}\overline{j}+\frac{1}{c}\frac{\partial \overline{D}}{\partial t}\qquad (2.1)\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-a4b732ebcf9c577dae0c8f70ee14f421_l3.png)
где
![Rendered by QuickLaTeX.com \[ \overline{H}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-785dac0f0eca31c703d823bdc44c20d1_l3.png)
-вектор магнитной напряженности,
![Rendered by QuickLaTeX.com \[ \overline{j}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-0d5407865818e9e6dd7f1f1ed0f04b54_l3.png)
— плотность электрического тока,
![Rendered by QuickLaTeX.com \[ \overline{D}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-a27bc6aede55a57e22ebae62d4e69258_l3.png)
— вектор электрического смещения.
Данное уравнение Максвелла является обобщением эмпирического закона Био-Савара о том, что магнитные поля возбуждаются электрическими токами. Смысл второго уравнения в том, что источником возникновения вихревого магнитного поля является также переменное электрическое поле, магнитное действие которого характеризуется током смещения. ( \frac{\partial \overline{D}}{\partial t}-плотность тока смещения).
В интегральном виде второе уравнение Максвелла (Теорема о циркуляции магнитного поля) представлено следующим образом:
![Rendered by QuickLaTeX.com \[ \[\oint_L{\overline{H}\cdot \overline{dl}} = \frac{4\pi}{c}\int_S{(j_n+\frac{1}{4\pi}\frac{\partial D_n}{\partial t})}ds\qquad (2.2)\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-1e99766fe4134648b2f4a317f4b36816_l3.png)
или
Циркуляция вектора напряжённости магнитного поля по произвольному контуру равна алгебраической сумме токов проводимости и тока смещения, сцепленных с контуром.
Когда Максвелл вводил уравнения (более ста лет тому назад!), природа электромагнитного поля была не понятна. В настоящее время природа поля выяснена, и стало ясно, что I_{shift} может быть названo «током» лишь формально. По pяду расчетных соображений такое название, не придавая ему прямого физического смысла, целесообразно сохранить, что в электротехнике и делается. По этой же причине вектор D, входящий в выражение для тока смещения, называют вектором электрического смещения.
Помимо первых двух уравнений в систему уравнений Максвелла входит теорема Гаусса-Остроградского для электрического и магнитного полей:
![Rendered by QuickLaTeX.com \[ \[div\overline{D}=4\pi \rho \qquad (3.1)\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-0583dfdf72c883c6a4344d07a7bba416_l3.png)
и
![Rendered by QuickLaTeX.com \[ \[div\overline{B}=0\qquad (4.1)\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-7951b58746ad17b823862e3fe6a72296_l3.png)
где
![Rendered by QuickLaTeX.com \[\rho —плотность электрического заряда. Что в интегральном виде представляет собой следующее: \[ \[\Phi_e=\oint_S{D_ndS}=4\pi q\qquad (3.2)\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-4eda9e7afd93f0d219105504ba5417a3_l3.png)
и
![Rendered by QuickLaTeX.com \[ \[\Phi_m=\oint_S{B_ndS}=0\qquad (4.2)\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-d397cf33409d0d86dcfe38ec0ff5ff8c_l3.png)
где
![Rendered by QuickLaTeX.com \[\Phi_e-поток электрического смещения \[\overline{D},\ \Phi_m\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-b0b637b8850a0ddb7f4c9f7b729cfade_l3.png)
— поток магнитной индукции
![Rendered by QuickLaTeX.com \[\overline{B}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-8000563a9026417a8f93a845b7a41990_l3.png)
сквозь замкнутую поверхность, охватывающую свободный заряд q.
Смысл уравнения 3.2. Электрический заряд – источник электрической индукции.
Уравнение 4.2 выражает факт отсутствия свободных магнитных зарядов.
Полная система уравнений Максвелла в дифференциальном виде (характеризует поле в каждой точке пространства):
![Rendered by QuickLaTeX.com \[ \[rot\overline{E}=-\frac{1}{c}\frac{\partial \overline{B}}{\partial t}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-398725d6b64d766341dbe99024bcae21_l3.png)
![Rendered by QuickLaTeX.com \[ \[rot\overline{H}=\frac{4\pi}{c}\overline{j}+\frac{1}{c}\frac{\partial \overline{D}}{\partial t}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-37a88186f81270e23ee736bb1f25a722_l3.png)
![Rendered by QuickLaTeX.com \[ \[div\overline{D}=4\pi \rho \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-41f289a1b91f76664fff095def5514ea_l3.png)
![Rendered by QuickLaTeX.com \[ \[div\overline{B}=0\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-39ddece54c5fd5589ce9b8db34fc3630_l3.png)
Полная система уравнений Максвелла в интегральном виде
Полная система уравнений Максвелла в интегральном виде (интегральная форма записи уравнений облегчает их физическую интерпретацию так ка делает их визуально ближе к известным эмпирическим законам):
![Rendered by QuickLaTeX.com \[ \[\oint_L{\overline{E}\cdot \overline{dl}=-\frac{1}{c}\int_S{\frac{\partial B_n}{\partial t}}}dS\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-f432c4f234fca38f37fd62cb3370852e_l3.png)
![Rendered by QuickLaTeX.com \[ \[\Phi_e=\oint_S{D_ndS}=4\pi q\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-6d28861433043913bfefe70393048096_l3.png)
![Rendered by QuickLaTeX.com \[ \[\Phi_m=\oint_S{B_ndS}=0\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-83a7b3ea01df3da9d361db3a9cace0ff_l3.png)
Систему уравнений Максвелла дополняют «материальными уравнениями», связывающими векторы
![Rendered by QuickLaTeX.com \[ \overline{E,\ } \overline{D,\ }\overline{B,\ } \overline{H\ } c величинами, описывающими электрические и магнитные свойства среды. \[ \[\overline{D}=\varepsilon {\varepsilon}_0\overline{E}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-554b05247f1dc8118734626e94f4e413_l3.png)
![Rendered by QuickLaTeX.com \[ \[\overline{B}=\mu {\mu}_0\overline{H}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-ca50fa6a86b6f32814919a79a5229091_l3.png)
![Rendered by QuickLaTeX.com \[ \[\overline{j}=\gamma \overline{E}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-47482a7dc8c3887d797b320932deba3d_l3.png)
где
![Rendered by QuickLaTeX.com \[\varepsilon - относительная диэлектрическая проницаемость, \mu - относительная магнитная проницаемость, \[\gamma\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-62d88edff65785387da798a48c7dfde0_l3.png)
-удельная электропроводность,
![Rendered by QuickLaTeX.com \[{\varepsilon}_0 - электрическая постоянная, \[{\mu}_0\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-aae73eb2dd53903f8dd5355807193787_l3.png)
– магнитная постоянная. Среда предполагается изотропной, неферрромагнитной, несегнетоэлектрической.
На границе раздела двух сред выполняются граничные условия:
![Rendered by QuickLaTeX.com \[ \[D_{1n}-D_{2n}=\sigma,\ B_{1n}=B_{2n}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-ac4c1ea49fc12503cae9b850da90acf2_l3.png)
![Rendered by QuickLaTeX.com \[ \[H_{1\tau}-H_{2\tau}=j_{pov},\ E_{1\tau}=E_{2\tau}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-0d4393f0c5c451165d93165c79e35c3c_l3.png)
где \sigma— поверхностная плотность свободных зарядов, n- единичный вектор нормали к границе раздела, проведенный из среды 2 в 1, \[\tau – единичный вектор, касательный к границе, \[j_{pov}— проекция вектора плотности поверхностных токов проводимости на единичный вектор.
Данные уравнения выражают непрерывность нормальных составляющих вектора магнитной индукции и скачок нормальных составляющих вектора смещения. Непрерывность касательных составляющих вектора напряженностей электрического поля на границе раздела и скачок этих составляющих для напряженности магнитного поля.
7.5. Система уравнений Максвелла
Уравнения Максвелла являются фундаментальными уравнениями классической макроскопической электродинамики, описывающими электромагнитные явления в любой среде и в вакууме. Они сформулированы Дж. Максвеллом в 60-х годах XIX века на основе обобщения эмпирических законов электрических и магнитных явлений и развития идеи М. Фарадея о том, что взаимодействия между электрически заряженными телами осуществляются посредством электромагнитного поля. Они связывают величины, характеризующие электромагнитное поле, с его источниками, т. е. с распределением в пространстве электрических зарядов и токов.
В вакууме электромагнитное поле характеризуется напряженностью электрического поля E и вектором магнитной индукции B, зависящими от пространственных координат и времени. Эти величины определяют силы, действующие со стороны поля на заряды и токи, распределение которых в пространстве задается объемной плотностью заряда и плотностью электрического тока j. Для описания электромагнитных процессов в материальной среде, кроме векторов E и B, вводятся вспомогательные векторные величины, зависящие от состояния и свойств среды: индукция электрического поля D и напряженность магнитного поля H.
Уравнения Максвелла позволяют определить основные характеристики электромагнитного поля (E, B, D и H) в каждой точке пространства в любой момент времени, если известны плотность тока и объемная плотность заряда как функции координат и времени. Они могут быть записаны в интегральной или дифференциальной форме.
7.5.1. Система уравнений Максвелла в интегральной форме
Уравнения Максвелла в интегральной форме определяют не векторы E, B, D и H в отдельных точках пространства, а некоторые интегральные величины, зависящие от распределения этих характеристик поля: циркуляцию векторов E и H вдоль произвольных замкнутых контуров и потоки векторов B и D через произвольные замкнутые поверхности.
1. Первое уравнение является обобщением на переменные электромагнитные поля эмпирического закона Био-Савара-Лапласа о возбуждении магнитного поля электрическими токами. Оно показывает, что источниками магнитного поля могут быть не только движущиеся в проводниках электрические заряды (электрические токи), но и изменяющиеся во времени электрические поля в диэлектриках или вакууме. Величина, пропорциональная скорости изменения электрического поля во времени, была названа Максвеллом током смещения, который возбуждает магнитное поле по тому же закону, что и ток проводимости. Полный ток, равный сумме тока проводимости и тока смещения, всегда является замкнутым. Первое уравнение Максвелла свидетельствует о том, что циркуляция вектора напряженности магнитного поля вдоль замкнутого контура L определяется полным током через произвольную поверхность S, ограниченную данным контуром. Первое уравнение Максвелла имеет вид
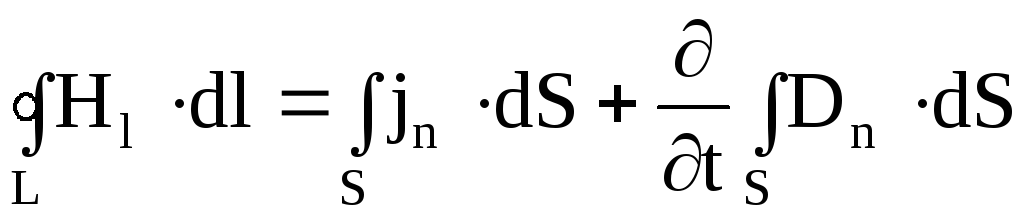 , (7.24)
, (7.24)
где 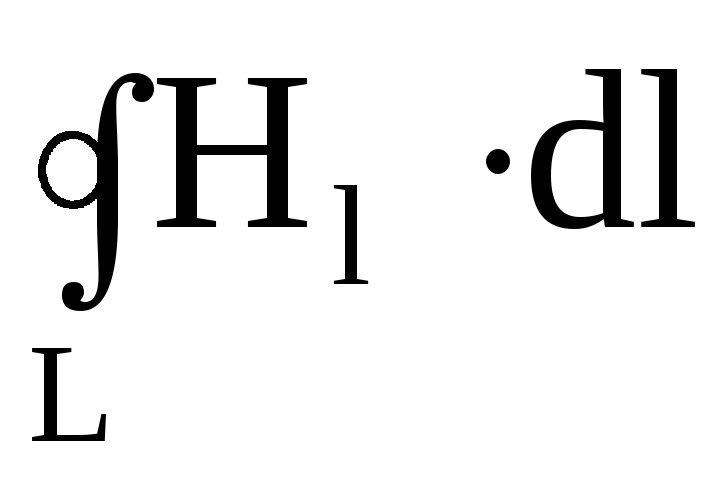 — циркуляция вектора напряженности
магнитного поля;
— циркуляция вектора напряженности
магнитного поля;
 — проекция вектора
плотности тока на направление положительной
нормали к бесконечно малой площадке
dS,
являющейся частью поверхности S;
— проекция вектора
плотности тока на направление положительной
нормали к бесконечно малой площадке
dS,
являющейся частью поверхности S;
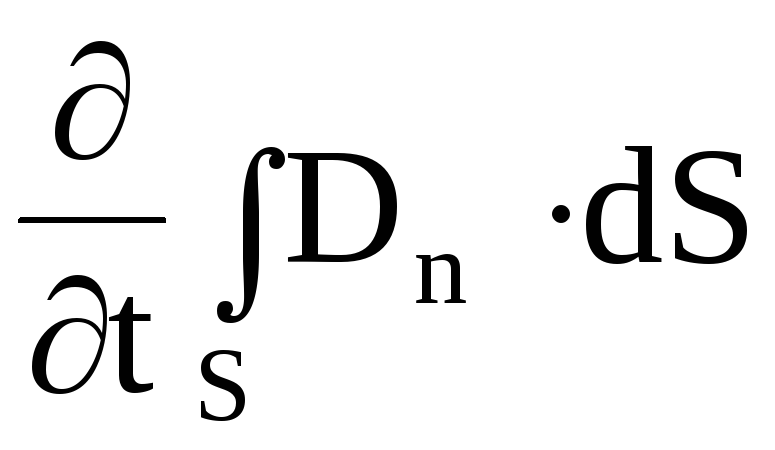 — проекция вектора
плотности тока смещения на ту же нормаль.
— проекция вектора
плотности тока смещения на ту же нормаль.
2. Второе уравнение является математической формулировкой закона электромагнитной индукции и записывается в виде
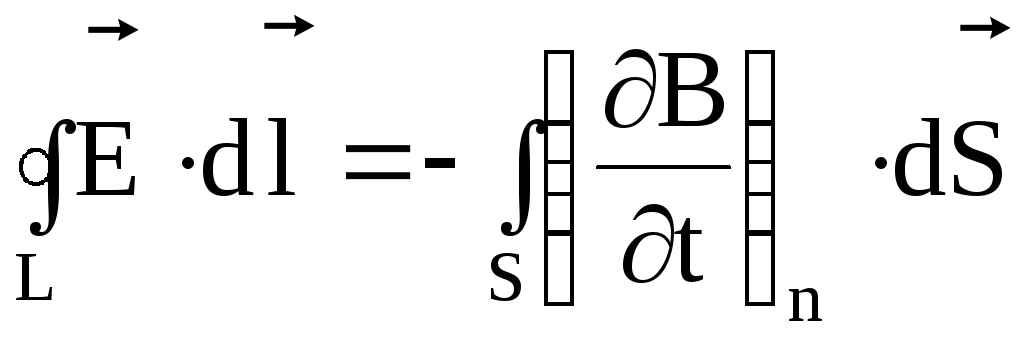 ,
(7.25)
,
(7.25)
где 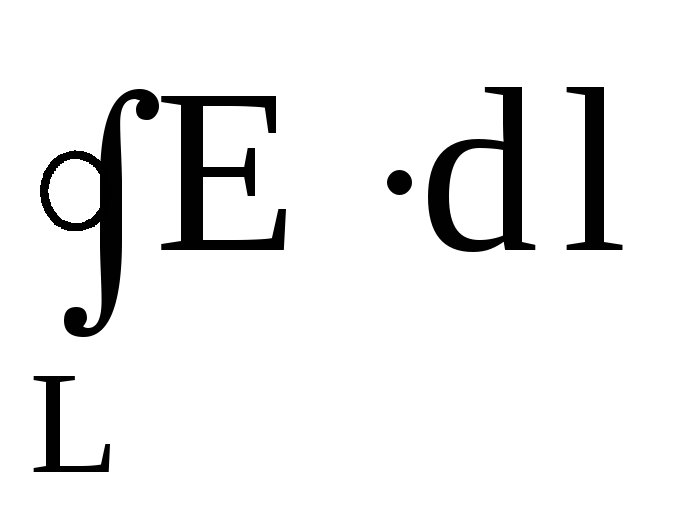 — циркуляция вектора напряженности
результирующего поля, потенциального
и вихревого;
— циркуляция вектора напряженности
результирующего поля, потенциального
и вихревого;
Bn – проекция вектора индукции магнитного поля на направление положительной нормали к бесконечно малой площадке dS, являющейся частью поверхности S;
Знак «минус» – соответствует закону (правилу) Ленца для определения направления индукционного тока.
Уравнение (7.25) утверждает, что циркуляция вектора напряженности результирующего электрического поля вдоль замкнутого контура L (ЭДС индукции) определяется скоростью изменения потока вектора магнитной индукции через поверхность S, ограниченную замкнутым контуром L.
3. Третье уравнение отражает то свойство вектора B, что его линии замкнуты или уходят в бесконечность (теорема Остроградского-Гаусса для магнитного поля). Это уравнение отображает опытные данные об отсутствии магнитных зарядов, аналогичных электрическим зарядам. Магнитное поле порождается только электрическим током. Математически его можно записать так:
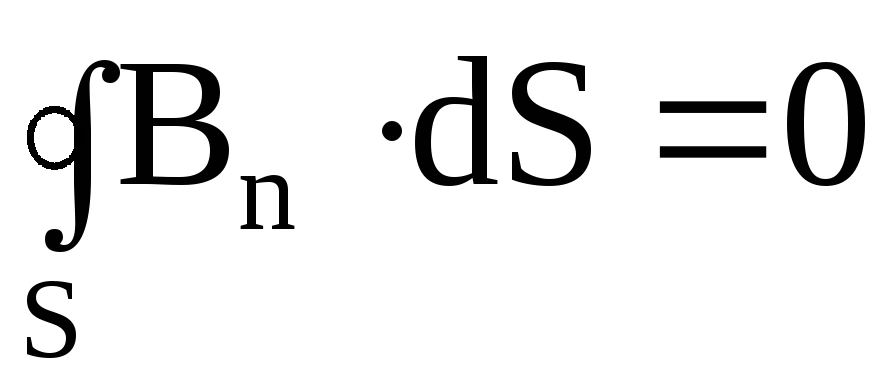 .
(7.26)
.
(7.26)
Таким образом, поток вектора магнитной индукции через произвольную замкнутую поверхность S равен нулю.
4. Четвертое уравнение показывает, что линии вектора D могут начинаться и оканчиваться на зарядах (теорема Остроградского-Гаусса для вектора D). Данное уравнение представляет собой обобщение закона взаимодействия неподвижных электрических зарядов (закона Кулона):
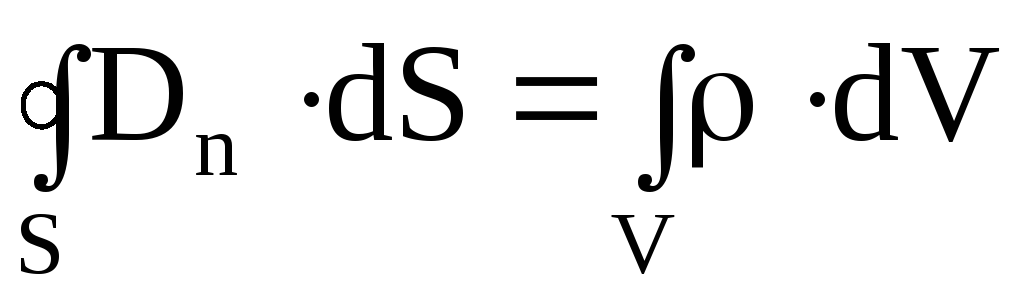 .
(7.27)
.
(7.27)
Поток вектора индукции электрического поля через произвольную замкнутую поверхность S определяется электрическим зарядом, находящимся внутри этой поверхности (в объеме V, ограниченном поверхностью S).
7.5.2. Система уравнений Максвелла в дифференциальной форме
Если считать, что векторы электромагнитного поля E, B, D и H являются непрерывными функциями координат, то, рассматривая циркуляцию E и H по бесконечно малым контурам и потоки векторов B и D через поверхности, ограничивающие бесконечно малые объемы, можно от системы уравнений Максвелла в интегральной форме перейти к системе уравнений Максвелла в дифференциальной форме, характеризующих поле в каждой точке пространства:
1) 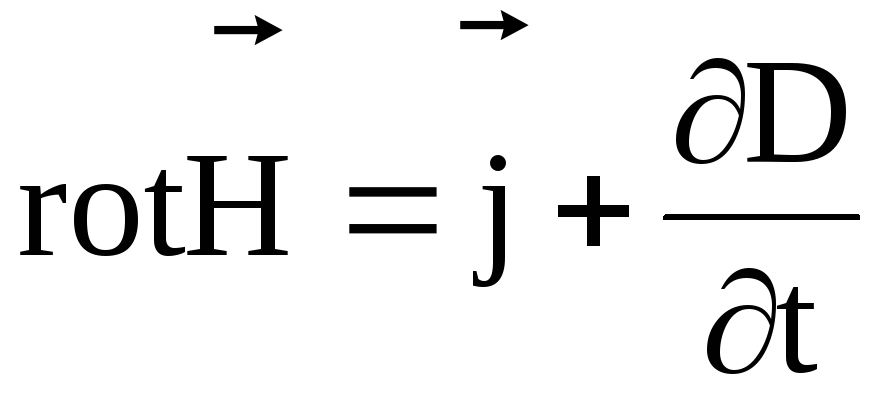 ;
(7.28)
;
(7.28)
2) 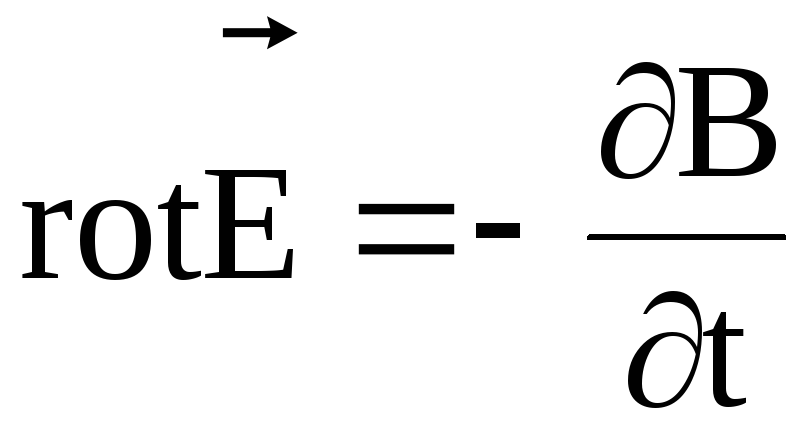 ;
(7.29)
;
(7.29)
3) 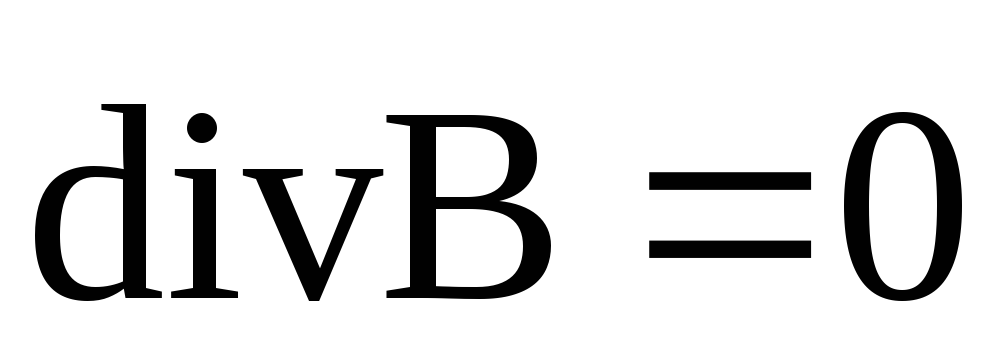 ;
(7.30)
;
(7.30)
4) 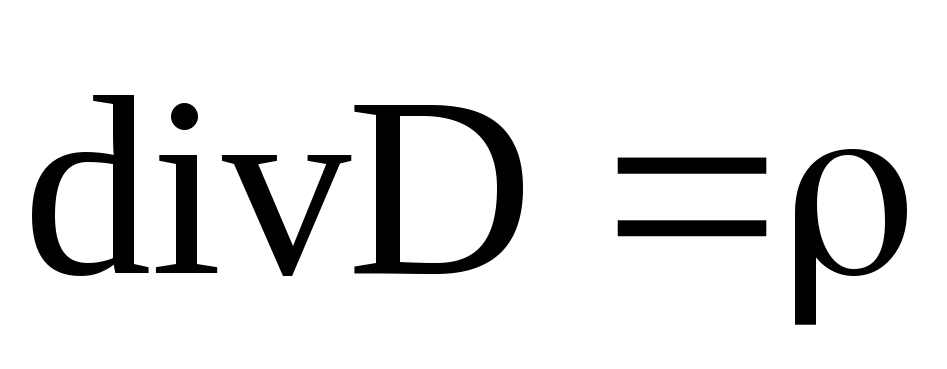 .
(7.31)
.
(7.31)
Физический смысл уравнений Максвелла в дифференциальной форме аналогичен физическому смыслу этих уравнений в интегральной форме.
7.5.3. Материальные уравнения
Уравнения Максвелла в интегральной и дифференциальной формах не образуют полной замкнутой системы, позволяющей рассчитывать электромагнитные процессы при наличии материальной среды. Поэтому систему уравнений Максвелла необходимо дополнить соотношениями, связывающими векторы E, B, D, H и j, которые являются независимыми. Связь между ними определяется свойствами среды и ее состоянием, причем векторы D и j выражаются через вектор E, а B – через H. Эти уравнения называются уравнениями состояния или материальными уравнениями. Они описывают электромагнитные свойства среды и для каждой конкретной среды имеют определенную форму. Для большинства изотропных сред, вплоть до значительных полей, уравнения состояния (материальные уравнения) имеют простую линейную связь:
1. Первое уравнение связывает векторы напряженности и индукции электрического поля:
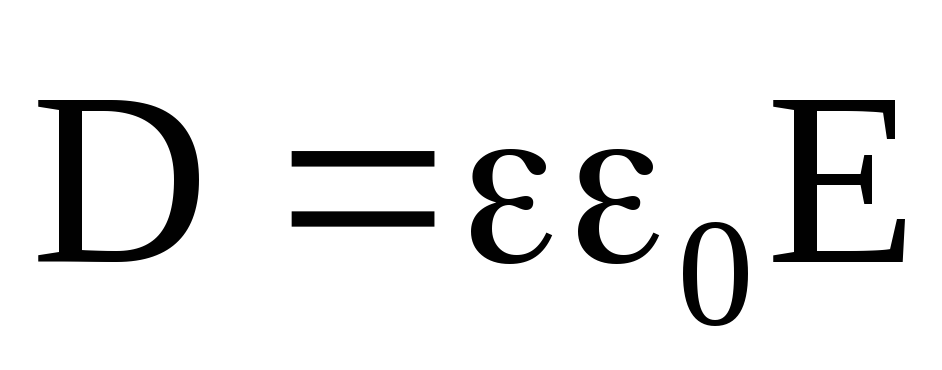 ,
(7.32)
,
(7.32)
где (x,y,z) –диэлектрическая проницаемость среды;
0 – диэлектрическая постоянная.
2. Второе уравнение связывает векторы индукции и напряженности магнитного поля:
 ,
(7.33)
,
(7.33)
где (x,y,z) – магнитная проницаемость среды;
0 – магнитная постоянная.
3. Третье уравнение выражает закон Ома в дифференциальной форме
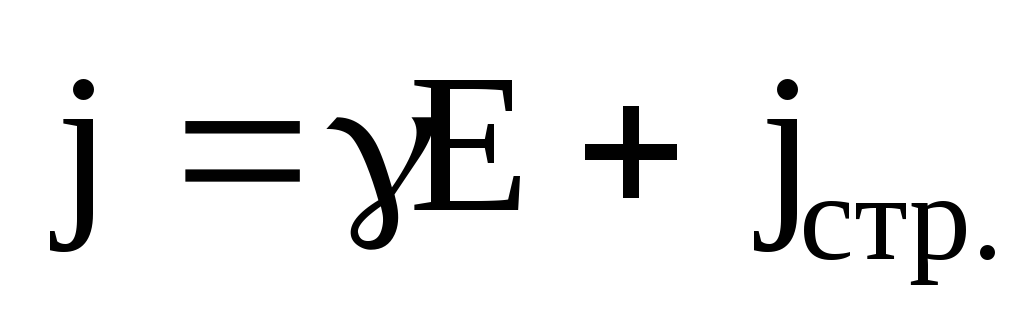 ,
(7.34)
,
(7.34)
где — удельная электропроводность;
jстр. – плотность так называемых сторонних токов, т.е. токов, поддерживаемых любыми силами, кроме сил электрического поля (например, магнитным полем, диффузией).
Проницаемости и определяют тот вклад в электромагнитное поле, который вносят связанные заряды, входящие в состав электрически нейтральных атомов и молекул вещества. Объемная плотность заряда и плотность тока j в материальных уравнениях – это плотности свободных зарядов и токов, причем вспомогательные векторы D и H, вводятся так, чтобы циркуляция вектора H определялась только движением свободных зарядов, а поток вектора D – плотностью распределения этих зарядов в пространстве. Материальные уравнения используются при решении уравнений Максвелла.
Из уравнений
Максвелла вытекает ряд законов сохранения:
закон сохранения электрического заряда,
закон сохранения электромагнитной
энергии. В частности, из уравнений 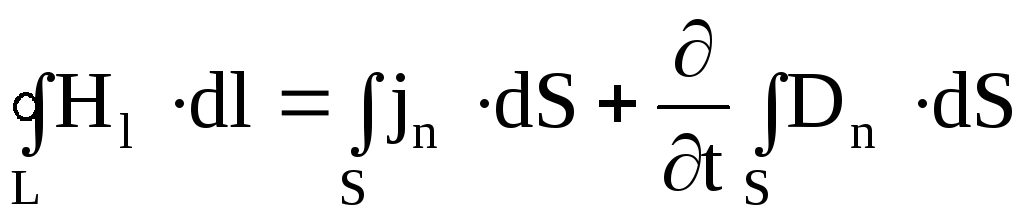 и
и 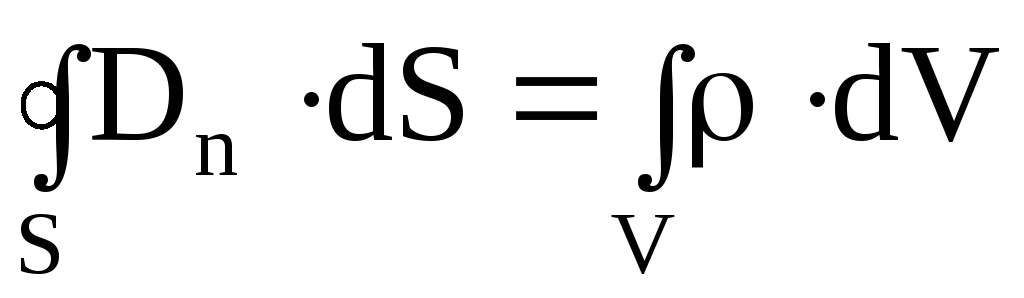 можно
получить уравнение непрерывности,
представляющее собой закон сохранения
электрического заряда:полный
ток, протекающий за единицу времени
через любую замкнутую поверхность S,
равен изменению заряда внутри объема V,
ограниченного поверхностью S.
Если ток через поверхность отсутствует,
то заряд в объеме V остается неизменным:
можно
получить уравнение непрерывности,
представляющее собой закон сохранения
электрического заряда:полный
ток, протекающий за единицу времени
через любую замкнутую поверхность S,
равен изменению заряда внутри объема V,
ограниченного поверхностью S.
Если ток через поверхность отсутствует,
то заряд в объеме V остается неизменным:
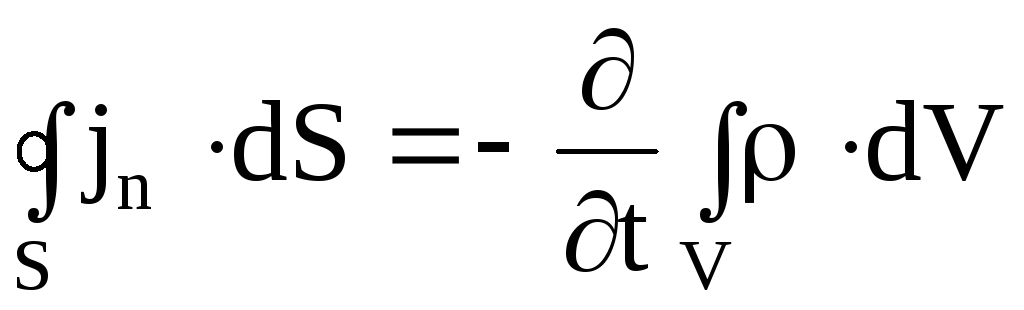 .
(7.35)
.
(7.35)
Если энергия электромагнитного поля не переходит в другие виды энергии, то, согласно уравнениям Максвелла, изменение энергии в некотором объеме за единицу времени равно потоку электромагнитной энергии через поверхность, ограничивающую этот объем.
Если внутри объема за счет энергии электромагнитного поля выделяется некоторое количество тепла, то закон сохранения энергии утверждает о том, что изменение энергии электромагнитного поля в некотором объеме V равно сумме потока энергии электромагнитного поля и количества теплоты, выделившейся в этом объеме:
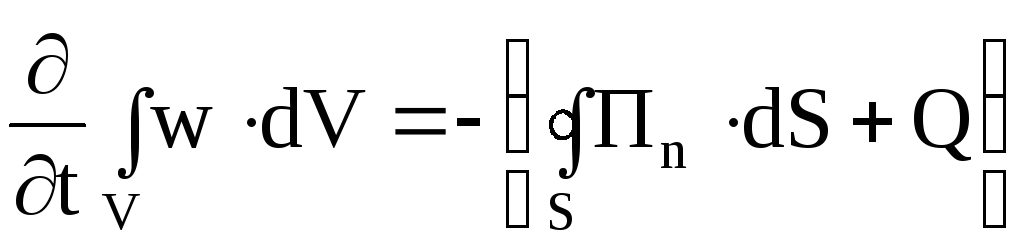 ,
(7.36)
,
(7.36)
где w – энергия поля в единице объема;
Пn – проекция вектора Умова-Пойтинга на направление положительной нормали к поверхности dS;
Q – количество тепла, выделяемое в единицу времени.
Уравнения Максвелла
приводят к фундаментальному выводу о
конечности скорости распространения
электромагнитных взаимодействий. Это
означает, что при изменении плотности
заряда или тока, порождающих электромагнитное
поле, в некоторой точке пространства
на расстоянии r
от них поле изменится спустя время 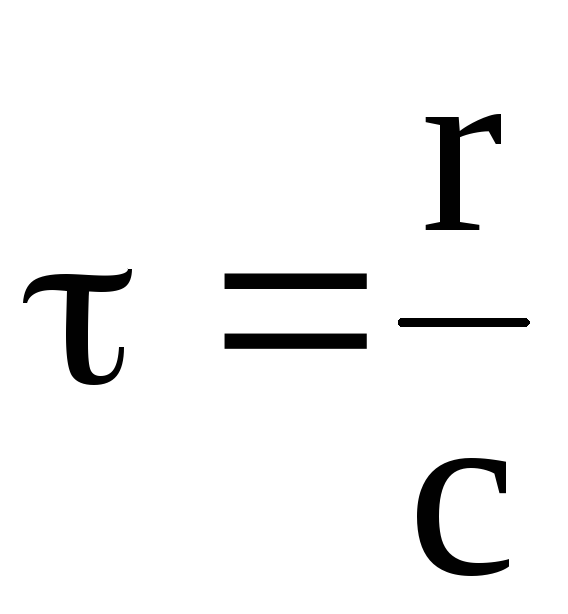 .
Вследствие конечной скорости
распространения электромагнитных
взаимодействий, следовательно, возможно
существование электромагнитных волн,
частным случаем которых является свет,
что было впервые доказано Максвеллом.
.
Вследствие конечной скорости
распространения электромагнитных
взаимодействий, следовательно, возможно
существование электромагнитных волн,
частным случаем которых является свет,
что было впервые доказано Максвеллом.
Это заключение называют вторым основным положением теории Максвелла: электромагнитное поле, возникнув в одном месте пространства, не остается локализованным в нем, а распространяется от этого места в виде электромагнитной волны. Векторы E и H электромагнитной волны взаимно перпендикулярны и перпендикулярны вектору скорости v, с которой распространяется электромагнитная волна.
7.5. Система уравнений Максвелла
Уравнения Максвелла являются фундаментальными уравнениями классической макроскопической электродинамики, описывающими электромагнитные явления в любой среде и в вакууме. Они сформулированы Дж. Максвеллом в 60-х годах XIX века на основе обобщения эмпирических законов электрических и магнитных явлений и развития идеи М. Фарадея о том, что взаимодействия между электрически заряженными телами осуществляются посредством электромагнитного поля. Они связывают величины, характеризующие электромагнитное поле, с его источниками, т. е. с распределением в пространстве электрических зарядов и токов.
В вакууме электромагнитное поле характеризуется напряженностью электрического поля E и вектором магнитной индукции B, зависящими от пространственных координат и времени. Эти величины определяют силы, действующие со стороны поля на заряды и токи, распределение которых в пространстве задается объемной плотностью заряда и плотностью электрического тока j. Для описания электромагнитных процессов в материальной среде, кроме векторов E и B, вводятся вспомогательные векторные величины, зависящие от состояния и свойств среды: индукция электрического поля D и напряженность магнитного поля H.
Уравнения Максвелла позволяют определить основные характеристики электромагнитного поля (E, B, D и H) в каждой точке пространства в любой момент времени, если известны плотность тока и объемная плотность заряда как функции координат и времени. Они могут быть записаны в интегральной или дифференциальной форме.
7.5.1. Система уравнений Максвелла в интегральной форме
Уравнения Максвелла в интегральной форме определяют не векторы E, B, D и H в отдельных точках пространства, а некоторые интегральные величины, зависящие от распределения этих характеристик поля: циркуляцию векторов E и H вдоль произвольных замкнутых контуров и потоки векторов B и D через произвольные замкнутые поверхности.
1. Первое уравнение является обобщением на переменные электромагнитные поля эмпирического закона Био-Савара-Лапласа о возбуждении магнитного поля электрическими токами. Оно показывает, что источниками магнитного поля могут быть не только движущиеся в проводниках электрические заряды (электрические токи), но и изменяющиеся во времени электрические поля в диэлектриках или вакууме. Величина, пропорциональная скорости изменения электрического поля во времени, была названа Максвеллом током смещения, который возбуждает магнитное поле по тому же закону, что и ток проводимости. Полный ток, равный сумме тока проводимости и тока смещения, всегда является замкнутым. Первое уравнение Максвелла свидетельствует о том, что циркуляция вектора напряженности магнитного поля вдоль замкнутого контура L определяется полным током через произвольную поверхность S, ограниченную данным контуром. Первое уравнение Максвелла имеет вид
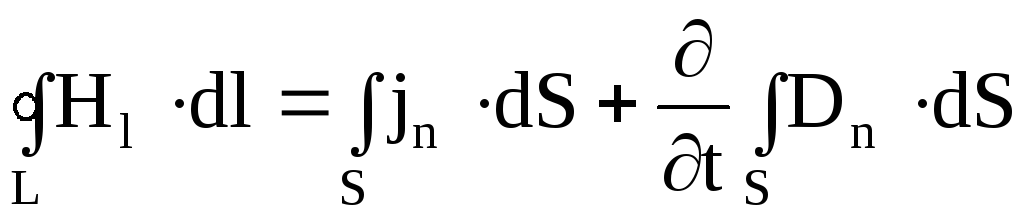 , (7.24)
, (7.24)
где  — циркуляция вектора напряженности
магнитного поля;
— циркуляция вектора напряженности
магнитного поля;
 — проекция вектора
плотности тока на направление положительной
нормали к бесконечно малой площадке
dS,
являющейся частью поверхности S;
— проекция вектора
плотности тока на направление положительной
нормали к бесконечно малой площадке
dS,
являющейся частью поверхности S;
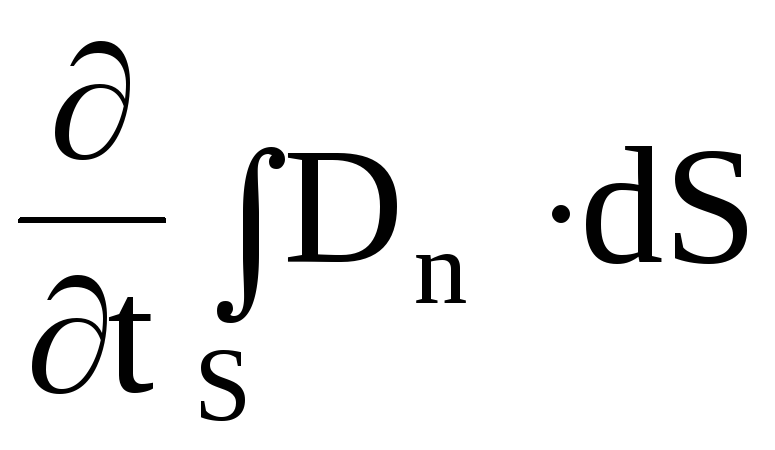 — проекция вектора
плотности тока смещения на ту же нормаль.
— проекция вектора
плотности тока смещения на ту же нормаль.
2. Второе уравнение является математической формулировкой закона электромагнитной индукции и записывается в виде
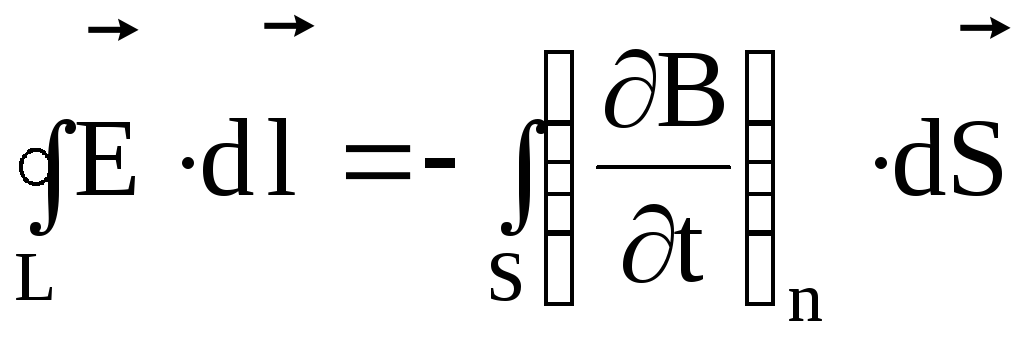 ,
(7.25)
,
(7.25)
где 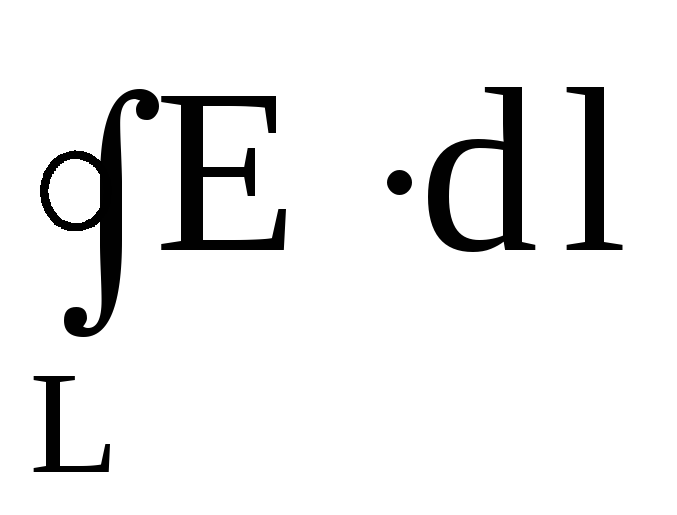 — циркуляция вектора напряженности
результирующего поля, потенциального
и вихревого;
— циркуляция вектора напряженности
результирующего поля, потенциального
и вихревого;
Bn – проекция вектора индукции магнитного поля на направление положительной нормали к бесконечно малой площадке dS, являющейся частью поверхности S;
Знак «минус» – соответствует закону (правилу) Ленца для определения направления индукционного тока.
Уравнение (7.25) утверждает, что циркуляция вектора напряженности результирующего электрического поля вдоль замкнутого контура L (ЭДС индукции) определяется скоростью изменения потока вектора магнитной индукции через поверхность S, ограниченную замкнутым контуром L.
3. Третье уравнение отражает то свойство вектора B, что его линии замкнуты или уходят в бесконечность (теорема Остроградского-Гаусса для магнитного поля). Это уравнение отображает опытные данные об отсутствии магнитных зарядов, аналогичных электрическим зарядам. Магнитное поле порождается только электрическим током. Математически его можно записать так:
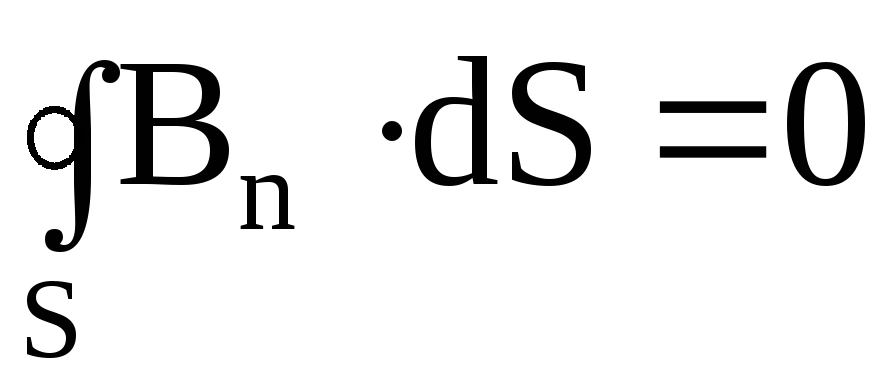 .
(7.26)
.
(7.26)
Таким образом, поток вектора магнитной индукции через произвольную замкнутую поверхность S равен нулю.
4. Четвертое уравнение показывает, что линии вектора D могут начинаться и оканчиваться на зарядах (теорема Остроградского-Гаусса для вектора D). Данное уравнение представляет собой обобщение закона взаимодействия неподвижных электрических зарядов (закона Кулона):
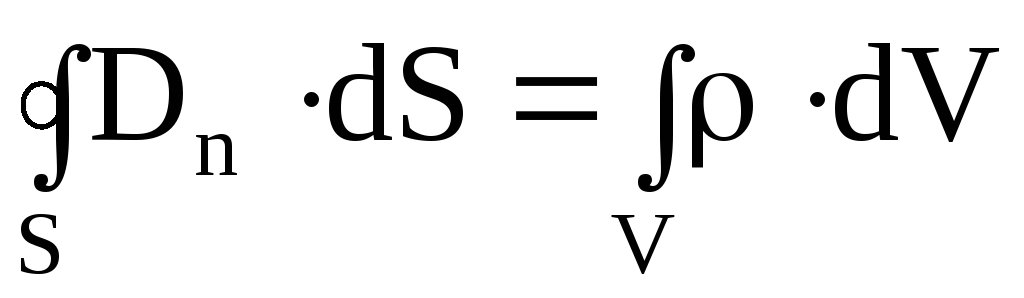 .
(7.27)
.
(7.27)
Поток вектора индукции электрического поля через произвольную замкнутую поверхность S определяется электрическим зарядом, находящимся внутри этой поверхности (в объеме V, ограниченном поверхностью S).
7.5.2. Система уравнений Максвелла в дифференциальной форме
Если считать, что векторы электромагнитного поля E, B, D и H являются непрерывными функциями координат, то, рассматривая циркуляцию E и H по бесконечно малым контурам и потоки векторов B и D через поверхности, ограничивающие бесконечно малые объемы, можно от системы уравнений Максвелла в интегральной форме перейти к системе уравнений Максвелла в дифференциальной форме, характеризующих поле в каждой точке пространства:
1) 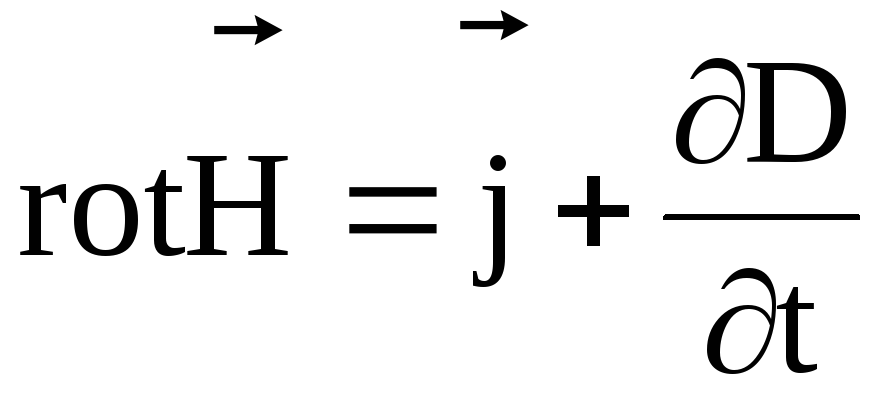 ;
(7.28)
;
(7.28)
2) 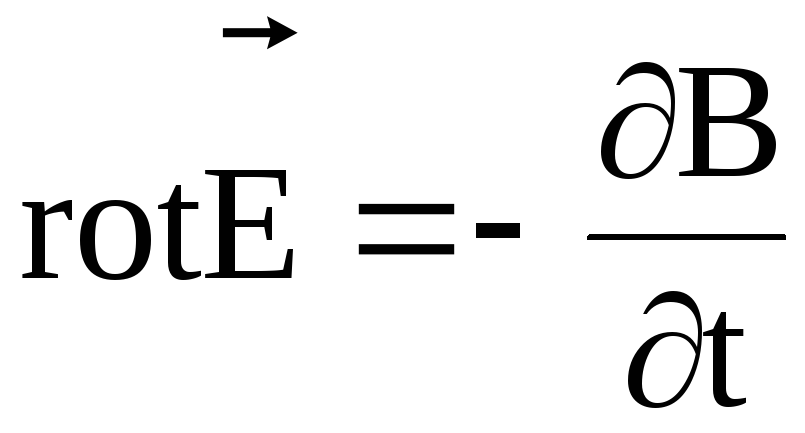 ;
(7.29)
;
(7.29)
3) 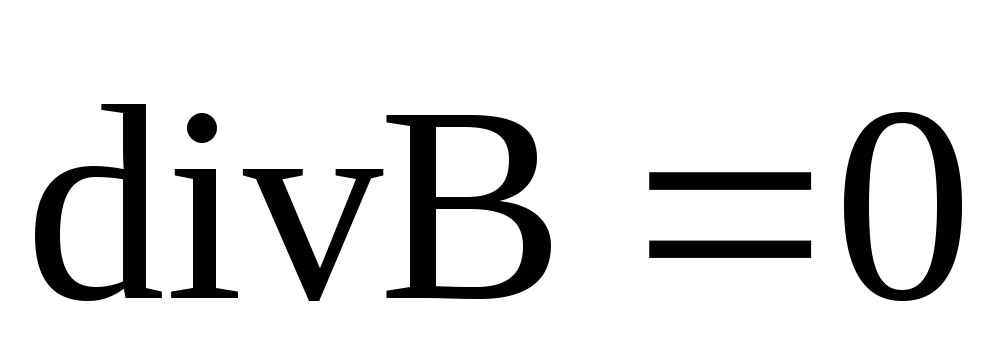 ;
(7.30)
;
(7.30)
4) 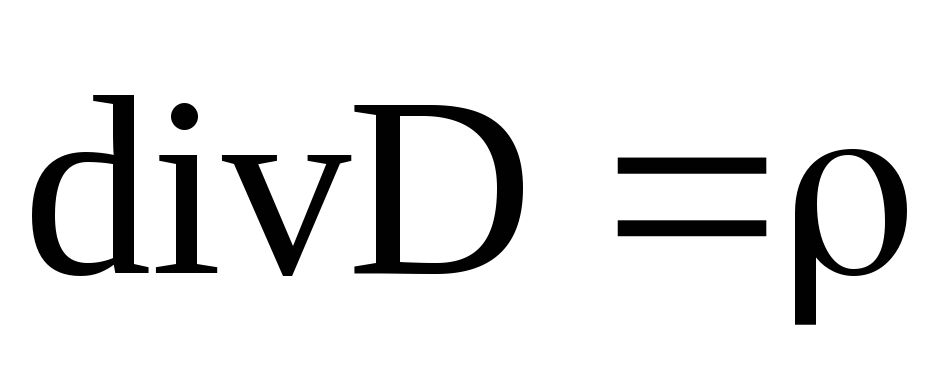 .
(7.31)
.
(7.31)
Физический смысл уравнений Максвелла в дифференциальной форме аналогичен физическому смыслу этих уравнений в интегральной форме.
7.5.3. Материальные уравнения
Уравнения Максвелла в интегральной и дифференциальной формах не образуют полной замкнутой системы, позволяющей рассчитывать электромагнитные процессы при наличии материальной среды. Поэтому систему уравнений Максвелла необходимо дополнить соотношениями, связывающими векторы E, B, D, H и j, которые являются независимыми. Связь между ними определяется свойствами среды и ее состоянием, причем векторы D и j выражаются через вектор E, а B – через H. Эти уравнения называются уравнениями состояния или материальными уравнениями. Они описывают электромагнитные свойства среды и для каждой конкретной среды имеют определенную форму. Для большинства изотропных сред, вплоть до значительных полей, уравнения состояния (материальные уравнения) имеют простую линейную связь:
1. Первое уравнение связывает векторы напряженности и индукции электрического поля:
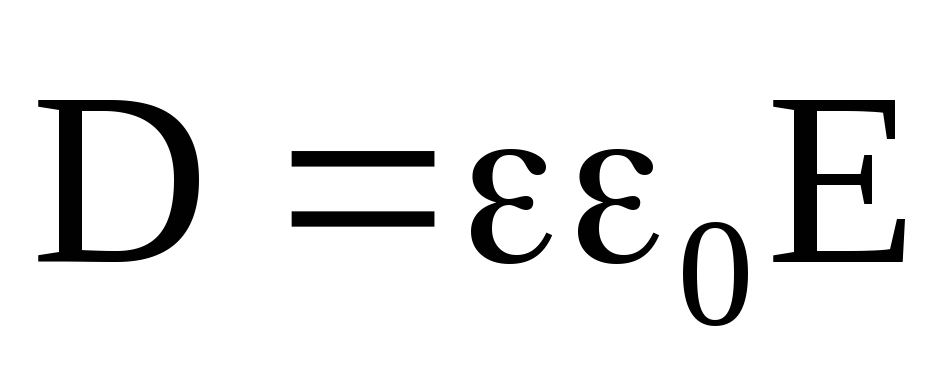 ,
(7.32)
,
(7.32)
где (x,y,z) –диэлектрическая проницаемость среды;
0 – диэлектрическая постоянная.
2. Второе уравнение связывает векторы индукции и напряженности магнитного поля:
 ,
(7.33)
,
(7.33)
где (x,y,z) – магнитная проницаемость среды;
0 – магнитная постоянная.
3. Третье уравнение выражает закон Ома в дифференциальной форме
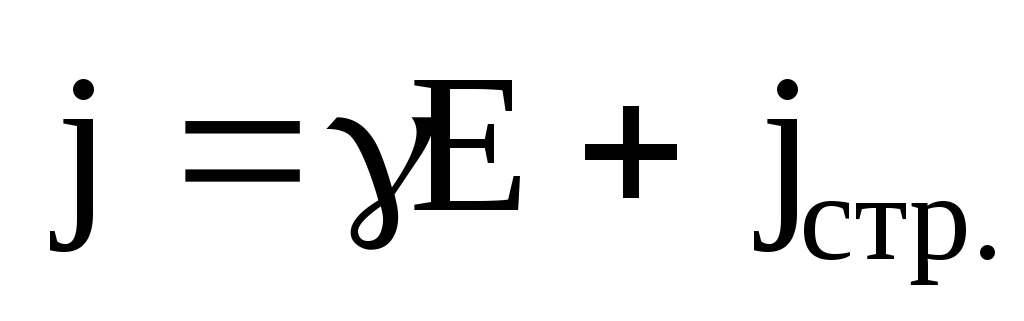 ,
(7.34)
,
(7.34)
где — удельная электропроводность;
jстр. – плотность так называемых сторонних токов, т.е. токов, поддерживаемых любыми силами, кроме сил электрического поля (например, магнитным полем, диффузией).
Проницаемости и определяют тот вклад в электромагнитное поле, который вносят связанные заряды, входящие в состав электрически нейтральных атомов и молекул вещества. Объемная плотность заряда и плотность тока j в материальных уравнениях – это плотности свободных зарядов и токов, причем вспомогательные векторы D и H, вводятся так, чтобы циркуляция вектора H определялась только движением свободных зарядов, а поток вектора D – плотностью распределения этих зарядов в пространстве. Материальные уравнения используются при решении уравнений Максвелла.
Из уравнений
Максвелла вытекает ряд законов сохранения:
закон сохранения электрического заряда,
закон сохранения электромагнитной
энергии. В частности, из уравнений 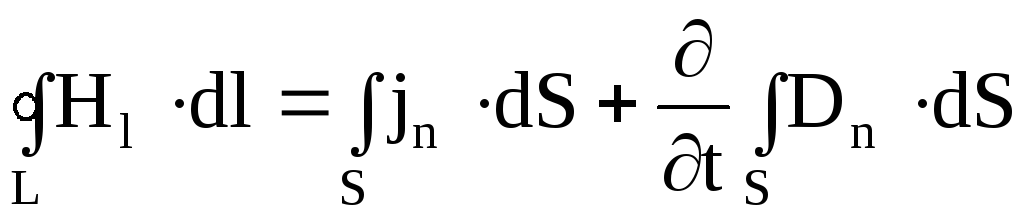 и
и 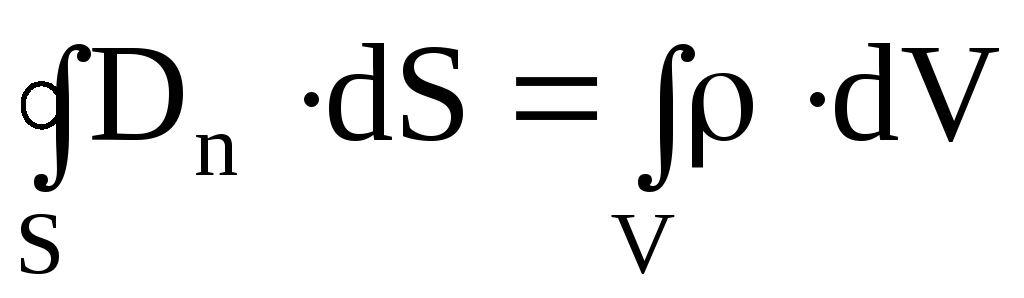 можно
получить уравнение непрерывности,
представляющее собой закон сохранения
электрического заряда:полный
ток, протекающий за единицу времени
через любую замкнутую поверхность S,
равен изменению заряда внутри объема V,
ограниченного поверхностью S.
Если ток через поверхность отсутствует,
то заряд в объеме V остается неизменным:
можно
получить уравнение непрерывности,
представляющее собой закон сохранения
электрического заряда:полный
ток, протекающий за единицу времени
через любую замкнутую поверхность S,
равен изменению заряда внутри объема V,
ограниченного поверхностью S.
Если ток через поверхность отсутствует,
то заряд в объеме V остается неизменным:
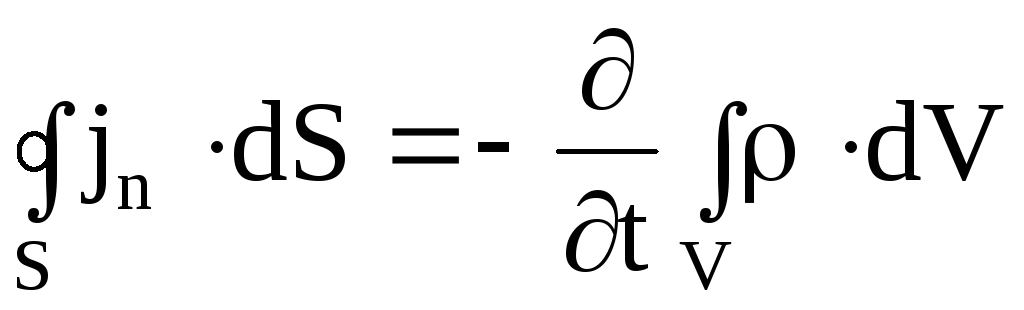 .
(7.35)
.
(7.35)
Если энергия электромагнитного поля не переходит в другие виды энергии, то, согласно уравнениям Максвелла, изменение энергии в некотором объеме за единицу времени равно потоку электромагнитной энергии через поверхность, ограничивающую этот объем.
Если внутри объема за счет энергии электромагнитного поля выделяется некоторое количество тепла, то закон сохранения энергии утверждает о том, что изменение энергии электромагнитного поля в некотором объеме V равно сумме потока энергии электромагнитного поля и количества теплоты, выделившейся в этом объеме:
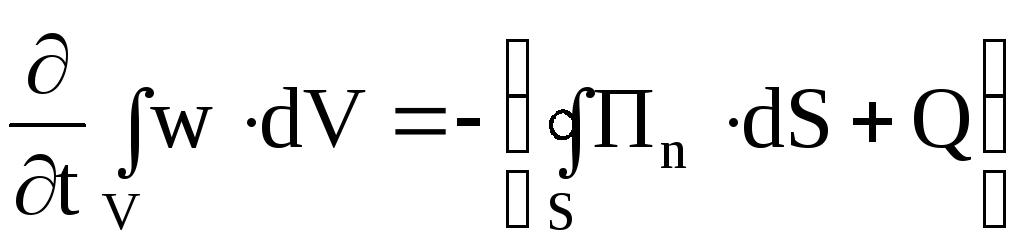 ,
(7.36)
,
(7.36)
где w – энергия поля в единице объема;
Пn – проекция вектора Умова-Пойтинга на направление положительной нормали к поверхности dS;
Q – количество тепла, выделяемое в единицу времени.
Уравнения Максвелла
приводят к фундаментальному выводу о
конечности скорости распространения
электромагнитных взаимодействий. Это
означает, что при изменении плотности
заряда или тока, порождающих электромагнитное
поле, в некоторой точке пространства
на расстоянии r
от них поле изменится спустя время 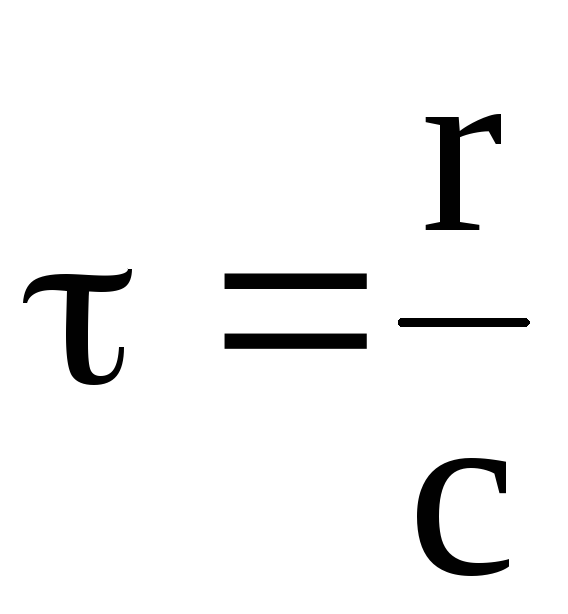 .
Вследствие конечной скорости
распространения электромагнитных
взаимодействий, следовательно, возможно
существование электромагнитных волн,
частным случаем которых является свет,
что было впервые доказано Максвеллом.
.
Вследствие конечной скорости
распространения электромагнитных
взаимодействий, следовательно, возможно
существование электромагнитных волн,
частным случаем которых является свет,
что было впервые доказано Максвеллом.
Это заключение называют вторым основным положением теории Максвелла: электромагнитное поле, возникнув в одном месте пространства, не остается локализованным в нем, а распространяется от этого места в виде электромагнитной волны. Векторы E и H электромагнитной волны взаимно перпендикулярны и перпендикулярны вектору скорости v, с которой распространяется электромагнитная волна.
Распределение Максвелла — Википедия
 Функция плотности распределения для 106 молекул кислорода при −100, 20, 600 градусах Цельсия
Функция плотности распределения для 106 молекул кислорода при −100, 20, 600 градусах ЦельсияРаспределе́ние Ма́ксвелла — общее наименование нескольких распределений вероятности, которые описывают статистическое поведение параметров частиц идеального газа. Вид соответствующей функции плотности вероятности диктуется тем, какая величина: скорость частицы, проекция скорости, модуль скорости, энергия, импульс и т.д. — выступает в качестве непрерывной случайной величины. В ряде случаев распределение Максвелла может быть выражено как дискретное распределение по множеству уровней энергии.
Наиболее значимое распределение Максвелла записывается для модуля скорости частицы v{\displaystyle v} в непрерывном случае и имеет плотность
- fv(x)=Bx2exp[−βx2](x≥0){\displaystyle f_{v}(x)=Bx^{2}\exp \left[-\beta x^{2}\right]\,\,(x\geq 0)} и fv(x)=0(x<0){\displaystyle f_{v}(x)=0\,\,(x<0)},
где x{\displaystyle x} — формальная переменная, фактор β>0{\displaystyle \beta >0} определяется типом частиц и температурой, а множитель B{\displaystyle B} подбирается в зависимости от β{\displaystyle \beta } для обеспечения нормировки. Именно это выражение считается максвелловским распределением в математике, хотя для других параметров частиц аналитический вид распределения Максвелла будет иным.
Распределение Максвелла лежит в основе кинетической теории газов, объясняющей многие фундаментальные свойства газов, включая давление и диффузию. С его помощью вычисляются средние и наиболее вероятные скорости и энергии молекул газа. Оно также применимо для описания электронных процессов переноса и других явлений в физике и химии. Распределение Максвелла может быть получено при помощи статистической механики (см. происхождение статсуммы). Данное распределение является реализующимся с наивысшей вероятностью распределением изучаемого параметра.
Сфера применения распределения Максвелла[править | править код]
Требования к описываемой системе, примеры[править | править код]
Вопрос о применимости распределения Максвелла к конкретной системе равносилен вопросу о том, может ли эта система считаться идеальным газом с достаточной точностью. При этом система должна
Такой набор требований удовлетворяется в первую очередь в газах, например в воздухе, при обычных условиях. Распределение Максвелла применимо к множеству свойств индивидуальных молекул в газе. В первую очередь о нём обычно думают как о распределении энергий молекул в газе, но оно может применяться к распределению скоростей и других параметров молекул. Чаще всего оно является непрерывным распределением по континууму изменения случайного параметра.
Во многих случаях, однако, условие доминирования упругих соударений над всеми другими процессами не выполняется даже приблизительно. Так, в физике ионосферы и космической плазмы, большое значение имеют процессы рекомбинации и столкновительного возбуждения (то есть излучательные процессы), в особенности для электронов. Использование распределения Максвелла в этом случае не только дало бы количественно неверные результаты, но и привело бы к качественно неправильной интерпретации соответствующих процессов.
Условия классического рассмотрения[править | править код]
В случаях, где квантовая дебройлева длина волны частиц газа не является малой по сравнению с расстоянием между частицами, наблюдаются отклонения от распределения Максвелла из-за квантовых эффектов. Поэтому важен вопрос о границах применимости классического рассмотрения.
Соотношение неопределённостей (нередко упрощённо записываемое в форме Δx⋅Δpx∼h{\displaystyle \Delta x\cdot \Delta p_{x}\sim h}, где Δx{\displaystyle \Delta x}, Δpx{\displaystyle \Delta p_{x}} — неопределённости координаты и x{\displaystyle x}-проекции импульса, h{\displaystyle h} — постоянная Планка) имеет трёхмерный аналог вида r⋅p∼h{\displaystyle r\cdot p\sim h}, где r{\displaystyle r} обозначает характерный линейный размер зоны локализации частицы. Чтобы неопределённости в координате и импульсе не играли роли и могла применяться классическая, а не квантовая механика, должно выполняться соотношение:
- V1/3⋅p≫h{\displaystyle V^{1/3}\cdot p\gg h},
где V{\displaystyle V} — объём, на который в среднем приходится одна частица, равный обратной концентрации n−1{\displaystyle n^{-1}} частиц газа. Если возвести обе части в квадрат, получится
- n−23h−2p2≫1{\displaystyle n^{-{\frac {2}{3}}}h^{-2}p^{2}\gg 1}.
Учитывая, что p2=2mE{\displaystyle p^{2}=2mE} и беря в качестве характерного значения энергии величину (3/2)kT{\displaystyle (3/2)kT}, придём к:
- T≫n23h33mk=Tdeg{\displaystyle T\gg {\frac {n^{\frac {2}{3}}h^{2}}{3mk}}=T_{deg}\qquad } (Tdeg{\displaystyle T_{deg}} — температура вырождения, а m{\displaystyle m} — масса частицы).
При температурах ниже Tdeg{\displaystyle T_{deg}} распределение Максвелла неприменимо.
Распределение Максвелла по состояниям[править | править код]
Распределение Максвелла можно записать как дискретное распределение по множеству состояний молекулы, нумеруемых символом i{\displaystyle i}:
- NiN=exp(−Ei/kT)∑jexp(−Ej/kT)(1){\displaystyle {\frac {N_{i}}{N}}={\frac {\exp \left(-E_{i}/kT\right)}{\sum _{j}^{}{\exp \left(-E_{j}/kT\right)}}}\qquad \qquad (1)}.
Через Ei{\displaystyle E_{i}} и Ni{\displaystyle N_{i}} обозначены энергия молекулы в i{\displaystyle i}-м состоянии и число таких молекул, T{\displaystyle T} — температура системы, N{\displaystyle N} — общее число молекул в системе и k{\displaystyle k} — постоянная Больцмана. (Бывает, что вышеупомянутое уравнение записывается с множителем gi{\displaystyle g_{i}}, обозначающим степень вырождения энергетических уровней. В этом случае i{\displaystyle i} нумерует не состояния, а энергии и сумма будет по энергиям, а не по состояниям). Поскольку скорость связана с энергией, последнее уравнение может использоваться для получения связи между температурой и скоростями молекул в газе. Знаменатель известен как каноническая статистическая сумма.
Разновидности непрерывного распределения Максвелла[править | править код]
Представленный в этом разделе вывод распределений Максвелла, естественный для современной учебно-методической литературы, сильно отличается от вывода, предложенного самим Джеймсом Клерком Максвеллом и позже описанного с меньшим количеством предположений Людвигом Больцманом. Исторический вывод будет приведён в конце статьи.
Распределение по вектору импульса[править | править код]
В случае идеального газа из невзаимодействующих молекул вся энергия находится в форме кинетической энергии. Кинетическая энергия соотносится с импульсом частицы как
- E=p22m(2){\displaystyle E={\frac {p^{2}}{2m}}\qquad \qquad (2)},
где p2{\displaystyle p^{2}} — квадрат вектора импульса p=[px,py,pz]{\displaystyle \mathbf {p} =[p_{x},p_{y},p_{z}]}, и уравнение (1) можно переписать как:
- NiN=1Zexp[−(px2+py2+pz2)2mkT](3){\displaystyle {\frac {N_{i}}{N}}={\frac {1}{Z}}\exp \left[{\frac {-(p_{x}^{2}+p_{y}^{2}+p_{z}^{2})}{2mkT}}\right]\qquad \qquad (3)},
где Z{\displaystyle Z} — статсумма, соответствующая знаменателю в уравнении (1), m{\displaystyle m} — масса молекулы.
Если уровни энергии расположены достаточно густо, факт дискретности становится непринципиальным и можно считать, что энергии распределены непрерывно. Тогда отношение Ni/N{\displaystyle N_{i}/N} пропорционально функции плотности вероятности fp{\displaystyle f_{\mathbf {p} }} нахождения молекулы в состоянии с этими значениями компонент импульса. Таким образом,
- fp(px,py,pz)=CZexp[−(px2+py2+pz2)2mkT](4){\displaystyle f_{\mathbf {p} }(p_{x},p_{y},p_{z})={\frac {C}{Z}}\exp \left[{\frac {-(p_{x}^{2}+p_{y}^{2}+p_{z}^{2})}{2mkT}}\right]\qquad \qquad (4)}.
Постоянная нормировки C, определяется из условия, в соответствии с которым вероятность того, что молекулы имеют какой-либо вообще импульс, должна быть равна единице. Поэтому интеграл уравнения (4) по всем значениям px,py{\displaystyle p_{x}\,,p_{y}} и pz{\displaystyle p_{z}} должен быть равен единице. Можно показать, что:
- ∭−∞+∞1Zexp[−(px2+py2+pz2)2mkT]dpxdpydpz=1Z(2πmkT)3/2(5){\displaystyle \iiint \limits _{-\infty }^{+\infty }{\frac {1}{Z}}\exp \left[{\frac {-(p_{x}^{2}+p_{y}^{2}+p_{z}^{2})}{2mkT}}\right]\,dp_{x}\,dp_{y}\,dp_{z}={\frac {1}{Z}}\left(2\pi mkT\right)^{3/2}\qquad \qquad (5)}.
Таким образом, чтобы интеграл в уравнении (4) имел значение 1 необходимо, чтобы
- C=Z(2πmkT)3(6){\displaystyle C={\frac {Z}{({\sqrt {2\pi mkT}})^{3}}}\qquad \qquad (6)}.
Подставляя выражение (6) в уравнение (4) и используя тот факт, что pi=mvi{\displaystyle p_{i}=mv_{i}}, мы получим
- fp(px,py,pz)=(12πmkT)3exp[−(px2+py2+pz2)2mkT](7){\displaystyle f_{\mathbf {p} }(p_{x},p_{y},p_{z})={\sqrt {\left({\frac {1}{2\pi mkT}}\right)^{3}}}\exp \left[{\frac {-(p_{x}^{2}+p_{y}^{2}+p_{z}^{2})}{2mkT}}\right]\qquad \qquad (7)}.
Распределение по вектору скорости[править | править код]
Учитывая, что плотность распределения по скоростям fv{\displaystyle f_{\mathbf {v} }} пропорциональна плотности распределения по импульсам:
- fvd3v=fp(dpdv)3d3v{\displaystyle f_{\mathbf {v} }d^{3}v=f_{\mathbf {p} }\left({\frac {dp}{dv}}\right)^{3}d^{3}v}
и используя p=mv{\displaystyle \mathbf {p} =m\mathbf {v} } мы получим:
- fv(vx,vy,vz)=(m2πkT)3exp[−m(vx2+vy2+vz2)2kT](8){\displaystyle f_{\mathbf {v} }(v_{x},v_{y},v_{z})={\sqrt {\left({\frac {m}{2\pi kT}}\right)^{3}}}\exp \left[{\frac {-m(v_{x}^{2}+v_{y}^{2}+v_{z}^{2})}{2kT}}\right]\qquad \qquad (8)},
что является распределением Максвелла по скоростям. Вероятность обнаружения частицы в бесконечно малом элементе dvx,dvy,dvz{\displaystyle dv_{x}\,,dv_{y}\,,dv_{z}} около скорости v=[vx,vy,vz]{\displaystyle \mathbf {v} =[v_{x},v_{y},v_{z}]} равна
- fv(vx,vy,vz)dvxdvydvz{\displaystyle f_{\mathbf {v} }\left(v_{x},v_{y},v_{z}\right)dv_{x}dv_{y}dv_{z}}
Распределение по модулю импульса[править | править код]
Интегрируя, мы можем найти распределение по абсолютной величине импульса
- fp=∫θ=0π∫ϕ=02π fpp2sin(θ)dθdϕ=4π(12πmkT)3 p2exp[−p22mkT]{\displaystyle f_{p}=\int _{\theta =0}^{\pi }\int _{\phi =0}^{2\pi }~f_{\mathbf {p} }p^{2}\sin(\theta )\,d\theta \,d\phi =4\pi {\sqrt {\left({\frac {1}{2\pi mkT}}\right)^{3}}}~p^{2}\exp \left[{\frac {-p^{2}}{2mkT}}\right]}
Распределение по энергии[править | править код]
Наконец, используя соотношения p2=2mE{\displaystyle p^{2}=2\,mE} и fEdE=fpdp{\displaystyle f_{E}\,dE=f_{p}\,dp}, мы получаем распределение по кинетической энергии:
- fE=fpdpdE=2π(πkT)3E exp[−EkT]{\displaystyle f_{E}=f_{p}{\frac {dp}{dE}}={\frac {2\pi }{\sqrt {(\pi kT)^{3}}}}{\sqrt {E}}{}~\exp \left[{\frac {-E}{kT}}\right]}
Распределение по проекции скорости[править | править код]
Распределение Максвелла для вектора скорости [vx,vy,vz]{\displaystyle [v_{x},v_{y},v_{z}]} — является произведением распределений для каждого из трех направлений:
- fv(vx,vy,vz)=fv(vx)fv(vy)fv(vz){\displaystyle f_{v}\left(v_{x},v_{y},v_{z}\right)=f_{v}(v_{x})f_{v}(v_{y})f_{v}(v_{z})},
где распределение по одному направлению:
- fv(vi)=m2πkTexp[−mvi22kT](9){\displaystyle f_{v}(v_{i})={\sqrt {\frac {m}{2\pi kT}}}\exp \left[{\frac {-mv_{i}^{2}}{2kT}}\right]\qquad \qquad (9)}
Это распределение имеет форму нормального распределения. Как и следует ожидать для покоящегося газа, средняя скорость в любом направлении равна нулю.
Распределение по модулю скорости[править | править код]
Обычно, более интересно распределение по абсолютному значению, а не по проекциям скоростей молекул. Модуль скорости, v определяется как:
- v=vx2+vy2+vz2(10){\displaystyle v={\sqrt {v_{x}^{2}+v_{y}^{2}+v_{z}^{2}}}\qquad \qquad (10)}
поэтому модуль скорости всегда будет больше или равен нулю. Так как все vi{\displaystyle v_{i}} распределены нормально, то v2{\displaystyle v^{2}} будет иметь хи-квадрат распределение с тремя степенями свободы. Если f(v){\displaystyle f(\mathbf {v} )} — функция плотности вероятности для модуля скорости, то:
- f(v)dv=P(χ2|3)dχ2{\displaystyle f\left(v\right)dv=P(\chi ^{2}|3)d\chi ^{2}},
где
- χ2=mv2kT{\displaystyle \chi ^{2}={\frac {mv^{2}}{kT}}}
таким образом, функция плотности вероятности для модуля скорости равна
- f(v)dv=4πv2(m2πkT)3/2exp(−mv22kT)dv(11){\displaystyle f(v)dv=4\pi v^{2}\left({\frac {m}{2\pi kT}}\right)^{3/2}\exp \left({\frac {-mv^{2}}{2kT}}\right)dv\qquad \qquad (11)}
Вид функции f(v){\displaystyle f(v)} соответствует приведённому в преамбуле с тем отличием, что там используется формальная переменная x{\displaystyle x} ради большей математической общности.