Уравнения Максвелла • Джеймс Трефил, энциклопедия «Двести законов мироздания»

Шотландский физик, один из самых выдающихся теоретиков XIX столетия. Родился в Эдинбурге, происходит из старинного дворянского рода. Учился в Эдинбургском и Кембриджском университетах. Первую научную статью (о методе начертания идеального овала) опубликовал в возрасте 14 лет. Максвелл занимал должность профессора кафедры экспериментальной физики Кембриджского университета, когда в 48 лет безвременно скончался от рака.

Первым большим теоретическим исследованием Клерка Максвелла, как его часто именуют, стала работа по теории цвета и цветного зрения. Он первым показал, что вся гамма видимых цветов может быть получена путем смешения трех основных цветов — красного, желтого и синего; объяснил природу дальтонизма (дефекта зрения, приводящего к нарушению восприятия цветовой гаммы) врожденным или приобретенным дефектом рецепторов сетчатки глаза. Он первым изобрел реально работающий цветной фотоаппарат (с использованием тартановой ленты в качестве светочувствительного материала) и продемонстрировал его работу на собрании Лондонского королевского общества в 1861 году.

Как бы между делом тщательно рассчитал возможную структуру колец Сатурна и доказал, что они не могут быть жидкими, как ранее считалось, а должны состоять из твердых частиц.

Максвелл внес важный вклад в развитие многих отраслей естествознания. Но, пожалуй, наиважнейшее его достижение состоит в развитии теории электромагнетизма и постановке ее на прочную математическую основу. Заниматься этим вопросом Максвелл начал в середине 1850-х годов. По иронии судьбы Максвелл твердо верил в существование светоносного эфира, и все свои уравнения выводил исходя из того, что эфир существует, и

в нем возбуждаются электромагнитные волны, имеющие, как следствие, конечную скорость распространения. До результатов опыта Майкельсона—Морли, опровергающих теорию существования эфира, Максвелл не дожил. (Как не дожил он и до безоговорочного признания своей теории. Окончательно волновая природа света и правильность уравнений Максвелла были подтверждены опытами Герца лишь в 1888 году, а до того времени большинство физиков, включая самого Герца, с недоверием относились к столь смелой теории.  — Примечание переводчика.) К счастью для него и для нас, теорию Максвелла этот опыт не отменил, поскольку уравнения Максвелла выполняются независимо от наличия или отсутствия эфира.

Наконец, Максвелл внес огромный вклад в становление статистической механики, найдя распределение молекул газа по скоростям, ставшее краеугольным камнем молекулярно-кинетической теории. Наконец, сам же Максвелл и подметил несовершенство этой теории, сформулировав парадокс, позже получивший название демона Максвелла.

Почему теорию Максвелла так трудно понять? / Хабр

Скромность не всегда добродетель

В 1865 году Джеймс Клерк Максвелл опубликовал свою статью “Динамическая теория электромагнитного поля» в «Философских трудах Королевского общества». Ему было тогда тридцать четыре года. Оглядываясь назад, мы можем заметить, что работа Максвелла была самым важным событием девятнадцатого века в истории физических наук. Если говорить в общем о естественных науках, то статья Максвелла была второй по значимости после «Происхождения видов» Дарвина.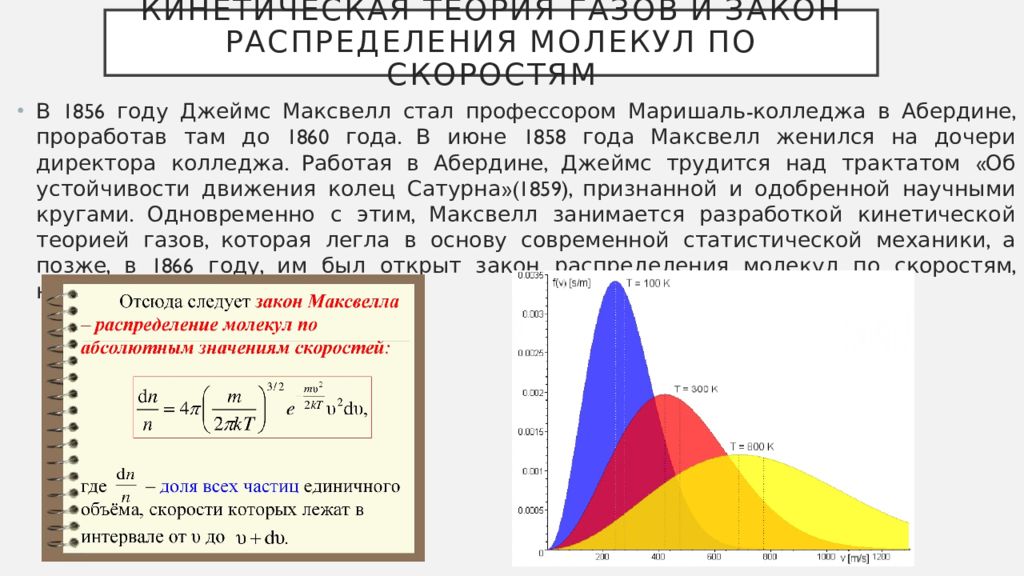 Но важность работ Максвелла не была очевидна для его современников. Более двадцати лет его теория электромагнетизма в основном игнорировалась. Физикам было трудно ее понять из-за обилия сложных уравнений. Математикам было трудно ее понять, потому что Максвелл использовал для объяснений физический язык. Этот труд был расценен как неясное предположение без должного количества экспериментальных доказательств. Физик Михаил Пупин в своей автобиографии «От иммигранта к изобретателю» описывает, как он путешествовал из Америки в Европу в 1883 году в поисках того, кто понимал Максвелла. Он отправился изучать теорию Максвелла, как рыцарь в поисках Святого Грааля.

Пупин сначала поступил в Кембридж с твердым намерением изучить теорию у самого Максвелла. Он не знал, что Максвелл умер четыре года назад. Узнав, что Максвелл умер, он остался в Кембридже и был назначен преподавателем колледжа. Но его наставник знал о теории Максвелла меньше, чем он сам, и был заинтересован только в том, чтобы научить Михаила решать математические задачи трипоса. Михаил Пупин был поражен, обнаружив, как он говорит, «как мало было физиков, которые уловили смысл теории, даже через двадцать лет после того, как она была сформулирована Максвеллом в 1865 году». В конце концов он бежал из Кембриджа в Берлин и поступил студентом к Герману фон Гельмгольцу. Гельмгольц понимал теорию и учил Пупина тому, что знал сам. Пупин вернулся в Нью-Йорк, стал профессором Колумбийского университета и обучал последующие поколения студентов, которые впоследствии распространили Евангелие Максвелла по всей Америке.

Открытка от Максвелла Питеру Тейту

Как случилось, что теория Максвелла была так широко проигнорирована? В конце концов, Максвелл не был похож на своего современника Грегора Менделя, монаха, работавшего в безвестном монастырском саду в Богемии. Максвелл был известным профессором, директором Кавендишской лаборатории в Кембридже, ведущей фигурой в британском научном сообществе. Свидетельством его высокого положения можно считать то, что он был президентом секции А (математические и физические науки) Британской ассоциации содействия развитию науки, когда ассоциация провела свое ежегодное собрание в Ливерпуле в 1870 году. Он выступил с президентской речью в Ливерпуле, которая была опубликована во втором томе недавно основанного журнала «Nature». Стиль его выступления показывает нам, почему его теорию не воспринимали всерьез. Можно было ожидать, что он воспользуется возможностью, предоставленной президентской платформой, чтобы объявить миру о важности открытий, которые он сделал пять лет назад. Он не сделал ничего подобного. Он был абсурдно и раздражающе скромен.

Максвелл в первую очередь объявил тему своего выступления — обзор последних достижений, которые были сделаны на границе между математикой и физикой. Затем он с большим энтузиазмом рассказал о вихревой теории молекул, недавно предложенной сэром Уильямом Томсоном (впоследствии ставшим лордом Кельвином).

Теория, которую сэр Уильям основал на великолепных гидродинамических теоремах Гельмгольца, ищет свойства молекул в кольцевых вихрях однородной несжимаемой жидкости без трения. Гельмгольц показал, что в идеальной жидкости такое кружащееся кольцо, если оно однажды возникло, будет продолжать кружиться вечно, всегда будет состоять из той же самой части жидкости, которая была сначала закручена, и никогда не может быть разрезана надвое какой-либо естественной причиной. Эти кольцевые вихри способны к таким разнообразным связям и узловатым самоинволюциям, что свойства различных узловатых вихрей должны быть столь же различны, как и свойства различных видов молекул.

И так далее. Максвелл объяснил, как древняя теория о том, что материя состоит из атомов, столкнулась с логическим парадоксом. С одной стороны, атомы должны были быть твердыми, непроницаемыми и неразрушимыми. С другой стороны, данные спектроскопии и химии показали, что атомы имеют внутреннюю структуру и находятся под влиянием внешних сил. Этот парадокс в течение многих лет блокировал прогресс в понимании природы материи. Теперь, наконец, вихревая теория молекул разрешила парадокс. Вихри в эфире мягкие и имеют внутреннюю структуру, и тем не менее, согласно Гельмгольцу, они индивидуальны и неразрушимы. Оставалось только вывести факты спектроскопии и химии из законов взаимодействия вихрей, предсказанных гидродинамикой идеальной жидкости. Максвелл считал эту вихревую теорию материи замечательным примером плодотворного взаимодействия математики и физики.

Неясно, верил ли Максвелл всерьез в то, что говорил о вихревой теории. Возможно, он хотел, чтобы его речь развлекала слушателей, а не просвещала их. У него было хитрое чувство юмора, и вполне возможно, что он хвалил теорию вихря, зная, что более проницательные члены аудитории поймут, что теория была шуткой. Только в конце своего выступления Максвелл кратко упомянул о своей теории электромагнетизма.

Другая теория электричества, которую я предпочитаю, отрицает действие на расстоянии и приписывает электрическое действие напряжениям и давлениям во всепроникающей среде, причем эти напряжения одинаковы по характеру с теми, которые известны инженерам, и среда идентична той, в которой предполагается распространение света.

Фраза «Другая теория электричества, которую я предпочитаю», кажется, намеренно скрывает тот факт, что это была его собственная теория. Неудивительно, что вихри Кельвина произвели на его слушателей большее впечатление, чем уравнения Максвелла.

Мораль этой истории заключается в том, что скромность не всегда является добродетелью. Максвелл и Мендель оба были чрезмерно скромны. Скромность Менделя задержала прогресс биологии на пятьдесят лет. Скромность Максвелла замедлила прогресс физики на двадцать лет. Для прогресса науки будет лучше, если люди, делающие великие открытия, не будут слишком скромны, чтобы трубить в свои собственные трубы. Если бы у Максвелла было такое же эго, как у Галилея или Ньютона, он бы позаботился о том, чтобы его работы не игнорировались. Максвелл был таким же великим ученым, как Ньютон, и гораздо более приятным человеком. Но, к сожалению, он не начал президентскую речь в Ливерпуле словами, подобными тем, которые Ньютон использовал, чтобы представить третий том своей Principia Mathematica: «… исходя из тех же принципов, я теперь демонстрирую структуру системы мира». Ньютон не называл свой закон всемирного тяготения «очередной теорией тяготения, которую я предпочитаю».

Теория Максвелла и квантовая механика

Помимо скромности Максвелла, были и другие причины, по которым его теорию было трудно понять. Он заменил ньютоновскую вселенную материальных объектов, взаимодействующих друг с другом на расстоянии, вселенной полей, простирающихся через пространство и взаимодействующих только локально с материальными объектами. Понятие поля было трудно понять, потому что поля неосязаемы. Ученые того времени, включая самого Максвелла, пытались представить поля как механические структуры, состоящие из множества маленьких колесиков и вихрей, простирающихся в пространстве. Эти структуры должны были переносить механические напряжения, которые электрические и магнитные поля передавали между электрическими зарядами и токами. Чтобы поля удовлетворяли уравнениям Максвелла, система колес и вихрей должна была быть чрезвычайно сложной.

Если попытаться визуализировать теорию Максвелла с помощью таких механических моделей, она выглядит как возврат к астрономии Птолемея с планетами, движущимися по циклам и эпициклам в небе. Это не похоже на изящную астрономию Ньютона. Уравнения Максвелла, записанные в неуклюжих обозначениях, которыми пользовался Максвелл, были пугающе сложными, а его механические модели — еще хуже. Для современников теория Максвелла была лишь одной из многих теорий электричества и магнетизма. Ее было трудно осмыслить, и, казалось, не было явного преимущества перед другими теориями, которые описывали электрические и магнитные силы в ньютоновском стиле как дальнодействие между зарядами и магнитами. Неудивительно, что мало кто из современников Максвелла прилагал усилия, чтобы изучить его теорию.

Теория Максвелла становится простой и понятной только тогда, когда вы отказываетесь мыслить в терминах механических моделей. Вместо того чтобы думать о механических объектах как о первичных, а об электромагнитных напряжениях как о вторичных следствиях, вы должны думать об электромагнитном поле как о первичном, а о механических силах как о вторичном конструкте. Мысль о том, что первичными составляющими Вселенной являются поля, не сразу пришла в голову физикам поколения Максвелла. Поля — это абстрактное понятие, далекое от привычного мира вещей и сил. Уравнения поля Максвелла являются уравнениями в частных производных. Они не могут быть выражены простыми словами, такими как закон движения Ньютона: сила равна массе, умноженной на ускорение. Теория Максвелла должна была ждать следующего поколения физиков, Герца, Лоренца и Эйнштейна, чтобы раскрыть свою силу и прояснить свои концепции. Следующее поколение выросло с уравнениями Максвелла и чувствовало себя как дома во вселенной, построенной из полей. Первенство полей было так же естественно для Эйнштейна, как первенство механических структур — для Максвелла.

https://ddcolrs.wordpress.com/2018/01/17/maxwells-equations-from-20-to-4/

Современный взгляд на мир, возникший из теории Максвелла, — это мир с двумя слоями. Первый слой, слой фундаментальных составляющих мира, состоит из полей, удовлетворяющих простым линейным уравнениям. Второй слой, слой вещей, которые мы можем непосредственно потрогать и измерить, состоит из механических напряжений, энергий и сил. Эти два слоя связаны, потому что величины во втором слое являются квадратичными или билинейными комбинациями величин в первом слое. Чтобы вычислить энергии или напряжения, вы берете квадрат напряженности электрического поля или умножаете одну составляющую поля на другую. Двухслойная структура мира — основная причина, по которой теория Максвелла казалась загадочной и трудной. Объекты на первом уровне, объекты, которые действительно фундаментальны, являются абстракциями, не доступными непосредственно нашим чувствам. Объекты, которые мы можем чувствовать и осязать, находятся на втором слое, и их поведение лишь косвенно определяется уравнениями, действующими на первом слое. Двухслойная структура мира подразумевает, что основные процессы природы скрыты от нашего взгляда.

Теперь мы считаем само собой разумеющимся, что электрические и магнитные поля являются абстракциями, не сводимыми к механическим моделям. Чтобы убедиться в этом, достаточно взглянуть на единицы измерения электрического и магнитного полей. Условная единица напряженности электрического поля — квадратный корень из джоуля на кубический метр. Джоуль — это единица энергии, а метр — единица длины, но квадратный корень из джоуля — это не единица чего-то осязаемого. Мы не можем представить себе, как можно измерить непосредственно квадратный корень из джоуля. Единица измерения напряженности электрического поля — это математическая абстракция, выбранная таким образом, что квадрат напряженности поля равен плотности энергии, которую можно измерить с помощью реальных приборов. Единицей плотности энергии является джоуль на кубический метр, и поэтому мы говорим, что единицей напряженности поля является квадратный корень из джоуля на кубический метр. Это не означает, что напряженность электрического поля можно измерить с помощью квадратного корня калориметра. Это означает, что напряженность электрического поля — абстрактная величина, несоизмеримая с любыми величинами, которые мы можем измерить непосредственно.

Через шестьдесят лет после того, как Максвелл опубликовал свою теорию, Шредингер, Гейзенберг и Дирак изобрели квантовую механику. Квантовая механика была принята гораздо быстрее, чем теория Максвелла, потому что она сделала множество определенных предсказаний об атомных процессах и эксперименты показали, что все предсказания были правильными. Через год-два все поверили в квантовую механику как в практический инструмент для расчета основных процессов физики и химии. Природа, очевидно, подчинялась законам квантовой механики. Но значение квантовой механики оставалось спорным. Хотя квантовая механика была быстро принята, она не была быстро понята. Резкие расхождения во мнениях по поводу интерпретации квантовой механики сохраняются на протяжении семидесяти лет.

И почему их никто не понимал?

Прошло около тридцати лет после Максвелла, прежде чем его уравнения стали понятны всем. Для достижения согласованного понимания квантовой механики потребуется по меньшей мере вдвое больше времени. Мы все еще ведем страстные споры между сторонниками различных интерпретаций квантовой механики, Копенгагенской интерпретации, многомировой интерпретации, декогерентной интерпретации, интерпретаций скрытых переменных и многих других. Причина этих споров заключается в том, что различные интерпретаторы пытаются описать квантовый мир словами повседневного языка, а язык не подходит для этой цели. Повседневный язык описывает мир таким, каким его видят люди. Наше восприятие мира целиком связано с макроскопическими объектами, которые ведут себя в соответствии с правилами классической физики. Все понятия, которые появляются в нашем языке, являются классическими. Каждая из интерпретаций квантовой механики — это попытка описать квантовую механику на языке, в котором отсутствуют соответствующие понятия. Битвы между соперничающими интерпретациями продолжаются безостановочно, и конца им не видно.

Для понимания квантовой механики может оказаться полезным подчеркнуть сходство между квантовой механикой и теорией Максвелла. В двух отношениях теория Максвелла может дать ключ к тайнам квантовой механики.

Во-первых, попытки понять квантовую механику в терминах языка, основанного на классических понятиях, аналогичны попыткам понять теорию Максвелла в терминах механических моделей. Теория Максвелла стала изящной и понятной только после того, как были оставлены попытки представить электромагнитные поля с помощью механических моделей. Точно так же квантовая механика становится изящной и понятной только после того, как попытки описать ее словами прекращаются. Чтобы увидеть красоту теории Максвелла, необходимо отойти от механических моделей и погрузиться в абстрактный мир полей. Чтобы увидеть красоту квантовой механики, необходимо отойти от словесных описаний и погрузиться в абстрактный мир геометрии. Математика — это язык, на котором говорит природа. Язык математики делает мир максвелловских полей и мир квантовых процессов одинаково прозрачными.

Вторая связь между теорией Максвелла и квантовой механикой заключается в глубоком сходстве структуры. Подобно теории Максвелла, квантовая механика делит Вселенную на два слоя. Первый слой содержит волновые функции Шредингера, матрицы Гейзенберга и векторы состояний Дирака. Величины в первом слое подчиняются простым линейным уравнениям. Их поведение можно точно рассчитать. Но их нельзя наблюдать непосредственно. Второй слой содержит вероятности столкновений и превращений частиц, интенсивности и поляризации излучения, математические ожидания энергий и спинов частиц. Величины во втором слое могут быть непосредственно наблюдаемы, но не могут быть непосредственно вычислены. Они не подчиняются простым уравнениям. Это либо квадраты величин первого слоя, либо произведения одной величины первого слоя на другую. В квантовой механике, как и в теории Максвелла, Природа живет в абстрактном математическом мире первого слоя, но мы, люди, живем в конкретном механическом мире второго слоя. Мы можем описать Природу только абстрактным математическим языком, потому что наш вербальный язык находится дома только во втором слое.

Как и в случае с теорией Максвелла, абстрактное качество величин первого слоя проявляется в единицах, в которых они выражаются. Например, волновая функция Шредингера выражается в единице, которая является квадратным корнем из обратного кубического метра. Уже один этот факт ясно показывает, что волновая функция — это абстракция, навсегда скрытая от нашего взгляда. Никто никогда не измерит напрямую квадратный корень из кубического метра. Конечная важность теории Максвелла гораздо больше, чем ее непосредственные достижения в объяснении и объединении явлений электричества и магнетизма. Его конечная важность состоит в том, чтобы стать прототипом для всех великих триумфов физики двадцатого века. Это прототип теории относительности Эйнштейна, квантовой механики, теории обобщенной калибровочной инвариантности Янга-Миллса и единой теории полей и частиц.

Все эти теории основаны на концепции динамических полей, введенной Максвеллом в 1865 году. Все они имеют одинаковую двухслойную структуру, отделяющую мир простых динамических уравнений от мира человеческого наблюдения. Все они воплощают в себе то же качество математической абстракции, которое сделало теорию Максвелла трудной для понимания его современниками. Мы можем надеяться, что глубокое понимание теории Максвелла приведет к рассеиванию тумана непонимания, который все еще окружает интерпретацию квантовой механики. И мы можем надеяться, что глубокое понимание теории Максвелла поможет проложить путь к дальнейшим триумфам физики в XXI веке.

Уравнения Максвелла

Уравнения Максвелла

Maxwell’s equations

    Уравнения Максвелла − уравнения классической электродинамики, описывающие динамику электромагнитного поля и его связь с зарядами и токами.

Уравнения Максвелла явились теоретическим обобщением экспериментальных законов: Кулона, Ампера, законов электромагнитной индукции и других.
    Уравнения Максвелла в гауссовой системе единиц имеют вид

	div B = 0,
	div D = 4πρ,

где E − напряжённость электрического поля, H − напряжённость магнитного поля, D − электрическая индукция, B − магнитная индукция, ρ − плотность электрического заряда, j − плотность электрического тока.

    Для того, чтобы использовать уравнения Максвелла для решения задач электродинамики в различных средах, необходимо учесть индивидуальные свойства среды.

D = εE,
B = μH,

ε − диэлектрическая проницаемость среды, μ − магнитная проницаемость среды, σ — электропроводность среды.
    В вакууме без зарядов и токов

D = ε0E,	B = μ0H,
div E = 0,	div H = 0,

    Эта система дифференциальных уравнений имеет решение — гармоническую плоскую волну.

Векторы электрического и магнитного полей перпендикулярны направлению распространения волны и друг другу и находятся в фазе. Волна распространяется со скоростью

c = (μ₀ε₀)^-1/2.

c − скорость света в вакууме, c = 2.99792458·10⁸ м/с,
ε₀ − электрическая постоянная, ε₀ = 8.85418782·10^-12 Ф/м,
μ₀ − магнитная постоянная, μ₀ = 1.25663706·10^-6 Гн/м.

---

 

 

МАКСВЕЛЛА УРАВНЕНИЯ • Большая российская энциклопедия

МА́КСВЕЛЛА УРАВНЕ́НИЯ, ос­но­во­по­ла­гаю­щие урав­не­ния клас­сич. мак­ро­ско­пич. элек­тро­ди­на­ми­ки, опи­сы­ваю­щие за­ко­но­мер­но­сти элек­тро­маг­нит­ных яв­ле­ний в сплош­ной сре­де или ва­куу­ме (в пре­неб­ре­же­нии кван­то­вы­ми яв­ле­ния­ми). Тео­рия элек­тро­маг­нит­но­го поля бы­ла раз­ра­бо­та­на Дж. К. Мак­свел­лом в 1856–73. В М. у. обоб­ще­ны ра­нее ус­та­нов­лен­ные опыт­ные за­ко­ны элек­трич.

и маг­нит­ных яв­ле­ний, и эти за­ко­ны объ­е­ди­не­ны с кон­цеп­ци­ей М. Фа­ра­дея об элек­тро­маг­нит­ном по­ле, обес­пе­чи­ваю­щем взаи­мо­дей­ст­вие ме­ж­ду уда­лён­ны­ми за­ря­жен­ны­ми те­ла­ми (т. н. тео­рия близ­ко­дей­ст­вия). В ори­ги­наль­ном из­ло­же­нии Мак­свел­ла бы­ло соз­на­тель­но при­ве­де­но из­бы­точ­ное чис­ло урав­не­ний; при этом Мак­свелл ис­поль­зо­вал ма­те­ма­тич. ап­па­рат ква­тер­нио­нов Га­миль­то­на. Совр. фор­му М. у. с ис­поль­зо­ва­ни­ем век­тор­но­го ис­чис­ле­ния при­да­ли Г. Р. Герц и О. Хе­ви­сайд. М. у. свя­зы­ва­ют век­тор­ные по­ле­вые ве­ли­чи­ны (яв­ляю­щие­ся функ­ция­ми ко­ор­ди­нат и вре­ме­ни) с ис­точ­ни­ка­ми элек­тро­маг­нит­но­го по­ля – рас­пре­де­лён­ны­ми в про­стран­ст­ве и из­ме­няю­щи­ми­ся во вре­ме­ни элек­трич. за­ря­да­ми и то­ка­ми. М. у. име­ют вид (диф­фе­рен­ци­аль­ная фор­ма М. у. в СИ): $$\textrm{rot}\,\boldsymbol E=-\frac{\partial \boldsymbol B}{\partial t},\quad \textrm{rot}\,\boldsymbol H=\boldsymbol j+\frac{\partial \boldsymbol D}{\partial t},\\ \textrm{div}\,\boldsymbol D=ρ,\quad \textrm{div}\,\boldsymbol B=0,$$ где $\boldsymbol E$ – на­пря­жён­ность элек­трич. по­ля, $\boldsymbol B$ – маг­нит­ная ин­дук­ция, $\boldsymbol H$ – на­пря­жён­ность маг­нит­но­го по­ля, $\boldsymbol D$ – элек­трич. ин­дук­ция, $\boldsymbol j$ – плот­ность элек­трич. то­ка, $ρ$  – объ­ём­ная плот­ность элек­трич. за­ря­да. Дей­ст­вие диф­фе­рен­ци­аль­ных опе­ра­то­ров $\textrm{rot}$ и $\textrm{div}$ на век­то­ры элек­тро­маг­нит­но­го по­ля мо­жет быть вы­ра­же­но че­рез век­тор­ное и ска­ляр­ное про­из­ве­де­ния опе­ра­то­ра Га­миль­то­на $\nabla$ (на­бла) и со­от­вет­ст­вую­ще­го по­ле­во­го век­то­ра; в де­кар­то­вой сис­те­ме ко­ор­ди­нат$$\nabla=\boldsymbol e_x\frac{\partial}{\partial x}+\boldsymbol e_y\frac{\partial}{\partial y}+\boldsymbol e_z\frac{\partial}{\partial z}$$(где $\boldsymbol e_x, \boldsymbol e_y, \boldsymbol e_z$ – еди­нич­ные век­то­ры соот­вет­ст­вую­щих ко­ор­ди­нат­ных осей), и для про­из­воль­ной век­тор­ной функ­ции $\boldsymbol f=\boldsymbol e_xf_x+\boldsymbol e_yf_y+\boldsymbol e_zf_z$ по­лу­ча­ем:$$\textrm{rot}\,\boldsymbol f=[\nabla \boldsymbol f]=\boldsymbol e_x \left( \frac{\partial f_z}{\partial y}-\frac{\partial f_y}{\partial z} \right) + \boldsymbol e_y \left( \frac{\partial f_x}{\partial z}-\frac{\partial f_z}{\partial x} \right) + \boldsymbol e_z \left( \frac{\partial f_y}{\partial x}-\frac{\partial f_x}{\partial y} \right),\\ \textrm{div}\,\boldsymbol f=\nabla \boldsymbol f=\frac{\partial f_x}{\partial x} + \frac{\partial f_y}{\partial y} + \frac{\partial f_z}{\partial z}. $$

Для то­го что­бы М. у. об­ра­зо­ва­ли ма­те­ма­ти­че­ски пол­ную сис­те­му урав­не­ний, они долж­ны быть до­пол­не­ны фи­зич. урав­не­ния­ми свя­зи ме­ж­ду по­ле­вы­ми век­то­ра­ми $\boldsymbol E$ и $\boldsymbol B$ (дос­та­точ­ны­ми для опи­са­ния элек­тро­маг­нит­но­го по­ля в ва­куу­ме) и по­ле­вы­ми век­то­ра­ми $\boldsymbol D$ и $\boldsymbol H$, за­ви­ся­щи­ми от элек­трич. и маг­нит­ных свойств ма­те­ри­аль­ной сре­ды, где рас­смат­ри­ва­ет­ся элек­тро­маг­нит­ное по­ле, а так­же урав­не­ния­ми свя­зи плот­но­сти то­ка $\boldsymbol j$, про­те­каю­ще­го в ма­те­ри­аль­ной сре­де, с элек­тро­маг­нит­ным по­лем. В об­щем слу­чае эти урав­не­ния яв­ля­ют­ся слож­ны­ми ин­те­граль­ны­ми со­от­но­ше­ния­ми, учи­ты­ваю­щи­ми, что ис­ко­мые по­ле­вые век­то­ры в дан­ной точ­ке про­стран­ст­ва и в дан­ный мо­мент вре­ме­ни мо­гут за­ви­сеть от элек­тро­маг­нит­но­го по­ля во всём про­стран­ст­ве и во все пред­ше­ст­вую­щие мо­мен­ты вре­ме­ни с учё­том за­паз­ды­ва­ния, вы­зван­но­го ко­неч­ной ско­ро­стью рас­про­стра­не­ния элек­трич.

{–7}$ Гн/м – маг­нит­ная по­сто­ян­ная, $c$ – ско­рость рас­про­стра­не­ния элек­тро­маг­нит­ных волн (ско­рость све­та) в ва­куу­ме, $ε$ – ди­элек­трич. про­ни­цае­мость, $μ$ – маг­нит­ная про­ни­цае­мость, $σ$ – элек­тро­про­вод­ность ма­те­ри­аль­ной сре­ды, $\boldsymbol j_{стор}$ – плот­ность элек­трич. то­ка (по­то­ка за­ря­жен­ных час­тиц), вы­зван­но­го не­элек­три­чес­ки­ми (сто­рон­ни­ми) при­чи­на­ми. Ма­те­ри­аль­ные ко­эф­фи­ци­ен­ты $ε$, $μ$ и $σ$ раз­ли­ча­ют­ся для раз­ных ма­те­ри­аль­ных сред и для кон­крет­ной сре­ды мо­гут быть кон­стан­та­ми или функ­ция­ми ко­ор­ди­нат и вре­ме­ни (ли­ней­ные сре­ды) или же до­пол­ни­тель­но за­ви­сеть от ве­ли­чин на­пря­жён­но­стей $\boldsymbol E$ и $\boldsymbol H$ (не­ли­ней­ные сре­ды). Для изо­троп­ных сред ма­те­ри­аль­ные ко­эф­фи­ци­ен­ты яв­ля­ют­ся ска­ля­ра­ми, для ани­зо­троп­ных (напр., кри­стал­ли­че­ских) – тен­зор­ны­ми ве­ли­чи­на­ми; для элек­тро­маг­нит­но­го по­ля в ва­куу­ме $ε=μ=1, σ=0$. Мик­ро­ско­пич. смысл ма­те­ри­аль­ных ко­эф­фи­ци­ен­тов и по­ле­вых век­то­ров $\boldsymbol D$ и $\boldsymbol H$, учи­ты­ваю­щих элек­тро­маг­нит­ные свой­ст­ва кон­крет­ной ма­те­ри­аль­ной сре­ды, вы­яв­ля­ет­ся при ус­ред­не­нии Ло­рен­ца – Мак­свел­ла урав­не­ний, рас­смат­ри­ва­ю­щих ма­те­ри­аль­ные сре­ды как со­во­куп­ность мик­ро­ско­пич. за­ря­жен­ных час­тиц.

При­ме­няя тео­ре­му Гри­на и фор­му­лу Га­ус­са – Ост­ро­град­ско­го к М. у. в диф­фе­рен­ци­аль­ной фор­ме, мож­но по­лу­чить М. у. в ин­те­граль­ной фор­ме:$$\oint\limits_L \boldsymbol E d \boldsymbol l =-\frac{d}{dt}\int\limits_S \boldsymbol Bd\boldsymbol S,\qquad (1)\\ \oint\limits_L \boldsymbol Hd\boldsymbol l=\int\limits_S \left( \boldsymbol j+\frac{\partial \boldsymbol D}{dt}\right)d\boldsymbol S,\qquad(2)\\ \oint\limits_S \boldsymbol D d \boldsymbol S=\int\limits_V ρdV,\qquad(3)\\ \oint\limits_S \boldsymbol B d \boldsymbol S=0\qquad(4)$$ В урав­не­ни­ях (1) и (2) $S$ – по­верх­ность про­из­воль­ной фор­мы, ог­ра­ни­чен­ная замк­ну­тым кон­ту­ром $L, d\boldsymbol l$ – век­тор эле­мен­тар­ной час­ти кон­ту­ра, на­прав­лен­ный по на­прав­ле­нию его об­хо­да в про­цес­се ин­тег­ри­ро­ва­ния, $d\boldsymbol S$ – век­тор эле­мен­тар­ной пло­щад­ки по­верх­но­сти $S$, чис­лен­но рав­ный пло­ща­ди пло­щад­ки и на­прав­лен­ный пер­пен­ди­ку­ляр­но по­верх­но­сти в на­прав­ле­нии, со­гла­со­ван­ном с на­прав­ле­ни­ем об­хо­да по пра­ви­лу вин­та. В урав­не­ни­ях (3) и (4) $S$ – замк­ну­тая по­верх­ность, ох­ва­ты­ваю­щая объ­ём $V, d\boldsymbol S$ – век­тор эле­мен­тар­ной пло­щад­ки, на­прав­лен­ный пер­пен­ди­ку­ляр­но по­верх­но­сти на­ру­жу от ох­ва­ты­вае­мо­го объ­ё­ма.

М. у. в ин­те­граль­ной фор­ме име­ют не­по­сред­ст­вен­ный фи­зич. смысл, пе­ре­но­си­мый и на со­от­вет­ст­вую­щие М. у. в диф­фе­рен­ци­аль­ной фор­ме. Урав­не­ние (1) обоб­ща­ет за­кон элек­тро­маг­нит­ной ин­дук­ции Фа­ра­дея, свя­зы­ваю­щий ско­рость из­ме­не­ния маг­нит­но­го по­то­ка (по­то­ка век­то­ра маг­нит­ной ин­дук­ции $\boldsymbol B$), сце­п­лен­но­го с не­ко­то­рым кон­ту­ром, с эдс ин­дук­ции, на­ве­дён­ной в этом кон­ту­ре. В от­ли­чие от опы­тов М. Фа­ра­дея, где кон­тур пред­став­лял со­бой ме­тал­лич. про­вод­ник, по ко­то­ро­му про­те­кал ре­ги­ст­ри­руе­мый ин­дук­ци­он­ный ток, Мак­свелл сфор­му­ли­ро­вал ут­вер­жде­ние, что эдс ин­дук­ции бу­дет так­же воз­ни­кать и при из­ме­не­нии маг­нит­но­го по­то­ка в ва­куу­ме или иной не­про­во­дя­щей сре­де. Т. о., со­глас­но урав­не­нию (1), из­ме­не­ние маг­нит­но­го по­ля во вре­ме­ни вы­зы­ва­ет воз­ник­но­ве­ние элек­трич. по­ля (так­же из­ме­няю­ще­го­ся во вре­ме­ни).

Урав­не­ние (2) яв­ля­ет­ся обоб­ще­ни­ем Био – Са­ва­ра за­ко­на о воз­бу­ж­де­нии маг­нит­но­го по­ля элек­трич. то­ком. Ана­ли­зи­руя про­хо­ж­де­ние пе­ре­мен­но­го то­ка по це­пи с кон­ден­са­то­ром, Мак­свелл пред­по­ло­жил, что для замк­ну­то­сти элек­трич. то­ка, кро­ме то­ка про­во­ди­мо­сти, обу­слов­лен­но­го дви­же­ни­ем за­ря­дов по про­вод­ни­ку, дол­жен су­ще­ст­во­вать до­пол­нит. ток (на­зван­ный им то­ком сме­ще­ния), плот­ность ко­то­ро­го рав­на $𝜕\boldsymbol D/𝜕t$ и ко­то­рый так­же дол­жен соз­да­вать маг­нит­ное по­ле. Эк­ви­ва­лент­ность маг­нит­но­го дей­ст­вия то­ка про­во­ди­мо­сти и то­ка сме­ще­ния бы­ла ус­та­нов­ле­на экс­пе­римен­таль­но А. А. Эй­хен­валь­дом в 1904 (см. Эй­хен­валь­да опыт). Т. о., со­глас­но урав­не­нию (2), маг­нит­ное по­ле воз­ни­ка­ет не толь­ко в слу­чае про­те­ка­ния элек­трич. то­ка, но и при из­ме­не­нии элек­трич. по­ля во вре­ме­ни; при этом воз­ни­каю­щее маг­нит­ное по­ле так­же из­ме­ня­ет­ся во вре­ме­ни.

Урав­не­ние (3) (Га­ус­са тео­ре­ма) вы­во­дит­ся с по­мо­щью Ку­ло­на за­ко­на (спра­вед­ли­во­го толь­ко для не­под­виж­ных за­ря­дов) и яв­ля­ет­ся его обоб­ще­ни­ем. Фи­зич. смысл урав­не­ния (3) – ис­точ­ни­ком элек­трич. по­ля яв­ля­ют­ся элек­трич. за­ря­ды [на­ря­ду с пе­ре­менным маг­нит­ным по­лем, см. урав­нение (1)]. Урав­не­ние (4) ана­ло­гич­но урав­не­нию (3) и яв­ля­ет­ся ма­те­ма­тич. вы­ра­же­ни­ем экс­пе­ри­мен­таль­но обос­но­вы­вае­мо­го ут­вер­жде­ния, что ис­точ­ни­ком маг­нит­но­го по­ля мо­гут быть толь­ко элек­трич. то­ки (про­во­ди­мо­сти и сме­ще­ния), а маг­нит­ные за­ря­ды (ана­ло­гич­ные элек­трич. за­ря­дам – ис­точ­ни­кам по­лей в тео­ре­ме Га­ус­са) в при­ро­де от­сут­ст­ву­ют. Пред­ска­за­ния не­ко­то­рых фи­зич. тео­рий о су­ще­ст­во­ва­нии отд. маг­нит­ных за­ря­дов (маг­нит­ных мо­но­по­лей) по­ка не по­лу­чи­ли экс­пе­рим. под­твер­ж­де­ния.

Как сле­ду­ет из фи­зич. смыс­ла урав­не­ний (1) и (2), пе­ре­мен­ное маг­нит­ное по­ле вы­зы­ва­ет воз­ник­но­ве­ние пе­ре­мен­но­го элек­трич. по­ля, а пе­ре­мен­ное элек­трич. по­ле – воз­ник­но­ве­ние пе­ре­мен­но­го маг­нит­но­го по­ля и, т. о., пе­ре­мен­ные элек­трич. и маг­нит­ные по­ля мо­гут под­дер­жи­вать друг дру­га, об­ра­зуя са­мо­сто­ятель­ный фи­зич. объ­ект – элек­тро­маг­нит­ную вол­ну, су­ще­ст­вую­щую уже не­за­ви­си­мо от пер­вич­ных ис­точ­ни­ков элек­трич. и маг­нит­но­го по­лей. Дж. К. Мак­свелл впер­вые по­лу­чил из М. у. вол­но­вое урав­не­ние для элек­тро­маг­нит­ной вол­ны и ус­та­но­вил, что элек­тро­маг­нит­ная вол­на рас­про­стра­ня­ет­ся в ва­куу­ме со ско­ро­стью, ко­то­рая сов­па­да­ет по ве­ли­чи­не с элек­тро­ди­на­мич. по­сто­ян­ной, вхо­дя­щей в ис­поль­зо­ван­ную Мак­свел­лом аб­со­лют­ную га­ус­со­ву сис­те­му еди­ниц. В. Э. Ве­бер и нем. фи­зик Р. Коль­ра­уш в 1856 ус­та­но­ви­ли, что элек­тро­ди­на­мич. по­сто­ян­ная рав­на ско­ро­сти све­та в ва­куу­ме; это по­зволи­ло Мак­свел­лу пред­по­ло­жить, что свет пред­став­ля­ет со­бой элек­тро­маг­нит­ные вол­ны. Это пред­по­ло­же­ние на­шло своё под­твер­жде­ние в даль­ней­шем раз­ви­тии уче­ния о све­те.

С по­мо­щью М. у. бы­ло ус­та­нов­ле­но, что элек­тро­маг­нит­ное по­ле об­ла­да­ет энер­ги­ей и им­пуль­сом. На­ли­чие им­пуль­са у элек­тро­маг­нит­ной вол­ны и, сле­до­ва­тель­но, его из­ме­не­ние при по­гло­ще­нии или от­ра­же­нии при­во­дит к воз­ник­но­ве­нию дав­ле­ния элек­тро­маг­нит­ной вол­ны на по­гло­щаю­щую или от­ра­жаю­щую по­верх­ность. Тео­ре­ти­че­ски пред­ска­зан­ное и ко­ли­че­ст­вен­но рас­счи­тан­ное Дж. К. Мак­свел­лом дав­ле­ние све­та впер­вые бы­ло экс­пе­ри­мен­таль­но об­на­ру­же­но и из­ме­ре­но П. Н. Ле­бе­де­вым в 1899. Ре­зуль­та­ты экс­пе­ри­мен­тов Ле­бе­де­ва, как и по­сле­дую­щие экс­пе­рим. ис­сле­до­ва­ния све­то­во­го дав­ле­ния, пол­но­стью под­твер­ди­ли ги­по­те­зу Мак­свел­ла об элек­тро­маг­нит­ном ха­рак­те­ре све­то­вых волн.

Осн. ха­рак­те­ри­сти­кой, опи­сы­ваю­щей про­цесс рас­про­стра­не­ния энер­гии и им­пуль­са элек­тро­маг­нит­но­го по­ля в про­стран­ст­ве, яв­ля­ет­ся Пойн­тин­га век­тор $\it {\mathbf Π}=[\boldsymbol E \boldsymbol H]$, на­прав­ле­ние ко­то­ро­го сов­па­да­ет с на­прав­ле­ни­ем им­пуль­са элек­тро­маг­нит­но­го по­ля и на­прав­ле­ни­ем рас­про­стра­не­ния его энер­гии, а ве­ли­чи­на рав­на плот­но­сти по­то­ка мощ­но­сти элек­тро­маг­нит­но­го по­ля – энер­гии, пе­ре­но­си­мой в еди­ни­цу вре­ме­ни че­рез еди­нич­ную пло­щад­ку, пер­пен­ди­ку­ляр­ную век­то­ру $\bf Π$ (или на­прав­ле­нию рас­про­стра­не­ния энер­гии).

Элек­тро­ди­на­ми­ка Мак­свел­ла ока­за­лась ис­то­ри­че­ски пер­вой ре­ля­ти­ви­ст­ской тео­ри­ей. Имен­но ана­лиз М. у. и ис­сле­до­ва­ние ме­то­дов их при­ме­не­ния к дви­жу­щим­ся сре­дам при­ве­ли к не­об­хо­ди­мо­сти пе­ре­строй­ки клас­сич. фи­зич. пред­став­ле­ний о про­стран­ст­ве и вре­ме­ни и соз­да­нию ча­ст­ной (спе­ци­аль­ной) тео­рии от­но­си­тель­но­сти. Ре­ля­ти­ви­ст­ский ха­рак­тер М. у. по­зво­ля­ет за­пи­сать их в ре­ля­ти­вист­ски ко­ва­ри­ант­ной (оди­на­ко­вой во всех инер­ци­аль­ных сис­те­мах от­счё­та) тен­зор­ной фор­ме, от­ку­да мо­гут быть по­лу­че­ны фор­му­лы пре­об­ра­зо­ва­ния по­ле­вых век­то­ров $\boldsymbol E, \boldsymbol B, \boldsymbol D$ и $\boldsymbol H$, а так­же $\boldsymbol j$ и $ρ$ при пе­ре­хо­де от од­ной инер­ци­аль­ной сис­те­мы от­счё­та к дру­гой.

М. у. по­слу­жи­ли тео­ре­тич. ос­но­вой для соз­да­ния и раз­ви­тия тех­ни­ки ра­дио­свя­зи и те­ле­ви­де­ния, элек­тро­тех­ни­ки, элек­тро­ни­ки и др. на­прав­ле­ний совр. нау­ки и тех­ни­ки.

1,2,3,4 уравнения Максвелла для электромагнитного поля, смысл, суть, решение

Уравнения Максвелла в электродинамике – это как законы Ньютона в классической механике или как постулаты Эйнштейна в теории относительности. Фундаментальные уравнения, в сущности которых мы сегодня будем разбираться, чтобы не впадать в ступор от одного их упоминания.

Полезная и интересная информация по другим темам – у нас в телеграм.

Уравнения Максвелла – это система уравнений в дифференциальной или интегральной форме, описывающая любые электромагнитные поля, связь между токами и электрическими зарядами в любых средах.

Уравнения Максвелла неохотно принимались и критически воспринимались учеными-современниками Максвелла. Все потому, что эти уравнения не были похожи ни на что из известного людям ранее.

Тем не менее, и по сей день нет никаких сомнений в правильности уравнений Максвелла, они «работают» не только в привычном нам макромире, но и в области квантовой механики.

Уравнения Максвелла совершили настоящий переворот в восприятии людьми научной картины мира. Так, они предвосхитили открытие радиоволн и показали, что свет имеет электромагнитную природу.

 

Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы. 

По порядку запишем и поясним все 4 уравнения. Сразу уточним, что записывать их будем в системе СИ.

Первое уравнение Максвелла

Современный вид первого уравнения Максвелла таков:

Тут нужно пояснить, что такое дивергенция. Дивергенция – это дифференциальный оператор, определяющий поток какого-то поля через определенную поверхность. Уместным будет сравнение с краном или с трубой. Например, чем больше диаметр носика крана и напор в трубе, тем большим будет поток воды через поверхность, которую представляет собой носик.

В первом уравнении Максвелла E – это векторное электрическое поле, а греческая буква «ро» – суммарный заряд, заключенный внутри замкнутой поверхности.

Так вот, поток электрического поля E через любую замкнутую поверхность зависит от суммарного заряда внутри этой поверхности. Данное уравнение представляет собой закон (теорему) Гаусса.

Третье уравнение Максвелла

Сейчас мы пропустим второе уравнение, так как третье уравнение Максвелла – это тоже закон Гаусса, только уже не для электрического поля, но для магнитного.

Оно имеет вид:

Что это значит? Поток магнитного поля через замкнутую поверхность равен нулю. Если электрические заряды (положительные и отрицательные) вполне могут существовать по отдельности, порождая вокруг себя электрическое поле, то магнитных зарядов в природе просто не существует.

Второе уравнение Максвелла

Второе уравнение Максвелла представляет собой ни что иное, как закон Фарадея. Его вид:

Ротор электрического поля (интеграл через замкнутую поверхность) равен скорости изменения магнитного потока, пронизывающего эту поверхность. Чтобы лучше понять, возьмем воду в ванной, которая сливается через отверстие. Вокруг отверстия образуется воронка. Ротор – это сумма (интеграл) векторов скоростей частиц воды, которые вращаются вокруг отверстия.

Как Вы помните, на основе закона Фарадея работают электродвигатели: вращающийся магнит порождает ток в катушке.

Четвертое уравнение Максвелла

Четвертое — самое важное из всех уравнений Максвелла. Именно в нем ученый ввел понятие тока смещения.

Это уравнение еще называется теоремой о циркуляции вектора магнитной индукции. Оно говорит нам о том, что электрический ток и изменение электрического поля порождают вихревое магнитное поле.

Приведем теперь всю систему уравнений и кратко обозначим суть каждого из них:

Первое уравнение: электрический заряд порождает электрическое поле

Второе уравнение: изменяющееся магнитное поле порождает вихревое электрическое поле

Третье уравнение: магнитных зарядов не существует

Четвертое уравнение: электрический ток и изменение электрической индукции порождают вихревое магнитное поле

Решая уравнения Максвелла для свободной электромагнитной волны, мы получим следующую картину ее распространения в пространстве:

Надеемся, эта статья поможет систематизировать знания об уравнениях Максвелла. А если понадобиться решить задачу по электродинамике с применением этих уравнений, можете смело обратиться за помощью в студенческий сервис. Подробное объяснение любого задания и отличная оценка гарантированы.

Электричество и магнетизм

Четыре уравнения, соответствующие нашим (модифицированным) утверждениям, называются уравнениями Максвелла в интегральной форме.

Выпишем их все рядом еще раз:

 

Чтобы получить уравнения Максвелла в среде, надо произвести замену:

,

то есть указать связь (так называемые «материальные» уравнения) между напряженностями и индукциями:  и  и дополнить систему уравнением закона Ома

.

Отметим, что приведенными выше простейшими соотношениями можно пользоваться не всегда. Ситуация заметно сложнее в присутствии таких веществ как сегнетоэлектрики, пьезоэлектрики, ферромагнетики, вещества анизотропные и тому подобное. Здесь наша цель показать, как формируется полная система уравнений, позволяющая (с учетом начальных и граничных условий, разумеется) рассчитать электромагнитное поле. 

От уравнений в интегральной форме можно с помощью теорем векторного анализа перейти к уравнениям в дифференциальной форме, связывающим значения полей  и  и их пространственных и временных производных со значениями плотностей заряда и тока. Этими уравнениями мы пользоваться не будем, но все же приведем их хотя бы как часть шутки, опубликованной в одном из журналов в дни юбилея Максвелла: 

«И сказал Бог:

И стал свет». 

Непонятные значки div (читается «дивергенция») и rot (читается «ротор») — это особые операции дифференцирования, выполняемые над векторными полями. Дивергенция — по латыни «расхождение». Эта операция описывает конфигурацию силовых линий типа «ежа», расходящихся из точек, где имеются электрические заряды. Слово «ротор» в переводе не нуждается, оно явно ассоциируется с вращением. Эта операция описывает вихревые поля (кольцеобразные — замкнутые силовые линии) вокруг их источников — токов или других полей, меняющихся во времени. 

Четыре интегральных уравнения и четыре дифференциальных эквивалентны. Максвелл показал, что все явления электромагнетизма можно полностью описать этими четырьмя уравнениями, являющимися обобщением экспериментальных фактов.

В приведенной шутке упоминался свет. Действительно, свет — это электромагнитное излучение определенного диапазона частот. Предсказание электромагнитных волн стало одним из величайших достижений теории Максвелла. Представим себе, что заряды и токи отсутствуют. Посмотрим на уравнения Максвелла в дифференциальной форме. Видно, что если поля не статические, но зависят от времени, то имеется вихревое электрическое и магнитные поля (соответствующие роторы отличны от нуля). Распространение полей без зарядов и токов — это и есть электромагнитные волны. И можно углядеть в уравнениях намек на скорость их распространения: туда входит комбинация e₀m₀, через которую может быть выражена скорость света в вакууме (см. (6.3))

Но об этом — позже, в следующей части нашего курса. 

В заключение же этой части процитируем слова Г. Герца об уравнениях Максвелла:

«Трудно избавиться от чувства, что эти математические формулы живут независимой жизнью и обладают своим собственным интеллектом, что они мудрее, чем мы сами, мудрее даже, чем их первооткрыватели, и что мы извлекаем из них больше, чем было заложено в них первоначально».

Уравнения Максвелла для электромагнитного поля

В линиях электропередач, электротехнических и электронных устройствах имеют место целые системы заряженных частиц, тел и контуров с токами, взаимодействующих друг с другом. В результате этих взаимодействий возникают электромагнитные явления, которые зависят не только от процессов в заряженных частицах, телах и контурах с токами, но и окружающей среды, в которой распространяется электромагнитное поле. Электрическое поле принято характеризовать вектором электрической напряжённости- Е, а магнитное поле вектором магнитной напряжённости – H.

В макроскопическом понимании (т.е. в целом) процессы в электромагнитных полях описывают уравнениями Максвелла, которые основаны на обобщении законов Ампера, Фарадея и Гаусса. Уравнения Максвелла, в интегральной форме, приведены ниже, в таблице 1.1.

Энергия, носителем которой выступает электромагнитное поле:

где  ε_а = εε₀, μ_а = μμ₀ — абсолютные электрическая и магнитная проницаемости среды, в которой находится электромагнитное поле ;  ε = ε_а / ε₀, μ = μ_а / μ₀ — значения относительной электрической и магнитной проницаемости ;  ε₀ = 8,854·10^-12 Ф/м, μ₀ = 1,257·10^-6 Гн/м — электрическая и магнитная проницаемость вакуума. В соответствующих физических таблицах, в зависимости от редакции, могут приводиться как относительные, так и абсолютные значения вышеупомянутых величин.

В вакууме, электромагнитные волны перемещаются со скоростью с = (ε₀μ₀)^-1/2 =2,999·10⁸ м/с, а в среде  со скоростью υ = с(ε·μ)^-1/2. Отношение скоростей распространения электромагнитных волн в вакууме и среде    n = c/υ=(ε·μ)^1/2 принято называть показателем преломления среды.

В уравнениях Максвелла, электромагнитные свойства среды, в общем случае, учитывают из опыта значениями удельной объёмной проводимости γ, электрической ε и магнитной μ проницаемостей в соответствии с уравнениями: δ_пр = γЕ, D = εE,  B = μH.

Где;  δ_пр — плотность электрического тока проводимости;

D – вектор индукции электрического поля;

B – вектор индукции магнитного поля.

До настоящего времени (с 1873г.) не было ни одного факта ставящего под сомнения уравнения Максвелла, хотя среди некоторых физиков и существует мнение об их некорректности. Применяют уравнения Максвелла не только для описания явлений электромагнитного поля.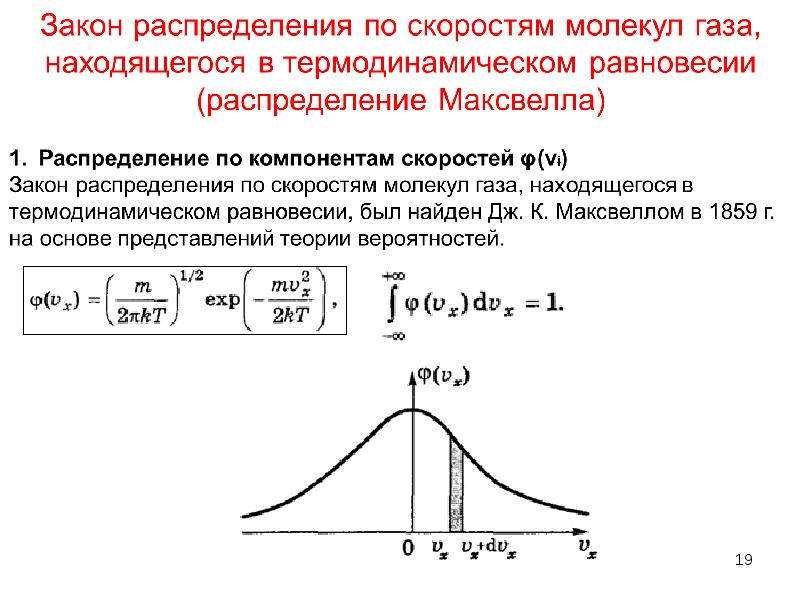 Они вошли и в квантовую механику, положив начало квантовой электродинамике, а также были одной из отправных точек при создании общей теории относительности Альберта Эйнштейна (отчасти от них попала в формулы теории относительности скорость света).

Уравнения Максвелла

Уравнения Максвелла — это набор из 4 сложных уравнений, описывающих мир электромагнетизма. Эти уравнения описывают, как электрические и магнитные поля распространяются, взаимодействуют и как на них влияют. по объектам.

Джеймс Клерк Максвелл [1831-1879] был гением уровня Эйнштейна / Ньютона, который взял набор известных экспериментальных законов (закон Фарадея, закон Ампера) и объединил их в симметричный согласованный набор уравнений, известных как Уравнения Максвелла.Максвелл одним из первых определил скорость распространения электромагнитных волн. (ЭМ) волны были такими же, как скорость света — и, следовательно, можно заключить, что ЭМ-волны и видимые свет были действительно то же самое.

Уравнения Максвелла имеют решающее значение для понимания антенн и Электромагнетизм. На них сложно смотреть — настолько сложно, что большинство инженеров-электриков и физиков даже толком не понимаю, что они означают. Окутанные сложной математикой (которая, вероятно, позволяет «интеллектуальным» людям чувствовать свое превосходство при их обсуждении) трудно прийти к истинному пониманию этих уравнений.

Это приводит к созданию этого веб-сайта — интуитивно понятному руководству по уравнениям Максвелла. Я буду избегать, если в все возможные математические трудности, которые возникают, и вместо этого опишите, что означают уравнения. А также не бойтесь — математика настолько сложна, что те, кто понимает сложное векторное исчисление, все еще не могут применять уравнения Максвелла в чем угодно, кроме простейших сценариев. По этой причине интуитивное знание Уравнения Максвелла намного превосходят знания, основанные на математических манипуляциях.Чтобы понять мир, вы должны понимать, что означают уравнения, а не просто знать математические конструкции. Я считаю принятым методы обучения электромагнетизму и уравнения Максвелла не дают понимания. И с этим, скажем что-нибудь об этих уравнениях.

Уравнения Максвелла — это законы, подобные закону всемирного тяготения. Эти уравнения — правила, которые использует вселенная. управлять поведением электрических и магнитных полей. Поток электрического тока произведет магнитное поле.Если текущий поток меняется со временем (как в случае любой волны или периодического сигнала), магнитное поле также вызовет электрическое поле. Уравнения Максвелла показывают, что разделенный заряд (положительный и отрицательный) вызывает электрическое поле — и если оно меняется со временем также вызовет распространяющееся электрическое поле, что в дальнейшем приведет к распространению магнитное поле.

Чтобы понять уравнения Максвелла на более интуитивном уровне, чем у большинства докторов технических наук или физики, щелкните по ссылкам и определениям выше.Вы обнаружите, что сложные математические маски внутренняя элегантность этих уравнений — и вы узнаете, как Вселенная управляет электромагнитным Машина.

Вот обучающее видео, интуитивно объясняющее уравнения Максвелла:

Вверху: уравнения Максвелла

уравнения Максвелла | Блестящая вики по математике и науке

Закон Лоренца, где qqq и v \ mathbf {v} v — электрический заряд и скорость частицы соответственно, определяет электрическое поле E \ mathbf {E} E и магнитное поле B \ mathbf {B} B, задавая общая электромагнитная сила F \ mathbf {F} F как

F = qE + qv × B.\ mathbf {F} = q \ mathbf {E} + q \ mathbf {v} \ times \ mathbf {B}. F = qE + qv × B.

По сути, одна часть электромагнитной силы, возникающая при взаимодействии с движущимся зарядом (qv q \ mathbf {v} qv), рассматривается как магнитное поле, а другая часть — как электрическое поле.

Закон Гаусса: Самым ранним из четырех уравнений Максвелла, которые были открыты (в эквивалентной форме закона Кулона), был закон Гаусса. В своей интегральной форме в единицах СИ он заявляет, что полный заряд, содержащийся внутри замкнутой поверхности, пропорционален общему электрическому потоку (сумме нормальной составляющей поля) через поверхность:

∫SE⋅da = 1ϵ0∫ρ dV, \ int_S \ mathbf {E} \ cdot d \ mathbf {a} = \ frac {1} {\ epsilon_0} \ int \ rho \, dV, ∫S E⋅da = ϵ0 1 ρdV,

, где коэффициент пропорциональности равен 1 / ϵ0, 1 / \ epsilon_0, 1 / ϵ0, обратной величине электрической постоянной.Полный заряд выражается как плотность заряда ρ \ rho ρ, проинтегрированная по области.

Закон Гаусса для магнетизма: Хотя магнитные диполи могут создавать аналогичный магнитный поток, который имеет аналогичную математическую форму, не существует эквивалентных магнитных монополей, и поэтому общий «магнитный заряд» во всем пространстве должен в сумме равняться нулю. Следовательно, закон Гаусса для магнетизма читается просто

.

∫SB⋅da = 0. \ int_S \ mathbf {B} \ cdot d \ mathbf {a} = 0. ∫S B⋅da = 0.

Закон Фарадея: Электрическое и магнитное поля переплетаются, когда поля претерпевают временную эволюцию.В 1820-х годах Фарадей обнаружил, что изменение магнитного потока создает электрическое поле по замкнутому контуру. Это соотношение теперь называется законом Фарадея:

∫loopE⋅ds = −ddt∫SB⋅da. \ int_ \ text {loop} \ mathbf {E} \ cdot d \ mathbf {s} = — \ frac {d} {dt} \ int_S \ mathbf {B} \ cdot d \ mathbf {a}. ∫loop E⋅ds = −dtd ∫S B⋅da.

При ориентации петли, определенной в соответствии с правилом правой руки, отрицательный знак отражает закон Ленца.

Закон Ампера: Наконец, закон Ампера предполагает, что постоянный ток через поверхность приводит к возникновению магнитного поля (выраженного в единицах потока).Вдобавок Максвелл определил, что быстрые изменения электрического потока (d / dt) E⋅da (d / dt) \ mathbf {E} \ cdot d \ mathbf {a} (d / dt) E⋅da также могут приводить к к изменениям магнитного потока. В целом закон Ампера с поправкой Максвелла утверждает, что

∫loopB⋅ds = μ0∫SJ⋅da + μ0ϵ0ddt∫SE⋅da. \ int _ {\ text {loop}} \ mathbf {B} \ cdot d \ mathbf {s} = \ mu_0 \ int_S \ mathbf {J} \ cdot d \ mathbf {a} + \ mu_0 \ epsilon_0 \ frac {d} {dt} \ int_S \ mathbf {E} \ cdot d \ mathbf {a}. ∫loop B⋅ds = μ0 ∫S J⋅da + μ0 ϵ0 dtd ∫S E⋅da.

Таким образом,

• Закон Гаусса: ∫SE⋅da = 1ϵ0∫ρ dV \ int_S \ mathbf {E} \ cdot d \ mathbf {a} = \ frac {1} {\ epsilon_0} \ int \ rho \, dV ∫ S E⋅da = ϵ0 1 ρdV
• Закон Гаусса для магнетизма: ∫SB⋅da = 0 \ int_S \ mathbf {B} \ cdot d \ mathbf {a} = 0 ∫S B⋅da = 0
• Закон Фарадея: ∫loopE⋅ds = −ddt∫SB⋅da \ int_ \ text {loop} \ mathbf {E} \ cdot d \ mathbf {s} = — \ frac {d} {dt} \ int_S \ mathbf {B} \ cdot d \ mathbf {a} ∫loop E⋅ds = −dtd ∫S B⋅da
• Закон Ампера: ∫loopB⋅ds = μ0∫SJ⋅da + ϵ0μ0ddt∫SE⋅da.\ int _ {\ text {loop}} \ mathbf {B} \ cdot d \ mathbf {s} = \ mu_0 \ int_S \ mathbf {J} \ cdot d \ mathbf {a} + \ epsilon_0 \ mu_0 \ frac {d} {dt} \ int_S \ mathbf {E} \ cdot d \ mathbf {a}. ∫loop B⋅ds = μ0 ∫S J⋅da + ϵ0 μ0 dtd ∫S E⋅da.

В своей интегральной форме уравнения Максвелла могут использоваться для определения области заряда или тока.

Уравнения Максвелла: предсказание и наблюдение электромагнитных волн

Цель обучения

К концу этого раздела вы сможете:

• Переформулируйте уравнения Максвелла.

Рис. 1. Джеймс Клерк Максвелл, физик 19-го века, разработал теорию, объясняющую взаимосвязь между электричеством и магнетизмом, и правильно предсказал, что видимый свет вызывается электромагнитными волнами. (кредит: Г. Дж. Стодарт)

Шотландец Джеймс Клерк Максвелл (1831–1879) считается величайшим физиком-теоретиком XIX века. (См. Рис. 1.) Хотя он умер молодым, Максвелл не только сформулировал полную электромагнитную теорию, представленную уравнениями Максвелла , он также разработал кинетическую теорию газов и внес значительный вклад в понимание цветового зрения и природы Сатурна. кольца.

Максвелл объединил всю работу, проделанную блестящими физиками, такими как Эрстед, Кулон, Гаусс и Фарадей, и добавил свои собственные идеи для разработки всеобъемлющей теории электромагнетизма. Уравнения Максвелла здесь перефразированы словами, потому что их математическая формулировка выходит за рамки этого текста. Однако уравнения показывают, как простые математические утверждения могут элегантно объединять и выражать множество концепций — почему математика является языком науки.

Уравнения Максвелла

1. Линии электрического поля берут начало от положительных зарядов и заканчиваются отрицательными зарядами. Электрическое поле определяется как сила, приходящаяся на единицу заряда испытательного заряда, а сила силы связана с электрической постоянной ε ₀ , также известной как диэлектрическая проницаемость свободного пространства. Из первого уравнения Максвелла мы получаем особую форму закона Кулона, известную как закон Гаусса для электричества.
2. Линии магнитного поля непрерывны, не имеют ни начала, ни конца.О существовании магнитных монополей не известно. Сила магнитной силы связана с магнитной постоянной μ ₀ , также известной как проницаемость свободного пространства. Это второе из уравнений Максвелла известно как закон Гаусса для магнетизма.
3. Изменяющееся магнитное поле индуцирует электродвижущую силу (ЭДС) и, следовательно, электрическое поле. Направление ЭДС противодействует изменению. Эта треть уравнений Максвелла является законом индукции Фарадея и включает в себя закон Ленца.
4. Магнитные поля создаются движущимися зарядами или изменяющимися электрическими полями. Эта четвертая часть уравнений Максвелла включает закон Ампера и добавляет еще один источник магнетизма — изменение электрических полей.

Уравнения Максвелла охватывают основные законы электричества и магнетизма. Что не так очевидно, так это симметрия, которую Максвелл ввел в свою математическую структуру. Особенно важно его добавление к гипотезе о том, что изменяющиеся электрические поля создают магнитные поля.Это в точности аналогично (и симметрично) закону индукции Фарадея и подозревалось в течение некоторого времени, но прекрасно вписывается в уравнения Максвелла.

Симметрия проявляется в самых разных ситуациях. В современных исследованиях симметрия играет важную роль в поиске субатомных частиц с использованием массивных многонациональных ускорителей частиц, таких как новый Большой адронный коллайдер в ЦЕРНе.

Налаживание связей: объединение сил

Полная и симметричная теория Максвелла показала, что электрические и магнитные силы не отдельные, а разные проявления одного и того же — электромагнитной силы.Это классическое объединение сил является одной из причин нынешних попыток объединить четыре основные силы в природе — гравитационное, электрическое, сильное и слабое ядерные взаимодействия.

Поскольку изменяющиеся электрические поля создают относительно слабые магнитные поля, их было нелегко обнаружить во время гипотезы Максвелла. Однако Максвелл понял, что колеблющиеся заряды, как в цепях переменного тока, создают изменяющиеся электрические поля. Он предсказал, что эти изменяющиеся поля будут распространяться от источника, как волны, создаваемые прыгающей рыбой в озере.

Волны, предсказанные Максвеллом, будут состоять из колеблющихся электрических и магнитных полей, определяемых как электромагнитная волна (электромагнитная волна). Электромагнитные волны будут способны воздействовать на заряды на большом расстоянии от их источника, и, таким образом, их можно будет обнаружить. Максвелл рассчитал, что электромагнитные волны распространяются со скоростью, задаваемой уравнением

.

[латекс] \ displaystyle {c} = \ frac {1} {\ sqrt {\ mu_ {0} \ epsilon_0}} \\ [/ latex]

Когда значения для μ ₀ и ε ₀ вводятся в уравнение для c , мы находим, что

[латекс] \ displaystyle {c} = \ frac {1} {\ sqrt {\ left (8.8 \ text {m / s} \\ [/ latex]

— скорость света. Фактически, Максвелл пришел к выводу, что свет — это электромагнитная волна с такой длиной волны, что ее можно обнаружить глазом.

Должны существовать другие длины волн — еще неизвестно, существуют ли они. Если так, теория Максвелла и его замечательные предсказания подтвердятся, что станет величайшим триумфом физики со времен Ньютона. Экспериментальная проверка произошла через несколько лет, но не раньше смерти Максвелла.

Наблюдения Герца

Немецкий физик Генрих Герц (1857–1894) был первым, кто генерировал и обнаруживал определенные типы электромагнитных волн в лаборатории.Начиная с 1887 года, он провел серию экспериментов, которые не только подтвердили существование электромагнитных волн, но и подтвердили, что они движутся со скоростью света.

Герц использовал схему AC RLC (резистор-индуктор-конденсатор), которая резонирует на известной частоте [латекс] f_0 = \ frac {1} {2 \ pi \ sqrt {LC}} \ [/ латекс] и подключена его к проволочной петле, как показано на рисунке 2. Высокое напряжение, индуцированное через зазор в петле, вызывало искры, которые были видимым свидетельством наличия тока в цепи и помогали генерировать электромагнитные волны.

Через лабораторию Герц подключил еще один контур к другому контуру RLC , который можно было настроить (как циферблат на радио) на ту же резонансную частоту, что и первый, и, таким образом, можно было заставить принимать электромагнитные волны. В этой петле также был зазор, в котором возникали искры, что давало твердое свидетельство приема электромагнитных волн.

Рис. 2. Устройство, которое Герц использовал в 1887 году для генерации и обнаружения электромагнитных волн. Схема RLC , подключенная к первому контуру, вызвала искры через разрыв в проводном контуре и генерировала электромагнитные волны.Искры в щели во второй петле, расположенной напротив лаборатории, свидетельствовали о том, что волны были приняты.

Герц также изучил картины отражения, преломления и интерференции генерируемых им электромагнитных волн, проверяя их волновой характер. Он смог определить длину волны из интерференционных картин и, зная их частоту, он мог вычислить скорость распространения, используя уравнение v = fλ (скорость — или скорость — равна частоте, умноженной на длину волны).Таким образом, Герц смог доказать, что электромагнитные волны распространяются со скоростью света. Единица измерения частоты в системе СИ, герц (1 Гц = 1 цикл / сек), названа в его честь.

Сводка раздела

• Электромагнитные волны состоят из колеблющихся электрических и магнитных полей и распространяются со скоростью света c . Их предсказал Максвелл, который также показал, что
  [латекс] \ displaystyle {c} = \ frac {1} {\ sqrt {{\ mu} _ {0} {\ epsilon} _ {0}}} \\ [ / латекс],
  , где μ ₀ — проницаемость свободного пространства, а ε ₀ — диэлектрическая проницаемость свободного пространства.
• Предсказание Максвелла об электромагнитных волнах стало результатом его формулировки полной и симметричной теории электричества и магнетизма, известной как уравнения Максвелла.
• Эти четыре уравнения перефразированы в этом тексте, а не представлены в числовом виде, и охватывают основные законы электричества и магнетизма. Первый — это закон Гаусса для электричества, второй — закон Гаусса для магнетизма, третий — закон индукции Фарадея, включая закон Ленца, и четвертый — закон Ампера в симметричной формулировке, который добавляет еще один источник магнетизма — изменение электрических полей.

Задачи и упражнения

1. Убедитесь, что правильное значение скорости света c получается, когда числовые значения проницаемости и диэлектрической проницаемости свободного пространства (μ ₀ и ε ₀ ) вводятся в уравнение [латекс] c = \ гидроразрыв {1} {\ sqrt {{\ mu} _ {0} {\ epsilon} _ {0}}} \\ [/ latex].
2. Покажите, что, когда вводятся единицы СИ для μ ₀ и ε ₀ , единицы, заданные правой частью уравнения в приведенной выше задаче, равны м / с.

Глоссарий

волны электромагнитные: излучение в виде волн электрической и магнитной энергии

Уравнения Максвелла: Набор из четырех уравнений, составляющих полную, всеобъемлющую теорию электромагнетизма

Цепь RLC: электрическая цепь, которая включает резистор, конденсатор и катушку индуктивности

герц: единица СИ, обозначающая частоту электромагнитной волны в циклах в секунду

скорость света: в вакууме, например в космосе, скорость света постоянна 3 × 10 ⁸ м / с

электродвижущая сила (ЭДС): энергия, вырабатываемая на единицу заряда, полученная из источника, производящего электрический ток

Линии электрического поля: шаблон воображаемых линий, которые проходят между источником электрического тока и заряженными объектами в окружающей области, со стрелками, направленными от положительно заряженных объектов к отрицательно заряженным объектам.Чем больше линий в узоре, тем сильнее электрическое поле в этой области

линии магнитного поля: узор из непрерывных воображаемых линий, которые выходят из противоположных магнитных полюсов и входят в них. Плотность линий указывает величину магнитного поля

уравнений Максвелла и свет

уравнения Максвелла и свет

Уравнения Максвелла и свет

Мы завершили изучение законов электричества и магнетизма.Все, что мы узнали можно суммировать в уравнениях, известных как уравнения Максвелла , вместе с формулами для электрических и магнитных сил на заряде. Один из нескольких способов преобразования уравнений Максвелла: написано отображается справа, чтобы вы могли сказать, что видели их. Первое уравнение — это закон Ампера (включая член в правой части, который мы не обсуждали в этом курсе). Второе уравнение — это закон Фарадея в сочетании с законом Ленца. Третье уравнение — это закон Гаусса, который выражает тот факт, что силовые линии электрического поля начинаются и заканчиваются только за плату.Четвертое уравнение является магнитным эквивалентом закона Гаусса, который выражает тот факт, что магнитные силовые линии никогда не начинаются и не заканчиваются (т. е. отсутствуют свободные магнитные заряды).

Используя некоторые не очень простые вычисления, уравнения Максвелла могут быть используется, чтобы показать, что электрическое и магнитное поля подчиняются волновым уравнениям. В скорость c электромагнитной волны определяется константами электричество и магнетизм, которые вы так хорошо знаете:
& nbsp c = 1 / ( e ₀ м ₀ ) ^1/2 = 2.998 X 10 ⁸ м / с .

Свет — это электромагнитная волна: это понял Максвелл примерно в 1864 году, как только уравнение c = 1 / (e ₀ м ₀ ) ^1/2 = 2.998 X 10 ⁸ м / с было обнаружено, поскольку к тому времени скорость света была точно измерена, и ее соответствие с c вряд ли было совпадением. Радиосигналы — это тоже электромагнитные волны; после открытия уравнений Максвелла потребовалось менее века, чтобы выяснить, как производить и обнаруживать их до такой степени, чтобы произвел революцию в нашей технологической цивилизации.Инфракрасный свет, ультрафиолетовый свет, рентгеновские лучи и гамма-лучи также являются примерами электромагнитных волн; подобно радиоволнам, они были неизвестны в то время, когда были открыты уравнения Максвелла.

Детали электромагнитной волны довольно сложно. Векторы электрического и магнитного полей указывают в направлениях, которые перпендикулярны друг другу и перпендикулярны направлению распространения волны. Если волна движется в направлении z , и электрическое поле колеблется в направлении x , затем магнитное поле колеблется в направлении y .Такая волна называется поляризованной в направлении , x , . (Поляризация описывается в терминах электрического поля, а не магнитного поля, потому что электрическое поле легче взаимодействует с большинством материалов.) На рисунке ниже показано поведение поляризованной электромагнитной волны. вдоль оси x и перемещаясь в z — направление.

Формулы для электрического и магнитного полей в этой волне:

, где частота и длина волны связаны соотношением c = f l .

---

Электромагнитный индекс волн Примеры Указатель лекций

Познакомьтесь с уравнениями Максвелла — вы их используете прямо сейчас | ПРОВОДНОЙ

Вот что произойдет, если магнит сломать пополам. Да, я обманул. На картинке выше показаны два стержневых магнита. Но поверьте мне — если разобьете магнит на две части, это будет выглядеть так.

Rhett Allain

Это еще диполь. Вы не можете заставить магнитное поле выглядеть как электрическое из-за точечного заряда, потому что нет отдельных магнитных зарядов (называемых магнитным монополем).По сути, это то, что гласит закон Гаусса для магнетизма — что не существует такой вещи, как магнитный монополь. Хорошо, здесь я должен быть ясным. Мы никогда не видели магнитного монополя . Они могут существовать.

Закон Фарадея

Ретт Аллен

Суперкороткая версия этого уравнения состоит в том, что есть еще один способ создать электрическое поле. Электрические поля создают не только электрические заряды. Фактически, вы также можете создать электрическое поле с изменяющимся магнитным полем. Это ОГРОМНАЯ идея, поскольку она устанавливает связь между электрическим и магнитным полями.

Позвольте мне начать с классической демонстрации. Вот магнит, катушка с проволокой и гальванометр (он в основном измеряет крошечные электрические токи). Когда я перемещаю магнит внутрь катушки или из нее, я получаю ток.

Ретт Аллен

Rhett Allain

Если просто удерживать магнит в катушке, ток не будет. Это должно быть изменяющееся магнитное поле . Ой, а где же электрическое поле? Что ж, способ создать электрический ток — это создать электрическое поле в направлении провода.Это электрическое поле внутри провода толкает электрические заряды, чтобы создать ток.

Но в этом электрическом поле есть нечто иное. Вместо того, чтобы указывать от положительных зарядов и указывать на отрицательные заряды, рисунок поля просто образует круги. Для такого случая я буду использовать название «фигурное электрическое поле» (я позаимствовал термин от моих любимых авторов учебников физики). При этом мы можем назвать электрическое поле, созданное из зарядов, «кулоновским полем» (из-за закона Кулона).

Законы Гаусса, Фарадея и Ампера с производными

Уравнения Максвелла были опубликованы ученым « Джеймс Клерк Максвелл » в 1860 году. Эти уравнения показывают, как заряженные атомы или элементы обеспечивают электрическую силу, а также силу магнитная сила для каждой единицы заряда. Энергия для каждого единичного заряда называется полем. Элементы могут быть неподвижными, в противном случае — двигаться. Уравнения Максвелла объясняют, как магнитные поля могут образовываться электрическими токами, а также зарядами, и, наконец, они объясняют, как электрическое поле может создавать магнитное поле и т. Д.Первичное уравнение позволяет определить электрическое поле, образованное зарядом. Следующее уравнение позволяет вам определить магнитное поле, а оставшиеся два объяснят, как поля протекают вокруг источников питания. В этой статье обсуждается теория Максвелла или закон Максвелла . В этой статье обсуждается обзор электромагнитной теории Максвелла .

Что такое уравнения Максвелла?

Вывод уравнения Максвелла состоит из четырех уравнений, каждое из которых соответственно объясняет один факт.Все эти уравнения не изобретены Максвеллом; однако он объединил четыре уравнения, составленные Фарадеем, Гауссом и Ампером. Хотя Максвелл включил одну часть информации в четвертое уравнение, а именно закон Ампера, это делает уравнение законченным.

Уравнения Максвелла

• Первый закон Закон Гаусса , предназначенный для статических электрических полей
• Второй закон также Закон Гаусса , предназначенный для статических магнитных полей
• Третий закон закон Фарадея , который говорит об изменении магнитного поля. field создаст электрическое поле.
• Четвертый закон закон Максвелла Ампера , который гласит, что изменение электрического поля приведет к возникновению магнитного поля.

Два уравнения 3 и 4 могут описывать электромагнитную волну , которая может распространяться сама по себе. Группировка этих уравнений говорит о том, что изменение магнитного поля может вызвать изменение электрического поля, а затем это приведет к дополнительному изменению магнитного поля. Поэтому эта серия продолжается, так как электромагнитный сигнал готов и распространяется по всему пространству.

Четыре уравнения Максвелла

Четыре уравнения Максвелла объясняют два поля, возникающие от источников электрического тока и тока. Поля бывают как электрическими, так и магнитными, и как они меняются во времени. Четыре уравнения Максвелла включают следующее.

• Первый закон: закон Гаусса для электричества
• Второй закон: закон Гаусса для магнетизма
• Третий закон: закон индукции Фарадея
• Четвертый закон: закон Ампера

Вышеупомянутые четыре уравнения Максвелла являются уравнениями Гаусса для электричества, Гаусс для магнетизма, закон Фарадея для индукции. Закон Ампера записывается по-разному, например, уравнения Максвелла в интегральной форме и уравнения Максвелла в дифференциальной форме , которые обсуждаются ниже.

Символы уравнения Максвелла

Символы, используемые в уравнении Максвелла, включают следующие:

• E обозначает электрическое поле
• M обозначает магнитное поле
• D обозначает электрическое смещение
• H обозначает напряженность магнитного поля
• Ρ обозначает плотность заряда
• i обозначает электрический ток
• ε0 обозначает диэлектрическую проницаемость
• J обозначает плотность тока
• μ0 обозначает проницаемость
• c обозначает скорость света
• M обозначает намагниченность
• P обозначает поляризацию

Первый закон: закон Гаусса для электричества

Первый закон Максвелла — это закон Гаусса , который используется для электричества.Закон Гаусса определяет, что электрический поток от любой замкнутой поверхности будет пропорционален всему заряду, заключенному на поверхности.

Интегральная форма закона Гаусса находит применение при расчете электрических полей в области заряженных объектов. Применяя этот закон к точечному заряду в электрическом поле, можно показать, что он зависит от закона Кулона.

Хотя первичная область электрического поля обеспечивает меру включенного чистого заряда, отклонение электрического поля дает меру компактности источников, а также включает значение, используемое для защиты заряда.

Второй закон: закон Гаусса для магнетизма

Закон Максвелла секунды — это закон Гаусса , который используется для магнетизма. Закон Гаусса гласит, что отклонение магнитного поля равно нулю. Этот закон применим к магнитному потоку через замкнутую поверхность. В этом случае вектор площади направлен от поверхности.

Магнитное поле из-за материалов будет генерироваться через узор, названный диполем. Эти полюса лучше всего обозначаются петлями тока, однако они похожи на положительные и отрицательные магнитные заряды, которые невидимо отражаются друг от друга.В условиях силовых линий этот закон гласит, что силовые линии магнитного поля не начинаются и не заканчиваются, а создают петли, в противном случае они расширяются до бесконечности и реверсируются. Другими словами, любая линия магнитного поля, которая проходит через данный уровень, должна где-то выходить из этого объема.

Этот закон может быть записан в двух формах: интегральной и дифференциальной. Эти две формы равны по теореме о расходимости.

Третий закон: Закон индукции Фарадея

Третий закон Максвелла — это закон Фарадея , который используется для индукции.Закон Фарадея гласит, как изменяющееся во времени магнитное поле создает электрическое поле. В интегральной форме он определяет, что усилие для каждого единичного заряда необходимо для перемещения заряда в области замкнутого контура, что равняется скорости уменьшения магнитного потока на замкнутой поверхности.

Подобно магнитному полю, электрически индуцированное электрическое поле включает замкнутые силовые линии, если на них не действует статическое электрическое поле. Эта функция электромагнитной индукции является принципом работы нескольких электрических генераторов : например, магнит с вращающимся стержнем создает изменение магнитного поля, которое, в свою очередь, создает электрическое поле в ближайшем проводе.

Четвертый закон: Закон Ампера

Четвертый закон Максвелла — это закон Ампера . Закон Ампера гласит, что создание магнитных полей может осуществляться двумя способами, а именно с помощью электрического тока, а также с помощью изменяющихся электрических полей. В интегральном типе индуцированное магнитное поле в области любого замкнутого контура будет пропорционально электрическому току и току смещения по всей замкнутой поверхности.

Закон Ампера Максвелла сделает систему уравнений точно надежной для нестатических полей без изменения законов Ампера, а также законов Гаусса для фиксированных полей.Но в результате ожидается, что изменение магнитного поля вызовет электрическое поле. Таким образом, эти математические уравнения позволят самодостаточной электромагнитной волне перемещаться через пустое пространство. Скорость электромагнитных волн можно измерить, и этого можно ожидать от токов, а также от экспериментов с зарядом, которые соответствуют скорости света, и это один из типов электромагнитного излучения.

∇ x B = J / ε0c2 + 1 / c2 ∂E / ∂t

Таким образом, это все уравнения Максвелла.Из приведенных выше уравнений, наконец, мы можем сделать вывод, что эти уравнения включают четыре закона, которые связаны с электрическим (E), а также с магнитным (B) полем, которые обсуждались выше. Уравнения Максвелла могут быть записаны как в форме эквивалентного интеграла, так и в форме дифференциала. Вот вам вопрос, каковы приложения уравнений Максвелла?

16.2: Уравнения Максвелла и электромагнитные волны

Цели обучения

К концу этого раздела вы сможете:

• Объясните исправление Максвеллом закона Ампера, включив в него ток смещения
• Сформулируйте и примените уравнения Максвелла в интегральной форме
• Опишите, как симметрия между изменяющимся электрическим и изменяющимся магнитным полями объясняет предсказание Максвелла об электромагнитных волнах.
• Опишите, как Герц подтвердил предсказание Максвелла об электромагнитных волнах.

Джеймс Клерк Максвелл (1831–1879) был одним из основных авторов физики девятнадцатого века (рисунок \ (\ PageIndex {1} \)).Хотя он умер молодым, он внес большой вклад в развитие кинетической теории газов, понимание цветового зрения и природу колец Сатурна. Он, вероятно, наиболее известен тем, что объединил существующие знания о законах электричества и магнетизма с собственными открытиями в полную всеобъемлющую электромагнитную теорию, представленную уравнениями Максвелла .

Рисунок \ (\ PageIndex {1} \): Джеймс Клерк Максвелл, физик девятнадцатого века, разработал теорию, объясняющую взаимосвязь между электричеством и магнетизмом, и правильно предсказал, что видимый свет состоит из электромагнитных волн.

Поправка Максвелла к законам электричества и магнетизма

Четыре основных закона электричества и магнетизма были открыты экспериментально благодаря работе таких физиков, как Эрстед, Кулон, Гаусс и Фарадей. Максвелл обнаружил логические несоответствия в этих более ранних результатах и ​​назвал их причиной неполноту закона Ампера.

Напомним, что согласно закону Ампера, интеграл магнитного поля вокруг замкнутого контура C пропорционален току I , проходящему через любую поверхность, граница которой представляет собой сам контур C :

\ [\ oint \ vec {B} \ cdot d \ vec {s} = \ mu_0 I.\ label {Eq1} \]

Существует бесконечно много поверхностей, которые можно присоединить к любой петле, и закон Ампера, сформулированный в уравнении \ ref {Eq1}, не зависит от выбора поверхности.

Рассмотрим установку, показанную на рисунке \ (\ PageIndex {2} \). Источник ЭДС резко подключается к конденсатору с параллельными пластинами, так что в проводе возникает зависящий от времени ток I . Предположим, мы применяем закон Ампера к контуру C , показанному перед тем, как конденсатор полностью заряжен, так что \ (I \ neq 0 \).Поверхность \ (S_1 \) дает ненулевое значение для замкнутого тока I , тогда как поверхность \ (S_2 \) дает ноль для замкнутого тока, потому что через него не проходит ток:

\ [\ underbrace {\ oint_C \ vec {B} \ cdot d \ vec {s} = \ mu_0 I} _ {\ text {если используется поверхность} S_1 \ text {}} \]

\ [\ underbrace {\, = 0} _ {\ text {если используется поверхность} S_2 \ text {}} \]

Ясно, что закон Ампера в его обычном виде здесь не работает. Это может быть неудивительно, потому что закон Ампера, применявшийся в предыдущих главах, требовал постоянного тока, тогда как ток в этом эксперименте меняется со временем и совсем не постоянный.

Рисунок \ (\ PageIndex {2} \): токи через поверхность \ (S_1 \) и поверхность \ (S_2 \) не равны, несмотря на наличие одного и того же граничного контура C .

Как можно изменить закон Ампера, чтобы он работал во всех ситуациях? Максвелл предложил включить дополнительный вклад, называемый током смещения \ (I_d \), в реальный ток I ,

\ [\ в коробке {\ oint_S \ vec {B} \ cdot d \ vec {s} = \ mu_0 (I + I_d)} \ label {EQ4} \]

, где ток смещения определен как

\ [\ в коробке {I_d = \ epsilon_0 \ dfrac {d \ Phi_E} {dt}.} \ label {EQ5} \]

Здесь \ (\ epsilon_0 \) — диэлектрическая проницаемость свободного пространства , а \ (\ Phi_E \) — электрический поток, определяемый как

.

\ [\ Phi_E = \ iint_ {Surface \, S} \ vec {E} \ cdot d \ vec {A}. \]

Ток смещения аналогичен реальному току в законе Ампера, таким же образом входя в закон Ампера. Однако он создается изменяющимся электрическим полем. Он учитывает изменяющееся электрическое поле, создающее магнитное поле, как и настоящий ток, но ток смещения может создавать магнитное поле даже там, где нет реального тока.Когда этот дополнительный член включен, модифицированное уравнение закона Ампера принимает вид

.

\ [\ oint_C \ vec {B} \ cdot d \ vec {s} = \ mu_0 I + \ epsilon_0 \ mu_0 \ dfrac {d \ Phi_E} {dt} \]

и не зависит от поверхности S , через которую измеряется ток I .

Теперь мы можем исследовать эту модифицированную версию закона Ампера, чтобы подтвердить, что он выполняется независимо от того, выбрана ли поверхность \ (S_1 \) или поверхность \ (S_2 \) на рисунке \ (\ PageIndex {2} \). Электрическое поле \ (\ vec {E} \), соответствующее потоку \ (\ Phi_E \) в уравнении \ ref {EQ5}, находится между пластинами конденсатора.Следовательно, поле \ (\ vec {E} \) и ток смещения через поверхность \ (S_1 \) равны нулю, и уравнение \ ref {EQ4} принимает форму

\ [\ oint_C \ vec {B} \ cdot d \ vec {s} = \ mu_0 I. \ label {16.5} \]

Теперь мы должны показать, что для поверхности \ (S_2 \), через которую фактически не протекает ток, ток смещения приводит к тому же значению \ (\ mu_0 I \) для правой части уравнения закона Ампера. Для поверхности \ (S_2 \) уравнение принимает вид

\ [\ oint_C \ vec {B} \ cdot d \ vec {s} = \ mu_0 \ dfrac {d} {dt} \ left [\ epsilon_0 \ iint_ {Surface \, S_2} \ vec {E} \ cdot d \ vec {A} \ right].\]

Закон Гаусса для электрического заряда требует замкнутой поверхности и обычно не может быть применен к поверхности вроде \ (S_1 \) отдельно или только \ (S_2 \). Но две поверхности \ (S_1 \) и \ (S_2 \) образуют замкнутую поверхность на рисунке \ (\ PageIndex {2} \) и могут использоваться в законе Гаусса. Поскольку электрическое поле равно нулю на \ (S_1 \), вклад потока через \ (S_1 \) равен нулю. Это дает нам

\ [\ begin {align} \ oint_ {Surface \, S_1 + S_2} \ vec {E} \ cdot d \ vec {A} & = \ iint_ {Surface \, S_1} \ vec {E} \ cdot d \ vec {A} + \ iint_ {Surface \, S_2} \ vec {E} \ cdot d \ vec {A} \\ [4pt] & = 0 + \ iint_ {Surface \, S_2} \ vec {E} \ cdot d \ vec {A} \\ [4pt] & = \ iint_ {Surface \, S_2} \ vec {E} \ cdot d \ vec {A}.\ end {align} \]

Следовательно, мы можем заменить интеграл по \ (S_2 \) в уравнении \ ref {16.5} на замкнутую гауссову поверхность \ (S_1 + S_2 \) и применить закон Гаусса, чтобы получить

\ [\ oint_ {S_1} \ vec {B} \ cdot d \ vec {s} = \ mu_0 \ dfrac {dQ_ {in}} {dt} = \ mu_0 I. \]

Таким образом, модифицированное уравнение закона Ампера такое же, как и для поверхности \ (S_2 \), где правая часть является результатом тока смещения, как и для поверхности \ (S_1 \), где вклад происходит от фактического поток электрического заряда.

Ток смещения в зарядном конденсаторе

Конденсатор с параллельными пластинами емкостью C, , пластины которого имеют площадь A, и расстояние между ними d , подключен к резистору R и батарее с напряжением В, . Ток начинает течь при \ (t = 0 \).

1. Найдите ток смещения между пластинами конденсатора в момент времени t .
2. Из свойств конденсатора найдите соответствующий реальный ток \ (I = \ dfrac {dQ} {dt} \) и сравните ответ с ожидаемым током в проводах соответствующей цепи RC .{-t / RC}. \ nonumber \] Этот ток такой же, как \ (I_d \), найденный в (a).

Уравнения Максвелла

С поправкой на ток смещения уравнения Максвелла принимают вид

\ [\ begin {align} \ oint \ vec {E} \ cdot d \ vec {A} & = \ dfrac {Q_ {in}} {\ epsilon_0} \, (\ text {закон Гаусса}) \ label { eq1} \\ [4pt] \ oint \ vec {B} \ cdot d \ vec {A} & = 0 \, (\ text {закон Гаусса для магнетизма}) \ label {eq2} \\ [4pt] \ oint \ vec {E} \ cdot d \ vec {s} & = — \ dfrac {d \ Phi_m} {dt} \, (\ text {закон Фарадея}) \ label {eq3} \\ [4pt] \ oint \ vec { B} \ cdot d \ vec {s} & = \ mu_0 I + \ epsilon_0I + \ epsilon_0 \ mu_0 \ dfrac {d \ Phi_E} {dt} (\ text {закон Ампера-Максвелла}).\ label {eq4} \ end {align} \]

После того, как поля были рассчитаны с использованием этих четырех уравнений, уравнение силы Лоренца

\ [\ vec {F} = q \ vec {E} + q \ vec {v} \ times \ vec {B} \]

дает силу, которую поля действуют на частицу с зарядом q , движущуюся со скоростью \ (\ vec {v} \). Уравнение силы Лоренца объединяет силу электрического поля и магнитного поля на движущийся заряд. Магнитные и электрические силы изучались в предыдущих модулях.Эти четыре уравнения Максвелла, соответственно:

Уравнения Максвелла

1. Закон Гаусса

Электрический поток через любую замкнутую поверхность равен электрическому заряду \ (Q_ {in} \), заключенному в поверхности. Закон Гаусса (уравнение \ ref {eq1}) описывает связь между электрическим зарядом и создаваемым им электрическим полем. Это часто изображают в виде линий электрического поля, исходящих от положительных зарядов и заканчивающихся отрицательными зарядами, и указывающих направление электрического поля в каждой точке пространства.

2. Закон Гаусса для магнетизма

Поток магнитного поля через любую замкнутую поверхность равен нулю (уравнение \ ref {eq2}). Это эквивалентно утверждению, что силовые линии магнитного поля непрерывны, не имеют ни начала, ни конца. Любая линия магнитного поля, входящая в область, ограниченную поверхностью, также должна покинуть ее. Не известно о существовании магнитных монополей, на которых линии магнитного поля заканчивались бы (см. Раздел «Магнитные поля и линии»).

3. Закон Фарадея

Изменяющееся магнитное поле индуцирует электродвижущую силу (ЭДС) и, следовательно, электрическое поле.Направление ЭДС противодействует изменению. Уравнение \ ref {eq3} является законом индукции Фарадея и включает закон Ленца. Электрическое поле от изменяющегося магнитного поля имеет силовые линии, которые образуют замкнутые контуры без начала и конца.

4. Закон Ампера-Максвелла

Магнитные поля создаются движущимися зарядами или изменяющимися электрическими полями. Четвертое из уравнений Максвелла, Equation \ ref {eq4}, включает закон Ампера и добавляет еще один источник магнитных полей, а именно изменяющиеся электрические поля.

Уравнения Максвелла и закон силы Лоренца вместе охватывают все законы электричества и магнетизма. Симметрия, которую Максвелл ввел в свою математическую структуру, может быть не сразу очевидна. Закон Фарадея описывает, как изменяющиеся магнитные поля создают электрические поля. Ток смещения, введенный Максвеллом, является результатом изменения электрического поля и учитывает изменяющееся электрическое поле, создающее магнитное поле. Уравнения для эффектов как изменяющихся электрических полей, так и изменяющихся магнитных полей отличаются по форме только там, где отсутствие магнитных монополей приводит к отсутствию членов.Эта симметрия между эффектами изменения магнитного и электрического полей важна для объяснения природы электромагнитных волн.

Более позднее применение теории относительности Эйнштейна к полной и симметричной теории Максвелла показало, что электрические и магнитные силы не разделены, а являются разными проявлениями одной и той же вещи — электромагнитной силы. Электромагнитная сила и слабая ядерная сила так же объединены, как и электрослабая сила. Это объединение сил было одной из причин попыток объединить все четыре основные силы в природе — гравитационное, электрическое, сильное и слабое ядерные взаимодействия (см. Физика элементарных частиц и космология).

Механизм распространения электромагнитных волн

Чтобы увидеть, как симметрия, введенная Максвеллом, объясняет существование комбинированных электрических и магнитных волн, распространяющихся в пространстве, представьте изменяющееся во времени магнитное поле \ (\ vec {B} _0 (t) \), создаваемое высокочастотным переменный ток показан на рисунке \ (\ PageIndex {3} \). Мы представляем \ (\ vec {B} _0 (t) \) на диаграмме одной из его силовых линий. Согласно закону Фарадея, изменяющееся магнитное поле через поверхность индуцирует изменяющееся во времени электрическое поле \ (\ vec {E} _0 (t) \) на границе этой поверхности.Источник тока смещения для электрического поля, как и источник закона Фарадея для магнитного поля, создает только замкнутые контуры силовых линий из-за математической симметрии, включенной в уравнения для индуцированного электрического и индуцированного магнитного полей. Показано линейное представление \ (\ vec {E} _0 (t) \). В свою очередь, изменяющееся электрическое поле \ (\ vec {E} _0 (t) \) создает магнитное поле \ (\ vec {B} _1 (t) \) согласно модифицированному закону Ампера. Это изменяющееся поле индуцирует \ (\ vec {E} _1 (t) \), которое индуцирует \ (\ vec {B} _2 (t) \) и так далее.Затем у нас есть самопродолжающийся процесс, который приводит к созданию изменяющихся во времени электрических и магнитных полей в областях все дальше и дальше от O . Этот процесс можно представить себе как распространение электромагнитной волны в пространстве.

Рисунок \ (\ PageIndex {3} \): Как изменяющиеся поля \ (\ vec {E} \) и \ (\ vec {B} \) распространяются в пространстве.

В следующем разделе мы покажем в более точных математических терминах, как уравнения Максвелла приводят к предсказанию электромагнитных волн, которые могут перемещаться в пространстве без материальной среды, подразумевая скорость электромагнитных волн, равную скорости света.

До работы Максвелла эксперименты уже показали, что свет — это волновое явление, хотя природа волн еще была неизвестна. В 1801 году Томас Янг (1773–1829) показал, что когда световой луч разделялся двумя узкими щелями и затем снова объединялся, на экране формировался узор, состоящий из ярких и темных полос. Янг объяснил это поведение, предположив, что свет состоит из волн, которые конструктивно складываются в одних точках и разрушительно в других (см. Интерференция).Впоследствии Жан Фуко (1819–1868) с измерениями скорости света в различных средах и Огюстен Френель (1788–1827) с подробными экспериментами, включающими интерференцию и дифракцию света, предоставили дополнительные убедительные доказательства того, что свет был волной. Итак, свет был известен как волна, и Максвелл предсказал существование электромагнитных волн, которые распространяются со скоростью света. Вывод казался неизбежным: свет должен быть формой электромагнитного излучения. Но теория Максвелла показала, что для электромагнитных волн возможны другие длины волн и частоты, отличные от света.Он показал, что электромагнитное излучение с теми же фундаментальными свойствами, что и видимый свет, должно существовать на любой частоте. Остальным оставалось проверить и подтвердить это предсказание.

Упражнение \ (\ PageIndex {1} \)

Когда ЭДС на конденсаторе включена и конденсатору позволяют заряжаться, когда магнитное поле, индуцированное током смещения, имеет наибольшую величину?

Максимально сразу после включения тока.Ток смещения и создаваемое им магнитное поле пропорциональны скорости изменения электрического поля между пластинами, которая максимальна, когда пластины впервые начинают заряжаться.

Наблюдения Герца

Немецкий физик Генрих Герц (1857–1894) был первым, кто генерировал и обнаруживал определенные типы электромагнитных волн в лаборатории. Начиная с 1887 года, он провел серию экспериментов, которые не только подтвердили существование электромагнитных волн, но и подтвердили, что они движутся со скоростью света.

Герц использовал схему переменного тока RLC (резистор-индуктор-конденсатор), которая резонирует на известной частоте \ (f_0 = \ dfrac {1} {2 \ pi \ sqrt {LC}} \), и подключил ее к петля провода, как показано на рисунке \ (\ PageIndex {4} \). Высокое напряжение, индуцированное через зазор в петле, вызывало искры, которые были видимым свидетельством наличия тока в цепи и помогали генерировать электромагнитные волны.

Через всю лабораторию Герц разместил еще одну петлю, присоединенную к другой схеме RLC , которую можно было настроить (как циферблат на радио) на ту же резонансную частоту, что и первая, и, таким образом, можно было заставить ее принимать электромагнитные волны.В этой петле также был зазор, в котором возникали искры, что давало твердое свидетельство приема электромагнитных волн.

Рисунок \ (\ PageIndex {4} \): устройство, которое Герц использовал в 1887 году для генерации и обнаружения электромагнитных волн.

Герц также изучил картины отражения, преломления и интерференции генерируемых им электромагнитных волн, подтвердив их волновой характер. Он смог определить длины волн по интерференционным картинам и, зная их частоты, он мог рассчитать скорость распространения, используя уравнение \ (v = f \ lambda \), где v — скорость волны, f — его частота, а \ (\ lambda \) — его длина волны.Таким образом, Герц смог доказать, что электромагнитные волны распространяются со скоростью света. Единица измерения частоты в системе СИ, герц \ ((1 \, Гц = 1 \, цикл / секунда) \), названа в его честь.

Упражнение \ (\ PageIndex {2} \)

Может ли чисто электрическое поле распространяться как волна через вакуум без магнитного поля? Обосновать ответ.

Нет. Изменяющееся электрическое поле в соответствии с модифицированной версией закона Ампера обязательно вызовет изменяющееся магнитное поле.

Авторы и авторство

• Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами. Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.