Курс общей физики, Т.3

Курс общей физики, Т.3

Савельев И. В. Курс общей физики: Учеб. пособие. В 3-х т. Т. 3. Квантовая оптика. Атомная физика. Физика твердого тела. Физика атомного ядра и элементарных частиц. 3-е изд., испр. — М.; Наука, Гл. ред. физ.-мат. лит., 1987. — 320 с. Третий том трехтомного курса общей физики, созданного профессором Московского инженерно-физического института, заслуженным деятелем науки. и техники РСФСР, лауреатом Государственной премии СССР И. В. Савельевым. Главная цель книги — познакомить студентов с основными идеями и методами физики. Особое внимание обращено на разъяснение смысла физических законов и на сознательное применение их. Для втузов с расширенной программой по физике, однако изложение построено так, что, опустив отдельные места, книгу можно использовать для втузов с обычной программой. Оглавление ПРЕДИСЛОВИЕ МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ЧАСТЬ 1. КВАНТОВАЯ ОПТИКА § 1. Тепловое излучение и люминесценция § 2. Закон Кирхгофа § 3. Равновесная плотность энергии излучения § 4. Закон Стефана — Больцмана и закон Вина § 5. Стоячие волны в пространстве трех измерений § 6. Формула Рэлея — Джинса § 7. Формула Планка ГЛАВА II. ФОТОНЫ § 8. Тормозное рентгеновское излучение § 9. Фотоэффект § 10. Опыт Боте. Фотоны § 11. Эффект Комптона ЧАСТЬ 2. АТОМНАЯ ФИЗИКА § 12. Закономерности в атомных спектрах § 13. Модель атома Томсона § 14. Опыты по рассеянию а-частиц. Ядерная модель атома § 15. Постулаты Бора. Опыт Франка и Герца § 16. Правило квантования круговых орбит § 17. Элементарная боровская теория водородного атома ГЛАВА IV. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ § 18. Гипотеза де-Бройля. Волновые свойства вещества § 19. Необычные свойства микрочастиц § 20. Принцип неопределенности § 21. Уравнение Шрёдингера § 22. Смысл пси-функции § 23. Квантование энергии § 24. Квантование момента импульса § 25. Принцип суперпозиции § 26. Прохождение частиц через потенциальный барьер § 27. Гармонический осциллятор ГЛАВА V. ФИЗИКА АТОМОВ И МОЛЕКУЛ § 28. Атом водорода § 29. Спектры щелочных металлов § 30. Ширина спектральных линий § 31. Мультиплетность спектров и спин электрона § 32. Результирующий механический момент многоэлектронного атома § 33. Магнитный момент атома § 34. Эффект Зеемана § 35. Электронный парамагнитный резонанс § 36. Принцип Паули. Распределение электронов по энергетическим уровням атома § 37. Периодическая система элементов Менделеева § 38. Рентгеновские спектры § 39. Энергия молекулы § 40. Молекулярные спектры § 41. Комбинационное рассеяние света § 42. Вынужденное излучение § 43. Лазеры § 44. Нелинейная оптика ЧАСТЬ 3. ФИЗИКА ТВЕРДОГО ТЕЛА § 45. Кристаллическая решетка. Индексы Миллера § 46. Теплоемкость кристаллов. Теория Эйнштейна § 47. Колебания систем с большим числом степеней свободы § 48. Теория Дебая § 49. Фононы § 50. Эффект Мёссбауэра ГЛАВА VII. ЗОННАЯ ТЕОРИЯ ТВЕРДЫХ ТЕЛ § 51. Квантовая теория свободных электронов в металле § 52. Распределение Ферми — Дирака § 53. Энергетические зоны в кристаллах § 54. Динамика электронов в кристаллической решетке ГЛАВА VIII. ЭЛЕКТРОПРОВОДНОСТЬ МЕТАЛЛОВ И ПОЛУПРОВОДНИКОВ § 55. Электропроводность металлов § 56. Сверхпроводимость § 57. Полупроводники § 58. Собственная проводимость полупроводников § 59. Примесная проводимость полупроводников ГЛАВА IX. КОНТАКТНЫЕ И ТЕРМОЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ § 60. Работа выхода § 61. Термоэлектронная эмиссия. Электронные лампы § 62. Контактная разность потенциалов § 63. Термоэлектрические явления § 64. Полупроводниковые диоды и триоды § 65. Внутренний фотоэффект ЧАСТЬ 4. ФИЗИКА АТОМНОГО ЯДРА И ЭЛЕМЕНТАРНЫХ ЧАСТИЦ § 66. Состав и характеристики атомного ядра § 67. Масса и энергия связи ядра § 68. Модели атомного ядра § 69. Ядерные силы § 70. Радиоактивность § 71. Ядерные реакции § 72. Деление ядер § 73. Термоядерные реакции ГЛАВА XI. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ § 74. Виды взаимодействий и классы элементарных частиц § 75. Методы регистрации элементарных частиц § 76. Космические лучи § 77. Частицы и античастицы § 78. Изотопический спин § 79. Странные частицы § 80. Несохранение четности в слабых взаимодействиях § 81. Нейтрино § 82. Систематика элементарных частиц § 83. Кварки § 84. Великое объединение ПРИЛОЖЕНИЯ I. ГРАВИТАЦИОННОЕ ВЗАИМОДЕЙСТВИЕ

1.2. Закон Кирхгофа. Формула Планка.

8. Методика определения интегральной поглощательной способности.

ЛИТЕРАТУРА

1. Савельев И. В. Курс общей физики. Т.3.

2. Сивухин Д.В. Общий курс физики. Оптика.

3. Ландсберг Г.С. Оптика.

Взято с сайта ФАЭ helper (URL: http://www.faehelper.narod.ru)

— 16 —

Министерство высшего и среднего специального образования РФ

НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Изучение законов теплового излучения c помощью оптического пирометра

Лабораторная работа №3-8

Нижний Новгород

1993 г.

Составители: А.Н. Мешков, А.М. Шутов, В.И. Шишко

УДК 621.373.8

Изучение законов теплового излучения с помощью оптического пирометра: Лабораторная работа по физике №3-8 для студентов всех специальностей/ НГТУ; Сост.

: А.Н. Мешков, А.М. Шутов, В.И. Шишко. Н.Новгород, 1993. 19 с.

Даны сведения о законах теплового излучения, оптической пирометрии. Описаны лабораторная установка, методика измерения температуры раскаленного тела.

Нижегородский политехнический ин-т. 603600, Н.Новгород, ул. Минина, 24.

Лаборатория офсетной печати ГПИ.603022,Н.Новгород, пр. Гагарина,1.

© Нижегородский Государственный Технический Университет, 1993

2.4.2. Определение истинной температуры Т.

1. Найти Т по формуле (15) и таблице 1. Записать в таблицу 2 значения a_λ,Т, которые принимались при вычислении Т.

2. Построить график Т(Р) совместно с Тя(Р).

2.4.3.Определение интегральной поглощательной способности.

1. Вычислить α_Т по формуле (18).

2. Построить график α_Т=f(T).

3. Оценить погрешность определения одного из значений α_Т как погрешность косвенных измерений, считая, что погрешности ∆T=10^-9, ∆S=5*10^-7 м².

Таблица 2

№, п/п	U, В	I, А	P, Вт	tя, 0 С	Tя, К		T, К	αТ
1
2
3
…. .
10

Отчет по лабораторной работе должен содержать схему установки, расчетные формулы, необходимые для составления расчетов с пояснениями, таблицу измерений, графики и расчет погрешностей.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Природа теплового излучения. Величины, характеризующие тепловое излучение.

2. Закон Кирхгофа, его проявление на опыте.

3. Формула Планка для функции Кирхгофа. Графическая зависимость излучательной способности от частоты излучения. Смысл численного значения функции Кирхгофа.

4. Законы Стефана-Больцмана и Вина, их проявление.

5. Радиационная, яркостная, цветовая температуры.

6. Принцип действия оптического пирометра и экспериментальной установки.

7. Методика определения температуры Т тела по яркостной температуре.

— 15 —

2.3. Указания по технике безопасности

2.3.1. При работе с установкой, опасным является напряжение сети 220 В, которым питается цепь накала исследуемой лапы и блок питания пирометра.

2.3.2. Прежде чем включать ЛАТР и блок питания пирометра в сеть, надо проверить соединение ЛАТРа, амперметра и исследуемой лампы.

2.3.3. Запрещается прикасаться к элементам схемы питания исследуемой лампы в процессе ее работы, за исключением ручки управления ЛАТРа.

2.4. Порядок выполнения работы

2.4.1. Измерение яркостной температуры Тя.

1. Установить ручку ЛАТРа регулировки напряжения нити накала исследуемой лампы в нулевое положение, повернув ее до отказа против часовой стрелки.

2. Проверить схему и включить ЛАТР и блок питания пирометра в сеть.

3. Поворотом ручки ЛАТРа установить напряжение нити лампы 60 В.

4. Подготовить пирометр к работе, для чего:

а) переключатель 5 пирометра поставить в положение

б) направить пирометр на исследуемый объект и перемещением объектива и окуляра добиться, что в поле зрения пирометра получилось четкое изображение нити исследуемой лампы.

5. Нажать кнопку 6 включения эталонной лампы. Вращая ручку пирометра 3 добиться, чтобы яркости эталонной и исследуемой нити были одинаковы, т.е. чтобы изображение границ пересечения эталонной нити и исследуемой нити исчезло. Отпустить кнопку 6.

6. Произвести отсчет температуры t_я в ⁰С по шкале 1 пирометра.

7. Показания вольтметра U, амперметра I и температуру tя0 С записать в таблицу 2.

8. Произвести измерения, измеряя напряжение U от 60 до 200 В через каждые 10-15 В. Всего следует произвести около 10 подобных измерений, все полученные результаты занести в таблицу 2.

9. Для каждого значения U вычислить по формуле (16) значения Тя в градусах по шкале Кельвина, результаты занести в таблицу 2.

10. Построить график Тя(Р).

— 14 –

Цель работы: изучить законы теплового излучения, понятия яркостной, радиационной, цветовой температуры, методику измерения температуры раскаленного тела пирометром.

1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

1.1. Природа теплового излучения. Основные характеристики теплового излучения

Излучение света происходит в результате переходов электронов вещества из состояния с большей энергией в состояние с меньшей энергией.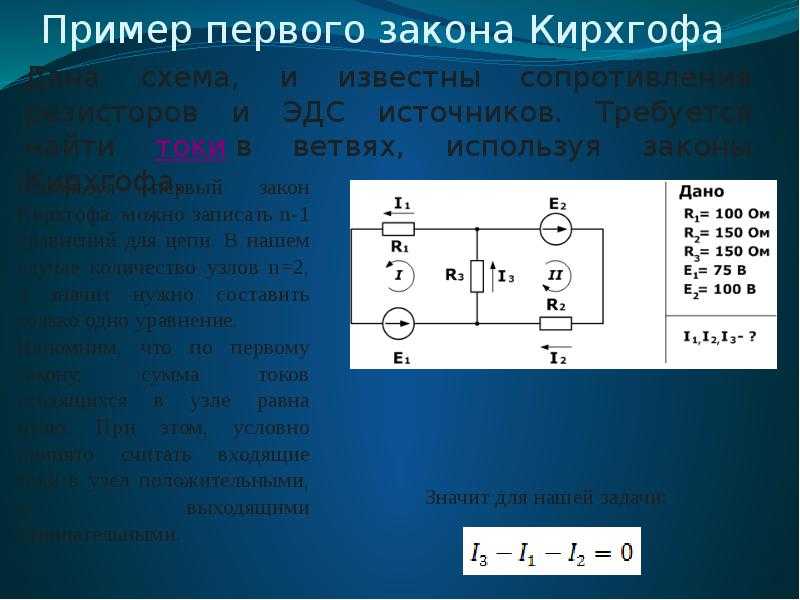 При каждом переходе выделяется квант энергии излучения hυ=∆W, где h=6,62*10^-34 Дж*с – постоянная Планка, υ – частота излучения, ∆W – разность энергий. Тепловое излучение обусловлено тем, что переход в состояние с большей энергией (в возбужденное состояние) происходит в результате теплового движения атомов.

Тело, нагретое до температуры в несколько тысяч градусов, имеет сплошной спектр излучения, занимающий область от невидимого инфракрасного излучения до невидимого ультрафиолетового. Доля энергии, приходящаяся на различные участки спектра, зависит от температуры излучающего тела. Тепловое излучение характеризуют следующими параметрами.

Энергетическая светимость R_T, Вт/м² – энергия излучения нагретого тела в единицу времени с единицы поверхности по всем направлением во всем интервале излучаемых длин волн. Индекс «Т», указывает на то, что энергетическая светимость зависит от температуры.

Испускательная способность

(1)

является функцией частоты и температуры, характеризует распределение энергии излучения по частотам. Чем выше r_υ,T при данной частоте υ и температуре Т, тем больше dR_T, а значит, больше энергии излучает тело на частотах, близких к υ (в диапазоне от υ до υ+dυ).

Очевидно, что

(2).

— 3 —

Поглощательная способность a_υ,Т, — характеризует способность тел поглощать падающее на них излучение. она показывает, какая доля энергии падающего излучения поглощается поверхностью на частотах, близких к υ. Поглощательная способность зависит от частоты и температуры. Для реальных тел 0<a<1. Тела, у которых a_υ,Т=1 для всех частот и температур (полное поглощение), называют абсолютно черными. Близки к ним в видимой области спектра – сажа, черный бархат. Абсолютно черное тело можно сделать искусственно в виде полости с малым отверстием (рис.1).

Излучение, попавшее извне в отверстие, полностью захватывается телом за счет многократных переотражений, при каждом из которых происходит частичное поглощение. Такая полость, разогретая до температуры Т, излучает из отверстия волны, характерные для абсолютно черного тела.

Рис.1

Между испускательной и поглощательной способностью существует взаимосвязь. Кирхгоф установил, что отношение испускательной и поглощательной способностей не зависит от природы тел и является универсальной для всех тел функцией частоты и температуры:

(3).

Это означает, что тело, сильнее поглощающее какие-либо лучи, будет эти лучи сильнее и испускать.

Закон Кирхгофа хорошо подтверждается на опыте. Если нагреть в печи кусок белого фарфора, наполовину покрытого черной краской, то, вынув кусок из печи, можно наблюдать в темноте собственное свечение – ярче светиться окрашенная часть. На свету – ярче выглядит часть керамики, не покрытая краской. Наблюдаемый эффект соответствует закону Кирхгофа, т.к. зачерненная поверхность является более поглощающей, а следовательно, и более излучающей.

• 4 –

2.2. Методика проведения измерений.

2.2.1. Измерение яркостной температуры Тя.

Пирометр непосредственно позволяет определить яркостную температуру нити исследуемой лампы в градусах Цельсия, затем ее пересчитывают в шкалу Кельвина. Если одновременно по приборам (рис.4,а) регулировать напряжение U и ток лампы I, а значит и мощность потребляемую нитью

, (16)

можно построить графики Tя=f(Р)

По формуле (15) и таблице 1 можно определить истинную температуру Т исследуемой нити и построить график Tя=f(Р).

2.2.3. Определение интегральной поглощательной способности α_Т

По определению (11) . При достаточно высокой температуре (при излучении видимого света) лишь небольшая часть мощности электропитания Р идет на передачу тепла через цоколь лампы, в основном она обеспечивает излучение лампы в видимом и инфракрасном диапазонах, т. е. в соответствии с определением электрической светимости,

, (17)

где S – площадь нити исследуемой лампы, имеет величину порядка 10^-4 м², точное значение указано на установке. Выразив из (17), а из (8), (9), найдем их отношения:

, (18)

что позволяет определить α_Т и построить график α_Т(Т).

Коэффициент α_Т показывает, какую долю энергии излучает нить реальной лампы от той энергии, которую бы излучала лампа с абсолютно черной нитью при той же температуре. На практике численные значения α_Т применяют при изменении температуры радиационным способом. Для металлов α_Т=0,1-0,9, для сплавов металлов и угля α_Т≈0,9.

— 13 —

(10)

Для сравнения энергетической светимости реальных тел и абсолютно черного можно ввести коэффициент , равный отношению интегралов (10) и (7), т. е.

(11)

Коэффициент иногда называют интегральной поглощательной способностью (или интегральным коэффициентом черноты). Он характеризует свойство реальных тел, что все они излучают меньше энергии (на всех вместе взятых частотах), чем абсолютно черное тело при той же температуре. Значения всегда меньше единицы, зависят от температуры, природы тела, состояния его поверхности.

Закон Стефана-Больцмана справедлив лишь для абсолютно черных тел. Для других тел закономерность (8) нарушается. Поэтому измерение постоянной δ, а затем через нее и h (см.(9)) проводят только на абсолютно черном теле или его искусственной модели (рис.1)

Правило соединения Кирхгофа: определение и уравнение

Правило соединения Кирхгофа: определение и уравнение | StudySmarter

Выберите язык

Предлагаемые языки для вас:

Немецкий (DE)

Дойч (Великобритания)

Европа

• английский (DE)
• английский (Великобритания)

Выберите язык

Предлагаемые языки для вас:

Немецкий (DE)

Дойч (Великобритания)

Европа

• английский (DE)
• английский (Великобритания)

StudySmarter — универсальное учебное приложение.

4.8 • Рейтинг +11k

Более 3 миллионов загрузок

Бесплатно

Правило соединения Кирхгофа

СОДЕРЖАНИЕ :

ОГЛАВЛЕНИЕ

При первом изучении основ принципиальных схем мы обычно рассматриваем простые последовательные и параллельные цепи. Однако, если бы вы открыли любой старый бытовой прибор, вы, вероятно, увидели бы, казалось бы, неразборчивую путаницу проводов и электрических компонентов. Большинство приборов состоят из чрезвычайно сложных цепей, которые не являются ни последовательными, ни параллельными цепями, где вычисление величин с \(V=IR\) заняло бы слишком много времени. Итак, как такие схемы разрабатываются и анализируются на практике? К счастью, есть два закона схемотехники, известные как законы Кирхгофа, которые можно применить к любой принципиальной схеме, какой бы сложной она ни была. В этой статье мы подробно рассмотрим первый из этих законов, известный как правило соединения Кирхгофа.

Определение первого закона Кирхгофа

В 1845 году прусский студент-физик Густав Кирхгоф исследовал поведение токов и разностей потенциалов в цепях, содержащих множество петель и узлов или соединений. Применив закон Ома к этим цепям, он сумел обобщить результаты в два простых закона, которые и по сей день невероятно полезны в области электротехники. Их основное применение — преобразование невероятно сложных принципиальных схем в наборы простых алгебраических выражений.

Рис. 1. Густав Кирхгоф (1824–1887) был прусским физиком, который внес важный вклад в понимание электрических цепей, в первую очередь в свои два закона.

Первый из этих законов, известный как Правило соединения Кирхгофа , касается тока, втекающего и выходящего из соединения цепи, и будет в центре внимания этой статьи. Напомним, что ток в проводе — это просто скорость, с которой заряд течет по этому проводу. Обычно цепи включают соединения, как показано на рисунке 2, в результате чего ток в проводе разделяется на два или более провода. Правило соединения Кирхгофа гарантирует, что ток, втекающий в соединение, всегда совпадает с током, выходящим из соединения.

Правило соединения Кирхгофа гласит, что сумма токов, встречающихся в соединении цепи, всегда должна быть равна нулю.

Рис. 2 – Пример соединения в цепи. Правило соединения Кирхгофа гласит, что \(i_2+i_3=i_1+i_4\).

Уравнение, описывающее правило соединения Кирхгофа

Если набор токов \(I_1,I_2,\dots,I_k\) встречается в соединении, то правило соединения Кирхгофа можно выразить алгебраически, присвоив знак \(\pm\) знаку каждый ток в зависимости от того, входят ли они в соединение или выходят из него. По соглашению токи, входящие в соединение, получают знак \(+\), а выходящие — знак \(-\). Тогда правило соединения Кирхгофа может быть выражено уравнением

\[\sum_{k,\text{входящий}} I_k-\sum_{l,\text{выходящий}}I_l=0\,\mathrm{A}. \]

Например, на рис. 2, \(i_2\) и \(i_3\) входят в перекресток, а \(i_1\) и \(i_4\) выходят из него, поэтому

\[\begin{align}&i_2+i_3-i_1-i_4= 0\,\mathrm{A}\,\\\iff &i_2+i_3=i_1+i_4,\end{align}\]

демонстрируя, что сумма токов, входящих в соединение, должна быть равна сумме токов выезд с развязки. И наоборот, если направление тока неизвестно, его можно определить по правилу соединения Кирхгофа, предполагая, что он входит или выходит из соединения и находит его знак. Если его значение отрицательное, предположение было неверным.

В качестве простого примера рассмотрим токи в последовательной цепи, как показано на рисунке 3. Мы должны помнить о том, как мы определяем знак тока в каждом соединении, поскольку один и тот же ток может иметь разный знак в зависимости от того, в каком соединении мы считаем. Если ток течет по часовой стрелке от положительной клеммы к отрицательной, то мы можем присвоить положительный знак токам, входящим в соединение, и отрицательные знаки тем, которые выходят из соединения. На рисунке 3 мы можем сказать, что каждый угол является соединением, поэтому каждое «соединение» имеет только один текущий вход и один текущий выход, поэтому правило соединения Кирхгофа говорит нам, что должно выполняться следующее:\[\begin{align} &I_1-I_2= 0\,\mathrm{A},\\ &I_2-I_3=0\,\mathrm{A},\\ &I_3-I_4=0\,\mathrm{A},\\&I_4-I_1=0\,\mathrm {A},\\\ подразумевает &I_1=I_2=I_3=I_4.\end{align}\]

Другими словами, ток в последовательной цепи одинаков во всех точках цепи.




Рис. 3. Правило соединения Кирхгофа требует, чтобы ток в последовательной цепи был везде одинаковым, то есть \(I_1=I_2=I_3=I_4\) в приведенной выше схеме.

Примеры правила соединения Кирхгофа

Давайте рассмотрим некоторые способы использования правила соединения Кирхгофа для анализа принципиальных схем и расчета недостающих токов.

Рис. 4. Правило соединения Кирхгофа позволяет нам решать схемы, подобные приведенной выше, не зная напряжения батареи.

Рассмотрим схему, приведенную выше, где мы хотим найти недостающие токи ветвей \(I_1,I_2,I_3\). Каждая ветвь содержит резистор разного сопротивления. Немедленно правило Кирхгофа о соединении говорит нам, что \(I_1=5\,\mathrm{A}\), поскольку ток, втекающий в батарею, должен быть таким же, как и ток, вытекающий из батареи (мы можем выбрать батарею в качестве соединения). и увидеть это непосредственно). Далее нам нужно найти токи \(I_2\) и \(I_3\). Глядя на правое соединение и предполагая, что оба тока \(I_2\) и \(I_3\) идут справа налево, правило соединения гласит, что \[\begin{align}I_1-I_2-I_3&=0\,\mathrm {A},\\\подразумевает I_2+I_3&=5\,\mathrm{A}.\end{align}\]

Мы можем использовать \(V=IR\), отметив, что потенциал в параллельных цепях одинаков во всех ветвях, чтобы найти долю тока, протекающего в каждой ветви. Поскольку ток обратно пропорционален сопротивлению, через резистор \(2\,\mathrm{\Omega}\) будет протекать вдвое больший ток, чем через резистор \(4\,\mathrm{\Omega}\). Следовательно, \(I_3=2I_2\) и, таким образом, \[\begin{align}3I_2&=5\,\mathrm{A},\\\ подразумевает I_2&=\frac{5}{3}\,\mathrm{A} ,\\\ подразумевает I_3&=\frac{10}{3}\,\mathrm{A}. \end{align}\]

Поскольку мы получаем положительные значения для неизвестных токов, мы знаем, что наше предположение об их направлении было верным, поэтому мы заключаем, что токи действительно текут справа налево.

Рис. 5. Правило соединения Кирхгофа особенно полезно для более сложных схем, где \(V=IR\) становится сложнее использовать.

В то время как использование \(V=IR\) для нахождения пропущенных величин обычно является самым простым методом решения схем, если схема особенно сложна, как показано на рисунке 5, то правило соединения Кирхгофа является наиболее эффективным методом. Давайте применим его, чтобы найти недостающие токи \(I_1,I_2,I_3\). Во-первых, мы можем применить правило соединения, чтобы найти \(I_1\). Поскольку \(I_1\) выходит из соединения, в которое входят потоки \(3\,\mathrm{A}\) и \(6\,\mathrm{A}\), мы знаем, что \[\begin{align} &-I_1+3\,\mathrm{A}+6\,\mathrm{A}=0\,\mathrm{A},\\\ подразумевает &I_1=9\,\mathrm{A}.\end{align}\]

Как и ожидалось, положительное значение, которое мы получаем для \(I_1\), говорит нам, что наше предположение было правильным, так что ток \(I_1\) должен вытекать перекрестка, справа налево.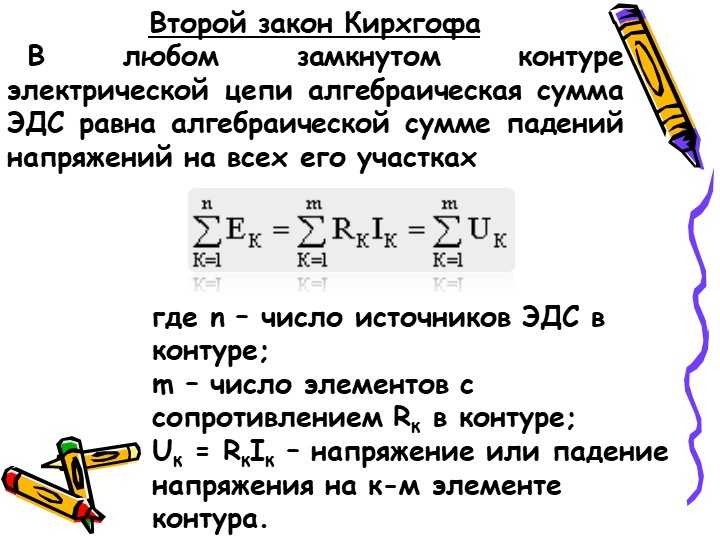

На следующем перекрестке, применяя правильный знак для направления тока, как указано на принципиальной схеме, мы находим \[\begin{align}I_1-I_2-2\,\mathrm{A}&=0\,\mathrm {A},\\\ подразумевает I_2=I_1-2\,\mathrm{A}&=7\,\mathrm{A}.\end{align}\]

Опять же, как и ожидалось, положительное значение подтверждает, что \(I_2\) вытекает из соединения вниз.

Есть два перекрестка, которые мы можем найти \(I_3\), давайте выберем нижний перекресток. Может показаться, что мы не знаем, каков третий ток на этом стыке вместе с \(I_2\) и \(I_3\). Однако обратите внимание, что между этим током и током \(3\,\mathrm{A}\), поступающим от нижней батареи, нет дальнейших соединений, поэтому это третий задействованный ток. Применение правила соединения, предполагающее, что \(I_3\) расположено слева направо (как показано на изображении), дает \[\begin{align}I_2+I_3-3\,\mathrm{A}&=0\,\mathrm{A },\\\подразумевает, что I_3=3\,\mathrm{A}-7\,\mathrm{A}&=-4\,\mathrm{A}.\end{align}\]

Подождите, мы получили отрицательное значение! Это означает, что наше предположение о направлении \(I_3\) было неверным. Мы заключаем, что \(I_3=4\,\mathrm{A}\), но его направление на самом деле справа налево. Изображение неправильное!

Это одно из самых полезных свойств законов Кирхгофа: они могут исправить любые неверные исходные предположения о направлении тока.

Правило соединения Кирхгофа: сохранение тока

Правило соединения Кирхгофа — это просто утверждение о сохранении тока в цепи. Сохранение тока само по себе является следствием основного закона сохранения заряда. Согласно фундаментальному закону сохранения, ни одна система не может нарушать закон сохранения заряда.

Закон сохранения тока гласит, что при фиксированных напряжении и сопротивлении ток не может быть создан или уничтожен в цепи.

Закон сохранения электрического заряда гласит, что общий электрический заряд изолированной системы, т. е. сумма всех отрицательных и положительных зарядов в системе, всегда должен оставаться постоянным. Например, общий заряд во Вселенной оставался постоянным с момента Большого взрыва.

Чтобы проиллюстрировать взаимосвязь между сохранением заряда и правилом соединения Кирхгофа, давайте представим сценарий, в котором правило соединения не выполняется.

Рассмотрим три потока \(I_1,I_2,I_3\), встречающиеся на узле, где \(I_1,I_2\) входят в узел и \(I_3\) выходят из него. Допустим,

\[I_1+I_2-I_3=x\,\mathrm{A},\text{ где } x\neq 0\,\mathrm{A}.\]

По определению тока это означает что каждую секунду \(x\,\mathrm{C}\) заряда самопроизвольно разрушается на стыке. Ясно, что это нарушает фундаментальный закон сохранения заряда, поэтому всегда должно выполняться правило соединения Кирхгофа.

Первый и второй закон Кирхгофа

Второй закон Кирхгофа, известный как правило цикла Кирхгофа, касается суммы разностей потенциалов вокруг контура в замкнутой цепи. При использовании в тандеме с правилом соединения Кирхгофа оно становится мощным инструментом для анализа сложных цепей и поиска неизвестных величин, таких как разности потенциалов, сопротивления и токи.

Правило петли Кирхгофа гласит, что сумма разностей потенциалов вокруг любой петли в цепи должна быть равна нулю: \[\sum_kV_k=0\,\mathrm{V}.\]

Правило петли Кирхгофа можно рассматривать как следствие закона сохранения энергии. Поскольку большинство параллельных цепей содержат несколько циклов, существует свобода выбора самого простого цикла для применения правила цикла Кирхгофа, которое часто значительно упрощает задачи. Чтобы применить правило контура, мы рассматриваем батареи как источники положительной разности потенциалов, в то время как компоненты, такие как резисторы, являются источниками отрицательной разности потенциалов. Давайте рассмотрим пример задачи, в которой мы можем применить оба правила для поиска недостающих величин. 9{-9}\,\mathrm{F}\) — емкость, а \(V\) — напряжение, которое нам пока неизвестно.

Мы можем применить оба закона Кирхгофа, чтобы найти недостающие разности потенциалов и токи в приведенной выше цепи, что также позволит нам найти заряд конденсатора.

Во-первых, правило пересечения Кирхгофа говорит нам, что токи \(I_1\) и \(I_2\), входящие и текущие \(I_3\), выходящие из перекрестка справа, должны удовлетворять \[\begin{align}I_1+I_2 -I_3&=0\,\mathrm{A},\\\ подразумевает I_1+I_2&=I_3.\end{align}\]

Левый узел — тот же самый случай, только знаки токов меняются местами, что приводит к эквивалентному уравнению.

Правило цикла Кирхгофа дает нам еще два условия, из которых мы можем найти все неизвестные переменные. Мы можем выбрать несколько разных контуров, но самый простой вариант — разделить цепь на два основных контура, верхний и нижний, оба в обход конденсатора. Мы знаем, что сумма разностей потенциалов вокруг каждой петли должна быть равна нулю, что дает следующие уравнения. \\3\,\mathrm{V}-V_2-V_3&=0\,\mathrm{V}.\end{align}\]

Мы можем выразить неизвестные разности потенциалов через токи и сопротивления резисторов, используя \(V=IR\), что в сочетании с уравнениями из правила соединения Кирхгофа образует набор решаемых одновременных уравнений.

\[\begin{align}&I_1+I_2=I_3\tag{1},\\&5\,\mathrm{V}-(3\,\mathrm{\Omega})I_1-(1\,\mathrm {\Omega})I_3=0\,\mathrm{V}\tag{2},\\&3\,\mathrm{V}-(1\,\mathrm{\Omega})I_3-(4\,\ mathrm{\Omega})I_2=0\,\mathrm{V}\tag{3}.\end{align}\]

Если мы разделим последние два уравнения на единицу \(\Omega\), мы получим три текущих уравнения:

\[\begin{align}&I_1+I_2=I_3\tag{1},\\&5\,\ mathrm{A}-3I_1-I_3=0\,\mathrm{A}\tag{2},\\&3\,\mathrm{A}-I_3-4I_2=0\,\mathrm{A}\tag{3 }.\end{align}\]

Подстановка \(I_3\) из первого уравнения в два других уравнения дает \[\begin{align}&5\,\mathrm{A}-4I_1-I_2=0 \,\mathrm{A}\tag{4},\\&3\,\mathrm{A}-I_1-5I_2=0\,\mathrm{A}\tag{5}.\end{align}\]

Мы можем изолировать \(I_2\), объединив \((4)\) и \((5)\) следующим образом\[\begin{align}(4)-4\times (5)&\ подразумевает -7\,\mathrm{A}+19I_2=0\,\mathrm{A},\\&\ подразумевает, что I_2=0,4\,\mathrm{A}.\end{align}\]Подставляя это в \(( 4)\) дает\[\begin{align}I_1=1.2\,\mathrm{A}.\end{align}\]

Соединяя все вместе в уравнение \((1)\), получаем, что все три тока равны \[I_1=1,2\,\mathrm{A},\, I_2=0,4\,\mathrm{A},\, I_3=1,5\,\mathrm{A}.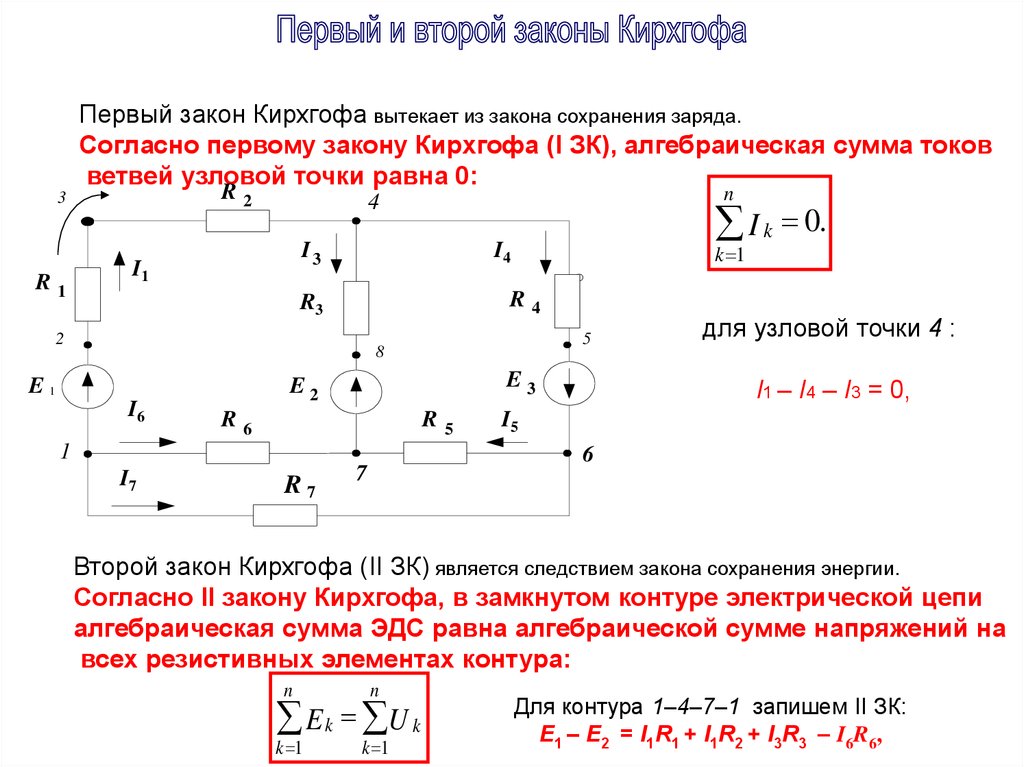 {-9}\,\mathrm{F}=7.6\,\mathrm{nC}.\]

Правило соединения Кирхгофа — основные выводы

• Соединение в цепи — это точка, в которой ток разделяется на несколько ветвей.
• Правило соединения Кирхгофа гласит, что сумма токов в соединении всегда должна быть равна нулю.
• По соглашению, токи, входящие в соединение, получают знак \(+\), а токи, выходящие из соединения, получают знак \(-\).
• Правило соединения — это просто следствие сохранения тока, которое само по себе является следствием сохранения заряда.
• Правило петли Кирхгофа гласит, что сумма разностей потенциалов вокруг любой петли цепи всегда должна быть равна нулю. Его можно использовать в тандеме с правилом соединений для решения сложных схем.

Ссылки

1. Рис. 1 — Густав Роберт Кирхофф (https://commons.wikimedia.org/wiki/File:Gustav_Robert_Kirchhoff.jpg) Смитсоновских библиотек находится в общественном достоянии.
2. Рис. 2 — Законы KCL-Kirchhoff’s Circuit Laws (https://commons. wikimedia.org/wiki/File:KCL_-_Kirchhoff%27s_circuit_laws.svg) от Pflodo под лицензией CC BY-SA 3.0 (https://creativecommons .org/licenses/by-sa/3.0/deed.en)
3. Рис. 3 — Серийная схема, StudySmarter Originals.
4. Рис. 4 – Параллельная схема, StudySmarter Originals.
5. Рис. 5 – Комплексная схема, StudySmarter Originals.
6. Рис. 6 — Схема конденсатора, StudySmarter Originals.

Часто задаваемые вопросы о правиле соединения Кирхгофа

Законы тока и напряжения Кирхгофа используются при анализе цепей для нахождения недостающих токов и напряжений. Они особенно полезны для анализа сложных схем, где В = ИК не подходит.

Правило соединения Кирхгофа гласит, что сумма токов, встречающихся в соединении цепи, всегда должна быть равна нулю.

Правило соединения Кирхгофа дает уравнение для множества токов {I_k}, встречающихся в соединении.

ΣI_k=0

Это можно изменить, чтобы найти отсутствующие токи, если другие известны.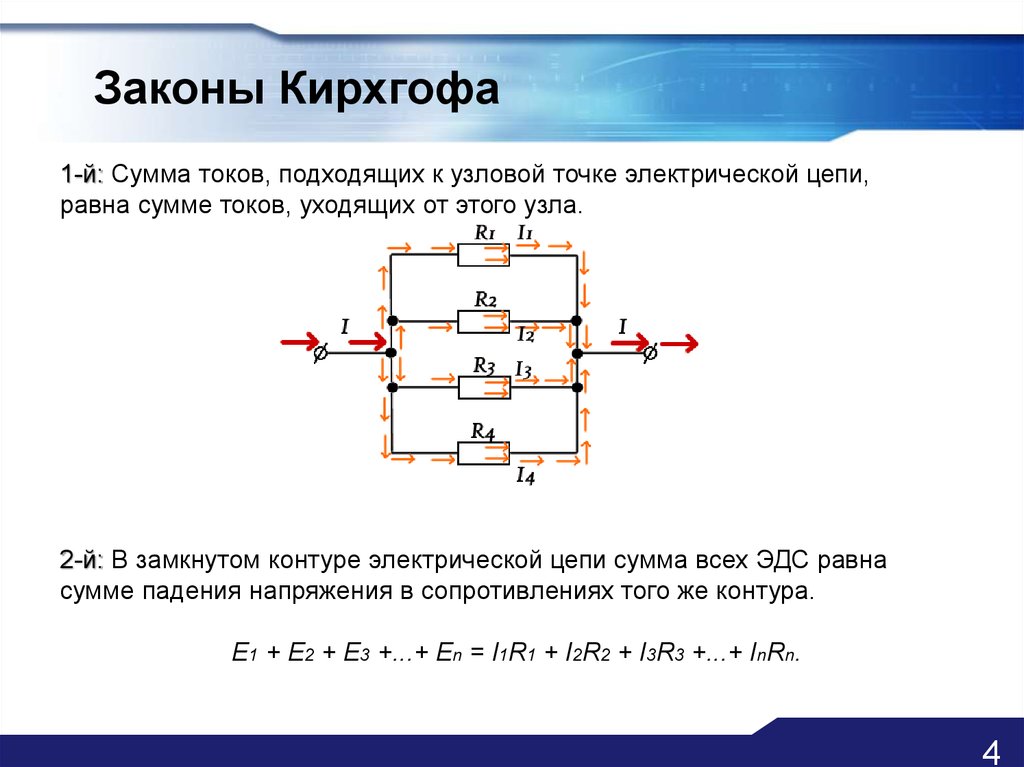

Есть два закона Кирхгофа. Правило соединения и правило цикла.

Для набора токов {I_k}, встречающихся на стыке,
ΣI_k=0.

Заключительная викторина по правилу соединения Кирхгофа

Вопрос

Укажите правило соединения Кирхгофа.

Показать ответ

Ответ

Сумма токов в узле всегда равна нулю с учетом их знаков в зависимости от того, идет ли ток в узел или от него.

Показать вопрос

Вопрос

Сформулировать правило петли Кирхгофа.

Показать ответ

Ответ

Сумма разностей потенциалов вокруг любого контура цепи равна нулю.

Показать вопрос

Вопрос

Три течения пересекаются на стыке. Если \(I_1=5\,\mathrm{A}\) и \(I_2=-3\,\mathrm{A}\), что такое \(I_3\)?

Показать ответ

Ответ

\(2\,\mathrm{A}\).

Показать вопрос

Вопрос

Ток \(10\,\mathrm{A}\) течет по проводу, который разделяется на две ветви. Если сопротивления ветвей равны \(R_1=1\,\mathrm{\Omega}\) и \(R_2=4\,\mathrm{\Omega}\) соответственно, каков ток через каждую ветвь?

Показать ответ

Ответ

\(I_1=8\,\mathrm{A}\) и \(I_2=2\,\mathrm{A}\).

Показать вопрос

Вопрос

Рассмотрим соединение с тремя токами \(I_1,\,I_2,\,I_3\). Первые два тока входят в узел и \(I_3\) выходят из него. Если \(I_1=I_3\), то что такое \(I_2\)?

Показать ответ

Ответ

\(I_2=0\,\mathrm{A}\).

Показать вопрос

Вопрос

Какое из этих утверждений верно для последовательных цепей?

Показать ответ

Ответ

Ток постоянен для всех компонентов.

Показать вопрос

Вопрос

Рассмотрим перекресток, содержащий четыре ответвления. Что из перечисленного не является возможной комбинацией токов?

Показать ответ

Ответ

\(+I,\,\frac{+I}{2},\,\frac{-I}{2},\,2I\).

Показать вопрос

Вопрос

Рассмотрим ответвление цепи с соединением на обоих концах. Если знак тока через ветвь \(+\) в одном переходе, то каков знак тока через другой переход?

Показать ответ

Ответ

\(-\).

Показать вопрос

Вопрос

Рассмотрим узел, в котором пересекаются 5 токов. Возможно ли, чтобы все токи имели одинаковую величину?

Показать ответ

Ответ

Показать вопрос

Вопрос

Следствием какого фундаментального закона сохранения является правило соединения Кирхгофа?

Показать ответ

Ответ

Сохранение электрического заряда.

Показать вопрос

Вопрос

Правило петли Кирхгофа является следствием какого фундаментального закона сохранения?

Показать ответ

Ответ

Сохранение энергии.

Показать вопрос

Вопрос

Количество ветвей, несущих ток в узел, должно быть равно количеству ветвей, несущих ток от узла.

Показать ответ

Ответ

Неверно.

Показать вопрос

Подробнее о правиле соединения Кирхгофа

Откройте для себя подходящий контент для ваших тем

Не нужно обманывать, если у вас есть все необходимое для успеха! Упаковано в одно приложение!

Учебный план

Будьте идеально подготовлены вовремя с индивидуальным планом.

Тесты

Проверьте свои знания с помощью игровых тестов.

Карточки

Создавайте и находите карточки в рекордно короткие сроки.

Заметки

Создавайте красивые заметки быстрее, чем когда-либо прежде.

Учебные наборы

Все учебные материалы в одном месте.

Документы

Загружайте неограниченное количество документов и сохраняйте их в Интернете.

Study Analytics

Определите сильные и слабые стороны вашего исследования.

Еженедельные цели

Ставьте индивидуальные учебные цели и зарабатывайте баллы за их достижение.

Умные напоминания

Хватит откладывать на потом наши напоминания об учебе.

Награды

Зарабатывайте очки, открывайте значки и повышайте уровень во время учебы.

Волшебный маркер

Создавайте карточки в заметках полностью автоматически.

Умное форматирование

Создавайте самые красивые учебные материалы, используя наши шаблоны.

Анализ законов цепей Кирхгофа и моделирование

Введение

Законы цепей Кирхгофа занимают центральное место в анализе цепей. У нас есть базовый инструмент для начала анализа цепей с помощью этих законов и уравнений для отдельных компонентов (резистора, конденсатора и катушки индуктивности). В этой статье мы рассмотрим законы тока и напряжения Кирхгофа и то, как их можно использовать при анализе цепей.

В модели электрических цепей с сосредоточенными элементами законы Кирхгофа о цепях представляют собой два равенства, которые имеют дело с током и разностью потенциалов, или напряжением. Немецкий физик Густав Кирхгоф впервые написал о них в 1845 году. Это произошло до исследования Джеймса Клерка Максвелла и обобщило выводы Георга Ома. Их часто называют законами Кирхгофа или просто законами Кирхгофа, и они широко используются в электротехнике. Эти правила служат основой для сетевого анализа и применимы как во временной, так и в частотной областях.

Зачем нужны законы Кирхгофа

Законы Кирхгофа можно использовать для расчета неизвестных величин в цепи, таких как ток и напряжение. Эти принципы полезны для поиска неизвестных значений в сложных схемах и сетях и могут применяться к любой схеме (с некоторыми ограничениями). Для определения значений тока и напряжения он также используется в узловом и сеточном анализе. Применение KVL (каждого контура) для вычисления тока через каждый независимый контур и подсчет всего тока для определения тока через любой компонент цепи (применимо в методе контурного тока). Чтобы лучше понять, как энергия движется по электрической цепи, обратитесь к законам Кирхгофа.

Расчет схемы по закону Кирхгофа

В этом эксперименте измерения напряжения и тока проводятся в последовательно-параллельной цепи. После этого закон Кирхгофа о петле и переходе проверяется путем сравнения теоретического расчета с фактическими измерениями напряжения и тока.

Оборудование и материалы:

• Блок питания
• Мультиметр
• Печатная плата
• 7 проводов для подключения
• 3 резистора (200, 400, 1K) Ом

Схема:

1. 
   Рис. 1. Схема по закону Кирхгофа

Процедура расчета схемы по закону Кирхгофа

Часть 1 Закон соединения:

1. Включите блок питания и установите напряжение 9,0 вольт. V 0 будет иметь это значение.
2. Соберите схему, показанную на рисунке выше, и соедините ее с блоком питания. Стоит отметить, что резисторы R1, R2 и R3 образуют последовательно-параллельную комбинацию.
3. Выберите режим амперметра на мультиметре. Амперметр следует подключать только последовательно к цепи на этом участке.
4. Подключите амперметр к точке B, соблюдая полярность, и запишите результат. Снова измерьте точки C, D, E, F и G.

Часть 2 Закон о петле:

1. Включите мультиметр в режим вольтметра. Вольтметр следует подключать к цепи параллельно только для этой части.
2. Соблюдая полярность, подключите вольтметр к точкам A и B, используя ту же схему, что и в части I, и запишите результаты.
3. Измерения следует повторить на участках C, D, а затем F, G соответственно.

Анализ закона Кирхгофа Цепь

Первый закон Кирхгофа Закон тока (KCL)

заряд, выходящий из узла, поскольку ему больше некуда идти, поскольку внутри узла заряд не тратится впустую». Другими словами, I(выход) + I(вход) = 0; алгебраическая сумма ВСЕХ токов, входящих и исходящих из узла, должна быть равна нулю. Теорию Кирхгофа часто называют законом сохранения заряда.

  I1 + I2 = I1

  I1 + I2=I1


«в любой сети с замкнутым контуром общее напряжение вокруг контура равно сумме всех падений напряжения внутри этого же контура», что также равно нулю. Другими словами, все напряжения внутри алгебраической суммы контура должны быть равны нулю. Теорию Кирхгофа называют законом сохранения энергии.


Рис. 3: KVL

Законы Кирхгофа о цепях занимают центральное место в анализе цепей постоянного тока. У нас есть базовый инструмент для начала анализа цепей с помощью этих законов и уравнений для отдельных компонентов (резистора, конденсатора и катушки индуктивности). В этой статье мы рассмотрим законы тока и напряжения Кирхгофа и то, как их можно использовать при анализе цепей. Законы Кирхгофа о цепях позволяют нам решать сложные проблемы с цепями, определяя набор фундаментальных сетевых законов и теорем для напряжений и токов в цепи. Мы можем рассчитать и найти токи и напряжения вокруг любой замкнутой цепи, используя закон Кирхгофа, относящийся к правилу соединения, и его правило замкнутого контура, если мы знаем значения электрических компонентов в ней. В учебнике по резисторам мы видели, что когда два или более резистора соединены последовательно, параллельно или в комбинации обоих, можно найти одно эквивалентное сопротивление (RT) и что эти цепи подчиняются закону Ома. Однако в сложных схемах, таких как мостовые или Т-образные сети, мы не всегда можем полагаться исключительно на закон Ома для определения напряжений или токов, циркулирующих в цепи.

Законы Кирхгофа о цепях Термины:

1. Цепь: Цепь представляет собой проводящую цепь с замкнутым контуром, по которой протекает электрический ток.
2.  Путь: одна линия, соединяющая два или более элементов или источников.
3. Узел: Узел — это соединение, соединение или терминал внутри цепи, где два или более элемента цепи соединены или соединены вместе, чтобы обеспечить точку соединения между двумя или более ветвями. Точка представляет собой узел.
4. Ветвь: Ветвь — это один или группа компонентов, соединенных между двумя узлами, такими как резисторы или источник.
5. Петля: Петля — это простой замкнутый путь в цепи, который не встречается ни с одним элементом или узлом цепи более одного раза.
6. Сетка: сетка представляет собой единый последовательный путь с замкнутым контуром, который лишен всех других путей.

Пример закона Кирхгофа о цепях

R3 40 Необходимо определить ток сопротивления. Схема имеет 3 ответвления, 2 узла (А и В) и 2 независимых контура. Уравнения представлены ниже с использованием закона тока Кирхгофа, сокращенно KCL:

I1 + I2 = I3 в узле A

I3 = I1 + I2 в узле B

Уравнения представлены ниже с использованием закона напряжения Кирхгофа, сокращенно KVL:

1-й контур выглядит следующим образом: R1 I1 + R3 I3 = 10I1 + 40 I3.

Дана петля 2n: R2 I2 + R3 I3 = 20 = 20I 2 + 40 I3

Дана петля 3: 10 – 20 = 10 I1 – 20 I2

Мы можем переписать уравнения следующим образом: Ур. № 1: 10 = 10I1 + 40(I1 + I2) = 50 I1 + 40 I2, так как I3 есть произведение I1 и I2.

Уравнение номер два: 20 = 20 I2 + 40 (I1 + I2) = 40 I1 + 60 I2

Используйте онлайн-симуляторы схем для моделирования и экспериментов с законами Кирхгофа. Онлайн-симуляторы схем могут упростить понимание законов Кирхгофа. Попробуйте виртуальную лабораторию от DCACLab бесплатно и нажмите кнопку инструмента анализа, чтобы отобразить все циклы и формулы.

Законы цепей Кирхгофа используются Пример 2:

Законы цепей Кирхгофа используются следующим образом для нахождения токов и напряжений в цепи, что называется «анализом» цепи.

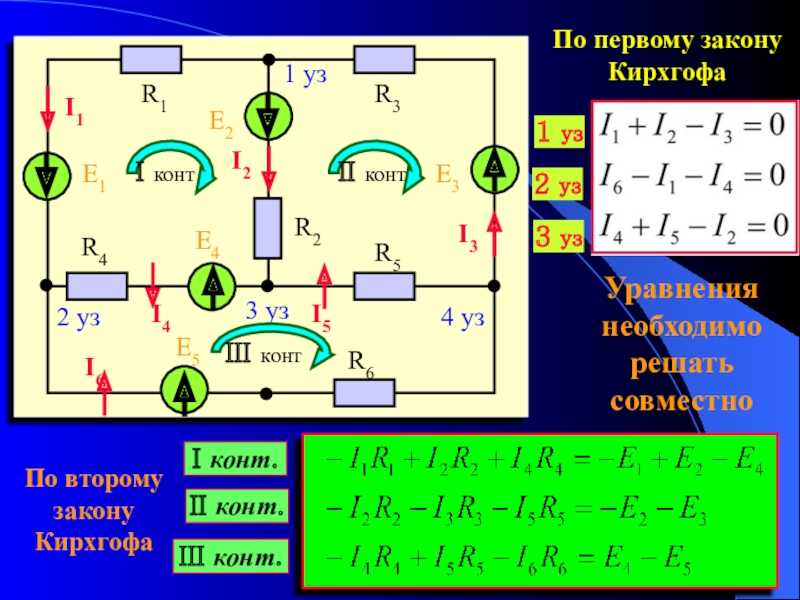
1. Предположим, что известны все сопротивления и напряжения. Если нет, напишите на них V1, V2, R1, R2 и т. д.
2. Распределяет ток (по часовой стрелке или против часовой стрелки) на каждую ветвь или сетку.