Второй закон Кирхгофа, теория и примеры

Онлайн калькуляторы

На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник

Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение

Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!

Главная Справочник Физика Второй закон Кирхгофа

Большое количество электрических цепей на практике являются сложными. Однако в цепь любого уровня сложности имеет элементы двух простейших видов. Это узлы и замкнутые контуры. Узел – это любая точка разветвления цепи, в которой сошлось три или более проводников, по которым текут токи.

Второе правило (закон) Кирхгофа является следствием обобщенного закона Ома. Так, если в изолированной замкнутой цепи есть один источник ЭДС, то сила тока в цепи будет такой, что сумма падения напряжения на внешнем сопротивлении и внутреннем сопротивлении источника будет равна сторонней ЭДС источника.

Если источников ЭДС несколько, то берут их алгебраическую сумму. Знак ЭДС выбирается положительным, если при движении по контуру в положительном направлении первым встречается отрицательный полюс источника. (За положительное направление обхода контура принимают направление обхода цепи либо по часовой стрелке, либо против нее).

Формулировка второго закона Кирхгофа

Произведение алгебраической величины силы тока (I) на сумму вешних и внутренних сопротивлений всех участков замкнутого контура равно сумме алгебраических значений сторонних ЭДС () рассматриваемого контура:

   

Каждое произведение определяет разность потенциалов, которая существовала бы между концами соответствующего участка, если бы ЭДС в нем была равно нулю. Величину называют падением напряжения, которое вызывается током.

Второй закон Кирхгофа иногда формулируют следующим образом:

Для замкнутого контура сумма падений напряжения есть сума ЭДС в рассматриваемом контуре.

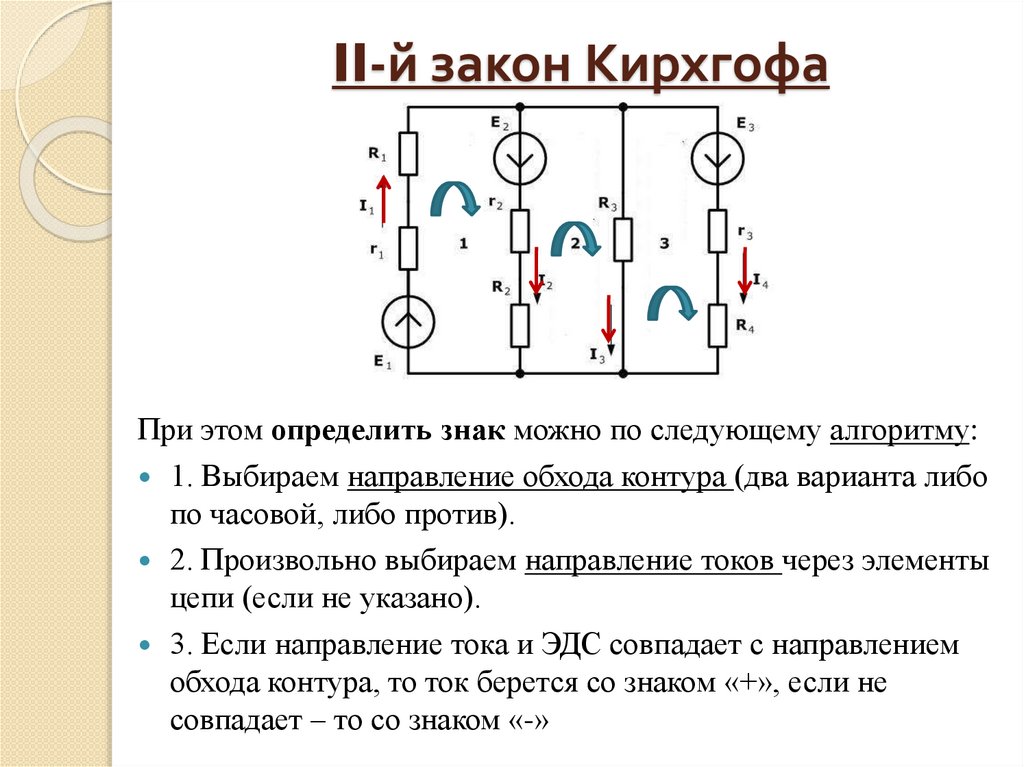
Правила Кирхгофа служат для того, чтобы составить систему уравнений, позволяющих найти силу тока для сложной цепи. Направление положительного обхода выбирают для всех контуров одинаковым. При составлении уравнений, используя правила Кирхгофа необходимо внимательно следить за расстановкой знаков токов и ЭДС.

Система уравнений, которая получается при использовании первого и второго закона Кирхгофа является полной и дает возможность отыскать все токи. При составлении уравнений, используя правила Кирхгофа, надо следить за тем, чтобы новое уравнение имело хотя бы одну величину, которая еще не вошла в предыдущие уравнения. Кроме того, необходимо, чтобы система уравнений имела число уравнений равное количеству неизвестных.

Второй закон Кирхгофа следует из того, что электрическое напряжение по замкнутому контуру равно нулю, то есть это правило является следствием основного свойства электростатического поля, которое заключается в том, что работа поля при движении заряда по замкнутой траектории равна нулю.

Примеры решения задач

Понравился сайт? Расскажи друзьям!

Уравнение по 2 закону кирхгофа

Два закона Кирхгофа вкупе с законом Ома составляют тройку законов, при помощи которых можно найти характеристики электрической цепи хоть какой трудности. Законы Кирхгофа мы будем инспектировать на примерах простых электрических схем, собрать которые не составит никакого труда. Для этого пригодится несколько резисторов, пара источников питания, в качестве которых подходят гальванические элементы (батарейки) и мультиметр.

1-ый закон Кирхгофа

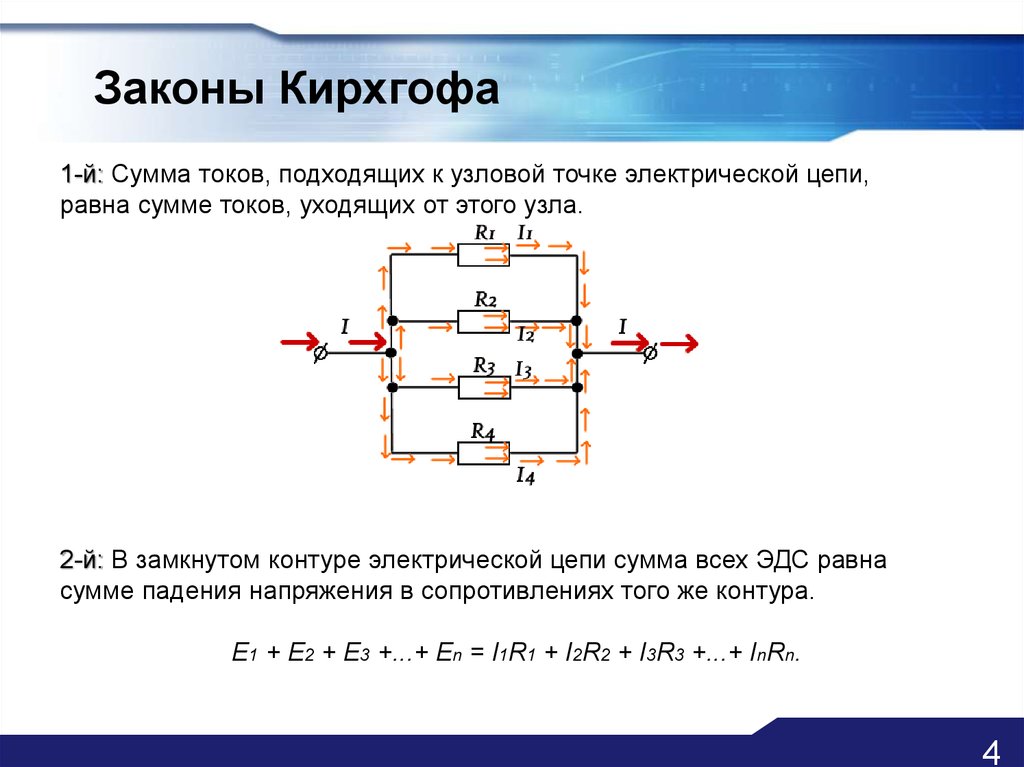
1-ый закон Кирхгофа гласит, что сумма токов в любом узле электрической цепи равна нулю. Существует и другая, подобная по смыслу формулировка: сумма значений токов, входящих в узел, равна сумме значений токов, выходящих из узла.

Давайте разберем произнесенное более тщательно. Узлом именуют место соединения 3-х и поболее проводников.

Ток, который втекает в узел, обозначается стрелкой, направленной в сторону узла, а выходящий из узла ток – стрелкой, направленной в сторону от узла.

Согласно первому закону Кирхгофа

Условно присвоили символ «+» всем входящим токам, а «-» ‑ все выходящим. Хотя это не принципно.

1 закон Кирхгофа согласуется с законом сохранения энергии, так как электрические заряды не могут скапливаться в узлах, потому, поступающие к узлу заряды покидают его.

Убедиться в справедливости 1-го закона Кирхгофа нам поможет обычная схема, состоящая из источника питания, напряжением 3 В (две последовательно соединенные батарейки по 1,5 В), три резистора различного номинала: 1 кОм, 2 кОм, 3,2 кОм (можно использовать резисторы всех других номиналов). Токи будем определять мультиметром в местах, обозначенных амперметром.

Если сложить показания 3-х амперметров с учетом символов, то, согласно первому закону Кирхгофа, мы должны получить ноль:

Либо показания первого амперметра А1 будет приравниваться сумме показаний второго А2 и третьего А3 амперметров.

2-ой закон Кирхгофа

2-ой закон Кирхгофа воспринимается начинающими радиолюбителями еще труднее, ежели 1-ый. Но на данный момент вы удостоверьтесь, что он довольно прост и понятен, если разъяснять его нормальными словами, а не заумными определениями.

Упрощенно 2 закон Кирхгофа гласит: сумма ЭДС в замкнутом контуре равна сумме падений напряжений

ΣE = ΣIR

Самый обычный случай данного закона разберем на примере батарейки 1,5 В и 1-го резистора.

Так как резистор всего один и одна батарейка, то ЭДС батарейки 1,5 В будет равна падению напряжения на резисторе.

Если мы возьмем два резистора одинакового номинала и подключим к батарейке, то 1,5 В распределятся поровну на резисторах, другими словами по 0,75 В.

Если возьмем три резистора опять одинакового номинала, к примеру по 1 кОм, то падение напряжения на них будет по 0,5 В.

Формулой это будет записано следующим образом:

Разглядим условно более непростой пример. Добавим в последнюю схему очередной источник питания E2, напряжением 4,5 В.

Направьте внимание, что оба источника соединены последовательно и согласно, другими словами плюс одной батарейки соединяется с минусом другой батарейки либо напротив. При таком методе соединения гальванических частей их электродвижущие силы складываются: E1 + E2 = 1,5 + 4,5 = 6 В, а падение напряжения на каждом сопротивлении составляет по 2 В. Формулой это описывается так:

И последний отличительный вариант, который мы разглядим в данной статье, подразумевает последовательное встречное соединение гальванических частей. При таком соединении источников питания из большей ЭДС отнимается значение наименьшей ЭДС. Поэтому к резисторам R1…R3 будет приложена разница E1 – E2, другими словами 4,5 – 1,5 = 3 В, – по одному вольту на каждый резистор.

2-ой закон Кирхгофа работает не зависимо от количества источников питания и нагрузок, также независимо от места их расположения в контуре схемы. Полезно будет собрать рассмотренные схемы и выполнить надлежащие измерения при помощи мультиметра.

Законы Кирхгофа действуют как для неизменного, так и для переменного тока.

При решении задач на законы Кирхгофа лучше придерживаться определенного метода: 1. найти число неведомых токов – столько уравнений должно быть в системе ; 2. найти количество узлов – уравнений по первому закону тогда необходимо составить на одно меньше; 3. проложить контуры и записать для них уравнения по второму закону. Кто желает разобраться конкретно – есть видео .

Задачка 1.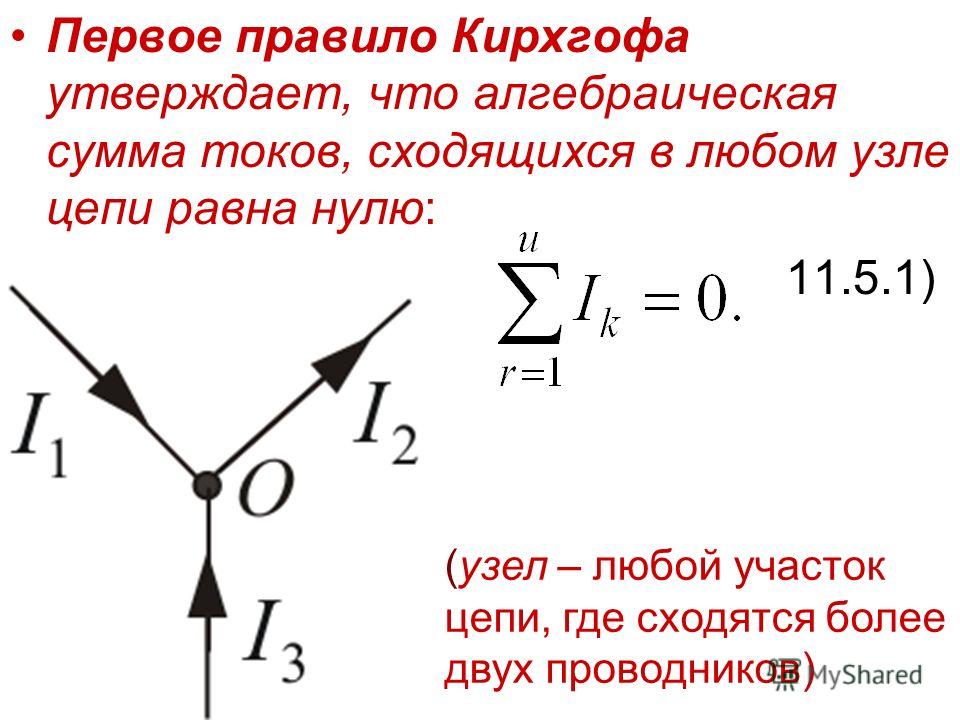 Два элемента с В и В соединены по схеме, показанной на рисунке . Сопротивление Ом. Внутреннее сопротивление частей идиентично Ом. Найти силу тока, идущего через сопротивление .

Обозначим токи в ветвях произвольно. По первому закону Кирхгофа сумма токов, сходящихся в узле, равна 0:

Будем обходить верхний контур против часовой стрелки. По второму закону Кирхгофа сумма падений напряжений в контуре равна сумме ЭДС:

Будем обходить 2-ой контур по часовой стрелке:

Неведомых токов – три, мы составили три уравнения. Этого довольно, дабы отыскать токи:

Выразим из второго уравнения, а – из третьего:

Подставим эти выражения в 1-ое уравнение:

Тогда токи и

Ответ: A, A, A.
Задачка 2. Отыскать силу тока на всех участках цепи‚ если В, В‚ В, Ом‚ Ом‚ Ом‚ Ом‚ Ом, Ом.

Обозначаем токи в ветвях произвольно, избираем направления обходов контуров и сами контуры. Составляем систему уравнений. Поначалу составим уравнение по первому закону Кирхгофа – у нас два узла, потому уравнение будет одно.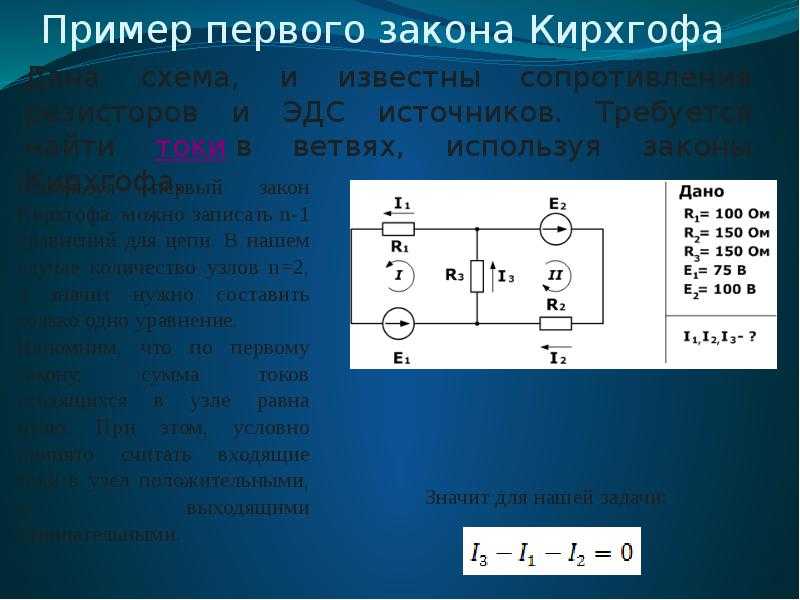

Потом, обходя контуры, составим два уравнения по второму закону: их необходимо составить два, так как неведомых токов в цепи три.

Решаем систему и находим ответ (я решала при помощи он-лайн калькулятора): , , .

Ответ: , , .

Задачка 3. В схеме, показанной на рисунке, отыскать силу тока через гальванометр, если В, кОм; В, кОм. Сопротивлением гальванометра пренебречь.

Нам непонятно сопротивление гальванометра, запишем для напряжения на нем два уравнения:

Заметим, что, если , то равенство будет выполнено. Таким макаром, ток через гальванометр не течет.

Ответ: .

Задачка 4. В цепи В‚ В, Ом, Ом. Отыскать рассредотачивание токов в цепи. Внутреннее сопротивление источников тока не учесть.

Обозначаем токи в ветвях произвольно, избираем направления обходов контуров и сами контуры. Составляем систему уравнений. Поначалу составим уравнение по первому закону Кирхгофа – у нас три узла, потому уравнений будет два. Потом, обходя контуры, составим три уравнения по второму закону: их необходимо составить конкретно три, так как неведомых токов в цепи 6.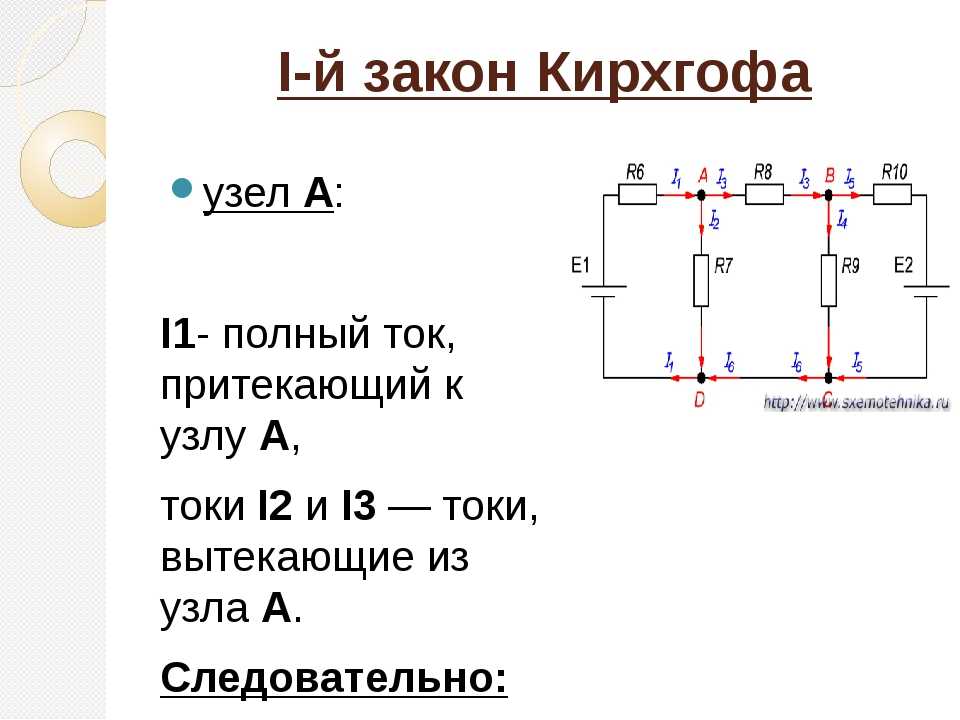

Решаем систему и находим ответ (я решала при помощи он-лайн калькулятора): , , , , , .

Ответ: , , , , , .
Задачка 5. Какую силу тока покажет амперметр в схеме, изображенной на рисунке? Сопротивлением амперметра пренебречь.

Обозначим токи в цепи произвольно. Обозначим направления обхода контуров. Запишем систему уравнений: составим три уравнения по первому закону (на одно меньше, чем количество узлов) и три уравнения по второму закону, так как неведомых токов 6 и система должна состоять из 6 уравнений.

Дабы пользоваться калькулятором, я задала Ом и В. В конечном итоге вышло: , , , , , .

Минусы свидетельствуют о обратном направлении тока в этой ветки тому, что мы нарисовали.

21.3 Правила Кирхгофа – Колледж физики

Резюме

• Проанализируйте сложную схему, используя правила Кирхгофа, используя соглашения для определения правильных знаков различных термов.

Многие сложные цепи, такие как схема на рис. 1, не могут быть проанализированы с помощью последовательно-параллельных методов, разработанных в главе 21.1 Резисторы в последовательном и параллельном соединении и главе 21.2 Электродвижущая сила: напряжение на клеммах. Однако есть два правила анализа цепей, которые можно использовать для анализа любой схемы, простой или сложной. Эти правила являются частными случаями законов сохранения заряда и сохранения энергии. Правила известны как

Правила Кирхгофа , в честь их изобретателя Густава Кирхгофа (1824–1887).

Рисунок 1. Эту схему нельзя свести к комбинации последовательного и параллельного соединений. Для его анализа можно использовать правила Кирхгофа, специальные приложения законов сохранения заряда и энергии. (Примечание: буква Е на рисунке обозначает электродвижущую силу, ЭДС.)

Правила Кирхгофа

• Первое правило Кирхгофа — правило пересечения. Сумма всех токов, входящих в соединение, должна равняться сумме всех токов, выходящих из соединения.
• Второе правило Кирхгофа — правило петли. Алгебраическая сумма изменений потенциала вокруг любой замкнутой цепи (петли) должна быть равна нулю.

Теперь будут даны объяснения двух правил, за которыми следуют советы по решению проблем для применения правил Кирхгофа и рабочий пример, который их использует.

Первое правило Кирхгофа (правило соединения ) представляет собой применение закона сохранения заряда к соединению; это показано на рис. 2. Ток — это поток заряда, а заряд сохраняется; таким образом, любой заряд, втекающий в соединение, должен вытекать наружу. Первое правило Кирхгофа требует, чтобы [латекс]\boldsymbol{I_1 = I_2 + I_3}[/латекс] (см. рисунок). Подобные уравнения могут и будут использоваться для анализа схем и решения схемных задач.

Установление соединений: законы сохранения

Правила Кирхгофа для анализа цепей представляют собой применение законов сохранения к цепям. Первое правило — применение закона сохранения заряда, а второе правило — применение закона сохранения энергии. Законы сохранения, даже используемые в конкретных приложениях, таких как анализ цепей, настолько просты, что составляют основу этого приложения.

Рисунок 2. Правило пересечения. На диаграмме показан пример первого правила Кирхгофа, в котором сумма токов, поступающих в соединение, равна сумме токов, выходящих из соединения. В этом случае ток, входящий в переход, разделяется и выходит в виде двух токов, так что I ₁ = I ₂ + I ₃ . Здесь I ₁ должно быть 11 А, так как I ₂ равно 7 А, а I ₃ 40 равно 9 А.

Второе правило Кирхгофа ( петлевое правило ) является применением закона сохранения энергии. Правило цикла сформулировано с точки зрения потенциала, [латекс]\boldsymbol{V}[/латекс], а не потенциальной энергии, но они связаны, поскольку [латекс]\boldsymbol{\textbf{PE}_{\textbf{ elec}} = qV}[/latex].

Напомним, что ЭДС — разность потенциалов источника при отсутствии тока. В замкнутом контуре любая энергия, поставляемая ЭДС, должна быть переведена в другие формы устройствами в контуре, поскольку нет других способов передачи энергии в контур или из него. На рис. 3 показаны изменения потенциала в простой последовательной цепи.

Второе правило Кирхгофа требует [латекс]\boldsymbol{\textbf{emf} — Ir — IR_1 — IR_2 = 0}[/latex]. В перестановке это [латекс]\boldsymbol{\textbf{ЭДС} = Ir + IR_1 + IR_2}[/latex], что означает, что ЭДС равна сумме [латекс]\boldsymbol{IR}[/латекс] (напряжение ) попадает в петлю.

Рисунок 3. Правило цикла. Пример второго правила Кирхгофа, согласно которому сумма изменений потенциала вокруг замкнутого контура должна быть равна нулю. (a) На этой стандартной схеме простой последовательной цепи ЭДС подает напряжение 18 В, которое сводится к нулю сопротивлениями, с 1 В на внутреннем сопротивлении и 12 В и 5 В на двух сопротивлениях нагрузки, для всего 18 В. (b) Этот вид в перспективе представляет потенциал как что-то вроде американских горок, где потенциал повышается за счет ЭДС и снижается за счет сопротивления. (Обратите внимание, что буква E означает emf.)

Применяя правила Кирхгофа, мы получаем уравнения, позволяющие находить неизвестные в цепях. Неизвестными могут быть токи, ЭДС или сопротивления. Каждый раз, когда применяется правило, создается уравнение. Если независимых уравнений столько же, сколько неизвестных, то задача решаема. При применении правил Кирхгофа вы должны принять два решения. Эти решения определяют знаки различных величин в уравнениях, которые вы получаете, применяя правила.

1. Применяя первое правило Кирхгофа, правило соединения, вы должны пометить ток в каждой ветви и решить, в каком направлении он течет. Например, на рис. 1, рис. 2 и рис. 3 токи помечены [латекс]\boldsymbol{I_1}[/латекс], [латекс]\boldsymbol{I_2}[/латекс], [латекс]\boldsymbol{I_3 }[/latex] и [latex]\boldsymbol{I}[/latex], а стрелки указывают их направления. Здесь нет никакого риска, потому что, если вы выберете неправильное направление, ток будет правильной величины, но отрицательным.
2. Применяя второе правило Кирхгофа, правило петли, вы должны определить замкнутую петлю и решить, в каком направлении ее обойти, по часовой или против часовой стрелки. Например, на рис. 3 петля была пройдена в том же направлении, что и ток (по часовой стрелке). Опять же, нет никакого риска; Обход цепи в противоположном направлении меняет знак каждого члена в уравнении, что похоже на умножение обеих частей уравнения на -1.

Рисунок 4 и следующие пункты помогут вам правильно расставить знаки плюс или минус при применении правила цикла. Обратите внимание, что резисторы и ЭДС пересекаются при переходе от a к b. Во многих схемах будет необходимо построить более одного контура. При обходе каждой петли необходимо следить за знаком изменения потенциала. (См. пример 1.)

Рисунок 4. Каждый из этих резисторов и источников напряжения проходит от a до b.

Возможные изменения показаны под каждым элементом и пояснены в тексте. (Обратите внимание, что буква E означает ЭДС.)

• Когда резистор перемещается в том же направлении, что и ток, изменение потенциала составляет [латекс]\жирный символ{-IR}[/латекс]. (См. рис. 4.)
• Когда резистор перемещается в направлении, противоположном току, изменение потенциала составляет [латекс]\boldsymbol{+IR}[/латекс]. (См. рис. 4.)
• Когда ЭДС перемещается от – к + (в том же направлении, что и положительный заряд), изменение потенциала составляет +ЭДС. (См. рис. 4.)
• Когда ЭДС перемещается от + к – (противоположно направлению движения положительного заряда), изменение потенциала равно −ЭДС. (См. рис. 4.)

Пример 1. Расчет тока: использование правил Кирхгофа

Найдите токи, протекающие в цепи на рисунке 5.

Рисунок 5. Эта цепь аналогична схеме на рисунке 1, но сопротивления и ЭДС заданы. (Каждая ЭДС обозначена буквой E.) Токи в каждой ветви помечены и предполагается, что они движутся в показанных направлениях. В этом примере для нахождения токов используются правила Кирхгофа.

Стратегия

Эта схема настолько сложна, что токи нельзя найти с помощью закона Ома и последовательно-параллельных методов — необходимо использовать правила Кирхгофа. На рисунке токи обозначены как [латекс]\boldsymbol{I_1}[/latex], [латекс]\boldsymbol{I_2}[/latex] и [латекс]\boldsymbol{I_3}[/latex]. сделал о своих направлениях. Места на схеме обозначены буквами от a до h. В решении мы будем применять правила соединения и петли, ища три независимых уравнения, которые позволят нам найти три неизвестных тока.

Решение

Начнем с применения первого правила Кирхгофа или правила соединения в точке а. Это дает

[latex]\boldsymbol{I_1 = I_2 + I_3} ,[/latex]

, так как [latex]\boldsymbol{I_1}[/latex] впадает в соединение, а [latex]\boldsymbol{I_2} [/latex] и [latex]\boldsymbol{I_3}[/latex] вытекают наружу. Применение правила соединения в точке e дает точно такое же уравнение, так что никакой новой информации не получается.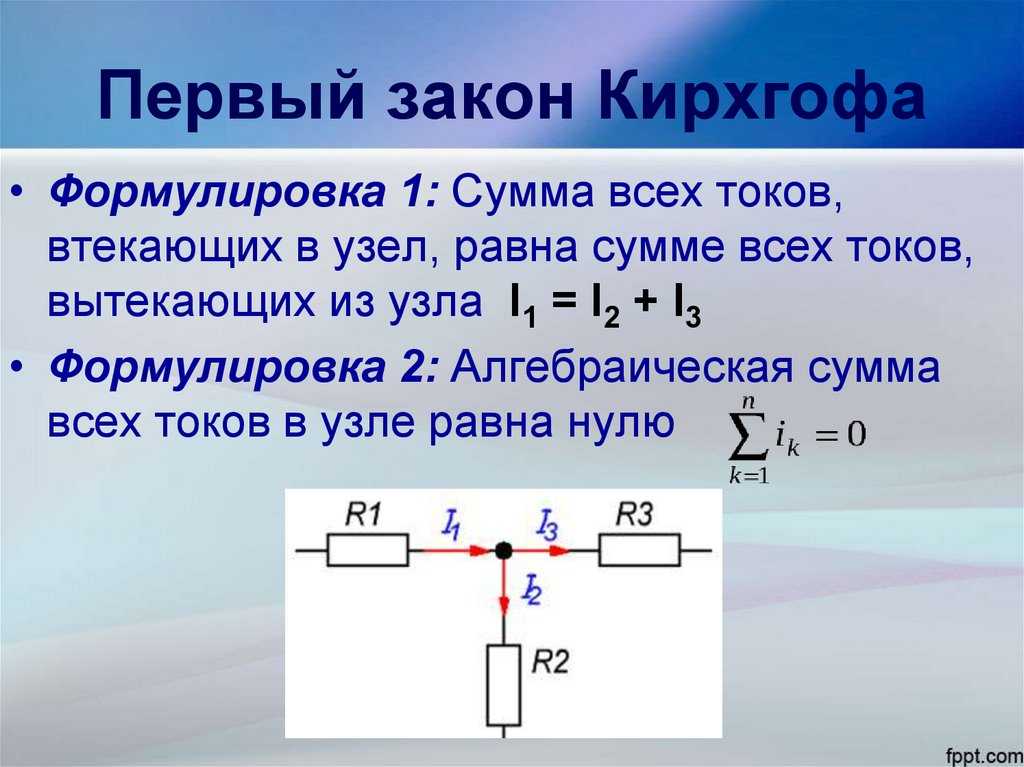 Это одно уравнение с тремя неизвестными — нужны три независимых уравнения, поэтому необходимо применить правило цикла.

Теперь рассмотрим цикл abcdea. Переходя от a к b, мы пересекаем [латекс]\boldsymbol{R_2}[/латекс] в том же (предполагаемом) направлении, что и текущий [латекс]\boldsymbol{I_2}[/латекс], поэтому изменение потенциала равно [латекс]\boldsymbol{-I_2R_2}[/латекс]. Затем, переходя от b к c, мы переходим от – к +, так что изменение потенциала составляет [латекс]\boldsymbol{+ \textbf{emf}_1}[/латекс]. Перемещение внутреннего сопротивления [латекс]\boldsymbol{r_1}[/латекс] от c к d дает [латекс]\boldsymbol{-I_2r_1}[/латекс]. Завершение цикла путем перехода от d к a снова пересекает резистор в том же направлении, что и его ток, что дает изменение потенциала [latex]\boldsymbol{-I_1R_1}[/latex].

Правило цикла гласит, что сумма изменений потенциала равна нулю. Таким образом,

[латекс]\boldsymbol{-I_2R_2 + \textbf{emf}_1 — I_2r_1 — I_1R_1 = -I_2(R_2 + r_1) + \textbf{emf}_1 — I_1R_1 = 0}. [/latex]

Подстановка сопротивлений и ЭДС значениями из принципиальной схемы и отмена единиц ампер дает

[латекс]\boldsymbol{-3I_2 + 18 -6I_1 = 0}.[/латекс]

Теперь применим правило цикла к aefgha ( мы могли бы выбрать и abcdefgha) аналогично дает

[латекс]\boldsymbol{+I_1R_1 + I_3R_3 + I_3r_2 — \textbf{emf}_2 = +I_1R_1 + I_3(R_3+r_2) — \textbf{emf}_2 = 0} .[/latex]

Обратите внимание, что знаки меняются местами по сравнению с другим циклом, потому что элементы проходятся в противоположном направлении. С введенными значениями это становится

[латекс]\boldsymbol{+6I_1 + 2I_3 — 45 = 0}.[/латекс]

Этих трех уравнений достаточно, чтобы решить для трех неизвестных токов. Сначала решим второе уравнение для [латекс]\boldsymbol{I_2}[/латекс]:

[латекс]\boldsymbol{I_2 = 6 — 2I_1}.[/latex]

Теперь решите третье уравнение для [латекс]\boldsymbol{I_3}[/латекс]:

[латекс]\boldsymbol{I_3 = 22.5 — 3I_1}.[/latex]

Подстановка этих двух новых уравнений в первое позволяет нам найти значение для [latex]\boldsymbol{I_1}[/latex]:

[latex]\boldsymbol{I_1 = I_2 + I_3 = (6 — 2I_1) + (22,5 — 3I_1) = 28,5 — 5I_1}. [/latex]

Объединение терминов дает

[latex]\boldsymbol{6I_1 = 28,5}[/latex] и

[латекс]\boldsymbol{I_1 = 4,75 \;\textbf{A}}.[/latex]

Подстановка этого значения вместо [латекс]\boldsymbol{I_1}[/латекс] обратно в четвертое уравнение дает

[латекс]\boldsymbol{I_2 = 6 — 2I_1 = 6 — 9,50}[/латекс]

[латекс]\boldsymbol{I_2 = -3,50 \;\textbf{A}}.[/latex]

Знак минус означает, что [латекс]\boldsymbol{I_2}[/латекс] течет в направлении, противоположном предполагаемому на рисунке 5.

Наконец, подстановка значения для [латекс]\жирныйсимвол{I_1}[/латекс] в пятое уравнение дает

[латекс]\boldsymbol{I_3 = 22,5 — 3I_1 = 22,5 — 14,25}[/latex]

[латекс]\boldsymbol{I_3 = 8,25 \;\textbf{A}}.[/latex]

Обсуждение

Просто для проверки отметим, что действительно [латекс]\boldsymbol{I_1 = I_2 + I_3}[/latex]. Результаты также можно проверить, введя все значения в уравнение для цикла abcdefgha.

Стратегии решения задач по правилам Кирхгофа

1. Убедитесь, что имеется четкая принципиальная схема, на которой вы можете отметить все известные и неизвестные сопротивления, ЭДС и токи. Если ток неизвестен, вы должны присвоить ему направление. Это необходимо для определения признаков потенциальных изменений. Если вы зададите направление неправильно, то обнаружится, что ток имеет отрицательное значение — никакого вреда не будет.
2. Применить правило соединения к любому соединению в цепи. Каждый раз, когда применяется правило соединения, вы должны получать уравнение с током, которого не было в предыдущем приложении — если нет, то уравнение избыточно.
3. Примените правило цикла к такому количеству циклов, которое необходимо для поиска неизвестных в задаче. (Независимых уравнений должно быть столько же, сколько и неизвестных.) Чтобы применить правило цикла, вы должны выбрать направление обхода цикла. Затем тщательно и последовательно определите знаки потенциальных изменений для каждого элемента, используя четыре маркированных пункта, рассмотренных выше в сочетании с рис. 4.9.0006
4. Решите уравнения для неизвестных. Это может включать в себя множество алгебраических шагов, требующих тщательной проверки и перепроверки.
5. Проверьте, разумны ли и последовательны ли ответы. Числа должны быть правильного порядка, ни чрезмерно большими, ни исчезающе малыми. Признаки должны быть разумными — например, отсутствие сопротивления не должно быть отрицательным. Убедитесь, что полученные значения удовлетворяют различным уравнениям, полученным в результате применения правил. Например, токи должны удовлетворять правилу соединения.

Теоретически материал в этом разделе верен. Мы должны быть в состоянии проверить это, произведя измерения тока и напряжения. На самом деле, некоторые из устройств, используемых для проведения таких измерений, представляют собой прямое применение принципов, рассмотренных до сих пор, и рассматриваются в следующих модулях. Как мы увидим, отсюда вытекает очень простой, даже глубокий факт: проведение измерения изменяет измеряемую величину.

• Правила Кирхгофа можно использовать для анализа любой схемы, простой или сложной.
• Первое правило Кирхгофа — правило соединения: сумма всех токов, входящих в соединение, должна равняться сумме всех токов, выходящих из соединения.
• Второе правило Кирхгофа — правило петли: алгебраическая сумма изменений потенциала вокруг любого замкнутого контура (петли) должна быть равна нулю.
• Два правила основаны соответственно на законах сохранения заряда и энергии.
• При расчете потенциала и тока по правилам Кирхгофа необходимо соблюдать ряд правил для определения правильных знаков различных членов.
• Простые ряды и параллельные правила являются частными случаями правил Кирхгофа.

Правила Кирхгофа

набор из двух правил, основанных на сохранении заряда и энергии, управляющих током и изменениями потенциала в электрической цепи

соединительная линейка

первое правило Кирхгофа, применяющее закон сохранения заряда к соединению; ток — это поток заряда; таким образом, любой заряд, втекающий в соединение, должен вытекать наружу; правило может быть сформулировано [латекс]\boldsymbol{I_1 = I_2 + I_3}[/latex]

правило цикла

Второе правило Кирхгофа, которое гласит, что в замкнутом контуре любая энергия, поставляемая ЭДС, должна быть переведена в другие формы устройствами в контуре, поскольку нет других способов передачи энергии в контур или из него. Таким образом, ЭДС равна сумме [latex]\boldsymbol{IR}[/latex] (напряжения) падений в контуре и может быть сформулирована следующим образом: [latex]\boldsymbol{\textbf{ЭДС} = Ir + IR_1 + IR_2 }[/латекс]

законы сохранения

требуют сохранения энергии и заряда в системе

 

Законы Кирхгофа, Закон Кирхгофа о напряжении и Закон Кирхгофа о токе

Базовая электроника

Энгр Фахад Отправить письмо 14 февраля 2020 г.

426

Содержание

1

Введение:

Законы Кирхгофа: эти законы используются для нахождения тока в различных ветвях электрической сети, которые могут быть легко решены с помощью закона Ома, Законы Кирхгофа два в числе

1. Первый закон Кирхгофа или действующий закон Кирхгофа «KCL»
2. Петлевой закон Кирхгофа или закон напряжения Кирхгофа или закон сетки Кирхгофа «KVL».

Законы Кирхгофа применимы как к переменному, так и к постоянному току.

1. Действующий закон Кирхгофа

Действующий закон Кирхгофа этот закон гласит, что в любой электрической сети

«Алгебраическая сумма токов, встречающихся в узле, узле или точке, равна нулю»

Или

Другими словами, «сумма токов, текущих к узлу, равна сумме токов, утекающих от узла ».

Рассмотрим расположение четырех проводов, соединенных вместе в точке «0», как показано на рис. ниже.

Стрелки указывают направление тока. Токи I ₁ и I ₄ идут к узлу, а ток I ₂ и I ₃ выходят из узла, мы принимаем (предположим) знак +ive для входящего тока и знак –ive для исходящего тока. Теперь по действующему закону Кирхгофа «KCL»

∑I=0

Теперь по рис. =0

I ₁ +I ₄ -I ₂ -I ₃ =0

I ₁ +I _{4 09 3} =I 903

Или входящие токи = исходящие токи

Задача 1:

Определить токи I3 и I4 для подающей цепи, используя закон тока Кирхгофа «KCL».

Решение:

в точке A By Kirchhoff’s

∑ I _{Входящее} = ∑ I _{, исходящие}

I ₁ +I ₂ = I9 3 ₁ +I ₂ = I _{3 3 111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111. I 3}

= I ₃ = 5

в точке «B» по закону Кирххоффа

∑ iincoming = ∑iouting

I ₃ + I ₅ = I ₄

5 + 1 = I ₄

9008 I _{8 4} 40404040404 4 40404 4 4040404 4 4 4 404 4 4 4 4 4 4 4 4. 6 _AMP

Проблема2:

Найти I ₁ , I ₃ , I ₄ , и I ₅ в сети

7

. Решение. а

I= I ₁ +I ₂

5=I ₁ +4

5-4=I1

I ₁ =1 _ампер

Так как R1 и R3 последовательно соединены пройти через каждый резистор, поэтому

I ₃ = 1 _ампер

И мы знаем, что R2 и R4 соединены последовательно, поэтому ток будет одинаковым, поэтому

I ₄ = 4 _ампер

40

0

0 Я ₅ = Я ₄ + Я ₃

I ₅ =4+1

I ₅ =5 _amp

Problem3:

Find the magnitude and direction of I ₃ and I ₄

I ₆ и I ₇ для сети, использующей текущий закон Кирхгофа KCL.

Решение:

Входящий ток I ₁ = 10 ампер

Исходящий ток I ₇ = 10 ампер

В точке b мы видим, что

I ₂ = I ₄ +I ₅

I ₂ = I ₄ +8

4 = I ₄

at Point D Wee

I ₀

. 7 = I ₅ + I ₆

10 = 8 + I ₆

10-8 = I ₆

I ₆ = 2 _AMP

AT AT AT C POTE см.

I ₆ + I ₃ = I ₄

2 +I ₃ = 4

I ₃ = 2 _ампер

2. Закон Кирхгофа о напряжении:

Этот закон гласит, что «алгебраическая сумма всех напряжений, взятых в заданном направлении по замкнутому контуру, равна нулю».

Математически

∑v=0

Замкнутая петля:

Замкнутая петля или замкнутый путь — это любой непрерывный путь, который достигает точки в одном направлении и возвращается в ту же точку в другом направлении, не выходя из цепи.