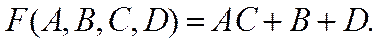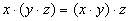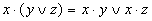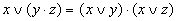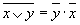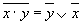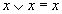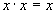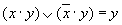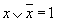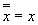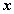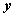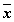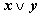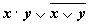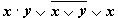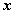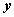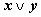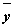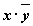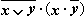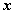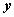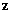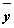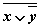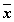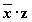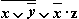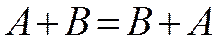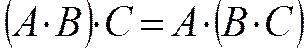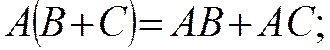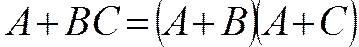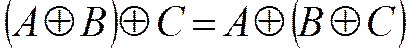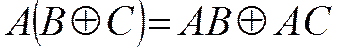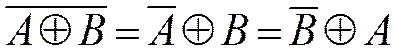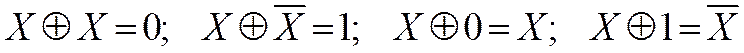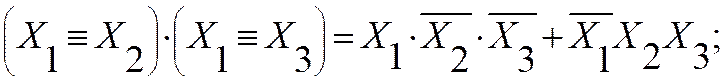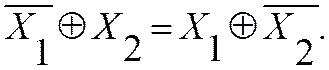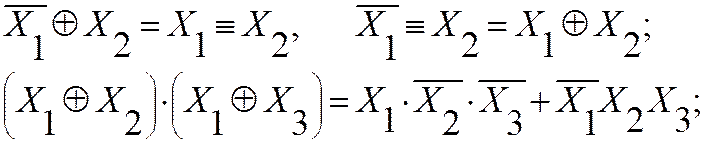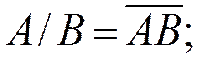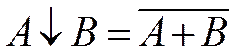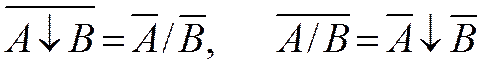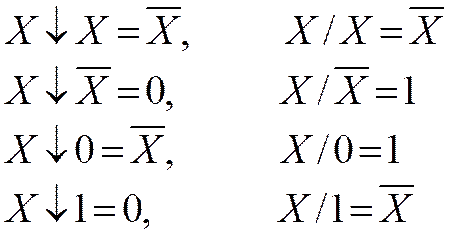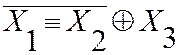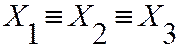_02Л_Законы АЛ

Основные законы булевой алгебры

В алгебре логики аналогично обычной математике раскрытие сложных выражений подчиняется определённым законам. Сложные логические выражения выполняются в следующей последовательности:

1)инверсия;

2. конъюнкция;

3. дизъюнкция.

Если необходимо изменить последовательность операций, то используются скобки. Операции в скобках выполняются в первую очередь. Если одни скобки вложены в другие, то вначале выполняются операции во внутренних скобках.

Над логическими выражениями производят тождественные преобразования с использованием законов булевой алгебры.

Две функции являются эквивалентными, если они принимают одинаковые значения на одних и тех же наборах входных переменных.

Две эквивалентные функции, приравненные друг к другу, называются тождеством.

1. Переместительный закон (аналогично обычной алгебре):

—для дизъюнкции

—для конъюнкции

От перемены мест логических слагаемых (сомножителей) их логическая сумма (логическое произведение) не меняется.

2. Сочетательный закон (аналогично обычной алгебре):

—для дизъюнкции

—для конъюнкции

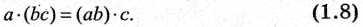
Можно различным образом группировать логические переменные при выполнении операции конъюнкции (дизъюнкции) при этом значение булевой переключательной функции не изменяется.

3. Распределительный закон

Распределительный закон здесь также справедлив, как и в обычной алгебре. Специфика его в булевой алгебре проявляется в некоторых частных случаях. Эти специфичные случаи и формулируются как распределительный закон булевой алгебры:

—для конъюнкции

конъюнкция переменной и дизъюнкции эквивалентна дизъюнкции конъюнкций;

—для дизъюнкции

(a v b)(a v c)=a v bc,

дизъюнкция переменной и конъюнкции равносильна конъюнкции дизъюнкций этой переменной с сомножителями.

Справедливость распределительного закона для дизъюнкции докажем следующими простейшими преобразованиями:

(a v b

)(a v c)= (aa v ac v ab v bc)=a v a(b v c) v bc=a(1 v (b v c)) v bc .

В результате получаем

(a v b)(a v c)=a v bc,

так как 1 v (b v c)=1 независимо от выражения в скобках.

4. Закон инверсии. Закон де Моргана.

—для дизъюнкции

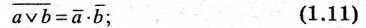
отрицание дизъюнкции логических переменных эквивалентно конъюнкции отрицаний этих переменных;

—для конъюнкции

отрицание конъюнкции переменных эквивалентно дизъюнкции отрицаний этих переменных.

Справедливость законов отрицания (де Моргана) докажем с помощью таблиц истинности.

Таблица. Закон отрицания (де Моргана) для дизъюнкции

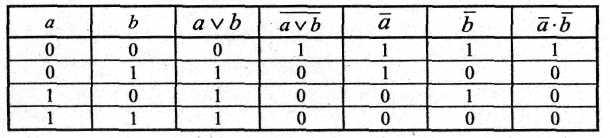
Таблица. Закон отрицания (де Моргана) для конъюнкции

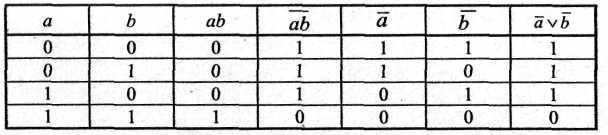
Таблицы 1.5; 1.6 показывают, что на одинаковых наборах переменных значения функций совпадает. Законы де Моргана доказаны.

5. Законы повторения

— для дизъюнкции.

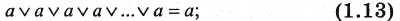
—для конъюнкции

Многократное логическое сложение (логическое умножение) одной переменной равно самой этой переменной.

Законы повторения булевой алгебры существенно отличаются от законов повторения обычной алгебры.

6. Закон двойного отрицания

Двойное отрицание логической переменной равно самой логической перемененной.

7. Соотношения с нулем и единицей

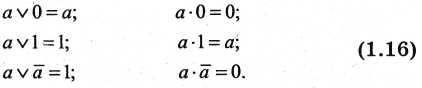
8. Закон склеивания:

Докажем законы склеивания эквивалентными преобразованиями

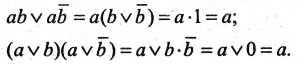
9. Законы поглощения

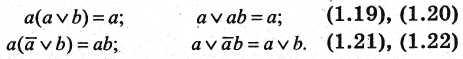
Доказательства законов поглощения

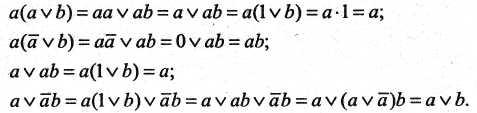
10. Умножение и сложение переменной и функции

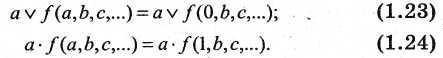
Формулы умножения и сложения позволяют существенно упростить техническую реализацию логического устройства, заменить переменную некоторой константой: логической 1 либо логическим 0.

Пример.

Правила алгебры логики позволяют преобразовать логическую функцию к виду, удобному для реализации в виде логического устройства.

Например, задана функция

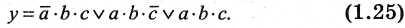
Для реализации функции в данном виде требуется два инвертора НЕ, три трехвходовых элемента ЗИ, один трехвходовый элемент ЗИЛИ (рис. 3).

Проведем эквивалентные преобразования с использованием закона поглощения

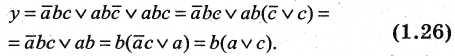
Очевидно, что после преобразования функция значительно упростилась. Для реализации теперь достаточно иметь один двухвходовый элемент 2И, один двухвходовый элемент 2ИЛИ (рис.3). Обе схемы позволяют реализовать одну и ту же функцию.

8.3. Логическая формул.Законы алгебрЫ логики

Логические формулы

С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой.

Всякая логическая переменная и символы «истина» («1») и «ложь» («0») — формулы.

Если  А и В — формулы,   то 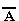  ,   А^. В ,   А v В ,   А B ,   А

В   —формулы.

Никаких других формул в алгебре логики нет.

В качестве примера рассмотрим высказывание «Если я куплю яблоки или абрикосы, то приготовлю фруктовый пирог«. Это высказывание формализуется в виде (A v B) C.

Как показывает анализ формулы (A v B) C, при определённых сочетаниях значений переменных A, B и C она принимает значение «истина», а при некоторых других сочетаниях — значение «ложь» (разберите самостоятельно эти случаи). Такие формулы называются

выполнимыми.

Некоторые формулы принимают значение «истина» при любых значениях истинности входящих в них переменных. Таковой будет, например, формула А v 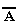, соответствующая высказыванию «Этот треугольник прямоугольный или косоугольный«. Эта формула истинна и тогда, когда треугольник прямоугольный, и тогда, когда треугольник не прямоугольный. Такие формулы называются тождественно истинными формулами или тавтологиями. Высказывания, которые формализуются тавтологиями, называются логически истинными высказываниями.

В качестве другого примера рассмотрим формулу А 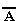^* , которой соответствует, например, высказывание«Катя самая высокая девочка в классе, и в классе есть девочки выше Кати«. Очевидно, что эта формула ложна, так как либо А, либо 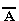обязательно ложно. Такие формулы называютсятождественно ложными формулами или противоречиями. Высказывания, которые формализуются противоречиями, называются логически ложными высказываниями.

Если две формулы А и В одновременно, то есть при одинаковых наборах значений входящих в них переменных, принимают одинаковые значения, то они называются равносильными.

Равносильность двух формул алгебры логики обозначается символом «=» или символом «» Замена формулы другой, ей равносильной, называетсяравносильным преобразованием данной формулы.

Основные законы алгебры логики

В алгебре логики выполняются следующие основные законы, позволяющие производить тождественные преобразования логических выражений (табл. 8.6):

Основные законы алгебры логики

Таблица 8. 6

Закон	Для   ИЛИ	Для И
Переместительный
Сочетательный
Распределительный
Правила де Моргана
Идемпотенции
Поглощения
Склеивания
Операция переменной с ее инверсией
Операция с константами
Двойного отрицания

8.4. Таблицы истинности

Таблица истинности логической формулы выражает соответствие между всевозможными наборами значений переменных и значениями формулы.

Для формулы, которая содержит две переменные, таких наборов значений переменных всего 2² — четыре: (0, 0),     (0, 1),     (1, 0),     (1, 1).

Если формула содержит три переменные, то возможных наборов значений переменных 2³ — восемь: (0, 0, 0),     (0, 0, 1),     (0, 1, 0),     (0, 1, 1),     (1, 0, 0),     (1, 0, 1),     (1, 1, 0),     (1, 1, 1).

Количество наборов для формулы с четырьмя переменными равно шестнадцати и т.д.

Удобной формой записи при нахождении значений формулы является таблица, содержащая кроме значений переменных и значений формулы также и значения промежуточных формул.

Пример 1

Составьте таблицу истинности для формулы , которая содержит две переменныеx и y. В двух первых столбцах таблицы запишите четыре возможных пары значений этих переменных, в последующих столбцах — значения промежуточных формул и в последнем столбце — значение формулы. В результате получите таблицу 8.7:

Таблица истинности для примера 1

Таблица 8. 7

Переменные		Промежуточные логические формулы					Формула
0	0	1	0	0	1	1	1
0	1	1	1	1	0	1	1
1	0	0	0	1	0	0	1
1	1	0	0	1	0	0	1

Из таблицы видно, что при всех наборах значений переменных x и y формула 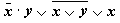принимает значение 1, то есть является тождественно истинной.

Пример 2

Таблица истинности для формулы приведена в табл. 8.8:

Таблица истинности для примера 2

Таблица 8. 8

Переменные		Промежуточные логические формулы				Формула
0	0	0	1	1	0	0
0	1	1	0	0	0	0
1	0	1	0	1	1	0
1	1	1	0	0	0	0

Из таблицы видно, что при всех наборах значений переменных x и y

формула принимает значение 0, то есть является тождественно ложной.

Пример 3

Таблица истинности для формулы приведена в табл. 8.9:

Таблица истинности для примера 3

Таблица 8. 9

Переменные			Промежуточные логические формулы					Формула
0	0	0	1	1	0	1	0	0
0	0	1	1	1	0	1	1	1
0	1	0	0	0	1	1	0	1
0	1	1	0	0	1	1	1	1
1	0	0	1	1	0	0	0	0
1	0	1	1	1	0	0	0	0
1	1	0	0	1	0	0	0	0
1	1	1	0	1	0	0	0	0

Из таблицы видно, что формула внекоторых случаях принимает значение 1, а в некоторых — 0, то есть является выполнимой.

Законы алгебры логики

Для преобразования логических формул к равносильным используются законы алгебры логики:

1. законы коммутативности
   • x ∧ y = y ∧ x
   • x ∨ y = y ∨ x
2. законы ассоциативности
   • (x ∧ y) ∧ z = x ∧ (y ∧ z)
3. (x ∨ y) ∨ z = x ∨ (y ∨ z)
4. законы поглощения (нуля и единицы)
5. законы дистрибутивности
   • x ∧ (y ∨ z) = (x ∧ y) ∨ (x ∧ z)
   • x ∨ (y ∧ z) = (x ∨ y) ∧ (x ∨ z)
6. закон противоречия
7. закон исключенного третьего
8. законы идемпотентности
9. закон двойного отрицания
10. законы де Моргана
    • ¬ (x ∧ y) = ¬ x ∨ ¬ y
    • ¬ (x ∨ y) = ¬ x ∧ ¬ y
11. законы поглощения
12. x ∧ (x ∨ y) = x

Законы алгебры логики достаточно просто доказываются с применением различных способов.

Пример 1. Докажем второй закон де Моргана с помощью таблицы истинности. Построим таблицу истинности для левой и правой части закона.

x	y	x ∨ y	¬ (x ∨ y)	¬ x	¬ y	¬ x ∧ ¬ y
0	0	0	1	1	1	1
0	1	1	0	1	0	0
1	0	1	0	0	1	0
1	1	1	0	0	0	0

Заметим, что результирующие столбцы в таблице истинности совпали. Таким образом, формулы в левой и правой части закона равносильны.

Пример 2. Докажем второй закон дистрибутивности (который несправедлив в алгебре чисел) путем тождественных преобразований.

1) Для доказательства раскроем скобки в правой части закона:
  (x + y) • (x + z) = x • x + x • z + y • x + y • z
2) Используем закон идемпотентности: x • x = x. В результате имеем,
  x + x • z + y • x + y • z
3) Применим закон поглощения x + x • z = x. После преобразования получим,
  x + y • x + y • z
4) Применим закон поглощения x + y • x = x. Окончательно получаем,
  x + y • z
Таким образом, (x + y) • (x + z) = x + y • z
Равенство доказано.

Законы алгебры логики. Последовательность выполнения операций в алгебре логики

1.4 Законы алгебры логики

Последовательность выполнения операций в алгебре логики: при наличии скобок сначала осуществляются операции внутри них, затем инверсии, после логические умножение и, затем, сложение (таблица 1.4.1).

Эквивалентность выражений в алгебре логики проверяется с помощью составления таблицы истинности для всех возможных наборов переменных, значения которых для сравниваемых выражений должны быть одинаковы.

Законы алгебры логики на примере логических функций И, ИЛИ                         Таблица 1.4.1

Переместительный
Сочетательный
Распределительный

1.4.1 Свойства логических функций (таблицы 1.4.2 ..1.4.6)

Свойства логических функций ИЛИ, И, НЕ                                                               Таблица 1.4.2

Правила и тождества  для функций И, ИЛИ, НЕ                                                       Таблица 1.4.3

Правила и тождества  для функций И, ИЛИ, НЕ (продолжение)                    

Законы алгебры логики для логической функции исключающее ИЛИ                  Таблица 1.4.4

Переместительный
Сочетательный
Распределительный

Свойства функций исключающее ИЛИ и эквивалентности                                     Таблица 1.4.5

Определение операции
Правило Де Моргана
Свойства
Тождества

Свойства функций стрелка Пирса, штрих Шеффера                                                 Таблица 1.4.6

Определение операций «/», «¯»
Правило Де Моргана
Свойства

1.4.2 Суперпозиция

подстановка в логические функции вместо переменных других логических выражений позволяет получить функции желательного числа переменных, например:

 

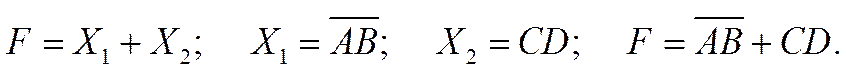1.4.3 Принцип двойственности

Из таблицы 1.3.2 следует, что у функций с взаимно дополняющими номерами i  и 15 – i значения для одинаковых наборов переменных являются инверсными друг к другу. В тоже время, инверсия всех значений функции – инверсия самой функции.

Пример для функций F₇ и F₈; F₆ и F₉:

 

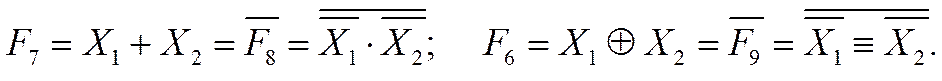Следовательно, при переходе от одной операции к другой (с взаимно дополняющими номерами) все переменные и выражение в целом должны инвертироваться.

Частный случай этого принципа – правило Де Моргана.

1.4.4 Примеры использования правил алгебры логики

Пример: преобразование логических операций и доказательство справедливости с помощью таблицы истинности.

 

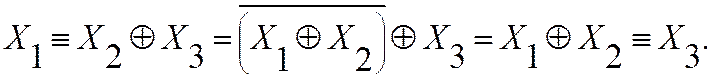Произошла замена операции сложения по модулю два на операцию эквивалентности и наоборот, что справедливо для любого нечетного количества переменных (в преобразованиях использовались тождества и определение операций).

Проверка справедливости первого аналитического выражения с помощью таблицы истинности (таблица 1.4.7):

Таблица истинности                                                                                               Таблица 1.4.7

№	X1	X2	X3
0	0	0	0	0	0	0
1	0	0	1	1	1	1
2	0	1	0	1	1	1
3	0	1	1	0	0	0
4	1	0	0	1	1	1
5	1	0	1	0	0	0
6	1	1	0	0	0	0
7	1	1	1	1	1	1

Например, для набора № 0 (первая строка), где все переменные равны логическому нулю, имеем:

 

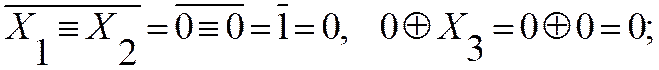Следовательно, на данном наборе (как и на других) выполненные преобразования верны.

Пример: доказать правило поглощения в аналитическом виде.

 

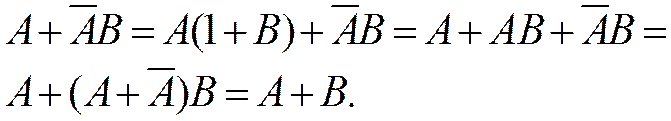Пример: упросить аналитическое выражение, используя законы алгебры логики:

1-й шаг. На основании переместительного закона во всех членах выражения размещаем переменные в одном и том же порядке (подчеркивание снизу для обозначения переменных, которые будут группироваться в следующем шаге):

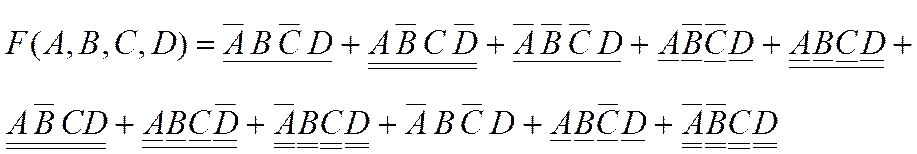
2-й шаг. Группируем члены таким образом, чтобы в каждую пару входили переменная, и ее инверсия:

3-й шаг. Руководствуясь распределительным законом, в каждой группе выносим за скобку одинаковые переменные:

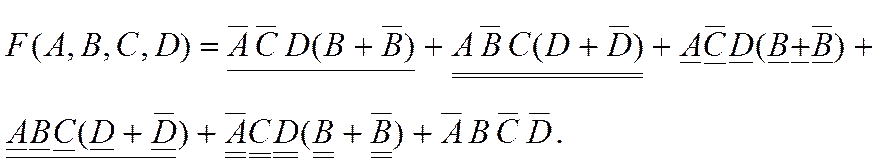
4-й шаг. Согласно свойствам логических функций (закон дополнения) имеем:

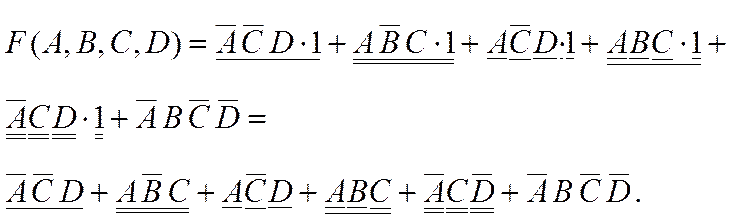
5-й шаг. Выполняя аналогичные преобразования, получаем:

6-й шаг. На основании закона поглощения пишем:

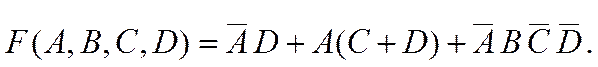
7-й шаг. Применив распределительный и сочетательный законы, имеем:

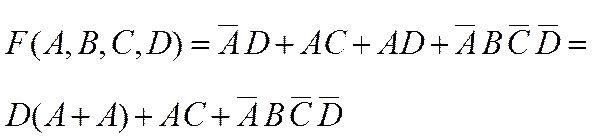
и, учитывая, что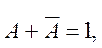 получаем:

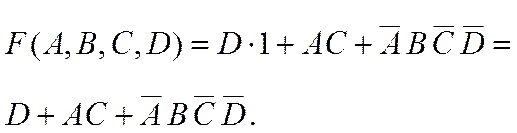
8-й шаг. В соответствии с сочетательным законом запишем:

Но по правилу поглощения:

Следовательно,

9-й шаг. Применив переместительный и сочетательный законы, имеем:

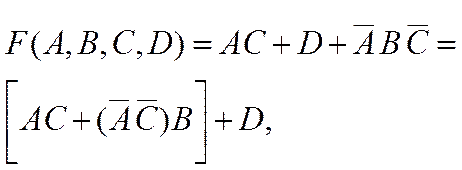
откуда по правилу поглощения: