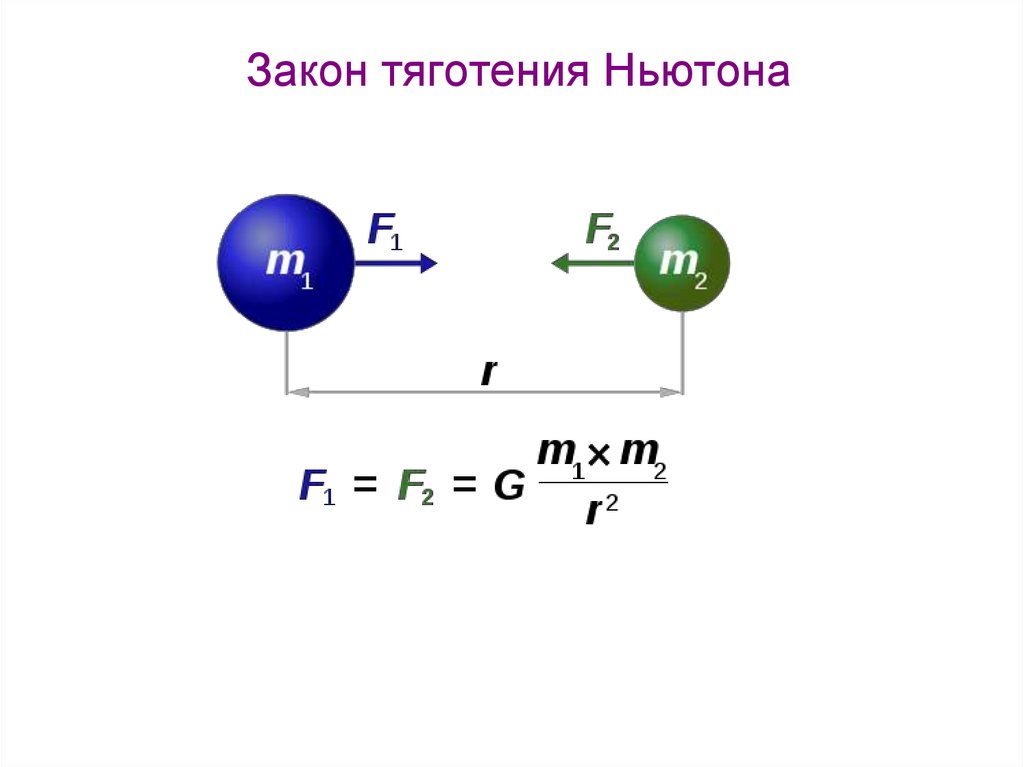
Закон всемирного тяготения Ньютона: в чем он заключается?
Существует популярная история о том, что когда Ньютон сидел под яблоней, ему на голову упало яблоко, и он вдруг подумал о законе всемирного тяготения. Как и во всех подобных легендах, это почти наверняка не соответствует действительности, но история содержит элементы того, что произошло на самом деле.
Никита Шевцев
Конечно, история с яблоком и Ньютоном — во многом выдумка. Но как на самом деле работает закон всемирного тяготения?
Что на самом деле произошло с яблоком?
Вероятно, более правильная версия истории заключается в том, что Ньютон, наблюдая за падением яблока с дерева, начал думать следующим образом: яблоко ускоряется, поскольку его скорость изменяется от нуля, когда оно висит на дереве и движется к земле. Таким образом, по второму закону Ньютона должна существовать сила, действующая на яблоко, и вызывающее это ускорение.
Давайте назовем эту силу «гравитацией», а связанное с ней ускорение — «ускорением под действием силы тяжести». Затем представьте, что яблоня в два раза выше. Опять же, мы ожидаем, что яблоко будет ускоряться по направлению к земле, так что это говорит о том, что эта сила, которую мы называем гравитацией, достигает верхушки самой высокой яблони.
Превосходнейшая идея сэра Исаака
Ньютону пришло поистине блестящее озарение: если сила тяжести достигает вершины самого высокого дерева, не может ли она простираться еще дальше; в частности, не может ли она достигать всей орбиты Луны! Тогда орбита Луны вокруг Земли может быть следствием гравитационной силы, потому что ускорение, вызванное гравитацией, может изменить скорость Луны именно таким образом, чтобы она следовала по орбите вокруг Земли.
Ньютон знал, что сила, которая вызывает ускорение яблока (гравитация), должна зависеть от массы яблока. И поскольку сила, действующая, чтобы вызвать ускорение яблока вниз, также вызывает ускорение Земли вверх (третий закон Ньютона), эта сила также должна зависеть от массы Земли.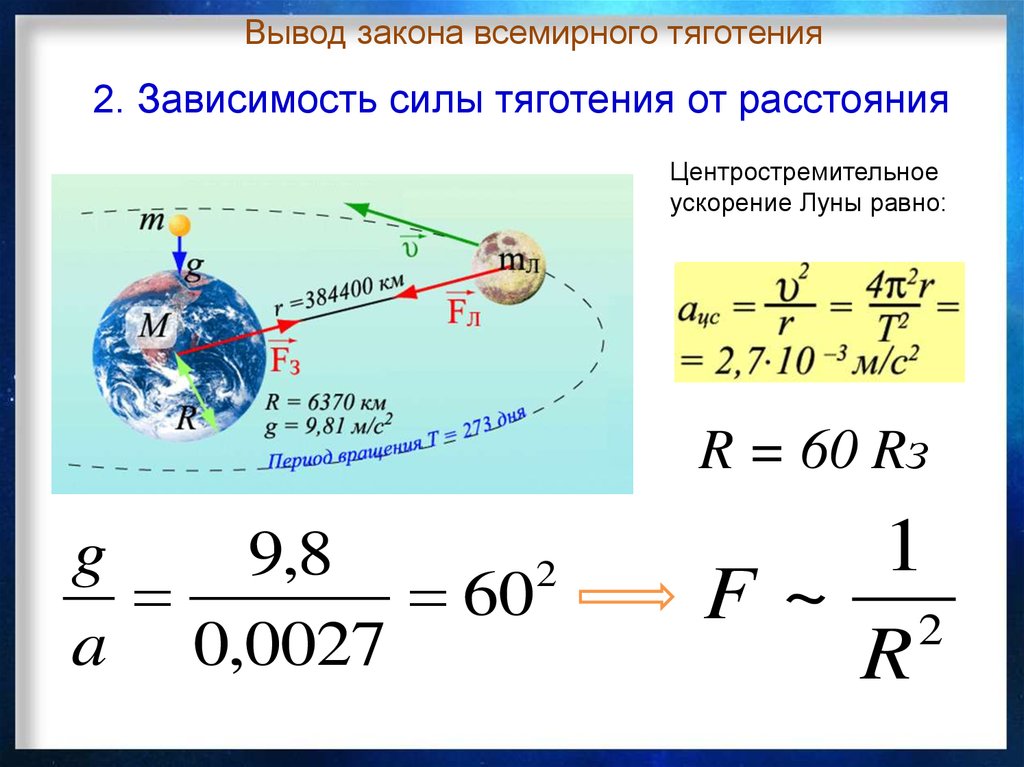
Таким образом, для Ньютона сила тяжести, действующая между Землей и любым другим объектом, прямо пропорциональна массе массе объекта и обратно пропорциональна квадрату расстояния от центра Земли до объекта.
Коэффициент пропорциональности или гравитационная постоянная — G. Ее числовое значение очень мало, что в основном является причиной того, что сила тяжести является самой слабой силой природы. Ее называют «универсальной постоянной», потому что считается, что она одинакова во всех местах и во все времена.
Но закон всемирного тяготения Ньютона распространяет гравитацию за пределы Земли. Согласно закону всемирного тяготения, любые объекты притягиваются друг к другу силой гравитационного притяжения. Гравитация универсальна. Эта сила гравитационного притяжения напрямую зависит от масс обоих объектов и обратно пропорциональна квадрату расстояния, разделяющего их центры.
Эксперимент, подвергающий сомнению Закон Всемирного тяготения
Описание эксперимента подтверждающий возможность движения тел по эллиптическим орбитам, без взаимодействия между телами
Физика
Статьи
Вуз: Пензенский государственный педагогический университет имени В.
Г. Белинского (ПГПУ им. ВГ. Белинского)
ID: 5756b45d5f1be7670cacce6d
UUID: 90b79a20-0ed3-0134-1051-525400003e20
Язык: Русский
Опубликовано: больше 6 лет назад
Просмотры: 226
Find:
Highlight allMatch case
Current View
Current View
Automatic ZoomActual SizeFit PageFull Width50%75%100%125%150%200%300%400%
Enter the password to open this PDF file:
File name:
—
File size:
—
Title:
—
—
Subject:
—
Keywords:
—
Creation Date:
—
Modification Date:
—
Creator:
—
PDF Producer:
—
PDF Version:
—
Page Count:
—
Эксперимент, подвергающий сомнению Закон всемирного тяготения.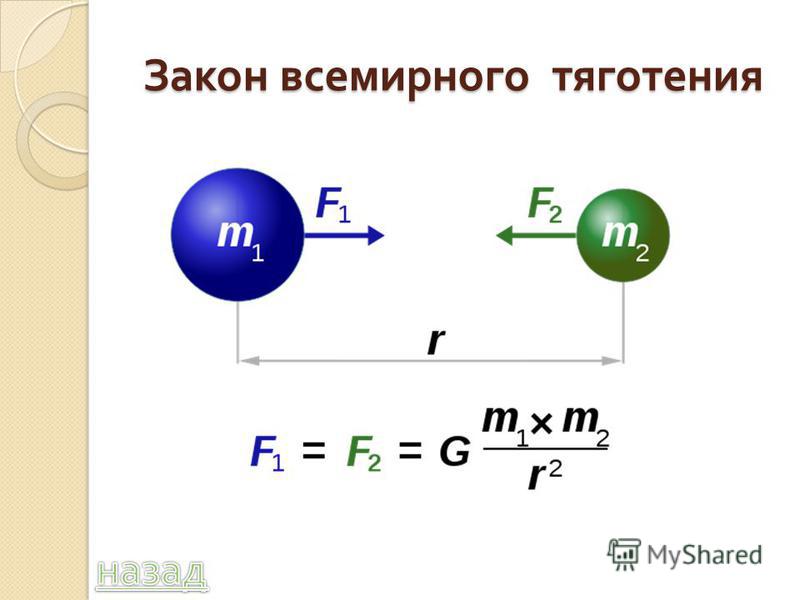
В панели вырезаем эллиптическое отверстие, по периметру эллипса делаем
ложбинку. Устанавливаем панель так, чтобы большая полуось эллипса была
перпендикулярна горизонтали Земли. В ложбинку укладываем шарик, и придаем
некоторый импульс. Шарик начнет движение по вырезанному эллипсу. На шарик
будет действовать сила тяжести Земли, реакция опоры, то есть панель не будет
давать возможность улететь шарику. Таким образом имеем три параметра,
которые определяют характер движения шарика:
— первоначальный импульс;
— сила реакция панели;
— сила Притяжения Земли.
Но если разместим в фокусе эллипса, который находится ниже, тело некоторой
массы, большей чем у шарика, то относительно этого тела движение шарика
можно описать законами Кеплера, которые основаны на законе Всемирного
тяготения. Хотя сила взаимного притяжения шарика и установленного в фокусе
тела имеют пренебрежимо малую величину.
Вывод: Вращение тел по эллиптическим орбитам может быть вызвано силами
несвязанными с телом, находящимся в фокусе орбиты тела малой массы.
Рецензии:
Авторизуйтесь, чтобы добавить рецензию
— у работы пока нет рецензий —
Закон всемирного тяготения Ньютона (Видео)
В 1686 году сэр Исаак Ньютон опубликовал Principia Mathematica , в котором представил свой Закон всемирного тяготения. Слово «универсальный» здесь важно, потому что он представлял закон, который будет работать и на Земле, и в космосе. У него была идея, что та же самая сила, которая управляет тем, как яблоки падают с дерева, отвечает за то, как Луна вращается вокруг Земли. Это противоречило философии того времени, согласно которой космос был совершенным и «небесным» и состоял из совершенно других материалов, чем те, что были найдены на Земле. Исаак Ньютон полагался на работу, проделанную Галилео Галилеем, который использовал телескоп, чтобы показать, что такие места в космосе, как Луна, такие же, как Земля. Ньютон использовал физические законы для дальнейшего объединения царств Земли и космоса.
Закон всемирного тяготения Ньютона, который часто называют просто «законом всемирного тяготения», гласит, что две вещи, обладающие массой, притягиваются друг к другу естественной силой, которую Ньютон назвал гравитацией. Эта сила между этими двумя вещами пропорциональна произведению их масс. Это означает, что большие массы обладают большей силой. Например, если вы держите руки рядом друг с другом, между вашими руками возникает гравитационная сила. Вы не почувствуете эту силу, потому что она такая крошечная. Однако в масштабах больших масс, таких как Луна и Земля, сила соизмеримо велика.
Кроме того, сила обратно пропорциональна квадрату расстояния между двумя массами. Это означает, что чем дальше две массы друг от друга, тем слабее будет сила между ними. Точнее, если два объекта переместить в два раза дальше друг от друга, сила тяжести уменьшится в четыре раза. Если объекты перемещаются в три раза дальше друг от друга, сила тяжести уменьшается в девять раз. Важной концепцией здесь является осознание того, что по мере того, как объекты удаляются друг от друга, сила гравитации между ними очень быстро уменьшается.
9{11}\). \(m\) в уравнении — это массы двух объектов. Например, если бы нам нужно было найти силу притяжения между Землей и Луной, одна из масс в уравнении была бы массой Земли, а другая — Луны. Как правило, более крупному объекту присваивается прописная буква M, а меньшему объекту — строчная \(m\), но математически не имеет значения, что куда идет. \(D\) относится к расстоянию между центрами двух объектов. Если вы бросите мяч на поверхность Земли, расстояние в этом уравнении будет от центра мяча до центра Земли. Поскольку Земля очень велика и для большинства людей мяч никогда не бывает слишком далеко от поверхности Земли, когда это уравнение применяется к объектам, падающим вблизи поверхности Земли, радиус Земли обычно используется в качестве расстояние.
До того, как Ньютон сформулировал гравитацию, Галилей обнаружил, что два объекта с разными массами падают на Землю с одинаковой скоростью. Миф утверждает, что Галилей сбросил два мяча с Пизанской башни, хотя он, вероятно, никогда не заходил так далеко.
Вместо этого он использовал деревянные шары, которые он мог открывать и помещать внутрь разные грузы, а затем катил эти шары по пандусам. Он не смог объяснить, почему шары с разной массой закончили свой забег в одно и то же время. Может показаться, что этот эксперимент показывает, что закон всемирного тяготения Ньютона не работает! В конце концов, мы только что сказали, что большие массы производят большие силы. Однако, как мы увидим, это наблюдение совпадает с тем, что мы должны ожидать, когда объединяем закон всемирного тяготения Ньютона с его законами движения.
Например, если у вас есть шар для боулинга, падающий на Землю, массы, которые вы использовали бы в уравнении гравитации, — это массы шара для боулинга и массы Земли. Если вместо этого вы уроните бейсбольный мяч, вы будете использовать массу бейсбольного мяча и массу Земли. Шар для боулинга с большей массой испытывает большую гравитационную силу. Совершенно верно, что когда вы роняете шар для боулинга и бейсбольный мяч, шар для боулинга ощущает большую силу Земли, чем бейсбольный мяч.
Верно также и то, что эти два мяча упали на землю одновременно. Этот результат согласуется со вторым законом движения Ньютона, который гласит, что сила, необходимая для перемещения объекта, равна произведению массы объекта на его ускорение. 9{2}}\)
Ускорение шара для боулинга зависит от гравитационной постоянной, массы Земли и расстояния между шаром для боулинга и центром Земли, которое мы обсуждали, по существу, радиус земли. Эти значения одинаковы для любого объекта вблизи поверхности Земли. Следовательно, ускорение свободного падения для любого объекта вблизи поверхности Земли одинаково. Если мы подставим значения, то обнаружим, что это ускорение равно девяти и восьми метрам в секунду в квадрате, или тридцати двум футам в секунду в квадрате. 9{2}\)
Это значение используется так часто, что ему присваивается собственный символ: строчная буква \(g\), называемая «маленькая \(g\)». Обратите внимание, что «немного \(g\)» отличается от гравитационной постоянной \(G\).
Один из экспериментов, проведенных астронавтами Аполлона-15 на Луне, состоял в том, чтобы сбросить молот и перо, чтобы показать, что они приземлились одновременно. Вы можете попробовать это сами и обнаружить, что это не работает! Для двух объектов с разной формой и массой здесь, на Земле, фактором будет сопротивление воздуха. Вот почему Галилей использовал одинаковые шары с разной массой, а Луна, не имеющая атмосферы, — идеальное место для проверки этой теории.
Теперь нужно время, чтобы привыкнуть к понятию различия между весом и массой. Вес не то же самое, что масса. Один из способов думать об этом состоит в том, что ваша масса связана с тем, сколько вас есть, а ваш вес связан с тем, где вы находитесь. Другими словами, ваш вес — это мера силы, с которой Земля притягивает вашу массу. Если бы вы отправились на Луну, ваша масса осталась бы прежней, но поскольку Луна имеет меньшую массу, чем Земля, сила между вами и Луной была бы меньше, чем сила между вами и Землей. Это означает, что вы будете меньше весить на Луне.
На самом деле вы можете использовать закон всемирного тяготения Ньютона, чтобы узнать, каким был бы ваш вес на разных планетах, лунах и других небесных телах.
Однако важно помнить, что расстояние также является частью уравнения. Другими словами, только потому, что объект более массивный, не означает, что вы испытаете больший вес. Отличным примером этого является Сатурн. На самом деле у Сатурна нет поверхности, на которой вы могли бы стоять, но давайте представим, что она есть. Сатурн имеет гораздо большую массу, чем Земля, но и радиус у него больше. Если бы вы могли стоять на «поверхности» Сатурна, вы бы на самом деле весили почти столько же, сколько и на Земле.
Закон всемирного тяготения Ньютона — полезный инструмент для определения силы между двумя объектами на основе их масс и расстояния между ними. Однако закон всемирного тяготения Ньютона неполный! Он отлично описывает движение почти всего, что мы видим и с чем взаимодействуем ежедневно, так чего же не хватает? Математически закон всемирного тяготения Ньютона является приближением, хотя и очень хорошим для большинства повседневных приложений.
Даже астронавтам нужно было всего лишь использовать законы Ньютона, чтобы добраться до Луны. Но Ньютон только систематизировал движение, которое он наблюдал, и определил уравнения для предсказания будущих наблюдений; он не объяснил, почему существует гравитация. Эйнштейн стремился сделать это в 1933 года, когда он опубликовал свою общую теорию относительности. В этой статье он сказал, что масса находится в четырехмерной ткани пространства-времени, и эта масса искажает ткань пространства-времени. Это искаженное пространство-время и есть то, что мы воспринимаем как гравитацию.
Насколько нам известно, концепция гравитации Эйнштейна полностью верна. Конечно, двести лет люди думали, что это верно и для закона всемирного тяготения Ньютона. Наука не перестает преподносить сюрпризы.
На этом обзоре все. Спасибо за просмотр и приятного изучения.
6.5 Универсальный закон всемирного тяготения Ньютона – College Physics
Глава 6 Равномерное круговое движение и гравитация
Резюме
- Объясните гравитационную силу Земли.
- Опишите гравитационное воздействие Луны на Землю.
- Обсудить невесомость в космосе.
- Изучить эксперимент Кавендиша
Что общего у ноющих ног, падающего яблока и орбиты Луны? Каждая из них вызвана силой гравитации. Наши ноги напряжены, поддерживая наш вес — силу земного притяжения, действующую на нас. Яблоко падает с дерева из-за той же силы, действующей на высоте нескольких метров над поверхностью Земли. А Луна вращается вокруг Земли потому, что гравитация способна обеспечить необходимую центростремительную силу на расстоянии сотен миллионов метров. На самом деле одна и та же сила заставляет планеты вращаться вокруг Солнца, звезды — вокруг центра галактики, а галактики — группироваться вместе. Гравитация — еще один пример лежащей в основе простоты природы. Это самая слабая из четырех основных сил, встречающихся в природе, и в некотором смысле наименее изученная. Это сила, действующая на расстоянии, без физического контакта, и выражается формулой, действующей повсюду во Вселенной, для масс и расстояний, которые варьируются от крошечных до огромных.
Сэр Исаак Ньютон был первым ученым, который точно определил гравитационную силу и показал, что она может объяснить как падающие тела, так и астрономические движения. См. рис. 1. Но Ньютон был не первым, кто заподозрил, что одна и та же сила вызывает и наш вес, и движение планет. Его предшественник Галилео Галилей утверждал, что падающие тела и движение планет имеют одну и ту же причину. Некоторые из современников Ньютона, такие как Роберт Гук, Кристофер Рен и Эдмунд Галлей, также добились определенного прогресса в понимании гравитации. Но Ньютон первым предложил точную математическую форму и с помощью этой формы показал, что движение небесных тел должно представлять собой конические сечения — окружности, эллипсы, параболы и гиперболы. Это теоретическое предсказание было большим триумфом — уже некоторое время было известно, что луны, планеты и кометы следуют по таким путям, но никто не мог предложить механизм, который заставлял бы их следовать именно по этим путям, а не по другим.
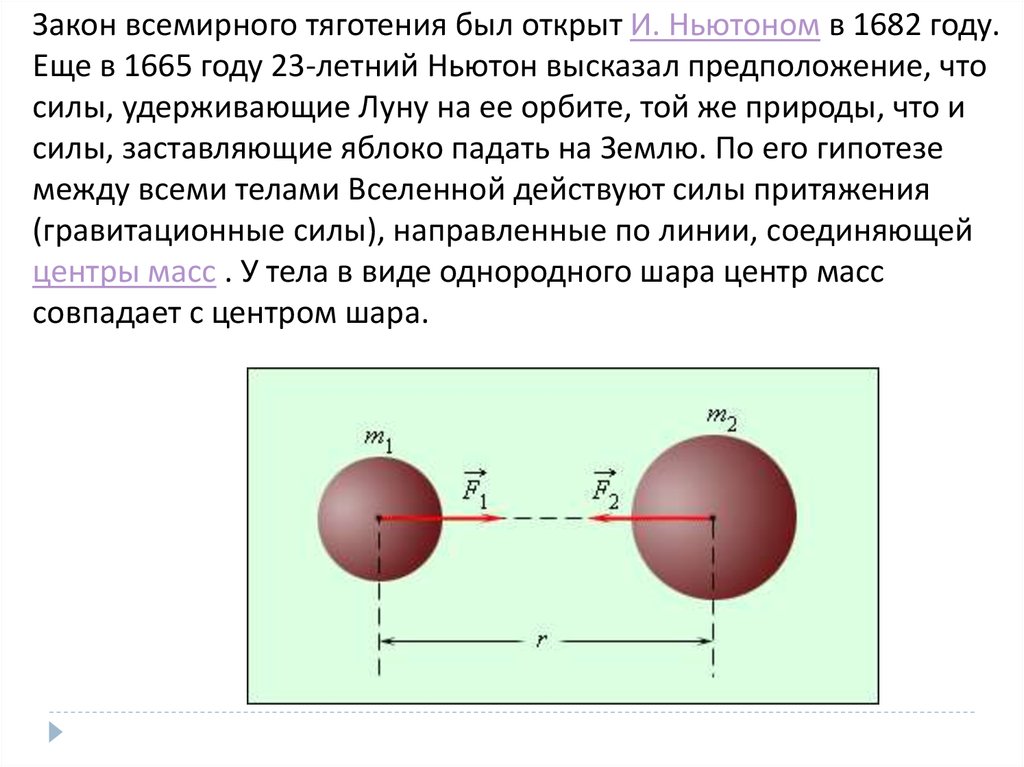Сила прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними. Рис. 2. Гравитационное притяжение происходит вдоль линии, соединяющей центры масс этих двух тел. Величина силы одинакова на каждом из них, что соответствует третьему закону Ньютона.ПРЕДУПРЕЖДЕНИЕ О НЕПРАВИЛЬНОМ КОНЦЕПЦИИ
Величина силы, действующей на каждый объект (один имеет большую массу, чем другой), одинакова, что соответствует третьему закону Ньютона.
Тела, с которыми мы имеем дело, имеют тенденцию быть большими. Для упрощения ситуации предположим, что тело ведет себя так, как будто вся его масса сосредоточена в одной определенной точке, называемой 92}.[/латекс]
Рисунок 3. Расстояние между центрами масс Земли и объектом на ее поверхности почти равно радиусу Земли, потому что Земля намного больше объекта. Это ожидаемое значение и не зависит от массы тела . Закон всемирного тяготения Ньютона продвигает наблюдение Галилея о том, что все массы падают с одинаковым ускорением, на шаг дальше, объясняя наблюдение с точки зрения силы, которая заставляет объекты падать, — фактически с точки зрения универсально существующей силы притяжения между массами.
ДОМАШНИЙ ЭКСПЕРИМЕНТ
Возьмите шарик, шарик и ложку и бросьте их с одинаковой высоты. Они падают на пол одновременно? Если вы также уроните лист бумаги, будет ли он вести себя как другие предметы? Объясните свои наблюдения.
УСТАНОВЛЕНИЕ СОЕДИНЕНИЙ
Все еще предпринимаются попытки понять силу гравитации. Как мы увидим в главе 33 «Физика элементарных частиц», современная физика исследует связи гравитации с другими силами, пространством и временем. Общая теория относительности меняет наш взгляд на гравитацию, заставляя нас думать о гравитации как о искривлении пространства и времени.
В следующем примере мы проводим сравнение, подобное тому, которое сделал сам Ньютон. Он отметил, что если сила гравитации заставляет Луну вращаться вокруг Земли, то ускорение свободного падения должно равняться центростремительному ускорению Луны на ее орбите. Ньютон обнаружил, что два ускорения совпадают «почти почти».
Пример 1. Сила тяготения Земли представляет собой центростремительную силу, заставляющую Луну двигаться по криволинейной траектории
(a) Найдите ускорение силы тяжести Земли на расстоянии от Луны.
8\text{м}}.[/латекс] 92},[/latex]
, где [latex]{\omega}[/latex] — угловая скорость Луны относительно Земли.
Решение для (b)
Учитывая, что период (время, необходимое для совершения одного полного оборота) орбиты Луны составляет 27,3 дня, (d) и используя
[latex]{1\text{ d }\times24}[/latex] [латекс]{\frac{\text{hr}}{\text{d}}}[/latex] [латекс]{\times\:60}[/latex] [латекс] {\ frac {\ text {мин}} {\ text {ч}}} [/ латекс] [латекс] {\ раз \: 60} [/ латекс] [латекс] {\ гидроразрыва {\ текст {s}} { \text{мин}}}[/латекс] [латекс]{=86 400\текст{ с}}[/латекс] 92} \end{array}[/latex]
Ускорение направлено к центру Земли.
Обсуждение
Центростремительное ускорение Луны, найденное в (б), отличается менее чем на 1% от ускорения силы тяжести Земли, найденного в (а). Это согласие является приблизительным, потому что орбита Луны слегка эллиптическая, а Земля не является стационарной (скорее, система Земля-Луна вращается вокруг своего центра масс, который расположен примерно на 1700 км ниже поверхности Земли).
Явный вывод состоит в том, что гравитационная сила Земли заставляет Луну вращаться вокруг Земли.
Почему Земля не остается неподвижной, когда Луна вращается вокруг нее? Это связано с тем, что, как и ожидалось из третьего закона Ньютона, если Земля воздействует на Луну, то Луна должна оказывать на Землю равную и противоположную силу (см. рис. 4). Мы не ощущаем влияние Луны на движение Земли, потому что гравитация Луны перемещает наши тела вместе с Землей, но на Земле есть и другие признаки, которые ясно показывают влияние гравитационной силы Луны, как обсуждалось в главе 6.6 Спутники и законы Кеплера. Аргумент в пользу простоты.
Рис. 4. (a) Земля и Луна вращаются примерно раз в месяц вокруг своего общего центра масс. (b) Их центр масс вращается вокруг Солнца по эллиптической орбите, но путь Земли вокруг Солнца имеет «изгибы». Подобные колебания на траекториях звезд наблюдались и считаются прямым свидетельством того, что планеты вращаются вокруг этих звезд.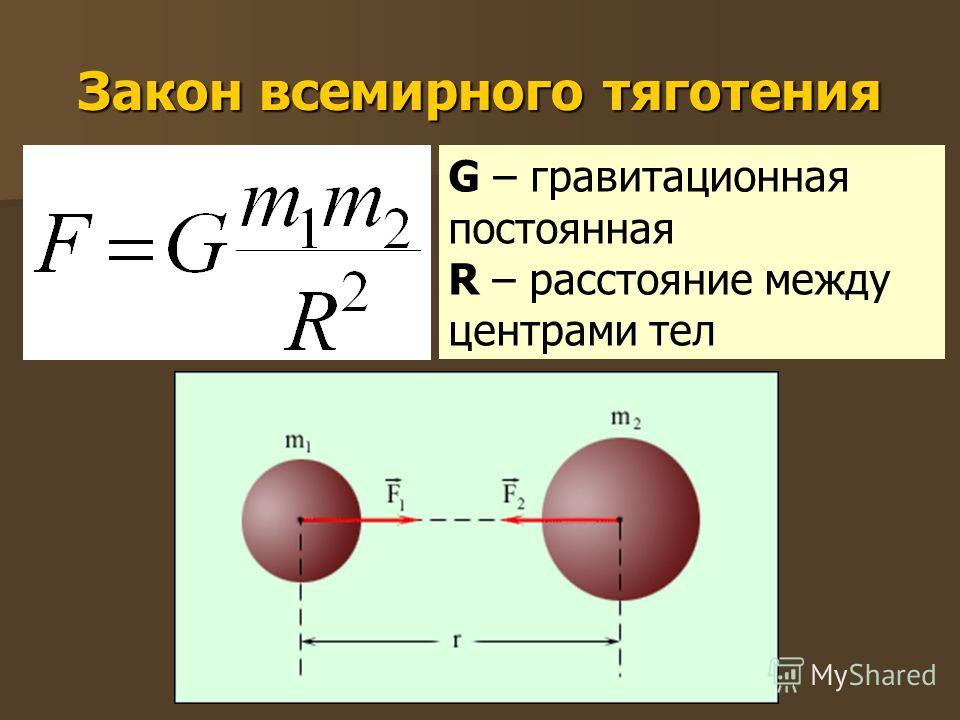
Это важно, потому что отраженный свет планет часто слишком тусклый, чтобы его можно было наблюдать. Океанские приливы — один из хорошо наблюдаемых результатов гравитации Луны, действующей на Землю. Рисунок 5 представляет собой упрощенный рисунок положения Луны относительно приливов. Поскольку вода легко течет по поверхности Земли, прилив создается на стороне Земли, ближайшей к Луне, где гравитационное притяжение Луны сильнее всего. Почему на противоположной стороне Земли также бывает прилив? Ответ заключается в том, что Земля притягивается к Луне больше, чем вода на дальней стороне, потому что Земля ближе к Луне. Таким образом, вода на стороне Земли, ближайшей к Луне, отрывается от Земли, а Земля отрывается от воды на дальней стороне. Когда Земля вращается, приливная выпуклость (воздействие приливных сил между вращающимся вокруг естественным спутником и основной планетой, вокруг которой он вращается) сохраняет свою ориентацию относительно Луны. Таким образом, в день бывает два прилива (фактический период прилива составляет около 12 часов 25,2 минуты, потому что Луна также движется по своей орбите каждый день).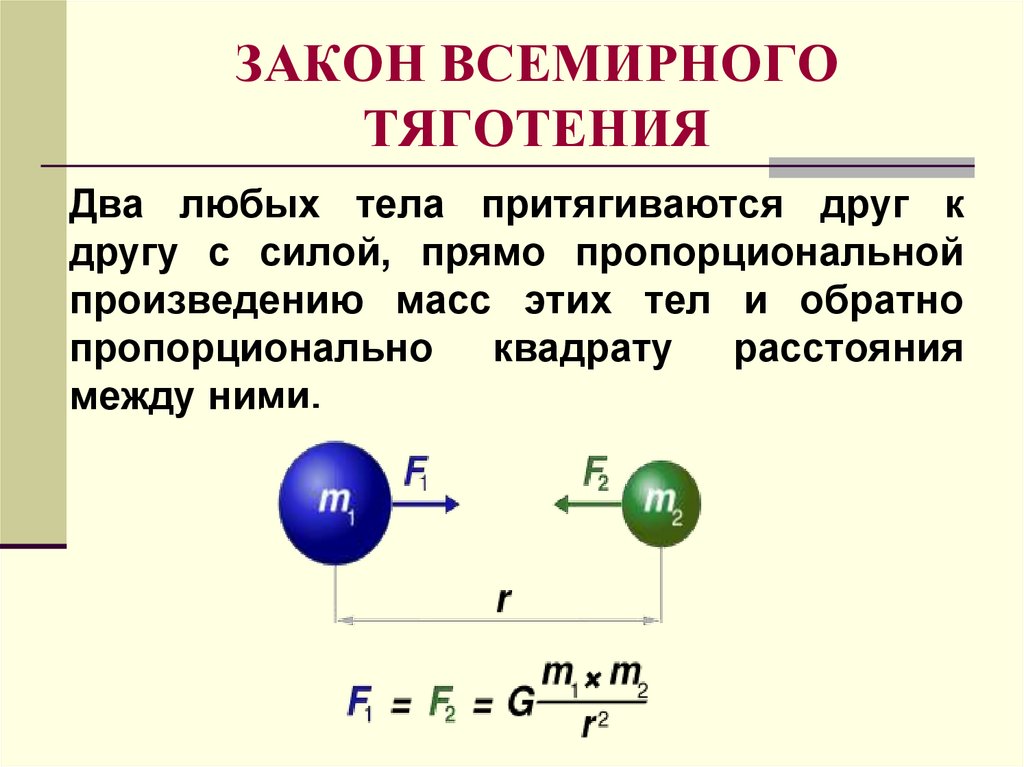
Солнце также влияет на приливы, хотя его влияние примерно вдвое меньше, чем у Луны. Однако самые большие приливы, называемые весенними приливами, происходят, когда Земля, Луна и Солнце выстраиваются на одной линии. Наименьшие приливы, называемые приливами, происходят, когда Солнце находится в [латексном]{90}[/latex] угол выравнивания Земля-Луна.
Рисунок 6. (a, b) Весенние приливы: самые высокие приливы возникают, когда Земля, Луна и Солнце выстраиваются на одной линии. (c) Квадрийский прилив: Самые низкие приливы возникают, когда Солнце находится на 90 90 223 0 90 224 по отношению к выравниванию Земли и Луны.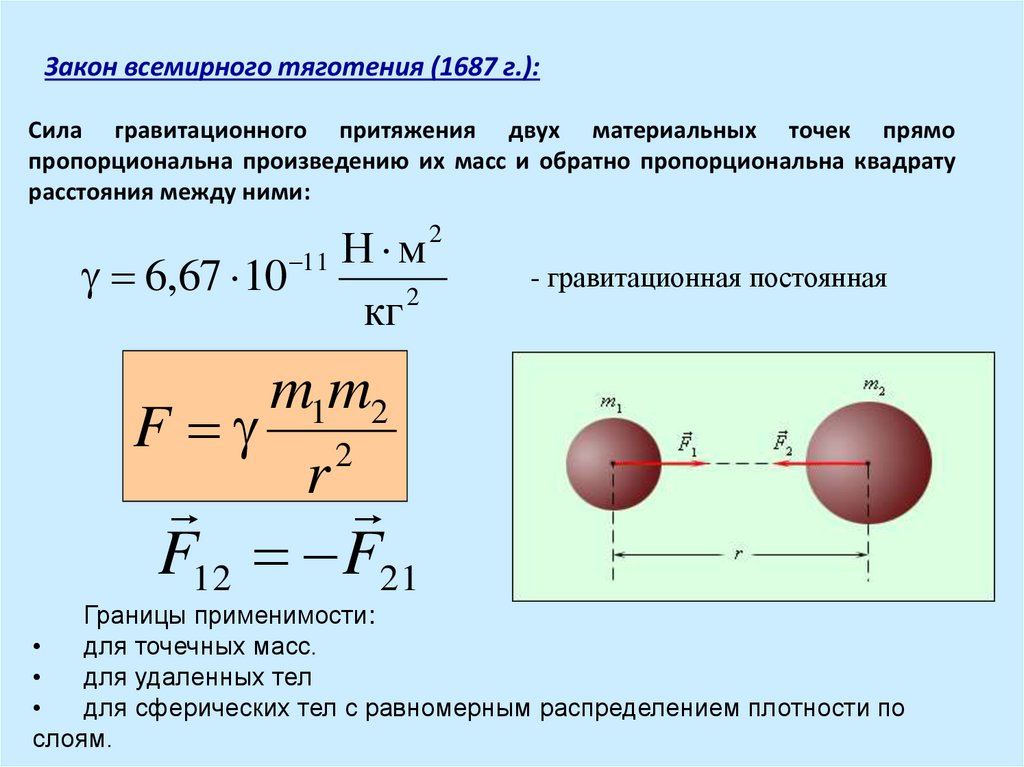
Обратите внимание, что этот рисунок выполнен не в масштабе.
Приливы и отливы характерны не только для Земли, но и для многих астрономических систем. Самые экстремальные приливы возникают там, где гравитационная сила наиболее сильна и изменяется наиболее быстро, например вблизи черных дыр (см. рис. 7). В нашей галактике наблюдалось несколько вероятных кандидатов в черные дыры. Они имеют массу больше, чем у Солнца, но имеют диаметр всего несколько километров в поперечнике. Приливные силы вблизи них настолько велики, что могут фактически оторвать материю от звезды-компаньона.
Рис. 7. Черная дыра — это объект с такой сильной гравитацией, что даже свет не может покинуть его. Эта черная дыра была создана сверхновой одной звезды в двухзвездной системе. Приливные силы, создаваемые черной дырой, настолько велики, что отрывают материю от звезды-компаньона. Это вещество сжимается и нагревается по мере того, как оно всасывается в черную дыру, создавая свет и рентгеновские лучи, наблюдаемые с Земли.
В отличие от огромной гравитационной силы вблизи черных дыр существует видимое гравитационное поле, с которым сталкиваются астронавты на орбите Земли. Как действует «невесомость» на космонавта, который месяцами находится на орбите? Или как насчет влияния невесомости на рост растений? Невесомость не означает, что на космонавта не действует гравитационная сила. На орбите космонавта нет «невесомости». Этот термин просто означает, что космонавт находится в свободном падении, ускоряясь с ускорением за счет силы тяжести. Если трос лифта порвется, пассажиры внутри окажутся в свободном падении и ощутят невесомость. Вы можете испытывать короткие периоды невесомости на некоторых аттракционах в парках развлечений.
Рис. 8. Астронавты испытывают невесомость на борту Международной космической станции. (кредит: НАСА) Микрогравитация относится к среде, в которой кажущееся суммарное ускорение тела мало по сравнению с ускорением, создаваемым Землей на ее поверхности.
Многие интересные темы биологии и физики были изучены за последние три десятилетия в условиях микрогравитации. Непосредственное беспокойство вызывает влияние на астронавтов длительного пребывания в открытом космосе, например, на Международной космической станции. Исследователи заметили, что в такой среде мышцы атрофируются (истощаются). Существует также соответствующая потеря костной массы. Продолжаются исследования адаптации сердечно-сосудистой системы к космическому полету. На Земле кровяное давление обычно выше в ногах, чем в голове, потому что более высокий столб крови оказывает на него нисходящую силу из-за гравитации. Когда вы стоите, 70% вашей крови находится ниже уровня сердца, а в горизонтальном положении происходит прямо противоположное. Какое значение имеет отсутствие этого перепада давления для сердца?
Некоторые открытия в области физиологии человека в космосе могут иметь клиническое значение для лечения заболеваний на Земле. С другой стороны, известно, что космический полет влияет на иммунную систему человека, что, возможно, делает членов экипажа более уязвимыми к инфекционным заболеваниям.
Эксперименты в космосе также показали, что некоторые бактерии растут быстрее в условиях микрогравитации, чем на Земле. Тем не менее, исследования показывают, что производство микробных антибиотиков может увеличиться в два раза в культурах, выращенных в космосе. Можно надеяться, что удастся понять эти механизмы, чтобы можно было добиться аналогичных успехов на местах. В другой области физических космических исследований в космическом пространстве были выращены неорганические кристаллы и кристаллы белков, которые имеют гораздо более высокое качество, чем любые, выращенные на Земле, поэтому кристаллографические исследования их структуры могут дать гораздо лучшие результаты.
Растения эволюционировали под воздействием силы тяжести и с помощью датчиков силы тяжести. Корни растут вниз, а побеги растут вверх. Растения могли бы обеспечить систему жизнеобеспечения для длительных космических миссий, восстанавливая атмосферу, очищая воду и производя пищу. Некоторые исследования показали, что гравитация не влияет на рост и развитие растений, но все еще существует неопределенность в отношении структурных изменений растений, выращенных в условиях микрогравитации.
Как отмечалось ранее, универсальная гравитационная постоянная [латекс]{G}[/латекс] определяется экспериментально. Это определение впервые дал Генри Кавендиш (1731–1810), английский ученый, в 179 г.8, более чем через 100 лет после того, как Ньютон опубликовал свой универсальный закон всемирного тяготения. Измерение [латекса]{G}[/латекса] очень простое и важное, поскольку оно определяет силу одной из четырех сил в природе. Эксперимент Кавендиша был очень сложным, потому что он измерил крошечное гравитационное притяжение между двумя массами обычного размера (не более десятков килограммов), используя прибор, подобный показанному на рис. 9. Примечательно, что его значение для [латекс]{G}[/латекс] отличается менее чем на 1% от лучшего современного значения. 92}{G}}.[/латекс]
Таким образом, [латекс]{M}[/латекс] можно рассчитать, поскольку все величины справа, включая радиус Земли [латекс]{r},[/латекс], известны из прямых измерений. В главе 6.6 «Спутники и законы Кеплера: аргумент в пользу простоты» мы увидим, что знание [латекс]{G}[/латекс] также позволяет определять астрономические массы.
Интересно, что из всех фундаментальных констант в физике [латекс]{G}[/латекс] определен наименее точно.
Эксперимент Кавендиша также используется для изучения других аспектов гравитации. Один из самых интересных вопросов заключается в том, зависит ли сила гравитации от вещества, а также от массы — например, оказывает ли один килограмм свинца такое же гравитационное притяжение, как один килограмм воды. Венгерский ученый по имени Роланд фон Этвёш начал это исследование в начале 20-го века. Он обнаружил с точностью до пяти частей на миллиард, что гравитационная сила не зависит от вещества. Такие эксперименты продолжаются и сегодня, и они улучшили измерения Этвеша. Эксперименты типа Кавендиша, такие как эксперименты Эрика Адельбергера и других в Вашингтонском университете, также наложили серьезные ограничения на возможность существования пятого взаимодействия и подтвердили главное предсказание общей теории относительности — гравитационная энергия вносит свой вклад в массу покоя. В текущих измерениях используются крутильные весы и параллельная пластина (а не сферы, как использовал Кавендиш), чтобы изучить, как закон тяготения Ньютона работает на субмиллиметровых расстояниях.
