Электродинамика
Электродинамика
ОглавлениеПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮВВЕДЕНИЕ ГЛАВА 1.  УРАВНЕНИЯ МАКСВЕЛЛА КАК РЕЗУЛЬТАТ ОБОБЩЕНИЯ ОПЫТНЫХ ФАКТОВ УРАВНЕНИЯ МАКСВЕЛЛА КАК РЕЗУЛЬТАТ ОБОБЩЕНИЯ ОПЫТНЫХ ФАКТОВЗакон Кулона для электрических зарядов. Взаимодействие магнитов и токов. Закон электромагнитной индукции Фарадея. Электромагнитные свойства вещества. § 2. УСЛОВИЕ МАКРОСКОПИЧНОСТИ И ЗАКОН СОХРАНЕНИЯ ЭЛЕКТРИЧЕСКОГО ЗАРЯДА § 3. ЗАКОН КУЛОНА И ЭЛЕКТРИЧЕСКОЕ ПОЛЕ § 4. МАГНИТНОЕ ПОЛЕ ПОСТОЯННЫХ ТОКОВ § 5. ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ ФАРАДЕЯ § 6. ТОК СМЕЩЕНИЯ И УРАВНЕНИЯ МАКСВЕЛЛА В ВАКУУМЕ § 7. ДИЭЛЕКТРИКИ. ЭЛЕКТРИЧЕСКАЯ ПОЛЯРИЗАЦИЯ § 8. МАГНЕТИКИ. НАМАГНИЧЕННОСТЬ § 9. УЧЕТ ТОКОВ НАМАГНИЧЕНИЯ И ПОЛЯРИЗАЦИИ § 11. ЗАКОН ОМА В ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ § 12. ГРАНИЧНЫЕ УСЛОВИЯ § 13. СИЛЫ, ДЕЙСТВУЮЩИЕ НА ЗАРЯДЫ И ТОКИ § 14. ЭНЕРГИЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ § 15. СИСТЕМЫ ЕДИНИЦ ГЛАВА 2. СТАЦИОНАРНЫЕ ПОЛЯ § 16. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ, СОЗДАВАЕМОЕ ЗАДАННЫМ РАСПРЕДЕЛЕНИЕМ ЗАРЯДОВ. УРАВНЕНИЕ ЛАПЛАСА § 17.  ПОТЕНЦИАЛ ПРОСТРАНСТВЕННО РАСПРЕДЕЛЕННЫХ ЗАРЯДОВ ПОТЕНЦИАЛ ПРОСТРАНСТВЕННО РАСПРЕДЕЛЕННЫХ ЗАРЯДОВ§ 18. ПОТЕНЦИАЛ ПОВЕРХНОСТНЫХ И ЛИНЕЙНЫХ ЗАРЯДОВ § 19. ПОТЕНЦИАЛ ОГРАНИЧЕННОЙ СИСТЕМЫ ЗАРЯДОВ (МУЛЬТИПОЛЬНОЕ РАЗЛОЖЕНИЕ) § 20. ПОТЕНЦИАЛ ДВОЙНОГО ЭЛЕКТРИЧЕСКОГО СЛОЯ § 22. ПОЛЕ ЗАРЯЖЕННЫХ ПРОВОДНИКОВ § 23. ЭНЕРГИЯ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ § 24. ЭНЕРГИЯ СИСТЕМЫ ЗАРЯЖЕННЫХ ПРОВОДНИКОВ § 25. ПРОВОДНИКИ И ДИЭЛЕКТРИКИ ВО ВНЕШНЕМ ПОЛЕ § 26. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ЭЛЕКТРОСТАТИКИ § 27. СИЛЫ, ДЕЙСТВУЮЩИЕ НА ПРОВОДНИКИ И ДИЭЛЕКТРИКИ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ § 28. МАГНИТНОЕ ПОЛЕ, СОЗДАВАЕМОЕ ЗАДАННЫМ РАСПРЕДЕЛЕНИЕМ ТОКОВ. ВЕКТОРНЫЙ ПОТЕНЦИАЛ § 29. МАГНИТНОЕ ПОЛЕ ОГРАНИЧЕННОЙ СИСТЕМЫ ТОКОВ (МАГНИТНОЕ МУЛЬТИПОЛЬНОЕ РАЗЛОЖЕНИЕ) § 30. ПОЛЕ ПОСТОЯННЫХ МАГНИТОВ § 31. МАГНИТНЫЕ СВОЙСТВА СВЕРХПРОВОДНИКОВ § 32. ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ ПОСТОЯННЫХ ТОКОВ § 34. СТАЦИОНАРНЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК § 35.  СИСТЕМА ИДЕАЛЬНЫХ ПРОВОДНИКОВ В СРЕДЕ С МАЛОЙ ПРОВОДИМОСТЬЮ СИСТЕМА ИДЕАЛЬНЫХ ПРОВОДНИКОВ В СРЕДЕ С МАЛОЙ ПРОВОДИМОСТЬЮ§ 36. ПОЛЕ ЦИЛИНДРИЧЕСКОГО ПРОВОДНИКА С ТОКОМ И ПРЕВРАЩЕНИЕ ЭНЕРГИИ В ЦЕПИ ПОСТОЯННОГО ТОКА § 37. ПРОСТЕЙШАЯ МОДЕЛЬ ОМИЧЕСКОГО СОПРОТИВЛЕНИЯ ПРОВОДНИКОВ ГЛАВА 3. ПЕРЕМЕННОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ § 38. ПЕРЕМЕННОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ В ОДНОРОДНОЙ СРЕДЕ ИЛИ ВАКУУМЕ § 39. ПЛОСКИЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ § 40. ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН НА ПЛОСКОЙ ГРАНИЦЕ РАЗДЕЛА ДВУХ СРЕД § 42. ЭЛЕКТРИЧЕСКИЙ И МАГНИТНЫЙ ВЕКТОРЫ ГЕРЦА § 43. ПОЛЯ ЭЛЕКТРИЧЕСКОГО И МАГНИТНОГО ВИБРАТОРОВ ГЕРЦА § 44. МУЛЬТИПОЛЬНОЕ РАЗЛОЖЕНИЕ ЗАПАЗДЫВАЮЩИХ ПОТЕНЦИАЛОВ § 45. ИЗЛУЧЕНИЕ ЛИНЕЙНОЙ АНТЕННЫ § 46. ПОЛЕ ПРОИЗВОЛЬНО ДВИЖУЩЕГОСЯ ЗАРЯДА § 47. СИЛА РЕАКЦИИ ИЗЛУЧЕНИЯ § 48. РАССЕЯНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН СВОБОДНЫМИ ЭЛЕКТРОНАМИ (ФОРМУЛА ТОМСОНА) ГЛАВА 4. КВАЗИСТАЦИОНАРНЫЕ ТОКИ И ПОЛЯ § 49. УРАВНЕНИЯ МАКСВЕЛЛА В КВАЗИСТАЦИОНАРНОМ СЛУЧАЕ § 50.  КВАЗИСТАЦИОНАРНЫЕ ТОКИ В ЛИНЕЙНЫХ ПРОВОДНИКАХ КВАЗИСТАЦИОНАРНЫЕ ТОКИ В ЛИНЕЙНЫХ ПРОВОДНИКАХ§ 51. ПРЕВРАЩЕНИЕ ЭНЕРГИИ В ЦЕПИ ЛИНЕЙНЫХ КВАЗИСТАЦИОНАРНЫХ ТОКОВ. ЭЛЕКТРОМЕХАНИЧЕСКАЯ АНАЛОГИЯ § 53. ДЛИННЫЕ ЛИНИИ § 54. КВАЗИСТАЦИОНАРНЫЕ ПОЛЯ В МЕДЛЕННО ДВИЖУЩИХСЯ ДЕФОРМИРУЮЩИХСЯ ПРОВОДНИКАХ (МАГНИТНАЯ ГИДРОДИНАМИКА) § 55. МАГНИТНАЯ КУМУЛЯЦИЯ ГЛАВА 5. ЭЛЕКТРОННАЯ ТЕОРИЯ СРЕД § 56. ОСНОВНЫЕ ПОЛОЖЕНИЯ ЭЛЕКТРОННОЙ ТЕОРИИ ЛОРЕНЦА § 57. УРАВНЕНИЯ МАКСВЕЛЛА—ЛОРЕНЦА И МАКРОСКОПИЧЕСКИЕ УРАВНЕНИЯ МАКСВЕЛЛА § 58. ДИЭЛЕКТРИКИ В ПОСТОЯННОМ ЭЛЕКТРИЧЕСКОМ ПОЛЕ § 59. ЭЛЕКТРОННАЯ ТЕОРИЯ НАМАГНИЧИВАНИЯ § 60. ТЕОРИЯ ФЕРРОМАГНЕТИЗМА ПО ВЕЙССУ § 61. ЭЛЕКТРОННАЯ ТЕОРИЯ ДИСПЕРСИИ И ПОГЛОЩЕНИЯ ЭЛЕКТРОМАГНИТНЫХ ВОЛН ГЛАВА 6. РЕЛЯТИВИСТСКАЯ КИНЕМАТИКА § 62. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ГАЛИЛЕЯ И ГИПОТЕЗА ЭФИРА § 64. ГИПОТЕЗЫ ФИЦДЖЕРАЛЬДА И ЛОРЕНЦА § 65. ПОСТУЛАТЫ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ § 66. ОБЩИЕ СВОЙСТВА ПРОСТРАНСТВА-ВРЕМЕНИ И ОПРЕДЕЛЕНИЕ ОДНОВРЕМЕННОСТИ § 67.  ВЫВОД ПРЕОБРАЗОВАНИЙ ЛОРЕНЦА—ЭЙНШТЕЙНА ВЫВОД ПРЕОБРАЗОВАНИЙ ЛОРЕНЦА—ЭЙНШТЕЙНА§ 68. ОБЩИЕ СЛЕДСТВИЯ ПРЕОБРАЗОВАНИЙ ЛОРЕНЦА § 69. ИЗМЕНЕНИЕ ДЛИНЫ ДВИЖУЩИХСЯ ТЕЛ § 70. ИЗМЕНЕНИЕ ХОДА ДВИЖУЩИХСЯ ЧАСОВ § 71. ПАРАДОКС ЧАСОВ § 72. ЧЕТЫРЕХМЕРНАЯ ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ПРЕОБРАЗОВАНИЙ ЛОРЕНЦА § 73. ЧЕТЫРЕХМЕРНЫЕ ВЕКТОРЫ И ТЕНЗОРЫ § 74. ЧЕТЫРЕХМЕРНЫЙ ВЕКТОРНЫЙ АНАЛИЗ § 75. ЧЕТЫРЕХМЕРНЫЕ СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ § 77. АБЕРРАЦИЯ И ЭФФЕКТ ДОПЛЕРА ДЛЯ СВЕТОВОЙ ВОЛНЫ ГЛАВА 7. РЕЛЯТИВИСТСКАЯ ЭЛЕКТРОДИНАМИКА И ДВИЖЕНИЕ ЗАРЯДА В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ § 78. ЗАКОН СОХРАНЕНИЯ ЭЛЕКТРИЧЕСКОГО ЗАРЯДА В КОВАРИАНТНОЙ ФОРМЕ § 79. КОВАРИАНТНАЯ ЗАПИСЬ УРАВНЕНИЙ ЭЛЕКТРОДИНАМИКИ § 80. ФОРМУЛЫ ПРЕОБРАЗОВАНИЯ ДЛЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ § 81. ИНВАРИАНТЫ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ § 82. ЧЕТЫРЕХМЕРНЫЙ ПОТЕНЦИАЛ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ § 83. КОВАРИАНТНАЯ ЗАПИСЬ УРАВНЕНИЙ МАКСВЕЛЛА В СРЕДЕ § 84. УРАВНЕНИЯ МИНКОВСКОГО § 85. УРАВНЕНИЯ ДВИЖЕНИЯ ЗАРЯДА ВО ВНЕШНЕМ ЭЛЕКТРОМАГНИТНОМ ПОЛЕ § 86.  § 87. ГАМИЛЬТОНОВА ФОРМА УРАВНЕНИЙ ДВИЖЕНИЯ ЗАРЯДА В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ § 88. СИЛА РЕАКЦИИ ИЗЛУЧЕНИЯ ГЛАВА 8. ЭНЕРГИЯ И ИМПУЛЬС В ЭЛЕКТРОДИНАМИКЕ И РЕЛЯТИВИСТСКОЙ МЕХАНИКЕ § 89. ЭНЕРГИЯ И ИМПУЛЬС ЭЛЕКТРОМАГНИТНОГО ПОЛЯ § 90. ЭЛЕКТРОМАГНИТНАЯ ТЕОРИЯ МАССЫ § 91. ЗАКОНЫ СОХРАНЕНИЯ ЭНЕРГИИ И ИМПУЛЬСА ДЛЯ СИСТЕМЫ ЧАСТИЦ И ПОЛЕЙ § 92. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ § 93. РЕЛЯТИВИСТСКИЕ ВСТРЕЧНЫЕ ПУЧКИ § 94. ПРИНЦИП НАИМЕНЬШЕГО ДЕЙСТВИЯ ДЛЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ § 95. ЗАКОНЫ СОХРАНЕНИЯ КАК СЛЕДСТВИЕ ВАРИАЦИОННОГО ПРИНЦИПА ПРИЛОЖЕНИЕ. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ВЕКТОРНОГО АНАЛИЗА 2П. ВАЖНЕЙШИЕ ФОРМУЛЫ И ТЕОРЕМЫ ВЕКТОРНОГО АНАЛИЗА ДОПОЛНЕНИЕ. МОЛЕКУЛЯРНАЯ ОПТИКА 2Д. Магнитооптика (эффекты Фарадея и Коттона-Мутона) |
Закон электромагнитной индукции — Remenergy.ru
В 1831 году мир узнал о понятии электромагнитной инфекции.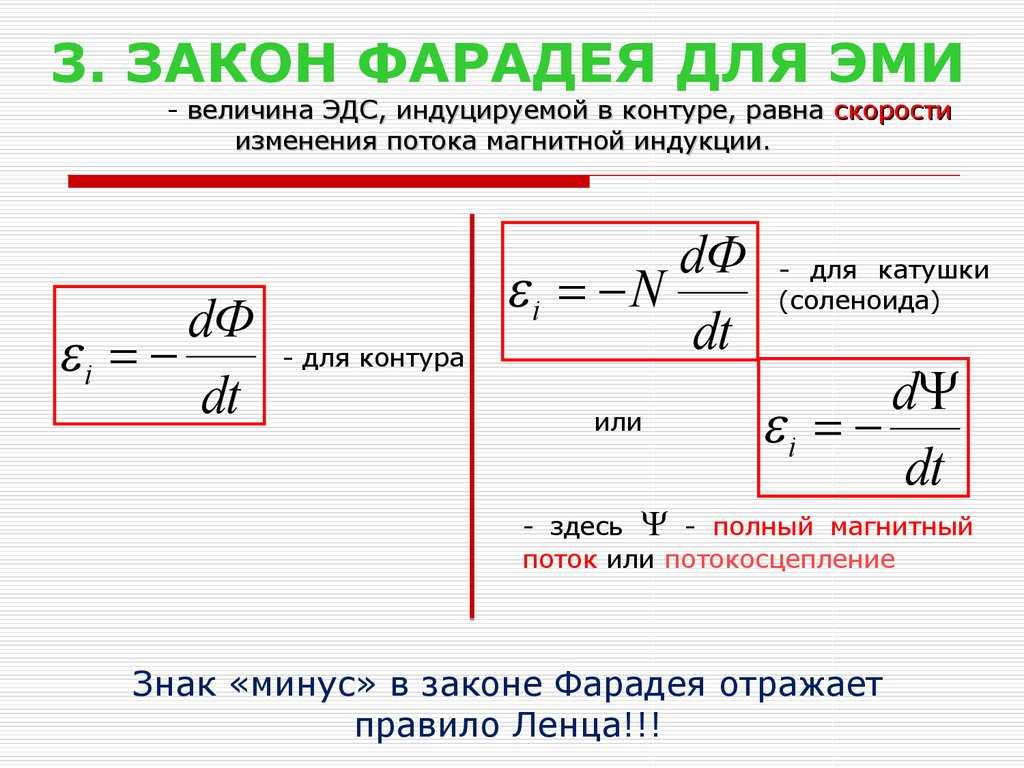 Именно тогда Майкл Фарадей обнаружил это явление, ставшее в конечном счете важным открытием в эмеледике.
Именно тогда Майкл Фарадей обнаружил это явление, ставшее в конечном счете важным открытием в эмеледике.
Содержание
- 1 История развития и опыты Фарадея
- 2 Закон Фарадея
- 3 Закон Фарадея-Максвелла
История развития и опыты Фарадея
ДО Середины XIX ВЕКА Считалось, что электрическое и магнитное поле не имеет связи, и по своей природе их блокировка различна. НЕТ М. Фарадей был уверен в единой природе полей и их свойств. Явление электромагнитной рассеянности, обнаруженное им, стало открытым фундаментом для устройства генераторов всех электростанций. Благодаря этому открытию знаний об электромагнетизме шагнули далеко вперед.
Фарадей проделал следующий опыт: он замыкал цепь в катушке I и вокруг возрастало магни Следующей причиной возникновения данной магнитной полярной сферы является катушка II, в результате которой возник случай
Рис. 1. Схема опыта Фарадея
В самом деле, одновременно с сарадеем, но независимо от него, другой ученый джозеф генри наблюдал это явление Однако Фарадей опубликовал свои исследования ранее. Таким образом, автором электромагнитного излучения стал Майкл Фарадей.
Таким образом, автором электромагнитного излучения стал Майкл Фарадей.
Фарадей, выброс однократного давления: для образования потребляемого тока важным является изменение магнитного потока, пронизывающего замкнутый проводящий контур (катушку).
Закон Фарадея
Явление выброса принимает решение об исключении тока в замкнутом электропроводящем контуре при использовании магнитного потока через этот обширный контур.
Основной закон фарадея соблюдается в том, что электродвижущая сила (эдс) прямо пропорциональна скорости изменения магнитного потока.
Формула федерального отклонения
Рис. 2. Формула рефлекса электромагнитной инфекции
И если Сама формула вопросов, поднимается из сказанных представителей не порождает выше, то знак «-» может вызывать сомнения. Оказывается, правило Ленца — Русского Ученого, Который проводил свои исследования, о скором приходе на фарадея. По Ленцу знак «-» нарушения направления вращения ЭДС, т.е привлекает внимание к воздействию потока, которое вызывает возбуждение тока.
Закон Фарадея-Максвелла
В 1873 г. Дж.К.Максвелл по-новому изложил показания электромагнитного поля. Уравнения, которые он вывел, легли в основу современной радиотехники и электротехники. Они рекомендуют:
- Edl = -dФ/dt – уравнение электродвижущей силы
- Hdl = -dN/dt – уравнение магнитодвижущей силы.
Где E – напряженность поля на участке dl; H – напряженность магнитного поля на участке dl; N – поток рассеяния, t – время.
Симметричный Датский тип включает в себя электрические и магнитные торговые сети, а также магнитные механизмы физический смысл, включает в себя все эти уравнения, может выражать чувства положени:я
- если электрическое поле колебаний, то это изменение всегда сопровождается магнитным полем.
- если магнитное поле меняется, то это изменение всегда связано с полем.
Рис. 3. Возникновение вихревого магнитного поля
Также Максвелл установил, что распространение электромагнитного поля равносильно распространению.
Закон Фарадея: формулировка, уравнение и применение
Что такое закон Фарадея
Закон электромагнитной индукции Фарадея гласит, что в проводнике индуцируется напряжение всякий раз, когда существует относительное движение между проводником и приложенным извне магнитным полем. Величина этого напряжения пропорциональна скорости изменения магнитного потока. Таким образом, закон устанавливает количественную связь между изменяющимся магнитным потоком и наведенным напряжением в электромагнитной цепи.
История
Этот закон приписывают английскому ученому Майклу Фарадею, внесшему значительный вклад в развитие электромагнетизма и электрохимии. В 1831 году Фарадей впервые продемонстрировал электромагнитную индукцию, обернув два провода вокруг противоположных сторон железного кольца. Один провод был подключен к батарее, которая давала ток, а другой провод к гальванометру. Ток в первом проводе создавал магнитное поле, которое проходило по второму проводу. При изменении магнитного потока во втором проводе индуцировался ток, регистрируемый гальванометром.
Уравнение закона Фарадея
Рассмотрим пример проводника, намотанного на катушку. Предположим, эта катушка помещена во внешнее магнитное поле, представленное магнитными силовыми линиями. Количество линий, проходящих через данную площадь поперечного сечения, определяется как магнитный поток. Есть несколько способов изменить этот поток.
Согласно закону Фарадея, изменение магнитного потока вызывает индуцированное напряжение, называемое электродвижущей силой (ЭДС). Математически закон задается следующей формулой.
ε = – Н dφ/dt
Где,
ε = ЭДС индукции
Н = число витков катушки
dφ/dt = мгновенное изменение магнитного потока во времени
4 СИ Единица ЭДС : Volts
Отрицательный знак связан с тем, что ЭДС индукции противодействует магнитному полю. Величина ЭДС определяется выражением
|ε| = N dφ/dt
Когда N = 1 и dφ/dt = 1 Втб/с, то |ε| = 1 В
Следовательно, ЭДС индукции представляет собой напряжение, создаваемое на катушке из одного витка при скорости потока 1 Втб/с. Закон Ленца определяет направление индукционного тока.
Закон Ленца определяет направление индукционного тока.
Дифференциальная форма закона Фарадея
Шотландский математик Джеймс Клерк Максвелл разработал набор уравнений в частных производных, которые описывают, как электрические и магнитные поля генерируются зарядами, токами и изменениями полей. Сегодня эти уравнения известны под общим названием уравнения Максвелла. Более ранняя версия уравнений была впервые опубликована в 1861 году. Уравнение Максвелла-Фарадея имеет вид
∇ X E = -∂ B /∂T
, где
E : Электрическое поле
B : Магнитное поле
Применение закона Фарадея
Фарадея является одним из самых основных законов. Этот закон находит свое применение в большинстве электрических устройств. Он может объяснить принцип работы трансформаторов, генераторов, катушек индуктивности и двигателей. Вот несколько вариантов использования и приложений, в том числе в повседневной жизни.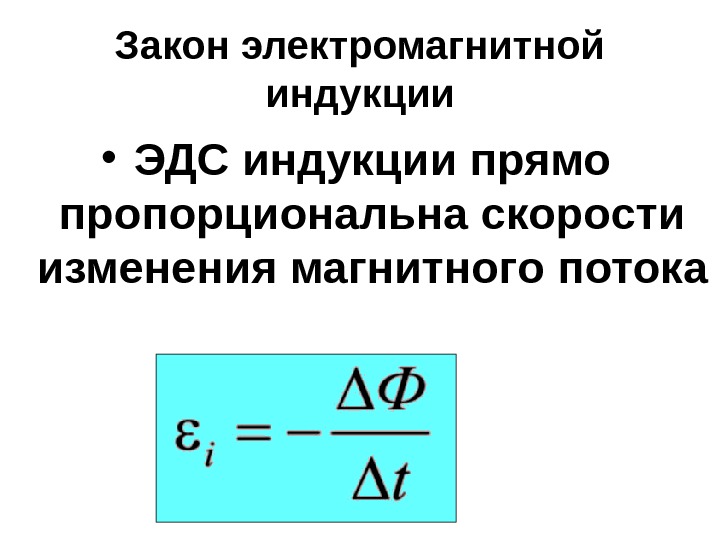
- Трансформатор : Он состоит из пары катушек, намотанных на квадратный сердечник. Переменный ток, проходящий через одну катушку, создает изменяющееся магнитное поле, в результате чего во второй катушке возникает индуцированный ток.
- Генератор : Устройство, преобразующее механическую энергию в электрическую, используемую во внешней цепи. Катушка проводника быстро вращается между полюсами подковообразного магнита. Вращающаяся катушка перехватывает магнитное поле, и в ней индуцируется ток.
- Индукционная плита : Используется для нагрева посуды с помощью индукции вместо пламени или электрической катушки. В нем используется понятие взаимной индуктивности, основанное на принципе взаимной индукции.
- Электрические звонки : Устройство, работающее от электромагнита. Молоток с электромагнитным приводом ударяет по колоколу, что приводит к звуку.
- Электромагнитный расходомер : Устройство, используемое для измерения скорости проводящих жидкостей с помощью приложения магнитного поля.
 ЭДС индукции пропорциональна скорости жидкости.
ЭДС индукции пропорциональна скорости жидкости.
Список литературы
Последний раз статья рецензировалась 2 февраля 2023 г.
Электромагнетизм — Закон Фарадея и электромагнитная индукция
Задавать вопрос
спросил
Изменено 2 года, 7 месяцев назад
Просмотрено 949 раз
$\begingroup$
Закон электромагнитной индукции Фарадея гласит, что скорость изменения магнитного потокосцепления пропорциональна индуцированной $\mathcal{ЭДС}$. Для проводника формула выглядит следующим образом:
$$\mathcal{ЭДС}=N\frac{\Delta\Phi}{\Delta t}$$
Где $N$ — количество витков в проводе, $\ Phi$ — это потокосцепление, а $t$ — это время.
Однако я не понимаю, как $N$ становится переменной в формуле. Принципом, лежащим в основе электромагнитной индукции, является скорость изменения потокосцепления, но $N$ не зависит от площади, хотя и связана с $B$, плотностью магнитного потока.
Через соотношение
$$\Phi=NBA$$
Это становится интуитивно понятным, если $N$ относится к числу витков соленоида $X$, создающего магнитное поле, а $B$ представляет собой магнитный поток плотности, обеспечиваемой единичной катушкой соленоида $X$, но я не совсем понимаю, как понимать формулу, если обстоятельства обратные,
Где $N$ — количество витков соленоида $Y$, в котором будет индуцироваться $\mathcal{ЭДС}$, а $B$ — плотность магнитного потока соленоида $X$, индуцирующего $\mathcal {ЭДС}.$
Я хочу пояснить переменную $N$ в этих типах явлений, потому что я не вижу интуитивного способа связать с ней концепцию магнитного потокосцепления и индуцированной $\mathcal{ЭДС}$.
- электромагнетизм
- электричество
- электромагнитная индукция
$\endgroup$
1
$\begingroup$
Я думаю, ваша проблема в том, почему ЭДС зависит от количества витков в катушке, не так ли?
Представьте себе такую ситуацию (извините за неудачную цифру). Я попытался сделать катушку из проволоки с N витками всего (все витки соединены, но если бы я сделал это, то изображение стало бы беспорядочным), а красные стрелки представляют линии магнитного поля. Поскольку каждая петля имеет одинаковую площадь, магнитный поток будет одинаковым во всех петлях (я рассматриваю магнитное поле B должен быть однородным внутри катушки), и любое изменение магнитного поля B вызовет одинаковое изменение магнитного потока во всех контурах. Таким образом, ЭДС , развиваемая в каждом контуре, определяется Законом Фарадея как $$ \mathcal{ЭДС} = -\frac{d\phi}{dt}~~~~~~~(1)$$ Теперь, так как у нас есть $N$ петель и в каждой петле ЭДС равна $-\frac{d\phi}{dt}$ поэтому общая ЭДС от А до В есть сумма этих ЭДС и, следовательно, $$ \mathcal{emf_{A ~to~ B} } = -N \frac{d\phi}{dt}$$
Ваша интуитивная проблема заключалась в том, почему ЭДС зависит от числа витков, когда экспериментально было установлено, что ЭДС зависит только от магнитного потока, который в свою очередь зависит от площади петли, ну как вы видели из математики сделанной выше, ЭДС равна вызванные в каждом контуре по закону Фарадея но за счет связности мы получили общую сумму всех э.
Я попытался сделать катушку из проволоки с N витками всего (все витки соединены, но если бы я сделал это, то изображение стало бы беспорядочным), а красные стрелки представляют линии магнитного поля. Поскольку каждая петля имеет одинаковую площадь, магнитный поток будет одинаковым во всех петлях (я рассматриваю магнитное поле B должен быть однородным внутри катушки), и любое изменение магнитного поля B вызовет одинаковое изменение магнитного потока во всех контурах. Таким образом, ЭДС , развиваемая в каждом контуре, определяется Законом Фарадея как $$ \mathcal{ЭДС} = -\frac{d\phi}{dt}~~~~~~~(1)$$ Теперь, так как у нас есть $N$ петель и в каждой петле ЭДС равна $-\frac{d\phi}{dt}$ поэтому общая ЭДС от А до В есть сумма этих ЭДС и, следовательно, $$ \mathcal{emf_{A ~to~ B} } = -N \frac{d\phi}{dt}$$
Ваша интуитивная проблема заключалась в том, почему ЭДС зависит от числа витков, когда экспериментально было установлено, что ЭДС зависит только от магнитного потока, который в свою очередь зависит от площади петли, ну как вы видели из математики сделанной выше, ЭДС равна вызванные в каждом контуре по закону Фарадея но за счет связности мы получили общую сумму всех э. д.с. от одного конца до другого.
д.с. от одного конца до другого.
Надеюсь, это поможет.
$\endgroup$
$\begingroup$
ЭДС замкнутого контура равна $$\mathscr E = -\frac {d\Phi}{dt}$$ в котором $$\Phi =\int_S \vec B.d\vec S$$ поверхностный интеграл вычисляется по любой поверхности, ограниченной петлей.
Вполне возможно применить этот так как стоит на катушку Н витков. Площадь S , ограниченная спиралью, образованной проводом катушки, почти равна N , умноженной на площадь одного витка, рассматриваемого как бы в одной плоскости. Таким образом, $$S=NA_{поворот}.$$
Преимущество написания уравнений в том виде, как я это сделал в начале, без явного появления $N$, заключается в том, что они формально правильны для ситуаций, в которых разные величины потока могут быть связаны с разными витками, как это может быть в случае соленоида. Интеграция позаботится об этом.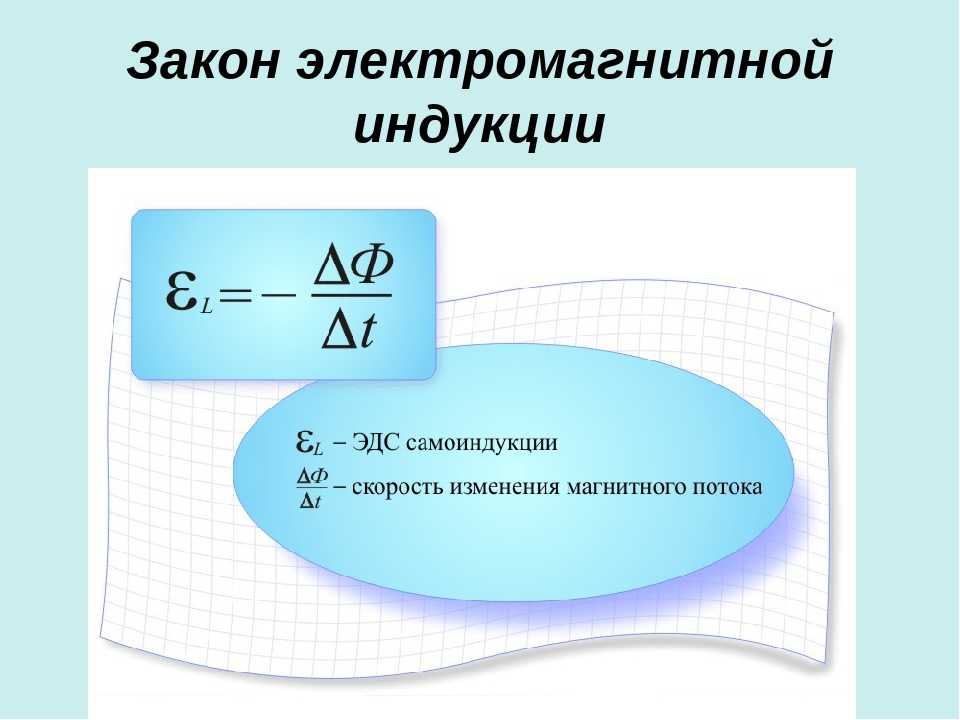


 ЭДС индукции пропорциональна скорости жидкости.
ЭДС индукции пропорциональна скорости жидкости.