Закон всемирного тяготения – кратко
Понимание закона всемирного тяготения – один из ключей к успешному изучению школьного курса физики. Гравитация действует абсолютно на все тела во Вселенной.
Сущность закона
Классическая механика, частью которой является теория Ньютона, описывает движение физических объектов во Вселенной. Объясняет, как взаимодействуют предметы при столкновении, при скатывании с наклонной плоскости, каким образом работают механизмы с шестерёнками и блоками и т. д. Данная модель была общепризнанной в XVII-XIX вв., её точности хватало для любых задач, возникавших перед людьми, таких как постройка зданий и создание механизмов. По сей день классическая механика изучается в школах и закладывает основы для дальнейшего образования инженеров и учёных.
Стоит отметить, что ньютоновский закон всемирного притяжения не объясняет природу возникновения гравитации, а всего лишь устанавливает количественные закономерности.
Описывается данное взаимодействие с помощью формулы:
, где:
m1 и m2 – масса первого и второго тела соответственно;
r – расстояние между их центрами тяжести;
G – гравитационная постоянная.
Измеряется сила гравитации в Ньютонах.
Гравитационная постоянная равна:
Малая величина гравитационной постоянной отражает низкую интенсивность взаимодействия, сила которого возрастает только при очень больших массах.
Ограничения по применению законов Ньютона
Формула, предложенная Ньютоном, может быть использована для решения задач только в нескольких случаях:
- Расчёт осуществляется для двух тел, размеры которых пренебрежительно малы по отношению к расстоянию, отделяющему их друг от друга.
- В случае когда оба объекта обладают шарообразной формой и равномерной плотностью.
- Первое тело – шар, масса и объём которого многократно превосходит соответствующие характеристики второго тела, а оно само находится вблизи него или лежит на его поверхности.
Третий случай описывает гравитационное взаимодействие между Землёй и любым предметом на её поверхности. Дистанция между объектами равна радиусу планеты, т. е. 6370 км. Сила притяжение вызывает ускорение движения при падении предметов на Землю.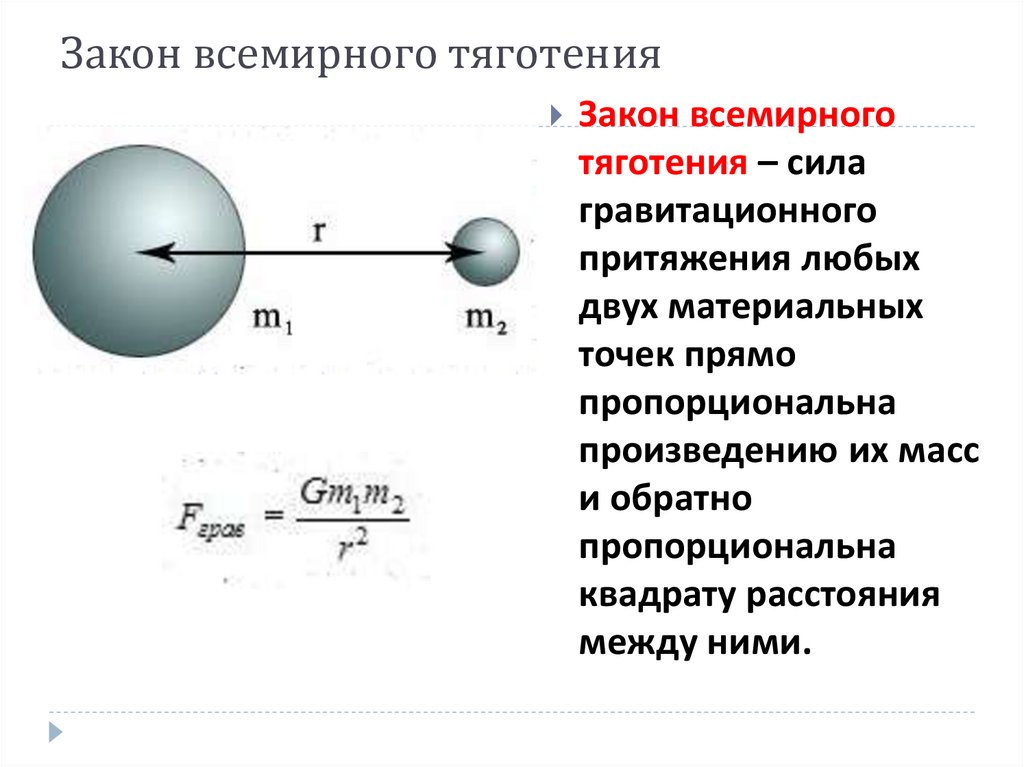
Сила тяжести
Это частный случай действия силы тяготения, который описывает притяжение, возникающее между планетами и малыми объектами.
m – масса тела, на которое действует притяжение планеты;
g – ускорение свободного падения.
Величина g не зависит от массы тела и является константой для каждой планеты. На Земле она примерно равна 9,8 м/с2. Есть незначительные колебания в зависимости от географического местоположения, наличия полезных ископаемых, высоты над уровнем моря и т. д.
История открытия
Идея о существовании некой силы, удерживающей планеты на орбитах и заставляющей тела притягиваться друг к другу, озвучивалась задолго до написания Ньютоном. Над этим размышляли ещё древнегреческие философы и учёные.
Свой труд «Математические начала натуральной философии» И. Ньютон основывает на эмпирических законах Кеплера. Однако английский физик не только выдвинул гипотезу, но и сумел предложить целостную математическую модель, описывающую движение тел и позволявшую вести точные расчёты. В неё вошли: три ньютоновских закона, система методов для математического исследования и закон тяготения.
В неё вошли: три ньютоновских закона, система методов для математического исследования и закон тяготения.
Найденные числовые закономерно неоднократно проверялись учёными XVIII –XIX вв. Одни использовали в экспериментах точные крутильные весы, как Г. Кавендиш, другие применяли закон гравитации для описания движения небесных тел или исследовали действие гравитационного поля при произвольном распределении вещества.
В научном сообществе того времени большинство приняло ньютоновскую модель в качестве наиболее точного описания фундаментального закона физики. Однако, у неё нашёлся ряд недостатков: необъяснимое дальнодействие, ненулевая средняя плотность вещества во Вселенной и др.
Дальнейшее развитие теория получила в работах С. Пуассона, У. Леверье и А. Эйнштейна. Общая теория относительности, предложенная последним, смогла преодолеть все ключевые недостатки теории Ньютона и стала основой для качественного скачка в понимании природы вещей.
Добавить комментарий
Закон всемирного тяготения (формула Ньютона).
 Постоянная тяготения (величина, единицы измерения).
Постоянная тяготения (величина, единицы измерения).Два тела действуют друг на друга с силой, которая обратно пропорциональна квадрату расстояния между ними и прямо пропорциональна произведению их масс.
Закон всемирного тяготения справедлив лишь для тел, которые можно считать материал.точками, т.е. для таких тел, размеры которых малы по сравнению с расстоянием между ними.
Значение G –фундам. Физ. Постоянная, принимаемая равной 6,6720 *10-11H*м2/кг2, т.е. два точечных тела массой по 1 кг каждое, находящиеся на расстоянии 1м друг от друга, притягиваются с силой 6,6720*10-11Н. Очень малая величина G показывает, что сила гравитац.взаимодействия может быть значительной только в случае больших масс.
Если тело расположено на высоте h от поверхности, R0-радиус земли, тогда
Вынужденные колебания.

Вынужденные колебания, колебания, возникающие в какой-либо системе под действием переменной внешней силы.
Fo/m — отношение амплитудного значения внешней вынуждающей силы
Инерциальные системы отсчёта. Первый закон Ньютона.
Инерциальная система отсчёта, система отсчёта, в которой справедлив закон инерции: материальная точка, когда на неё не действуют никакие силы (или действуют силы взаимно уравновешенные), находится в состоянии покоя или равномерного прямолинейного движения.
Первый
закона Ньютона (закон
инерции)
выполняется только в инерцсис
отсчета: существуют
такие системы отсчета, относительно
которых тело (материальная точка) при
отсутствии на неё внешних воздействий
(или при их взаимной компенсации)
сохраняет состояние покоя или равномерного
прямолинейного движения.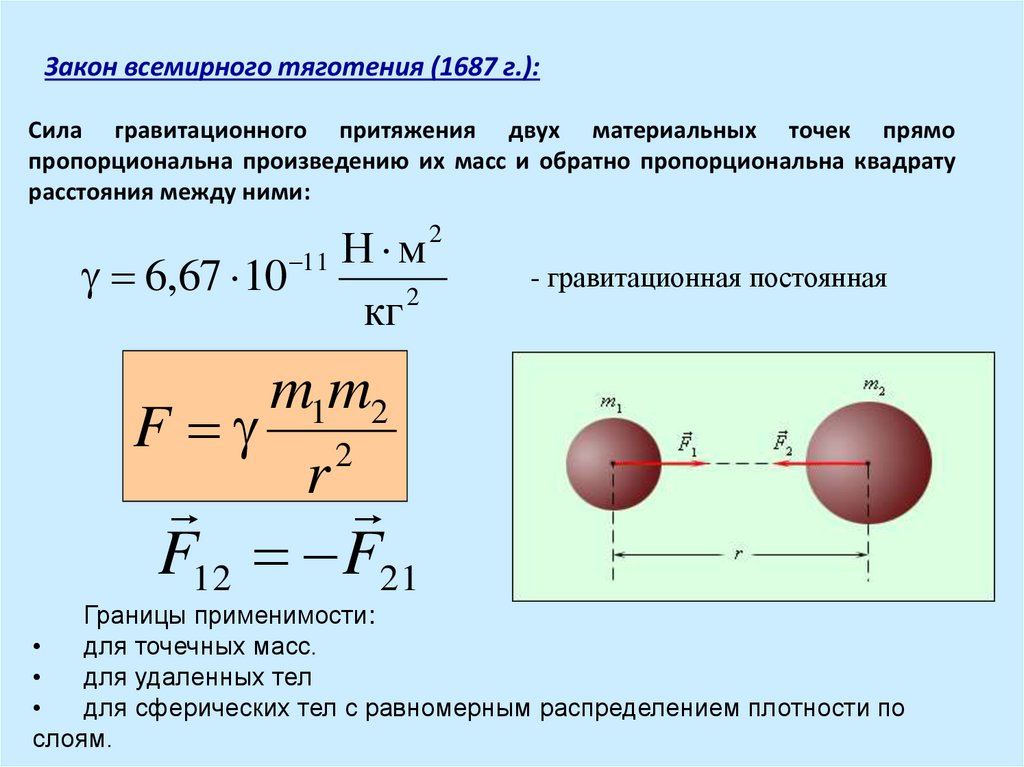 Свойство
тел сохранять свою скорость при отсутствии
действия на него других тел называется
инерцией. Поэтому первый
закон Ньютона называют
законом инерции.
Свойство
тел сохранять свою скорость при отсутствии
действия на него других тел называется
инерцией. Поэтому первый
закон Ньютона называют
законом инерции.
Каноническое уравнение свободных затухающих колебаний.
затухающие свободные колебания — колебания с уменьшающейся энергией из-за сопротивления среды
уравнение затухающих колебаний маятника: , где
-коэффициент затухания, w-частота
, где (r — коэффициент сопротивления), Коэффициент затухания — величина обратная пропорциональная времени в течении которого амплитуда уменшилась в е раз.
Второй закон Ньютона. Сила, масса, плотность тела (определение, единицы измерения)
2ой
закон Ньютона-основной закон динамики
поступательного движения. 2ой закон
отвечает на вопрос, как изменится
механическое движение матер.точки(тела)
под действием приложенных к ней сил.
Если
рассмотреть действие различных сил на
одно и то же тело, то оказывается, что
ускорение, приобретаемое телом, всегда
прямо пропорционально равнодействующей
приложенных сил:
При
действии одной и той же силы на тела с
разными массами их ускорения оказываются
различными, а именно а
~ 1/т
(F =
const).
сила и ускорение—величины векторные, можем записать а = kF/m.
Соотношение (6.3) выражает второй закон Ньютона: ускорение, приобретаемое материальной точкой (телом), пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела). В СИ коэффициент пропорциональности k= 1. Тогда A=F/m или (6.4) Учитывая, что масса материальной точки (тела) в классической механике есть величина постоянная, в выражении (6.4) ее можно внести под знак производной: (6.5) Векторная величина (6.6)- численно равная произведению массы материальной точки на ее скорость и имеющая направление скорости, называется импульсом (количеством движения) этой материальной точки. Подставляя (6.6) в (6.5), получим(6.7) Это выражение —
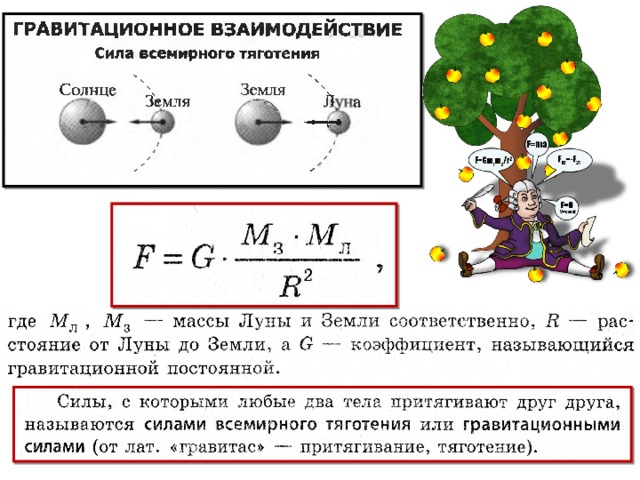 7) называетсяуравнением
движения материальной точки.
Единица
силы в СИ — ньютон (Н):
1 Н — сила, которая массе 1 кг сообщает
ускорение 1 м/с2 в направлении действия
силы:
1Н=1кг*м/c2
Второй закон Ньютона справедлив
только в инерциальных системах
отсчета. Первый
закон Ньютона можно получить из второго.
Действительно, в случае равенства
нулю равнодействующей сил (при отсутствии
воздействия на тело со стороны других
тел) ускорение (см. (6.3)) также равно нулю.
Однако
7) называетсяуравнением
движения материальной точки.
Единица
силы в СИ — ньютон (Н):
1 Н — сила, которая массе 1 кг сообщает
ускорение 1 м/с2 в направлении действия
силы:
1Н=1кг*м/c2
Второй закон Ньютона справедлив
только в инерциальных системах
отсчета. Первый
закон Ньютона можно получить из второго.
Действительно, в случае равенства
нулю равнодействующей сил (при отсутствии
воздействия на тело со стороны других
тел) ускорение (см. (6.3)) также равно нулю.
Однако Сила-векторная величина, являющ. мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму или размеры.Единицы измерения в СИ –ньютоны.
Масса-физическая
величина, являющаяся однйо из основных
характеристик матери, определяющая ее
инерционные и гравитационные свойства.
Плотность-скалярная физическая величина, определяемая как отношение массы тела к занимаемому этим телом объёму или площади(поверхностная плотность).Ед.измерения в СИ-кг/м3.
Объяснение урока: Закон всемирного тяготения Ньютона
В этом объяснении мы узнаем, как применить закон всемирного тяготения Ньютона, чтобы найти гравитационную силу между двумя массами.
Рассмотрим две массы 𝑚 и 𝑚, разделенные расстоянием 𝑟. Затем каждый из этих масс оказывает силу притяжения на другую, называемую гравитационной силой . Эта сила возникает между любой парой тел с ненулевыми массами и обратно пропорциональна квадрату расстояния между двумя массами. Эта сила возникает как прямой результат третьего закона движения Ньютона.
Определение: Третий закон движения Ньютона
Третий закон движения Ньютона гласит, что когда одно тело действует с силой на
второе тело, второе тело одновременно прикладывает силу, равную
по величине и противоположно по направлению на первом теле.
Для гравитационных сил, действующих на пару тел, эти условия могут быть дополнены некоторыми дополнительными условиями, которые вместе составляют определение закона всемирного тяготения Ньютона.
Давайте теперь определим закон всемирного тяготения Ньютона.
Определение: Закон всемирного тяготения Ньютона
Два тела действуют гравитационные силы друг на друга, где направление сила, действующая на любое тело, направлена к центру масс другого тела.
Величины сил задаются формулой 𝐹=𝐺𝑚𝑚𝑟, где 𝐹 — сила, измеряемая в ньютонах, 𝑚 и 𝑚 — массы тел измеряется в килограммах, 𝑟 — расстояние между центрами масс тел, измеряемых в метрах, а 𝐺 — постоянная, где 𝐺≈6,67×10⋅/.Нмкг
𝐺 известна как универсальная гравитационная постоянная.
Примечание. Если два объекта должны соприкасаться, чтобы действовала сила, сила известна.
как контактная сила. Если в этом нет необходимости, силы называются бесконтактными.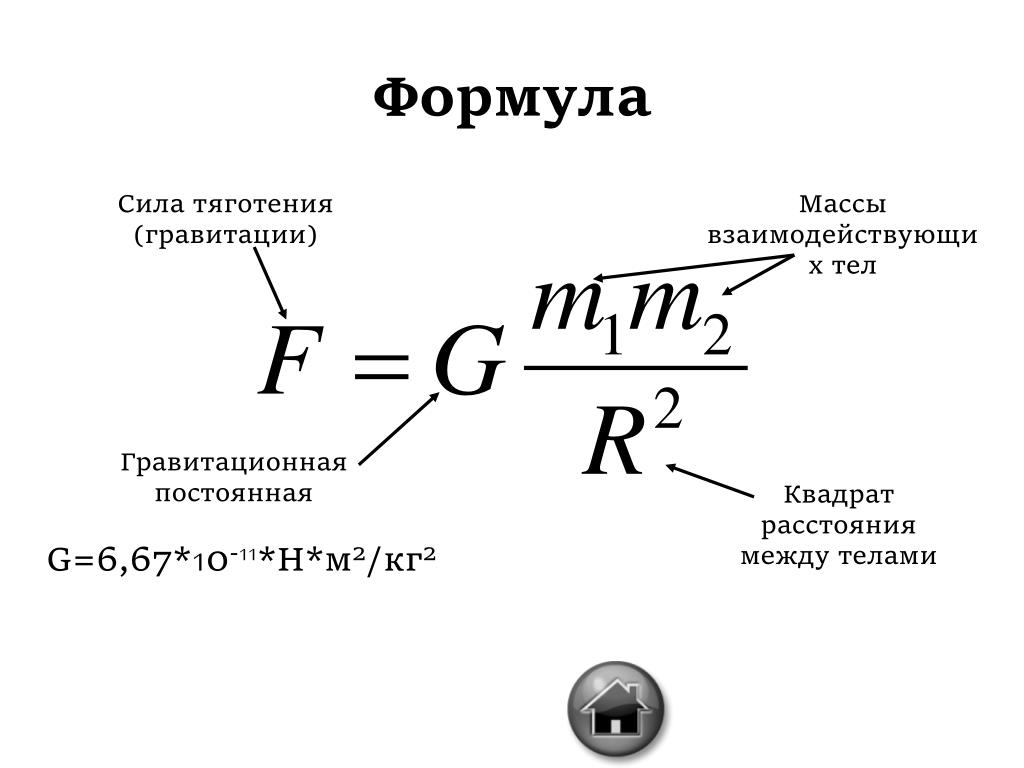
Давайте рассмотрим пример, в котором гравитационная сила возникает между определяется два тела.
Пример 1. Расчет силы притяжения между двумя телами
Определите силу притяжения между двумя одинаковыми шарами, каждый из которых масса 3,01 кг, если расстояние между их центрами равно 15,05 см, а универсальная гравитационная постоянная равна 6,67×10 Н⋅м 2 /кг 2 .
Ответ
Расстояние между центрами масс шаров, 𝑟, должны быть измерены в метрах, чтобы соответствовать единице всемирного тяготения постоянная, 𝐺. Тогда значение 𝑟 равно 0,1505 м.
Подставляя значения, указанные в вопросе, находим, что 𝐹=6,67×103,010,1505=2,668×10,N
Теперь рассмотрим пример, в котором гравитационная сила между
двух тел используется для определения расстояния между их центрами масс.
Пример 2: Расчет расстояния между двумя телами при наличии силы тяжести между ними
При условии, что сила тяжести между двумя телами масс 4,6 кг и 2,9кг было 3,2×10 N, найдите расстояние между их центрами. Возьмем универсальную гравитационную постоянную 𝐺=6,67×10⋅/Нмкг.
Ответ
Формула для определения силы тяготения между телами, 𝐹=𝐺𝑚𝑚𝑟, можно переставить, чтобы сделать 𝑟 предметом следующим образом: 𝑟=𝐺𝑚𝑚𝐹𝑟=𝐺𝑚𝑚𝐹.
Подставляя значения, указанные в вопросе, находим, что 𝑟=6,67×104,6(2,9)3,2×10𝑟=√6,67×10(4,16875×10)𝑟=√2,78055625𝑟=1,6675.м
Расстояние между центрами тел равно 166,75 см.
Давайте теперь рассмотрим пример, в котором гравитационная сила возникает между два тела определяются, где одно из тел Земля.
Пример 3: расчет гравитационной силы между Землей и спутником
Спутник массы
2 415 кг
вращается вокруг Земли на высоте 540 км над ее поверхностью. Учитывая, что универсальная гравитационная постоянная
составляет 6,67×10 Н⋅м 2 /кг 2 а масса и радиус Земли равны
6×10 кг и
6 360 км, определить силу гравитации
воздействия Земли на спутник.
Учитывая, что универсальная гравитационная постоянная
составляет 6,67×10 Н⋅м 2 /кг 2 а масса и радиус Земли равны
6×10 кг и
6 360 км, определить силу гравитации
воздействия Земли на спутник.
Ответ
Силу можно определить по формуле 𝐹=𝐺𝑚𝑚𝑟.
Расстояние между Землей и спутником, 𝑟, должно измеряться в метров, чтобы соответствовать значению всемирного гравитационного постоянная, 𝐺.
Поскольку 𝑟 в формуле — это расстояние между центрами масс, значение 𝑟 есть сумма расстояний от спутника до поверхность Земли и радиус Земли: 𝑟=(6360+540)×10=6,9×10.
Подставляя значения, указанные в вопросе, находим, что 𝐹=6,67×1024156×10(6,9×10)𝐹=6,67×101,449×10(6,9×10)𝐹=6,67×103,0434783×10=20300, N
Ускорение тела за счет силы тяжести между ним и
другое тело можно определить, приравняв силы между телами
и результирующая сила, действующая на тело, ускорение которого определяется. У нас есть то, что
𝐹=𝐺𝑚𝑚𝑟,
и
𝐹=𝑚𝑎,
где тело, ускорение которого определяется, имеет массу 𝑚. Отсюда получаем
𝑚𝑎=𝐺𝑚𝑚𝑟.
У нас есть то, что
𝐹=𝐺𝑚𝑚𝑟,
и
𝐹=𝑚𝑎,
где тело, ускорение которого определяется, имеет массу 𝑚. Отсюда получаем
𝑚𝑎=𝐺𝑚𝑚𝑟.
Поскольку 𝑚≠0, мы можем разделить на 𝑚. Следовательно, 𝑎=𝐺𝑚𝑟.
Мы видим, что ускорение тела массой 𝑚 не зависят от значения 𝑚.
Определение: Напряженность гравитационного поля точечной массы
Напряженность гравитационного поля – это гравитационная сила, приходящаяся на единицу массы масса, 𝑚, на теле, центр масс которого находится на расстоянии 𝑟 из 𝑚. Это дано 𝑔=𝐺𝑚𝑟.
Напряжённость гравитационного поля — это свойство любой точки поля, соприкасаются ли они с поверхностью гравитирующего тела или нет.
На Земле ускорение свободного падения составляет примерно
9,8 м/с 2 . Это значение, известное как 𝑔, можно определить по массе,
𝑚=5,97×10кг,
и радиус, 𝑟 = 6,37 × 10 м, Земли следующим образом:
𝑔=6,67×105,97×10(6,37×10),
что составляет 9,8 с точностью до одного десятичного знака.
Теперь рассмотрим пример, в котором коэффициент ускорения за счет гравитации на Земле и другой планете определяется.
Пример 4: Сравнение ускорения силы тяжести на Земле и на другой планете
Учитывая, что масса и диаметр планеты в 3 и 6 раз больше земные, соответственно, рассчитывают соотношение между ускорение силы тяжести на этой планете и на Земле.
Ответ
Ускорение свободного падения на поверхности однородной сферы можно определить по формуле 𝑎=𝐺𝑚𝑟, где 𝑚 — масса сферы, а 𝑟 — ее радиус.
Принимая 𝑚 за массу Земли и 𝑟 за радиус Земли,
ускорение свободного падения на планете с массой в 3 раза больше
Земли и диаметром в 6 раз больше, чем у Земли, выражается
𝑎=𝐺3𝑚(6𝑟),
так как умножение диаметра сферы на константу умножает
радиус сферы на ту же постоянную. Выражение для
ускорение силы тяжести на планете можно выразить как
ускорение силы тяжести на Земле, умноженное на постоянную, следующим образом:
𝑎=𝐺3𝑚36𝑟=𝐺𝑚12𝑟=112𝐺𝑚𝑟.
Поскольку ускорение свободного падения на планете равно 112 из что на Земле отношение ускорения свободного падения на планеты к ускорению свободного падения на Земле 1∶12.
Давайте теперь рассмотрим пример, в котором радиус планеты равен определяется по ускорению силы тяжести на планете.
Пример 5. Определение радиуса планеты по информации о сброшенном объекте
Космонавт сбросил объект с высоты 2 352 см над поверхностью планеты, и он достиг поверхности через 8 с. Масса планеты составляет 7,164×10 кг, в то время как Земля 5,97×10 кг, а радиус Земли равен 6,34×10 м. При условии гравитационный ускорение Земли равно 𝑔=9,8/мс, найти радиус другая планета.
Ответ
Ускорение вблизи поверхности планеты может быть аппроксимировано
используя ускорение силы тяжести планеты на ее поверхности. Тогда ускорение свободного падения на поверхности однородной
сферы можно определить по формуле
𝑎=𝐺𝑚𝑟,
где 𝑚 — масса сферы и
𝑟 — его радиус.
Тогда ускорение свободного падения на поверхности однородной
сферы можно определить по формуле
𝑎=𝐺𝑚𝑟,
где 𝑚 — масса сферы и
𝑟 — его радиус.
Ускорение свободного падения на планете, которую посещает космонавт можно определить по движению падающего предмета по формуле 𝑠=𝑢𝑡+12𝑎𝑡, где 𝑠 — перемещение брошенного предмета, 𝑢 является начальным скорость объекта, 𝑡 — время, в течение которого объект движется для, а 𝑎 — ускорение объекта.
Объект падает с точки 2 352 см над поверхностью планеты. Чтобы соответствовать универсальному гравитационная постоянная, это смещение преобразуется в значение в метров 23,52 м. Объект падает из состояния покоя; следовательно, мы имеем это 23,52=12𝑎8,𝑎=2(23,52)64=0,735/.мс
Мы можем сделать 𝑟 предметом формулы, 𝑎=𝐺𝑚𝑟, давая нам 𝑟=𝐺𝑚𝑎,𝑟=𝐺𝑚𝑎.
Подставляя найденное ускорение, известную массу планеты, и принимая 𝐺=6,67×10⋅/,Нмкг у нас есть 𝑟=6,67×107,164×100,735,𝑟≈2,55×10,m
Важно отметить, что вопрос не дает значения
из 𝐺 использовать.
Способ определения радиуса планеты без знаний значения 𝐺 можно получить, сравнивая выражения для ускорения свободного падения на планете и на Земле.
На Земле у нас есть это 𝑎=𝐺𝑚𝑟,ЕЕЕ где 𝑎E — ускорение свободного падения на Земле, 𝑚E — масса Земли, а 𝑟E — радиус Земли.
Эквивалентно, на планете у нас есть это 𝑎=𝐺𝑚𝑟,PPP где 𝑎P — ускорение свободного падения на планете, 𝑚P — масса планеты, а 𝑟P — радиус планеты.
Мы можем разделить 𝑎E на 𝑎P, чтобы получить 𝑎𝑎=𝐺𝐺𝑎𝑎=𝑎𝑎=𝑚𝑚𝑟𝑟.EPEPEPEPPEEEPPEEEEPPEE0003
Мы можем сделать 𝑟P предметом выражения следующим образом: 𝑟=𝑎𝑎𝑚𝑚𝑟𝑟=𝑎𝑎𝑚𝑚𝑟.PEPPEEPEPPEE
Подставляя значения 𝑎E, 𝑚E, 𝑟E, 𝑚P и 𝑎P, получаем 𝑟=9,80,7357,164×105,97×10(6,34×10)𝑟=9,80,7357,1645,97(6,34×10)𝑟=2,536×10,ППС m
Это значение 𝑟P немного отличается от полученного с помощью
стандартное значение 𝐺, как значение, рассчитанное при сравнении выражений
для ускорения свободного падения на Земле и на планете зависит от
точность, используемая при указании значения радиуса и массы
Земли, а не на значение всемирной гравитационной постоянной.
Важно отметить, что кинематическое уравнение, используемое для определения 𝑎P только приблизительно правильно, так как ускорение свободного падения при точка 23,52 м над поверхностью планеты не равна ускорение силы тяжести у поверхности планеты. Следовательно, значение ускорения свободного падения на планете определяется формулой сброс объекта с поверхности планеты приведет к недооценке ускорение и, следовательно, переоценить радиус планеты.
Давайте теперь обобщим некоторые ключевые понятия из этого объяснения.
Ключевые моменты
- Два тела действуют друг на друга с гравитационными силами, где
направление силы, действующей на любое тело, направлено к центру масс
другое тело. Величины сил задаются выражением
𝐹=𝐺𝑚𝑚𝑟,
где 𝐹 — сила, измеренная в
ньютоны, 𝑚
𝑚 – массы тел, измеренные в
килограммы,
𝑟 — расстояние между центрами
масса тел измеряется в
метров и 𝐺
константа, где
𝐺≈6,67×10⋅/.
 Nmkg𝐺 известна как универсальная гравитационная постоянная.
Nmkg𝐺 известна как универсальная гравитационная постоянная. - Ускорение тела за счет силы тяжести между собой а другое тело можно определить, приравняв силы между телами и результирующая сила, действующая на тело, ускорение которого определяется: 𝑚𝑎=𝐺𝑚𝑚𝑟. Следовательно, 𝑎=𝐺𝑚𝑟, где 𝑎 — ускорение свободного падения тела массы 𝑚 и 𝑟 — расстояние между центры масс 𝑚 и 𝑚.
- Для двух тел с массами 𝑚 и 𝑚 и радиусов 𝑟 и 𝑟 отношение ускорений свободного падения этих тел равно 𝑎𝑎=𝑚𝑚𝑟𝑟.
6.5 Универсальный закон всемирного тяготения Ньютона – Колледж физики
Глава 6 Равномерное круговое движение и гравитация
Резюме
- Объясните гравитационную силу Земли.
- Опишите гравитационное воздействие Луны на Землю.
- Обсудить невесомость в космосе.
- Изучите эксперимент Кавендиша
Что общего у ноющих ног, падающего яблока и орбиты Луны? Каждая из них вызвана силой гравитации. Наши ноги напряжены, поддерживая наш вес — силу земного притяжения, действующую на нас. Яблоко падает с дерева из-за той же силы, действующей на высоте нескольких метров над поверхностью Земли. А Луна вращается вокруг Земли потому, что гравитация способна обеспечить необходимую центростремительную силу на расстоянии сотен миллионов метров. На самом деле одна и та же сила заставляет планеты вращаться вокруг Солнца, звезды — вокруг центра галактики, а галактики — группироваться вместе. Гравитация — еще один пример лежащей в основе простоты природы. Это самая слабая из четырех основных сил, встречающихся в природе, и в некотором смысле наименее изученная. Это сила, действующая на расстоянии, без физического контакта, и выражается формулой, действующей повсюду во Вселенной, для масс и расстояний, которые варьируются от крошечных до огромных.
Наши ноги напряжены, поддерживая наш вес — силу земного притяжения, действующую на нас. Яблоко падает с дерева из-за той же силы, действующей на высоте нескольких метров над поверхностью Земли. А Луна вращается вокруг Земли потому, что гравитация способна обеспечить необходимую центростремительную силу на расстоянии сотен миллионов метров. На самом деле одна и та же сила заставляет планеты вращаться вокруг Солнца, звезды — вокруг центра галактики, а галактики — группироваться вместе. Гравитация — еще один пример лежащей в основе простоты природы. Это самая слабая из четырех основных сил, встречающихся в природе, и в некотором смысле наименее изученная. Это сила, действующая на расстоянии, без физического контакта, и выражается формулой, действующей повсюду во Вселенной, для масс и расстояний, которые варьируются от крошечных до огромных.
Сэр Исаак Ньютон был первым ученым, который точно определил гравитационную силу и показал, что она может объяснить как падающие тела, так и астрономические движения. См. рис. 1. Но Ньютон был не первым, кто заподозрил, что одна и та же сила вызывает и наш вес, и движение планет. Его предшественник Галилео Галилей утверждал, что падающие тела и движение планет имеют одну и ту же причину. Некоторые из современников Ньютона, такие как Роберт Гук, Кристофер Рен и Эдмунд Галлей, также добились определенного прогресса в понимании гравитации. Но Ньютон первым предложил точную математическую форму и с помощью этой формы показал, что движение небесных тел должно представлять собой конические сечения — окружности, эллипсы, параболы и гиперболы. Это теоретическое предсказание было большим триумфом — уже некоторое время было известно, что луны, планеты и кометы следуют по таким путям, но никто не мог предложить механизм, который заставлял бы их следовать именно по этим путям, а не по другим.
См. рис. 1. Но Ньютон был не первым, кто заподозрил, что одна и та же сила вызывает и наш вес, и движение планет. Его предшественник Галилео Галилей утверждал, что падающие тела и движение планет имеют одну и ту же причину. Некоторые из современников Ньютона, такие как Роберт Гук, Кристофер Рен и Эдмунд Галлей, также добились определенного прогресса в понимании гравитации. Но Ньютон первым предложил точную математическую форму и с помощью этой формы показал, что движение небесных тел должно представлять собой конические сечения — окружности, эллипсы, параболы и гиперболы. Это теоретическое предсказание было большим триумфом — уже некоторое время было известно, что луны, планеты и кометы следуют по таким путям, но никто не мог предложить механизм, который заставлял бы их следовать именно по этим путям, а не по другим.
 Вдохновение яблоком Ньютона является частью мирового фольклора и даже может быть основано на фактах. Этому придается большое значение, потому что универсальный закон тяготения Ньютона и его законы движения ответили на очень старые вопросы о природе и оказали огромную поддержку представлению о лежащей в основе простоте и единстве природы. Ученые по-прежнему ожидают, что их непрекращающиеся исследования природы проявят лежащую в их основе простоту.
Вдохновение яблоком Ньютона является частью мирового фольклора и даже может быть основано на фактах. Этому придается большое значение, потому что универсальный закон тяготения Ньютона и его законы движения ответили на очень старые вопросы о природе и оказали огромную поддержку представлению о лежащей в основе простоте и единстве природы. Ученые по-прежнему ожидают, что их непрекращающиеся исследования природы проявят лежащую в их основе простоту.Гравитационная сила относительно проста. Она всегда притягательна и зависит только от вовлеченных масс и расстояния между ними. Говоря современным языком, универсальный закон тяготения Ньютона утверждает, что каждая частица во Вселенной притягивает каждую другую частицу с силой вдоль линии, соединяющей их. Сила прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними.
Рис. 2. Гравитационное притяжение происходит вдоль линии, соединяющей центры масс этих двух тел. Величина силы одинакова на каждом из них, что соответствует третьему закону Ньютона.
Величина силы одинакова на каждом из них, что соответствует третьему закону Ньютона.ПРЕДУПРЕЖДЕНИЕ О НЕПРАВИЛЬНОМ КОНЦЕПЦИИ
Величина силы, действующей на каждый объект (один имеет большую массу, чем другой), одинакова, что соответствует третьему закону Ньютона.
Тела, с которыми мы имеем дело, имеют тенденцию быть большими. Для упрощения ситуации предположим, что тело ведет себя так, как будто вся его масса сосредоточена в одной определенной точке, называемой 92}.[/латекс]
Рис. 3. Расстояние между центрами масс Земли и объектом на ее поверхности почти равно радиусу Земли, потому что Земля намного больше объекта. Это ожидаемое значение и не зависит от массы тела . Закон всемирного тяготения Ньютона продвигает наблюдение Галилея о том, что все массы падают с одинаковым ускорением, на шаг дальше, объясняя наблюдение с точки зрения силы, которая заставляет объекты падать, — фактически с точки зрения универсально существующей силы притяжения между массами.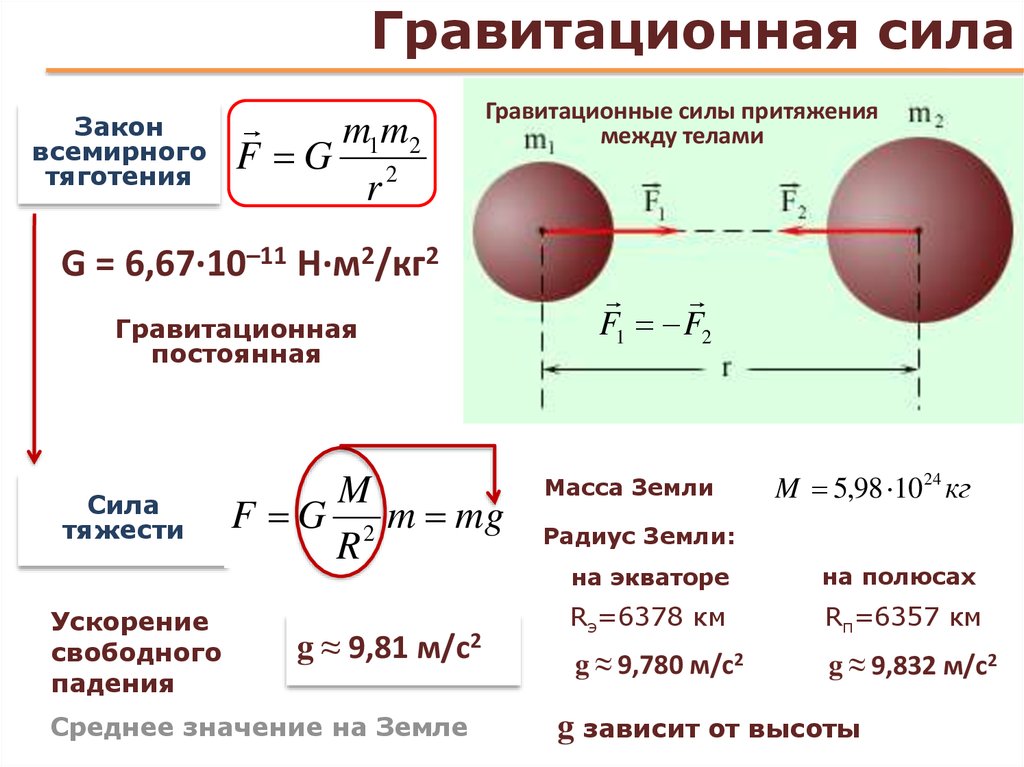
ДОМАШНИЙ ЭКСПЕРИМЕНТ
Возьмите шарик, шарик и ложку и бросьте их с одной высоты. Они падают на пол одновременно? Если вы также уроните лист бумаги, будет ли он вести себя как другие предметы? Объясните свои наблюдения.
УСТАНОВЛЕНИЕ СОЕДИНЕНИЙ
Все еще предпринимаются попытки понять силу гравитации. Как мы увидим в главе 33 «Физика элементарных частиц», современная физика исследует связи гравитации с другими силами, пространством и временем. Общая теория относительности меняет наш взгляд на гравитацию, заставляя нас думать о гравитации как о искривлении пространства и времени.
В следующем примере мы проводим сравнение, подобное тому, которое сделал сам Ньютон. Он отметил, что если сила гравитации заставляет Луну вращаться вокруг Земли, то ускорение свободного падения должно равняться центростремительному ускорению Луны на ее орбите. Ньютон обнаружил, что два ускорения совпадают «почти почти».
Пример 1. Сила тяготения Земли представляет собой центростремительную силу, заставляющую Луну двигаться по криволинейной траектории
(a) Найдите ускорение силы тяжести Земли на расстоянии от Луны. 8\text{м}}.[/латекс] 92},[/latex]
8\text{м}}.[/латекс] 92},[/latex]
, где [latex]{\omega}[/latex] — угловая скорость Луны относительно Земли.
Решение для (b)
Учитывая, что период (время, необходимое для совершения одного полного оборота) орбиты Луны составляет 27,3 дня, (d) и используя
[latex]{1\text{ d }\times24}[/latex] [латекс]{\frac{\text{hr}}{\textbf{d}}}[/latex] [латекс]{\times\:60}[/latex] [латекс] {\ frac {\ text {мин}} {\ text {ч}}} [/ латекс] [латекс] {\ раз \: 60} [/ латекс] [латекс] {\ гидроразрыва {\ текст {s}} { \text{мин}}}[/латекс] [латекс]{=86 400\текст{ с}}[/латекс] 92} \end{array}[/latex]
Ускорение направлено к центру Земли.
Обсуждение
Центростремительное ускорение Луны, найденное в (б), отличается менее чем на 1% от ускорения силы тяжести Земли, найденного в (а). Это согласие является приблизительным, потому что орбита Луны слегка эллиптическая, а Земля не является стационарной (скорее, система Земля-Луна вращается вокруг своего центра масс, который расположен примерно на 1700 км ниже поверхности Земли). Явный вывод состоит в том, что гравитационная сила Земли заставляет Луну вращаться вокруг Земли.
Явный вывод состоит в том, что гравитационная сила Земли заставляет Луну вращаться вокруг Земли.
Почему Земля не остается неподвижной, когда Луна вращается вокруг нее? Это связано с тем, что, как и ожидалось из третьего закона Ньютона, если Земля воздействует на Луну, то Луна должна оказывать на Землю равную и противоположную силу (см. рис. 4). Мы не ощущаем влияние Луны на движение Земли, потому что гравитация Луны перемещает наши тела вместе с Землей, но на Земле есть и другие признаки, которые ясно показывают влияние гравитационной силы Луны, как обсуждалось в главе 6.6 Спутники и законы Кеплера. Аргумент в пользу простоты.
Рис. 4. (а) Земля и Луна вращаются примерно раз в месяц вокруг своего общего центра масс. (b) Их центр масс вращается вокруг Солнца по эллиптической орбите, но путь Земли вокруг Солнца имеет «изгибы». Подобные колебания на траекториях звезд наблюдались и считаются прямым свидетельством того, что планеты вращаются вокруг этих звезд. Это важно, потому что отраженный свет планет часто слишком тусклый, чтобы его можно было наблюдать.
Это важно, потому что отраженный свет планет часто слишком тусклый, чтобы его можно было наблюдать. Океанские приливы — один из хорошо наблюдаемых результатов гравитации Луны, действующей на Землю. Рисунок 5 представляет собой упрощенный рисунок положения Луны относительно приливов. Поскольку вода легко течет по поверхности Земли, прилив создается на стороне Земли, ближайшей к Луне, где гравитационное притяжение Луны сильнее всего. Почему на противоположной стороне Земли также бывает прилив? Ответ заключается в том, что Земля притягивается к Луне больше, чем вода на дальней стороне, потому что Земля ближе к Луне. Таким образом, вода на стороне Земли, ближайшей к Луне, отрывается от Земли, а Земля отрывается от воды на дальней стороне. Когда Земля вращается, приливная выпуклость (воздействие приливных сил между вращающимся вокруг естественным спутником и основной планетой, вокруг которой он вращается) сохраняет свою ориентацию относительно Луны. Таким образом, в день бывает два прилива (фактический период прилива составляет около 12 часов 25,2 минуты, потому что Луна также движется по своей орбите каждый день).
Солнце также влияет на приливы, хотя его влияние примерно вдвое меньше, чем у Луны. Однако самые большие приливы, называемые весенними приливами, происходят, когда Земля, Луна и Солнце выстраиваются на одной линии. Наименьшие приливы, называемые приливами, происходят, когда Солнце находится в [латексном]{9{\circ}}[/latex] угол выравнивания Земля-Луна.
Рис. 6. (a, b) Весенние приливы: самые высокие приливы возникают, когда Земля, Луна и Солнце выстраиваются на одной линии. (c) Квадрийский прилив: самые низкие приливы возникают, когда Солнце находится в точке 90 0 по отношению к выравниванию Земля-Луна. Обратите внимание, что этот рисунок выполнен не в масштабе.
Обратите внимание, что этот рисунок выполнен не в масштабе.
Приливы и отливы характерны не только для Земли, но и для многих астрономических систем. Самые экстремальные приливы возникают там, где гравитационная сила наиболее сильна и изменяется наиболее быстро, например вблизи черных дыр (см. рис. 7). В нашей галактике наблюдалось несколько вероятных кандидатов в черные дыры. Они имеют массу больше, чем у Солнца, но имеют диаметр всего несколько километров в поперечнике. Приливные силы вблизи них настолько велики, что могут фактически оторвать материю от звезды-компаньона.
Рис. 7. Черная дыра — это объект с такой сильной гравитацией, что даже свет не может покинуть его. Эта черная дыра была создана сверхновой одной звезды в двухзвездной системе. Приливные силы, создаваемые черной дырой, настолько велики, что отрывают материю от звезды-компаньона. Это вещество сжимается и нагревается по мере того, как оно всасывается в черную дыру, создавая свет и рентгеновские лучи, наблюдаемые с Земли.
В отличие от огромной гравитационной силы вблизи черных дыр существует видимое гравитационное поле, с которым сталкиваются астронавты на орбите Земли. Как действует «невесомость» на космонавта, который месяцами находится на орбите? Или как насчет влияния невесомости на рост растений? Невесомость не означает, что на космонавта не действует гравитационная сила. На орбите космонавта нет «невесомости». Этот термин просто означает, что космонавт находится в свободном падении, ускоряясь с ускорением за счет силы тяжести. Если трос лифта порвется, пассажиры внутри окажутся в свободном падении и ощутят невесомость. Вы можете испытывать короткие периоды невесомости на некоторых аттракционах в парках развлечений.
Рис. 8. Астронавты испытывают невесомость на борту Международной космической станции. (кредит: НАСА) Микрогравитация относится к среде, в которой кажущееся чистое ускорение тела мало по сравнению с ускорением, создаваемым Землей на ее поверхности. Многие интересные темы биологии и физики были изучены за последние три десятилетия в условиях микрогравитации. Непосредственное беспокойство вызывает влияние на астронавтов длительного пребывания в открытом космосе, например, на Международной космической станции. Исследователи заметили, что в такой среде мышцы атрофируются (истощаются). Существует также соответствующая потеря костной массы. Продолжаются исследования адаптации сердечно-сосудистой системы к космическому полету. На Земле кровяное давление обычно выше в ногах, чем в голове, потому что более высокий столб крови оказывает на него нисходящую силу из-за гравитации. Когда вы стоите, 70% вашей крови находится ниже уровня сердца, а в горизонтальном положении происходит прямо противоположное. Какое значение имеет отсутствие этого перепада давления для сердца?
Многие интересные темы биологии и физики были изучены за последние три десятилетия в условиях микрогравитации. Непосредственное беспокойство вызывает влияние на астронавтов длительного пребывания в открытом космосе, например, на Международной космической станции. Исследователи заметили, что в такой среде мышцы атрофируются (истощаются). Существует также соответствующая потеря костной массы. Продолжаются исследования адаптации сердечно-сосудистой системы к космическому полету. На Земле кровяное давление обычно выше в ногах, чем в голове, потому что более высокий столб крови оказывает на него нисходящую силу из-за гравитации. Когда вы стоите, 70% вашей крови находится ниже уровня сердца, а в горизонтальном положении происходит прямо противоположное. Какое значение имеет отсутствие этого перепада давления для сердца?
Некоторые открытия в области физиологии человека в космосе могут иметь клиническое значение для лечения заболеваний на Земле. С другой стороны, известно, что космический полет влияет на иммунную систему человека, что, возможно, делает членов экипажа более уязвимыми к инфекционным заболеваниям. Эксперименты в космосе также показали, что некоторые бактерии растут быстрее в условиях микрогравитации, чем на Земле. Тем не менее, исследования показывают, что производство микробных антибиотиков может увеличиться в два раза в культурах, выращенных в космосе. Можно надеяться, что удастся понять эти механизмы, чтобы можно было добиться аналогичных успехов на местах. В другой области физических космических исследований в космическом пространстве были выращены неорганические кристаллы и кристаллы белков, которые имеют гораздо более высокое качество, чем любые, выращенные на Земле, поэтому кристаллографические исследования их структуры могут дать гораздо лучшие результаты.
Эксперименты в космосе также показали, что некоторые бактерии растут быстрее в условиях микрогравитации, чем на Земле. Тем не менее, исследования показывают, что производство микробных антибиотиков может увеличиться в два раза в культурах, выращенных в космосе. Можно надеяться, что удастся понять эти механизмы, чтобы можно было добиться аналогичных успехов на местах. В другой области физических космических исследований в космическом пространстве были выращены неорганические кристаллы и кристаллы белков, которые имеют гораздо более высокое качество, чем любые, выращенные на Земле, поэтому кристаллографические исследования их структуры могут дать гораздо лучшие результаты.
Растения эволюционировали под воздействием силы тяжести и с помощью датчиков силы тяжести. Корни растут вниз, а побеги растут вверх. Растения могли бы обеспечить систему жизнеобеспечения для длительных космических миссий, восстанавливая атмосферу, очищая воду и производя пищу. Некоторые исследования показали, что гравитация не влияет на рост и развитие растений, но все еще существует неопределенность в отношении структурных изменений растений, выращенных в условиях микрогравитации.
Как отмечалось ранее, универсальная гравитационная постоянная [латекс]{G}[/латекс] определяется экспериментально. Это определение впервые дал Генри Кавендиш (1731–1810), английский ученый, в 179 г.8, более чем через 100 лет после того, как Ньютон опубликовал свой универсальный закон всемирного тяготения. Измерение [латекса]{G}[/латекса] очень простое и важное, поскольку оно определяет силу одной из четырех сил в природе. Эксперимент Кавендиша был очень сложным, потому что он измерил крошечное гравитационное притяжение между двумя массами обычного размера (не более десятков килограммов), используя прибор, подобный показанному на рис. 9. Примечательно, что его значение для [латекс]{G}[/латекс] отличается менее чем на 1% от лучшего современного значения. 92}{G}}.[/латекс]
Таким образом, [латекс]{M}[/латекс] можно рассчитать, поскольку все величины справа, включая радиус Земли [латекс]{r},[/латекс], известны из прямых измерений. В главе 6.6 «Спутники и законы Кеплера: аргумент в пользу простоты» мы увидим, что знание [латекс]{G}[/латекс] также позволяет определять астрономические массы. Интересно, что из всех фундаментальных констант в физике [латекс]{G}[/латекс] определен наименее точно.
Интересно, что из всех фундаментальных констант в физике [латекс]{G}[/латекс] определен наименее точно.
Эксперимент Кавендиша также используется для изучения других аспектов гравитации. Один из самых интересных вопросов заключается в том, зависит ли сила гравитации от вещества, а также от массы — например, оказывает ли один килограмм свинца такое же гравитационное притяжение, как один килограмм воды. Венгерский ученый по имени Роланд фон Этвёш начал это исследование в начале 20-го века. Он обнаружил с точностью до пяти частей на миллиард, что гравитационная сила не зависит от вещества. Такие эксперименты продолжаются и сегодня, и они улучшили измерения Этвеша. Эксперименты типа Кавендиша, такие как эксперименты Эрика Адельбергера и других в Вашингтонском университете, также наложили серьезные ограничения на возможность существования пятого взаимодействия и подтвердили главное предсказание общей теории относительности — гравитационная энергия вносит свой вклад в массу покоя. В текущих измерениях используются крутильные весы и параллельная пластина (а не сферы, как использовал Кавендиш), чтобы изучить, как закон тяготения Ньютона работает на субмиллиметровых расстояниях.



 Nmkg𝐺 известна как универсальная гравитационная постоянная.
Nmkg𝐺 известна как универсальная гравитационная постоянная.