Презентация к уроку Закон всемирного тяготения доклад, проект
Какие явления вы наблюдали? Что общего между этими явлениями?
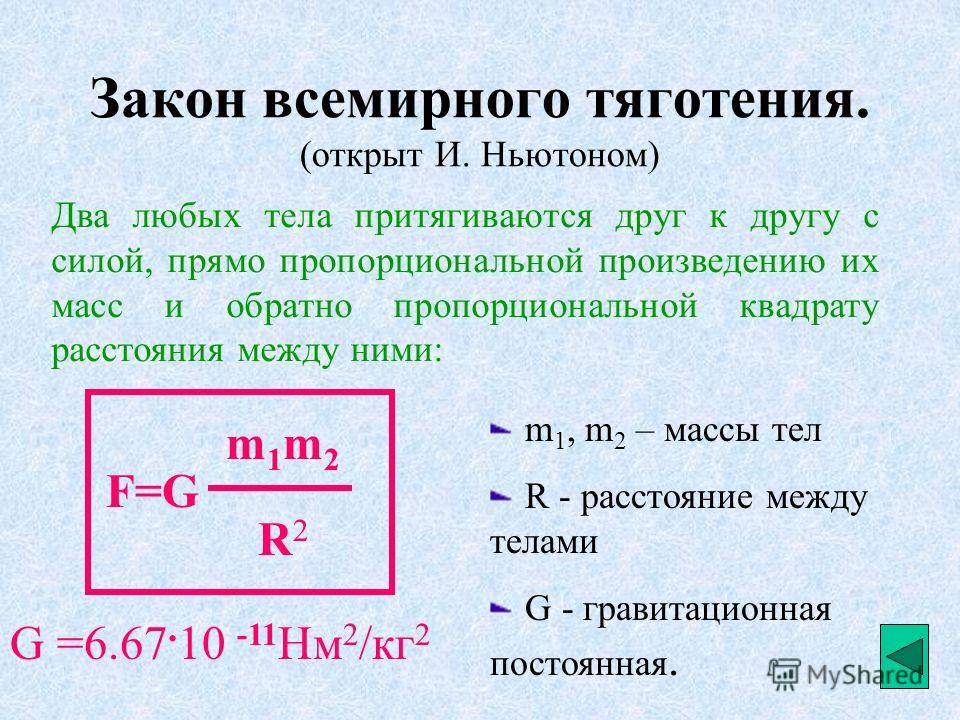
Закон всемирного тяготения
Сформулировать закон всемирного тяготения.
У знать историю открытия закона.
Найти примеры проявления сил тяготения.
Установить границы его применения.
Законы Ньютона
МОДЕЛИ ВСЕЛЕННОЙ
1 вариант
Геоцентрическая система мира
Клавдий Птолемей, II век
Неподвижная Земля – центр мироздания, вокруг нее вращаются все небесные тела
1 вариант
Гелиоцентрическая система мира
Николай Коперник, XVI век
Солнце является центральным небесным телом, вокруг которого обращается Земля и другие планеты
2 вариант
Джордано Бруно
(1548-1600)
Вселенная бесконечна
звезды – это далекие Солнца
на других планетах может существовать жизнь
Тихон Браге (1546 — 1601) Датский астроном многие годы наблюдал за движением планет, накопил многочисленные данные, но не сумел их объяснить.
Галилео Галилей
Законы Кеплера
Сформулировал законы движения планет
1-ый Закон
2-ой Закон
3-ий Закон
Кеплер подошел к формулировке закона
тяготения, но не описал его математически
Окинув единым мысленным взором «земное» и «небесное», Ньютон предположил, что существует единый закон всемирного тяготения, которому подвластны все тела во Вселенной — от яблок до планет!
Вывод закона всемирного тяготения 1. Зависимость силы тяготения от массы
Зависимость силы тяготения от массы
g = F ∕ m
g — const
F~ m F~ m1 m2
F1= F2
Третий закон Ньютона
Центростремительное ускорение Луны равно:
R = 60 Rз
2. Зависимость силы тяготения от расстояния
Вывод закона всемирного тяготения
F~m1 ∙ m2
F~ 1/R²
Закон всемирного тяготения
m1 , m2 — массы взаимодействующих тел,
R – расстояние между ними,
G – гравитационная постоянная
Сила взаимного притяжения двух тел прямо пропорциональна произведению масс этих тел и обратно пропорциональна квадрату расстояния между ними
1798 г.
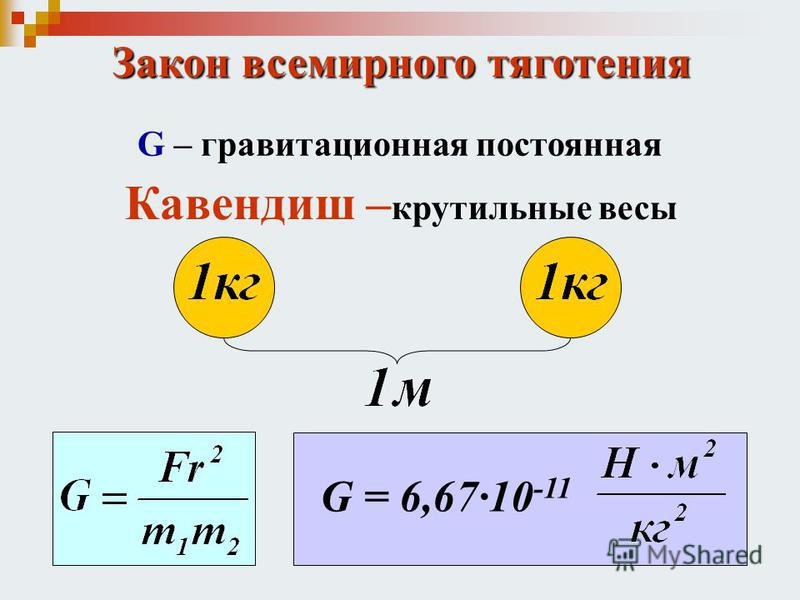
Генри Кавендиш
Опыт Кавендиша
Гравитационная постоянная
Физический смысл гравитационной постоянной.
Гравитационная постоянная численно равна
силе гравитационного притяжения двух тел, массой по 1 кг каждое, находящихся на расстоянии 1 м одного от другого.
Запомни, что . . .Н
Гравитационное взаимодействие –это взаимодействие ,свойственное всем телам Вселенной и проявляющееся в их взаимном притяжении друг к другу.
Гравитационное поле – особый вид материи, осуществляющее гравитационное взаимодействие.
1 вариант
1. Закон всемирного тяготения открыл:
Закон всемирного тяготения открыл:
А.И.Ньютон Б. Г.Галилей
2.Значение гравитационной постоянной:
А. G=1,67*10-11 Н*м2/кг2
Б.G= 6,67*10-11 Н*м2/кг2
3.С увеличением расстояния между телами, сила притяжения….
А.увеличивается
4.Как изменится сила всемирного тяготения при увеличении расстояния между телами в 2 раза?
А.увеличится в 2 раза
Б.уменьшится в 4 раза
5.Явление всемирного тяготения заключается в том, что
А.все тела во Вселенной имеют вес
Б.между всеми телами во Вселенной действуют силы притяжения
Взаимопроверка
Критерии оценок : Нет ошибок – 1 балл 1 ошибка – 0,5 балла 2 ошибки – 0,25 балла 3 ошибки – 0 баллов
Открытие Ньютоном закона всемирного тяготения явилось важнейшим событием в истории физики.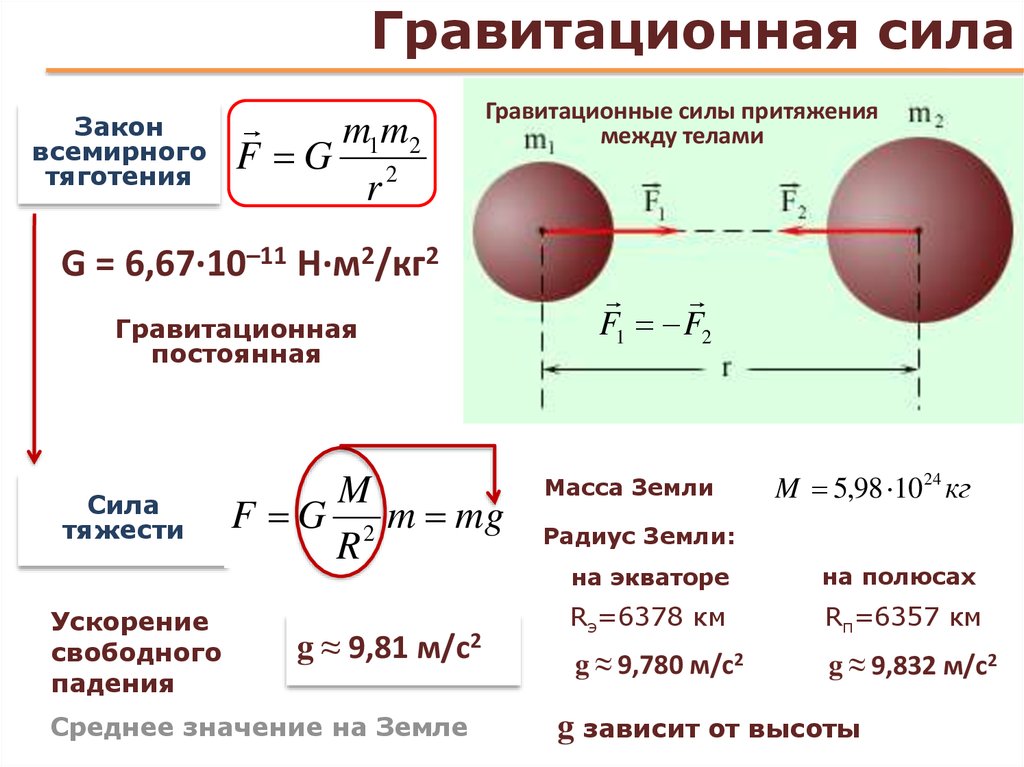
На основе закона всемирного тяготения:
открыты планеты Нептун и Плутон
На основе закона всемирного тяготения:
определены массы Солнца, планет и других небесных тел
На основе закона всемирного тяготения:
раскрыты загадки движения комет, тайны приливов
На основе закона всемирного тяготения:
вычисляются параметры движения космических аппаратов, искусственных спутников Земли
ЛОГИКА НАУЧНОГО ПОЗНАНИЯ
Явления взаимного притяжения любых тел на
расстоянии: Луны и Земли, яблока и Земли и др.
ФАКТЫ
Действие земли на тела; сила тяжести FT =mg
как характеристика этого действия.
Объяснение природы движения планет.
Выяснение причины приливов на Земле
Понимание «незаметности» силы всемирного
тяготения для обычных тел.
СЛЕДСТВИЯ
Границы применимости
закона всемирного тяготения?
Какими были задачи нашего урока?
Сформулировать закон всемирного тяготения.
У знать историю открытия закона.
Найти примеры проявления сил тяготения.
Установить границы его применения.
Домашнее задание
1. Учить опорный конспект.
2.Решить 2 задачи
Задача 1
А на море корабли
В дрейф давно уже легли.
Коль закон ты не забыл,
Силу ты сумей найти,
Что сближает корабли.
Знай, что эти корабли-
Каждый массой тонн пяти.
1морская миля= 1,852км
20 миль=37 км
той. Массы учеников 50 кг
Задача 2
Рассчитайте силу всемирного тяготения между двумя учениками, сидящими за одной партой. Массы учеников 50 кг, расстояние 1 м?
Массы учеников 50 кг, расстояние 1 м?
Продолжи предложение:
Что заинтересовало вас сегодня на уроке?
Сегодня на уроке я научился…
На уроке я закрепил… …
Теперь я могу …
Моя группа работала …
РЕФЛЕКСИЯ
§ 10. Примеры решения задач «Закон всемирного тяготения»
Задача 1. Средняя плотность Венеры , радиус планеты. Найдите ускорение свободного падения на поверхности Венеры.
Краткая запись условия задачи: ,.
Найти:
Решение. При рассмотрении закона всемирного тяготении был получен следующий результат:
=
Очевидно, что это выражение справедливо для любой другой планета, например, для Венеры, т.е.
=
Учитывая, что и, получим:
Следовательно,
=
или
=
Задача 2. Каков период
обращения искусственного спутника на
высоте
от поверхности? Массу и радиус Земли
считать известными.
Каков период
обращения искусственного спутника на
высоте
от поверхности? Массу и радиус Земли
считать известными.
Краткая запись условия задачи:, , .
Найти:
Решение. При рассмотрении первой космической скорости был получен следующий результат:
С другой стороны, из кинематики вращательного движения
но
Тогда
Приравнивая полученное равенство и выражение для первой космической скорости, получим:
Следовательно,
Одной
из сил, действующих на тело только вблизи
Земли, всегда является сила тяжести.
Поэтому при рассмотрении вопросов,
связанных с равновесием (и не только
с равновесием) абсолютно твердого тела,
важно знать точку приложения этой силы.
До сих пор, говоря о силе тяжести, мы
прикладывали ее к точке, которая казалась
нам наиболее подходящей для этого. Так,
рассматривая равновесие балки, мы
приложили силу тяжести к ее середине. Оказывается,
в этом случае (полагая, что балка
однородная) сила тяжести действительно
приложена к этой точке: если, разбив
балку на одинаковые частицы, сложить
действующие на них элементарные силы
тяжести, то равнодействующая этих
сил — сила тяжести балки
— будет приложена в точкеC (рис.
20а).
Но далеко не всегда мы можем «угадать»
положение точки приложения силы тяжести.
Как быть, скажем, в тех случаях, когда
тело неоднородное или имеет неправильную
форму?
Так,
рассматривая равновесие балки, мы
приложили силу тяжести к ее середине. Оказывается,
в этом случае (полагая, что балка
однородная) сила тяжести действительно
приложена к этой точке: если, разбив
балку на одинаковые частицы, сложить
действующие на них элементарные силы
тяжести, то равнодействующая этих
сил — сила тяжести балки
— будет приложена в точкеC (рис.
20а).
Но далеко не всегда мы можем «угадать»
положение точки приложения силы тяжести.
Как быть, скажем, в тех случаях, когда
тело неоднородное или имеет неправильную
форму?
Обратимся
к хорошо известному нам случаю равновесия
тела, подвешенного на нити (рис.20б). Действующие
на него силы тяжести
и
натяжения нити
равны по модулю
и лежат на одной прямой, иначе
бы тело не находилось в равновесии.
Поэтому линия действия
силы тяжести совпадает с нитью. Этим
обстоятельством мы и воспользуемся
для определения положения
точки приложения силы тяжести
опытным путем.
Вырежем из картона фигуру произвольной формы и подвесим ее к нити (рис. 21а). Проведем карандашом на ней прямую, совпадающую с вертикалью, вдоль которой расположена нить. Тем самым мы найдем линию действия силы тяжести. Подвесим тело за какие-нибудь другие точки (рис. 21, б и в) и точно также определим линии действия силы тяжести. Мы увидим, что все три линии пересекутся в одной и той же точке С.
З
рис.21
начит, как бы мы ни поворачивали тело, линия действия силы тяжести всегда будет проходить через точку С. Естественно поэтому и считать ее точкой приложения силы тяжести. Эта точка называется центром тяжести.
Итак, центром тяжести тела называется точка, через которую проходит линия действия силы тяжести при любом положении тела.
Если
бы мы проделали такие же опыты с телами
правильной геометрической формы, то
обнаружили бы, что у треугольника центр
тяжести совпадает с точкой пересечения
его медиан, у круга — с его центром, у
параллелограмма — с точкой пересечения
его диагоналей. Центр тяжести симметричных
тел всегда находится в центре
симметрии (если, конечно, эти тела
однородные). У таких объемных тел, как
шар
или куб, центр тяжести совпадает с их
центром. Но центр тяжести может находиться
и вне тел, — например, у кольца, у пустой
банки, у циркуля, ножки которого
раздвинуты, и т.д.
Центр тяжести симметричных
тел всегда находится в центре
симметрии (если, конечно, эти тела
однородные). У таких объемных тел, как
шар
или куб, центр тяжести совпадает с их
центром. Но центр тяжести может находиться
и вне тел, — например, у кольца, у пустой
банки, у циркуля, ножки которого
раздвинуты, и т.д.
В случае, когда размеры тела малы по сравнению с расстоянием до центра Земного шара, центр тяжести совпадает с центром масс тела.
А как же найти центр масс неоднородного тела? Ответим на этот вопрос, решив следующую задачу.
Задача. Одна часть цилиндрического стержня длиной 5 см и массой 3 кг состоит из алюминия, другая часть – из стали длиной 2 см и массой 4 кг. Определите положение центра масс стержня.
Краткая запись условия задачи: кг,м,кг,м.
Найти:Решение: Выберем систему отсчёту так, как показано
на рисунке
22.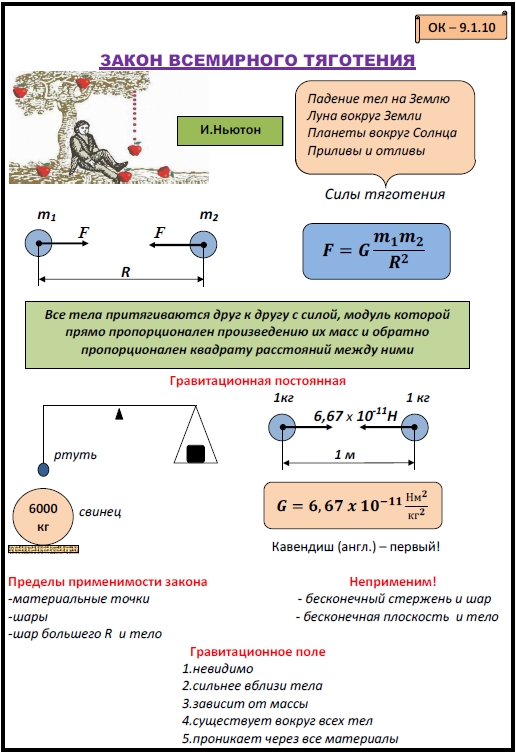 Обозначим
за
расстояние от начала системы координат
до центра масс тела. За ось вращения
примем прямую, проходящую через точкуC.
Выразим моменты каждой силы.
Обозначим
за
расстояние от начала системы координат
до центра масс тела. За ось вращения
примем прямую, проходящую через точкуC.
Выразим моменты каждой силы.
;
Так цилиндрический стержень находится в равновесии, то
Тогда
Причем,
;
Следовательно,
(м)
Таким образом, в случае разнородных тел центр масс системы находится по формуле:
=,
где xi,mi– координаты, массы элементов тел.
Раздел динамики. Три закона Ньютона. Закон всемирного тяготения – StudyWay
В настоящее время ЕГЭ по физике проходит в виде решения задач. Задание, содержащиеся в КИМах определяются согласно кодификатору элементов содержания и требований к подготовке выпускников к проведению ЕГЭ.
Для успешной подготовки к ЕГЭ, в этой статье рассмотрена физика, а именно раздел динамики, включая формулы для подготовки к ЕГЭ, статья охватывает следующие темы:
– Первый закон И. Ньютона;
Ньютона;
– Второй закон И. Ньютона;
– Третий закон И. Ньютона;
– Закон всемирного тяготения;
– Сила упругости. Закон Гука.
Приступим к изучению тем и примеров решения задач.
В динамике выделяют три закона открытых И. Ньютоном, они позволяют определить движение для любой системы.
Первый закон Ньютона
Первый закон открыт в конце 17 века. Закон звучит следующим образом: существуют инерциальные системы отсчёта, в которых тела движутся равномерно и прямо по линии, если на них не оказывают влияние другие силы.
Закон инерции: в случае, когда на тело не оказывают влияния внешние воздействий, то у данного тела сохраняется состояние покоя. Это значит, что все тела могут оставаться в первоначальном состоянии, то есть если тело находится в движении, то оно будет в таком же состоянии. Если оно неподвижно, то продолжает стоять без изменений, пока не появится сила, заставляющая его двигаться.
Инерциальной системой отсчёта называют систему, находящуюся в состоянии движении или покое.
Неинерциальной системой называют движущуюся с ускорением систему.
Инерциальными считаются системы, находящиеся в состоянии покоя или движения, при этом, движение должно быть равномерным и прямолинейным.
Неинерциальными считаются системы, имеющие ускорение.
Существует также гелиоцентрическая модель отсчёта, в ней начало координат совмещено с солнцем.
Первый закон Ньютона не содержит формул, поэтому рассмотрим примеры:
– Наиболее популярным объяснением является резкое торможение. Тело движется в направлении автомобиля, поэтому при резком торможении автомобиль сильно дёргается. Если же автомобиль плавно затормозит, соответственно, его движение будет нерезким;
– Движение наверх и вниз. Американские горки поднимаются наверх за счёт накопленной потенциальной энергии при крутом спуске.
Второй закон Ньютона
Второй закон открыт около 1666 года, он гласит: В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, является пропорциональным вызывающим его силам. 2
2
m = 50 кг.
Помним формулу второго закона: F = mа. Далее подставляет известные значения.
F = 50 кг * 0,6 = 30 H.
Ответ: F = 30 H.
Третий закон Ньютона
Третий закон открыли в 1725 году: действию F всегда есть противодействие, то есть взаимодействия двух дел равны и направлены по прямой в противоположные стороны. Формула: F12 = -F21.
Пример. Для строительства моста нужно высчитать нагрузку. Данную нагрузку можно узнать с помощью третьего закона. При этом, на мост давят держащие опоры, поэтому строительство ведётся по определённой схеме, которая рассчитывает большую выносливость.
Рассмотрим пример решения задачи: на стуле стоит портфель. На него действуют силы равные 500 H. Согласно третьему закону сверху на него действует та же сила, равная 500 H.
Следует, что F1 = F2. То есть, чем больше масса тела, тем меньше его ускорение.
Следует помнить о том, что третий закон применяется исключительно в инерциальных системах отсчёта.
Закон всемирного тяготения
В школьной программе изучение закона всемирного тяготения при подготовке к ЕГЭ является важной темой. Издавна люди смотрели на звёзды и понимали, что ими что-то движет. Но люди не догадывались, что притяжением управляет один закон. В 1687 году И. Ньютон открыл закон всемирного тяготения.
Издавна люди смотрели на звёзды и понимали, что ими что-то движет. Но люди не догадывались, что притяжением управляет один закон. В 1687 году И. Ньютон открыл закон всемирного тяготения.
Согласно известной всем версии, Ньютон увидел падающее с дерева яблоко. Он стал размышлять о том, что на все тела действует некая определённая сила, которая позволяет им притягиваться к Земле.
Формула данного закона выглядит таким образом: F=G*(m1*m2)/r2. При этом, G – постоянная гравитации, равная 6,67408(31)•10−11. Это величина, которая воздействует на любой объект нашей планеты.
Позднее закон всемирного тяготения стали применять в астрономии и механике, так как с его помощью объясняется процесс движения различных тел. Любой объект будет находиться в невесомости, объясняется это тем, что объект находится в космосе и сила притяжения на него не действует.
Примером закона всемирного тяготения является запуск в космос спутника (это произошло в 1957 году). При этом, спутник постоянно находился в равном расстоянии над Землёй, это обусловлено тем, что наша планета притягивает одинаково в различных направлениях. 2 = 2,4 H
2 = 2,4 H
Ответ: 2,4 H.
Сила упругости. Закон Гука
Закон Гука является основным в теории упругости. Немаловажное значение в процессе подготовки к сдаче ЕГЭ по физике имеет тема о силе упругости, открытая Робертом Гуком – английский учёный, данный закон открыл в 1660 году в возрасте двадцати пяти лет.
Закон гласит: сила упругости, которая возникает при растяжении или сжатии тела является пропорциональной значению по изменению длины тела.
Сила упругости – это сила, которая возникает при деформации тела, данная сила возвращает тело в его первоначальное состояние.
При деформации тело пытается вернуться в первоначальное состояние, это объясняется электромагнитным воздействием на молекулярном уровне.
Формула закона: пусть х – упругость тела, тогда Fx = -kx, k – жёсткость тела.
Жёсткость зависит от материала и размера тела, она составляет ньютон на метр (1Н / м). Чем больше жёсткость, тем меньше оно подвержено деформации под воздействием сил. Стоит помнить о том, что закон Гука достоверно применяют при упругой деформации, т. е. деформация должна быть малой. При большой деформации тела длина перестаёт быть прямо пропорциональной силе, а при сильной деформации тело разрушается.
е. деформация должна быть малой. При большой деформации тела длина перестаёт быть прямо пропорциональной силе, а при сильной деформации тело разрушается.
Рассмотрим пример задачи: проволоку разрезали ровно пополам, её жёсткость составляет 90 H/m. Нужно найти жёсткость обеих проволок.
Решение: k = F/x.
Согласно условию задачи, жёсткость пропорциональна длине проволоки.
k1 = 2k = 180 H/m.
Ответ: 180 H/m.
Таким образом, мы рассмотрели одни из важных тем раздела динамики: три закона Исаака Ньютона, закон всемирного тяготения и силу упругости, закон Роберта Гука. Изучив данные материалы по теме и просмотрев примеры решения задач, вы сможете решить схожие задание на ЕГЭ по физике.
Закон всемирного тяготения Ньютона — определение, характеристики, примеры и ответы на часто задаваемые вопросы Вдохновением сэра Исаака Ньютона для вывода революционного закона всемирного тяготения было яблоко, упавшее с дерева. Мы все хорошо знакомы с историей Ньютона и тем, как он открыл гравитацию.
 Падение яблока заставило его открыть гравитацию Ньютона и закон всемирного тяготения. Закон всемирного тяготения Ньютона играет важную роль в механике.
Падение яблока заставило его открыть гравитацию Ньютона и закон всемирного тяготения. Закон всемирного тяготения Ньютона играет важную роль в механике.Ньютон из любопытства задал простой вопрос: почему яблоко падает, а не вбок или вверх!!! Позже Ньютон понял, что земля должна быть ответственна за падение яблока вниз перпендикулярно земле. Это был главный поворотный момент, и тогда он разработал закон всемирного тяготения.
Сила притяжения между любыми двумя телами. По сути, все объекты во Вселенной притягиваются друг к другу с определенной силой, но в большинстве случаев сила либо слишком слаба, либо слишком мала, чтобы ее можно было наблюдать из-за очень большого расстояния между ними. 9{2}}\].
(Изображение скоро будет загружено)
Что такое закон всемирного тяготения Ньютона?
Закон всемирного тяготения является важным открытием в области физики. Это дает представление о взаимосвязи между массой и силой. Закон тяготения гласит, что каждый объект во Вселенной притягивает любой другой объект так, что прилагаемая сила будет пропорциональна произведению масс и обратно пропорциональна квадрату расстояния между ними.
Закон тяготения гласит, что каждый объект во Вселенной притягивает любой другой объект так, что прилагаемая сила будет пропорциональна произведению масс и обратно пропорциональна квадрату расстояния между ними.
(\[m_{1}~и~m_{2}\]) — это массы двух частиц, которые обычно измеряются в килограммах.
r — расстояние по прямой между двумя частицами, которое обычно измеряется в метрах.
В соответствии с законом всемирного тяготения Ньютона
Математически запишем:
Рассмотрим два объекта с массами \[m_{1}~и~m_{2}\], разделенные расстоянием r, как показано на рисунке.
(Изображение скоро будет загружено) 9{2}\]
Уравнение (4) известно как математическая форма закона тяготения Ньютона или закона гравитационной силы. Из уравнения (4) находим, что силы, действующие друг на друга, будут прямо пропорциональны произведению масс точек и обратно пропорциональны квадрату расстояния между ними. Он также известен как закон обратных квадратов. В некоторых статьях его также называют первым законом всемирного тяготения.
Он также известен как закон обратных квадратов. В некоторых статьях его также называют первым законом всемирного тяготения.
Гравитационная сила, действующая между двумя объектами, обусловлена только их массой. Гравитационная сила является одной из четырех основных сил физики. Иногда ее также называют гравитацией Ньютона или гравитацией Ньютона. Сила гравитации действует во всей Вселенной. Для значительной гравитационной силы один из двух объектов должен быть больше другого.
Характеристики Силы Гравитации
Ниже приведены характеристики Силы Гравитации:
Сила Гравитации является центральной силой.
Гравитационная сила – это взаимная сила.
Гравитационная сила зависит от массы.
Гравитационная сила является силой притяжения.

Гравитационная сила не зависит от присутствия других массовых тел.
Сила гравитации действует на большие расстояния.
Гравитационная сила является универсальной силой.
Гравитационная сила является самой слабой среди основных сил природы.
Сила гравитации всегда притягивает и направлена вдоль линии соединения двух взаимодействующих тел.
Гравитационная сила не зависит от среды и окружающей среды.
Сила гравитации действительна для больших расстояний, таких как расстояние между двумя планетами, и для коротких расстояний, таких как межатомные расстояния.
 {th}\].
{th}\].
Вес
Из закона всемирного тяготения или закона тяготения Ньютона мы поняли, что масса является важнейшей сущностью. Между массой и весом всегда происходит путаница, мы считаем массу и вес одним и тем же, но на самом деле они взаимосвязаны, но отличны друг от друга.
Вес — это гравитационная сила, действующая на любой объект определенной массы. Вес объекта можно оценить, умножив массу m объекта на ускорение силы тяжести g на поверхности Земли. Измеренное ускорение силы тяжести у поверхности Земли составляет около \[9{2}\].
Мера того, сколько материи содержится в объекте, называется массой, а вес является мерой гравитационной силы, действующей на материал в данном гравитационном поле; таким образом, масса и вес пропорциональны друг другу.

W ∝ M
, где,
M — масса объекта
W = MG
, где,
. 9{4}\]
F = 19,59 Н
Следовательно, сила притяжения между Землей и человеком равна 882,3 Н.
2. Почему Луна не врезается в Землю? Какова величина гравитации на Луне в ньютонах?
Ответ: Луна — естественный спутник Земли. Силы скорости и гравитации удерживают Луну на постоянной орбите вокруг Земли. Кажется, что Луна вращается вокруг Земли, не подвергаясь влиянию гравитации. Однако причина, по которой Луна остается на орбите, точна из-за гравитации.
 Теперь значение гравитации на Луне можно рассчитать, используя закон всемирного тяготения Ньютона.
Теперь значение гравитации на Луне можно рассчитать, используя закон всемирного тяготения Ньютона.Это все о законах гравитационных сил Ньютона, объясненных на решенных примерах. Сосредоточьтесь на том, как термины используются для определения формулы и значения гравитационной постоянной.
Гравитация
Гравитация Ньютон :Ньютон расширил работу Галилея, чтобы лучше определить взаимосвязь между энергией и движение. В частности, он разработал следующие понятия:
- изменение скорости = ускорение -> вызванное силой
- инерция = сопротивление
к изменению скорости и пропорциональна массе
объект
- импульс = количество энергии движения и равен массе, умноженной на скорость
- закон сохранения импульса = полный импульс (масса x скорость) взаимодействия сохраняется -> то же самое до и после
Следствием идей Ньютона была так называемая Заводная Вселенная.  модель. Концепция, утверждающая, что полный импульс Вселенной
сохраняется, взаимодействия перераспределяют импульс, но сумма никогда
изменения. В этой модели Бог только запускает часы (первопричина),
затем он работает сам по себе в остальное время.
модель. Концепция, утверждающая, что полный импульс Вселенной
сохраняется, взаимодействия перераспределяют импульс, но сумма никогда
изменения. В этой модели Бог только запускает часы (первопричина),
затем он работает сам по себе в остальное время.Законы движения Ньютона:
- 1-й закон: тело остается в покое или движется прямолинейно постоянная скорость, пока на него не действуют внешние силы
- 2-й закон: тело, на которое действует сила, будет ускоряться так, что сила
равно массе, умноженной на ускорение (F=ma)
- 3-й закон: для каждого действия существует равное и противоположное реакция
 Именно эта «дельта-ви» производит
эллиптическая кривизна, то есть орбита.
Именно эта «дельта-ви» производит
эллиптическая кривизна, то есть орбита.Кроме того, согласно второму закону Ньютона, когда бейсболист ударяет по мячу, он прикладывает силу F к мячу массой m. Скажем, он бьет в теннис шар массой одной десятой массы обычного бейсбольного мяча (1/10 м). какая результирующее ускорение? В десять раз быстрее обычного бейсбольный мяч и, следовательно, в десять раз больше конечной скорости и в десять раз больше дальний удар. Вы оказались в ловушке на ледяном озере с мешком с песком. Вспомнив 3-й закон Ньютона, как спастись?
Закон всемирного тяготения Ньютона :
Галилей первым заметил, что объекты «притягиваются» к центр Земли, но Ньютон показал, что эта же сила (гравитация) отвечала за орбиты планет в Солнечной Система.
Объекты во Вселенной притягиваются друг к другу с разной силой. прямо пропорционально произведению их масс и обратно пропорционально квадрату их расстояния
Все массы, независимо от размера, притягивают другие массы силой тяжести.  Ты
не замечайте силы от близлежащих объектов, потому что их масса настолько
мало по сравнению с массой Земли. Рассмотрим следующее
пример:
Ты
не замечайте силы от близлежащих объектов, потому что их масса настолько
мало по сравнению с массой Земли. Рассмотрим следующее
пример:Используя векторное исчисление, Ньютон смог разработать космологию, которая включил основную причину движения планет, гравитацию, завершил модель солнечной системы началось вавилонянами и ранними греками. Математическая формулировка Ньютоновская динамическая модель Солнечной системы стала наукой о небесная механика, величайшая из детерминистических наук.
Хотя ньютоновская механика была великим достижением 1700-х годов, она отнюдь не был окончательным ответом. Например, уравнения орбит можно решить для двух тел, а можно не решить за троих или несколько тел. Задача трех тел озадачивал астрономов в течение многих лет, пока не стало известно, что некоторые математические проблемы страдают от детерминированного хаос, где динамические системы имеют явно случайные или непредсказуемые поведение (см. ниже). 
Дифференциальные гравитационные силы (приливы) :
Приливы вызваны взаимодействием движения тела вокруг планеты или Солнце и внутренняя сила тяжести.
Приливы :
Водяные приливы вызваны тем, что вода на Земле поверхность легче деформируется приливными силами, чем каменистая кора. А сила приливов зависит от трех факторов:
- расположение на поверхности Земли
- ориентация Солнца и Луны (оба имеют примерно
равное приливное воздействие на поверхность Земли)
- географические особенности (форма бухты, заливов и т. д.)
Лимит Рош :
Что происходит, когда приливные силы становятся больше внутренней гравитации объекта? Объект разорван. Это происходит, когда луна подходит слишком близко к своей основной. Приливные силы возрастают по мере того, как R расстояние между планетой и Луной становится меньше, пока Луна не распадается на множество мелких тел.
 Это происхождение колец
вокруг Сатурна и других юпитерианских миров.
Это происхождение колец
вокруг Сатурна и других юпитерианских миров.В небесной механике предел Роша — это расстояние, в пределах которого небесное тело, скрепленное только собственной гравитацией, распадется из-за приливных сил второго небесного тела, превышающих силы первого тела гравитационное самопритяжение. Внутри предела Роша орбитальный материал рассеивается и образует кольца, тогда как вне предела материал имеет тенденцию к сливаться.
Задача трех тел и сложность :
Детерминированные законы, такие как законы движения Ньютона, предполагают предсказуемость только в идеализированном пределе бесконечной точности. Сама Вселенная не может знать свою собственную работу с абсолютной точностью, и там нельзя предсказать, что будет дальше во всех деталях. Детерминированный хаос кажется случайным, потому что мы неизбежно невежественны. сверхтонких деталей, как и сама Вселенная.
Поведение сложных систем на самом деле не случайно, а просто что конечное состояние настолько чувствительно к начальным условиям, что оно невозможно предсказать будущее поведение без бесконечных знаний всех движений и энергии (например, бабочка в Южной Америке влияет на штормы в Северной Атлантике).

Даже игры с простыми правилами могут привести к сложному поведению, как показано на рис. следующий пример:
Хотя это «всего лишь» математическая игра, есть много примеров той же формы и сложного поведения, встречающегося в природе.
общая теория относительности — Чем лучше объясняется Закон всемирного тяготения?
Правда в том, что ни Ньютон, ни Эйнштейн на самом деле не объяснили гравитационное притяжение . Они оба дали нам некоторые уравнения, но ни один из них не дал объяснения относительно истинного механизма лежащей в основе силы. (Вот почему физика до сих пор так отчаянно пытается объединить ОТО и КМ и почему она не может избавиться от понятия гравитона.)
Ньютон просто дал нам уравнение для силы, действующей на расстоянии. Мы можем рассчитать ускорение, которое яблоко дает Земля, но нам не объясняют, откуда яблоко знает, что в нескольких метрах от него находится гораздо более «массивное» (что бы это ни значило) тело, и что такого привлекательного в этом большем друге, что наш красивое яблоко решает подойти поближе и пообщаться с ним.

Эйнштейн сделал попытку, и он значительно приблизил расстояние, но так и не смог объяснить саму силу. Потому что искривление пространства (времени) само по себе просто не может заставить яблоко двигаться (к другому телу или просто к точке). Если искривление производит движение, то только потому, что под ним находится гравитация. Вот почему яблоко, положенное на землю, скатывается по склону. Для этого требуется кривизна (земли), а также гравитация под (землей). Если убрать силу и оставить только искривление… с яблоком ничего не произойдет; он останется там, где был, пока не почувствует настоящую силу. Так что кривизна не может заменить гравитационное притяжение, она не может заменить реальную силу. (Если кто-то применит к ней тензор Эйнштейна, пожалуйста, сначала прочитайте, поскольку я буду ссылаться на это позже).
Вы также можете узнать, что превращение пространства в пространство-время меняет все. Что добавление компонента времени к пространству заставляет вещи двигаться.
 И если вы все еще не можете понять, как это возможно, вас отправят на визуализацию, показывающую, что время ортогонально всем физическим измерениям, и скажут, что в пространстве-времени мы находимся в постоянном движении через одно или все четыре измерения, но всегда через время (кроме света). Так что на самом деле мы все равно находимся в постоянном движении. Но откуда мы это знаем? Что ж, никто, вероятно, даже не задаст этот вопрос, поскольку мы все настолько привыкли к графикам ускорения (или простой скорости), которые показывают время как ортогональное к оси $x$, что делает прекрасную визуализацию изменения скорости в форму кривой, на которую мы отвечаем: «О, теперь я понял! Теперь я знаю, как работает ускорение». Только то, что когда мы видим, как машина ускоряется на улице, ее следы не оставляют кривой. Они идут просто как свисток. Таким образом, кажется, что время не ортогонально ни одному физическому измерению. Следовательно, визуализация ненастоящая, и мы не можем сделать из нее никаких выводов.
И если вы все еще не можете понять, как это возможно, вас отправят на визуализацию, показывающую, что время ортогонально всем физическим измерениям, и скажут, что в пространстве-времени мы находимся в постоянном движении через одно или все четыре измерения, но всегда через время (кроме света). Так что на самом деле мы все равно находимся в постоянном движении. Но откуда мы это знаем? Что ж, никто, вероятно, даже не задаст этот вопрос, поскольку мы все настолько привыкли к графикам ускорения (или простой скорости), которые показывают время как ортогональное к оси $x$, что делает прекрасную визуализацию изменения скорости в форму кривой, на которую мы отвечаем: «О, теперь я понял! Теперь я знаю, как работает ускорение». Только то, что когда мы видим, как машина ускоряется на улице, ее следы не оставляют кривой. Они идут просто как свисток. Таким образом, кажется, что время не ортогонально ни одному физическому измерению. Следовательно, визуализация ненастоящая, и мы не можем сделать из нее никаких выводов. Потому что время просто не заставляет вещи двигаться. Время – это скорее индикатор движения. И это скорее движение, необходимое для операционального объяснения времени.
Потому что время просто не заставляет вещи двигаться. Время – это скорее индикатор движения. И это скорее движение, необходимое для операционального объяснения времени.На это можно было бы возразить аргументами, что движение производится энергией, выраженной тензором Эйнштейна, являющимся результатом тензора энергии-импульса. Ну, я попытался решить этот вопрос здесь: В какой точке Вселенной $R_{\mu \nu}=0$, если есть источник гравитации (точечная масса). Из ответа Муфрида и последующего обсуждения вы можете видеть, что даже уравнения поля Эйнштейна считаются «неполными» и фактически вводят в заблуждение. В учебниках говорится, что уравнение показывает кривизну пространства (времени) через тензор Риччи, метрический тензор и космологическую постоянную. Однако, если вы спросите дальше, вам скажут, что уравнение на самом деле относится не к пространству вообще, а только к материи … Вам скажут, что полная кривизна пространства описывается тензором Римана, состоящим из тензора Риччи (нуль для вакуума) и тензор Вейля.
 Но если потом вы решите копнуть еще глубже и зададите вполне очевидный вопрос, а отвечает ли тензор Вейля за искривление пространства, заставляющее массивные тела сближаться, то ответ будет… тишина…
Но если потом вы решите копнуть еще глубже и зададите вполне очевидный вопрос, а отвечает ли тензор Вейля за искривление пространства, заставляющее массивные тела сближаться, то ответ будет… тишина…Еще одной попыткой объяснения является гипотетический гравитон, который будет «опосредовать» гравитационное поле. Однако до сих пор не объяснено, как это «посредничество» должно вообще заставить вещи двигаться, особенно то, что гравитон не имеет массы, чтобы оказать реальную силу на яблоко (и как эта сила будет действовать в обратном направлении, против направления движения). «носителя» силы?).
Очевидно, физика не очень-то охотно признает все это, что вполне понятно. Он произвел тонны эзотерических концепций, математики, исправлений, но до сих пор не дал ответа на основные вопросы.
Итак, возвращаясь к вопросу: кто лучше объяснил гравитацию — Ньютон или Эйнштейн, ответ снова — ни тот, ни другой. Для меня версия Ньютона, при всех ее недостатках, была, по крайней мере, более честной и не претендовала на решение той проблемы, на которую не решалась.
 Потому что гравитация по-прежнему является действием на расстоянии, и только ньютоновская пустота между двумя притягивающимися телами теперь заполнена тоннами захватывающих математических расчетов, которые ровно ничего не объясняют.
Потому что гравитация по-прежнему является действием на расстоянии, и только ньютоновская пустота между двумя притягивающимися телами теперь заполнена тоннами захватывающих математических расчетов, которые ровно ничего не объясняют.В качестве дополнения, я думаю, вы должны увидеть мой ответ здесь: Почему закон всемирного тяготения Ньютона является действительным законом? Что заставляет любые два тела во Вселенной притягивать друг друга с силой? и посмотрите видео Фейнмана по ссылке.
Чтобы убедиться, это не говорит о том, что физика совершенно бесполезна и все обманывают. Все, что я имею в виду, это то, что физике лучше признать, что она не знает некоторых фундаментальных вещей, и не только потому, что они не могут быть познаны или что они являются метафизикой. Потому что такой ответ означает просто уклонение от ответа. И отсутствие поиска ответов делает физику полностью открытой для полных сюрпризов, таких как «темная материя». Просчет материи-энергии Вселенной на какие-то 95% — явное свидетельство ее дефицита в этой области.




 {th}\].
{th}\].
 Теперь значение гравитации на Луне можно рассчитать, используя закон всемирного тяготения Ньютона.
Теперь значение гравитации на Луне можно рассчитать, используя закон всемирного тяготения Ньютона. модель. Концепция, утверждающая, что полный импульс Вселенной
сохраняется, взаимодействия перераспределяют импульс, но сумма никогда
изменения. В этой модели Бог только запускает часы (первопричина),
затем он работает сам по себе в остальное время.
модель. Концепция, утверждающая, что полный импульс Вселенной
сохраняется, взаимодействия перераспределяют импульс, но сумма никогда
изменения. В этой модели Бог только запускает часы (первопричина),
затем он работает сам по себе в остальное время. Именно эта «дельта-ви» производит
эллиптическая кривизна, то есть орбита.
Именно эта «дельта-ви» производит
эллиптическая кривизна, то есть орбита. Ты
не замечайте силы от близлежащих объектов, потому что их масса настолько
мало по сравнению с массой Земли. Рассмотрим следующее
пример:
Ты
не замечайте силы от близлежащих объектов, потому что их масса настолько
мало по сравнению с массой Земли. Рассмотрим следующее
пример: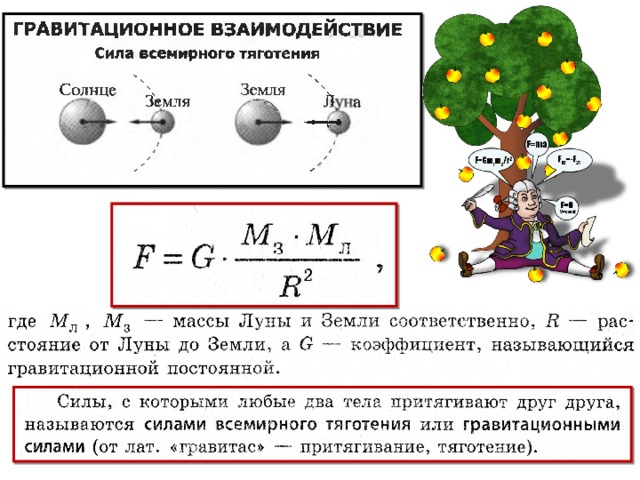
 Это происхождение колец
вокруг Сатурна и других юпитерианских миров.
Это происхождение колец
вокруг Сатурна и других юпитерианских миров.

 И если вы все еще не можете понять, как это возможно, вас отправят на визуализацию, показывающую, что время ортогонально всем физическим измерениям, и скажут, что в пространстве-времени мы находимся в постоянном движении через одно или все четыре измерения, но всегда через время (кроме света). Так что на самом деле мы все равно находимся в постоянном движении. Но откуда мы это знаем? Что ж, никто, вероятно, даже не задаст этот вопрос, поскольку мы все настолько привыкли к графикам ускорения (или простой скорости), которые показывают время как ортогональное к оси $x$, что делает прекрасную визуализацию изменения скорости в форму кривой, на которую мы отвечаем: «О, теперь я понял! Теперь я знаю, как работает ускорение». Только то, что когда мы видим, как машина ускоряется на улице, ее следы не оставляют кривой. Они идут просто как свисток. Таким образом, кажется, что время не ортогонально ни одному физическому измерению. Следовательно, визуализация ненастоящая, и мы не можем сделать из нее никаких выводов.
И если вы все еще не можете понять, как это возможно, вас отправят на визуализацию, показывающую, что время ортогонально всем физическим измерениям, и скажут, что в пространстве-времени мы находимся в постоянном движении через одно или все четыре измерения, но всегда через время (кроме света). Так что на самом деле мы все равно находимся в постоянном движении. Но откуда мы это знаем? Что ж, никто, вероятно, даже не задаст этот вопрос, поскольку мы все настолько привыкли к графикам ускорения (или простой скорости), которые показывают время как ортогональное к оси $x$, что делает прекрасную визуализацию изменения скорости в форму кривой, на которую мы отвечаем: «О, теперь я понял! Теперь я знаю, как работает ускорение». Только то, что когда мы видим, как машина ускоряется на улице, ее следы не оставляют кривой. Они идут просто как свисток. Таким образом, кажется, что время не ортогонально ни одному физическому измерению. Следовательно, визуализация ненастоящая, и мы не можем сделать из нее никаких выводов. Потому что время просто не заставляет вещи двигаться. Время – это скорее индикатор движения. И это скорее движение, необходимое для операционального объяснения времени.
Потому что время просто не заставляет вещи двигаться. Время – это скорее индикатор движения. И это скорее движение, необходимое для операционального объяснения времени.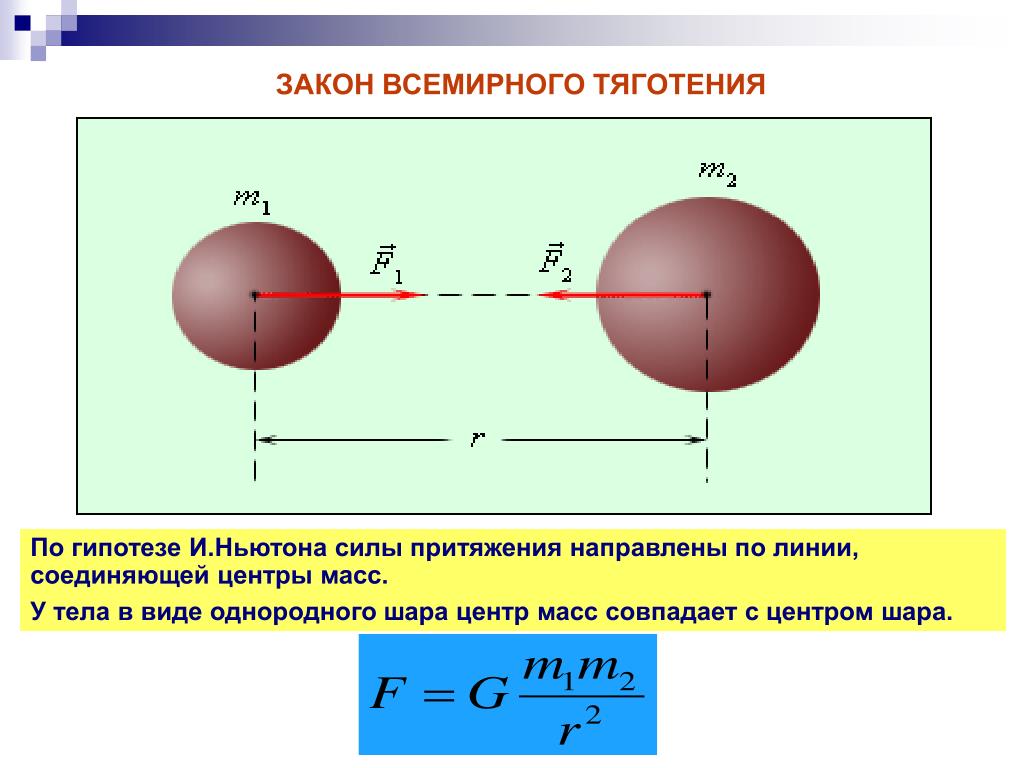 Но если потом вы решите копнуть еще глубже и зададите вполне очевидный вопрос, а отвечает ли тензор Вейля за искривление пространства, заставляющее массивные тела сближаться, то ответ будет… тишина…
Но если потом вы решите копнуть еще глубже и зададите вполне очевидный вопрос, а отвечает ли тензор Вейля за искривление пространства, заставляющее массивные тела сближаться, то ответ будет… тишина… Потому что гравитация по-прежнему является действием на расстоянии, и только ньютоновская пустота между двумя притягивающимися телами теперь заполнена тоннами захватывающих математических расчетов, которые ровно ничего не объясняют.
Потому что гравитация по-прежнему является действием на расстоянии, и только ньютоновская пустота между двумя притягивающимися телами теперь заполнена тоннами захватывающих математических расчетов, которые ровно ничего не объясняют.