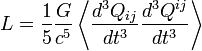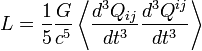Закон тяготения — это… Что такое Закон тяготения?

Гравита́ция (всеми́рное тяготе́ние, тяготе́ние) (от лат. gravitas — «тяжесть») — дальнодействующее фундаментальное взаимодействие в природе, которому подвержены все материальные тела. По современным данным, является универсальным взаимодействием в том смысле, что, в отличие от любых других сил, всем без исключения телам независимо от их массы придаёт одинаковое ускорение. Главным образом гравитация играет определяющую роль в космических масштабах. Термин гравитация используется также как название раздела физики, изучающего гравитационное взаимодействие. Наиболее успешной современной физической теорией в классической физике, описывающей гравитацию, является общая теория относительности, квантовая теория гравитационного взаимодействия пока не построена.

Гравитационное взаимодействие

Гравитационное взаимодействие — одно из четырёх фундаментальных взаимодействий в нашем мире. В рамках классической механики, гравитационное взаимодействие описывается законом всемирного тяготения

Ньютона, который гласит, что сила гравитационного притяжения между двумя материальными точками массы m₁ и m₂, разделёнными расстоянием R, пропорциональна обеим массам и обратно пропорциональна квадрату расстояния — то есть

.

Здесь G — гравитационная постоянная, равная примерно м³/(кг•с²). Знак минус означает, что сила, действующая на тело, всегда равна по направлению радиус-вектору, направленному на тело, то есть гравитационное взаимодействие приводит всегда к притяжению любых тел.

Закон всемирного тяготения — одно из приложений закона обратных квадратов, встречающегося так же и при изучении излучений (см. например, Давление света), и являющимся прямым следствием квадратичного увеличения площади сферы при увеличении радиуса, что приводит к квадратичному же уменьшению вклада любой единичной площади в площадь всей сферы.

Поле тяжести потенциально. Это значит, что можно ввести потенциальную энергию гравитационного притяжения пары тел, и эта энергия не изменится после перемещения тел по замкнутому контуру. Потенциальность поля тяжести влечёт за собой закон сохранения суммы кинетической и потенциальной энергии и при изучении движения тел в поле тяжести часто существенно упрощает решение. В рамках ньютоновской механики гравитационное взаимодействие является дальнодействующим. Это означает, что как бы массивное тело ни двигалось, в любой точке пространства гравитационный потенциал зависит только от положения тела в данный момент времени.

Большие космические объекты — планеты, звезды и галактики имеют огромную массу и, следовательно, создают значительные гравитационные поля.

Гравитация — слабейшее взаимодействие. Однако, поскольку оно действует на любых расстояниях и все массы положительны, это тем не менее очень важная сила во Вселенной. Для сравнения: полный электрический заряд этих тел ноль, так как вещество в целом электрически нейтрально.

Также гравитация, в отличие от других взаимодействий, универсальна в действии на всю материю и энергию. Не обнаружены объекты, у которых вообще отсутствовало бы гравитационное взаимодействие.

Из-за глобального характера гравитация ответственна и за такие крупномасштабные эффекты, как структура галактик, черные дыры и расширение Вселенной, и за элементарные астрономические явления — орбиты планет, и за простое притяжение к поверхности Земли и падения тел.

Гравитация была первым взаимодействием, описанным математической теорией. В античные времена Аристотель считал, что объекты с разной массой падают с разной скоростью. Только много позже Галилео Галилей экспериментально определил, что это не так — если сопротивление воздуха устраняется, все тела ускоряются одинаково. Закон всеобщего тяготения Исаака Ньютона (1687) хорошо описывал общее поведение гравитации. В 1915 году Альберт Эйнштейн создал Общую теорию относительности, более точно описывающую гравитацию в терминах геометрии пространства-времени.

Небесная механика и некоторые её задачи

Раздел механики, изучающий движение тел в пустом пространстве только под действием гравитации называется небесной механикой.

Наиболее простой задачей небесной механики является гравитационное взаимодействие двух тел в пустом пространстве. Эта задача решается аналитически до конца; результат её решения часто формулируют в виде трёх законов Кеплера.

При увеличении количества взаимодействующих тел задача резко усложняется. Так, уже знаменитая задача трёх тел (то есть движение трёх тел с ненулевыми массами) не может быть решена аналитически в общем виде. При численном же решении, достаточно быстро наступает неустойчивость решений относительно начальных условий. В применении к Солнечной системе, эта неустойчивость не позволяет предсказать движение планет на масштабах, превышающих сотню миллионов лет.

В некоторых частных случаях удаётся найти приближённое решение. Наиболее важным является случай, когда масса одного тела существенно больше массы других тел (примеры: солнечная система и динамика колец Сатурна). В этом случае в первом приближении можно считать, что лёгкие тела не взаимодействуют друг с другом и движутся по кеплеровым траекториям вокруг массивного тела. Взаимодействия же между ними можно учитывать в рамках теории возмущений, и усреднять по времени. При этом могут возникать нетривиальные явления, такие как резонансы, аттракторы, хаотичность и т. д. Наглядный пример таких явлений — нетривиальная структура колец Сатурна.

Несмотря на попытки описать поведение системы из большого числа притягивающихся тел примерно одинаковой массы, сделать этого не удаётся из-за явления динамического хаоса.

Сильные гравитационные поля

В сильных гравитационных полях, при движении с релятивистскими скоростями, начинают проявляться эффекты общей теории относительности:

Гравитационное излучение

Одним из важных предсказаний ОТО является гравитационное излучение, наличие которого до сих пор не подтверждено прямыми наблюдениями. Однако, имеются косвенные наблюдательные свидетельства в пользу его существования, а именно: потери энергии в двойной системе с пульсаром PSR B1913+16 — пульсаром Халса-Тейлора — хорошо согласуются с моделью, в которой эта энергия уносится гравитационным излучением.

Гравитационное излучение могут генерировать только системы с переменным квадрупольным или более высокими мультипольными моментами, этот факт говорит о том, что гравитационное излучение большинства природных источников направленное, что существенно усложняет его обнаружение. Мощность гравитационного l-польного источника пропорциональна (v / c)^{2l + 2}, если мультиполь имеет электрический тип, и (v / c)^{2l + 4}

 — если мультиполь магнитного типа ^[1], где v — характерная скорость движения источников в излучающей системе, а c — скорость света. Таким образом, доминирующим моментом будет квадрупольный момент электрического типа, а мощность соответствующего излучения равна:

где Q_ij — тензор квадрупольного момента распределения масс излучающей системы. Константа  (1/Вт) позволяет оценить порядок величины мощности излучения.

Начиная с 1969 года (эксперименты Вебера (англ.)) и до настоящего времени (февраль 2007) предпринимаются попытки прямого обнаружения гравитационного излучения. В США, Европе и Японии в настоящий момент существует несколько действующих наземных детекторов (GEO 600), а также проект космического гравитационного детектора [2] республики Татарстан.

Тонкие эффекты гравитации

Помимо классических эффектов гравитационного притяжения и замедления времени, общая теория относительности предсказывает существование других проявлений гравитации, которые в земных условиях весьма слабы и их обнаружение и экспериментальная проверка поэтому весьма затруднительны. До последнего времени преодоление этих трудностей представлялось за пределами возможностей экспериментаторов.

Среди них, в частности, можно назвать увлечение инерциальных систем отсчета (или эффект Лензе-Тирринга) и гравитомагнитное поле. В 2005 году автоматический аппарат НАСА Gravity Probe B провёл беспрецедентный по точности эксперимент по измерению этих эффектов вблизи Земли, но его полные результаты пока не опубликованы.

Квантовая теория гравитации

Несмотря на более чем полувековую историю попыток, гравитация — единственное из фундаментальных взаимодействий, для которого пока ещё не построена непротиворечивая перенормируемая квантовая теория. Впрочем, при низких энергиях, в духе квантовой теории поля, гравитационное взаимодействие можно представить как обмен гравитонами — калибровочными бозонами со спином 2.

Стандартные теории гравитации

Подробней см. статью Теории гравитации

В связи с тем, что квантовые эффекты гравитации чрезвычайно малы даже в самых экстремальных экспериментальных и наблюдательных условиях, до сих пор не существует их надёжных наблюдений. Теоретические оценки показывают, что в подавляющем большинстве случаев можно ограничиться классическим описанием гравитационного взаимодействия.

Существует современная каноническая^[3] классическая теория гравитации — общая теория относительности, и множество уточняющих её гипотез и теорий различной степени разработанности, конкурирующих между собой (см. статью Альтернативные теории гравитации). Все эти теории дают очень похожие предсказания в рамках того приближения, в котором в настоящее время осуществляются экспериментальные тесты. Далее описаны несколько основных, наиболее хорошо разработанных или известных теорий гравитации.

Общая теория относительности

В стандартном подходе общей теории относительности (ОТО) гравитация рассматривается изначально не как силовое взаимодействие, а как проявление искривления пространства-времени. Таким образом, в ОТО гравитация интерпретируется как геометрический эффект, причём пространство-время рассматривается в рамках неевклидовой римановой (точнее псевдо-римановой) геометрии. Гравитационное поле (обобщение ньютоновского гравитационного потенциала) иногда называемое также полем тяготения, в ОТО отождествляется с тензорным метрическим полем или метрикой четырехмерного пространства-времени, а напряженность гравитационного поля — с аффинной связностью пространства-времени, определяемой метрикой. Стандартной задачей ОТО является определение компонент метрического тензора, в совокупности задающих метрику пространства-времени, по известному распределению источников энергии-импульса в рассматриваемой системе четырехмерных координат. В свою очередь знание метрики позволяет рассчитывать движение пробных частиц, что эквивалентно знанию свойств поля тяготения в данной системе. В связи с тензорным характером уравнений ОТО, а также со стандартным фундаментальным обоснованием ее формулировки, считается, что гравитация также носит тензорный характер. Одним из следствий является то, что гравитационное излучение должно быть не ниже квадрупольного порядка. Известно, что в ОТО имеются затруднения с объяснением факта неинвариантности энергии гравитационного поля, поскольку данная энергия не описывается тензором. В классической ОТО также возникает проблема описания спин-орбитального взаимодействия. Считается, что существуют определенные проблемы с однозначностью результатов и обоснованием непротиворечивости. Однако экспериментально ОТО считается подтверждающейся до самого последнего времени. Кроме того, многие альтернативные эйнштейновскому, но стандартные для современной физики, подходы к формулировке теории гравитации приводят к результату, совпадающему с ОТО в низкоэнергетическом приближении, которое в основном и доступно экспериментальной проверке.

Теория Эйнштейна-Картана

Теория Эйнштейна-Картана (ЭК) была разработана как расширение ОТО, внутренне включающее в себя описание воздействия на пространство-время кроме энергии-импульса также и спина объектов.^[4] В теории ЭК вводится аффинное кручение, а вместо псевдоримановой геометрии для пространства-времени используется геометрия Римана-Картана. В результате от метрической теории переходят к аффинной теории пространства-времени. Результирующие уравнения для описания пространства-времени распадаются на два класса. Один из них аналогичен ОТО, с тем отличием, что в тензор кривизны включены компоненты с аффинным кручением. Второй класс уравнений задаёт связь тензора кручения и тензора спина материи и излучения. Получаемые поправки к ОТО настолько малы, что пока не видно даже гипотетических путей для их измерения.

Релятивистская теория гравитации

Релятивистская теория гравитации (РТГ) разрабатывается академиком Логуновым А. А. с группой сотрудников. ^[5] В ряде работ они утверждают, что РТГ имеет следующие отличия от ОТО^[6] :

• Гравитация есть не геометрическое поле, а реальное физическое силовое поле, описываемое тензором.

• Гравитационные явления следует рассматривать в рамках плоского пространства Минковского, в котором однозначно выполняются законы сохранения энергии-импульса и момента количества движения. Тогда движение тел в пространстве Минковского эквивалентно движению этих тел в эффективном римановом пространстве.

• В тензорных уравнениях для определения метрики следует учитывать массу гравитона, а также использовать калибровочные условия, связанные с метрикой пространства Минковского. Это не позволяет уничтожить гравитационное поле даже локально выбором какой-то подходящей системы отсчёта.

Как и в ОТО, в РТГ под веществом понимаются все формы материи (включая и электромагнитное поле), за исключением самого гравитационного поля. Следствия из теории РТГ таковы: чёрных дыр как физических объектов, предсказываемых в ОТО, не существует; Вселенная плоская, однородная, изотропная, неподвижная и евклидовая.

C другой стороны, существуют не менее убедительные аргументы противников РТГ, сводящиеся к следующим положениям:

• РТГ есть биметрическая теория, в случае безмассового гравитона эквивалентная так называемой полевой трактовке ОТО как надстройке над ненаблюдаемым пространством Минковского: «В релятивистской теории гравитации… фигурируют в точности те же лагранжианы…, которые приводят к уравнениям гравитационного поля»^[7], «математическое содержание РТГ сводится к математическому содержанию ОТО (в полевой формулировке)» ^[8]. Этот аргумент в таком изложении, правда, по-видимому не учитывает возможных топологических различий между обычной моделью ОТО и такой моделью, или же, по крайней мере, маскирует их.
• Случай массивного гравитона в РТГ не даёт правильного ньютоновского предела при переходе к массе равной 0, и, следовательно, бессмыслен.
• Дополнительные уравнения РТГ представляют собой всего лишь координатные условия: «Весь набор уравнений РТГ в терминах метрики искривленного пространства-времени можно свести к уравнениям Эйнштейна плюс гармоническое координатное условие, столь успешно использовавшееся Фоком» ^[8].
• Вышеприведённые следствия из РТГ являются лишь следствием неточностей: несуществование чёрных дыр — следствием невозможности покрыть одной координатной картой, эквивалентной пространству-времени Минковского, пространство-время сколлапсировавшего в чёрную дыру объекта; космологических предсказаний — следствием принятых координатных условий в сочетании с совершенно произвольным дополнительным допущением о вложенности световых конусов реального пространства в конусы пространства Минковского. (Как видим, этот аргумент явно противоречит первому, показывая расхождение РТГ и ОТО, которые вполне ощутимы; и, если оставить соображения, очевидно исходящие просто изнутри обычной логики ОТО, или суждения о произвольности постулатов, то решение о верности одного из этих подходов остается за экспериментом, если конечно не будет всё же доказана достаточно неочевидная их полная эквивалентность в области наблюдаемого).

Теория Бранса — Дикке

В скалярно-тензорных теориях, самой известной из которых является теория Бранса — Дикке (или Йордана — Бранса — Дикке), гравитационное поле как эффективная метрика пространства-времени определяется воздействием не только тензора энергии-импульса материи, как в ОТО, но и дополнительного гравитационного скалярного поля. Источником скалярного поля считается свёрнутый тензор энергии-импульса материи. Следовательно, скалярно-тензорные теории, как ОТО и РТГ, относятся к метрическим теориям, дающим объяснение гравитации, используя только геометрию пространства-времени и его метрические свойства. Наличие скалярного поля приводит к двум тензорным уравнениям для метрики. Теория Бранса — Дикке вследствие наличия скалярного поля может рассматриваться также как действующая в пятимерном многообразии, состоящем из пространства-времени и скалярного поля.^[9]

Подобное имеет место и в РТГ, где второе тензорное уравнение вводится для учёта связи между неевклидовым пространством и пространством Минковского^[10]. Благодаря наличию безразмерного подгоночного параметра в теории Йордана — Бранса — Дикке, появляется возможность выбрать его так, чтобы результаты теории совпадали с результатами гравитационных экспериментов.

Теории гравитации

Источники и примечания

1. ↑ См. аналогии между слабым гравитационным полем и электромагнитным полем в статье гравитомагнетизм
2. ↑ http://dulkyn.org.ru/ru/about.html
3. ↑ Канонической эта теория является в том смысле, что она наиболее хорошо разработана и широко используется в современной небесной механике, астрофизике и космологии, причём количество надёжно установленных противоречащих ей экспериментальных результатов практически равно нулю.
4. ↑ Иваненко Д. Д., Пронин П. И., Сарданашвили Г. А., Калибровочная теория гравитации. — М., Изд. МГУ, 1985.
5. ↑ Логунов А. А., Мествиришвили М. А. Релятивистская теория гравитации. — М: Наука, 1989.
6. ↑ Логунов А. А., Мествиришвили М. А. Тензор энергии-импульса материи как источник гравитационного поля. — Теоретическая и математическая физика, 1997, Т. 110, Вып. 1, Стр. 5 — 24.
7. ↑ Зельдович Я. Б., Грищук Л. П. ТЯГОТЕНИЕ, ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ И АЛЬТЕРНАТИВНЫЕ ТЕОРИИ. УФН, 1986, Т. 149, № 4, с. 695—707. С. 704.
8. ↑ ^{1 2} Зельдович Я. Б., Грищук Л. П. Общая теория относительности верна! УФН, 1988, Т. 155, № 3, с. 517—527. С. 521, 524.
9. ↑ Brans, C. H.; Dicke, R. H. (November 1 1961). «Mach’s Principle and a Relativistic Theory of Gravitation». Physical Review 124 (3): 925—935. DOI:10.1103/PhysRev.124.925. Retrieved on 2006-09-23.
10. ↑ С ортодоксальной точки зрения это уравение представляет собой координатное условие, см. выше.

Литература

• Визгин В. П. Релятивистская теория тяготения (истоки и формирование, 1900—1915). М.: Наука, 1981. — 352c.
• Визгин В. П. Единые теории в 1-й трети ХХ в. М.: Наука, 1985. — 304c.
• Иваненко Д. Д., Сарданашвили Г. А. Гравитация, 3-е изд. М.:УРСС, 2008. — 200с.

См. также

Ссылки

Wikimedia Foundation. 2010.

Закон всемирного тяготения — это… Что такое Закон всемирного тяготения?

Гравита́ция (всеми́рное тяготе́ние, тяготе́ние) (от лат. gravitas — «тяжесть») — дальнодействующее фундаментальное взаимодействие в природе, которому подвержены все материальные тела. По современным данным, является универсальным взаимодействием в том смысле, что, в отличие от любых других сил, всем без исключения телам независимо от их массы придаёт одинаковое ускорение. Главным образом гравитация играет определяющую роль в космических масштабах. Термин гравитация используется также как название раздела физики, изучающего гравитационное взаимодействие. Наиболее успешной современной физической теорией в классической физике, описывающей гравитацию, является общая теория относительности, квантовая теория гравитационного взаимодействия пока не построена.

Гравитационное взаимодействие

Гравитационное взаимодействие — одно из четырёх фундаментальных взаимодействий в нашем мире. В рамках классической механики, гравитационное взаимодействие описывается законом всемирного тяготения Ньютона, который гласит, что сила гравитационного притяжения между двумя материальными точками массы m₁ и m₂, разделёнными расстоянием R, пропорциональна обеим массам и обратно пропорциональна квадрату расстояния — то есть

.

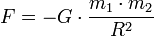Здесь G — гравитационная постоянная, равная примерно 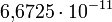м³/(кг•с²). Знак минус означает, что сила, действующая на тело, всегда равна по направлению радиус-вектору, направленному на тело, то есть гравитационное взаимодействие приводит всегда к притяжению любых тел.

Закон всемирного тяготения — одно из приложений закона обратных квадратов, встречающегося так же и при изучении излучений (см. например, Давление света), и являющимся прямым следствием квадратичного увеличения площади сферы при увеличении радиуса, что приводит к квадратичному же уменьшению вклада любой единичной площади в площадь всей сферы.

Поле тяжести потенциально. Это значит, что можно ввести потенциальную энергию гравитационного притяжения пары тел, и эта энергия не изменится после перемещения тел по замкнутому контуру. Потенциальность поля тяжести влечёт за собой закон сохранения суммы кинетической и потенциальной энергии и при изучении движения тел в поле тяжести часто существенно упрощает решение. В рамках ньютоновской механики гравитационное взаимодействие является дальнодействующим. Это означает, что как бы массивное тело ни двигалось, в любой точке пространства гравитационный потенциал зависит только от положения тела в данный момент времени.

Большие космические объекты — планеты, звезды и галактики имеют огромную массу и, следовательно, создают значительные гравитационные поля.

Гравитация — слабейшее взаимодействие. Однако, поскольку оно действует на любых расстояниях и все массы положительны, это тем не менее очень важная сила во Вселенной. Для сравнения: полный электрический заряд этих тел ноль, так как вещество в целом электрически нейтрально.

Также гравитация, в отличие от других взаимодействий, универсальна в действии на всю материю и энергию. Не обнаружены объекты, у которых вообще отсутствовало бы гравитационное взаимодействие.

Из-за глобального характера гравитация ответственна и за такие крупномасштабные эффекты, как структура галактик, черные дыры и расширение Вселенной, и за элементарные астрономические явления — орбиты планет, и за простое притяжение к поверхности Земли и падения тел.

Гравитация была первым взаимодействием, описанным математической теорией. В античные времена Аристотель считал, что объекты с разной массой падают с разной скоростью. Только много позже Галилео Галилей экспериментально определил, что это не так — если сопротивление воздуха устраняется, все тела ускоряются одинаково. Закон всеобщего тяготения Исаака Ньютона (1687) хорошо описывал общее поведение гравитации. В 1915 году Альберт Эйнштейн создал Общую теорию относительности, более точно описывающую гравитацию в терминах геометрии пространства-времени.

Небесная механика и некоторые её задачи

Раздел механики, изучающий движение тел в пустом пространстве только под действием гравитации называется небесной механикой.

Наиболее простой задачей небесной механики является гравитационное взаимодействие двух тел в пустом пространстве. Эта задача решается аналитически до конца; результат её решения часто формулируют в виде трёх законов Кеплера.

При увеличении количества взаимодействующих тел задача резко усложняется. Так, уже знаменитая задача трёх тел (то есть движение трёх тел с ненулевыми массами) не может быть решена аналитически в общем виде. При численном же решении, достаточно быстро наступает неустойчивость решений относительно начальных условий. В применении к Солнечной системе, эта неустойчивость не позволяет предсказать движение планет на масштабах, превышающих сотню миллионов лет.

В некоторых частных случаях удаётся найти приближённое решение. Наиболее важным является случай, когда масса одного тела существенно больше массы других тел (примеры: солнечная система и динамика колец Сатурна). В этом случае в первом приближении можно считать, что лёгкие тела не взаимодействуют друг с другом и движутся по кеплеровым траекториям вокруг массивного тела. Взаимодействия же между ними можно учитывать в рамках теории возмущений, и усреднять по времени. При этом могут возникать нетривиальные явления, такие как резонансы, аттракторы, хаотичность и т. д. Наглядный пример таких явлений — нетривиальная структура колец Сатурна.

Несмотря на попытки описать поведение системы из большого числа притягивающихся тел примерно одинаковой массы, сделать этого не удаётся из-за явления динамического хаоса.

Сильные гравитационные поля

В сильных гравитационных полях, при движении с релятивистскими скоростями, начинают проявляться эффекты общей теории относительности:

Гравитационное излучение

Одним из важных предсказаний ОТО является гравитационное излучение, наличие которого до сих пор не подтверждено прямыми наблюдениями. Однако, имеются косвенные наблюдательные свидетельства в пользу его существования, а именно: потери энергии в двойной системе с пульсаром PSR B1913+16 — пульсаром Халса-Тейлора — хорошо согласуются с моделью, в которой эта энергия уносится гравитационным излучением.

Гравитационное излучение могут генерировать только системы с переменным квадрупольным или более высокими мультипольными моментами, этот факт говорит о том, что гравитационное излучение большинства природных источников направленное, что существенно усложняет его обнаружение. Мощность гравитационного l-польного источника пропорциональна (v / c)^{2l + 2}, если мультиполь имеет электрический тип, и (v / c)^{2l + 4} — если мультиполь магнитного типа ^[1], где v — характерная скорость движения источников в излучающей системе, а c — скорость света. Таким образом, доминирующим моментом будет квадрупольный момент электрического типа, а мощность соответствующего излучения равна:

где Q_ij — тензор квадрупольного момента распределения масс излучающей системы. Константа 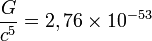 (1/Вт) позволяет оценить порядок величины мощности излучения.

Начиная с 1969 года (эксперименты Вебера (англ.)) и до настоящего времени (февраль 2007) предпринимаются попытки прямого обнаружения гравитационного излучения. В США, Европе и Японии в настоящий момент существует несколько действующих наземных детекторов (GEO 600), а также проект космического гравитационного детектора [2] республики Татарстан.

Тонкие эффекты гравитации

Помимо классических эффектов гравитационного притяжения и замедления времени, общая теория относительности предсказывает существование других проявлений гравитации, которые в земных условиях весьма слабы и их обнаружение и экспериментальная проверка поэтому весьма затруднительны. До последнего времени преодоление этих трудностей представлялось за пределами возможностей экспериментаторов.

Среди них, в частности, можно назвать увлечение инерциальных систем отсчета (или эффект Лензе-Тирринга) и гравитомагнитное поле. В 2005 году автоматический аппарат НАСА Gravity Probe B провёл беспрецедентный по точности эксперимент по измерению этих эффектов вблизи Земли, но его полные результаты пока не опубликованы.

Квантовая теория гравитации

Несмотря на более чем полувековую историю попыток, гравитация — единственное из фундаментальных взаимодействий, для которого пока ещё не построена непротиворечивая перенормируемая квантовая теория. Впрочем, при низких энергиях, в духе квантовой теории поля, гравитационное взаимодействие можно представить как обмен гравитонами — калибровочными бозонами со спином 2.

Стандартные теории гравитации

Подробней см. статью Теории гравитации

В связи с тем, что квантовые эффекты гравитации чрезвычайно малы даже в самых экстремальных экспериментальных и наблюдательных условиях, до сих пор не существует их надёжных наблюдений. Теоретические оценки показывают, что в подавляющем большинстве случаев можно ограничиться классическим описанием гравитационного взаимодействия.

Существует современная каноническая^[3] классическая теория гравитации — общая теория относительности, и множество уточняющих её гипотез и теорий различной степени разработанности, конкурирующих между собой (см. статью Альтернативные теории гравитации). Все эти теории дают очень похожие предсказания в рамках того приближения, в котором в настоящее время осуществляются экспериментальные тесты. Далее описаны несколько основных, наиболее хорошо разработанных или известных теорий гравитации.

Общая теория относительности

В стандартном подходе общей теории относительности (ОТО) гравитация рассматривается изначально не как силовое взаимодействие, а как проявление искривления пространства-времени. Таким образом, в ОТО гравитация интерпретируется как геометрический эффект, причём пространство-время рассматривается в рамках неевклидовой римановой (точнее псевдо-римановой) геометрии. Гравитационное поле (обобщение ньютоновского гравитационного потенциала) иногда называемое также полем тяготения, в ОТО отождествляется с тензорным метрическим полем или метрикой четырехмерного пространства-времени, а напряженность гравитационного поля — с аффинной связностью пространства-времени, определяемой метрикой. Стандартной задачей ОТО является определение компонент метрического тензора, в совокупности задающих метрику пространства-времени, по известному распределению источников энергии-импульса в рассматриваемой системе четырехмерных координат. В свою очередь знание метрики позволяет рассчитывать движение пробных частиц, что эквивалентно знанию свойств поля тяготения в данной системе. В связи с тензорным характером уравнений ОТО, а также со стандартным фундаментальным обоснованием ее формулировки, считается, что гравитация также носит тензорный характер. Одним из следствий является то, что гравитационное излучение должно быть не ниже квадрупольного порядка. Известно, что в ОТО имеются затруднения с объяснением факта неинвариантности энергии гравитационного поля, поскольку данная энергия не описывается тензором. В классической ОТО также возникает проблема описания спин-орбитального взаимодействия. Считается, что существуют определенные проблемы с однозначностью результатов и обоснованием непротиворечивости. Однако экспериментально ОТО считается подтверждающейся до самого последнего времени. Кроме того, многие альтернативные эйнштейновскому, но стандартные для современной физики, подходы к формулировке теории гравитации приводят к результату, совпадающему с ОТО в низкоэнергетическом приближении, которое в основном и доступно экспериментальной проверке.

Теория Эйнштейна-Картана

Теория Эйнштейна-Картана (ЭК) была разработана как расширение ОТО, внутренне включающее в себя описание воздействия на пространство-время кроме энергии-импульса также и спина объектов.^[4] В теории ЭК вводится аффинное кручение, а вместо псевдоримановой геометрии для пространства-времени используется геометрия Римана-Картана. В результате от метрической теории переходят к аффинной теории пространства-времени. Результирующие уравнения для описания пространства-времени распадаются на два класса. Один из них аналогичен ОТО, с тем отличием, что в тензор кривизны включены компоненты с аффинным кручением. Второй класс уравнений задаёт связь тензора кручения и тензора спина материи и излучения. Получаемые поправки к ОТО настолько малы, что пока не видно даже гипотетических путей для их измерения.

Релятивистская теория гравитации

Релятивистская теория гравитации (РТГ) разрабатывается академиком Логуновым А. А. с группой сотрудников. ^[5] В ряде работ они утверждают, что РТГ имеет следующие отличия от ОТО^[6] :

• Гравитация есть не геометрическое поле, а реальное физическое силовое поле, описываемое тензором.

• Гравитационные явления следует рассматривать в рамках плоского пространства Минковского, в котором однозначно выполняются законы сохранения энергии-импульса и момента количества движения. Тогда движение тел в пространстве Минковского эквивалентно движению этих тел в эффективном римановом пространстве.

• В тензорных уравнениях для определения метрики следует учитывать массу гравитона, а также использовать калибровочные условия, связанные с метрикой пространства Минковского. Это не позволяет уничтожить гравитационное поле даже локально выбором какой-то подходящей системы отсчёта.

Как и в ОТО, в РТГ под веществом понимаются все формы материи (включая и электромагнитное поле), за исключением самого гравитационного поля. Следствия из теории РТГ таковы: чёрных дыр как физических объектов, предсказываемых в ОТО, не существует; Вселенная плоская, однородная, изотропная, неподвижная и евклидовая.

C другой стороны, существуют не менее убедительные аргументы противников РТГ, сводящиеся к следующим положениям:

• РТГ есть биметрическая теория, в случае безмассового гравитона эквивалентная так называемой полевой трактовке ОТО как надстройке над ненаблюдаемым пространством Минковского: «В релятивистской теории гравитации… фигурируют в точности те же лагранжианы…, которые приводят к уравнениям гравитационного поля»^[7], «математическое содержание РТГ сводится к математическому содержанию ОТО (в полевой формулировке)» ^[8]. Этот аргумент в таком изложении, правда, по-видимому не учитывает возможных топологических различий между обычной моделью ОТО и такой моделью, или же, по крайней мере, маскирует их.
• Случай массивного гравитона в РТГ не даёт правильного ньютоновского предела при переходе к массе равной 0, и, следовательно, бессмыслен.
• Дополнительные уравнения РТГ представляют собой всего лишь координатные условия: «Весь набор уравнений РТГ в терминах метрики искривленного пространства-времени можно свести к уравнениям Эйнштейна плюс гармоническое координатное условие, столь успешно использовавшееся Фоком» ^[8].
• Вышеприведённые следствия из РТГ являются лишь следствием неточностей: несуществование чёрных дыр — следствием невозможности покрыть одной координатной картой, эквивалентной пространству-времени Минковского, пространство-время сколлапсировавшего в чёрную дыру объекта; космологических предсказаний — следствием принятых координатных условий в сочетании с совершенно произвольным дополнительным допущением о вложенности световых конусов реального пространства в конусы пространства Минковского. (Как видим, этот аргумент явно противоречит первому, показывая расхождение РТГ и ОТО, которые вполне ощутимы; и, если оставить соображения, очевидно исходящие просто изнутри обычной логики ОТО, или суждения о произвольности постулатов, то решение о верности одного из этих подходов остается за экспериментом, если конечно не будет всё же доказана достаточно неочевидная их полная эквивалентность в области наблюдаемого).

Теория Бранса — Дикке

В скалярно-тензорных теориях, самой известной из которых является теория Бранса — Дикке (или Йордана — Бранса — Дикке), гравитационное поле как эффективная метрика пространства-времени определяется воздействием не только тензора энергии-импульса материи, как в ОТО, но и дополнительного гравитационного скалярного поля. Источником скалярного поля считается свёрнутый тензор энергии-импульса материи. Следовательно, скалярно-тензорные теории, как ОТО и РТГ, относятся к метрическим теориям, дающим объяснение гравитации, используя только геометрию пространства-времени и его метрические свойства. Наличие скалярного поля приводит к двум тензорным уравнениям для метрики. Теория Бранса — Дикке вследствие наличия скалярного поля может рассматриваться также как действующая в пятимерном многообразии, состоящем из пространства-времени и скалярного поля.^[9]

Подобное имеет место и в РТГ, где второе тензорное уравнение вводится для учёта связи между неевклидовым пространством и пространством Минковского^[10]. Благодаря наличию безразмерного подгоночного параметра в теории Йордана — Бранса — Дикке, появляется возможность выбрать его так, чтобы результаты теории совпадали с результатами гравитационных экспериментов.

Теории гравитации

Источники и примечания

1. ↑ См. аналогии между слабым гравитационным полем и электромагнитным полем в статье гравитомагнетизм
2. ↑ http://dulkyn.org.ru/ru/about.html
3. ↑ Канонической эта теория является в том смысле, что она наиболее хорошо разработана и широко используется в современной небесной механике, астрофизике и космологии, причём количество надёжно установленных противоречащих ей экспериментальных результатов практически равно нулю.
4. ↑ Иваненко Д. Д., Пронин П. И., Сарданашвили Г. А., Калибровочная теория гравитации. — М., Изд. МГУ, 1985.
5. ↑ Логунов А. А., Мествиришвили М. А. Релятивистская теория гравитации. — М: Наука, 1989.
6. ↑ Логунов А. А., Мествиришвили М. А. Тензор энергии-импульса материи как источник гравитационного поля. — Теоретическая и математическая физика, 1997, Т. 110, Вып. 1, Стр. 5 — 24.
7. ↑ Зельдович Я. Б., Грищук Л. П. ТЯГОТЕНИЕ, ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ И АЛЬТЕРНАТИВНЫЕ ТЕОРИИ. УФН, 1986, Т. 149, № 4, с. 695—707. С. 704.
8. ↑ ^{1 2} Зельдович Я. Б., Грищук Л. П. Общая теория относительности верна! УФН, 1988, Т. 155, № 3, с. 517—527. С. 521, 524.
9. ↑ Brans, C. H.; Dicke, R. H. (November 1 1961). «Mach’s Principle and a Relativistic Theory of Gravitation». Physical Review 124 (3): 925—935. DOI:10.1103/PhysRev.124.925. Retrieved on 2006-09-23.
10. ↑ С ортодоксальной точки зрения это уравение представляет собой координатное условие, см. выше.

Литература

• Визгин В. П. Релятивистская теория тяготения (истоки и формирование, 1900—1915). М.: Наука, 1981. — 352c.
• Визгин В. П. Единые теории в 1-й трети ХХ в. М.: Наука, 1985. — 304c.
• Иваненко Д. Д., Сарданашвили Г. А. Гравитация, 3-е изд. М.:УРСС, 2008. — 200с.

См. также

Ссылки

Wikimedia Foundation. 2010.

Закон всемирного тяготения. Примеры силы тяготения в повседневной жизни и в космосе

Содержание статьи:

При изучении школьного курса физики важной темой раздела механики является Закон всемирного тяготения. В данной статье подробнее рассмотрим, что он собой представляет, и с помощью какой математической формулы описывается, а также приведем примеры силы тяготения в повседневной жизни человека и космических масштабах.

Кто открыл Закон всемирного тяготения

Прежде чем приводить примеры силы всемирного тяготения, расскажем кратко, кому приписывают ее открытие.

С давних времен люди наблюдали за звездами и планетами и знали, что они движутся по определенным траекториям. Кроме того, любой человек, не обладающий специальными знаниями, понимал, что как бы далеко и высоко он не бросал камень или другой предмет, тот всегда падал на землю. Но ни один из людей даже не догадывался, что процессами на Земле и небесными телами управляет один и тот же природный закон.

Вам будет интересно:Лорд — это… Значение и происхождение слова

В 1687 году сэр Исаак Ньютон опубликовал научный труд, в котором впервые изложил математическую формулировку Закона всемирного тяготения. Конечно же, Ньютон не самостоятельно пришел к этой формулировке, что признавал лично. Он использовал некоторые идеи своих современников (например, существование обратной пропорциональности от квадрата расстояния силы притяжения между телами), а также накопленный экспериментальный опыт о траекториях движения планет (три закона Кеплера). Гений Ньютона проявил себя в том, что проанализировав весь имеющийся опыт, ученый смог его оформить в виде стройной и практически пригодной теории.

Формула силы тяготения

Кратко сформулировать Закон всемирного тяготения можно так: между всеми телами во Вселенной существует сила притяжения, которая обратно пропорциональна квадрату дистанции между их центрами масс и прямо пропорциональна произведению самих масс тел. Для двух тел с массами m1 и m2, которые друг от друга находятся на расстоянии r, изучаемый закон запишется в виде:

F = G*m1*m2/r2.

Здесь величина G — это постоянная гравитации.

Силу притяжения можно рассчитывать по этой формуле во всех случаях, если расстояния между телами достаточно велики по сравнению с их размерами. В противном случае, а также в условиях сильной гравитации вблизи массивных космических объектов (нейтронных звезд, черных дыр) следует использовать разработанную Эйнштейном теорию относительности. Последняя рассматривает гравитацию как результат искажения пространства-времени. В классическом же законе Ньютона гравитация — это результат взаимодействия тел с некоторым энергетическим полем, подобно электрическому или магнитному полям.

Проявление силы тяготения: примеры из повседневной жизни

Во-первых, в качестве таких примеров можно назвать любые падения тел с некоторой высоты. Например, листа или знаменитого яблока с дерева, падение камня, капель дождя, явления горных обвалов и оползней. Во всех этих случаях тела стремятся к центру нашей планеты.

Во-вторых, когда учитель просит учащихся: «Приведите примеры силы тяготения», то им также следует вспомнить о существовании у всех тел веса. Когда телефон лежит на столе или когда человек взвешивается на весах, в этих случаях тело давит на опору. Вес тела — это яркий пример проявления силы тяготения, который совместно с реакцией опоры образует пару уравновешивающих друг друга сил.

Если формулу из предыдущего пункта использовать для земных условий (подставить в нее массу планеты и ее радиус), то можно получить следующее выражение:

F = m*g

Именно его используют при решении задач с силой тяжести. Здесь g — это ускорение, сообщаемое всем телам независимо от их массы при свободном падении. Если бы не существовало сопротивления воздуха, то тяжелый камень и легкое перышко падали бы за одно и то же время с одинаковой высоты.

Тяготение во Вселенной

Каждый знает, что Земля вместе с другими планетами вращается вокруг Солнца. В свою очередь, Солнце, находясь в одном из рукавов спиральной галактики Млечный путь, вращается вместе с сотнями миллионов звезд вокруг ее центра. Сами галактики также приближаются друг к другу в так называемых местных скоплениях. Если вернуться назад в масштабах, то следует вспомнить спутники, которые вращаются вокруг своих планет, астероиды, которые на эти планеты падают или пролетают рядом. Все перечисленные случаи можно вспомнить, если учитель просит школьников: «Приведите примеры силы тяготения».

Отметим, что в последние десятилетия вопрос главной силы в космическом масштабе поставлен под сомнение. В локальном космосе ею без сомнения является сила гравитации. Однако, рассматривая вопрос на уровне галактики, в игру вступает иная, пока еще неизвестная сила, связанная с темной материей. Последняя проявляет себя в виде антигравитации.

Источник

Закон всемирного тяготения — это… Что такое Закон всемирного тяготения?

Гравита́ция (всеми́рное тяготе́ние, тяготе́ние) (от лат. gravitas — «тяжесть») — дальнодействующее фундаментальное взаимодействие в природе, которому подвержены все материальные тела. По современным данным, является универсальным взаимодействием в том смысле, что, в отличие от любых других сил, всем без исключения телам независимо от их массы придаёт одинаковое ускорение. Главным образом гравитация играет определяющую роль в космических масштабах. Термин гравитация используется также как название раздела физики, изучающего гравитационное взаимодействие. Наиболее успешной современной физической теорией в классической физике, описывающей гравитацию, является общая теория относительности, квантовая теория гравитационного взаимодействия пока не построена.

Гравитационное взаимодействие

Гравитационное взаимодействие — одно из четырёх фундаментальных взаимодействий в нашем мире. В рамках классической механики, гравитационное взаимодействие описывается законом всемирного тяготения Ньютона, который гласит, что сила гравитационного притяжения между двумя материальными точками массы m₁ и m₂, разделёнными расстоянием R, пропорциональна обеим массам и обратно пропорциональна квадрату расстояния — то есть

.

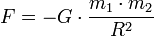Здесь G — гравитационная постоянная, равная примерно 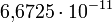м³/(кг•с²). Знак минус означает, что сила, действующая на тело, всегда равна по направлению радиус-вектору, направленному на тело, то есть гравитационное взаимодействие приводит всегда к притяжению любых тел.

Закон всемирного тяготения — одно из приложений закона обратных квадратов, встречающегося так же и при изучении излучений (см. например, Давление света), и являющимся прямым следствием квадратичного увеличения площади сферы при увеличении радиуса, что приводит к квадратичному же уменьшению вклада любой единичной площади в площадь всей сферы.

Поле тяжести потенциально. Это значит, что можно ввести потенциальную энергию гравитационного притяжения пары тел, и эта энергия не изменится после перемещения тел по замкнутому контуру. Потенциальность поля тяжести влечёт за собой закон сохранения суммы кинетической и потенциальной энергии и при изучении движения тел в поле тяжести часто существенно упрощает решение. В рамках ньютоновской механики гравитационное взаимодействие является дальнодействующим. Это означает, что как бы массивное тело ни двигалось, в любой точке пространства гравитационный потенциал зависит только от положения тела в данный момент времени.

Большие космические объекты — планеты, звезды и галактики имеют огромную массу и, следовательно, создают значительные гравитационные поля.

Гравитация — слабейшее взаимодействие. Однако, поскольку оно действует на любых расстояниях и все массы положительны, это тем не менее очень важная сила во Вселенной. Для сравнения: полный электрический заряд этих тел ноль, так как вещество в целом электрически нейтрально.

Также гравитация, в отличие от других взаимодействий, универсальна в действии на всю материю и энергию. Не обнаружены объекты, у которых вообще отсутствовало бы гравитационное взаимодействие.

Из-за глобального характера гравитация ответственна и за такие крупномасштабные эффекты, как структура галактик, черные дыры и расширение Вселенной, и за элементарные астрономические явления — орбиты планет, и за простое притяжение к поверхности Земли и падения тел.

Гравитация была первым взаимодействием, описанным математической теорией. В античные времена Аристотель считал, что объекты с разной массой падают с разной скоростью. Только много позже Галилео Галилей экспериментально определил, что это не так — если сопротивление воздуха устраняется, все тела ускоряются одинаково. Закон всеобщего тяготения Исаака Ньютона (1687) хорошо описывал общее поведение гравитации. В 1915 году Альберт Эйнштейн создал Общую теорию относительности, более точно описывающую гравитацию в терминах геометрии пространства-времени.

Небесная механика и некоторые её задачи

Раздел механики, изучающий движение тел в пустом пространстве только под действием гравитации называется небесной механикой.

Наиболее простой задачей небесной механики является гравитационное взаимодействие двух тел в пустом пространстве. Эта задача решается аналитически до конца; результат её решения часто формулируют в виде трёх законов Кеплера.

При увеличении количества взаимодействующих тел задача резко усложняется. Так, уже знаменитая задача трёх тел (то есть движение трёх тел с ненулевыми массами) не может быть решена аналитически в общем виде. При численном же решении, достаточно быстро наступает неустойчивость решений относительно начальных условий. В применении к Солнечной системе, эта неустойчивость не позволяет предсказать движение планет на масштабах, превышающих сотню миллионов лет.

В некоторых частных случаях удаётся найти приближённое решение. Наиболее важным является случай, когда масса одного тела существенно больше массы других тел (примеры: солнечная система и динамика колец Сатурна). В этом случае в первом приближении можно считать, что лёгкие тела не взаимодействуют друг с другом и движутся по кеплеровым траекториям вокруг массивного тела. Взаимодействия же между ними можно учитывать в рамках теории возмущений, и усреднять по времени. При этом могут возникать нетривиальные явления, такие как резонансы, аттракторы, хаотичность и т. д. Наглядный пример таких явлений — нетривиальная структура колец Сатурна.

Несмотря на попытки описать поведение системы из большого числа притягивающихся тел примерно одинаковой массы, сделать этого не удаётся из-за явления динамического хаоса.

Сильные гравитационные поля

В сильных гравитационных полях, при движении с релятивистскими скоростями, начинают проявляться эффекты общей теории относительности:

Гравитационное излучение

Одним из важных предсказаний ОТО является гравитационное излучение, наличие которого до сих пор не подтверждено прямыми наблюдениями. Однако, имеются косвенные наблюдательные свидетельства в пользу его существования, а именно: потери энергии в двойной системе с пульсаром PSR B1913+16 — пульсаром Халса-Тейлора — хорошо согласуются с моделью, в которой эта энергия уносится гравитационным излучением.

Гравитационное излучение могут генерировать только системы с переменным квадрупольным или более высокими мультипольными моментами, этот факт говорит о том, что гравитационное излучение большинства природных источников направленное, что существенно усложняет его обнаружение. Мощность гравитационного l-польного источника пропорциональна (v / c)^{2l + 2}, если мультиполь имеет электрический тип, и (v / c)^{2l + 4} — если мультиполь магнитного типа ^[1], где v — характерная скорость движения источников в излучающей системе, а c — скорость света. Таким образом, доминирующим моментом будет квадрупольный момент электрического типа, а мощность соответствующего излучения равна:

где Q_ij — тензор квадрупольного момента распределения масс излучающей системы. Константа 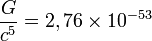 (1/Вт) позволяет оценить порядок величины мощности излучения.

Начиная с 1969 года (эксперименты Вебера (англ.)) и до настоящего времени (февраль 2007) предпринимаются попытки прямого обнаружения гравитационного излучения. В США, Европе и Японии в настоящий момент существует несколько действующих наземных детекторов (GEO 600), а также проект космического гравитационного детектора [2] республики Татарстан.

Тонкие эффекты гравитации

Помимо классических эффектов гравитационного притяжения и замедления времени, общая теория относительности предсказывает существование других проявлений гравитации, которые в земных условиях весьма слабы и их обнаружение и экспериментальная проверка поэтому весьма затруднительны. До последнего времени преодоление этих трудностей представлялось за пределами возможностей экспериментаторов.

Среди них, в частности, можно назвать увлечение инерциальных систем отсчета (или эффект Лензе-Тирринга) и гравитомагнитное поле. В 2005 году автоматический аппарат НАСА Gravity Probe B провёл беспрецедентный по точности эксперимент по измерению этих эффектов вблизи Земли, но его полные результаты пока не опубликованы.

Квантовая теория гравитации

Несмотря на более чем полувековую историю попыток, гравитация — единственное из фундаментальных взаимодействий, для которого пока ещё не построена непротиворечивая перенормируемая квантовая теория. Впрочем, при низких энергиях, в духе квантовой теории поля, гравитационное взаимодействие можно представить как обмен гравитонами — калибровочными бозонами со спином 2.

Стандартные теории гравитации

Подробней см. статью Теории гравитации

В связи с тем, что квантовые эффекты гравитации чрезвычайно малы даже в самых экстремальных экспериментальных и наблюдательных условиях, до сих пор не существует их надёжных наблюдений. Теоретические оценки показывают, что в подавляющем большинстве случаев можно ограничиться классическим описанием гравитационного взаимодействия.

Существует современная каноническая^[3] классическая теория гравитации — общая теория относительности, и множество уточняющих её гипотез и теорий различной степени разработанности, конкурирующих между собой (см. статью Альтернативные теории гравитации). Все эти теории дают очень похожие предсказания в рамках того приближения, в котором в настоящее время осуществляются экспериментальные тесты. Далее описаны несколько основных, наиболее хорошо разработанных или известных теорий гравитации.

Общая теория относительности

В стандартном подходе общей теории относительности (ОТО) гравитация рассматривается изначально не как силовое взаимодействие, а как проявление искривления пространства-времени. Таким образом, в ОТО гравитация интерпретируется как геометрический эффект, причём пространство-время рассматривается в рамках неевклидовой римановой (точнее псевдо-римановой) геометрии. Гравитационное поле (обобщение ньютоновского гравитационного потенциала) иногда называемое также полем тяготения, в ОТО отождествляется с тензорным метрическим полем или метрикой четырехмерного пространства-времени, а напряженность гравитационного поля — с аффинной связностью пространства-времени, определяемой метрикой. Стандартной задачей ОТО является определение компонент метрического тензора, в совокупности задающих метрику пространства-времени, по известному распределению источников энергии-импульса в рассматриваемой системе четырехмерных координат. В свою очередь знание метрики позволяет рассчитывать движение пробных частиц, что эквивалентно знанию свойств поля тяготения в данной системе. В связи с тензорным характером уравнений ОТО, а также со стандартным фундаментальным обоснованием ее формулировки, считается, что гравитация также носит тензорный характер. Одним из следствий является то, что гравитационное излучение должно быть не ниже квадрупольного порядка. Известно, что в ОТО имеются затруднения с объяснением факта неинвариантности энергии гравитационного поля, поскольку данная энергия не описывается тензором. В классической ОТО также возникает проблема описания спин-орбитального взаимодействия. Считается, что существуют определенные проблемы с однозначностью результатов и обоснованием непротиворечивости. Однако экспериментально ОТО считается подтверждающейся до самого последнего времени. Кроме того, многие альтернативные эйнштейновскому, но стандартные для современной физики, подходы к формулировке теории гравитации приводят к результату, совпадающему с ОТО в низкоэнергетическом приближении, которое в основном и доступно экспериментальной проверке.

Теория Эйнштейна-Картана

Теория Эйнштейна-Картана (ЭК) была разработана как расширение ОТО, внутренне включающее в себя описание воздействия на пространство-время кроме энергии-импульса также и спина объектов.^[4] В теории ЭК вводится аффинное кручение, а вместо псевдоримановой геометрии для пространства-времени используется геометрия Римана-Картана. В результате от метрической теории переходят к аффинной теории пространства-времени. Результирующие уравнения для описания пространства-времени распадаются на два класса. Один из них аналогичен ОТО, с тем отличием, что в тензор кривизны включены компоненты с аффинным кручением. Второй класс уравнений задаёт связь тензора кручения и тензора спина материи и излучения. Получаемые поправки к ОТО настолько малы, что пока не видно даже гипотетических путей для их измерения.

Релятивистская теория гравитации

Релятивистская теория гравитации (РТГ) разрабатывается академиком Логуновым А. А. с группой сотрудников. ^[5] В ряде работ они утверждают, что РТГ имеет следующие отличия от ОТО^[6] :

• Гравитация есть не геометрическое поле, а реальное физическое силовое поле, описываемое тензором.

• Гравитационные явления следует рассматривать в рамках плоского пространства Минковского, в котором однозначно выполняются законы сохранения энергии-импульса и момента количества движения. Тогда движение тел в пространстве Минковского эквивалентно движению этих тел в эффективном римановом пространстве.

• В тензорных уравнениях для определения метрики следует учитывать массу гравитона, а также использовать калибровочные условия, связанные с метрикой пространства Минковского. Это не позволяет уничтожить гравитационное поле даже локально выбором какой-то подходящей системы отсчёта.

Как и в ОТО, в РТГ под веществом понимаются все формы материи (включая и электромагнитное поле), за исключением самого гравитационного поля. Следствия из теории РТГ таковы: чёрных дыр как физических объектов, предсказываемых в ОТО, не существует; Вселенная плоская, однородная, изотропная, неподвижная и евклидовая.

C другой стороны, существуют не менее убедительные аргументы противников РТГ, сводящиеся к следующим положениям:

• РТГ есть биметрическая теория, в случае безмассового гравитона эквивалентная так называемой полевой трактовке ОТО как надстройке над ненаблюдаемым пространством Минковского: «В релятивистской теории гравитации… фигурируют в точности те же лагранжианы…, которые приводят к уравнениям гравитационного поля»^[7], «математическое содержание РТГ сводится к математическому содержанию ОТО (в полевой формулировке)» ^[8]. Этот аргумент в таком изложении, правда, по-видимому не учитывает возможных топологических различий между обычной моделью ОТО и такой моделью, или же, по крайней мере, маскирует их.
• Случай массивного гравитона в РТГ не даёт правильного ньютоновского предела при переходе к массе равной 0, и, следовательно, бессмыслен.
• Дополнительные уравнения РТГ представляют собой всего лишь координатные условия: «Весь набор уравнений РТГ в терминах метрики искривленного пространства-времени можно свести к уравнениям Эйнштейна плюс гармоническое координатное условие, столь успешно использовавшееся Фоком» ^[8].
• Вышеприведённые следствия из РТГ являются лишь следствием неточностей: несуществование чёрных дыр — следствием невозможности покрыть одной координатной картой, эквивалентной пространству-времени Минковского, пространство-время сколлапсировавшего в чёрную дыру объекта; космологических предсказаний — следствием принятых координатных условий в сочетании с совершенно произвольным дополнительным допущением о вложенности световых конусов реального пространства в конусы пространства Минковского. (Как видим, этот аргумент явно противоречит первому, показывая расхождение РТГ и ОТО, которые вполне ощутимы; и, если оставить соображения, очевидно исходящие просто изнутри обычной логики ОТО, или суждения о произвольности постулатов, то решение о верности одного из этих подходов остается за экспериментом, если конечно не будет всё же доказана достаточно неочевидная их полная эквивалентность в области наблюдаемого).

Теория Бранса — Дикке

В скалярно-тензорных теориях, самой известной из которых является теория Бранса — Дикке (или Йордана — Бранса — Дикке), гравитационное поле как эффективная метрика пространства-времени определяется воздействием не только тензора энергии-импульса материи, как в ОТО, но и дополнительного гравитационного скалярного поля. Источником скалярного поля считается свёрнутый тензор энергии-импульса материи. Следовательно, скалярно-тензорные теории, как ОТО и РТГ, относятся к метрическим теориям, дающим объяснение гравитации, используя только геометрию пространства-времени и его метрические свойства. Наличие скалярного поля приводит к двум тензорным уравнениям для метрики. Теория Бранса — Дикке вследствие наличия скалярного поля может рассматриваться также как действующая в пятимерном многообразии, состоящем из пространства-времени и скалярного поля.^[9]

Подобное имеет место и в РТГ, где второе тензорное уравнение вводится для учёта связи между неевклидовым пространством и пространством Минковского^[10]. Благодаря наличию безразмерного подгоночного параметра в теории Йордана — Бранса — Дикке, появляется возможность выбрать его так, чтобы результаты теории совпадали с результатами гравитационных экспериментов.

Теории гравитации

Источники и примечания

1. ↑ См. аналогии между слабым гравитационным полем и электромагнитным полем в статье гравитомагнетизм
2. ↑ http://dulkyn.org.ru/ru/about.html
3. ↑ Канонической эта теория является в том смысле, что она наиболее хорошо разработана и широко используется в современной небесной механике, астрофизике и космологии, причём количество надёжно установленных противоречащих ей экспериментальных результатов практически равно нулю.
4. ↑ Иваненко Д. Д., Пронин П. И., Сарданашвили Г. А., Калибровочная теория гравитации. — М., Изд. МГУ, 1985.
5. ↑ Логунов А. А., Мествиришвили М. А. Релятивистская теория гравитации. — М: Наука, 1989.
6. ↑ Логунов А. А., Мествиришвили М. А. Тензор энергии-импульса материи как источник гравитационного поля. — Теоретическая и математическая физика, 1997, Т. 110, Вып. 1, Стр. 5 — 24.
7. ↑ Зельдович Я. Б., Грищук Л. П. ТЯГОТЕНИЕ, ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ И АЛЬТЕРНАТИВНЫЕ ТЕОРИИ. УФН, 1986, Т. 149, № 4, с. 695—707. С. 704.
8. ↑ ^{1 2} Зельдович Я. Б., Грищук Л. П. Общая теория относительности верна! УФН, 1988, Т. 155, № 3, с. 517—527. С. 521, 524.
9. ↑ Brans, C. H.; Dicke, R. H. (November 1 1961). «Mach’s Principle and a Relativistic Theory of Gravitation». Physical Review 124 (3): 925—935. DOI:10.1103/PhysRev.124.925. Retrieved on 2006-09-23.
10. ↑ С ортодоксальной точки зрения это уравение представляет собой координатное условие, см. выше.

Литература

• Визгин В. П. Релятивистская теория тяготения (истоки и формирование, 1900—1915). М.: Наука, 1981. — 352c.
• Визгин В. П. Единые теории в 1-й трети ХХ в. М.: Наука, 1985. — 304c.
• Иваненко Д. Д., Сарданашвили Г. А. Гравитация, 3-е изд. М.:УРСС, 2008. — 200с.

См. также

Ссылки

Wikimedia Foundation. 2010.