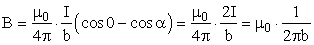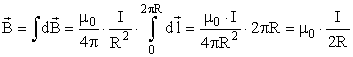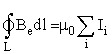1.3. Закон Био – Савара – Лапласа и его применение к расчету магнитного поля. @
Вопрос второй.
Магнитостатика. Магнитное поле в вакууме.
2.1.Магнитное поле и его источники. Вектор магнитной индукции,свойства магнитного поля.
Многочисленные опыты начала XIX века показали, что каждый проводник с током и постоянный магнит способны оказывать силовое воздействие через пространство на другие проводники с током или магниты. Это происходит из-за того, что вокруг проводников с током и магнитов возникает поле, которое было названо магнитным.
Рассмотрим ряд опытов, которые позволили установить основные свойства магнитного поля:
Если заряженный шарик из диэлектрика подвесить на нити вблизи магнитной стрелки, стрелка и шарик остаются неподвижными. Следовательно, постоянные магниты не действуют на неподвижные заряды и неподвижные заряды не создают магнитного поля.
Если магнитную стрелку поместить под прямолинейным проводником с током, то она будет поворачиваться, стремясь расположиться перпендикулярно проводнику (опыт Эрстеда). Смена направления тока на противоположное вызовет переориентацию стрелки на 180˚С.
 Рис.1.2 Силовые линии
Рис.1.2 Силовые линиимагнитного поля прямолинейного тока и правило правой руки.
Пучок движущихся электронов оказывает действие на магнитную стрелку аналогичное проводнику с током (опыт Иоффе).
Конвекционные токи, образуемые движущимися заряженными телами, по своему действию на магнитную стрелку подобны токам проводимости (опыт Эйхенвальда).
На основании данных опытов был сделан вывод о том, что магнитное поле создается только движущимися зарядами или движущимися заряженными телами, а также постоянными магнитами.
Основной
характеристикой магнитного поля является вектор магнитной индукции 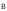 .За направление магнитной индукции в
данной точке поля принимают направление,
по которому в данной точке располагается
ось магнитной стрелки отS кN (рис.1.1). Графически
магнитные поля изображаются силовыми
линиями магнитной индукции, то есть
кривыми, касательные к которым в каждой
точке совпадают с направлением вектора
В.
.За направление магнитной индукции в
данной точке поля принимают направление,
по которому в данной точке располагается
ось магнитной стрелки отS кN (рис.1.1). Графически
магнитные поля изображаются силовыми
линиями магнитной индукции, то есть
кривыми, касательные к которым в каждой
точке совпадают с направлением вектора
В.
Как
определить направление вектора 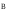 около проводника с током? Это можно
сделать с помощьюправила правой
руки,которое иллюстрируется
рис. 1.2. Большой палец
правой руки ориентируют в направлении
тока, тогда остальные пальцы в согнутом
положении указывают направление силовых
линий магнитного поля.
около проводника с током? Это можно
сделать с помощьюправила правой
руки,которое иллюстрируется
рис. 1.2. Большой палец
правой руки ориентируют в направлении
тока, тогда остальные пальцы в согнутом
положении указывают направление силовых
линий магнитного поля.
Магнитная индукция  в системе СИ измеряется в Н/(А∙м), этой
величине присвоено специальное
наименование – тесла [Tл].
в системе СИ измеряется в Н/(А∙м), этой
величине присвоено специальное
наименование – тесла [Tл].
2.2 Сила Ампера, сила Лоренца.
В 1820 г. А.Ампер установил, что сила, с
которой магнитное поле действует на
элементарный проводник с током Iи длиной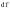 :
:
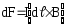 .
.
Вектор 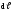 совпадает по направлению с током. Данная
формула выражаетзакон Ампера:сила,
действующая на элемент проводника с
током в магнитном поле, равна произведению
силы тока на векторное произведение
элемента длины проводника и магнитной
индукции поля.
совпадает по направлению с током. Данная
формула выражаетзакон Ампера:сила,
действующая на элемент проводника с
током в магнитном поле, равна произведению
силы тока на векторное произведение
элемента длины проводника и магнитной
индукции поля.
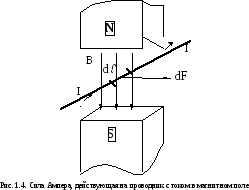
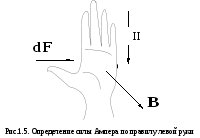
Если поместить проводник
с током между полюсов постоянного
магнита, то сила Ампера будет действовать
на него в направлении, показанном на
рис. 1.4. Направление 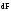
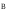 был направлен в ладонь, а четыре вытянутых
пальца указывали направление тока в
проводнике, то отставленный под прямым
углом большой палец укажет направление
силы, действующей на элемент проводника
с током (рис.4.5).
был направлен в ладонь, а четыре вытянутых
пальца указывали направление тока в
проводнике, то отставленный под прямым
углом большой палец укажет направление
силы, действующей на элемент проводника
с током (рис.4.5).
Модуль силы Ампера вычисляется по формуле:
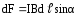 ,
где α –угол между векторами
,
где α –угол между векторами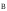
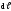 .
Чтобы найти силу, действующую на проводник
конечной длины
.
Чтобы найти силу, действующую на проводник
конечной длины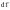 в магнитном поле, необходимо определить
геометрическую сумму сил, действующих
на все малые элементы данного проводника,
т.е.
в магнитном поле, необходимо определить
геометрическую сумму сил, действующих
на все малые элементы данного проводника,
т.е.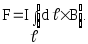
Пусть элемент проводника
с током перпендикулярен направлению
магнитного поля. Тогда sinα=1 и dF=IВ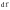
Последнее выражение
помогает определить физический смысл
величины В: магнитная индукция
численно равна силе, действующей со
стороны магнитного поля на 1 м проводника,
по которому течет ток в 1 А и который
расположен перпендикулярно направлению
магнитного поля.Таким образом,
магнитная индукция является силовой
характеристикой магнитного поля. 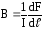
Из закона Ампера следует, что магнитные силы нецентральные, так как они направлены перпендикулярно силовым линиям магнитного поля. Напомним, что электростатические силы – центральные.
Сила Лоренца
Так как электрический ток представляет собой упорядоченное движение зарядов, то действие магнитного поля на проводник с током есть результат его действия на отдельные движущиеся заряды.
Силу, действующую со стороны магнитного поля на движущиеся в нем заряды, называют силой Лоренца.
Сила Лоренца определяется соотношением:
Fл = q·V·B·sin
где q –величина движущегося заряда; V — модуль его скорости; B — модуль вектора индукции магнитного поля; — угол между вектором скорости заряда и вектором магнитной индукции.
Обратите внимание, что сила Лоренца перпендикулярна скорости и поэтому она не совершает работы, не изменяет модуль скорости заряда и его кинетической энергии. Но направление скорости изменяется непрерывно
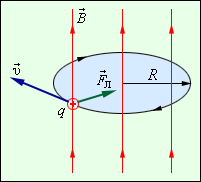
Сила Лоренца перпендикулярна векторам В и v , и её направление определяется с помощью того же правила левой руки, что и направление силы Ампера: если левую руку расположить так, чтобы составляющая магнитной индукции В, перпендикулярная скорости заряда, входила в ладонь, а четыре пальца были направлены по движению положительного заряда (против движения отрицательного), то отогнутый на 90 градусов большой палец покажет направление действующей на заряд силы Лоренца F л.
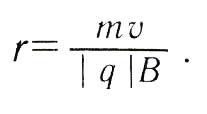
Сила Лоренца зависит от модулей скорости частицы и индукции магнитного поля. Эта сила перпендикулярна скорости и, следовательно, определяет центростремительное ускорение частицы. Частица равномерно движется по окружности радиуса r.
2.3 Закон Био-Савара-Лапласса и его применение к расчету магнитного поля.
Французские физики Ф.
Савар и Ж.Б. Био изучали магнитное поле,
создаваемое проводниками с постоянным
током различной формы. На основании
многочисленных опытов они пришли к
выводу, что магнитная индукция поля
проводника с током пропорциональна
силе тока I, зависит от формы и размеров
проводника, а также от расположения
рассматриваемой точки по отношению к
проводнику. Био и Савар пытались получить
самый общий закон – для проводника
любой формы и любой точки поля. Однако
сделать это им не удалось. По их просьбе
этой проблемой занялся французский
математик П.С.Лаплас. Он высказал важную
гипотезу о том, что при наложении
магнитных полей справедлив принцип
суперпозиции, т.е. принцип независимости
действия полей. Если имеется несколько
проводников с током, каждый из которых
создает в исследуемой точке магнитное
поле с индукциями 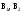
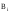
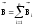 .
Если перейти к малым отрезкам провода
с током, то суммирование надо заменить
интегрированием и тогда индукция
.
Если перейти к малым отрезкам провода
с током, то суммирование надо заменить
интегрированием и тогда индукция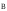 ,
создаваемая всем проводником с токомI, будет равна:
,
создаваемая всем проводником с токомI, будет равна: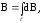 где
где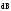 –
индукция, создаваемая элементом длины
проводникаdℓ, интегрирование
проводится по всей длине проводника.Лаплас обобщил экспериментальные
результаты Био и Савара в виде
дифференциального закона, называемого
законом Био – Савара – Лапласа, по
которому магнитная индукция
–
индукция, создаваемая элементом длины
проводникаdℓ, интегрирование
проводится по всей длине проводника.Лаплас обобщил экспериментальные
результаты Био и Савара в виде
дифференциального закона, называемого
законом Био – Савара – Лапласа, по
которому магнитная индукция 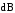 ,
создаваемая в некоторой точке А элементом
проводникаdℓ
с током I,
определяется формулой
,
создаваемая в некоторой точке А элементом
проводникаdℓ
с током I,
определяется формулой
Выберем произвольную
точку А вблизи проводника. Вектор  направлен в точке А перпендикулярно
плоскости, построенной на векторах
направлен в точке А перпендикулярно
плоскости, построенной на векторах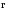 и
и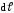 по
правилу правого винта (буравчика), и
совпадает с направлением касательной
к линии индукции в точке А (пунктирный
круг) (рис.1.7). Коэффициент пропорциональностиkзависит от выбора системы
единиц. В СИ это размерная величина,
равная μ0/4π, где μ0 — магнитная
постоянная, равная 4π∙10-7Гн/м. Все
выше изложенное относится к вакууму.
по
правилу правого винта (буравчика), и
совпадает с направлением касательной
к линии индукции в точке А (пунктирный
круг) (рис.1.7). Коэффициент пропорциональностиkзависит от выбора системы
единиц. В СИ это размерная величина,
равная μ0/4π, где μ0 — магнитная
постоянная, равная 4π∙10-7Гн/м. Все
выше изложенное относится к вакууму.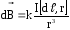
Таким образом, магнитную индукцию поля, создаваемую в вакууме током I, текущим по проводу конечной длины ℓ и любой формы, можно найти по формуле
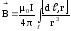
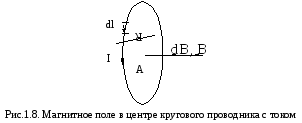
1.Магнитное
поле в центре кругового проводника с
током.Рассмотрим круговой проводник
с током, изображенный на рис.1.8. Все
элементы данного проводникаdℓ
создают в его центре (точке А) магнитные
поля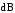 одинакового направления – вдоль нормали
к площади витка. Поэтому, как и в предыдущем
случае, сложение векторов можно заменить
сложением их модулей. Элементыdℓ
перпендикулярныRиsinα=1.
Используя закон Био-Савара-Лапласа,
получим:
одинакового направления – вдоль нормали
к площади витка. Поэтому, как и в предыдущем
случае, сложение векторов можно заменить
сложением их модулей. Элементыdℓ
перпендикулярныRиsinα=1.
Используя закон Био-Савара-Лапласа,
получим:
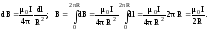
2.Магнитное
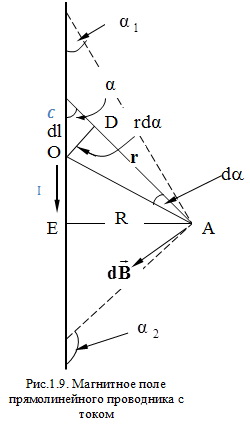
поле прямолинейного проводника с током. Представим себе ток, текущий по
тонкому прямому проводу бесконечной
длины (рис. 1.9). Возьмем произвольную
точку А на расстоянииRот проводника. Согласно правилу правого
винта (буравчика), векторы от каждого элемента токаdℓiимеют одинаковое направление,
перпендикулярное плоскости чертежа
(на нас). Поэтому сложение векторов
от каждого элемента токаdℓiимеют одинаковое направление,
перпендикулярное плоскости чертежа
(на нас). Поэтому сложение векторов можно заменить сложением их модулей.
При суммировании всех
можно заменить сложением их модулей.
При суммировании всех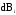 будет меняться уголαмеждуrиdℓ,
поэтому выберемαв
качестве переменной интегрирования.
Выразим черезαвсе
остальные величины, полагая, что отрезок
АD≈rиз-за
малостиdℓ.
будет меняться уголαмеждуrиdℓ,
поэтому выберемαв
качестве переменной интегрирования.
Выразим черезαвсе
остальные величины, полагая, что отрезок
АD≈rиз-за
малостиdℓ.
Итак, из
треугольника АСЕ выразим rчерез известное нам расстояниеRи переменнуюα: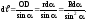
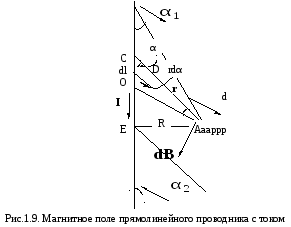
По закону Био-Савара-Лапласа получим: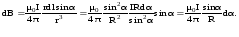
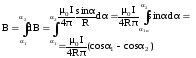
В данном выражении α1и α2 — значения угла α для крайних точек проводника. Если прямолинейный проводник бесконечно длинный, то α1 = 0, α2= π. Магнитная индукция в любой точке поля такого проводника с током:
Напомним,
что линии магнитной индукции поля
прямого тока представляют собой систему
охватывающих провод концентрических
окружностей.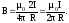
3.Магнитное поле соленоида. Если витки соленоида расположены вплотную друг к другу, то соленоид можно рассматривать как систему последовательно соединенных круговых токов одинакового радиуса с общей осью. Обозначим черезLдлину соленоида, а черезn- число витков, приходящихся на единицу длины соленоида. Магнитная индукция поля соленоида В равна геометрической сумме магнитных индукций Вiполей всех его витков. ЕслиL>>R(радиуса витков), тогда В в точке А, лежащей на оси вдали от концов такого соленоида, вычисляется по формуле (без вывода): В = μ0nI.
2.4 Расчет магнитных полей для простейших систем. ХРЕН ЗНАЕТ ТО ИЛИ НЕ ТО,ДРУГОГО НЕТ! Или это то,что выше….то,что под цифрами 1,2,3
Законы Био
– Савара – Лапласа и Ампера применяются
для определения силы взаимодействия
двух параллельных проводников с током.
Рассмотрим два бесконечных прямолинейных
проводника с токами I1 и I2 , расстояние
между которыми равно а. На рис. 1.10
проводники расположены перпендикулярно
чертежу. Токи в них направлены одинаково
(из-за чертежа на нас) и обозначены
точками. Каждый из проводников создает
магнитное поле, которое действует на
другой проводник. Ток I1 создает вокруг
себя магнитное поле, линии магнитной
индукции которого представляют собой
концентрические окружности. Направление 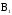 определяется правилом правого винта,
а его модуль по закону Био – Савара –
Лапласа . Согласно проведенным выше
расчетам модуль равен с
определяется правилом правого винта,
а его модуль по закону Био – Савара –
Лапласа . Согласно проведенным выше
расчетам модуль равен с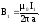 Тогда, согласно закону Ампера, dF1=I2B1dl
или
Тогда, согласно закону Ампера, dF1=I2B1dl
или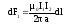 и аналогично
и аналогично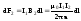 .
Направление силы
.
Направление силы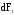 ,
с которой поле
,
с которой поле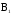 действует на участокdℓ
второго проводника с токомI2(рис.1.10), определяется по правилу левой
руки (см. разд. 1.2). Как видно из рис.1.10 и
расчетов, силы
действует на участокdℓ
второго проводника с токомI2(рис.1.10), определяется по правилу левой
руки (см. разд. 1.2). Как видно из рис.1.10 и
расчетов, силы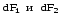 одинаковы
по модулю и противоположны по направлению.
В нашем случае они направлены навстречу
друг другу и проводники притягиваются.
Если токи текут в противоположных
направлениях, то возникающие между ними
силы отталкивают проводники друг от
друга. Итак, параллельные токи (одного направления)
притягиваются, а антипараллельные (
противоположных направлений ) —
отталкиваются. Для определения
силы F, действующей
на проводник конечной длины ℓ, необходимо
проинтегрировать полученное равенство
по ℓ от 0 до ℓ :
одинаковы
по модулю и противоположны по направлению.
В нашем случае они направлены навстречу
друг другу и проводники притягиваются.
Если токи текут в противоположных
направлениях, то возникающие между ними
силы отталкивают проводники друг от
друга. Итак, параллельные токи (одного направления)
притягиваются, а антипараллельные (
противоположных направлений ) —
отталкиваются. Для определения
силы F, действующей
на проводник конечной длины ℓ, необходимо
проинтегрировать полученное равенство
по ℓ от 0 до ℓ : 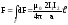 При магнитном взаимодействии выполняется
закон действия и противодействия, т.е.
третий закон Ньютона:
При магнитном взаимодействии выполняется
закон действия и противодействия, т.е.
третий закон Ньютона: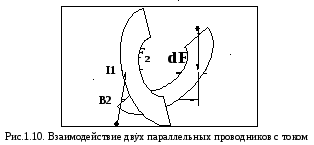

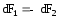 .
.
2.5 Работа по перемещению проводника с током в магнитном поле. ВРОДЕ ТО,ХЗ
1.3 Закон Био — Савара
1.3. Закон Био – Савара – Лапласа и его применение к расчету магнитного поля.
Французские физики Ф. Савар и Ж.Б. Био изучали магнитное поле, создаваемое проводниками с постоянным током различной формы. На основании многочисленных опытов они пришли к выводу, что магнитная индукция поля проводника с током пропорциональна силе тока I, зависит от формы и размеров проводника, а также от расположения рассматриваемой точки по отношению к проводнику. Био и Савар пытались получить самый общий закон – для проводника любой формы и любой точки поля. Однако сделать это им не удалось. По их просьбе этой проблемой занялся французский математик П.С.Лаплас. Он высказал важную гипотезу о том, что при наложении магнитных полей справедлив принцип суперпозиции, т.е. принцип независимости действия полей. Если имеется несколько проводников с током, каждый из которых создает в исследуемой точке магнитное поле с индукциями 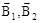 …, то результирующая магнитная индукция будет равна векторной сумме всех
…, то результирующая магнитная индукция будет равна векторной сумме всех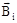 :
: 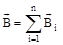 . Если перейти к малым отрезкам провода с током, то суммирование надо заменить интегрированием и тогда индукция
. Если перейти к малым отрезкам провода с током, то суммирование надо заменить интегрированием и тогда индукция 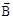 , создаваемая всем проводником с током I, будет равна:
, создаваемая всем проводником с током I, будет равна: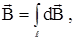 где
где – индукция, создаваемая элементом длины проводника dℓ, интегрирование проводится по всей длине проводника.
– индукция, создаваемая элементом длины проводника dℓ, интегрирование проводится по всей длине проводника.
Лаплас обобщил экспериментальные результаты Био и Савара в виде дифференциального закона, называемого законом Био – Савара – Лапласа, по которому магнитная индукция 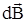 , создаваемая в некоторой точке А элементом проводника dℓ с током I, определяется формулой
, создаваемая в некоторой точке А элементом проводника dℓ с током I, определяется формулой
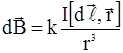
Выберем произвольную точку А вблизи проводника. Вектор 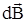 направлен в точке А перпендикулярно плоскости, построенной на векторах
направлен в точке А перпендикулярно плоскости, построенной на векторах 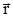 и
и 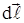 по правилу правого винта (буравчика), и совпадает с направлением касательной к линии индукции в точке А (пунктирный круг) (рис.1.7). Коэффициент пропорциональности k зависит от выбора системы единиц. В СИ это размерная величина, равная μ0/4π, где μ0 — магнитная постоянная, равная 4π∙10-7Гн/м. Все выше изложенное относится к вакууму.
по правилу правого винта (буравчика), и совпадает с направлением касательной к линии индукции в точке А (пунктирный круг) (рис.1.7). Коэффициент пропорциональности k зависит от выбора системы единиц. В СИ это размерная величина, равная μ0/4π, где μ0 — магнитная постоянная, равная 4π∙10-7Гн/м. Все выше изложенное относится к вакууму.
Таким образом, магнитную индукцию поля, создаваемую в вакууме током I, текущим по проводу конечной длины ℓ и любой формы, можно найти по формуле
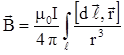 |
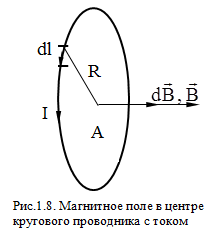
Магнитное поле в центре кругового проводника с током. Рассмотрим круговой проводник с током, изображенный на рис.1.8. Все элементы данного проводника dℓ создают в его центре (точке А) магнитные поля 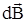 одинакового направления – вдоль нормали к площади витка. Поэтому, как и в предыдущем случае, сложение векторов можно заменить сложением их модулей. Элементы dℓ перпендикулярны R и sinα=1. Используя закон Био-Савара-Лапласа, получим:
одинакового направления – вдоль нормали к площади витка. Поэтому, как и в предыдущем случае, сложение векторов можно заменить сложением их модулей. Элементы dℓ перпендикулярны R и sinα=1. Используя закон Био-Савара-Лапласа, получим:
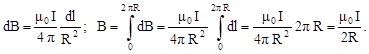 |
Магнитное поле прямолинейного проводника с током. Представим себе ток, текущий по тонкому прямому проводу бесконечной длины (рис. 1.9). Возьмем произвольную точку А на расстоянии R от проводника. Согласно правилу правого винта (буравчика), векторы 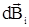 от каждого элемента тока dℓi имеют одинаковое направление, перпендикулярное плоскости чертежа (на нас). Поэтому сложение векторов
от каждого элемента тока dℓi имеют одинаковое направление, перпендикулярное плоскости чертежа (на нас). Поэтому сложение векторов 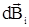 можно заменить сложением их модулей. При суммировании всех
можно заменить сложением их модулей. При суммировании всех 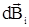 будет меняться угол α между r и dℓ, поэтому выберем α в качестве переменной интегрирования. Выразим через α все остальные величины, полагая, что отрезок АD ≈ r из-за малости dℓ.
будет меняться угол α между r и dℓ, поэтому выберем α в качестве переменной интегрирования. Выразим через α все остальные величины, полагая, что отрезок АD ≈ r из-за малости dℓ.
Итак, из треугольника АСЕ выразим r через известное нам расстояние R и переменную α: 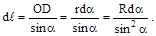
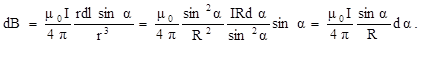
По закону Био-Савара-Лапласа получим:
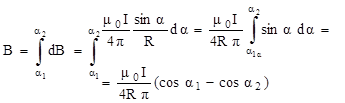 |
В данном выражении α1 и α2 — значения угла α для крайних точек проводника. Если прямолинейный проводник бесконечно длинный, то α1 = 0, α2 = π. Магнитная индукция в любой точке поля такого проводника с током:
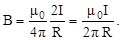 |
Напомним, что линии магнитной индукции поля прямого тока представляют собой систему охватывающих провод концентрических окружностей.
Магнитное поле соленоида. Если витки соленоида расположены вплотную друг к другу, то соленоид можно рассматривать как систему последовательно соединенных круговых токов одинакового радиуса с общей осью. Обозначим через L длину соленоида, а через n — число витков, приходящихся на единицу длины соленоида. Магнитная индукция поля соленоида В равна геометрической сумме магнитных индукций Вi полей всех его витков. Если L>>R (радиуса витков), тогда В в точке А, лежащей на оси вдали от концов такого соленоида, вычисляется по формуле (без вывода): В = μ0nI.
ЛК-№7-Законы_Био-Савара-Лапласа_Ампера
4
Тема 3. Магнитное поле.
Лекция_№7.
1. Магнитное поле и его характеристики.
2. Закон Био — Савара — Лапласа.
3. Закон Ампера, взаимодействие параллельных токов.
1. Магнитное поле и его характеристики.
Определение 1.
Магнитным полем называется силовое поле, возникающее в пространстве, окружающем токи и постоянные магниты,
Наличие магнитного поля обнаруживается по силовому действию на внесенные в него проводники с током или постоянные магниты.
Название «магнитное поле» связывают с ориентацией магнитной стрелки под действием поля, создаваемого током (это явление впервые обнаружено датским физиком X. Эрстедом (1777—1851)).
Электрическое поле действует как на неподвижные, так и на движущиеся в нем электрические заряды.
Важнейшая особенность магнитного поля состоит в том, что оно действует только на движущиеся в этом поле электрические заряды.
При исследовании магнитного поля используется замкнутый плоский контур с током (рамка с током), линейные размеры которого малы по сравнению с расстоянием до токов, образующих магнитное поле.
О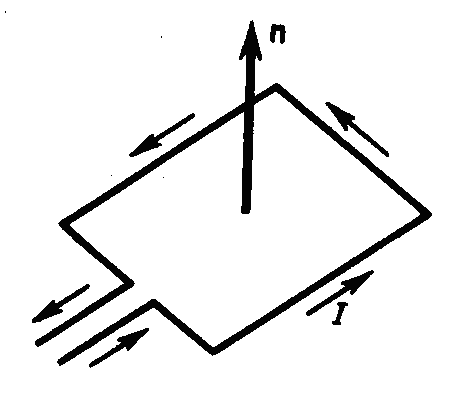 риентация
контура в пространстве определяется
направлением нормали к контуру.
Направление нормали определяется
правилом правого винта: за положительное
направление нормали принимается
направление поступательного движения
винта, головка которого вращается в
направлении тока, текущего в рамке
(рисунок слева).
риентация
контура в пространстве определяется
направлением нормали к контуру.
Направление нормали определяется
правилом правого винта: за положительное
направление нормали принимается
направление поступательного движения
винта, головка которого вращается в
направлении тока, текущего в рамке
(рисунок слева).
Опыты показывают, что магнитное поле оказывает на рамку с током ориентирующее действие, поворачивая ее определенным образом.
Этот результат используется для выбора направления магнитного поля.
О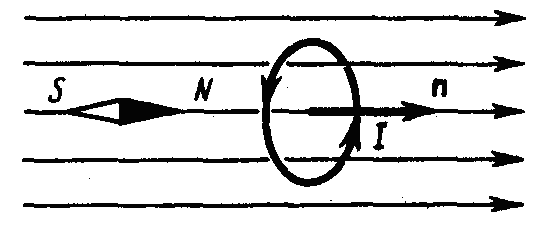 пределение
2.
пределение
2.
За направление магнитного поля в данной точке принимается направление, вдоль которого располагается положительная нормаль к рамке (рисунок слева).
Примечание. За направление магнитного поля может быть также принято направление, совпадающее с направлением силы, которая действует на северный полюс магнитной стрелки, помещенной в данную точку. Так как оба полюса магнитной стрелки лежат в близких точках поля, то силы, действующее на оба полюса, равны друг другу. Следовательно, на магнитную стрелку действует пара сил, поворачивающая ее так, чтобы ось стрелки, соединяющая южный полюс с северным, совпадала с направлением поля.
Рамкой с током можно воспользоваться также и для количественного описания магнитного поля.
Определение 3.
Магнитным моментом
плоского контура с током называется
физическая величина, равная 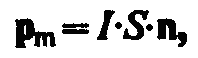 где S — площадь поверхности контура (рамки), n —
единичный вектор нормали к поверхности
рамки.
где S — площадь поверхности контура (рамки), n —
единичный вектор нормали к поверхности
рамки.
Примечание. Направление рm совпадает с направлением положительной нормали.
Если в данную точку магнитного поля помещать рамки с различными магнитными моментами, то на них действуют различные вращающие моменты, однако отношение Мmax/рm (Мmax— максимальный вращающий момент) для всех контуров будет одинаковым!
И, следовательно, данное отношение может служить характеристикой магнитного поля!
Определение 4.
Магнитной индукцией магнитного поля называется физическая величина, равная отношению максимального вращающего момента, действующего на плоский контур с током, к магнитному моменту этого контура, то есть,
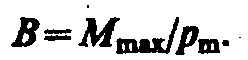
Так как магнитное поле является силовым, то его, по аналогии с электрическим, изображают с помощью линий магнитной индукции — линий, касательные к которым в каждой точке совпадают с направлением вектора В.
Примечание. Линии магнитной индукции можно «проявить» с помощью железных опилок, намагничивающихся в исследуемом поле и ведущих себя подобно маленьким магнитным стрелкам.
Линии магнитной индукции всегда замкнуты и охватывают проводники с током. Этим они отличаются от линий напряженности электростатического поля, которые являются разомкнутыми.
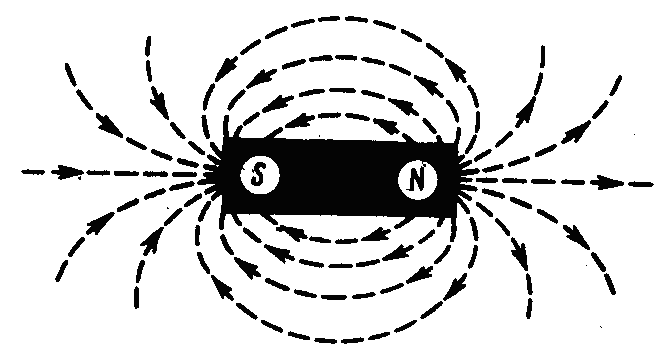
На рисунке слева изображены линии магнитной индукции полосового магнита; они выходят из северного полюса и входят в южный, но «замыкаются» на бесконечности!
Примечание. опыты показали, что, разрезая магнит на части, его полюсы разделить нельзя. Это означает, что, в отличие от электрических зарядов, свободные магнитные «заряды» не существуют!.
Поле в веществе.
Согласно предположению французского физика А. Ампера (1775—1836), в любом теле существуют микроскопические токи, обусловленные движением электронов в атомах и молекулах.
Эти микротоки создают свое магнитное поле. И если вблизи какого-то тела поместить проводник с током (макроток), то под действием его магнитного поля микротоки во всех атомах будут ориентироваться определенным образом, усиливая внешнее магнитное поле . макротока.
Вектор магнитной индукции В характеризует результирующее магнитное поле, создаваемое всеми макро- и микротоками.
Магнитное поле макротоков описывается, так называемым, вектором напряженности Н.
Резюме.
1.Силовой
характеристикой магнитного поля в
вакууме является вектор напряжённости
магнитного поля –  .
.
2.Силовой
характеристикой магнитного поля в
веществе является вектор индукции
магнитного поля –  .
.
3. Связь между
напряжённостью и индукцие магнитного
поля даётся, так называемым, материальным
соотношением 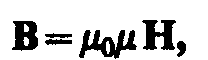 где 0 — магнитная постоянная, — безразмерная величина — магнитная
проницаемость среды, показывающая,
во сколько раз магнитное поле макротоков Н усиливается за счет поля микротоков
среды.
где 0 — магнитная постоянная, — безразмерная величина — магнитная
проницаемость среды, показывающая,
во сколько раз магнитное поле макротоков Н усиливается за счет поля микротоков
среды.
Примечание. Сравнивая векторные характеристики электростатического (Е и D) и магнитного (В и Н) полей, укажем, что аналогом вектора напряженности электростатического поля Е является вектор напряженности Н магнитного поля. Аналогом вектора электрического смещения D является вектор магнитной индукции В, так как векторы D и В зависят от свойств среды.
2. Закон Био — Савара — Лапласа.
Магнитное поле постоянных токов различной формы изучалось французскими учеными Ж.Био (1774—1862) и Ф.Саваром (1791—1841). Результаты этих опытов были обобщены выдающимся французским математиком и физиком П.Лапласом.
З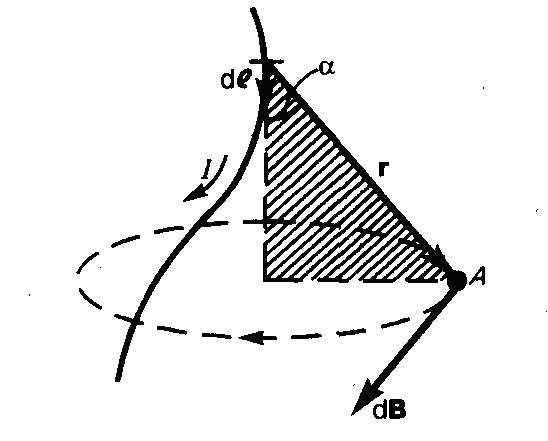 акон
Био — Савара — Лапласа для проводника с током I,
элемент dl которого создает в некоторой точке т.А (рисунок слева) индукцию поля dB, записывается в виде
акон
Био — Савара — Лапласа для проводника с током I,
элемент dl которого создает в некоторой точке т.А (рисунок слева) индукцию поля dB, записывается в виде
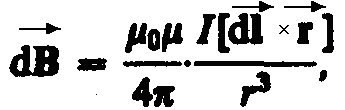 (1)
(1)
где dl — вектор, совпадающий по направлению с током, r — радиус-вектор, проведенный из элемента dl проводника в точку т.А поля.
Направление dB перпендикулярно плоскости векторов  и
и 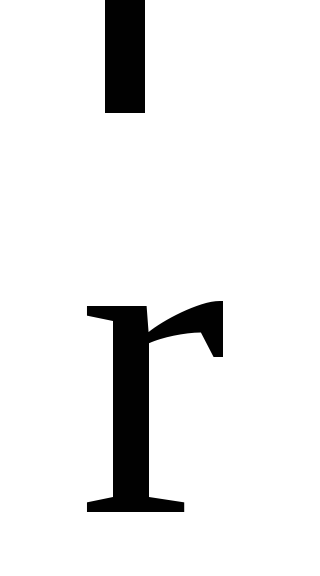 ,
и совпадает с касательной к линии
магнитной индукции.
,
и совпадает с касательной к линии
магнитной индукции.
Примечание.Это направление может быть найдено по «правилу правого винта». Направление вращения головки винта дает направление dB, если поступательное движение винта соответствует направлению тока в элементе.
Модуль вектора dB определяется выражением
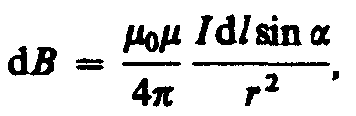
где — угол между векторами dl и r.
Для магнитного поля, как и для электрического, справедлив принцип суперпозиции.
Магнитная индукция результирующего поля, создаваемого несколькими токами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током в отдельности:
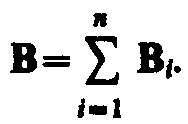
3. Закон Ампера, взаимодействие параллельных токов.
Обобщая результаты исследования действия магнитного поля на различные проводники с током, французский физик Ампер установил, что сила dF, с которой магнитное поле действует на элемент проводника dl с током, находящегося в магнитном поле, равна
 (1)
(1)
где d l—векторный элемент с током, В — вектор магнитной индукции.
Направление вектора силы взаимодействия – dF может быть найдено по определению векторного произведения векторов.
Примечание. Направление вектора dF может быть найдено по правилу левой руки. Если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток.
Модуль силы Ампера вычисляется по формуле
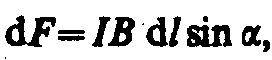 (2)
(2)
где — угол между векторами dl и В.
Рассмотрим два бесконечных прямолинейных параллельных тока I1 и I2, расстояние между которыми равно R.
Согласно закону Ампера сила взаимодействия двух элементарных токов (элементов длины – dl) будет равна
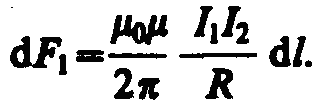 (3)
(3)
Знак плюс в формуле (3) соответствует притяжению, минус – отталкиванию.
Собственно знак определяется взаимной ориентацией токов в проводниках,
Два параллельных тока одинакового направления притягиваются друг к другу с силой, определяемой выражением (3).
Если токи имеют противоположные направления, то между ними действует сила отталкивания, определяемая формулой (3).
Примечание. Силовое взаимодействие параллельных токов используется в современных
обрабатывающих технологиях автомобильного производства («Ford
Motor Comp», США, «Volkswagen», Германия), а также в создании
оборудования для внешнего бесконтактного удаления вмятин в
автомобильных кузовах («Beulentechnik AG», Швейцария, Австралия).
9.2. Закон Био-Савара- Лапласа и его применение к расчету полей прямого и кругового токов.
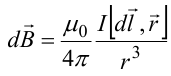
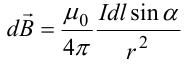
Направление вектора dB определяется правилом правого винта, которое заключается в
следующем: буравчик с правым винтом (штопор) нужно вращать от вектора dl к вектору r по
кратчайшему пути, тогда на правление движения острия бу равчика rпокажет ориентацию вектора dB .
Магнитное поле прямого тока
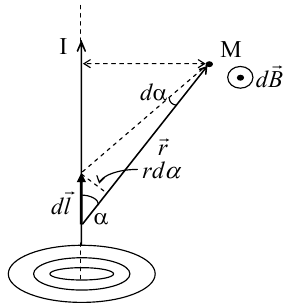 Рассчитаем,
используя закон Био-Савара-Лапласа,
магнит ное поле, создаваемое бесконечным
прямым проводником с то ком, в точке М,
отстоящей на расстоянии а от проводника.
Рассчитаем,
используя закон Био-Савара-Лапласа,
магнит ное поле, создаваемое бесконечным
прямым проводником с то ком, в точке М,
отстоящей на расстоянии а от проводника.
Выделим элемент проводника dl. Пусть элемент dl виден из точки М под малым углом dα. Положение точки М относительно элемента dl определяется вектором r. Из
рис. видно, что выполняются следующие соотношения
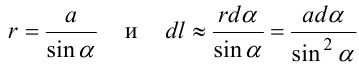
Используя закон Био-Савара-Лапласа, запишем индукцию магнитного поля, создаваемого элементом тока dl в точке М
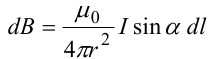
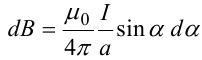
Для того, чтобы найти индукцию магнитного поля, создаваемого всем проводом, нужно, используя принцип суперпозиции, найти сумму векторов dBi от всех элементов dli.
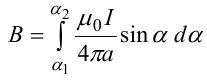
В случае бесконечного прямого тока α1=0 и α2=π, тогда
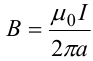
В общем случае индукция магнитного поля, создаваемого прямым проводником с ток конечной длины равна
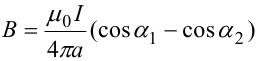
odmin
Магнитное поле на оси кругового витка с током.
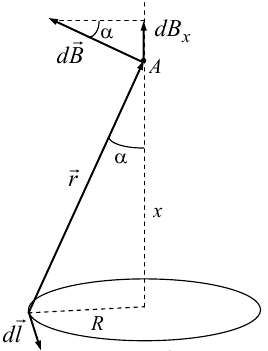 Возьмем
на оси кругового витка точку А, отстоящую
от плоскости витка на расстоянии х.
Выберем ось х вдоль оси витка. Выделим
на витке с током элемент тока dl. Оче
видно, что при суммировании векторов
dB от всех элементов витка горизонтальные
составляющие векторов dB взаимно
компенсируются, а вертикальные
составляющие (dBx) складываются скалярно.
Тогда индукция магнитного поля в точке
А будет
Возьмем
на оси кругового витка точку А, отстоящую
от плоскости витка на расстоянии х.
Выберем ось х вдоль оси витка. Выделим
на витке с током элемент тока dl. Оче
видно, что при суммировании векторов
dB от всех элементов витка горизонтальные
составляющие векторов dB взаимно
компенсируются, а вертикальные
составляющие (dBx) складываются скалярно.
Тогда индукция магнитного поля в точке
А будет
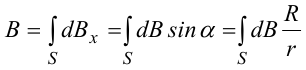
здесь S − длина витка, R − его радиус.
Согласно закону Био-Савара-Лапласа
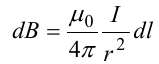
(угол между векторами r и dl равен π/2).
Окончательно
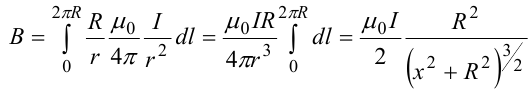
10.1. Закон полного тока (теорема о циркуляции вектора магнитной индукции).
В случае нескольких токов вrсилу принципа суперпозиции
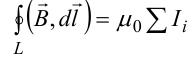
применение к расчету полей соленоида
10.2. Применение к расчету поля соленоида.
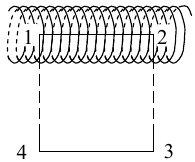 Рассмотрим
бесконечно длинный соленоид по которому
течет ток I и который имеет n витков на
единицу длины. Выберем прямоугольный
контур интегрирования 1-2-3-4. Сторона 1-2
совпадает с осью соленоида, а 3-4 удалена
на очень большое расстояние от оси. В
силу симметрии вектор B внутри соленоида
дол жен быть параллелен его оси, т.е.
Внутри соленоида магнитное поле должно
быть однородно.
Рассмотрим
бесконечно длинный соленоид по которому
течет ток I и который имеет n витков на
единицу длины. Выберем прямоугольный
контур интегрирования 1-2-3-4. Сторона 1-2
совпадает с осью соленоида, а 3-4 удалена
на очень большое расстояние от оси. В
силу симметрии вектор B внутри соленоида
дол жен быть параллелен его оси, т.е.
Внутри соленоида магнитное поле должно
быть однородно.
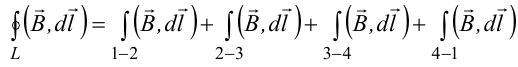
Последний интеграл в правой части равен нулю, т.к. На большом расстоянии от соленоида В=0. Второй и третий интегралы в правой части также равны нулю, т.к. для каждого элемента dl выполняется условие B ⊥ dl , а на участке 1-2, очевидно, B параллелен dl r. Тогда
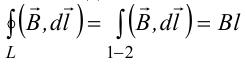
, где l − длина участка 1-2.
С другой стороны, полученное выражение должно быть пропорционально сумме токов, охватываемых контуром 1-2-3-4. Рассматриваемый контур охватывает nl витков, в
каждом из которых течет ток I, тогда
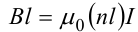
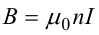
Откуда
10.3. Поле тороида.
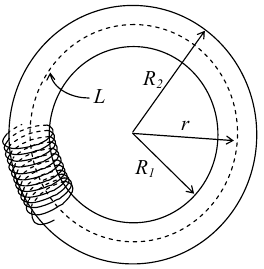 Пусть
мы имеем тороид (”бублик”) с плотно
намотанными на него N витками тонкого
провода с током I. Пусть R1 и R2 − внешний
и внутренний радиусы то роида. Найдем
индукцию магнитного поля на средней
линии тороида, т.е. на окружности радиуса
r=(R1+R2)/2.
Пусть
мы имеем тороид (”бублик”) с плотно
намотанными на него N витками тонкого
провода с током I. Пусть R1 и R2 − внешний
и внутренний радиусы то роида. Найдем
индукцию магнитного поля на средней
линии тороида, т.е. на окружности радиуса
r=(R1+R2)/2.
В качестве контура интегрирования L выберем саму среднюю линию. В силу симметрии вектор индукции магнитного поля B в каждой точке контура L должен быть направлен по касательной к этому контуру и быть постоянным по модулю. Выбранный нами контур охватывает все N витков.
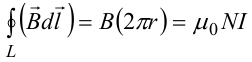
Откуда
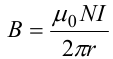
1. 3. Закон Био-Савара-Лапласа и его применение
Французские ученые Био и Савар в 1820 г. провели экспериментальное исследование магнитных полей токов, текущих по тонким проводам различной формы. Лаплас проанализировал полученные результаты и нашел, что поле любого тока может быть вычислено как векторная сумма (суперпозиция) полей, создаваемых отдельными элементарными участками токов.
| | (5) |
Для магнитной индукции поля, создаваемого элементом dl тока I в некоторой точке А , была получена формула, которая носит название закона Био-Савара-Лапласа в дифференциальной форме
| | (6) |
где
I – сила тока в проводнике; dl –
участок проводника с током, направленный
по оси элемента тока; 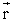 –
радиус–вектор, проведенный от элемента
проводника
–
радиус–вектор, проведенный от элемента
проводника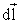 в
точку А; μ0 –
магнитная постоянная. Вектор
в
точку А; μ0 –
магнитная постоянная. Вектор  направлен
перпендикулярно к плоскости, проходящей
через
направлен
перпендикулярно к плоскости, проходящей
через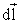 и
и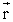 .
Его направление определяется по правилу
буравчика: направление вращения ручки
буравчика совпадает с направлением
.
Его направление определяется по правилу
буравчика: направление вращения ручки
буравчика совпадает с направлением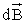 ,
если поступательное движение буравчика
соответствует направлению тока в
проводнике (рис. 12).
,
если поступательное движение буравчика
соответствует направлению тока в
проводнике (рис. 12). Рис.
12 Модуль вектора
Рис.
12 Модуль вектора определяется
как:
определяется
как:
| | (7) |
где
α — угол между элементом с током и
радиус-вектором. Закон Био-Савара-Лапласа
(6) в сочетании с принципом суперпозиции
(5) позволяет произвести расчет магнитной
индукции некоторых конкретных полей. 1.
Применение закона Био-Савара-Лапласа
к расчету поля прямого тока Рассмотрим
поле, созданное тонким прямым проводником
с током бесконечной длины (рис. 13).
Значение индукции магнитного поля  в
точке А, созданного элементом
в
точке А, созданного элементом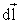 тока
I , определяется формулой (6) или в скалярном
выражении – формулой (7). Для того,
чтобы определить индукцию магнитного
поля
тока
I , определяется формулой (6) или в скалярном
выражении – формулой (7). Для того,
чтобы определить индукцию магнитного
поля ,
нужно сложить согласно (5) все элементарные
векторы
,
нужно сложить согласно (5) все элементарные
векторы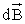 .
.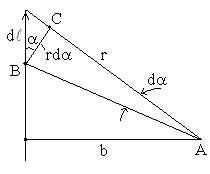 рис.
13 Все векторы
рис.
13 Все векторы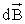 в
точке А имеют одинаковое направление
(см. рис. 13), поэтому сложение векторов
можно заменить сложением их модулей.
Сделаем некоторые преобразования:
в
точке А имеют одинаковое направление
(см. рис. 13), поэтому сложение векторов
можно заменить сложением их модулей.
Сделаем некоторые преобразования: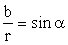 ;
;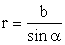 Учитывая,
что угол dα , под которым виден участок
проводника dl из точки А, мал, можно
принять АВ ≈ АС; ВС = rdα, тогда
Учитывая,
что угол dα , под которым виден участок
проводника dl из точки А, мал, можно
принять АВ ≈ АС; ВС = rdα, тогда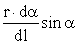
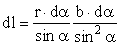 . Подставим
полученные выражения для r и dl в формулу
(7), а затем в (5).
. Подставим
полученные выражения для r и dl в формулу
(7), а затем в (5).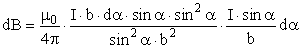
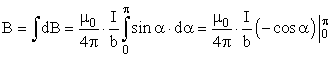 Угол
α для всех элементов бесконечного
прямого тока изменяется в пределах от
0 до π.В итоге:
Угол
α для всех элементов бесконечного
прямого тока изменяется в пределах от
0 до π.В итоге:
| | (8) |
2.
Расчет магнитного поля кругового
тока Поле
в центре кругового тока. По
круговому контуру радиуса R течет ток
I, требуется найти индукцию магнитного
поля в центре контура, в точке О (рис.
14).  рис.
14 Рассмотрим элемент контура
рис.
14 Рассмотрим элемент контура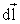 с
током I. Созданная им элементарная
индукция будет равна:
с
током I. Созданная им элементарная
индукция будет равна: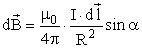 ,
где α = π/2, значит sin π = 1. Направление
векторов
,
где α = π/2, значит sin π = 1. Направление
векторов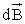 от
всех элементов
от
всех элементов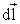 кругового
тока совпадает с направлением положительной
нормали к контуру. После интегрирования
получим:
кругового
тока совпадает с направлением положительной
нормали к контуру. После интегрирования
получим:
| | (9) |
1. 4. Циркуляция вектора индукции магнитного поля по замкнутому контуру. Вихревой характер магнитного поля
В
электростатическом поле циркуляция
вектора 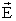 по
замкнутому контуру равна нулю.
по
замкнутому контуру равна нулю.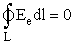 Найдем
циркуляцию вектора
Найдем
циркуляцию вектора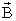 по
замкнутому контуру в магнитном поле.
Рассмотрим магнитное поле прямого тока
(рис. 16). Ток уходит за чертеж. Линии
индукции охватывают контур, их направление
связано с направлением тока правилом
правого винта (буравчика).
по
замкнутому контуру в магнитном поле.
Рассмотрим магнитное поле прямого тока
(рис. 16). Ток уходит за чертеж. Линии
индукции охватывают контур, их направление
связано с направлением тока правилом
правого винта (буравчика).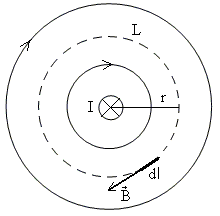 Рис.
16 Выберем мысленно замкнутый контур
в форме окружности радиуса r. На рисунке
16 он изображен штриховой линией. Вычислим
циркуляцию вектора
Рис.
16 Выберем мысленно замкнутый контур
в форме окружности радиуса r. На рисунке
16 он изображен штриховой линией. Вычислим
циркуляцию вектора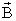 по
выбранному контуру. Значение индукции
магнитного поля прямого тока на расстоянии
r от него задается уравнением (9):
по
выбранному контуру. Значение индукции
магнитного поля прямого тока на расстоянии
r от него задается уравнением (9):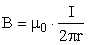 .
Выражение для циркуляции вектора
.
Выражение для циркуляции вектора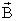 по
контуру запишем в виде:
по
контуру запишем в виде: , так
как вектор
, так
как вектор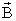 в
каждой точке линии магнитной индукции
направлен по касательной, угол между
элементом контура dl и
в
каждой точке линии магнитной индукции
направлен по касательной, угол между
элементом контура dl и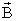 равен
нулю, тогда косинус угла между этими
векторами равен единице. Подстановка
уравнения (9) приводит к
выражению:
равен
нулю, тогда косинус угла между этими
векторами равен единице. Подстановка
уравнения (9) приводит к
выражению: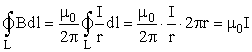
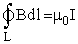 Циркуляция
вектора
Циркуляция
вектора по
замкнутому контуру равна произведению
магнитной постоянной μ0 на
ток, охватываемый контуром. Если контур
охватывает несколько токов (рис. 17), то
берется алгебраическая сумма токов.
по
замкнутому контуру равна произведению
магнитной постоянной μ0 на
ток, охватываемый контуром. Если контур
охватывает несколько токов (рис. 17), то
берется алгебраическая сумма токов. 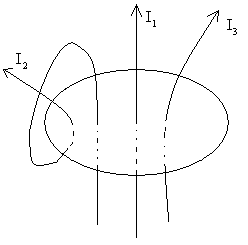 рис.
3.17
рис.
3.17
| | (13) |
Это
выражение носит название закона полного
тока в вакууме. Для поля в веществе
учитываются еще молекулярные
токи. Положительным считается ток,
направление которого связано с
направлением обхода контура правилом
правого винта, ток противоположного
направления считается отрицательным.
Например для системы токов, изображенных
на рис. 17 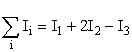 Сравнивая
выражения для циркуляции векторов
Сравнивая
выражения для циркуляции векторов и
и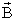 видим,
что электростатическое и магнитное
поля имеют принципиальное различие.
Циркуляция вектора
видим,
что электростатическое и магнитное
поля имеют принципиальное различие.
Циркуляция вектора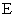 всегда
равна нулю, электростатическое поле
потенциальное. Циркуляция вектора
всегда
равна нулю, электростатическое поле
потенциальное. Циркуляция вектора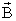 не
равна нулю, такое поле называется
вихревым. Теорема о циркуляции
вектора
не
равна нулю, такое поле называется
вихревым. Теорема о циркуляции
вектора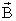 имеет
в учении о магнитном поле такое же
значение, как теорема Остроградского-Гаусса
в электростатике. Она позволяет находить
магнитную индукцию поля, не применяя
закон Био-Савара-Лапласа.
^
имеет
в учении о магнитном поле такое же
значение, как теорема Остроградского-Гаусса
в электростатике. Она позволяет находить
магнитную индукцию поля, не применяя
закон Био-Савара-Лапласа.
^
§ 110. Закон Био — Савара — Лапласа и его применение к расчету магнитного поля
Магнитное поле постоянных токов различной формы изучалось французскими учеными Ж. Био (1774—1862) и Ф. Саваром (1791 —1841). Результаты этих опытов были обобщены выдающимся французским математиком и физиком П. Лапласом.
Закон Био — Савара — Лапласа для проводника с током I, элемент которого dl создает в некоторой точке А (рис. 164) индукцию поля dB, записывается в виде
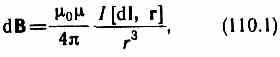
где dl — вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током, r — радиус-вектор,
179
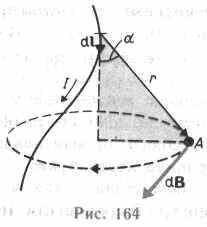
проведенный из элемента dl проводника в точку А поля, r — модуль радиуса-вектора г. Направление dB перпендикулярно dl и r, т. е. перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление вращения головки винта дает направление dB, если поступательное движение винта соответствует направлению тока в элементе.
Модуль вектора dB определяется выражением
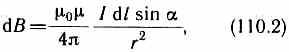
где а — угол между векторами dl и г.
Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности:

Расчет характеристик магнитного поля (В и Н) по приведенным формулам в общем случае довольно сложен. Однако если распределение тока имеет определенную симметрию, то применение закона Био — Савара — Лапласа совместно с принципом суперпозиции позволяет довольно просто рассчитать конкретные поля. Рассмотрим два примера.
1. Магнитное поле прямого тока — тока, текущего по тонкому прямому про-
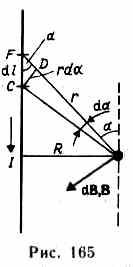
воду бесконечной длины (рис. 165). В произвольной точке А, удаленной от оси проводника на расстояние R, векторы dB от всех элементов тока имеют одинаковое направление, перпендикулярное плоскости чертежа («к нам»). Поэтому сложение векторов dB можно заменить сложением их модулей. В качестве постоянной интегрирования выберем угол а (угол между векторами dl и r), выразив через него все остальные величины. Из рис. 165 следует, что
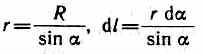
(радиус дуги CD вследствие малости dl равен r, и угол FDC по этой же причине можно считать прямым). Подставив эти выражения в (110.2), получим, что магнитная индукция, создаваемая одним элементом проводника, равна
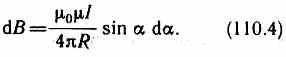
Так как угол а для всех элементов прямого тока изменяется в пределах от 0 до я, то, согласно (110.3) и (110.4),
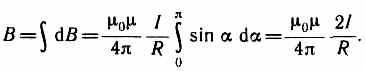
Следовательно, магнитная индукция поля прямого тока
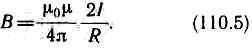
2. Магнитное поле в центре кругового проводника с током (рис. 166). Как следует из рисунка, все элементы кругового проводника с током создают в центре магнитное поле одинакового направления — вдоль нормали от витка.
180
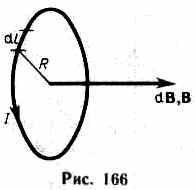
Поэтому сложение векторов dB можно заменить сложением их модулей. Так как все элементы проводника перпендикулярны радиусу-вектору (sin=1) и расстояние всех элементов проводника до центра кругового тока одинаково и равно R, то, согласно (110.2),
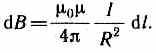
Тогда
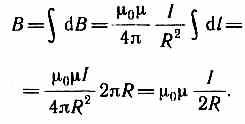
Следовательно, магнитная индукция поля в центре кругового проводника с током
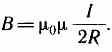
20.Закон Био-Савара-Лапласа и его применение к расчету магнитных полей. Принцип суперпозиции
Закон Био-Савара-Лапласа и его применение к расчету полей. В 1820г французские ученые Ж.Био и Ф.Савар установили зависимость силы, действующей на магнитную стрелку, от расстояния до провода, по которому протекал постоянный ток. Они выяснили:
1. во всех случаях индукция магнитного поля пропорциональна силе тока в проводнике;
2. величина индукции магнитного поля зависит от формы и размеров проводника с током;
3. индукция магнитного поля в произвольной точке зависит от расположения этой точки по отношению к проводнику с током.
Био и Савар пытались получить общий закон, который позволял бы вычислить магнитную индукцию в любой точке поля, создаваемого током, текущим по проводнику любой формы. В этом им помог Лаплас, который предложил применить принцип суперпозиции, т.е. принцип независимого действия полей, создаваемых отдельными участками проводника с током. Лаплас обобщил результаты опытов Био-Савара, установив закон, позволяющий найти вектор индукции магнитного поля, создаваемого малым линейным проводником с постоянным током (элементом тока), который был назван законом Био-Савара-Лапласа:
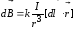 ,
,
1)магнитная индукция поля прямого тока
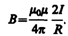
2)магнитная индукция поля в центре кругового проводника с током
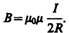
21. Закон Ампера. Взаимодействие параллельных токов
Зако́н Ампе́ра — закон взаимодействия электрических токов. Впервые был установленАндре Мари Ампером в 1820 для постоянного тока. Из закона Ампера следует, что параллельные проводники с электрическими токами, текущими в одном направлении, притягиваются, а в противоположных — отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током.
F = BIlsina (a — угол между направлением тока и индукцией магнитного поля ). Эта формула закона Ампера оказывается справедливой для прямолинейного проводника и однородного поля.
Сила Ампера направлена перпендикулярно плоскости, в которой лежат векторы dl и B.
Для определения направления силы, действующей на проводник с током, помещенный в магнитное поле, применяется правило левой руки.:
если
расположить левую руку так, чтобы вектор 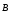 входил в ладонь, а четыре сложенных
вместе пальца были направлены вдоль
тока, то отставленный в сторону большой
палец укажет направление силы
входил в ладонь, а четыре сложенных
вместе пальца были направлены вдоль
тока, то отставленный в сторону большой
палец укажет направление силы
два параллельных тока одинакового направления притягиваются друг к другу с силой
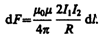
Если токи имеют противоположные направления, то, используя правило левой руки, можно показать, что между ними действует сила отталкивания,определяемая формулой
22. Действие магнитного поля на движущийся заряд. Сила Лоренца. Движение заряженных частиц в магнитном поле. Ускорители заряженных частиц.
Опыт показывает, что магнитное поле действует не только на проводники с током, но и на отдельные заряды, движущиеся в магнитном поле.
Сила,
с которой магнитное поле действует на
движущийся со скоростью 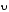 зарядQ называется силой
Лоренца и
выражается формулой:
зарядQ называется силой
Лоренца и
выражается формулой:
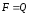
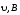 . (10)
. (10)
Модуль силы Лоренца:
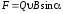 ,
,
Направление
силы Лоренца определяется по
правилу левой руки:
если ладонь левой руки расположить так,
чтобы в нее входил вектор 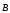 ,
а четыре вытянутых пальца направить
вдоль вектора
,
а четыре вытянутых пальца направить
вдоль вектора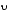 ,
то отогнутый большой палец покажет
направление силы, действующей на
положительный заряд
На отрицательный
заряд сила действует в противоположном
направлении.
,
то отогнутый большой палец покажет
направление силы, действующей на
положительный заряд
На отрицательный
заряд сила действует в противоположном
направлении.
Движение заряженных частиц в магнитном поле:
1. Частица движется в магнитном поле вдоль линий магнитной индукции.
Запишем
выражение для силы Лоренца: 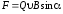 .
При
.
При  или
или 
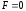 .
.
Вывод: частица движется равномерно и прямолинейно.
2. Частица
движется в магнитном поле перпендикулярно
вектору магнитной индукции 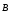 .
.
Вывод:
период вращения частицы в однородном
магнитном поле определяется только
величиной, обратной удельному заряду 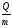 частицы, и магнитной индукции поля, но
не зависит от ее скорости. На этом
основано действие циклических ускорителей
заряженных частиц.
частицы, и магнитной индукции поля, но
не зависит от ее скорости. На этом
основано действие циклических ускорителей
заряженных частиц.
3.
Частица движется в магнитном поле под
углом к вектору 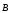 .
.
Движение частицы можно представить в виде суперпозиции:
1. равномерного прямолинейного движения вдоль поля со скоростью
=  ;
;
Вывод: при последовательном соединении конденсаторов суммируются величины, обратные емкостям. Результирующая емкость всегда меньше наименьшей емкости, используемой в батарее.
2. равномерного движения со скоростью
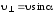
по окружности в плоскости, перпендикулярной полю.


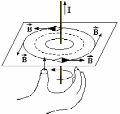 Рис.1.2 Силовые линии
Рис.1.2 Силовые линии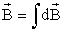
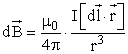
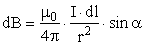 ,
,