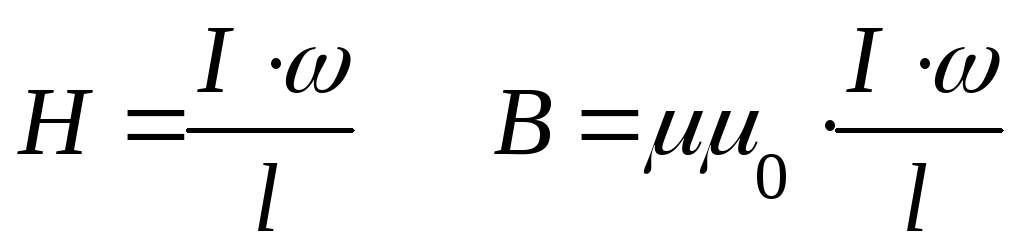Закон полного тока | Электрикам


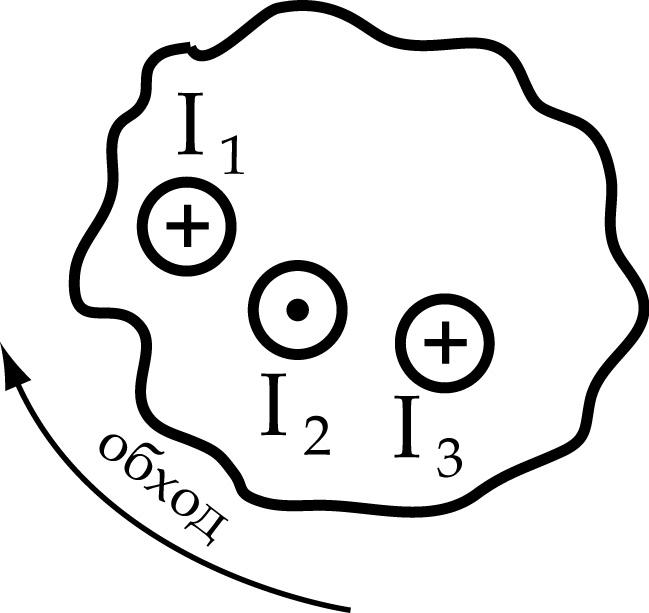
Полным током называют алгебраическую сумму токов, пронизывающих поверхность, ограниченную замкнутым контуром.
Приняв произвольно выбранное направление обхода какого-либо контура в магнитном поле за положительное, будем считать токи, пронизывающие этот контур, положительными, если их направление совпадает с направлением поступательного движения буравчика, рукоятка которого вращается в положительном направлении обхода контура.
Например, на рис. 1 ток I1— положительный, а ток I2 —


отрицательный. Полный ток, пронизывающий контур,


Рис 1. Токи, пронизывающие поверхность, ограниченную контуром
Рис 2. Напряженность магнитного поля провода с током
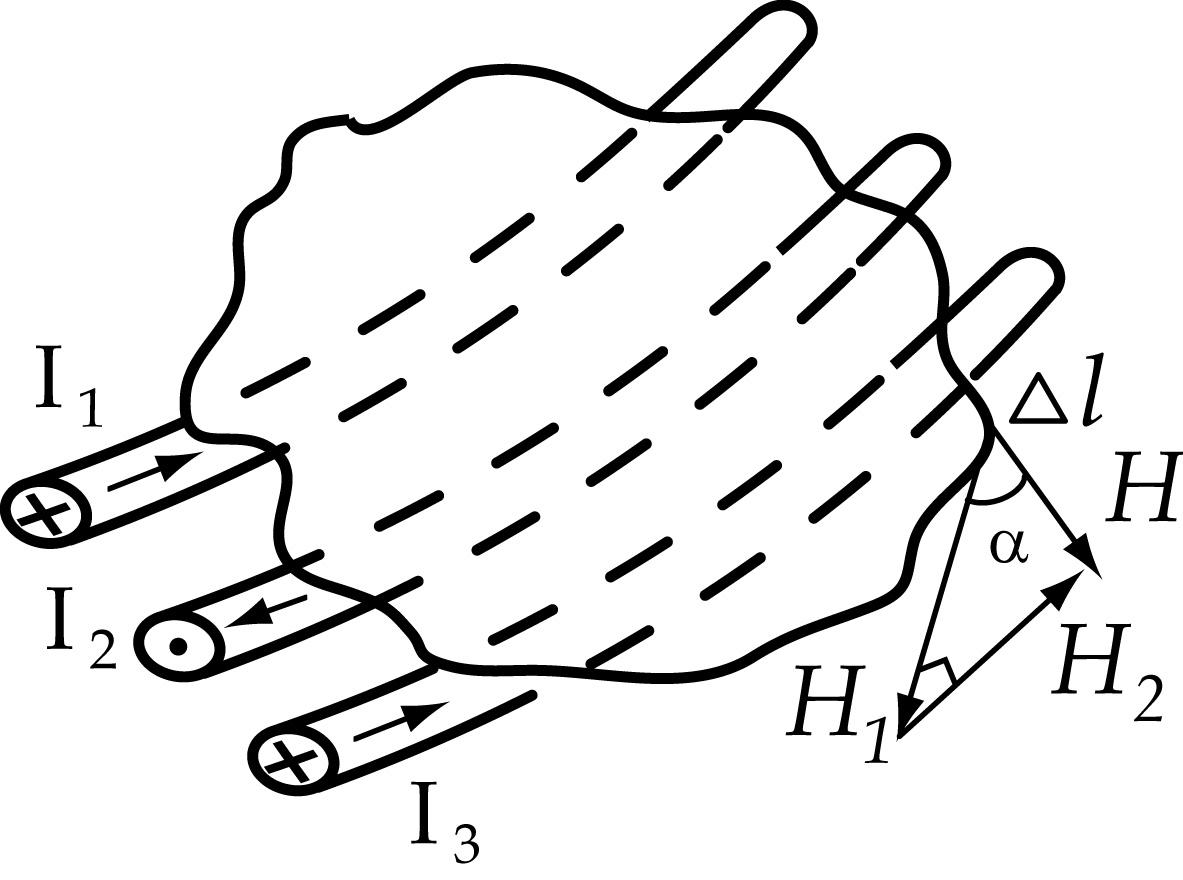
Магнитная индукция и напряженность поля в отдельных точках, расположенных на контуре, могут иметь или различные или одинаковые значения Допустим, что в точке а вектор индукции и пропорциональный ему вектор напряженности поля образует с элементом длины контура dl угол α. При этом HL = H cosα будет представлять собой касательную к контуру составляющую вектора напряженности магнитного поля. Магнитное напряжение HLdl на элементарном участке контура dl положительно, если направление вектора НL совпадает c выбранным направлением обхода контура, в противном случае оно будет отрицательным.
По закону полного тока МДС F вдоль контура равна полному току, который проходит сквозь поверхность ограниченную этим контуром, т. е.

 или
или 

Если контур совпадает с магнитной линией, то направление вектора напряженности поля совпадает с касательной к контуру и, следовательно, HL=H.
Если, кроме того, индукция B и напряжённость поля H во всех точках контура одинаковы, как вследствие симметрии при обходе вдоль контура рис. 5.17, то в формуле (5 23
напряженность можно вынести за знак суммирования и написать:


где знак 
 обозначает сумму элементарных длин замкнутого контура, т. е. длину этого контура L; следовательно в этом случае
обозначает сумму элементарных длин замкнутого контура, т. е. длину этого контура L; следовательно в этом случае


Выражение 
 иногда называют циркуляцией вектора напряженности магнитного поля по замкнутому контуру. В соответствии с этим изменяют и формулировку закона полного тока.
иногда называют циркуляцией вектора напряженности магнитного поля по замкнутому контуру. В соответствии с этим изменяют и формулировку закона полного тока.
Закон полного тока для магнитного поля: физический смысл, формулы
В электрических цепях всегда присутствует магнитное поле, которое оказывает электромагнитное взаимодействие с токами этих цепей. Данный фактор учитывается при расчетах цепей, а закон полного тока для магнитного поля является инструментом для подобных вычислений.
Если поднести магнитную стрелку к проводнику, по которому течёт ток, её положение изменится. Это говорит о наличии вокруг проводника кроме электрического ещё и магнитного поля. В результате многочисленных исследований электромагнитных явлений установлено, что существует взаимное влияние полей, имеющих электрическую и магнитную природу.
Физический смысл закона
Рассмотрим упрощённый вариант влияния магнитной индукции на электрическое поле. Для этого представим себе два параллельных проводника, по которым циркулируют постоянные токи, например, I1 и I2. Вблизи этих проводников образуется поле, которое мысленно можно ограничить неким контуром L – воображаемой замкнутой фигурой, плоскость которой пересекает потоки движущихся зарядов.
В пределах плоскости, охватываемой контуром L, формируется магнитное поле, напряжённость которого распределена в соответствии с направлениями токов. При этом циркуляция вектора магнитного поля в плоскости замкнутого контура прямо пропорциональна сумме токов, пронзающих данный контур. Полный электрический ток равен векторной сумме его составляющих:

Направления векторов I1 и I2 определяется по правилу буравчика.
Приведённые выше рассуждения можно рассматривать в качестве примера изображающего упрощённую модель частного случая рассматриваемого закона. В действительности же, процессы взаимного влияния магнитных и электрических полей намного сложнее, и они описываются интегральными и дифференциальными уравнениями Максвелла.
Упрощенный подход
Выразить закон в дифференциальном представлении довольно сложно. Потребуется вводить дополнительные компоненты. Необходимо учитывать влияние молекулярных токов. Наличие вихревых токов является причиной образования магнитного вихревого поля в пределах контура.
Вектор электрического смещения сравним с вектором напряжённости присутствующего магнитного поля H. При этом Ориентация вектора смещения зависит от быстроты изменения магнитной индукции.
Для упрощения вычислений на практике часто пользуются формулами закона для магнитного поля полных токов, представленных в виде суммирования предельно малых участков контура, с учётом влияния вихревых полей. При реализации этого метода контур мысленно разбивают на бесконечно малые отрезки. На этих отрезках проводники считаются прямолинейными, а магнитное поле на таких участках контура считают однородным.
На одном дискретном участке вектор напряженности Um определяется по формуле: Um= HL×ΔL, где HL– циркуляция вектора напряжённости на участке ΔL контура L. Тогда суммарная напряжённость UL вдоль всего контура вычисляется по формуле:
Закон в интегральном представлении
Рассмотрим бесконечно прямой проводник, по которому циркулирует электрический ток, образующий поле, ограниченное контуром в виде окружности. Плоскость, пронизывающая проводник, – это круг, очерчённый линией данной окружности (см. рис. 1).
 Рис. 1. Поле бесконечно прямого тока
Рис. 1. Поле бесконечно прямого токаВоспользуемся методом разбиения контура на мизерные участки dl (элементарные векторы длины контура). Пусть φ – угол между векторами dl и B. В нашем случае, при суммировании отрезков, вектор индукции B поворачивается так, что он очерчивает круг, то есть угол φ
Из теоремы Остроградского-Гаусса вытекает формула:

Учитывая, что cos φ = 1,

следовательно:

Данная формула – постулат, подтверждённый экспериментально. Согласно этому постулату, циркуляция вектора B по окружности, то есть по замкнутому контуру, равна μ
Ориентация вектора dB определяется путём применения правила буравчика. Это направление всегда перпендикулярно вектору плотности. Если проводников будет несколько (например, N), тогда

Каждый ток, с учётом знака, необходимо учитывать такое количество раз, которое соответствует числу его охватов контуром.
Ток берётся со знаком «+», если он по направлению обхода образует правовинтовую систему. При этом, отрицательным считается ток противоположного направления.
Заметим, что формула справедлива только для вакуума. В обычных условиях необходимо учитывать проницаемость среды.
Если ток распределён в пространстве (произвольный ток), тогда

где S – натянутая на контур поверхность, j – объёмная плотность тока. С учётом последнего выражения, формулу полного тока в вакууме можно записать:


Отсюда вытекает:
- Закон справедлив не только для бесконечно прямолинейного проводника, но и для контуров, произвольной конфигурации.
- Циркуляция вектора магнитной индукции B сориентированного вдоль магнитных линий, всегда отлична от нуля.
- Ненулевая циркуляция свидетельствует о том, что магнитное поле прямолинейного, бесконечно длинного проводника не потенциально. Такое поле называют вихревым, либо соленоидным.
Влияние среды
На результат взаимодействия магнитных потоков и постоянных токов влияет среда. Вещества обладают магнитной проницаемостью в потоке вектора индукции, что вносит коррективы на взаимодействие магнитной среды с токами проводимости. В однородной изотопной среде, где значение вектора электромагнитной индукции одинаково во всех точках, векторы B и H связаны между собой следующим соотношением:

где H — напряжённость магнитного поля, символом μ обозначена магнитная проницаемость.
Носители электрических зарядов создают собственные микротоки. Циркуляция вектора, характеризующего электростатическое поле, всегда нулевая. Поэтому электростатические поля, в отличие от магнитных, являются потенциальными.
Вектор B отображает результирующее значение полей макро- и микротоков. Линии электростатической индукции всегда остаются замкнутыми, в том числе и на положительных зарядах.
 Рис. 3. Закон полного тока в веществе
Рис. 3. Закон полного тока в веществеДля полей, которые действуют в среде, состоящей из разных веществ, необходимо учитывать микротоки, характерные именно для конкретных структур, образующих данную среду.
Утверждение, изложенное выше, верно для полей соленоидов или любой другой структуры, обладающей свойствами конечной магнитной проницаемости.
Торойд
В электротехнике часто приходится иметь дело с катушками разных видов и размеров. Катушка, образованная витками намотанными на сердечник тороидальной формы (в виде бублика), называется тороидом. Важными характеристиками сердечника тора являются его радиусы — внутренний (R
Поле внутри соленоида на расстоянии r от центра равно:

Выводы
На основании изложенного, приходим к заключению:
- Закон полного тока устанавливает зависимость между напряжённостью магнитного поля и перемещением в этом поле электрических зарядов.
- Действие закона распространяется на все среды, при допустимых плотностях тока.
- Закон также выполняется в полях постоянных магнитов.
При вычислениях не имеет значения, какую формулу мы используем – суть закона остаётся неизменной: он выражает взаимодействия, которые происходят между токами и создаваемыми ими магнитными полями, пронизывающими замкнутый контур.
Выводы закона учитываются при конструировании электромагнитных устройств. Наличие завихрений в электромагнитных полях приводит к снижению КПД. Кроме того, вихревые поля негативно влияют на работоспособность электронных элементов, расположенных в зоне их действий.
Конструкторы электротехнических приборов стремятся свести к минимуму таких влияний. Например, вместо обычных соленоидов применяют тороидальные катушки, за пределами которых отсутствуют электромагнитные поля.
Закон полного тока
Дата публикации: .
Категория: Электротехника.
Пусть произвольная замкнутая линия l пронизывает проводник с током (рисунок 1), то есть они сцепляются друг с другом как два звена цепи. Вокруг проводника возникает магнитное поле.

Рисунок 1. Закон полного тока
Построим вектор напряженности H, создаваемой током в точке А, расположенной на линии l. Если линия охватывает несколько проводников с током, то для каждого тока строятся векторы напряженности в данной точке линии. Складывая геометрически отдельные векторы напряженности, находим вектор результирующей напряженности магнитного поля.
Вектор результирующей напряженности H в общем случае образует с элементом длины Δl угол α. Поэтому продольная или тангенциальная составляющая Hl результирующей напряженности H будет:
Hl = H × cos α.
Если разбить замкнутую линию на n элементов длины и сложить произведения длин всех элементов на тангенциальные составляющие результирующей напряженности в этих элементах, получим следующую сумму:

Эту сумму можно представить так:

где знак  означает сумму от k = 1 до k = n.
означает сумму от k = 1 до k = n.
В теоретической электротехнике доказывается, что указанная сумма равна алгебраической сумме токов, сцепляющихся с контуром суммирования подобно тому, как сцепляются между собой два смежных звена цепи.
Следовательно, можно записать так:

Эта формулировка называется законом полного тока. Для случая, когда контур многократно пронизывает один и тот же виток, как, например, при наличии обмотки с числом витков w, полный ток будет:


Если замкнутый контур суммирования совпадает с магнитной линией, то вектор напряженности в любой точке контура будет направлен по касательной к элементу длины Δl.
В этом случае


и закон полного тока принимает вид:


Если значение напряженности для всех точек контура при этом одинаково, а сумма Δl по контуру равна l, то формула закона полного тока запишется так:


Закон полного тока является основным законом при расчете магнитных цепей и дает возможность в некоторых случаях легко определять напряженность поля.
Например, применяя закон полного тока для определения напряженности на расстоянии a от прямолинейного проводника с током, имеем:


l = 2 × π × a .
Поэтому
H × 2 × π × a = I ,
откуда


  |
| Рисунок 2. К определению напряженности поля катушки, намотанной на кольцо |
Чтобы определить напряженность поля внутри катушки, намотанной на кольцо (рисунок 2), воспользуемся опять законом полного тока. Контуром здесь является окружность радиуса r. Контур пронизывает w витков с токами одного направления:
H × 2 × π × r = I × w .
Обозначая длину средней линии кольца через l = 2 × π × r , получаем:
H × l = I × w ,
откуда


Таким образом, напряженность поля катушки пропорциональна произведению числа ампер на число витков или числу ампер-витков. I × w называется намагничивающей силой и обозначается буквой F. Так как w – число отвлеченное, то намагничивающая сила измеряется в амперах.
Магнитная индукция внутри катушки будет:


Если площадь поперечного сечения кольца по всей длине одинакова и равна S, то, зная магнитную индукцию B, можно определить магнитный поток Ф:


Эту же формулу можно представить в ином виде:


По своему строению эта формула напоминает формулу Ома. Выше было указано, что произведение I × w называется намагничивающей силой. Выражение 
 стоящее в знаменателе, называется магнитным сопротивлением и обозначается буквой Rм:
стоящее в знаменателе, называется магнитным сопротивлением и обозначается буквой Rм:

Из этой формулы видно, что магнитное сопротивление пропорционально длине пути и обратно пропорционально сечению материала, по которому проходит магнитный поток.
Таким образом, магнитный поток Ф пропорционален намагничивающей силе F и обратно пропорционален магнитному сопротивлению Rм:




Рисунок 3. Закон полного тока для вакуума
Источник: Кузнецов М.И., «Основы электротехники» — 9-е издание, исправленное — Москва: Высшая школа, 1964 — 560с.
Закон полного тока простыми словами
Содержание статьи:
Суть закона
Рассматриваемый закон, применимый в магнитных цепях, определяет следующую количественную связь между входящими в него составляющими. Циркуляция вектора магнитного поля по замкнутому контуру пропорциональна сумме токов, пронизывающих его. Чтобы понять физический смысл закона полного тока – потребуется ознакомиться с графическим представлением описываемых им процессов.
Из рисунка видно, что около двух проводников с протекающими по ним токами I1 и I2 образуется поле, ограниченное контуром L. Оно вводится как мысленно представляемая замкнутая фигура, плоскость которой пронизывают проводники с движущимися зарядами. Простыми словами этот закон можно выразить так. При наличии нескольких потоков электричества через мысленное представляемую поверхность, охватываемую контуром L, в ее пределах формируется магнитное поле с заданным распределением напряженности.
За положительное направление движения вектора в соответствии с законом для контура магнитной цепи выбирается ход часовой стрелки. Оно также является мысленно представляемым.
Такое определение создаваемого токами вихревого поля предполагает, что направление каждого из токов может быть произвольным.
Для справки! Вводимую полевую структуру и описывающий ее аппарат следует отличать от циркуляции электростатического вектора «Е», который при обходе контура всегда равен нулю. Вследствие этого такое поле относится к потенциальным структурам. Циркуляция же вектора «В» магнитного поля никогда не бывает нулевой. Именно поэтому оно называется «вихревым».
Основные понятия
В соответствии с рассматриваемым законом для расчета магнитных полей применяется следующий упрощенный подход. Полный ток представляется в виде суммы нескольких составляющих, протекающих через поверхность, охватываемую замкнутым контуром L. Теоретические выкладки могут быть представлены следующим образом:
- Полный электрический поток, пронизывающих конур Σ I – это векторная сумма I1 и I2.
- В рассматриваемом примере для его определения используется формула:
ΣI = I1- I2 (минус перед вторым слагаемым означает, что направления токов противоположны). - Они, в свою очередь, определяются по известному в электротехнике закону (правилу) буравчика.
Напряженность магнитного поля вдоль контура вычисляется на основании полученных выкладок по специальным методикам. Для ее нахождения придется проинтегрировать этот параметр по L, используя уравнение Максвелла, представленное в одной из форм.Оно может быть применено и в дифференциальной форме, но это несколько усложнит выкладки.
Упрощенный подход в интегральном виде
Если воспользоваться дифференциальным представлением – выразить закон полного тока в упрощенном виде будет очень сложно (в этом случае в него приходится вводить дополнительные компоненты). Добавим к этому, что магнитное вихревое поле, создаваемое движущимся в пределах контура токами, определяется в этом случае с учетом тока смещения, зависящего от скорости изменения электрической индукции.
Поэтому на практике в ТОЭ большей популярностью пользуется представление формул для полных токов в виде суммирования микроскопически малых отрезков контура с создаваемыми в них вихревыми полями. Этот подход предполагает применение уравнения Максвелла в интегральной форме. При его реализации контур разбивается на мелкие отрезки, в первом приближении считающиеся прямолинейными (согласно закону предполагается, что магнитное поле однородно). Эта величина, обозначаемая как Um для одного дискретного участка длиной ΔL магнитного поля, действующего в вакууме, определяется так:
Um= HL*ΔL
Суммарная напряженность вдоль полного контура L, представленная кратко в интегральном виде, находится по следующей формуле:
UL= Σ HL*ΔL.
Закон полного тока для вакуума
В окончательном виде, оформленном по всем правилам интегрирования, закон полного тока выглядит так. Циркуляция вектора «В» по замкнутому контуру может быть представлена как произведение магнитной постоянной m на сумму токов:
Интеграл от B по dL = интегралу от Bl по dL= m Σ In
где n – это обще число проводников с разнонаправленными токами, охватываемыми мысленно представляемым контуром L произвольной формы.
Каждый ток учитывается в этой формуле столько раз, сколько он полностью охватывается данным контуром.
На окончательный вид полученных выкладок для закона полного тока большое влияние оказывает среда, в которой действует наведенная электромагнитная сила (поле).
Влияние среды
Рассмотренные отношения для закона токов и полей, действующих не в вакууме, а в магнитной среде, приобретают несколько иной вид. В этом случае помимо основных токовых составляющих вводится понятие микроскопических токов, возникающих в магнетике, например, или в любом подобном ему материале.
Нужное соотношение в полном виде выводится из теоремы о векторной циркуляции магнитной индукции B. Простым языком она выражается в следующем виде. Суммарное значение вектора B при интегрировании по выбранному контуру равно сумме охватываемых им макро токов, умноженной на коэффициент магнитной постоянной.
В итоге формула для «В» в веществе определяется выражением:
Интеграл от B по dL = интегралу от Bl по dL= m(I+I1)
где: dL – дискретный элемент контура, направленный вдоль его обхода, Вl– составляющая в направлении касательной в произвольной точке,бI и I1 – ток проводимости и микроскопический (молекулярный) ток.
Если поле действует в среде, состоящей из произвольных материалов – должны учитываться микроскопические токи, характерные именно для этих структур.
Эти выкладки также верны для поля, создаваемого в соленоиде или в любой другой среде, обладающей конечной магнитной проницаемостью.
Для справки
В самой полной и объемлющей системе измерений СГС напряженность магнитного поля представляется в эрстедах (Э). В другой действующей системе (СИ) она выражается в амперах на один метр (А/метр). Сегодня эрстед постепенно вытесняется более удобной в работе единицей – ампером на метр. При переводе результатов измерений или расчетов из СИ в СГС используется следующее соотношение:
1 Э = 1000/(4π) А/м ≈ 79,5775 Ампер/метр.
В заключительной части обзора отметим, что независимо от того, какая используется формулировка закона полных токов – суть его остается неизменной. Своими словами это можно представить так: он выражает отношения между токами, пронизывающими данный контур и создаваемыми в веществе магнитными полями.
Напоследок рекомендуем просмотреть полезное видео по теме статьи:
Источник
Вероятно эти статьи вам также будут интересны:
Закон полного тока для магнитного поля: формулы и определение
Знакомый многим предмет под названием «Электротехника» содержит в своей программе ряд основополагающих законов, определяющих принципы физического взаимодействия для магнитного поля. Они распространяют свое действие на различные элементы электротехнических устройств, а также на входящие в их состав структуры и среды. Физика происходящих в них процессов касается таких базовых понятий, как потоки электричества и поля. Закон полного тока устанавливает зависимость между перемещением электрических зарядов и создаваемым им магнитным полем (точнее – его напряженностью). Современная наука утверждает, что его применение распространяется практически на все среды.
Суть закона
Рассматриваемый закон, применимый в магнитных цепях, определяет следующую количественную связь между входящими в него составляющими. Циркуляция вектора магнитного поля по замкнутому контуру пропорциональна сумме токов, пронизывающих его. Чтобы понять физический смысл закона полного тока – потребуется ознакомиться с графическим представлением описываемых им процессов.

Из рисунка видно, что около двух проводников с протекающими по ним токами I1 и I2 образуется поле, ограниченное контуром L. Оно вводится как мысленно представляемая замкнутая фигура, плоскость которой пронизывают проводники с движущимися зарядами. Простыми словами этот закон можно выразить так. При наличии нескольких потоков электричества через мысленное представляемую поверхность, охватываемую контуром L, в ее пределах формируется магнитное поле с заданным распределением напряженности.
За положительное направление движения вектора в соответствии с законом для контура магнитной цепи выбирается ход часовой стрелки. Оно также является мысленно представляемым.
Такое определение создаваемого токами вихревого поля предполагает, что направление каждого из токов может быть произвольным.
Для справки! Вводимую полевую структуру и описывающий ее аппарат следует отличать от циркуляции электростатического вектора «Е», который при обходе контура всегда равен нулю. Вследствие этого такое поле относится к потенциальным структурам. Циркуляция же вектора «В» магнитного поля никогда не бывает нулевой. Именно поэтому оно называется «вихревым».
Основные понятия
В соответствии с рассматриваемым законом для расчета магнитных полей применяется следующий упрощенный подход. Полный ток представляется в виде суммы нескольких составляющих, протекающих через поверхность, охватываемую замкнутым контуром L. Теоретические выкладки могут быть представлены следующим образом:
- Полный электрический поток, пронизывающих конур Σ I – это векторная сумма I1 и I2.
- В рассматриваемом примере для его определения используется формула:
ΣI = I1- I2 (минус перед вторым слагаемым означает, что направления токов противоположны). - Они, в свою очередь, определяются по известному в электротехнике закону (правилу) буравчика.
Напряженность магнитного поля вдоль контура вычисляется на основании полученных выкладок по специальным методикам. Для ее нахождения придется проинтегрировать этот параметр по L, используя уравнение Максвелла, представленное в одной из форм.Оно может быть применено и в дифференциальной форме, но это несколько усложнит выкладки.
Упрощенный подход в интегральном виде
Если воспользоваться дифференциальным представлением – выразить закон полного тока в упрощенном виде будет очень сложно (в этом случае в него приходится вводить дополнительные компоненты). Добавим к этому, что магнитное вихревое поле, создаваемое движущимся в пределах контура токами, определяется в этом случае с учетом тока смещения, зависящего от скорости изменения электрической индукции.
Поэтому на практике в ТОЭ большей популярностью пользуется представление формул для полных токов в виде суммирования микроскопически малых отрезков контура с создаваемыми в них вихревыми полями. Этот подход предполагает применение уравнения Максвелла в интегральной форме. При его реализации контур разбивается на мелкие отрезки, в первом приближении считающиеся прямолинейными (согласно закону предполагается, что магнитное поле однородно). Эта величина, обозначаемая как Um для одного дискретного участка длиной ΔL магнитного поля, действующего в вакууме, определяется так:
Um= HL*ΔL
Суммарная напряженность вдоль полного контура L, представленная кратко в интегральном виде, находится по следующей формуле:
UL= Σ HL*ΔL.
Закон полного тока для вакуума
В окончательном виде, оформленном по всем правилам интегрирования, закон полного тока выглядит так. Циркуляция вектора «В» по замкнутому контуру может быть представлена как произведение магнитной постоянной m на сумму токов:
Интеграл от B по dL = интегралу от Bl по dL= m Σ In
где n – это обще число проводников с разнонаправленными токами, охватываемыми мысленно представляемым контуром L произвольной формы.
Каждый ток учитывается в этой формуле столько раз, сколько он полностью охватывается данным контуром.
На окончательный вид полученных выкладок для закона полного тока большое влияние оказывает среда, в которой действует наведенная электромагнитная сила (поле).
Влияние среды
Рассмотренные отношения для закона токов и полей, действующих не в вакууме, а в магнитной среде, приобретают несколько иной вид. В этом случае помимо основных токовых составляющих вводится понятие микроскопических токов, возникающих в магнетике, например, или в любом подобном ему материале.
Нужное соотношение в полном виде выводится из теоремы о векторной циркуляции магнитной индукции B. Простым языком она выражается в следующем виде. Суммарное значение вектора B при интегрировании по выбранному контуру равно сумме охватываемых им макро токов, умноженной на коэффициент магнитной постоянной.
В итоге формула для «В» в веществе определяется выражением:
Интеграл от B по dL = интегралу от Bl по dL= m(I+I1)
где: dL – дискретный элемент контура, направленный вдоль его обхода, Вl– составляющая в направлении касательной в произвольной точке,бI и I1 – ток проводимости и микроскопический (молекулярный) ток.
Если поле действует в среде, состоящей из произвольных материалов – должны учитываться микроскопические токи, характерные именно для этих структур.
Эти выкладки также верны для поля, создаваемого в соленоиде или в любой другой среде, обладающей конечной магнитной проницаемостью.
Для справки
В самой полной и объемлющей системе измерений СГС напряженность магнитного поля представляется в эрстедах (Э). В другой действующей системе (СИ) она выражается в амперах на один метр (А/метр). Сегодня эрстед постепенно вытесняется более удобной в работе единицей – ампером на метр. При переводе результатов измерений или расчетов из СИ в СГС используется следующее соотношение:
1 Э = 1000/(4π) А/м ≈ 79,5775 Ампер/метр.
В заключительной части обзора отметим, что независимо от того, какая используется формулировка закона полных токов – суть его остается неизменной. Своими словами это можно представить так: он выражает отношения между токами, пронизывающими данный контур и создаваемыми в веществе магнитными полями.
Напоследок рекомендуем просмотреть полезное видео по теме статьи:
Материалы по теме:
О законе полного тока: формула для магнитных цепей
В радиоэлектронике применяется ряд законов и постулатов для анализа, как цепей, так и устройств. Сталкиваясь с необходимостью исследования магнитных цепей, применяют закон полного тока для магнитного поля.
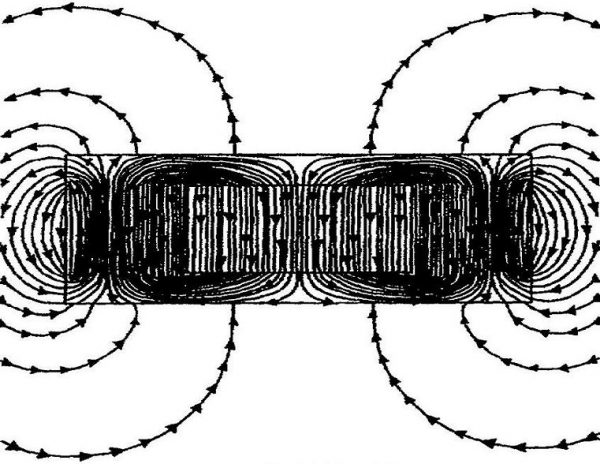
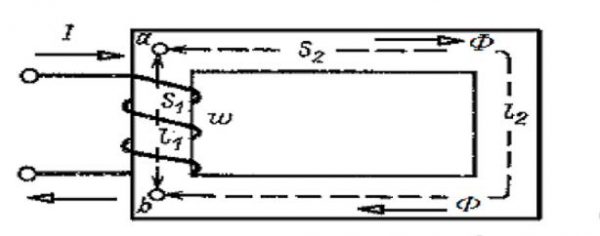
Магнитные потоки трансформатора
Суть закона полного тока
Данный постулат характеризует взаимосвязь между током электрической цепи и магнитным полем, появляющимся в связи с протеканием этого тока.
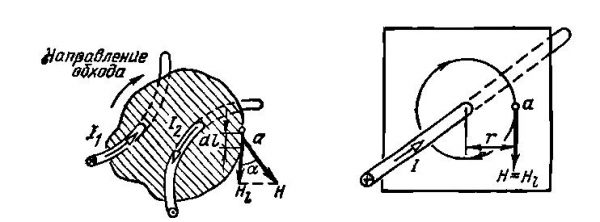
Контур с проводниками под током
Для понимания закона полного тока необходимо представить некоторое число проводников, по которым протекает электрический ток. Множество проводников охватывает некоторый контур, и, соответственно, ограничивает мнимую поверхность S, согласно картинке выше. Направление огибания контура, согласно правилу буравчика, ориентировано по ходу часовой стрелки. Поскольку множество токов является величиной дискретной, то закон полного тока определяется как связь суммарного электрического тока через закольцованный контур L и напряженности магнитного поля, сформированного этим током, и определяется по формуле:
∫LHdl=I∑, где:
- H – вектор напряженности магнитного поля;
- dl – направленный элементарный линейный участок, взятый вдоль контура;
- I∑ – суммарная сила тока.
Сущностью закона полного тока является то, что передвижение вектора напряженности магнитного поля по кольцевому контуру приравнивается сумме всех токов, которые находятся в этом контуре. Это выражение является интегральной формой закона полного тока.
Дополнительная информация. Интеграл произведения вектора напряженности магнитного поля и направленного элементарного линейного участка по кольцевому контуру называется циркуляцией вектора Н.
Если заданный контур пронизывает непрерывный пространственный поток движущихся заряженных частиц с плотностью электрического тока J, то общая величина тока, проходящего сквозь площадку, измеряется по выражению:
I∑=∫sJdS, где dS – элементарная площадка контура S.
Произведение JdS характеризует поток вектора плотности тока J, проходящего через поверхность dS.
Помимо интегральной формы, применяется дифференциальная форма закона полного тока. С целью получения дифференциальной формы выражения полного тока следует заменить интеграл по контуру L на интеграл по площади S. Поскольку теорема Стокса в векторном анализе выражается как:
∫LАdl=∫s rotАdS, то ∫LНdl=∫s rotНdS.
Объединив эти выражения с законом полного тока, в интегральной форме получается:
∫s rotНdS =∫s J∑dS.
Поскольку контур L взят произвольным образом, то интегралы в левой и правой частях выражения равны, если равны подынтегральные выражения. Исходя из этого, выражение преобразовывается в:
rotН=J∑.
Данной формулой выражается закон полного тока в дифференциальной форме.
Практическое применение в расчетах
Закон полного тока является основным законом при расчете магнитных цепей и дает возможность без особых усилий определять напряженность поля.
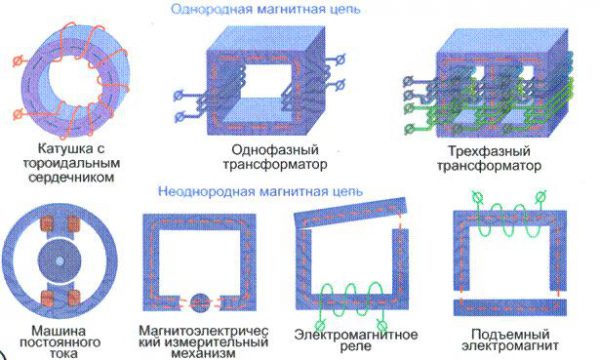
Примеры магнитных цепей
Магнитная цепь являет собой комплекс физических тел, обладающих сильно выраженными магнитными свойствами, магнитодвижущих сил и других условий, по которым смыкается магнитный поток. Магнитодвижущая сила определяется как произведение количества витков катушки на протекающий в ней электрический ток:
F=Iω, где:
- F – магнитодвижущая сила;
- ω – количество витков в катушке;
- I – электрический ток.
Подобно тому, как электродвижущая сила электрической цепи провоцирует возникновение тока, так и магнитодвижущая сила магнитной цепи вызывает магнитный поток. Направление магнитодвижущей силы в схемотехнике определяется на основании правила буравчика.
Параметры, описывающие характеристики магнитной или электрической цепи, являются тождественными. Аналогичными являются и мероприятия по расчету цепей. Постоянные токи в электрических цепях возникают благодаря электродвижущей силе. В магнитных цепях эту функцию выполняет магнитодвижущая сила обмоток. Характеристика сопротивления току в электрической цепи имеет свою аналогию в магнитной цепи в виде магнитного сопротивления.
Неразветвленная магнитная цепь
Согласно закону полного тока, выражение, описывающее процессы в магнитной цепи (рис. выше), выглядит так:
Iω=h2L1+h3L2, где:
- h2 – напряженность поля первого участка;
- h3 – напряженность поля второго участка;
- L1 – длина первого однородного участка;
- L2 – длина второго однородного участка.
Поскольку напряженность магнитного поля и магнитная индукции на первом и втором участках равны:
- h2=B1/µа1, где:
- B1 – магнитная индукция;
- µа1 – магнитная проницаемость первого участка.
- B 1=Φ/S1, где:
- Φ – магнитный поток;
- S1 – площадь поперечного сечения первого участка.
- h3=B2/µа2, где:
- B2 – магнитная индукция второго участка;
- µа2 – магнитная проницаемость второго участка.
- B 2=Φ/S2, где:
- Φ – магнитный поток;
- S2 – площадь поперечного сечения второго участка.
выражение, описывающее закон полного тока, преобразовывается в:
Iω=ΦL1/µа1S1+ ΦL2/µа2S2=ΦRм1+ΦRм2, где:
- Rм1=L1/µа1S1 – магнитное сопротивление первого участка;
- Rм2=L2/µа2S2 – магнитное сопротивление второго участка.
Проводя аналогии с электрической цепью, произведение магнитного потока на магнитное сопротивление является магнитным напряжением:
Uм2=ΦRм2=h3L2.
Если выделить из формулы магнитный поток, получается формула, представляющая собой закон Ома для магнитной цепи:
Φ= Iω/Rм1+Rм2= Iω/∑Rм.
Для магнитной цепи, не имеющей магнитодвижущей силы, выражение будет выглядеть как:
Uм=ΦRм=HL.
Аналогично электрическим цепям на магнитные цепи распространяются постулаты Кирхгофа:
- Сумма магнитных потоков, втекающих в узел, равна сумме магнитных потоков, вытекающих из узла. Выражение выглядит как ∑Φк=0;
- Сумма магнитодвижущих сил, находящихся в контуре, равна сумме падений напряжений на всех отрезках цепи, что соответствует выражению ∑Iω=∑Uм=∑HL.
Закон полного тока для магнитных цепей стоит на одном уровне с основными законами, касающимися электрических цепей. Понимание закона полного тока позволит с легкостью проводить расчет и подбор необходимых устройств, в основе работы которых лежат магнитные потоки.
Видео
Оцените статью:Закон полного тока
Магнитное поле, создаваемое током, и ток в проводнике неразрывно связаны между собой, следовательно, и величины, характеризующие магнитное поле (магнитный поток, магнитная индукция и т.д.) также связаны с током в проводнике.
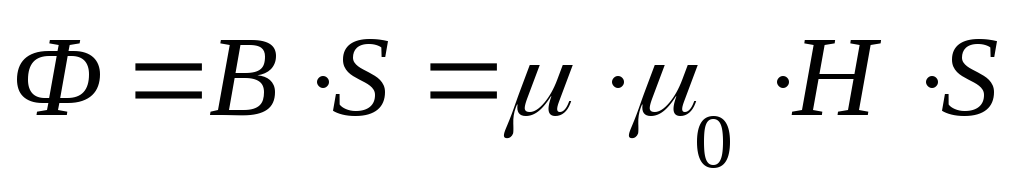
Закон полного тока и устанавливает зависимость между током в проводнике и напряженностью магнитного поля.
Полным токомназывают алгебраическую сумму токов, пронизывающих поверхность, ограниченную контуром ((I)– полный ток).
|
Если ток создает магнитное поле, направление которого совпадает с произвольно выбранным направлением обхода контура, то он берется со знаком «+», а если нет – со знаком «-» |
| Магнитное
поле во всех точках контура будет
различным и по значению
и по направлению, поэтому выделим на
контуре элементарный участок |
с
участком  угол.
Вектор Н можно разложить на две составляющие,
одна из которых совпадает с участком
угол.
Вектор Н можно разложить на две составляющие,
одна из которых совпадает с участком  ,
а вторая – перпендикулярна ему.
,
а вторая – перпендикулярна ему.
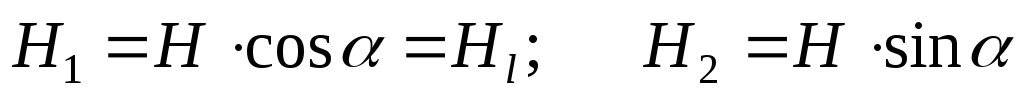
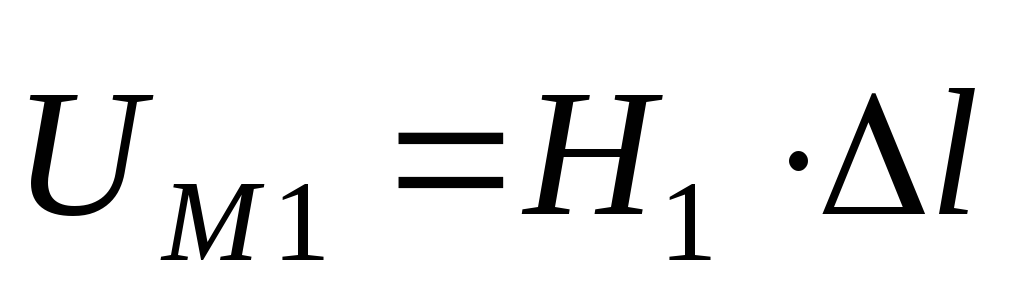
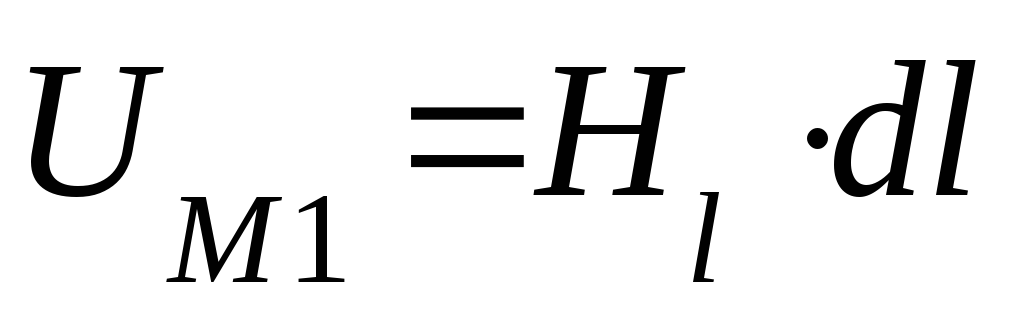
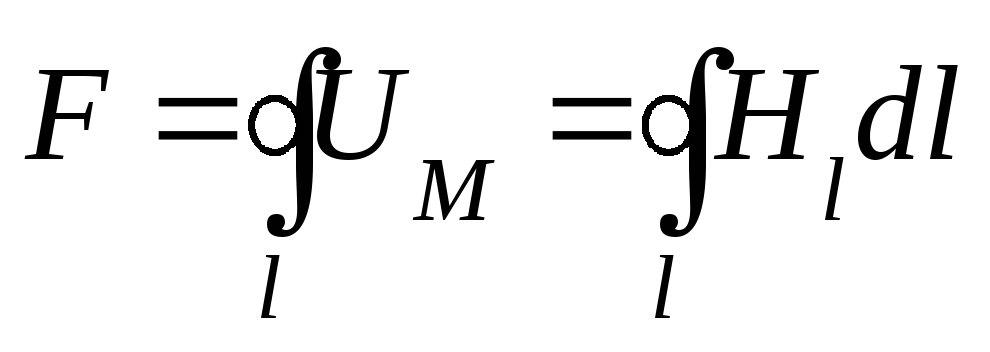
Для определения намагничивающей силы для замкнутого контура необходимо просуммировать (проинтегрировать) все магнитные напряжения, вычисленные вдоль этого контура.
Опытным путем установлено, что намагничивающая сила, вычисленная вдоль замкнутого контура, равна полному току (алгебраической сумме токов, пронизывающих поверхность, ограниченную магнитной силовой линией, по которой вычислена намагничивающая сила).
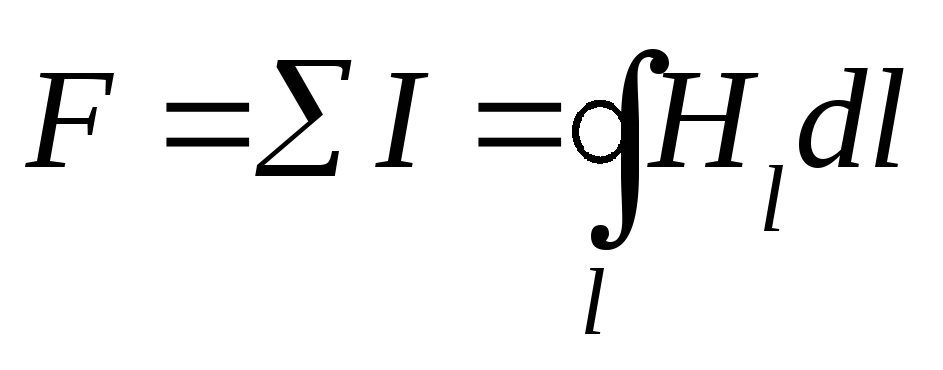
Применение закона полного тока
1. Магнитное поле вокруг прямолинейного проводника с током
| Необходимо определить напряженность поля вокруг проводника в т.А, расположенной от проводника на расстоянии х. Для этого проведем аксонометрическую окружность с радиусом х. Полный ток здесь равен току в проводнике.
|
|
Длина контура равна длине окружности, таким образом, чем дальше точка удалена от проводника, тем напряженность поля в ней будет меньше.
2. Напряженность поля внутри цилиндрического проводника
| Необходимо определить напряженность поля внутри проводника в т.А, расположенной на расстояниихот центра проводника (х<R). Плотность
тока |
проводника
одинакова, поэтому протекающий через
площадь, ограниченную окружностью с
радиусом х,
ток равен 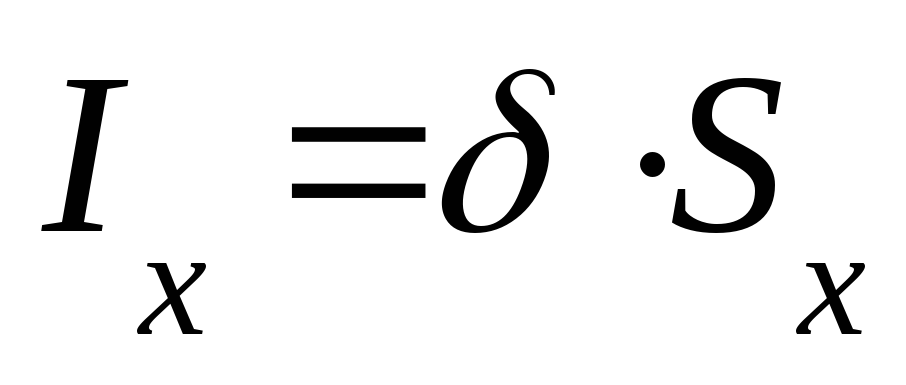 .
С другой стороны плотность тока
.
С другой стороны плотность тока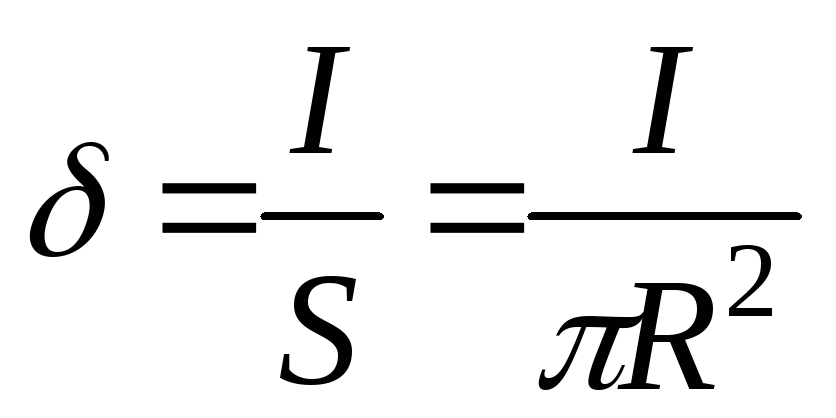 ,
а площадь, ограниченная контуром с
радиусомх:
,
а площадь, ограниченная контуром с
радиусомх: 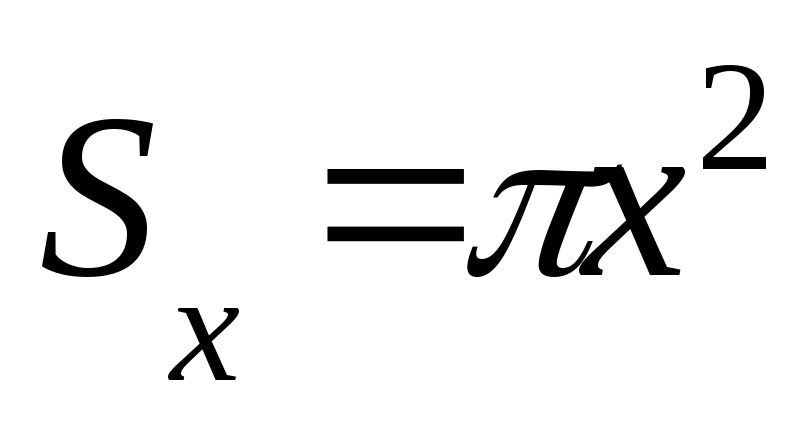 .
.
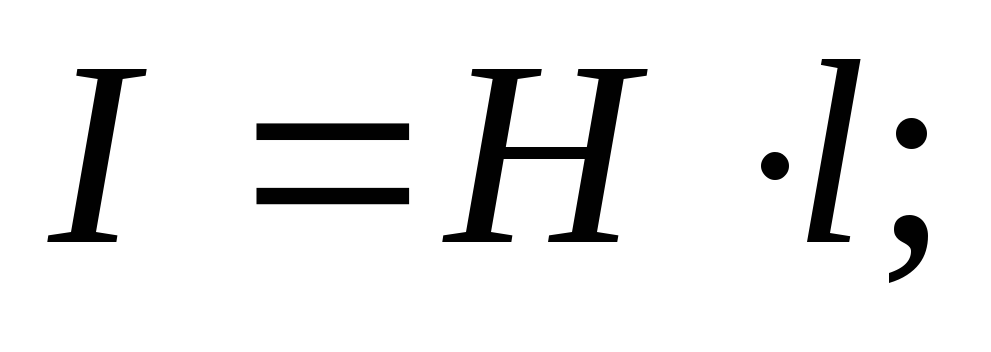 где
где 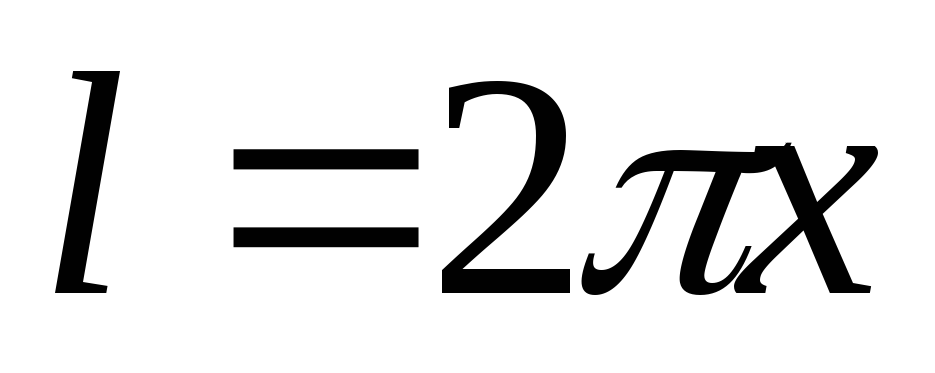
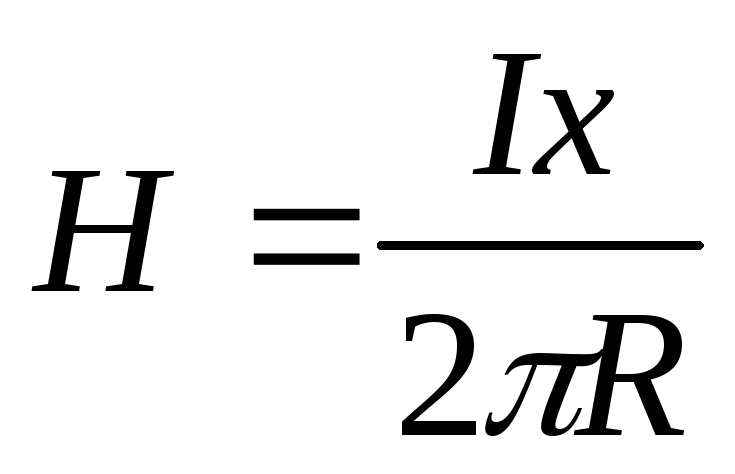
Напряженность поля внутри проводника увеличивается от нуля в центре проводника до максимального значения на его поверхности, а затем по мере удаления от поверхности проводника опять уменьшается.
| Магнитную
индукцию можно определить как |
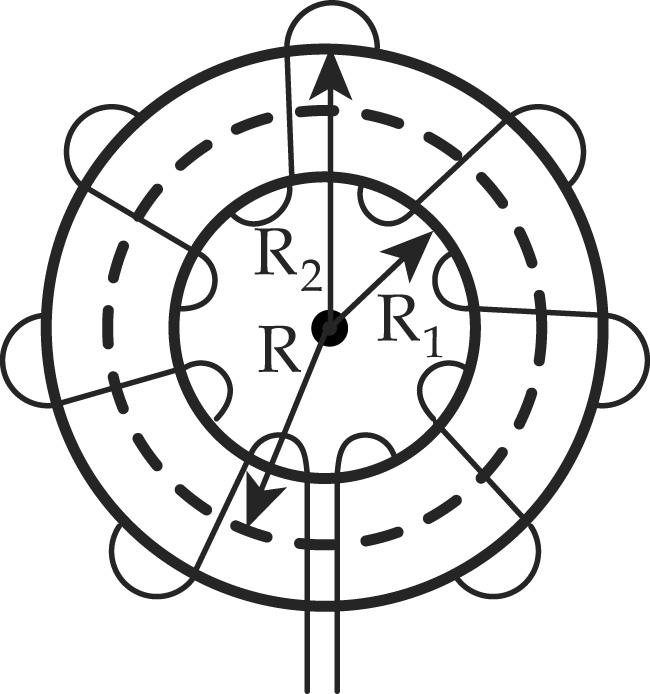
3. Магнитное поле кольцевой и цилиндрической катушек
| На
кольцевой катушке равномерно намотана
обмотка, имеющая витков. Напряженность поля внутри
сердечника на расстоянии R благодаря симметрии во всех точках
будет одинакова согласно закону
полного тока ( |
Полный
ток 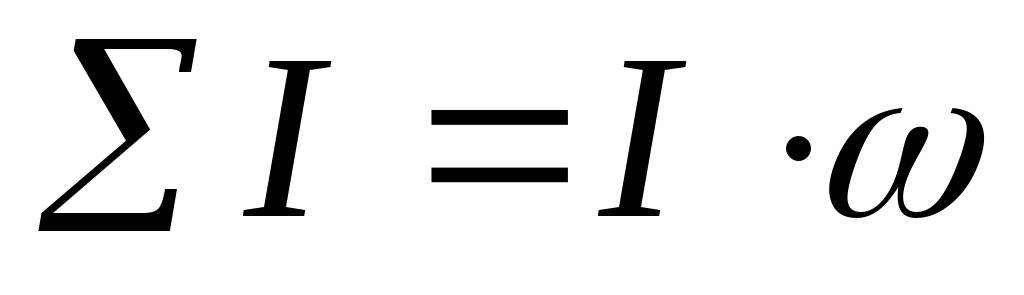 ,
где — число витков.
,
где — число витков.
 ,
тогда
,
тогда 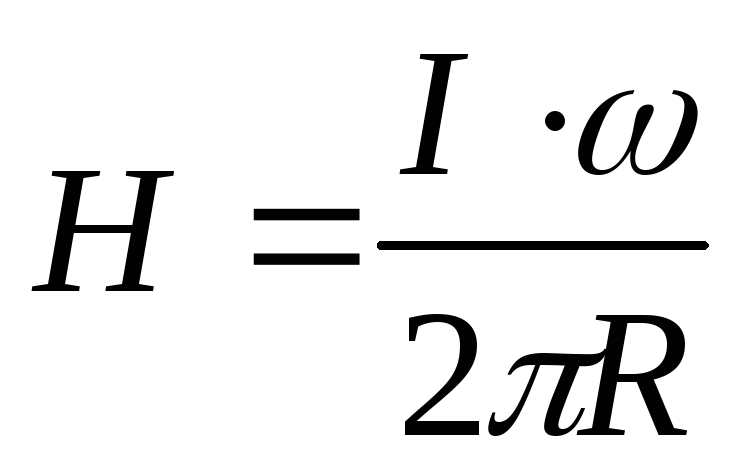
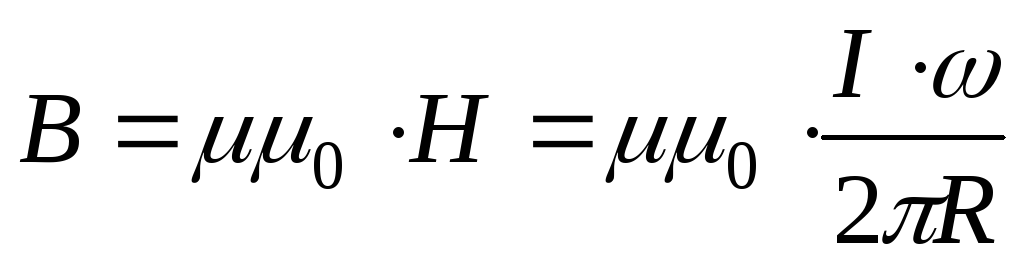
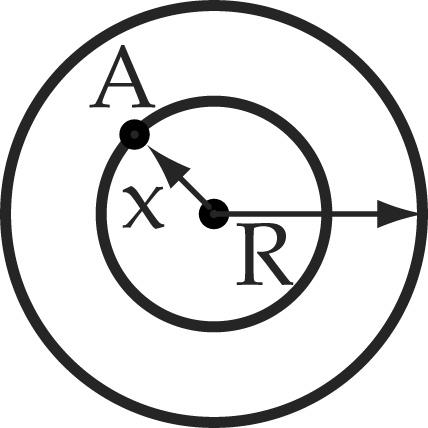
Наибольшая
напряженность и магнитная индукция
будут на внутренней поверхности кольца,
а наименьшие – на внешней поверхности
кольца. Если взять контур с радиусом 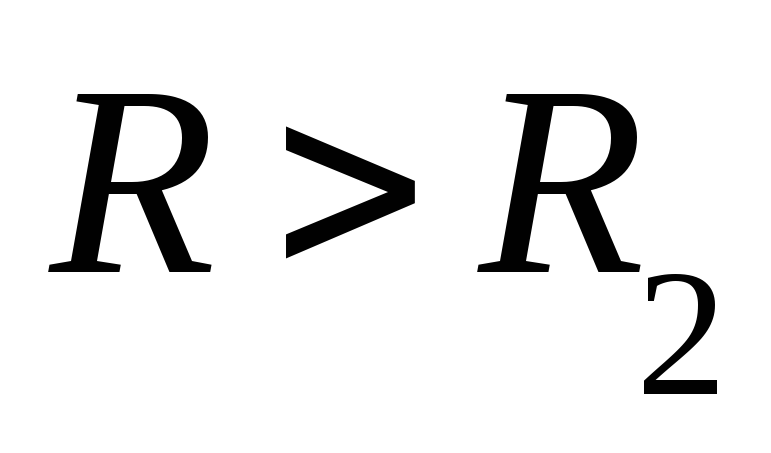 или с радиусом
или с радиусом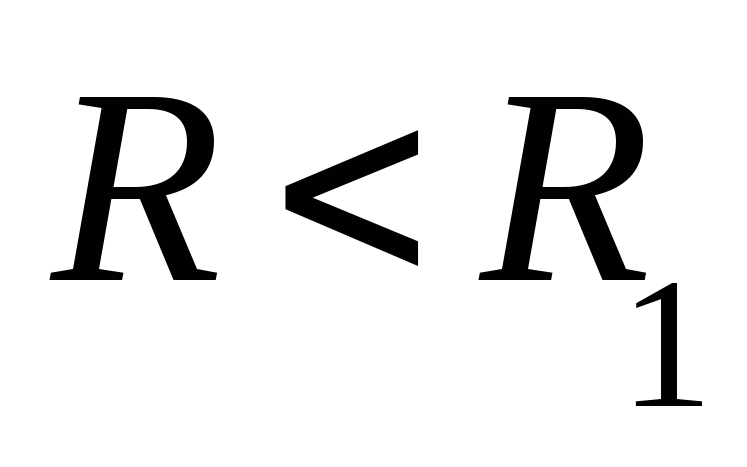 ,
то напряженность и магнитная индукция
в этих точках будут равны нулю, т.к. эти
точки не пронизываются токами.
,
то напряженность и магнитная индукция
в этих точках будут равны нулю, т.к. эти
точки не пронизываются токами.
| Цилиндрические
катушки можно рассматривать
как кольцевую с бесконечно большим
радиусом. Поэтому напряженность поля
цилиндрической катушки определяется
как: |
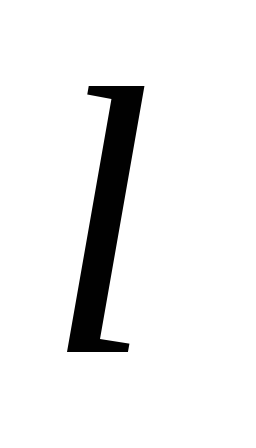 — длина катушки;
— длина катушки;
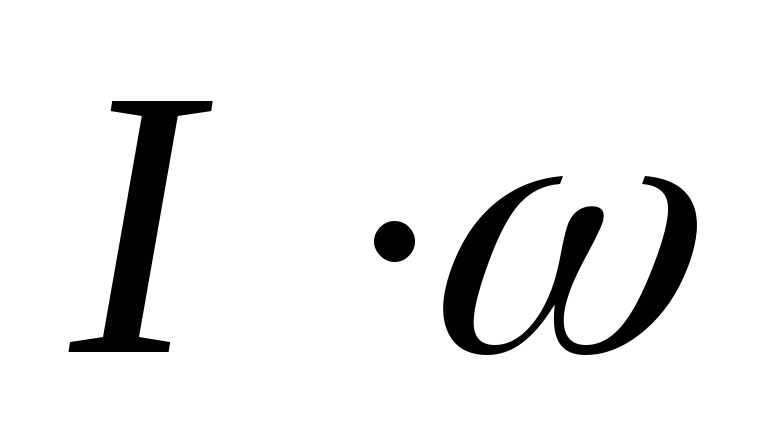 — полный ток.
— полный ток.
Сила взаимодействия двух параллельных проводников с токами
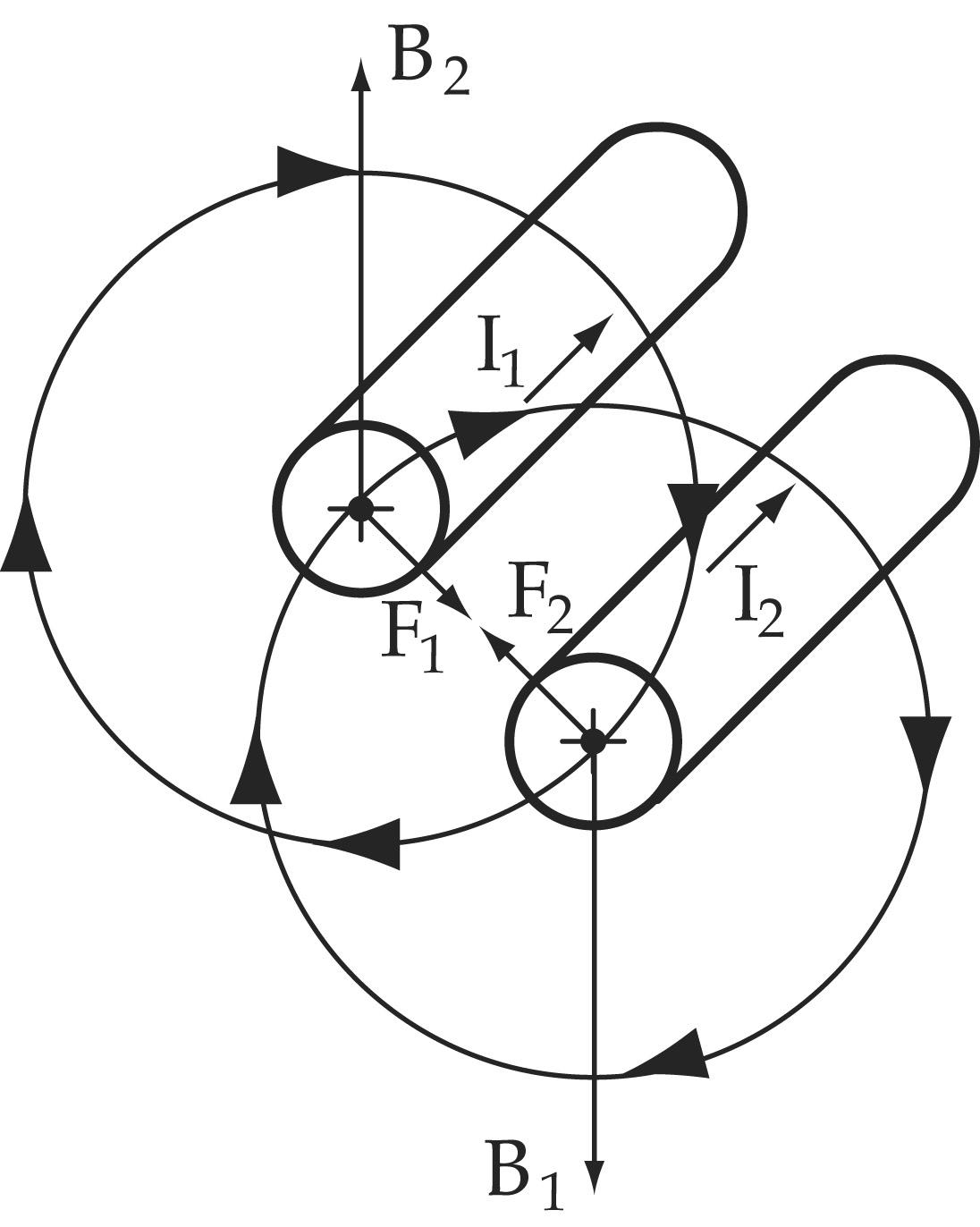
Если взять два параллельных проводника с токами, расположенных на расстоянии а друг от друга, то вокруг каждого из них будет возникать собственное магнитное поле, причем проводник с током I1 окажется в магнитном поле проводника с током I2 и наоборот. В результате на проводники будут действовать электромагнитные силы F1 и F2, направление которых определяется по правилу левой руки.
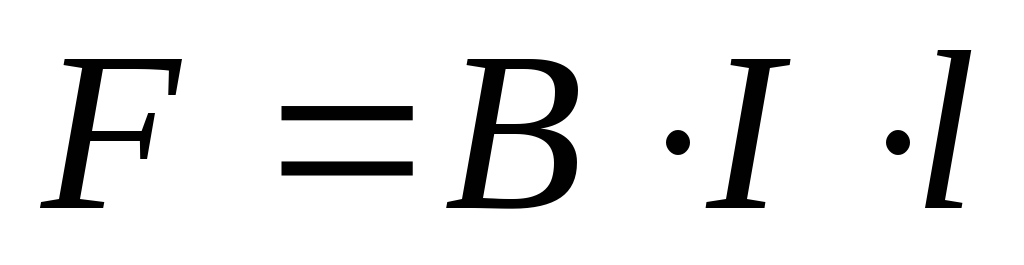
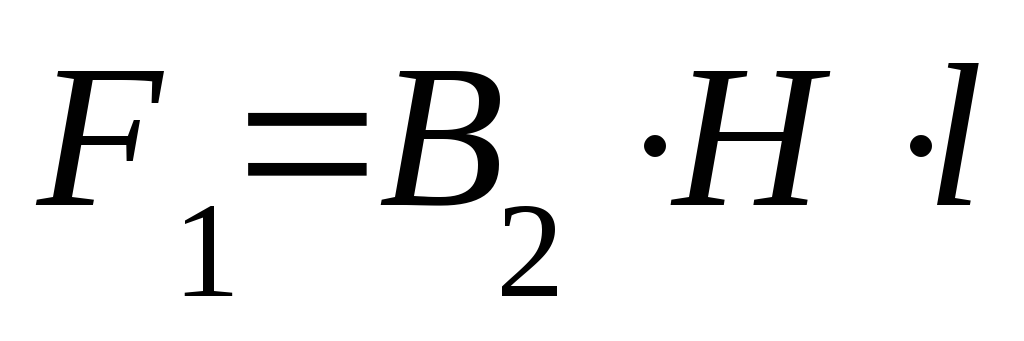
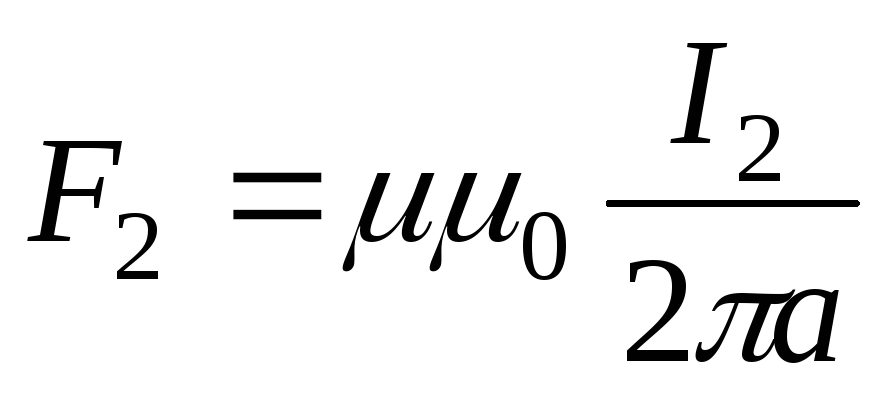
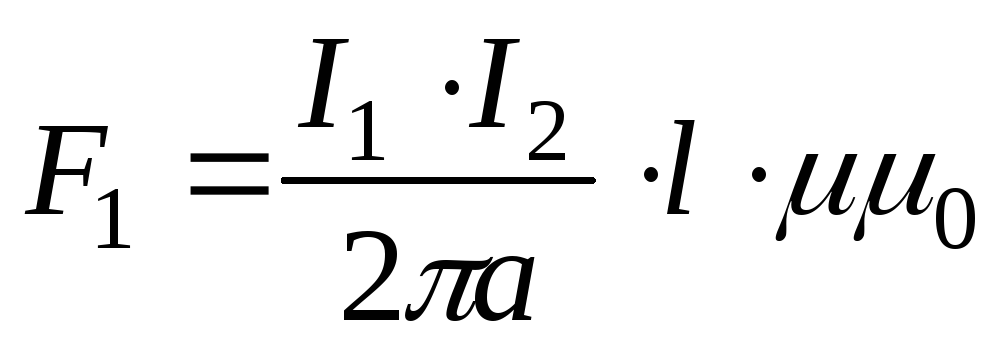
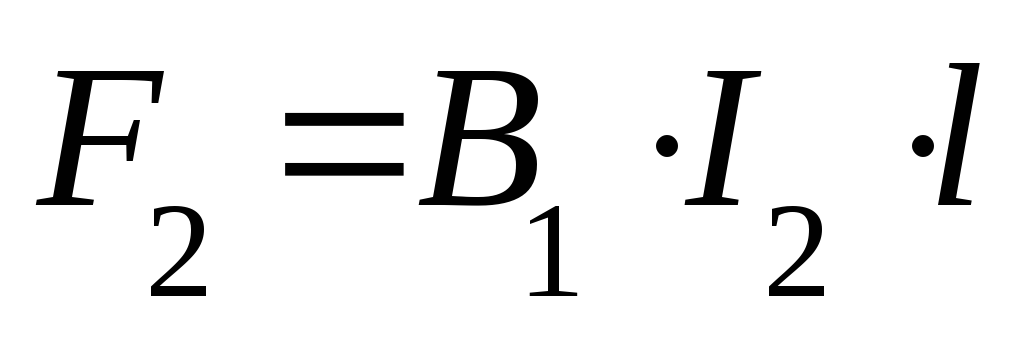
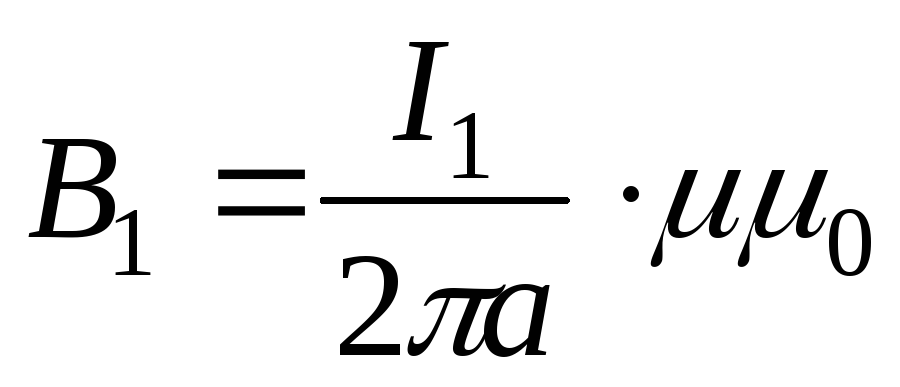
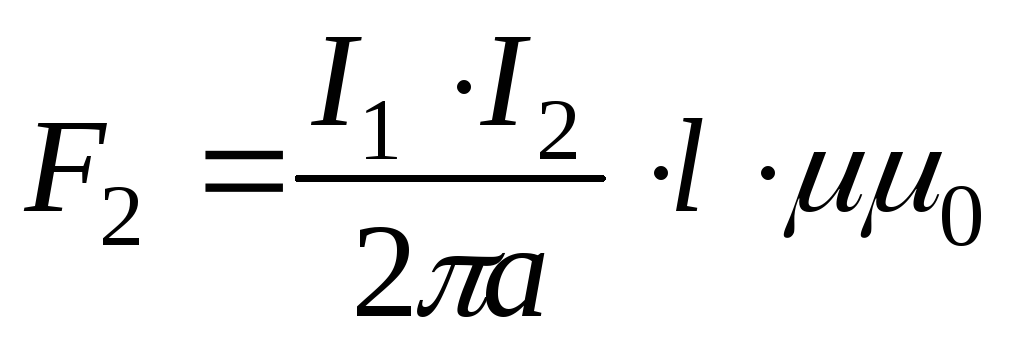


провода с токами
одинакового направления притягиваются
друг к другу с силой F.
провода с токами
одинакового направления притягиваются
друг к другу с силой F.


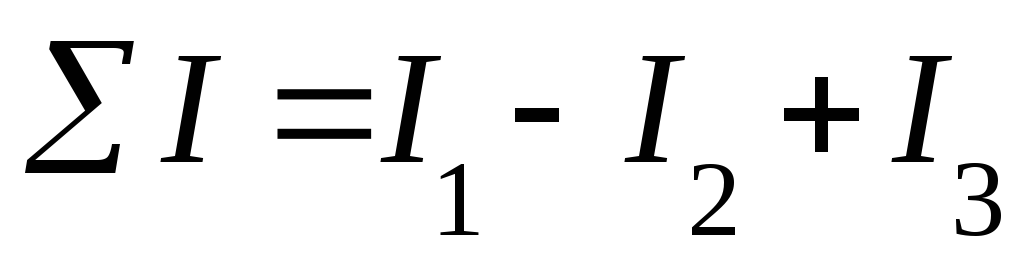
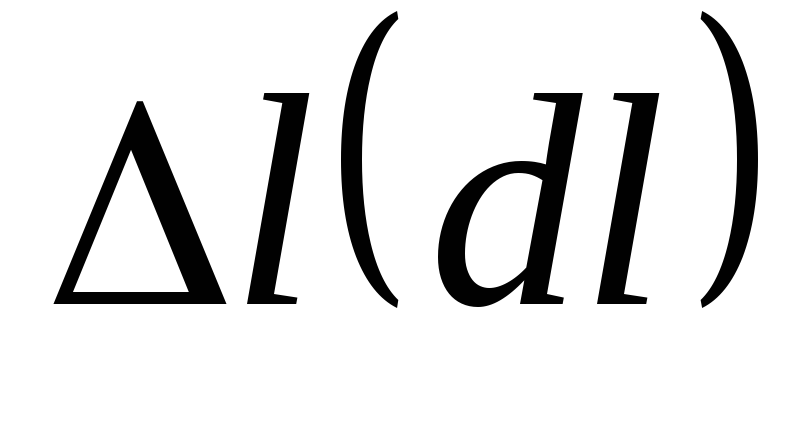 и допустим, что вектор напряжен-ности
в этой точке образует
и допустим, что вектор напряжен-ности
в этой точке образует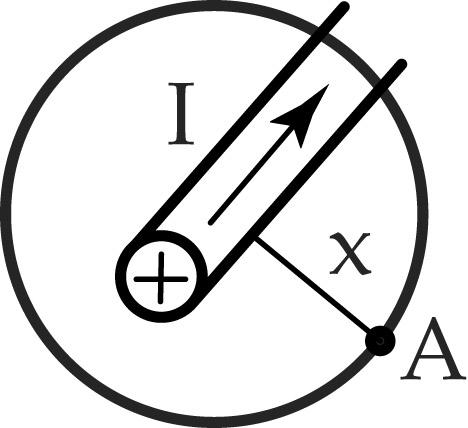
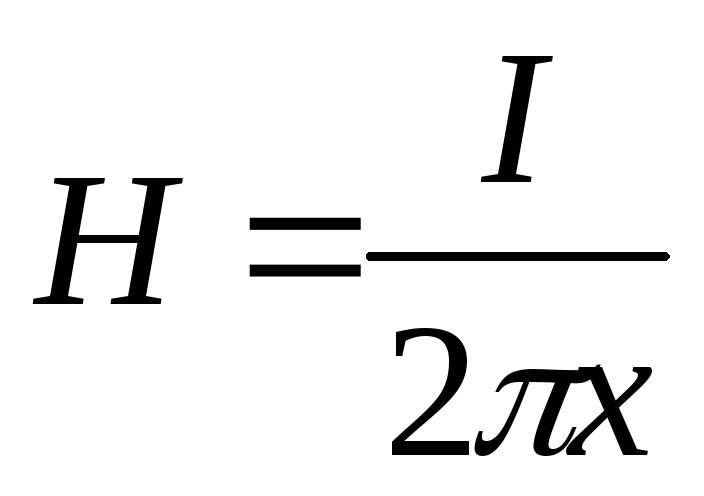
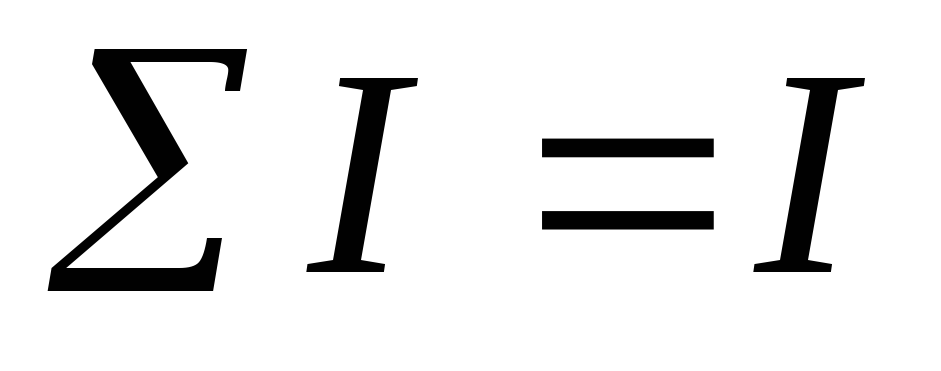
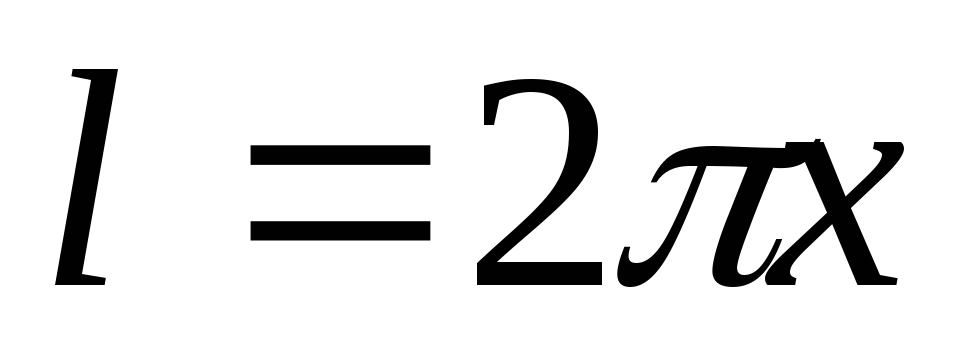
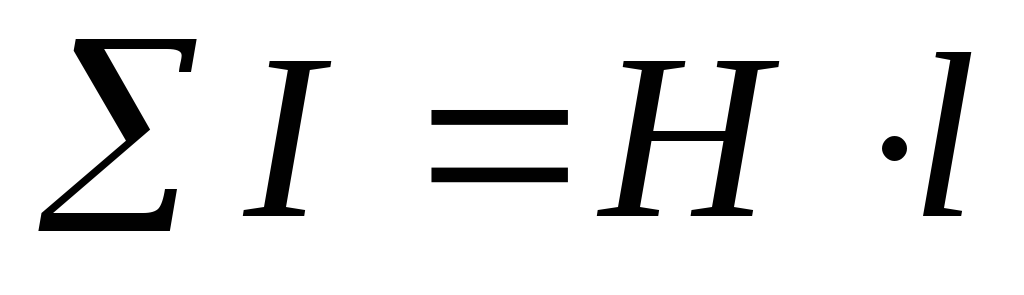
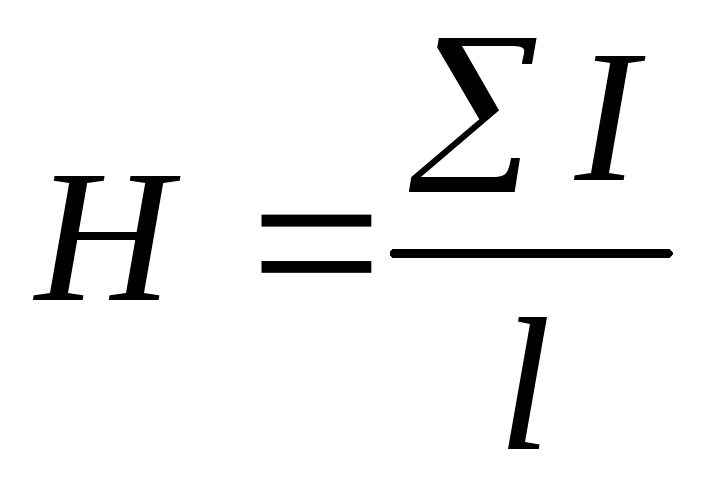
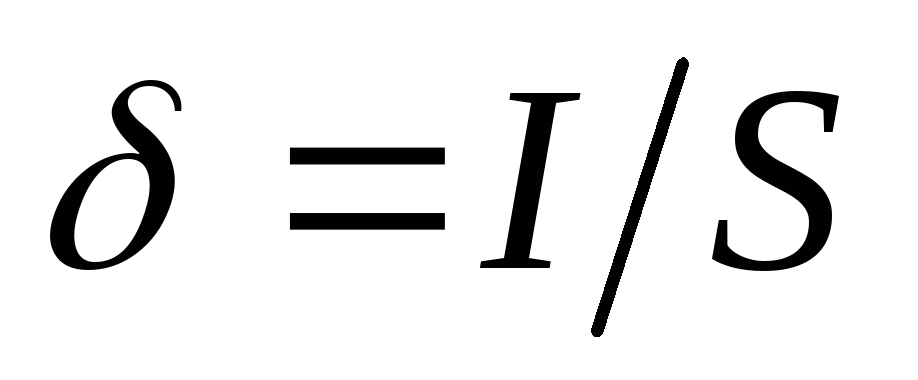 по всему сечению
по всему сечению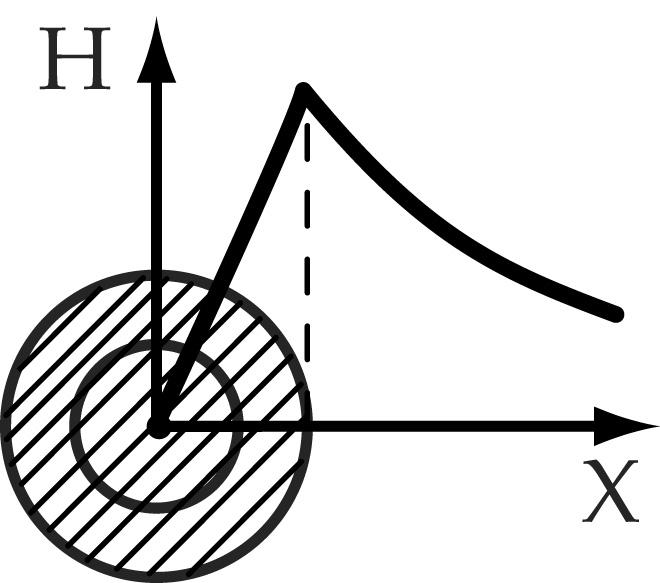
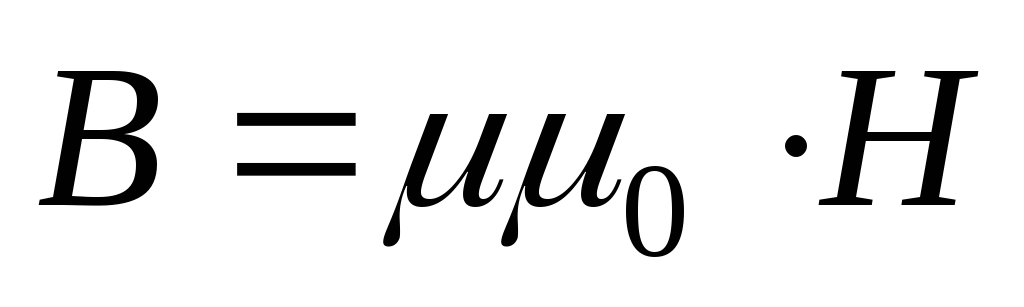 и для прямолинейного проводника с
током магнитная индукция будет равна
и для прямолинейного проводника с
током магнитная индукция будет равна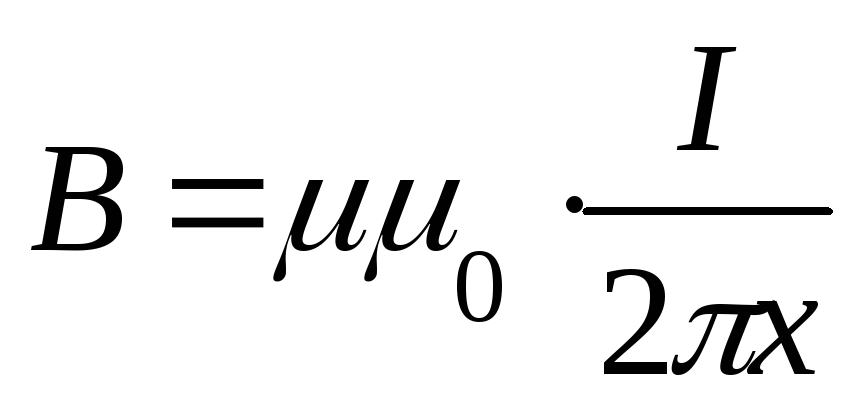 ,
а внутри проводника с током –
,
а внутри проводника с током –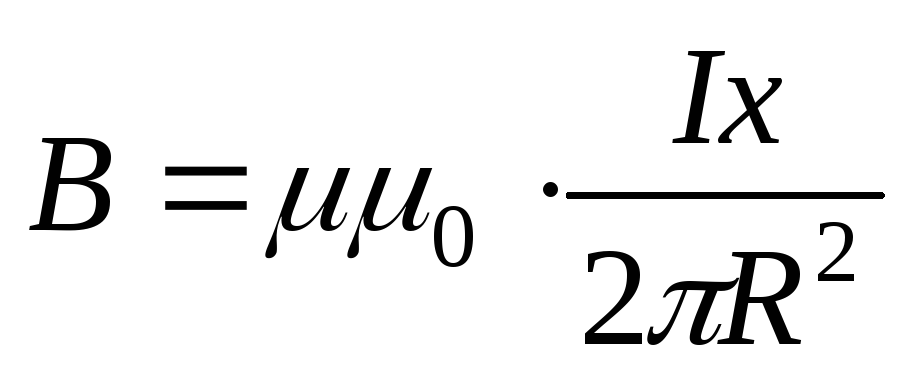
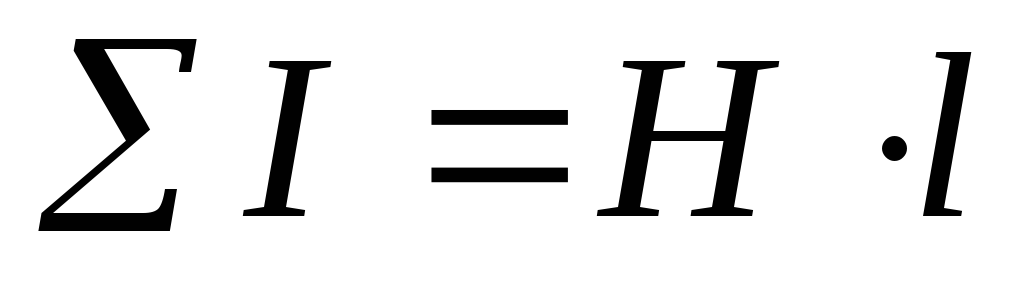 —
для однородного поля). Определим
напряженность поляН внутри кольцевой катушки.
—
для однородного поля). Определим
напряженность поляН внутри кольцевой катушки.