Глава 21. Электрический ток. Законы Ома и Джоуля-Ленца
Для решения задач ЕГЭ на постоянный ток надо знать определения тока, напряжения, сопротивления, закон Ома для участка цепи и замкнутой цепи, закон Джоуля-Ленца, а также уметь находить эквивалентные сопротивления простейших электрически цепей. Рассмотрим эти вопросы.
Электрическим током называют упорядоченное движение заряженных частиц. Силой тока в некотором сечении проводника называется отношение заряда , протекшего через это сечение за интервал времени , к этому интервалу времени
(21.1) |
Чтобы в проводнике тек электрический ток, в проводнике должно быть электрическое поле, или, другими словами, потенциалы различных точек проводника должны быть разными. Но при движении электрических зарядов по проводнику потенциалы различных точек проводника будут выравниваться (см. гл. 19). Поэтому для протекания тока в течение длительного времени на каких-то участках цепи необходимо обеспечить движение зарядов в направлении противоположном полю. Такое движение может быть обеспечено только силами неэлектрической природы, которые в этом контексте принято называть сторонними. В гальванических элементах («батарейках») сторонние силы возникают в результате электрохимических превращений на границах электродов и электролита. Эти превращения обеспечивают перемещение заряда противоположно направлению поля, поддерживая движение зарядов по замкнутому пути.
Сила тока в однородном участке проводника пропорциональна напряженности электрического поля внутри проводника. А поскольку напряженность поля внутри проводника связана с разностью потенциалов его концов (или электрическим напряжением на проводнике ), то
(21.2) |
Коэффициент пропорциональности , который принято записывать в знаменатель формулы (21.2), является характеристикой проводника и называется его сопротивлением. В результате формула (21.2) принимает вид
(21.3) |
Формула (21.3) называется законом Ома для однородного участка цепи, а сам участок цепи часто называют резистором (от английского слова resistance — сопротивление).
Если проводник является однородным и имеет цилиндрическую форму (провод), то его сопротивление пропорционально длине и обратно пропорционально площади сечения
(21.4) |
где коэффициент пропорциональности зависит только от материала проводника и называется его удельным сопротивлением.
Если участок цепи представляет собой несколько последовательно соединенных однородных проводников с сопротивлениями (см. рисунок), то сила тока через каждый проводник будет одинаковой , электрическое напряжение на всем участке цепи равно сумме напряжений на каждом проводнике , а эквивалентное сопротивление всего участка равно сумме сопротивлений отдельных проводников
(21.4) |
Если участок цепи представляет собой несколько однородных проводников с сопротивлениями , соединенных параллельно (см. рисунок), то электрическое напряжение на каждом проводнике будет одинаковым , ток через участок будет равен сумме токов, текущих через каждый проводник , а величина, обратная эквивалентному сопротивлению всего участка, равно сумме обратных сопротивлений отдельных проводников
(21.5) |
Рассмотрим теперь закон Ома для замкнутой электрической цепи. Пусть имеется замкнутая электрическая цепь, состоящая из источника сторонних сил с внутренним сопротивлением и внешнего сопротивления . Пусть при прохождении заряда через источник сторонние силы совершают работу . Электродвижущей силой источника (часто используется аббревиатура ЭДС) называется отношение работы сторонних сил к заряду
(21.6) |
В этом случае сила тока в цепи равна
(21.7) |
Формула (21.7) называется законом Ома для замкнутой электрической цепи.
При прохождении электрического тока через участок цепи электрическое поле совершает работу (часто эту работу называют работой тока, хотя термин этот не очень точный). Очевидно, вся эта работа превращается в тепло. Поэтому если через участок цепи прошел заряд , где — сила тока в цепи, — время, то количество выделившейся теплоты равно
(21.8) |
(для получения последнего и предпоследнего равенств использован закон Ома для участка цепи). Формулы (21.8) называются законом Джоуля-Ленца. Из формулы (21.8) следует, что количество выделившейся при протекании электрического тока теплоты линейно зависит от времени наблюдения. Поэтому отношение
(21.9) |
которое называется мощностью тока, не зависит от времени наблюдения. Формулу (21.9) также называют законом Джоуля-Ленца.
Рассмотрим теперь задачи.
Структура металла кратко обсуждалась в гл. 16: положительно заряженные ионы расположены в узлах кристаллической решетки, образовавшиеся в результате диссоциации валентные электроны могут свободно перемещаться по проводнику (свободные электроны). Они и осуществляют проводимость металла (задача 21.1.1 — ответ 2).
Согласно определению (21.1) находим среднюю силу тока в канале молнии (
(ответ 2).
Если за 1 мин через сечение проводника протекает заряд 60 Кл (задача 21.1.3), то сила тока в этом проводнике равна А. Применяя далее к этому проводнику закон Ома для участка цепи, получаем В (ответ 2).
По закону Ома для участка цепи имеем для силы тока через участок цепи после изменения его сопротивления и электрического напряжения на нем (задача 21.1.4)
Таким образом, сила тока уменьшилась в 4 раза (ответ
Согласно закону Ома для участка цепи сопротивление — это коэффициент пропорциональности между напряжением на этом участке и силой тока в нем. Поэтому в задаче 21.1.5 имеем, например, используя крайнюю точку графика
(ответ 2). Из-за линейной зависимости тока от напряжения вычисления можно было выполнить и по другим точкам графика, ответ был бы таким же.
Согласно формуле (21.4) имеем для первой проволоки в задаче 21.1.6
где — удельное сопротивление меди, — длина проводника, — его радиус. Для медной проволоки с вдвое большей длиной и втрое бóльшим радиусом сечения имеем
(ответ 3).
Как следует из формулы (21.4) при двукратном уменьшении длины проводника вдвое уменьшается его сопротивление. Поэтому из закона Ома для участка цепи (21.3) заключаем, что при двукратном уменьшении напряжения на проводнике и двукратном уменьшении его длины (задача 21.1.7) сила тока в проводнике не изменится (ответ 4).
В задаче 21.1.8 следует использовать закон Ома для замкнутой электрической цепи (21.7). Имеем
где — ЭДС источника, — сопротивлении е внешней цепи, — сопротивление источника (ответ 1).
В задаче 21.1.9 следует применить закон Ома для замкнутой электрической цепи (21.7) к какому-нибудь значению внешнего сопротивления, по графику найти силу тока в цепи, а затем и ЭДС источника. Проще всего применить закон Ома к случаю . Из графика находим силу тока . Поэтому
где — внутреннее сопротивление источника (ответ 3).
Из формулы (21.9) следует, что при фиксированном сопротивлении участка цепи увеличение электрического напряжения в 2 раза (
В задаче 21.2.1 удобно использовать вторую из формул (21.9) . Имеем Вт (ответ 3).
Часто школьники не могут ответить на такой вопрос: из формулы для мощности тока следует, что мощность линейно растет с ростом сопротивления, а из формулы — убывает с ростом сопротивления. А как же в действительности мощность зависит от сопротивления? Давайте разберемся в этом вопросе на примере задачи 21.2.2. Конечно, оба предложенных «решения» неправильны: в них молчаливо предполагалось, что сила тока, текущего через это сопротивление, или напряжение на этом сопротивлении не зависят от его величины. А на самом деле эти величины от сопротивления зависят, причем эти зависимости могут быть разными для разных источников тока. Внутреннее сопротивление бытовых электрических сетей очень мало. В этом случае из законов Ома для замкнутой цепи и участка цепи (21.7), (21.3) следует, что напряжение на любом элементе, включенном в такую сеть, не зависит от сопротивления этого элемента и равно номинальному напряжению сети . Поэтому из формулы заключаем, что мощность, которая выделяется на таком элементе обратно пропорциональна его сопротивлению (ответ
Если бы внутреннее сопротивление источника было бы много больше внешнего сопротивления, ток в цепи определялся бы, главным образом, внутренним сопротивлением источника, а от внешнего сопротивления зависел бы слабо. В этом случае мощность тока была бы прямо пропорциональна сопротивлению участка цепи.
Как обсуждалось в решении предыдущей задачи, сопротивление элемента, работающего в бытовой электросети равно , где — номинальная мощность данного элемента, — напряжение в сети. Поэтому отношение сопротивлений ламп мощностью Вт и Вт, рассчитанных на работу в одной и той же бытовой электрической сети (задача 21.2.3) равно
(ответ 2).
Поскольку резисторы в задаче 21.2.4 соединены последовательно, то сила тока в них одинакова. Поэтому из закона Ома для участка цепи заключаем, что
(ответ 2).
При параллельном соединении ламп (задача 21.2.5) напряжение на них одинаково (см. введение к настоящей главе). Поэтому из закона Ома для участка цепи следует, что
(ответ 1).
Рассматриваемый в задаче 21.2.6 участок представляет собой два последовательных соединенных элемента, один из которых есть резистор 6 Ом, второй — два таких же резистора, соединенных параллельно. По правилам сложения сопротивлений находим эквивалентное сопротивление второго участка
а затем и эквивалентное сопротивление всей цепи
(ответ 3).
При разомкнутом ключе сопротивление участка цепи, данного в задаче 21.2.7, можно найти как в предыдущей задаче , где — сопротивление каждого резистора. Если ключ замкнут, то цепь сводится к одному резистору (т.к. параллельно двум резисторам включается проводник с пренебрежимо малым сопротивлением). Поэтому в этом случае сопротивление цепи равно . Таким образом, сопротивление второй цепи составляет две трети от сопротивления первой (ответ 1).
Как обсуждалось в решении задачи 21.2.2, сопротивление элемента номинальной мощности , работающего в бытовой электросети равна
где В — напряжение сети. Из этой формулы следует, что чем больше номинальная мощность элемента, тем меньше должно быть его сопротивление. Если две лампы накаливания включены последовательно (задача 21.2.8), то сила тока в них одинакова и отношение мощностей тока в этих лампах равно отношению их сопротивлений. Отсюда следует, что отношение реально выделяемых в лампах мощностей и обратно отношению номинальных мощностей этих ламп:
(ответ 2).
Работа, совершаемая электрическим полем в проводнике при протекании по нему электрического тока, превращается в энергию тока, которая затем превращается в тепловую энергию. Поэтому работу поля можно найти из закона Джоуля-Ленца. Для работы поля за время получаем . Из этой формулы находим сопротивление проводника в задаче 21.2.9 —
(ответ 1).
Поскольку при последовательном соединении резисторов ток через каждый из них одинаков, из закона Джоуля-Ленца (22.8) заключаем, что из двух сопротивлений и (задача 21.2.10; см. рисунок) наибольшей будет мощность тока на сопротивлении , из двух сопротивлений и — на сопротивлении . Сравним мощности тока на этих сопротивлениях. Учитывая, что при параллельном соединении элементов электрическое напряжение на каждом элементе одинаковое, а при последовательном — складываются значения сопротивлений, получим из законов Ома для верхнего и нижнего участков цепи и закона Джоуля-Ленца
где — электрическое напряжение, приложенное ко всей цепи. Поскольку то в представленной схеме наибольшая мощность будет выделяться на сопротивлении (ответ 2).
Законы Кирхгофа, Ома, Джоуля — Ленца.
Законы Кирхгофа являются одной из форм закона сохранения энергии и потому относятся к фундаментальным законам природы.
Первый закон Кирхгофа является следствием принципа непрерывности электрического тока, в соответствии с которым суммарный поток зарядов через любую замкнутую поверхность равен нулю, т.е. количество зарядов выходящих через эту поверхность должно быть равно количеству входящих зарядов.
Можно считать токи направленные к узлу положительными, а от узла отрицательными. Тогда для узла рис. 1 уравнение Кирхгофа будет иметь вид I3+I4—I1—I2 = 0 или I3+I4=I1+I2 .
Обобщая сказанное на произвольное число ветвей сходящихся в узле, можно сформулировать первый закон Кирхгофа следующим образом:
- алгебраическая сумма токов в любом узле электрической цепи равна нулю
| (1) |
- в любом узле сумма токов направленных к узлу равна сумме токов направленных от узла
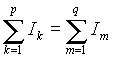 , где p+q=n. , где p+q=n.
| (2) |
в пределах описания одной электрической цепи нельзя для разных узлов использовать разные знаки для токов направленных к узлам или от узлов.
Второй закон Кирхгофа связан с понятием потенциала электрического поля, как работы, совершаемой при перемещении единичного точечного заряда в пространстве. Если такое перемещение совершается по замкнутому контуру, то суммарная работа при возвращении в исходную точку будет равна нулю. В противном случае путем обхода контура можно было бы получать положительную энергию, нарушая закон ее сохранения.
Сформулируем оба варианта второго закона Кирхгофа, т.к. они принципиально равноценны:
- алгебраическая сумма падений напряжения вдоль любого замкнутого контура электрической цепи равна нулю
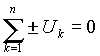 |
знак + выбирается перед падением напряжения на резисторе, если направление протекания тока через него и направление обхода контура совпадают; для падений напряжения на источниках ЭДС знак + выбирается, если направление обхода контура и направление действия ЭДС встречны независимо от направления протекания тока;
- алгебраическая сумма ЭДС вдоль любого замкнутого контура равна алгебраической сумме падений напряжения на резисторах в этом контуре
| , где p+q=n | (4) |
знак + для ЭДС выбирается в том случае, если направление ее действия совпадает с направлением обхода контура, а для напряжений на резисторах знак + выбирается, если в них совпадают направление протекания тока и направление обхода.
Закон Ома — это закон, устанавливающий связь между падением напряжения U на любом неразветвленном (не содержащем узлов) участке электрической цепи и величиной тока I, протекающего по этому участку.
Если зависимость U(I) или I(U) какого-либо элемента электрической цепи линейна, то такой элемент называют линейным, а электрическую цепь, состоящую только из линейных элементов — линейной цепью.
Для линейного элемента справедливо
где r=1/g и g=1/r — некоторые постоянные коэффициенты имеющие размерность соответственно В/А=Ом (омы) и А/В=См (сименсы).Коэффициент r называется сопротивлением, а g — проводимостью. В резисторе ток и падение напряжения (напряжение) всегда имеют одинаковое направление (рис. 1).
Закон Джоуля-Ленца. Если по активному сопротивлению (проводнику) течет постоянный ток, то работа тока на этом участке идет на преобразование электрической энергии во внутреннюю. Увеличение внутренней энергии проводника приводит к повышению его температуры (проводник нагревается).
Мощность тепла, выделяемого в единице объёма среды при протекании электрического тока, пропорциональна произведению плотности электрического тока на величину электрического поля
Математически может быть выражен в следующей форме:
где w — мощность выделения тепла в единице объёма, 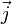 — плотность электрического тока,
— плотность электрического тока, 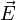 — напряжённость электрического поля, σ — проводимость среды.
— напряжённость электрического поля, σ — проводимость среды.
Закон также может быть сформулирован в интегральной форме для случая протекания токов в тонких проводах[3]:
Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивлению участка
В математической форме этот закон имеет вид
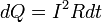
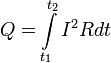
где dQ — количество теплоты, выделяемое за промежуток времени dt, I — сила тока, R — сопротивление, Q — полное количество теплоты, выделенное за промежуток времени от t1 до t2. В случае постоянных силы тока и сопротивления:
3.Анализ электрического состояния цепей постоянного тока В соответствии с методом свертывания, отдельные участки схемы упрощают и постепенным преобразованием приводят схему к одному эквивалентному (входному) сопротивлению, включенному к зажимам источника. Схема упрощается с помощью замены группы последовательно или параллельно соединенных сопротивлений одним, эквивалентным по сопротивлению. Определяют ток в упрощенной схеме, затем возвращаются к исходной схеме и определяют в ней токи.
Рассмотрим схему на рис. 3.1. Пусть известны величины сопротивлений R1, R2, R3, R4, R5, R6, ЭДС Е. Необходимо определить токи в ветвях схемы.
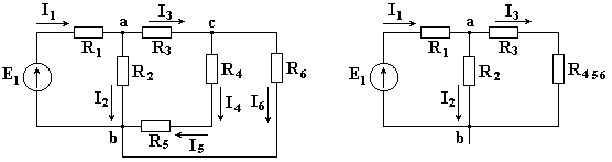
Рис. 3.1 Рис. 3.2 Сопротивления R4 и R5 соединены последовательно, а сопротивление R6 — параллельно с ними, поэтому их эквивалентное сопротивление
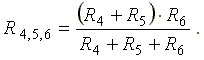
После проведенных преобразований схема принимает вид, показанный на рис. 3.2, а эквивалентное сопротивление всей цепи
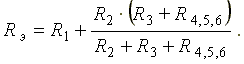
Ток I1 в неразветвленной части схемы определяется по формуле:
Найдем токи I2 и I3 в схеме на рис. 3.2 по формулам:
I3 = I1 — I2 — формула получается из уравнения, составленного по первому закону Кирхгофа:
I1 — I2 — I3 = 0.
Переходим к исходной схеме на рис. 3.1 и определим токи в ней по формулам:
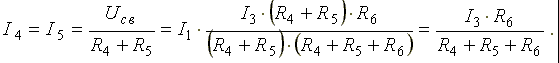
I6 = I3 — I4 (в соответствии с первым законом Кирхгофа I3 — I4 — I6 =0).
4.Применение законов Кирхгофа и Ома для расчетов электрических цепей .Самое распространенное применение законов Кирхгофа мы наблюдаем в так называемых последовательных и параллельных цепях. В последовательной цепи (яркий пример такой цепи — елочная гирлянда, состоящая из последовательно соединенных между собой лампочек) электроны от источника питания по серии проводов последовательно проходят через все лампочки, и на сопротивлении каждой из них напряжение падает согласно закону Ома.
В параллельной цепи провода, напротив, соединены таким образом, что на каждый элемент цепи подается равное напряжение от источника питания, а это означает, что в каждом элементе цепи сила тока своя, в зависимости от его сопротивления. Пример параллельной цепи является — ламп «лесенкой»: напряжение подается на шины, а лампы смонтированы на поперечинах. Токи, проходящие через каждый узел такой цепи, определяются по второму закону Кирхгофа.
Все те, кто знаком с основами электротехники, представляют себе значение закона Ома в теории и практике электрических цепей. Не вдаваясь в подробности, перечислим некоторые примеры использования закона Ома при изучении электрических цепей.
В первую очередь, как уже упоминалось, закон Ома в виде 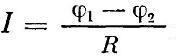
служит для определения сопротивления проводника. При наличии амперметра и вольтметра эта операция даже для неопытного экспериментатора не представит трудностей. Одним из наиболее точных и чувствительных способов определения сопротивления является метод мостовых схем, расчет которых производится также с использованием закона Ома.
Применяя закон Ома для полной цепи, можно, изменяя внешнее сопротивление, вычислить ЭДС и внутреннее сопротивление источника тока, решив для этого систему двух соответствующих выражений:
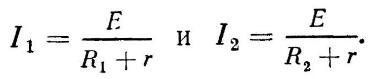
ПоказанияI1 и I2 при этом снимают с амперметра, включенного в цепь. Сопротивление R1 и R2 внешних участков цепи можно найти, измеряя вольтметром падение напряжения на этих участках и применяя формулу закона Ома для участка цепи.
Этот же закон позволяет рассчитать электрическую цепь, источником тока в которой является батарея, составленная из нескольких элементов.
В настоящее время в электротехнике широко применяются правила Кирхгофа, с помощью которых рассчитывают разветвленные цепи. Зная эти правила, можно, например, определить силу и направление тока в любой части разветвленной системы проводников, если заданы сопротивления и ЭДС всех его участков. Второе правило Кирхгофа получено в результате применения закона Ома к различным участкам замкнутой цепи. Первое правило также следует из теоретических рассуждений Ома, изложенных им в работе «Теоретические исследования электрических цепей».
Изучение нелинейных цепей обязано своим прогрессом также закону Ома. Важнейшие характеристики электронных ламп и полупроводниковых приборов — крутизна характеристики, внутреннее сопротивление — определяется в соответствии с законом Ома.
Закон Ома применяется ко всей цепи. Его можно применять для расчёта гидравлических, пневматических, магнитных, электрических, световых, тепловых потоков и т. д., также, как и Правила Кирхгофа
5.Метод эквивалентного преобразования схем . Эквивалентным называется преобразование, при котором напряжения и токи в частях схемы, не подвергшихся преобразованию, не меняются.
Последовательное соединение элементов
электрических цепей
На рис. 2.1 изображена электрическая цепь с последовательно соединенными сопротивлениями.
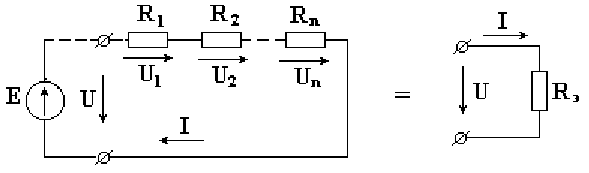
Рис. 2.1
Напряжение на зажимах источника ЭДС равно величине электродвижущей силы. Поэтому часто источник на схеме не изображают.
Падения напряжений на сопротивлениях определяются по формулам 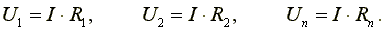 В соответствии со вторым законом Кирхгофа, напряжение на входе электрической цепи равно сумме падений напряжений на сопротивлениях цепи.
В соответствии со вторым законом Кирхгофа, напряжение на входе электрической цепи равно сумме падений напряжений на сопротивлениях цепи. 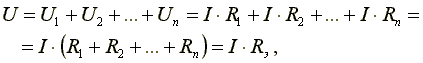 где
где 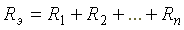 — эквивалентное сопротивление.
— эквивалентное сопротивление.
Эквивалентное сопротивление электрической цепи, состоящей из n последовательно включенных элементов, равно сумме сопротивлений этих элементов.
Параллельное соединение элементов
электрических цепей
На рис. 2.2 показана электрическая цепь с параллельным соединением сопротивлений.
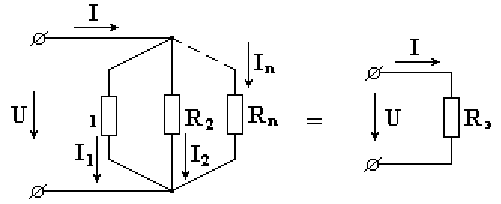
Рис. 2.2
Токи в параллельных ветвях определяются по формулам:
где 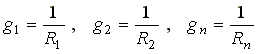 — проводимости 1-й, 2-й и n-й ветвей.
— проводимости 1-й, 2-й и n-й ветвей.
В соответствии с первым законом Кирхгофа, ток в неразветвленной части схемы равен сумме токов в параллельных ветвях.
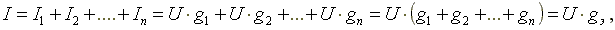 где
где 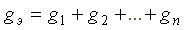
Эквивалентная проводимость электрической цепи, состоящей из n параллельно включенных элементов, равна сумме проводимостей параллельно включенных элементов.
Эквивалентным сопротивлением цепи называется величина, обратная эквивалентной проводимости 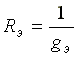
Пусть электрическая схема содержит три параллельно включенных сопротивления.
Эквивалентная проводимость
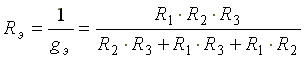 Эквивалентное сопротивление схемы, состоящей из n одинаковых элементов, в n раз меньше сопротивлений R одного элемента
Эквивалентное сопротивление схемы, состоящей из n одинаковых элементов, в n раз меньше сопротивлений R одного элемента
Возьмем схему, состоящую из двух параллельно включенных сопротивлений (рис. 2.3). Известны величины сопротивлений и ток в неразветвленной части схемы. Необходимо определить токи в параллельных ветвях.
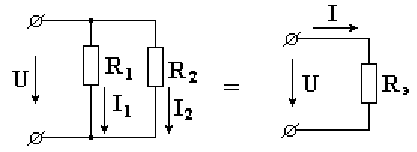
Рис. 2.3 Эквивалентная проводимость схемы
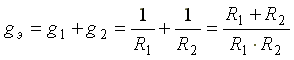 ,
,
а эквивалентное сопротивление 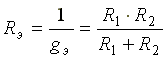 Напряжение на входе схемы
Напряжение на входе схемы 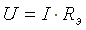 Токи в параллельных ветвях
Токи в параллельных ветвях
Аналогично
Ток в параллельной ветви равен току в неразветвленной части схемы, умноженному на сопротивление противолежащей, чужой параллельной ветви и деленному на сумму сопротивлений чужой и своей параллельно включенных ветвей.
Преобразование треугольника сопротивлений
в эквивалентную звезду
Встречаются схемы, в которых отсутствуют сопротивления, включенные последовательно или параллельно, например, мостовая схема, изображенная на рис. 2.4. Определить эквивалентное сопротивление этой схемы относительно ветви с источником ЭДС описанными выше методами нельзя. Если же заменить треугольник сопротивлений
R1-R2-R3, включенных между узлами 1-2-3, трехлучевой звездой сопротивлений, лучи которой расходятся из точки 0 в те же узлы 1-2-3, эквивалентное сопротивление полученной схемы легко определяется.
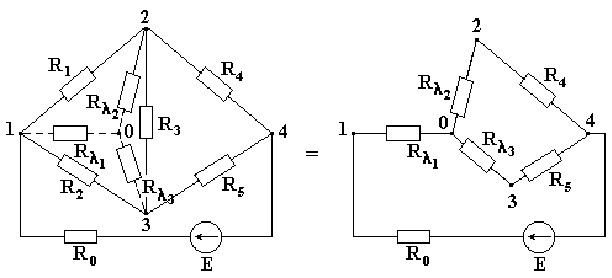
Рис. 2.4 Сопротивление луча эквивалентной звезды сопротивлений равно произведению сопротивлений прилегающих сторон треугольника, деленному на сумму сопротивлений всех сторон треугольника.
В соответствии с указанным правилом, сопротивления лучей звезды определяются по формулам:
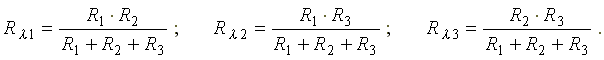 Эквивалентное соединение полученной схемы определяется по формуле
Эквивалентное соединение полученной схемы определяется по формуле
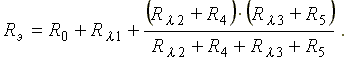 Сопротивления R0 и R?1 включены последовательно, а ветви с сопротивлениями R?1 + R4 и R?3 + R5 соединены параллельно.
Сопротивления R0 и R?1 включены последовательно, а ветви с сопротивлениями R?1 + R4 и R?3 + R5 соединены параллельно.
Преобразование звезды сопротивлений
в эквивалентный треугольник
Иногда для упрощения схемы полезно преобразовать звезду сопротивлений в эквивалентный треугольник.
Рассмотрим схему на рис. 2.5. Заменим звезду сопротивлений R1-R2-R3 эквивалентным треугольником сопротивлений R?1-R?2-R?3, включенных между узлами 1-2-3.
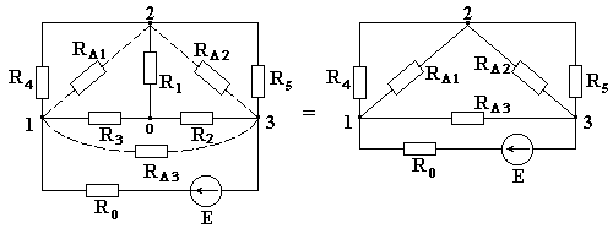
2.5. Преобразование звезды сопротивлений
в эквивалентный треугольник
Сопротивление стороны эквивалентного треугольника сопротивлений равно сумме сопротивлений двух прилегающих лучей звезды плюс произведение этих же сопротивлений, деленное на сопротивление оставшегося (противолежащего) луча. Сопротивления сторон треугольника определяются по формулам:
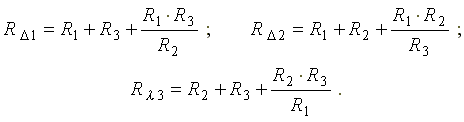
Эквивалентное сопротивление преобразованной схемы равно
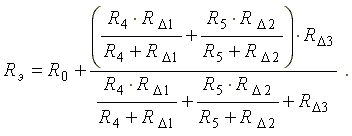
При решении схемы методом непосредственного преобразования элементов используют серию эквивалентных преобразований схемы, направленных на упрощение схемы. Понятие эквивалентного преобразования подразумевает такое изменение состава и/или топологии фрагментасхемы, при котором не изменяются электрические показатели (токи и напряжения) в остальных частях схемы, не затронутых преобразованием. Такое обстоятельство означает, что величины, найденные для одной из эквивалентных схем (искомые или вспомогательные), действительны и для любой другой из эквивалентных схем.
Читайте также:
Рекомендуемые страницы:
Поиск по сайту
Вопрос№13. Электрически ток и его характеристики. Условия существования тока. Закона Ома и Джоуля-Ленца в дифференциальной форме.
⇐ ПредыдущаяСтр 3 из 6Следующая ⇒Электрический ток – любое упорядоченное движение заряженных частиц. В проводнике под действием приложенного электрического поля 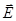 свободные электрические заряды перемещаются: положительные – по полю, отрицательные – против поля – идет ток проводимости.
свободные электрические заряды перемещаются: положительные – по полю, отрицательные – против поля – идет ток проводимости.
Виды электрического тока:
1. ток проводимости— движение свободных электрических зарядов заряженных макроскопических тел;
2. конвекционный ток — перенос электрических зарядов заряженными макроскопическими телами;
3. ток в жидкости — упорядоченное движение положительных и отрицательных ионов;
4. ток в газах (газовый разряд) — упорядоченное движение положительных и отрицательных ионов;
5. ток поляризации— возникает при малом перемещении связанных зарядов в диэлектрике;
6. ток смещения в вакууме — условный ток, объясняющий магнитное действие переменного электрического тока
Для возникновения и существования тока необходимо:
— наличие свободных носителей зарядов;
— наличие разности потенциалов, т.е. электрического поля, энергия которого затрачивалась бы на перемещение зарядов.
Сила тока — заряд, проходящий, через всё поперечное сечение S проводника в единицу времени:
а) для постоянного тока
б) для переменного тока , размерность – ампер.
Плотность тока — заряд, прошедший через единицу площади поперечного сечения проводника в единицу времени;
а) равномерное распределение по сечению
б) неравномерное распределение по сечению 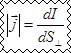
Закон Ома. (для плотности тока)
Приложенное к проводнику напряжение U вызывает электрический ток I. Как физически будет развиваться этот процесс. Зависимость тока I(U) участка цепи называется вольт — амперной характеристикой. Немецкий ученый Георг Ом установил что для металла величина тока I линейно зависит от U.
Закон Ома можно представить в дифференциальной форме. Подставив выражение для сопротивления в закон Ома, получим
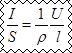 ,где величина, обратная удельному сопротивлению, — называется удельной электрической проводимостью вещества проводника. Учитывая, что — напряженность электрического поля в проводнике, — плотность тока, закон Ома можно записать в виде
,где величина, обратная удельному сопротивлению, — называется удельной электрической проводимостью вещества проводника. Учитывая, что — напряженность электрического поля в проводнике, — плотность тока, закон Ома можно записать в виде 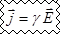
Закон Джоуля — Ленца дифференциальной форме
Если электрический ток проходит по неподвижному омическому проводнику, то вся работа по перемещению заряда идет на его нагревание.
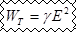 закон Джоуля — Ленца в дифференциальной форме.
закон Джоуля — Ленца в дифференциальной форме.
Вопрос№14.Стороние силы. ЭДС. Закон Ома для участка цепи с источником ЭДС. Закон Джоуля-Ленца в интегральной форме.
Сторонние силы. Э.Д.С.,
Против сил электрического поля могут действовать только силы неэлектрического происхождения, поэтому такие силы называются сторонними.
Сторонние силы — это силы неэлектрического происхождения, которые в отличие от кулоновских сил вызывают не соединение, а разделение разноименных электрических зарядов и поддерживают разность потенциалов проводников.
Примеры сторонних сил: — механические; — химические; — магнитные; — теплового движения и т.д.
Электродвижущая сила – численно равна работе, совершаемой сторонними силами при перемещении по участку цепи единичного положительного заряда. 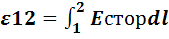 –электродвижущая сила, действующая на участок цепи.
–электродвижущая сила, действующая на участок цепи.
а) цепь замкнута: 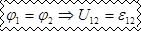
б) Э.Д.С. на участке отсутствует: 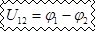
Участок на котором отсутствует Э.Д.С. называется однородным, а участок содержащий Э.Д.С. называется неоднородным.
Закон Джоуля — Ленца в интегральной и дифференциальной форме.
Если электрический ток проходит по неподвижному омическому проводнику, то вся работа по перемещению заряда идет на его нагревание. Пусть к однородному проводнику приложено напряжение, тогда работа по перемещению заряда q, равна Из соотношения 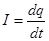 следует
следует
Для омического проводника U=IR
dA=I2Rdt, мы полагаем, что вся работа идет на образование тепла, то есть dA=dQ 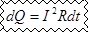
Тепловая мощность 
Количество теплоты, выделяемое постоянным током в участке цепи, равно произведению квадрата силы тока на время его прохождения и электрическое сопротивление этого участка цепи.
Закон Ома для участка цепи
Для участка цепи содержащей ЭДС будет иметь вид

Вопрос№15. Правила Киргофа и расчет электрических цепей.
Электрическая цепь- это система соединенных между собой токопроводящих элементов цепи. Если цепь состоит только из линейных элементов, то она линейна, если же цепь содержит хотя бы один нелинейный элемент, то она становится нелинейной. Электрическая цепь изображается графически в виде своей эквивалентной электрической схемы, на которой показано условное изображение её элементов и соединение их друг с другом.
Физической основой расчёта электрической цепи, как линейной так и нелинейной являются законы Кирхгофа, первый из которых относится к узлам цепи, а второй — к простым контурам.
Первый закон Кирхгофа (для узлов): алгебраическая сумма притекающих и вытекающих токов для любого узла цепи равна нулю:
(1)
В уравнении (1) притекающие и вытекающие токи берутся с противоположными знаками.
Второй закон Кирхгофа (для контуров): алгебраическая сумма падений напряжений на элементах цепи вдоль любого замкнутого контура равна алгебраической сумме ЭДС, действующих в данном контуре
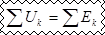 (2)
(2)
В уравнении (2) знаки величин Uk и Ek определяются по отношению к выбранному направлению обхода контура. Если ток Ik совпадает с направлением обхода, то падение напряжения на данном элементе Uk считается положительным, в противном случае оно отрицательно. Электродвижущая сила Ek считается положительной, если её поле сторонних сил совпадает с направлением обхода контура, в противном случае она отрицательна. (Поле сторонних сил всегда направлено внутри источника от отрицательного к положительному полюсу).
Если элемент цепи не генерирует ЭДС, то падение напряжения на нём совпадает с разностью потенциалов на элементе. Для линейного элемента оно определяется1 из закона Ома по заданному току и сопротивлению . Для нелинейного элемента, не подчиняющегося закону Ома, такое определение падения напряжения невозможно, в данном случае оно определяется только из ВАХ нелинейного элемента по заданному току.
Законы Ома и Джоуля-Ленца в классической теории
Объяснение закона Ома в классической теории
В классической теории электропроводности металлов считается, что дополнительная энергия, которую приобретает электрон, при нахождении проводника во внешнем электрическом поле:
где $q_e$,$\ m_e$ — заряд и масса электрона, $E$ — напряженность внешнего электрического поля. Исходя из уравнения (2), получим, что к концу своего пробега скорость электрона в среднем будет равна:
где $\tau $ — среднее время, которое проходит между двумя последовательными соударениями электрона с ионами решетки.
Друде, основавший классическую теорию электропроводности металлов, не учитывал распределения электронов по скоростям и приписывал им всем одинаковые скорости $v$. В таком случае можно считать, что:
где $\left|\overrightarrow{v}\right|\approx \left|\overrightarrow{v}+\overrightarrow{u}\right|$. Подставим выражение (4) в формулу (3), имеем:
Получилось, что скорость $u$ изменяется линейно за время пробега. Значит, ее среднее значение за пробег равно:
Подставим среднюю скорость из формулы (6) в выражение для плотности тока:
в результате получим:
Мы получили, что $j\sim E$. То есть пришли к закону Ома, где удельная проводимость ($\sigma $) вычисляется как:
В том случае, если бы столкновения электронов с ионами не было, то длина свободного пробега была бесконечно большой ($\lambda \to \infty $), значит бесконечно большой была бы проводимость. Из классической теории проводимости можно сделать вывод о том, что сопротивление металлов вызвано столкновениями свободных электронов с ионами узлов кристаллической решетки.
Закон Джоуля — Ленца
К окончанию свободного пробега электрон имеет дополнительную кинетическую энергию (${\triangle W}_k$), среднее значение которой равно:
По теории, когда электрон сталкивается с ионом, он полностью передает дополнительную энергию (${\triangle W}_k$) кристаллической решетке. Энергия, которая при этом сообщается решетке, расходуется на увеличение внутренней энергии металла, что проявляется в его нагревании.
Каждый электрон совершает в среднем за секунду $\frac{1}{\tau }=\frac{v}{\lambda }$ ударов. Каждый раз он сообщает решетке энергию $\left\langle {\triangle W}_k\right\rangle $ (10). Это значит, что в единице объема за единицу времени выделяется тепло (назовем его удельным) равное:
где $n$ — концентрация электронов проводимости. $Q_{ud}$ — удельная тепловая мощность тока. Используя выражение (9), формулу (11) можно записать как:
\[Q_{ud}=\sigma E^2=\rho j^2\left(12\right),\]где $\rho =\frac{1}{\sigma }$ — удельное сопротивление. Выражение (12) — дифференциальная форма закона Джоуля — Ленца.
Так, мы получили, что классическая теория проводимости смогла объяснить законы Ома и закон Джоуля — Ленца.
Пример 1
Задание: Получите выражение, связывающее абсолютную температуру проводника и его удельную проводимость.
Решение:
Согласно классической теории электропроводности считаем, что к электронам в металле применима классическая статистическая механика. Тогда средняя энергия поступательного движения электронов в электронном газе (одноатомном) зависит только от абсолютной температуры (T) и равна:
\[W_k=\frac{m_ev^2}{2}=\frac{3}{2}kT\left(1.1\right).\]Выразим из (1.1) скорость, получим:
\[v=\sqrt{\frac{3kT}{m_e}}\left(1.2\right).\]Выражение для удельной проводимости, полученное в рамках теоретического материала имеет вид:
\[у=\frac{{{nq}_e}^2}{2m_e}\frac{\lambda }{v}\left(1.3\right).\]Подставим в (1.3) выражение для скорости (1.2), имеем:
\[\sigma =\frac{{{nq}_e}^2}{2m_e}\frac{\lambda }{\sqrt{\frac{3kT}{m_e}}}=\frac{{{n\lambda q}_e}^2}{2\sqrt{3kTm_e}}.\]Ответ: $\sigma =\frac{{{n\lambda q}_e}^2}{2\sqrt{3kTm_e}}$. Из полученного выражения видно, что сопротивление металлов должно расти пропорционально квадратному корню от температуры. Для предположения о том, что $n\ и\ \lambda $ зависят от температуры, в классической теории электропроводности снований нет. То есть классическая теория не смогла объяснить эмпирические данные, согласно которым сопротивление металлов пропорционально первой степени температуры.
Пример 2
Задание: Объясните, почему металлы оказывают сопротивление электрическому току.
Решение:
Если бы электроны не испытывали ни каких помех при своём движении, то после приведения их однажды их в упорядоченное движение, они двигались бы по инерции бесконечное время без воздействия внешнего электрического поля. Однако в действительности электроны испытывают соударения с ионами кристаллической решетки. При чем, до удара электрон обладает некоторой скоростью упорядоченного движения, после соударения электроны отскакивают в произвольных направлениях, скорость упорядоченного движения становится равной нулю. После выключения внешнего поля упорядоченное движение электронов (ток) скоро прекратится. Для того чтобы получить ток, текущий сколько ни будь длительное время, необходимо чтобы после каждого удара электрона о ион, на электрон действовала сила, то есть необходимо существование внешнего поля. Причем плотность тока в проводнике тем выше, чем больше напряженность приложенного поля.
Закон Джоуля — Ленца — это… Что такое Закон Джоуля — Ленца?
Закон Джоуля — Ленца — физический закон, дающий количественную оценку теплового действия электрического тока. Открыт в 1840 году независимо Джеймса Джоуля и Эмилия Ленца.
В словесной формулировке звучит следующим образом[1]
Мощность тепла, выделяемого в единице объёма среды при протекании электрического тока, пропорциональна произведению плотности электрического тока на величину электрического поля
Математически может быть выражен в следующей форме:
где w — мощность выделения тепла в единице объёма, — плотность электрического тока, — напряжённость электрического поля, σ — проводимость среды.
Закон также может быть сформулирован в интегральной форме для случая протекания токов в тонких проводах[2]:
Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивлению участка
В математической форме этот закон имеет вид
где dQ — количество теплоты, выделяемое за промежуток времени dt, I — сила тока, R — сопротивление, Q — полное количество теплоты, выделенное за промежуток времени от t1 до t2. В случае постоянных силы тока и сопротивления:
Практическое значение
Снижение потерь энергии
При передаче электроэнергии тепловое действие тока является нежелательным, поскольку ведёт к потерям энергии. Поскольку передаваемая мощность линейно зависит как от напряжения, так и от силы тока, а мощность нагрева зависит от силы тока квадратично, то выгодно повышать напряжение перед передачей электроэнергии, понижая в результате силу тока. Однако, повышение напряжения снижает электробезопасность линий электропередачи.
Для применения высокого напряжения в цепи для сохранения прежней мощности на полезной нагрузке приходится увеличивать сопротивление нагрузки. Подводящие провода и нагрузка соединены последовательно. Сопротивление проводов () можно считать постоянным. А вот сопротивление нагрузки () растёт при выборе более высокого напряжения в сети. Также растёт соотношение сопротивления нагрузки и сопротивления проводов. При последовательном включении сопротивлений (провод — нагрузка — провод) распределение выделяемой мощности () пропорционально сопротивлению подключённых сопротивлений.
Ток в сети для всех сопротивлений постоянен. Следовательно, выполняются соотношение
и для в каждом конкретном случае являются константами. Следовательно, мощность, выделяемая на проводах, обратно пропорциональна сопротивлению нагрузки, то есть уменьшается с ростом напряжения, так как . Откуда следует, что . В каждом конкретном случае величина является константой, следовательно, тепло выделяемое на проводе обратно пропорционально квадрату напряжения на потребителе.
Выбор проводов для цепей
Тепло, выделяемое проводником с током, в той или иной степени выделяется в окружающую среду. В случае, если сила тока в выбранном проводнике превысит некоторое предельно допустимое значение, возможен столь сильный нагрев, что проводник может спровоцировать возгорание находящихся рядом с ним объектов или расплавиться сам. Как правило, при сборке электрических цепей достаточно следовать принятым нормативным документам, которые регламентируют, в частности, выбор сечения проводников.
Электронагревательные приборы
Если сила тока одна и та же на всём протяжении электрической цепи, то в любом выбранном участке будет выделять тепла тем больше, чем выше сопротивление данного участка.
За счёт сознательного увеличения сопротивления участка цепи можно добиться локализованного выделения тепла в этом участке. По этому принципу работают электронагревательные приборы. В них используется нагревательный элемент — проводник с высоким сопротивлением. Повышение сопротивления достигается (совместно или по отдельности) выбором сплава с высоким удельным сопротивлением (например, нихром, константан), увеличением длины проводника и уменьшением его поперечного сечения. Подводящие провода имеют обычное низкое сопротивление и поэтому их нагрев, как правило, незаметен.
Плавкие предохранители
Для защиты электрических цепей от протекания чрезмерно больших токов используется отрезок проводника со специальными характеристиками. Это проводник относительно малого сечения и из такого сплава, что при допустимых токах нагрев проводника не перегревает его, а при чрезмерно больших перегрев проводника столь значителен, что проводник расплавляется и размыкает цепь.

