Закон Ома | Все формулы

Сообщение от администратора:

Ребята! Кто давно хотел выучить английский?
Переходите по моей ссылке и получите два бесплатных урока в школе английского языка SkyEng! 
Занимаюсь там сам — очень круто. Прогресс налицо.

В приложении можно учить слова, тренировать аудирование и произношение.

Попробуйте. Два урока бесплатно по моей ссылке!
Жмите СЮДА

Закон Ома для полной цепи — физический закон, определяющий связь между Электродвижущей силой источника или напряжением с силой тока и сопротивлением проводника.

Закон Ома — сила тока в электрической цепи будет прямо пропорциональна напряжению приложенному к этой цепи, и обратно пропорциональна сумме внутреннего сопротивления источника электропитания и общему сопротивлению всей цепи.

Из закона Ома для полной цепи вытекают следующие следствия:

Следствие 1 : При r < < R Сила тока в цепи обратно пропорциональна её сопротивлению. А сам источник в ряде случаев может быть назван источником напряжения

Следствие 2 : При r > > R Сила тока от свойств внешней цепи (от величины нагрузки) не зависит. И источник может быть назван источником тока.

Электродвижущая сила в замкнутой цепи, по которой течёт ток равняется:

То есть сумма падений напряжения на внутреннем сопротивлении источника тока и на внешней цепи равна ЭДС источника. Последний член в этом равенстве специалисты называют «напряжением на зажимах», поскольку именно его показывает вольтметр, измеряющий напряжение источника между началом и концом присоединённой к нему замкнутой цепи. В таком случае оно всегда меньше ЭДС.

Так же изучите :

Закон Ома в дифференциальной форме :

Закон Ома для переменного тока :

В Формуле мы использовали :

— ЭДС источника напряжения

— Внутреннее сопротивление источника напряжения

— Сила тока в цепи

— Сопротивление

— Напряжение в цепи

— Вектор плотности тока

— Удельная проводимость

— Вектор напряжённости электрического поля

— Сопротивление

— Напряжение в цепи

Обсуждение:Закон Ома — Википедия

Материал из Википедии — свободной энциклопедии

Э… Это не совсем закон Ома.

На самом деле Ом экспериментальным путем установил что:
Сила электрического тока в проводнике пропорциональна приложенному напряжению:

 I ~ U

где:
I — сила тока,
U — приложенное напряжение.

Ом сформулировал свой закон безотносительно к системе единиц.

Закон Ома можно сформулировать в нескольких формах (в том числе и в дифференциальной), но на самом деле закон имеет именно такую форму.

В системе Си закон Ома имеет вид:

I = U/R

где:
I — сила тока в Амперах,
U — приложенное напряжение в Вольтах,
R — сопротивление в Омах.

В других системах единиц закон Ома имеет, конечно же, другой вид.

Проводники — это такие вещества. Резистор — это устройство. К закону Ома отношения не имеет. snv

Согласен с тем, что единицы измерения тут указывать не следует. Убрал. Изменил резистор на проводник. Остальное считаю правильным. Закон Ома — в его современной формулировке (а не так, как его сам Ом формулировал) — есть именно равенство (I = U/R), которое можно записать в любой системе единиц, а не пропорциональность. Igorivanov 16:22, 12 Окт 2004 (UTC)

В системе Си коэффициен пропорциональности 1/R. В других системах едениц коэффициент пропорциональности другой. Хотя за последние 10 лет система Си стала настолько популярной, что я даже сходу не могу привести пример систем едениц в которых коэффициент пропорциональности отличен от 1/R.snv 16:42, 12 Окт 2004 (UTC)

Вовсе нет. Этот коэффициент пропорциональности есть просто определение сопротивления. Т.е. активное сопротивление (ну или эе проводимость) проводника есть, по определению, этот самый коэффициент. От системы единиц зависит, в чем его выражать. Igorivanov 16:54, 12 Окт 2004 (UTC)

Г-н Panaioty, подписи в статье не стоит ставить. Описывайте вашу правку и её причины в обсуждении. Булат Ш. 05:02, 24 июня 2008 (UTC)

Не статья, а какое-то дурное нагромождение разрозненных фактов из учебника ТОЭ. Собственно закон Ома приведён только в пятой (!) формуле, зато в первом же предложении мы зачем-то узнаём про 1826 год и как звали Ома. Надо полагать, до 1826 года этот закон не действовал, а Омов в науке как Поповых в Архангельской губернии. Сравните этот вики-срам хотя бы с английской версией. Там сначала — сам закон, внятно сформулированный и наглядно проиллюстрированный, а затем уже история открытия, имя Ома, размер его ноги и прочая лирика. 89.105.158.250 01:48, 14 октября 2014 (UTC)

Эмпирическая сущность закона Ома[править код]

Закон Ома является эмпирическим, а не фундаментальным, что я отразил во вводной части и в разделе «Трактовка и пределы применимости». Заодно дополнил этот раздел примерами нарушения закона Ома. Raoul NK 16:46, 22 июня 2013 (UTC)

Стрелки, указывающие направления тока и напряжения, должны быть направлены в одну сторону. См. Рис. 3-11 Л.Р. Нейман, К.С. Демирчян Теоретические основы электротехники, т.1, Л., Энергоиздат, 1981 Vnbiryukov (обс.) 13:59, 13 апреля 2017 (UTC)vnbiryukov

Этот рисунок, вообще, не несёт никакого смысла. Стрелки есть у векторов. У напряжения нет стрелок. Alexander Mayorov (обс.) 15:11, 13 апреля 2017 (UTC)

фраза про «математически корректное утверждение…», которое «физически ложно» очень понравилась. Показал его многим коллегам, все (позитивно) оценили. Автору огромное спасибо, как ныне говорят «респект»! 92.243.107.243 07:58, 7 марта 2019 (UTC)АИ.

ЗАКОН ОМА

На рисунке показана схема знакомой вам простейшей электрической цепи. Эта замкнутая цепь состоит из трех элементов: источника напряжения — батареи GB, потребителя тока — нагрузки R, которой может быть, например, нить накала электрической лампы или резистор, и проводников, соединяющих источник напряжения с нагрузкой. Между прочим, если эту цепь дополнить выключателем, то получится полная схема карманного электрического фонаря.

Нагрузка R, обладающая определенным сопротивлением, является участком цепи. Значение тока на этом участке цепи зависит от действующего на нем напряжения и его сопротивления: чем больше напряжение и меньше сопротивление, тем большим ток будет идти по участку цепи. Эта зависимость тока от напряжения и сопротивления выражается следующей формулой:

I = U/R

где I — ток, выраженный в амперах, А; U — напряжение в вольтах, В; R — сопротивление в омах, Ом. Читается это математическое выражение так: ток на участке цепи прямо пропорционален напряжению на нем и обратно пропорционален его сопротивлению. Это основной закон электротехники, именуемый законом Ома (по фамилии Г. Ома), для участка электрической цепи. Используя закон Ома, можно по двум известным электрическим величинам узнать неизвестную третью. Вот несколько примеров практического применения закона Ома.

Первый пример: На участке цепи, обладающем сопротивлением 5 Ом, действует напряжение 25 В. Надо узнать значение тока на этом участке цепи.
Решение: I = U/R = 25 / 5 = 5 А.
Второй пример: На участке цепи действует напряжение 12 В, создавая в нем ток, равный 20 мА. Каково сопротивление этого участка цепи? Прежде всего ток 20 мА нужно выразить в амперах. Это будет 0,02 А. Тогда R = 12 / 0,02 = 600 Ом.
Третий пример: Через участок цепи сопротивлением 10 кОм течет ток 20 мА. Каково напряжение, действующее на этом участке цепи? Здесь, как и в предыдущем примере, ток должен быть выражен в амперах (20 мА = 0,02 А), сопротивление в омах (10кОм = 10000Ом). Следовательно, U = IR = 0,02 х 10000 = 200 В. На цоколе лампы накаливания плоского карманного фонаря выштамповано: 0,28 А и 3,5 В. О чем говорят эти сведения? О том, что лампочка будет нормально светиться при токе 0,28 А, который обусловливается напряжением 3,5 В, Пользуясь законом Ома, нетрудно подсчитать, что накаленная нить лампочки имеет сопротивление R = 3,5 / 0,28 = 12,5 Ом. Это, подчеркиваю, сопротивление накаленной нити лампочки. А сопротивление остывшей нити значительно меньше. Закон Ома справедлив не только для участка, но и для всей электрической цепи. В этом случае в значение R подставляется суммарное сопротивление всех элементов цепи, в том числе и внутреннее сопротивление источника тока. Однако при простейших расчетах цепей обычно пренебрегают сопротивлением соединительных проводников и внутренним сопротивлением источника тока.

В связи с этим приведу еще один пример: Напряжение электроосветительной сети 220 В. Какой ток потечет в цепи, если сопротивление нагрузки равно 1000Ом? Решение: I = U/R = 220 / 1000 = 0,22 А. Примерно такой ток потребляет электрический паяльник.
Всеми этими формулами, вытекающими из закона Ома, можно пользоваться и для расчета цепей переменного тока, но при условии, если в цепях нет катушек индуктивности и конденсаторов.
Закон Ома и производные от него расчетные формулы, достаточно легко запомнить, если пользоваться вот этой графической схемой, т. н. треугольник закона Ома:

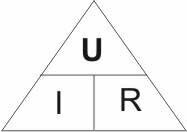
>Пользоваться этим треугольником легко, достаточно четко запомнить, что горизонтальная линия в треугольнике означает знак деления (по аналогии дробной черты), а вертикальная линия в треугольнике означает знак умножения.

Теперь рассмотрим такой вопрос: как влияет на ток резистор, включаемый в цепь последовательно с нагрузкой или параллельно ей? Разберем такой пример. У нас имеется лампочка от круглого электрического, фонаря, рассчитанная на напряжение 2,5 В и ток 0,075 А. Можно ли питать эту лампочку от батареи 3336Л, начальное напряжение которой 4,5 В? Нетрудно подсчитать, что накаленная нить этой лампочки имеет сопротивление немногим больше 30 Ом. Если же питать ее от свежей батареи 3336Л, то через нить накала лампочки, по закону Ома, пойдет ток, почти вдвое превышающий тот ток, на который она рассчитана. Такой перегрузки нить не выдержит, она перекалится и разрушится. Но эту лампочку все же можно питать от батареи 336Л, если последовательно в цепь включить добавочный резистор сопротивлением 25 Ом, как это показано на рис..

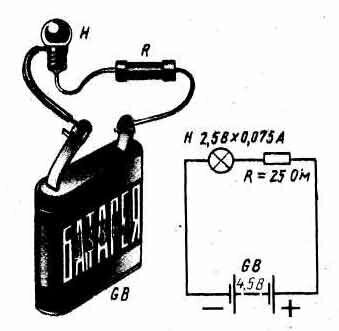
В этом случае общее сопротивление внешней цепи будет равно примерно 55 Ом, т.е. 30 Ом — сопротивление нити лампочки Н плюс 25 Ом — сопротивление добавочного резистора R. В цепи, следовательно, потечет ток, равный примерно 0,08 А, т.е. почти такой же, на который рассчитана нить накала лампочки. Эту лампочку можно питать от батареи и с более высоким напряжением и даже от электроосветительной сети, если подобрать резистор соответствующего сопротивления. В этом примере добавочный резистор ограничивает ток в цепи до нужного нам значения. Чем больше будет его сопротивление, тем меньше будет и ток в цепи. В данном случае в цепь было включено последовательно два сопротивления: сопротивление нити лампочки и сопротивление резистора. А при последовательном соединении сопротивлений ток одинаков во всех точках цепи. Можно включать амперметр в любую точку цепи, и всюду он будет показывать одно значение. Это явление можно сравнить с потоком воды в реке. Русло реки на различных участках может быть широким или узким, глубоким или мелким. Однако за определенный промежуток времени через поперечное сечение любого участка русла реки всегда проходит одинаковое количество воды.
Добавочный резистор, включаемый в цепь последовательно с нагрузкой (как, например, на рис. выше), можно рассматривать как резистор, «гасящий» часть напряжения, действующего в цепи. Напряжение, которое гасится добавочным резистором или, как говорят, падает на нем, будет тем большим, чем больше сопротивление этого резистора. Зная ток и сопротивление добавочного резистора, падение напряжения на нем легко подсчитать все по той же знакомой вам формуле U = IR, Здесь U — падение напряжения, В; I — ток в цепи, A; R — сопротивление добавочного резистора, Ом. Применительно к нашему примеру резистор R ( на рис.) погасил избыток напряжения: U = IR = 0,08 х 25 = 2 В. Остальное напряжение батареи, равное приблизительно 2,5 В, упало на нити лампочки. Необходимое сопротивление резистора можно найти по другой знакомой вам формуле R = U/I, где R — искомое сопротивление добавочного резистора, Ом; U-напряжение, которое необходимо погасить, В; I — ток в цепи, А. Для нашего примера сопротивление добавочного резистора равно: R = U/I = 2/0,075, 27 Ом. Изменяя сопротивление, можно уменьшать или увеличивать напряжение, которое падает на добавочном резисторе, и таким образом регулировать ток в цепи. Но добавочный резистор R в такой цепи может быть переменным, т.е. резистором, сопротивление которого можно изменять (см. рис. ниже).

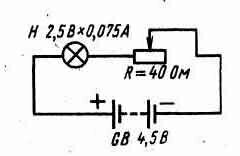
В этом случае с помощью движка резистора можно плавно изменять напряжение, подводимое к нагрузке Н, а значит, плавно регулировать ток, протекающий через эту нагрузку. Включенный таким образом переменный резистор называют реостатом, С помощью реостатов регулируют токи в цепях приемников, телевизоров и усилителей. Во многих кинотеатрах реостаты использовали для плавного гашения света в зрительном зале. Есть, однако, и другой способ подключения нагрузки к источнику тока с избыточным напряжением — тоже с помощью переменного резистора, но включенного потенциометром, т.е. делителем напряжения, как показано на рис..

Здесь R1 — резистор, включенный потенциометром, a R2 — нагрузка, которой может быть та же лампочка накаливания или какой — то другой прибор. На резисторе R1 происходит падение напряжения источника тока, которое частично или полностью может быть подано к нагрузке R2. Когда движок резистора находится в крайнем нижнем положении, к нагрузке напряжение вообще не подается (если это лампочка, она гореть не будет). По мере перемещения движка резистора вверх мы будем подавать все большее напряжение к нагрузке R2 (если это лампочка, ее нить будет накаливаться). Когда же движок резистора R1 окажется в крайнем верхнем положении, к нагрузке R2 будет подано все напряжение источника тока (если R2 — лампочка карманного фонаря, а напряжение источника тока большое, нить лампочки перегорит). Можно опытным путем найти такое положение движка переменного резистора, при котором к нагрузке будет подано необходимое ей напряжение. Переменные резисторы, включаемые потенциометрами, широко используют для регулирования громкости в приемниках и усилителях. Резистор может быть непосредственно подключен параллельно нагрузке. В таком случае ток на этом участке цепи разветвляется и идет двумя параллельными путями: через добавочный резистор и основную нагрузку. Наибольший ток будет в ветви с наименьшим сопротивлением. Сумма же токов обеих ветвей будет равна току, расходуемому на питание внешней цепи. К параллельному соединению прибегают в тех Случаях, когда надо ограничить ток не во всей цепи, как при последовательном включении добавочного резистора, а только на каком — то участке. Добавочные резисторы подключают, например, параллельно миллиамперметрам, чтобы ими можно было измерять большие токи. Такие резисторы называют шунтирующими или шунтами. Слово шунт означает ответвление.

Спасибо lessonradio.narod.ru

Закон Ома для магнитной цепи — Википедия

Материал из Википедии — свободной энциклопедии

Зако́н О́ма для магни́тной цепи́ (зако́н Го́пкинсона) — физический закон для магнитной цепи, аналогичный закону Ома для электрической цепи. Определяет связь между магнитодвижущей силой, магнитным сопротивлением и магнитным потоком в магнитной цепи.

В неразветвлённой магнитной цепи магнитный поток прямо пропорционален магнитодвижущей силе и обратно пропорционален полному магнитному сопротивлению^[1].

Рассмотрим неразветвлённую магнитную цепь, состоящую из ярма с площадью поперечного сечения S{\displaystyle S} из материала c магнитной проницаемостью μ{\displaystyle \mu } и зазора из другого материала, имеющего то же сечение и магнитную проницаемость μ1{\displaystyle \mu _{1}}. На ярмо надета катушка с числом витков N{\displaystyle N}, по которой идёт ток i{\displaystyle i}. Рассмотрим среднюю линию магнитной цепи и применим теорему о циркуляции магнитного поля.

Hl+h2l1=4πNic.(1){\displaystyle Hl+H_{1}l_{1}={\frac {4\pi Ni}{c}}.\qquad (1)}

Здесь H{\displaystyle H} — напряжённость магнитного поля внутри ярма, h2{\displaystyle H_{1}} — напряжённость магнитного поля внутри зазора, l{\displaystyle l} — длина ярма, измеренная вдоль средней линии индукции, l1{\displaystyle l_{1}} — длина зазора. Так как линии индукции непрерывны, то значения магнитного потока Φ{\displaystyle \Phi } внутри ярма и внутри зазора одинаковы. Из соотношений Φ=BS,B=μH{\displaystyle \Phi =BS,B=\mu H} выражаем напряжённость магнитного поля через поток H=Φ/(μS),{\displaystyle H=\Phi /(\mu S),} h2=Φ/(μ1S).{\displaystyle H_{1}=\Phi /(\mu _{1}S).} Подставляя эти выражения в формулу (1), получаем из неё значение магнитного потока Φ{\displaystyle \Phi }:

Φ=4πNiclμS+l1μ1S.{\displaystyle \Phi ={\frac {\frac {4\pi Ni}{c}}{{\frac {l}{\mu S}}+{\frac {l_{1}}{\mu 1S}}}}.}

Полученная формула подобна закону Ома для замкнутой электрической цепи. При этом величина Fm=4πNic{\displaystyle F_{m}={\frac {4\pi Ni}{c}}} играет роль электродвижущей силы и поэтому по аналогии она получила название магнитодвижущей силы. Её отличие от электродвижущей силы состоит в том, что в магнитном потоке не движутся никакие частицы. Сумма Rm=lμS+l1μ1S{\displaystyle R_{m}={\frac {l}{\mu S}}+{\frac {l_{1}}{\mu _{1}S}}} входит в формулу так же, как полное сопротивление электрической цепи в законе Ома, и поэтому её называют полным магнитным сопротивлением цепи. Итак, закон Ома для магнитной цепи можно записать в виде Φ=FmRm.{\displaystyle \Phi ={\frac {F_{m}}{R_{m}}}.} В неразветвлённой магнитной цепи магнитный поток равен частному от деления магнитодвижущей силы на полное магнитное сопротивление.

Идею о том, что величину магнитного потока в магнитной цепи можно записать аналогично закону Ома для электрической цепи, первым высказал американский физик Генри Роуланд в 1873 году^[2]. Закон часто называют формулой Гопкинсона или законом Гопкинсона в честь английского физика и инженера Джона Гопкинсона (Хопкинсона), который вместе со своим братом Эдвардом в 1886 году разработал формализм для расчёта магнитных цепей.

разница с выражением для участка контура, определение, формула

Среди известных широкой общественности физических формул лидирует E=mc². По популярности с ней может соперничать только U=IR. Это простое выражение имеет фундаментальное значение для электротехники и описывает математически соотношение между параметрами участка электрической цепи. Менее известен закон Ома для полной цепи, который рассматривает нагрузку неотделимо от источника напряжения.

Основные понятия

Электрический ток течёт, когда замкнутый контур позволяет электронам перемещаться от высокого потенциала к более низкому в цепи. Иначе говоря, ток требует источника электронов, обладающего энергией для приведения их в движение, а также точки их возвращения отрицательных зарядов, для которой характерен их дефицит. Как физическое явление ток в цепи характеризуется тремя фундаментальными величинами:

• напряжение;
• сила тока;
• сопротивление проводника, по которому движутся электроны.

Сила и напряжение

Сила тока (I, измеряется в Амперах) есть объём электронов (заряд), перемещающихся через место в цепи за единицу времени. Иными словами, измерение I — это определение количества электронов, находящихся в движении. Важно понимать, что термин относится только к движению: статические заряды, например, на клеммах неподсоединённой батареи, не имеют измеряемого значения I. Ток, который протекает в одном направлении, называется постоянным (DC), а периодически изменяющий направление — переменным (AC).

Вольт — единица измерения, применяемая для электрической разницы потенциалов, самого потенциала и электродвижущей силы. Термин напряжение (U) относится к электрической разности потенциалов между точками. Любые статические заряды имеют значение в Вольтах, а величина их разности определяется как U.

Напряжение можно проиллюстрировать таким явлением, как давление, или как разность потенциальной энергии предметов под воздействием гравитации. Для того чтобы создать этот дисбаланс, нужно затратить предварительно энергию, которая и будет реализована в движении при соответствующих обстоятельствах. Например, в падении груза с высоты реализуется работа по его подъёму, в гальванических батареях разность потенциалов на клеммах образуется за счёт преобразования химической энергии, в генераторах — в результате воздействия электромагнитного поля.

Сопротивление проводников

Независимо от того, насколько хорош обычный проводник, он никогда не будет пропускать сквозь себя электроны без какого-либо сопротивления их движению. Можно рассматривать сопротивление как аналог механического трения, хотя это сравнение не будет совершенным. Когда ток протекает через проводник, некоторая разность потенциалов преобразуется в тепло, поэтому всегда будет падение напряжения на резисторе. Электрические обогреватели, фены и другие подобные устройства предназначены исключительно для рассеивания электрической энергии в виде тепла.

Упрощённо сопротивление (обозначается как R) является мерой того, насколько поток электронов тормозится в цепи. Оно измеряется в Омах. Проводимость резистора или другого элемента определяется двумя свойствами:

• геометрией;
• материалом.

Форма имеет важнейшее значение, это очевидно на гидравлической аналогии: протолкнуть воду через длинную и узкую трубу гораздо тяжелее, чем через короткую и широкую. Материалы играют определяющую роль. Например, электроны могут свободно перемещаться в медном проводе, но не способны протекать вообще через такие изоляторы, как каучук, независимо от их формы. Кроме геометрии и материала, существуют и другие факторы, влияющие на проводимость.

Закон для участка цепи

Существует фундаментальная связь между напряжением, током и проводимостью. Это знаменитое уравнение называется законом Ома, и его можно отобразить тремя эквивалентными способами:

Выраженный в словах он звучит так: ток, протекающий через проводник между двумя контактами, прямо пропорционален напряжению на этих контактах. Первые два выражения фиксируют константу пропорциональности между током и напряжением. Последнее можно рассматривать как определение для единичного резистора — элемента, позволяющего протекать единице тока под единичным напряжением.

Приведённые математические соотношения — основа для электротехники и электроники. Закон был назван в честь немецкого физика Георга Симона Ома, который в монографии, опубликованной в 1827 г., описал измерения приложенного напряжения и тока с помощью простых электрических цепей, состоящих из проводов различной длины.

Исследователь объяснил свои экспериментальные результаты несколько сложнее, чем отражено в приведённых уравнениях, известных в современной физике как неполный закон Ома. Для того чтобы сформулировать закон Ома для полной электрической цепи, необходимо оперировать понятиями внутреннего сопротивления источника тока и электродвижущей силы.

Электродвижущая сила

Перемещение электронов в любом источнике создаётся с помощью сторонних сил. Их природа может быть различной. В гальванических элементах или аккумуляторах они возникают в результате электрохимических процессов. В генераторах тока они появляются как результат движения проводников в магнитном поле. Источник тока в электрической схеме играет ту же роль, что и насос, перекачивающий жидкость в замкнутой гидравлической системе.

Под воздействием внешних сил заряды двигаются внутри источника тока против сил электростатического поля. Это позволяет поддерживать постоянный ток в замкнутом контуре до тех пор, пока работают внешние силы. Физическая величина, равная отношению затраченной энергии сторонних сил на перемещение заряда, называется электродвижущей силой источника тока. Она может быть представлена формулой ℰ = A/q. В этом выражении:

• ℰ — ЭДС в вольтах;
• A — работа в джоулях;
• q — заряд в кулонах.

По аналогии с замкнутой гидравлической системой и насосом, электрические заряды протекают непрерывно по всему контуру, и привести их в движение могут только внешние силы. Это означает, что работу по перемещению заряда любым источником можно рассматривать как ЭДС и измерять в вольтах. Вывод о модели цепи с источником, в которой протекает ток, как о замкнутом контуре крайне важен для понимания закона Ома для полного участка цепи.

Внешнее и внутреннее сопротивление

Все батареи и генераторы обладают внутренним сопротивлением: электроды и электролиты неабсолютные проводники, как и провода обмоток электрических машин. Оно может варьироваться от тысячных долей ома до нескольких ом. Этот физический параметр является ключевым в законе Ома для всей цепи. В качестве математических моделей для рассмотрения и иллюстрации электрических процессов различают:

• Идеальный источник тока (ИИТ). Генерирует электрический ток, не зависящий от изменений напряжения. Внутреннее сопротивление ИИТ бесконечно, напряжение полностью определяется подключённой схемой. Ни один физический источник тока не может работать в условиях разрыва цепи, поэтому ИИТ возможен только в качестве абстрактной модели.
• Идеальный источник напряжения (ИИН). Представляет собой устройство, поддерживающее постоянное выходное напряжение независимо от тока, протекающего по контуру. Обладает нулевым внутренним сопротивлением. ИИН удобен для моделирования практических источников, которые можно представить как ИНН с подключённым резистором.

Внутренне сопротивление источника электрической энергии является фактором обеспечения максимальной мощности для подключённой к нему нагрузки. Наиболее эффективный перенос энергии происходит, когда внешнее сопротивление значительно превышает внутреннее у источника.

Например, свинцово-кислотные аккумуляторы автомобиля, благодаря низкому внутреннему сопротивлению, способны создавать относительно высокие токи при сравнительно низком напряжении. Однако, с другой стороны, высоковольтные источники должны иметь высокое внутренне сопротивление, чтобы ограничить количество тока, протекающего в результате случайного короткого замыкания.

Полный закон

Выражение U=IR описывает явления во фрагменте электрической цепи, через которую протекает ток. В этом уравнении не принимается во внимание наличие источников. Если исправить такое упрощение, то можно получить формулу закона Ома для полной цепи: ℰ =I (R+r).

В этом уравнении предусмотрено наличие в контуре источника питания электродвижущей силы ℰ c внутренним сопротивлением r. Поскольку ЭДС — практически величина, зависящая от внешних сил, то физический смысл имеет расчёт силы тока для полной цепи при помощи выражения: I=ℰ/(R+r).

Таким образом, полный постулат Ома гласит о зависимости силы тока в замкнутом контуре от внутреннего сопротивления его источника, то есть учитывает сопротивление электролита и электродов для гальванических элементов и проводимость обмоток генераторов. Основное практическое применение — расчёт силы тока в линейных электрических цепях DC, определение мощности и импеданса любых элементов цепи.

Закон Ома — это… Что такое Закон Ома?

V — напряжение,
I — сила тока,
R — сопротивление.

Зако́н О́ма — физический закон, определяющий связь электродвижущей силы источника или электрического напряжения с силой тока и сопротивлением проводника. Экспериментально установлен в 1826 году, и назван в честь его первооткрывателя Георга Ома.

В своей оригинальной форме он был записан его автором в виде : ,

Здесь X — показания гальванометра, т.е в современных обозначениях сила тока I, a — величина, характеризующая свойства источника тока, постоянная в широких пределах и не зависящая от величины тока, то есть в современной терминологии электродвижущая сила (ЭДС) , l — величина, определяемая длиной соединяющих проводов, чему в современных представлениях соответствует сопротивление внешней цепи R и, наконец, b параметр, характеризующий свойства всей установки, в котором сейчас можно усмотреть учёт внутреннего сопротивления источника тока r^[1].

В таком случае в современных терминах и в соответствии с предложенной автором записи формулировка Ома (1) выражает

Закон Ома для полной цепи:

, (2)

где:

Из закона Ома для полной цепи вытекают следствия:

• При r<<R сила тока в цепи обратно пропорциональна её сопротивлению. А сам источник в ряде случаев может быть назван источником напряжения
• При r>>R сила тока от свойств внешней цепи (от величины нагрузки) не зависит. И источник может быть назван источником тока.

Часто^[2] выражение:

(3)

(где есть напряжение или падение напряжения, или, что то же, разность потенциалов между началом и концом участка проводника) тоже называют «Законом Ома».

Таким образом, электродвижущая сила в замкнутой цепи, по которой течёт ток в соответствии с (2) и (3) равняется:

(4)

То есть сумма падений напряжения на внутреннем сопротивлении источника тока и на внешней цепи равна ЭДС источника. Последний член в этом равенстве специалисты называют «напряжением на зажимах», поскольку именно его показывает вольтметр, измеряющий напряжение источника между началом и концом присоединённой к нему замкнутой цепи. В таком случае оно всегда меньше ЭДС.

К другой записи формулы (3), а именно:

(5)

Применима другая формулировка:

Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи.

Выражение (5) можно переписать в виде:

(6)

где коэффициент пропорциональности G назван проводимость или электропроводность. Изначально единицей измерения проводимости был «обратный Ом» — Mо^[3], впоследствии переименованный в Си́менс (обозначение: См, S).

Мнемоническая диаграмма для Закона

Схема, иллюстрирующая три составляющие закона Ома Диаграмма, помогающая запомнить закон Ома. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления

В соответствии с этой диаграммой формально может быть записано выражение:

(7)

Которое всего лишь позволяет вычислить (применительно к известному току, создающему на заданном участке цепи известное напряжение), сопротивление этого участка. Но математически корректное утверждение о том, что сопротивление проводника растёт прямо пропорционально приложенному к нему напряжению и обратно пропорционально пропускаемому через него току, физически ложно.

В специально оговорённых случаях сопротивление может зависеть от этих величин, но по умолчанию оно определяется лишь физическими и геометрическими параметрами проводника:

(8)

где:

•  — удельное сопротивление материала, из которого сделан проводник,
•  — его длина
•  — площадь его поперечного сечения

Закон Ома и ЛЭП

Одним из важнейших требований к линиям электропередач (ЛЭП) является уменьшение потерь при доставке энергии потребителю. Эти потери в настоящее время заключаются в нагреве проводов, то есть переходе энергии тока в тепловую энергию, за что ответственно омическое сопротивление проводов. Иными словами задача состоит в том, чтобы довести до потребителя как можно более значительную часть мощности источника тока = при минимальных потерях мощности в линии передачи = , где , причём на этот раз есть суммарное сопротивление проводов и внутреннего сопротивления генератора, (последнее всё же меньше сопротивления линии передач).

В таком случае потери мощности будут определяться выражением:

= (9)

Отсюда следует, что при постоянной передаваемой мощности её потери растут прямо пропорционально длине ЛЭП и обратно пропорционально квадрату ЭДС. Таким образом желательно всемерное её увеличение, что ограничивается электрической прочностью обмотки генератора. И повышать напряжение на входе линии следует уже после выхода тока из генератора, что для постоянного тока является проблемой. Однако, для переменного тока эта задача много проще решается с помощью использования трансформаторов, что и предопределило повсеместное распространение ЛЭП на переменном токе. Однако при повышении напряжения в ней возникают потери на коронирование и возникают трудности с обеспечением надёжности изоляции от земной поверхности. Поэтому наибольшее, практически используемое, напряжение в дальних ЛЭП не превышает миллиона вольт.

Кроме того, любой проводник, как показал Дж. Максвелл, при изменении силы тока в нём, излучает энергию в окружающее пространство, и потому ЛЭП ведёт себя как антенна, что заставляет в ряде случаев наряду с омическими потерями брать в расчёт и потери на излучение.

Закон Ома в дифференциальной форме

Сопротивление зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника.

Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем:

где:

Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость является тензором ранга (1, 1).

Раздел физики, изучающий течение электрического тока в различных средах, называется электродинамикой сплошных сред.

Закон Ома для переменного тока

Вышеприведённые соображения о свойствах электрической цепи при использовании источника (генератора) с переменной во времени ЭДС остаются справедливыми. Специальному рассмотрению подлежит лишь учёт специфических свойств потребителя, приводящих к разновремённости достижения напряжением и током своих максимальных значений, то есть учёта фазового сдвига.

Если ток является синусоидальным с циклической частотой , а цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), то закон Ома обобщается; величины, входящие в него, становятся комплексными:

где:

• U = U₀e^iωt — напряжение или разность потенциалов,
• I — сила тока,
• Z = Re^−iδ — комплексное сопротивление (импеданс),
• R = (R_a² + R_r²)^1/2 — полное сопротивление,
• R_r = ωL − 1/(ωC) — реактивное сопротивление (разность индуктивного и емкостного),
• R_а — активное (омическое) сопротивление, не зависящее от частоты,
• δ = − arctg (R_r/R_a) — сдвиг фаз между напряжением и силой тока.

При этом переход от комплексных переменных в значениях тока и напряжения к действительным (измеряемым) значениям может быть произведён взятием действительной или мнимой части (но во всех элементах цепи одной и той же!) комплексных значений этих величин. Соответственно, обратный переход строится для, к примеру, подбором такой что Тогда все значения токов и напряжений в схеме надо считать как

Если ток изменяется во времени, но не является синусоидальным (и даже периодическим), то его можно представить как сумму синусоидальных Фурье-компонент. Для линейных цепей можно считать компоненты фурье-разложения тока действующими независимо.

Также необходимо отметить, что закон Ома является лишь простейшим приближением для описания зависимости тока от разности потенциалов и от сопротивления и для некоторых структур справедлив лишь в узком диапазоне значений. Для описания более сложных (нелинейных) систем, когда зависимостью сопротивления от силы тока нельзя пренебречь, принято обсуждать вольт-амперную характеристику. Отклонения от закона Ома наблюдаются также в случаях, когда скорость изменения электрического поля настолько велика, что нельзя пренебрегать инерционностью носителей заряда.

Трактовка закона Ома

Закон Ома можно просто объяснить при помощи теории Друде:

Здесь:

См. также

Примечания

Ссылки

Закон Ома.

Закон Ома.

Программа КИП и А

В программу «КИП и А», в разделе «Электрика» включен блок расчета закона Ома для постоянного и переменного тока. Сначала немного теории..

Для постоянного тока

Закон Ома определяет зависимость между током (I), напряжением (U) и сопротивлением (R) в участке электрической цепи. Наиболее популярна формулировка:

Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи, т.е.

I = U / R	где	I — сила тока, измеряемая в Амперах, (A)
		U — напряжение, измеряемое в Вольтах, (V)
		R — сопротивление, измеряется в Омах, (Ω)

Закон Ома, является основополагающим в электротехнике и электронике. Без его понимания также не представляется работа подготовленного специалиста в области КИП и А. Когда-то была даже распространена такая поговорка, — «Не знаешь закон Ома, — сиди дома..».

Помимо закона Ома, важнейшим является понятие электрической мощности, P:

Мощность постоянного тока (P) равна произведению силы тока (I) на напряжение (U), т.е.

P = I × U	где	P — эл. мощность, измеряемая в Ваттах, (W)
		I — сила тока, измеряемая в Амперах, (A)
		U — напряжение, измеряемое в Вольтах, (V)

Комбинируя эти две формулы, выведем зависимость между силой тока, напряжением, сопротивлением и мощностью, и создадим таблицу:

Сила тока,	I=	U/R	P/U	√(P/R)
Напряжение,	U=	I×R	P/I	√(P×R)
Сопротивление,	R=	U/I	P/I²	U²/P
Мощность,	P=	I×U	I²×R	U²/R

Практический пример использования таблицы: Покупая в магазине утюг, мощностью 1 кВт (1 кВт = 1000 Вт), высчитываем на какой минимальный ток должна быть рассчитана розетка в которую предполагается включать данную покупку:
Несмотря на то, что утюг включается в сеть переменного тока, пренебрегаем его реактивным сопротивлением (см. ниже), и используем упрощенную формулу для постоянного тока. Находим в таблице I = P / U. Получаем: 1000 кВт / 220 В (напряжение сети) = 4,5 Ампера. Это и есть минимальный ток, который должна выдерживать розетка, при подключении к ней нагрузки мощностью 1 кВт.

Наиболее распространенные множительные приставки:

• Сила тока, Амперы (A): 1 килоампер (1 kА) = 1000 А. 1 миллиампер (1 mA) = 0,001 A. 1 микроампер (1 µA) = 0,000001 A.
• Напряжение, Вольты (V): 1 киловольт (1kV) = 1000 V. 1 милливольт (1 mV) = 0,001 V. 1 микровольт (1 µV) = 0,000001 V.
• Сопротивление, Омы (Om): 1 мегаом (1 MOm) = 1000000 Om. 1 килоом (1 kOm) = 1000 Om.
• Мощность, Ватты (W): 1 мегаватт (1 MW) = 1000000 W. 1 киловатт (1 kW) = 1000 W. 1 милливатт (1 mW) = 0,001 W.

Для переменного тока

В цепи переменного тока закон Ома может иметь некоторые особенности, описанные ниже.

Импеданс, Z

В цепи переменного тока, сопротивление кроме активной (R), может иметь как емкостную (C), так и индуктивную (L) составляющие. В этом случае вводится понятие электрического импеданса, Z (полного или комплексного сопротивления для синусоидального сигнала). Упрощенные схемы комплексного сопротивления приведены на рисунках ниже, слева для последовательного, справа для параллельного соединения индуктивной и емкостной составляющих.

Последовательное включение R, L, C
Параллельное включение R, L, C

Также, полное сопротивление, Z зависит не только от емкостной (C), индуктивной (L) и активной (R) составляющих, но и от частоты переменного тока.

Импеданс, Полное сопротивление, Z
При последовательном включении R, L, C	При параллельном включении R, L, C
Z=√(R2+(ωL-1/ωC)2)	Z=1/ √(1/R2+(1/ωL-ωC)2)
где,
ω = 2πγ — циклическая, угловая частота; γ — частота переменного тока.

Коэффициент мощности, Cos(φ)

Коэффициент мощности, в самом простом понимании, это отношение активной мощности (P) потребителя электрической энергии к полной (S) потребляемой мощности, т. е.

Cos(φ) = P / S

Он также показывает насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения.
Изменяется от 0 до 1. Если нагрузка не содержит реактивных составляющих (емкостной и индуктивной), то коэффициент мощности равен единице.
Чем ближе Cos(φ) к единице, тем меньше потерь энергии в электрической цепи.

Исходя из вышеперечисленных понятий импеданса Z и коэффициента мощности Cos(φ), характерных для переменного тока, выведем формулу закона Ома, коэффициента мощности и их производные для цепей переменного тока:

I = U / Z	где	I — сила переменного тока, измеряемая в Амперах, (A)
		U — напряжение переменного тока, измеряемое в Вольтах, (V)
		Z — полное сопротивление (импеданс), измеряется в Омах, (Ω)

Производные формулы:

Сила тока,	I=	U/Z	P/(U×Cos(φ))	√(P/Z)
Напряжение,	U=	I×Z	P/(I×Cos(φ))	√(P×Z)
Полное сопротивление, импеданс	Z=	U/I	P/I²	U²/P
Мощность,	P=	I²×Z	I×U×Cos(φ)	U²/Z

Программа «КИП и А» имеет в своем составе блок расчета закона Ома как для постоянного и переменного тока, так и для расчета импеданса и коэффициента мощности Cos(φ). Скриншоты представлены на рисунках внизу:

Закон Ома для постоянного тока
Закон Ома для переменного тока
Расчет полного сопротивления
Расчет коэффициента мощности Cos(φ)