2.11. Закон Ома в комплексной форме записи

Комплексное сопротивление Z включено в цепь переменного тока с напряжением (рис. 2.18). Точка над буквой Z не ставится, точку принято ставить над комплексными величинами, которые представляют синусоидальные функции времени.

Ток в цепи определяется по закону Ома:

,

где: R – активное сопротивление цепи;

X – реактивное сопротивление цепи, которое может быть индуктивным или емкостным;

z – модуль комплексного сопротивления;

φ – угол сдвига по фазе.

Рис. 2.18. Цепь переменного тока с комплексным сопротивлением Z

2.12. Комплексная проводимость

Под комплексной проводимостью Y понимают величину, обратную комплексному сопротивлению Z:

,

где: – активная проводимость;

–реактивная проводимость цепи.

Если X положительно, то и b положительно, при отрицательном X, b также отрицательно.

Аналогично треугольнику сопротивлений строим треугольник проводимостей (рис. 2.19). Треугольник проводимостей – графическая интерпретация связи между модулем полной проводимости у и ее активной и реактивной составляющими: .

Рис. 2.19. Треугольник проводимостей

При использовании комплексной проводимости закон Ома записывается следующим образом:

=∙.

2.13. Активная, реактивная и полная мощность цепи переменного тока

Под активной мощностью Р понимают среднее значение мгновенной мощности р за период Т:

,

где: и = U_msin(ωt + φ) ; i = I_msinωt.

Активная мощность – это энергия, которая определяется в единицу времени (предполагается, что в 1 секунду укладывается целое число периодов Т) в резисторе R:

P = I²R [Вт].

Реактивная мощность Q = UIsinφ [вар].

Если sinφ > 0, то и Q > 0, если sinφ < 0, то Q < 0.

Полная мощность определяется из треугольника мощностей (рис. 2.20), который подобен треугольнику сопротивлений:

или S = U·I [В·А].

Рис.2.20. Треугольник мощностей

Из треугольника мощностей получаем:

.

2.14. Комплексная форма записи мощности

Допустим, что к электрической цепи (см. рис. 2.18) подведено напряжение , по цепи протекает ток .

Представим эти два вектора на комплексной плоскости(рис. 2.21).

Рис. 2.21. Комплексные напряжение и ток

Комплексная мощность

,

где: – сопряженный комплекс тока;

s – модуль комплексной мощности.

2.15. Законы Кирхгофа в комплексной форме записи.

Для цепей переменного тока справедливы законы Кирхгофа, сформулированные ранее для цепей постоянного тока, см. 1.5, п. 1.6.

Согласно первому закону сумма комплексных токов в узле равна нулю:

.

Второй закон применяется к любому замкнутому контуру цепи:

,

где:

–алгебраическая сумма комплексных э.д.с. источников напряжения;

–падения напряжений на комплексных сопротивлениях Z_k отдельных участков.

2.16. Цепь переменного тока с последовательным соединением элементов

Согласно второму закону Кирхгофа для цепи рис. 2.22 можно записать

Рис. 2.22. Цепь переменного тока с последовательным соединением R

, L, С

Для действующих значений

,

где: X_L – X_C = X – реактивное сопротивление цепи.

Ток в цепи определяется по закону Ома:

или в комплексной форме записи:

,

где: – напряжение, приложенное к цепи;

Z – комплексное сопротивление цепи.

В данной цепи возможны следующие три варианта.

1. Индуктивное сопротивление больше емкостного X_L > Х_C , следовательно,

U_L > U_C .

Векторная диаграмма для этого случая представлена на рис. 2.23, а. Вектор для наглядности изображен рядом с вектором, в действительности компенсирует . Угол в данном случае положительный, вектор напряжения опережает вектор тока на угол φ.

Рис. 2.23. Векторные диаграммы для цепи с последовательным соединением

R, L, C: a – X_L

> X_C ; б – X_L < X_C; в – X_L = X_C

2. Индуктивное сопротивление меньше емкостного Х_L < Х_C, следовательно, U_L < U_c (рис. 2.23, б), угол φ отрицательный, вектор тока опережает вектор напряжения на угол φ, по отношению к сети нагрузка является активно-емкостной.

3. Индуктивное сопротивление равно емкостному X_L = Х_с – условие резонанса напряжений (рис. 2.23, в).

Реактивное сопротивление цепи X = X_L – Х_с = 0, полное сопротивление равно активному Z = R. Ток в цепи определяется величиной активного сопротивления и намного превышает номинальное значение тока для данной цепи. Напряжения на реактивных элементах равны U_L= X_L I = U

_C = Х_с Iи превышают в раз напряжение сети U=U_R. Угол сдвига фаз φ = 0, следовательно, cosφ = 1.

Активная мощность цепи равна полной Р = UIcosφ = UI = S, а реактивная Q = UIsinφ = 0.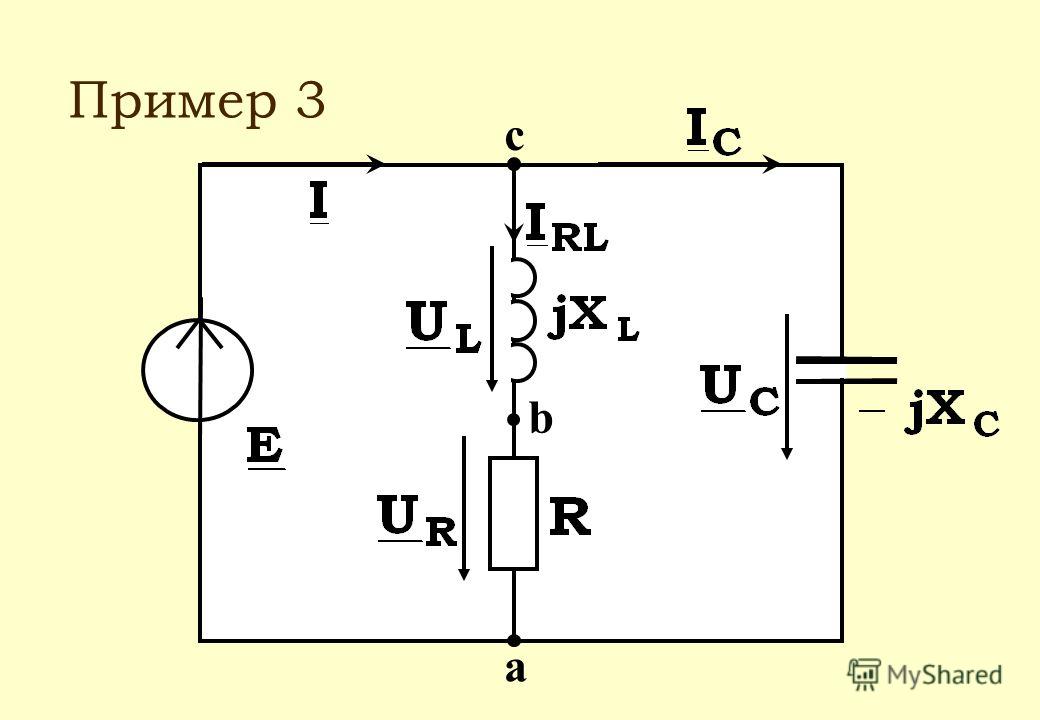

Резонансная частота последовательного колебательного контура зависит от величины индуктивностиL и емкости С.

Явление резонанса напряжений широко используют в различных электрорадиотехнических устройствах.

2.4 Закон Ома в комплексной форме для цепей синусоидального тока

Составными элементами цепей синусоидального тока являются активное сопротивление, индуктивность и емкость. Термин сопротивление для цепей синусоидального тока не полный, т. к. сопротивление переменному току оказывают не только элементы цепи, в которых выделяется энергия в виде тепла (активные сопротивления), но и элементы, в которых энергия запасается в электрическом и магнитном полях. Такие элементы называются реактивными сопротивлениями и ими обладают индуктивность и емкость.

Синусоидальный ток в активном сопротивлении

Рассмотрим случай, когда начальные фазы отличаются от нуля.

Ток и напряжение определены формулами

; ,

(2.20)

а начальные фазы тока и напряжения равны , т. е. ток и напряжение совпадают по фазе.

В комплексном виде ток и напряжение на резистивном элементе:

и

(2.21)

т. к. начальные фазы равны, то закон Ома для действующих величин в комплексной форме для резистивного элемента будет:

(2.22)

Рисунок 2.6 – Изменение мгновенных значений тока и напряжения на активном сопротивлении и векторная диаграмма при наличии начальной фазы

Индуктивность в цепи синусоидального тока

Любая обмотка (катушка) обладает индуктивностью L и активным сопротивлением R. . На схеме замещения катушку представляют в виде последовательно соединенных индуктивности и сопротивления.

Выделим из схемы одну индуктивность, удалив активное сопротивление. Если в индуктивном элементе течет ток:

,

(2.23)

то в катушке наводится ЭДС самоиндукции и появляется напряжение:

(2.24)

При этом амплитуды тока и напряжения соотносятся как:

,

(2.25)

где величина – индуктивное сопротивление [Ом].

Разность фаз показывает, что ток отстает по фазе от напряжения на угол .

,

(2.26)

Комплексные величины тока и напряжения равны:

и

(2.27)

Закон Ома в комплексной форме для индуктивного элемента

,

(2.28)

где – комплексное сопротивление индуктивного элемента.

Если начальный угол тока равен нулю, то графики мгновенных значений и векторная диаграмма выглядят следующим образом (рисунок 2.7). Но для реальной катушки индуктивности падение напряжение равно сумме напряжений на индуктивности () и на активном сопротивлении (). Тогда суммарный вектор напряжениябудет опережать ток на угол. Причем, гдеQ – добротность катушки.

Рисунок 2.7 – Изменение мгновенных значений тока и напряжения на индуктивном элементе и векторная диаграмма при начальном угле тока

Конденсатор в цепи синусоидального тока

Если приложенное к конденсатору напряжение не меняется во времени, то заряды на его обкладках неизменны и ток через конденсатор не проходит (). При изменении напряжения по синусоидальному закону

(2.29)

по этому же закону будет изменяться и заряд q конденсатора, который будет периодически перезаряжаться. Периодическая перезарядка конденсатора сопровождается протеканием через него зарядного тока:

(2. 30)

Отсюда видно, что ток на конденсаторе опережает по фазе напряжение на 90⁰, т. е. разность фаз между током и напряжением

.

(2.31)

Амплитуды тока и напряжения связаны соотношением:

,

(2.32)

разделив которые на , получим соотношение для действующих значений:

(2.33)

где – емкостное сопротивление [Ом].

Закон Ома в комплексной форме записи:

,

(2. 34)

где – комплексное емкостное сопротивление.

При прохождении синусоидального тока через конденсатор предполагается, что диэлектрик, разделяющий его пластины, является идеальным. Однако в реальном диэлектрике всегда имеются потери энергии, связанные c вязким трением при повороте дипольных молекул, а также наличием небольшой проводимости. Эти потери относительно малы, но если их требуется учесть, то составляют схему замещения, где параллельно емкости включают активное сопротивление, потери в котором имитируют потери энергии в реальном диэлектрике.

Тогда суммарный ток через конденсатор равен геометрической сумме двух токов: – через емкость и– через активное сопротивление.

Рисунок 2.8 – Схема замещения (а) и векторная диаграмма (б)

конденсатора, заполненного диэлектриком

В конденсаторе с диэлектриком ток опережает напряжение на угол (90⁰— δ), где δ называется углом диэлектрических потерь. Для реальных конденсаторов он выражается через tgδ и указывается в таблицах.

Импеданс

. Как закон Ома распространяется на Z, если Z комплексное?

Когда кто-то узнает о цепях, он сталкивается с двумя вариантами закона Ома. Первый — это \$V = IR\$, который применяется только к резисторам, рассматриваемым изолированно. Если вы используете базовые методы анализа цепи на чисто резистивной цепи, уравнение, которое вы получите, будет в основном иметь вид \$\mathcal{E} — IR = 0\$. Однако, когда вы вводите конденсаторы, катушки индуктивности и источники переменного напряжения, анализ схемы начинает давать вам 9{i\omega t}\tag{2}$$

Если вы определяете \$\tilde I(t)\$ так, что \$I(t) = \operatorname{Re}\tilde{I}(t) \$, то вы заметите, что уравнение (1) — это всего лишь действительная часть уравнения (2). Но уравнение (2) решить проще, потому что с экспоненциальными функциями работать легче, чем с синусом и косинусом. Итак, мы решаем уравнение (1), решая уравнение (2), а затем беря действительную часть. {i \ omega t} \end{выравнивание}$$

Итак, , предполагая, что \$\tilde{I}\$ является экспонентой этой формы, вы можете выразить уравнения (3) как

$$\begin{align} \tilde{V}_C &= \underbrace{\frac{1}{i\omega C}}_{Z_C}\tilde{I} & \tilde{V}_R &= \underbrace{R}_{Z_R}\tilde{I} & \tilde{V}_L &= \underbrace{i\omega L}_{Z_L} \tilde{I} \end{align}$$

Это источник комплексного импеданса: предположим, что \$\tilde{I}\$ является комплексной экспонентой, действительная часть которой представляет действительный ток, тогда \$\tilde{V}\$ представляет собой комплексную экспоненту, действительная часть которой представляет фактическое напряжение, и вы можете рассчитать ее как \$\tilde{V} = Z\tilde{I}\$, где \$Z\$ – комплексная величина, зависящая от схемы рассматриваемый элемент. Это удобно, потому что не только легче решать соответствующие дифференциальные уравнения, используя комплексные экспоненты, но и экспонента также включает временную зависимость синусоидального тока или напряжения.

Обобщение импеданса, чтобы распространить закон Ома на конденсаторы и катушки индуктивности

Используйте понятие импеданса, чтобы обобщить закон Ома в векторной форме, чтобы вы могли применить и распространить закон на конденсаторы и катушки индуктивности. После описания импеданса вы используете векторные диаграммы, чтобы показать разность фаз между напряжением и током. Эти диаграммы показывают, как фазовое соотношение между напряжением и током различается для резисторов, конденсаторов и катушек индуктивности.

Закон Ома и импеданс

Для цепи, состоящей только из резисторов, закон Ома гласит, что напряжение равно произведению тока на сопротивление, или В = IR . Но когда вы добавляете в схему запоминающие устройства, соотношение i-v становится немного сложнее. Резисторы избавляются от энергии в виде тепла, а конденсаторы и катушки индуктивности накапливают энергию.

Конденсаторы сопротивляются изменениям напряжения, а катушки индуктивности сопротивляются изменениям тока.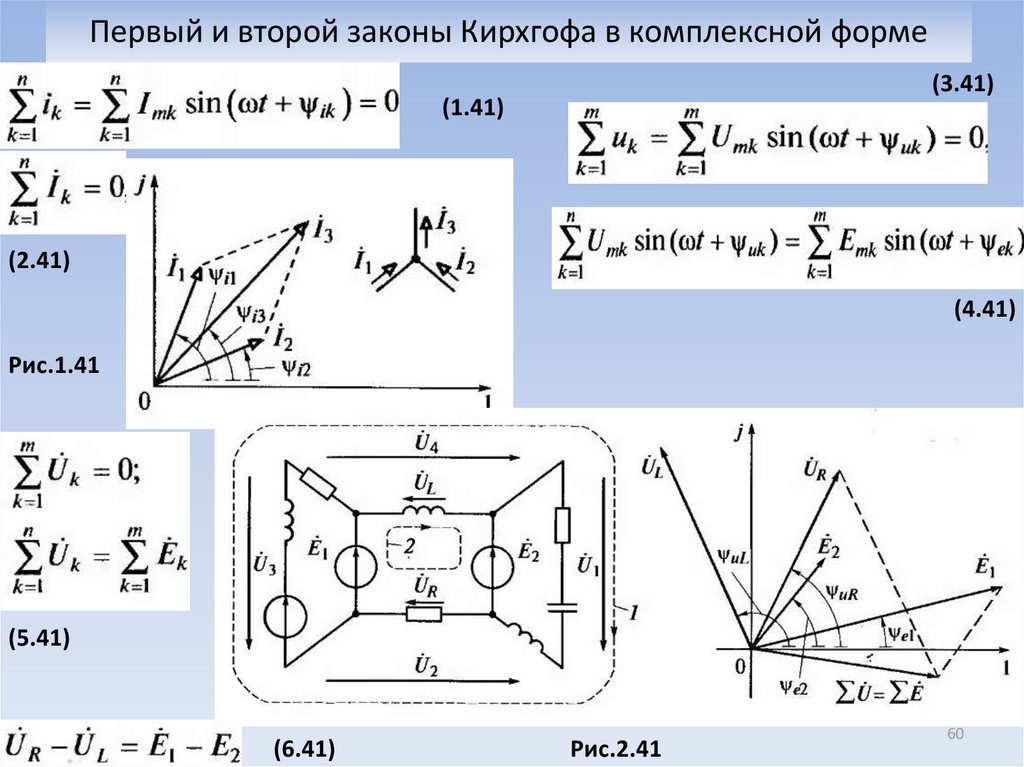 Импеданс обеспечивает прямую связь между напряжением и током для резисторов, конденсаторов и катушек индуктивности при анализе цепей с векторами напряжения или тока.

Как и сопротивление, импеданс можно рассматривать как константу пропорциональности, которая связывает векторное напряжение В и векторный ток I в электрическом устройстве. С точки зрения закона Ома, вы можете связать V , I и импеданс Z следующим образом:

В = I Z

Импеданс Z представляет собой комплексное число:

Z = R + jX

Вот какие действительные и мнимые части числа Z означает:

• Действительная часть R это сопротивление резисторов . Вы никогда не вернете энергию, потерянную при протекании тока через резистор. Когда у вас есть резистор, соединенный последовательно с конденсатором, начальное напряжение конденсатора постепенно уменьшается до 0, если к цепи не подключена батарея.

  Почему? Потому что резистор использует первоначальную накопленную энергию конденсатора в виде тепла, когда ток течет по цепи. Точно так же резисторы заставляют начальный ток катушки индуктивности постепенно снижаться до 0,

• Мнимая часть X является реактивным сопротивлением , возникающим из-за воздействия конденсаторов или катушек индуктивности . Всякий раз, когда вы видите мнимое число для импеданса, оно имеет дело с устройствами хранения. Если мнимая часть импеданса отрицательна, то в мнимой части импеданса преобладают конденсаторы. Если он положительный, в импедансе преобладают катушки индуктивности.

Когда у вас есть конденсаторы и катушки индуктивности, импеданс меняется в зависимости от частоты. Это большое дело! Почему? Вы можете проектировать схемы для приема или отклонения определенных диапазонов частот для различных приложений. Когда в этом контексте используются конденсаторы или катушки индуктивности, цепи называются фильтрами. Вы можете использовать эти фильтры для таких вещей, как создание причудливых рождественских витрин с мигающими разноцветными огнями и танцами под музыку.

Обратная величина импеданса Z называется адмиттансом Y :

Действительная часть G называется проводимостью , а мнимая часть B называется активной проводимостью .

Векторные диаграммы и резисторы, конденсаторы и катушки индуктивности

Векторные диаграммы объясняют различия между резисторами, конденсаторами и катушками индуктивности, где напряжение и ток либо совпадают по фазе, либо не совпадают по фазе на 90 ^o . Напряжение и ток резистора совпадают по фазе, потому что мгновенное изменение тока соответствует мгновенному изменению напряжения.

Но для конденсаторов напряжение не меняется мгновенно, поэтому, даже если ток изменяется мгновенно, напряжение будет отставать от тока. Для катушек индуктивности ток не изменяется мгновенно, поэтому при мгновенном изменении напряжения ток отстает от напряжения.

Вот векторные диаграммы для этих трех устройств. Для резистора ток и напряжение совпадают по фазе, поскольку векторное описание резистора равно В _R = I _Ч Ч . Напряжение конденсатора отстает от тока на 90 ^o за счет – Дж /(ω Кл) , а напряжение дросселя опережает ток на 90 ^o за счет Дж 4 4 .

Представить закон Ома для конденсаторов в векторной форме

Для конденсатора с емкостью C у вас есть следующий ток:

Поскольку производная вектора просто умножает вектор на j ω , векторное описание конденсатора:

Описание вектора для конденсатора имеет форму, аналогичную закону Ома, показывающую, что импеданс конденсатора равен

.

Ранее вы видели векторную диаграмму конденсатора. Напряжение конденсатора отстает от тока на 90 ^o , как видно из формулы Эйлера:

Думайте о воображаемом числе j как об операторе, который поворачивает вектор на 90 ^o против часовой стрелки. А –j поворачивает вектор по часовой стрелке. Также следует отметить, что j ² поворачивает вектор на 180 ^o и равно –1.

Мнимая составляющая конденсатора отрицательна. По мере увеличения частоты ω в радианах импеданс конденсатора снижается. Поскольку частота батареи равна 0, а батарея имеет постоянное напряжение, полное сопротивление конденсатора бесконечно. Конденсатор действует как разомкнутая цепь для источника постоянного напряжения.

Представить закон Ома для катушек индуктивности в векторной форме

Для индуктора с индуктивностью л напряжение

Соответствующее описание вектора для катушки индуктивности:

.

Импеданс катушки индуктивности равен

.

Z _L =jωL

Ранее вы видели векторную диаграмму катушки индуктивности. Напряжение катушки индуктивности опережает ток на 90 ^o по формуле Эйлера:

Мнимая составляющая положительна для катушек индуктивности.