27. Обобщенный закон Ома в интегральной форме для участка цени и полной цепи

Закон Ома в интегральной форме подразумевает, что рассматривается полный ток, протекающий в цепи и величина тока со временем не меняется. Очевидно, что количество заряда, протекающее по проводнику, обратно пропорционально сопротивлению проводника. Количество заряда протекающее в проводнике, прямо пропорционально напряженности или разности потенциалов, создающих внешнее электрическое поле.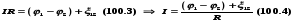

Выражение (100.3) или (100.4) представляет собой закон Ома для неоднородного участка цепи в интегральной форме, который является обобщенным законом Ома.

Если на данном участке цепи источник тока отсутствует (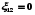), то из (100.4) приходим к закону Ома для однородного участка цепи:

.

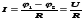
(при отсутствии сторонних сил напряжение на концах участка равно разности потенциалов). Если же электрическая цепь замкнута, то выбранные точки 1 и 2 совпадают, 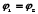; тогда из (100.4) получаем закон Ома для замкнутой цепи: 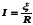, где ξ— э.д.с., действующая в цепи, R — суммарное сопротивление всей цепи. В общем случае R = r+R1, где r — внутреннее сопротивление источника э.д.с., R1 — сопротивление внешней цепи. Поэтому закон Ома для замкнутой цепи будет иметь вид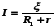

.

Если цепь разомкнута и, следовательно, в ней ток отсутствует (I=0), то из закона Ома (100.4) получим, что 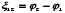т. е. э.д.с., действующая в разомкнутой цепи, равна разности потенциалов на ее концах. Следовательно, для того чтобы найти э.д.с. источника тока, надо измерить разность потенциалов на его клеммах при разомкнутой цепи.

1) Суммарное сопротивление проводников и элементов цепи без э.д.с. обозначается на схеме. 2) Если участок цепи включает в себя э.д.с, то собственное сопротивление источника тока выделяется и обозначается r.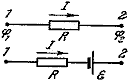

Тогда закон Ома для участка цепи, содержащей э.д.с., имеет вид: .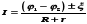

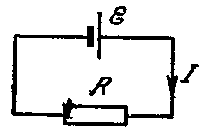
3) Если замкнутый участок цепи, содержит э.д.с., тогда 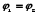, и получаем:

– закон Ома для замкнутого участка цепи, содержащего э.д.с.

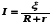
В целом участок цепи, содержащей множество э.д.с. и разных деталей представлен законом Ома в виде: .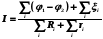

Если при напряжении на концах участка цепи в 1В по цепи протекает ток в 1А, то говорят, что сопротивление цепи равно одному Ому.

28. Правила Кирхгофа, их применение для решения задач с разветвленными цепями

Правила КИРХГОФА устанавливают соотношения для токов и напряжений в разветвлённых электрич. цепях постоянного или квазистационарного тока. Сформулированы Г. Р. Кирхгофом в 1847.

Для упрощения расчетов сложных электрических цепей, содержащих неоднородные участки, используются правила Кирхгофа, которые являются обобщением закона Ома на случай разветвленных цепей. В разветвленных цепях можно выделить узловые точки (узлы), в которых сходятся не менее трех проводников (рис. 4.10.1). Токи, втекающие в узел, принято считать положительными; токи, вытекающие из узла – отрицательными.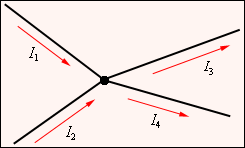

В узлах цепи постоянного тока не может происходить накопление зарядов. Отсюда следует первое правило Кирхгофа: Алгебраическая сумма сил токов для каждого узла в разветвленной цепи равна нулю:

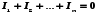
Первое правило Кирхгофа является следствием закона сохранения электрического заряда. В разветвленной цепи всегда можно выделить некоторое количество замкнутых путей, состоящих из однородных и неоднородных участков. Такие замкнутые пути называются контурами. На разных участках выделенного контура могут протекать различные токи.

Второе правило Кирхгофа можно сформулировать так: алгебраическая сумма произведений сопротивления каждого из участков любого замкнутого контура разветвленной цепи постоянного тока на силу тока на этом участке равна алгебраической сумме ЭДС вдоль этого контура. Второе правило Кирхгофа является следствием обобщенного закона Ома.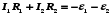

.

Первое и второе правила Кирхгофа, записанные для всех независимых узлов и контуров разветвленной цепи, дают в совокупности необходимое и достаточное число алгебраических уравнений для расчета электрической цепи.

Таким образом, правила Кирхгофа сводят расчет разветвленной электрической цепи к решению системы линейных алгебраических уравнений. Это решение не вызывает принципиальных затруднений, однако, бывает весьма громоздким даже в случае достаточно простых цепей. Если в результате решения сила тока на каком-то участке оказывается отрицательной, то это означает, что ток на этом участке идет в направлении, противоположном выбранному положительному направлению.

Законы Кирхгофа справедливы для линейных и нелинейных цепей при любом характере изменения во времени токов и напряжений.

18.Закон Ома для однородного участка цепи. Сопротивление. Соединения проводников. Электрическое напряжение. Закон Ома в дифференциальной форме.

Закон Ома для однородного участка цепи (не содержащего источника тока): сила тока в проводнике прямо про­порциональна приложенному напряжению и обратно про­порциональна сопротивлению проводника: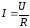

Электри́ческое сопротивле́ние — скалярная физическая величина, характеризующая свойства проводника и равная отношению напряжения на концах проводника к силе электрического тока, протекающему по нему.

В международной системе единиц (СИ) единицей сопротивления является Ом (Ω, Ом). В системе СГС единица сопротивления не имеет специального названия. Сопротивление (часто обозначается буквой R или r) считается, в определённых пределах, постоянной

величиной для данного проводника; её можно определить как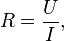

где

R — сопротивление;

U — разность электрических потенциалов на концах проводника, измеряется в вольтах;

I — ток, протекающий между концами проводника под действием разности потенциалов, измеряется в амперах.

Обратной величиной по отношению к сопротивлению является электропроводность, единицей измерения которой служит сименс.

Высокая электропроводность металлов связана с тем, что в них имеется громадное количество носителей тока — электронов проводимости, образующихся из валентных электронов атомов металла, которые не принадлежат определённому атому. Электрический ток в металле возникает под действием внешнего электрического поля, которое вызывает упорядоченное движение электронов. Движущиеся под действием поля электроны рассеиваются на неоднородностях ионной решётки (на примесях, дефектах решётки, а также нарушениях периодической структуры, связанной с тепловыми колебаниями ионов). При этом электроны теряют импульс, а энергия их движения преобразуются во внутреннюю энергию кристаллической решётки, что и приводит к нагреванию проводника при прохождении по нему электрического тока.

В других средах (полупроводниках, изоляторах, электролитах, неполярных жидкостях, газах и т. д.) в зависимости от природы носителей заряда физическая причина сопротивления может быть иной. Линейная зависимость, выраженная законом Ома, соблюдается не во всех случаях.

Сопротивление проводника при прочих равных условиях зависит от его геометрии и от удельного электрического сопротивления материала, из которого он состоит.

Сопротивление однородного проводника постоянного сечения зависит от свойств вещества проводника, его длины, сечения и вычисляется по формуле: 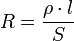где ρ — удельное сопротивление вещества проводника, L — длина проводника, а S — площадь сечения.

Сопротивление однородного проводника также зависит от температуры.

Удельное сопротивление — скалярная физическая величина, численно равная сопротивлению однородного цилиндрического проводника единичной длины и единичной площади.

Сопротивление металлов снижается при понижении температуры; при температурах порядка нескольких кельвинов сопротивление большинства металлов и сплавов стремится или становится равным нулю (эффект сверхпроводимости). Напротив, сопротивление полупроводников и изоляторов при снижении температуры растёт. Сопротивление также меняется по мере увеличения тока/напряжения, протекающего через проводник/полупроводник.

Последовательное и параллельное соединение в электротехнике — два основных способа соединения элементов электрической цепи. При последовательном соединении все элементы связаны друг с другом так, что включающий их участок цепи не имеет ни одного узла. При параллельном соединении все входящие в цепь элементы объединены двумя узлами и не имеют связей с другими узлами. При последовательном соединении проводников сила тока во всех проводниках одинакова.

При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов. При этом величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.

Последовательное соединение

При последовательном соединении проводников сила тока в любых частях цепи одна и та же: I = I1 = I2

Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника тока, равно сумме напряжений на отдельных участках цепи: U = U1 + U2

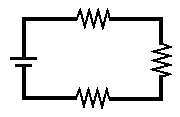последовательное соединение

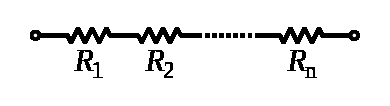
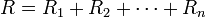
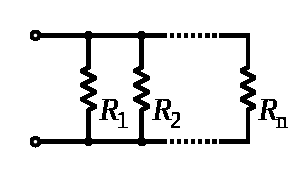
Параллельное соединение

Сила тока в неразветвленной части цепи равна сумме сил токов в отдельных параллельно соединенных проводниках: I = I1 + I2

Напряжение на участках цепи АВ и на концах всех параллельно соединенных проводников одно и то же: U = U1 = U2

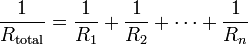
Электрическое напряжение

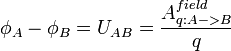Напряже́ние (разность потенциалов, падение потенциалов) между точками A и B — отношение работы электрического поля при переносе пробного электрического заряда из точки A в точку B к величине пробного заряда. При этом считается, что перенос пробного заряда не изменяет распределения зарядов на источниках поля.(по определению пробного заряда)

Альтернативное определение (для электростатического поля) — 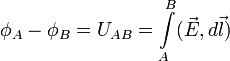— интеграл от проекции поля (напряжённости поля 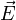) на расстояние между точками A и B вдоль любой траектории, идущей из точки A в точку B.

Единицей измерения напряжения в системе СИ является вольт.

Напряжение показывает, какую работу совершает электрическое поле при перемещении единичного положительного заряда из одной точки в другую.Закон Ома в дифференциальной форме. Сопротивление 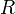зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника.

Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем:

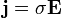
где:

-удельная проводимость,

Е-вектор напряжённости электрического поля.

Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость является тензором ранга. Раздел физики, изучающий течение электрического тока в различных средах, называется электродинамикой сплошных сред.

Закон Ома для однородного участка цепи

Немецкий физик Георг Ом (1826) экспериментально установил, что сила тока,

текущего по однородному металлическому проводнику, пропорциональна напряжению U на концах проводника и обратно пропорциональна сопротивлению R проводника:

I	U
	R	-закон Ома для однородного участка цепи.

Напряжение U (в случае однородного проводника) совпадает с разностью потенциалов.

U12 1 2

Найдем связь между векторами j (вектор плотности тока) и Е (напряженность поля)

водной и той же точке проводника. Так как в изотропном проводнике носители тока

вкаждой точке движутся в направлении вектора Е, то направления j и Е совпадают

Напряжение, приложенное концам проводника, равно Edl, а его сопротивление

	dR dl
	S
	Подставив эти выражения в формулу I U
	.				R
	запишем	I Edl	S	1	ES ES
		dl

Ток I это суммарный ток через S — площадь поперечного сечения проводника. Тогда ток dI ток через элементарную площадку dS

dI EdS

Разделив левую и правую часть на dS, получим слева плотность тока.

j dSdI E

или в векторном виде

j E

Это выражение представляет собой закон Ома в дифференциальной форме для

однородного участка цепи.

Этот закон связывает плотность тока в любой точке внутри проводника с напряженностью электрического поля в этой же точке.

Это соотношение справедливо и для переменных полей.

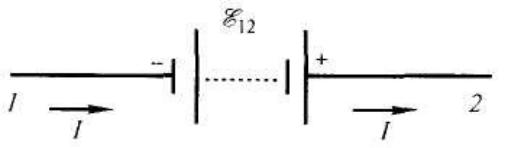
Чтобы перейти к интегральной форме закона Ома, рассмотрим случай, когда электрический ток течет вдоль тонких проводов. Тогда направление тока совпадает с направлением оси провода, и плотность тока j одинакова во всех точках сечения провода. Участок цепи 1-2 выбран произвольно, и в цепи имеется источник ЭДС.

	Умножим слева и справа выражение			j E ECT
	на элемент провода dl	jdl E ECT dl
	затем разделив на γ,
			jdl
	jdl			E	ECT dl

					jdl
	jdl						E ECT dl
проинтегрируем полученное выражение по длине провода от точки 1 до точки 2:
	2	2								2			2
	jdl		E ECT dl									Edl	ECT dl
	1	1								1			1
Левая часть этого уравнения
2	2		2					2 I
											dl
jdl	jdl			j dl
1	1		1					1 S

	2		I		2		I dl		2		dl		2
														R12 сопротивление
				dl					I				I dR IR12
							S				S
	1		S		1				1				1	участке 1-2.

Получив выражение закона Ома, преобразуем правую часть.

правая часть	2			2
	IR12 Edl			ECT dl
	1			1

Первый интеграл в правой части уравнения Второй интеграл

	2			2
	Edl 1		2
				ECT dl 12
	1
				1

где ξ12 — ЭДС, действующая на участке цепи 1-2

IR12 1	2	12	Это выражение представляет собой закон
			Ома для неоднородного участка цепи в

интегральной форме. Это выражение также называют обобщенным законом Ома.

Если в цепи на участке 1-2 отсутствует источник, то ξ равно нулю Выражение IR12 1 2 12

приобретает вид : IR12 1 2 U12

I U12 R12

Если цепь замкнута, выбранные точки 1 и 2 совпадают и 1 = 2,

IR

I

R

В общем случае R = r + R1

r — внутреннее сопротивление источника ЭДС

R1 – полное сопротивление «внешних» (не источника ЭДС) элементов цепи.

Закон Ома для замкнутой цепи будет иметь вид

I

R r R1

Если цепь разомкнута и, следовательно, в ней ток отсутствует ток (I = 0), то

IR12 0 1 2 12

2 1 12

ЭДС, действующая в разомкнутой цепи, равна разности потенциалов на ее концах. Чтобы найти ЭДС источника тока, надо измерить разность потенциалов на его клеммах при разомкнутой цепи.

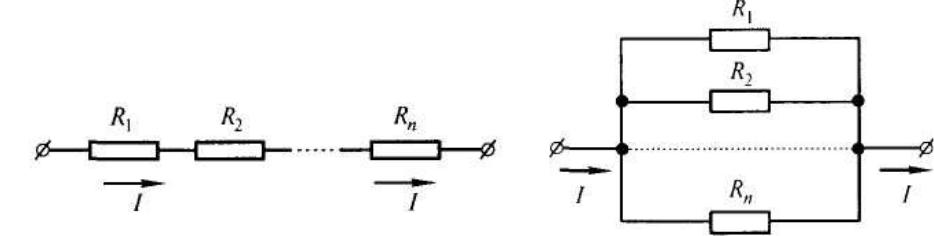
Соединения резисторов и источников ЭДС

Резистор — элемент электрической цепи, основное назначение которого оказывать сопротивление электрическому току с целью регулирования тока и напряжения в цепи. В идеале он характеризуется только сопротивлением электрическому току, и для резистора в любой момент времени должен выполняться закон Ома.. Резисторы в электрических цепях постоянного тока соединяют последовательно и параллельно.

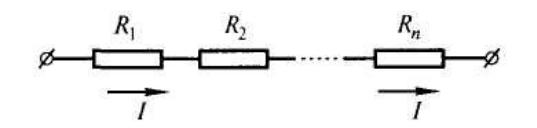
При последовательном соединении п проводников конец первого проводника соединяют с началом второго и т. д

В данном случае сила тока I одинакова во всех резисторах,

I1 I2 ….. In 1 In

напряжение на концах цепи равно сумме напряжений во всех последовательно включенных проводниках

n

UU1 U2 ….. Un 1 Un Ui

i 1

12.3. Закон Ома для однородного участка цепи. Сопротивление проводников.

Г. Ом в 1826 г. экспериментально установил закон, который называется законом Ома для однородного участка цепи: Ток, текущий по однородному металлическому проводнику, пропорционален падению напряжения на проводнике.

I=(), (12-14)

где R — сопротивление проводника, измеряется в СИ в омах [Ом]; из (12-14) следует, что 1Ом =1 В/1 А.

Сопротивление проводника

R =ρl / S , (12-15)

где — удельное сопротивление, измеряется в СИ в Ом м. Оно зависит от температуры: =T, где — удельное сопротивление при температуре t = 0°С, — температурный коэффициент сопротивления, близкий к 1/273 К, T- термодинамическая температура; так что с ростом температуры сопротивление металлических проводников увеличивается. Качественная температурная зависимость удельного сопротивления металлического проводника представлена на рис.12.3

Найдем связь между векторами и. Для этого мыслен­но выделим в окрестности некоторой точки проводника элемен­тарный цилиндрический объем с образующими, параллельными векторам и, (рис.12.4).

Между концами проводника длиной dl напряжение U = Edl, под действием которого через его поперечное сечение площадью dS течет ток I = jdS.

Сопротивление цилиндрического проводника, в нашем случае, равно

R = .

Используя закон Ома для участка цепи I = , находим:

jdS = ,

откуда и получаем закон Ома в дифференциальной форме

= =, (12-16)

где =удельная электропроводность; [] = 1 / (Ом м).

12.4. Закон Ома для неоднородного участка цепи

На неоднородном участке цепи плотность тока пропорциональна сумме напряженностей электростатического поля и поля сторонних сил, т.е.

. (12-17)

Рассмотрим цилиндрический проводник длиной l с площадью поперечного сечения S. Ум­ножим обе части равенства (12-17) на перемещение dl вдоль оси проводника и проинтегрируем получившееся соотношение по длине проводника от 0 до l:

что дает

j l = (+). (12-18)

Заменив j на I/S, а на , из (12-18) получим I =+ , откуда следует закон Ома для неоднородного участка цепи

I = (+) / R (12-19)

где R=l / S — сопротивление участка цепи 12. Для замкнутой цепи формула (12-19) запишется в виде

I = / R (12-20)

где R — суммарное сопротивление всей цепи; — ЭДС источника.

Пусть замкнутая цепь состоит из источника электрической энергии с ЭДС и внут­ренним сопротивлением r, а также внешней цепи потребителя, имеющей сопротивление R. Согласно (12-20)

I = / (R + r). (12-21)

азность потенциалов на электродах источника, рис.12.5, равна напряжению на внешнем участке цепи:

U == IR =- Ir. (12-22)

Если цепь разомкнуть, то ток в ней прекратится и напряжение U на зажимах источника станет равным его ЭДС, т.е. U = .

Таким образом, напряжение на внешнем участке цепи, будет равно

U = IR = R / (R + r).(12-23)

В пределе, когда R 0 (источник тока замкнут накоротко), то в этом случае, в соот­ветствии с (12-21), ток максимален

I= I= / R, (12-24)

а напряжение во внешней цепи равно нулю.

В противоположном предельном случае, R, цепь разомкнута и ток отсутствует: I=lim[/ (R+r)]=0,а напряжение на зажимах источника максимально и равно его ЭДС:

U = R / (R + r)= , т. к. lim R / (R + r) = 1. (12-25)