Закон Ома для цепи переменного тока. Резонанс в электрической цепи. Школьный курс физики

Главная | Физика 11 класс | Закон Ома для цепи переменного тока

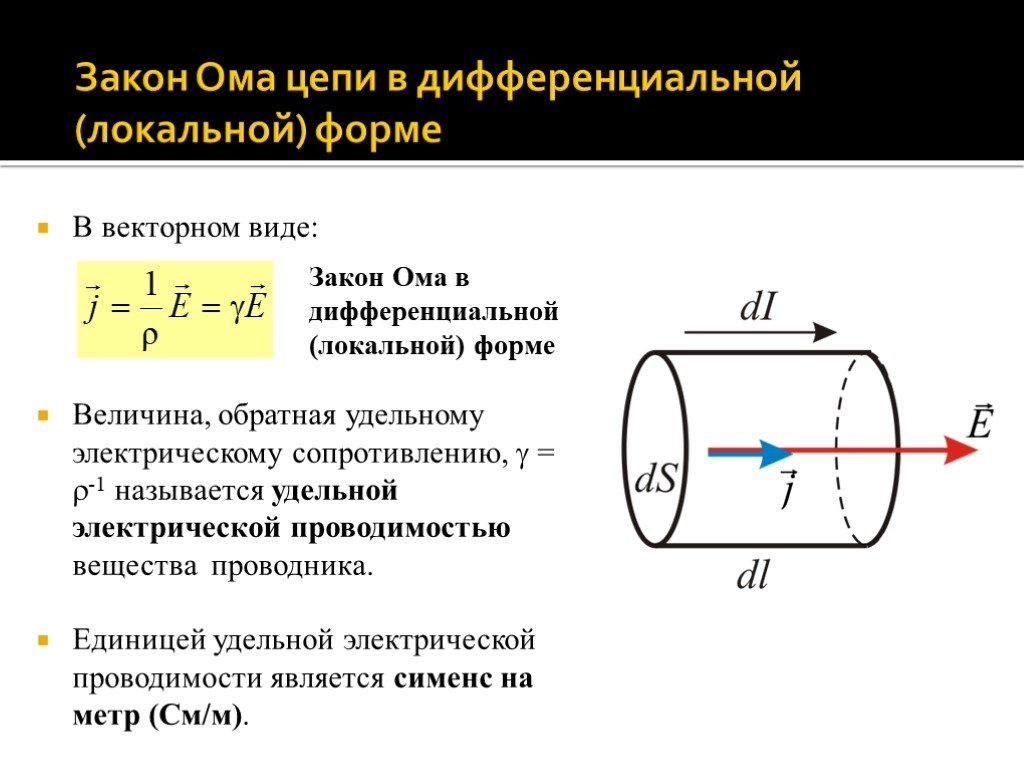
Закон Ома для цепи переменного тока.

Рассмотрим более общий случай электрической цепи, в которую последовательно включены проводник с активным сопротивлением R и малой индуктивностью, катушка с большой индуктивностью L и малым активным сопротивлением и конденсатор ёмкостью С. Если напряжение на концах такой цепи меняется по закону u = U_msin ωt, то сила тока в цепи меняется по закону

i = I_msin (ωt-φ_c),

где φ_c — разность фаз между колебаниями силы тока и колебаниями напряжения в цепи.

В результате математических преобразований можно получить соотношение между амплитудами колебаний силы тока и напряжения в RLC-контуре:

Сдвиг фаз

φ_c будет определяться выражением

Выражение (1) имеет вид закона Ома I_m = U_m / Z, где

Величина Z — это полное сопротивление цепи. Закон Ома для цепи переменного тока (1) записан для амплитудных значений силы тока и напряжения.

Резонанс в цепи переменного тока ¹.

---

¹ Существуют два основных вида резонанса в цепи переменного тока: резонанс напряжений, который возникает при последовательном соединении элементов цепи, и резонанс токов, происходящий при их параллельном соединении. В этом параграфе будет рассмотрен резонанс напряжений.

Аналогия между законами механических и электромагнитных колебаний позволяет сделать заключение о существовании резонанса в колебательном контуре, обладающем определённой собственной частотой колебаний.

Амплитуда силы тока при вынужденных электромагнитных колебаниях в контуре, совершающихся под действием внешнего гармонически изменяющегося напряжения, определяется формулой (1). При фиксированном напряжении U_m и заданных значениях R, L и C амплитуда колебаний силы тока достигает максимума при частоте ω, удовлетворяющей соотношению

Знаменатель в формуле (1) становится при этом минимальным, и амплитуда колебаний силы тока достигает максимального значения:

Амплитуда силы тока особенно велика при малом R. Из уравнения (3) можно определить циклическую частоту переменного тока, при которой сила тока максимальна:

Эта частота совпадает с частотой свободных колебаний в контуре с малым активным сопротивлением (см. § 31 «Свободные электромагнитные колебания. Колебательный контур»).

Резкое возрастание амплитуды установившихся вынужденных колебаний силы тока в колебательном контуре с малым активным сопротивлением происходит при совпадении частоты внешнего переменного напряжения с собственной частотой колебательного контура. В этом состоит

явление резонанса в колебательном контуре.

Резонанс выражен тем отчётливее, чем меньше энергетические потери в цепи, т. е. чем меньше сопротивление R. При R → 0 резонансное значение силы тока неограниченно возрастает: I_рез → ∞.

C увеличением R максимальное значение силы тока уменьшается, и при больших R говорить о резонансе уже не имеет смысла.

Зависимость амплитуды силы тока от частоты при различных сопротивлениях показана на рисунке 6.28 (R₁ < R₂ < R₃).

Рис. 6.28

Одновременно с увеличением силы тока при резонансе резко возрастают напряжения на конденсаторе и катушке индуктивности. Они становятся одинаковыми и во много раз превосходят внешнее напряжение, которое связано с резонансной силой тока следующим образом:

При резонансе сдвиг фаз между силой тока и напряжением становится, согласно формуле (2), равным нулю. Наглядно это можно пояснить так. Колебания напряжения на катушке индуктивности и конденсаторе всегда происходят в противофазе. Резонансные амплитуды этих напряжений одинаковы. В результате напряжения на катушке и конденсаторе полностью компенсируют друг друга

(u_L = -u_C), и падение напряжения происходит только на участке с активным сопротивлением.

Явление электрического резонанса учитывают в радиотехнике при расчётах электрических цепей, в схемах настройки радиоприёмников, радиопередатчиков, усилителей, генераторов высокочастотных колебаний.

В некоторых случаях резонанс в электрической цепи может принести большой вред. Если цепь не рассчитана на работу в условиях резонанса, то возникновение резонанса приведёт к аварии. Чрезмерно большие токи могут перегреть провода, а большие напряжения приведут к пробою изоляции.

Вопросы:

1. Что представляет собой RLC-контур?

2. Какое соотношение выражает закон Ома для цепи переменного тока?

3. В чём заключается явление резонанса в электрическом колебательном контуре?

Вопросы для обсуждения:

1.Как будет изменяться накал нити лампы при изменении частоты переменного тока от 0 до ∞ в цепях, изображённых на рисунке 6.29? Амплитуда колебаний напряжения источника переменного тока не изменяется.

  

Рис. 6.29

2. Можно ли установить режим резонанса в цепи переменного тока, не изменяя индуктивности катушки и ёмкости конденсатора в цепи? Если да, то как это сделать?

3. Сравните явление резонанса в механических и электрических колебательных системах.

Пример решения задачи

Катушка с активным сопротивлением 10 Ом и индуктивностью 0,05 Гн соединена последовательно с конденсатором ёмкостью 2 мкФ. К цени подведено напряжение с амплитудой 100 В при частоте переменного тока, равной 50 Гц (рис. 6.30). Определите амплитуду силы тока в цепи.

Рис. 6.30

Запишем закон Ома для цени переменного тока и найдём силу тока:

Ответ: I_m ≈ 0,06 А.

Упражнения:

1. Электрическая цепь состоит из последовательно соединённых резистора сопротивлением 4 Ом, катушки с индуктивным сопротивлением 8 Ом И конденсатора с ёмкостным сопротивлением 5 Ом. К концам цени приложено переменное напряжение 120 В. Найдите силу тока в цепи и напряжения на всех участках цепи.

2. В цепь включены последовательно катушка индуктивностью 50 мГн и конденсатор ёмкостью 20 мкФ.

Какой частоты переменный ток нужно пропустить через эту цепь, чтобы наступил резонанс?

3. Конденсатор и катушка соединены последовательно в цепи переменного тока. Индуктивность катушки равна 0,01 Гн. При какой ёмкости конденсатора сила тока частотой 1 кГц будет максимальной?

4. Конденсатор и катушка соединены последовательно в цепи переменного тока. Ёмкостное сопротивление конденсатора равно 5000 Ом. Какой должна быть индуктивность катушки, чтобы резонанс наступил в цепи при частоте тока 20 кГц?

5. Резонансная частота колебательного контура равна 50 кГц. Как нужно изменить расстояние между пластинами плоского конденсатора в этом контуре, чтобы резонансная частота стала равной 70 кГц?

Предыдущая страницаСледующая страница

Нарушение закона Ома и анализ цепи | Блог Advanced PCB Design

 

Несмотря на то, что эксперименты с использованием закона Ома являются фундаментальной частью обучения любого инженера-электрика, закон Ома имеет свои ограничения. На высокой частоте в полупроводниковых устройствах и в некоторых схемах с обратной связью схема фактически будет демонстрировать нелинейный отклик на возбуждающее напряжение. Это иллюстрирует несостоятельность закона Ома, поскольку он больше не описывает правильно ток, индуцируемый в цепи. В результате использование SPICE-моделирования для схем с нелинейными элементами усложняется и требует специальных методов.

Нарушение закона Ома и основы анализа цепей

Любой, кто посещал базовые курсы физики или электроники, знает закон Ома. Этот простой эмпирический закон связывает проводимость материала с плотностью тока, хотя инженеры обычно рассматривают его с точки зрения напряжения и тока, используя уравнение V = IR. Этот фундаментальный закон анализа цепей определяет линейную зависимость между напряжением и током в цепи. Хотя это обычно обсуждается с точки зрения цепей постоянного тока, это также относится к цепям переменного тока. При этом используется эквивалентное уравнение V = IZ, где Z — импеданс рассматриваемого элемента схемы.

Обратите внимание, что импеданс является функцией частоты сигнала переменного тока, который распространяется в цепи, но это не меняет линейности зависимости между напряжением и током.

Поскольку закон Ома определяет линейную зависимость между напряжениями, он не работает в любом устройстве с непостоянной крутизной. Это означает, что ток в рассматриваемом элементе схемы больше не прямо пропорционален напряжению, используемому для управления элементом схемы. Вместо того, чтобы график зависимости напряжения от силы тока представлял собой прямую линию, график показывает кривую зависимость. Элементы, демонстрирующие такое поведение, называются элементами нелинейной схемы.

Более общее описание поведения любой цепи — использование законов Кирхгофа. Этим законам все равно, является ли связь между током и напряжением линейной или нелинейной. Они касаются только напряжения вокруг петли в цепи (закон напряжения Кирхгофа) или распределения тока в узле цепи (закон тока Кирхгофа). Оба утверждения связаны с фундаментальными законами сохранения в физике. В случае нелинейных элементов схемы ток в данном элементе цепи является функцией падения напряжения на элементе. Это усложняет расчет поведения нелинейной цепи, но такой метод, как анализ малых сигналов, идеален для моделирования поведения схемы при определенном значении падения напряжения.

Здесь важно различать цепи переменного тока. Тот факт, что ток в цепи переменного тока (или ток через конкретный элемент цепи) является нелинейной функцией частоты, не требует, чтобы ток также был нелинейной функцией напряжения. Рассмотрим конденсатор в цепи переменного тока; импеданс зависит только от частоты, но не от напряжения, поэтому конденсатор по-прежнему имеет линейную зависимость напряжения от тока, и закон Ома по-прежнему выполняется.

 

Схема триггера Шмитта является одним из примеров, иллюстрирующих нарушение закона Ома

 

Нелинейность и нарушение закона Ома

Как бы нам ни хотелось думать, что некоторые природные явления линейны, это просто не правда в реальности.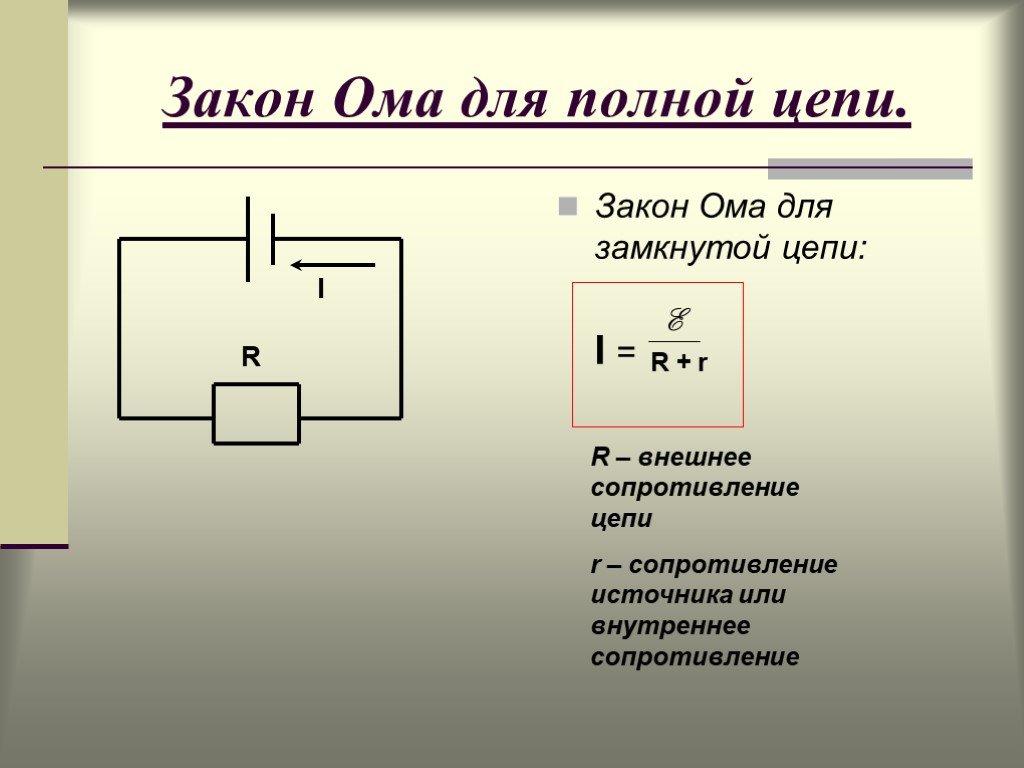 Каждая линейная система имеет свои пределы; в электронике нелинейные эффекты берут верх и ограничивают реакцию элемента схемы, когда напряжение на элементе схемы становится очень большим. Несмотря на то, что резисторы определены как чисто линейные элементы, реальные резисторы будут демонстрировать нелинейность при высокой частоте и высоком напряжении.

 

Что касается высокого падения напряжения на резисторе, то так получилось, что номинальная мощность большинства резисторов такова, что резистор сгорит до того, как вы сможете достоверно наблюдать нелинейный ток, когда на резистор подается постоянное напряжение. В цепи переменного тока или в цепи, управляемой потоком цифровых импульсов, шероховатость резистивной пленки внутри резистора и в местах его пайки может привести к интермодуляционным продуктам, которые искажают форму сигнала и генерируют боковые полосы из-за нелинейного смешения частот на очень высоких частотах. высокие частоты возбуждения (в аналоговых схемах) и с высокими скоростями переключения и скоростью передачи данных (в цифровых схемах).

Диод, пожалуй, самый популярный пример элемента нелинейной схемы. Выходной ток диода является простой экспоненциальной функцией входного напряжения. Другие элементы схемы, демонстрирующие нелинейный отклик, включают электронные лампы, транзисторы, ферритовые трансформаторы и катушки индуктивности, работающие за пределами насыщения, а также усилители, работающие на высоких уровнях сигнала.

 

Нелинейная зависимость между выходным током диода и падением напряжения на диоде, иллюстрирующая нарушение закона Ома

 

Анализ нелинейных элементов и цепей

Правильный способ рассмотрения поведения нелинейного устройства в цепи — использовать анализ малых сигналов. Это относится к анализу постоянного и переменного тока нелинейных устройств. Этот метод основан на линеаризации, когда ток в нелинейном элементе цепи аппроксимируется как линейная функция падения напряжения на этом элементе с использованием разложения в ряд Тейлора при определенном рабочем смещении. Это позволяет рассчитать крутизну (или трансимпеданс для частотно-зависимых элементов) для каждого элемента схемы при определенном уровне смещения.

Когда у вас есть эти значения крутизны / крутизны для каждого элемента в цепи, вы можете затем выполнить развертку постоянного или переменного тока для вашей цепи в определенных диапазонах напряжения и / или частоты с помощью симулятора на основе SPICE. Моделирование выведет результаты того же типа, что и для типичной линейной схемы.

Будьте осторожны с интерпретацией этих результатов; сдвиг смещения постоянного тока или амплитуды переменного тока слишком далеко от рабочего смещения приведет к менее точным результатам. Результаты анализа малых сигналов точны только в пределах определенного диапазона значений напряжения. Хороший способ оценить точность — сравнить линеаризованное напряжение и ток в конкретном элементе схемы с реальной нелинейной зависимостью между напряжением и током.

Всякий раз, когда вы сталкиваетесь с нарушением закона Ома во время анализа схемы, вам понадобится адаптируемая программа, такая как PSpice Designer от OrCAD, для анализа ваших проектов по мере их усложнения.