Закон Ома для участка цепи – конспект урока – Корпорация Российский учебник (издательство Дрофа – Вентана)
авторы: Ульяна Валерьевна Демура , учитель астрономии, информатики, физики, Приморский край
Разработки уроков (конспекты уроков)
Линия УМК А.В. Перышкина. Физика (7-9)
Физика
Внимание! Администрация сайта rosuchebnik.ru не несет ответственности за содержание методических разработок, а также за соответствие разработки ФГОС.
Цели урока:
Образовательная: Изучить закон Ома.
Развивающая: формировать умение проведения измерений (исследование зависимости одной физической величины от другой), умение наблюдать, сравнивать, обобщать результаты эксперимента.
Воспитательная:
- воспитать аккуратность при работе с физическими приборами
- познавательный интерес к предмету.
Задачи урока:
- Научиться определять силу тока, напряжение по графики между этими величинами и по нему же — сопротивление проводника.

- Установить зависимость силы тока от напряжения на концах проводника.
- Установить зависимость силы тока от напряжения.
- Научиться решать задачи по данной теме.
Оборудование. Интерактивная доска и интерактивная модель (интернет-ресурс «классная физика»), проектор, ПК, мультимедийная презентация, лабораторное оборудование: вольтметр, амперметр, источник питания 1,5 в, источник питания 4,5 в, лампочка, ключ, провода – 5 комплектов..
Тип урока: урок изучения нового материала.
План урока:
|
Этапы урока |
Деятельность учителя |
Деятельность ученика |
|
1. |
Сообщение плана работы на уроке. |
|
|
2. Актуализация знаний. |
Опрос учащихся. |
Заполняют «Ступенчатую карточку индивидуального опроса» (карточка № 1). |
|
3. Изложение нового материала. |
Рассказ с опорой на интерактивную презентацию. |
Внимательно смотрят, проводят интерактивные опыты. |
|
Установление зависимости между I, U, R. |
Слушают учителя, проводят практический эксперимент. |
|
|
Демонстрация опытов, заполнение таблиц. |
Наблюдают, делают выводы, заполняют «Экспериментальную карточку» (карточка № 2). |
|
|
Общий вывод закона. |
Заполняют «Экспериментальную карточку». |
|
|
4. Закрепление. |
Решение задач. |
Решают задачи по вариантам (карточка № 3), проверяют решение на интерактивной модели. |
|
5. Подведение итога урока. |
Беседа с учащимися. |
Отвечают на вопросы для самоконтроля (карточка № 4). |
|
6. Домашнее задание. |
Записывает на доске. |
Записывают в дневник. |
1. Организационный момент. (слайд 1)
— Здравствуйте, меня зовут Ульяна Валерьевна. Сегодня, я проведу у вас урок физики, надеюсь, наша работа будет плодотворной. (слайд 2) Мы познакомимся и изучим закон Ома. Установим зависимость силы тока от напряжения и сопротивления и закрепим полученные знания.
2. Актуализация знаний.
(слайд 3) Но, чтобы узнать новое необходимо вспомнить изученное. Перед вами расположен индивидуальный набор карточек. Обратите внимание на «Ступенчатую карточку индивидуального опроса» (карточка № 1). Подпишите её: ФИ. Выберите свою ступень заданий: на оценку 3,4 или 5 и ответьте на её вопросы. На работу 3 минуты. Вопросы есть?
На работу 3 минуты. Вопросы есть?
— Готовы? А теперь давайте посмотрим, кто на какой ступени себя ощущает. Поднимите руки, кто…
У нас получилось…надеюсь, что к завершению нашего занятия, количество «жильцов» ступеней: 4,5 увеличится.
— Двигаемся дальше!
3. Изложение нового материала.
— (слайд 4) Знаете кто это?
— Разрешите представить: это немецкий физик Георг Ом, человек который в 1827г. вывел теоретически и подтвердил на опыте закон, выражающий связь между силой тока, напряжением и сопротивлением цепи.
Чтобы рассмотреть зависимость между силой тока, напряжением и сопротивлением, предлагаю повести опыт. Согласны? Наш опыт состоит из двух частей: интерактивной и практической.
Но для начала, мне понадобятся помощники. Назначаю активистов групп, которые на протяжении урока будут записывать самых активных и результативных участников своей группы (фи).
Сначала я, с вашей помощью, проведу интерактивный эксперимент, мы с вместе построим график, на основе полученных данных, сформулируем первую часть закона Ома. А потом вы в группах на практике установите вторую часть закона Ома. Понятно?
(слайд 5) Опыт 1. – Откройте карточку №2- экспериментальную. Верхнюю часть листа мы заполним вместе, а нижнюю- заполните самостоятельно.
— Проверим, как зависит сила тока в цепи от сопротивления.
— Перед нами электрическая цепь, не полная. Наша задача: включить различные сопротивления и наблюдать, что покажут приборы.
— Обратите внимание, не все деления на шкале подписаны и чтобы точно знать показания, какую величину мы должны вычислить?
-Напоминаю, чтобы вычислить цену деления нужно…
Проведение интерактивного эксперимента, запись результатов, построение графика, формулировка вывода.
Какой отсюда следует вывод? А теперь посмотрите на график. Какую зависимость он показывает?
— Было сложно? Не привычно? Устали? Предлагаю провести физкультминутку (слайд 6).
-Располагаемся удобно, можно остаться в сидячем положении. Физкультминутка юмористическая. Самые спортивные, добавят балл к своей отметке.
-Здорово! Отдохнули?
-(слайд 7) Вторую часть закона Ома, то есть, как связаны между собой сила тока и напряжение нам поможет установить практический эксперимент. Вы работаете самостоятельно, перед вами стоит оборудование, к нему прилагается инструкционная карта. Прочитайте её, вспомните, пожалуйста, правила ТБ ( на слайде дублирую).
-Обратите внимание, электрическая цепь собрана, только не хватает источника питания. У вас на выбор два источника напряжением: 1,5 и 4,5 в. Ваша задача, их правильно соединить, соблюдая полярность, снять показания с амперметра, не забывайте про цену деления, проанализировать полученные значения, по ним построить график (у вас будет две точки) и сформулировать вывод — как зависит сила тока от напряжения.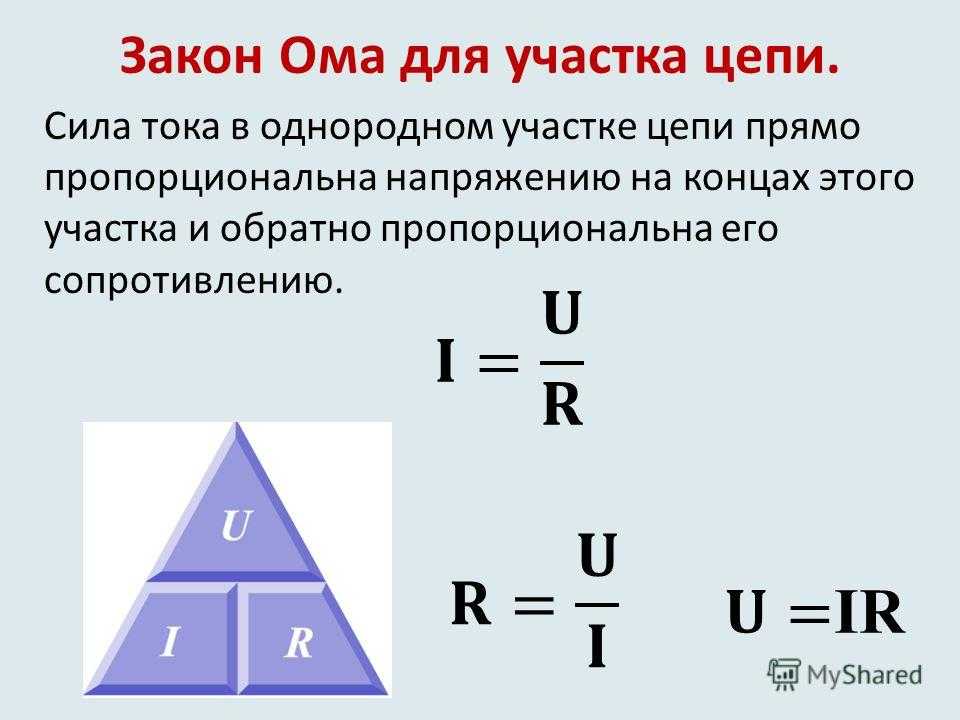 На работу 10 минут.
На работу 10 минут.
НЕ СТЕСНЯЙТЕСЬ ЗАДАВАТЬ ВОПРОСЫ, только руку поднимайте.
Приступаем
— Давайте проверим, что у Вас получилось?
— Итак, какой вывод следует?
А теперь соберем вместе две части закона Ома и попробуем его сформулировать.
Молодцы! Запишем общий вывод в специальное окошко на карточке. (Напомнить правила пользования треугольником формул.)
4. Закрепление
— Давайте закрепим, полученные знания с помощью задач. Открываем карточку №3, у каждого свой вариант, на основе закона Ома решаем задачи самостоятельно.
Напоминаю: внимательно прочитайте условие и по картинке определите, что дано и что необходимо найти. А потом, используя только что выведенный закон и математический аппарат, найдите искомую величину. На решение — 5 минут.
На решение — 5 минут.
После решения мы с Вами проверим, верность вашего ответа ответ. В этом нам помогут интерактивные электрические схемы.
— Готовы? Порошу запомнить полученный результат, а индивидуальный набор карточек, за исключением последней сдать активисту.Я их соберу для выставления отметок за урок, так же собираю «активные карточки»- прибавляющие баллы.
— Молодцы, все справились.
5. Домашнее задание.
Откройте, пожалуйста, дневники, запишите домашнее задание (слайд 9):
Параграфы 42,44; упражнение 29
6. Поведение итогов урока.
— Вы сегодня большие молодцы. Особо хочется отметить:… Спасибо активистам.
У меня к вам последняя просьба: возьмите карточку №4 «Лист самоконтроля» и заполните её. Со звонком работы соберу, на работу минут (слайд 10).
7. Звонок.
— Ребята искренне благодарю за урок, светлого Вам пути! (слайд 11)
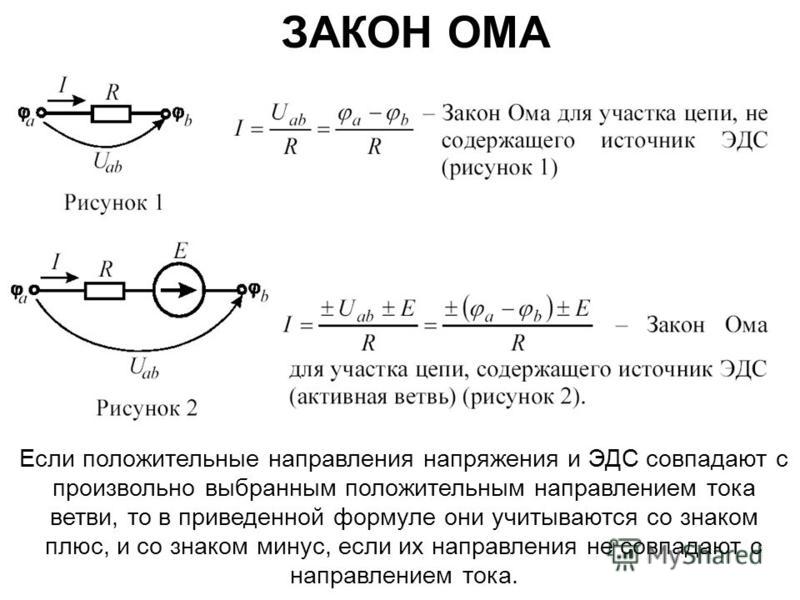
Закон Ома для участка цепи
Закон Ома для участка цепи- Кочкина Олеся Сергеевна, Учитель физики и информатики
Разделы: Физика, Конкурс «Презентация к уроку», Мастер-класс
Ключевые слова: Закон Ома
Презентация к уроку
Загрузить презентацию (428 кБ)
Предмет: Физика.
Класс: 8.
Тип урока: урок открытия и первичного закрепления нового знания.
Цель урока: усвоение учащимися основных физических зависимостей силы тока от напряжения на основе закона Ома во время решения задач.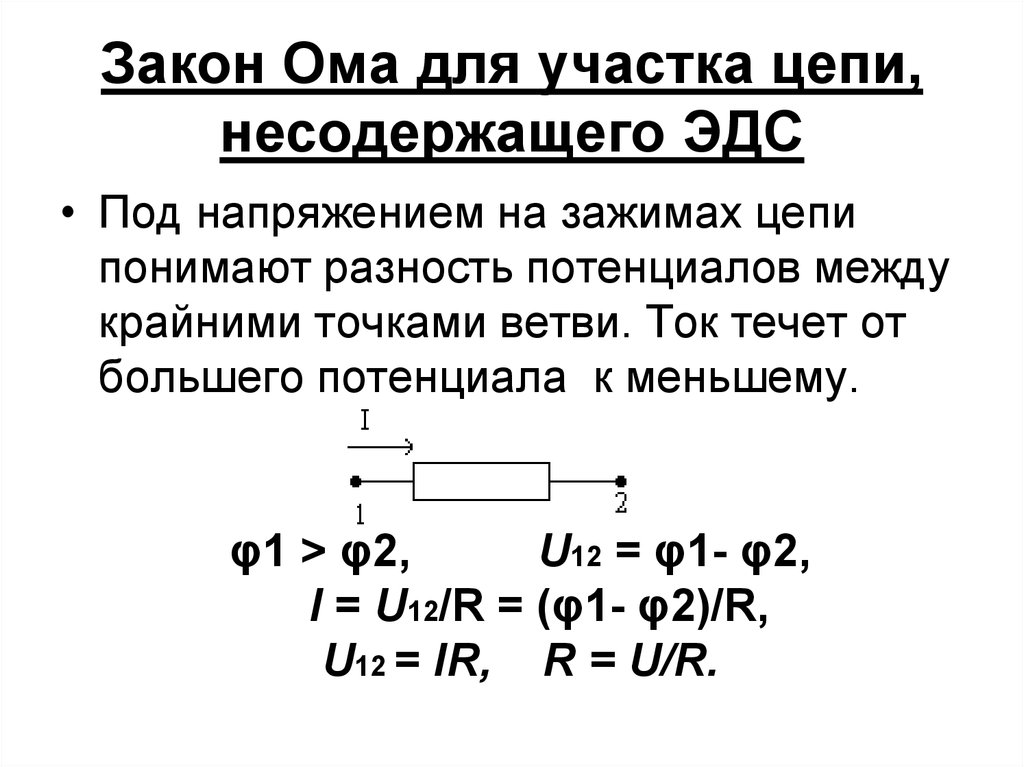
Задачи:
- обучающие: изучить один из важнейших законов электрического тока — закон Ома для участка цепи; применять полученные знания в новых условиях; формировать умение вычислять силу тока, напряжение, сопротивление.
- развивающие: развивать навыки обобщения изученного материала, систематизации знаний; способствовать развитию познавательной компетентности.
- воспитательные: формировать умение высказывать и аргументировать свою точку зрения; прививать культуру умственного труда и умение работать в коллективе.
Технология — проблемное обучение.
Принципы технологии: Создание под руководством учителя проблемной ситуации.
- Активная деятельность учащихся.
- Развитие мыслительных способностей учащихся.
Формы работы: фронтальная, работа в группах, индивидуальная.
Оборудование урока: учебник, компьютер, мультимедийное оборудование.
План урока
Этапы | Содержание | Формы и методы |
Организация начала урока | Приветствие. | Беседа. |
Мотивация учебной деятельности | Повторение пройденного раннее материала, необходимого для изучения новой темы. | Проблемная ситуация. Фронтальный опрос. |
Подготовка учащихся к актуализации опорных знаний | Подготовка учащихся к усвоению новых знаний. | Смысловое чтение текста/ Использование мультимедийных технологий |
Изучение нового материала | Формирование закона Ома | Беседа. Использование мультимедийных технологий. |
Первичная проверка усвоения знаний | Умение найти необходимую информацию в учебнике. | Проблемная ситуация. |
Первичное закрепление знаний | Умение учащихся воспроизводить, полученные на уроке знания. | Беседа. Фронтальный опрос. |
Контроль и самопроверка знаний | Проверка умение учащихся воспроизводить, полученные на уроке знания. | Индивидуальная работа. |
Информация о домашнем задании. | Сообщение домашнего задания, инструктаж учащихся по его выполнению. | Беседа. Работа с учебником. |
Подведение итогов урока. Рефлексия. | Возращение к целям урока. Выявление успешности овладения содержанием урока. | Беседа. Индивидуальная работа. |
Ход урока
Деятельность учителя | Деятельность обучающегося |
Организация начала урока (1 мин) | |
Здравствуйте. | Проверяют свою готовность. |
Мотивация учебной деятельности (6 мин) | |
Давайте заполним таблицу (см. Приложение № 1). | Заполняют таблицу |
Подготовка учащихся к актуализации опорных знаний (3 мин) | |
О чем мы будем говорить сегодня на уроке? | Высказывают свои предположения. Формулируют тему урока и цели. |
Изучение нового материала (5 мин) | |
Определим зависимость трех физических величин. Сформулируем закон Ома. Запишем физический закон. | Высказывают свои варианты, обсуждают. |
Закон Ома: сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению. I — сила тока в участке цепи [А] | |
Первичная проверка усвоения знаний (5 мин) | |
По пройденному материалу предлагается заполнить кластер (см. | Работают с учебником и материалом на доске. Заполняют кластер по основным терминам и величинам. |
Первичное закрепление знаний (5 мин) | |
Решение задачи на доске с объяснением (см. Приложение № 3) | Запись решения в тетрадь, анализируют ход решения задачи, задают вопросы. |
Контроль и самопроверка знаний (10 мин) | |
Предлагается решить задачи самостоятельно (см. Приложение № 4) | Решают в тетради задачу, выполняют взаимопроверку у доски. |
Информация о домашнем задании (2 мин) | |
§ 45, Упр. | Записывают задание в дневник. |
Подведение итогов урока. Рефлексия (3 мин) | |
С какими основными понятиями мы сегодня познакомились? | |
Электрические цепи: проверка закона Ома — 2133 слов
Введение
Анализ состоит из трех разделов, где первая часть использовалась для экспериментальной проверки закона Ома. Второй и третий эксперименты были проведены для оценки цепей делителя напряжения и тока. В целом, целью CEN201: Лабораторный эксперимент 1 – Электрические цепи было:
- Экспериментальная проверка закона Ома путем поддержания постоянного напряжения и изменения сопротивления.

- Экспериментально проверить формулу делителя напряжения.
- Для экспериментальной проверки формулы делителя тока.
Теоретическая основа
Закон Ома определяет зависимость между напряжением и током идеального проводника. Эта взаимосвязь была впервые обнаружена немецким физиком Георгом Омом в 1826 году (Engineermaths, nd; University of Kentucky, nd). Закон гласит, что ток, проходящий через электрическую цепь, прямо пропорционален напряжению и обратно пропорционален сопротивлению системы при постоянной температуре (Engineermaths, nd; Technical Books Pdf, nd). Соотношение закона Ома представлено уравнением 1, которое иллюстрирует, что если известны два значения напряжения, тока или сопротивления, можно определить недостающую величину (Технические книги Pdf, n.d). Графическое представление закона Ома называется треугольником закона Ома, показанным на рисунке 1. На рисунке 2 показаны различные комбинации законов Ома, показывающие, как могут быть рассчитаны различные параметры.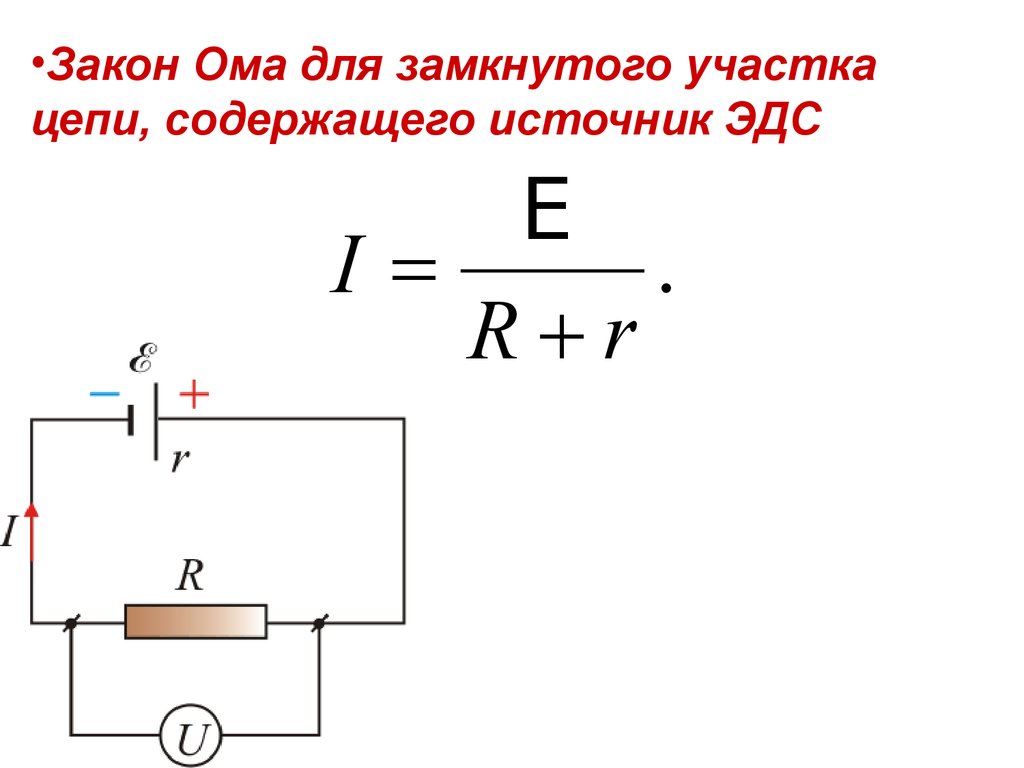
I = V/R (уравнение 1), где
- I = ток в амперах (А)
- В = напряжение в вольтах (В)
- R = сопротивление в Омах (Ом)
Закон Ома широко используется в расчетах и проектах электроники. Устройства, которые подчиняются закону Ома, называются омическими, тогда как те, которые не подчиняются, называются неомическими (Университет Кентукки, nd). Резисторы и кабели являются примерами омических устройств, тогда как диоды и транзисторы относятся к категории неомических (Университет Кентукки, nd). Взаимосвязь различных факторов закона Ома может быть установлена экспериментально. В связи с этим первая часть эксперимента заключалась в проверке закона Ома путем определения тока через разное сопротивление при постоянном напряжении. В анализе использовалась простая схема, подобная той, что показана на рис. 3, где график зависимости тока от сопротивления был построен по строгому закону Ома.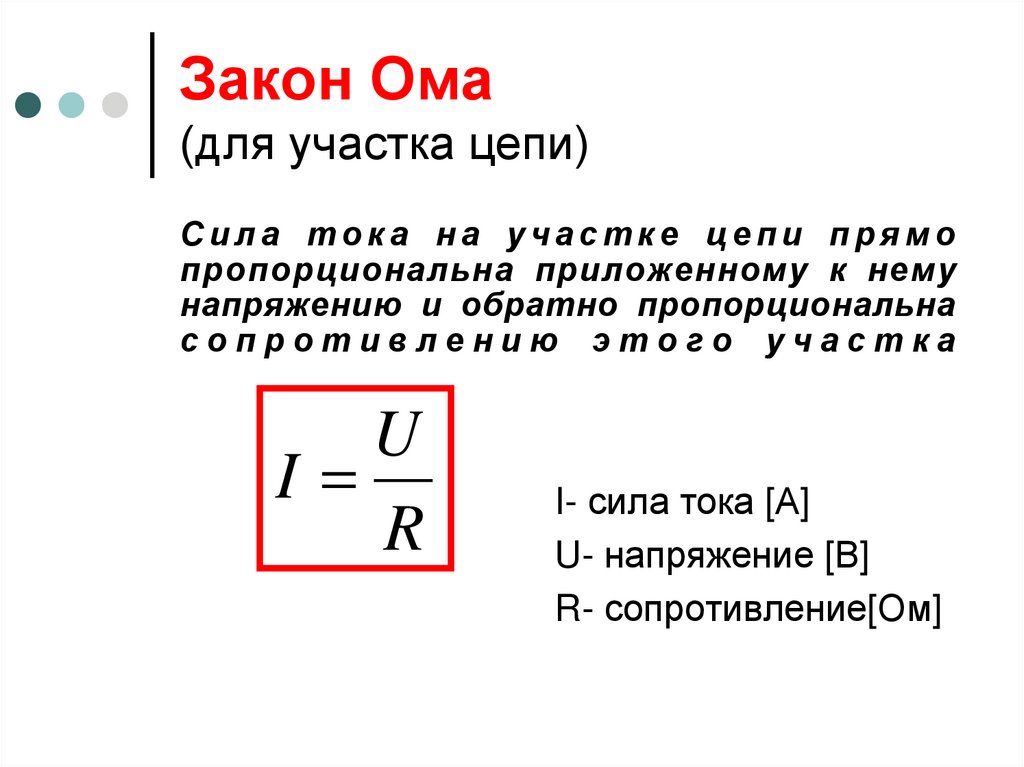
Второй эксперимент использовался для исследования схемы делителя напряжения и проверки ее формул. Формула делителя напряжения показывает, как напряжение делится между последовательно соединенными резисторами. Рассмотрим схему на рисунке 3, ток, протекающий через цепь, можно рассчитать с помощью уравнения 2. Общее сопротивление цепи будет суммой номиналов резисторов 1 и 2, поскольку они соединены последовательно, как показано в уравнении 2. Напряжение на резисторе 2 можно рассчитать с помощью уравнения 4. Подставив уравнения 2 и 3 в уравнение 4, значение напряжения на резисторе 2 можно рассчитать с помощью выражения 5, которое представляет собой формулу делителя напряжения. Уравнение показывает, что напряжение на последовательных резисторах равно произведению отношения его сопротивления к суммарному значению всех резисторов, умноженному на общее напряжение (Калифорнийский университет, nd). Та же процедура может быть использована для определения напряжения на резисторе 1, которое дано в уравнении 6. Формула делителя напряжения была проверена экспериментально в этом анализе.
Формула делителя напряжения была проверена экспериментально в этом анализе.
I8 = Vs/Req (уравнение 2)
Req = R1 + R2 (уравнение 3)
V2 = R2I8 (уравнение 4)
/ R+R8 = R+R8 (Уравнение 5)V1 = R1 / R1+R2 = V8 (Уравнение 6), где
- i с = ток, проходящий через цепь
- v с = напряжение в цепи
- Req = эквивалентное сопротивление (общее сопротивление системы)
- R1 = значение сопротивления резистора 1
- R2 = значение сопротивления резистора 2
- v 2 = напряжение на резисторе 2 напряжение на резисторе 1
Третий эксперимент был использован для анализа схемы делителя тока и проверки ее формул. Формула делителя тока показывает, как делится ток при прохождении через параллельные резисторы. Рассмотрим схему на рис. 4. Общее сопротивление можно рассчитать по уравнению 7. Напряжение в точках 1 и 2 равно выражению 8. Применив законы Ома к каждому резистору, можно определить ток по уравнению 9.и 10 для резисторов 1 и 2 соответственно (Университет Саймона Фрейзера, nd). Формулы делителя показывают, что ток, проходящий через набор резисторов в параллельной конфигурации, разделяется таким образом, что большее количество течет по пути с меньшим сопротивлением. Если один из резисторов имеет нулевое сопротивление (короткое замыкание), весь ток проходит через другой. Текущая формула делителя была проверена экспериментально в исследовании.
4. Общее сопротивление можно рассчитать по уравнению 7. Напряжение в точках 1 и 2 равно выражению 8. Применив законы Ома к каждому резистору, можно определить ток по уравнению 9.и 10 для резисторов 1 и 2 соответственно (Университет Саймона Фрейзера, nd). Формулы делителя показывают, что ток, проходящий через набор резисторов в параллельной конфигурации, разделяется таким образом, что большее количество течет по пути с меньшим сопротивлением. Если один из резисторов имеет нулевое сопротивление (короткое замыкание), весь ток проходит через другой. Текущая формула делителя была проверена экспериментально в исследовании.
Треб. = R1R2 / R1 + R2 (уравнение 7)
V12 = I8Req (уравнение 8)
I1 = V12/R1 = Треб./R1*I8 = R1 / R1 + R2*I8 (уравнение 9) )
I2 = V12 / R2 = Req / R2 * I8 = R1 / R1 + R2 * I8 (уравнение 10) где,
- i с = ток, проходящий через цепь
- v с = напряжение в цепи
- Req = эквивалентное сопротивление (общее сопротивление системы)
- R1 = значение сопротивления резистора 1
- R2 = значение сопротивления резистора 2
- В 12 = напряжение между точками 1 и 2
- i 1 = ток, протекающий через резистор 1
Методика
Аппаратура
Эксперимент проводился с использованием передовой электронной экспериментальной платформы, платы электрических сетей и мультиметра, которые представлены на рисунках 5.
Процедура
Анализ состоит из трех частей, где первая часть использовалась для проверки закона Ома, а во второй и третьей части были исследованы цепи делителя напряжения и тока соответственно. Первый эксперимент начался с отключения питания модуля усовершенствованной электронной экспериментальной платформы. Перемычка между розетками 1.6 и 1.7 была подключена. После этого также был подключен лид между 1.10 и 1.12. Мультиметр в режиме постоянного тока был подключен между гнездом 1. 13 (плюс) и 1.2 (общий). Схема, рассмотренная для этого эксперимента, представлена на рисунке 6. Значение переменного резистора было установлено на 100 Ом. Был включен модуль питания усовершенствованной электронной экспериментальной платформы. Значение тока было измерено и записано в Таблицу 1. Эксперимент был повторен для различных значений сопротивления (200 Ом, 300 Ом, 400 Ом, 500 Ом, 600 Ом, 700 Ом и 800 Ом).
13 (плюс) и 1.2 (общий). Схема, рассмотренная для этого эксперимента, представлена на рисунке 6. Значение переменного резистора было установлено на 100 Ом. Был включен модуль питания усовершенствованной электронной экспериментальной платформы. Значение тока было измерено и записано в Таблицу 1. Эксперимент был повторен для различных значений сопротивления (200 Ом, 300 Ом, 400 Ом, 500 Ом, 600 Ом, 700 Ом и 800 Ом).
Вторая часть анализа была использована для исследования схемы делителя напряжения и проверки формулы. Эксперимент начался с того, что питание модуля усовершенствованной электронной экспериментальной платформы было отключено. После этого были подключены закорачивающие перемычки между розетками 3.2 и 3.3, а также между розетками 3.8 и 3.11. Напряжения на резисторах 6 и 7 были рассчитаны с использованием уравнений, аналогичных уравнениям 5 и 6, и записаны в Таблицу 2. Блок питания модуля усовершенствованной электронной экспериментальной платформы был включен, и напряжения на резисторах R6 и R7 были измерены и записаны в Таблицу 2.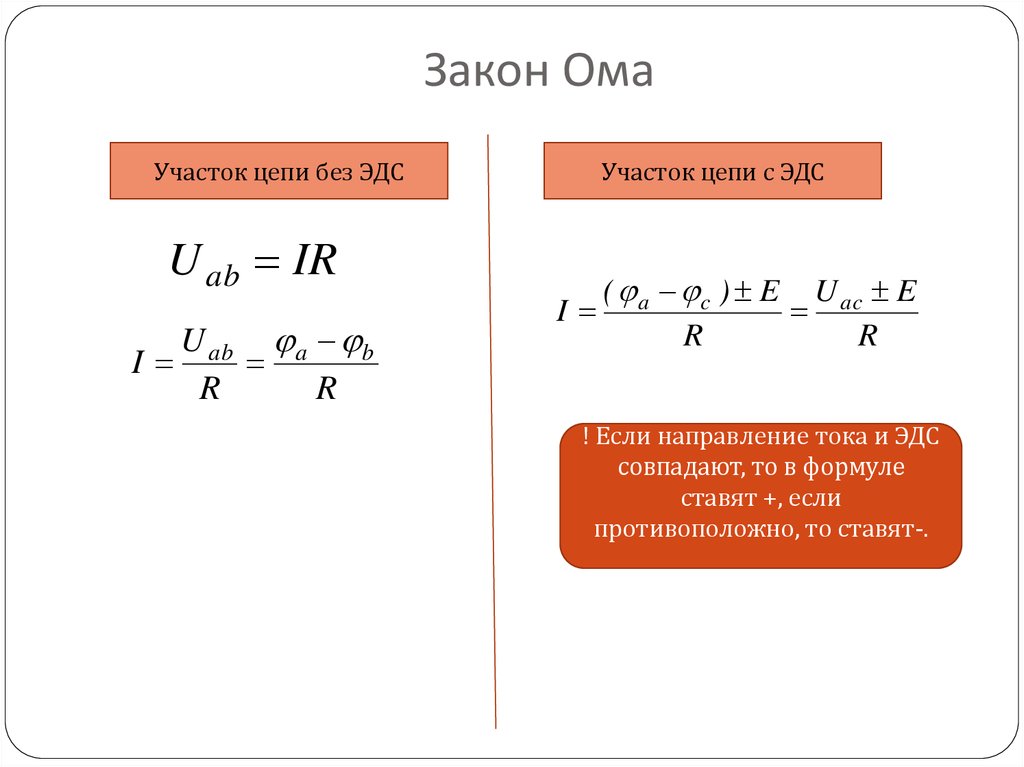 На Рисунке 7 показана схема делителя напряжения, рассматриваемая при анализе.
На Рисунке 7 показана схема делителя напряжения, рассматриваемая при анализе.
Третий эксперимент был использован для исследования схемы делителя и проверки формулы. Упражнение началось с отключения питания модуля усовершенствованной электронной экспериментальной платформы. Провода между розетками 3.3 и 3.6, 3.5 и 3.13, а также между 3.2 и 3.3 были подключены, как описано в лабораторном руководстве. В анализе использовалась схема делителя тока, представленная на рис. 8. Используя аналогичные уравнения для 9и 10, ток, проходящий через R6 и R8 . После этого был включен источник питания модуля усовершенствованной электронной экспериментальной платформы, а также токи через R6 и R8 с помощью мультиметра в соответствии с подключениями, указанными в лабораторном руководстве. Расчетные и измеренные значения занесены в Таблицу 3.
Рис. 8. Схема делителя тока, рассматриваемая при анализе.
Результаты
Результаты проверки закона Ома, формулы делителя напряжения и тока были записаны в таблицы 1, 2 и 3 соответственно.
Таблица 1. Результаты эксперимента по проверке закона Ома
Пример расчета;
Учитывая первый эксперимент с сопротивлением 100 Ом.
I = V/R
- I = ток
- V = напряжение = 12 В
- R = 100 Ом
I = V/R = 12/100 = 0,12 A = 1204 мА 9000 = погрешность Теоретическое значение – Экспериментальное значение / Теоретическое значение * 100 = 120 – 119,986 / 120 * 100 = 0,012%
Рисунок 9. График зависимости тока от сопротивления.Таблица 2. Результаты были получены в результате эксперимента с делителем напряжения.
Пример расчета;
Расчетное напряжение на резисторе R6
V6 = R6 / R7 + R6 * V8 = 1000 / 1000 + 1500 * 12 = 4,8 В
Погрешность в процентах = Теоретическое значение – Экспериментальное значение / Теоретическое значение * 100 = 4,800 – 4,900 / Теоретическое значение * 100 = 2,10%
Расчетное напряжение на R7
V7 = R7 / R6 + R7 * V8 = 1500 / 1000 + 1500 * 12 = 7,2 вольта
Процентная ошибка = Теоретическое значение – Экспериментальное значение / Теоретическое значение * 100 = 7,200 – 7,257 / 7,200 * 100 = 0,80%
Процентная ошибка для полного напряжения;
Процентная ошибка = Теоретическое значение – Экспериментальное значение / Теоретическое значение * 100 = 12,000 – 12,157 / 12,000 * 100 = 1,31%
Таблица 3. Результаты, полученные в ходе эксперимента с делителем тока.
Результаты, полученные в ходе эксперимента с делителем тока.
Пример расчета;
Расчетный ток в R6
I6 = V12 / V6 = 12/100 = 12 мА
Процентная ошибка = Теоретическое значение – Экспериментальное значение / Теоретическое значение * 100 = 12,000 – 12,367 / 12,000 * 100 = 0,031%
Расчетный ток в R7
I8 = V12/R8 = 12/60 = Теоретическое значение – Экспериментальное значение / Теоретическое значение * 100 = 17,650 – 18,162 / 17,650 * 100 = 2,90%
Расчетный общий ток;
Req = R1R2 / R1+R2 = 1000 * 680 / 1000 + 680 = 404,762 Ом
V12 = IsReq = 12 v = Is * 404,762 Ом
I S = 12 В / 404,762 ω = 29,650 мА
Процент ошибка = теоретическое значение — Экспериментальное значение / Тэретическое значение * 100 = 29,650 — 30,503 / 29,650 * 100 = 2,88%
. В эксперименте закон Ома определяли путем измерения тока через различные сопротивления при постоянном напряжении. Как измеренные, так и рассчитанные значения показывают, что ток уменьшается с увеличением сопротивления, как показано на рисунке 9.
 . Было обнаружено, что существует небольшая разница между измеренным и рассчитанным током, проходящим через различные сопротивления. Измеренный ток оказался выше расчетных значений, что может быть связано с некоторым сопротивлением соединительных кабелей и измерительных устройств, которое предполагается при теоретическом рассмотрении. Второй эксперимент показывает, что напряжение на резисторе R7 (7,257 вольта) было выше, чем на резисторе R6 (4,901 вольта). Результаты показывают, что напряжение разделяется в зависимости от значения сопротивления. Чем больше номинал резистора, тем больше напряжение на нем. В третьем эксперименте было обнаружено, что больший ток проходит через R8, который имеет меньшее сопротивление, чем R6. Таким образом, формула делителя тока была проверена экспериментально.
. Было обнаружено, что существует небольшая разница между измеренным и рассчитанным током, проходящим через различные сопротивления. Измеренный ток оказался выше расчетных значений, что может быть связано с некоторым сопротивлением соединительных кабелей и измерительных устройств, которое предполагается при теоретическом рассмотрении. Второй эксперимент показывает, что напряжение на резисторе R7 (7,257 вольта) было выше, чем на резисторе R6 (4,901 вольта). Результаты показывают, что напряжение разделяется в зависимости от значения сопротивления. Чем больше номинал резистора, тем больше напряжение на нем. В третьем эксперименте было обнаружено, что больший ток проходит через R8, который имеет меньшее сопротивление, чем R6. Таким образом, формула делителя тока была проверена экспериментально.Заключение
Цели анализа были достигнуты, и в первой части эксперимента был сделан вывод, что ток, проходящий через электрическую цепь, обратно пропорционален сопротивлению системы.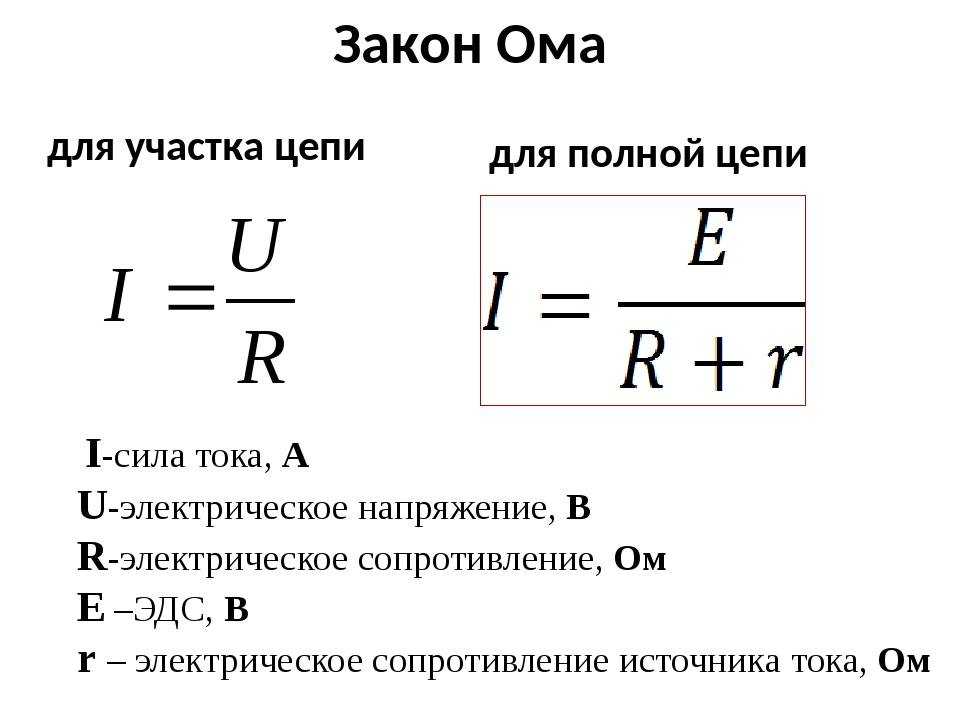 Формула делителя напряжения была проверена экспериментально, и был сделан вывод, что напряжение делится пропорционально величине сопротивления. В третьем эксперименте было установлено, что ток разделяется таким образом, что большее его количество протекает через путь с меньшим сопротивлением для резисторов, расположенных параллельно в цепи делителя.
Формула делителя напряжения была проверена экспериментально, и был сделан вывод, что напряжение делится пропорционально величине сопротивления. В третьем эксперименте было установлено, что ток разделяется таким образом, что большее его количество протекает через путь с меньшим сопротивлением для резисторов, расположенных параллельно в цепи делителя.
Послелабораторные вопросы
- Вопрос 1.1: Сопротивление обратно пропорционально току для источника постоянного напряжения.
- Вопрос 1.2: Ток уменьшится, если напряжение, подаваемое на переменный резистор, уменьшится вдвое, потому что эти два параметра прямо пропорциональны по закону Ома.
- Вопрос 2.1: Напряжение прямо пропорционально номиналу каждого резистора в цепи делителя.
- Вопрос 3.1: В цепи делителя больший ток протекает по пути с меньшим сопротивлением. Через R6 проходит меньший ток по сравнению с R7.
Ссылки
Инженерная математика, (без даты). Введение в закон Ома .
Введение в закон Ома .
Университет Саймона Фрейзера. (н.д). КВЛ Пример резисторного делителя напряжения .
Университет Кентукки. (н.д). Закон Ома и сопротивление .
Технические книги Pdf. (н.д). Формула закона Ома .
Калифорнийский университет. (н.д). Делители напряжения и тока .
Закон Ома – определения, эксперимент, примеры
Прохождение электрического тока через проводник зависит от разности потенциалов на его концах. При определенной температуре сила тока, протекающего через него, прямо пропорциональна разности потенциалов на его концах. Это известно как закон Ома.
Это известно как закон Ома.
Я ∝ В
или V ∝ I V = разность потенциалов
V = RI R = сопротивление
или R = V/I, I = ток
Здесь R — константа пропорциональности, которая зависит от размера, природы материала и температуры. R называется электрическим сопротивлением или сопротивлением проводника.
- Соберите цепь, как показано на рисунке, состоящую из нихромовой проволоки XY длиной, скажем, 0,5 м, амперметра, вольтметра и четырех ячеек по 1,5 В каждая. (Нихром представляет собой сплав никеля, хрома, марганца и металлического железа.)
- Сначала используйте только одну ячейку в качестве источника в цепи. Обратите внимание на показания амперметра I для тока и показания вольтметра V для разности потенциалов на нихромовой проволоке XY в цепи. Табулируйте их.
- Затем подключите две ячейки в цепь и запишите соответствующие показания амперметра и вольтметра для значений тока через нихромовую проволоку и разности потенциалов на нихромовой проволоке.

- Повторите вышеуказанные шаги, используя три ячейки, а затем четыре ячейки в цепи по отдельности.
- Рассчитайте отношение V к I для каждой пары разности потенциалов (V) и тока (I).
- Постройте график между V и I и обратите внимание на характер графика.
Таким образом, V/I — это постоянное отношение, которое называется сопротивлением (R). Он известен как закон Ома.
СОПРОТИВЛЕНИЕ ПРОВОДНИКА:
Электрический ток представляет собой поток электронов через проводник. Когда электроны перемещаются из одной части проводника в другую, они сталкиваются с другими электронами, а также с атомами и ионами, присутствующими в теле проводника. Из-за этих столкновений возникает некоторое препятствие или противодействие потоку электронов через проводник.
Свойство проводника, благодаря которому он противодействует протеканию по нему тока, называется сопротивлением. Сопротивление проводника численно равно отношению разности потенциалов на его концах к протекающему по нему току.
Сопротивление = разность потенциалов/ток или R = V/I
ЕДИНИЦА СОПРОТИВЛЕНИЯ
Единицей сопротивления в системе СИ является Ом (Ом)
1 Ом (Ом) = 1 вольт (1 В)/ ампер (1 А)
Говорят, что сопротивление проводника равно одному ому, если по нему протекает ток в один ампер, когда к его концам приложена разность потенциалов в один вольт.
ПРОВОДНИКИ, РЕЗИСТОРЫ И ИЗОЛЯТОРЫ:
По электрическому сопротивлению все вещества можно разделить на три группы:
проводники, резисторы и изоляторы.
Проводники:
Те вещества, которые имеют очень низкое электрическое сопротивление, называются проводниками. Проводник позволяет электричеству легко проходить через него. Серебряный металл является лучшим проводником электричества. Медь и алюминий также являются хорошими проводниками. Электрические провода сделаны из меди или алюминия, потому что они имеют очень низкое электрическое сопротивление.
Резисторы:
Те вещества, которые обладают сравнительно большим электрическим сопротивлением, называются резисторами. Такие сплавы, как нихром, манганин и константан (или урека), имеют довольно высокое сопротивление, поэтому они используются для изготовления тех электрических устройств, где требуется высокое сопротивление. Резистор уменьшает ток в цепи.
Такие сплавы, как нихром, манганин и константан (или урека), имеют довольно высокое сопротивление, поэтому они используются для изготовления тех электрических устройств, где требуется высокое сопротивление. Резистор уменьшает ток в цепи.
Изоляторы:
Те вещества, которые обладают бесконечно большим электрическим сопротивлением, называются изоляторами. Изолятор не пропускает через себя электричество. Резина — отличный изолятор. Электрики носят резиновые перчатки при работе с электричеством, потому что резина является изолятором и защищает их от поражения электрическим током. Дерево также является хорошим теплоизолятором.
ПРИЧИНА СОПРОТИВЛЕНИЯ:
В проводнике много свободных электронов. Они двигаются хаотично, когда через них не проходит электрический ток. Но когда через него проходит ток, они, будучи отрицательно заряженными, начинают двигаться к положительному концу проводника со скоростью, называемой дрейфовой скоростью. Во время этого движения они сталкиваются с атомами или ионами проводника и таким образом их скорость замедляется. Это замедление из-за препятствия называется Сопротивлением.
Это замедление из-за препятствия называется Сопротивлением.
Упражнение, чтобы показать, что количество тока через электрический компонент зависит от его сопротивления:
- Возьмите нихромовую проволоку, лампу накаливания, лампочку на 10 Вт и амперметр (диапазон 0-5 А), штепсельный ключ и несколько соединительных проводов.
- Соберите цепь, последовательно соединив четыре сухих элемента по 1,5 В каждый с амперметром, оставив в цепи зазор XY, как показано на рисунке.
- Завершите цепь, подключив нихромовую проволоку в разрыв XY. Вставьте ключ. Запишите показания амперметра. Выньте ключ из вилки. [Примечание: Всегда вынимайте ключ из вилки после измерения тока в цепи.]
- Замените в цепи нихромовую проволоку с лампой накаливания и найдите силу тока через нее, измерив показания амперметра.
- Теперь повторите описанный выше шаг с лампочкой мощностью 10 Вт в зазоре XY.
- Вы заметите, что показания амперметра различаются для разных компонентов, подключенных через зазор XY.

- Вы можете повторить это действие, оставив любой материальный компонент в промежутке. В каждом случае наблюдайте за показаниями амперметра. Проанализируйте наблюдения.
Таким образом, мы приходим к выводу, что ток через электрический компонент зависит от его сопротивления.
ФАКТОРЫ, ВЛИЯЮЩИЕ НА СОПРОТИВЛЕНИЕ ПРОВОДНИКА
Сопротивление зависит от следующих факторов:
(i) Длина проводника.
(ii) Площадь поперечного сечения проводника (или толщина проводника).
(iii) Природа материала проводника.
(iv) Температура проводника.
Математически: Экспериментально установлено, что:
(i) Сопротивление данного проводника прямо пропорционально его длине, т.е.
R ∝ l ….(i)
(ii) Сопротивление данного проводника обратно пропорционально площади его поперечного сечения, т.е.
R ∝ 1/A ….(ii)
Из (i) и (ii), R ∝ 1/A
R = ρ x 1/A…(iii)
Где ρ (rho) — постоянная, известная как удельное сопротивление материала проводника.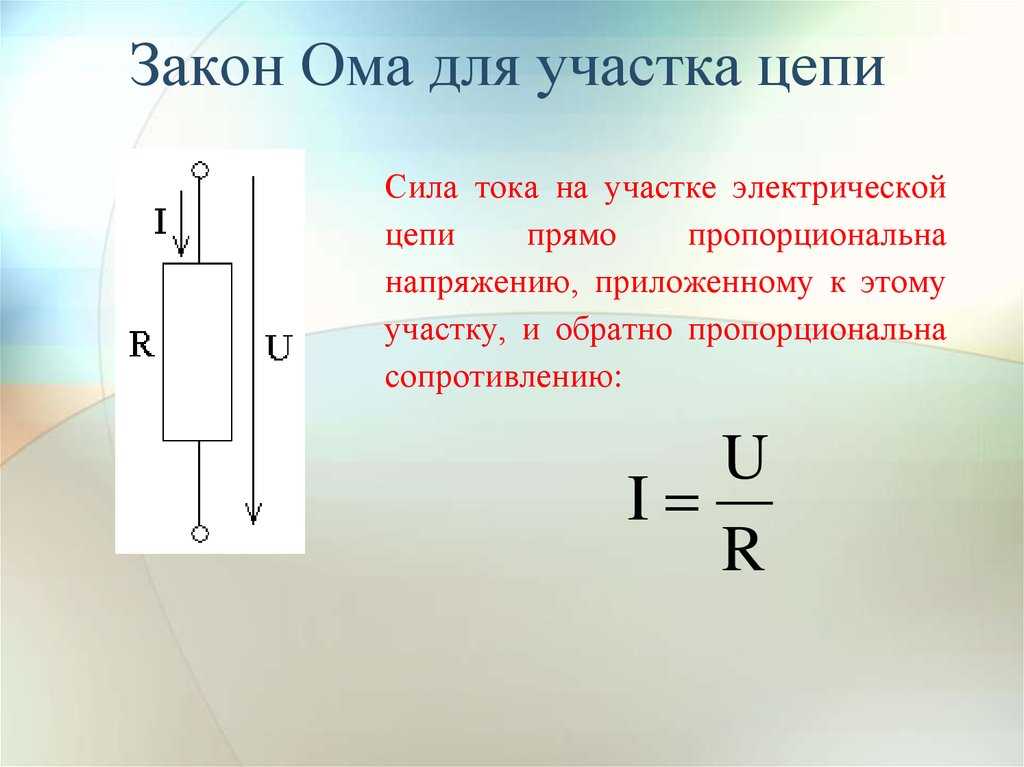 Удельное сопротивление также известно как удельное сопротивление.
Удельное сопротивление также известно как удельное сопротивление.
ЗАВИСИМОСТЬ СОПРОТИВЛЕНИЯ ОТ ТЕМПЕРАТУРЫ:
Если R 0 — сопротивление проводника при 0°C, а R1 — сопротивление проводника при t°C, то отношение между R0 и R1 определяется выражением
. R 1 = R o (1 + θαΔt) [здесь Δt = t – 0 = t]
Или
Здесь a = коэффициент удельного сопротивления, t = температура в °C
Опыт, чтобы показать, что сопротивление проводника зависит от его длины, площади поперечного сечения и природы его материала.
- Замкните электрическую цепь, состоящую из ячейки, амперметра, нихромовой проволоки длиной [обозначена (1)] и штепсельного ключа, как показано на рисунке.
- Теперь вставьте ключ. Обратите внимание на силу тока амперметра.
- Замените нихромовую проволоку другой нихромовой проволокой той же толщины, но в два раза большей длины, то есть 2 [отмечено (2) на рисунке].

- Обратите внимание на показания амперметра.
- Теперь замените проволоку более толстой нихромовой проволокой той же длины [обозначено (3)]. Более толстый провод имеет большую площадь поперечного сечения. Снова запишите ток в цепи.
- Вместо нихромовой проволоки подключите в цепь медную проволоку [обозначена (4) на рисунке]. Пусть проволока будет той же длины и той же площади поперечного сечения, что и первая нихромовая проволока [обозначена (1)]. Обратите внимание на значение тока.
- Обратите внимание на разницу в токе во всех случаях.
- Заметим, что сила тока зависит от длины проводника.
- Мы также заметили, что сила тока зависит от площади поперечного сечения используемого провода.
СОПРОТИВЛЕНИЕ:
Удельное сопротивление, ρ = R x A/1….(iv)
Используя эту формулу, мы теперь получим определение удельного сопротивления. Возьмем проводник с единичной площадью поперечного сечения 1 м2 и единичной длиной 1 м. Итак, положив A= 1 и l = 1 в уравнении (iv),
Итак, положив A= 1 и l = 1 в уравнении (iv),
получаем:
Удельное сопротивление, ρ = R
Удельное сопротивление вещества численно равно сопротивлению стержня из этого вещества длиной 1 метр и квадратным сечением 1 метр.
Единица удельного сопротивления,
Единицей удельного сопротивления в СИ является ом-метр, который записывается символами как Ω — м.
Удельное сопротивление вещества не зависит от его длины или толщины. Это зависит только от природы вещества. Удельное сопротивление вещества является его характерным свойством. Таким образом, мы можем использовать значения удельного сопротивления для сравнения сопротивлений двух или более веществ.
Значение удельного сопротивления:
Хороший проводник электричества должен иметь низкое удельное сопротивление, а плохой проводник электричества должен иметь высокое удельное сопротивление. Удельное сопротивление сплавов намного выше, чем у чистых металлов. Именно из-за их высокого удельного сопротивления сплавы манганина и константана используются для изготовления резистивных проводов, используемых в электронных приборах для уменьшения тока в электрической цепи.
Сплав нихрома используется для изготовления нагревательных элементов электроприборов, таких как электрические утюги, комнатные обогреватели, водонагреватели, тостеры и т. д., поскольку он имеет очень высокое удельное сопротивление и не подвергается окислению (или горению) даже в раскаленном состоянии.
Влияние температуры на удельное сопротивление:
Удельное сопротивление проводников (например, металлов) очень низкое. Удельное сопротивление большинства металлов увеличивается с температурой. С другой стороны, удельное сопротивление изоляторов, таких как эбонит, стекло и алмаз, очень велико и не изменяется при изменении температуры. Удельное сопротивление полупроводников, таких как кремний и германий, находится между сопротивлениями проводников и изоляторов и уменьшается при повышении температуры. Полупроводники приобретают большое практическое значение из-за заметного изменения их проводящих свойств с температурой и концентрацией примесей.
СПЕЦИАЛЬНОЕ ИСПОЛЬЗОВАНИЕ НЕКОТОРЫХ ПРОВОДЯЩИХ МАТЕРИАЛОВ:
Вольфрам: Имеет высокую температуру плавления 3380ºC и излучает свет при 2127ºC. Таким образом, он используется в качестве нити накаливания в лампах.
Таким образом, он используется в качестве нити накаливания в лампах.
Нихром: Обладает высоким удельным сопротивлением и температурой плавления. Используется как элемент в отопительных приборах.
Константан и манганин: имеют модулированное удельное сопротивление. Таким образом, они используются для изготовления сопротивлений и реостатов.
Олово-свинец Сплав: Имеет низкое удельное сопротивление и низкую температуру плавления. Таким образом, он используется в качестве плавкого предохранителя.
1. При подключении батареи 12 В через неизвестный резистор в цепи возникает ток 2,5 мА. Найдите значение сопротивления резистора.
Решение: Учитывая, что напряжение батареи V = 12 В
Ток цепи I = 2,5 мА = 2,5 × 10 -3 А
∴ Значение сопротивления R = V/I = 12/ 2,5 x 10 3 = 4800 Ом
2. Перерисуйте схему на рис. 11, вставив амперметр для измерения тока через резисторы и вольтметр для измерения разности потенциалов на резисторах 12 Ом.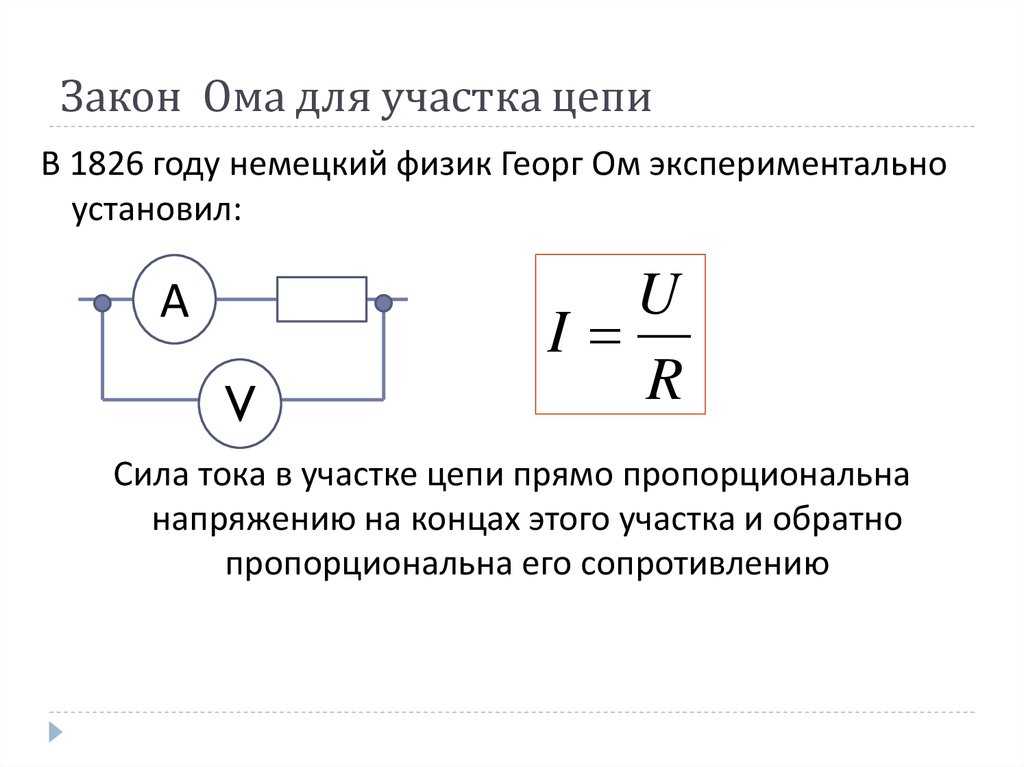



 Организационный момент.
Организационный момент.

 Формулировка цели урока.
Формулировка цели урока.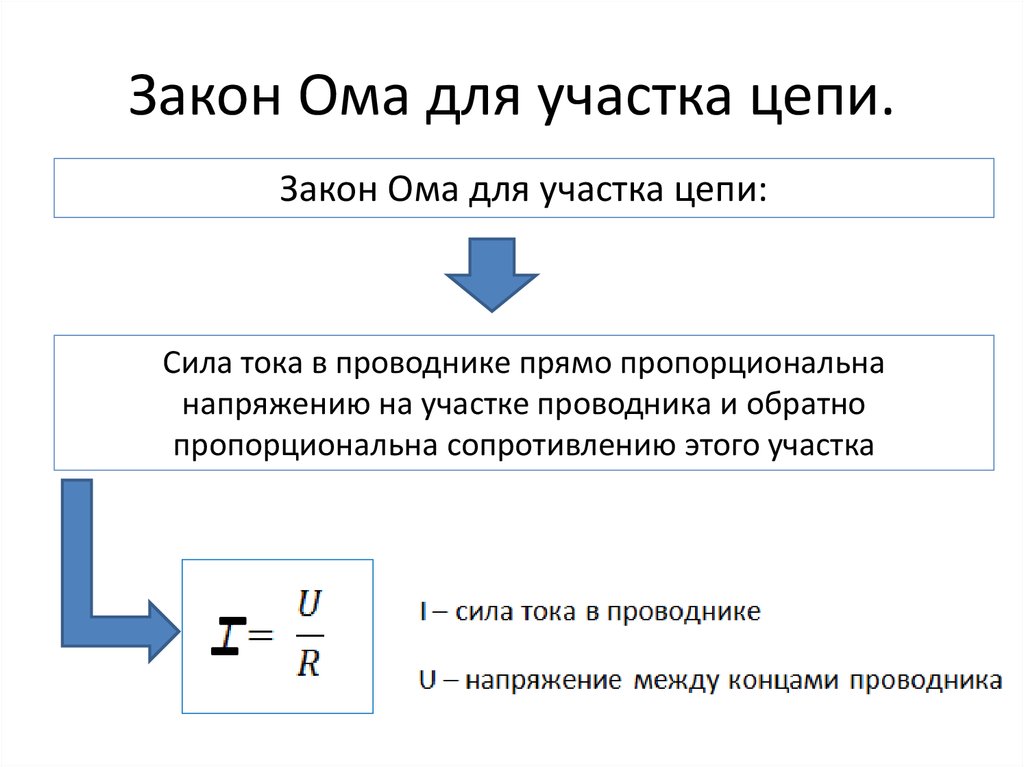


 Приложение № 2)
Приложение № 2) 29 (1,2,3).
29 (1,2,3).


