Закон Ома для участка цепи – формула, определение сопротивления
4.3
Средняя оценка: 4.3
Всего получено оценок: 286.
4.3
Средняя оценка: 4.3
Всего получено оценок: 286.
Наравне с законами Кирхгофа, закон Ома для участка цепи – один из ключевых во всей электротехники. При проектировании электросетей любой сложности закон Ома становится необходимым инструментом, так как позволяет рассчитывать требуемые для нужного результата параметры сети.
Сущность закона
Эксперименты с электрическими цепями, в которых были источник тока и элемент сопротивления, позволили Георгу Ому установить некоторые закономерности, которые легли в основу закона, названного его именем. Приведем их:
- При увеличении напряжения сила тока на участке цепи возрастала линейно.
- Сила тока уменьшалась при увеличении сопротивления участка.
Поэтому математическая формула закон Ома для участка цепи выглядит следующим образом:
$I = \frac {U}{R}$, где I – сила тока, измеряемая в амперах, U – напряжение, измеряемое в вольтах и R – сопротивление, измеряемое в омах.
Из фигурирующих в уравнении величин ключевой является сопротивление. Оно зависит от параметров проводника:
- Становится больше с увеличением длинны проводника
- Уменьшается с ростом проводимости проводника и его площади сечения.
Объяснить это очень просто: чем больше путь, проходимый электронами, тем больше вероятность столкновений с атомами в узлах решетки. Это мешает движению тока. С другой стороны, увеличение площади сечения дает больше вариантов пути электронам, уменьшается вероятность соударений. Проводимость же – исключительно свойства проводящего вещества. Например, медь оказывает меньшее сопротивление, чем железо, поскольку является более проводимым.
Закон Ома с точностью справедлив лишь для цепей, где действует идеальный источник тока. То есть такой, в котором нет внутреннего сопротивления.
В противном случае применяется закон Ома для полной цепи.
Рассмотрим участок электрической цепи (рис. 2). В узлах 1 и 2 – потенциалы электрического поля $\phi_1$ и $\phi_2$. Между ними заключен элемент с сопротивлением R – резистор. К участку также подсоединен вольтметр.
Тогда падением напряжения на данном участке электрической цепи будем называть величину, выраженную через закон Ома:
$U = I \cdot R$
Падение напряжения – определение, сложившееся исторически. Речь идет об изменении значения потенциала электрического поля по мере продвижения вдоль проводника.
Для запоминания закона Ома используют правило, называемое треугольником Ома.
Рис. 3. Треугольник Ома.Техника работы с ним проста. Ту величину, которую нужно найти, закрываем пальцем, а две другие дают формулу для ее нахождения. Закрыв I, получим $\frac {U}{R}$.
Задачи
- Сопротивление проводника – 2 Ом. Напряжение – 10 В. Какова сила тока? Какой будет сила тока, если увеличить длину проводника в два раза?
Решение:
Запишем закон Ома для участка цепи:
$I = \frac {U}{R}$
Подставив в него известные величины, получим:
$I = \frac {10}{2} = 5 \: А$
Теперь, зная, что сопротивление прямо пропорционально длине проводника, запишем:
$I = \frac {U}{2R} = 2,5 А$
- Амперметр показал, что сила тока на участке цепи – 0,1 А.
Решение:
Запишем закон Ома для участка цепи:
$I = \frac {U}{R}$
Подставив в него известные величины и выразив R, получим:
$R = \frac {U}{I} = \frac {200}{0,1} = 2000 Ом \: А$
Что мы узнали?
В ходе урока дали математическую и словесную формулировки закона Ома для участка цепи, рассмотрели значение сопротивления для участка цепи, а также разобрались с треугольником Ома. Для закрепления материала решили задачу.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Ринат Баишев
10/10
Денис Иванов
9/10
Мария Кшевач
7/10
Оценка доклада
4.3
Средняя оценка: 4.3
Всего получено оценок: 286.
А какая ваша оценка?
Закон Ома для участка цепи
В § 8-и мы начали знакомство с физической величиной «электрическое сопротивление».
Продолжим его – проделаем опыт. Нам потребуются источник электроэнергии, амперметр, вольтметр, реостат и два резистора (две нихромовые спирали) с различными сопротивлениями.
Соберём цепь, как показано на рисунке слева или на схеме в конце параграфа. Перемещая движок реостата, поочерёдно установим значения силы тока 0,4 А, 0,6 А, 0,8 А, 1 А. Запишем показания амперметра и вольтметра в таблицу. Повторим опыт, заменив резистор, и дополним таблицу:
| Первый резистор | Второй резистор | |||||||
| I , A | 0,4 | 0,6 | 0,8 | 1,0 | 0,4 | 0,6 | 0,8 | 1,0 |
| U , В | 1,6 | 2,4 | 3,2 | 4,0 | 2,4 | 3,6 | 4,8 | 6,0 |
| Поделив напряжение на силу тока, обнаружим закономерность: | ||||||||
| R = U/I | 4 | 4 | 4 | 4 | 6 | 6 | 6 | 6 |
Закономерность в том, что вне зависимости от значений напряжения и силы тока их частное остаётся постоянным для каждого резистора.
Проверьте: после деления каждого числа строки (U, В) на расположенное над ним число строки (I, А) получаются одинаковые результаты во всех колонках левой половины таблицы: 4 В/А и во всех колонках правой половины таблицы: 6 В/А. Это показывает, что величина R является характеристикой именно изучаемого участка цепи – резистора.
Заметим, что эта закономерность всегда справедлива для металлических проводников в твёрдом или жидком состоянии; для других проводников она справедлива не всегда. Однако величину R, равную отношению U/I, всегда называют электрическим сопротивлением проводника независимо от его материала и состояния, а 1 В/А называют 1 Ом. Следовательно, 1 Ом – сопротивление такого проводника, в котором возникнет ток 1 А, если на концах проводника напряжение 1 В.
Связь между величинами U, I, R обычно записывается в виде формулы, известной как закон Ома для участка цепи:
» border=»0″ cellspacing=»0″ cellpadding=»0″>U – приложенное напряжение, В
R – сопротивление участка цепи, Ом
Чтобы выяснить, как следует прочитать эту формулу, вспомним знания по алгебре о видах пропорциональности величин.
| прямая пропорциональность: | Y = k · X | → | I = 1/R · U |
| обратная пропорциональность: | Y = k / X | → | I = U / R |
Из первой строки следует: при постоянном сопротивлении величина 1/R тоже постоянна, поэтому сила тока прямо пропорциональна напряжению на концах участка цепи.
Из второй строки: при постоянном напряжении сила тока обратно пропорциональна сопротивлению участка цепи. Объединяя это, получаем формулировку закона Ома для участка цепи: сила тока в участке цепи прямо пропорциональна напряжению на его концах и обратно пропорциональна сопротивлению этого участка.
Примечание. С точки зрения алгебры, формулу закона Ома можно записать в такой форме: U=I·R. Применим её для изучения цепи, изображённой на схеме. Допустим, клеммы A и B присоединены к источнику с напряжением 10 В, однако вольтметр позволяет измерить напряжение не более 6 В (см. рисунок в начале параграфа). Поэтому нам нужно создать падение напряжения на реостате на 4 В или более. Как это сделать? Чем правее мы смещаем движок, тем больше сопротивление реостата, и, согласно формуле U=I·R, больше напряжение на реостате, которое и называют падением напряжения.
В результате на резисторе напряжение снижается и может стать менее 6 В, что нам и нужно.
20.2: Закон Ома. Сопротивление и простые схемы
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 2680
- OpenStax
- OpenStax
Цели обучения
К концу этого раздела вы сможете:
- Объяснить происхождение закона Ома.
- Расчет напряжения, тока или сопротивления по закону Ома.
- Объясните, что такое омический материал.
- Опишите простую схему.
Что управляет током? Мы можем думать о различных устройствах, таких как батареи, генераторы, настенные розетки и т.
д., которые необходимы для поддержания тока. Все такие устройства создают разность потенциалов и в широком смысле называются источниками напряжения. Когда источник напряжения подключен к проводнику, он применяет разность потенциалов \(V\), которая создает электрическое поле. Электрическое поле, в свою очередь, воздействует на заряды, вызывая ток.
Закон Ома
Ток, протекающий через большинство веществ, прямо пропорционален приложенному к нему напряжению \(V\). Немецкий физик Георг Симон Ом (1787–1854) был первым, кто экспериментально продемонстрировал, что ток в металлической проволоке прямо пропорционален приложенному напряжению :
\[I \propto V . \label{20.3.1}\]
Это важное соотношение известно как закон Ома . Его можно рассматривать как причинно-следственную связь, где напряжение является причиной, а ток — следствием. Это эмпирический закон, аналогичный закону трения — экспериментально наблюдаемому явлению. Такая линейная зависимость не всегда имеет место.
Сопротивление и простые схемы
Если напряжение управляет током, что этому препятствует? Электрическое свойство, препятствующее току (примерно похожее на трение и сопротивление воздуха), называется сопротивлением \(R\). Столкновения движущихся зарядов с атомами и молекулами в веществе передают энергию веществу и ограничивают ток. Сопротивление определяется как обратно пропорциональное току, или
\[I \propto \frac{1}{R} . \label{20.3.2}\]
Таким образом, например, ток уменьшается вдвое, если сопротивление удваивается. Сочетание отношений тока к напряжению и тока к сопротивлению дает
\[I = \frac{V}{R} . \label{20.3.3}\]
Это соотношение также называют законом Ома. Закон Ома в этой форме действительно определяет сопротивление для определенных материалов. Закон Ома (как и закон Гука) не является универсальным. Многие вещества, для которых выполняется закон Ома, называются омическими . К ним относятся хорошие проводники, такие как медь и алюминий, и некоторые плохие проводники при определенных обстоятельствах.
Омические материалы имеют сопротивление \(R\), которое не зависит от напряжения \(V\) и тока \(I\). Объект, который имеет простое сопротивление, называется резистор , даже если его сопротивление мало. Единицей измерения сопротивления является Ом и обозначается символом \(\Омега\) (греческая омега в верхнем регистре). Перестановка \(I = V/R\) дает \(R = V/I\), поэтому единицами сопротивления являются 1 Ом = 1 вольт на ампер:
\[1 \Omega = 1 \frac{V} {А} . \label{20.3.4} \]
На рисунке \(\PageIndex{1}\) показана схема простой цепи. Простая схема имеет один источник напряжения и один резистор. Провода, соединяющие источник напряжения с резистором, можно считать имеющими пренебрежимо малое сопротивление, или их сопротивление можно включить в \(R\).
Рисунок \(\PageIndex{1}\): Простая электрическая цепь, в которой замкнутый путь для протекания тока обеспечивается проводниками (обычно металлическими проводами), соединяющими нагрузку с клеммами батареи, представленными красными параллельными линиями.
. Зигзагообразный символ представляет одиночный резистор и включает любое сопротивление в соединениях с источником напряжения.Пример \(\PageIndex{1}\): Расчет сопротивления: Автомобильная фара:
Каково сопротивление автомобильной фары, через которую протекает ток 2,50 А при подаче на нее напряжения 12,0 В?
Стратегия
Мы можем преобразовать закон Ома в формулу \(I = V/R\) и использовать его для нахождения сопротивления.
Решение:
Преобразование уравнения \ref{20.3.3} и подстановка известных значений дает
\[\begin{align*} R &= \frac{V}{I} \\[5pt] &= \frac{12,0 В}{2,50 А} \\[5pt] &= 4,80 \Омега . \end{align*}\]
Обсуждение:
Это относительно небольшое сопротивление, но оно больше, чем сопротивление холода фары. Как мы увидим, сопротивление металлов обычно 9{-5} \Омега\), а сверхпроводники вообще не имеют сопротивления (они неомические). Сопротивление связано с формой объекта и материалом, из которого он состоит, как будет показано в разделе «Сопротивление и удельное сопротивление».
Дополнительное понимание достигается путем решения \(I = V/R\) для \(V\), что дает
\[V = IR . \label{20.3.5}\]
Выражение для \(V\) можно интерпретировать как падение напряжения на резисторе, вызванное низким током \(I\). Фраза \(IR\) 9Для этого напряжения часто используется падение 0050 . Например, фара в примере имеет падение \(IR\) 12,0 В. Если измерить напряжение в различных точках цепи, будет видно, что оно увеличивается на источнике напряжения и уменьшается на резисторе. Напряжение аналогично давлению жидкости. Источник напряжения подобен насосу, создающему перепад давления, вызывающему ток — поток заряда. Резистор подобен трубе, которая снижает давление и ограничивает поток из-за своего сопротивления. Сохранение энергии имеет здесь важные последствия. Источник напряжения поставляет энергию (вызывая электрическое поле и ток), а резистор преобразует ее в другую форму (например, в тепловую энергию). В простой цепи (одна с одним простым резистором) напряжение, подаваемое источником, равно падению напряжения на резисторе, так как \(PE = q \Delta V\), и одно и то же \(q\) протекает через каждый .
Таким образом, энергия, подаваемая источником напряжения, и энергия, преобразуемая резистором, равны (рис. \(\PageIndex{2}\)).
ВЫПОЛНЕНИЕ СОЕДИНЕНИЙ: СОХРАНЕНИЕ ЭНЕРГИИ
В простой электрической цепи единственный резистор преобразует энергию, поступающую от источника, в другую форму. О сохранении энергии здесь свидетельствует тот факт, что вся энергия, подаваемая источником, преобразуется в другую форму одним только резистором. Мы обнаружим, что закон сохранения энергии имеет и другие важные применения в цепях и является мощным инструментом анализа цепей.
Резюме
- Простая цепь — это цепь, в которой есть один источник напряжения и одно сопротивление.
- Одно из утверждений закона Ома дает отношение между током \(I\), напряжением \(V\) и сопротивлением \(R\) в простой цепи как \(I = \frac{V}{R}. \)
- Сопротивление выражается в омах (\(\Омега\)), связанных с вольтами и амперами как \(1 \Омега = 1 В/А \).
- Падение напряжения или \(IR\) на резисторе, вызванное протеканием через него тока, определяемое выражением \(V = IR\).
Глоссарий
- Закон Ома
- эмпирическое соотношение, утверждающее, что ток I пропорционален разности потенциалов В , ∝ В ; его часто записывают как I = V/R , где R — сопротивление
- сопротивление
- электрическое свойство, препятствующее току; для омических материалов это отношение напряжения к току, Р = В/И
- Ом
- единица сопротивления, определяемая как 1 Ом = 1 В/А
- омический
- тип материала, для которого действует закон Ома
- простая схема
- схема с одним источником напряжения и одним резистором
Эта страница под названием 20.
2: Закон Ома — Сопротивление и простые схемы распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать оглавление
- нет
- Теги
- Ом
- Закон Ома
- омический
- сопротивление
- простая схема
- источник@https://openstax.
Анализ цепи, часть 3: Закон Ома, мощность и энергия | Джейсон Холл
Во второй части этой серии я представил введение в электрическое сопротивление. В этой статье я повторю некоторые принципы закона Ома, которые были представлены в предыдущих статьях, и представлю электрическую мощность и энергию. Я также кратко расскажу о программах SPICE и их использовании для анализа цепей.
Георг Ом определил, что ток (I) в цепи прямо пропорционален приложенному напряжению (E) и обратно пропорционален сопротивлению (R). Закон Ома гласит, что I = E/R. Уравнение можно изменить для решения любой из трех переменных:
Обычно источник напряжения показан слева, а нагрузка (в данном случае резистор) показана справа со стрелкой, указывающей направление тока (обычное направление):
На принципиальных схемах вы часто увидите напряжение, представленное как E, так и V. Различие здесь заключается в том, что источники напряжения обозначаются буквой E, а нагрузки обозначаются буквой V.
Часто также указывается полярность напряжения:
Электрическая мощность (P) — скорость, с которой электрическая энергия передается по электрической цепи. Единицей мощности в системе СИ является ватт.
Легко рассчитать мощность в ваттах, подводимую к нагрузке, используя уравнения для мощности. Допустим, у вас есть цепь с источником 120 В и нагрузкой с сопротивлением 15 Ом. Как вы можете видеть ниже, существует несколько способов расчета подаваемой мощности:
С точки зрения электричества, энергия – это просто мера мощности, подаваемой в единицу времени. Например, если лампочка мощностью 100 Вт горит в течение пятнадцати часов, энергия, используемая лампочкой, составляет (100 Вт) (15 часов) = 1500 Втч (ватт-часов).
В Северной Америке энергия измеряется в киловатт-часах, поэтому эквивалент равен 1500 Втч/1000 = 1,5 кВтч.
Программное обеспечение SPICE (Программа моделирования с акцентом на интегральные схемы) часто используется в промышленности для проектирования схем и имитации их поведения.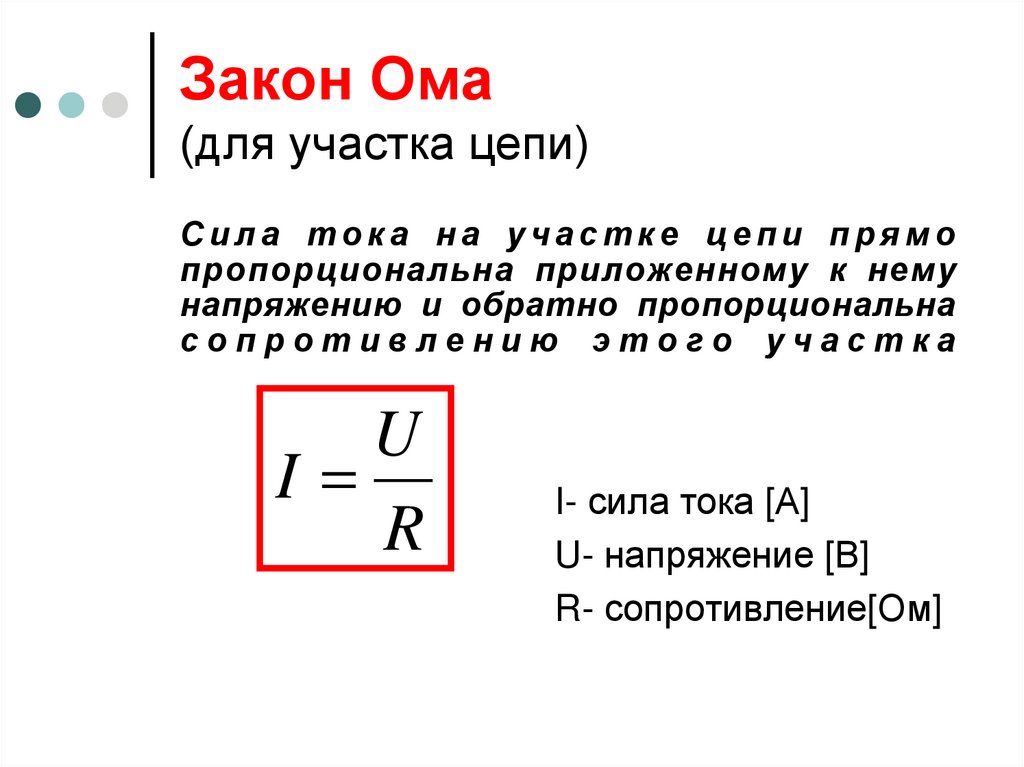
Существует множество продуктов, использующих SPICE, и в будущих статьях я буду использовать одну из этих программ под названием 9.0056 Multisim , чтобы проиллюстрировать сделанные выводы. LTspice — альтернатива Multisim с открытым исходным кодом.
Я создал простую резистивную цепь сверху в Multisim и подключил ваттметр для измерения мощности, подаваемой на нагрузку. Обратите внимание, что ток измеряется последовательно с нагрузкой (красные провода), а напряжение измеряется на нагрузке (синие провода):
- Ток в резистивной цепи пропорционален приложенному напряжению и обратно пропорционален сопротивлению.
- Закон Ома можно использовать для определения напряжения, силы тока и сопротивления.
- Источники напряжения часто обозначаются буквой E, а нагрузки обозначаются буквой V.
- Электрическая мощность — это скорость, с которой электрическая энергия передается в цепи, и измеряется в ваттах.
- Энергия является единицей измерения электрической мощности в единицу времени и измеряется в ватт-часах.
