Закон Ома для неоднородного участка цепи. Закон Ома для замкнутого контура.
Вернёмся ещё раз к рис. 7.1. Здесь изображена замкнутая проводящая цепь. На участке цепи 1-а-2 движение носителей заряда происходит под действием только электростатической силы=q. Такие участки называютсяоднородными.
Совсем по-другому обстоят дела на участке контура 2-b-1. Здесь на заряды действует не только электростатическая, но и сторонняя сила. Полную силунайдем, сложив эти две:
.
Участок замкнутого контура, где наряду с электростатической силой действуют и сторонние силы, называют неоднородным.
Можно показать, что на однородном участке цепи средняя скорость направленного движения носителей заряда пропорциональна действующей на них силе. Для этого достаточно сравнить формулы, полученные на прошлой лекции: =(6.3) и=(6.13).
Пропорциональность скорости силе, а
плотности тока — напряжённости сохранится
и в случае неоднородного участка цепи.
. (7.5)
Это уравнение закона Ома в локальной дифференциальной форме для неоднородногоучастка цепи.
Теперь перейдём к закону Ома для неоднородного участка цепи в интегральной форме.
Выделим двумя близкими сечениями Sучастокdlтрубки тока (рис. 7.3.). Сопротивление этого участка:
,
а плотность тока можно связать с силой тока:
.
Эти два выражения используем в уравнении (7.5), спроецировав его предварительно на линию тока:
Проинтегрировав последнее уравнение по неоднородному участку 1-2, получим:
.
Произведение IR1-2=U— напряжение на участке 1-2;
первый интеграл справа ==1–2— разность потенциалов на концах участка;
второй интеграл
==1-2— э. д.с.
источника тока.
д.с.
источника тока.
Учтя всё это, конечный результат запишем в виде:
. (7.6)
Это закон Ома для неоднородного участка цепи в интегральной форме. Обратите внимание, что напряжение на неоднородном участке цепиUне совпадает с разностью потенциалов на его концах (1–2):
IR1-2=U1-2= (1–2) +1-2. (7.7)
Эти две величины равны только в случае однородного участка, где источники тока отсутствуют и 1-2= 0. Тогда:
U1-2
Для замкнутого контура уравнение закона Ома (7.6) несколько видоизменяется, так как разность потенциалов в этом случае равна нулю:
. (7.8)
В законе Ома для замкнутой цепи (7.8) R — полное сопротивление контура, складывающееся из внешнего сопротивления цепи R0 и внутреннего сопротивления источника r:
R=R0+r.
Рассмотренные нами законы постоянного тока позволяют рассчитать токи в сложных разветвлённых электрических цепях. Эти расчёты упрощаются, если пользоваться правилами Кирхгофа.
Правил Кирхгофа два: правило токовиправило напряжений.
Правило токов относится к узлам цепи, то есть, к таким точкам схемы, где сходятся не менее трёх проводников (рис. 7.4.). Правило токов гласит: алгебраическая сумма токов в узле равняется нулю:
. (7.9)
Рис. 7.4.
При составлении соответствующего уравнения, токи, втекающие в узел, берутся со знаком плюс, а покидающие его — со знаком минус. Так, для узла
I1–I2–I3+I4–I5= 0.
Это первое правило Кирхгофа является
следствием уравнения непрерывности
(см. (6.7)) или закона сохранения электрического
заряда.
(6.7)) или закона сохранения электрического
заряда.
Правило напряженийотносится к любому замкнутому контуру разветвлённой цепи.
Выделим, например, в разветвлённой
сложной цепи замкнутый элемент 1-2-3-1
(рис. 7.5.). Произвольно обозначим в ветвях
контура направления токов I
Участок .
Здесь R1,R2,R3—полноесопротивление соответствующих ветвей. Сложив эти уравнения, получим формулу второго правила Кирхгофа:
I1R1–I2R2–I3R3=1+2–3–4+5.
Правило напряжений формулируется
так: в любом замкнутом контуре
алгебраическая сумма падений напряжения
равна алгебраической сумме э.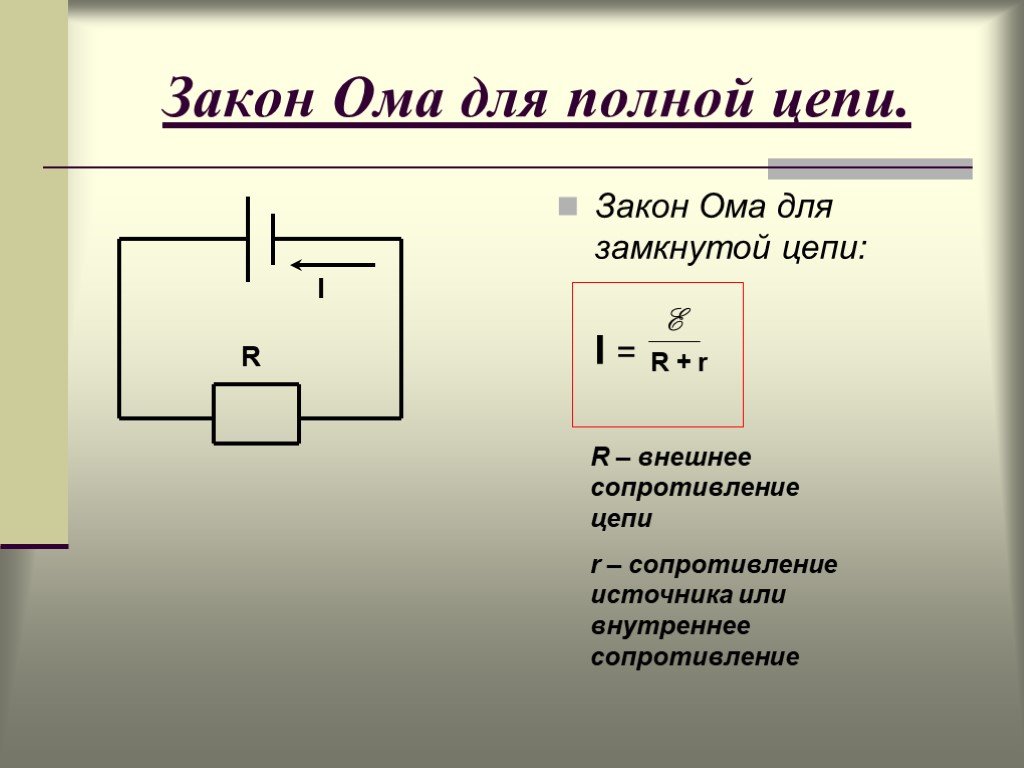
. (7.10)
Рис. 7.5.
При составлении уравнения (7.10) второго правила Кирхгофа задаются направлением обхода: в нашем примере — по часовой стрелке. Токи, совпадающие с направлением обхода, берутся со знаком плюс (I1), токи противоположного направления — со знаком минус (–I2, –I3).
Э.д.с. источника берётся со знаком плюс,
если он создаёт ток, совпадающий с
направлением обхода (+
В качестве примера составим уравнения
правил Кирхгофа для конкретной
электрической схемы — измерительного
моста Уитстона (рис. 7.6.). Мост образуют
четыре резистора R1,R2,R3,R4. В точкахAиBк мосту подключен
источник питания (,r), а в диагоналиBD — измерительный гальванометр с
сопротивлениемRg.
Рис. 7.6.
Во всех ветвях схемы произвольнообозначим направления токовI1,I2, I3, I4, Ig, I.
В схеме четыре узла: точки A,B,C,D. Для трёх из них составим уравнения первого правила Кирхгофа — правила токов:
точка А: I – I1 – I4 = 0; (1)
точка B: I1 – I
точка D: I4 + Ig – I3 = 0. (3)
Для трёх контуров цепи ABDA,BCDBиADCAсоставим уравнения второго правила Кирхгофа.
 Во всех контурах направление
обхода по часовой стрелке.
Во всех контурах направление
обхода по часовой стрелке.
ABDA: I1R1 + IgRg – I4R4 = 0; (4)
BCDB: I2
ADCA: I4R4 + I3R3 + Ir = . (6)
Таким образом, мы получили систему шести уравнений, решая которую можно найти все шесть неизвестных токов.
Но чаще мост Уитстона используется для измерения неизвестного сопротивления RxR1. В этом случае резисторыR2,R3иR4— переменные. Меняя их сопротивления, добиваются того, чтобы ток в измерительной диагонали моста оказался равным нулю
 Это означает, что:
Это означает, что:I1=I2см. (1),
I3=I4см.(3),
I1R1 = I4R4 см. (4),
I2R2 = I3R3 см. (5).
Учитывая эти упрощающие обстоятельства, приходим к выводу, что:
,
или:
.
Замечательно, что для определения неизвестного сопротивления нужно знать лишь сопротивления резисторов моста R2,R3иR4. Э.д.с. источника, его внутреннее сопротивление, как и сопротивление гальванометра при таком измерении не играют никакой роли.
Основы электротехники и электроники: Курс лекций, страница 3
Электротехника \ Основы электротехники и электроники
При свертке
параллельных ветвей эквивалентное сопротивление всегда меньше наименьшего из
сворачиваемых.
Если параллельно соединены n одинаковых сопротивлений (Рис. 3.3), эквивалентное сопротивление в n раз меньше сопротивления любой из ветвей.
Рис. 3.3
Если на участке цепи параллельно соединены лишь два элемента (Рис. 3.4), выражение (3.2) упрощается. В этом случае эквивалентное сопротивление можно определить как отношение произведения двух сопротивлений к их сумме:
Рис. 3.4
4. ОСНОВНЫЕ ЗАКОНЫ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
К основным законам электрических цепей относятся закон Ома и законы Кирхгофа.
Закон Ома
Если в ветви
не содержится ЭДС, к ней применим уже известный закон Ома для пассивного участка
цепи (1.1). Его можно сформулировать и следующим образом. Ток в ветви, не содержащей
ЭДС, равен падению напряжения в ветви, деленному на сопротивление ветви (Рис. 4.1):
4.1):
Рис. 4.1
Закон Ома для ветви, содержащей ЭДС, позволяет найти ток этой ветви по известной разности потенциалов на концах ветви. Ток в ветви, содержащей ЭДС, равен дроби, знаменатель которой – это сопротивление ветви. В числителе дроби – напряжение на концах ветви плюс алгебраическая сумма ЭДС, заключенных между концами ветви. С плюсом берутся напряжения и ЭДС, направление которых совпадает с направлением тока, с минусом – противоположные.
В частности, ток в ветви, изображенной на Рис. 4.2, равен:
.
Рис. 4.2
Первый закон Кирхгофа
В любом узле цепи алгебраическая сумма токов равна нулю. При этом, токи, направленные к узлу, принято считать положительными, токи, направленные от узла, принято считать отрицательными (Рис. 4.3).
Рис. 4.3
4.3
По первому закону Кирхгофа можно написать столько уравнений, сколько узлов содержит схема. Но не все они будут независимыми. Если схема содержит узлов, независимыми будут уравнений. Оставшееся уравнение будет являться следствием всех предыдущих.
Второй закон Кирхгофа
В любом замкнутом контуре цепи алгебраическая сумма напряжений равна алгебраической сумме ЭДС, включенных в контур.
При этом, положительными считаются те напряжения и ЭДС, которые совпадают с направлением обхода контура, отрицательными считаются напряжения и ЭДС, которые противоположны направлению обхода контура. Направление обхода контура можно выбирать произвольно.
Алгоритм составления уравнения по второму закону Кирхгофа для замкнутого контура цепи
Для заданного контура (Рис. 4.4 а) уравнение по второму закону Кирхгофа составляется в следующем порядке:
Рис. 4.4 а
4.4 а
- Задается направление токов в ветвях (Рис. 4.4 б).
Рис. 4.4 б
- Выбирается направление обхода контура (Рис. 4.4 в).
Рис. 4.4 в
- Записывается уравнение, в левой части которого – сумма падений напряжений на сопротивлениях ветвей. В правой части – сумма ЭДС контура.
Примечание: Падение напряжения на сопротивлении ветви записывается в соответствии с известным уже законом Ома (1.1):
Применение второго закона Кирхгофа для незамкнутого участка цепи
Второй закон
Кирхгофа справедлив только для замкнутого контура. При этом, любой незамкнутый
участок цепи можно дополнить до замкнутого контура с помощью напряжения в разрыве
незамкнутого участка.
Пример 4.1:
Незамкнутый участок цепи abcd изображен на Рис. 4.5 а.
а)
б)
Рис. 4.5
Дополняем участок до замкнутого контура, добавляя напряжение между незамкнутыми точками c и d (Рис. 4.5 б). Теперь для контура abcd можно записать второй закон Корхгофа:
Применение законов Кирхгофа при наличии в цепи источника тока
Источник тока имеет бесконечно большое сопротивление, поэтому не образует замкнутого контура и не может входить в уравнения второго закона Кирхгофа. Однако, в уравнениях первого закона Кирхгофа источник тока должен содержаться обязательно.
При
необходимости записать уравнение по второму закону Кирхгофа для контура, содержащего
источник тока, его заменяют напряжением на выводах источника тока.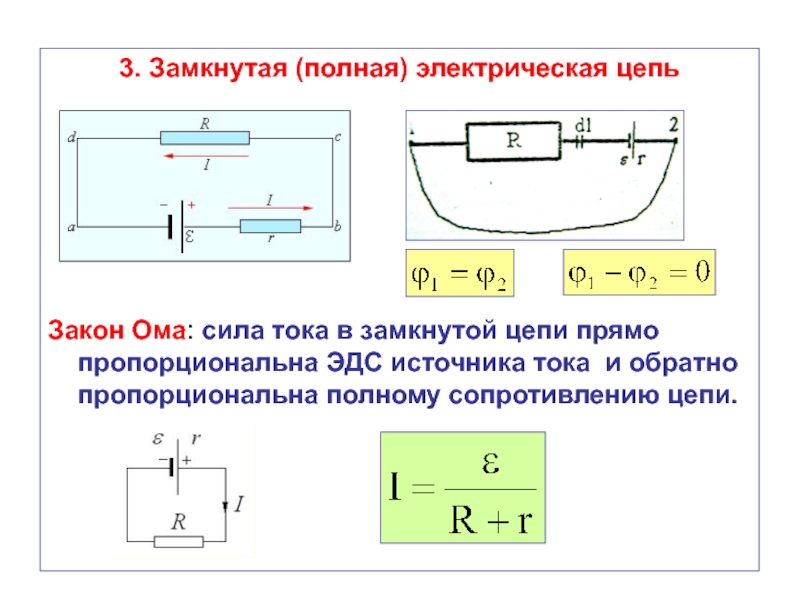
Пример 4.2:
Написать уравнение по первому закону Кирхгофа для узла a и уравнение по второму закону Кирхгофа для контура abcd (Рис. 4.6 а).
а)
б)
Рис. 4.6
Уравнение по первому закону Кирхгофа для узла a содержит источник тока и имеет вид:
Для того чтобы написать уравнение по второму закону Кирхгофа для контура abcd, заменяем источник тока напряжением на его выводах (Рис. 4.6 б), задаем направление обхода контура против часовой стрелки и получаем:
Для упрощения расчетов источник тока с параллельным сопротивлением можно заменить на эквивалентный источник ЭДС (Рис. 4.7). После расчета необходимо обязательно вернуться к исходной схеме.
Рис. 4.7
4.7
Независимый контур цепи
В принципе, по второму закону Кирхгофа можно составить столько уравнений, сколько контуров содержит цепь. Но не все эти уравнения будут независимыми. Для определения независимости уравнений по второму закону Кирхгофа вводится такое понятие как независимый контур цепи.
Независимый контур цепи – это такой контур, который содержит хотя бы одну новую ветвь, не вошедшую в другие контуры цепи.
Независимые контуры в общем случае выбираются произвольно, но проще всего выбирать их так, чтобы они совпадали с ячейками цепи (Рис. 4.8 б).
а)
б)
Рис. 4.8
Если схема содержит ветвей и узлов, число независимых контуров равно
.
Схема на Рис. 4.8 б содержит три независимых контура.
5. СИСТЕМА
УРАВНЕНИЙ ПО ЗАКОНАМ КИРХГОФА ДЛЯ РАСЧЕТА ТОКОВ ЦЕПИ
СИСТЕМА
УРАВНЕНИЙ ПО ЗАКОНАМ КИРХГОФА ДЛЯ РАСЧЕТА ТОКОВ ЦЕПИ
Законы Кирхгофа можно использовать для расчета токов в ветвях цепи. Главное требование при этом – получение системы независимых уравнений, в которой число неизвестных равно количеству токов, подлежащих определению.
Алгоритм составления системы уравнений по законам Кирхгофа
Скачать файл
Выбери свой ВУЗ
- АлтГТУ 419
- АлтГУ 113
- АмПГУ 296
- АГТУ 267
- БИТТУ 794
- БГТУ «Военмех» 1191
- БГМУ 172
- БГТУ 603
- БГУ 155
- БГУИР 391
- БелГУТ 4908
- БГЭУ 963
- БНТУ 1070
- БТЭУ ПК 689
- БрГУ 179
- ВНТУ 120
- ВГУЭС 426
- ВлГУ 645
- ВМедА 611
- ВолгГТУ 235
- ВНУ им.
 Даля 166
Даля 166 - ВЗФЭИ 245
- ВятГСХА 101
- ВятГГУ 139
- ВятГУ 559
- ГГДСК 171
- ГомГМК 501
- ГГМУ 1966
- ГГТУ им. Сухого 4467
- ГГУ им. Скорины 1590
- ГМА им. Макарова 299
- ДГПУ 159
- ДальГАУ 279
- ДВГГУ 134
- ДВГМУ 408
- ДВГТУ 936
- ДВГУПС 305
- ДВФУ 949
- ДонГТУ 498
- ДИТМ МНТУ 109
- ИвГМА 488
- ИГХТУ 131
- ИжГТУ 145
- КемГППК 171
- КемГУ 508
- КГМТУ 270
- КировАТ 147
- КГКСЭП 407
- КГТА им.
 Дегтярева 174
Дегтярева 174 - КнАГТУ 2910
- КрасГАУ 345
- КрасГМУ 629
- КГПУ им. Астафьева 133
- КГТУ (СФУ) 567
- КГТЭИ (СФУ) 112
- КПК №2 177
- КубГТУ 138
- КубГУ 109
- КузГПА 182
- КузГТУ 789
- МГТУ им. Носова 369
- МГЭУ им. Сахарова 232
- МГЭК 249
- МГПУ 165
- МАИ 144
- МАДИ 151
- МГИУ 1179
- МГОУ 121
- МГСУ 331
- МГУ 273
- МГУКИ 101
- МГУПИ 225
- МГУПС (МИИТ) 637
- МГУТУ 122
- МТУСИ 179
- ХАИ 656
- ТПУ 455
- НИУ МЭИ 640
- НМСУ «Горный» 1701
- ХПИ 1534
- НТУУ «КПИ» 213
- НУК им.
 Макарова 543
Макарова 543 - НВ 1001
- НГАВТ 362
- НГАУ 411
- НГАСУ 817
- НГМУ 665
- НГПУ 214
- НГТУ 4610
- НГУ 1993
- НГУЭУ 499
- НИИ 201
- ОмГТУ 302
- ОмГУПС 230
- СПбПК №4 115
- ПГУПС 2489
- ПГПУ им. Короленко 296
- ПНТУ им. Кондратюка 120
- РАНХиГС 190
- РОАТ МИИТ 608
- РТА 245
- РГГМУ 117
- РГПУ им.
 Герцена 123
Герцена 123 - РГППУ 142
- РГСУ 162
- «МАТИ» — РГТУ 121
- РГУНиГ 260
- РЭУ им. Плеханова 123
- РГАТУ им. Соловьёва 219
- РязГМУ 125
- РГРТУ 666
- СамГТУ 131
- СПбГАСУ 315
- ИНЖЭКОН 328
- СПбГИПСР 136
- СПбГЛТУ им. Кирова 227
- СПбГМТУ 143
- СПбГПМУ 146
- СПбГПУ 1599
- СПбГТИ (ТУ) 293
- СПбГТУРП 236
- СПбГУ 578
- ГУАП 524
- СПбГУНиПТ 291
- СПбГУПТД 438
- СПбГУСЭ 226
- СПбГУТ 194
- СПГУТД 151
- СПбГУЭФ 145
- СПбГЭТУ «ЛЭТИ» 379
- ПИМаш 247
- НИУ ИТМО 531
- СГТУ им.
 Гагарина 114
Гагарина 114 - СахГУ 278
- СЗТУ 484
- СибАГС 249
- СибГАУ 462
- СибГИУ 1654
- СибГТУ 946
- СГУПС 1473
- СибГУТИ 2083
- СибУПК 377
- СФУ 2424
- СНАУ 567
- СумГУ 768
- ТРТУ 149
- ТОГУ 551
- ТГЭУ 325
- ТГУ (Томск) 276
- ТГПУ 181
- ТулГУ 553
- УкрГАЖТ 234
- УлГТУ 536
- УИПКПРО 123
- УрГПУ 195
- УГТУ-УПИ 758
- УГНТУ 570
- УГТУ 134
- ХГАЭП 138
- ХГАФК 110
- ХНАГХ 407
- ХНУВД 512
- ХНУ им.
 Каразина 305
Каразина 305 - ХНУРЭ 325
- ХНЭУ 495
- ЦПУ 157
- ЧитГУ 220
- ЮУрГУ 309
Ома — EEmaginations
Приведенное выше изображение является одним из лучших изображений, которые я видел, определяя фундаментальное уравнение, связывающее напряжение, ток и сопротивление, которое мы называем законом Ома.
Закон Ома определяется как \(V = IR\).
Хотя эта форма уравнения сформулирована просто, поскольку напряжение равно произведению тока на сопротивление, смысл уравнения гораздо глубже. Давайте посмотрим поближе.
Сопротивление (резисторы) В замкнутой цепи резисторы, измеряемые в Омах, в основном используются для ограничения протекания тока в цепи.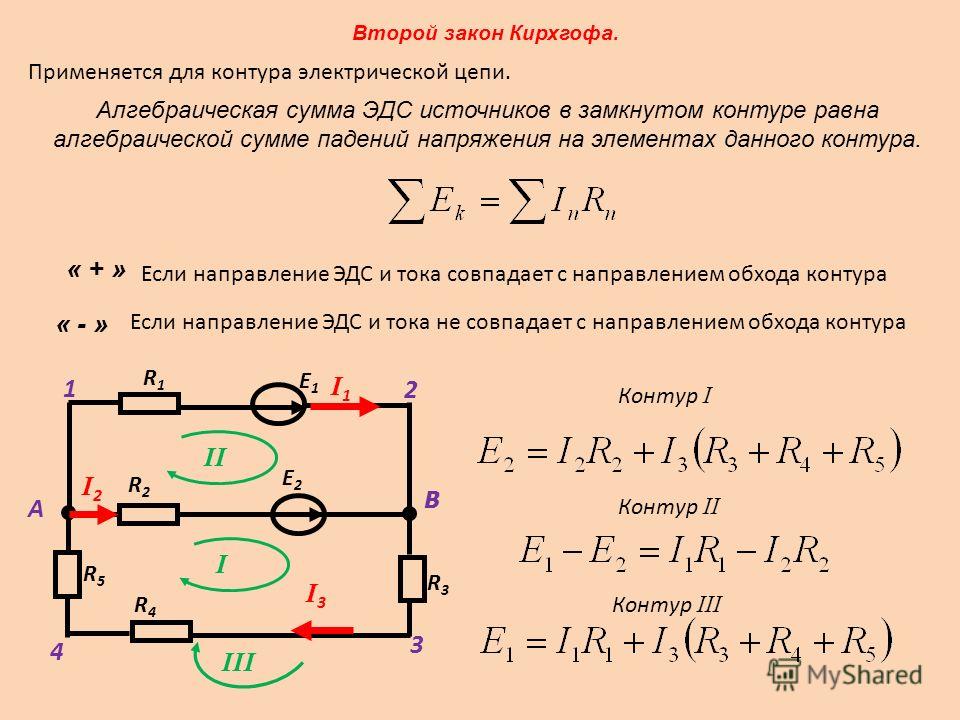 Это легко визуализировать на картинке выше, поскольку мы видим, как резистор сжимает трубу, что позволяет току течь через нее. При фиксированном напряжении, чем больше сопротивление, тем меньше ток будет течь по цепи.
Это легко визуализировать на картинке выше, поскольку мы видим, как резистор сжимает трубу, что позволяет току течь через нее. При фиксированном напряжении, чем больше сопротивление, тем меньше ток будет течь по цепи.
Электрический ток измеряется в амперах (амперах) и определяется как скорость потока электрических зарядов в цепи по отношению ко времени. Электрические заряды измеряются в кулонах, а ампер измеряется в кулонах в секунду. Переписав закон Ома для определения тока, мы видим, что ток в цепи равен напряжению, деленному на сопротивление. Ток прямо пропорционален напряжению и косвенно пропорционален сопротивлению. Следовательно, при фиксированном напряжении ток в цепи будет уменьшаться по мере увеличения сопротивления, а ток будет увеличиваться при уменьшении сопротивления. При постоянном сопротивлении ток будет увеличиваться с увеличением напряжения и уменьшаться с уменьшением напряжения. На картинке выше это тоже хорошо видно.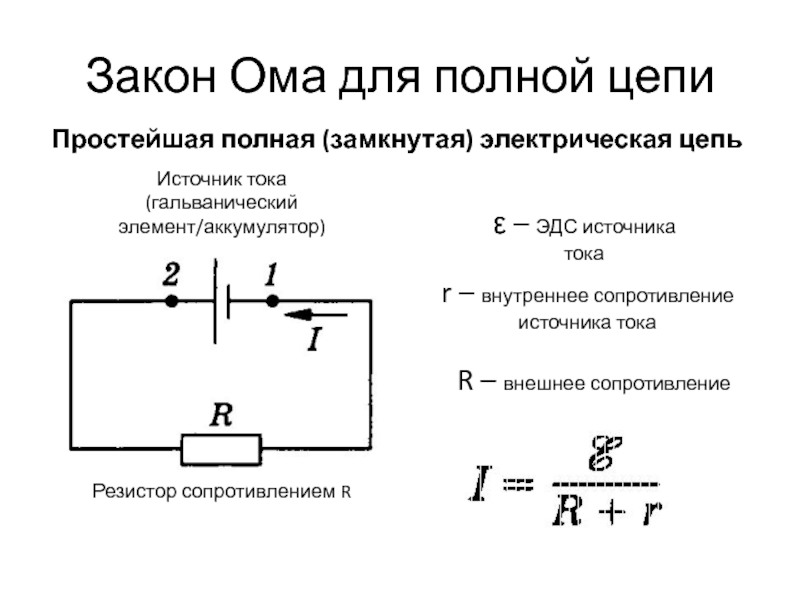 Чем больше сопротивление, тем меньший ток будет течь при фиксированном напряжении.
Чем больше сопротивление, тем меньший ток будет течь при фиксированном напряжении.
Напряжение, измеряемое в вольтах, может быть трудно осмыслить. Напряжение можно рассматривать как количество энергии, необходимое для «проталкивания» тока по цепи. Закон Ома гласит, что напряжение прямо пропорционально току и сопротивлению. Чтобы поддерживать фиксированный ток в цепи, увеличение сопротивления цепи требует увеличения напряжения. Точно так же уменьшение сопротивления требует уменьшения напряжения для поддержания того же тока в цепи. Следовательно, большее сопротивление означает больший «толчок», а меньшее сопротивление означает меньший толчок. Картинка выше дает обоснование этой концепции.
Аналогия потока жидкости Изображение предоставлено: https://learn.sparkfun.com/tutorials/transistors/extending-the-water-analogy Жидкость, текущая по трубе, является механической аналогией электрического тока, протекающего по цепи из электрических проводников (обычно медных проводов). Количество жидкости, протекающей по трубе, является синонимом количества тока, протекающего по проводам цепи. Размер трубы является синонимом размера резистора. Уменьшение размера трубы ограничит поток жидкости через трубу так же, как увеличение сопротивления ограничит прохождение электрического тока через цепь. Увеличение давления между трубами требуется для поддержания тока, протекающего по трубе, по мере уменьшения размера трубы. Это синонимично увеличению напряжения, необходимого для поддержания протекания электрического тока в цепи при увеличении электрического сопротивления.
Количество жидкости, протекающей по трубе, является синонимом количества тока, протекающего по проводам цепи. Размер трубы является синонимом размера резистора. Уменьшение размера трубы ограничит поток жидкости через трубу так же, как увеличение сопротивления ограничит прохождение электрического тока через цепь. Увеличение давления между трубами требуется для поддержания тока, протекающего по трубе, по мере уменьшения размера трубы. Это синонимично увеличению напряжения, необходимого для поддержания протекания электрического тока в цепи при увеличении электрического сопротивления.
Вопрос о законе индукции Фарадея для замкнутого пути
Индукция: Где бы ни случилось, чтобы существовало переменное магнитное поле и неважно, почему оно случилось бы или изменилось, тогда в том же самом месте в том же самом время также возникает электрическое поле. Электрическое поле курчавое, т.е. это происходит как замкнутые петли. Векторный ротор индуцированного электрического поля показан в уравнениях Максвелла и равен производной по времени от плотности магнитного потока.
Для уравнений Максвелла не существует универсального решения, все случаи разные. Но многие практически важные геометрические фигуры хорошо изучены, и ваша петля — одна из них. Величины индуктивность и взаимная индуктивность переносят действие индукции в теорию цепей — там электричество мыслится не как поля между проводами, а как напряжения и токи. Это удобно, но за всем по-прежнему стоят электрические и магнитные векторные поля.
Вы хотели напряжения на резисторах прямо из индуцированного электрического поля без малейшего намека и использования тока (и, я думаю, плотности тока), который вызывает электрическое поле. Это, к сожалению, невозможно. Из полученной формулы напряжения можно исключить ток, но вывод этой формулы без тока невозможен. Это потому, что, говоря «они резисторы», вы берете ток с собой. Значимой мерой для резистора является сопротивление, и оно определяется как U / I, нет более фундаментальных критериев для того, чтобы быть или не быть резистором.
Распространено предположение о существовании более фундаментального определения сопротивления. Возможность существования такого определения заложена в предложении «Резисторы подчиняются закону Ома I=U/R». Георг Ом обнаружил, что многие материалы ведут себя в электрическом поле таким образом, что ток через кусок и напряжение на этом куске пропорциональны. Коэффициент пропорциональности U/I, сопротивление, зависит от используемого материала и размеров. По сути, Георг Ом обнаружил, что многие детали действуют как резисторы, и объявил, что значит быть резистором.
Возможность существования такого определения заложена в предложении «Резисторы подчиняются закону Ома I=U/R». Георг Ом обнаружил, что многие материалы ведут себя в электрическом поле таким образом, что ток через кусок и напряжение на этом куске пропорциональны. Коэффициент пропорциональности U/I, сопротивление, зависит от используемого материала и размеров. По сути, Георг Ом обнаружил, что многие детали действуют как резисторы, и объявил, что значит быть резистором.
О событиях в ваших петлях:
Предполагая, что размеры настолько малы, а переходные процессы настолько медленны, что мы можем опустить радиоволны и резонансы, все индуцированное напряжение в вашей разомкнутой петле действительно возникает через промежуток. Это потому, что индуцированное электрическое поле перемещает электроны. Они накапливаются на конце провода до тех пор, пока поле, вызванное неравномерно распределенным зарядом, не уравновесится с индуцированным полем. Процесс накопления фактически является текущим. Это не мгновенно, это требует времени. Процесс можно смоделировать с помощью цепи, которая содержит источник напряжения, вызванный внешним магнитным полем, емкостью провода, сопротивлением провода и индуктивностью. Индуктивность предназначена для индукции в магнитном поле тока накопления. Ток в петле изменяется, и он также индуцирует E, что частично компенсирует внешне индуцированный E.
Это не мгновенно, это требует времени. Процесс можно смоделировать с помощью цепи, которая содержит источник напряжения, вызванный внешним магнитным полем, емкостью провода, сопротивлением провода и индуктивностью. Индуктивность предназначена для индукции в магнитном поле тока накопления. Ток в петле изменяется, и он также индуцирует E, что частично компенсирует внешне индуцированный E.
В вашем замкнутом контуре большую роль играет сопротивление, оно легко скрывает эффект емкости и резонансное поведение емкости и индуктивности — по крайней мере, если частота составляет всего 60 Гц, размер контура всего несколько метров, а резисторы — кОм. . Поле смещенных электронов все еще частично компенсирует индуцированную Е, но не полностью.
Теория цепей дает нам модель индукции как внешнего магнитного поля, так и поля, вызванного током контура. Мы можем думать, что существующее внешнее магнитное поле вызвано током в другой цепи, и между этой цепью и вашей петлей существует взаимная индуктивность.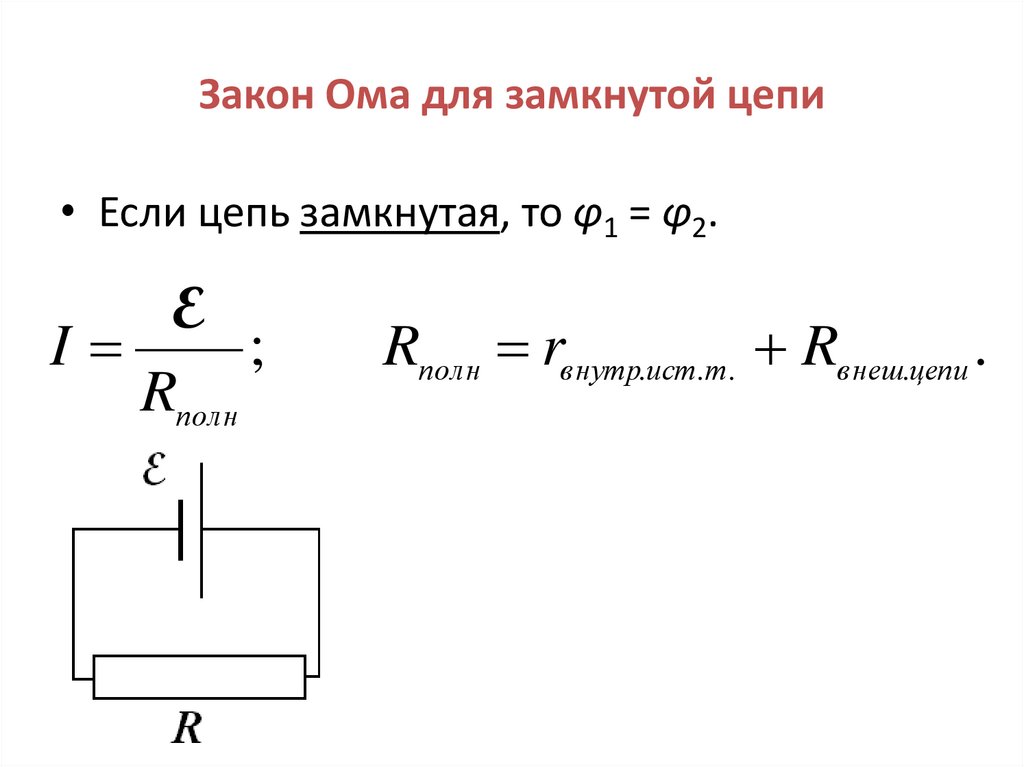 Для удобства мы предполагаем, что емкость пренебрежимо мала. Также мы предполагаем, что внешний «первичный» контур настолько массивен, что взаимную индукцию необходимо учитывать только в вашем контуре. Вот схема:
Для удобства мы предполагаем, что емкость пренебрежимо мала. Также мы предполагаем, что внешний «первичный» контур настолько массивен, что взаимную индукцию необходимо учитывать только в вашем контуре. Вот схема:
Представьте себе слабосвязанный трансформатор с резистивной нагрузкой R = общее сопротивление контура. Первичная цепь имеет ток I1, ваша петля имеет ток I2, а также взаимная индуктивность M и индуктивность петли L2. А=площадь петли.
В верхней строке 2 векторных уравнения для синусоидального тока и напряжения. Напряжение U2 на полном сопротивлении записывается двояко. Это по закону Ома и наведенным напряжениям вместе. Мы можем устранить ток контура и получить общее напряжение на резисторах. Он записывается как вектор и как абсолютное значение вектора, среднеквадратичное напряжение.
Предполагается, что внешнее магнитное поле является синусоидальным. B — его плотность (среднеквадратичное значение), а H — напряженность поля, также среднеквадратичное значение.


 Во всех контурах направление
обхода по часовой стрелке.
Во всех контурах направление
обхода по часовой стрелке. Даля 166
Даля 166 Дегтярева 174
Дегтярева 174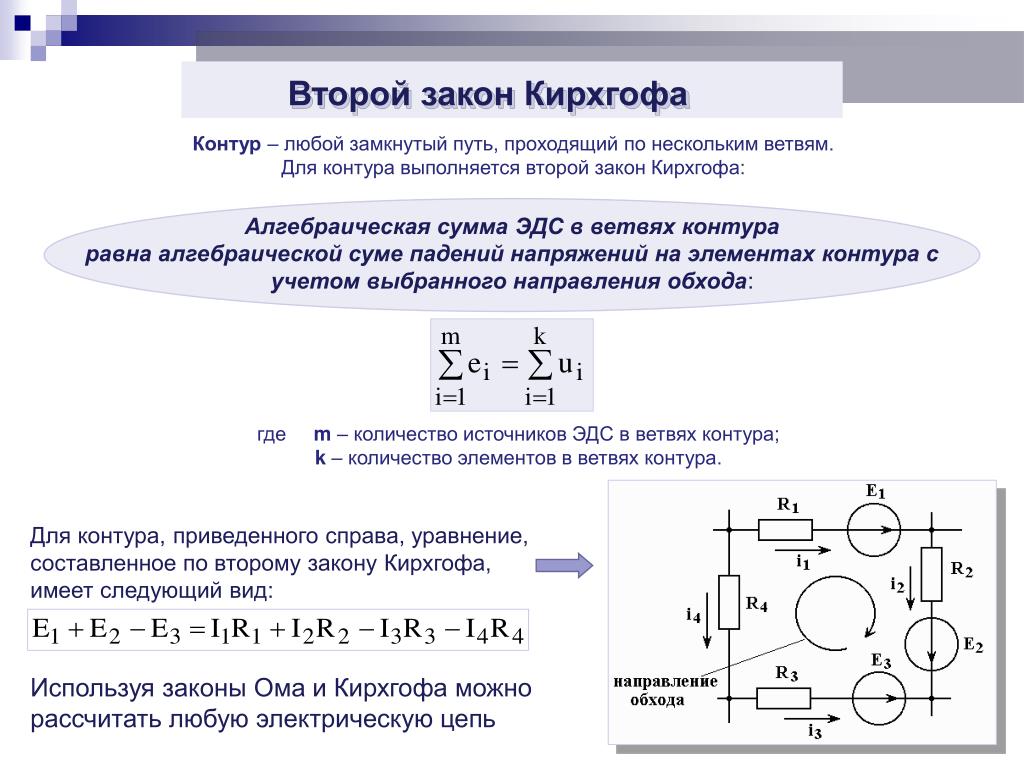 Макарова 543
Макарова 543 Герцена 123
Герцена 123 Гагарина 114
Гагарина 114 Каразина 305
Каразина 305