Курс общей физики, Т.2
Курс общей физики, Т.2
ОглавлениеПРЕДИСЛОВИЕМЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ЧАСТЬ 1. ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ § 1. Электрический заряд § 2. Закон Кулона § 3. Системы единиц § 4. Рационализованная запись формул § 5. Электрическое поле. Напряженность поля § 6. Потенциал § 7. Энергия взаимодействия системы зарядов § 8. Связь между напряженностью электрического поля и потенциалом § 9. Диполь § 10. Поле системы зарядов на больших расстояниях § 11. Описание свойств векторных полей Дивергенция. Циркуляция. Теорема Стокса. § 12. Циркуляция и ротор электростатического поля § 13. Теорема Гаусса Поле двух разноименно заряженных плоскостей. Поле заряженной сферической поверхности. Поле объемно-заряженного шара. ГЛАВА II. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ДИЭЛЕКТРИКАХ § 15. Полярные и неполярные молекулы § 16. Поляризация диэлектриков § 17.  Поле внутри диэлектрика§ 18. Объемные и поверхностные связанные заряды § 19. Вектор электрического смешения § 20. Примеры на вычисление поля в диэлектриках § 21. Условия на границе двух диэлектриков § 22. Силы, действующие на заряд в диэлектрике ГЛАВА III. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ § 24. Равновесие зарядов на проводнике § 25. Проводник во внешнем электрическом поле § 26. Электроемкость § 27. Конденсаторы ГЛАВА IV. ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ § 28. Энергия заряженного проводника § 29. Энергия заряженного конденсатора § 30. Энергия электрического поля ГЛАВА V. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК § 31. Электрический ток § 32. Уравнение непрерывности § 33. Электродвижущая сила § 34. Закон Ома. Сопротивление проводников § 35. Закон Ома для неоднородного участка цепи § 36. Разветвленные цепи. Правила Кирхгофа § 37. Мощность тока ГЛАВА VI. МАГНИТНОЕ ПОЛЕ В ВАКУУМЕ § 39.  Взаимодействие токов§ 40. Магнитное поле § 41. Поле движущегося заряда § 42. Закон Био — Савара § 43. Сила Лоренца § 44. Закон Ампера § 45. Магнитное взаимодействие как релятивистский эффект § 46. Контур с током в магнитном поле § 47. Магнитное поле контура с током § 48. Работа, совершаемая при перемещении тока в магнитном § 49. Дивергенция и ротор магнитного поля § 50. Поле соленоида и тороида ГЛАВА VII. МАГНИТНОЕ ПОЛЕ В ВЕЩЕСТВЕ § 51. Намагничение магнетика § 53. Вычисление поля в магнетиках § 54. Условия на границе двух магнетиков § 55. Виды магнетиков § 56. Магнитомеханические явления § 57. Диамагнетизм § 58. Парамагнетизм § 59. Ферромагнетизм ГЛАВА VIII. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ § 60. Явление электромагнитной индукции § 61. Электродвижущая сила индукции § 62. Методы измерения магнитной индукции § 63. Токи Фуко § 64. Явление самоиндукции § 65.  Ток при замыкании и размыкании цепи§ 66. Взаимная индукция § 67. Энергия магнитного поля ГЛАВА IX. УРАВНЕНИЯ МАКСВЕЛЛА § 69. Вихревое электрическое поле § 70. Ток смещения § 71. Уравнения Максвелла ГЛАВА X. ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В ЭЛЕКТРИЧЕСКИХ И МАГНИТНЫХ ПОЛЯХ § 72. Движение заряженной частицы в однородном магнитном поле § 73. Отклонение движущихся заряженных частиц электрическим и магнитным полями § 74. Определение заряда и массы электрона § 75. Определение удельного заряда ионов. Масс-спектрографы § 76. Ускорители заряженных частиц ГЛАВА XI. КЛАССИЧЕСКАЯ ТЕОРИЯ ЭЛЕКТРОПРОВОДНОСТИ МЕТАЛЛОВ § 77. Природа носителей тока в металлах § 78. Элементарная классическая теория металлов § 79. Эффект Холла ГЛАВА XII. ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ § 81. Несамостоятельный газовый разряд § 82. Ионизационные камеры и счетчики § 83.  Процессы, приводящие к появлению носителей тока при самостоятельном разряде§ 84. Газоразрядная плазма § 85. Тлеющий разряд § 86. Дуговой разряд § 87. Искровой и коронный разряды ГЛАВА XIII. ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ § 88. Квазистационарные токи § 89. Свободные колебания в контуре без активного сопротивления § 90. Свободные затухающие колебания § 91. Вынужденные электрические колебания § 92. Переменный ток § 93. Распространение волн в упругой среде § 94. Уравнения плоской и сферической волн § 95. Уравнение плоской волны, распространяющейся в произвольном направлении § 96. Волновое уравнение § 97. Скорость упругих волн в твердой среде § 98. Энергия упругой волны § 99. Стоячие волны § 100. Колебания струны § 101. Звук § 102. Скорость звука в газах § 103. Эффект Доплера для звуковых волн ГЛАВА XV. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ § 104. Волновое уравнение для электромагнитного поля § 105. 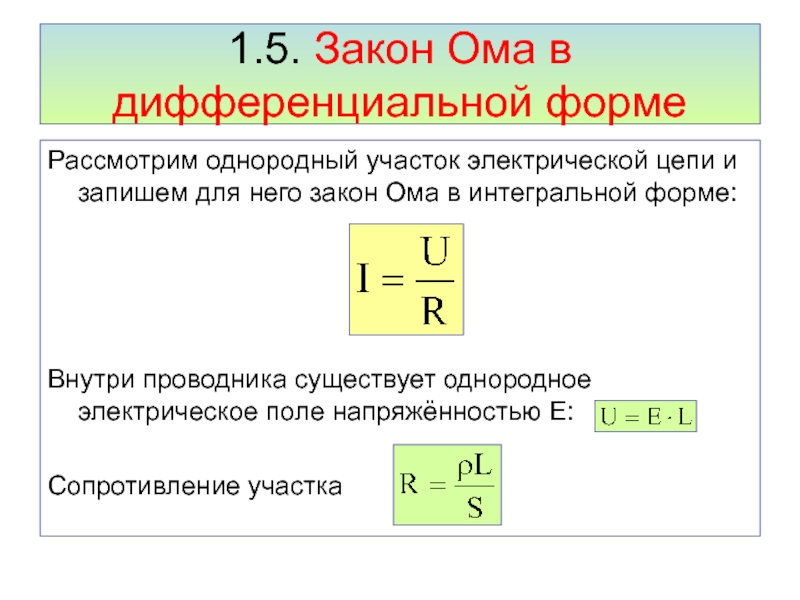 Плоская электромагнитная волна§ 107. Энергия электромагнитных волн § 108. Импульс электромагнитного поля § 109. Излучение диполя ЧАСТЬ 3. ОПТИКА § 110. Световая волна § 111. Представление гармонических функций с помощью экспонент § 112. Отражение и преломление плоской волны на границе двух диэлектриков § 113. Световой поток § 114. Фотометрические величины и единицы § 115. Геометрическая оптика § 116. Центрированная оптическая система § 117. Тонкая линза § 118. Принцип Гюйгенса ГЛАВА XVII. ИНТЕРФЕРЕНЦИЯ СВЕТА § 119. Интерференция световых волн § 120. Когерентность § 121. Способы наблюдения интерференции света § 123. Интерферометр Майкельсона § 124. Многолучевая интерференция ГЛАВА XVIII. ДИФРАКЦИЯ СВЕТА § 126. Принцип Гюйгенса—Френеля § 127. Зоны Френеля § 128. Дифракция Френеля от простейших преград § 129.  Дифракция Фраунгофера от щели§ 130. Дифракционная решетка § 131. Дифракция рентгеновских лучей § 132. Разрешающая сила объектива § 133. Голография ГЛАВА XIX. ПОЛЯРИЗАЦИЯ СВЕТА § 134. Естественный и поляризованный свет § 135. Поляризация при отражении и преломлении § 136. Поляризация при двойном лучепреломлении § 138. Прохождение плоскополяризованного света через кристаллическую пластинку § 139. Кристаллическая пластинка между двумя поляризаторами § 140. Искусственное двойное лучепреломление § 141. Вращение плоскости поляризации ГЛАВА XX. ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН С ВЕЩЕСТВОМ § 142. Дисперсия света § 143. Групповая скорость § 144. Элементарная теория дисперсии § 145. Поглощение света § 146. Рассеяние света § 147. Эффект Вавилова — Черенкова ГЛАВА XXI. ОПТИКА ДВИЖУЩИХСЯ СРЕД § 148. Скорость света § 149. Опыт Физо § 150. Опыт Майкельсона § 151.  ПРИЛОЖЕНИЯ I. Единицы электрических и магнитных величин в СИ и в гауссовой системе Приложение II. Основные формулы электромагнетизма в СИ и в гауссовой системе Приложение III. Векторный потенциал |
Закон Ома в интегральной и дифференциальной форме
Нужна помощь в написании работы?
Узнать стоимость
Закон Ома в интегральной форме для однородного участка цепи (не содержащего ЭДС)
(7.6.1) |
Для однородного линейного проводника выразим
, | (7.6.2) |
ρ – удельное объемное сопротивление; = .
Найдем связь между и в бесконечно малом объеме проводника – закон Ома в дифференциальной форме.
В изотропном проводнике (в данном случае с постоянным сопротивлением) носители зарядов движутся в направлении действия силы, т.
е. вектор плотности тока и вектор напряженности поля сонаправлены(рис. 7.6).
: Исходя из закона Ома (7.6.1), имеем
А мы знаем, что или . Отсюда можно записать
, | (7.6.3) |
это запись закона Ома в дифференциальной форме.
Здесь – удельная электропроводность., Размерность σ – .
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы.
Расчет стоимостиГарантииОтзывы
Плотность тока можно выразить через заряд электрона е, количество зарядов n и дрейфовую скорость :
.
Обозначим , тогда ;
(7.6.4) |
Теперь, если удельную электропроводность σ выразить через е, n и b: то вновь получим выражение закона Ома в дифференциальной форме:
-вектор плотности тока
Закон Джоуля Ленца
Мощность тепла, выделяемого в единице объёма среды при протекании электрического тока, пропорциональна произведению плотности электрического тока на величину напряженности электрического поля
Математически может быть выражен в следующей форме:
где — мощность выделения тепла в единице объёма, — плотность электрического тока, — напряжённость электрического поля, σ — проводимость среды, а точкой обозначено скалярное произведение.
Поможем написать любую работу на аналогичную тему
Реферат
Закон Ома в интегральной и дифференциальной форме
От 250 руб
Контрольная работа
Закон Ома в интегральной и дифференциальной форме
От 250 руб
Курсовая работа
Закон Ома в интегральной и дифференциальной форме
От 700 руб
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Поделись с друзьями
Закон Гаусса — Интеграл и Дифференциал | Электричество
30-секундное резюме
Закон Гаусса
Закон Гаусса утверждает, что суммарный электрический поток через любую гипотетическую замкнутую поверхность равен 1/ε 0 раз суммарный электрический заряд внутри этой замкнутой поверхности.
Φ E = Q/ε 0
Мы вычисляем электрический поток через каждый элемент и интегрируем результаты, чтобы получить общий поток.
Электрический поток Φ E определяется как поверхностный интеграл электрического поля.
О законе Гаусса
В электромагнетизме Закон Гаусса , также известный как Теорема Гаусса о потоках , связывает распределение электрического заряда с результирующим электрическим полем. В своей интегральной форме закон Гаусса связывает заряд, заключенный в замкнутой поверхности (часто называемой гауссовой поверхностью), с полным потоком через эту поверхность. Когда электрическое поле из-за его симметрии постоянно на этой поверхности и перпендикулярно ей, можно найти точное электрическое поле.
Закон Гаусса включает понятие электрического потока, которое относится к электрическому полю, проходящему через данную область. Другими словами:
Закон Гаусса гласит, что суммарный электрический поток через любую гипотетическую замкнутую поверхность равен 1/ε 0 , умноженному на суммарный электрический заряд внутри этой замкнутой поверхности.
Φ E = Q/ε 0
изображенный точкой заряд, излучающий «линии потока». Они называются линиями Гаусса. Обратите внимание, что линии поля представляют собой графическую иллюстрацию напряженности и направления поля и не имеют физического смысла. Плотность этих линий соответствует напряженности электрического поля, которую также можно назвать плотностью электрического потока: числом «линий» на единицу площади. Электрический поток пропорционален общему числу силовых линий электрического поля, проходящих через поверхность.
Электрический поток зависит от напряженности электрического поля, E , площади поверхности и взаимной ориентации поля и поверхности. Для однородного электрического поля E , проходящего через площадь A, электрический поток E определяется как:
Φ = E x A
определение электрического потока для однородного электрического поля по:
Φ = E x A x cosφ (электрический поток для однородной E, плоской поверхности)
Что произойдет, если электрическое поле не является однородным, а меняется от точки к точке по площади? Или что, если это часть изогнутой поверхности? Для неоднородного электрического поля электрический поток dΦ E через небольшую площадь поверхности d A определяется выражением:
dΦ 900 27 E = E x dA
Мы вычисляем электрический поток через каждый элемент и интегрируем результаты, чтобы получить общий поток.
Тогда электрический поток Φ E определяется как поверхностный интеграл электрического поля:
закон сс связывает заряд, заключенный в замкнутую поверхности к полному потоку через эту поверхность. Точное соотношение между электрическим потоком через замкнутую поверхность и суммарным зарядом Q encl , заключенное внутри этой поверхности, определяется законом Гаусса:
, где ε 0 — это та же константа (диэлектрическая проницаемость свободного пространства), которая фигурирует в законе Кулона. Интеграл слева находится по значению E на любой замкнутой поверхности, и мы выбираем эту поверхность для нашего удобства в любой данной ситуации. Заряд Qencl представляет собой чистый заряд, заключенный в этой поверхности.
Неважно, где и как распределяется заряд внутри поверхности. Любой заряд за пределами этой поверхности не должен учитываться.
Заряд вне выбранной поверхности может повлиять на положение линий электрического поля, но не повлияет на чистое количество линий, входящих или выходящих из поверхности.
Закон Гаусса можно использовать в его дифференциальной форме, которая гласит, что дивергенция электрического поля пропорциональна локальной плотности заряда. Эта теорема о дивергенции также известна как теорема Гаусса-Остроградского.
Часто задаваемые вопросы
Каково основное применение закона Гаусса?
Закон Гаусса полезен для определения электрических полей, когда распределение заряда очень симметрично. При выборе поверхности всегда пользуйтесь преимуществом симметрии распределения заряда, чтобы E можно было убрать из интеграла.
Какой закон аналогичен закону Гаусса.
Подобно закону Ампера, аналогичному закону магнетизма, закон Гаусса является одним из четырех уравнений Максвелла (первое) и, следовательно, фундаментальным для классической электродинамики.
Какова единица электрического заряда?
Кулон (обозначение: C) — это единица измерения электрического заряда в Международной системе единиц (СИ). Кулон был определен как количество электричества, переносимого за одну секунду силой тока в один ампер: 1 Кл = 1 А × 1 с
Следующий Статья
Какая математика используется в электротехнической карьере?
Математика, физика и алгебра имеют решающее значение для всего, что делает электрик, будь то измерения или расчет напряжения и мощности. Любой, кто хочет стать электриком, должен знать основы математики. Это формирует основную математику, используемую в рутинных измерениях и расчетах на работе. Ниже приведены различные виды математики, используемые в карьере электрика:
Понимание математики имеет решающее значение для успеха электрика.
Тригонометрия и геометрия
Электрики используют принципы тригонометрии и базовой геометрии при установке, ремонте и техническом обслуживании.
Тригонометрия — это раздел математики, изучающий стороны и углы треугольников. Электрики могут применять тангенциальные функции, чтобы определить идеальные углы для изгиба секций кабелепровода вдоль правильного маршрута проводки.
Тригонометрия имеет ряд других операций, которым обучают во время обучения электриков.
Учащиеся могут вычислять различные уравнения и функции и без труда применять их при электромонтаже здания в реальных ситуациях. Простые геометрические понятия, такие как теорема Пифагора, также важны для понимания электриками основ переменного тока. В большинстве учебных программ используется тригонометрия с упором на функции и аспекты, используемые электриком в повседневной работе.
Алгебра и исчисление
Алгебра позволяет электрикам комфортно работать с неизвестными переменными при вычислении известных. Есть много ситуаций, когда электрики и инженеры-электрики используют свои алгебраические навыки для решения сложных задач. Вводная алгебра, изучаемая в средней школе, является отправной точкой.
У электриков есть более надежные уравнения и переменные для факторизации, включая булевую алгебру и числа с действительными и мнимыми корнями.
Исчисление — еще одна важная математика, используемая в электротехнике. Это математика изменений и часть многих расчетов электриков. Расчет может определить количество ампер и лампочек, необходимых для проекта. Это также важно при расчете мощности и напряжения. Студенты, желающие стать инженерами-электриками, изучат продвинутое интегральное и дифференциальное исчисление.
Закон ОМ
С Законом ОМ можно столкнуться на уроках физики, но физика включает в себя много математики, и они часто пересекаются. Любой, кто хочет стать электриком, должен освоить закон Ома, поскольку это уравнение является синонимом электрических цепей. Основное уравнение (E = I x R) или (напряжение = ток x сопротивление) выражает, почему закон Ома жизненно важен при изучении электрических цепей и расчете тока, сопротивления и напряжения.
Электрикам нужны точные цифры при расчете требований и ограничений по току, напряжению и сопротивлению.
