Закон Ома в интегральной и дифференциальной форме — Студопедия

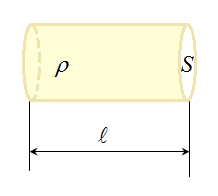
Рис.3.16

Пусть по проводнику длиной l и сечением S течет ток I. В проводнике создается электрическое поле напряженности E, а j1 и j2 – потенциалы на концах проводника (рис.3.16). В случае однородного проводника величину j1 — j2 = U можно назвать падением напряжения на участке проводника.

Закон Ома: сила тока, текущего по однородному участку проводника, прямо пропорциональна падению напряжения на проводнике:

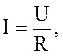(3.47)

где R – электрическое сопротивление проводника.

(3.47) – закон Ома в интегральной форме.

Размерность сопротивления в СИ: [R] = В/А = Ом.

Ом – сопротивление такого проводника, в котором при напряжении в 1 В течет ток 1А.

Сопротивление зависит от геометрических размеров и формы проводников, материала и температуры проводников. Для цилиндрического проводника

(3.48)

где r — удельное сопротивление проводника.

Удельное сопротивление численно равно сопротивлению проводника длиной 1 м и площадью поперечного сечения 1 м². Размерность удельного сопротивления в СИ: [r] = Ом×м.

Величина, обратная сопротивлению, называется проводимостью.

Величина, обратная удельному сопротивлению, называется удельной проводимостью:

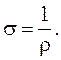(3.49)

Единица, обратная Ом, называется Сименсом [См].

Учитывая (3.46) — (3.49), а также 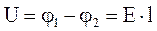, получим:

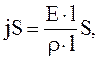
(3.50)

(3.50) – закон Ома в дифференциальной форме.

Закон Ома для однородного участка цепи в интегральной и дифференциальной форме. Сопротивление проводников

Ом экспериментально установил закон, согласно которому сила тока, текущего по однородному металлическому проводнику, пропорциональна падению напряжения

U на проводнике:

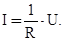(Интегральная форма закона) (20.10)

Однородным называется проводник, в котором не действуют сторонние силы, т.е. отсутствуют источники ЭДС. В этом случае, как мы видели, напряжение U совпадает с разностью потенциалов j₁ — j₂, поддерживаемой на концах проводника. Величина Rназывается электрическим сопротивлением проводника. Единицей сопротивления служит Oм, равный сопротивлению такого проводника, в котором при напряжении в 1 В течет ток силой в 1 А

.

Величина сопротивления зависит от формы и размеров проводника, а также от свойств материала, из которого он сделан. Для однородного цилиндрического проводника

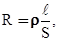(20.11)

где l — длина проводника, S — площадь его поперечного сечения, r — зависящий от свойств материала коэффициент, называемый удельным электрическим сопротивлением вещества. В СИ r измеряется в омо-метрах (Ом×м). На практике часто характеризуют материал сопротивлением при

l = 1 м и S == 1 мм², т. е. выражают r в

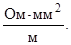
Закон Ома можно записать в дифференциальной форме.

Это уравнение устанавливает связь между дифференциальными характеристиками поля и тока, т.е. между j и Ев одной и той же точке проводника.

Преобразуем выражение (20.10) применительно к цилиндрическому проводнику, являющемуся однородным участком электрической цепи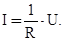

Если поле однородно, то U = E×l,

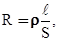и тогда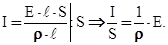

Обозначим и назовем удельной проводимостью, а 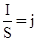— плотность тока.

В результате получаем j = g×E . Вполне справедлива и векторная форма записи

(20.12)

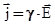
В анизотропных телах направления векторов j и Е могут не совпадать.

Электрический ток. Сила и плотность тока. Основные законы постоянного тока. Законы Ома и Джоуля-Ленца в интегральной и дифференциальной формах. Плотность тока и скорость носителей тока.

I. Любое упорядоченное (направленное) движение электрических зарядов называется ЭЛЕКТРИЧЕСКИМ ТОКОМ. При приложении внешнего электрического поля Е в проводнике начинается движение зарядов, т.е. возникает электрический ток. При этом положительные заряды движутся по полю, а отрицательные — против поля. За направление тока принимают направление движения положительных зарядов. Для возникновения и существования электрического тока необходимо выполнение двух условий :

1. наличие свободных носителей зарядов (т.е. вещество должно быть проводником или полупроводником при высоких температурах),

2.Наличие внешнего электрического поля.

Для количественного описания электрического тока вводится — СИЛА ТОКА – скалярная физическая велична, равная количеству электрического заряда, переносимосму за единицу времени через поперечное сечение проводника S.

— для постоянного тока, и

— для переменного тока.

Ток, сила и направление которого не изменяются со временем, называется

постоянным.

ПЛОТНОСТЬ ТОКА — векторная физическая величина, численно равная силе тока, проходящего через единицу площади, перпендикулярной к току:

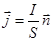
1. Закон Ома для однородного участка цепи.

Однороднымназывается участок не содержащий ЭДС.

Сила тока на однородном участке цепи прямо пропорциональна напряжению и обратно пропорциональна сопротивлению цепи

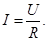
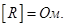
1 Ом – сопротивление такого проводника, в котором при напряжении 1 В течёт ток 1 А.

G — электрическая проводимость. 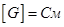(Сименс).

Сопротивление R проводника зависит от его размеров и формы, а также от материала проводника.

,

где ρ — удельное сопротивление проводника — сопротивление единицы длины проводника.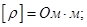

ℓ — длина проводника; S — площадь поперечного сечения проводника.

2.Закон Ома для неоднородного участка цепи

НЕОДНОРОДНЫМназывается участок цепи, содержащий ЭДС.

 

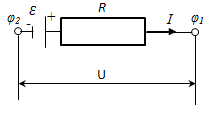
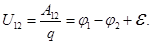
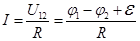
— Закон Ома для неоднородного участка цепи в интегральной форме.

3. Закон Ома для замкнутой цепи (для полной цепи).

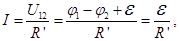
где

где R — сопротивление внешней цепи,

г — сопротивление источника ЭДС, тогда

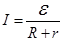— Закон Ома для полной цепи

4. Закон Ома в дифференциальной форме.

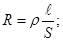
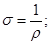
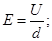
σ — удельная электропроводность;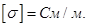

— Закон Ома в дифференциальной форме.

Плотность тока прямо пропорциональна напряженности электрического поля Е, Коэффициент пропорциональности σ — удельная электропроводность.

Если в проводнике течет постоянный ток и проводник остается неподвижным, то работа сторонних сил расходуется на его нагревание. Опыт показывает, что в любом проводнике происходит выделение теплоты, равное работе, совершаемой электрическими силами по переносу заряда вдоль проводника. Если на концах участка проводника имеется разность потенциалов , тогда работу по переносу заряда q на этом участке равна

По определению I= q/t. откуда q= I t. Следовательно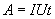

Так как работа идет па нагревание проводника, то выделяющаяся в проводнике теплота Q равна работе электростатических сил

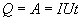
(17.13)

Соотношение (17.13) выражает закон Джоуля-Ленца в интегральной форме. Введем плотность тепловой мощности 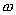, равную энергии выделенной за единицу время прохождения тока в каждой единице объема проводника

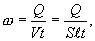
где S — поперечное сечение проводника, 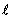— его длина. Используя (1.13) и соотношение , получим . Но — плотность тока, а , тогда с учетом закона Ома в дифференциальной форме 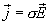, окончательно получаем

(17.14)

Формула (17.14) выражает закон Джоуля-Ленца в дифференциальной форме: объемная плотность тепловой мощности тока в проводнике равна произведению его удельной электрической проводимости на квадрат напряженности электрического поля.

Подвижность (скорость) носителей тока в твёрдом теле, отношение скорости направленного движения электронов проводимости и дырок (дрейфовой скорости υ_др), вызванного электрическим полем, к напряжённости Е этого поля:

μ = υ_др/Е.

У разных типов носителей в одном и том же веществе μ различны, а в анизотропных кристаллахразличны μ каждого типа носителей для разных направлений поля Е. Величина μ определяется процессамирассеяния электронов в кристалле. Рассеяние происходит на заряженных и нейтральных примесныхчастицах и дефектах кристаллической решётки, а также на тепловых колебаниях кристаллической решётки (фононах). Испуская или поглощая фонон, носитель изменяетсвой Квазиимпульс и, следовательно, скорость. Поэтому μ сильно изменяется при изменении температуры.При T ≥ 300 К преобладает рассеяние на фононах, с понижением температуры вероятность этого процессападает и доминирующим становится рассеяние на заряженных примесях или дефектах, вероятностькоторого растет с уменьшением энергии носителей.

 

Законы Кирхгофа.

Первый закон Кирхгофа.

1) Первый закон (правило) Кирхгофа — алгебраическая сумма токов сходящихся в узле равна нулю.

Ветви — это проводящие участки цепи между узлами.

Узел — это область соединения двух (или трёх) и более ветвей.

Алгебраическая сумма — это значит в неё входят слагаемые со знаком плюс и со знаком минус.

На рисунке ниже показан узел в котором соединяются четыре ветви с токами: I1, I2, I3, I4.

Рисунок 1 — Узел с ветвями
Направления токов показаны стрелочками. От узла направлены токи I1 и I2, к узлу направлены токи I3 и I4. Примем направления к узлу — положительными, а от узла — отрицательными. Запишем, с учётом выбранных положительных и отрицательных направлений токов, уравнение по первому закону Кирхгофа для узла на рисунке 1:

Ток I1 вошел в уравнение (1) со знаком минус так как этот ток направлен от узла (см. рисунок 1).

Ток I2 входит в уравнение (1) со знаком минус по той же причине. Токи I3 и I4 входят в уравнение (1) со знаком плюс так как они направлены к узлу (см. рисунок 1). Вся эта алгебраическая сумма равна нулю.

Токи I1 и I2 можно перенести в правую часть уравнения с противоположным знаком:

Также можно поступить и с любым уравнением записанным по первому закону Кирхгофа.

Учитывая это можно дать другое определение первого закона (правила) Кирхгофа:

2) сумма токов входящих в узел равна сумме токов выходящих из него.

Уравнение (2) можно привести к виду:

перенеся в правую часть уравнения токи I3 и I4 с противоположным знаком.
Уравнение (3) можно привести к виду:

Тоже самое можно проделать с любым уравнением записанным по первому закону Кирхгофа. Это значит что не имеет значения то какое направление (от узла или к узлу) принято за положительное а какое за отрицательное, главное чтобы все одинаковые направления имели один знак а все противоположные другой.

Иногда бывает так что один узел принимается за два и более при невнимательном осмотре схемы что приводит к ошибкам в расчётах. Рассмотрим схему на рисунке 2:

Рисунок 2 — Схема с одним узлом

В этой схеме один узел, для этого узла можно составить уравнение по первому закону Кирхгофа:

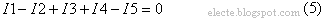Токи в узлах не протекают т.к. узел имеет один потенциал на всем его протяжении и на всей его площади.



Закон Ома для однородного участка цепи в интегральной и дифференциальной формах.

Немецкий физик Г. Ом экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (т. е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению U на концах проводника: I = U/R, где R — электрическое сопротивление проводника. Это уравнение выражает закон Ома для участка цепи (не содержащего источника тока): сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротив­лению проводника. Формула позволяет установить единицу сопротивления — ом (Ом): 1 Ом — сопротивление такого проводника, в котором при напряжении 1 В течет постоянный ток 1 А. Величина

G = 1/R называется электрической проводимостью проводника. Единица проводимости — сименс (См): 1 См — проводимость участка электрической цепи сопротивлением 1 Ом.

Сопротивление проводников зависит от его размеров и формы, а также от матери­ала, из которого проводник изготовлен. Для однородного линейного проводника сопротивление R прямо пропорционально его длине l и обратно пропорционально площади его поперечного сечения S:

R = ρl/S, где r — коэффициент пропорциональности, характеризующий материал проводника и называемыйудельным электрическим сопротивлением. Единица удельного элект­рического сопротивления — ом×метр (Ом×м). Наименьшим удельным сопротивлением обладают серебро (1,6×10^–8 Ом×м) и медь (1,7×10^–8 Ом×м). На практике наряду с медными применяются алюминиевые провода.

Закон Ома можно представить в дифференциальной форме. Подставив выражение для сопротивления в закон Ома, получим

I/S = U/ρl, где величина, обратная удельному сопротивлению, γ = 1/ρ называетсяудельной электрической проводимостью вещества проводника. Ее едини­ца — сименс на метр (См/м). Учитывая, что U/l = Е — напряженность электрического поля в проводнике, I/S = j — плотность тока, формулу можно записать в виде

j= γE. Так как в изотропном проводнике носители тока в каждой точке движутся в направле­нии вектора Е, то направления j и Е совпадают.

Последняя формула — закон Ома в дифференциальном форме, связывающий плотность тока в любой точке внутри проводника с напряженностью электрического поля в этой же точке. Это соотношение справедливо и для переменных полей.

Опыт показывает, что в первом приближении изменение удельного сопротивления, а значит и сопротивления, с температурой описывается линейным законом:

ρ = ρ₀(1+αt), R = R₀(1+αt), где r и r₀, R и R₀ — соответственно удельные сопротивления и сопротивления провод­ника при t и 0°С, a —температурный коэффициент сопротивления, для чистых металлов (при не очень низких температурах) близкий к 1/273 К^–1. Следовательно, температур­ная зависимость сопротивления может быть представлена в виде R = R₀αT

где Т — термодинамическая температура.

Впоследствии было обнаружено, что сопротивление многих металлов (например, Al, Pb, Zn и др.) и их сплавов при очень низких температурах T_K (0,14—20 К), называемыхкритическими, характерных для каждого вещества, скачко­образно уменьшается до нуля, т. е. металл становится абсолютным провод­ником. Явление сверхпроводимости объясняется на основе квантовой теории. Практическое использование сверхпроводящих материалов (в об­мотках сверхпроводящих магнитов, в системах памяти ЭВМ и др.) затруднено из-за их низких критических температур. В настоящее время обнаружены и активно исследуют­ся керамические материалы, обладающие сверхпроводимостью при температуре выше 100 К.

Закон Ома ? для участка цепи, формула. Закон Ома ? в дифференциальной форме для полной цепи и её участка

Автор Даниил Леонидович На чтение 5 мин. Просмотров 2.3k. Опубликовано 18 ноября

Физический закон ома получен путём экспериментов. 3 формулировки ома – одни из основополагающих в физике, устанавливающие связь между электротоком, сопротивлением и энергонапряжением. Год открытия – 1826. Впервые все 3 физических закона ома сформулировал физик-экспериментатор немецкого происхождения Георг Ом, с фамилией которого связано их определение.

Мнемоническая схема

Согласно мнемосхеме, чтобы высчитать электросопротивление по закону ома для участка цепи постоянного тока, необходимо комплексное напряжение на участке цепи разделить на силу тока для полной цепи. Однако, с физико-математической точки зрения, формулу ома для участка цепи для вычисления только по первому закону ома принято считать неполной.

Альтернативный способ вычислить токовое сопротивление по закону ома кратко подразумевает умножение электросопротивления материи, из которой выполнен проводник, на длину с последующим делением на площадь пересекающегося сечения.

Для выполнения вычислений сформулируйте по закону ома для участка цепи уравнение, исходя из имеющихся числовых данных:

Применение на линии электропередач

В процессе доставки на линию электропередач потери энергии должны быть минимизированы. Причиной энергетических потерь является нагрев провода, во время которого энергия электротока превращается в теплоэнергию.

Чтобы дать определение по закону ома потерянной мощности, необходимо показатель электрической мощности во второй степени умножить на внутреннее сопротивление источника напряжения и разделить на ЭДС в квадрате.

Из этого следует, что рост потери энергомощности осуществляется пропорционально протяжённости линии электропередач и квадрату электродвижущей силы.

Поскольку электродвижущую силу ограничивает прочность обмотки генератора, то повышение энергонапряжения возможно после того, как из генератора выйдет электроток, на участке входа линии.

Переменный ток легче всего распределяется по линии через трансформатор. Однако, поскольку следствием повышения энергонапряжения является потеря коронирования, а надёжность изоляции обеспечивается с трудом, напряжение на участке цепи протяжённой линии электропередач не превышает миллиона вольт.

Внимание!

Поведение линии электропередач в пространстве подобно антенне, ввиду чего берётся во внимание потеря на излучение.

Отображение в дифференциальной форме

На подсчёт сопротивления влияет тип материи, по которой протекает электроток, а также геометрические габариты проводника.

Дифференциальная форма формулировки Ома, записывающаяся достаточно кратко, отображает электропроводящие характеристики изотропных материалов и заключается в умножении удельной проводимости на вектор напряжённости электрополя с целью вычисления вектора плотности энерготока.

Для выполнения требуемых вычислений, уравнение сформулируйте по закону ома:

Интересно!

Если исходить из научных данных, следует сделать вывод о законе ома в дифференциальной форме об отсутствии зависимого соотношения геометрических габаритов.

При использовании анизотропеновых электроэлементов нередко встречается несовпадение вектора плотности токового энергонапряжения. Данное суждение справедливо для закона ома в интегральной и дифференциальной формах.

Переменный ток

Величины являются комплексными, если речь идёт о синусоидальных формах энерготока с циклической частотой, в цепях которых присутствуют активная ёмкость с индуктивностью.

В перечень комплексных величин входят:

• разность между потенциалами;
• сила тока;
• комплексное электросопротивление;
• модуль импеданса;
• разность индуктивного и ёмкостного сопротивлений;
• омическое электросопротивление;
• фаза импеданса.

Если несинусоидальный энерготок допустимо измерить временными показателями, закон ома для неполной электрической цепи может быть представлен в виде сложенных синусоидальных Фурье-компонентов. В линейной цепи составные элементы фурье-разложения являются независимо функционирующими. В нелинейных цепях образуются гармоники и множество колебаний. Таким образом, можно сделать вывод о невозможности выполнения правила Ома для нелинейной электроцепи.

Внимание!

Гармоника – это колебание, частота которого кратна частоте напряжения.

Как трактуется правило Ома

Так как обобщённая формула ома не считается основополагающей, правило применяется для описания разновидностей проводников в условиях приближения незначительной частоты, плотности тока и напряжения электрополя. Следует отметить, что в ряде случаев как первый закон, так и второй закон, применяемый для полной цепи, не соблюдаются.

Существует теория Друде, для выражения которой используются следующие величины:

• удельная электропроводимость;
• концентрированное размещение электронов;
• показатель элементарного заряда;
• время затихания по импульсам;
• эффективная масса электрона.

Внимание!

Все формулы Ома – первый, второй физический закон ома и третий распространяются на омические компоненты.

Перечень условий, при которых становится невозможным соблюдения правила Ома:

1. высокие частоты с чрезмерно большой скоростью изменения электротока;
2. пониженная температура сверхпроводимого вещества;
3. перегрев проводника проходящим электротоком;
4. в ситуации пробоя, возникшего в результате подсоединения к проводниковому элементу высокого напряжения;
5. в вакуумной или газонаполненной электролампе;
6. для гетерогенного полупроводникового прибора;
7. при образовании пространственного диэлектрического заряда в контакте металлического диэлектрика.

Интерпретация

Определяющаяся действием приложенного напряжения мощностная сила тока является пропорциональной показателю его напряжения. К примеру, при двойном увеличении приложенного напряжения, интенсивность постоянного тока также удваивается.

Интересно!

Наиболее часто правило Ома применяется для металла и керамики.

Методы запоминания формулы

Чтобы легче запомнить формулу расчёта напряжения на участке цепи, следует выписать на бумажном листе все величины, из которых она состоит, в которую также входит сопротивление и сила тока. Искомую величину закрыть пальцем, вследствие чего соотношение оставшихся величин будет отображать действие, которое необходимо совершить для её вычисления.

Ниже будет представлено видео с подробным объяснением всех правил и формул, относящихся к рассматриваемой теме.

Закон Ома – один из самых несложных для понимания, который входит в программу школьных учебников физики начального уровня. Пользуясь графическим приёмом расчёта величин – при необходимости или для самопроверки, можно получить безошибочные результаты вычислений.

Закон Ома для однородного участка цепи в интегральной и дифференциальной формах.

 

Сила тока в однородном участке цепи прямо пропорциональна напряжению при постоянном сопротивлении участка и обратно пропорциональна сопротивлению участка при постоянном напряжении.

 В диф:  

 В интегральной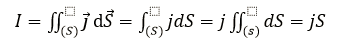

Электросопротивление, его температурная зависимость. Сверхпроводимость. Свойства сверхпроводников. Высокотемпературные сверхпроводники

Электри́ческое сопротивле́ние — физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока и равная отношению напряжения на концах проводника к силе тока, протекающего по нему

Удельное сопротивление меняется с изменением температуры ΔT:

Сверхпроводи́мость — свойство некоторых материалов обладать строго нулевым электрическим сопротивлением при достижении ими температуры ниже определённого значения

Свойства сверхпроводников: 

· Нулевое сопротивление

· Фазовый переход в сверхпроводящее состояние

· Эффект Мейсснера

· Изотопический эффект

· Момент Лондона

Высокотемпературные сверхпроводники- сверхпроводящие соединения, имеющие рекордно высокие критические температуры тс перехода в сверхпроводящее состояние

 

Закон Ома для неоднородного участка цепи.    , правила Кирхгофа

Произведение силы тока I на сопротивление участка цепи R равно сумме разности потенциалов на этом участке и ЭДС всех источников тока, включенных на данном участке цепи  

Разветвленная цепь состоит из совокупности однородных и неоднородных участков цепи, электрическое соединение которых происходит в узлах. Узлом в разветвленной цепи называется точка, в которой имеется более двух возможных направлений тока . В узле сходится более двух проводников.

Правила Кирхгофа:

1. Алгебраическая сумма токов в узле равна 0

2. Алгебраическая сумма падений напряжений на элементах замкнутого контура равна сумме ЭДС

3. Выбирают направление обхода контура и берут токи с (+) , которые совпадают с направлением обхода и т.е ЭДС которых гонят ток в том же направлении

 

Обобщенный закон Ома в интегральной и дифференциальной формах.

Обобщенный закон Ома в интегральной и дифференциальной  формах.

Немецкий физик Г. Ом (1787-1854) экспериментально установил, что сила тока в однородном проводнике пропорциональна разности потенциалов на его концах и обратно пропорциональна сопротивлению проводника (закон Ома для участка цепи): 

 где R – электрическое сопротивление проводника, определяющее упорядоченность перемещения свободных носителей тока.

 Электрическое сопротивление металлического проводника обусловлено тем, что свободные электроны при своем движении взаимодействуют (соударяются) с положительными ионами кристаллической решетки. Поэтому сопротивление проводников зависит прежде всего от материала проводника, т.е. строения его кристаллической решетки. Для однородного цилиндрического проводника длиной l и площадью поперечного сечения S сопротивление определяется по формуле 

Удельное электрическое сопротивление проводника зависит не только от рода вещества, но и от температуры (по Цельсию):

  У чистых металлов α = 1/273  1/K

Для полной цепи, содержащей ЭДС, справедлив обобщенный закон Ома в интегральной форме

Для участка с источником тока и для участка с внешним сопротивлением будем иметь

Сложив, получим     закон Ома для полной цепи

  I(r+R)=ε

Разности потенциалов сократились, потому что работа электростатических сил по замкнутому контуру равна нулю. В случае многих источников направление тока заранее неизвестно; выбираем его произвольно и проходим контур в этом направлении. Записав соответствующие уравнения, получим

 I∑Ri=∑±εi
Если сила тока окажется отрицательной, то направление тока надо изменить на противоположное.

Закон Фарадея — Электромагнитная геофизика

Такое поведение описывается законом Фарадея. Закон Фарадея назван в честь английского ученого Майкла Фарадея (1791-1867), и описывает способ, которым изменяющиеся во времени магнитные поля вызывают вращательные электрические поля. Это объясняет электромагнитную индукцию явление, которое является основным механизмом возбуждения индуктивного источник.

Интегральная форма во временной области

Закон Фарадея в интегральной форме можно выразить с помощью следующего уравнения:

(55) \ [\ oint_C {\ bf e} \ cdot {\ bf d} {\ bf l} = — \ int_S \ frac {\ partial {\ bf b}} {\ partial t} \ cdot \ hat {\ bf n} \, da, \]

где:

• \ (\ mathbf {e} \) — электрическое поле, определенное вокруг замкнутого пути \ (C \)

• \ (\ mathbf {b} \) — плотность магнитного потока, определенная над замкнутой поверхностью \ (A \), очерченной \ (C \)

• \ (\ hat n \) — единичный вектор внешней нормали, перпендикулярный \ (da \)

• \ (\ d \ mathbf {l} \) — векторный элемент длины по контуру \ (C \)

Ур.(55) утверждает, что зависящая от времени скорость изменения магнитного потока через поверхность, ограниченную замкнутым путем, отрицательно пропорциональна линейному интегралу электрического поля, которое он наводит на этом пути.

Дифференциальная форма во временной области

Применяя теорему Стокса к левой части уравнения. (55), можно получить дифференциальную форму уравнения Фарадея закон:

(56) \ [\ nabla \ times {\ bf e} = — \, \ frac {\ partial {\ bf b}} {\ partial t} \]

Ур. (56) утверждает, что изменяющиеся во времени магнитные поля будут индуцируют вращательные электрические поля.Кроме того, ротор индуцированной электрические поля противодействуют зависящим от времени изменениям индуцирующего магнитного поля.

Закон Фарадея в частотной области

Частотное представление закона Фарадея может быть получено применяя преобразование Фурье к уравнениям. (55) и (56). Интегральная форма закона Фарадея в частотная область:

(57) \ [\ oint_C {\ bf E} \ cdot d {\ bf l} = — \, i \ omega \ int_A {\ bf B} \ cdot \ hat n \, da \]

Аналогичным образом, используя теорему Стокса, дифференциальная форма закона Фарадея:

(58) \ [\ nabla \ times {\ bf E} = — \, i \ omega {\ bf B} \]

где \ (\ omega \) — угловая частота, \ ({\ bf E} \) — частотно-зависимое электрическое поле, а \ ({\ bf B} \) — частотно-зависимое зависимая плотность магнитного потока.

Из уравнения. (58), мы можем вывести две вещи:

1. Наведенные вращательные электрические поля пропорциональны угловой частоте; это означает, что электромагнитная индукция больше на более высоких частотах.

2. Индуцированные вращательные электрические поля и отвечающие за них частотно-зависимые магнитные поля сдвинуты по фазе на 90 градусов.

Открытие закона Фарадея

Закон Фарадея лучше всего понять с помощью трех экспериментов, которые Фарадей проведено и обобщено в 1831 г.Для каждого из этих экспериментов электромагнит использовался для создания зависящего от времени магнитного поля, которое мы представим с использованием плотности магнитного потока \ ({\ bf {b}} \). Петля провод с областью \ (A \), очерченный замкнутым контуром \ (C \), затем удерживался в непосредственной близости от электромагнита. Это привело к магнитному потоку \ ({\ boldsymbol \ Phi_b} \) определяется по: s

(59) \ [{\ boldsymbol \ Phi_b} = \ int_A {\ bf b} \ cdot \ hat {\ bf {n}} \, da \]

Затем Фарадей провел следующие три эксперимента:

1. Проволочная петля была закрыта, а электромагнит оставался неподвижным.

2. Электромагнит перемещался, при этом проволочная петля оставалась неподвижной.

3. Как проволочная петля, так и электромагнит оставались неподвижными, однако сила магнитного поля изменялась как функция времени.

Фарадей заметил, что во всех трех экспериментах электродвижущая сила \ (\ mathcal {E} \) был индуцирован в проводе, что привело к измеримому электрический ток. Электродвижущая сила \ (\ mathcal {E} \) может быть определена через электрическое поле \ ({\ bf e} \) путем интегрирования по пути провод следующим образом:

(60) \ [\ mathcal {E} = — \ oint_C {\ bf e} \ cdot d {\ bf l}.

Закон Гаусса: определение, уравнение, приложения и проблемы

Закон Гаусса гласит, что: «Полный электрический поток через любую замкнутую поверхность равен 1 / ε0, умноженному на полный заряд, заключенный на поверхности». Применение закона Гаусса приведены ниже.

Это дано Карлом Фридрихом Гауссом, названным в его честь, который дал связь между электрическим потоком через замкнутую поверхность и чистым зарядом, заключенным на поверхности. Он применяется для расчета электрической напряженности из-за различных конфигураций заряда.Во всех таких случаях рассматривается воображаемая замкнутая поверхность, электрическая напряженность которой должна оцениваться. Эта замкнутая поверхность называется гауссовой поверхностью. Его выбор таков, что поток через него можно легко оценить. Она задается формулой

Φ = q / ∈0

где ∈0 — относительная диэлектрическая проницаемость вакуума в свободном пространстве.

Вывод уравнения закона Гаусса

Предположим, точечные заряды q _1, q _2, q ₃ , ……., q _n произвольно распределены на замкнутой поверхности произвольной формы, показанной на рисунке. Используя идею о том, что электрический поток, проходящий через замкнутую поверхность, равен:

Это математическое выражение закона Гаусса, которое можно сформулировать следующим образом: «Поток через любую замкнутую поверхность в 1 / ∈ ₀ раз больше полный заряд, заключенный в нем ».

Где Q = q ₁ + q ₂ + q ₃ + ……. + Q _n, — общий заряд, заключенный на замкнутой поверхности.

интегральная форма закона Гаусса

Поскольку объемная плотность заряда определяется как:

Уравнение (4) является интегральной формой закона Гаусса.

дифференциальная форма закона Гаусса

Если заряд распределен в объеме, имеющем однородную объемную плотность заряда ‘ρ’, то согласно дифференциальной форме закона Гаусса:

Мы знаем по теореме дивергенции:

Это дифференциальная форма закона Гаусса.

применения закона Гаусса в электростатике

Закон Гаусса применяется для расчета электрической напряженности, обусловленной различными конфигурациями заряда. Во всех таких случаях рассматривается воображаемая замкнутая поверхность, проходящая через точку, в которой должна быть оценена электрическая напряженность. Эта замкнутая поверхность называется гауссовой поверхностью. Его выбор таков, что поток через него можно легко оценить. Затем рассчитывается заряд, заключенный в гауссовой поверхности, и, наконец, вычисляется электрическая напряженность с применением закона Гаусса.

поле внутри полых заряженных сфер

Предположим, что полая проводящая сфера радиуса R получает положительный заряд + Q. Мы хотим вычислить

.

Дифференциальные уравнения — основные понятия

Онлайн-заметки Павла

Ноты Быстрая навигация Скачать

• Перейти к
• Ноты
• Задачи практики и задания еще не написаны.Пока позволяет время, я работаю над ними, однако у меня нет того количества свободного времени, которое я имел раньше, поэтому пройдет некоторое время, прежде чем здесь что-нибудь появится.
• Показать / Скрыть
• Показать все решения / шаги / и т. Д.
• Скрыть все решения / шаги / и т. Д.

• Разделы
• Введение в DE второго порядка
• Настоящие и отчетливые корни
• Разделы
• DE Первого Ордена
• Преобразование Лапласа
• Классы
• Алгебра
• Исчисление I
• Исчисление II
• Исчисление III
• Дифференциальные уравнения
• Дополнительно
• Алгебра и триггерный обзор
• Распространенные математические ошибки
• Праймер комплексных чисел
• Как изучать математику
• Шпаргалки и таблицы
• Разное
• Свяжитесь со мной
• Справка и настройка MathJax
• Мои студенты

• Notes Загрузки
• Полная книга
• Текущая глава
• Текущий раздел
• Practice Problems Загрузок
• Проблем пока не написано.
• Проблемы с назначением Загрузок
• Проблем пока не написано.
• Прочие товары
• Получить URL для загружаемых элементов

• Распечатать страницу в текущем виде (по умолчанию)
• Показать все решения / шаги и распечатать страницу
• Скрыть все решения / шаги и распечатать страницу

• Дом
• Классы
• Алгебра
  • Отборочные
    • Целочисленные экспоненты
    • Рациональные экспоненты
    • Радикалы
    • Полиномы
    • Факторинговые многочлены
    • Рациональные выражения
    • Комплексные числа
  • Решение уравнений и неравенств
    • Решения и наборы решений
    • Линейные уравнения
    • Приложения линейных уравнений
    • Уравнения с более чем одной переменной
    • Квадратные уравнения — Часть I
    • Квадратные уравнения — Часть II
    • Квадратные уравнения: сводка
    • Приложения квадратных уравнений
    • Уравнения, сводимые к квадратичным в форме
    • Уравнения с радикалами
    • Линейные неравенства
    • Полиномиальные неравенства
    • Рациональные неравенства
    • Уравнения абсолютных значений
    • Неравенства абсолютных значений
  • Графики и функции
    • График
    • Строки
    • Круги
    • Определение функции
    • Графические функции
    • Комбинирование функций
    • Обратные функции
  • Общие графы
    • Прямые, окружности и кусочные функции
    • Параболы
    • Эллипсы
    • Гиперболы
    • Разные функции
    • Преобразования
    • Симметрия
    • Рациональные функции
  • Полиномиальные функции
    • Делительные многочлены
    • Нули / корни многочленов
    • Графические полиномы
    • Нахождение нулей многочленов
    • Частичные дроби
  • Экспоненциальные и логарифмические функции
    • Экспоненциальные функции
    • Логарифмических функций
    • Решение экспоненциальных уравнений
    • Решение логарифмических уравнений
    • Приложения
  • Системы уравнений
    • Линейные системы с двумя переменными
    • Линейные системы с тремя переменными
    • Расширенные матрицы
    • Подробнее об Augmen

.

Что такое процентное дифференциальное реле? Определение, рабочие, рабочие характеристики и типы

Определение: Процентное дифференциальное реле определяется как реле, которое работает от разности фаз двух или более одинаковых электрических величин. Это усовершенствованная форма реле дифференциальной защиты. Единственная разница между ними — сдерживающая катушка. Процентное дифференциальное реле состоит из ограничительной катушки для преодоления проблем, возникающих из-за разницы в соотношении токов при высоком значении внешнего тока короткого замыкания.

Система процентного дифференциала состоит из ограничительной катушки, подключенной к управляющему проводу, как показано на рисунке ниже, и через нее протекает ток, наведенный в обоих трансформаторах тока. Катушка управления находится между средней точкой удерживающей катушки.

Ограничивающая катушка контролирует чувствительную характеристику реле. Это ограничивает нежелательное отключение трансформатора из-за тока дисбаланса. Ограничивающая катушка также ограничивает гармоники в пусковом токе.

Работа реле процентного дифференциала

Крутящий момент из-за ограничительной катушки предотвращает замыкание цепи отключения, в то время как крутящий момент из-за рабочей катушки стремится замкнуть контакты цепи отключения. В нормальных рабочих условиях и в условиях нагрузки крутящий момент, развиваемый удерживающей катушкой, превышает крутящий момент рабочей катушки. Таким образом реле остается в нерабочем состоянии.

Когда происходит внутренняя неисправность, рабочий крутящий момент превышает ограничивающий момент, тогда контакты цепи отключения замыкаются, чтобы размыкать автоматический выключатель.Ограничивающий момент можно регулировать, изменяя количество оборотов ограничительной катушки.

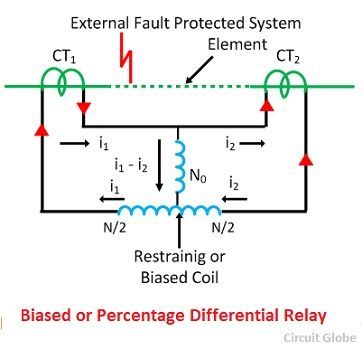Дифференциальный ток, необходимый для использования этого реле, является переменной величиной из-за действия ограничительной катушки. Дифференциальный ток в рабочей катушке пропорционален (I ₁ -I ₂ ), а ограничивающая катушка пропорциональна (I ₁ -I ₂ ) / 2, поскольку рабочий ток подключен к середина ограничительной катушки. При внешних неисправностях увеличиваются как I ₁ , так и I ₂ , и тем самым увеличивается сдерживающий момент, что предотвращает неправильную работу.

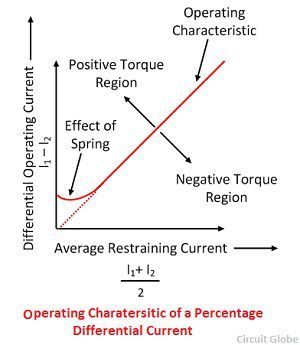
Рабочие характеристики реле процентного дифференциала

Рабочие характеристики реле показаны на рисунке ниже. График выше показывает, что соотношение их рабочего тока и тока ограничения фиксировано. Это реле также называется дифференциальным реле смещения, потому что ограничивающая катушка также называется катушкой смещения, поскольку она обеспечивает дополнительный магнитный поток.

Типы реле процентного дифференциала

Процентное дифференциальное реле в основном подразделяется на два типа.Они

1. Применение трехполюсной системы процентного дифференциального реле.
2. Дифференциальное реле с индукционным смещением.

Такие типы реле используют для защиты генераторов, трансформаторов, фидеров, линий электропередачи и т. Д.

1. Применение трех клеммной системы — Это реле может применяться к элементу, имеющему более двух клемм. Каждая из трех клемм имеет одинаковое количество витков, и каждая из этих катушек развивает крутящий момент, независимый друг от друга.Их крутящие моменты складываются арифметически.

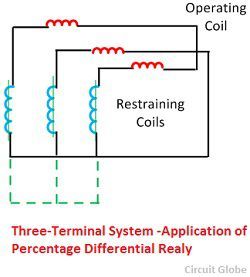Характеристика крутизны в процентах реле будет изменяться в зависимости от распределения тока между ограничивающими катушками. Эти реле бывают мгновенными или высокоскоростными.

2. Дифференциальное реле со смещением индукционного типа — Это реле состоит из поворотного диска, который перемещается в воздушных зазорах двух электромагнитов. Часть каждого полюса снабжена медным кольцом. Это кольцо может двигаться дальше от полюса, в него или из него.

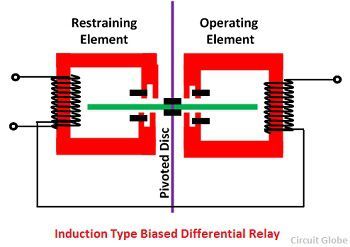Диск испытывает два крутящих момента — один из-за рабочего элемента, а другой из-за ограничивающего элемента. Если бы затеняющее кольцо находилось в одном и том же положении каждого элемента, то сдерживающий момент, испытываемый кольцом, был бы равен нулю. Но если затемненное кольцо ограничивающего элемента было продвинуто дальше в стальной сердечник, крутящий момент, создаваемый ограничивающим элементом, превысит крутящий момент ограничивающего момента.

.