Закон Ома для однородного и неоднородного участка цепи

Дифференциальная форма закона Ома. Найдем связь между плотностью тока j и напряженностью поля Е в одной и той же точке проводника. В изотропном проводнике упорядоченное движение носителей тока происходит в направлении вектора Е. Поэтому направления векторов j и Е совпадают. Рассмотрим в однородной изотропной среде элементарный объем с образующими, параллельными вектору Е, длиной , ограниченной двумя эквипотенциальными сечениями 1 и 2 (рис. 4.3).

Обозначим их потенциалы  и , а среднюю площадь сечения через . Используя закон Ома, получим для тока , или для плотности тока , следовательно 

.

Перейдем к пределу при , тогда рассматриваемый объем можно считать цилиндрическим, а поле внутри него однородным, так что

,

где Е — напряженность электрического поля внутри проводника. Учитывая, что j и Есовпадают по направлению, получаем

.

Это соотношение является дифференциальной формой закона Ома для однородного участка цепи. Величина  называется удельной проводимостью. На неоднородном участке цепи на носители тока действуют, кроме электростатических сил , еще и сторонние силы , следовательно, плотность тока в этих участках оказывается пропорциональной сумме напряженностей. Учет этого приводит к дифференциальной форме закон Ома для неоднородного участка цепи.

.

При прохождении электрического тока в замкнутой цепи на свободные заряды действуют силы со стороны стационарного электрического поля и сторонние силы. При этом на отдельных участках этой цепи ток создается только стационарным электрическим полем. Такие участки цепи называются 

однородными. На некоторых участках этой цепи, кроме сил стационарного электрического поля, действуют и сторонние силы. Участок цепи, на котором действуют сторонние силы, называют неоднородным участком цепи.

Для того чтобы выяснить, от чего зависит сила тока на этих участках, необходимо уточнить понятие напряжения.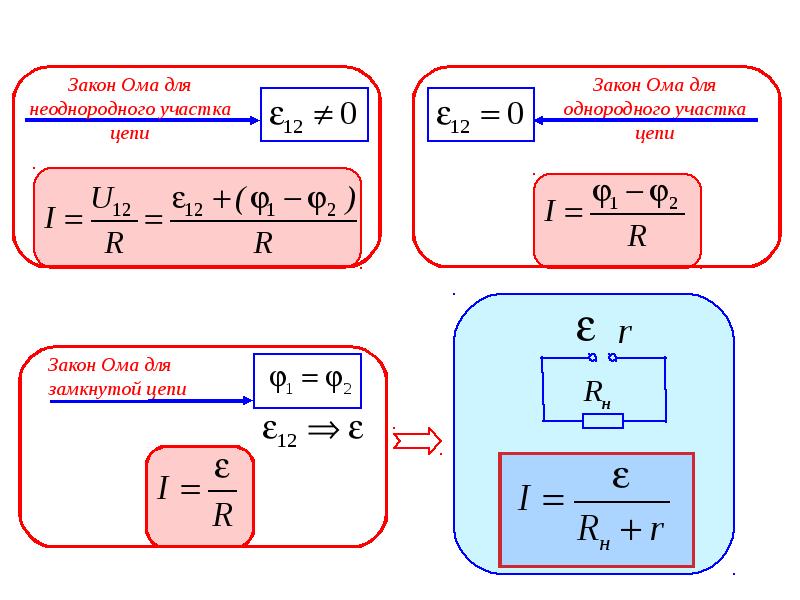

Рис. 1

Рассмотрим вначале однородный участок цепи (рис. 1, а). В этом случае работу по перемещению заряда совершают только силы стационарного электрического поля, и этот участок характеризуют разностью потенциалов Δ

φ. Разность потенциалов на концах участка  Δφ=φ1−φ2=AKq, где A_K — работа сил стационарного электрического поля. Неоднородный участок цепи (рис. 1, б) содержит в отличие от однородного участка источник ЭДС, и к работе сил электростатического поля на этом участке добавляется работа сторонних сил. По определению,  Aelq=φ1−φ2, где q — положительный заряд, который перемещается между любыми двумя точками цепи;  φ1−φ2 — разность потенциалов точек в начале и конце рассматриваемого участка;  Astq=ε. Тогда говорят о напряжении для напряженности:  E_{стац. э. п.} = E_{э/стат. п.} + E_стор. Напряжение U на участке цепи представляет собой физическую скалярную величину, равную суммарной работе сторонних сил и сил электростатического поля по перемещению единичного положительного заряда на этом участке:

 U=AKq+Astorq=φ1−φ2+ε.

Из этой формулы видно, что в общем случае напряжение на данном участке цепи равно алгебраической сумме разности потенциалов и ЭДС на этом участке. Если же на участке действуют только электрические силы (

ε = 0), то  U=φ1−φ2. Таким образом, только для однородного участка цепи понятия напряжения и разности потенциалов совпадают.

Закон Ома для неоднородного участка цепи имеет вид:

 I=UR=φ1−φ2+εR,

где R — общее сопротивление неоднородного участка.

ЭДС ε может быть как положительной, так и отрицательной. Это связано с полярностью включения ЭДС в участок: если направление, создаваемое источником тока, совпадает с направлением тока, проходящего в участке (направление тока на участке совпадает внутри источника с направлением от отрицательного полюса к положительному), т.

е. ЭДС способствует движению положительных зарядов в данном направлении, то ε > 0, в противном случае, если ЭДС препятствует движению положительных зарядов в данном направлении, то ε < 0.

Закон Ома для однородного участка цепи – формула

4.5

Средняя оценка: 4.5

Всего получено оценок: 98.

4.5

Средняя оценка: 4.5

Всего получено оценок: 98.

Упорядоченное движение электрических зарядов (электронов, ионов) или заряженных макроскопических тел называется электрическим током. Движение зарядов возникает под воздействием на них электрического поля, созданного в проводнике приложенным к его концам напряжением

U. Какова зависимость величины электрического тока I от величины напряжения U ? Ответ на этот вопрос впервые дал немецкий ученый Георг Симон Ом, открывший закон, названный в последствии его именем. Для начала рассмотрим закон Ома для однородного участка цепи.

Свойства электрического тока

Направлением электрического тока принято считать движение свободных положительных зарядов. Ток называется постоянным, если его направление и сила постоянны во времени.

Электрическое поле величиной E действует на заряд величиной q с силой F, которая равна:

$ F = q * E $ (1).

В результате в проводнике возникает электрический ток. Для создания электрического поля E, к концам проводника должно быть приложено напряжение U, которое равно разности потенциалов φ₁ и φ₂ на концах проводника:

$ U = φ2 – φ1 $ (2),

при этом φ₂ > φ₁.

Единица электрического тока — ампер (А) — названа в честь французского физика Ампера. Эта единица является одной семи основных единиц в Международной системе СИ. Единицей измерения напряжений является вольт (В), названная в честь итальянского исследователя Алессандро Вольта.

Опыты Георга Ома

В 1826 г. Георг Ом на основании данных своих многочисленных экспериментов открыл однозначную связь между силой тока I и напряжением U. Ученый измерял зависимости тока от напряжения (вольт-амперные характеристики) и строил графики, из которых он обнаружил не просто пропорциональность (чем больше напряжение, тем больше ток), а линейную математическую зависимость тока от напряжения, т.е. I ∼ U.

Рис. 1. График линейной зависимости силы тока от напряжения в проводниках:.

Из графиков было видно, что угол наклона линейных зависимостей для разных материалов разный, т.е. каждый проводник обладал различной степенью сопротивляемости или проводимости. Эта величина была названа электрическим сопротивлением

R. Формула закона Ома для однородного участка цепи выглядит следующим образом:

$ I = {U \over R} $ (3).

Полностью формулировка закона Ома звучит так: сила тока I для проводника на однородном участке цепи прямо пропорциональна напряжению U на этом участке и обратно пропорциональна сопротивлению проводника R.

Любую электрическую цепь можно разделить на отдельные участки. Участки цепи, на которых отсутствует действие сторонних сил (т.е. участки, где отсутствуют источники тока), называются однородными. Участки цепи, на которых имеются источники тока, называются неоднородными.

Сопротивление

Сопротивление проводников и других веществ (полупроводников и диэлектриков) обусловлено тем, что заряженные частицы взаимодействуют (сталкиваются) с узлами кристаллической решетки и атомами разных примесей и дефектов, что приводит к торможению зарядов.

Наблюдения показали, что сопротивление проводника прямо пропорционально его длине L и обратно пропорционально площади поперечного сечения S:

$ R = ρ * { L \over S } $ (5),

Рис. 2. Электрический ток I в металлическом цилиндрическом проводнике, длиной

L, площадью S, электрическое поле E.

Единицей измерения сопротивления является Ом, равный:

$ [1 Ом] = {[1 В]\over [1 A] } $ (6).

Единица измерения удельного сопротивления ρ показывает какое сопротивление имеет проводник длиной 1 метр с площадью поперечного сечения 1 м². Удельные сопротивления всех известных материалов измерены и сведены в справочные таблицы.

Рис. 3. Пример справочной таблицы удельных проводимостей разных веществ

Значения ρ в справочных таблицах приводятся обычно для нормальной, температуры 20

0С, т.к. величина удельного сопротивления зависит от температуры внешней среды T, и описывается формулой:

$ ρ = ρ_0 * (1 + α * T) $ (7),

где: ρ₀ — удельное сопротивление при 0⁰K, α — температурный коэффициент сопротивления.

Что мы узнали?

Итак, мы узнали, что закон Ома для однородного участка цепи формулируется так: сила тока I для проводника на однородном участке цепи прямо пропорциональна напряжению U на этом участке и обратно пропорциональна сопротивлению проводника R. Участки электрической цепи, на которых отсутствуют источники тока, называются однородными. Удельное электрическое сопротивление вещества ρ — величина, характеризующая способность вещества к сопротивлению.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.5

Средняя оценка: 4.5

Всего получено оценок: 98.

---

А какая ваша оценка?

Статья о сопротивлении+измерении из The Free Dictionary

Сопротивление+измерение | Статья о сопротивлении+измерении от The Free Dictionary Сопротивление+измерение | Статья о сопротивлении+измерении из The Free Dictionary

---

Слово, не найденное в Словаре и Энциклопедии.

Возможно, Вы имели в виду:

Пожалуйста, попробуйте слова отдельно:

сопротивление измерение

Некоторые статьи, соответствующие вашему запросу:

Не можете найти то, что ищете? Попробуйте выполнить поиск по сайту Google или помогите нам улучшить его, отправив свое определение.

Полный браузер ?

• ▲
• Силовые тренировки и ходьба
• Преобразователь сопротивления
• Коэффициент передачи сопротивления
• Коэффициент передачи сопротивления
• Коэффициент передачи сопротивления
• Коэффициент передачи сопротивления
• Коэффициент передачи сопротивления
• Коэффициент передачи сопротивления
• Коэффициент передачи сопротивления
• блок сопротивления
• блок сопротивления
• Сопротивление Vasculaire Rénale
• Война Сопротивления против Америки
• Война Сопротивления против Америки
• Война Сопротивления против Америки
• Война Сопротивления против Америки
• Тренировка с отягощениями
• Тренировка с отягощениями
• Тренировка с отягощениями
• Ассоциация производителей сварочных аппаратов сопротивлением

• Сварка сопротивлением
• Сварка сопротивлением
• Сварка сопротивлением
• Сварка сопротивлением
• Сварка сопротивлением
• Сварка сопротивлением
• Компания по сварке сопротивлением
• Производственный альянс контактной сварки
• Провод сопротивления
• Провод сопротивления
• сопротивление+измерение
• сопротивление, акустика
• Сопротивление, Акустика
• Сопротивление переменного тока
• Сопротивление, емкость и индуктивность
• Сопротивление, индуктивность и емкость
• Сопротивление, индуктивность, емкость
• Сопротивление, индуктивность, емкость и проводимость
• Сопротивление, индуктивность, проводимость, емкость
• Сопротивление, омическое
• Сопротивление, омическое

• Сопротивление, восстание и смерть
• Сопротивление-Емкость
• Цепь сопротивления-емкости
• константа сопротивления-емкости
• усилитель с емкостной связью
• Резистивно-емкостной фильтр
• резистивно-емкостная сеть
• резистивно-емкостной генератор
• усилитель с резистивной связью
• фактор, вызывающий резистентность
• фактор, вызывающий резистентность
• фактор, вызывающий резистентность
• Сопротивление-индуктивность
• расходомер сопротивления
• двигатель с пусковым сопротивлением
• коэффициент передачи сопротивления
• эписомы, передающие резистентность
• Сопротивление: Падение человека
• Сопротивление: Альянс молодых социалистов
• Сопротивления
• ▼

Сайт: Следовать:

Делиться:

Открыть / Закрыть

 

источников тока в однородной и изотропной среде | Электрические поля мозга: нейрофизика ЭЭГ

Фильтр поиска панели навигации Oxford Academic Электрические поля мозга: нейрофизика ЭЭГ (2-е изд. ) Нейроэндокринология и вегетативная нервная система Нейронаучные методы Oxford Scholarship OnlineBooksJournals Мобильный телефон Введите поисковый запрос

Закрыть

Фильтр поиска панели навигации Oxford Academic Электрические поля мозга: нейрофизика ЭЭГ (2-е изд.) Нейроэндокринология и вегетативная нервная система Нейронаучные методы Oxford Scholarship OnlineBooksJournals Введите поисковый запрос

Расширенный поиск

• Иконка Цитировать Цитировать

• Разрешения

• Делиться
  • Фейсбук
  • Твиттер
  • LinkedIn
  • Электронная почта

Укажите

Нуньес, Пол Л. и Рамеш Шринивасан, «Источники тока в однородной и изотропной среде», Электрические поля мозга: нейрофизика ЭЭГ , 2-е изд. (

New York , 2006; онлайн-издание, Oxford Academic, 1 мая 2009 г.), https://doi.org/10.1093/acprof:oso/9780195050387.003.0005, по состоянию на 3 июня 2023 г.

Выберите формат Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)

Закрыть

Фильтр поиска панели навигации Oxford Academic Электрические поля мозга: нейрофизика ЭЭГ (2-е изд.) Нейроэндокринология и вегетативная нервная система. Нейронаучные методы. Оксфордская стипендия. Мобильный телефон Введите поисковый запрос

Закрыть

Фильтр поиска панели навигации Oxford Academic Электрические поля мозга: нейрофизика ЭЭГ (2-е изд.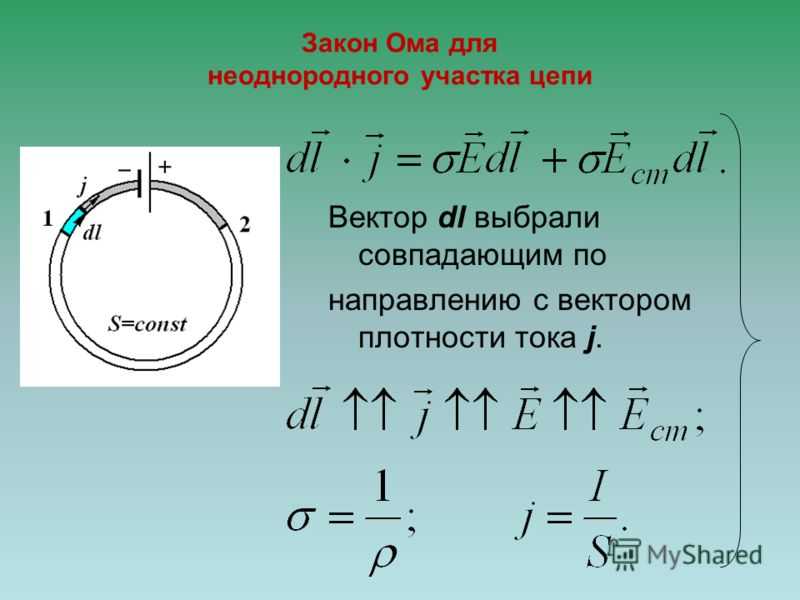 ) Нейроэндокринология и вегетативная нервная система. Нейронаучные методы. Оксфордская стипендия. Введите поисковый запрос

Advanced Search

Abstract

В этой главе демонстрируется взаимосвязь источников тока с зарегистрированными потенциалами в объемных проводниках с использованием простого эксперимента в аквариуме с морской водой, состоящего из дипольного источника тока и отдельной измерительной цепи. В такой проводящей среде поведение потенциалов определяется только геометрическим расположением источников и стоков тока. Примеры включают монополь, диполь и различные распределенные системы источник-сток, в том числе распределение источника потенциала действия и примеры «замкнутого поля». Эти идеализированные конфигурации источников связаны с хорошо известными моделями разветвленных дендритов Ралла потенциалов внеклеточного поля. Показано, что теоретические модели источников приблизительно согласуются с истинными потенциалами, зарегистрированными в мозге кошки (верхняя олива) и вблизи изолированного активного седалищного нерва лягушки. Фактические экспериментальные потенциалы представляют собой средние пространственные значения по объему кончика электрода. Записанная динамика может быть чувствительной к масштабу или фрактальной; динамическое поведение, зарегистрированное в одном масштабе, не обязательно должно совпадать с поведением в других масштабах.

Ключевые слова: монополь, диполь, дипольный слой, источники потенциала действия, закрытое поле, дендритные источники, седалищный нерв

Субъект

Нейроэндокринология и вегетативная нервная система Нейронаучные методы

Коллекция: Оксфордская стипендия онлайн

В настоящее время у вас нет доступа к этой главе.

Войти

Получить помощь с доступом

Получить помощь с доступом

Доступ для учреждений

Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:

Доступ на основе IP

Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.

Войдите через свое учреждение

Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.

1. Нажмите Войти через свое учреждение.
2. Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
3. При посещении сайта учреждения используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic.
4. После успешного входа вы вернетесь в Oxford Academic.

Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.

Войти с помощью читательского билета

Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.

Члены общества

Доступ члена общества к журналу достигается одним из следующих способов:

Войти через сайт сообщества

Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:

1. Щелкните Войти через сайт сообщества.
2. При посещении сайта общества используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic.
3. После успешного входа вы вернетесь в Oxford Academic.

Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.

Вход через личный кабинет

Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. См. ниже.

Личный кабинет

Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.

Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.

Просмотр учетных записей, вошедших в систему

Щелкните значок учетной записи в правом верхнем углу, чтобы:

• Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.