Формула выражающая закон ома для участка цепи
Сила тока I — скалярная величина, равная отношению заряда q, прошедшего через поперечное сечение проводника, к промежутку времени t, в течение которого шёл ток.
Неизменный ток — электрический ток, не изменяющийся с течением времени.
Последовательное соединение проводников. При последовательном соединении электрическая цепь не имеет разветвлений. Все проводники включают в цепь попеременно вереницей.
Параллельное соединение проводников. При параллельном соединении концы проводников присоединены к одной паре точек.
Смешанное соединение проводников — это такое соединение, когда в цепи находится и последовательное, и параллельное соединение.
Узел – это точка электрической цепи, где сходится более 3-х веток.
Свойство проводника ограничивать силу тока в цепи, другими словами противодействовать электрическому току, именуют электрическим сопротивлением проводника.
Резистор либо проводник — элемент электрических цепей, владеющий определённым либо переменным значением электрического сопротивления.
Основная и дополнительная литература по теме урока:
1. Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 335 – 340.
2. Рымкевич А.П. Сборник задач по физике. 10-11 класс. — М.: Дрофа, 2009. – С. 105 – 109.
3. Простый учебник физики. Учебное пособие в 3 томах под редакцией академика Ландсберга Г.С.: Т.2. Электричество и магнетизм. – 12-е изд. – М.: ФИЗМАТЛИТ, 2001. С. 110 – 115.
4. Тульчинский М.Е. Высококачественные задачи по физике в средней школе. Пособие для учителей. Изд. 4-е, переработ. и доп. М. «Просвещение», 1972. С. 83 – 87.
5. Савельев И.В. Курс общей физики, том II. Электричество. М.: Изд. «Наука», 1970 г. С. 108.
Открытые электронные ресурсы:
Теоретический материал для дополнительного исследования
Трудно представить нашу жизнь без электрического тока. Каждый денек, не задумываясь, мы используем разные электрические приборы, в базе работы которых лежат обыкновенные и сложные электрические цепи. Какому закону подчиняются главные характеристики электрических цепей? Как высчитать эти цепи, дабы приборы работали исправно?
Какому закону подчиняются главные характеристики электрических цепей? Как высчитать эти цепи, дабы приборы работали исправно?
Вы уже понимаете, электрическим током именуют упорядоченное (направленное) движение заряженных частиц.
Для появления и существования электрического тока в проводнике нужно:
- наличие свободных заряженных частиц;
- сила, действующая на них в определённом направлении, другими словами наличие электрического поля в проводнике.
Различают следующие деяния электрического тока:
- термическое ;
- хим ;
- магнитное .
Неизменный ток — электрический ток, у которого сила тока и направление не меняются с течением времени.
Сила тока I равна отношению электрического заряда q, прошедшего через поперечное сечение проводника, ко времени его прохождения t:
За направление электрического тока условно выбрано направление движения положительно заряженных частиц, другими словами в сторону, обратную направлению движения электронов.
Для каждого проводника – твердого, водянистого и газообразного – существует определённая зависимость силы тока от приложенной разности потенциалов (напряжения) на концах проводника. Эту зависимость выражает, так именуемая, вольт-амперная черта проводника.
Для широкого класса проводников (в т. ч. металлов ) при постоянной температуре справедлив закон Ома для участка цепи:
Сила тока на участке цепи прямо пропорциональна приложенному напряжению U и назад пропорциональна сопротивлению этого участка цепи:
Закон имеет ординарную форму, но обосновать экспериментально его справедливость достаточно тяжело.
Закон Ома является основой всей электротехники неизменных токов. Из закона Ома вытекает, что замыкать обыденную осветительную сеть проводником малого сопротивления небезопасно.
Основная электрическая черта проводника – сопротивление. От этой величины зависит сила тока в проводнике при данном напряжении. Предпосылкой электрического сопротивления является взаимодействие электронов при их движении по проводнику с ионами кристаллической решетки.
Электрическое сопротивление металлов прямо пропорционально длине проводника и назад пропорционально площади его поперечного сечения:
где величина ρ – удельное сопротивление проводника — величина, зависящая от рода вещества и его состояния (от температуры прежде всего). Удельное сопротивление веществ приводятся в справочных таблицах.
Омметр – устройство для измерения сопротивления.
От источника тока энергия может быть передана по проводам к устройствам, потребляющим энергию. Для этого составляют электрические цепи различной трудности. Различают последовательное, параллельное, смешанное соединения проводников.
Последовательное соединение проводников. При последовательном соединении электрическая цепь не имеет разветвлений. Все проводники включают в цепь попеременно вереницей. Основная особенность последовательного соединения состоит в том, что через все проводники протекает однообразный ток. Если через один проводник протекает ток определенной величины, то таковой же ток протекает и через все другие. Если хотя бы в одном проводнике отсутствует ток, то он непременно отсутствует и во всех других. Напряжение на концах последовательно соединенных проводников складывается. Полное сопротивление всего участка цепи при последовательном соединении равно сумме сопротивлений всех проводников.
Если через один проводник протекает ток определенной величины, то таковой же ток протекает и через все другие. Если хотя бы в одном проводнике отсутствует ток, то он непременно отсутствует и во всех других. Напряжение на концах последовательно соединенных проводников складывается. Полное сопротивление всего участка цепи при последовательном соединении равно сумме сопротивлений всех проводников.
Электрический ток. Закон Ома
При помещении изолированного проводника в электрическое поле E → на свободные заряды q в проводнике будет действовать сила F → = q E → . Это провоцирует появление краткосрочных перемещений свободных зарядов. Процесс заканчивается, когда собственное поле электрических зарядов будет возмещено наружным. Электростатическое поле снутри проводника станет равным нулю.
Есть определенные условия, при которых появляется непрерывное упорядоченное движение свободных носителей заряда. Оно получило название электрического тока.
За направление электрического тока принято брать направление движения положительных свободных зарядов. При наличии электрического поля произойдет появление электрического тока в проводнике.
При наличии электрического поля произойдет появление электрического тока в проводнике.
Силой тока именуют скалярную физическую величину I , равняющуюся отношению заряда ∆ q , протекающего по сечению проводника за время ∆ t :
При неизменяемых силе тока и направлении за промежуток времени ток именуют неизменным. Следует уделять свое внимание на его свойства.
Набросок 1 . 8 . 1 . Упорядоченное движение электронов в железном проводнике и ток I . S – площадь поперечного сечения проводника, – электрическое поле.
В системе С И I измеряется в амперах ( А ) , а единица измерения 1 А устанавливается по магнитному взаимодействию 2-ух параллельных проводников.
Законы неизменного тока. Формулы
Неизменный электрический ток создается в замкнутой цепи, где свободные носители заряда проходят по замкнутым траекториям.
Различные точки цепи владеют постоянным по времени электрическим полем, исходя из главных законов неизменного тока. Другими словами в таковой цепи оно ассоциируется с замороженным электростатическим полем. Когда электрический заряд перемещается по замкнутой линии движения, то работа сил приравнивается нулю.
Когда электрический заряд перемещается по замкнутой линии движения, то работа сил приравнивается нулю.
Дабы неизменный ток имел место на существование, необходимо наличие такового устройства в цепи, которое будет создавать и поддерживать разности потенциалов различных участков цепи с помощью работы сил неэлектростатического происхождения. Их именуют источниками неизменного тока. Такие силы, действующие на свободные носители заряда со стороны источников тока, получили название посторониих сил.
Их природа различна. Гальванические элементы либо батареи владеют посторонними силами, возникающими из-за химических процессов. В генераторах это обстоит по-другому: возникновение посторониих сил может быть при движении проводников в магнитном поле. Источник тока сравним с насосом, перекачивающим жидкость замкнутой гидравлической системы. Электрические заряды снутри источника под действием посторониих сил движутся против сил электростатического поля. Вот поэтому замкнутая цепь может владеть неизменным током.
Перемещаясь по цепи неизменного тока, электрические заряды посторониих сил действуют на источники тока, другими словами совершают работу.
Физическую величину, равную отношению посторониих сил A с т при перемещении заряда q от отрицательного полюса источника к положительной величине этого заряда, именуют электродвижущей силой источника (ЭДС):
Э Д С = δ = A с т q .
Отсюда следует, что ЭДС определяется совершаемой посторонними силами работой при перемещении единичного положительного заряда. ЭДС измеряется в вольтах ( В ) .
Если по замкнутой цепи движется единично положительный разряд, то работа посторониих сил приравнивается сумме ЭДС, которая действует в данной цепи с работой электростатического поля, имеющего значение 0 .
Цепь с неизменной величиной тока следует разбивать на участки. Если на них отсутствует действие посторониих сил, тогда участки именуют однородными, если находятся, то неоднородными.
Когда единичный положительный заряд перемещается по определенному участку цепи, то работу совершают кулоновские и посторонние силы. Запись работы электростатических сил приравнивается разности потенциалов ∆ φ 12 = φ 1 — φ 2 исходной и конечной точек неоднородного участка. Работу посторониих сил приравнивают к электродвижущей данного участка по закону Ома. Тогда полная работа запишется как:
Запись работы электростатических сил приравнивается разности потенциалов ∆ φ 12 = φ 1 — φ 2 исходной и конечной точек неоднородного участка. Работу посторониих сил приравнивают к электродвижущей данного участка по закону Ома. Тогда полная работа запишется как:
U 12 = φ 1 — φ 2 + δ 12 .
Величина U 12 именуется напряжением участка цепи 1 — 2 . Если данный участок однородный, тогда напряжение фиксируется как разность потенциалов:
В 1826 году Г. Ом при помощи опыта установил, что сила тока I , текущая по однородному железному проводнику (отсутствие деяния посторониих сил), пропорциональна напряжению на U концах проводника.
I = 1 R U либо R I = U , где R = c o n s t .
R именуют электрическим сопротивлением.
Проводник, имеющий электрическое сопротивление, получил название резистора.
Связь между R и I гласит о формулировке законе Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и назад пропорциональна сопротивлению.
Обозначение сопротивления по системе С И выражается омами ( О м ) .
Если на участке цепи имеется сопротивление в 1 О м , тогда при напряжении 1 В во время измерения появляется ток силой 1 А .
Нужна помощь педагога?
Опиши задание — и наши специалисты для тебя посодействуют!
Обрисовать задание
Электрический ток и его свойства
Проводники, которые подчинены закону Ома, получили название линейных.
Для изображения графической зависимости силы тока I от U (графики именуют вольт-амперными чертами, ВАХ) применяется ровная линия, проходящая через начало координат.
Есть устройства, не подчиняющиеся закону Ома. К ним относят полупроводниковый диодик либо газоразрядную лампу. Железные проводники имеют отличия от закона Ома при токах большой силы. Это связано с ростом температуры.
Участок цепи, содержащий ЭДС, позволяет записывать закон Ома таким макаром:
I R = U 12 = φ 1 — φ 2 + δ = ∆ φ 12 + δ .
Формула получила название обобщенного закона Ома либо закон Ома для неоднородного участка цепи.
Набросок 1 . 8 . 2 указывает замкнутую цепь с неизменным током, при этом ток цепи ( c d ) считается однородным.
Набросок 1 . 8 . 2 . Цепь неизменного тока.
Исходя из закона Ома I R = ∆ φ c d , участок ( a b ) содержит источник тока с ЭДС, равной δ . Тогда для неоднородного участка формула воспримет вид I r = ∆ φ a b + δ . Сумма обоих равенств дает в итоге выражение I ( R + r ) = ∆ φ c d + ∆ φ a b + δ . Но ∆ φ c d = ∆ φ b a = — ∆ φ a b , тогда I = δ R + r .
Формула I = δ R + r выражает закон Ома для полной цепи. Запишем ее, как определение: сила тока в полной цепи приравнивается электродвижущей силе источника, деленной на сумму сопротивлений однородного и неоднородного участков цепи.
Набросок 1 . 8 . 2 гласит о том, что R неоднородного тела может быть рассмотрено как внутреннее сопротивление источника тока. Тогда ( a b ) участок будет являться внутренним участком источника.
При замыкании a и b при помощи проводника с малым по сопоставлению с внутренним сопротивлением источника получим, что в цепи имеется ток недлинного замыкания I к з = δ r .
Сила тока недлинного замыкания является наибольшей, получаемой от источника с ЭДС и внутренним сопротивлением r . Если внутренне сопротивление не много, тогда ток недлинного замыкания может вызвать разрушение электрической цепи либо источника.
Свинцовые батареи автомобилей имеют силу тока недлинного замыкания в несколько сотен ампер. Необыкновенную опасность представляют замыкания в осветительных сетях, которые имеют подпитку от подстанций. Во избежание разрушительных действий предусмотрены предохранители либо автоматы для защиты сетей.
Дабы при превышении допустимых значений силы тока не вышло недлинного замыкания, применяют наружное сопротивление. Если сопротивление r приравнивается сумме внутреннего и наружного сопротивления источника, сила тока не будет превосходить норму.
При наличии разомкнутой цепи разность потенциалов на полюсах разомкнутой батареи приравнивается ее ЭДС. Когда наружное R включено и ток I подается через батарею, то разность потенциалов на полюсах запишется, как ∆ φ b a = δ — I r .
Набросок 1 . 8 . 3 дает четкое схематическое изображение источника неизменного тока с ЭДС, равной δ , внутренним r в 3-х режимах: «холостой ход», работа на нагрузку, режим недлинного замыкания. E → является напряженностью снутри электрического поля снутри батареи, a – силами, действующими на положительные заряды, F с т → – посторонней силой. Исчезновение электрического поля появляется при маленьком замыкании.
Набросок 1 . 8 . 3 . Схематическое изображение источника неизменного тока: 1 – батарея разомкнута;
2 – батарея замкнута на наружное сопротивление R ; 3 – режим недлинного замыкания.
Вольтметр и амперметр
Используются измерительные приборы для напряжения тока в электрических цепях, именуемые вольтметрами и амперметрами.
Вольтметр определяет разности потенциалов, приложенные к его клеммам.
Подключение к цепи делается параллельно. Любой из устройств такового типа имеет внутреннее сопротивление R B . Дабы перераспределение токов не было приметно, необходимо проследить за тем, дабы внутреннее сопротивление было больше, чем на участках подключаемой цепи.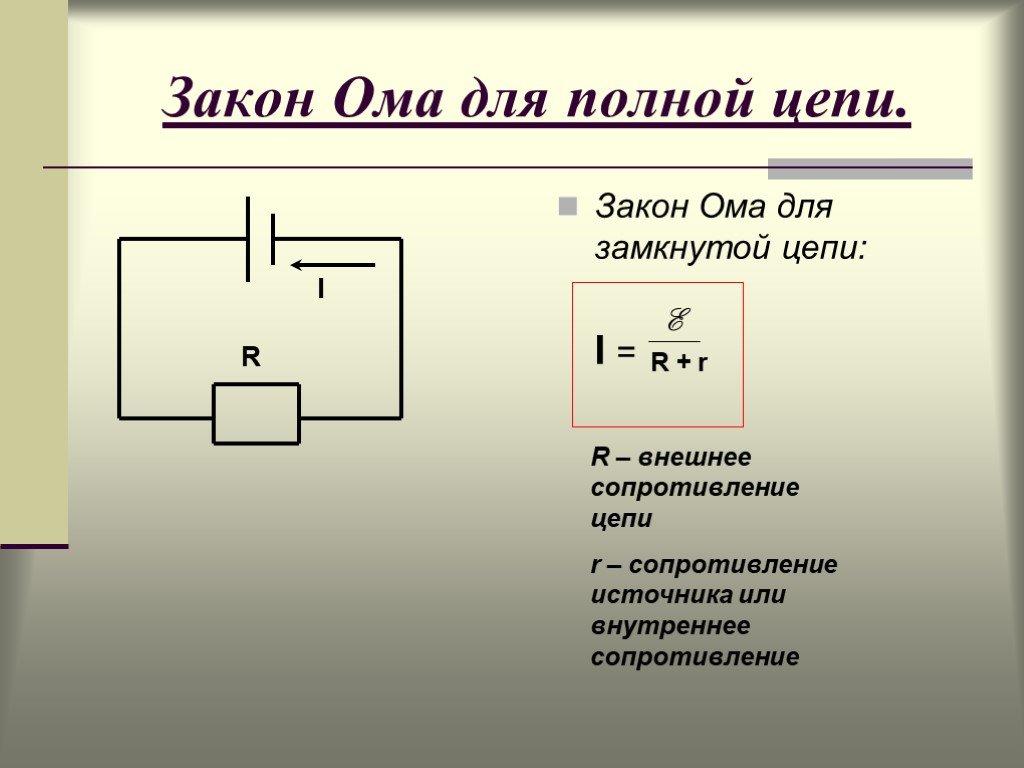 На рисунке 1 . 8 . 4 изображена такая цепь, тогда данное условие можно записать как R B ≫ R 1 .
На рисунке 1 . 8 . 4 изображена такая цепь, тогда данное условие можно записать как R B ≫ R 1 .
Это значит, что ток I B = ∆ φ c d R B , протекающий через вольтметр, меньше тока I = ∆ φ c d R 1 , проходящего по данному участку цепи.
Снутри устройства также не действуют посторонние силы, потому разность потенциалов его клемм совпадет со значением напряжения. Отсюда следует, что вольтметр определяет напряжение.
Амперметр предназначается для измерения силы тока в цепи.
Его подключение к цепи делается последовательно для прохождения всего измеряемого тока. Внутреннее сопротивление устройства обозначается как R A . В отличие от вольтметра обязано иметь малые значения относительно полного сопротивления цепи. На рисунке 1 . 8 . 4 показано, что сопротивление амперметра подходит к условию R A ≪ ( r + R 1 + R 2 ) . При включении устройства ток в цепи не должен изменяться.
Измерительные приборы подразделяют на стрелочные и цифровые, последние из которых являются сложными электронными устройствами и в состоянии давать очень четкие значения при измерении.
Набросок 1 . 8 . 4 . Включение амперметра ( А ) и вольтметра ( В ) в электрическую цепь.
Закон Ома
Закон Ома связывает величину напряжения (или ЭДС) и силы тока в цепях, владеющих сопротивлением.
Существует два варианта закона Ома — для участка цепи и для всей цепи.
Содержание
Закон Ома для участка цепи
Закон Ома для участка цепи говорит, что сила тока в участке цепи помноженная на сопротивление участка равна напряжению между его концами.
» />
» /> — напряжение между концами участка цепи, » /> — сила тока, протекающий через участок цепи, » /> — сопротивление участка цепи.
Закон Ома для всей цепи
Закон ома для всей цепи говорит, что сила тока циркулирующего по неразветвлённой замкнутой цепи, помноженная на суммарное сопротивление этой цепи равна суммарной ЭДС источников в ней.
>=IR,>» />
Закон Ома для переменного тока
Закон Ома применим как к неизменному току, так и к моментальным значениям напряжения и тока:
» />
Более того, закон Ома применим и к таким величинам, как амплитудное, действующее, среднее, малое, наибольшее значение, размах напряжения и тока, связывая надлежащие величины между собой. Так амплитуда напряжения » /> будет связана с амплитудой тока » /> выражением
Так амплитуда напряжения » /> будет связана с амплитудой тока » /> выражением
» />
среднее значение напряжения » /> и тока » /> — выражением:
» />
и т. д. Неважно какая линейная функция тока и напряжения будет подчиняться закону Ома, если закону Ома подчиняется секундное значение.
«Реактивный» закон Ома
При протекании тока через такие элементы, как конденсаторы и катушки индуктивности закон Ома для моментальных значений тока и напряжения не осуществляется. Но, если рассматривать действие на такие элементы напряжения, подчиняющемуся гармоническому закону:
» />
в силу их линейности ток также будет гармоническим, но со сдвигом фазы >>» />:
>).>» />
При всем этом амплитудные значения напряжения » /> и тока » /> будут пропорциональны (при отрицательном сдвиге фаз её значение будет отрицательным), так что можно можно написать для них следующую формулу:
» />
где коэффициент пропорциональности » /> именуется реактивным сопротивлением.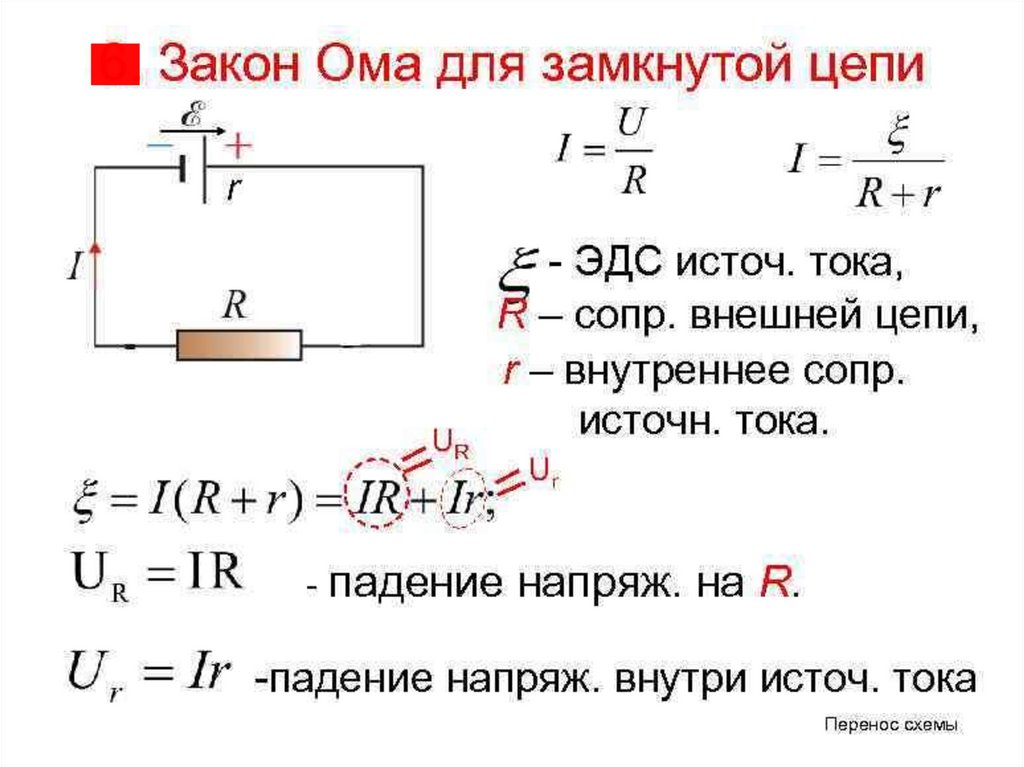 Его можно вычислить по формулам:
Его можно вычислить по формулам:
=2\pi fL=\omega L>» /> для катушки с индуктивностью » /> и =-<2\pi fC>>=-<\omega C>>>» /> для конденсатора с ёмкостью » />,
где » /> — частота в герцах, » /> — радиальная частота гармонического сигнала.
Закон Ома для всеохватывающих амплитуд
В пределах способа всеохватывающих амплитуд удалось обобщить действие закона Ома на цепи владеющие не только лишь активным, но и реактивным сопротивлением. Для этого вводится понятие всеохватывающего импеданса >>» />, выражаемого в виде
>=R+iX,>» />
ФИЗИЧЕСКИЙ 126
ФИЗИЧЕСКИЙ 126ФАКУЛЬТЕТ НАУК, ЗИМА 2008PHYS 126 LEC B3: Жидкости, поля и излучение (Инструктор: Марк де Монтиньи)
- Раздел 21-1: Электрический ток
- стр. 696, экв. 21-1, I = ΔQ/Δt. ΔQ — количество заряда, протекающего через данной точки провода за время Δt.
- Стр.
696, Единица СИ: 1 ампер или ампер (А) = 1 Кл/с.
- Направление I определяется направлением движения положительных пробных зарядов, как показано на рисунке 21-4.
- Цепи постоянного тока (постоянный ток): ток всегда течет в одном направлении.
- Цепи переменного тока (переменного тока): токи периодически меняют свое направление. Более подробно обсуждается в главе 24.
- Электродвижущая сила
- Стр. 697, Электродвижущая сила (ЭДС, ε) – разность потенциалов между две клеммы идеальной батареи. Разность потенциалов V между клеммами реальной батареи обычно меньше ε, как обсуждалось на стр. 707.
- Источник ЭДС поддерживает разность потенциалов, обычно из-за неэлектрических (например, химические, магнитные, солнечные элементы, топливные элементы, ядерные) источники.
- Несмотря на свое название, ЭДС НЕ является силой. Единицей ЭДС является Вольт.
- На этом рисунке показан символ батареи, или источник ЭДС, где более длинный вывод соответствует более высокому потенциалу, а более короткая клемма имеет меньший потенциал, т.
е. V A B.
- Обратите внимание, что ток не обязательно течет от — к +. Например, если система состоит из двух батарей с противоположной полярностью. Это аналогично силам: ускорение не обязательно указывает в направлении действия силы.
- стр. 698, Рис. 21-3 иллюстрирует механическую аналогию схема на рис. 21-4: человек подъем воды соответствует источнику ЭДС, а весло соответствует лампочке. (или сопротивление), которое рассеивает мощность. Также как этот человек выполняет какую-то работу, чтобы поднять вода, когда идеальная батарея перемещает заряд ΔQ по цепи, он совершает работу W = ∆Qε. Эта фигура показ аналогии с водой будет полезен, когда мы будем обсуждать резисторы параллельно и последовательно.
- стр. 726, задача 7
- Раздел 21-2: Сопротивление и закон Ома
- стр. 699, экв. 21-2, Закон Ома: V = RI.
- R — сопротивление. Единица измерения: 1 Ом (Ом) = 1 В/А.
- На этом рисунке показан символ сопротивления.
Электрический потенциал уменьшается при перемещении через резистор в направлении тока, т. е. V C > V D . (См. начало стр. 712.)
- На этом рисунке показано, что график V как функции I — линия с наклоном R.
- Закон Ома не универсален; это справедливо только для так называемых омических материалов. Тем не менее, неомические материалы могут быть весьма полезными, т.е. Светоизлучающие диоды (LED). Это не закон физики, как закон сохранения энергии.
- На этом рисунке показаны резисторы, аналогичные используемым в своих лабораторных экспериментах. Конвертер цветового кода резистора [Конечно, не нужно запоминать это.]
- Простое моделирование
- стр. 700, экв. 21-3, Удельное сопротивление ρ определяется как R = ρL/A.
- СИ Единицей измерения ρ является Ом•м.
- Некоторые удельные сопротивления перечислены в таблице 21-1.
- [Опущено: для многих материалов удельное сопротивление зависит от температуры следующим образом: ρ = ρ 0 (1 + α ΔT), где α называется температурный коэффициент удельного сопротивления, а ρ 0 – другой коэффициент, который зависит от материала.
- стр. 726, задача 14
- стр. 726, задача 17
- стр. 726, задача 73
- стр. 727, задача 18
- Раздел 21-3: Энергия и мощность в электрических цепях
- стр. 702, экв. 21-4, Электрическая мощность: P = IV. [Единица P, ватт (Вт)]
- Экв. 21-4 следует из P = ΔU/Δt, где ΔU — изменение потенциальной энергии при движении заряда ΔQ через разность потенциалов V. Тогда P = ΔQ V/Δt = IV.
- стр. 703, экв. 21-5, P = I 2 R (омический материал)
- стр. 703, экв. 21-6, P = V 2 /R (омический материал)
- стр. 727, задача 22
- стр. 727, задача 25
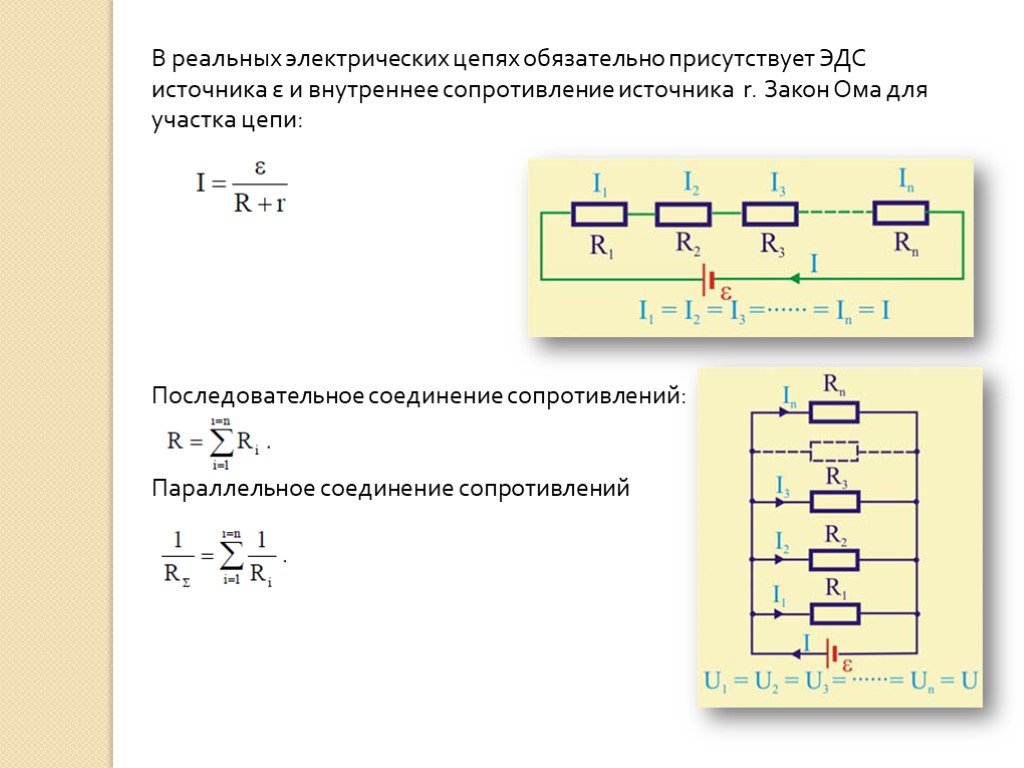
- Раздел 21-4: Резисторы последовательно и параллельно
- Резисторы последовательно:
- стр. 706, экв. 21-7, Резисторы последовательно: R eq = R 1 + R 2 + …
- стр. 706, Рис. 21-6 иллюстрирует сопротивление R eq эквивалентен трем резисторам.
- Этот рисунок иллюстрирует аналогию между водопадами и два резистора последовательно.
- Один и тот же ток I протекает через каждый последовательно соединенный резистор. Потенциальные различия добавить.
- Обратите внимание, что для резисторов, соединенных последовательно, R eq больше, чем наибольшее сопротивление в комбинация, то есть увеличивает сопротивление.
- Параллельные резисторы:
- стр. 708, экв. 21-10, Параллельные резисторы: 1/R eq = 1/R 1 + 1/R 2 + …
- стр. 708, Рис. 21-9 иллюстрирует сопротивление R eq эквивалентен трем резисторам.
- Этот рисунок иллюстрирует аналогию между водопадами и два резистора последовательно.
- Резисторы подключены параллельно через одну и ту же разность потенциалов.
- Обратите внимание, что для резисторов, включенных параллельно, R eq меньше наименьшего сопротивления в комбинация, то есть уменьшает сопротивление.
- стр. 728, задача 43
- стр. 707, Рис. 21-7 иллюстрирует важный пример последовательно соединенные резисторы: внутреннее сопротивление r настоящей батареи. Это объясняет внутренние потери и случай, когда разность потенциалов между клеммами меньше ЭДС ε и зависеть от тока в батарее.
- Запуск автомобиля с батарейками для фонарика
- Раздел 21-5: Правила Кирхгофа
- С. 711, Правила Кирхгофа
- Правило соединения: алгебраическая сумма всех токов в любом соединении. в цепи должен равняться нулю. «Алгебраический» означает, что входящие и исходящие токи имеют разный знак. Это правило является следствием сохранения заряда.
- Правило петли: алгебраическая сумма всех разностей потенциалов вокруг любого замкнутый контур в цепи должен равняться нулю. «Алгебраический» означает, что знак разности потенциалов зависит от того, увеличивается она или уменьшается в направлении движения по кругу. Это правило является следствием сохранения энергии.
- стр. 728, задача 48
- стр. 728, задача 50
- Воздействие тока на организм человека
- Раздел 21-6: Цепи, содержащие конденсаторы
- стр. 714, Параллельные конденсаторы
- стр. 714, рис. 21-17
- стр. 714, экв. 21-14: С экв. = С 1 + С 2 + …
- Каждый конденсатор имеет одинаковую разность потенциалов. Общий заряд – это сумма обвинений.
- стр. 716, Конденсаторы в серии
- стр. 716, рис. 21-18
- стр. 716, экв. 21-10, Конденсаторы последовательно: 1/C eq = 1/C 1 + 1/C 2 + …
- Конденсаторы имеют одинаковый заряд. Разности потенциалов складываются.
- стр. 729, задача 58
- стр. 729, задача 60
- Дополнительная проблема
- Раздел 21-7: RC-цепи
- Зарядка конденсатора
- стр.
717, на рис. 21-19 показана RC-цепь. На рис. 21-20 показана зависимость заряда от времени.
- стр. 717, экв. 21-18, Зарядный конденсатор: q(t) = Cε (1 — e -t/RC )
- RC обычно называют «постоянной времени цепи» и обозначают греческой буквой буква тау, τ (тот же символ, что и крутящий момент в PHYS 124).
- стр. 718, экв. 21-19, Ток в зарядном конденсаторе: I(t) = (ε/R) e -t/RC
- Разрядка конденсатора
- стр. 719, На рис. 21-22 показана RC-цепь, где батарея снята и конденсатор разряжен. На рис. 21-21 показана зависимость тока от времени. Обратите внимание, что заряд ведет себя так же.
- стр. 719, экв. 21-20, Разрядный конденсатор: q(t) = Q e -t/RC
- стр. 729, задача 62
- стр. 731, задача 96
- Раздел 21-8: Амперметры и вольтметры
- С.720: Амперметр включен последовательно с участком цепи в котором измеряется ток.
Идеальный амперметр имеет внутреннюю сопротивление равно нулю. стр. 720, рис. 21-23.
- P.720: Вольтметр подключен параллельно участку цепи в котором измеряется разность потенциалов. Идеальный вольтметр имеет внутреннюю сопротивление, которое бесконечно. стр. 720, рис. 21-24.
Вернуться к Веб-страница PHYS 126, LEC B3
Видео урока: Электродвижущая сила и внутреннее сопротивление
Стенограмма видео
В этом уроке мы говорим о
электродвижущая сила и внутреннее сопротивление. Эта тема даст нам внутри
информация о том, как работают электрические цепи. И конкретно, мы будем учиться
о батареях и элементах в этих цепях. Приступая к работе, давайте рассмотрим
эта простая электрическая цепь, состоящая из батареи и резистора с
сопротивление 𝑅. Термин батарея иногда
указывает на одну ячейку в такой схеме. Или это может указывать на несколько ячеек
натянуты встык вот так. Для наших целей в этом видео
мы будем считать батарею единой единицей, одной ячейкой.
Для наших целей в этом видео
мы будем считать батарею единой единицей, одной ячейкой.
Итак, батарея, как мы помним, представляет собой
устройство, преобразующее накопленную химическую энергию в электрическую. Через химическую реакцию
В процессе электроны направляются к одному концу батареи, называемому анодом. И это оставляет другой конец с
относительно положительный заряд. Этот конец называется катодом
батарея. Итак, когда его внутренняя химия
работает хорошо, много отрицательных зарядов, электронов, накапливаются на одном конце
батарея. А это значит, что на другом конце есть
большая концентрация положительного заряда. Если мы возьмем такую батарею и
мы вставляем его в электрическую цепь, тогда весь отрицательный заряд накапливается одновременно
конец батареи, называемый одной из клемм батареи, стремится оттолкнуть любой
другие близлежащие отрицательные заряды. Это означает, что мобильный негатив
заряд, скажем, в этой точке нашей цепи испытал бы силу от отрицательного
клемма аккумулятора, которая толкает его вправо.
Это означает, что мобильный негатив
заряд, скажем, в этой точке нашей цепи испытал бы силу от отрицательного
клемма аккумулятора, которая толкает его вправо.
И, в конечном счете, эта плата будет
нажимается по часовой стрелке по всей цепи. Это поток отрицательного заряда
по цепи, называемой электрическим током. Как примечание, другой
Клемма нашей батареи, положительная, оказывает такую же силу отталкивания.
на соседних положительных зарядах в цепи. Но в отличие от отрицательных зарядов,
электроны, положительные заряды, как правило, не подвижны. Это верно не для каждого типа
поток заряда, но это верно для электрических цепей, подобных этой. Вот почему мы говорим, что электрический
ток на самом деле состоит из отрицательных зарядов, а не положительных зарядов. Для цепей, соединенных металлом
провода, как этот, это отрицательные заряды, которые делают движение.
Теперь предположим, что общая ток в этой цепи определяется значением 𝐼. С учетом этой информации, что общий ток в цепи равен 𝐼, а полное сопротивление в цепи равно 𝑅. Если бы нас попросили решить разность потенциалов на нашей батарее, мы могли бы назвать эту разность потенциалов 𝑉. Тогда мы могли бы подумать о законе Ома и напомним, что полная разность потенциалов в цепи равна общий ток в этой цепи, умноженный на сопротивление цепи. Итак, мы могли бы тогда сказать, что 𝐼 раз 𝑅 равно 𝑉, разности потенциалов на нашей батарее. Этот анализ точен, но внутри батареи происходит больше. Давайте рассмотрим эту батарею один раз более.
Когда эта батарея подключена к
замкнутая цепь, то он управляет потоком отрицательного заряда вокруг этой цепи. Эти отрицательные заряды, электроны,
двигаться в петле.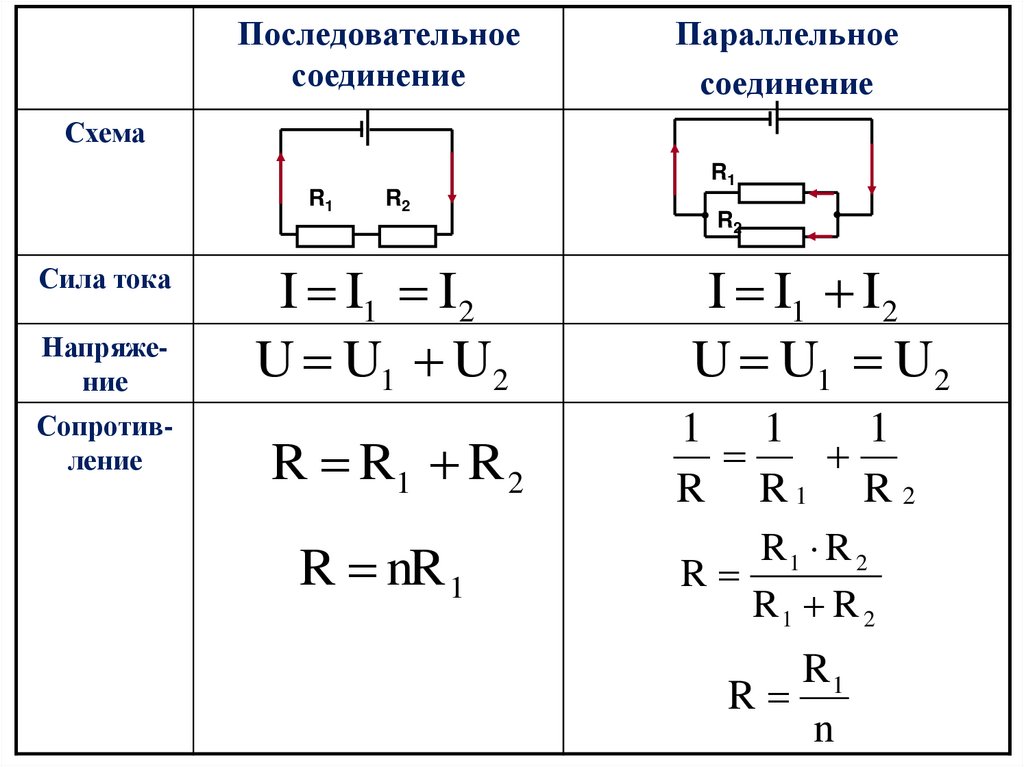 Но потом мы удивляемся, что происходит
когда они достигают плюсовой клеммы аккумулятора? Электрически говоря, кажется
как будто электроны хотели бы остаться здесь и не двигаться дальше. Это потому, что электроны, с
их отрицательный заряд будет притягиваться к положительному полюсу батареи.
и отталкивается от отрицательной клеммы. Тогда с этой точки зрения мы
можно представить, что как только электрон пробился с одного конца
аккумулятор к другому, то он остановится здесь. И электроны будут просто добры
накапливаться вокруг этой положительной клеммы.
Но потом мы удивляемся, что происходит
когда они достигают плюсовой клеммы аккумулятора? Электрически говоря, кажется
как будто электроны хотели бы остаться здесь и не двигаться дальше. Это потому, что электроны, с
их отрицательный заряд будет притягиваться к положительному полюсу батареи.
и отталкивается от отрицательной клеммы. Тогда с этой точки зрения мы
можно представить, что как только электрон пробился с одного конца
аккумулятор к другому, то он остановится здесь. И электроны будут просто добры
накапливаться вокруг этой положительной клеммы.
Но если бы это случилось, все эти
накопленные отрицательные заряды начнут нейтрализовать эту положительную батарею
Терминал. Сам терминал станет
все меньше положительно заряжены. И поскольку это произошло, это означало бы
что другой терминал, который изначально был отрицательным, будет становиться все более и более
положительно заряжен.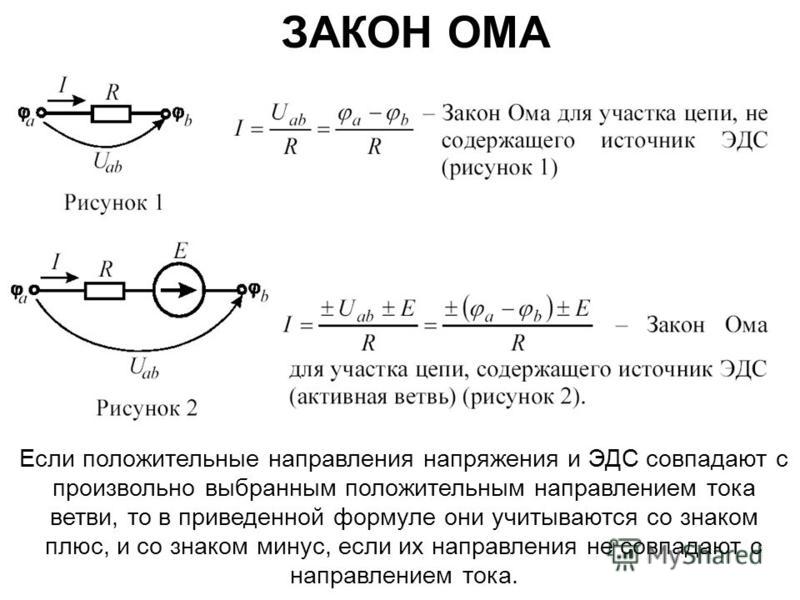 Это было бы связано с тем, что
накопление отрицательного заряда здесь означает наличие относительно положительного заряда.
налипание на минусовой клемме аккумулятора. Эти условия нейтрализуют
полярность, можно сказать, этой батареи. И это быстро привело бы к
конец потока заряда через нашу электрическую цепь. Это отключило бы ток.
Это было бы связано с тем, что
накопление отрицательного заряда здесь означает наличие относительно положительного заряда.
налипание на минусовой клемме аккумулятора. Эти условия нейтрализуют
полярность, можно сказать, этой батареи. И это быстро привело бы к
конец потока заряда через нашу электрическую цепь. Это отключило бы ток.
Поскольку мы этого не наблюдаем
явления в электрических цепях, должно происходить что-то еще. И действительно, что-то есть. Так как отрицательно заряженные электроны
вводим плюсовую клемму нашего аккумулятора, внутри идет химическая реакция
батарея, которая преодолевает естественную склонность электронов прилипать к
положительный терминал. Вместо этого, благодаря этой реакции,
электроны на самом деле движутся слева направо от положительного к отрицательному в нашем
батарея. Когда это продолжается, заряд не
построить, как мы нарисовали его здесь. Поэтому ионы, несущие заряд
может продолжать протекать через батарею, а заряд может продолжать протекать через
остальная часть цепи.
Поэтому ионы, несущие заряд
может продолжать протекать через батарею, а заряд может продолжать протекать через
остальная часть цепи.
То, что мы говорим, это то, что наш
сама батарея является частью нашей общей цепи, и этот ток существует в батарее
тоже в том же направлении и с той же величиной, что и везде. Заряд течет не только в
аккумулятор, но при этом он также сталкивается с некоторым сопротивлением. Часто мы говорим об этом сопротивлении
со строчной 𝑟. Имя, которое мы даем для этого,
внутреннее сопротивление. Мы называем это так, потому что это
сопротивление, которое исходит от батареи или самой ячейки в нашей цепи. Внутреннее сопротивление влияет
на некоторые свойства электрической цепи. Во-первых, если наша батарея
действительно имеет некоторое внутреннее сопротивление, строчная буква 𝑟, тогда, когда мы применим закон Ома к
цепи, это сопротивление, которое мы должны принять во внимание.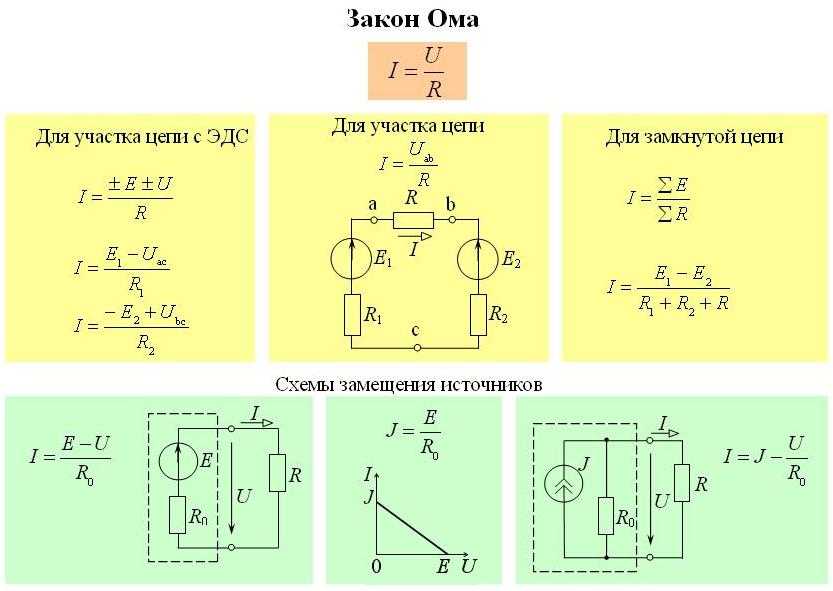
В случае с этой схемой мы видим здесь допустим, что 𝑉 — это разность потенциалов, обеспечиваемая батареей. Другими словами, если бы мы измерьте электрический потенциал на положительной клемме аккумулятора, а затем измерьте электрический потенциал на отрицательной клемме, эти значения будут разные. И эта разница называется разность потенциалов на аккумуляторе. Другое название этого потенциала разница в напряжении на клеммах. И это то, что мы обычно символизировать с помощью заглавной 𝑉. это разность потенциалов подается в цепь вне батареи.
Итак, возвращаемся к нашей схеме
вот это напряжение на клеммах, разность потенциалов на нашем аккумуляторе, уже
учитывает внутреннее сопротивление аккумулятора, строчная 𝑟. Мы могли бы тогда сказать, что это
напряжение на клеммах — это то, что остальная часть цепи, цепь, которая начинается здесь и
заканчивается здесь все это вне батареи, опыты.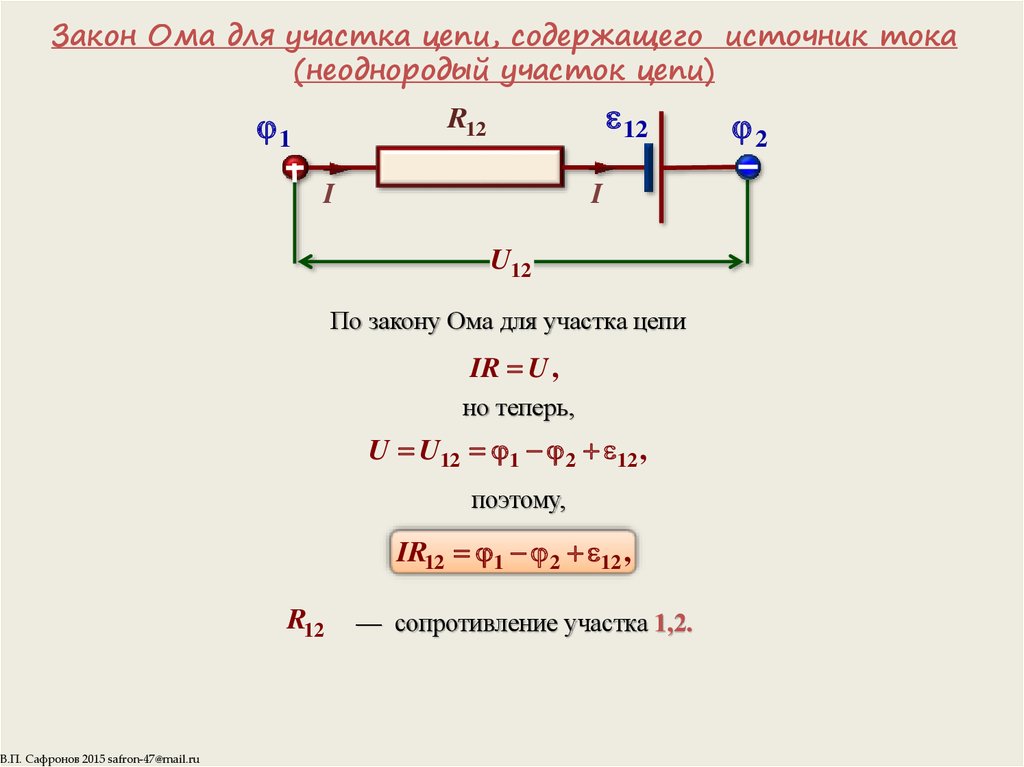 Поскольку заглавная 𝑉 является терминалом
напряжение нашей батареи, которое уже отражает уменьшение этого напряжения благодаря
к внутреннему сопротивлению батареи. Следуя закону Ома, мы
действительно можно написать, что напряжение на клеммах нашего аккумулятора равно току
протекающий через нашу цепь, умноженный на внешнее сопротивление, капитал 𝑅.
Поскольку заглавная 𝑉 является терминалом
напряжение нашей батареи, которое уже отражает уменьшение этого напряжения благодаря
к внутреннему сопротивлению батареи. Следуя закону Ома, мы
действительно можно написать, что напряжение на клеммах нашего аккумулятора равно току
протекающий через нашу цепь, умноженный на внешнее сопротивление, капитал 𝑅.
А как же напряжение
через нашу батарею до того, как внутреннее сопротивление отнимет у нее кусок, поэтому, чтобы
разговаривать? Там есть имя, данное этому
определенное количество напряжения; это электродвижущая сила. Эту силу также называют ЭДС для
короче, и обычно обозначается греческой буквой 𝜀. И первое, на что стоит обратить внимание
дело в том, что хотя мы и называем это силой, мы измеряем ее в вольтах. Действительно, электродвижущая сила
является разностью потенциалов. В частности, это потенциал
разница между аккумулятором, когда в нем нет тока.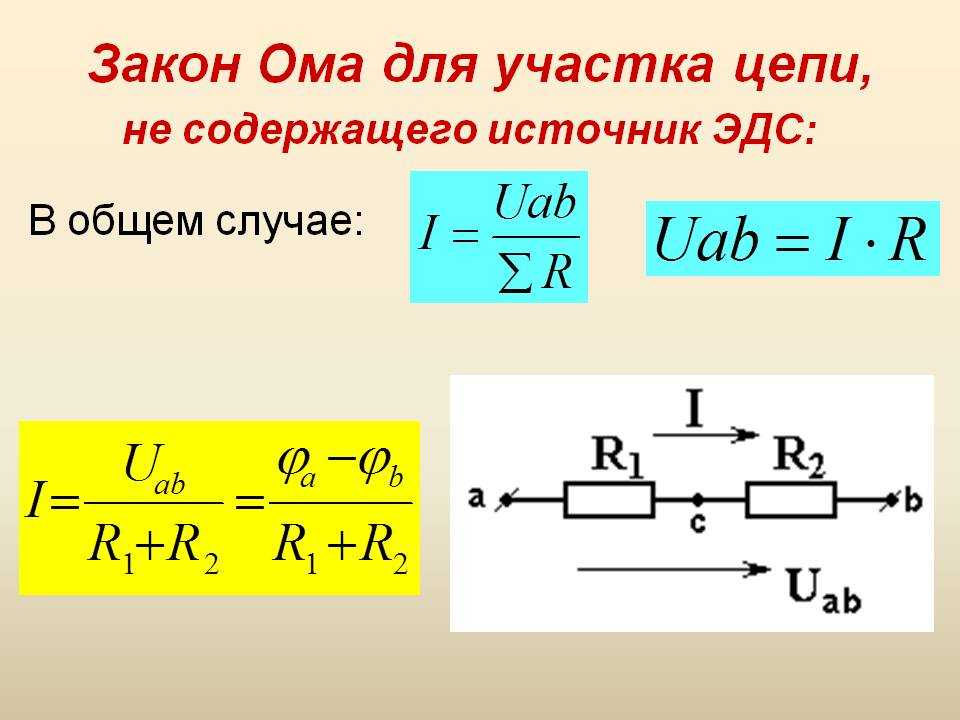
Вот как мы можем думать о это. Скажем, у нас есть батарея, которая не является частью электрической цепи. Это всего лишь батарея сам. Эта батарея, когда она работает правильно, тем не менее, будет иметь положительный и отрицательный вывод. То есть отрицательный заряд будет накапливаться вверх на одном конце и положительный заряд на другом. Это накопление заряда создает разность потенциалов на аккумуляторе. И эта разность потенциалов электродвижущая сила 𝜀. Но тогда, если бы мы соединили наши батареи, так что теперь она была частью электрической цепи, эта разность потенциалов 𝜀, электродвижущая сила, это не разность потенциалов, что остальная часть цепь вне батареи испытала бы. То есть ЭДС не совпадает с напряжение 𝑉.
Помните, что когда аккумулятор
включен в цепь, и заряд течет, это означает, что отрицательный заряд движется
через батарею.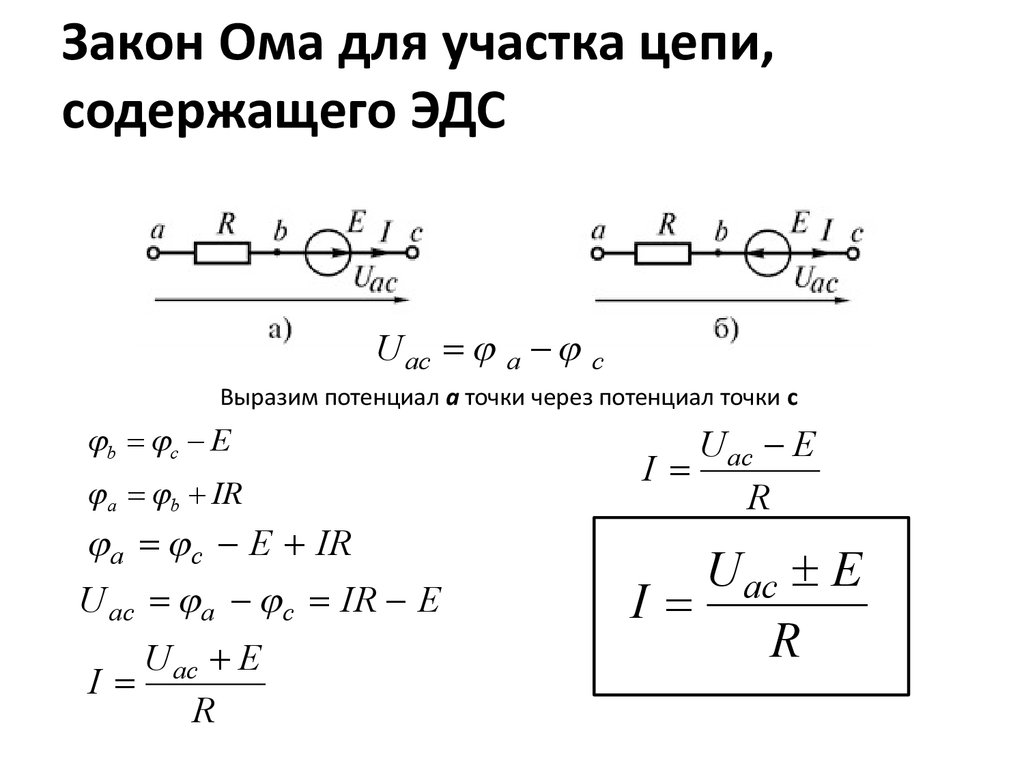 И этот поток, который путешествует
через батарею такой же, как ток, который проходит через все остальное в
схема. Мы назвали эту текущую столицу
𝐼, поэтому мы можем дать ему то же имя здесь. Поток капитала 𝐼 находится в
батарея. Так как батарея имеет некоторое ненулевое значение
хотя внутреннее сопротивление в 𝐼 раз больше, чем внутреннее сопротивление представляет собой напряжение
потеря.
И этот поток, который путешествует
через батарею такой же, как ток, который проходит через все остальное в
схема. Мы назвали эту текущую столицу
𝐼, поэтому мы можем дать ему то же имя здесь. Поток капитала 𝐼 находится в
батарея. Так как батарея имеет некоторое ненулевое значение
хотя внутреннее сопротивление в 𝐼 раз больше, чем внутреннее сопротивление представляет собой напряжение
потеря.
Итак, вот что мы делаем. Берем нашу электродвижущую силу 𝜀
и отнимаем от него 𝐼 умноженное на строчную 𝑟, внутренний аккумулятор
сопротивление. Ток в цепи
умноженное на внутреннее сопротивление батареи, называется потерянным напряжением. Вот сколько потенциала
разница падает просто на самой батарее. Итак, мы начинаем с 𝜀, а затем
вычитаем из него потерянное напряжение. И это то, что равно
к 𝑉, разности потенциалов, испытываемой остальной частью цепи.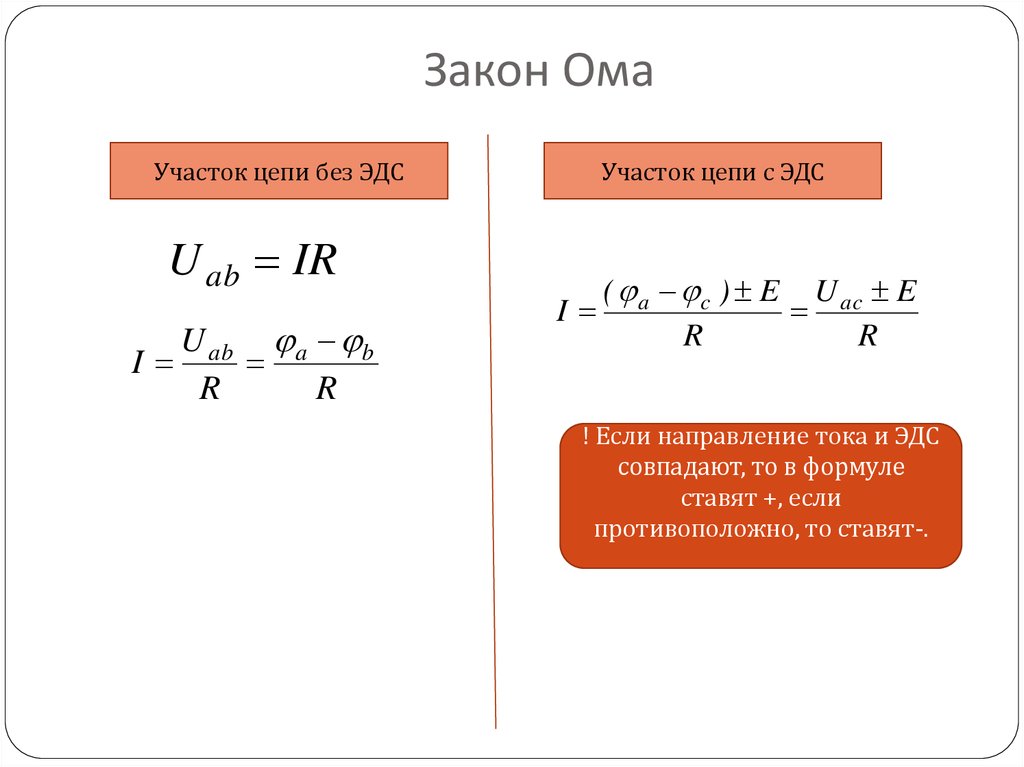
Теперь, если мы рассмотрим это уравнение для электродвижущей силы вместе с этой мы нашли из применения закона Ома к В остальной части нашей схемы мы видим, что происходит что-то интересное. Во-первых, обратите внимание, что мы можем написать наш уравнение для электродвижущей силы, как это. ЭДС равна столичной 𝑉 плюс 𝐼 раз внутреннее сопротивление нашей батареи. Но потом мы видим эту столицу 𝑉 можно заменить на 𝐼, умноженное на 𝑅, где 𝐼 — ток в нашей цепи, а заглавная 𝑅 — сопротивление всей цепи вне батареи. Затем мы видим, что мы можем сгруппировать эти два члена вместе, так как они имеют общий делитель текущего 𝐼.
И теперь, когда мы смотрим на это, мы видим
что это уравнение очень похоже на наше уравнение закона Ома, 𝑉 равно 𝐼 раз
𝑅. Здесь у нас есть потенциал
разница, в частности, разность потенциалов на нашей батарее, когда нет заряда
движется через него.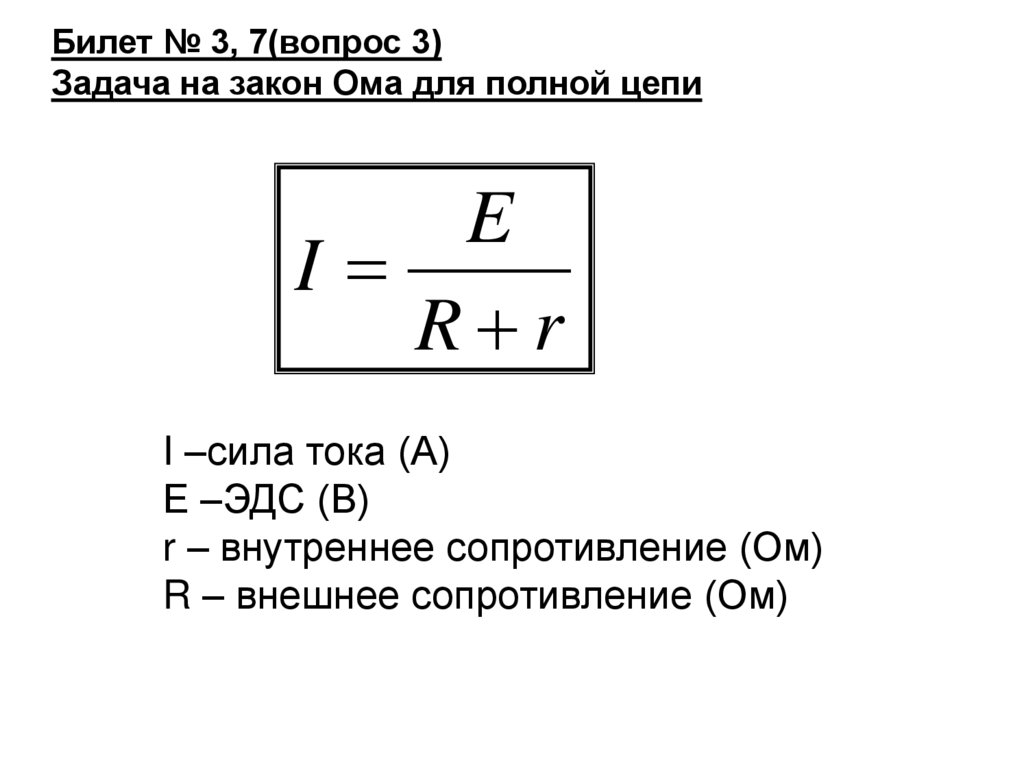 Здесь у нас есть наша общая схема
ток. А если объединить заглавную 𝑅 и
строчная 𝑟, имеем общее сопротивление в цепи. Так что везде закон Ома
очередной раз. Но на этот раз мы учитываем
внутреннее сопротивление нашей батареи. Зная все это, давайте немного
практики с этими идеями через пример.
Здесь у нас есть наша общая схема
ток. А если объединить заглавную 𝑅 и
строчная 𝑟, имеем общее сопротивление в цепи. Так что везде закон Ома
очередной раз. Но на этот раз мы учитываем
внутреннее сопротивление нашей батареи. Зная все это, давайте немного
практики с этими идеями через пример.
Какое из следующих утверждений является правильным описанием электродвижущей силы, ЭДС, батареи? а) ЭДС батареи – это напряжение, которое он прикладывает к цепи, к которой он подключен. б) ЭДС батареи – это напряжение, необходимое для преодоления его внутреннего сопротивления. в) ЭДС батареи – это ток внутри аккумулятора. А (D) ЭДС батареи равна разность потенциалов на его клеммах, когда он не производит ток.
Итак, мы начали вычислять
какой из этих четырех вариантов является правильным описанием электродвигателя
сила или ЭДС батареи, давайте освободим немного места в верхней части нашего экрана. Теперь, когда мы говорим о батарее,
иногда этот термин относится к отдельной единице, или к отдельной ячейке, подобной этой, или к другому
раз это может относиться к нескольким ячейкам, расположенным встык. Для простоты будем ссылаться
к этому единственному блоку в качестве батареи. И мы хотим определить правильный
описание ЭДС этой батареи. Батарейка, как мы помним, это
устройство, преобразующее химическую энергию в электрическую. Он делает это химически
отделяя электрические заряды, посылая отрицательные заряды к одному концу
батарея называется отрицательной клеммой. И это оставляет обилие
положительные заряды на другой клемме.
Теперь, когда мы говорим о батарее,
иногда этот термин относится к отдельной единице, или к отдельной ячейке, подобной этой, или к другому
раз это может относиться к нескольким ячейкам, расположенным встык. Для простоты будем ссылаться
к этому единственному блоку в качестве батареи. И мы хотим определить правильный
описание ЭДС этой батареи. Батарейка, как мы помним, это
устройство, преобразующее химическую энергию в электрическую. Он делает это химически
отделяя электрические заряды, посылая отрицательные заряды к одному концу
батарея называется отрицательной клеммой. И это оставляет обилие
положительные заряды на другой клемме.
Мы видим, что эта батарея, как
то есть не является частью электрической цепи. Это означает, что нет заряда
течет через аккумулятор. В этих условиях, если бы мы
для измерения электрического потенциала на положительном конце батареи, положительный
терминале, а также произвести измерение электрического потенциала на отрицательном
Терминал.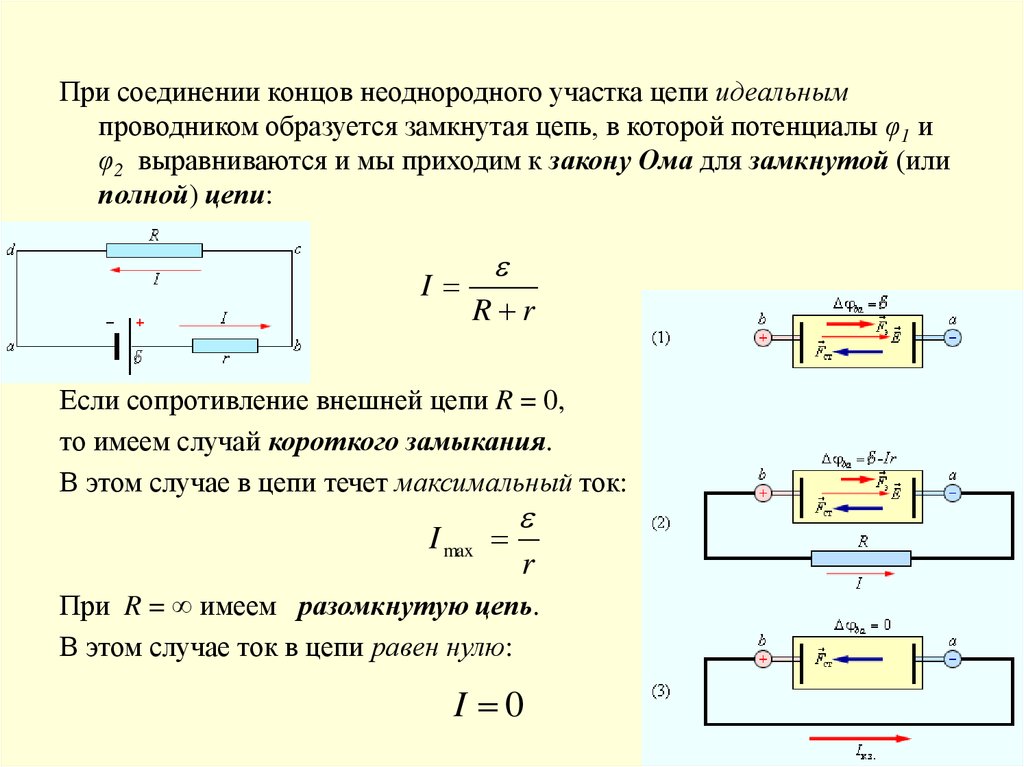 Мы могли бы назвать потенциал в
положительная клемма 𝑉 саб плюс и потенциал на отрицательной клемме 𝑉 саб
минус. Тогда ЭДС нашей батареи равна
равно величине разности этих двух потенциалов. Другими словами, ЭДС представляет собой потенциал
разница. Просматривая наши варианты ответов,
мы видим, что это совпадает с вариантом (D). Но давайте посмотрим на другой
варианты ответов, чтобы понять, почему они неверны.
Мы могли бы назвать потенциал в
положительная клемма 𝑉 саб плюс и потенциал на отрицательной клемме 𝑉 саб
минус. Тогда ЭДС нашей батареи равна
равно величине разности этих двух потенциалов. Другими словами, ЭДС представляет собой потенциал
разница. Просматривая наши варианты ответов,
мы видим, что это совпадает с вариантом (D). Но давайте посмотрим на другой
варианты ответов, чтобы понять, почему они неверны.
Вариант (А) говорит о том, что ЭДС
Батарея – это напряжение, которое она прикладывает к цепи, к которой она подключена.
связано. Итак, возвращаясь к нашей батарее,
скажем, что мы соединили его так, что теперь он является частью электрической цепи, такой как
это. Вариант (А) говорит о том, что
ЭДС батареи — это напряжение, которое она прикладывает к цепи, к которой она подключена.
связано. Другими словами, это потенциал
разницу, создаваемую батареей в этой внешней части цепи, мы могли бы
назови это. Проблема с этим определением заключается в том,
он игнорирует тот факт, что сама батарея может иметь внутреннее сопротивление. Мы часто представляем это внутреннее
сопротивление со строчной 𝑟. И это внутреннее сопротивление,
в сочетании с током внутри батареи уменьшает ЭДС так, что напряжение
батарея распространяется на остальную часть цепи на самом деле меньше, чем
э.д.с.
Другими словами, это потенциал
разницу, создаваемую батареей в этой внешней части цепи, мы могли бы
назови это. Проблема с этим определением заключается в том,
он игнорирует тот факт, что сама батарея может иметь внутреннее сопротивление. Мы часто представляем это внутреннее
сопротивление со строчной 𝑟. И это внутреннее сопротивление,
в сочетании с током внутри батареи уменьшает ЭДС так, что напряжение
батарея распространяется на остальную часть цепи на самом деле меньше, чем
э.д.с.
Если ток в этой цепи
равен капиталу 𝐼, то этот ток, умноженный на внутреннее сопротивление 𝑟, должен
быть добавлено к напряжению, которое мы обычно называем 𝑉, чтобы добавить к ЭДС
созданный батареей. Вариант ответа (А) описывает
напряжение, которое прикладывается к остальной части цепи, к которой подключен аккумулятор.
связано.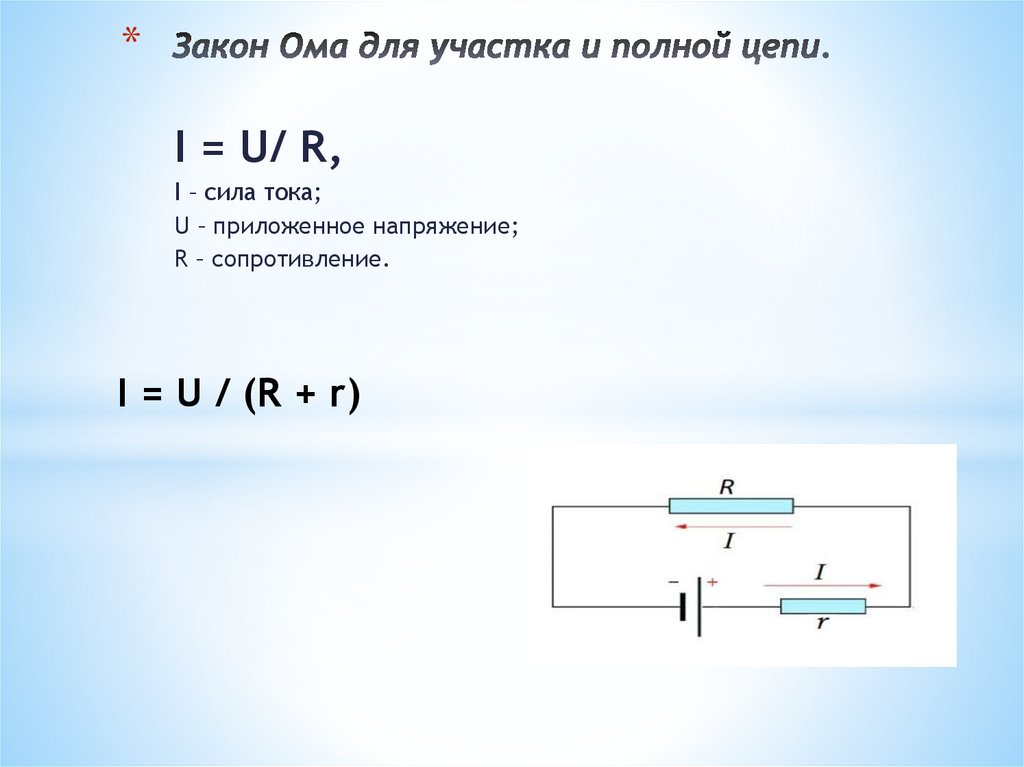 Это напряжение представлено этим
заглавная 𝑉 здесь. И мы видим, что это
отличается от э.д.с. Единственный способ, которым 𝑉 будет равен
ЭДС, если бы внутреннее сопротивление нашей батареи было равно нулю. Хотя практически это
это не так. И поэтому вариант ответа (А)
не будет нашим выбором.
Это напряжение представлено этим
заглавная 𝑉 здесь. И мы видим, что это
отличается от э.д.с. Единственный способ, которым 𝑉 будет равен
ЭДС, если бы внутреннее сопротивление нашей батареи было равно нулю. Хотя практически это
это не так. И поэтому вариант ответа (А)
не будет нашим выбором.
Переходим к варианту ответа (B),
это говорит о том, что ЭДС батареи — это напряжение, необходимое для преодоления ее внутренней
сопротивление. Ну, это правда, что ЭДС
напряжение, что может показаться удивительным, учитывая, что его название — сила. Но оглядываясь назад на наше уравнение
для ЭДС мы могли бы сказать, что напряжение, необходимое для преодоления внутренней
сопротивление равно 𝐼 умноженному на строчную букву 𝑟, это значение внутреннего сопротивления. Однако мы видим, что это не
вся история, когда дело доходит до ЭДС.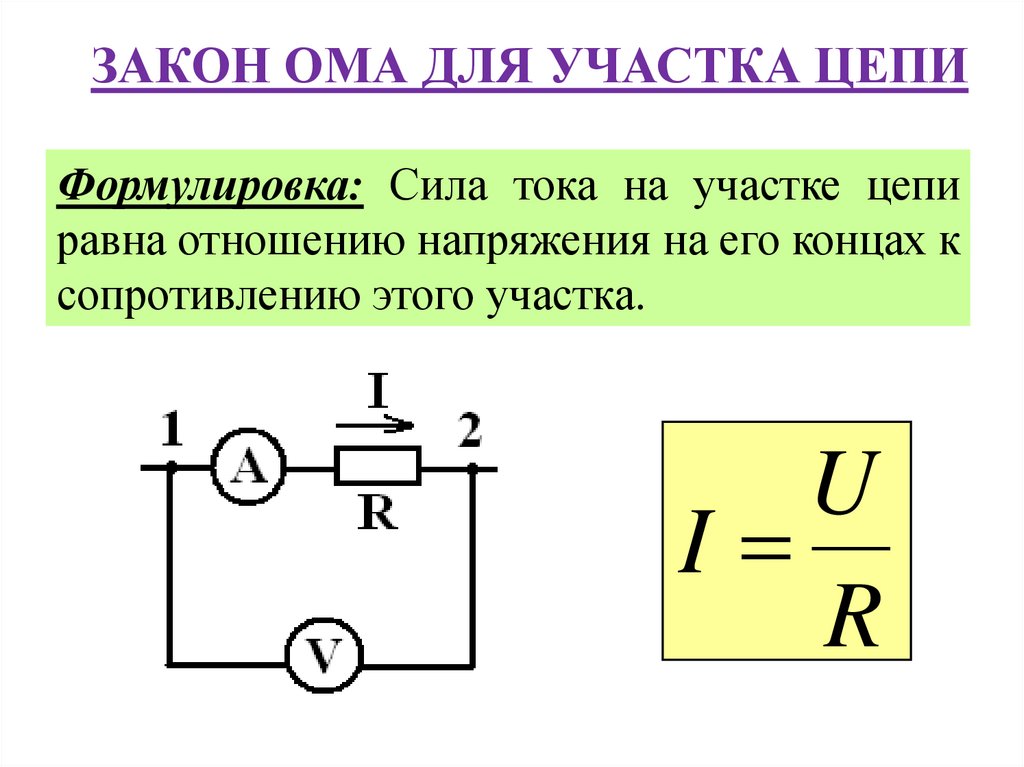 ЭДС также включает в себя напряжение, подаваемое на
остальная часть цепи. Когда мы рассматриваем только один из этих
два термина в нашем описании ЭДС, это описание является неполным. Мы не выберем вариант (Б)
либо.
ЭДС также включает в себя напряжение, подаваемое на
остальная часть цепи. Когда мы рассматриваем только один из этих
два термина в нашем описании ЭДС, это описание является неполным. Мы не выберем вариант (Б)
либо.
Вариант (С) сообщает нам, что ЭДС батарея — это ток внутри батареи. Но мы уже видели, что ЭДС напряжение, поэтому называть его током также не может быть правильным описанием. По этой причине мы не будем выбирать вариант (С). Это подтверждает наш выбор варианта (D), что ЭДС батареи представляет собой разность потенциалов на ее клеммах, когда он не производит никакого тока. И это согласуется с нашим уравнением для ЭДС, потому что если мы установим ток 𝐼 равным нулю, то ЭДС будет равна 𝑉.
Давайте на минутку
обобщить то, что мы узнали об электродвижущей силе и внутреннем сопротивлении. Начиная, мы видели, что когда
батарея подключена к электрической цепи, она создает ток в этой цепи, и
также то, что батареи обладают некоторым внутренним сопротивлением, называемым с помощью
строчная 𝑟. Более того, мы видели, что потенциал
разница между аккумулятором, когда через него не протекает заряд, называется его
электродвижущая сила. Это также известно как его ЭДС, и
это представлено символически с помощью буквы 𝜀.
Более того, мы видели, что потенциал
разница между аккумулятором, когда через него не протекает заряд, называется его
электродвижущая сила. Это также известно как его ЭДС, и
это представлено символически с помощью буквы 𝜀.
Если у нас есть сценарий, в котором батарея подключена к цепи и по цепи течет заряд, то ЭДС батареи равна 𝑉, разность потенциалов на остальных цепи вне батареи плюс ток в цепи, умноженный на внутреннее сопротивление батареи.
Далее мы увидели, что если мы сможем
представить 𝑉 как произведение тока в цепи на внешнее сопротивление
цепи, то есть ее сопротивление вне батареи. Тогда мы можем переписать это уравнение
для ЭДС следующим образом: ток в цепи 𝐼 умножить на величину, внешний
сопротивление в цепи плюс внутреннее сопротивление. И здесь внешнее и внутреннее
см.



 696, Единица СИ: 1 ампер или ампер (А) = 1 Кл/с.
696, Единица СИ: 1 ампер или ампер (А) = 1 Кл/с. е. V A B.
е. V A B. Электрический потенциал уменьшается при перемещении через резистор в направлении
тока, т. е. V C > V D . (См. начало стр. 712.)
Электрический потенциал уменьшается при перемещении через резистор в направлении
тока, т. е. V C > V D . (См. начало стр. 712.)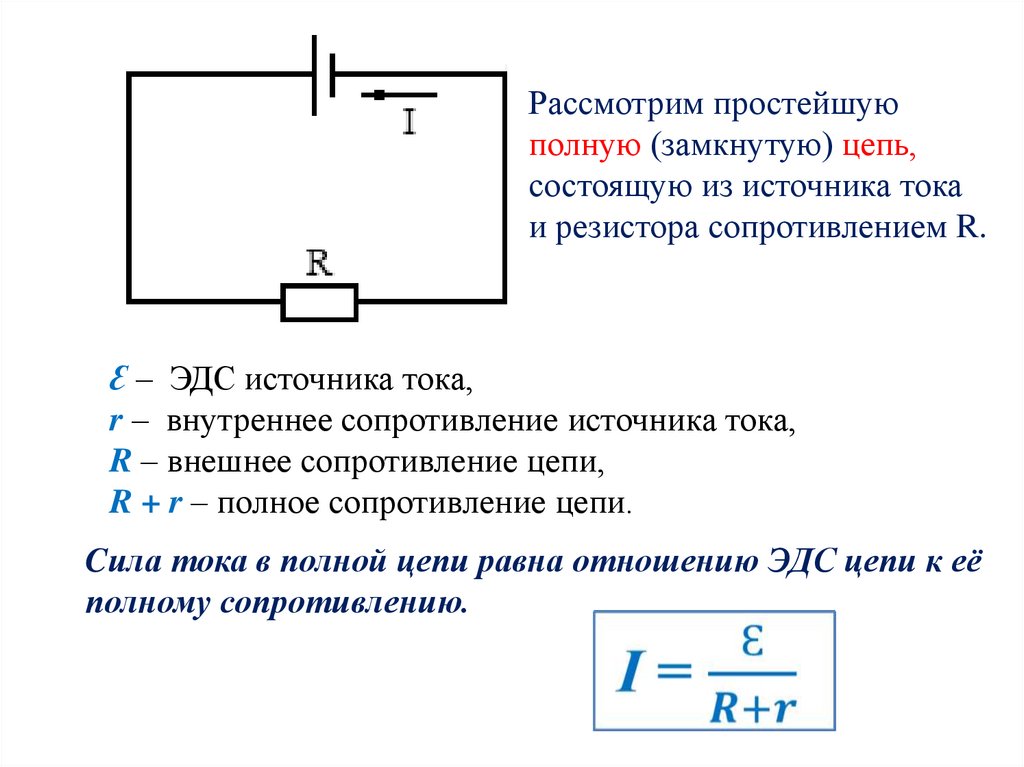


 717, на рис. 21-19 показана RC-цепь.
На рис. 21-20 показана зависимость заряда от времени.
717, на рис. 21-19 показана RC-цепь.
На рис. 21-20 показана зависимость заряда от времени. Идеальный амперметр имеет внутреннюю
сопротивление равно нулю. стр. 720, рис. 21-23.
Идеальный амперметр имеет внутреннюю
сопротивление равно нулю. стр. 720, рис. 21-23.