3.Закон Ома для участка цепи, не содержащего эдс:
I = U/R . (1.4)
Рассмотрим участок цепи с ЭДС (Error: Reference source not found).
Рис.1.5. Линейный участок цепи, содержащий ЭДС
Из состава сложной электрической цепи выделим ветвь, содержащую источник энергии и потребитель. Для определенности примем, что направления тока и источника ЭДС совпадают. При условно выбранных положительных направлениях тока и ЭДС в ветви имеем:
1 > a 1 – a = IR, 0(1.5)
2 > a 2 – a =
0(1.6)Вычтем из уравнения ( 1 .5) уравнение ( 1 .6) и тогда получим:
1 – 2 = IR – E = U12;
. 0(1.7)
Полученное выражение представляет собой закон Ома для участка цепи с ЭДС. В случае несовпадения направления тока в ветви с направлениями напряжения и ЭДС перед ними появляется знак «минус».
Первый закон Кирхгофа алгебраическая сумма токов в узле равна нулю:
. 0(1.8)
Второй закон Кирхгофа алгебраическая сумма падений напряжений вдоль замкнутого контура равна алгебраической сумме ЭДС, действующих в этом контуре:
0(1.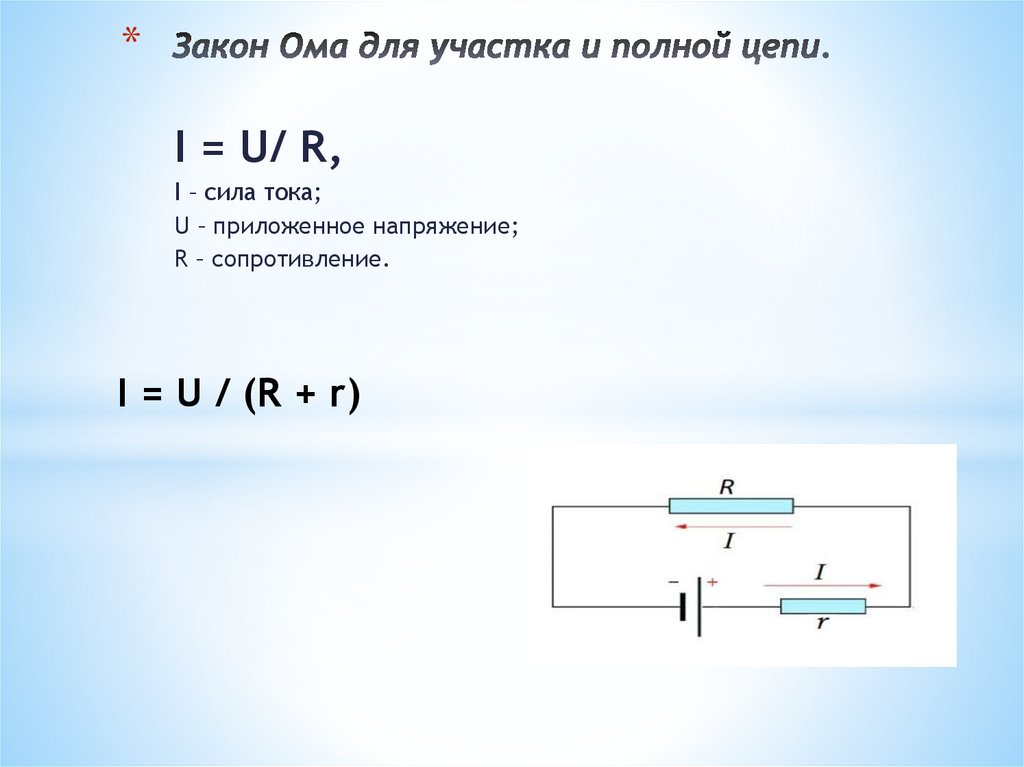
9)
Второй закон Кирхгофа работает как для замкнутого, так и для разомкнутого контура.
Уравнение баланса мощности:
0 (1.10)
В левой части этого уравнения стоит арифметическая сумма мощностей, которые выделяются на сопротивлениях от токов, которые по ним протекают. В правой части – мощность, отданная источниками в сеть.
При этом возможна такая ситуация, когда одно из слагаемых суммы справа может оказаться отрицательным. Это будет означать, что в данной ситуации источник становится потребителем. Она возникает в случае, когда ток, протекающий по источнику, направлен встречно направлению ЭДС.
Закон
Джоуля — Ленца — физический
закон,
дающий количественную
оценку теплового действия электрического
тока.
Установлен в 1841
году Джеймсом
Джоулем и
независимо от него в 1842
году Эмилием
Ленцом[1].
В словесной формулировке звучит следующим образом[2]
Мощность тепла, выделяемого в единице объёма среды при протекании электрического тока, пропорциональна произведению плотности электрического тока на величину электрического поля
Математически может быть выражен в следующей форме:
где — мощность выделения тепла в единице объёма, — плотность электрического тока, — напряжённость электрического поля,
Закон также может быть сформулирован в интегральной форме для случая протекания токов в тонких проводах[3]:
Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке исопротивлению участка
В математической форме этот закон имеет вид
где dQ — количество теплоты, выделяемое за промежуток времени dt, I — сила тока, R — сопротивление, Q — полное количество теплоты, выделенное за промежуток времени от t1 до
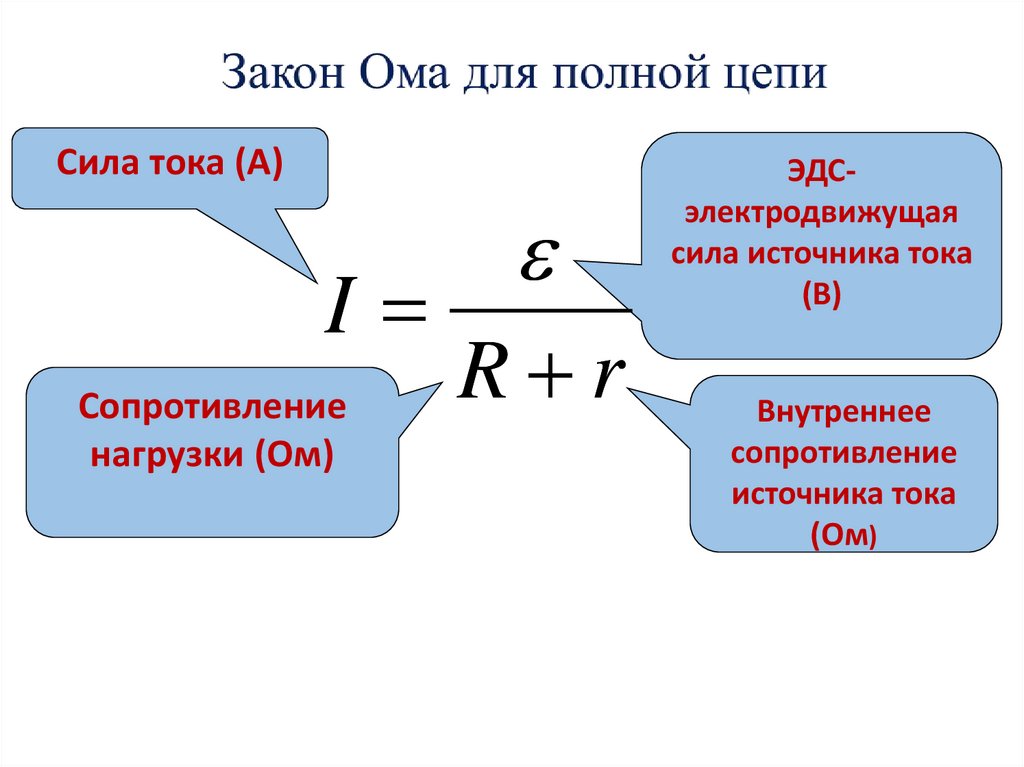В случае постоянных силы тока и
сопротивления:4.
5.
6. Последовательное и параллельное соединения в электротехнике — два основных способа соединения элементов электрической цепи. При последовательном соединении все элементы связаны друг с другом так, что включающий их участок цепи не имеет ни одного узла. При параллельном соединении все входящие в цепь элементы объединены двумя узлами и не имеют связей с другими узлами, если это не противоречит условию.
При последовательном соединении проводников сила тока во всех проводниках одинакова.
При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов. При этом величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Закон Ома для участка цепи с источником ЭДС. (Лекция N 5)
Возьмем два участка цепи a—bи c—d (см.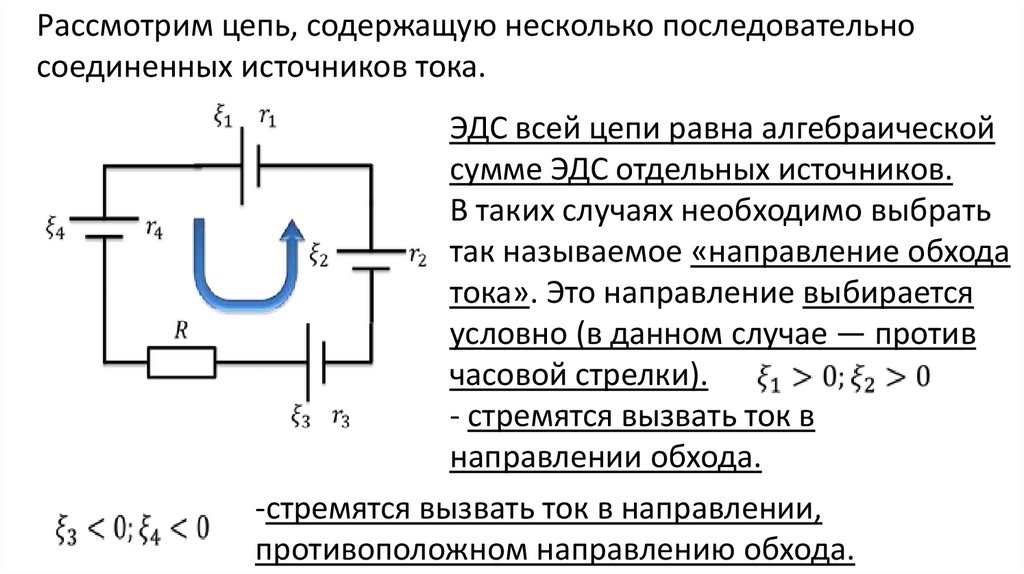
рис. 1) и составим для них уравнения в комплексной форме с учетом указанных на
рис. 1 положительных направлений напряжений
и токов.
Объединяя оба случая, получим
| (1) |
или для постоянного тока
| . | (2) |
Формулы (1) и (2) являются аналитическим выражением закона Ома для участка
цепи с источником ЭДС, согласно которому ток на участке цепи с источником
ЭДС равен алгебраической сумме напряжения на зажимах участка цепи и ЭДС, деленной
на сопротивление участка. В случае переменного тока все указанные величины суть
комплексы. При этом ЭДС и напряжение берут со знаком “+”, если их направление
совпадает с выбранным направлением тока, и со знаком “-”, если их направление
противоположно направлению тока.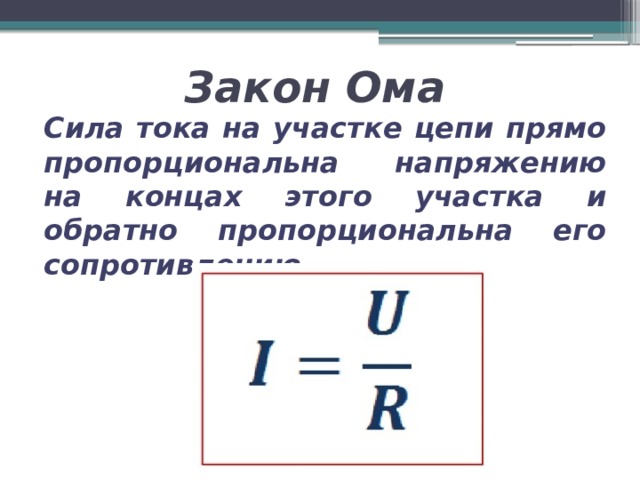
Основы символического метода расчета цепей
синусоидального тока
Расчет цепей переменного синусоидального тока может производиться не только путем построения векторных диаграмм, но и аналитически – путем операций с комплексами, символически изображающими
Символический метод расчета цепей синусоидального тока основан на законах Кирхгофа и законе Ома в комплексной форме.
Уравнения, выражающие законы Кирхгофа в комплексной форме, имеют совершенно такой же вид, как и соответствующие уравнения для цепей постоянного тока. Только токи, ЭДС, напряжения и сопротивления входят в уравнение в виде комплексных величин.
1.
| . | (3) |
2. Второй закон Кирхгофа в комплексной форме:
| (4) |
или применительно к схемам замещения с источниками ЭДС
| . | (5) |
3. Соответственно матричная запись законов Кирхгофа в комплексной форме имеет вид:
§ первый закон Кирхгофа:
| . ; | (6) |
§ второй закон Кирхгофа
. |
(7) |
Пример.
Дано:
Рис. 2
| Определить:
2) токи |
Решение:
1. .
2. .
3.
.
4. Принимая начальную фазу напряжения за нуль, запишем:
.
Тогда
.
5. Поскольку ток распределяется обратно пропорционально сопротивлению ветвей (это вытекает из закона Ома), то
6. .
7. Аналогичный результат можно получить, составив для данной схемы уравнения по законам Кирхгофа в комплексной форме
или после подстановки численных значений параметров схемы
Специальные методы расчета
Режим работы любой цепи полностью характеризуется уравнениями, составленными
на основании законов Кирхгофа.
При этом необходимо составить и решить систему
с n неизвестными, что может оказаться
весьма трудоемкой задачей при большом числе n ветвей схемы. Однако, число уравнений, подлежащих решению, может
быть сокращено, если воспользоваться специальными методами расчета, к
которым относятся методы контурных токов и узловых потенциалов.
Метод контурных токов
Идея метода контурных токов: уравнения составляются только по второму закону
Кирхгофа, но не для действительных, а для воображаемых токов, циркулирующих
по замкнутым контурам, т.е. в случае выбора главных контуров равных токам ветвей
связи. Число уравнений равно числу независимых контуров, т.е. числу ветвей связи
графа . Первый закон Кирхгофа выполняется автоматически.
Контуры можно выбирать произвольно, лишь бы их число было равно и чтобы каждый новый контур содержал хотя
бы одну ветвь, не входящую в предыдущие.
Такие контуры называются независимыми.
Их выбор облегчает использование топологических понятий дерева и ветвей связи.
Направления истинных и контурных токов выбираются произвольно. Выбор положительных направлений перед началом расчета может не определять действительные направления токов в цепи. Если в результате расчета какой-либо из токов, как и при использовании уравнений по законам Кирхгофа, получится со знаком “-”, это означает, что его истинное направление противоположно.
Пусть имеем схему по рис. 3.
Выразим токи ветвей через контурные токи:
;
; ;
; .
Обойдя контур aeda, по второму закону Кирхгофа имеем
.
Поскольку ,
то
.
Таким образом, получили уравнение для первого контура относительно контурных токов. Аналогично можно составить уравнения для второго, третьего и четвертого контуров:
совместно с первым решить их относительно контурных токов и затем по уравнениям,
связывающим контурные токи и токи ветвей, найти последние.
Однако данная система уравнений может быть составлена формальным путем:
При составлении уравнений необходимо помнить следующее:
— сумма сопротивлений, входящих в i-й контур;
— сумма сопротивлений, общих для i-го и k-го контуров, причем ;
члены на главной диагонали всегда пишутся со знаком “+”;
знак “+” перед остальными членами ставится в случае, если через общее сопротивление i-й и k- й контурные токи проходят в одном направлении, в противном случае ставится знак “-”;
если i-й и k- й контуры не имеют общих сопротивлений, то ;
в правой части уравнений записывается алгебраическая сумма ЭДС, входящих в контур: со знаком “+”, если направление ЭДС совпадает с выбранным направлением контурного тока, и “-”, если не совпадает.
В нашем случае, для первого уравнения системы, имеем:
Следует обратить внимание на то, что, поскольку , коэффициенты контурных уравнений всегда
симметричны относительно главной диагонали.
Если в цепи содержатся помимо источников ЭДС источники тока, то они учитываются в левых частях уравнений как известные контурные токи: k- й контурный ток, проходящий через ветвь с k- м источником тока равен этому току .
Метод узловых потенциалов
Данный метод вытекает из первого закона Кирхгофа. В качестве неизвестных принимаются потенциалы узлов, по найденным значениям которых с помощью закона Ома для участка цепи с источником ЭДС затем находят токи в ветвях. Поскольку потенциал – величина относительная, потенциал одного из узлов (любого) принимается равным нулю. Таким образом, число неизвестных потенциалов, а следовательно, и число уравнений равно , т.е. числу ветвей дерева .
Пусть имеем схему по рис. 4, в которой примем .
Допустим, что и известны. Тогда значения токов на основании закона Ома для участка цепи с источником ЭДС
Запишем уравнение по первому закону Кирхгофа для узла а:
и подставим значения входящих в него токов, определенных выше:
.
Сгруппировав соответствующие члены, получим:
.
Аналогично можно записать для узла b:
.
Как и по методу контурных токов, система уравнений по методу узловых потенциалов может быть составлена формальным путем. При этом необходимо руководствоваться следующими правилами:
1. В левой части i-го уравнения записывается со знаком “+”потенциал i-го узла, для которого составляется данное i-е уравнение, умноженный на сумму проводимостей ветвей, присоединенных к данному i-му узлу, и со знаком “-”потенциал соседних узлов, каждый из которых умножен на сумму проводимостей ветвей, присоединенных к i-му и k-му узлам.
Из сказанного следует, что все члены , стоящие на главной диагонали в левой части
системы уравнений, записываются со знаком “+”, а все остальные – со знаком “-”,
причем .
Последнее равенство по аналогии с методом
контурных токов обеспечивает симметрию коэффициентов уравнений относительно
главной диагонали.
2. В правой части i-го уравнения записывается так называемый узловой ток , равный сумме произведений ЭДС ветвей, подходящих к i-му узлу, и проводимостей этих ветвей. При этом член суммы записывается со знаком “+”, если соответствующая ЭДС направлена к i-му узлу, в противном случае ставится знак “-”. Если в подходящих к i-му узлу ветвях содержатся источники тока, то знаки токов источников токов, входящих в узловой ток простыми слагаемыми, определяются аналогично.
В заключение отметим,
что выбор того или иного из рассмотренных методов определяется тем, что следует
найти, а также тем, какой из них обеспечивает меньший порядок системы уравнений.
При расчете токов при одинаковом числе уравнений предпочтительнее использовать
метод контурных токов, так как он не требует дополнительных вычислений с использованием
закона Ома.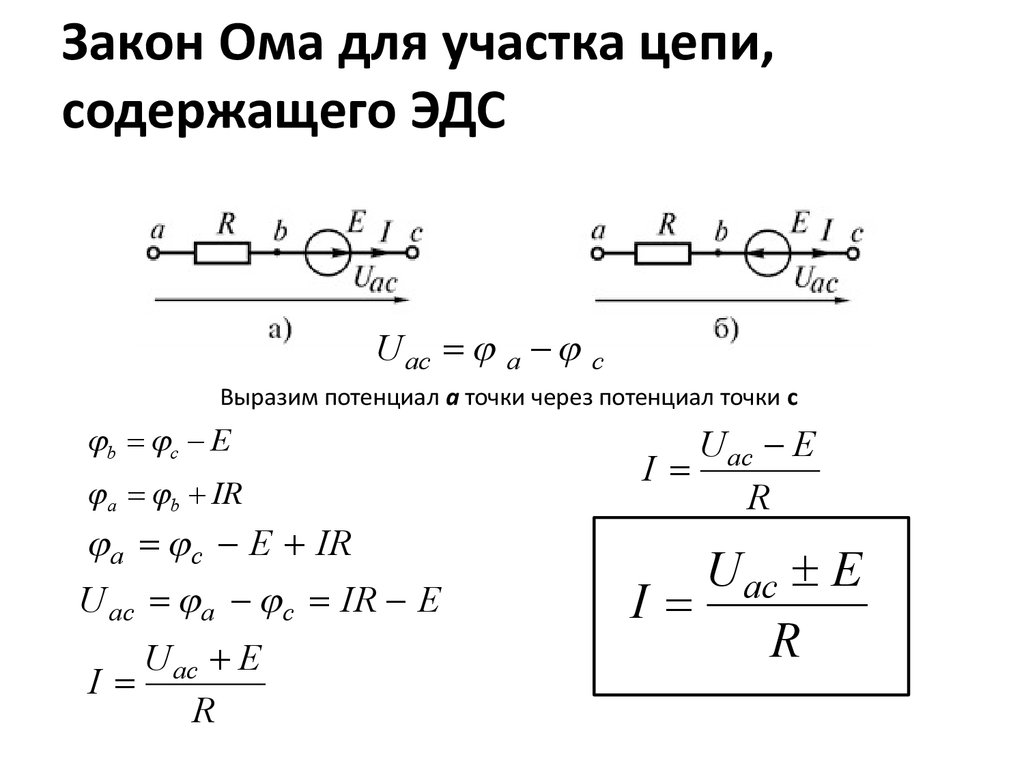
Метод узловых потенциалов очень удобен при расчетах многофазных
цепей, но не удобен при расчете цепей со взаимной индуктивностью.
Литература
1. Основы теории цепей: Учеб.для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
2. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с
.
Контрольные вопросы и задачи
1. В ветви на рис. 1 . Определить ток .
Ответ: .
2. В чем заключается сущность символического метода расчета цепей синусоидального тока?
3. В чем состоит сущность метода контурных токов?
4.
В
чем состоит сущность метода узловых потенциалов?
5. В цепи на рис. 5 ; ;
; . Методом контурных токов определить комплексы действующих значений токов ветвей.
Ответ: ; ; .
6. В цепи на рис. 6 . Рассчитать токи в ветвях, используя метод узловых потенциалов.
Ответ: ; ; ; ; ; ; .
электромагнетизм — Закон Ома и индуцированные поля
спросил
Изменено 2 года, 7 месяцев назад
Просмотрено 139 раз
$\begingroup$
Рассмотрим простую схему: батарея и резистор, где резистор подключен между точками A и B.
Тогда мы имеем: 9{b}-\vec{E}.\vec{dl}= iR$$
Будет ли иметь место то же выражение, если $\vec{E}$ является «индуцированным электрическим полем»? Например, рассмотрим стационарную петлю , содержащую резистор, охватывающий область A, и изменяющееся магнитное поле через область. Допустимо ли выражение $i=A/R*(dB/dt)$?
- электромагнетизм
- электрические цепи
- электрический ток
- электрическое сопротивление
- уравнения Максвелла
$\endgroup$ 9b{-\vec{E}·d\vec{\ell}}=iR$$ не всегда действительно, особенно когда электродвижущая сила (ЭДС) вдоль цепи движущая .
Рассмотрим следующую схему, в которой резистивный стержень скользит со скоростью $\vec{v}$ в постоянном однородном магнитном поле $\vec{B}$. Все остальные провода в идеале (сопротивления нет). В этом случае отсутствует электрическое поле , управляющее током. Магнитный поток через контур меняется, поэтому вдоль контура индуцируется (движущая) ЭДС, и через $R$ протекает некоторый ток $i$.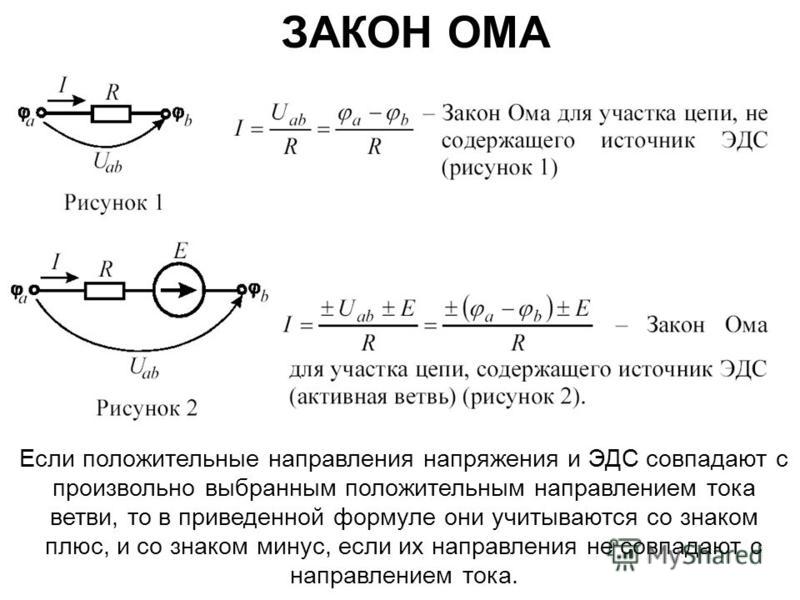
b{-\vec{f}_{mag}·d\vec{\ell}}=iR,$$
где $\vec{f}_{mag}$ — сила, приложенная к единице заряда магнитным полем, т. е. $\vec{f}_{mag}=\vec{v}’\times\vec{B }$, где $\vec{v}’$ — скорость заряда. Это дает
$$BvL=iR$$
где $L$ — длина стержня.
Короче говоря, закон Ома на самом деле утверждает $\mathcal{E}=Ri$, где $\mathcal{E}$ — ЭДС вдоль резистора.
Чтобы ответить на ваш второй вопрос: да, $i=A\frac{dB}{dt}/R$ по-прежнему действует (при условии, что $\frac{dB}{dt}$ постоянна или собственная индуктивность цепь незначительна). Это потому, что $\mathcal{E} = A\frac{dB}{dt}$.
$\endgroup$
2
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
|
| |||||||||||||||||||||||||||||||
Он дал свое имя. единица измерения электродвижущей силы — ВОЛЬТ.
Ампер, француз, измерил текущий дефект и дал ему свое имя. измерительный блок
тока — АМПЕР. Немец по имени Ом измерил сопротивление электрических цепей.
и проводников и дал свое имя единице измерения сопротивления — ОМ. Ом
делал больше, чем экспериментировал с сопротивлением — он связывал свои открытия с
у Вольты и Ампера. В результате получился ЗАКОН ОМА. Убедитесь, что вы понимаете каждый
одна из трех величин в электричестве — они составляют Закон Ома. На следующем
страница представляет собой таблицу этих важных величин, их символов, их единиц, их
аббревиатуры и их влияние на схему.
или усил.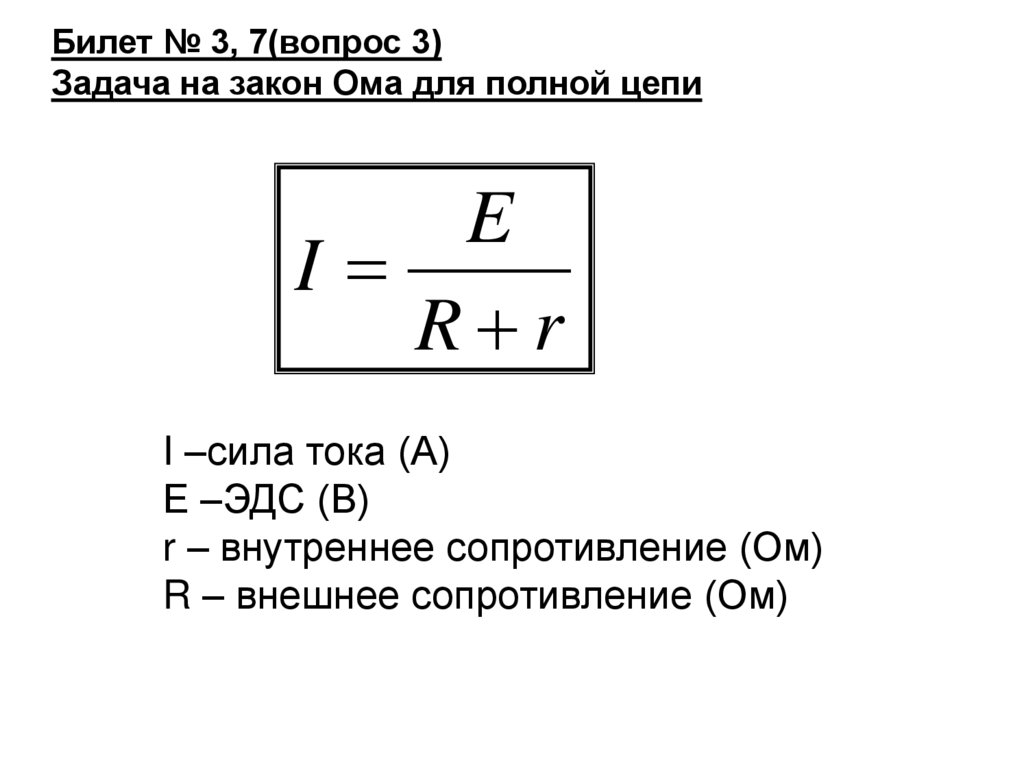
31. — Простая схема, постоянное напряжение.
ЕСЛИ
ВЫ ПОДДЕРЖИВАЕТЕ СОПРОТИВЛЕНИЕ ПОСТОЯННЫМ И УМЕНЬШАЕТЕ НАПРЯЖЕНИЕ, ТОК УМЕНЬШАЕТСЯ
ПРОПОРЦИОНАЛЬНО. ПОНИЖЕНИЕ НАПРЯЖЕНИЯ. 
Закон Ома расскажет вам, как
течет большой ток. 
