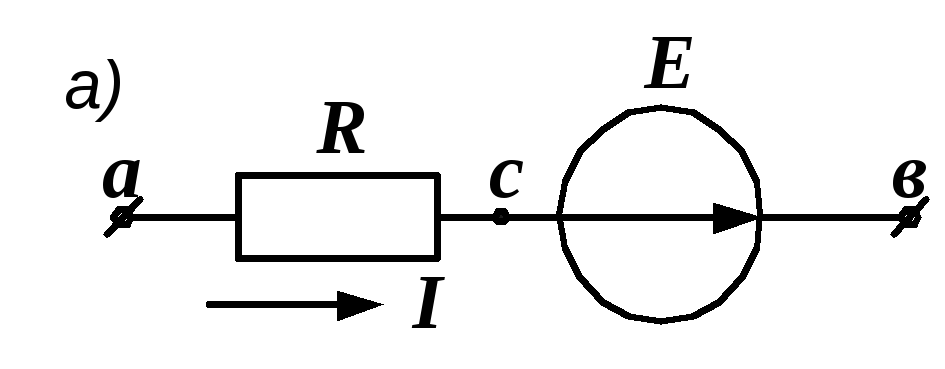
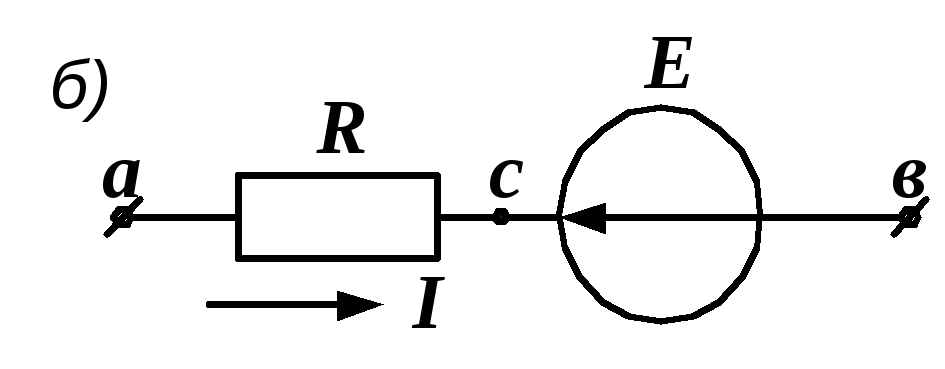
Закон Ома для участка цепи с Э.Д.С

Возьмем два участка цепи a—b  и c—d (см. рис.  1) и составим для них уравнения в комплексной форме с учетом указанных на рис. 1 положительных направлений напряжений и токов.

                 

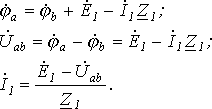
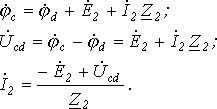
Объединяя оба случая, получим

(1)

или для постоянного тока

.

(2)

 

Формулы (1) и (2) являются аналитическим выражением закона Ома для участка цепи с источником ЭДС, согласно которому ток на участке цепи с источником ЭДС равен алгебраической сумме напряжения на зажимах участка цепи и ЭДС, деленной на сопротивление участка. В случае переменного тока все указанные величины суть комплексы. При этом ЭДС и напряжение берут со знаком “+”, если их направление совпадает с выбранным направлением тока, и со знаком “-”, если их направление противоположно направлению тока.

Закон (правило) Ома для участка цепи, содержащего источник ЭДС, позволяет найти ток этого участка по известной разности потенциалов фи(а) – фи(с) на концах участка цепи и имеющейся на этом участке ЭДС Е.

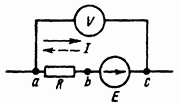
Рис. 2.7

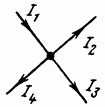
Рис. 2.8

Так, по уравнению (1.2) для схемы рис. 2.6, а

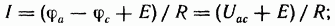
по уравнению (2.2а) для схемы рис. 2.6, б

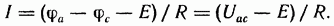
В общем случае

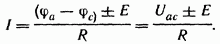
Уравнение (2.3а) математически выражает закон Ома для участка цепи, содержащего источник ЭДС; знак плюс перед Е соответствует рис. 2.6,а, знак минус — рис. 2.6, б. В частном случае при Е=0 уравнение (2.3а) переходит в уравнение (2.3).

Пример 9. К зажимам а и с схемы рис. 2.7 подключен вольтметр, имеющий очень большое, теоретически бесконечно большое сопротивление (следовательно, его подключение или отключение не влияет на режим работы цепи).

Если ток I=10A течет от точки а к точке с, то показание вольтметра U’ac=-18В; если этот ток течет от точки с к точке а, то U»ac=-20В. Определить сопротивление R и ЭДС ?.

Решение. В первом режиме  во втором U’ac=-18В=-E+IR=-E+10R, во втором U»ac=-20В=-E-IR=-E-10R. Совместное решение дает E=19В, R=0,1Ом.

 

Электротехника. Основы. Закон Ома — Всё об энергетике

Электротехника. Основы. Закон Ома

В электротехнике, как и в любой другой науке, существуют базовые понятия, без понимания которых не удастся овладеть этой областью знаний. Здесь такими понятиями являются электрическое напряжение, электрический ток и электрическое сопротивление.

Закон Ома

Закон Ома был открыт в результате экспериментов Георга Ома с гальванометром и простой электрической цепью из источника ЭДС и сопротивления. Со временем формула полученная Омом претерпела несколько изменений.

Закон Ома для участка цепи без ЭДС

Может быть сформулирован через сопротивление [1, стр.33][2, стр.15]:

\begin{equation} I = {U_{ab}\over R}; \end{equation}

Где:

• I — ток через участок ab электрической цепи;
• U_ab — напряжение на участке ab электрической цепи;
• R — сопротивление участка ab электрической цепи.

Или через проводимость:

\begin{equation} I = U_{ab} × G; \end{equation}

Где:

• G — проводимость участка ab электрической цепи.

Формула (1, 2) справедлива для электрической цепи представленной ниже на рисунке 1.

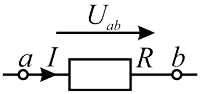
Рисунок 1 — Участок цепи без ЭДС

Закон Ома для участка цепи содержащего ЭДС

Или обобщённый закон Ома. Формулируется следующим образом [1, стр.34][2, стр.17]:

\begin{equation} I = {U_{ab} + E\over R}; \end{equation}

Где:

• I — ток через участок ac электрической цепи;
• U_ab — напряжение на участке
  ab электрической цепи;
• E — ЭДС на участке bс электрической цепи;
• R — сопротивление участка ab электрической цепи.

Или через проводимость:

\begin{equation} I = {(U_{ab} + E) × G}; \end{equation}

Где:

• G — проводимость участка ab электрической цепи.

Формула (3, 4) справедлива для электрической цепи представленной ниже на рисунке 2.

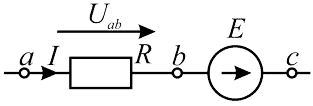
Рисунок 2 — Участок цепи содержащий ЭДС

Закон Ома для полной цепи

Закон формулируется следующим образом [1, стр.34][2, стр.17]:

\begin{equation} I = {E\over {R + r}}; \end{equation}

Где:

• I — ток в электрической цепи;
• E — ЭДС электрической цепи;
• R — сопротивление электрической цепи;
• r — внутреннее сопротивление источника ЭДС.

Формулировка выражения (5) через проводимость неудобна и здесь приведена не будет. Ниже на рисунке 3 изображена схема электрической цепи для которой справедливо выражение (5).

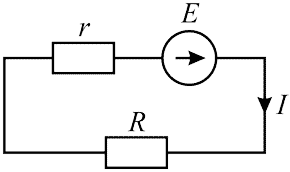
Рисунок 3 — Полная цепь

На схеме видно, что R и r соединены последовательно, а в формуле это отражено как сумма R

(сопротивления цепи) и r (внутреннего сопротивления источника ЭДС). Заменим выражение R + r на R_п

\begin{equation} I = {E\over R_п}; \end{equation}

Где:

• R_п — полное сопротивление электрической цепи (включая сопротивление источника ЭДС).

Закон Ома в дифференциальной форме

Закон Ома в дифференциальной форме, представленный в выражении (7), справедлив для неоднородного, но изотропного вещества [3].

\begin{equation} \vec E = {ρ × \vec\jmath}; \end{equation}

Где:

• \(\vec\jmath\) — плотность тока;
• ρ — удельное сопротивление;
• \(\vec E\) — напряжённость электрического поля.

Примеры применения

Ниже приведены несколько примеров для демонстрации применения разных формулировок закона Ома.

Пример 1

Схема задания приведена на рисунке 4. На схеме R = 5,2 Ом, U = 26 В. Определить I.

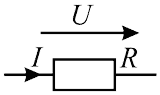
Рисунок 4 — Схема к 1 и 2-му примеру

Для решения задания воспользуемся выражением (1):

\begin{equation} I = {U\over R} = {26\over 5,2} = {5 \ А;} \end{equation}

Пример 2

Схема задания приведена на рисунке 4. К данному участку цепи приложено напряжение 24 В и по нему протекает ток 1,5 А. Определить проводимость участка цепи.

Для решения задания преобразуем выражение (2) относительно

G:

\begin{equation} I = {U × G} \ \Rightarrow \ G = {I\over U} = {1,5\over 24} = {0,0625 \ См;} \end{equation}

Пример 3

Схема задания приведена на рисунке 5. На схеме U = 220 В, I = 0,5 А, R = 140 Ом. Определить E.

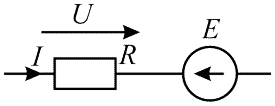
Рисунок 5 — Схема к 3-му примеру

Для решения задания преобразуем выражение (3) относительно E:

\begin{equation} I = {U — E\over R} \ \Rightarrow \ {I × R} = {U — E} \ \Rightarrow \ E = {U — I × R}; \end{equation}

Подставим в выражение (10) известные величины:

\begin{equation} E = {U — I × R} = {220 — 0,5 × 140} = {150 \ В;} \end{equation}

Пример 4

Сопротивление электрической цепи, приведенной на рисунке 3 составляет 12 Ом, напряжение источника ЭДС включенного в цепь — 9 В. Измерения показали, что по цепи протекает ток 0,72 А. Необходимо определить внутреннее сопротивление источника ЭДС.

Преобразуем выражение (5) относительно r:

\begin{equation} I = {E\over {R + r}} \ \Rightarrow \ {I × (R + r)} = E \ \Rightarrow \ {I × r} = {E — I × R} \ \Rightarrow \ r = {E — I × R\over I}; \end{equation}

Определим внутренней сопротивление источника ЭДС, подставив в выражение (10) известные величины:

\begin{equation} r = {E — I × R\over I} = {9 — 0,72 × 12\over 0,72} = {0,36\over 0,72} = {0,5 \ Ом;} \end{equation}

Использованные термины

Электрический потенциал точки:

Физическая величина, равная потенциальной энергии, которой обладает элементарный положительный заряд, помещенный в электрическое поле.

Потенциал обозначается буквой φ греческого алфавита и измеряется в вольтах (В). Он не имеет направления и записывается как скаляр.

Электрическое напряжение:

Физическая величина, равная количеству энергии, затраченной на перенос единичного заряда из точки А в точку Б электромагнитного поля, определяемая как разность потенциалов этих точек: U_ab = φ_a — φ_b.

Напряжение обозначается буквой U (u) латинского алфавита и измеряется в вольтах (В). Напряжение — скалярная величина, но на электрических схемах указывают его положительное направление.

Электродвижущая сила (ЭДС):

Также как и напряжение это физическая величина, равная количеству энергии, затраченной на перенос единичного заряда из одной точки электромагнитного поля в другую.

ЭДС обозначается буквой E (e) латинского алфавита и измеряется в вольтах (В). ЭДС — скалярная величина, но на электрических схемах указывают её положительное направление. Она численно равна напряжению на зажимах не подключенного источника.

Электрическое ток:

Физическая величина, равная количеству заряженных частиц прошедших через поперечное сечение проводника за единицу времени. Как явление — направленное движение заряженных частиц.

Напряжение обозначается буквой I (i) латинского алфавита и измеряется в амперах (А). Ток, так же как и напряжение, величина скалярная, и на электрических схемах тоже указывают его положительное направление [2, стр.11].

Плотность тока:

Физическая величина, имеющая смысл силы электрического тока, протекающего через элемент поверхности единичной площади.

Плотность тока обозначается буквой \(\vec\jmath\) латинского алфавита и измеряется в амперах на метр квадратный (А/м²). Плотность тока — векторная величина [4].

Электрическое сопротивление:

Физическая величина, характеризующая способность проводника препятствовать прохождению по нему тока.

Сопротивление обозначается буквами R (r), X (x) или Z (z) латинского алфавита (последние два обозначения применяются для реактивного и комплексного сопротивления соответственно) и измеряется в омах (Ом). Как и предыдущие, сопротивление — скалярная величина.

Электрическая проводимость:

Физическая величина, характеризующая насколько хорошо проводник проводит электрический ток, является обратной сопротивлению: G = 1/R.

Проводимость обозначается буквами G (g) латинского алфавита и измеряется в сименсах (См). Так же как и сопротивление проводимость — скалярная величина.

Удельное сопротивление:

Физическая величина, численно равная сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 м².

Удельная проводимость обозначается буквами ρ греческого алфавита и измеряется в омах на метр (Ом×м). Является скалярной величиной. [3].

В дальнейшем при использовании вышеперечисленных терминов слово «электрический» будет упускаться.

Список использованных источников

1. Бессонов, Л.А. Теоретические основы электротехники: учебник / Л.А. Бессонов — Москва: Высшая школа, 1996. — 623 с.
2. Иванова, С.Г. Теоретические основы электротехники: Версия 1.0 [Электронный ресурс] : учеб. пособие / С. Г. Иванова, В. В. Новиков – Красноярск: ИПК СФУ, 2008. — 318 с.
3. Википедия — Удельное электрическое сопротивление [электронный ресурс] — Режим доступа: https://ru.wikipedia.org/wiki/Удельное_электрическое_сопротивление
4. Википедия — Плотность тока [электронный ресурс] — Режим доступа: https://ru.wikipedia.org/wiki/Плотность_тока

1.2. Закон Ома для участка цепи с эдс

На практике часто встречается задача, когда требуется определить ток в некоторой ветви при известных ее параметрах и потенциалах ее зажимов.

Пусть в схеме на рис. 1.8, а заданы R, E, _a, _b, и требуется определить ток.

Рис. 1.8. Варианты ветви с ЭДС

Между R и E отметим промежуточную точку с и выразим ее потенциал через потенциалы точек а и b.

Так как в резисторе ток протекает слева направо, то потенциал точки а выше потенциала точки с на величину падения напряжения в активном сопротивлении:

_a = _с + IR. (1.4)

Точка b находится на положительном полюсе источника, а с – на отрицательном. Поэтому

_b = _с + E. (1.5)

Беря разность левых и правых частей выражений (1.4) и (1.5), получим

_a – _b = IR – Е,

откуда

.

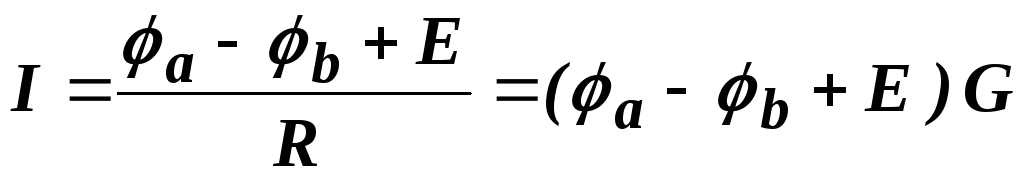Для цепи на рис. 1.8, б после аналогичных рассуждений будем иметь

I = (_a – _b – E) G.

В двух последних формулах ЭДС записывается с плюсом, если ее направление на схеме совпадает с направлением тока, и с минусом – в противоположном случае.

1.3. Расчет сложных электрических цепей постоянного тока

1.3.1. Метод уравнений Кирхгофа

Этот метод сводится к решению системы уравнений, количество которых равно числу неизвестных токов (числу ветвей). Покажем его применение на примере схемы, изображенной на рис. 1.9.

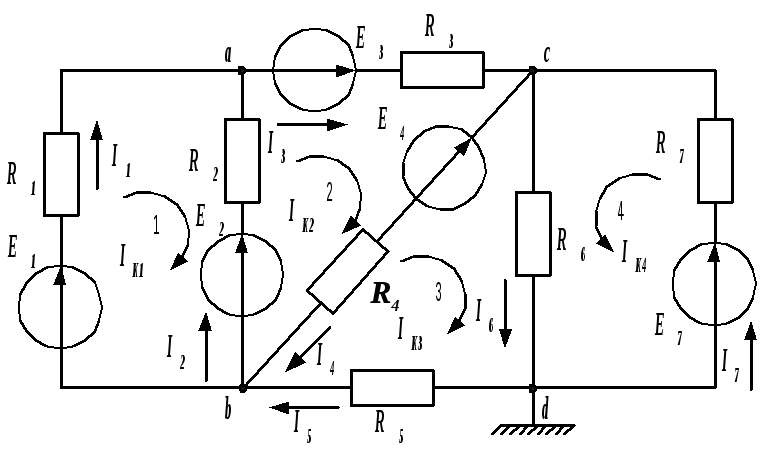
Рис. 1.9. Сложная электрическая цепь

Первый закон Кирхгофа: в узле электрической цепи алгебраическая сумма токов равна нулю.

Произвольно задавшись направлениями токов в ветвях и принимая токи, подтекающие к узлу, положительными, а оттекающие от узла – отрицательными, записываем:

узел а:

узел b:

узел с:

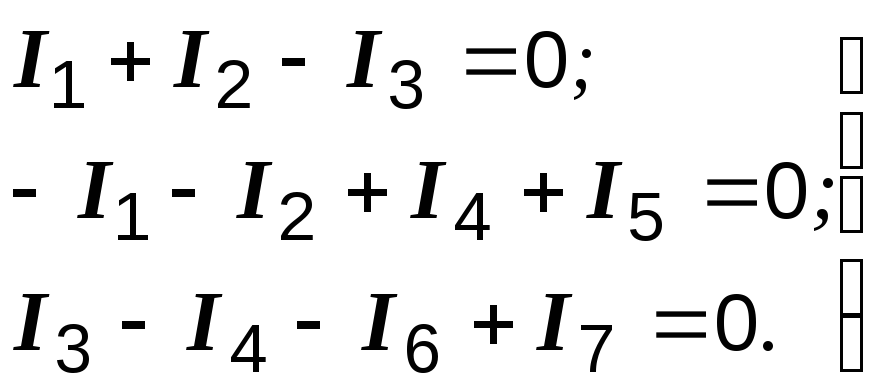(1.6)

Число независимых уравнений в первом законе Кирхгофа – на единицу меньше числа узлов, поэтому для последнего узла d уравнение не пишем.

В заданной схеме семь ветвей, семь неизвестных токов. Система (1.6) содержит только три уравнения. Недостающие четыре записываем по второму закону Кирхгофа.

Второй закон Кирхгофа: в замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на всех сопротивлениях контура.

Число уравнений, составляемых по этому закону, равно числу взаимно независимых контуров. При рассмотрении схемы каждый последующий контур является независимым относительно предыдущих, если он отличается от них хотя бы одной новой ветвью. В заданной схеме таких контуров четыре. Они отмечены пронумерованными дугообразными стрелками. Любой другой контур новых ветвей не содержит, поэтому не является независимым. Дугообразные стрелки показывают произвольно выбранные направления обхода контуров. Если направления ЭДС и токов совпадают с направлением обхода контура, то они записываются с плюсом, если не совпадают – то с минусом.

контур 1:

контур 2:

контур 3:

контур 4:

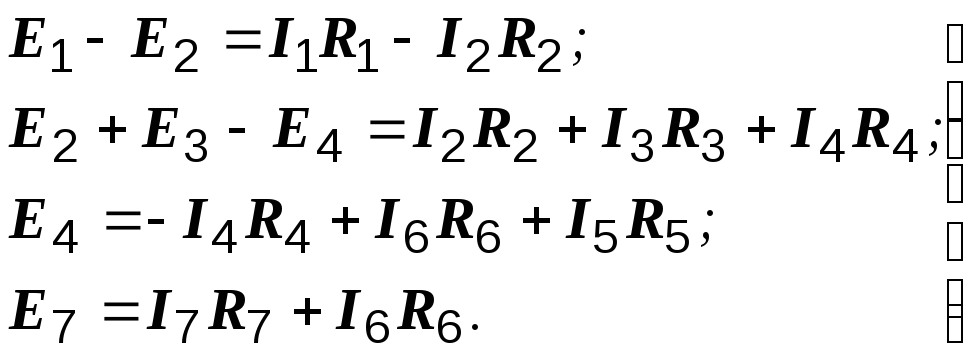(1.7)

Системы (1.6) и (1.7) дают достаточное количество уравнений для отыскания всех неизвестных токов.

1.3.2. Метод узловых потенциалов

Уравнения, составляемые по этому методу, называются узловыми уравнениями. В качестве неизвестных они содержат потенциалы узлов, причем один из них задается заранее – обычно принимается равным нулю. Пусть таким узлом будет узел d: _d = 0. Равенство нулю какой-то точки схемы обычно показывается как ее заземление.

Запишем для каждой ветви выражение закона Ома:

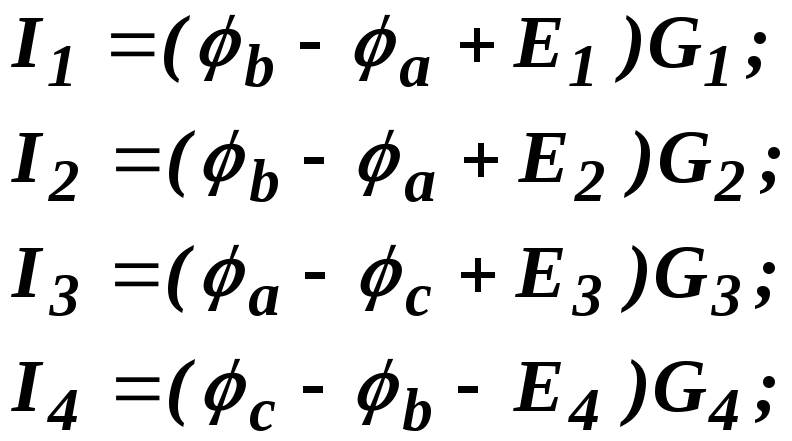
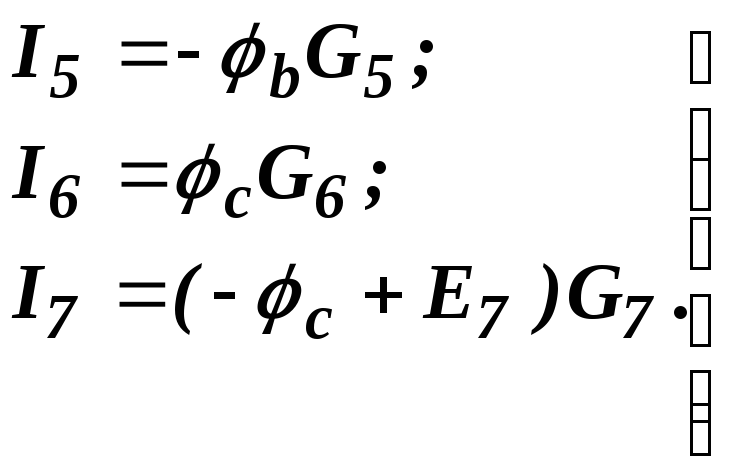(1.8)

Подставляя формулы (1.8) в систему (1.6) после несложных преобразований получаем следующие уравнения, количество которых на единицу меньше числа узлов:

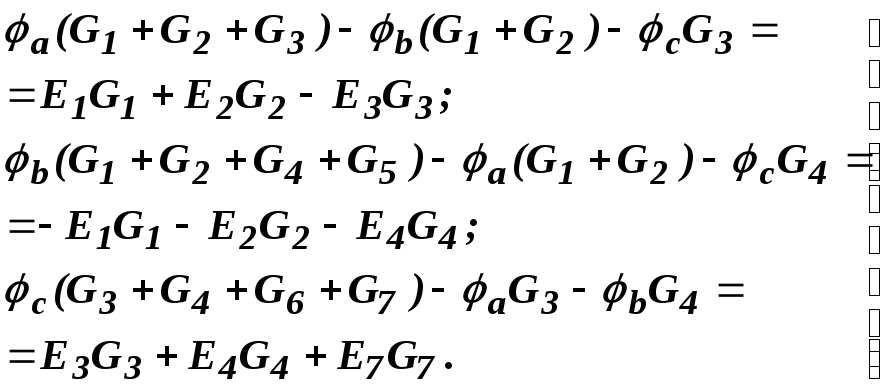(1.9)

При решении практических задач указанный вывод не делают, а узловые уравнения записывают сразу, пользуясь следующим правилом.

Потенциал узла, для которого составляется уравнение (например, в первом уравнении последней системы – это узел а), умножается на сумму проводимостей ветвей, присоединенных к этому узлу: _а (G₁+G₂+G₃).Это произведение записывается в левой части уравнения со знаком плюс. Потенциал каждого соседнего узла (b и с) умножается на проводимости ветвей, лежащих между этим (соседним) узлом и узлом, для которого составляется уравнение.

Эти произведения _b (G₁ + G₂) и _сG₃ записываются со знаком минус. В правой части уравнения стоит алгебраическая сумма произведений ЭДС на проводимости тех ветвей, которые присоединены к рассматриваемому узлу: E₁G₁, E₂G₂ и E₃G₃. Эти произведения записываются с плюсом, если ЭДС направлены к узлу, и с минусом, если от узла.

Найдя из (1.9) потенциалы узлов и подставляя их в (1.8), определяем токи ветвей.

Закон Ома для участка цепи с одной эдс.

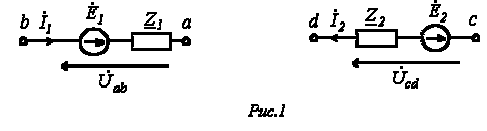
Возьмем два участка цепи a-b и c-d (см. рис. 1) и составим для них уравнения в комплексной форме с учетом указанных на рис. 1 положительных направлений напряжений и токов.

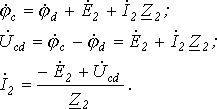
Объединяя оба случая, получим (1)

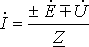
или для постоянного тока . (2)

Формулы (1) и (2) являются аналитическим выражением закона Ома для участка цепи с источником ЭДС, согласно которому ток на участке цепи с источником ЭДС равен алгебраической сумме напряжения на зажимах участка цепи и ЭДС, деленной на сопротивление участка. В случае переменного тока все указанные величины суть комплексы. При этом ЭДС и напряжение берут со знаком “+”, если их направление совпадает с выбранным направлением тока, и со знаком “-”, если их направление противоположно направлению тока.

5.Закон Ома и его применение для расчета разветвленной цепи постоянного тока.?????

6.Законы Кирхгофа и их применение.

Первый закон Кирхгофа

Алгебраическая сумма токов в ветвях, сходящихся к любому узлу электрической цепи, тождественно равна нулю. Согласно этому закону, если к некоторому узлу цепи подсоединено n ветвей с токами i₁, i₂, …, i_n, то в любой момент времени

,

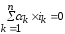где 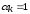, если направление тока положительно и ориентировано от узла (ток выходит из узла), или 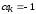, если ток входит в узел. Таким образом, любому узлу цепи соответствует уравнение, связывающее токи в ветвях цепи, соединенных с данным узлом.

В качестве примера приведем схему на рисунке 1.

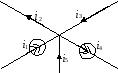
Рис.1.

В соответствии с первым законом Кирхгофа:

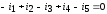.Общее число уравнений, которое можно составить по первому закону Кирхгофа для цепи, равно числу узлов цепи .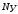

Так, для четырех узлов графа (рисунок 2) можно составить следующие четыре уравнения:

Рис.2.

узел 1: 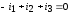,узел 2: ,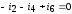

узел 3: 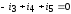,узел 4: .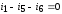

Первый закон Кирхгофа часто называют законом Кирхгофа для токов и сокращенно в тексте обозначают ЗКТ.Число независимых уравнений равно трем, так как любое из этих уравнений отличается от суммы трех остальных только знаком. Итак, если цепь содержит 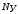узлов, то для неё можно составить по первому закону Кирхгофа 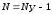независимых уравнений. Совокупность из N узлов цепи, уравнения для которых образуют систему линейно независимых уравнений, называют совокупностью независимых узлов цепи.

Примеры на применение первого закона Кирхгофа. Параллельное соединение элементов

В качестве примера на применение первого закона Кирхгофа рассмотрим параллельное соединение нескольких элементов активных сопротивлений, конденсаторов, катушек индуктивности.Особенностью параллельного соединения нескольких элементов является равенство напряжений, приложенных к зажимам любого из элементов, входящих в соединение. Цепь при таком соединении характеризуется только одним независимым узлом.Пусть параллельно соединены n элементов активного сопротивления. Если выбрать направления отчетов токов в элементах такими как это показано на рисунке 3, то согласно первому закону Кирхгоффа при параллельном соединении элементов запишем:

Рис.3.

u

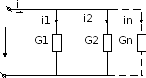
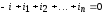;учитывая, что 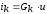, имеем 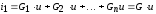,где .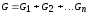

Зависимость 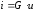не отличается от зависимости между напряжением на зажимах и током в элементе активного сопротивления с проводимостью G. Следовательно, цепь, составленная из нескольких сопротивлении, включенных параллельно, может быть заменена одним активным сопротивлением, при этом проводимость эквивалентного элемента равна сумме проводимостей элементов, входящих в соединение.

При параллельном соединении конденсаторов (рисунок 4) ток ветви можно определить по формуле: .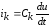

Рис.4.

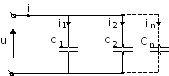
Для вычисления общего тока необходимо просуммировать токи ветвей:

,

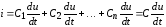где _..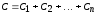

Таким образом, при параллельном соединении нескольких конденсаторов эквивалентная ёмкость равна сумме емкостей, входящих в соединение.

В случае параллельного соединения катушек индуктивностей (рисунок 5) ток каждой из ветвей равен: .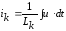

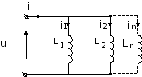
Рис.5.

Уравнение для вычисления общего тока имеет вид:

.

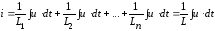Следовательно 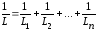, то есть .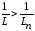

Это означает, что значение эквивалентной индуктивности будит меньше наименьшего из значений соединённых параллельно индуктивностей.

Второй закон Кирхгофа

Второй закон Кирхгофа формулируется следующим образом: алгебраическая сумма напряжений ветвей в любом контуре цепи тождественно равна нулю. Для замкнутого контура, изображённого на рисунке 6, можно записать соотношение:

.

Рис.6.

В соответствии со вторым законом Кирхгофа при обходе контура по часовой стрелке справедливо соотношение: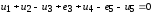.Изменение направления обхода эквивалентно изменению знаков напряжений на противоположные (умножению на минус единицу).

Примеры на применение второго закона Кирхгофа

1.3. Закон Ома для участка цепи, не содержащего э.Д.С.

Закон Ома устанавливает связь между током и напряжением на некотором участке цепи. Так, применительно к участку цепи рис. 1.6, запишем:

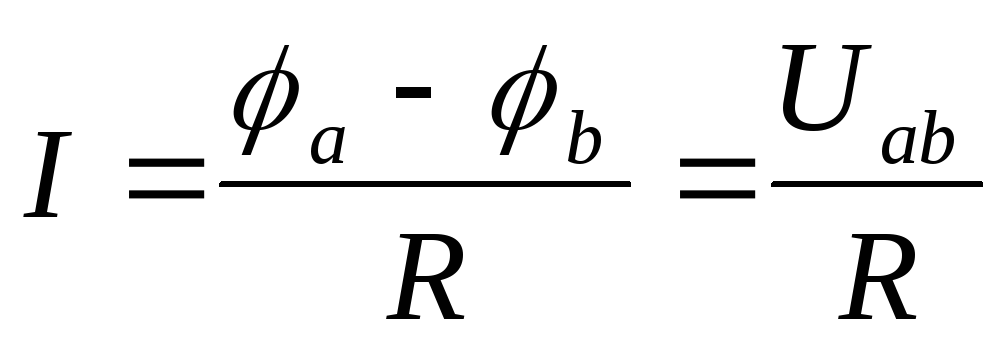
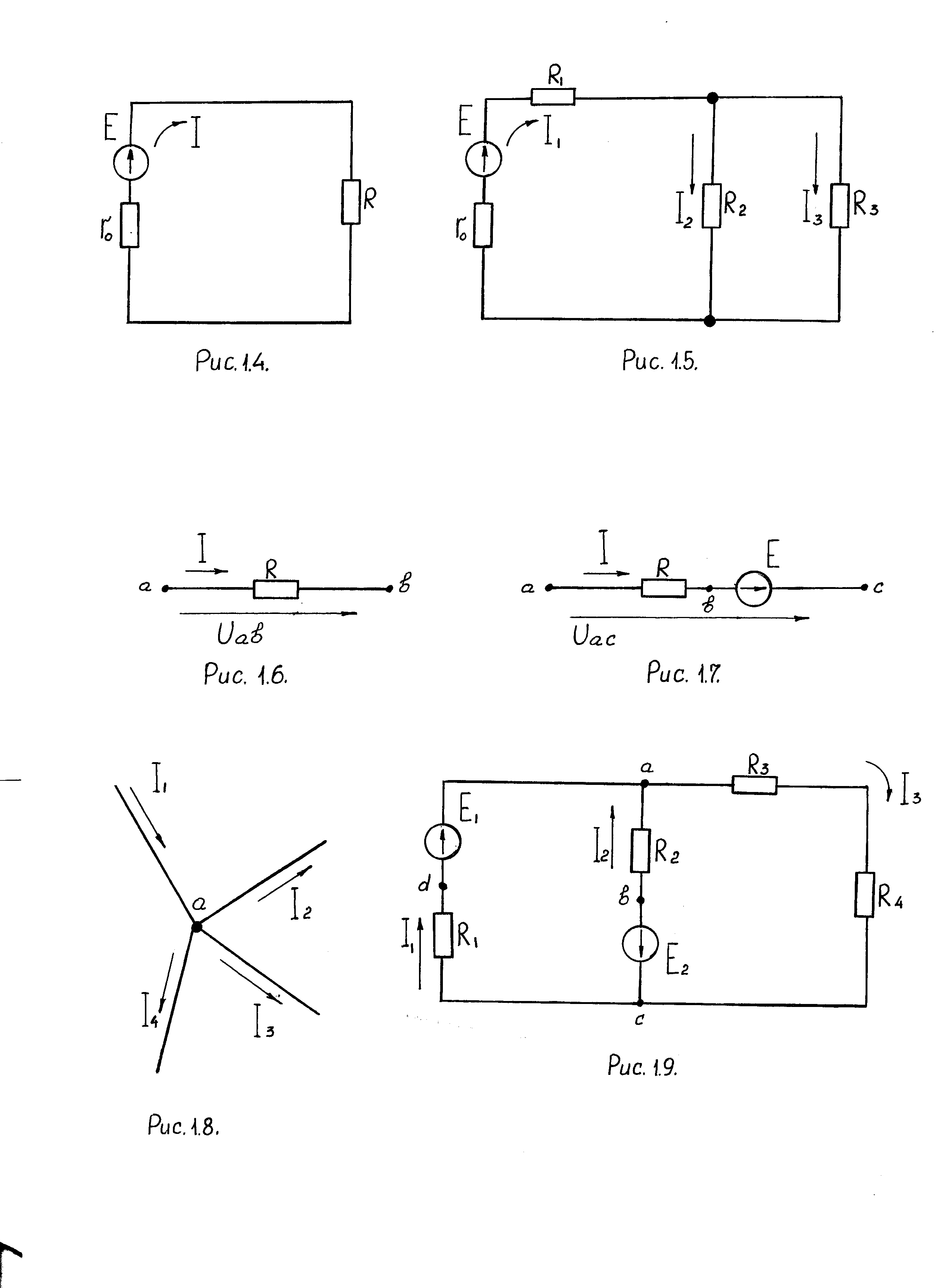
Рис. 1.6. Участок цепи, не содержащий э. д. с.

1.4. Закон Ома для участка цепи, содержащего э.д.с.

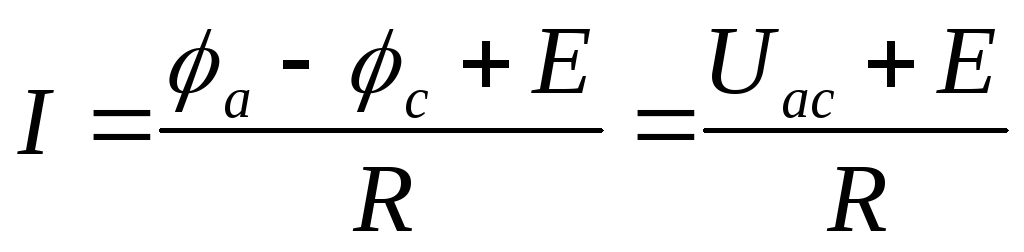
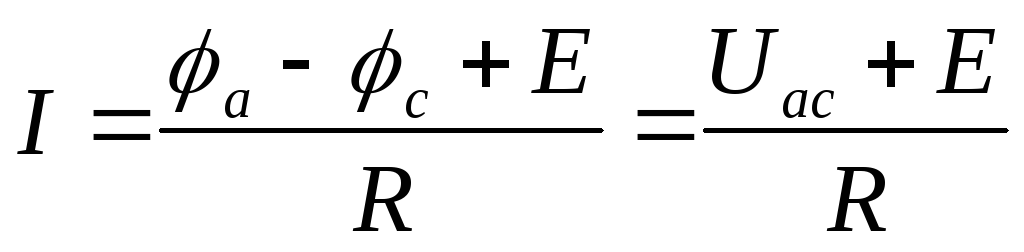Закон Ома для участка цепи, содержащего э.д.с. (рис. 1.7), позволяет найти ток по известной разности потенциалов (φ_а – φ_с) на концах участка цепи:

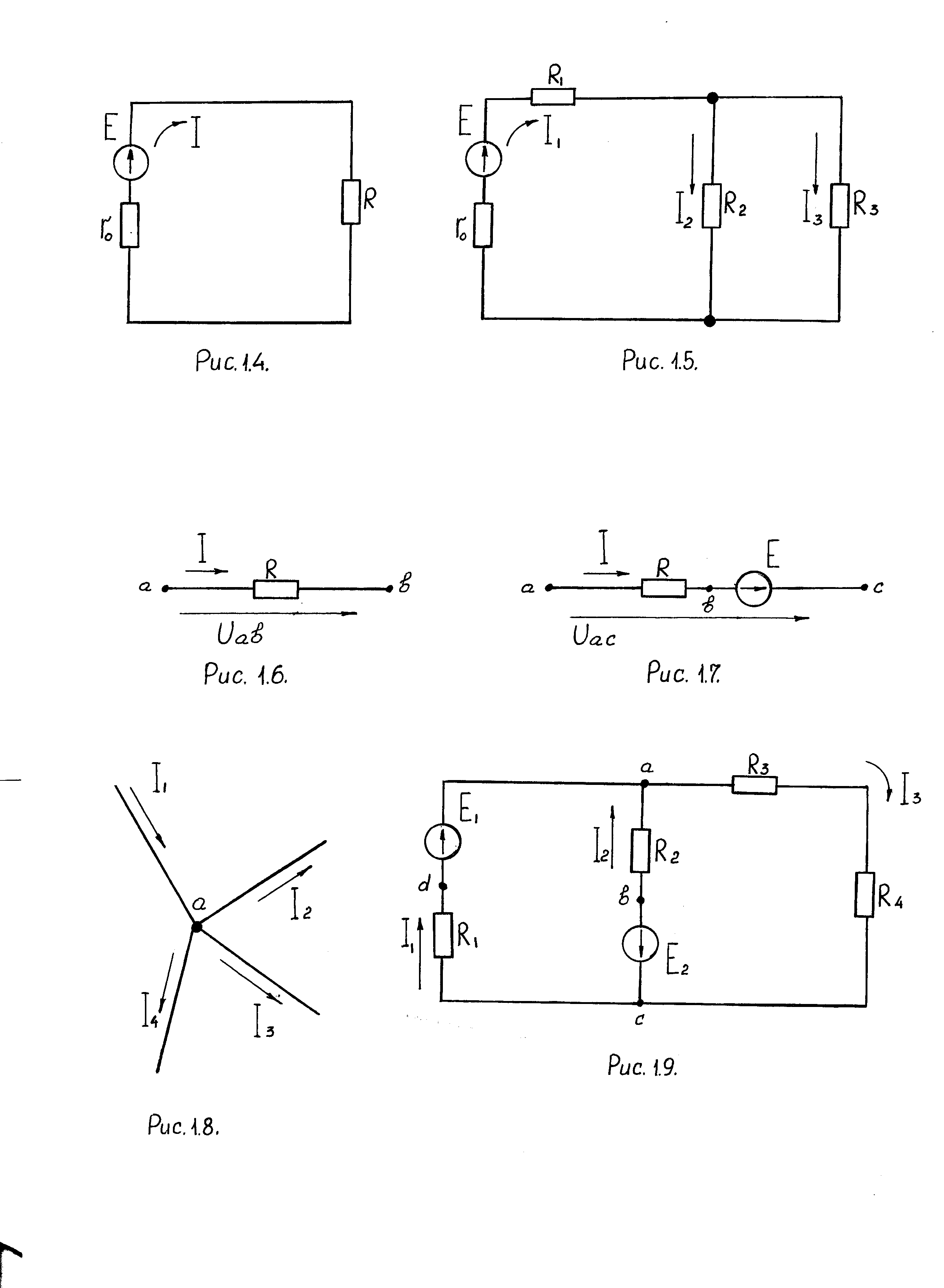
Рис. 1. 7. Участок цепи, содержащий э.д.с.

Если э.д.с. Е имеет противоположное направление, то

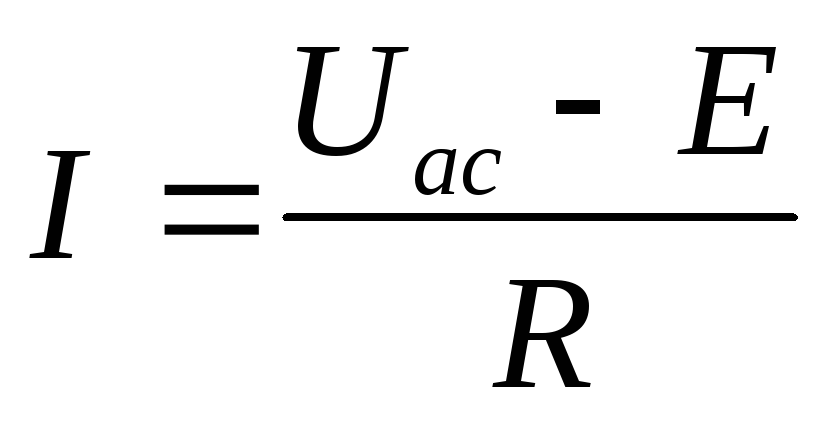
1.5. Первый закон Кирхгофа

Алгебраическая сумма токов в узле равняется нулю (рис. 1.8):

Σ I = 0

I₁ – I₂ – I₃ – I₄= 0 или I₁ = I₂ + I₃ + I₄

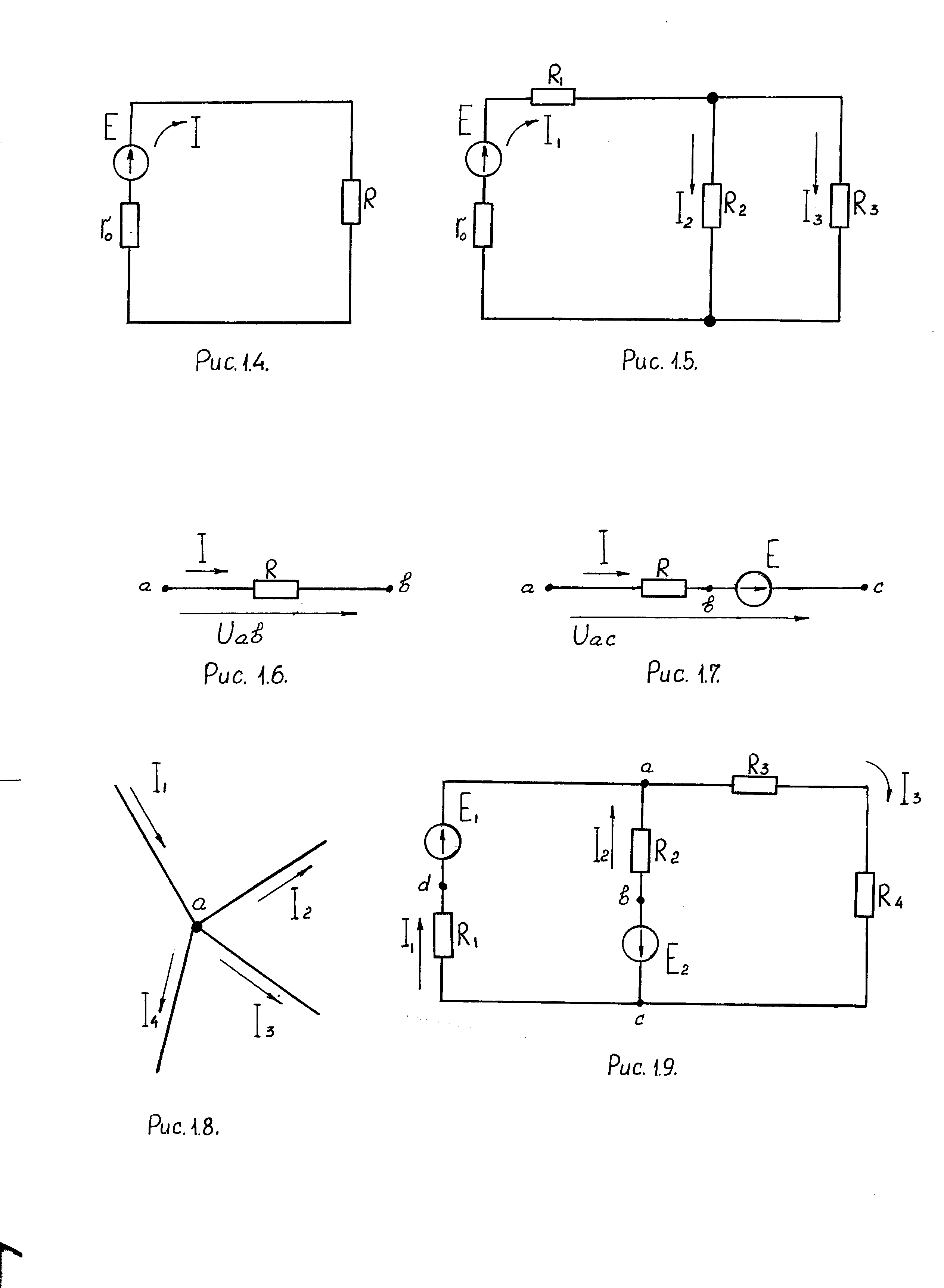
Рис. 1.8. Узел электрической цепи

1.6. Второй закон Кирхгофа

Алгебраическая сумма падений напряжений в любом замкнутом контуре равняется алгебраической сумме э.д.с. вдоль того же контура:

Σ IR = Σ E,

или алгебраическая сумма напряжений вдоль любого замкнутого контура равна нулю:

Σ U_x = 0.

Любой замкнутый путь, проходящий по нескольким ветвям, называется контуром. Так, для схемы 1.9 имеем:

I₃R₃ + I₃R₄ + I₁R₁ – U_da= 0

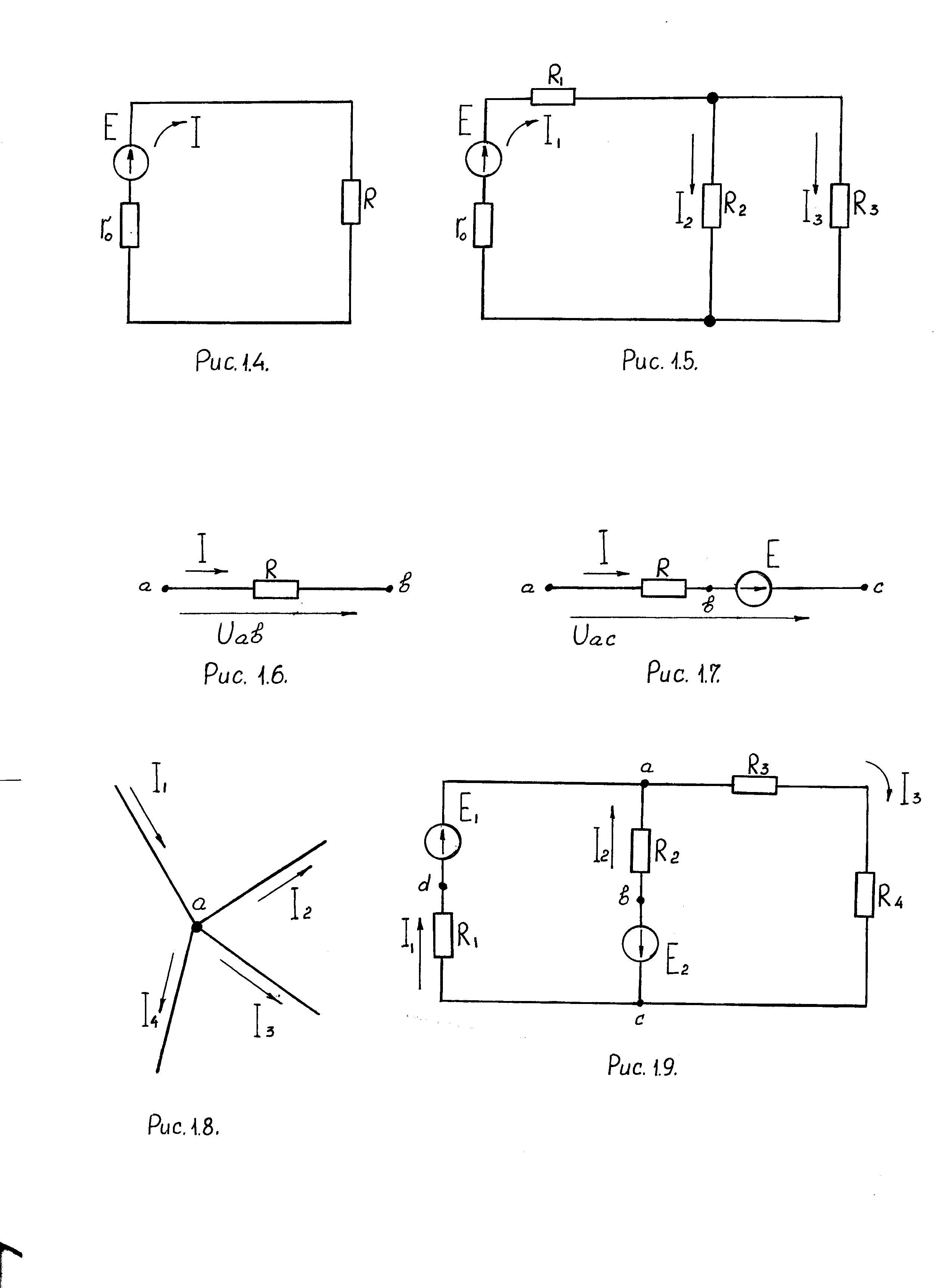
Рис.1.9. Схема двухконтурной цепи постоянного тока

1.7. Составление уравнений для расчета токов в схемах при помощи законов Кирхгофа

Законы Кирхгофа используются для нахождения токов в ветвях схемы. Так как в каждой ветви схемы протекает свой ток, то число неизвестных токов равняется числу ветвей схем. Перед тем как составлять уравнения, необходимо:

1. Произвольно выбрать положительные направления токов в ветвях и обозначить их на схеме.

2. Выбрать положительные направления обхода контуров для составления уравнений по второму закону Кирхгофа.

Для единообразия рекомендуется положительные направления обхода контуров выбрать одинаковыми для всех контуров, например, по часовой стрелке.

Обозначим число ветвей схем буквой b и число узлов у. Для того чтобы получить линейно-независимые уравнения, по первому закону Кирхгофа составляется число уравнений, равное числу узлов минус единица, т.е. у-1. По второму закону Кирхгофа составляется число уравнений, равное числу ветвей за вычетом числа уравнений, составленных по первому закону Кирхгофа, т.е.

b – (у – 1).

При составлении уравнений по второму закону Кирхгофа необходимо следить за тем, чтобы были охвачены все ветви схемы.

Рассмотрим применение законов Кирхгофа для схемы рис. 1.9. Произвольно выбираем положительные направления токов и обозначаем их на схеме. В схеме два узла, следовательно, по первому закону Кирхгофа достаточно составить только одно уравнение:

I₁ + I₂ = I₃ .

По второму закону Кирхгофа необходимо составить b – (у – 1) = 3 – (2 – 1) – 2 уравнения. Положительные направления обхода контуров выбираем по часовой стрелке.

Для контура R₁E₁R₂E₂ : I₁R₁ – I₂R₂ = E₁ + E₂.

Знак «плюс» перед I₁R₁взят потому, что направление тока I₁ совпадает с направлением обхода контура. Знак «минус» перед I₂R₂ – потому, что направление I₂встречно обходу контура. Для контура Е₂R₂R₃R₄ :

I₂R₂ + I₃ (R₃ + R₄) = – E₂ .

Поскольку положительные направления токов выбираются произвольно, то в результате расчета один или несколько токов могут оказаться отрицательными, т.е. в реальной схеме эти токи протекают в обратном направлении.

2.3 Закон Ома для участка цепи, содержащего источники эдс

Это специальное правило, позволяющее вычислять величину тока в ветви, если известно напряжение на ее зажимах.

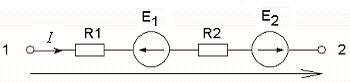
По второму закону Кирхгофа для фиктивного контура:

=>

,

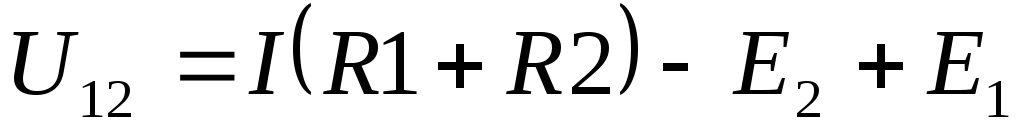
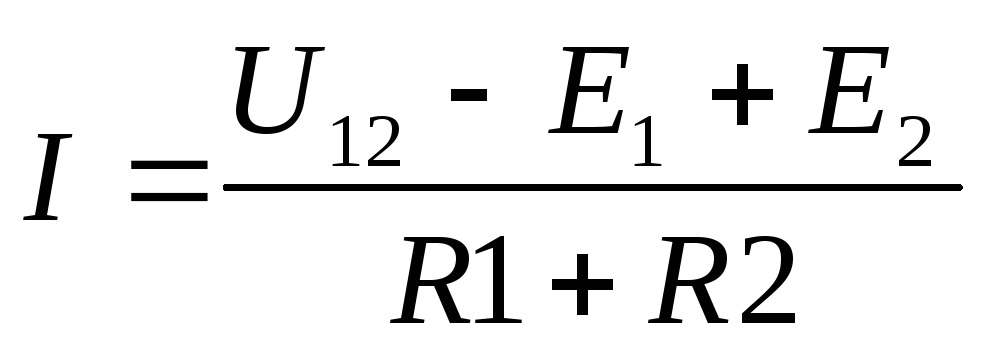т.е.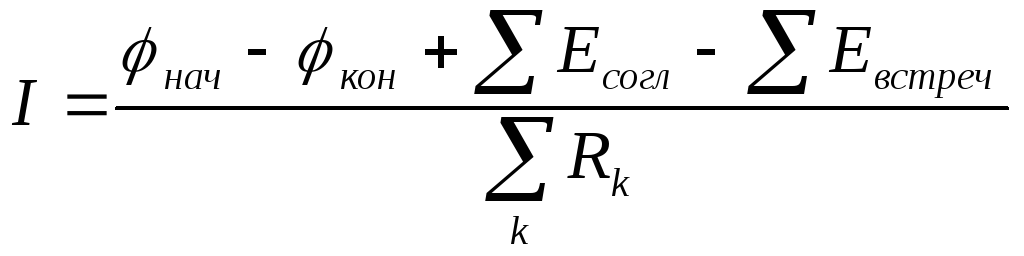

2.4 Метод узловых потенциалов

Этот метод позволяет сократить число совместно решаемых уравнений по сравнению с методом уравнений Кирхгофа.

Идея метода состоит в следующем: если выразить ток каждой ветви по закону Ома для ветви, содержащей ЭДС и подставить полученное выражение в (n_У — 1) число уравнений первого закона Кирхгофа, получится система уравнений в относительно узловых потенциалов. Правда число потенциалов будет на единицу больше числа уравнений. Эту проблему решают так: т.к. ток в ветви зависит от разности потенциалов ее концов, не изменяя режима цепи, можно все потенциалы узлов схемы изменить на одну и ту же величину, причем на столько, чтобы один из потенциалов стал равен нулю (заземлить какой-то узел). После этого получаются уравнения стандартного вида.

Для некоторого узла k получится уравнение

,

где 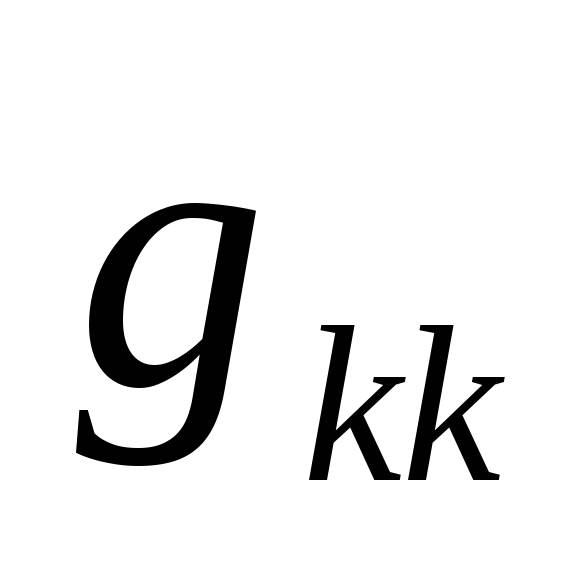— собственная узловая проводимостьk-ого узла, она равна сумме проводимостей всех ветвей, подключенных к этому узлу;

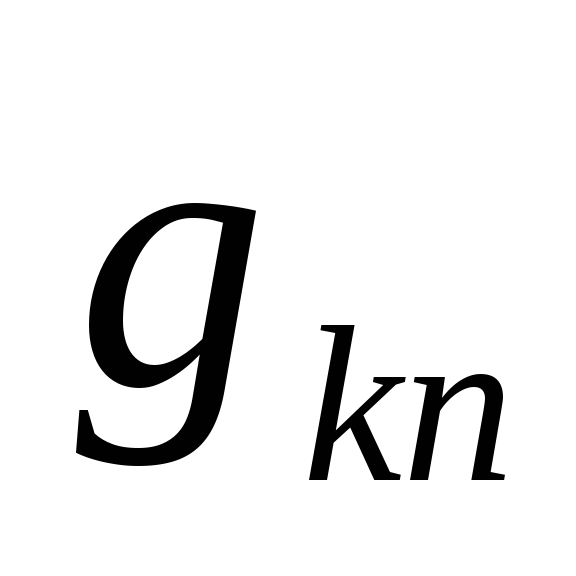— межузловая проводимость k-ого и n-ого узлов, она равна сумме проводимостей ветвей непосредственно соединяющих n-ый узел с узлом k для которого пишется уравнение;

— алгебраическая сумма величин источников тока, стоящих в ветвях, присоединенных к k-ому узлу;

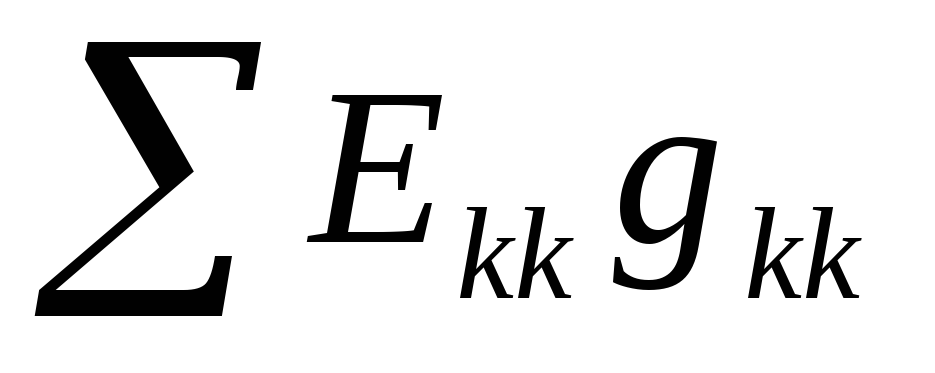— алгебраическая сумма произведений ЭДС, стоящих в ветвях присоединенных к k-ому узлу на проводимости этих ветвей.

У любого источника берется знак «+», если он направлен к узлу, для которого пишется уравнение.

Проводимость ветви есть величина обратная сопротивлению этой ветви.

Пример:

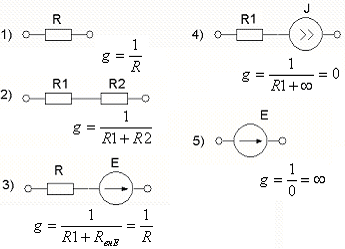
Ветвь 5) называется ветвью типа Е и проводимость вычисляется по особому правилу. Рекомендуемый порядок действий:

1. Выбирают узел, потенциал которого принимают равным нулю. Возможны 3 случая.

а. В схеме нет ветвей типа Е, тогда заземляют любой узел схемы. Записывают (n_У — 1) уравнений МУП, где n_У — число узлов схемы.

б. В схеме есть одна или несколько ветвей типа Е, но если их несколько, то все они между собой непосредственно соединены. Тогда обязательно заземляют один из узлов этих ветвей. Остальные узлы будут иметь известные потенциалы. Записывают ((n_У -1)— n_Е) уравнений

МУП, где n_Е – число ветвей типа Е.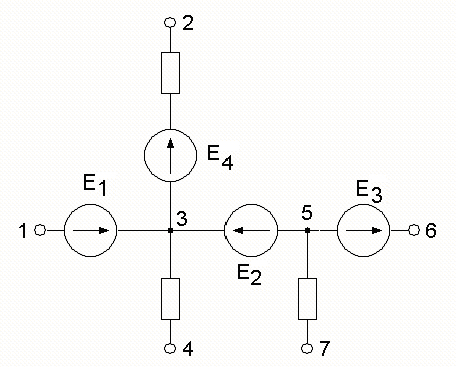

,

,

,

,

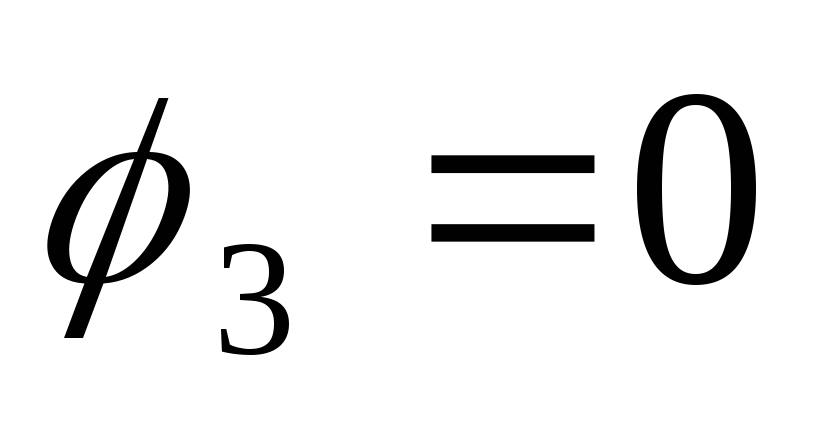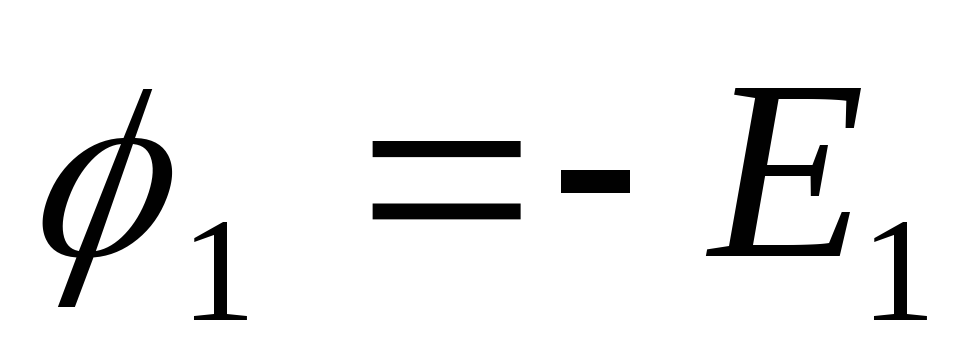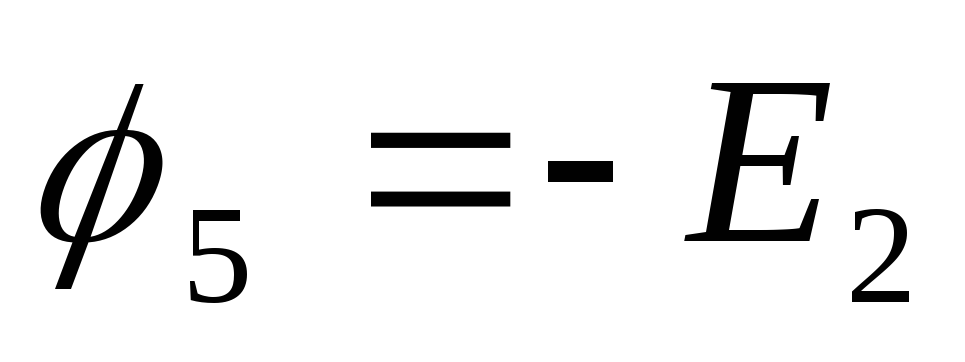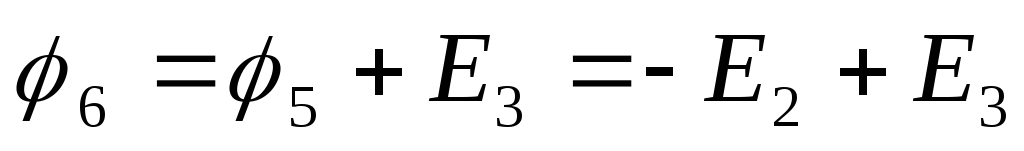в. В схеме есть несколько ветвей типа Е, но не все они между собой соединены – решать задачу МУП нельзя.

2. Для узлов, потенциалы которых остались неизвестными, записывают уравнения МУП стандартного вида и решают полученную систему.

Система уравнений должна быть полной – содержать столько уравнений, сколько неизвестных.

3. Токи ветвей записывают по закону Ома для участка цепи, содержащего ЭДС. В ветвях типа Е токи по закону Ома определить нельзя.

.

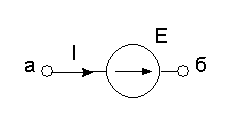
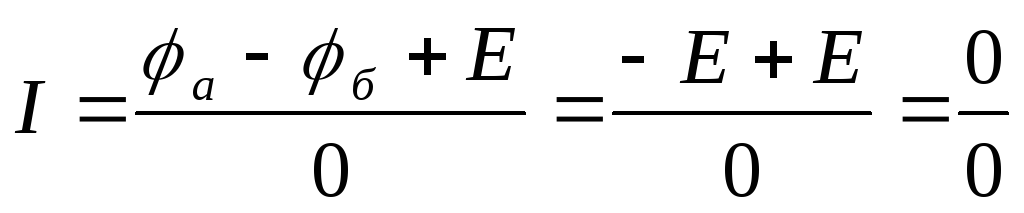Примечание: в ветвях типа Е токи находят по первому закону Кирхгофа в последнюю очередь.

Если в схеме есть управляемые источники, то к системе уравнений по МУП приписывают уравнения связи, в которых величины управляемых источников выражаются через узловые потенциалы.

Пример: Дано: 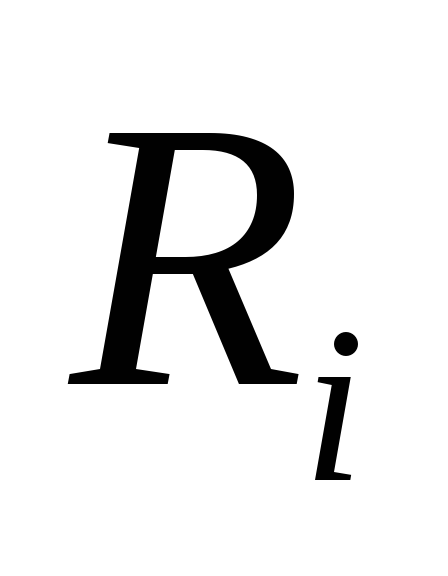,,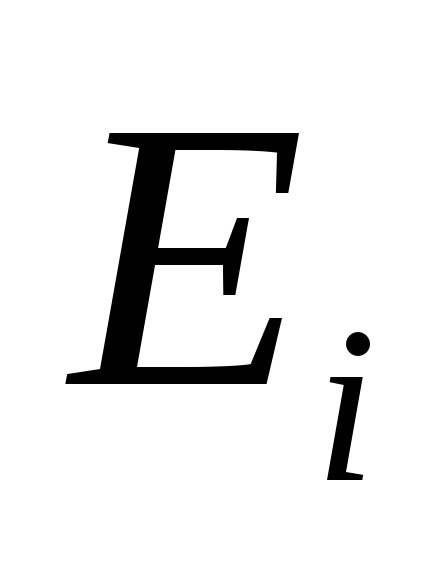. Найти:.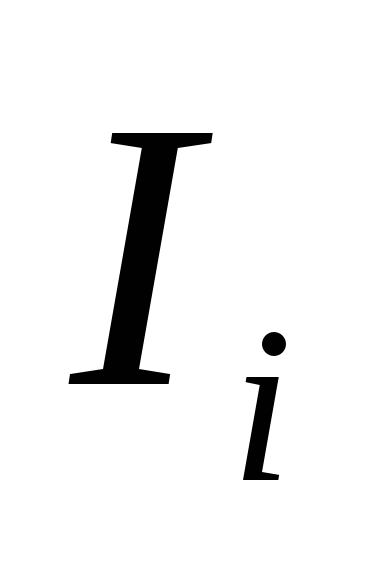

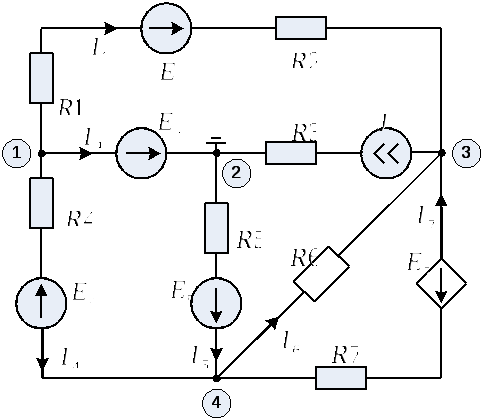
Пусть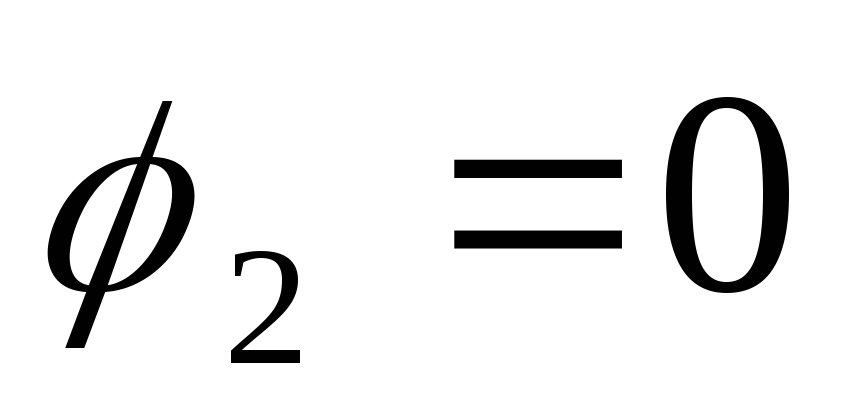

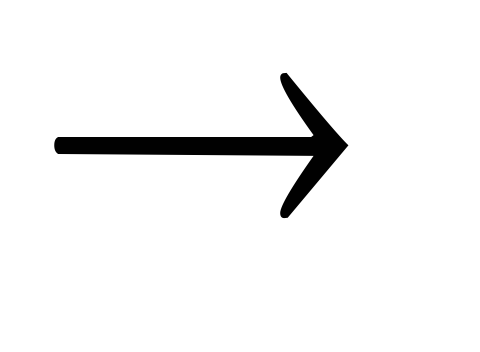
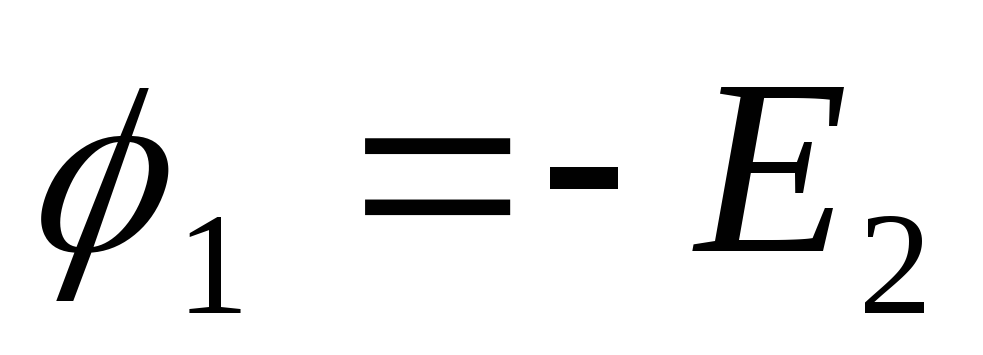
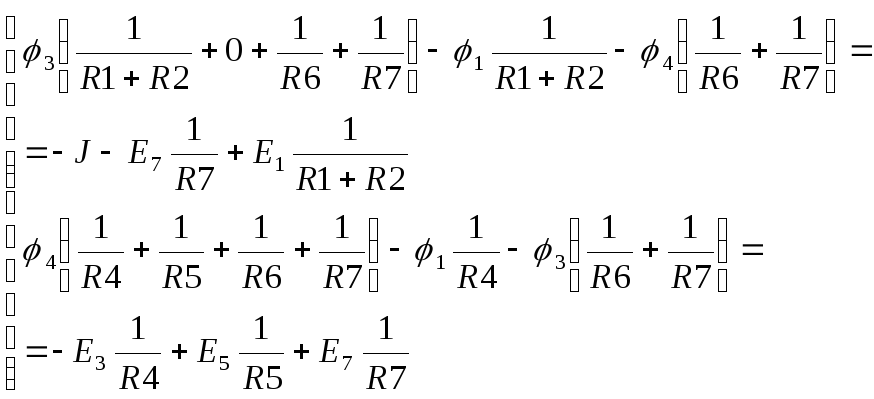
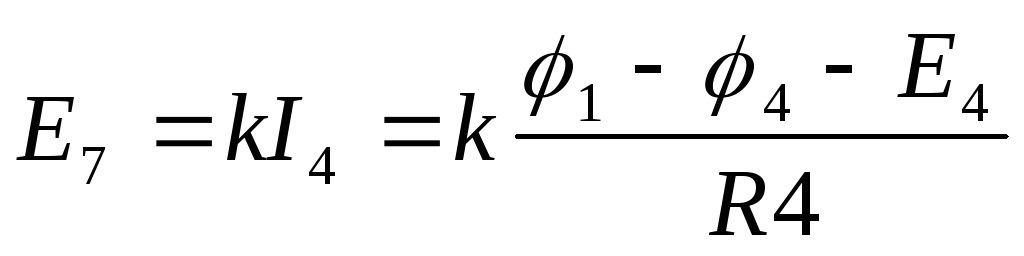
Решают эту систему и находят потенциалы и. После этого находят токи ветвей:

, ,,,,

=> .

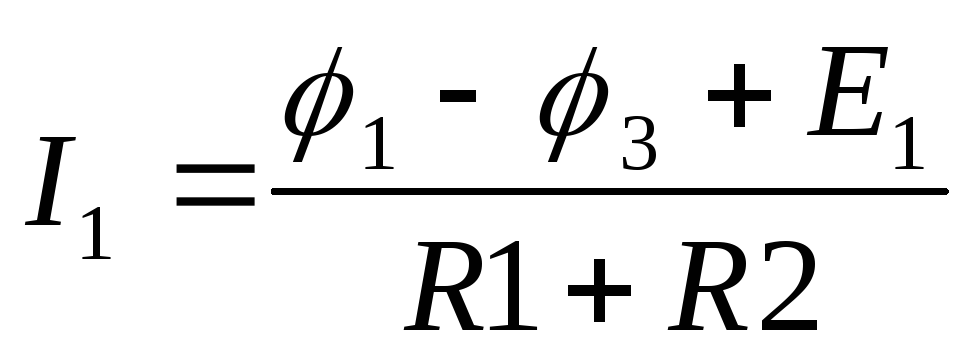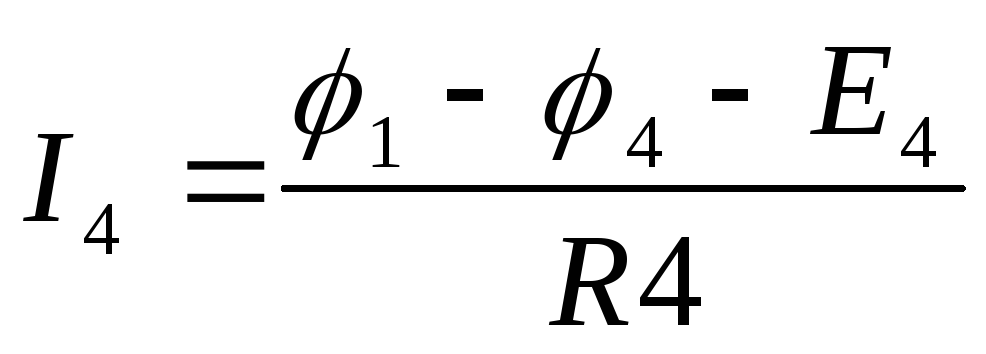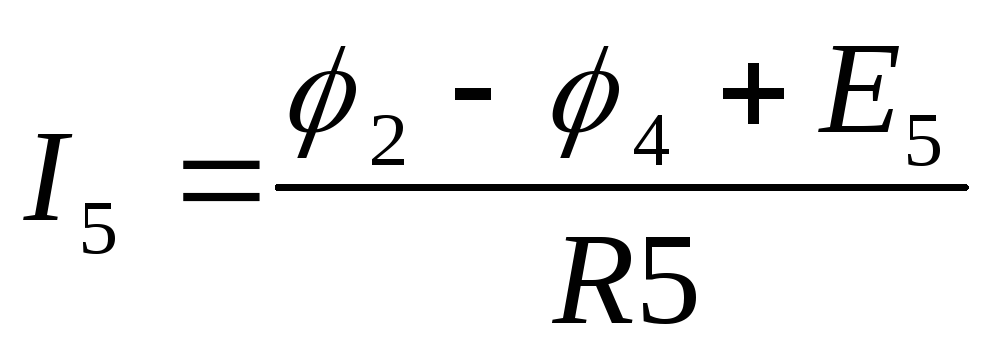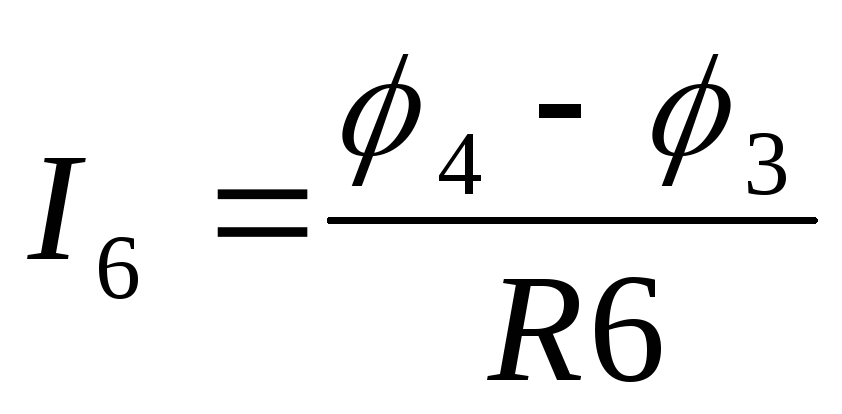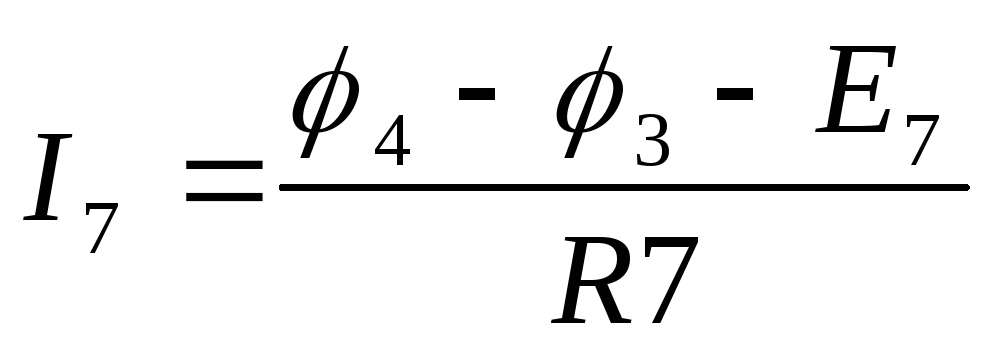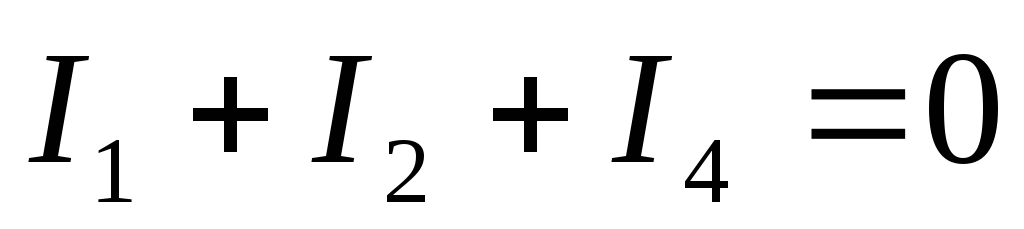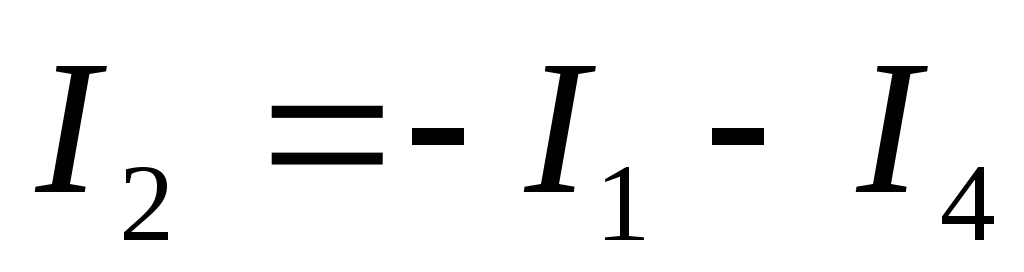3.Закон Ома для участка цепи, не содержащего эдс:

I = U/R . (1.4)

Рассмотрим участок цепи с ЭДС (Error: Reference source not found).

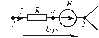
Рис.1.5. Линейный участок цепи, содержащий ЭДС

Из состава сложной электрической цепи выделим ветвь, содержащую источник энергии и потребитель. Для определенности примем, что направления тока и источника ЭДС совпадают. При условно выбранных положительных направлениях тока и ЭДС в ветви имеем:

₁ > _a  ₁ – _a = IR, 0(1.5)

₂ > _a  ₂ – _a = E. 0(1.6)

Вычтем из уравнения ( 1 .5) уравнение ( 1 .6) и тогда получим:

₁ – ₂ = IR – E = U₁₂;

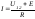. 0(1.7)

Полученное выражение представляет собой закон Ома для участка цепи с ЭДС. В случае несовпадения направления тока в ветви с направлениями напряжения и ЭДС перед ними появляется знак «минус».

Законы Кирхгофа

Первый закон Кирхгофа  алгебраическая сумма токов в узле равна нулю:

. 0(1.8)

где k – номер ветви, n – общее их количество.

Второй закон Кирхгофа  алгебраическая сумма падений напряжений вдоль замкну­того контура равна алгебраической сумме ЭДС, действующих в этом контуре:

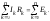0(1.9)

Второй закон Кирхгофа работает как для замкнутого, так и для разомк­нутого контура.

Уравнение баланса мощности:

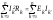0 (1.10)

Уравнение баланса мощности является модификацией закона сохранения энергии для электрических цепей. Это базовое уравнение для проверки правильности выполненных расчетов тех или иных цепей.

В левой части этого уравнения стоит арифметическая сумма мощностей, которые выделяются на сопро­тивлениях от токов, которые по ним протекают. В правой части – мощность, отданная источниками в сеть.

При этом возможна такая ситуация, когда одно из сла­гаемых суммы справа мо­жет оказаться отрицательным. Это будет означать, что в данной ситуации источник становится пот­ребителем. Она возникает в случае, когда ток, проте­кающий по источнику, направлен встречно направлению ЭДС.

Закон Джоуля — Ленца — физический закон, дающий количественную оценку теплового действия электрического тока. Установлен в 1841 году Джеймсом Джоулем и независимо от него в 1842 году Эмилием Ленцом^[1].

В словесной формулировке звучит следующим образом^[2]

Мощность тепла, выделяемого в единице объёма среды при протекании электрического тока, пропорциональна произведению плотности электрического тока на величину электрического поля

Математически может быть выражен в следующей форме:

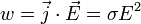
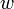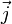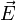где  — мощность выделения тепла в единице объёма,  — плотность электрического тока,  — напряжённость электрического поля, σ — проводимость среды.

Закон также может быть сформулирован в интегральной форме для случая протекания токов в тонких проводах^[3]:

Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке исопротивлению участка

В математической форме этот закон имеет вид

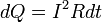
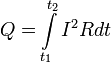
где dQ — количество теплоты, выделяемое за промежуток времени dt, I — сила тока, R — сопротивление, Q — полное количество теплоты, выделенное за промежуток времени от t₁ доt₂. В случае постоянных силы тока и сопротивления:

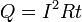
4.

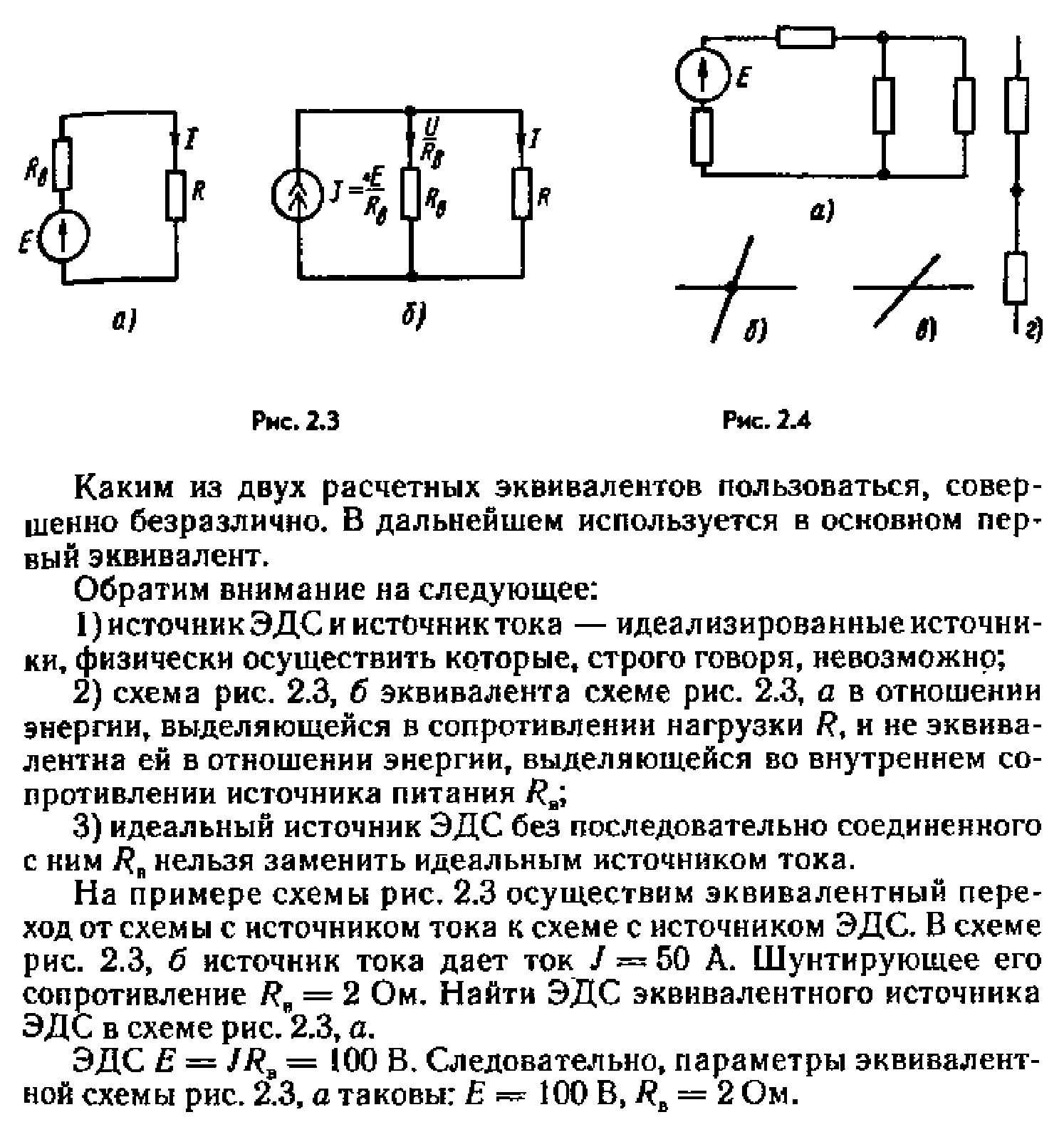
5.

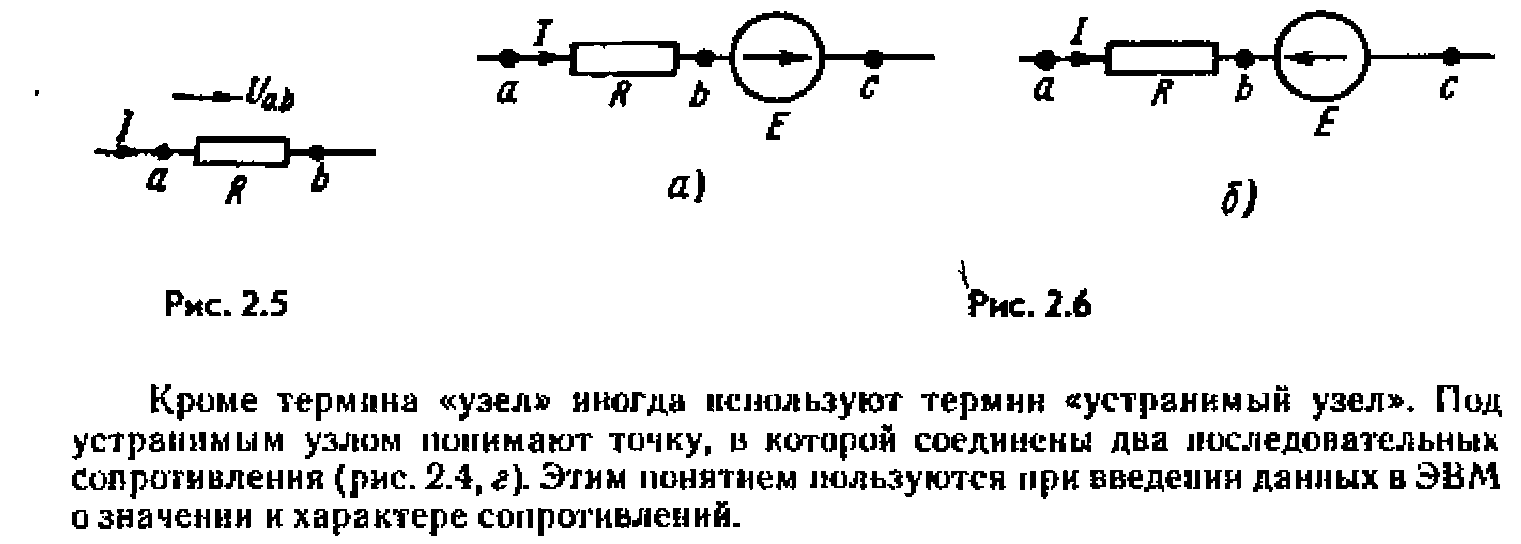
6. Последовательное и параллельное соединения в электротехнике — два основных способа соединения элементов электрической цепи. При последовательном соединении все элементы связаны друг с другом так, что включающий их участок цепи не имеет ни одного узла. При параллельном соединении все входящие в цепь элементы объединены двумя узлами и не имеют связей с другими узлами, если это не противоречит условию.

При последовательном соединении проводников сила тока во всех проводниках одинакова.

При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов. При этом величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
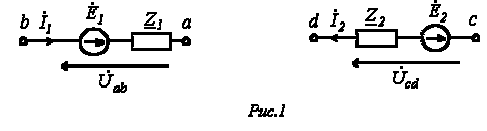
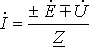
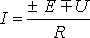