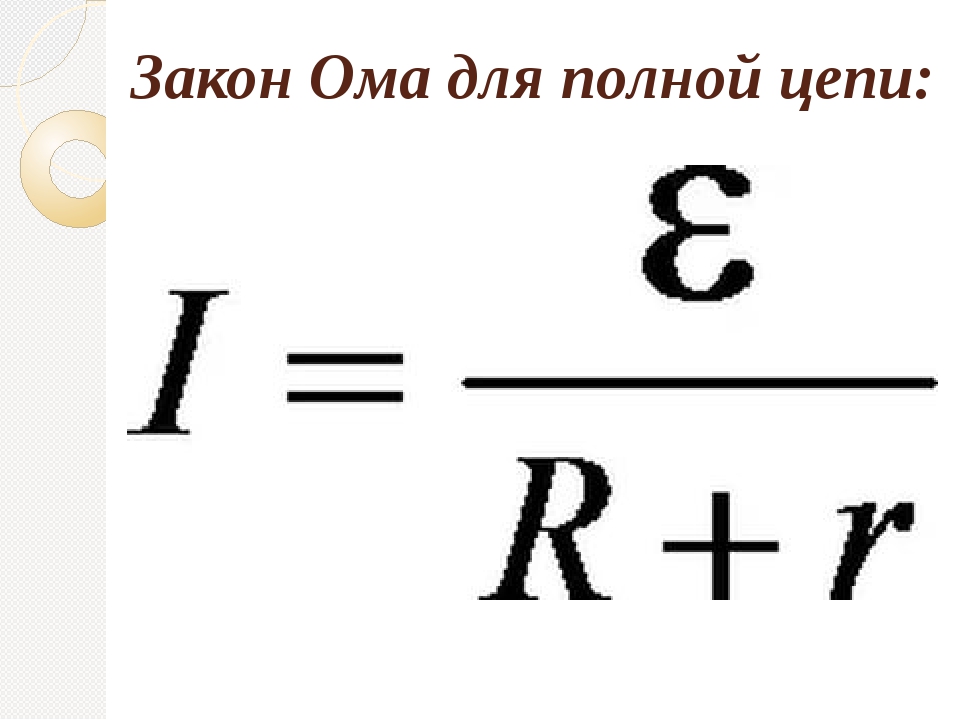Закон Ома для полной цепи – формула, определение
4.6
Средняя оценка: 4.6
Всего получено оценок: 150.
4.6
Средняя оценка: 4.6
Всего получено оценок: 150.
Закон Ома связывает в одной формуле электрические параметры, с помощью которых можно определить токи и напряжения на каждом элементе цепи. Данный закон можно распространить на всю электрическую цепь. Рассмотрим, как это происходит.
Источник ЭДС в полной цепи
Для возникновения электрического тока в замкнутой цепи, эта цепь должна содержать хотя бы один особый элемент, в котором будет происходить работа по переносу зарядов между его полюсами. Силы, переносящие заряды внутри этого элемента, делают это против электрического поля, а значит, их природа должна быть отлична от электрической. Поэтому такие силы называются сторонними.
Рис. 1. Сторонние силы в физике.Элемент электрической цепи, в котором происходит работа сторонних сил по переносу зарядов против действия электрического поля, называется источником тока.
Значение ЭДС источника тока равно отношению сторонних сил по переносу заряда к величине этого заряда:
$$\mathscr{E}={A_{ст}\over q}$$
Поскольку смысл ЭДС очень близок к смыслу электрического напряжения (напомним, напряжение – это отношение работы, совершаемой электрическим полем, переносящим заряд, к величине этого заряда), то ЭДС так же, как и напряжение, измеряется в Вольтах:
$$1В={Дж\overКл}$$
Второй важнейшей электрической характеристикой реального источника тока является его внутреннее сопротивление. При переносе зарядов между клеммами происходит их взаимодействие с веществом источника ЭДС, а поэтому, источник для электрического тока также представляет некоторое сопротивление. Внутреннее сопротивление, как и обычное сопротивление, измеряется в Омах, но обозначается малой латинской буквой $r$.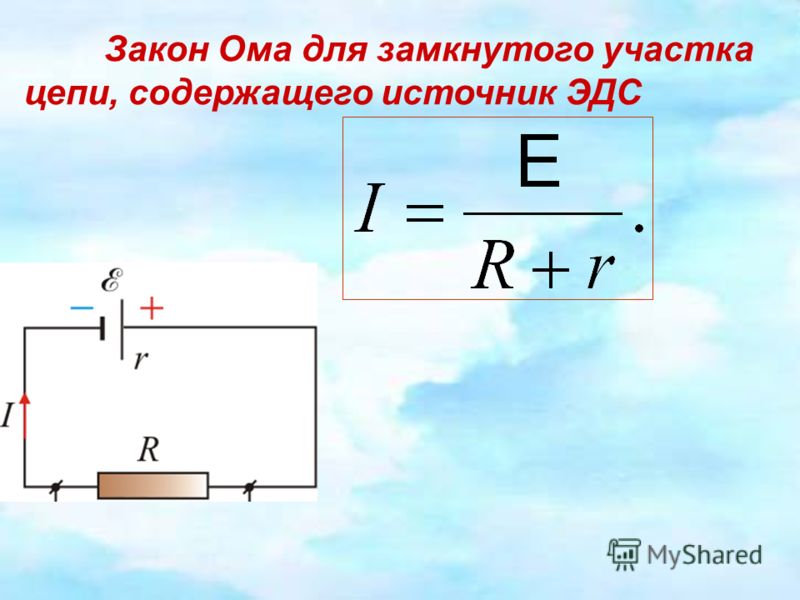
Сокращая и перенося значение тока влево, окончательно получаем формулу Закона Ома для полной цепи:
$$I={\mathscr{E}\over R+r}$$
Сила тока в замкнутой цепи равна отношению ЭДС источника тока к сумме сопротивления цепи и внутреннего сопротивления источника.
Внутреннее сопротивление реальных источников тока очень невелико (доли ома), поэтому для небольших мощностей оно почти не оказывает влияния на электрическую цепь. Однако, если мощность цепи велика, то пренебрегать этим сопротивлением нельзя, на нем может выделяться заметное количество тепла.
Сложные цепи с несколькими источниками тока
В замкнутой цепи может быть не один источник тока.
В этом случае полная ЭДС цепи равна алгебраической сумме ЭДС источников. В цепи произвольно выбирается направление обхода, и если источник вызывает ток в этом направлении, его ЭДС считается положительной, а иначе – отрицательной. Сопротивление не имеет направления, а поэтому внешние и внутренние сопротивления всегда суммируются.
В реальных сложных электрических цепях может быть много разветвлений и контуров, причем, источники тока могут находиться в различных местах. Для определения токов на всех ветвях цепи используются системы уравнений, построенные на основе специальных правил (законов) Кирхгофа.
Рис. 3. Сложные цепи и законы Кирхгофа.Что мы узнали?
Реальные источники тока обладают внутренним сопротивлением. Согласно Закону Ома для полной цепи, ток в замкнутой цепи равен отношению ЭДС источника тока к сумме сопротивления цепи и внутреннего сопротивления источника. Если в простой цепи несколько источников ЭДС, то общая ЭДС равна алгебраической сумме ЭДС источников. Для сложных цепей используются системы уравнений на основе правил Кирхгофа.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.6
Средняя оценка: 4. 6
6
Всего получено оценок: 150.
А какая ваша оценка?
Закон ома для полной цепи: формула для расчета
В электрике и электронике действует несколько основных физических законов, объясняющих и регулирующих все текущие процессы. К наиболее значимым относится закон Ома для полной цепи, описывающий взаимодействия меду током, напряжением и сопротивлением. Эти положения широко применяются на практике при расчетах всевозможных электронных схем.
Содержание
Отдельный участок и полная электрическая цепь
Закон Ома, применительно к участку или всей цепи, может рассматриваться в двух вариантах расчетов:
- Отдельный краткий участок. Является частью схемы без источника ЭДС.
- Полная цепь, состоящая из одного или нескольких участков. Сюда же входит источник ЭДС со своим внутренним сопротивлением.
Расчет тока участка электрической схемы
В этом случае применяется основная формула I = U/R, в которой I является силой тока, U – напряжением, R – сопротивлением.
Электрический ток, проходящий через некоторый участок цепи, находится в прямой пропорции с приложенным напряжением, и в обратной пропорции – с сопротивлением.
Данная формулировка является основой для многих других формул, представленных на так называемой «ромашке» в графическом исполнении. В секторе Р – определяется мощность, в секторах I, U и R – проводятся действия, связанные с силой тока, напряжением и сопротивлением.
Каждое выражение – и основное и дополнительные, позволяют рассчитать точные параметры элементов, предназначенных для использования в схеме.
Специалисты, работающие с электрическими цепями, выполняют быстрое определение любого из параметров по методике треугольников, изображенных на рисунке.
В расчетах следует учитывать сопротивление проводников, соединяющих между собой элементы участка. Поскольку они изготавливаются из разных материалов, данный параметр будет отличаться в каждом случае. Если же потребуется сформировать полную схему, то основная формула дополняется параметрами источника напряжения, например, аккумуляторной батареи.
Если же потребуется сформировать полную схему, то основная формула дополняется параметрами источника напряжения, например, аккумуляторной батареи.
Вариант расчета для полной цепи
Полная цепь состоит из отдельно взятых участков, объединенных в единое целое вместе с источником напряжения (ЭДС). Таким образом, существующее сопротивление участков дополняется внутренним сопротивлением подключенного источника. Следовательно, основная трактовка, рассмотренная ранее, будет читаться следующим образом: I = U / (R + r). Здесь уже добавлен резистивный показатель (r) источника ЭДС.
С точки зрения чистой физики этот показатель считается очень малой величиной. Однако, на практике, рассчитывая сложные схемы и цепи, специалисты вынуждены его учитывать, поскольку дополнительное сопротивление оказывает влияние на точность работы. Кроме того, структура каждого источника очень разнородная, в результате, сопротивление в отдельных случаях может выражаться достаточно высокими показателями.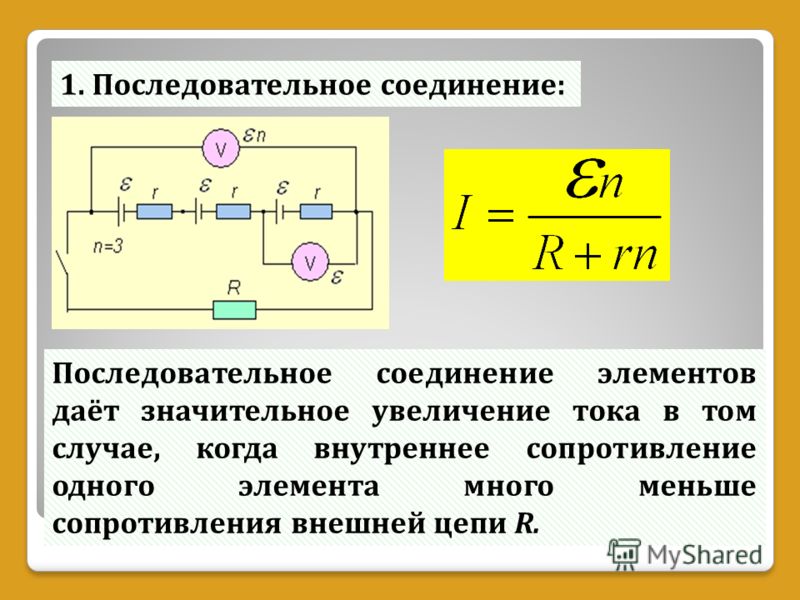
Приведенные расчеты выполняются применительно к цепям постоянного тока. Действия и расчеты с переменным током производятся уже по другой схеме.
Действие закона к переменной величине
При переменном токе сопротивление цепи будет представлять из себя так называемый импеданс, состоящий из активного сопротивления и реактивной резистивной нагрузки. Это объясняется наличием элементов с индуктивными свойствами и синусоидальной величиной тока. Напряжение также является переменной величиной, действующей по своим коммутационным законам.
Следовательно, схема цепи переменного тока по закону Ома рассчитывается с учетом специфических эффектов: опережения или отставания величины тока от напряжения, а также наличия активной и реактивной мощности. В свою очередь, реактивное сопротивление включает в себя индуктивную или емкостную составляющие.
Все этим явлениям будет соответствовать формула Z = U / I или Z = R + J * (XL – XC), в которой Z является импедансом; R – активной нагрузкой; XL , XC – индуктивной и емкостной нагрузками; J – поправочный коэффициент.
Последовательное и параллельное включение элементов
Элементы полной цепи или участка цепи могут соединяться последовательно или параллельно. Для каждого варианта действие тока и напряжения будет разным, поэтому закон Ома для замкнутой цепи в обоих случаях тоже отличается. Данный физические свойства комбинированно используются в различных электрических схемах.
Цепь последовательно включенных резистивных элементов
Если в качестве примера взять два элемента на отдельном участке, то поведение основных величин можно записать в следующем виде:
- I = I1= I2 (силы токов равны)
- U = U1+ U2 (общее напряжение состоит из суммы напряжений)
- R = R1+ R2 (общее сопротивление также является суммой двух сопротивлений)
Отсюда можно сделать вывод, что вне зависимости от количества резистивных элементов 1, 2 или 3, соединенных последовательно, сила тока на участке остается неизменной. Общее значение напряжения эквивалентно источнику ЭДС, а для каждого компонента определяется основной формулой закона Ома.
Цепь параллельно включенных резистивных элементов
При параллельном подключении действие закона Ома происходит несколько иначе:
- I = I1+ I2 … (силы токов, проходящих через элементы, складываются)
- U = U1= U2 … (все напряжения равны между собой)
- 1 / R = 1 / R1+ 1 / R2 + … (сопротивление суммируется по отдельной схеме)
Довольно часто используются смешанные схемы подключения, в которых используются оба варианта, объединенные в замкнутый контур. В этом случае сначала рассчитывается общий резистивный номинал на участке с параллельным подключением, после чего к полученному результату добавляется значение резистора на последовательном соединении.
Интегральная и дифференциальная формы закона
Все варианты, рассмотренные выше, подходят ближе к идеальным условиям, где каждый элемент имеет свой постоянный показатель. В том числе и в проводниках рассматривается однородная структура, хотя на практике такое встречается очень редко. Большинство схем состоят из множества участков, на которых используются разные проводники, отличающиеся материалом и сечением.
Большинство схем состоят из множества участков, на которых используются разные проводники, отличающиеся материалом и сечением.
Интегральная форма расчетов практически совпадает с действием закона Ома для полной цепи и других его производных. Следовательно, сила тока, протекающего в проводнике, будет зависеть от разности потенциалов на его концах и его полного сопротивления. То есть, напряжение можно определить: I * R = φ1 – φ2 + έ или же U=I x R.
Дифференциальная форма используется в основном для изучения и теоретических расчетов бесконечно малых проводников на ничтожно малом участке цепи. Коротко это можно написать в таком виде:
- ej = aE
В этом выражении А является удельной теплопроводностью, E – напряженностью электрического поля, j – плотностью потока частиц с электрическим зарядом. Следовательно, произведение ej будет плотностью электрического тока. Поскольку Закон Ома в данном случае касается лишь одной точки, поэтому он и получил название дифференциальной формы.
Выводы
В данной статье мы постарались дать простое объяснение закона Ома для полной цепи. Знание этих на первый взгляд простых вещей может сослужить Вам неплохую службу на экзамене. Специалисты в области электрики и электроники в своей работе постоянно используют закон Ома для полной электрической цепи и ее отдельных участков.
Видеоинструкция
Закон Ома для полной цепи и для участка цепи: формулы, описание и объяснение
Закон Ома — мощность
Когда через резистор протекает электрический ток, он рассеивает определенную часть мощности в виде тепла.
Мощность является функцией протекающего тока I (А) и приложенного напряжения V (В):
где
Р — мощность в ваттах (В)
В сочетании с законом Ома для участка цепи, формулу можно преобразовать в следующий вид:
или
Идеальный резистор рассеивает всю энергию и не сохраняет электрическую или магнитную энергию. Каждый резистор имеет предел мощности, которая может быть рассеяна, не оказывая повреждение резистору. Это мощность называется номинальной.
Каждый резистор имеет предел мощности, которая может быть рассеяна, не оказывая повреждение резистору. Это мощность называется номинальной.
Окружающие условия могут снизить или повысить это значение. Например, если окружающий воздух горячий, то способность рассеять излишнее тепло у резистора снижается, и на оборот, при низкой температуре окружающего воздух рассеиваемая способность резистора возрастает.
На практике, резисторы редко имеют обозначение номинальной мощности. Тем не менее, большинство из резисторов рассчитаны на 1/4 или 1/8 Вт.
Ниже приведена круговая диаграмма, которая поможет вам быстро определить связь между мощностью, силой тока, напряжением и сопротивлением. Для каждого из четырех параметров показано, как вычислить свое значение.
Параллельное и последовательное соединение
В электрике элементы соединяются либо последовательно — один за другим, либо параллельно — это когда к одной точке подключены несколько входов, к другой — выходы от тех же элементов.
Закон Ома для параллельного и последовательного соединения
Последовательное соединение
Как работает закон Ома для этих случаев? При последовательном соединении сила тока, протекающая через цепочку элементов, будет одинаковой. Напряжение участка цепи с последовательно подключенными элементами считается как сумма напряжений на каждом участке. Как можно это объяснить? Протекание тока через элемент — это перенос части заряда с одной его части в другую. То есть, это определенная работа. Величина этой работы и есть напряжение. Это физический смысл напряжения. Если с этим понятно, двигаемся дальше.
Последовательное соединение и параметры этого участка цепи
При последовательном соединении приходится переносить заряд по очереди через каждый элемент. И на каждом элементе это определенный «объем» работы. А чтобы найти объем работы на всем участке цепи, надо работу на каждом элементе сложить. Вот и получается, что общее напряжение — это сумма напряжений на каждом из элементов.
Точно так же — при помощи сложения — находится и общее сопротивление участка цепи. Как можно это себе представить? Ток, протекая по цепочке элементов, последовательно преодолевает все сопротивления. Одно за другим. То есть чтобы найти сопротивление, которое он преодолел, надо сопротивления сложить. Примерно так. Математический вывод более сложен, а так понять механизм действия этого закона проще.
Параллельное соединение
Параллельное соединение — это когда начала проводников/элементов сходятся в одной точке, а в другой — соединены их концы. Постараемся объяснить законы, которые справедливы для соединений этого типа. Начнем с тока. Ток какой-то величины подается в точку соединения элементов. Он разделяется, протекая по всем проводникам. Отсюда делаем вывод, что общий ток на участке равен сумме тока на каждом из элементов: I = I1 + I2 + I3.
Теперь относительно напряжения. Если напряжение — это работа по перемещению заряда, тоо работа, которая необходима на перемещение одного заряда будет одинакова на любом элементе. То есть, напряжение на каждом параллельно подключенном элементе будет одинаковым. U = U1=U2=U3. Не так весело и наглядно, как в случае с объяснением закона Ома для участка цепи, но понять можно.
То есть, напряжение на каждом параллельно подключенном элементе будет одинаковым. U = U1=U2=U3. Не так весело и наглядно, как в случае с объяснением закона Ома для участка цепи, но понять можно.
Законы для параллельного соединения
Для сопротивления все несколько сложнее. Давайте введем понятие проводимости. Это характеристика, которая показывает насколько легко или сложно заряду проходить по этому проводнику. Понятно, что чем меньше сопротивление, тем проще току будет проходить. Поэтому проводимость — G — вычисляется как величина обратная сопротивлению. В формуле это выглядит так: G = 1/R.
Для чего мы говорили о проводимости? Потому что общая проводимость участка с параллельным соединением элементов равна сумме проводимости для каждого из участков. G = G1 + G2 + G3 — понять несложно. Насколько легко току будет преодолеть этот узел из параллельных элементов, зависит от проводимости каждого из элементов. Вот и получается, что их надо складывать.
Теперь можем перейти к сопротивлению. Так как проводимость — обратная к сопротивлению величина, можем получить следующую формулу: 1/R = 1/R1 + 1/R2 + 1/R3.
Так как проводимость — обратная к сопротивлению величина, можем получить следующую формулу: 1/R = 1/R1 + 1/R2 + 1/R3.
Что нам дает параллельное и последовательное соединение?
Теоретические знания — это хорошо, но как их применить на практике? Параллельно и последовательно могут соединяться элементы любого типа. Но мы рассматривали только простейшие формулы, описывающие линейные элементы. Линейные элементы — это сопротивления, которые еще называют «резисторы». Итак, вот как можно использовать полученные знания:
Если в наличии нет резистора большого номинала, но есть несколько более «мелких», нужное сопротивление можно получить соединив последовательно несколько резисторов. Как видите, это полезный прием.
Для продления срока жизни батареек, их можно соединять параллельно. Напряжение при этом, согласно закону Ома, останется прежним (можно убедиться, измерив напряжение мультиметром). А «срок жизни» сдвоенного элемента питания будет значительно больше, нежели у двух элементов, которые сменят друг друга
Только обратите внимание: параллельно соединять можно только источники питания с одинаковым потенциалом.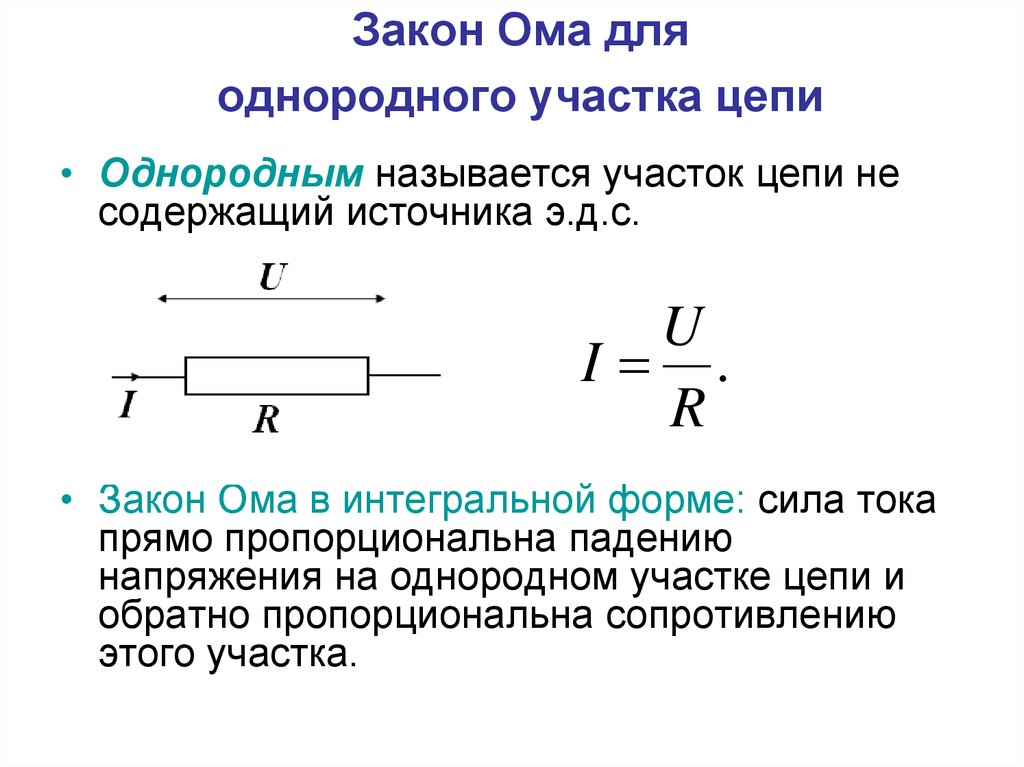 То есть, севшую и новую батарейки соединять нельзя
То есть, севшую и новую батарейки соединять нельзя
Если все-таки соединить, та батарейка которая имеет больший заряд, будет стремиться зарядить менее заряженную. В результате общий их заряд упадет до низкого значения.
В общем, это наиболее распространенные варианты использования этих соединений.
Параметры постоянного тока
Как и всякая физическая величина, постоянный электрический ток характеризуется целым рядом параметров, имеющих непосредственное к нему отношение и отношение к взаимосвязанным с ним величинам.
Величина постоянного тока (сила тока)
Прежде чем говорить о силе тока, определимся с таким понятием, как электрический заряд, выражающий способность тел участвовать в электромагнитных явлениях типа создания электромагнитного поля и электромагнитного взаимодействия.
Впервые это понятие было введено в конце XVIII века французским учёным Шарлем Кулоном, сформулировавшим тогда же свой знаменитый закон о силе взаимодействия между точечными зарядами в зависимости от разделяющего их расстояния. В честь него единица измерения электрического заряда (количества электричества) стала называться «Кулон» (Кл).
В честь него единица измерения электрического заряда (количества электричества) стала называться «Кулон» (Кл).
Только опираясь на понятие электрического заряда, можно говорить о величине (силе) тока, формула расчёта которого (для равномерного движения зарядов) выглядит следующим образом:
I = Q/t
Что можно выразить следующими словами: сила тока прямо пропорциональна количеству зарядов, проходящих через поперечное сечение проводника за единицу времени. Здесь:
- I – ток, измеряемый в амперах (Андре Мари-Ампер – ещё один французский физик, внёсший значительный вклад в теорию электромагнетизма).
- Q – электрический заряд, измеряемый в кулонах или ампер-часах (А·ч). 1 А·ч = 3600 Кл.
- t – единица времени.
Для измерения силы тока используются амперметры, включаемые последовательно с источником электрического тока.
Плотность тока
Ещё одно важное понятие, необходимое в целях правильного выбора токопроводящего сечения линий электропередачи.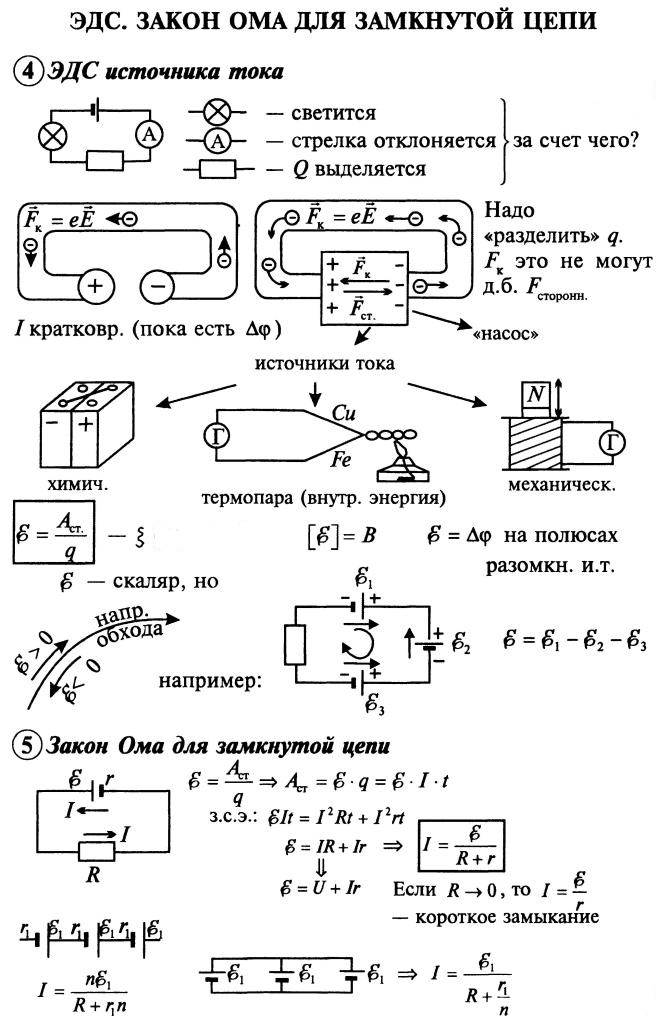 Плотность тока это:. j = I/S
Плотность тока это:. j = I/S
j = I/S
Где: I – сила тока в амперах. S – площадь поперечного сечения в м2. J – плотность тока в А/м2 или А/мм2.
Электродвижущая сила (ЭДС)
Электродвижущая сила (ЭДС) – это величина, характеризующая работу первичного источника электрической энергии по созданию постоянного электрического тока.
E = A/Q
E – электродвижущая сила (ЭДС), измеряемая в вольтах (Алессандро Вольта – известнейший итальянский физик). A – работа, измеряемая в джоулях (Джеймс Прескотт Джоуль – английский физик, внёсший значительный вклад в развитие термодинамики).
Электрическое напряжение
Электрическое напряжение – это величина, показывающая работу эффективного электрического поля, затраченную на перенос единичного пробного заряда из точки A в точку B.
UAB = φA – φB + EAB
φA – φB – разница потенциалов между точками A и B. EAB – электродвижущая сила, возникающая на искомом участке цепи постоянного тока. Здесь все величины измеряются в вольтах. Для определения величины напряжения применяются вольтметры, подключаемые параллельно участку измерения напряжения.
Для определения величины напряжения применяются вольтметры, подключаемые параллельно участку измерения напряжения.
Использование на практике
Закон Ома лежит в основе всех расчетов производимых в электронике и электротехнике. Будущих специалистов с первых дней учат, как использовать так называемый треугольник. Чтобы найти какую-то искомую величину, должны выполняться простые арифметические действия. Если два оставшихся параметра находятся в одной строке – они перемножаются. Если на разных уровнях, то верхний всегда делится на нижний.
Самые простые вычисления производятся на основе данных измерительных приборов. На участке цепи измерение тока выполняется амперметром, а напряжения – вольтметром. После этого найти сопротивление математическим путем не составит труда.
Для замеров сопротивления тоже есть прибор – омметр. Полученное выражение, подставляется в одну из формул, после чего находятся величины силы тока или напряжения. Точность омметра зависит от стабильности напряжения, подаваемого источником тока. Стабилизация проводится путем добавления резистора, выполняющего функцию регулятора.
Стабилизация проводится путем добавления резистора, выполняющего функцию регулятора.
Иногда требуется исключить из схемы какой-нибудь элемент без демонтажа. С этой целью проводится шунтирование, когда приходится устанавливать проводник на входных клеммах ненужного резистора. Ток начинает идти через шунт с меньшим сопротивлением, а напряжение на резисторе падает до нуля.
Закон Ома используется в защитных системах. Это делается с помощью уставок, обеспечивающих нормальную работу и отключающих питание лишь в аварийных ситуациях.
Неоднородный участок цепи постоянного тока
Неоднородную структуру имеет такой участок цепи, где помимо проводников и элементов, присутствует источник тока. Его ЭДС необходимо учитывать при расчетах общей силы тока на данном участке.
Существует формула, которая дает определение основным параметрам и процессам неоднородного участка: q = q0 x n x V. Ее показатели характеризуются следующим образом:
- В процессе перемещения зарядов (q) они приобретают определенную плотность.
 Ее показатели зависят от силы тока и площади поперечного сечения проводника (S).
Ее показатели зависят от силы тока и площади поперечного сечения проводника (S). - В условиях определенной концентрации (n) можно точно указать численность единичных зарядов (q0), которые были перемещены за единичный отрезок времени.
- Для расчетов проводник условно считается цилиндрическим участком, имеющим какой-то объем (V).
При подключении проводника к аккумулятору, последний через некоторое время будет разряжен. То есть, движение электронов постепенно замедляется и, в конце концов, прекратится совсем. Этому способствует молекулярная решетка проводника, оказывающая противодействие, столкновения электронов между собой и другие факторы. Для преодоления такого сопротивления следует дополнительно приложить определенные сторонние силы.
Во время расчетов эти силы суммируются с кулоновскими. Кроме того, для перенесения единичного заряда q из 1-й точки во 2-ю потребуется выполнение работы А1-2 или просто А12. С этой целью создается разница потенциалов (ϕ1 – ϕ2).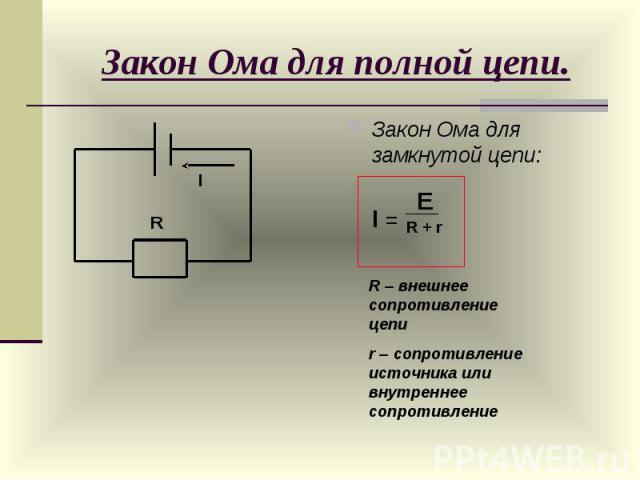 Под действием источника постоянного тока возникает ЭДС, перемещающая заряды по цепи. Величина общего напряжения будет состоять из всех сил, отмеченных выше.
Под действием источника постоянного тока возникает ЭДС, перемещающая заряды по цепи. Величина общего напряжения будет состоять из всех сил, отмеченных выше.
Полярность подключения к источнику постоянного тока нужно учитывать в расчетах. При изменении клемм будет меняться и ЭДС, ускоряющая или замедляющая перемещение зарядов.
Закон Ома для переменного тока
При наличии индуктивности или ёмкости в цепи переменного тока необходимо учитывать их реактивное сопротивление.В таком случае запись Закона Ома будет иметь вид:
I = U/Z
Здесь Z — полное (комплексное) сопротивление цепи — импеданс. В него входит активная R и реактивная X составляющие.Реактивное сопротивление зависит от номиналов реактивных элементов, от частоты и формы тока в цепи.Более подробно ознакомится с комплексным сопротивлением можно на страничке импеданс.
С учётом сдвига фаз φ, созданного реактивными элементами, для синусоидального переменного тока обычно записывают Закон Ома в комплексной форме:— комплексная амплитуда тока. = Iampe jφ— комплексная амплитуда напряжения. = Uampe jφ— комплексное сопротивление. Импеданс.φ — угол сдвига фаз между током и напряжением.e — константа, основание натурального логарифма.j — мнимая единица.Iamp , Uamp — амплитудные значения синусоидального тока и напряжения.
= Iampe jφ— комплексная амплитуда напряжения. = Uampe jφ— комплексное сопротивление. Импеданс.φ — угол сдвига фаз между током и напряжением.e — константа, основание натурального логарифма.j — мнимая единица.Iamp , Uamp — амплитудные значения синусоидального тока и напряжения.
Для ЭДС
Перед тем как рассмотреть закон Ома для полной (замкнутой) цепи приведу правило знаков для ЭДС, которое гласит:Если внутри источника ЭДС ток идет от катода (-) к аноду (+) (направление напряженности поля сторонних сил совпадает с направлением тока в цепи, то ЭДС такого источника считается положительной. В противном случае – ЭДС считается отрицательной.
Практическим применением этого правила является возможность приведения нескольких источников ЭДС в цепи к одному с величиной E=E1+E2+…+En, естественно, с учетом знаков, определяемых по вышеприведенному правилу. Например (рис.3.3) E=E1+E2-E3. При отсутствии встречно включенного источника E3 (на практике так почти никогда не бывает) имеем широко распространенное последовательное включение элементов питания, при котором их напряжения суммируются.
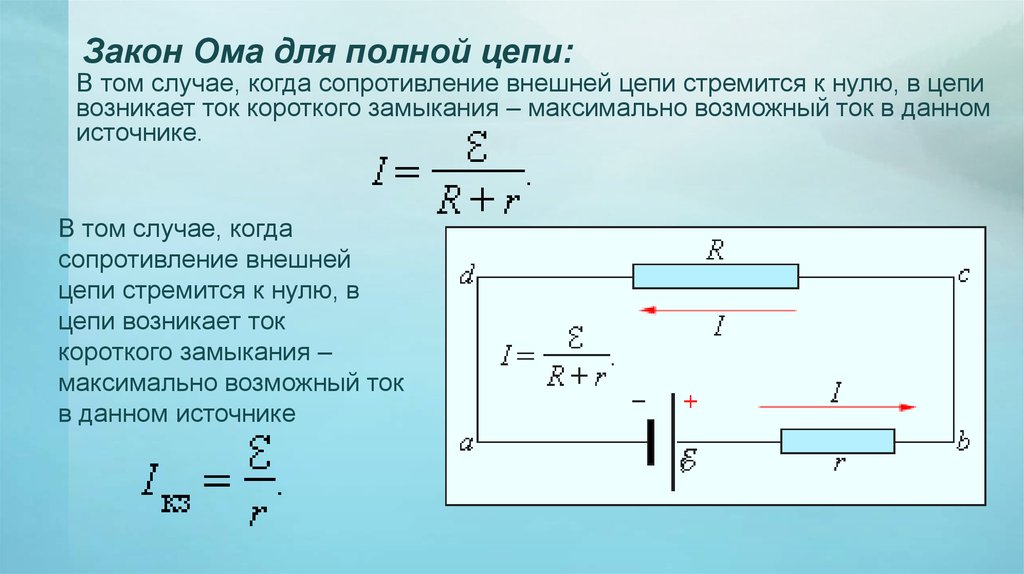
Закон Ома для полной цепи – его еще можно назвать закон ома для замкнутой цепи, имеет вид I=E/(R+r). Приведенная формула закона Ома содержит обозначение r, которое еще не упоминалось. Это внутреннее сопротивление источника ЭДС. Оно достаточно мало, в большинстве случаев при практических расчетах им можно пренебречь (при условии, что R>>r – сопротивление цепи много больше внутреннего сопротивления источника). Однако, когда они соизмеримы, пренебрегать величиной r нельзя.
Как вариант можно рассмотреть случай, при котором R=0 (короткое замыкание). Тогда приведенная формула закона Ома для полной цепи примет вид: I=E/r, то есть величина внутреннего сопротивления будет определять ток короткого замыкания. Такая ситуация вполне может быть реальной. Закон Ома рассмотрен здесь достаточно бегло, но приведенных формул достаточно для проведения большинства расчетов, примеры которых, по мере размещения других материалов я буду приводить.
Полноценную цепь составляет уже участок (участки), а также источник ЭДС. То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС. Поэтому логичным является некоторое изменение выше рассмотренной формулы:
То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС. Поэтому логичным является некоторое изменение выше рассмотренной формулы:
I = U / (R + r)
Конечно, значение внутреннего сопротивления ЭДС в законе Ома для полной электрической цепи можно считать ничтожно малым, правда во многом это значение сопротивления зависит от структуры источника ЭДС. Тем не менее, при расчетах сложных электронных схем, электрических цепей с множеством проводников, наличие дополнительного сопротивления является важным фактором.
Как для участка цепи, так и для полной схемы следует учитывать естественный момент – использование тока постоянной или переменной величины. Если отмеченные выше моменты, характерные для закона Ома, рассматривались с точки зрения использования постоянного тока, соответственно с переменным током всё выглядит несколько иначе.
Как найти с помощью формулы напряжение
Людей, интересующихся электричеством и физикой, всегда волнует вопрос, как найти напряжения, если известны другие характеристики. Его можно найти через многие формулы: в соответствии с законом Ома, через работу тока, путём сложения всех напряжений в электрической цепи и практическим способом – с помощью вольтметра. Как вычислить показатель с помощью последнего способа было описано выше.
Его можно найти через многие формулы: в соответствии с законом Ома, через работу тока, путём сложения всех напряжений в электрической цепи и практическим способом – с помощью вольтметра. Как вычислить показатель с помощью последнего способа было описано выше.
Важно! В цепях с последовательным соединением общее напряжение – сумма значений каждой нагрузки. При параллельном соединении общее напряжение равно значению каждой лампочки, у которых оно также эквивалентно
Вам это будет интересно WAGO соединители
Измерение напряжения
По каким формулам вычисляется напряжение через работу и сама сила тока, рассказывают на уроках физики, так как эти величины считаются базовыми. Работа тока равна произведению напряжения и заряда: A = U*q. Также, из этой формулы выводится A = U*I*t, так как заряд – произведение силы тока и времени. Из них следует, что U = A/q или U = A/(I*t). Кроме того, одной из основных является формула напряжения, выведенная из закона Ома: U = R/I.
Важно! Определить напряжение можно и через мощность электрического тока. Мощность равна A/t, и, так как A = U*I*t, конечная формула выглядит, как P = (U*I*t)/t
Мощность равна A/t, и, так как A = U*I*t, конечная формула выглядит, как P = (U*I*t)/t
Здесь t сократится, и останется P = U*I, из которой следует, что U = P/I.
Отдельный участок и полная электрическая цепь
Закон Ома, применительно к участку или всей цепи, может рассматриваться в двух вариантах расчетов:
- Отдельный краткий участок. Является частью схемы без источника ЭДС.
- Полная цепь, состоящая из одного или нескольких участков. Сюда же входит источник ЭДС со своим внутренним сопротивлением.
Расчет тока участка электрической схемы
В этом случае применяется основная формула I = U/R, в которой I является силой тока, U – напряжением, R – сопротивлением. По ней можно сформулировать общепринятую трактовку закона Ома:
Данная формулировка является основой для многих других формул, представленных на так называемой «ромашке» в графическом исполнении. В секторе Р – определяется мощность, в секторах I, U и R – проводятся действия, связанные с силой тока, напряжением и сопротивлением.
Каждое выражение – и основное и дополнительные, позволяют рассчитать точные параметры элементов, предназначенных для использования в схеме.
Специалисты, работающие с электрическими цепями, выполняют быстрое определение любого из параметров по методике треугольников, изображенных на рисунке.
В расчетах следует учитывать сопротивление проводников, соединяющих между собой элементы участка. Поскольку они изготавливаются из разных материалов, данный параметр будет отличаться в каждом случае. Если же потребуется сформировать полную схему, то основная формула дополняется параметрами источника напряжения, например, аккумуляторной батареи.
Вариант расчета для полной цепи
Полная цепь состоит из отдельно взятых участков, объединенных в единое целое вместе с источником напряжения (ЭДС). Таким образом, существующее сопротивление участков дополняется внутренним сопротивлением подключенного источника. Следовательно, основная трактовка, рассмотренная ранее, будет читаться следующим образом: I = U / (R + r). Здесь уже добавлен резистивный показатель (r) источника ЭДС.
Здесь уже добавлен резистивный показатель (r) источника ЭДС.
С точки зрения чистой физики этот показатель считается очень малой величиной. Однако, на практике, рассчитывая сложные схемы и цепи, специалисты вынуждены его учитывать, поскольку дополнительное сопротивление оказывает влияние на точность работы. Кроме того, структура каждого источника очень разнородная, в результате, сопротивление в отдельных случаях может выражаться достаточно высокими показателями.
Приведенные расчеты выполняются применительно к цепям постоянного тока. Действия и расчеты с переменным током производятся уже по другой схеме.
Действие закона к переменной величине
При переменном токе сопротивление цепи будет представлять из себя так называемый импеданс, состоящий из активного сопротивления и реактивной резистивной нагрузки. Это объясняется наличием элементов с индуктивными свойствами и синусоидальной величиной тока. Напряжение также является переменной величиной, действующей по своим коммутационным законам.
Следовательно, схема цепи переменного тока по закону Ома рассчитывается с учетом специфических эффектов: опережения или отставания величины тока от напряжения, а также наличия активной и реактивной мощности. В свою очередь, реактивное сопротивление включает в себя индуктивную или емкостную составляющие.
Все этим явлениям будет соответствовать формула Z = U / I или Z = R + J * (XL – XC), в которой Z является импедансом; R – активной нагрузкой; XL , XC – индуктивной и емкостной нагрузками; J – поправочный коэффициент.
Закон Джоуля-Ленца
Закон Джоуля-Ленца устанавливает связь между током «бегающему» по проводнику, его сопротивлению и теплом которое при этом выделяется.
В математическом символизме закон Джоуля-Ленца выглядит так:
Q=I2×R×t,где Q это количество выделяемого тепла в проводнике, в Джоулях;I-сила тока;R-сопротивление проводника;t-время прохождения тока в секундах.
В качестве информации: Ленц это русский физик Эмилий Христианович Ленц. Русский физик, электротехник, физический географ.1804-1865 года жизни.
Русский физик, электротехник, физический географ.1804-1865 года жизни.
Говоря о практическом применении закона Джоуля-Ленца, трудно назвать в какой части электрики он не проявляется. Электрические обогреватели, электрические водонагреватели, тепловые завесы, выбор автоматов защиты, тепловые реле в автоматике и многое другое.
Конечно это не все основные законы электрики. На по своему значению эти законы имеют фундаментальное значение.
Другие статьи сайта
- Автоматы защиты
- Виды опор линий электропередачи по материалу
- Виды опор по назначению
- Воздушные линии электропередачи проводами СИП
- Деревянные опоры воздушных линий электропередачи
- Железобетонные опоры линий электропередачи
- Железобетонные опоры линий электропередачи
- Защита человека от поражения электрическим током, прямое и косвенное прикосновение
- Как получает электроэнергию потребитель низкого напряжения 380 Вольт
- Колодцы кабельной сети этапы установки
Единицы измерения: вольт, ампер и ом
Чтобы иметь возможность делать осмысленные утверждения об этих величинах в цепях, нам нужно уметь описывать их количества так же, как мы могли бы количественно определить массу, температуру, объем, длину или любые другие физические величины. Для массы мы можем использовать единицы «килограмм» или «грамм». Для температуры мы можем использовать градусы Фаренгейта или градусы Цельсия. В таблице ниже приведены стандартные единицы измерения электрического тока, напряжения и сопротивления:
Для массы мы можем использовать единицы «килограмм» или «грамм». Для температуры мы можем использовать градусы Фаренгейта или градусы Цельсия. В таблице ниже приведены стандартные единицы измерения электрического тока, напряжения и сопротивления:
Единицы измерения тока, напряжения, сопротивления в таблице:
| Величина | Символ | Единица измерения | Сокращение единицы измерения |
| Ток | I | Ампер | А |
| Напряжение | V | Вольт | В |
| Сопротивление | R | Ом | Ом |
«Символ», присвоенный каждой величине, представляет собой стандартную букву латинского алфавита, используемую для представления этой величины в формулах. Подобные стандартизированные буквы распространены во всех физических и технических дисциплинах и признаны во всем мире. «Сокращение единицы измерения» для каждой величины представляет собой алфавитный символ(ы), используемый в качестве сокращенного обозначения конкретной единицы измерения.
Каждая единица измерения названа в честь известного экспериментатора в области электричества: ампер в честь француза Андре М. Ампера, вольт в честь итальянца Алессандро Вольта, а ом в честь немца Георга Симона Ома.
Математический символ для каждой величины также имеет значение. «R» для сопротивления и «V» для напряжения говорят сами за себя («Resistance» и «Voltage», соответственно), тогда как «I» для тока кажется немного странным. Предполагается, что буква «I» должна представлять «интенсивность» («Intensity»)(потока заряда). Судя по исследованиям, которые мне удалось провести, кажется, что есть некоторые разногласия по поводу значения слова «I». Другой символ напряжения, «E», означает «электродвижущую силу» («Electromotive force»). Символы «E» и «V» по большей части взаимозаменяемы, хотя в некоторых текстах «E» зарезервировано для обозначения напряжения на источнике (таком как батарея или генератор), а «V»– для обозначения напряжения на любом другом элементе.
Все эти символы выражаются заглавными буквами, за исключением случаев, когда величина (особенно напряжение или ток) описывается в терминах короткого периода времени (так называемые «мгновенные» значения). Например, напряжение батареи, которое стабильно в течение длительного периода времени, будет обозначаться заглавной буквой «E», тогда как пиковое напряжения при ударе молнии в тот самый момент, когда она попадает в линию электропередачи, скорее всего, будет обозначаться строчной буквой «е» (или строчной буквой «v»), чтобы отметить это значение как имеющееся в один момент времени. Это же соглашение о нижнем регистре справедливо и для тока: строчная буква «i» представляет ток в некоторый момент времени. Однако большинство измерений в цепях постоянного тока, которые стабильны во времени, будут обозначаться заглавными буквами.
Например, напряжение батареи, которое стабильно в течение длительного периода времени, будет обозначаться заглавной буквой «E», тогда как пиковое напряжения при ударе молнии в тот самый момент, когда она попадает в линию электропередачи, скорее всего, будет обозначаться строчной буквой «е» (или строчной буквой «v»), чтобы отметить это значение как имеющееся в один момент времени. Это же соглашение о нижнем регистре справедливо и для тока: строчная буква «i» представляет ток в некоторый момент времени. Однако большинство измерений в цепях постоянного тока, которые стабильны во времени, будут обозначаться заглавными буквами.
Источник ЭДС в полной цепи
Для возникновения электрического тока в замкнутой цепи, эта цепь должна содержать хотя бы один особый элемент, в котором будет происходить работа по переносу зарядов между его полюсами. Силы, переносящие заряды внутри этого элемента, делают это против электрического поля, а значит, их природа должна быть отлична от электрической. Поэтому такие силы называются сторонними.
Поэтому такие силы называются сторонними.
Рис. 1. Сторонние силы в физике.
Элемент электрической цепи, в котором происходит работа сторонних сил по переносу зарядов против действия электрического поля, называется источником тока. Главная его характеристика – это величина сторонних сил. Для ее характеристики вводится специальная мера – Электродвижущая Сила (ЭДС), она обозначается буквой $\mathscr{E}$.
Значение ЭДС источника тока равно отношению сторонних сил по переносу заряда к величине этого заряда:
$$\mathscr{E}={A_{ст}\over q}$$
Поскольку смысл ЭДС очень близок к смыслу электрического напряжения (напомним, напряжение – это отношение работы, совершаемой электрическим полем, переносящим заряд, к величине этого заряда), то ЭДС так же, как и напряжение, измеряется в Вольтах:
$$1В={Дж\overКл}$$
Второй важнейшей электрической характеристикой реального источника тока является его внутреннее сопротивление. При переносе зарядов между клеммами происходит их взаимодействие с веществом источника ЭДС, а поэтому, источник для электрического тока также представляет некоторое сопротивление. Внутреннее сопротивление, как и обычное сопротивление, измеряется в Омах, но обозначается малой латинской буквой $r$.
Внутреннее сопротивление, как и обычное сопротивление, измеряется в Омах, но обозначается малой латинской буквой $r$.
Рис. 2. Примеры источников тока.
Просадка напряжения
Итак, знакомьтесь, автомобильный аккумулятор!
Для дальнейшего его использования, припаяем к нему два провода: красный на плюс, черный на минус
Наш подопечный готов к бою.
Теперь берем автомобильную лампочку-галогенку и тоже припаяем к ней два проводка с крокодилами. Я припаялся к клеммам на “ближний” свет.
Первым делом давайте замеряем напряжение на клеммах аккумулятора
12,09 вольт. Вполне нормально, так как наш аккумулятор выдает именно 12 вольт. Забегу чуток вперед и скажу, что сейчас мы замерили именно ЭДС.
Подключаем галогенную лампу к аккумулятору и снова замеряем напряжение:
Видели да? Напряжение на клеммах аккумулятора просело до 11,79 Вольт!
А давайте замеряем, сколько потребляет тока наша лампа в Амперах. Для этого составляем вот такую схемку:
Желтый мультиметр у нас будет замерять напряжение, а красный мультиметр – силу тока. Как замерять с помощью мультиметра силу тока и напряжение, можно прочитать в этой статье.
Как замерять с помощью мультиметра силу тока и напряжение, можно прочитать в этой статье.
Смотрим на показания приборов:
Как мы видим, наша лампа потребляет 4,35 Ампер. Напряжение просело до 11,79 Вольт.
Давайте вместо галогенной лампы поставим простую лампочку накаливания на 12 Вольт от мотоцикла
Смотрим показания:
Лампочка потребляет силу тока в 0,69 Ампер. Напряжение просело до 12 Вольт ровно.
Какие выводы можно сделать? Чем больше нагрузка потребляет силу тока, тем больше просаживается напряжение на аккумуляторе.
ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ
Расчет параметров электрической цепи
при параллельном соединении сопротивлений:
1. сила тока в неразветвленном участке цепи равна сумме сил токов
во всех параллельно соединенных участках
2. напряжение на всех параллельно соединенных участках цепи одинаково
3. при параллельном соединении сопротивлений складываются величины, обратные сопротивлению :
( R — сопротивление проводника,
1/R — электрическая проводимость проводника)
Если в цепь включены параллельно только два сопротивления, то:
( при параллельном соединении общее сопротивление цепи меньше меньшего из включенных сопротивлений )
4. работа электрического тока в цепи, состоящей из параллельно соединенных участков,
работа электрического тока в цепи, состоящей из параллельно соединенных участков,
равна сумме работ на отдельных участках:A=A1+A2
5. мощность электрического тока в цепи, состоящей из параллельно соединенных участков,
равна сумме мощностей на отдельных участках:P=P1+P2
Для двух сопротивлений:
т.е. чем больше сопротивление, тем меньше в нём сила тока.
Домашняя работа.
Задание 1. Ответить на вопросы.
- Какое соединение проводников называют последовательным? Изобразите его на схеме.
- Какая электрическая величина одинакова для всех проводников, соединённых последовательно?
- Как найти общее сопротивление цепи, зная сопротивление отдельных проводников, при последовательном соединении?
- Как найти напряжение участка цепи, состоящего из последовательно соединённых проводников, зная напряжение на каждом?
- Какое соединение проводников называют параллельным? Изобразите его на схеме.
- Какая из электрических величин одинакова для всех проводников, соединённых параллельно?
- Как выражается сила тока в цепи до её разветвления через силы токов в отдельных ветвях разветвления?
- Как изменяется общее сопротивление разветвления после увеличения числа проводников в разветвлении?
- Какое соединение проводников применяется в жилых помещениях? Какие напряжения используются для бытовых нужд?
Задание 2.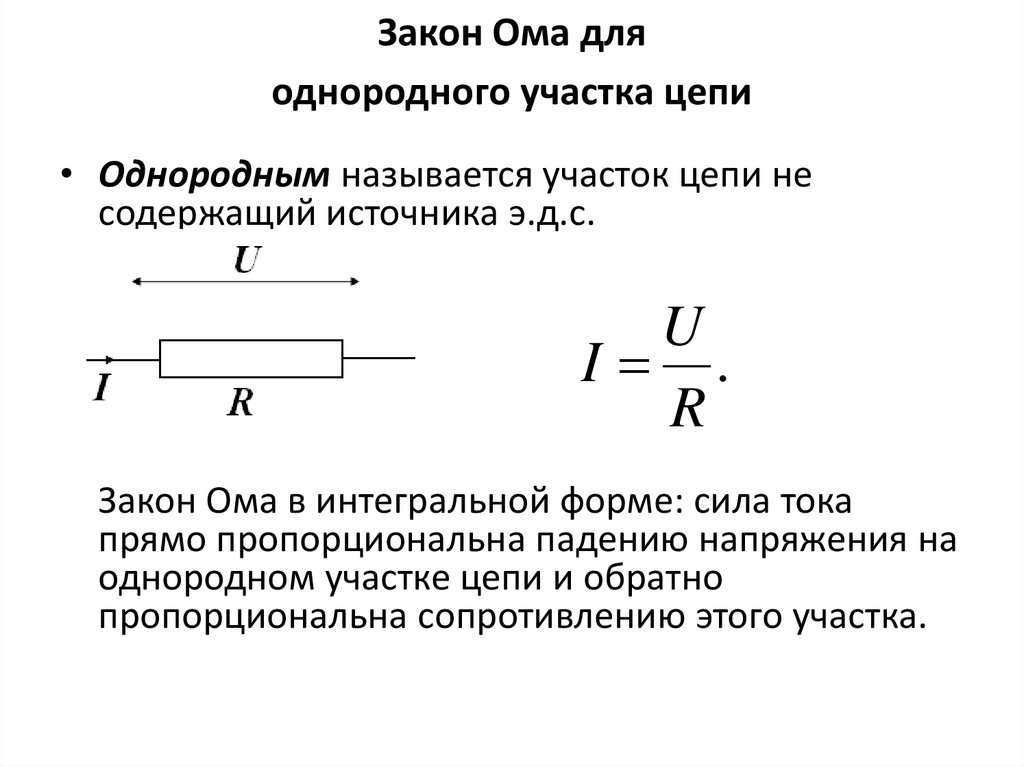 Решите задачи.
Решите задачи.
1. Две лампочки соединены последовательно. Сила тока на первой лампочке 2А. Найдите общее напряжение и напряжение на каждой из ламп, если сопротивление на первой лампе 3Ом, а на второй 4Ом.
2. Две лампочки соединены параллельно. Напряжение на второй лампочке10В. Найдите силу тока в цепи и на каждой из ламп, если сопротивление на первой лампе 1Ом, а на второй 2Ом.
- http://www.tepka.ru/
- http://class-fizika.narod.ru
- http://znaika.ru/catalog/10-klass/physics/
- https://www.youtube.com/watch?v=NB7hOVYe7h0
- https://www.youtube.com/watch?v=cVKE9NItreo
- https://www.youtube.com/watch?v=0hFWeR8ybxs
- https://www.youtube.com/watch?v=EDI8DzWSSWY
- https://www.youtube.com/watch?v=bH_-qGnjJqc
Электродвижущая сила источника тока
Двигая разноименные частицы к противоположным полюсам ИТ, сторонние силы преодолевают сопротивление электростатического поля. Следовательно, они совершают некую работу Ас. Она пропорциональна заряду q, перемещаемому за тот же промежуток времени вдоль электроцепи.
Она пропорциональна заряду q, перемещаемому за тот же промежуток времени вдоль электроцепи.
Что такое электродвижущая сила
Иными словами, Ас/q остается постоянным при любом значении данных величин, а следовательно, это соотношение может выступать характеристикой ИТ. Называют ее электродвижущей силой (ЭДС) и обозначают литерой Ԑ = Ас / q
Важно понимать условность данного термина. ЭДС – это не механическая сила, а энергетический параметр ИТ
ЭДС измеряется в тех же единицах, что и разность потенциалов (напряжение) – в вольтах (В). Например, у пальчиковой батарейки с полным зарядом, Ԑ составляет 1,5 В.
Формулировка для полной цепи
Трактовка для полной цепи будет несколько иной, чем для участка, поскольку в законе, составленном Омом, еще учитывает параметр «r», это сопротивление источника ЭДС. На рисунке ниже проиллюстрирована подобная схема.
Схема с подключенным с источником
Учитывая «r» ЭДС, формула предстанет в следующем виде:
Заметим, если «R» сделать равным 0, то появляется возможность рассчитать «I», возникающий во время короткого замыкания.
Напряжение будет меньше ЭДС, определить его можно по формуле:
Собственно, падение напряжения характеризуется параметром «I*r». Это свойство характерно многим гальваническим источникам питания.
Просадка напряжения
Итак, знакомьтесь, автомобильный аккумулятор!
Для дальнейшего его использования, припаяем к нему два провода: красный на плюс, черный на минус
Наш подопечный готов к бою.
Теперь берем автомобильную лампочку-галогенку и тоже припаяем к ней два проводка с крокодилами. Я припаялся к клеммам на «ближний» свет.
Первым делом давайте замеряем напряжение на клеммах аккумулятора
12,09 вольт. Вполне нормально, так как наш аккумулятор выдает именно 12 вольт. Забегу чуток вперед и скажу, что сейчас мы замерили именно ЭДС.
Забегу чуток вперед и скажу, что сейчас мы замерили именно ЭДС.
Подключаем галогенную лампу к аккумулятору и снова замеряем напряжение:
Видели да? Напряжение на клеммах аккумулятора просело до 11,79 Вольт!
А давайте замеряем, сколько потребляет тока наша лампа в Амперах. Для этого составляем вот такую схемку:
Желтый мультиметр у нас будет замерять напряжение, а красный мультиметр — силу тока. Как замерять с помощью мультиметра силу тока и напряжение, можно прочитать в этой статье.
Смотрим на показания приборов:
Как мы видим, наша лампа потребляет 4,35 Ампер. Напряжение просело до 11,79 Вольт.
Давайте вместо галогенной лампы поставим простую лампочку накаливания на 12 Вольт от мотоцикла
Смотрим показания:
Лампочка потребляет силу тока в 0,69 Ампер. Напряжение просело до 12 Вольт ровно.
Какие выводы можно сделать? Чем больше нагрузка потребляет силу тока, тем больше просаживается напряжение на аккумуляторе.
Переменный ток
Мы уже рассмотрели закон Ома для всей цепи для постоянного тока. Как же изменится формула при переменном токе? Прежде чем мы это узнаем, давайте охарактеризуем само понятие. Переменный ток – это движение электрически заряженных частиц, направление и значение которых изменяется с течением времени. В отличие от постоянного он сопровождается дополнительными факторами, порождающими новый вид сопротивления (реактивного). Свойственно оно конденсаторам и катушкам индуктивности.
Закон Ома для полной цепи для переменного тока имеет вид:
I = U / Z,
где Z – комплексное сопротивление, состоящее из активных и реактивных.
простое объяснение для чайников с формулой и понятиями. Закон Ома для электрической цепи
Автор Andrey Ku На чтение 31 мин Опубликовано
Содержание
- Закон Ома для цепи
- Для ЭДС
- Для полной цепи
- Для переменного тока
- Для замкнутой цепи
- Сфера применения
- Закон Ома для замкнутой цепи
- Закон Ома для неоднородного участка цепи
- Закон Ома для переменного тока
- Метода треугольника закона Ома
- Значение Закона Ома
- Сопротивление
- Таблица удельных сопротивлений различных материалов
- Резистор
- Реостат
- Закон Ома для участка цепи
- Закон Ома для полной цепи
- Что такое ЭДС и откуда она берется
- Когда «сопротивление бесполезно»
- Формула Закона Джоуля-Ленца
- Преобразованные формулы Закона Ома и Джоуля-Ленца
- Применение закона Ома на практике
- Таблица-шпаргалка
- Последовательное и параллельное включение элементов
- Цепь последовательно включенных резистивных элементов
- Цепь параллельно включенных резистивных элементов
- Интегральная и дифференциальная формы закона
- Параллельное и последовательное соединение
- Последовательное соединение
- Параллельное соединение
- Что нам дает параллельное и последовательное соединение?
- Интегральная и дифференциальная формы закона
Закон Ома для цепи
Закон Ома для участка цепи, безусловно, можно описать известной из школьного курса физики формулой: I=U/R, но некоторые изменения и уточнения внести, думаю, стоит. Возьмем замкнутую электрическую цепь и рассмотрим ее участок между точками 1-2. Для простоты я взял участок электрической цепи, не содержащий источников ЭДС (Е).
Возьмем замкнутую электрическую цепь и рассмотрим ее участок между точками 1-2. Для простоты я взял участок электрической цепи, не содержащий источников ЭДС (Е).
Итак, закон Ома для рассматриваемого участка цепи имеет вид:
φ1-φ2=I*R, где
- I – ток, протекающий по участку цепи.
- R – сопротивление этого участка.
- φ1-φ2 – разность потенциалов между точками 1-2.
Если учесть, что разность потенциалов это напряжение, то приходим к производной формулы закона Ома, которая приведена в начале страницы: U=I*R. Это формула закона Ома для пассивного участка цепи (не содержащего источников электроэнергии).
Интересно по теме: Как проверить стабилитрон.
В неразветвленной электрической цепи (рис.2) сила тока во всех участках одинакова, а напряжение на любом участке определяется его сопротивлением:
- U1=I*R1
- U2=I*R2
- Un=I*Rn
- U=I*(R1+R2+…+Rn
Отсюда можно получить формулы, которые пригодятся при практических вычислениях. Например:
Например:
U=U1+U2+…+Un или U1/U2/…/Un=R1/R2/…/Rn
Расчет сложных (разветвленных) цепей осуществляется с помощью законов Кирхгофа.
Закон Ома для участка цепи.
Для ЭДС
Перед тем как рассмотреть закон Ома для полной (замкнутой) цепи приведу правило знаков для ЭДС, которое гласит:
Если внутри источника ЭДС ток идет от катода (-) к аноду (+) (направление напряженности поля сторонних сил совпадает с направлением тока в цепи, то ЭДС такого источника считается положительной. В противном случае – ЭДС считается отрицательной.
Практическим применением этого правила является возможность приведения нескольких источников ЭДС в цепи к одному с величиной E=E1+E2+…+En, естественно, с учетом знаков, определяемых по вышеприведенному правилу. Например (рис.3.3) E=E1+E2-E3. При отсутствии встречно включенного источника E3 (на практике так почти никогда не бывает) имеем широко распространенное последовательное включение элементов питания, при котором их напряжения суммируются.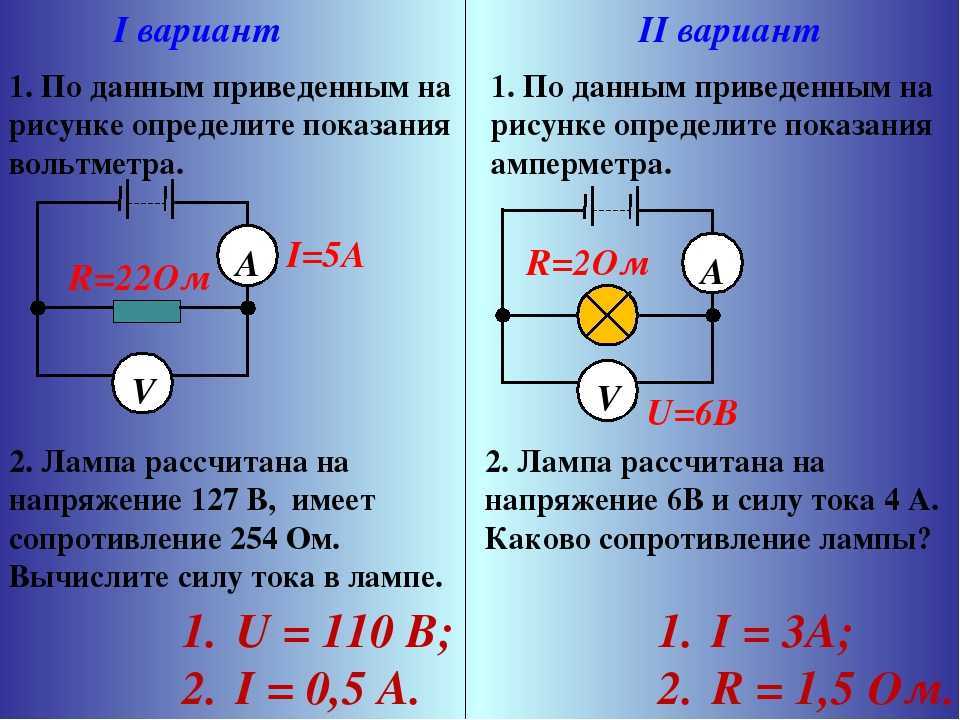
Для полной цепи
Закон Ома для полной цепи – его еще можно назвать закон ома для замкнутой цепи, имеет вид I=E/(R+r). Приведенная формула закона Ома содержит обозначение r, которое еще не упоминалось. Это внутреннее сопротивление источника ЭДС. Оно достаточно мало, в большинстве случаев при практических расчетах им можно пренебречь (при условии, что R>>r – сопротивление цепи много больше внутреннего сопротивления источника). Однако, когда они соизмеримы, пренебрегать величиной r нельзя.
Как вариант можно рассмотреть случай, при котором R=0 (короткое замыкание). Тогда приведенная формула закона Ома для полной цепи примет вид: I=E/r, то есть величина внутреннего сопротивления будет определять ток короткого замыкания. Такая ситуация вполне может быть реальной. Закон Ома рассмотрен здесь достаточно бегло, но приведенных формул достаточно для проведения большинства расчетов, примеры которых, по мере размещения других материалов я буду приводить.
Полноценную цепь составляет уже участок (участки), а также источник ЭДС. То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС. Поэтому логичным является некоторое изменение выше рассмотренной формулы:
То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС. Поэтому логичным является некоторое изменение выше рассмотренной формулы:
I = U / (R + r)
Конечно, значение внутреннего сопротивления ЭДС в законе Ома для полной электрической цепи можно считать ничтожно малым, правда во многом это значение сопротивления зависит от структуры источника ЭДС. Тем не менее, при расчетах сложных электронных схем, электрических цепей с множеством проводников, наличие дополнительного сопротивления является важным фактором.
Как для участка цепи, так и для полной схемы следует учитывать естественный момент – использование тока постоянной или переменной величины. Если отмеченные выше моменты, характерные для закона Ома, рассматривались с точки зрения использования постоянного тока, соответственно с переменным током всё выглядит несколько иначе.
youtube.com/embed/f2rpF5ztAr0?feature=oembed»>Для переменного тока
Переменный ток отличается от постоянного тем, что он изменяется с определенными временными периодами. Конкретно он изменяет свое значение и направление. Чтобы применить закон Ома здесь нужно учитывать, что сопротивление в цепи с постоянным током может отличатся от сопротивления в цепи с током переменным. И отличается оно в том случае если в цепи применены компоненты с реактивным сопротивлением. Реактивное сопротивление может быть индуктивным (катушки, трансформаторы, дроссели) и емкостными (конденсатор).
Если мы схематически представим, как с течением времени меняются эти два значения, у нас получится синусоида. И напряжение, и сила тока от нуля поднимаются до максимального значения, затем, опускаясь, проходят через нулевое значение и достигают максимального отрицательного значения. После этого снова поднимаются через нуль до максимального значения и так далее. Когда говорится, что сила тока или напряжение имеет отрицательное значение, здесь имеется ввиду, что они движутся в обратном направлении.
Весь процесс происходит с определенной периодичностью. Та точка, где значение напряжения или силы тока из минимального значения поднимаясь к максимальному значению проходит через нуль называется фазой.
Для замкнутой цепи
На самом деле, это только предисловие. Вернемся к реактивному и активному сопротивлению. Отличие активного сопротивления от реактивного в том, что в цепи с активным сопротивлением фаза тока совпадает с фазой напряжения. То есть, и значение силы тока, и значение напряжения достигают максимума в одном направлении одновременно. В таком случае наша формула для расчета напряжения, сопротивления или силы тока не меняется.
Следствия закона Ома.
Если же цепь содержит реактивное сопротивление, фазы тока и напряжения сдвигаются друг от друга на ¼ периода. Это означает, что, когда сила тока достигнет максимального значения, напряжение будет равняться нулю и наоборот. Когда применяется индуктивное сопротивление, фаза напряжения «обгоняет» фазу тока. Когда применяется емкостное сопротивление, фаза тока «обгоняет» фазу напряжения.
Когда применяется емкостное сопротивление, фаза тока «обгоняет» фазу напряжения.
Формула для расчета падения напряжения на индуктивном сопротивлении:
U = I ⋅ ωL
Где L – индуктивность реактивного сопротивления, а ω – угловая частота (производная по времени от фазы колебания).
Формула для расчета падения напряжения на емкостном сопротивлении:
U = I / ω ⋅ С
С – емкость реактивного сопротивления.
Эти две формулы – частные случаи закона Ома для переменных цепей.
Полный же будет выглядеть следующем образом:
I = U / Z
Здесь Z – полное сопротивление переменной цепи известное как импеданс.
Сфера применения
Закон Ома не является базовым законом в физике, это лишь удобная зависимость одних значений от других, которая подходит почти в любых ситуациях на практике. Поэтому проще будет перечислить ситуации, когда закон может не срабатывать:
- Если есть инерция носителей заряда, например, в некоторых высокочастотных электрических полях;
- В сверхпроводниках;
- Если провод нагревается до такой степени, что вольтамперная характеристика перестает быть линейной.
 Например, в лампах накаливания;
Например, в лампах накаливания; - В вакуумных и газовых радиолампах;
- В диодах и транзисторах.
Закон Ома для замкнутой цепи
Подобная интерпретация подразумевает наличие источника питания, а также проводника, по которому протекает ток. В этом случае, помимо сопротивления на отдельно взятом участке следует учитывать и то, которое возникает в ИП. Учитывая эти факторы, можно сказать, что сила тока будет равна отношению электродвижущей силы к сумме сопротивлений.
I = E/ Rвн+r,
где Е – ЭДС, Rвн – внешнее сопротивление, а r соответственно внутреннее.
Закон Ома для замкнутой цепи можно объяснить доступным языком. Электродвижущая сила по определению должна полноценно обеспечивать постоянную разницу потенциалов, и эта сила может иметь неприродное происхождение: химическое, если в качестве источника используется батарейка или механическая, в случае подключения к электрической цепи генератора. При подключении медной проволоки с идентичным сечением к батарейке и аккумулятору. Эффект должен быть таким, что по этому проводнику, в котором сопротивление практически отсутствует, должен пойти ток с величиной, стремящейся к бесконечности. Однако этого не происходит и разница в показателях будет существенной, а во втором случае, проволока и вовсе может перегореть. Именно поэтому в расчет берется внутреннее сопротивление источника питания, чтобы описать подобное явление.
Эффект должен быть таким, что по этому проводнику, в котором сопротивление практически отсутствует, должен пойти ток с величиной, стремящейся к бесконечности. Однако этого не происходит и разница в показателях будет существенной, а во втором случае, проволока и вовсе может перегореть. Именно поэтому в расчет берется внутреннее сопротивление источника питания, чтобы описать подобное явление.
Закон Ома для неоднородного участка цепи
Перед тем, как записать формулу для подобной интерпретации закона, следует разобраться в таких понятиях, как линейные и нелинейные участки цепи.
Если сопротивление никаким образом не зависит от тока и подаваемого напряжения, то с ростом второго параметра, первый будет прямо пропорционально возрастать и наоборот, то есть зависимость можно описать прямой линией. Подобная зависимость относится к линейным участкам цепи и сопротивление имеет аналогичное название.
Однако вышеизложенный вариант считается идеальным и его можно смоделировать лишь в идеальных условиях, что фактически невозможно, ведь, как минимум, окружающая среда вносит свои коррективы. В этом случае, рост напряжения не будет прямо пропорциональным силе тока и на графике зависимость будет изображаться в виде кривой.
В этом случае, рост напряжения не будет прямо пропорциональным силе тока и на графике зависимость будет изображаться в виде кривой.
На рисунке изображено два графика, первый из которых описывает линейную зависимость, а второй нелинейную.
Чтобы отчетливо понимать разницу между этими понятиями, рассмотрим принцип работы обычной электрической лампы накаливания. При прохождении тока по нити, температура в значительной степени повышается, что приводит к заметному росту сопротивления. Соответственно, при возрастании напряжения, сила тока будет увеличиваться медленнее, то есть не линейно.
Примечание: в некоторых ситуациях, некоторыми внешними факторами пренебрегают по причине того, что они очень незначительны и в числовом эквиваленте никоим образом не могут повлиять на общую картину. Это значит, что нелинейная зависимость на графике фактически совпадает с линейной.
Учитывая вышесказанное, можно установить следующую зависимость:
I = U/ R = (f1 – f2) + E/ R,
Где f1 и f2 – потенциалы (соответственно f1 – f2 называется разницей потенциалов), E – ЭДС неоднородного участка цепи, а R – суммарное сопротивление на этом же участке.
Нужно упомянуть и о том, что электродвижущая сила не всегда в этом случае будет иметь положительное значение. Если направление тока источника будет аналогичным с направлением в электрической сети, протонов будет больше, чем электронов (положительных и отрицательных частиц), то в этом случае величина E будет иметь значение со знаком «+», в иной ситуации, этот параметр будет со знаком «-».
Закон Ома для переменного тока
Если в электроцепи имеется емкость или инертность, то этот факт следует однозначно учитывать при расчётах силы тока. Они имеют собственные показатели сопротивления, что приводит к ситуации, которая будет иметь переменный характер. В случае Закона Ома для переменного тока формула записывается следующим образом:
I = U/ Z, где
I – сила тока, U – напряжение, а Z – суммарное значение сопротивления на всех участках электрической цепи (этот параметр именуется еще, как импеданс).
Как говорилось изначально, закон Ома считается эмпирическим. Это обозначает то, что он может не всегда работать и выполнять вычисления на его основе не представляется возможным. Подобная ситуация может сложиться в нескольких случаях:
Подобная ситуация может сложиться в нескольких случаях:
- в ситуации, когда электросеть имеет высокую частоту и электромагнитное поле может сильно изменяться за короткие промежутки времени;
- при наличии проводников, которые обладают свойствами сверхпроводимости, расположенных в условиях низких температурных показателей;
- при перегреве проводника под воздействием проходящего по нему тока, отношение напряжения и сопротивления может носить переменный, неоднородный характер;
- если проводник (диэлектрик) находится под высоким напряжением;
- светодиодных лампах;
- в полупроводниках и аналогичных устройствах.
На основе этого закона, можно произвести вывод некоторых формул математическим путем. С их помощью можно производить разнообразные расчеты.
Метода треугольника закона Ома
Закон Ома – очень простой и полезный инструмент для анализа электрических цепей. Он так часто используется при изучении электричества и электроники, что студент должен запомнить его. Если вы не очень хорошо умеете работать с формулами, то для его запоминания существует простой прием, помогающий использовать его для любой величины, зная две других. Сначала расположите буквы E, I и R в виде треугольника следующим образом:
Если вы не очень хорошо умеете работать с формулами, то для его запоминания существует простой прием, помогающий использовать его для любой величины, зная две других. Сначала расположите буквы E, I и R в виде треугольника следующим образом:
Рисунок 5 – Треугольник закона Ома
Если вы знаете E и I и хотите определить R, просто удалите R с картинки и посмотрите, что осталось:
Рисунок 6 – Закон Ома для определения R
Если вы знаете E и R и хотите определить I, удалите I и посмотрите, что осталось:
Рисунок 7 – Закон Ома для определения I
Наконец, если вы знаете I и R и хотите определить E, удалите E и посмотрите, что осталось:
Рисунок 8 – Закон Ома для определения E
В конце концов, вам придется научиться работать с формуми, чтобы серьезно изучать электричество и электронику, но этот совет может облегчить запоминание ваших первых вычислений. Если вам удобно работать с формулами, всё, что вам нужно сделать, это зафиксировать в памяти E = IR и вывести из нее две другие формулы, когда они вам понадобятся!
Значение Закона Ома
Закон Ома определяет силу тока в электрической цепи при заданном напряжении и известном сопротивлении. Он позволяет рассчитать тепловые, химические и магнитные действия тока, так как они зависят от силы тока.
Он позволяет рассчитать тепловые, химические и магнитные действия тока, так как они зависят от силы тока.
Закон Ома является чрезвычайно полезным в технике(электронной/электрической), поскольку он касается трех основных электрических величин: тока, напряжения и сопротивления. Он показывает, как эти три величины являются взаимозависимыми на макроскопическом уровне.
Если бы было можно охарактеризовать закон Ома простыми словами, то наглядно это выглядело бы так:
Из закона Ома вытекает, что замыкать обычную осветительную сеть проводником малого сопротивления опасно. Сила тока окажется настолько большой, что это может иметь тяжелые последствия.
Задача 1.1
Рассчитать силу тока, проходящую по медному проводу длиной 100 м, площадью поперечного сечения 0,5 мм2, если к концам провода приложено напряжение 12 B.
Задачка простая, заключается в нахождении сопротивления медной проволоки с последующим расчетом силы тока по формуле закона Ома для участка цепи. Приступим.
Приступим.
Сопротивление
Представьте, что есть труба, в которую затолкали камни. Вода, которая протекает по этой трубе, станет течь медленнее, потому что у нее появилось сопротивление. Точно также будет происходить с электрическим током.
- Сопротивление — физическая величина, которая показывает способность проводника пропускать электрический ток. Чем выше сопротивление, тем ниже эта способность.
Теперь сделаем «каменный участок» длиннее, то есть добавим еще камней. Воде будет еще сложнее течь.
Сделаем трубу шире, оставив количество камней тем же — воде полегчает, поток увеличится.
Теперь заменим шероховатые камни, которые мы набрали на стройке, на гладкие камушки из моря. Через них проходить тоже легче, а значит сопротивление уменьшается.
Электрический ток реагирует на эти параметры аналогичным образом: при удлинении проводника сопротивление увеличивается, при увеличении поперечного сечения (ширины) проводника сопротивление уменьшается, а если заменить материал — изменится в зависимости от материала. 2.
2.
Знайте!СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение составляет килограмм с приставкой «кило».
- Удельное сопротивление проводника — это физическая величина, которая показывает способность материала пропускать электрический ток. Это табличная величина, она зависит только от материала.
Таблица удельных сопротивлений различных материалов
| Удельное сопротивление ρ, Ом*мм2/м | Удельное сопротивление ρ, Ом*мм2/м |
| Алюминий | 0,028 |
| Бронза | 0,095 – 0,1 |
| Висмут | 1,2 |
| Вольфрам | 0,05 |
| Железо | 0,1 |
| Золото | 0,023 |
| Иридий | 0,0474 |
| Константан ( сплав Ni-Cu + Mn) | 0,5 |
| Латунь | 0,025 – 0,108 |
| Магний | 0,045 |
| Манганин (сплав меди марганца и никеля – приборный) | 0,43 – 0,51 |
| Медь | 0,0175 |
| Молибден | 0,059 |
| Нейзильбер (сплав меди цинка и никеля) | 0,2 |
| Натрий | 0,047 |
| Никелин ( сплав меди и никеля) | 0,42 |
| Никель | 0,087 |
| Нихром ( сплав никеля хрома железы и марганца) | 1,05 – 1,4 |
| Олово | 0,12 |
| Платина | 0. 107 107 |
| Ртуть | 0,94 |
| Свинец | 0,22 |
| Серебро | 0,015 |
| Сталь | 0,103 – 0,137 |
| Титан | 0,6 |
| Хромаль | 1,3 – 1,5 |
| Цинк | 0,054 |
| Чугун | 0,5-1,0 |
Резистор
Все реальные проводники имеют сопротивление, но его стараются сделать незначительным. В задачах вообще используют словосочетание «идеальный проводник», а значит лишают его сопротивления.
Из-за того, что проводник у нас «кругом-бегом-такой-идеальный», чаще всего за сопротивление в цепи отвечает резистор. Это устройство, которое нагружает цепь сопротивлением.
Вот так резистор изображается на схемах:
В школьном курсе физики используют Европейское обозначение, поэтому запоминаем только его. Американское обозначение можно встретить, например, в программе Micro-Cap, в которой инженеры моделируют схемы.
Вот так резистор выглядит в естественной среде обитания:
Полосочки на нем показывают его сопротивление.
На сайте компании Ekits, которая занимается продажей электронных модулей, можно выбрать цвет резистора и узнать значение его сопротивления:
Источник: сайт компании Ekits
О том, зачем дополнительно нагружать сопротивлением цепь, мы поговорим в этой же статье чуть позже.
Реостат
Есть такие выключатели, которые крутишь, а они делают свет ярче-тусклее. В такой выключатель спрятан резистор с переменным сопротивлением — реостат.
Стрелка сверху — это ползунок. По сути, он отсекает ту часть резистора, которая находится от него справа. То есть, если мы двигаем ползунок вправо — мы увеличиваем длину резистора, а значит и сопротивление. И наоборот — двигаем влево и уменьшаем.
По формуле сопротивления это очень хорошо видно, так как длина проводника находится в числителе:
| Сопротивление R = ρ l/S R — сопротивление [Ом] l — длина проводника [м] S — площадь поперечного сечения [мм^2] ρ — удельное сопротивление [Ом*мм^2/м] |
Закон Ома для участка цепи
С камушками в трубе все понятно, но не только же от них зависит сила, с которой поток воды идет по трубе — от насоса, которым мы эту воду качаем, тоже зависит. Чем сильнее качаем, тем больше течение. В электрической цепи функцию насоса выполняет источник тока.
Чем сильнее качаем, тем больше течение. В электрической цепи функцию насоса выполняет источник тока.
Например, источником может быть гальванический элемент (привычная батарейка). Батарейка работает на основе химических реакций внутри нее. Эти реакции выделяют энергию, которая потом передается электрической цепи.
У любого источника обязательно есть полюса — «плюс» и «минус». Полюса — это его крайние положения, по сути клеммы, к которым присоединяется электрическая цепь. Собственно, ток как раз течет от «+» к «-».
У нас уже есть две величины, от которых зависит электрический ток в цепи — напряжение и сопротивление. Кажется, пора объединять их в закон.
Сила тока в участке цепи прямо пропорциональна напряжению на его концах и обратно пропорциональна его сопротивлению.
Математически его можно описать вот так:
| Закон Ома для участка цепи I = U/R I — сила тока [A] U — напряжение [В] R — сопротивление [Ом] |
Напряжение измеряется в Вольтах и показывает разницу между двумя точками цепи: от этой разницы зависит, насколько сильно будет течь ток — чем больше разница, тем выше напряжение и ток будет течь сильнее. 2/м
2/м
Обратимся к таблице удельных сопротивлений материалов, чтобы выяснить, из какого материала сделана эта нить накаливания.
Закон Ома для полной цепи
Мы разобрались с законом Ома для участка цепи. А теперь давайте узнаем, что происходит, если цепь полная: у нее есть источник, проводники, резисторы и другие элементы.
В таком случае вводится Закон Ома для полной цепи: сила тока в полной цепи равна отношению ЭДС цепи к ее полному сопротивлению.
Так, стоп. Слишком много незнакомых слов — разбираемся по-порядку.
Что такое ЭДС и откуда она берется
ЭДС расшифровывается, как электродвижущая сила. Обозначается греческой буквой ε и измеряется, как и напряжение, в Вольтах.
- ЭДС — это сила, которая движет заряженные частицы в цепи. Она берется из источника тока. Например, из батарейки.
Химическая реакция внутри гальванического элемента (это синоним батарейки) происходит с выделением энергии в электрическую цепь. Именно эта энергия заставляет частицы двигаться по проводнику.
Зачастую напряжение и ЭДС приравнивают и говорят, что это одно и то же. Формально, это не так, но при решении задач чаще всего и правда нет разницы, так как эти величины обе измеряются в Вольтах и определяют очень похожие по сути своей процессы.
В виде формулы Закон Ома для полной цепи будет выглядеть следующим образом:
| Закон Ома для полной цепи I = ε/(R + r) I — сила тока [A] ε — ЭДС [В] R — сопротивление [Ом] r — внутреннее сопротивление источника [Ом] |
Любой источник не идеален. В задачах это возможно («источник считать идеальным», вот эти вот фразочки), но в реальной жизни — точно нет. В связи с этим у источника есть внутреннее сопротивление, которое мешает протеканию тока.
Решим задачу на полную цепь.
Задачка
Найти силу тока в полной цепи, состоящей из одного резистора сопротивлением 3 Ом и источником с ЭДС равной 4 В и внутренним сопротивлением 1 Ом
Решение:
Возьмем закон Ома для полной цепи:
I = ε/(R + r)
Подставим значения:
I = 4/(3+1) = 1 A
Ответ: сила тока в цепи равна 1 А.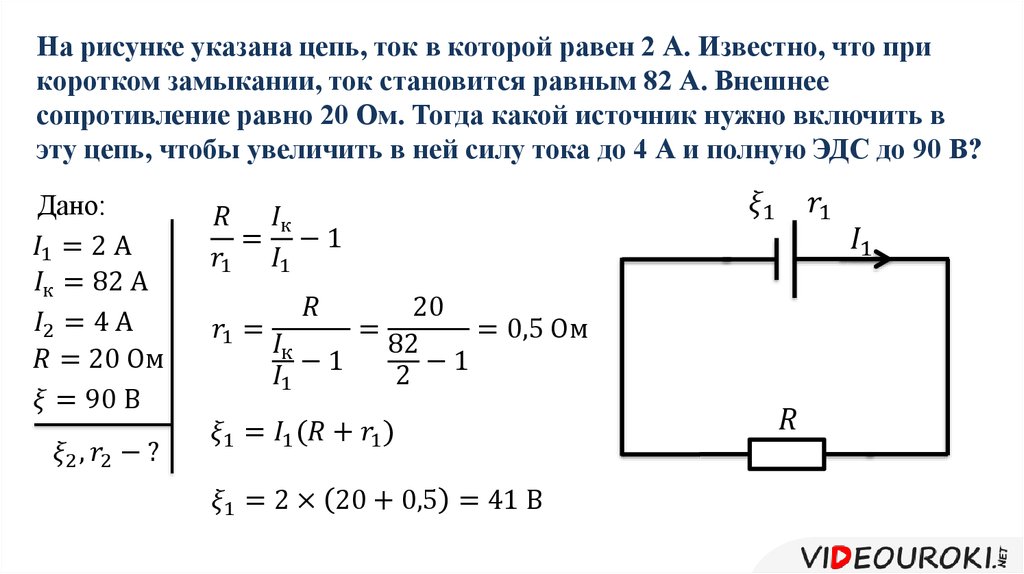
Когда «сопротивление бесполезно»
Электрический ток — умный и хитрый парень. Если у него есть возможность обойти резистор и пойти по идеальному проводнику без сопротивления, он это сделает. При этом с резисторами просто разных номиналов это не сработает: он не пойдет просто через меньшее сопротивление, а распределится согласно закону Ома — больше тока пойдет туда, где сопротивление меньше, и наоборот.
А вот на рисунке ниже сопротивление цепи равно нулю, потому что ток через резистор не пойдет.
Ток идет по пути наименьшего сопротивления.
Теперь давайте посмотрим на закон Ома для участка цепи еще раз.
| Закон Ома для участка цепи I = U/R I — сила тока [A] U — напряжение [В] R — сопротивление [Ом] |
Подставим сопротивление, равное 0. Получается, что знаменатель равен нулю, а на математике говорят, что на ноль делить нельзя. Но мы вам раскроем страшную тайну, только не говорите математикам: на ноль делить можно. Если совсем упрощать такое сложное вычисление (а именно потому что оно сложное, мы всегда говорим, что его нельзя производить), то получится бесконечность.
Если совсем упрощать такое сложное вычисление (а именно потому что оно сложное, мы всегда говорим, что его нельзя производить), то получится бесконечность.
То есть:
I = U/0 = ∞
Такой случай называют коротким замыканием — когда величина силы тока настолько велика, что можно устремить ее к бесконечности. В таких ситуациях мы видим искру, бурю, безумие — и все ломается.
Это происходит, потому что две точки цепи имеют между собой напряжение (то есть между ними есть разница). Это как если вдоль реки неожиданно появляется водопад. Из-за этой разницы возникает искра, которую можно избежать, поставив в цепь резистор.
Именно во избежание коротких замыканий нужно дополнительное сопротивление в цепи.
Формула Закона Джоуля-Ленца
Величину резистора для изготовления блока нагрузки для блока питания компьютера мы рассчитали, но нужно еще определить какой резистор должен быть мощности? Тут поможет другой закон физики, который, независимо друг от друга открыли одновременно два ученых физика. В 1841 году Джеймс Джоуль, а в 1842 году Эмиль Ленц. Этот закон и назвали в их честь – Закон Джоуля-Ленца.
В 1841 году Джеймс Джоуль, а в 1842 году Эмиль Ленц. Этот закон и назвали в их честь – Закон Джоуля-Ленца.
Потребляемая нагрузкой мощность прямо пропорциональна приложенной величине напряжения и протекающей силе тока. Другими словами, при изменении величины напряжения и тока будет пропорционально будет изменяться и потребляемая мощность.
где P – мощность, измеряется в ваттах и обозначается Вт;U – напряжение, измеряется в вольтах и обозначается буквой В;I – сила ток, измеряется в амперах и обозначается буквой А.
Зная напряжения питания и силу тока, потребляемую электроприбором, можно по формуле определить, какую он потребляет мощность. Достаточно ввести данные в окошки ниже приведенного онлайн калькулятора.
Закон Джоуля-Ленца позволяет также узнать силу тока, потребляемую электроприбором зная его мощность и напряжение питания. Величина потребляемого тока необходима, например, для выбора сечения провода при прокладке электропроводки или для расчета номинала.
Например, рассчитаем потребляемый ток стиральной машины. По паспорту потребляемая мощность составляет 2200 Вт, напряжение в бытовой электросети составляет 220 В. Подставляем данные в окошки калькулятора, получаем, что стиральная машина потребляет ток величиной 10 А.
Еще один пример, Вы решили в автомобиле установить дополнительную фару или усилитель звука. Зная потребляемую мощность устанавливаемого электроприбора легко рассчитать потребляемый ток и правильно подобрать сечение провода для подключения к электропроводке автомобиля. Допустим, дополнительная фара потребляет мощность 100 Вт (мощность установленной в фару лампочки), бортовое напряжение сети автомобиля 12 В. Подставляем значения мощности и напряжения в окошки калькулятора, получаем, что величина потребляемого тока составит 8,33 А.
Разобравшись всего в двух простейших формулах, Вы легко сможете рассчитать текущие по проводам токи, потребляемую мощность любых электроприборов – практически начнете разбираться в основах электротехники.
Преобразованные формулы Закона Ома и Джоуля-Ленца
Встретил в Интернете картинку в виде круглой таблички, в которой удачно размещены формулы Закона Ома и Джоуля-Ленца и варианты математического преобразования формул. Табличка представляет собой не связанные между собой четыре сектора и очень удобна для практического применения
По таблице легко выбрать формулу для расчета требуемого параметра электрической цепи по двум другим известным. Например, нужно определить ток потребления изделием по известной мощности и напряжению питающей сети. По таблице в секторе тока видим, что для расчета подойдет формула I=P/U.
А если понадобится определить напряжение питающей сети U по величине потребляемой мощности P и величине тока I, то можно воспользоваться формулой левого нижнего сектора, подойдет формула U=P/I.
Подставляемые в формулы величины должны быть выражены в амперах, вольтах, ваттах или Омах.
Применение закона Ома на практике
На практике часто приходится определять не силу тока I, а величину сопротивления R.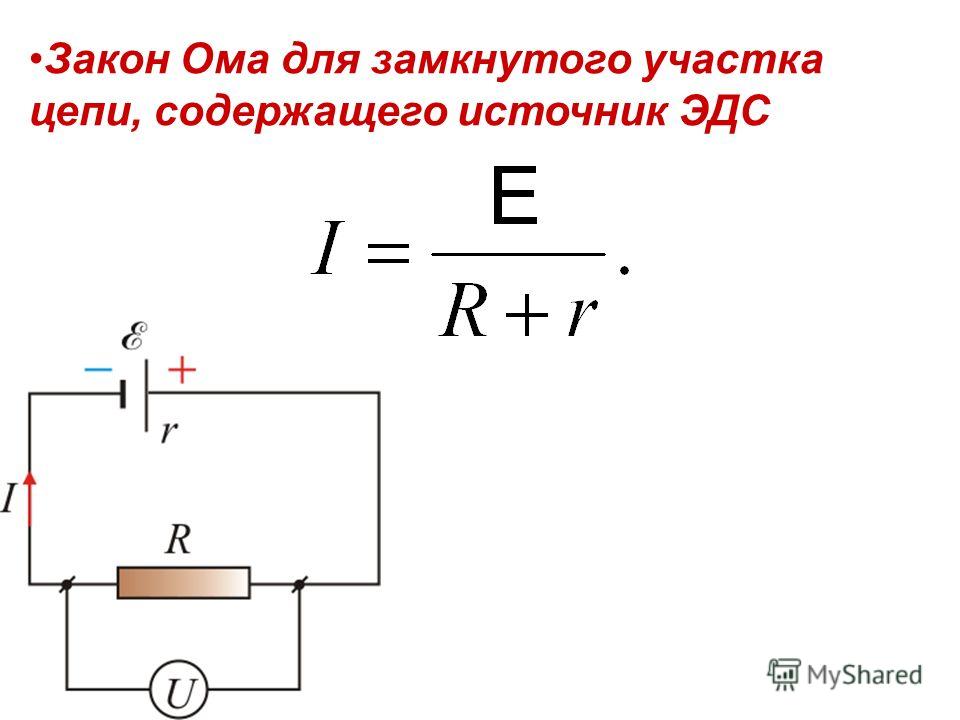 Преобразовав формулу Закона Ома, можно рассчитать величину сопротивления R, зная протекающий ток I и величину напряжения U.
Преобразовав формулу Закона Ома, можно рассчитать величину сопротивления R, зная протекающий ток I и величину напряжения U.
Величину сопротивления может понадобится рассчитать, например, при изготовлении блока нагрузок для проверки блока питания компьютера. На корпусе блока питания компьютера обычно есть табличка, в которой приведен максимальный ток нагрузки по каждому напряжению. Достаточно в поля калькулятора ввести данные величины напряжения и максимальный ток нагрузки и в результате вычисления получим величину сопротивления нагрузки для данного напряжения. Например, для напряжения +5 В при максимальной величине тока 20 А, сопротивление нагрузки составит 0,25 Ом.
Таблица-шпаргалка
Используя закон Ома для участка цепи, а также формулу для мощности электрического тока: P = U*I – я подготовил для вас полезную таблицу-шпаргалку, которая позволяет соотносить между собой сопротивление (R), силу тока (I), напряжение (U) и мощность электрического тока (P). Будет точно полезно не только школьникам!
| Известные величины | R (сопротивление) | I (сила тока) | U (напряжение) | P (мощность) |
| Ток и сопротивление | U = I × R | P = I2 × R | ||
| Напряжение и ток | R = U / I | P = U × I | ||
| Мощность и ток | R = P / I2 | U = P / I | ||
| Напряжение и сопротивление | I = U / R | P = U2 / R | ||
| Мощность и сопротивление | I = P / R | |||
| Напряжение и мощность | R = U2 / R | I = P / U |
Последовательное и параллельное включение элементов
Для элементов электрической цепи (участка цепи) характерным моментом является последовательное либо параллельное соединение. Соответственно, каждый вид соединения сопровождается разным характером течения тока и подводкой напряжения. На этот счёт закон Ома также применяется по-разному, в зависимости от варианта включения элементов.
Соответственно, каждый вид соединения сопровождается разным характером течения тока и подводкой напряжения. На этот счёт закон Ома также применяется по-разному, в зависимости от варианта включения элементов.
Цепь последовательно включенных резистивных элементов
Применительно к последовательному соединению (участку цепи с двумя компонентами) используется формулировка:
- I = I1= I2 ;
- U = U1+ U2 ;
- R = R1+ R2
Такая формулировка явно демонстрирует, что, независимо от числа последовательно соединенных резистивных компонентов, ток, текущий на участке цепи, не меняет значения. Величина напряжения, приложенного к действующим резистивным компонентам схемы, является суммой и составляет в целом значение источника ЭДС.
При этом напряжение на каждом отдельном компоненте равно: Ux = I * Rx. Общее сопротивление следует рассматривать как сумму номиналов всех резистивных компонентов цепи.
youtube.com/embed/PBI9RxyDpi8?feature=oembed»>Цепь параллельно включенных резистивных элементов
На случай, когда имеет место параллельное включение резистивных компонентов, справедливой относительно закона немецкого физика Ома считается формулировка:
- I = I1+ I2 … ;
- U = U1= U2 … ;
- 1 / R = 1 / R1+ 1 / R2 + …
Не исключаются варианты составления схемных участков «смешанного» вида, когда используется параллельное и последовательное соединение. Для таких вариантов расчет обычно ведется изначальным расчетом резистивного номинала параллельного соединения. Затем к полученному результату добавляется номинал резистора, включенного последовательно.
Интегральная и дифференциальная формы закона
Все вышеизложенные моменты с расчетами применимы к условиям, когда в составе электрических схем используются проводники, так сказать, «однородной» структуры. Между тем на практике нередко приходится сталкиваться с построением схематики, где на различных участках структура проводников меняется. К примеру, используются провода большего сечения или, напротив, меньшего, сделанные на основе разных материалов.
К примеру, используются провода большего сечения или, напротив, меньшего, сделанные на основе разных материалов.
Для учёта таких различий существует вариация, так называемого, «дифференциально-интегрального закона Ома». Для бесконечно малого проводника рассчитывается уровень плотности тока в зависимости от напряженности и величины удельной проводимости.
Под дифференциальный расчет берется формула: J = ό * E. Для интегрального расчета, соответственно, формулировка: I * R = φ1 – φ2 + έ Однако эти примеры скорее уже ближе к школе высшей математики и в реальной практике простого электрика фактически не применяются.
Параллельное и последовательное соединение
В электрике элементы соединяются либо последовательно — один за другим, либо параллельно — это когда к одной точке подключены несколько входов, к другой — выходы от тех же элементов.
Закон Ома для параллельного и последовательного соединения
Последовательное соединение
Как работает закон Ома для этих случаев? При последовательном соединении сила тока, протекающая через цепочку элементов, будет одинаковой.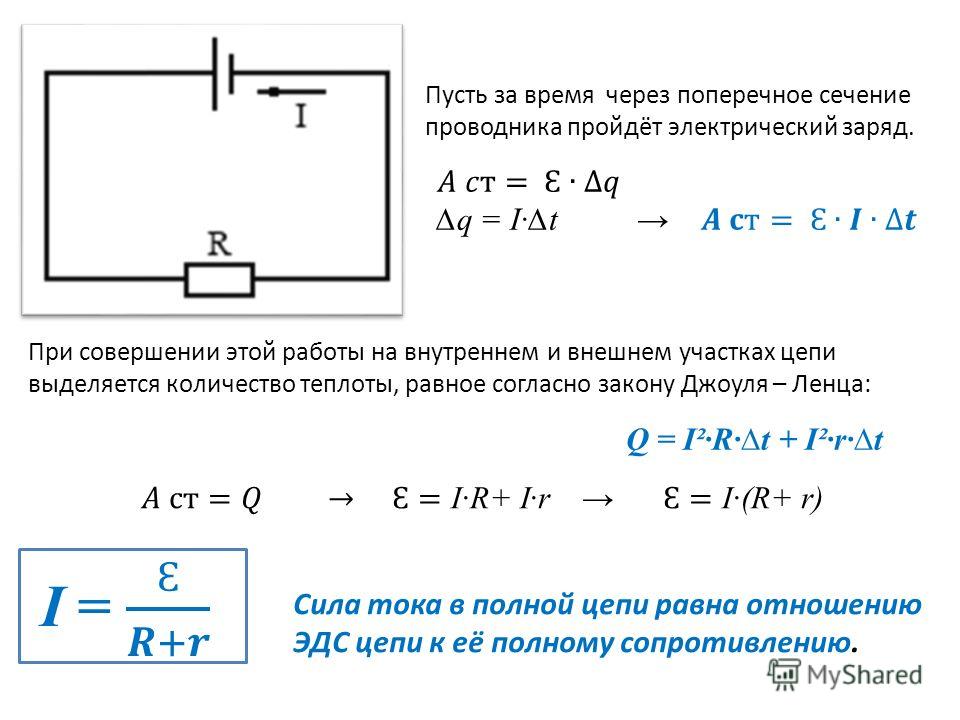 Напряжение участка цепи с последовательно подключенными элементами считается как сумма напряжений на каждом участке. Как можно это объяснить? Протекание тока через элемент — это перенос части заряда с одной его части в другую. То есть, это определенная работа. Величина этой работы и есть напряжение. Это физический смысл напряжения. Если с этим понятно, двигаемся дальше.
Напряжение участка цепи с последовательно подключенными элементами считается как сумма напряжений на каждом участке. Как можно это объяснить? Протекание тока через элемент — это перенос части заряда с одной его части в другую. То есть, это определенная работа. Величина этой работы и есть напряжение. Это физический смысл напряжения. Если с этим понятно, двигаемся дальше.
Последовательное соединение и параметры этого участка цепи
При последовательном соединении приходится переносить заряд по очереди через каждый элемент. И на каждом элементе это определенный «объем» работы. А чтобы найти объем работы на всем участке цепи, надо работу на каждом элементе сложить. Вот и получается, что общее напряжение — это сумма напряжений на каждом из элементов.
Точно так же — при помощи сложения — находится и общее сопротивление участка цепи. Как можно это себе представить? Ток, протекая по цепочке элементов, последовательно преодолевает все сопротивления. Одно за другим. То есть чтобы найти сопротивление, которое он преодолел, надо сопротивления сложить. Примерно так. Математический вывод более сложен, а так понять механизм действия этого закона проще.
Примерно так. Математический вывод более сложен, а так понять механизм действия этого закона проще.
Параллельное соединение
Параллельное соединение — это когда начала проводников/элементов сходятся в одной точке, а в другой — соединены их концы. Постараемся объяснить законы, которые справедливы для соединений этого типа. Начнем с тока. Ток какой-то величины подается в точку соединения элементов. Он разделяется, протекая по всем проводникам. Отсюда делаем вывод, что общий ток на участке равен сумме тока на каждом из элементов: I = I1 + I2 + I3.
Теперь относительно напряжения. Если напряжение — это работа по перемещению заряда, тоо работа, которая необходима на перемещение одного заряда будет одинакова на любом элементе. То есть, напряжение на каждом параллельно подключенном элементе будет одинаковым. U = U1=U2=U3. Не так весело и наглядно, как в случае с объяснением закона Ома для участка цепи, но понять можно.
Законы для параллельного соединения
Для сопротивления все несколько сложнее. Давайте введем понятие проводимости. Это характеристика, которая показывает насколько легко или сложно заряду проходить по этому проводнику. Понятно, что чем меньше сопротивление, тем проще току будет проходить. Поэтому проводимость — G — вычисляется как величина обратная сопротивлению. В формуле это выглядит так: G = 1/R.
Давайте введем понятие проводимости. Это характеристика, которая показывает насколько легко или сложно заряду проходить по этому проводнику. Понятно, что чем меньше сопротивление, тем проще току будет проходить. Поэтому проводимость — G — вычисляется как величина обратная сопротивлению. В формуле это выглядит так: G = 1/R.
Для чего мы говорили о проводимости? Потому что общая проводимость участка с параллельным соединением элементов равна сумме проводимости для каждого из участков. G = G1 + G2 + G3 — понять несложно. Насколько легко току будет преодолеть этот узел из параллельных элементов, зависит от проводимости каждого из элементов. Вот и получается, что их надо складывать.
Теперь можем перейти к сопротивлению. Так как проводимость — обратная к сопротивлению величина, можем получить следующую формулу: 1/R = 1/R1 + 1/R2 + 1/R3.
Что нам дает параллельное и последовательное соединение?
Теоретические знания — это хорошо, но как их применить на практике? Параллельно и последовательно могут соединяться элементы любого типа.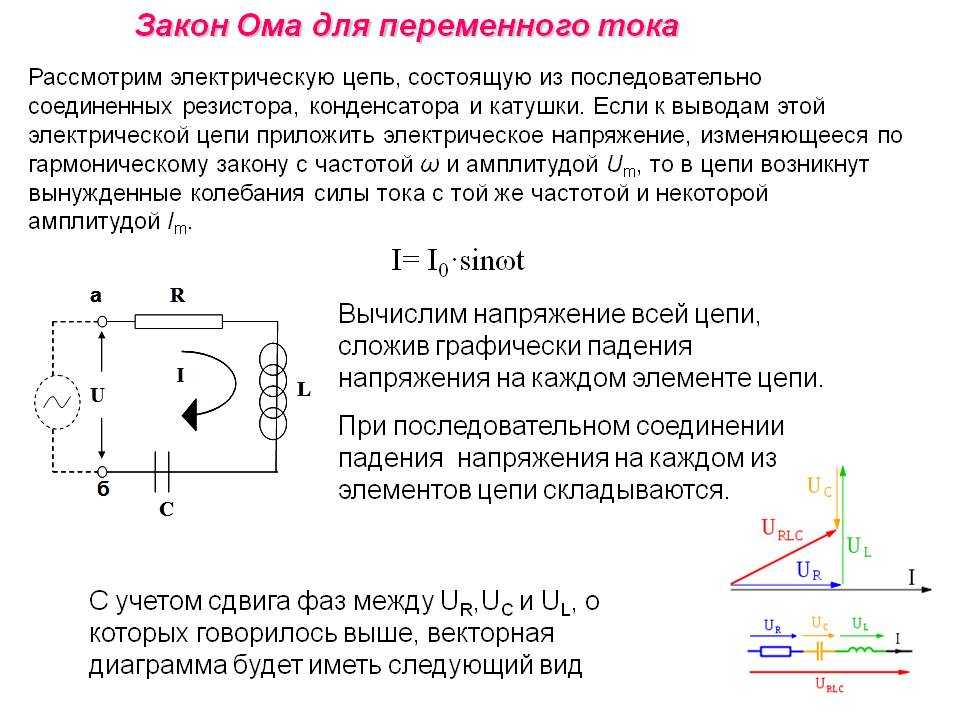 Но мы рассматривали только простейшие формулы, описывающие линейные элементы. Линейные элементы — это сопротивления, которые еще называют «резисторы». Итак, вот как можно использовать полученные знания:
Но мы рассматривали только простейшие формулы, описывающие линейные элементы. Линейные элементы — это сопротивления, которые еще называют «резисторы». Итак, вот как можно использовать полученные знания:
- Если в наличии нет резистора большого номинала, но есть несколько более «мелких», нужное сопротивление можно получить соединив последовательно несколько резисторов. Как видите, это полезный прием.
- Для продления срока жизни батареек, их можно соединять параллельно. Напряжение при этом, согласно закону Ома, останется прежним (можно убедиться, измерив напряжение мультиметром). А «срок жизни» сдвоенного элемента питания будет значительно больше, нежели у двух элементов, которые сменят друг друга. Только обратите внимание: параллельно соединять можно только источники питания с одинаковым потенциалом. То есть, севшую и новую батарейки соединять нельзя. Если все-таки соединить, та батарейка которая имеет больший заряд, будет стремиться зарядить менее заряженную. В результате общий их заряд упадет до низкого значения.

Практическое применение закона Ома: можно создавать источники питания с нужным напряжением и силой тока
В общем, это наиболее распространенные варианты использования этих соединений.
Интегральная и дифференциальная формы закона
Все вышеизложенные моменты с расчетами применимы к условиям, когда в составе электрических схем используются проводники, так сказать, «однородной» структуры. Между тем на практике нередко приходится сталкиваться с построением схематики, где на различных участках структура проводников меняется. К примеру, используются провода большего сечения или, напротив, меньшего, сделанные на основе разных материалов.
Для учёта таких различий существует вариация, так называемого, «дифференциально-интегрального закона Ома». Для бесконечно малого проводника рассчитывается уровень плотности тока в зависимости от напряженности и величины удельной проводимости.
Под дифференциальный расчет берется формула: J = ό * E. Для интегрального расчета, соответственно, формулировка: I * R = φ1 – φ2 + έ Однако эти примеры скорее уже ближе к школе высшей математики и в реальной практике простого электрика фактически не применяются.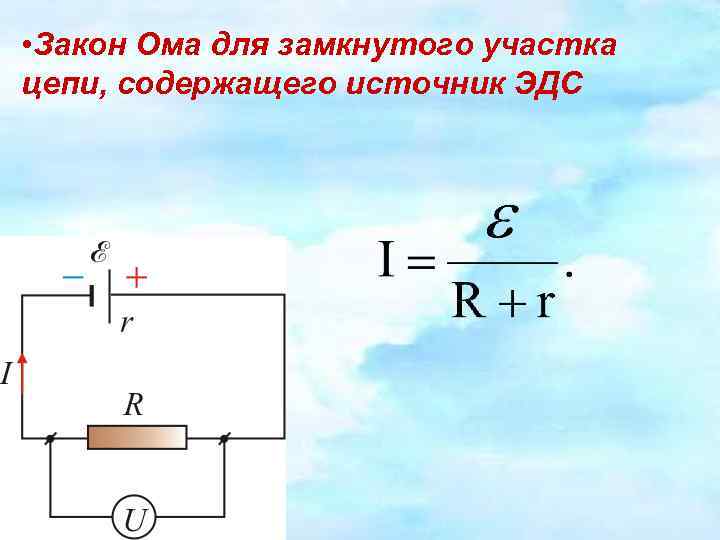
Источники
- https://ElectroInfo.net/teorija/vse-o-zakone-oma-prostymi-slovami-s-primerami-dlja-chajnikov.html
- https://uelektrika.ru/osnovy-yelektrotekhniki/zakon-oma-dlya-yelektricheskoy-cepi/
- https://serp1.ru/kak-ponjat-zakon-oma-prostoe-objasnen/
- https://skysmart.ru/articles/physics/zakon-oma
- https://mnogoformul.ru/zakon-oma
- https://www.asutpp.ru/zakon-oma-dlya-uchastka-tsepi.html
Закон Ома для полной цепи и для участка цепи: формулы, описание и объяснение
Содержание
Формула Закона Джоуля-Ленца
Величину резистора для изготовления блока нагрузки для блока питания компьютера мы рассчитали, но нужно еще определить какой резистор должен быть мощности? Тут поможет другой закон физики, который, независимо друг от друга открыли одновременно два ученых физика. В 1841 году Джеймс Джоуль, а в 1842 году Эмиль Ленц. Этот закон и назвали в их честь – Закон Джоуля-Ленца.
Потребляемая нагрузкой мощность прямо пропорциональна приложенной величине напряжения и протекающей силе тока. Другими словами, при изменении величины напряжения и тока будет пропорционально будет изменяться и потребляемая мощность.
Другими словами, при изменении величины напряжения и тока будет пропорционально будет изменяться и потребляемая мощность.
гдеP – мощность, измеряется в ваттах и обозначается Вт;U – напряжение, измеряется в вольтах и обозначается буквой В;I – сила ток, измеряется в амперах и обозначается буквой А.
Зная напряжения питания и силу тока, потребляемую электроприбором, можно по формуле определить, какую он потребляет мощность. Достаточно ввести данные в окошки ниже приведенного онлайн калькулятора.
ЗаконДжоуля-Ленца позволяет также узнать силу тока, потребляемую электроприбором зная его мощность и напряжение питания. Величина потребляемого тока необходима, например, для выбора сечения провода при прокладке электропроводки или для расчета номинала.
Например, рассчитаем потребляемый ток стиральной машины. По паспорту потребляемая мощность составляет 2200 Вт, напряжение в бытовой электросети составляет 220 В. Подставляем данные в окошки калькулятора, получаем, что стиральная машина потребляет ток величиной 10 А.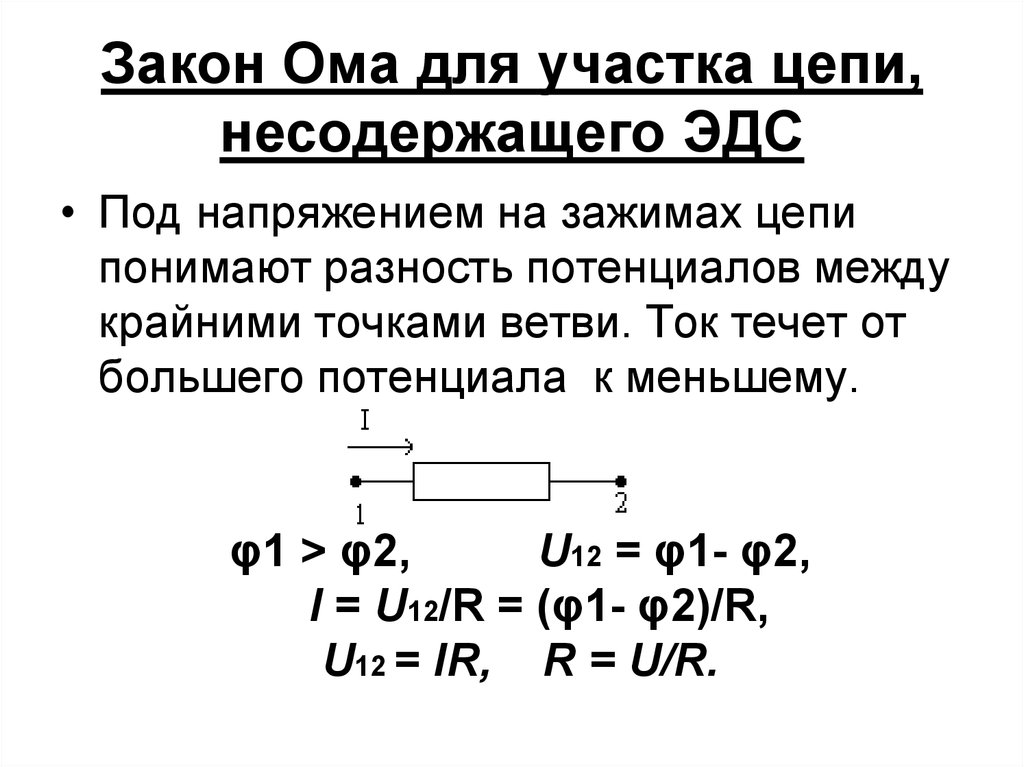
Еще один пример, Вы решили в автомобиле установить дополнительную фару или усилитель звука. Зная потребляемую мощность устанавливаемого электроприбора легко рассчитать потребляемый ток и правильно подобрать сечение провода для подключения к электропроводке автомобиля. Допустим, дополнительная фара потребляет мощность 100 Вт (мощность установленной в фару лампочки), бортовое напряжение сети автомобиля 12 В. Подставляем значения мощности и напряжения в окошки калькулятора, получаем, что величина потребляемого тока составит 8,33 А.
Разобравшись всего в двух простейших формулах, Вы легко сможете рассчитать текущие по проводам токи, потребляемую мощность любых электроприборов – практически начнете разбираться в основах электротехники.
Условные обозначения источников электрической энергии и элементов цепей
| Условное обозначение | Элемент |
| Идеальный источник ЭДС Е — электродвижущая сила, Е = const Ro = 0 — внутреннее сопротивление | |
| Идеальный источник тока I = const Rвн- внутреннее сопротивление источника тока, Rвн>>Rнаг | |
| Активное сопротивление R = const | |
| Индуктивность L = const | |
| Емкость С = const |
К химическим источникам тока относят гальванические элементы и аккумуляторы.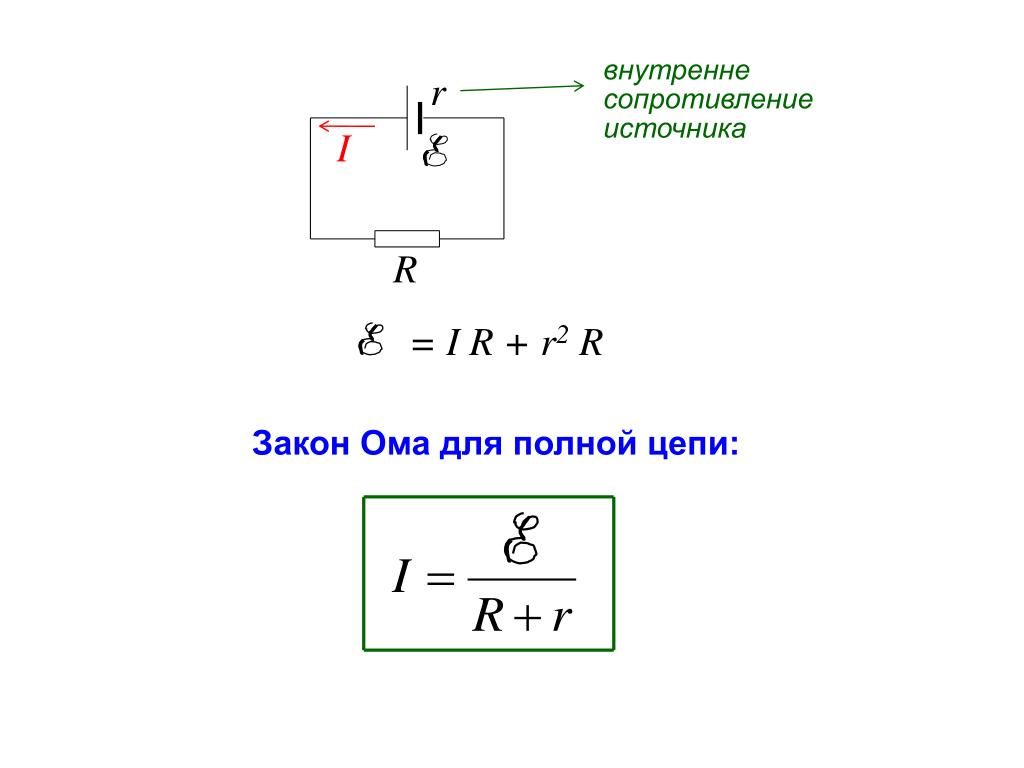 В них заряды переносятся в результате химических реакций. При этом в гальваническом элементе реагенты расходуются необратимо, а в аккумуляторе они могут восстанавливаться путем пропускания через аккумулятор электрического тока противоположного направления от других источников.
В них заряды переносятся в результате химических реакций. При этом в гальваническом элементе реагенты расходуются необратимо, а в аккумуляторе они могут восстанавливаться путем пропускания через аккумулятор электрического тока противоположного направления от других источников.
Источники электрической энергии относятся к группе активных элементов электротехнических устройств. Если Rо=0 и электродвижущая сила (ЭДС) Е=const, то источник называется идеальным. Аккумуляторная батарея по своим параметрам близка к идеальному источнику ЭДС.
К группе пассивных элементов относятся: активное сопротивление R, индуктивность L и емкость С.
В электротехнических устройствах одновременно протекают три энергетических процесса:
1 В активном сопротивлении в соответствии с законом Джоуля — Ленца происходит преобразование электрической энергии в тепло.
Мощность, по определению равна отношению работы к промежутку времени, за который эта работа совершается. Следовательно, мощность тока для участка цепи
p = A/t = ui
Полная мощность, вырабатываемая генератором, равна
где R- полное сопротивление замкнутой цепи, называемое омическим или активным;
Р, I — мощность и ток в цепи постоянного тока.
р, i, и — мгновенные значения активной мощности, тока и напряжения в цепи переменного тока,
g — активная проводимость или величина, обратная сопротивлению g=1/R измеряется в сименсах (См).
В соответствии с законом сохранения энергии работа есть мера изменения различных видов энергии. Так, в электродвигателе за счет работы тока возникает механическая энергия, протекают химические реакции и т. д. На резисторах происходит необратимое преобразование энергии электрического тока во внутреннюю энергию проводника.
Если в проводнике под действием тока не происходит химических реакций, то температура проводника должна измениться. Изменение внутренней энергии проводника (количество теплоты) Q равно работе А, которую совершает суммарное поле при перемещении зарядов:
Q = А = uit
Воспользовавшись законом Ома, получим два эквивалентных выражения:
Это и есть закон Джоуля — Ленца.
Если нужно сравнить два резистора по характеру тепловых процессов, происходящих в них, то нужно предварительно выяснить: протекает ли по ним одинаковый ток или они находятся под одинаковым напряжением?
Если по двум резисторам протекают одинаковые токи, то согласно формуле за одно и то же время больше возрастает внутренняя энергия резистора с большим сопротивлением. С таким случаем мы встречаемся, например, в цепи с последовательным соединением резисторов. Последнее обстоятельство следует учитывать при включении в сеть нагрузки (электроплиток, утюгов, электродвигателей и т. д.). Сопротивление подводящих проводов при этом должно быть значительно меньше, чем сопротивление нагрузки. При несоблюдении этого условия в проводах выделится большое количество теплоты, что может привести к их загоранию.
С таким случаем мы встречаемся, например, в цепи с последовательным соединением резисторов. Последнее обстоятельство следует учитывать при включении в сеть нагрузки (электроплиток, утюгов, электродвигателей и т. д.). Сопротивление подводящих проводов при этом должно быть значительно меньше, чем сопротивление нагрузки. При несоблюдении этого условия в проводах выделится большое количество теплоты, что может привести к их загоранию.
Если же оба резистора находятся под одинаковым напряжением, то согласно формуле быстрее будет нагреваться резистор с меньшим сопротивлением. Такой эффект, в частности, наблюдают при параллельном соединении резисторов.
Термин «сопротивление» применяется для условного обозначения элемента электрической цепи и для количественной оценки величины R.
Сопротивление измеряется в омах (Ом). 1 Ом — это сопротивление проводника, сила тока в котором равна 1 А, если на концах его поддерживается разность потенциалов 1 В:
1 Ом = 1 В/1 А
Электрическое сопротивление R материалов с изменением температуры меняется. Сопротивление металлических проводников линейно возрастает с температурой. У полупроводников и электролитов с увеличением температуры удельное сопротивление уменьшается, причем нелинейно.
Сопротивление металлических проводников линейно возрастает с температурой. У полупроводников и электролитов с увеличением температуры удельное сопротивление уменьшается, причем нелинейно.
Для сравнения проводников по степени зависимости их сопротивления от температуры t вводится величина a, называемая температурным коэффициентом сопротивления. Отсюда
Для практических расчетов в электрических цепях величину R можно принимать постоянной. В этом случае зависимость напряжения на сопротивлении R от силы тока (вольт-амперная характеристика) будет называться линейной. Электрические цепи, в которые включены постоянные по величине сопротивления, также будут линейными.
Законы Кирхгофа
Законы Кирхгофа (или правила Кирхгофа) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи. Правила Кирхгофа позволяют рассчитывать любые электрические цепи постоянного и квазистационарного тока. Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения любых электротехнических задач.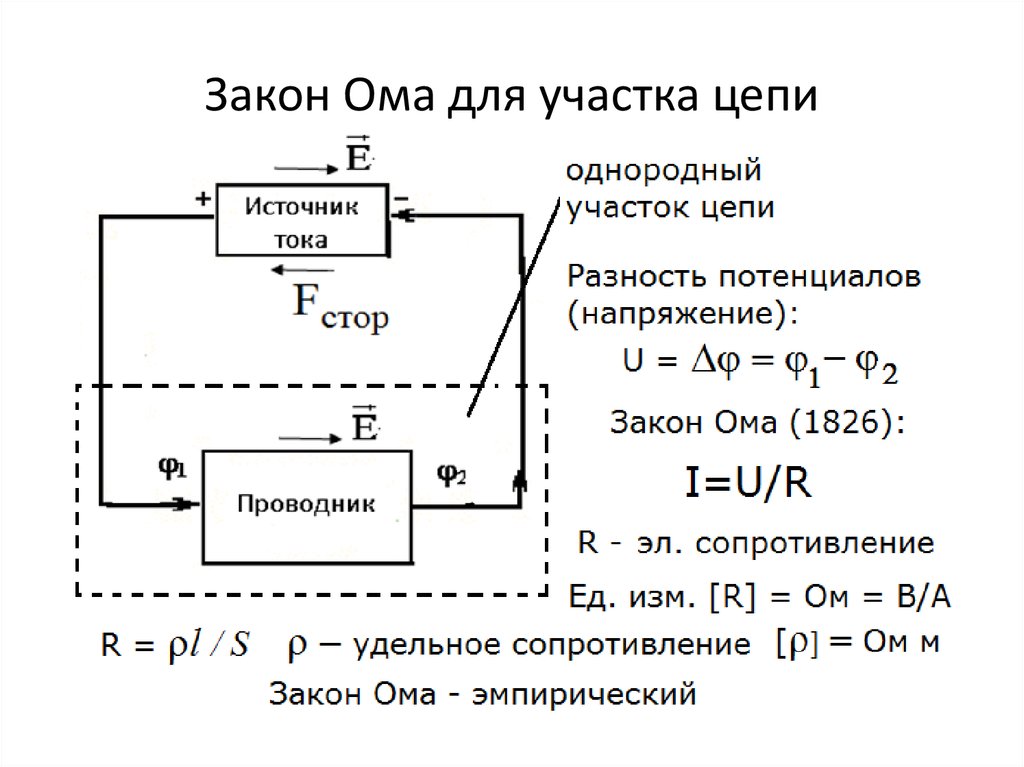 Применение правил Кирхгофа к цепи позволяет получить систему линейных уравнений относительно токов, и соответственно, найти значение токов на всех ветвях цепи.
Применение правил Кирхгофа к цепи позволяет получить систему линейных уравнений относительно токов, и соответственно, найти значение токов на всех ветвях цепи.
Для формулировки законов Кирхгофа, в электрической цепи выделяются узлы — точки соединения трёх и более проводников и контуры — замкнутые пути из проводников. При этом каждый проводник может входить в несколько контуров. В этом случае законы формулируются следующим образом.
Первый закон (ЗТК, Закон токов Кирхгофа) гласит, что алгебраическая сумма токов в любом узле любой цепи равна нулю (значения вытекающих токов берутся с обратным знаком):
Иными словами, сколько тока втекает в узел, столько из него и вытекает. Данный закон следует из закона сохранения заряда. Если цепь содержит p узлов, то она описывается p − 1 уравнениями токов. Этот закон может применяться и для других физических явлений (к примеру, водяные трубы), где есть закон сохранения величины и поток этой величины.
Второй закон (ЗНК, Закон напряжений Кирхгофа) гласит, что алгебраическая сумма падений напряжений по любому замкнутому контуру цепи равна алгебраической сумме ЭДС, действующих вдоль этого же контура. Если в контуре нет ЭДС, то суммарное падение напряжений равно нулю:
Если в контуре нет ЭДС, то суммарное падение напряжений равно нулю:
для постоянных напряжений:
для переменных напряжений:
Иными словами, при обходе цепи по контуру, потенциал, изменяясь, возвращается к исходному значению. Если цепь содержит ветвей, из которых содержат источники тока ветви в количестве , то она описывается уравнениями напряжений. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи.
Законы Кирхгофа справедливы для линейных и нелинейных цепей при любом характере изменения во времени токов и напряжений.
На этом рисунке для каждого проводника обозначен протекающий по нему ток (буквой «I») и напряжение между соединяемыми им узлами (буквой «U»)
Например, для приведённой на рисунке цепи, в соответствии с первым законом выполняются следующие соотношения:
Обратите внимание, что для каждого узла должно быть выбрано положительное направление, например здесь, токи, втекающие в узел, считаются положительными, а вытекающие — отрицательными. В соответствии со вторым законом, справедливы соотношения:. В соответствии со вторым законом, справедливы соотношения:
В соответствии со вторым законом, справедливы соотношения:. В соответствии со вторым законом, справедливы соотношения:
В соответствии со вторым законом, справедливы соотношения:
Если направление тока совпадает с направлением обхода контура (которое выбирается произвольно), перепад напряжения считается положительным, в противном случае — отрицательным.
Законы Кирхгофа, записанные для узлов и контуров цепи, дают полную систему линейных уравнений, которая позволяет найти все токи и напряжения.
Существует мнение, согласно которому «Законы Кирхгофа» следует именовать «Правилами Кирхгофа», ибо они не отражают фундаментальных сущностей природы (и не являются обобщением большого количества опытных данных), а могут быть выведены из других положений и предположений.
Напряжение на участке цепи формула
Закон Ома
Со школьного курса физики всем хорошо известна классическая трактовка Закона Ома: Сила тока в проводнике прямо пропорциональна напряжению на концах проводника и обратно пропорциональна его сопротивлению. Это значит, если к концам проводника сопротивлением R = 1 Ом приложено напряжение U = 1 Вольт, тогда величина тока I в проводнике будет равна 1/1 = 1 Ампер. Отсюда следуют ещё два полезных соотношения: Если в проводнике, сопротивлением 1 Ом, протекает ток 1 Ампер, значит на концах проводника напряжение 1 Вольт (падение напряжения). Если на концах есть напряжение 1 Вольт и по нему протекает ток 1 Ампер, значит сопротивление проводника равно 1 Ом.
Это значит, если к концам проводника сопротивлением R = 1 Ом приложено напряжение U = 1 Вольт, тогда величина тока I в проводнике будет равна 1/1 = 1 Ампер. Отсюда следуют ещё два полезных соотношения: Если в проводнике, сопротивлением 1 Ом, протекает ток 1 Ампер, значит на концах проводника напряжение 1 Вольт (падение напряжения). Если на концах есть напряжение 1 Вольт и по нему протекает ток 1 Ампер, значит сопротивление проводника равно 1 Ом.
Вышеописанные формулы в таком виде могут быть применимы для переменного тока лишь в том случае, если цепь состоит только из активного сопротивления R .
Напряжение на участке цепи формула
Для широкого класса проводников (в т. ч. металлов) сила тока в проводнике прямо пропорциональна напряжению ( закон Ома ): Коэффициент пропорциональности R называется электрическим сопротивлением и измеряется в омах (Ом). Причиной электрического сопротивления является взаимодействие электронов при их движении по проводнику с ионами кристаллической решетки.
Электрическое сопротивление металлов прямо пропорционально длине проводника и обратно пропорционально площади его поперечного сечения: Коэффициент пропорциональности ρ – удельное сопротивление – зависит только от вида металла. Общее сопротивление R последовательно соединенных проводников R 1 и R 2 равно сумме их сопротивлений: Рис. 4. Расчет сопротивления сложной цепи Для того, чтобы в замкнутой цепи постоянного тока поддерживалась непрерывная циркуляция зарядов (то есть протекал электрический ток) в этой цепи должны действовать силы неэлектростатического происхождения, так как работа электрического поля при перемещении зарядов по замкнутому пути равна нулю.
Закон Ома для участка цепи
Знание этого закона позволит нам беспрепятственно и безошибочно определять значения силы тока, напряжения (разности потенциалов) и сопротивления на участке цепи.
Кто такой Ом? Немного истории Закон Ома открыл всем известный немецкий физик Георг Симон Ом в 1826 году.
Вот так он выглядел.
Всю биографию Георга Ома я рассказывать Вам не буду. Про это Вы можете узнать на других ресурсах более подробно.
Скажу только самое главное. Его именем назван самый основной закон электротехники, который мы активно применяем в сложных расчетах при проектировании, на производстве и в быту.
В этом случае э. д. с.
Е источника в формуле (7) должна быть заменена разностью потенциалов между началом и концом рассматриваемого участка, т. е. напряжением U, а вместо сопротивления всей цепи в формулу должно быть подставлено сопротивление R данного участка.
В этом случае закон Ома формулируется следующим образом. Сила тока I на данном участке электрической цепи равна напряжению U, приложенному к участку, поделенному на сопротивление R этого участка: Рис 14. Прохождение электрического тока по проводникам аналогично прохождению воды по трубам Прохождение электрического тока по проводникам полностью аналогично прохождению воды по трубам (рис.
14). Чем больше разность уровней воды при входе и выходе из трубы (напор) и чем больше поперечное сечение трубы, тем больше воды протекает сквозь трубу в единицу времени.
Глава 21
Чтобы в тек электрический ток, в проводнике должно быть электрическое поле, или, другими словами, потенциалы различных точек проводника должны быть разными.
Но при движении электрических зарядов по проводнику потенциалы различных точек проводника будут выравниваться (см. гл. 19). Поэтому для протекания тока в течение длительного времени на каких-то участках цепи необходимо обеспечить движение зарядов в направлении противоположном полю.
Такое движение может быть обеспечено только силами неэлектрической природы, которые в этом контексте принято называть сторонними.
В гальванических элементах («батарейках») сторонние силы возникают в результате электрохимических превращений на границах электродов и электролита.
Говорим о напряжении
Не менее важно понять что такое напряжение. Давайте сразу начнем с аналогии и снова используем воду
Пусть в воронке находится вода. Она просачивается через узкое горлышко, которое создает сопротивление. Если представить, что на воду уложили груз, движение воды ускорится. Этот груз — и есть напряжение. И теперь тоже понятно, почему чем выше напряжение, тем сильнее ток — чем сильнее давление, тем быстрее будет двигаться вода. То есть, зависимость прямая: больше напряжение — больше ток. И именно это положение отражает закон Ома — «давление» стоит в числителе (в верхней части дроби).
Если представить, что на воду уложили груз, движение воды ускорится. Этот груз — и есть напряжение. И теперь тоже понятно, почему чем выше напряжение, тем сильнее ток — чем сильнее давление, тем быстрее будет двигаться вода. То есть, зависимость прямая: больше напряжение — больше ток. И именно это положение отражает закон Ома — «давление» стоит в числителе (в верхней части дроби).
Можно попробовать представить напряжение по-другому. Есть все те же электроны, которые скопились на одном краю источника питания. На втором краю их мало. Так как каждый из электронов имеет какой-то заряд, там, где их много, суммарный заряд больше, где мало — меньше. Разница между зарядами и есть напряжение. Это тоже несложно представить. С точки зрения электричества — это более корректное представление, хоть и не точное.
На тему закона Ома есть немало забавных картинок, позволяющих чуть лучше понять все эти явления. Одна из них перед вами и иллюстрирует, как ток зависит от напряжения и сопротивления. Смотрите что получается: сопротивление старается уменьшить ток (обратная зависимость), а с ростом напряжения он увеличивается (прямая зависимость). Это и есть закон Ома, но переданный простыми словами.
Смотрите что получается: сопротивление старается уменьшить ток (обратная зависимость), а с ростом напряжения он увеличивается (прямая зависимость). Это и есть закон Ома, но переданный простыми словами.
Благодаря картинке просто понять зависимость тока от напряжения и сопротивления
Если вы хотите убедиться и в этой зависимости, тоже надо создать простенькую цепь. Но нужен будет либо регулируемый источник питания, либо несколько батареек, которые выдают разное напряжение. Или можно последовательно включать несколько батареек — тоже вариант. Но менять/подпаивать батарейки надо при разорванной цепи (выключенном тумблере).
В этой схеме используются два измерительных прибора: амперметр включается последовательно с нагрузкой (резистор на схеме ниже), вольтметр параллельно нагрузке.
Схема для иллюстрации закона Ома
Так как другие параметры цепи остаются в норме, при увеличении напряжения мы увидим увеличение силы тока. Чем больше напряжение подаем, тем больше отклоняются стрелки вольтметра и амперметра. Если задаться целью построить график, он будет в виде прямой. Если поставить другое сопротивление, график также будет в виде прямой, но угол наклона ее изменится.
Если задаться целью построить график, он будет в виде прямой. Если поставить другое сопротивление, график также будет в виде прямой, но угол наклона ее изменится.
Сверхпроводимость
Сверхпроводимость – это свойство некоторых материалов обладать строго нулевым электрическим сопротивлением при достижении ими температуры меньше определённой, так называемой критической температуры.
Существует несколько сотен материалов, которые могут переходить в сверхпроводящее состояние при определённой температуре.
Ранее среди физиков бытовало мнение, что при уменьшении температуры сопротивление должно плавно уменьшаться, а при достижении температуры, близкой к абсолютному нулю, электроны вообще перестают двигаться, следовательно, ток перестанет течь по проводникам. Однако 8 апреля 1911 года обнаружилось, что при температуре 3 К С электрическое сопротивление ртути практически равно нулю. Более точные измерения показали, что резкий спад сопротивления до нуля происходит при температуре 4,15 К.
Однако 8 апреля 1911 года обнаружилось, что при температуре 3 К С электрическое сопротивление ртути практически равно нулю. Более точные измерения показали, что резкий спад сопротивления до нуля происходит при температуре 4,15 К.
Для постоянного электрического тока электрическое сопротивление сверхпроводника равно нулю. Это было продемонстрировано в ходе эксперимента, где в замкнутом сверхпроводнике был индуцирован электрический ток, который протекал в нём без затухания в течение 2,5 лет. Эксперимент был прерван забастовкой рабочих, подвозивших криогенную жидкость (сжиженный газ с температурой ниже 120 К).
В технике применяются сверхпроводники на основе сплавов ниобия (см. Рис. 7)
Отсутствие потерь на нагревание при прохождении постоянного тока через сверхпроводник делает привлекательным применение сверхпроводящих кабелей (см. Рис. для доставки электричества, так как один такой тонкий кабель способен передавать мощность, которую традиционным методом можно передать с помощью цепи линий электропередач с несколькими более толстыми кабелями.
Рис. 7. Сплав ниобия
Проблемами, препятствующими широкому использованию сверхпроводящих кабелей, являются высокая стоимость кабеля и его обслуживание (через сверхпроводящие линии необходимо постоянно перекачивать жидкий азот). Однако в Нью-Йорке в конце июня 2008 года была запущена первая коммерческая сверхпроводящая линия электропередач.
Рис. 8. Сверхпроводящий кабель
Заказать решение ТОЭ
- Метрология Электрические измерения
- Пигарев А.Ю. РГЗ по электротехнике и электронике в Multisim
- Теория линейных электрических цепей ТЛЭЦ — Теория линейных электрических цепей железнодорожной автоматики, телемеханики и связи: задание на контрольные работы № 1 и 2 с методическими указаниями для студентов IV курса специальности Автоматика, телемеханика и связь на железнодорожном транспорте — Контрольная работа №1
- — Контрольная работа №2
Электротехника и основы электроники
- — Электротехника и основы электроники: Методические указания и контрольные задания для студентов-заочников инженерно-технических специальностей высших учебных заведений / Соколов Б.
 П., Соколов В.Б. – М.: Высш. шк., 1985. – 128 с, ил — Контрольная работа № 1 Электрические цепи
П., Соколов В.Б. – М.: Высш. шк., 1985. – 128 с, ил — Контрольная работа № 1 Электрические цепи
— Контрольная работа № 2 Трансформаторы и электрические машины
— Контрольная работа № 3 Основы электроники
Теоретические основы электротехники ТОЭ
- — Артеменко Ю.П., Сапожникова Н.М. Теоретические основы электротехники: Пособие по выполнению курсовой работы МГТУ ГА 2009
— Переходные процессы Переходные процессы в электрических цепях
— Теоретические основы электротехники Методические указания и контрольные задания для студентов технических специальностей вузов — Задание 1 Линейные электрические цепи постоянного и синусоидального тока — Задача 1.1 Линейные электрические цепи постоянного тока
— Задача 1.2 Линейные электрические цепи синусоидального тока
— Задание 2 Четырехполюсники, трехфазные цепи, периодические несинусоидальные токи, электрические фильтры, цепи с управляемыми источниками
— Теоретические основы электротехники сб. заданий Р. Я. Сулейманов Т.А. Никитина Екатеринбург УрГУПС 2010
Я. Сулейманов Т.А. Никитина Екатеринбург УрГУПС 2010
— Трехфазные цепи. Расчет трехфазных цепей
— УГТУ-УПИ Решение ТОЭ Билеты по ТОЭ
— Электромагнитное поле Электростатическое поле Электростатическое поле постоянного тока в проводящей среде Магнитное поле постоянного тока
Советуем изучить Рекуперация или преобразование кинетической энергии торможения
Закон ома для неоднородного участка цепи
Перед тем, как записать формулу для подобной интерпретации закона, следует разобраться в таких понятиях, как линейные и нелинейные участки цепи.
Если сопротивление никаким образом не зависит от тока и подаваемого напряжения, то с ростом второго параметра, первый будет прямо пропорционально возрастать и наоборот, то есть зависимость можно описать прямой линией. Подобная зависимость относится к линейным участкам цепи и сопротивление имеет аналогичное название.
Однако вышеизложенный вариант считается идеальным и его можно смоделировать лишь в идеальных условиях, что фактически невозможно, ведь, как минимум, окружающая среда вносит свои коррективы.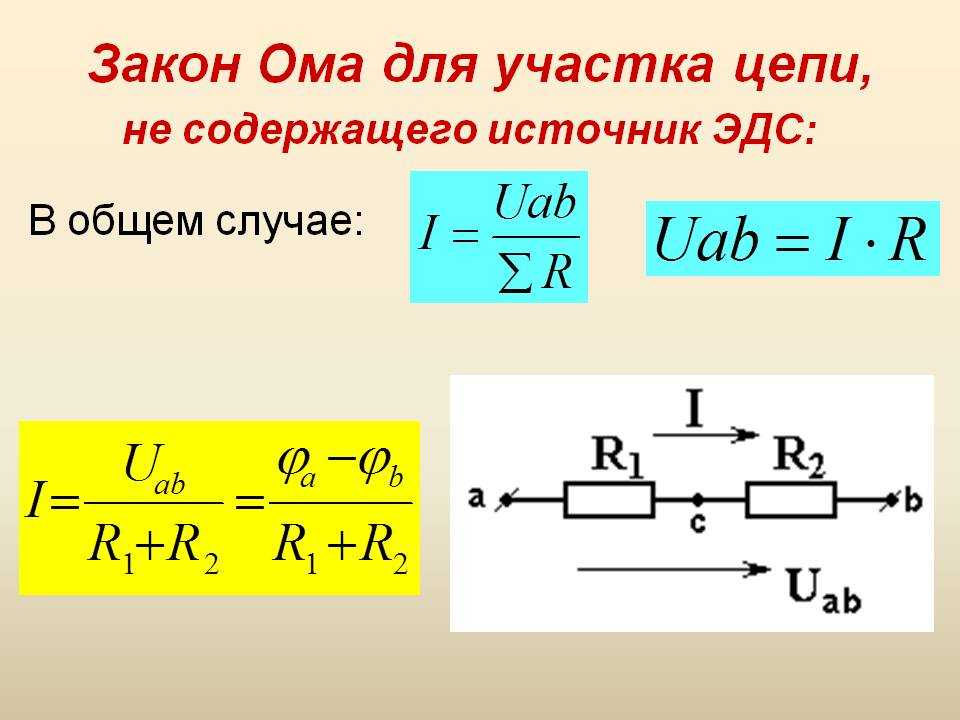 В этом случае, рост напряжения не будет прямо пропорциональным силе тока и на графике зависимость будет изображаться в виде кривой.
В этом случае, рост напряжения не будет прямо пропорциональным силе тока и на графике зависимость будет изображаться в виде кривой.
На рисунке изображено два графика, первый из которых описывает линейную зависимость, а второй нелинейную.
Чтобы отчетливо понимать разницу между этими понятиями, рассмотрим принцип работы обычной электрической лампы накаливания. При прохождении тока по нити, температура в значительной степени повышается, что приводит к заметному росту сопротивления. Соответственно, при возрастании напряжения, сила тока будет увеличиваться медленнее, то есть не линейно.
Учитывая вышесказанное, можно установить следующую зависимость:
I = U/ R = (f1 – f2) + E/ R,
Где f1 и f2 – потенциалы (соответственно f1 – f2 называется разницей потенциалов), E – ЭДС неоднородного участка цепи, а R – суммарное сопротивление на этом же участке.
Нужно упомянуть и о том, что электродвижущая сила не всегда в этом случае будет иметь положительное значение. Если направление тока источника будет аналогичным с направлением в электрической сети, протонов будет больше, чем электронов (положительных и отрицательных частиц), то в этом случае величина E будет иметь значение со знаком «+», в иной ситуации, этот параметр будет со знаком «-».
Закон Ома для полной цепи
- Подробности
- Просмотров: 432
«Физика — 10 класс»
Сформулируйте закон Ома для участка цепи.
Из каких элементов состоит электрическая цепь?
Для чего служит источник тока?
Рассмотрим простейшую полную (т. е. замкнутую) цепь, состоящую из источника тока (гальванического элемента, аккумулятора или генератора) и резистора сопротивлением R (рис. 15.10). Источник тока имеет ЭДС Ε и сопротивление r.
В генераторе r — это сопротивление обмоток, а в гальваническом элементе сопротивление раствора электролита и электродов.
Сопротивление источника называют внутренним сопротивлением в отличие от внешнего сопротивления R цепи.
Закон Ома для замкнутой цепи связывает силу тока в цепи, ЭДС и полное сопротивление цепи R + r. Эта связь может быть установлена теоретически, если использовать закон сохранения энергии и закон Джоуля—Ленца (15.14).
Пусть за время Δt через поперечное сечение проводника проходит электрический заряд Δq. Тогда работу сторонних сил при перемещении заряда Δq можно записать так: Аст = ΕΔq. Согласно определению силы тока (15.1) Δq = IΔt. Поэтому
Тогда работу сторонних сил при перемещении заряда Δq можно записать так: Аст = ΕΔq. Согласно определению силы тока (15.1) Δq = IΔt. Поэтому
Аст = ΕIΔt. (15.17)
При совершении этой работы на внутреннем и внешнем участках цепи, сопротивления которых г и Я, выделяется некоторое количество теплоты. По закону Джоуля—Ленца оно равно:
Q = I2RΔt + I2rΔt. (15.18)
По закону сохранения энергии Аст = Q, откуда получаем
Ε = IR + 1r. (15.19)
Произведение силы тока и сопротивления участка цепи называют падением напряжения на этом участке.
Таким образом, ЭДС равна сумме падений напряжения на внутреннем и внешнем участках замкнутой цепи.
Закон Ома для замкнутой цепи:
Сила тока в замкнутой цепи равна отношению ЭДС источника тока к полному сопротивлению цепи.
Согласно этому закону сила тока в цепи зависит от трёх величин: ЭДС Ε сопротивлений R внешнего и г внутреннего участков цепи. Внутреннее сопротивление источника тока не оказывает заметного влияния на силу тока, если оно мало по сравнению с сопротивлением внешней части цепи (R >> r). При этом напряжение на зажимах источника примерно равно ЭДС: U = IR = Ε — Ir ≈ Ε
Внутреннее сопротивление источника тока не оказывает заметного влияния на силу тока, если оно мало по сравнению с сопротивлением внешней части цепи (R >> r). При этом напряжение на зажимах источника примерно равно ЭДС: U = IR = Ε — Ir ≈ Ε
При коротком замыкании, когда R ≈ 0, сила тока в цепи и определяется именно внутренним сопротивлением источника и при электродвижущей силе в несколько вольт может оказаться очень большой, если r мало (например, у аккумулятора r ≈ 0,1 — 0,001 Ом). Провода могут расплавиться, а сам источник выйти из строя.
Если цепь содержит несколько последовательно соединённых элементов с ЭДС Ε1, Ε2, Ε3 и т. д., то полная ЭДС цепи равна алгебраической сумме ЭДС отдельных элементов.
Для определения знака ЭДС любого источника нужно вначале условиться относительно выбора положительного направления обхода контура.
На рисунке (15.11) положительным (произвольно) считают направление обхода против часовой стрелки.
Если при обходе цепи данный источник стремится вызвать ток в направлении обхода, то его ЭДС считается положительной: Ε > 0.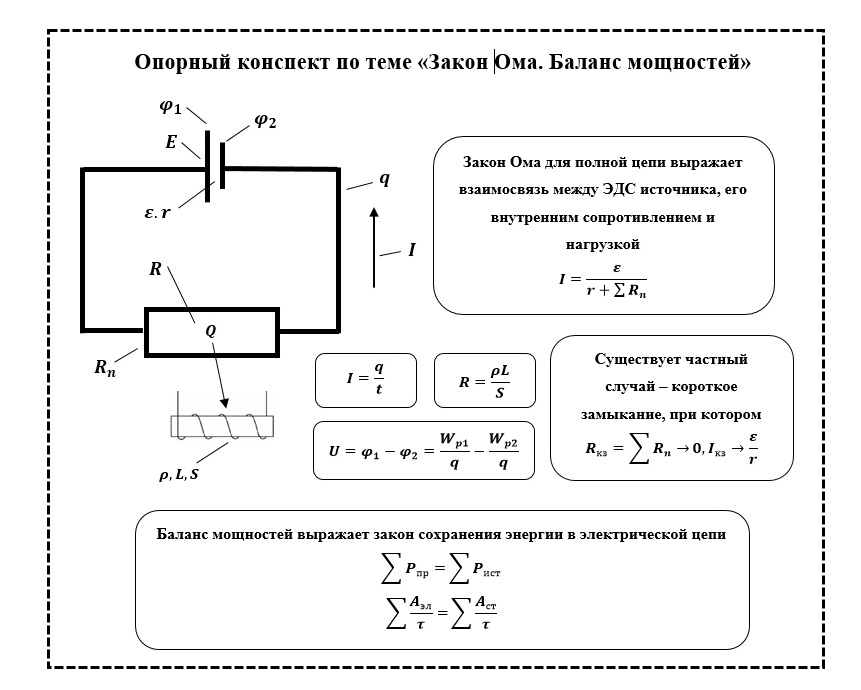 Сторонние силы внутри источника совершают при этом положительную работу.
Сторонние силы внутри источника совершают при этом положительную работу.
Если же при обходе цепи данный источник вызывает ток против направления обхода цепи, то его ЭДС будет отрицательной: Ε < 0. Сторонние силы внутри источника совершают отрицательную работу. Так, для цепи, изображённой на рисунке 15.11, при обходе контура против часовой стрелки получаем следующее уравнение:
Εп = Ε1 + Ε2 + Ε3 = lΕ1| — |Ε2| + |Ε3|
Если Εп > 0, то согласно формуле (15.20) сила тока I > 0, т. е. направление тока совпадает с выбранным направлением обхода контура. При Εп < 0, наоборот, направление тока противоположно выбранному направлению обхода контура. Полное сопротивление цепи Rп равно сумме всех сопротивлений (см. рис. 15.11):
Rп = R + r1 + r2 + r3.
Для любого замкнутого участка цепи, содержащего несколько источников токов, справедливо следующее правило: алгебраическая сумма падений напряжения равна алгебраической сумме ЭДС на этом участке (второе правило Кирхгофа):
I1R1+ I2R2 + … + InRn = Ε1 + Ε2 + … + Εm
Следующая страница «Примеры решения задач по теме «Работа и мощность постоянного тока. Закон Ома для полной цепи»»
Закон Ома для полной цепи»»
Назад в раздел «Физика — 10 класс, учебник Мякишев, Буховцев, Сотский»
Законы постоянного тока — Физика, учебник для 10 класса — Класс!ная физика
Электрический ток. Сила тока —
Закон Ома для участка цепи. Сопротивление —
Электрические цепи. Последовательное и параллельное соединения проводников —
Примеры решения задач по теме «Закон Ома. Последовательное и параллельное соединения проводников» —
Работа и мощность постоянного тока —
Электродвижущая сила —
Закон Ома для полной цепи —
Примеры решения задач по теме «Работа и мощность постоянного тока. Закон Ома для полной цепи»
Как трактуется правило Ома
Так как обобщённая формула ома не считается основополагающей, правило применяется для описания разновидностей проводников в условиях приближения незначительной частоты, плотности тока и напряжения электрополя. Следует отметить, что в ряде случаев как первый закон, так и второй закон, применяемый для полной цепи, не соблюдаются.
Существует теория Друде, для выражения которой используются следующие величины:
- удельная электропроводимость;
- концентрированное размещение электронов;
- показатель элементарного заряда;
- время затихания по импульсам;
- эффективная масса электрона.
Перечень условий, при которых становится невозможным соблюдения правила Ома:
- высокие частоты с чрезмерно большой скоростью изменения электротока;
- пониженная температура сверхпроводимого вещества;
- перегрев проводника проходящим электротоком;
- в ситуации пробоя, возникшего в результате подсоединения к проводниковому элементу высокого напряжения;
- в вакуумной или газонаполненной электролампе;
- для гетерогенного полупроводникового прибора;
- при образовании пространственного диэлектрического заряда в контакте металлического диэлектрика.
Параллельное и последовательное соединение
В электрике элементы соединяются либо последовательно — один за другим, либо параллельно — это когда к одной точке подключены несколько входов, к другой — выходы от тех же элементов.
Закон Ома для параллельного и последовательного соединения
Последовательное соединение
Как работает закон Ома для этих случаев? При последовательном соединении сила тока, протекающая через цепочку элементов, будет одинаковой. Напряжение участка цепи с последовательно подключенными элементами считается как сумма напряжений на каждом участке. Как можно это объяснить? Протекание тока через элемент — это перенос части заряда с одной его части в другую. То есть, это определенная работа. Величина этой работы и есть напряжение. Это физический смысл напряжения. Если с этим понятно, двигаемся дальше.
Последовательное соединение и параметры этого участка цепи
При последовательном соединении приходится переносить заряд по очереди через каждый элемент. И на каждом элементе это определенный «объем» работы. А чтобы найти объем работы на всем участке цепи, надо работу на каждом элементе сложить. Вот и получается, что общее напряжение — это сумма напряжений на каждом из элементов.
Точно так же — при помощи сложения — находится и общее сопротивление участка цепи. Как можно это себе представить? Ток, протекая по цепочке элементов, последовательно преодолевает все сопротивления. Одно за другим. То есть чтобы найти сопротивление, которое он преодолел, надо сопротивления сложить. Примерно так. Математический вывод более сложен, а так понять механизм действия этого закона проще.
Параллельное соединение
Параллельное соединение — это когда начала проводников/элементов сходятся в одной точке, а в другой — соединены их концы. Постараемся объяснить законы, которые справедливы для соединений этого типа. Начнем с тока. Ток какой-то величины подается в точку соединения элементов. Он разделяется, протекая по всем проводникам. Отсюда делаем вывод, что общий ток на участке равен сумме тока на каждом из элементов: I = I1 + I2 + I3.
Теперь относительно напряжения. Если напряжение — это работа по перемещению заряда, тоо работа, которая необходима на перемещение одного заряда будет одинакова на любом элементе. То есть, напряжение на каждом параллельно подключенном элементе будет одинаковым. U = U1=U2=U3. Не так весело и наглядно, как в случае с объяснением закона Ома для участка цепи, но понять можно.
То есть, напряжение на каждом параллельно подключенном элементе будет одинаковым. U = U1=U2=U3. Не так весело и наглядно, как в случае с объяснением закона Ома для участка цепи, но понять можно.
Законы для параллельного соединения
Для сопротивления все несколько сложнее. Давайте введем понятие проводимости. Это характеристика, которая показывает насколько легко или сложно заряду проходить по этому проводнику. Понятно, что чем меньше сопротивление, тем проще току будет проходить. Поэтому проводимость — G — вычисляется как величина обратная сопротивлению. В формуле это выглядит так: G = 1/R.
Для чего мы говорили о проводимости? Потому что общая проводимость участка с параллельным соединением элементов равна сумме проводимости для каждого из участков. G = G1 + G2 + G3 — понять несложно. Насколько легко току будет преодолеть этот узел из параллельных элементов, зависит от проводимости каждого из элементов. Вот и получается, что их надо складывать.
Теперь можем перейти к сопротивлению. Так как проводимость — обратная к сопротивлению величина, можем получить следующую формулу: 1/R = 1/R1 + 1/R2 + 1/R3.
Так как проводимость — обратная к сопротивлению величина, можем получить следующую формулу: 1/R = 1/R1 + 1/R2 + 1/R3.
Что нам дает параллельное и последовательное соединение?
Теоретические знания — это хорошо, но как их применить на практике? Параллельно и последовательно могут соединяться элементы любого типа. Но мы рассматривали только простейшие формулы, описывающие линейные элементы. Линейные элементы — это сопротивления, которые еще называют «резисторы». Итак, вот как можно использовать полученные знания:
Если в наличии нет резистора большого номинала, но есть несколько более «мелких», нужное сопротивление можно получить соединив последовательно несколько резисторов. Как видите, это полезный прием.
Для продления срока жизни батареек, их можно соединять параллельно. Напряжение при этом, согласно закону Ома, останется прежним (можно убедиться, измерив напряжение мультиметром). А «срок жизни» сдвоенного элемента питания будет значительно больше, нежели у двух элементов, которые сменят друг друга
Только обратите внимание: параллельно соединять можно только источники питания с одинаковым потенциалом.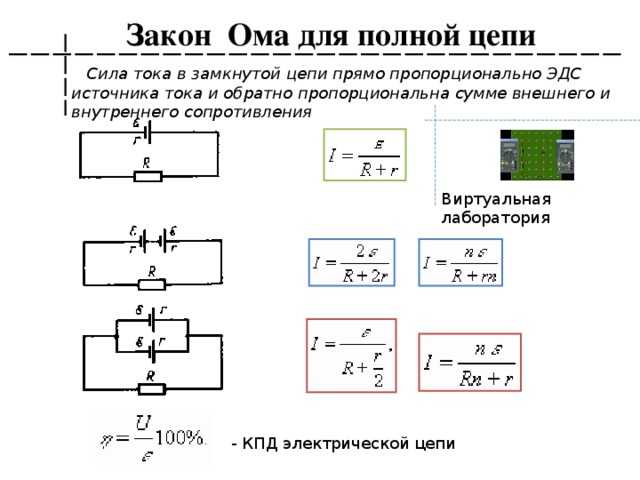 То есть, севшую и новую батарейки соединять нельзя
То есть, севшую и новую батарейки соединять нельзя
Если все-таки соединить, та батарейка которая имеет больший заряд, будет стремиться зарядить менее заряженную. В результате общий их заряд упадет до низкого значения.
В общем, это наиболее распространенные варианты использования этих соединений.
Вывод
Внутреннее сопротивление бывает не только у различных химических источников напряжения. Внутренним сопротивлением также обладают и различные измерительные приборы. Это в основном вольтметры и осциллографы.
Дело все в том, что если подключить нагрузку R, сопротивление у которой будет меньше или даже равно r, то у нас очень сильно просядет напряжение. Это можно увидеть, если замкнуть клеммы аккумулятора толстым медным проводом и замерять в это время напряжение на клеммах. Но я не рекомендую этого делать ни в коем случае! Поэтому, чем высокоомнее нагрузка (ну то есть чем выше сопротивление нагрузки R ), тем меньшее влияние оказывает эта нагрузка на источник электрической энергии.
Вольтметр и осциллограф при замере напряжения тоже чуть-чуть просаживают напряжение замеряемого источника напряжения, потому как являются нагрузкой с большим сопротивлением. Именно поэтому самый точный вольтметр и осциллограф имеют ну очень большое сопротивление между своими щупами.
Физика Электрический ток. Условия, необходимые для его существования. Закон Ома для участка цепи. Сопротивление
Материалы к уроку
53. Электрический ток. Условия, необходимые для его существования. Закон Ома для участка цепи. Сопротивление.doc
57 KBСкачать- Закон Ома для участка цепи. Сопротивление.ppt»>53. Электрический ток. Условия, необходимые для его существования. Закон Ома для участка цепи. Сопротивление.ppt8.12 MBСкачать
Конспект урока
Мы живём в век научно-технического прогресса, в век, когда уровень жизни каждого отдельного человека напрямую зависит от достижений науки и техники. В очень далёкие времена, когда горели лучины и топились печи по «чёрному», люди не представляли себе, в каком светлом и тёплом будущем будут жить их потомки. Сейчас не можем представить наш мир без электричества. А если попробовать?
Вдруг что-то произойдет, и электричество просто исчезнет. Жизнь просто остановится!
Электрические законы, открытые чуть позже тех далёких времён, являются и сейчас самыми важными, и мы живём среди них.
Неподвижные электрические заряды редко используются на практике. Для того чтобы заставить электрические заряды служить нам, их нужно привести в движение – создать электрический ток. Электрическим током называется упорядоченное движение, направленное движение заряженных частиц. За направление тока принимают направление движения положительно заряженных частиц.
Электрическим током называется упорядоченное движение, направленное движение заряженных частиц. За направление тока принимают направление движения положительно заряженных частиц.
Движение частиц в проводнике мы непосредственно не видим. О наличии электрического тока приходится судить по тем действиям или явлениям, которые его сопровождают.
Во-первых, проводник, по которому течет ток, нагревается.
Во- вторых, электрический ток может изменять химический состав проводника, например, выделять его химические составные части (медь из раствора медного купороса и т.д.).
В-третьих, ток оказывает силовое воздействие на соседние токи и намагниченные тела.
Если в цепи устанавливается электрический ток, то это означает, что через поперечное сечение проводника все время переносится электрический заряд. Заряд, перенесенный в единицу времени, служит основной количественной характеристикой тока, называемой силой тока. Таким образом, сила тока равна отношению заряда (дельта кю) Δq , переносимого через поперечное сечение проводника за интервал времени (дельта т) Δt, к этому интервалу времени.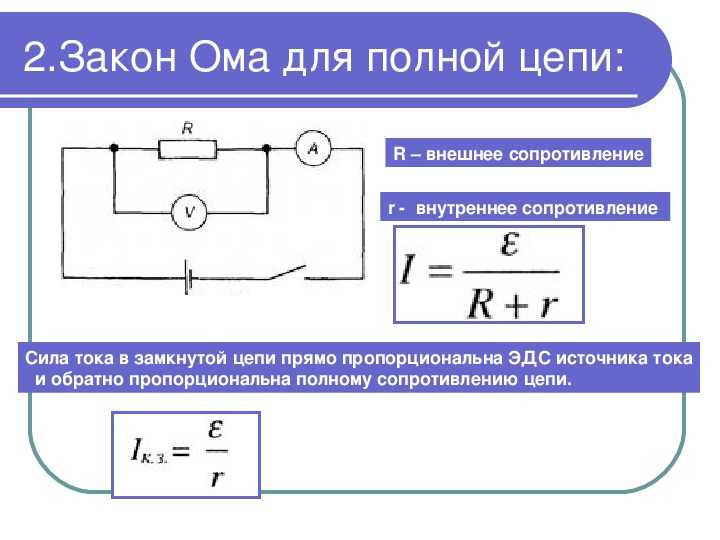
Решим задачу. Сила тока в спирали лампы накаливания составляет 0,5 А (ампера). Какой заряд протекает за 1 мин. через лампу? Воспользовавшись формулой, найдем заряд: он составит 30 Кулонов.
Сила тока, подобно заряду,- величина скалярная. Она может быть, как положительной, так и отрицательной. Сила тока зависит от заряда, переносимого каждой частицей, концентрации частиц, скорости их направленного движения и площади поперечного сечения проводника.
Ввел в физику понятие «электрический ток Андре Ампер
(1775-1836). Французский физик и математик. Он создал первую теорию, которая выражала связь электрических и магнитных явлений. Амперу принадлежит гипотеза о природе магнетизма, он ввел в физику понятие «электрический ток».
В международной системе единиц силу тока выражают в амперах. Эту единицу устанавливают на основе магнитного взаимодействия токов. Измеряют силу тока амперметрами. Принцип устройства этих приборов основан на магнитном действии тока.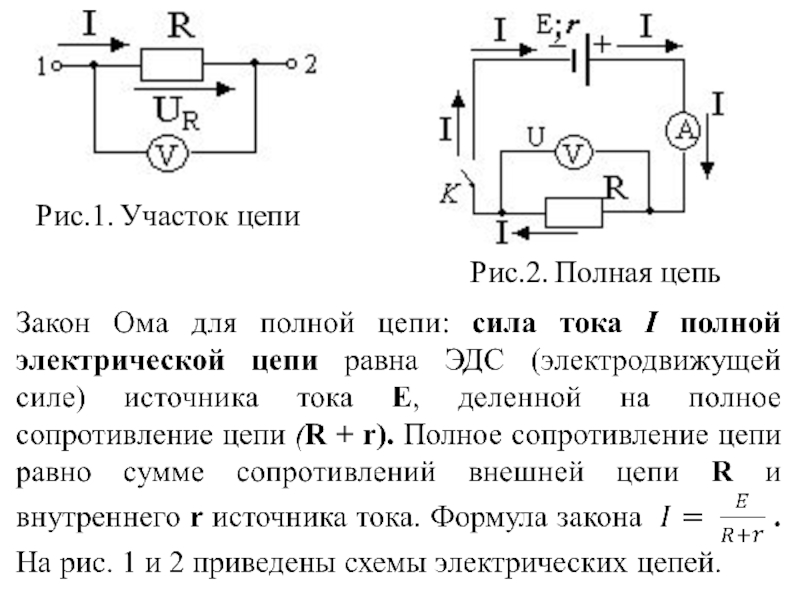
Электрический ток может быть получен только в таком веществе, в котором имеются свободные заряженные частицы. Чтобы эти частицы пришли в упорядоченное движение, нужно создать в проводнике электрическое поле. Значит, для существования тока в проводнике необходимо создать разность потенциалов на его концах с помощью источника тока.
Для измерения напряжения существует специальный измерительный прибор — вольтметр.
Условное обозначение вольтметра на электрической схеме.
При включении вольтметра в электрическую цепь необходимо соблюдать два правила.
1. Вольтметр подключается параллельно участку цепи, на котором будет измеряться напряжение.
2. Соблюдать полярность: «+» вольтметра подключается к «+» источника тока,
а «минус» вольтметра — к «минусу» источника тока.
Для измерения напряжения источника питания вольтметр присоединяют непосредственно к его зажимам.
Меру противодействия проводника установлению в нем электрического тока назовают сопротивлением.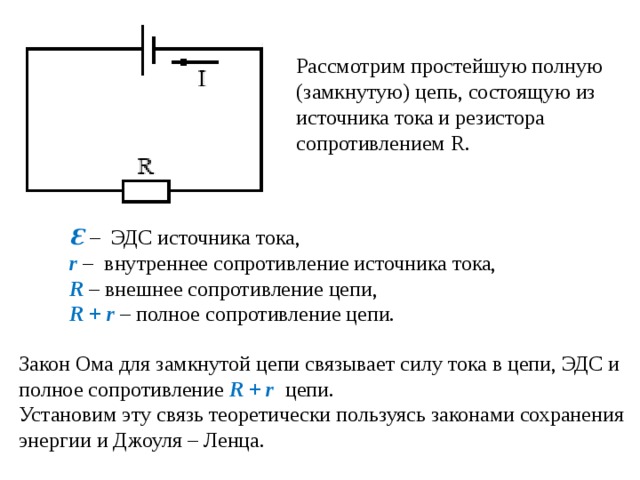 Это основная характеристика проводника. Сопротивление зависит от материала проводника длиной (эль) с постоянной площадью поперечного сечения (эс) S , где (ро) p — удельное сопротивление проводника – величина, зависящая от рода вещества и его состояния (от температуры в первую очередь).То есть сопротивление проводника прямо пропорционально отношению длины проводника к площади поперечного сечения. Проводник имеет сопротивление 1 Ом, если при разности потенциалов 1 В сила тока в нем 1 А. Единицей удельного сопротивления является 1 Ом на м.
Это основная характеристика проводника. Сопротивление зависит от материала проводника длиной (эль) с постоянной площадью поперечного сечения (эс) S , где (ро) p — удельное сопротивление проводника – величина, зависящая от рода вещества и его состояния (от температуры в первую очередь).То есть сопротивление проводника прямо пропорционально отношению длины проводника к площади поперечного сечения. Проводник имеет сопротивление 1 Ом, если при разности потенциалов 1 В сила тока в нем 1 А. Единицей удельного сопротивления является 1 Ом на м.
Для каждого проводника — твердого, жидкого и газообразного – существует определенная зависимость силы тока от приложенной разности потенциалов на концах проводника. Эту зависимость выражает вольт-амперная характеристика проводника. Впервые (для металлов) ее установил немецкий ученый Георг Ом, поэтому зависимость силы тока от напряжения носит название закона Ома.
Установим опытным путём зависимости между физическими величинами. Во-первых, определим зависимость между силой тока и напряжением. Соберем цепь, как показано на рисунке. То есть, соединим последовательно источник тока, ключ и резистор или другой потребитель тока. Последовательно к потребителю подключим амперметр, параллельно — вольтметр. Снимем показания амперметра при напряжениях в 5 вольт, 10 вольт и 20 вольт.
Во-первых, определим зависимость между силой тока и напряжением. Соберем цепь, как показано на рисунке. То есть, соединим последовательно источник тока, ключ и резистор или другой потребитель тока. Последовательно к потребителю подключим амперметр, параллельно — вольтметр. Снимем показания амперметра при напряжениях в 5 вольт, 10 вольт и 20 вольт.
Теперь, не меняя напряжение, посмотрим, как меняется сила тока при изменении сопротивления.
Если построить график зависимости силы тока от напряжения, то легко заметить, что сила тока прямо пропорциональна напряжению.
Продолжая анализировать результат эксперимента, приходим к выводу, что сила тока обратно пропорциональна сопротивлению.
Согласно закону Ома для участка цепи сила тока прямо пропорциональна приложенному напряжению (у) U и обратно пропорциональна сопротивлению проводника (эр) R.
Закон Ома – основа всей электротехники постоянных токов. Ее легче запомнить, пользуясь магическим треугольником.
Закон Ома: Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению.
Следствия из закона Ома:
1) напряжение на концах участка цепи равно произведению силе тока и сопротивлению проводника;
2) сопротивление проводника находят отношением напряжения на концах проводника к силе тока.
Решим задачу.
Сопротивление вольтметра равно 12000 Ом. Какова сила тока, протекающая через вольтметр, если он показывает напряжение, равное 120В?
По формуле найдем силу тока в проводнике.
Подставив данные, получим ответ сила тока =0,01A
На рисунке изображены графики зависимости силы тока от напряжения для двух проводников А и В. Какой из этих проводников обладает большим сопротивлением?
Зависимость между силой тока и сопротивлением в проводнике при постоянном напряжении — обратная. Возьмем на этих двух прямых точки с одинаковой координатой по оси U. У проводника А сила тока будет больше. Следовательно, проводник В обладает большим сопротивлением.
У проводника А сила тока будет больше. Следовательно, проводник В обладает большим сопротивлением.
Проверим это, подставив числовые значения.
Возьмем на этих прямых точки с напряжением равным 6 В.
По графику определим для этих точек силу тока.
Для проводника А сила тока равна 3А.
Для проводника В сила тока равна 1А.
Рассчитаем сначала сопротивление для проводника А, потом для проводника В.
Ответ: RB>RA.
Человечество впервые увидело электрическое освещение всего 138 лет тому назад. 23 марта 1876 года Павел Николаевич Яблочков (1847 – 1894) получил свой первый патент на изобретение электрической лампы, в ней под действием электрического тока вольфрамовая нить раскаляется до яркого свечения и освещает комнату. Этот день стал исторической датой. Лампу П.Н. Яблочкова в Европе современники называли «русским светом», а в России – «русским солнцем». Время шло, лампы видоизменялись, совершенствовались. В наше время появились энергосберегающие лампочки, которые состоят из колбы, наполненной парами ртути и аргоном. При нагревании ртуть начинает создавать ультрафиолетовое излучение, которое преобразуется в видимый свет. Энергосберегающая лампа светится по всей своей площади. Благодаря чему свет получается мягкий и равномерный, более приятен для глаз и лучше распространяется по помещению. При использовании энергосберегающих ламп нужно помнить, что отработав, они требуют специальной утилизации, так как содержат пары ртути и выбрасывать их категорически запрещено.
При нагревании ртуть начинает создавать ультрафиолетовое излучение, которое преобразуется в видимый свет. Энергосберегающая лампа светится по всей своей площади. Благодаря чему свет получается мягкий и равномерный, более приятен для глаз и лучше распространяется по помещению. При использовании энергосберегающих ламп нужно помнить, что отработав, они требуют специальной утилизации, так как содержат пары ртути и выбрасывать их категорически запрещено.
Одним из первых, кто ощутил на себе действие тока, был голландский физик П. Мушенбрук, живший в 18 веке. Получив удар током, он заявил, что «не согласился бы подвергнуться ещё раз такому испытанию даже за королевский трон Франции.
Следует помнить, что электрический ток вызывает изменения в нервной системе, выражающиеся в ее раздражении
или параличе, возникают судорожные спазмы мышц. Ток «держит» человека. Происходит судорожный спазм диафрагмы; действие тока на мозг может вызвать потерю сознания; электрический ток оказывает тепловое действие, выражающееся в ожогах 3-ей степени…
Электрошок — электрическое раздражение мозга, с помощью которого лечат некоторые психические заболевания.
Дефибрилляторы — электрические медицинские приборы, используемые при восстановлении
нарушений ритма сердечной деятельности посредством воздействия на организм кратковременными высоковольтными электрическими разрядами
Гальванизация — пропускание через организм слабого постоянного тока, оказывающего болеутоляющий эффект и улучшающий кровообращение.
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитора
Определение, формула, применение, примечания и практические вопросы
Закон Ома — это формула, которая устанавливает соотношение между током (I), напряжением (V) и сопротивлением (R) в электрической цепи. В 1826 году Георг Симон Ом в результате эксперимента сформулировал закон Ома. Он заметил, что ток, протекающий по цепи, прямо пропорционален напряжению и обратно пропорционален сопротивлению, если температура остается постоянной. Закон Ома используется в нашей повседневной жизни в электрических предохранителях для защиты цепей путем управления током или для управления скоростью вентилятора путем изменения сопротивления.
Он заметил, что ток, протекающий по цепи, прямо пропорционален напряжению и обратно пропорционален сопротивлению, если температура остается постоянной. Закон Ома используется в нашей повседневной жизни в электрических предохранителях для защиты цепей путем управления током или для управления скоростью вентилятора путем изменения сопротивления.
Закон Ома гласит, что разность потенциалов на концах проводника прямо пропорциональна току, протекающему в проводнике, при условии, что все физические условия, особенно температура, остаются постоянными.
В ∝ I
Формула закона Ома, Напряжение (В) = Ток (I) × Сопротивление (R) , помогает найти пропущенное значение третьей переменной, когда любое из двух значений напряжение, ток или сопротивление известны. Это один из самых основных законов электричество , которое помогает в расчете мощности, тока, КПД, напряжения и сопротивления элемента электрической цепи.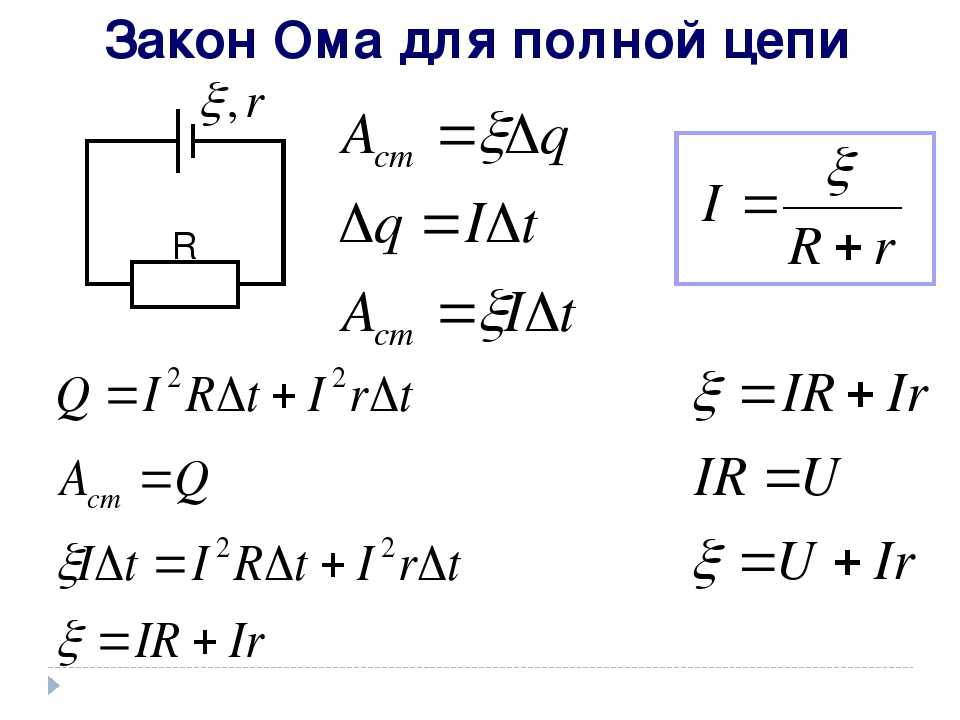
Нажмите здесь, чтобы прочитать Закон о Ом на хинди
Таблица Содержания
|
Ключевые члены: . Проводник
Проводник
Что такое закон Ома?
[Нажмите здесь, чтобы просмотреть примеры вопросов]
Закон Ома гласит, что разность потенциалов на концах металлического провода прямо пропорциональна току, протекающему через него, при условии, что все физические условия и температура остаются постоянными.
- Закон Ома определяет соотношение между током (I) и разностью потенциалов (V) на клеммах проводника.
- Закон Ома используется во всех отраслях электротехники для расчета номинала резисторов , необходимых в электрических цепях .
- Его также можно использовать для определения тока, протекающего в цепи, где можно легко измерить напряжение на известном резисторе.
Омические и неомические проводники
- Закон Ома выполняется только в том случае, если другие физические факторы и температура остаются постоянными.
- В некоторых случаях увеличение тока приводит к повышению температуры.

- Например, в нити накаливания лампочки температура повышается по мере увеличения тока. В этом случае закон Ома не может быть применен в этом сценарии. Таким образом, нить накала лампочки нарушает закон Ома.
Формула закона Ома
Поскольку ток и разность потенциалов являются скалярными величинами, закон Ома представлен в скалярной форме. Математически уравнение для закона Ома в скалярной форме представлено следующим образом: поток заряда от источника положительного заряда к источнику отрицательного заряда.
R или константа пропорциональности известна как Сопротивление. Он представлен в омах с символом Ω. R является константой для омических проводников, которые подчиняются закону Ома . Формулу Ома можно переписать для расчета сопротивления и тока соответственно следующим образом:
Формулу Ома можно переписать для расчета сопротивления и тока соответственно следующим образом:
ПримерЕсли к одному концу проводника приложить 10 В, а к другому концу — 0, то по нему потечет ток силой 1 А. Теперь, если мы увеличим разность потенциалов на одном конце с 10 до 20 В, оставив на другом 0, что произойдет с током в проводнике? Решение : Покажем это на схеме Из-за разности потенциалов электроны текут от одного конца проводника к другому, что вызывает протекание тока в проводнике. Итак, по закону Ома сила тока пропорциональна разности потенциалов. Таким образом, если разность потенциалов удвоится, ток также удвоится. Итак, ток в проводнике теперь равен 2А. |
Ohm’s Law Units
The units of elements of Ohm’s law are as follows –
| Element | Symbol | Units |
|---|---|---|
| Current | I | Ampere |
| Напряжение | В | Volts |
| Сопротивление | R | OHMS |
Click здесь, чтобы прочитать Закон о Бенгали
.
 Vector Vector Vector of o ohms vector of ohms vector of ohms vector of ohms vector of ohms vector of ohms vector of ohms vector of ohms vector of ohms vector of ohms. материаловедение и электромагнетизм. Закон Ома в векторной форме представлен как,
Vector Vector Vector of o ohms vector of ohms vector of ohms vector of ohms vector of ohms vector of ohms vector of ohms vector of ohms vector of ohms vector of ohms. материаловедение и электромагнетизм. Закон Ома в векторной форме представлен как,\(\overrightarrow{J} = \sigma \overrightarrow{E} \)
- Где, \(\overrightarrow{J}\) — плотность тока, которая является векторным эквивалентом из текущих
- \(\overrightarrow{E}\) – это электрическое поле – векторный эквивалент разности потенциалов
- , а σ – проводимость, обратная удельному сопротивлению \(\rho\) – векторный эквивалент сопротивления
Микроскопическая форма закона Ома задается как Дж = σE , где σ представляет собой электрическую проводимость, E — электрическое поле, а J — плотность тока
Состояние Закон Ома Закон Ома гласит, что напряжение или разность потенциалов на проводнике прямо пропорциональны току, протекающему по нему, при условии, что все физические условия и температура остаются постоянными. Уравнение закона ОмаV = IR , где V обозначает напряжение на проводнике, I обозначает протекающий ток, а R обозначает сопротивление, оказываемое проводником протеканию тока. |
Подробнее:
Зависимость между напряжением, током и сопротивлением
[Нажмите здесь, чтобы просмотреть примеры вопросов]
Согласно закону Ома, зависимость между напряжением и током определяется как В ∝ I
или, V/I = Константа = R
V = IR
Связь между напряжением, током и сопротивлением . Точно так же мы замечаем, что удвоение общего сопротивления вдвое уменьшает ток в цепи.
Закон Ома Магический треугольник
Чтобы найти переменные V , I , и R , мы можем использовать магический треугольник, по которому мы можем легко найти значения. Магический треугольник представлен ниже:
Закон Ома Магический треугольник
Если запрашивается значение напряжения и предоставляются значения тока и сопротивления, мы можем определить его с помощью I × R.
\(I = {V \над R}\)
\(R = {V \over I}\)
Пример закона Ома 900 Ом?Решение: Нам дано V = 220 В и R = 1200 Ом. Теперь у нас есть ток Через него протекает электрический ток силой 2А. Считая токопроводящие провода без сопротивления, рассчитать сопротивление электроприбора. Решение: Чтобы определить значение сопротивления при наличии напряжения и тока, мы закрываем R в магическом треугольнике. Это оставляет нам значение V и I и формулу V ÷ I. Подставляя значения в уравнение закона Ома, мы получаем R = V ÷ I R = 8 В ÷ 2 A R = 4 Ω |
Водопровод Аналогия закона Ома
[Щелкните здесь, чтобы просмотреть примеры вопросов]
Закон Ома описывает протекание тока через сопротивление, когда на конце каждого сопротивления приложено различное напряжение.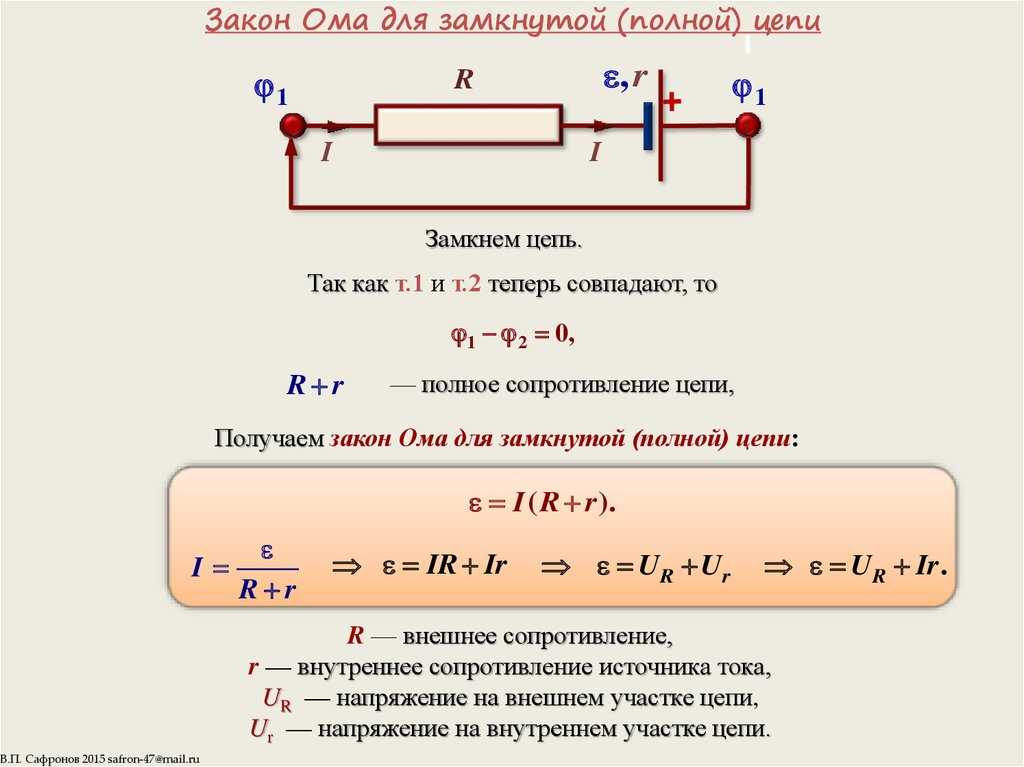 Так как мы не можем видеть электронов , аналогия закона Ома с водопроводной трубой помогает нам лучше понять электрические цепи .
Так как мы не можем видеть электронов , аналогия закона Ома с водопроводной трубой помогает нам лучше понять электрические цепи .
Закон Ома Аналогия водопроводной трубы
- Вода, текущая по трубам, представляет собой механическую систему, которая может быть аналогична электрической цепи .
- Приложенное напряжение аналогично давлению воды , ток можно принять как количество воды, протекающей по трубе, а 0003 сопротивление можно понимать как размер трубы .
- При большем давлении или напряжении по трубе будет течь больше воды или тока, и чем больше труба, тем меньше сопротивление.
Закон Ома Рукописные заметки
Закон Ома PDF – Рукописные заметки
Экспериментальная проверка закона Ома
0007
Требуется материал: Резистор, Ammeter , батарея , вольтметр, реостат, клавиша подключения
Группа Ом. Схема закона Ома
Схема закона Ома
Процедура:
- Ключ K изначально закрыт, и реостат настраивается для получения минимального показания амперметра (A) и вольтметра (V).
- Ток в цепи постепенно увеличивается за счет перемещения скользящего вывода реостата.
- Во время этого процесса записывается ток, протекающий в цепи, и соответствующее значение разности потенциалов на проводе сопротивления.
- Таким образом получают различные значения напряжения и тока.
- Для каждого набора значений V и I рассчитывается отношение V/I.
- Когда вы рассчитаете V/I для каждого случая, вы обнаружите, что они почти одинаковы. Итак, V/I = R, что является константой.
- Постройте график зависимости силы тока от разности потенциалов. График будет представлять собой прямую линию.
- Следовательно, ток пропорционален разности потенциалов.
График закона Ома: Таким образом, мы получаем прямой график V-I, подтверждающий закон Ома
Пример закона Ома
Пример. Рассмотрим резистор 1 Ом в цепи с падением напряжения от 100 до 10 В на его клеммах. Какой ток через резистор?
Рассмотрим резистор 1 Ом в цепи с падением напряжения от 100 до 10 В на его клеммах. Какой ток через резистор?
Решение: Формула сопротивления тока напряжения дается законом OHM’s AS — I = VR
= (100 — 10) .1
= 90
Расчет электроэнергии с использованием закона OHM’s
Расчет электроэнергии. [Нажмите здесь, чтобы получить ответы на важные вопросы о законе Ома]
Электроэнергия – это скорость, с которой электрическая энергия преобразуется в другую форму энергии, такую как Тепло, , Магнитная или Механическая энергия. Мы можем найти значение электрической мощности, используя закон Ома. Измеряется в ваттах. Формулы для нахождения мощности:
- P = VI , когда заданы значения напряжения и тока.
- P = V 2 /R , когда даны значения напряжения и сопротивления.
- P = I 2 R , если даны значения тока и сопротивления.

Треугольник силы
Применение закона Ома
[Нажмите здесь, чтобы просмотреть примеры вопросов]
0007
- Закон Ома используется для определения значения напряжения, сопротивления или тока электрической цепи .
- Используется для поддержания требуемого падения напряжения на электронных компонентах.
- Закон Ома используется в амперметрах постоянного тока и других шунтах постоянного тока для отвода тока.
- Используется для расчета значения потребляемой мощности.
Закон Ома и закон КирхгофаЗакон Ома и Законы Кирхгофа являются важными законами для объяснения функционирования электрических цепей. Уравнения электрической цепи определяются с помощью закона Ома.
|
Ограничения закона Ома
[Нажмите здесь, чтобы получить ответы на важные вопросы о законе Ома]
Ограничения закона Ома следующие: как диоды и транзисторы ).
Ohm’s Law Graph for Gases
Ohm’s Law ProofAs we know, i = v d enA
|
Matrix Table of Ohm’s Law
[Click Here for Important Questions on Ohm’s Law]
Ohm’s Law Calculation can be condensed in a matrix form which is as given below:
| Known Значения | Сопротивление (R) | Ток (I) | Voltage (V) | Power (P) |
|---|---|---|---|---|
| Current & Resistance | — | — | R = I X R | P = I 2 X R |
| Напряжение и ток | r = V/I | — | — | P = V X I |
| Power & Current | R = P/I 2 | — | 2— | .0033 —|
| напряжение и сопротивление | — | I = V/R | — | P = V 2 /R |
| Power & Resistance | /R||||
.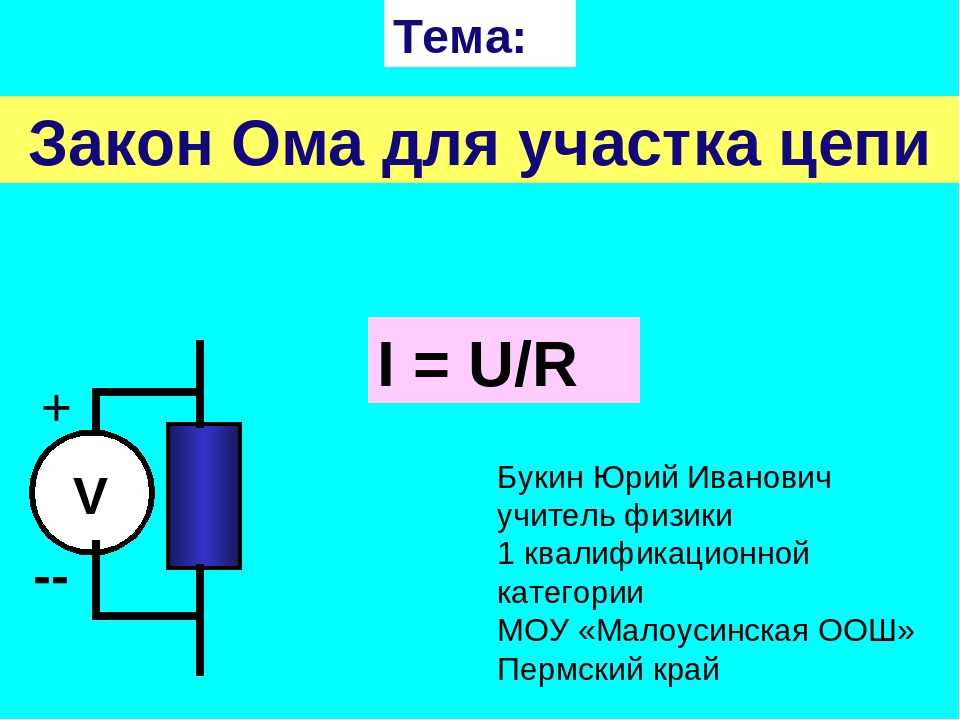 | V = √Z X R | — | ||
| Voltage & Power | R = V 2 /P | I = P/V | — | — |
Read More:
Круговая диаграмма закона Ома
Связь между различными параметрами закона Ома можно понять с помощью круговой диаграммы закона Ома, которая выглядит следующим образом:
Что нужно помнить разница в электрической цепи.
Закон Ома Важные вопросы
Щелкните здесь, чтобы получить дополнительные вопросы о законе Ома
|
Примеры вопросов
Вопрос 1: Государственная микроскопическая форма закона Ома . Какова разность потенциалов по закону Ома? (1 балл)
Какова разность потенциалов по закону Ома? (1 балл)
Ответ: Микроскопическая форма закона Ома: Дж = σE.
Разница между количеством энергии, которую носители заряжают между двумя точками цепи. Это электроны вдоль проводников, которые генерируются клеткой на ее клеммах.
Обозначается буквой V, где V = выполненная работа (Вт)/заряд (Q).
Вопрос 2. Является ли закон Ома универсальным? (2 балла)
Ответ: Нет, закон Ома не является универсально применимым, поскольку он применим только к омическим проводникам, таким как железо и медь, но неприменим к неомическим проводникам.
Закон Ома неприменим к полупроводниковым устройствам, поскольку они являются нелинейными устройствами, что означает, что отношение напряжения к току не остается постоянным при изменении напряжения.
Вопрос 3: Существуют ли какие-либо методы, с помощью которых мы можем найти значения V, I, R и P, используя закон Ома? (1 балл)
Ответ: Да, есть некоторые методы, такие как магический треугольник закона Ома, треугольник мощности, круговая диаграмма закона Ома и таблица матрицы закона Ома, с помощью которых мы можем найти значения V, I, R , и P легко.
Вопрос 4. Разность потенциалов между клеммами электронагревателя составляет 120 В, когда он потребляет от источника ток силой 8 А. Если разность потенциалов увеличить на 240 В, то ток, потребляемый нагревателем, равен? (5 баллов)
Ответ. Дано, разность потенциалов V = 120 В, ток I = 8 А.
По закону Ома,
R = VI
Расчет по закону Ома
= 120 В x 8 А
= 15 Ом разница увеличивается до 240 В, ток равен
Ток = VR
= 240 В x 15 Ом
= 16 А
Ток через нагреватель становится 16 А.
Вопрос 5. Есть 2 резистора R 1 и R 2 , которые включены последовательно и имеют сопротивление 10 Ом и 20 Ом соответственно. Напряжение на резисторе R 1 равно 4В. Найти ток, протекающий через резистор R 2 , и напряжение на этом же резисторе. (5 баллов)
(5 баллов)
Решение: Мы используем закон Ома, чтобы найти ток I1, проходящий через резистор R1:
V = RI получает 4 = 10.I1
Теперь найдем I1
I1 = 4/10 = 0,4 А
Через них проходит одинаковый ток, так как два резистора включены последовательно. Следовательно, ток I2 через R2 равен 0,4 А (поскольку I1 = I2).
Используйте закон Ома, чтобы найти напряжение V 2 на резисторе R 2 .
В 2 = R 2 I 2
= 20(0,4)
= 50 В
Ques 6. Это. Найдите напряжение между двумя точками. (5 баллов)
Ответ. Используя магический треугольник, чтобы вычислить значение напряжения со значением тока и сопротивления, мы покрываем V треугольником.
Теперь у нас есть I × R.
Следовательно, для вычисления V:
V = I × R
Вопрос 7. Если к резистору 500 Ом приложить напряжение 10 В, какой ток будет течь? (3 балла)
Ответ. Поскольку мы знаем, что I = V/R = 10/500
Поскольку мы знаем, что I = V/R = 10/500
= 0,02 А
= 20 мА
Следовательно, ток, протекающий через резистор 500 Ом, равен 20 мА.
Вопрос 8. Рассчитайте сопротивление цепи с напряжением 10 вольт и силой тока 0,1 А. (3 балла)
Ответ. По закону Ома R=V/I
R = 10/0,1
= 100 Ом
Вопрос 9. Какова величина 1 Ом? (1 балл)
Ответ. Один ом эквивалентен одному килограмму в квадрате на метр в секунду в кубе на ампер в квадрате (1 кг м 2 с -3 А -2 . Ом также эквивалентен вольту на ампер (В/А).
Вопросы 10. Сформулируйте и объясните закон Ома . Какое значение имеет закон Ома? (2 балла)
Отв. Определение закона Ома – закон Ома гласит, что сила тока в цепи прямо пропорциональна напряжению и обратно пропорциональна сопротивлению в цепи. Закон Ома важен, поскольку —
- Он помогает нам определить напряжение, сопротивление или ток в электрической цепи, когда известны две другие величины.

- Упрощает расчет мощности.
Вопрос 11. Рассчитайте сопротивление электрической цепи при напряжении 10 В и токе 5 мА. (3 балла)
Отв. дано: В = 10 В,
I = 5 мА = 0,005 A
R = V/I
= 10 В/0,005 A
= 2000 ω
= 2 KОм
. Закон Ома не применим к полупроводникам? (2 балла)
Отв. Закон Ома не применяется к полупроводникам, поскольку они являются нелинейными устройствами. Следовательно, отношение напряжения к току не остается постоянным при изменении напряжения.
Вопрос 13. Когда нарушается закон Ома? (2 балла)
Отв. Закон Ома не может объяснить поведение односторонних устройств, таких как диоды и полупроводники. Закон Ома также может не сработать, если физические условия, такие как давление и температура, не поддерживаются постоянными.
Вопрос 14. Почему закон Ома неприменим для электролитов и электронных ламп? (3 балла)
Отв.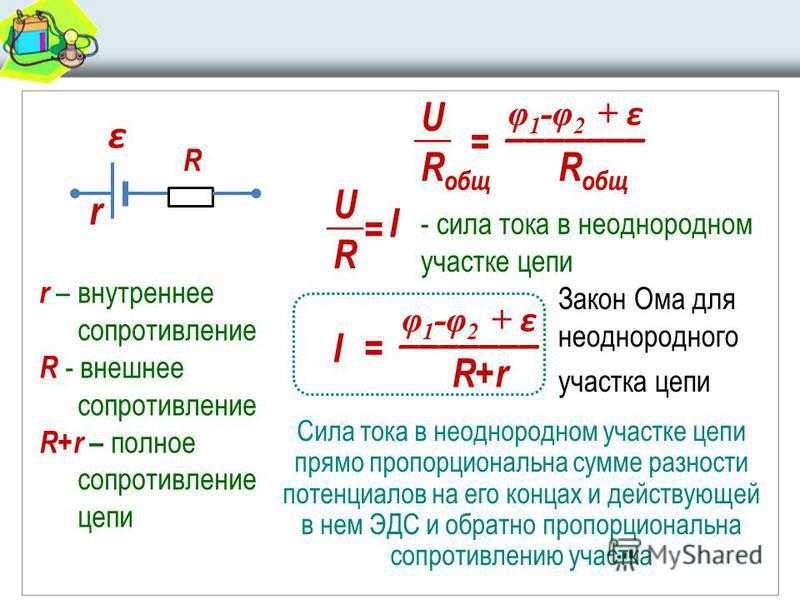 Закон Ома применим только к ограниченному кругу проводников. Для применения закона Ома отношение напряжения к току должно быть постоянным для изменений напряжения. Если отношение меняется, то закон Ома не применяется. Материалы, к которым применяется закон Ома, известны как «линейные» или «омические» устройства; те, к которым это не относится, известны как «нелинейные» или «неомические» устройства. Поэтому закон Ома неприменим к электролитам и электронным лампам.
Закон Ома применим только к ограниченному кругу проводников. Для применения закона Ома отношение напряжения к току должно быть постоянным для изменений напряжения. Если отношение меняется, то закон Ома не применяется. Материалы, к которым применяется закон Ома, известны как «линейные» или «омические» устройства; те, к которым это не относится, известны как «нелинейные» или «неомические» устройства. Поэтому закон Ома неприменим к электролитам и электронным лампам.
Вопрос 15. Найдите ток I, протекающий через резистор сопротивлением 2 Ом, если напряжение на резисторе равно 6 В. (3 балла)
Ответ. Подставив значения R и V в формулу закона Ома V = R I.
6 = 2 I
Найдите I
I = 6 / 2
= 3 A
Вопрос 16. Ток, проходящий через резистор, равен 0,01 A при напряжении 5 В. Какая сила тока проходит через него, когда напряжение на нем составляет 7,5 В? (3 балла)
Ответ. Используйте закон Ома V = RI, чтобы найти резистор R в этой цепи.
5 = R (0,01)
Решите для R
R = 5 / 0,01
= 500 Ом
Используя определение закона Ома, V = RI, чтобы найти ток при напряжении 7,5.
7,5 = 500 I
Найдите I
I = 7,5 / 500
= 0,015 А
Вопрос 17. Кто открыл закон Ома? (1 балл)
Ответ. Закон Ома был разработан Георгом Симоном Омом.
Вопросы 18. Сколько стоит 1 Ом? (1 балл)
Ответ. При переводе в базовые единицы 1 Ом эквивалентен одному килограммовому метру в квадрате на секунду в кубе на ампера в квадрате.
Вопросы 19. Может ли напряжение быть отрицательным? (1 балл)
Ответ. Величина напряжения может быть как положительной, так и отрицательной.
Вопросы 20. Каковы 3 формы закона Ома? (2 балла)
Отв. Формула закона Ома может быть представлена в трех формах:
- ΔV = IR
- R = V/I
- I = V/R
Вопрос 21. Докажите векторную форму закона Ома. (5 баллов)
Докажите векторную форму закона Ома. (5 баллов)
Как известно, i = v d enA
Где i = ток, v d = дрейфовая скорость, e = заряд электрона, n = количество свободных электронов в единице объема и A = площадь поперечного сечения
Теперь скорость дрейфа, vd = эВ\(\тау \)/мл
Где V = разность потенциалов на концах проводника, m = масса электрона, l = длина проводника и \ (\ тау\) = среднее время релаксации 92 \tau}\) = удельное сопротивление или \(\rho\)
Следовательно, \(\overrightarrow{ E} = \rho \overrightarrow{J}\)
или \( \overrightarrow{J} = \sigma \overrightarrow{ E} \)
, поскольку проводимость \(\sigma\) является обратной величиной удельного сопротивления.
Сделать проверку:
Q = It E = QV расчеты Закон Ома V = IR исследование факторов, влияющих на сопротивление График ВАХ диод омический проводник лампа накаливания igcse/gcse 9-1 Примечания к пересмотру физики
Электричество Часть 3 Закон Ома, экспериментальные исследования сопротивления а также Графики ВАХ и расчеты с использованием I = V/R, Q = It и E = QV IGCSE AQA GCSE Physics Edexcel GCSE Physics OCR GCSE Gateway Science Physics OCR GCSE 21st Century Science Physics Примечания к пересмотру школьной физики Дока Брауна: GCSE физика, физика IGCSE, физика уровня O, ~8, 9 классы СШАи 10 школьные курсы по естествознанию или эквивалентные для ~ 14-16 летних учащихся физика Что такое закон Ома? Как вы выполняете расчеты по закону Ом/с? Какие факторы влияют на сопротивление схема? Как построить и использовать схему для изучить закон Ома? Как рассчитать количество электроэнергии заряд движется по цепи? Субиндекс для этой страницы
ВСЕ мои заметки по физике Найдите свой GCSE научный курс для получения дополнительной помощи, ссылки на примечания к редакции Используй свой
мобильный телефон или iPad и т. это БОЛЬШОЕ веб-сайте, вам нужно потратить время на его изучение [Поиск по веб-сайту Коробка] электронный документ коричневый — комментарий — запрос? 1а. Ома Закон (и упоминание других единиц, рассматриваемых в других разделах)
1б. Простой эксперимент по измерению сопротивления одного компонента
1с. Примеры расчеты с помощью Ома Закон V = IR
ВЕРХ СТРАНИЦЫ и субиндекс 2. Движение заряда 2а. Расчет заряда, проходящего через точку цепи Q = It
2б. Примеры расчетных вопросов с участием уравнение Q = It
ВЕРХ СТРАНИЦЫ и субиндекс 3. Разница потенциалов и передача энергии 3а. Введение в электрическую энергию передача Передача энергии на единицу заряда = разность потенциалов (pd) и расчеты на основе Э = КВ
3б. Еще одно уравнение для расчета электрического передача энергии
Просто мимоходом и несколько напоминаний:
3в. Q1 Электродвигатель Модель автомобиля питается от аккумулятора 1,5 В.
Q2 Какое количество
заряд необходим для передачи 500 Дж энергии, если п.
Q3 Какой потенциал разница требуется в цепи для передачи 2000 Дж энергии с заряд 50 кулонов?
4 квартал Батарейка 12,0 В пропускает через лампу ток силой 2,0 А в течение 5 минут.
Q5 Прибор имеет мощность 1,5 кВт и работает от сети 230 В.
3д. Еще немного о разности потенциалов — влияние двух последовательно соединенных резисторов
ВЕРХ СТРАНИЦЫ и субиндекс 4. Электрическое сопротивление — эксперименты по исследовать ВАХ различных сопротивлений и достоверность, или в противном случае по закону Ома 4а. Что влияет на сопротивление провода? Сопротивление постоянный?
ВЕРХ СТРАНИЦЫ и субиндекс 4б. Исследование электрического сопротивления провода — изменение длины или ширины Схема 30 показывает, как исследовать сопротивление провода .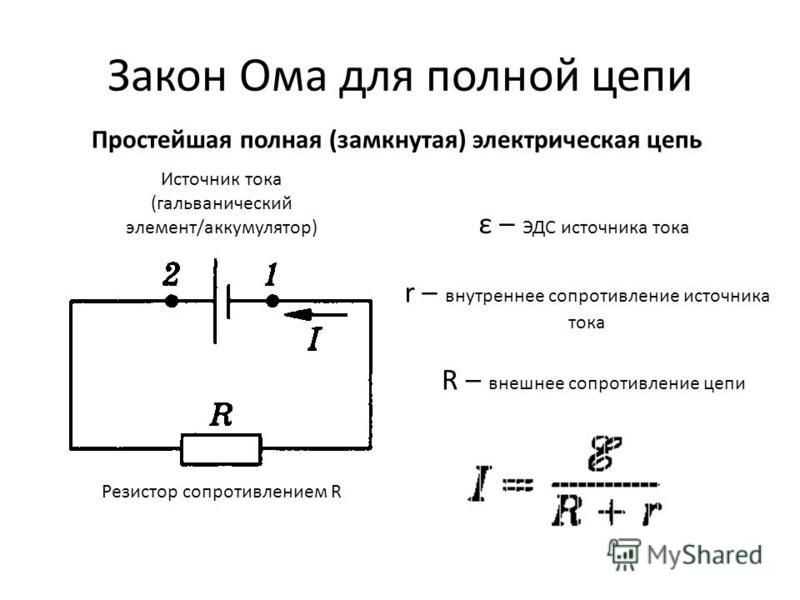
ВЕРХ СТРАНИЦЫ и субиндекс 4в. Расследование ток — напряжение характеристики провода
Схема 31 показано, как исследовать, как I зависит от V для сопротивления .
ВЕРХ СТРАНИЦЫ и субиндекс 4д.
Исследование вольтамперных характеристик металла
лампа накаливания
ВЕРХ СТРАНИЦЫ и субиндекс 4е. Исследование вольтамперных характеристик диода
ВЕРХ СТРАНИЦЫ и субиндекс Практическая работа по помощь в развитии ваших навыков и понимания может включать следующее:
ПРИЛОЖЕНИЕ 1: Важные определения, описания,
формулы и
ед.
ВЕРХ СТРАНИЦЫ и подиндекс Что дальше? Электричество и ревизия магнетизма индекс нот
Версия IGCSE
примечания Закон Ома исследования сопротивления V = IR Q = It расчеты KS4 физика Научные примечания по
Исследование сопротивления по закону Ома V = IR Q = It
расчеты GCSE руководство по физике
примечания к закону Ома исследования сопротивления V = IR Q = It
расчеты для школ, колледжей, академий, курсов естественных наук, репетиторов, изображений
диаграммы рисунков для исследования сопротивления по закону Ома V = IR Q =
Он вычисляет примечания к научному пересмотру
Исследование сопротивления по закону Ома V = IR Q = It
расчеты для повторения модулей по физике примечания к темам по физике для помощи в понимании
Исследование сопротивления по закону Ома V = IR Q = It
расчеты университетские курсы по физике
карьера в научной физике работа в машиностроении
технический лаборант
ученичество инженер стажировки по физике США 8 класс США 9 класс10 класс AQA
GCSE 9-1 примечания к пересмотру закона Ома по физике
исследования сопротивления V = IR Q = It расчеты GCSE
примечания к закону Ома исследования сопротивления V = IR Q = It
расчеты Edexcel GCSE 9-1 физика естествознание примечания к пересмотру
Исследование сопротивления по закону Ома V = IR Q = It
расчеты по ОКР GCSE 9-1 21 век
физика научные заметки об исследованиях сопротивления по закону Ома
V = IR Q = It расчеты OCR GCSE
9-1 Шлюз физика наука
примечания к пересмотру исследований сопротивления по закону Ома V = IR
Q = Это расчеты WJEC gcse science CCEA/CEA gcse science повторение конспектов по физике для 14-16 школьных классов AQA Edexcel
OCR IGCSE/GCSE 9-1 Модули тем курса естественных наук для
изучение электрических расчетов, как решать задачи с помощью
формула Q = It E = QV, как делать расчеты на основе Ома
закон V = IR, как исследовать эксперименты по факторам
воздействие на электрическое сопротивление провода, волочение и
объяснение тока по сравнению с p. | ||||||||||||||||||||||||||
электрическое сопротивление. Любая ли конечная схема «разрешима» с использованием закона Ома и правил цикла Кирхгофа?
$\begingroup$
Всякий раз, когда я решал схемы (только ячейки, резисторы и провода), необходимо было использовать только закон Ома (или вещи, вытекающие из закона Ома, например, как два резистора $R_1$ и $R_2$ имеют эффективное сопротивление $R_1 +R_2$ в целом) и правила цикла Кирхгофа. Однако мне было любопытно, всегда ли это работает.
То есть:
Для любой цепи конечного размера, состоящей только из проводов (с нулевым сопротивлением), батарей (с известным напряжением) и (омических) резисторов (с известным сопротивлением), всегда ли возможно использовать закон Ома и правила Кирхгофа для контуров и соединений для расчета ток в любой точке цепи и напряжение между любыми двумя точками?
Я не понимаю, почему это не так, но я не знаю никаких окончательных доказательств.
(Это может слишком сильно опираться на логику, особенно на идею полноты, поэтому, если этот вопрос не подходит, я перенесу его на MSE.)
- электрические цепи
- электрические сопротивления
- батареи
$\endgroup$
4
$\begingroup$
В других ответах указано, что общее количество уравнений правильное, но на самом деле этого недостаточно, чтобы гарантировать уникальное решение. Есть по крайней мере две причины, по которым что-то может выйти из строя:
- Уравнения несовместимы. Например, рассмотрим схему, состоящую из двух идеальных батарей по 1 вольту, направленных по часовой стрелке. Тогда правило цикла Кирхгофа $1+1 = 0$ не имеет решения.
- Уравнения неполные. Предположим, что где-то в вашей цепи есть замкнутый контур с нулевым сопротивлением и, возможно, группа батарей, ЭДС которых равна нулю.
 (Например, возьмите предыдущий пример и переверните одну из батарей.) Тогда правило цикла Кирхгофа: $0 = 0$, что вообще ничего не говорит; ток в этой цепи не определен.
(Например, возьмите предыдущий пример и переверните одну из батарей.) Тогда правило цикла Кирхгофа: $0 = 0$, что вообще ничего не говорит; ток в этой цепи не определен.
На самом деле отсутствие решений или неуникальные решения довольно часто встречаются в простых физических моделях. Часто это означает, что идеализация, используемая в этой модели, не работает. Проблемы, о которых я упоминал, можно решить, придав всем батареям и проводам маленькое внутреннее сопротивление.
$\endgroup$
2
$\begingroup$
С одной батареей и любой комбинацией резисторов, которые не закорачивают батарею, есть уникальное решение для напряжений и токов.
Идея суперпозиции для цепи с любым количеством батарей позволяет найти вклад в токи и напряжения от каждой батареи независимо, при условии, что батарея не замкнута накоротко.
Токи и напряжения, создаваемые каждой отдельной батареей, затем можно сложить вместе, чтобы найти токи и напряжения для всей цепи.
Итак, как показано в схеме, ответ на вопрос «Разрешима» ли каждая конечная схема с помощью закона Ома и правил Кирхгофа для контуров? , только с резисторами и батарейками в схеме, это «да».
Я, возможно, недостаточно ясно объяснил, что я имел в виду под фразой при условии, что батарея не закорочена.
Короткое замыкание могло произойти при параллельном подключении двух аккумуляторов. Единственная конфигурация, которая будет работать с двумя батареями параллельно, — это если они будут соединены вместе с одинаковой полярностью и будут иметь одинаковую ЭДС, тогда две батареи можно будет рассматривать как одну.
$\endgroup$
2
$\begingroup$
Ответ Кристофа действительно великолепен, но если он слишком запутан для вас, инженерный способ выразить этот факт состоит в том, чтобы сказать, что в любой такой схеме количество неизвестных в уравнении схемы равно количеству известных, поэтому алгебраическое решение всегда существует.
$\endgroup$
$\begingroup$
Соотношение Эйлера для планарного графа (Википедия), вероятно, является важным компонентом доказательства. Обозначим $e$ количество ребер, $f$ количество граней и $n$ количество узлов, соотношение Эйлера утверждает, что $$n-e+f=2$$ Обратите внимание, что в этом определении $f=2$ для одной петли, потому что одна грань находится внутри петли, а другая — снаружи.
Предположим, что электрическая цепь является частным случаем плоского графа. Мы хотим вычислить интенсивность потока в каждой ветви (или ребре) этого графа. Таким образом, есть переменные $e$. В каждом узле сумма интенсивностей должна обращаться в нуль (закон Кирхгофа). Обратите внимание, что если у нас есть два узла, соединенных одним или несколькими ребрами, два закона Кирхгофа, записанные для этих двух узлов, фактически идентичны. Число независимых законов Кирхгофа равно не $e$, а $e-1$.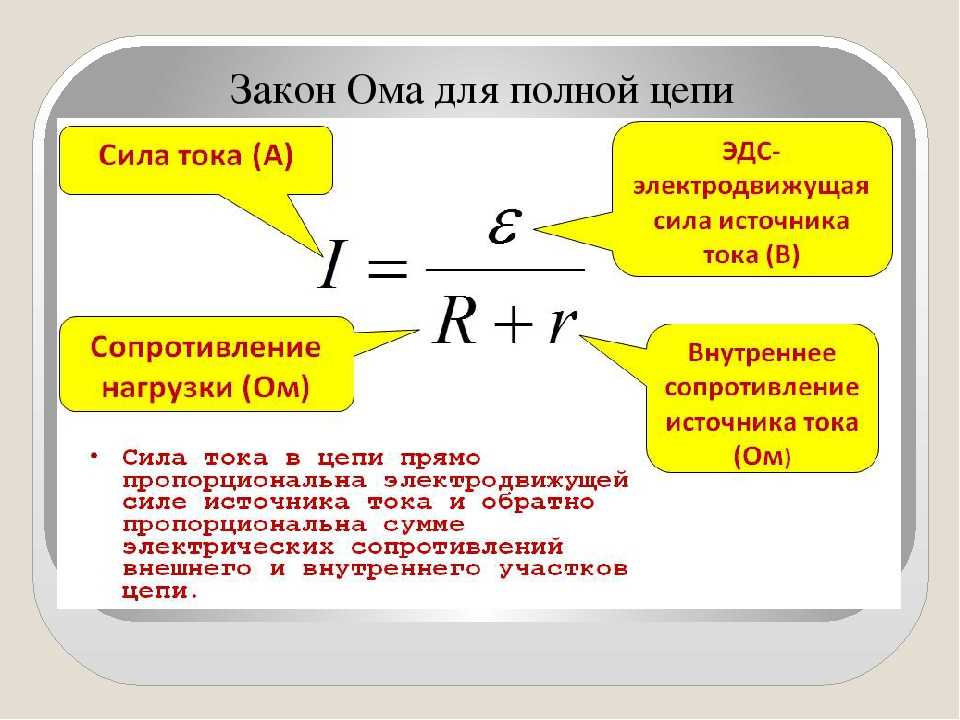
Вокруг каждой грани графика сумма электрических напряжений должна исчезнуть (закон напряжения Кирхгофа). Из-за определения числа граней плоского графа в наших схемах действует $f-1$ (а не $f$) закон Кирхгофа о напряжении.
Итак, имеем $(n-1)+(f-1)$ уравнений. Согласно соотношению Эйлера количество уравнений $n+f-2$ равно количеству переменных.
Возможно, еще предстоит некоторая работа, чтобы сделать это строгим (любая помощь в улучшении приветствуется), но это может быть идеей доказательства.
Приложение Полное и доступное доказательство можно найти в статье PDF
. $\endgroup$
4
$\begingroup$
Доказательство, которое вам нужно, состоит в том, что смысл «решения схемы» состоит в том, чтобы найти значения для всех неизвестных, которые удовлетворяют уравнениям ограничений. Закон Кирхгофа о напряжении охватывает все эти ограничения. Доказательством этого является немного отрицательное доказательство. Обычно вы доказываете это, показывая, что вам удобно моделировать реальную схему с идеальными батареями, идеальными проводами и идеальными резисторами.
Закон Кирхгофа о напряжении охватывает все эти ограничения. Доказательством этого является немного отрицательное доказательство. Обычно вы доказываете это, показывая, что вам удобно моделировать реальную схему с идеальными батареями, идеальными проводами и идеальными резисторами.
Нетрудно показать, что , а не моделирует каждую возможную схему, но вы обнаружите, что это довольно хорошая модель во всех случаях. Несмотря на это, ваша формулировка постановки задачи указывает на то, что предполагается, что этой модели достаточно.
Получив это, вы можете продемонстрировать, что все эти ограничения являются линейными, поэтому вы решаете систему линейных уравнений.
Мы можем, конечно, продемонстрировать , когда мы можем решить схему с этими формами, представив эти ограничения в матричной форме, а затем спросив, является ли матрица обратимой. Если да, то система разрешима. И, конечно же, как отмечали другие, это разрешимо, когда:
- Уравнений столько, сколько переменных
- В системе нет противоречий или повторяющихся уравнений (что сделает матрицу сингулярной)
Эти вещи не будут происходить в правильно сформированных цепях, но могут появиться, когда вы делаете такие вещи, как короткое замыкание батареи или два провода, которые проходят между одними и теми же узлами (таким образом, вы не знаете, сколько тока проходит каждый) . Мы обычно решаем последнее, объединяя провода вместе, а первое решаем либо делая схему менее ужасной, либо используя более полные модели батарей и проводов.
Мы обычно решаем последнее, объединяя провода вместе, а первое решаем либо делая схему менее ужасной, либо используя более полные модели батарей и проводов.
$\endgroup$
Закон Ома: определение, формула, примеры решения
- Автор Shikha Pandey
- Последнее изменение 19-07-2022
- Автор Шиха Пандей
- Последнее изменение 19-07-2022
Закон Ома: Закон Ома — один из фундаментальных законов физики, управляющий электрическими и электронными цепями. Известно, что закон Ома представляет собой зависимость между напряжением и током. Закон гласит, что напряжение в проводнике прямо пропорционально силе тока через него.
Например, когда мы увеличиваем количество ячеек в факеле, увеличивается яркость лампочки. С другой стороны, когда мы пользуемся фонариком в течение длительного времени, мы наблюдаем, что яркость лампочки постепенно уменьшается. Это происходит потому, что ток, протекающий через колбу фонаря, зависит от приложенной к ней разности потенциалов. Если студенты не уверены в точном определении закона Ома и его применении, мы включили все подробности в эту статью.
Если студенты не уверены в точном определении закона Ома и его применении, мы включили все подробности в эту статью.
Изучите концепции 11-го экзамена CBSE
| Последнее обновление: ? Ожидается, что результаты первого семестра CBSE будут опубликованы в январе 2022 года. ? Экзамены за второй семестр начнутся в марте/апреле. Вскоре в феврале 2022 года комиссия выпустит карточку допуска и лист с датами экзамена. Закон Ома представляет собой соотношение между электрическим током и разностью потенциалов. Эта связь между разностями тока и потенциалов была установлена немецким физиком Георгом Симоном Омом \((1787-1854).\) Определение закона ОмаЗакон Ома утверждает, что ток, протекающий в цепи, прямо пропорционален приложенной разности потенциалов и обратно пропорционален сопротивлению в цепи. Если \(I\) — ток, протекающий по проводнику, а \(V\) — разность потенциалов на концах проводника, то по закону Ома (при постоянной температуре): Магический треугольник закона Ома С помощью магического треугольника закона Ома мы можем выучить различные уравнения закона Ома, которые используются для решения таких переменных, как \(V, I, R. Закон Ома — сопротивление проводникаСопротивление – это свойство проводника сопротивляться протеканию через него тока. Единицей сопротивления в СИ является Ом, который обозначается греческой буквой \(\Омега). Согласно закону Ома, сопротивление проводника постоянно для данной температуры и других условий. \(R = \frac{V}{I}\) \(1\) Ом — сопротивление проводника, по которому протекает ток \(1\) ампер при приложении к его концам разности потенциалов \(1\) вольт. Практика 11-го экзамена CBSE Вопросы Экспериментальная проверка закона Ома Возьмите пять или шесть сухих элементов, резистор с выводами \(A\) и \(B,\), вольтметр, амперметр, ключ (переключатель) и несколько соединительных проводов. Соберите электрическую цепь, аккуратно соединив все эти компоненты, но используя только один элемент, как показано на рисунке (а) ниже. Амперметр измеряет ток \(I\), протекающий по цепи, а вольтметр измеряет напряжение на концах резистора \(\left( {AB} \right).\) Обратите внимание на показания амперметра и вольтметра . Теперь соедините две ячейки последовательно, как показано на рисунке (б), и снова отметьте новые показания амперметра и вольтметра. Согласно закону Ома, мы обнаружим, что при увеличении количества последовательно соединенных элементов напряжение на выводах резистора увеличивается, и, следовательно, увеличивается ток через него. Поэтому показания на вольтметре и амперметре тоже увеличиваются. Повторите опыт, подключив третью ячейку, четвертую ячейку и так далее. Обратите внимание на чтение для каждого случая. Теперь, когда мы найдем отношение напряжения к току для каждого случая, мы обнаружим, что оно почти одинаково. Следовательно, мы можем заключить, что утверждение закона Ома справедливо для данного проводника или резистора, где \(R\) постоянна. Если мы построим вольтамперный график, используя эти значения тока и напряжения, мы получим прямую линию. Омические материалыЗакон Ома не является фундаментальным законом. Закон Ома применим для большого числа проводников. Эти проводящие материалы называются омическими материалами. Металлы и их сплавы относятся к омическим материалам. Электрическая цепь из омического материала называется линейной цепью. Попытка пробных тестов Неомические материалы Существует много полезных проводящих материалов и устройств, которые не подчиняются закону Ома. Они называются неомическими проводниками и считаются одним из ограничений закона Ома. Вакуумные лампы, кварцевые выпрямители, термисторы и транзисторы являются примерами неомических материалов. Эти материалы и устройства демонстрируют отклонение от линейного поведения вольт-амперной кривой. Например, для полупроводниковых диодов при положительном напряжении протекает большой ток, а при обратном напряжении течет очень небольшой ток. Закон Ома — факторы, влияющие на сопротивлениеКогда температура и другие физические условия остаются неизменными, то по закону Ома сопротивление проводника остается постоянным. Ниже приведены коэффициенты, от которых зависит сопротивление проводника:
Математически, Удельное или удельное сопротивление Удельное сопротивление определяется как сопротивление на концах проводника единичной длины и единичного поперечного сечения. Закон Ома выполняется при постоянной температуреУдельное сопротивление проводника зависит от температуры. Это связано с тем, что с повышением температуры средняя скорость положительных ионов увеличивается, что увеличивает вероятность столкновения с электронами, вызывающими ток. Изменение сопротивления в зависимости от температуры в основном связано с изменением сопротивления в зависимости от температуры. По закону Ома сопротивление постоянно, поэтому закон Ома применяется только при постоянной температуре. Формула закона Ома: расчет мощности с использованием закона ОмаЗнание закона Ома поможет рассчитать стоимость электроэнергии. Проверьте формулу для расчета мощности снизу: Когда известны значения напряжения и тока: Формула для расчета тока, если известны мощность и напряжение: Формула для расчета напряжения, если известны мощность и ток: Практические экзаменационные вопросы Таблица матрицы закона Ома Напряжение/ток/сопротивление/мощность можно рассчитать по формулам, полученным из закона Ома.
Примеры решения закона Ома Q. Q.2. Ток через проводник сопротивлением \(250\,{\rm{\Omega}}\) равен \(3\;{\rm{A}}.\) Если мы хотим удвоить ток, то какая разность потенциалов должна быть приложена к проводнику? Попытка 11-го экзамена CBSE Пробные тесты Часто задаваемые вопросы по закону ОмаНиже приведены часто задаваемые вопросы по закону Ома: Q. Q.2: Государственный закон Ома. Q.3: Определите сопротивление проводника. Q.4: В каких условиях действует закон Ома? Q.5: Что такое 1 Ом? Q.6: Что такое неомические материалы? Q.7: Каковы ограничения закона Ома? Учитесь в Embibe Концепция закона Ома обычно вводится в классе 10. Кроме того, некоторые концепции закона Ома также объясняются в классе 12. Таким образом, чтобы помочь вам понять все концепции классов с 10 по 12, Embibe предлагает бесплатный пробный тест и практику. Вопросы. Таким образом, учащиеся 10-12 классов могут решить Практические вопросы или попробуйте 10 пробных тестов на Embibe бесплатно, что очень поможет вам в подготовке к экзамену. Теперь, когда вы получили всю информацию о законе Ома, мы надеемся, что эта подробная статья окажется вам полезной. Если у вас есть какие-либо вопросы о законе Ома, напишите нам через поле для комментариев ниже, и мы свяжемся с вами как можно скорее. Практические вопросы по закону Ома с советами и решениями Сопротивление и простые схемы – Физика Колледжа Дугласа 1207Глава 4 Электрический ток, сопротивление и закон Ома Резюме
Что управляет током? Мы можем думать о различных устройствах, таких как батареи, генераторы, настенные розетки и т. д., которые необходимы для поддержания тока. Все такие устройства создают разность потенциалов и в широком смысле называются источниками напряжения. Ток, протекающий через большинство веществ, прямо пропорционален приложенному к нему напряжению В . Немецкий физик Георг Симон Ом (1787–1854) первым экспериментально продемонстрировал, что сила тока в металлической проволоке прямо пропорциональна приложенному напряжению : .И В Это важное соотношение известно как закон Ома. Его можно рассматривать как причинно-следственную связь, где напряжение является причиной, а ток — следствием. Это эмпирический закон, аналогичный закону трения — экспериментально наблюдаемому явлению. Такая линейная зависимость не всегда имеет место. Если напряжение управляет током, что этому препятствует? Электрическое свойство, препятствующее току (в общих чертах похожее на трение и сопротивление воздуха), называется сопротивлением R . Так, например, ток уменьшается вдвое, если сопротивление удваивается. Сочетание отношений тока к напряжению и тока к сопротивлению дает Это соотношение также называют законом Ома. Закон Ома в этой форме действительно определяет сопротивление для определенных материалов. Закон Ома (как и закон Гука) не является универсальным. Многие вещества, для которых выполняется закон Ома, называются омическими. К ним относятся хорошие проводники, такие как медь и алюминий, и некоторые плохие проводники при определенных обстоятельствах. Омические материалы имеют сопротивление Ом , которое не зависит от напряжения В и тока I . Объект, который имеет простое сопротивление, называется резистор , даже если его сопротивление мало. Единицей сопротивления является ом, который обозначается символом Ом (греческая омега в верхнем регистре). На рис. 1 ниже показана схема простой цепи. Простая схема имеет один источник напряжения и один резистор. Провода, соединяющие источник напряжения с резистором, можно считать имеющими пренебрежимо малое сопротивление, или их сопротивление можно включить в Р . Рисунок 1. Простая электрическая цепь, в которой замкнутый путь для протекания тока обеспечивается проводниками (обычно металлическими проводами), соединяющими нагрузку с клеммами батареи, представленными красными параллельными линиями. Зигзагообразный символ представляет одиночный резистор и включает любое сопротивление в соединениях с источником напряжения.Пример 1. Расчет сопротивления: автомобильная фараКаково сопротивление автомобильной фары, через которую протекает ток 2,50 А при подаче на нее напряжения 12,0 В? Стратегия Мы можем преобразовать закон Ома в соответствии с формулой I = V/R и использовать его для определения сопротивления. Решение Перестановка I = V/R и подстановка известных значений дает Обсуждение Это относительно небольшое сопротивление, но оно больше, чем морозостойкость фары. Как мы увидим в разделе «Сопротивление и удельное сопротивление», сопротивление обычно увеличивается с температурой, поэтому при первом включении лампочка имеет более низкое сопротивление и будет потреблять значительно больший ток в течение короткого периода прогрева. Диапазон сопротивлений превышает многие порядки. Некоторые керамические изоляторы, например те, которые используются для поддержки линий электропередач, имеют сопротивление 10 12 Ом или более. У сухого человека сопротивление руки к ноге может составлять 10 5 Ω , тогда как сопротивление человеческого сердца составляет около 10 3 Ω . Метровый отрезок медного провода большого диаметра может иметь сопротивление 10 -5 Ом , а сверхпроводники вообще не имеют сопротивления (они неомические). Дополнительную информацию можно получить, решив I = V/R , что даст В = I R. Это выражение для В можно интерпретировать как падение напряжения на резисторе, вызванное протеканием тока I . Для этого напряжения часто используется фраза IR drop . Например, фара в примере 1 имеет падение напряжения IR , равное 12,0 В. Если измерить напряжение в различных точках цепи, будет видно, что оно увеличивается на источнике напряжения и уменьшается на резисторе. Напряжение аналогично давлению жидкости. Источник напряжения подобен насосу, создающему перепад давления, вызывающему ток — поток заряда. Резистор подобен трубе, которая снижает давление и ограничивает поток из-за своего сопротивления. Соединения: сохранение энергии В простой электрической цепи единственный резистор преобразует энергию, поступающую от источника, в другую форму. О сохранении энергии здесь свидетельствует тот факт, что вся энергия, подаваемая источником, преобразуется в другую форму одним только резистором. Мы обнаружим, что закон сохранения энергии имеет и другие важные применения в цепях и является мощным инструментом анализа цепей. PhET Исследования: Закон ОмаПосмотрите, как формула закона Ома соотносится с простой цепью. Отрегулируйте напряжение и сопротивление и посмотрите, как изменится ток в соответствии с законом Ома. Размеры символов в уравнении изменяются в соответствии с принципиальной схемой. Прямая ссылка: https://phet.colorado.edu/sims/html/ohms-law/latest/ohms-law_en.html Рисунок 3. Закон Ома
Закон Ома – определение, формулы и примеры Согласно определению закона Ома в физике, напряжение или разность потенциалов между двумя точками в цепи пропорциональны току электричества, протекающему через сопротивление. Обычно тремя наиболее фундаментальными компонентами электричества являются напряжение, ток и сопротивление в цепи. Формулировка закона Ома:«Закон Ома гласит, что приложенное к проводнику напряжение прямо пропорционально протекающему по нему току при условии, что все физические условия и температура остаются постоянными» Заметно, что закон Ома может выполняться только в том случае, если температура и другие физические факторы остаются постоянными. В некоторых компонентах при увеличении тока в цепи также повышается температура. Формула закона Ома:Теперь вы должны подумать о том, какова формула закона Ома. Посмотрите на приведенное ниже уравнение закона Ома: В = ИК Где,
Кроме того, вы можете найти значение напряжения (V), тока (I) и сопротивления (R) по формуле, используя онлайн-калькулятор закона Ома. Экспериментальная проверка закона Ома:Георг Симон Ом, немецкий физик (1789-1854), был первым, кто экспериментально проверил закон Ома. Давайте теперь объясним закон Ома с помощью эксперимента, в том числе: Требуемый аппарат:
Схема: Процедура:
Вы также можете использовать онлайн-калькулятор трансформатора , чтобы рассчитать напряжение, токи нагрузки и различные потери, связанные с трансформатором. Треугольник закона Ома:Математическая зависимость между напряжением (V, иногда обозначается как U или E), сопротивлением (R) и током (I) в электрической цепи называется треугольником закона Ома. Вы можете использовать треугольник закона Ома, чтобы запомнить различные уравнения закона Ома для решения различных переменных (V, I, R).
Решенные примеры: Теперь обсудите примеры, связанные с законом Ома, которые описаны ниже, чтобы прояснить вашу концепцию. Пример №1: Если сопротивление (R) электрического утюга равно 100 Ом и через сопротивление электрического утюга протекает ток силой 4,2 А. Найдите напряжение между двумя точками. Решение: Используя формулу закона Ома для расчета значения V: V = I × R Подставляя значения в уравнение закона Ома, получаем В = 4,2 А × 100 Ом = 420 В Отсюда напряжение электрического утюга = 420 В Пример №2: К резистивному электроприбору (лампочке накаливания) подключен источник ЭДС напряжением 6,0 В. Через него протекает электрический ток 2,0 А. Токопроводящие провода считать без сопротивления. Рассчитайте сопротивление электроприбора (лампочки). Решение: Чтобы рассчитать значение сопротивления, вы можете использовать формулу закона Ома, которая задается как: R = V ÷ I Подставляя значения в уравнение закона Ома, получаем R = V ÷ I R = 6 ÷ 2 A = 3 Ом Следовательно, сопротивление электроприбора = 3 Ом. Расчет электрической мощности по закону Ома:Электроэнергия: Скорость, с которой энергия передается по электрической цепи в единицу времени, называется электрической мощностью. 92R (когда требуются ток и сопротивление) Кроме того, онлайн-калькулятор лошадиных сил поможет вам оценить стоимость ручной силы за пару секунд. Как правило, основные применения закона Ома приведены ниже: Существуют некоторые ограничения закона Ома, которые описаны ниже: |


 Ее показатели зависят от силы тока и площади поперечного сечения проводника (S).
Ее показатели зависят от силы тока и площади поперечного сечения проводника (S). Например, в лампах накаливания;
Например, в лампах накаливания;
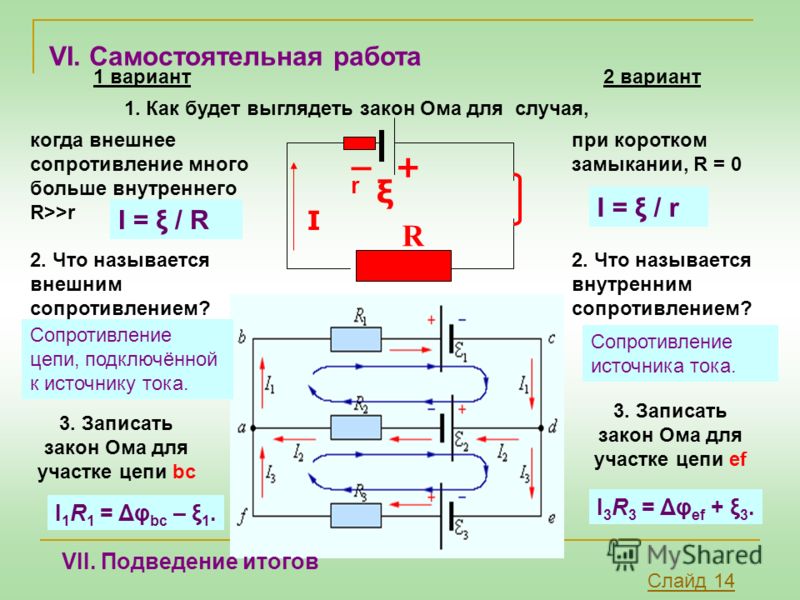 П., Соколов В.Б. – М.: Высш. шк., 1985. – 128 с, ил — Контрольная работа № 1 Электрические цепи
П., Соколов В.Б. – М.: Высш. шк., 1985. – 128 с, ил — Контрольная работа № 1 Электрические цепи


 (V = IR)
(V = IR)
 Как это можно проверить экспериментально?
Как это можно проверить экспериментально? 

 Закон Ома,
простая схема исследования и вычисления V= IR
Закон Ома,
простая схема исследования и вычисления V= IR д. в альбомной ориентации
д. в альбомной ориентации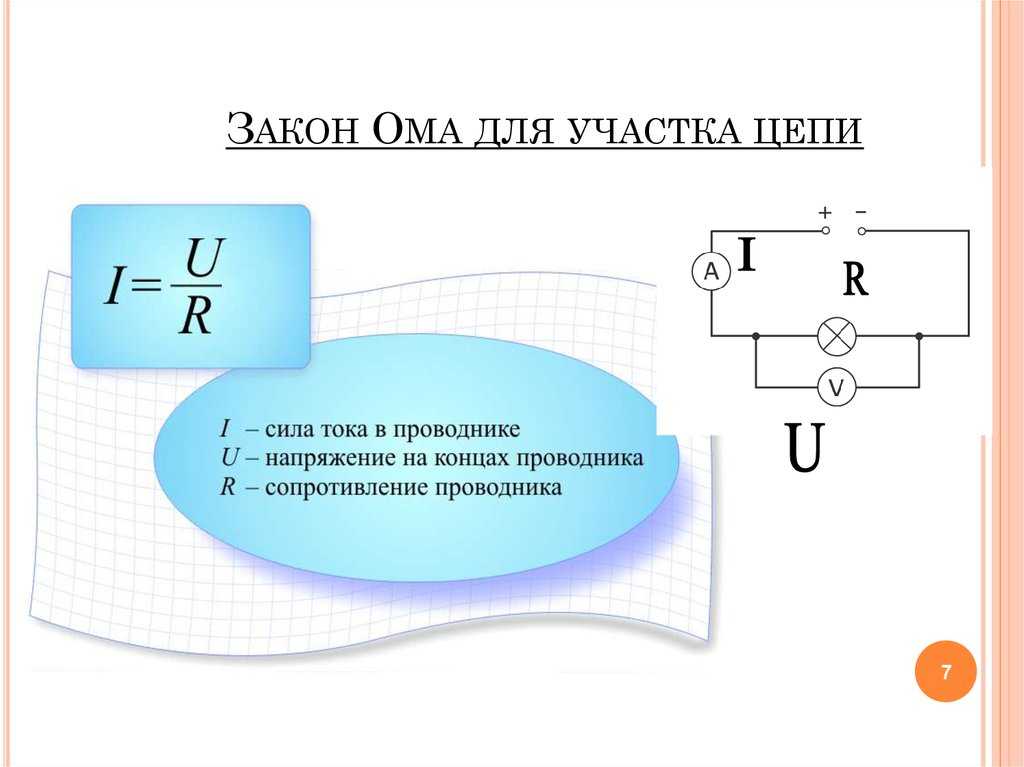
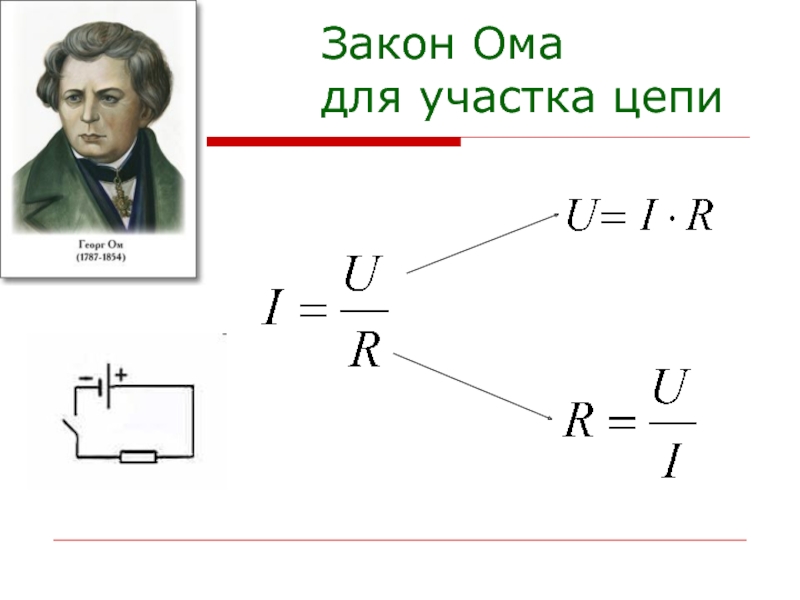
 графики, а также как получить сопротивление графическим методом — см. указатель
вверху страницы.
графики, а также как получить сопротивление графическим методом — см. указатель
вверху страницы.
 заряд вокруг цепи.
заряд вокруг цепи.  д. 15,0 В.
д. 15,0 В.


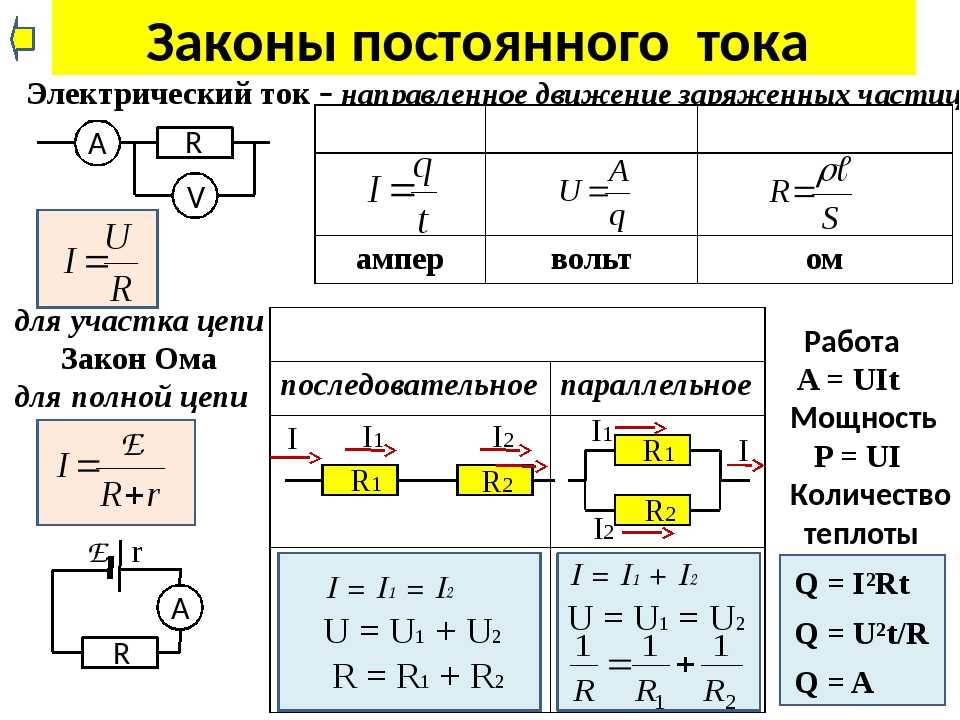

 Расчет q вопрос на основе E = QV (иногда с участием других уравнений электричества)
Расчет q вопрос на основе E = QV (иногда с участием других уравнений электричества) д. схемы
24,0 В?
д. схемы
24,0 В?

 описывает и объясняет несколько примеров
графиков ВАХ, которые можно исследовать с помощью схемы 31 (справа)
описывает и объясняет несколько примеров
графиков ВАХ, которые можно исследовать с помощью схемы 31 (справа) 

 температура
последствия).
температура
последствия).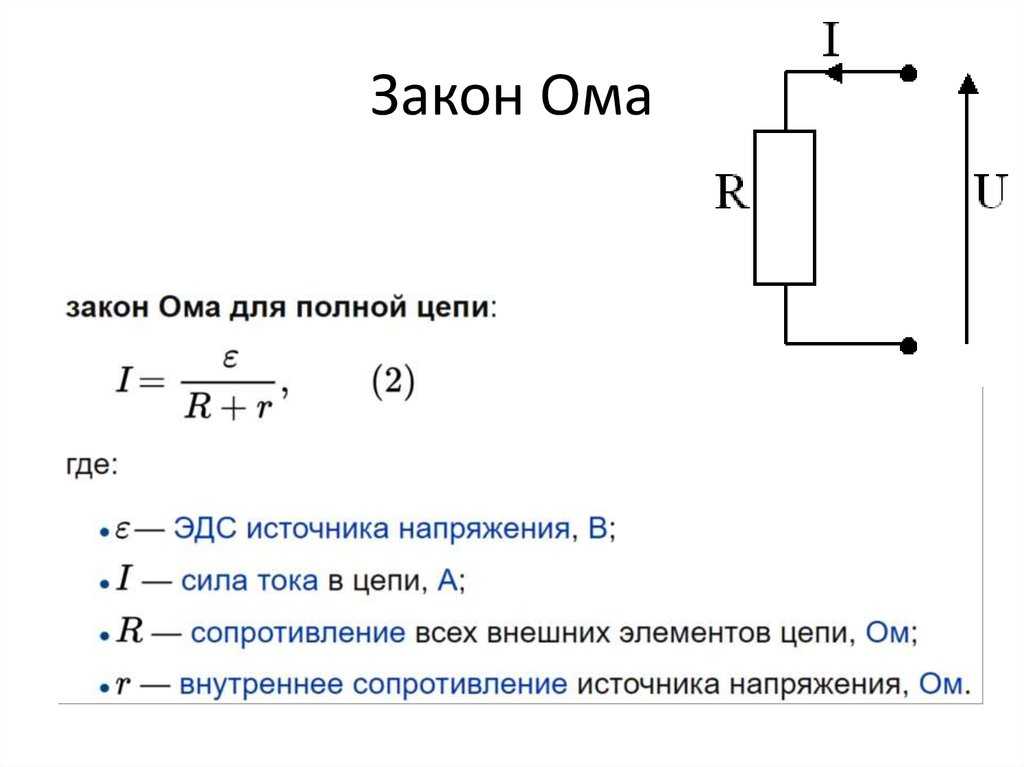
 (правый график).
(правый график).


 d. В измеряется в вольтах ( В ).
d. В измеряется в вольтах ( В ). Это нелинейный график .
Это нелинейный график . По мере увеличения тока вибрации увеличиваются, вызывая больше
электрической энергии, подлежащей преобразованию в тепло, — увеличение
температура И сопротивление металлической нити, тем самым
снижая ток еще больше.
По мере увеличения тока вибрации увеличиваются, вызывая больше
электрической энергии, подлежащей преобразованию в тепло, — увеличение
температура И сопротивление металлической нити, тем самым
снижая ток еще больше.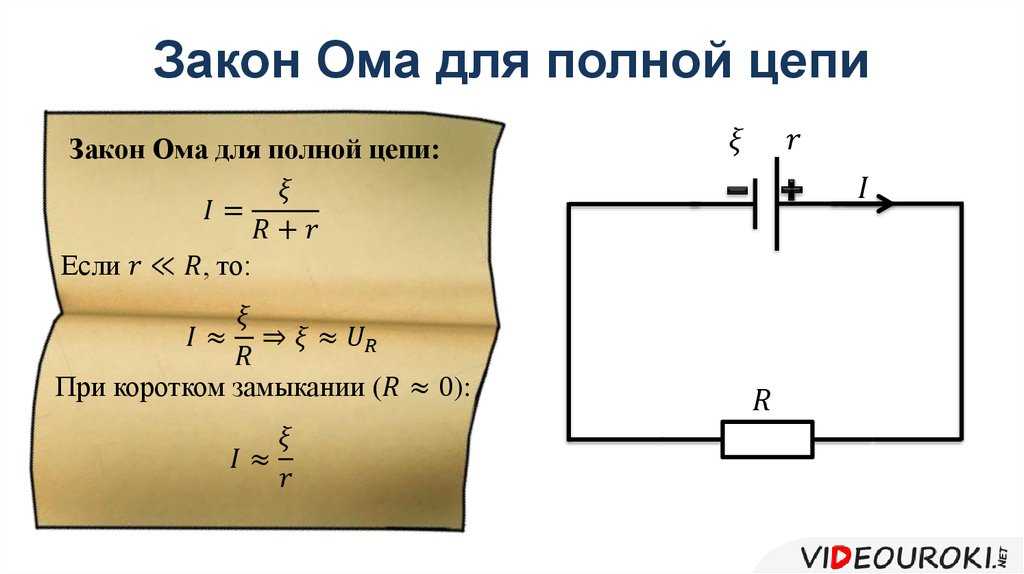 инертный газ
например, аргон или азот добавляют, чтобы уменьшить это испарение — любой
испарившиеся атомы вольфрама попали в нереакционноспособный (и, следовательно, неокисляющий) Ar
или № 2 молекул и, надеюсь, снова сконденсируются на нити.
инертный газ
например, аргон или азот добавляют, чтобы уменьшить это испарение — любой
испарившиеся атомы вольфрама попали в нереакционноспособный (и, следовательно, неокисляющий) Ar
или № 2 молекул и, надеюсь, снова сконденсируются на нити. d. В измеряется в вольтах ( В ).
d. В измеряется в вольтах ( В ).

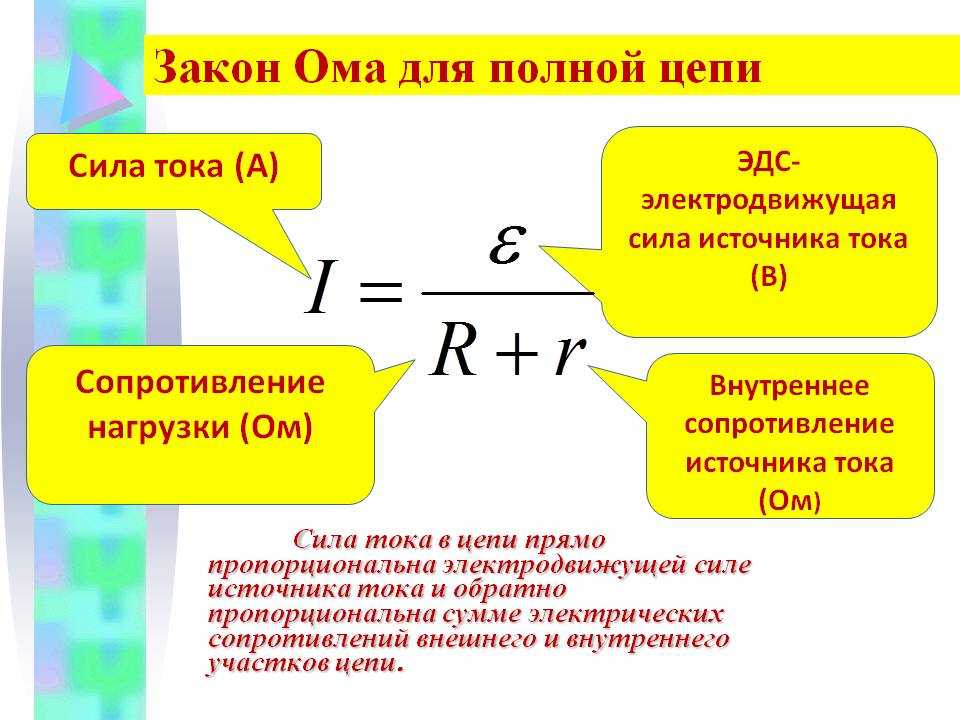
 также P = E/t ниже)
также P = E/t ниже) Полезность электроэнергии, безопасность, передача энергии, расчет стоимости и мощности, P = IV = I 2 Р,
E = Pt, E=IVt
Полезность электроэнергии, безопасность, передача энергии, расчет стоимости и мощности, P = IV = I 2 Р,
E = Pt, E=IVt Статическое электричество и электрические поля, применение
и опасности статического электричества gcse
примечания к пересмотру физики
Статическое электричество и электрические поля, применение
и опасности статического электричества gcse
примечания к пересмотру физики d. графики напряжения, график ВАХ
характеристики диода, что такое омический проводник, ВАХ
график для лампы накаливания, влияние изменения температуры на
сопротивление провода, цепи, не подчиняющиеся закону Ома,
исследование схемы и расчеты V= IR для расчета
сопротивление от показаний тока и напряжения, движения и единиц измерения
электрического заряда, кулон, единица электрического заряда,
расчет переноса заряда по формуле Q = It, Potential
разность и формула передачи электрической энергии E = QV
расчеты, исследование факторов, влияющих на сопротивление
проволоки при постоянной температуре путем изменения длины или ширины,
ток — напряжение поведение провода — измерение графика и
объяснение поведения тока и напряжения металлической нити накала
график лампы, исследование зависимости тока от напряжения
диод — объяснение графика
d. графики напряжения, график ВАХ
характеристики диода, что такое омический проводник, ВАХ
график для лампы накаливания, влияние изменения температуры на
сопротивление провода, цепи, не подчиняющиеся закону Ома,
исследование схемы и расчеты V= IR для расчета
сопротивление от показаний тока и напряжения, движения и единиц измерения
электрического заряда, кулон, единица электрического заряда,
расчет переноса заряда по формуле Q = It, Potential
разность и формула передачи электрической энергии E = QV
расчеты, исследование факторов, влияющих на сопротивление
проволоки при постоянной температуре путем изменения длины или ширины,
ток — напряжение поведение провода — измерение графика и
объяснение поведения тока и напряжения металлической нити накала
график лампы, исследование зависимости тока от напряжения
диод — объяснение графика  Фил Браун 2000+. Все авторские права защищены на примечания к редакции, изображения,
викторины, рабочие листы и т. д. Копирование материалов веб-сайта НЕ
разрешенный. Резюме пересмотренных экзаменов и ссылки на спецификации курса естественных наук
являются неофициальными.
Фил Браун 2000+. Все авторские права защищены на примечания к редакции, изображения,
викторины, рабочие листы и т. д. Копирование материалов веб-сайта НЕ
разрешенный. Резюме пересмотренных экзаменов и ссылки на спецификации курса естественных наук
являются неофициальными. (Например, возьмите предыдущий пример и переверните одну из батарей.) Тогда правило цикла Кирхгофа: $0 = 0$, что вообще ничего не говорит; ток в этой цепи не определен.
(Например, возьмите предыдущий пример и переверните одну из батарей.) Тогда правило цикла Кирхгофа: $0 = 0$, что вообще ничего не говорит; ток в этой цепи не определен. \) Здесь разность потенциалов, \(V = IR,\) произведение силы тока и сопротивления. Отсюда мы также можем получить ток \(I = \frac{V}{R}\) и сопротивление, \(R = \frac{V}{I}\)
\) Здесь разность потенциалов, \(V = IR,\) произведение силы тока и сопротивления. Отсюда мы также можем получить ток \(I = \frac{V}{R}\) и сопротивление, \(R = \frac{V}{I}\) Теперь замкните электрическую цепь с помощью ключа.
Теперь замкните электрическую цепь с помощью ключа.
 Сверхпроводники имеют нулевое сопротивление, как только по ним начинает течь ток.
Сверхпроводники имеют нулевое сопротивление, как только по ним начинает течь ток. Его можно измерить омметром. 9{ – 1}}} \right)\) Электропроводность обратна удельному сопротивлению. Он представлен \(\сигма.\) Хорошие проводники электричества имеют высокую проводимость. Они оказывают меньшее сопротивление протеканию тока через них.
Его можно измерить омметром. 9{ – 1}}} \right)\) Электропроводность обратна удельному сопротивлению. Он представлен \(\сигма.\) Хорошие проводники электричества имеют высокую проводимость. Они оказывают меньшее сопротивление протеканию тока через них.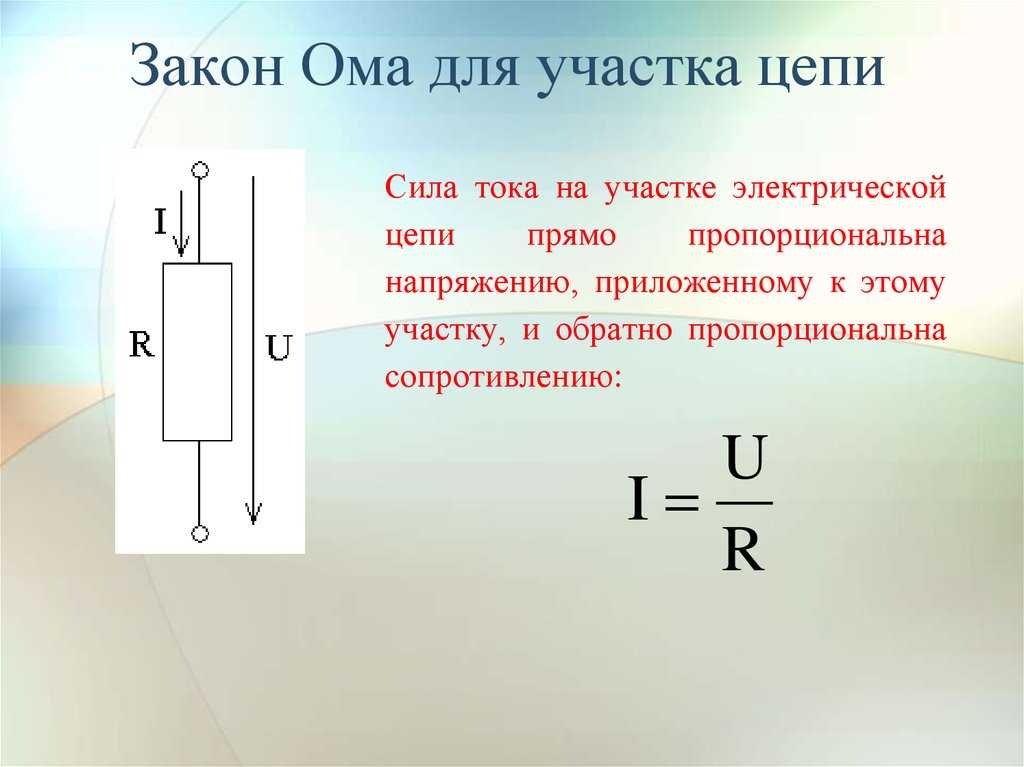 Проверьте формулы из таблицы ниже:
Проверьте формулы из таблицы ниже: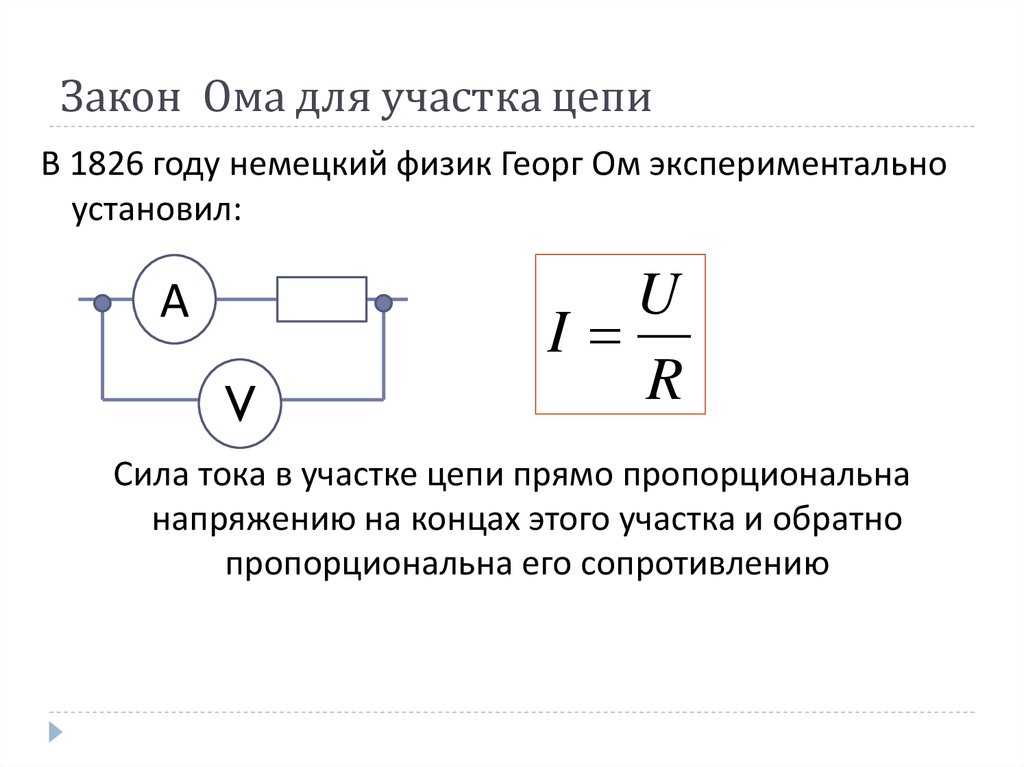 1. Разность потенциалов \(15\;{\rm{V}}\) приложена к проводу с неизвестным сопротивлением. Если ток через провод \(0,2\;{\rm{A}}\) , то каково сопротивление провода?
1. Разность потенциалов \(15\;{\rm{V}}\) приложена к проводу с неизвестным сопротивлением. Если ток через провод \(0,2\;{\rm{A}}\) , то каково сопротивление провода?  1: Напишите формулу закона Ома.
1: Напишите формулу закона Ома. 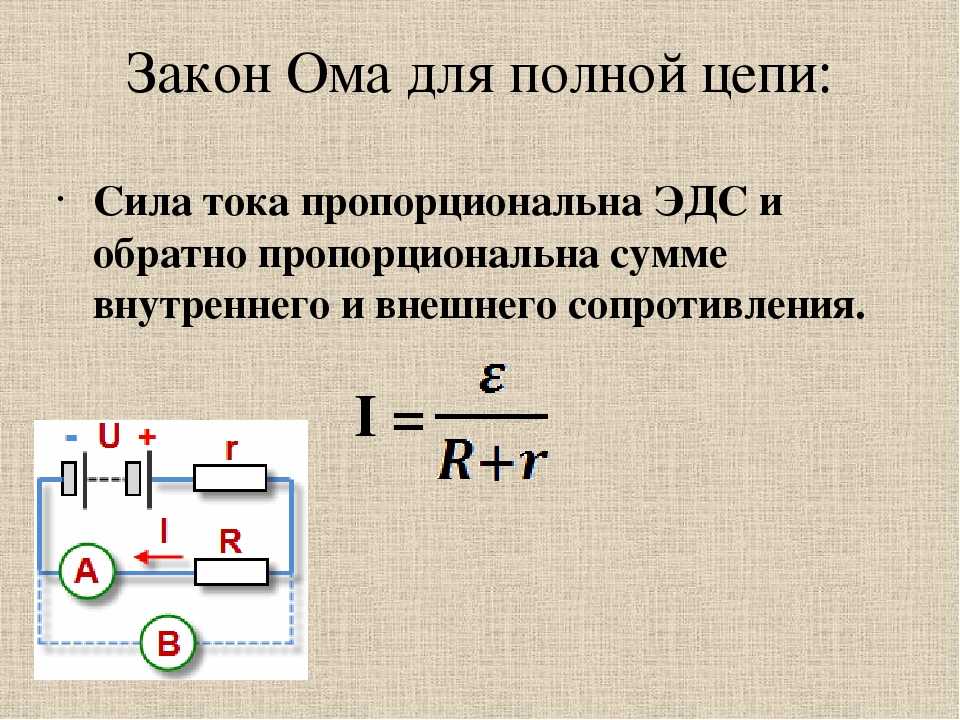
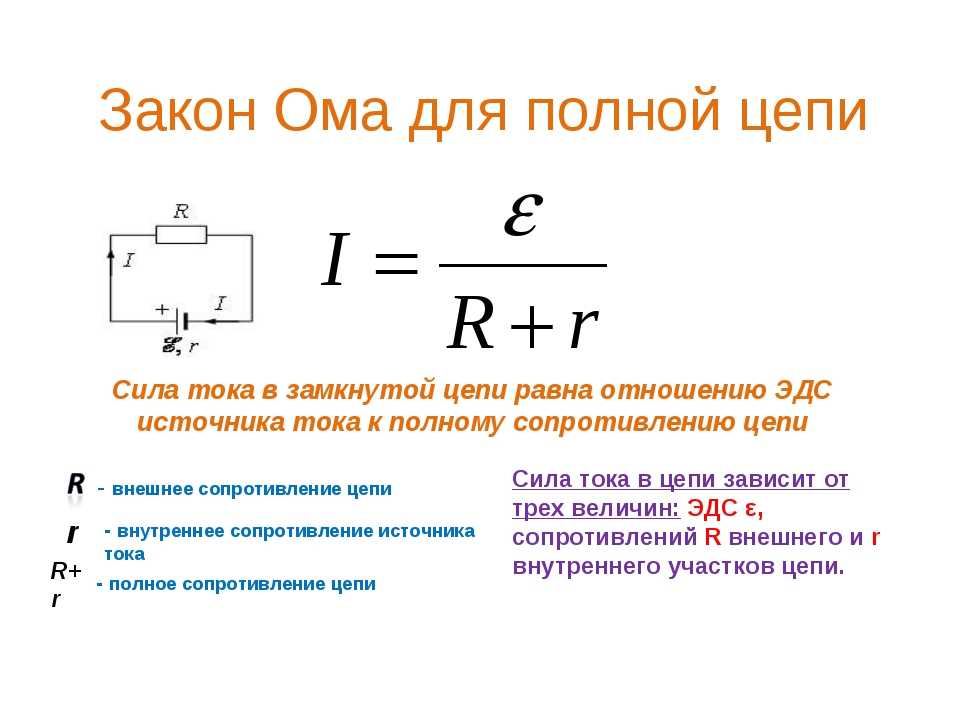
 Когда источник напряжения подключен к проводнику, он создает разность потенциалов В , создающее электрическое поле. Электрическое поле, в свою очередь, воздействует на заряды, вызывая ток.
Когда источник напряжения подключен к проводнику, он создает разность потенциалов В , создающее электрическое поле. Электрическое поле, в свою очередь, воздействует на заряды, вызывая ток. Столкновения движущихся зарядов с атомами и молекулами в веществе передают энергию веществу и ограничивают ток. Сопротивление определяется как обратно пропорциональное току, или
Столкновения движущихся зарядов с атомами и молекулами в веществе передают энергию веществу и ограничивают ток. Сопротивление определяется как обратно пропорциональное току, или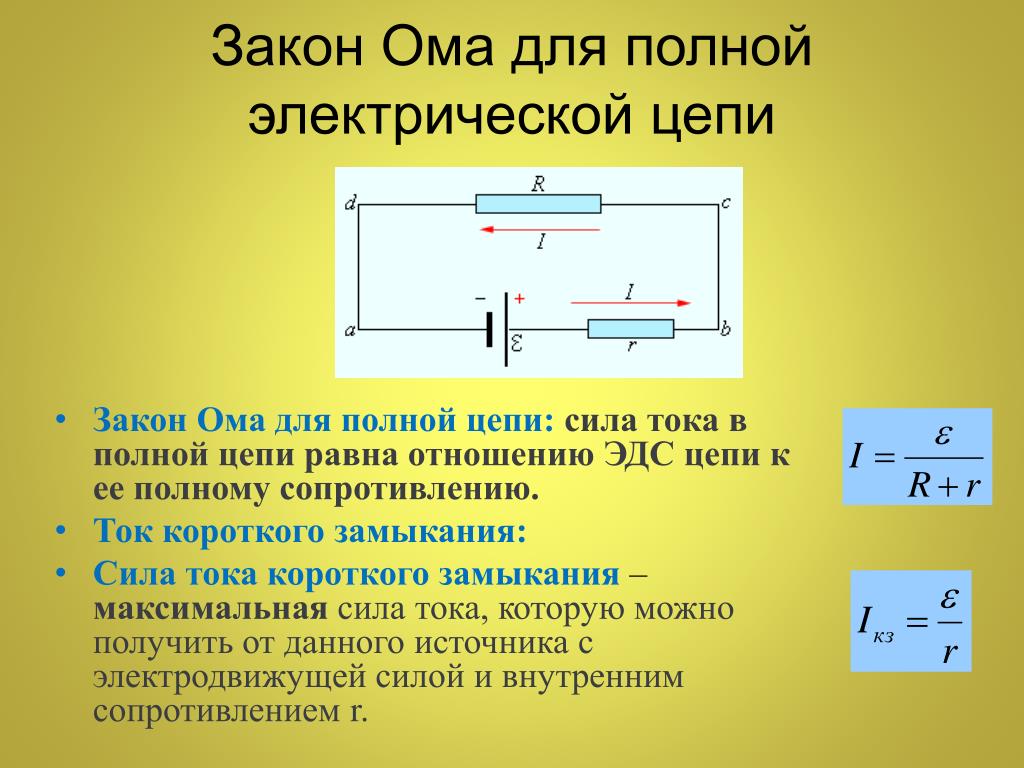 Преобразование I = V/R дает R = V/I , поэтому единицами сопротивления являются 1 Ом = 1 вольт на ампер:
Преобразование I = V/R дает R = V/I , поэтому единицами сопротивления являются 1 Ом = 1 вольт на ампер: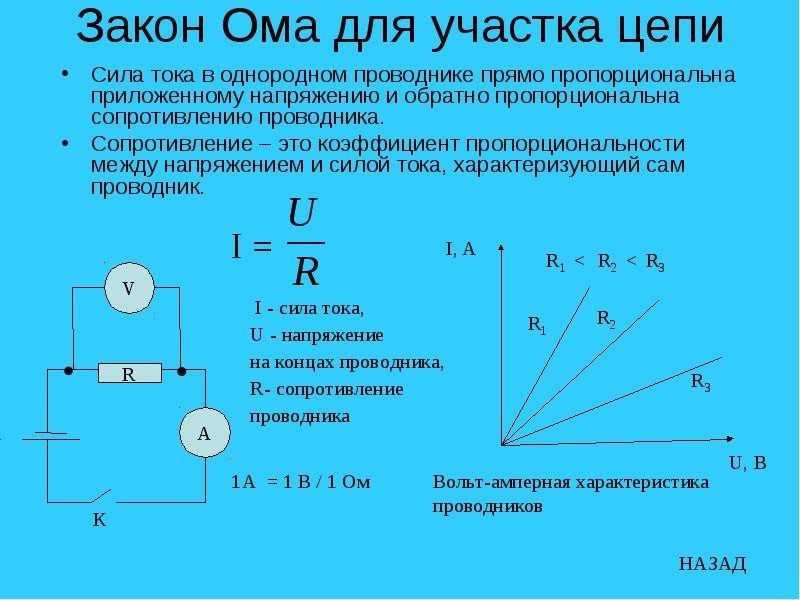
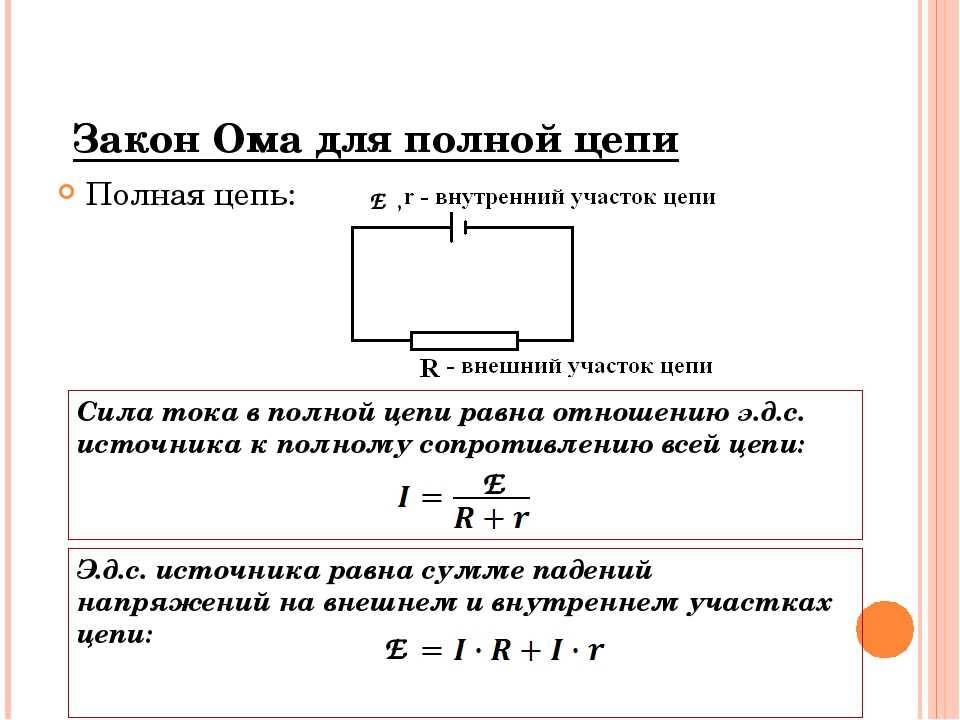 Сопротивление связано с формой объекта и материалом, из которого он состоит, как будет показано в главе 20.3 Сопротивление и удельное сопротивление.
Сопротивление связано с формой объекта и материалом, из которого он состоит, как будет показано в главе 20.3 Сопротивление и удельное сопротивление. Сохранение энергии имеет здесь важные последствия. Источник напряжения поставляет энергию (вызывая электрическое поле и ток), а резистор преобразует ее в другую форму (например, в тепловую энергию). В простой цепи (с одним простым резистором) напряжение, подаваемое источником, равно падению напряжения на резисторе, поскольку Потенциальная энергия = PE = q ΔV , и через каждый протекает одно и то же q . Таким образом, энергия, подаваемая источником напряжения, и энергия, преобразуемая резистором, равны. См. рисунок ниже.
Сохранение энергии имеет здесь важные последствия. Источник напряжения поставляет энергию (вызывая электрическое поле и ток), а резистор преобразует ее в другую форму (например, в тепловую энергию). В простой цепи (с одним простым резистором) напряжение, подаваемое источником, равно падению напряжения на резисторе, поскольку Потенциальная энергия = PE = q ΔV , и через каждый протекает одно и то же q . Таким образом, энергия, подаваемая источником напряжения, и энергия, преобразуемая резистором, равны. См. рисунок ниже.
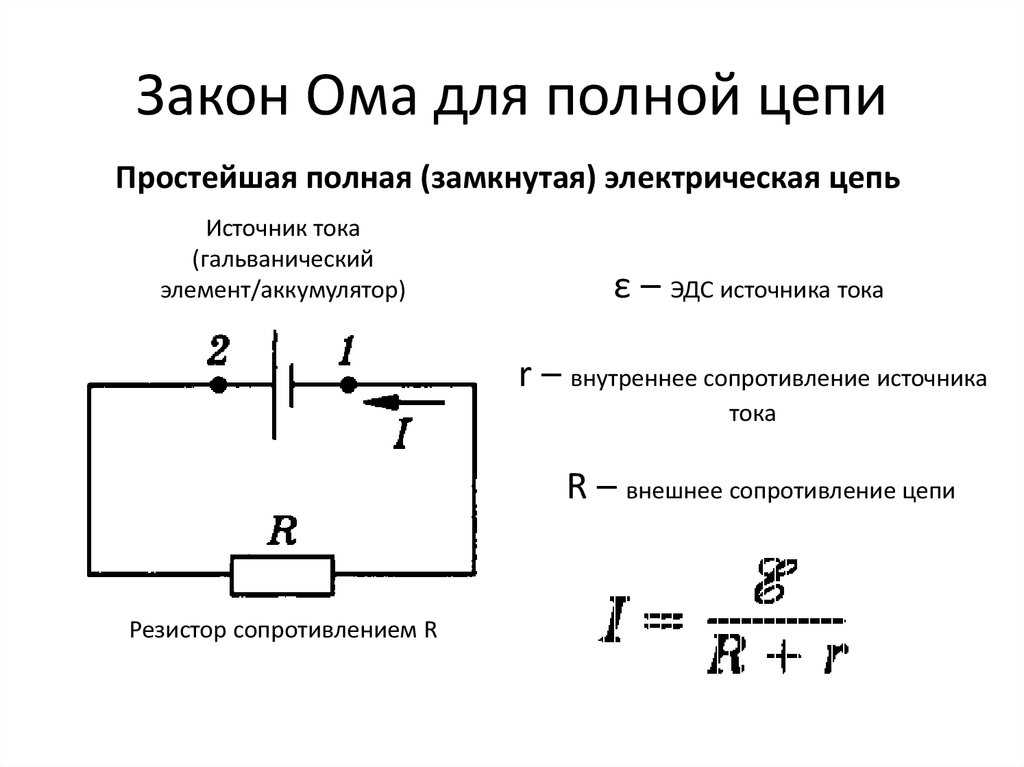
 Закон Ома описывает прямую связь между этими тремя переменными.
Закон Ома описывает прямую связь между этими тремя переменными.
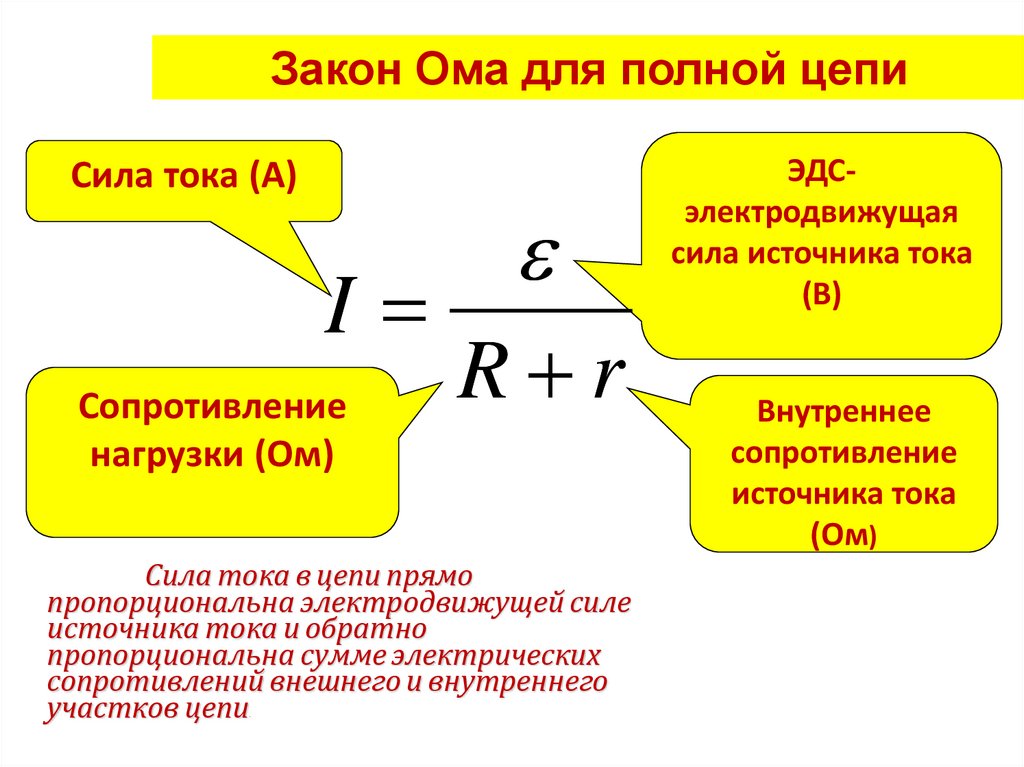
 Давай двигаться!
Давай двигаться!