Закон Ома для однородного участка цепи – формула

4.5

Средняя оценка: 4.5

Всего получено оценок: 89.

4.5

Средняя оценка: 4.5

Всего получено оценок: 89.

Упорядоченное движение электрических зарядов (электронов, ионов) или заряженных макроскопических тел называется электрическим током. Движение зарядов возникает под воздействием на них электрического поля, созданного в проводнике приложенным к его концам напряжением U. Какова зависимость величины электрического тока I от величины напряжения U ? Ответ на этот вопрос впервые дал немецкий ученый Георг Симон Ом, открывший закон, названный в последствии его именем. Для начала рассмотрим закон Ома для однородного участка цепи.

Свойства электрического тока

Направлением электрического тока принято считать движение свободных положительных зарядов. Ток называется постоянным, если его направление и сила постоянны во времени.

Электрическое поле величиной E действует на заряд величиной q с силой

F, которая равна:

$ F = q * E $ (1).

В результате в проводнике возникает электрический ток. Для создания электрического поля E, к концам проводника должно быть приложено напряжение U, которое равно разности потенциалов φ₁ и φ₂ на концах проводника:

$ U = φ2 – φ1 $ (2),

при этом φ₂ > φ₁.

Единица электрического тока — ампер (А) — названа в честь французского физика Ампера. Эта единица является одной семи основных единиц в Международной системе СИ. Единицей измерения напряжений является вольт (В), названная в честь итальянского исследователя Алессандро Вольта.

Опыты Георга Ома

В 1826 г. Георг Ом на основании данных своих многочисленных экспериментов открыл однозначную связь между силой тока I и напряжением U. Ученый измерял зависимости тока от напряжения (вольт-амперные характеристики) и строил графики, из которых он обнаружил не просто пропорциональность (чем больше напряжение, тем больше ток), а линейную математическую зависимость тока от напряжения, т. е. I ∼ U.

Рис. 1. График линейной зависимости силы тока от напряжения в проводниках:.

Из графиков было видно, что угол наклона линейных зависимостей для разных материалов разный, т.е. каждый проводник обладал различной степенью сопротивляемости или проводимости. Эта величина была названа электрическим сопротивлением

R. Формула закона Ома для однородного участка цепи выглядит следующим образом:

$ I = {U \over R} $ (3).

Полностью формулировка закона Ома звучит так: сила тока I для проводника на однородном участке цепи прямо пропорциональна напряжению U на этом участке и обратно пропорциональна сопротивлению проводника R.

Любую электрическую цепь можно разделить на отдельные участки. Участки цепи, на которых отсутствует действие сторонних сил (т.е. участки, где отсутствуют источники тока), называются однородными. Участки цепи, на которых имеются источники тока, называются неоднородными.

Сопротивление

Сопротивление проводников и других веществ (полупроводников и диэлектриков) обусловлено тем, что заряженные частицы взаимодействуют (сталкиваются) с узлами кристаллической решетки и атомами разных примесей и дефектов, что приводит к торможению зарядов.

Наблюдения показали, что сопротивление проводника прямо пропорционально его длине L и обратно пропорционально площади поперечного сечения S

:

$ R = ρ * { L \over S } $ (5),

Рис. 2. Электрический ток I в металлическом цилиндрическом проводнике, длиной L, площадью S, электрическое поле E.

Единицей измерения сопротивления является Ом, равный:

$ [1 Ом] = {[1 В]\over [1 A] } $ (6).

Единица измерения удельного сопротивления ρ показывает какое сопротивление имеет проводник длиной 1 метр с площадью поперечного сечения 1 м². Удельные сопротивления всех известных материалов измерены и сведены в справочные таблицы.

Рис. 3. Пример справочной таблицы удельных проводимостей разных веществ

Значения ρ в справочных таблицах приводятся обычно для нормальной, температуры 20⁰С, т.к. величина удельного сопротивления зависит от температуры внешней среды

T, и описывается формулой:

$ ρ = ρ_0 * (1 + α * T) $ (7),

где: ρ₀ — удельное сопротивление при 0⁰K, α — температурный коэффициент сопротивления.

Что мы узнали?

Итак, мы узнали, что закон Ома для однородного участка цепи формулируется так: сила тока I для проводника на однородном участке цепи прямо пропорциональна напряжению U на этом участке и обратно пропорциональна сопротивлению проводника R. Участки электрической цепи, на которых отсутствуют источники тока, называются однородными. Удельное электрическое сопротивление вещества

ρ — величина, характеризующая способность вещества к сопротивлению.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.5

Средняя оценка: 4.5

Всего получено оценок: 89.

---

А какая ваша оценка?

Закон Ома для однородного участка цепи. Сопротивление проводников.

Однородным называется проводник, в котором не действуют сторонние силы, т. е. нет источника тока.

В 1826 году Ом экспериментально установил закон, согласно которому сила тока, текущего по однородному металлическому проводнику пропорциональна падению напряжения U на проводнике.

(1)

U-напряжение, или падение напряжения, оно равно разности потенциалов ,поддерживаемой на концах проводника.

Величина R называется электрическим сопротивлением проводника. Единицей сопротивления в системе СИ является Ом.

; СИ: 1Ом=;

Величина сопротивления зависит от формы и размеров проводника, а также от свойств материала, из которого сделан проводник. Для однородного цилиндрического проводника

ρ- зависящий от свойств материала коэффициент, называемый удельным сопротивлением вещества.

В СИ сопротивление измеряется в Ом*м, часто измеряют в ; Сопротивление зависит от температуры. Для большинства металлов  растет с температурой по линейному закону

Уравнение (1) определяет соотношение между током и напряжением для конечного участка цепи и поэтому иногда называется законом Ома в интегральной форме.

Закон Ома можно записать также в дифференциальной форме.

Выделим мысленно в окрестности некоторой точки внутри проводника элементарный цилиндрический объем с образующими, параллельными вектору плотности тока в данной точке.

Тогда закон Ома в применении к такому элементарному участку проводника можно записать так:

dI = (2)

dI = jdS ; dU = Edl ; dR = (dl/dS)

Подставляя все эти выражения в (2) , получим:

jdS = ; (3)

Носители заряда в каждой точке движутся в направлении . Поэтому направления и совпадают, и следовательно можно записать в векторном виде

(4)

коэффициент электропроводности или просто проводимость материала.

Формула (4) выражает закон Ома для однородного участка цепи в дифференциальной форме.

Участок цепи, в котором действуют сторонние силы, то есть, например, включен гальванический элемент, называется неоднородным. Обозначим через

Е* =

напряженность поля сторонних сил. При наличии сторонних сил закон Ома в дифференциальной форме примет более общий вид

(1)

(1)- закон Ома для неоднородного участка цепи в дифференциальной форме.

Перейдем к интегральной форме.

Умножим скалярно обе части равенства (1) на вектор , численно равный элементу dl длины проводника и направленный в направлении .

(2)

Е-проекция на направление

С учетом этих соотношений и заменяя (2) можно переписать в виде:

Интегрируя по длине l проводника от сечения 1 до сечения 2, получаем: (3)

Рассмотрим физический смысл всех членов входящих в уравнение (3)

— численно равен работе, совершаемой кулоновскими (т.е. электрическими) силами при перенесении единичного положительного заряда из точки 1 в точку 2.

В электростатике мы нашли связь между напряженностью поля и потенциалом

;

(4)

где и — значения потенциала в точках 1 и 2.

Аналогичный интеграл содержащий вектор напряженности поля сторонних сил называется электродвижущей силой (ЭДС) действующей на участке цепи 1-2.

(5)

ЭДС численно равна работе, совершаемой сторонними силами при перемещении по проводнику единичного положительного заряда из точки 1 в точку 2. Эта работа производится за счет энергии, затрачиваемой в источнике тока.

Падением напряжения U₂₁ или просто напряжением, на участке цепи 1-2 называется физическая величена, численно равная работе, совершаемой суммарным полем кулоновских и сторонних сил при перемещении вдоль цепи единичного положительного заряда из точки 1 в точку 2.

(6)

Если на участке не приложена ЭДС, т.е. участок однородный, то напряжение равно разности потенциалов на концах этого участка.

Интеграл

(7)

представляет собой сопротивление участка цепи между сечениями 1 и2. Для однородного линейного проводника =const , S =const и

,

где l₂₁ – длина проводника между сечениями 1 и 2

Из ф. (3) – (7) следует, что

I (8)

Или

Формула (8) выражает собой закон Ома в интегральной форме для неоднородного участка цепи.

Рассмотрим частные случаи формулы (8) :

1. ,это означает, что точки 1 и 2 совпадают, т.е. цепь замкнута.

При этом сопротивление всей цепи

(9)

Часто R_общ. представляют в виде суммы внешнего сопротивления R и внутреннего сопротивления источника тока r

закон Ома для замкнутой цепи.

2. Если , то из (8) получается закон Ома для однородного участка цепи.

или

3.Если цепь разомкнута, и след.I=0, то из (8) следует, что

это значит, что ЭДС равна разности потенциалов на концах разомкнутой цепи. Поэтому при точных измерениях ЭДС применяются схемы, при которых ток через измеряемую ЭДС делается равным нулю. Разность потенциалов на её концах дает при этом точное значение ЭДС.

Приближенно ЭДС измеряют с помощью вольтметра. По закону Ома для замкнутой цепи:

Вольтметр в данном случае показывает напряжение во внешней цепи, т.е. на самом себе

Поскольку R_v>>r, то U_vε

электромагнетизм — Закон Ома в проводнике

Задай вопрос

спросил 5 лет, 1 месяц назад

Изменено 3 года, 6 месяцев назад

Просмотрено 507 раз

$\begingroup$

Предположим, установившиеся условия и однородный проводник. Тогда dp/dt = 0, где p — объемная плотность заряда. Если в проводнике действует закон Ома, то

$${\rm div}\ \bar{J} = {\rm div}\ \bar{E} = 0$$

мы знаем, что по поверхности проводника течет постоянный ток; это означает, что на поверхности:

${\rm div}\ \bar{J} = 0 $ , ${\rm div}\ \bar{E} \neq 0 $

Таким образом, закон Ома кажется неприменимым на поверхности проводника. Где я ошибаюсь?

• электромагнетизм
• электростатика
• электрическое сопротивление
• проводники

$\endgroup$

2

$\begingroup$

Закон Ома действительно не действует на поверхности проводника. Это связано с тем, что электрическое поле имеет ненулевую нормальную составляющую на поверхности, но нормальная составляющая плотности электрического тока там равна нулю, поскольку заряды не будут выскакивать из проводника в вакуум (если только электрическое поле не является экстремальным). Закон Ома обычно справедлив внутри металлического проводника, по которому течет ток, а не по его поверхности, где он (в случае установившегося тока) не течет.

$\endgroup$

$\begingroup$

Для постоянного тока не обязательно требуется электрическое поле. Электроны, движущиеся в вакууме где-то во Вселенной или в сверхпроводящем кольце, не нуждаются в силе, когда они ускоряются. Если бы в сверхпроводящем кольце существовало поле E, энергия, переданная электрону, была бы равна нулю для полного цикла. Поле E — если оно есть — сразу за поверхностью (идеального) проводника всегда перпендикулярно поверхности в электростатических условиях. Это важное ограничение уравнений Максвелла.

$\endgroup$

3

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

электрических цепей — Закон Ома Интуиция

Когда мы выводим закон Ома, используя модель Друде, мы предполагаем в какой-то момент времени, что E=V/L, когда на самом деле E=dV/dL, если только E не является постоянным, и в этом случае предположение E=V/L правда. Но я не понимаю, почему электрическое поле в проводнике должно быть постоянным при протекании тока.

Как правило, электрическое поле в проводнике не должно быть постоянным (во времени или пространстве) при протекании тока. Если изменение электрического поля во времени достаточно велико, это может вызвать быстрое изменение потока, что, в свою очередь, может привести к тому, что электрическое поле станет функцией пространства. В этом случае закон Ома в традиционном понимании ($V=IR$) не работает и приходится применять теорию линий передачи. Давайте на секунду вернемся назад и посмотрим, как мы можем избежать этого общего случая и остаться в пределе, где напряжение четко определено.

Исходя из закона Фарадея, мы знаем, что:

$\nabla \times E = -\frac{\partial B}{\partial t}$

Что можно переписать как:

$\oint E \cdot dl = -\int{\frac{\partial B}{\partial t}}\cdot dA$

Итак, если правая часть этих уравнений пренебрежимо мала, мы знаем, что сумма изменений напряжения на любом замкнутом пути (например, в цепи, состоящей из батареи с двумя последовательно соединенными резисторами) должен равняться нулю. Кроме того, обратите внимание, что $\nabla \times E = 0$ также требуется для того, чтобы мы могли написать $E = — \nabla V$. Если $\nabla \times E$ не равно нулю, то мы не можем определить эту связь между электрическими полями и напряжением таким образом, потому что $\nabla \times \nabla V$ всегда должно быть равно нулю (это просто тождество векторного исчисления).

Теперь, даже с этим ограничением, E не обязательно должно быть постоянным в пространстве по всей цепи. По сути, он постоянен в среде, такой как резистор, потому что эта среда однородна (я скоро к этому вернусь).

Кроме того, если предположение V=E/L имеет смысл, я могу понять, почему закон Ома должен работать для однородной электрической цепи. Однако я не понимаю, почему это должно работать для гетерогенной схемы — возможно, с двумя последовательно соединенными резисторами. И, пожалуйста, не используйте аналогию с пробкой. Конечно, должен быть более теоретический способ объяснить это (используя классическую физику).

Я дам вам классическую физическую картину, которая объяснит, почему E = постоянная в пределах однородного резистора, и объяснит, почему закон Ома выполняется для последовательной комбинации. Проницательный способ вывести закон Ома состоит в том, чтобы начать с уравнения Лоренца и применить его к объемным электронам в резистивной среде (не к отдельному электрону, а к массе, предполагая, что они движутся вместе):

$F = n m \frac {dv}{dt} = n q (E + v \times B)$

Электрон ускоряется электрическим полем, а для нашей идеальной цепи магнитного поля не существует, поэтому второй член опустим (это иногда называется членом Холла и приводит к эффекту Холла). Заметим, что $n$ в приведенном выше выражении — объемная электронная плотность. Теперь мы знаем, что это объемное движение не может продолжать ускоряться бесконечно — электроны будут отдавать свою энергию при столкновении внутри среды. Мы можем смоделировать это, добавив член потерь в приведенное выше уравнение. Электроны имеют импульс $n m v$ и с некоторой скоростью теряют этот импульс; назовем это $\nu$. Это дает:

$F = n m \frac{dv}{dt} = n q E — n m v \nu$

Обратите внимание, что в $\nu$ используются обратные секунды. На данный момент это просто определение. Нам нужно вычислить $\nu$, думая о том, сколько времени требуется среднему электрону, чтобы потерять импульс, равный $m v$ (согласно нашему собственному определению проблемы). Как рассчитывается это значение, выходит за рамки этого поста и зависит от среды. Для некоторых материалов нам нужно только принять во внимание отдельные колламбовые столкновения и спросить, сколько времени требуется среднему электрону, чтобы потерять импульс, равный $m v$.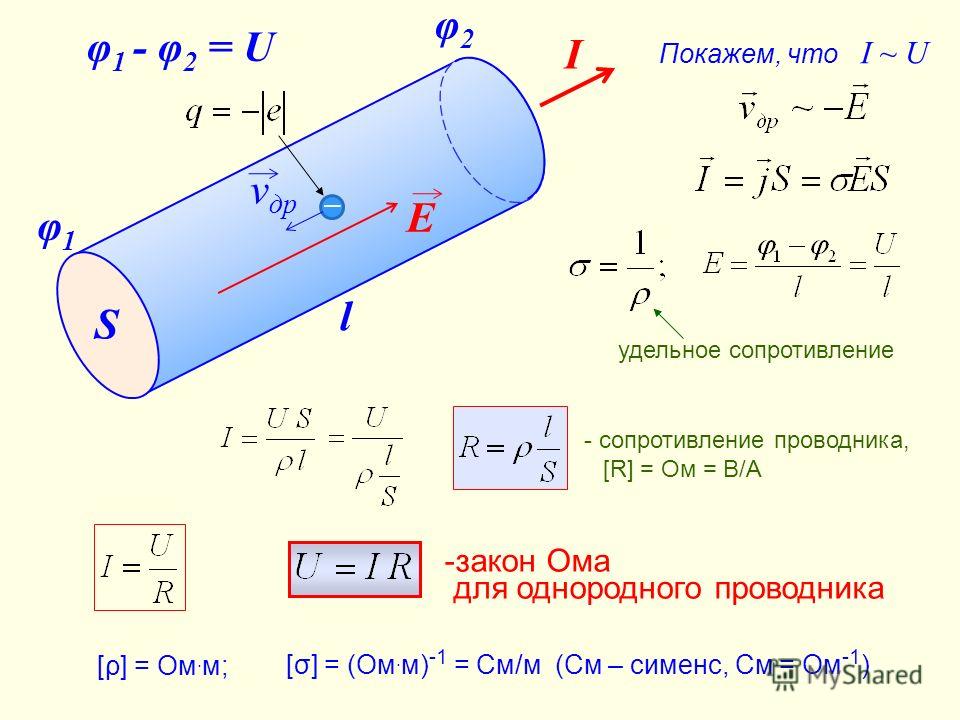 Для других материалов могут иметь место другие эффекты, которые могут привести к потере энергии электроном. В любом случае, однако, мы можем свалить всю эту физику в $\nu$, а последний может быть функцией температуры, массы, заряда и т. д. Тогда мы можем задать вопрос, учитывая приведенное выше уравнение силы для объема электронов, какова стационарная скорость? Чтобы найти это, мы установим $\frac{dv}{dt} = 0$ и переставим члены: 92}{m \nu}$

Это определение для всей протяженности резистора имеет смысл только в том случае, если плотность носителей заряда n постоянна и имеет одинаковую массу по всему резистору. Тогда мы можем сказать, что $\sigma$ постоянна в пространстве, что означает, что $E$ и $J$ постоянны в пространстве. Лежащая в основе физическая картина связана с потерей энергии электронами; если эта потеря происходит равномерно, то $\sigma$ равномерна в пространстве. Так что теперь, если у вас есть два разных материала последовательно, вы можете применить это уравнение к каждому материалу независимо.