§ 100. Закон Ома для неоднородного участка цепи
Рассмотрим неоднородный участок цепи, где действующую э.д.с. на участке 1—2 обозначим через ξ12, а приложенную на концах участка разность потенциалов — через 1-2.
Если ток проходит по неподвижным проводникам, образующим участок 1—2, то работа A12 всех сил (сторонних и электростатических), совершаемая над носителями тока, по закону сохранения и превращения энергии равна теплоте, выделяющейся на участке. Работа сил, совершаемая при перемещении заряда Q0 на участке 1—2, согласно (97.4),
A12=Q0ξ12 + Q0(1—2).
Э.д.с. ξ12, как и сила тока I,— величина скалярная. Ее необходимо брать либо с положительным, либо с отрицательным знаком в зависимости от знака работы, совершаемой сторонними силами. Если
э.д.с. способствует движению положительных зарядов в выбранном направлении (в направлении 1—2), то ξ12>0. Если э.д.с. препятствует движению положительных зарядов в данном направлении, то
ξ12<0.
За время t в проводнике выделяется теплота (см. (99.5))
Q=I2Rt=IR(It)=IRQ0. (100.2) Из формул (100.1) и (100.2) получим
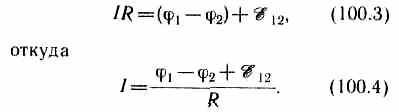
Выражение (100.3) или (100.4) представляет собой закон Ома для неоднородного участка цепи в интегральной форме, который является обобщенным законом Ома.
Если на данном участке цепи источник тока отсутствует (ξ12=0), то из (100.4) приходим к закону Ома для однородного участка цепи (98.1):
I=(1-2)/R=U/R
(при отсутствии сторонних сил напряжение на концах участка равно разности потенциалов (см. §97)). Если же электрическая цепь
I=ξ/R,
где ξ— э.д.с., действующая в цепи, R — суммарное сопротивление всей цепи. В общем случае R = r+R1, где r — внутреннее сопротивление источника э.д.с., R1 — сопротивление внешней цепи. Поэтому закон Ома для замкнутой цепи будет иметь вид
I=ξ/(r+R1).
Если цепь разомкнута и, следовательно, в ней ток отсутствует (I=0), то из закона Ома (100.4) получим, что ξ12=2-1 т. е. э.д.с., действующая в разомкнутой цепи, равна разности потенциалов на ее концах. Следовательно, для того чтобы найти э.д.с. источника тока, надо измерить разность потенциалов на его клеммах при разомкнутой цепи.
§ 99. Работа и мощность тока. Закон Джоуля — Ленца
Рассмотрим однородный проводник, к концам которого приложено напряжение U. За время At через сечение проводника переносится заряд dq = Idt. Так как ток представляет собой перемещение заряда dq под действием электрического поля, то, по формуле (84.6), работа тока
dA=Udq=IUdt. (99.1)
Если сопротивление проводника R, то, используя закон Ома (98.1), получим
dA=I2Rdt=(U2/r)dt. (99.2)
Из (99.1) и (99.2) следует, что мощность тока
P=dA/dt=UI=I2R=U2/R. (99.3)
Если
сила тока выражается в амперах, напряжение
— в вольтах, сопротивление — в омах,
то работа тока выражается в джоулях, а
мощность — в ваттах. На практике
применяются также внесистемные
единицы работы тока: ватт-час (Вт•ч) и
киловатт-час (кВт•ч). 1 Вт•ч — работа
тока мощностью в 1 Вт в течение 1 ч: 1 Вт•ч
= 3600 Вт•с = 3,6•10
Если ток проходит по неподвижному металлическому проводнику, то вся работа тока идет на его нагревание и, по закону сохранения энергии,
dQ=dA. (99.4)
Таким образом, используя выражения (99.4), (99.1) и (99.2), получим

Выражение (99.5) представляет собой закон Джоуля — Ленца,
Выделим в проводнике элементарный цилиндрический объем dV=dSdl (ось цилиндра совпадает с направлением тока),
сопротивление которого R= (dl/dS). По закону Джоуля — Ленца, за время dt в этом объеме выделится теплота
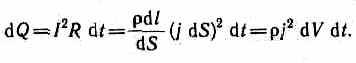
Количество теплоты, выделяющееся за единицу времени в единице объема, называется удельной тепловой мощностью тока. Она равна
w=j2. (99.6)
w =jE =E2. (99.7)
Формулы (99.6) и (99.7) являются обобщенным выражением закона Джоуля — Ленца в дифференциальной форме, пригодным для любого проводника.
Тепловое действие тока находит широкое применение в технике, которое началось с открытия в 1873 г. русским инженером А. Н. Лодыгиным (1847—1923) лампы накаливания. На нагревании, проводников электрическим током основано действие электрических муфельных печей, электрической дуги (открыта русским инженером В. В. Петровым (1761 — 1834)), контактной электросварки, бытовых электронагревательных приборов и т. д.
Закон Ома для неоднородного участка цепи
Закон Ома для неоднородного участка цепи.
При прохождении электрического тока в замкнутой цепи на свободные заряды действуют силы со стороны стационарного электрического поля и сторонние силы. При этом на отдельных участках этой цепи ток создается только стационарным электрическим полем. Такие участки цепи называются однородными. На некоторых участках этой цепи, кроме сил стационарного электрического поля, действуют и сторонние силы. Участок цепи, на котором действуют сторонние силы, называют неоднородным участком цепи.
Для того чтобы выяснить, от чего зависит сила тока на этих участках, необходимо уточнить понятие напряжения.
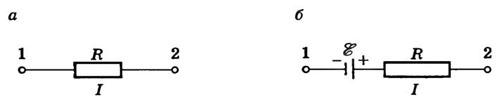 Рис.
1
Рис.
1
Рассмотрим
вначале однородный участок цепи (рис.
1, а). В этом случае работу по перемещению
заряда совершают только силы стационарного
электрического поля, и этот участок
характеризуют разностью потенциалов
Δφ. Разность потенциалов на концах
участка 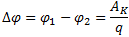 ,
где AK — работа сил стационарного
электрического поля. Неоднородный
участок цепи (рис. 1, б) содержит в отличие
от однородного участка источник ЭДС, и
к работе сил электростатического поля
на этом участке добавляется работа
сторонних сил. По определению,
,
где AK — работа сил стационарного
электрического поля. Неоднородный
участок цепи (рис. 1, б) содержит в отличие
от однородного участка источник ЭДС, и
к работе сил электростатического поля
на этом участке добавляется работа
сторонних сил. По определению, 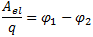
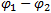 —
разность потенциалов точек в начале и
конце рассматриваемого участка;
—
разность потенциалов точек в начале и
конце рассматриваемого участка; 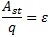 .
Тогда говорят о напряжении для
напряженности: Eстац. э. п. = Eэ/стат. п. +
Eстор. Напряжение U на участке цепи
представляет собой физическую скалярную
величину, равную суммарной работе
сторонних сил и сил электростатического
поля по перемещению единичного
положительного заряда на этом участке:
.
Тогда говорят о напряжении для
напряженности: Eстац. э. п. = Eэ/стат. п. +
Eстор. Напряжение U на участке цепи
представляет собой физическую скалярную
величину, равную суммарной работе
сторонних сил и сил электростатического
поля по перемещению единичного
положительного заряда на этом участке: 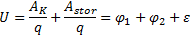
Из этой формулы видно, что в общем случае напряжение на данном участке цепи равно алгебраической сумме разности потенциалов и ЭДС на этом участке. Если же на участке действуют только электрические силы (ε = 0), то . Таким образом, только для однородного участка цепи понятия напряжения и разности потенциалов совпадают.
Закон Ома для неоднородного участка цепи имеет вид:
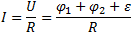
где R — общее сопротивление неоднородного участка.
ЭДС ε может быть как положительной, так и отрицательной. Это связано с полярностью включения ЭДС в участок: если направление, создаваемое источником тока, совпадает с направлением тока, проходящего в участке (направление тока на участке совпадает внутри источника с направлением от отрицательного полюса к положительному), т.е. ЭДС способствует движению положительных зарядов в данном направлении, то ε > 0, в противном случае, если ЭДС препятствует движению положительных зарядов в данном направлении, то ε < 0.
20. Закон Джоуля-Ленца (интегральная и дифференциальная формы).
Теперь подробнее обсудим величину DU (которая представляет в расчетах изменение внутренней энергии) применительно к проводнику, по которому начинает течь ток.
Постепенно, выбранный проводник будет нагреваться, а это значит, что будет увеличиваться его внутренняя энергия. По мере нагрева разность между температурой проводника и окружающей его среды будет увеличиваться. Согласно закономерности Ньютона, вместе с этим возрастать будет и мощность теплоотдачи проводника. Таким образом, через какое-то время температура проводника, достигнув определенного значения, перестанет увеличиваться. В этот момент величина DU будет равной нулю, и перестанет изменяться внутренняя энергия проводника.
Тогда для этого состояния первый закон термодинамики будет выглядеть так: A = – Q. То есть когда не меняется внутренняя энергия проводника, работа тока целиком превращается в теплоту. Используя этот вывод, можем записать все три рассмотренные формулы для расчета работы тока в несколько ином виде, в конечном итоге получаем закон Джоуля-Ленца в интегральной форме:
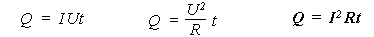 На
первый взгляд все формулы могут считаться
равноправными, однако только последняя
справедлива всегда, поэтому она и
считается законом. А вот остальные две
справедливы только при определенных
условиях, поэтому законом считаться не
могут.
На
первый взгляд все формулы могут считаться
равноправными, однако только последняя
справедлива всегда, поэтому она и
считается законом. А вот остальные две
справедливы только при определенных
условиях, поэтому законом считаться не
могут.
Закон Джоуля-Ленца в дифференциальной форме выглядит совершенно по-иному, мы рассмотрим только общий вариант, без дополнительных выведений и вычислений, который выглядит так:
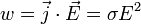 Где:
Где:
 —
является мощностью тепла, выделяемого
в единице объёма;
—
является мощностью тепла, выделяемого
в единице объёма; —
плотность электрического тока;
—
плотность электрического тока; —
это напряжённость электрического поля;
—
это напряжённость электрического поля; —
проводимость выбранной среды.
—
проводимость выбранной среды.
Так в общих чертах выглядит закон Джоуля-Ленца и его интегральная и дифференциальная формы. Хотя, если проводить дальнейшие вычисления, то закон может принимать и другие формы.
21. Закон Ома для неоднородного участка цепи (обобщенный закон Ома). Закон Ома для замкнутой цепи.
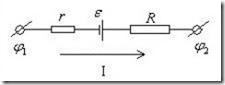
Участок цепи, содержащий источник ЭДС, называется неоднородным(рис.5.11). Всякий источник ЭДС характеризуется величиной ЭДС ε ивнутренним сопротивлением r.
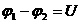 —
напряжение на концах участка цепи.
—
напряжение на концах участка цепи.
Рис.5.11. Неоднородный участок цепи.
Закон Ома для неоднородного участка цепи имеет вид:
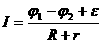
При
соединении концов неоднородного участка
цепи идеальнымпроводником
образуется замкнутая цепь, в
которой потенциалы φ1 иφ2 выравниваются
и мы приходим к закону
Ома для замкнутой (или полной) цепи:
потенциалы φ1 иφ2 выравниваются
и мы приходим к закону
Ома для замкнутой (или полной) цепи:
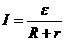
Если
сопротивление внешней цепи 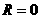 ,
то имеем случай короткого
замыкания.
В этом случае в цепи течетмаксимальный ток:
,
то имеем случай короткого
замыкания.
В этом случае в цепи течетмаксимальный ток:

При 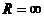 имеем разомкнутую цепь.
В этом случае ток в цепи равен
нулю:
имеем разомкнутую цепь.
В этом случае ток в цепи равен
нулю:
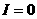
22. Правила Кирхгофа для разветвленных цепей постоянного тока
Правило 1: в любом узле сумма входящих токов и выходящих равна нулю. Оно учитывает закон сохранения электрического заряда.
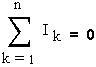
При этом токи, идущие к узлу, и токи, исходящие из узла, следует считать величинами разных знаков.
Правило 2: алгебраическая сумма произведений сил токов на сопротивления при обходе контура равна сумме ЭДС в контуре. Учитывается закон сохранения энергии.
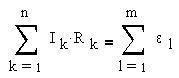
Для упрощения расчетов сложных электрических цепей, содержащих неоднородные участки, используются правила Кирхгофа, которые являются обобщением закона Ома на случай разветвленных цепей.
В разветвленных цепях можно выделить узловые точки (узлы), в которых сходятся не менее трех проводников (рис. 1.10.1). Токи, втекающие в узел, принято считать положительными; вытекающие из узла – отрицательными.
|
Рисунок 1.10.1. Узел электрической цепи. I1, I2 > 0; I3,I4 < 0 |
В узлах цепи постоянного тока не может происходить накопление зарядов. Отсюда следует первое правило Кирхгофа:
Алгебраическая сумма сил токов для каждого узла в разветвленной цепи равна нулю:
|
Первое правило Кирхгофа является следствием закона сохранения электрического заряда.
В разветвленной цепи всегда можно выделить некоторое количество замкнутых путей, состоящих из однородных и неоднородных участков. Такие замкнутые пути называются контурами. На разных участках выделенного контура могут протекать различные токи. На рис. 1.10.2 представлен простой пример разветвленной цепи. Цепь содержит два узла a и d, в которых сходятся одинаковые токи; поэтому только один из узлов является независимым (a или d).
|
Рисунок 1.10.2. Пример разветвленной электрической цепи. Цепь содержит один независимый узел (a или d) и два независимых контура (например, abcd и adef) |
В цепи можно выделить три контура abcd, adef и abcdef. Из них только два являются независимыми (например, abcd и adef), так как третий не содержит никаких новых участков.
Второе правило Кирхгофа является следствием обобщенного закона Ома.
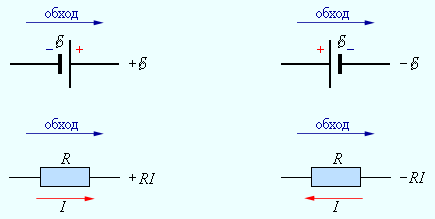
Запишем обобщенный закон Ома для участков, составляющих один из контуров цепи, изображенной на рис. 1.10.2, например, abcd. Для этого на каждом участке нужно задать положительное направление тока и положительное направление обхода контура. При записи обобщенного закона Ома для каждого из участков необходимо соблюдать определенные «правила знаков», которые поясняются на рис. 1.10.3.
|
Рисунок 1.10.3. «Правила знаков» |
Для участков контура abcd обобщенный закон Ома записывается в виде:
Для
участка bc: I1R1 = Δφbc – 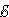 1.
1.
Для
участка da: I2R2 = Δφda – 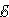 2.
2.
Складывая левые и правые части этих равенств и принимая во внимание, что Δφbc = – Δφda , получим:
I1R1 + I2R2 = Δφbc + Δφda – |
Аналогично, для контура adef можно записать:
– I2R2 + I3R3 = |
Второе правило Кирхгофа можно сформулировать так: алгебраическая сумма произведений сопротивления каждого из участков любого замкнутого контура разветвленной цепи постоянного тока на силу тока на этом участке равна алгебраической сумме ЭДС вдоль этого контура.
Первое и второе правила Кирхгофа, записанные для всех независимых узлов и контуров разветвленной цепи, дают в совокупности необходимое и достаточное число алгебраических уравнений для расчета значений напряжений и сил токов в электрической цепи. Для цепи, изображенной на рис. 1.10.2, система уравнений для определения трех неизвестных токов I1, I2 и I3 имеет вид:
I1R1 + I2R2 = – |
– I2R2 + I3R3 = |
– I1 + I2 + I3 = 0 |
Закон Ома для однородного и неоднородного участка цепи
Дифференциальная
форма закона Ома.
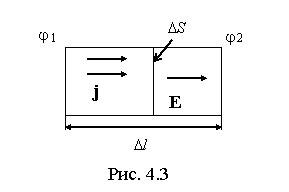
Найдем связь между плотностью тока j и
напряженностью поля Е в
одной и той же точке проводника. В
изотропном проводнике упорядоченное
движение носителей тока происходит в
направлении вектора Е.
Поэтому направления
векторов j и Е совпадают.
Рассмотрим
в однородной изотропной среде элементарный
объем с образующими, параллельными
вектору Е,
длиной 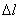 ,
ограниченной двумя эквипотенциальными
сечениями 1 и 2 (рис. 4.3).
,
ограниченной двумя эквипотенциальными
сечениями 1 и 2 (рис. 4.3).
Обозначим
их потенциалы 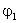 и
и 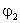 ,
а среднюю площадь сечения через
,
а среднюю площадь сечения через 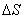 .
Используя закон Ома, получим для тока
.
Используя закон Ома, получим для тока 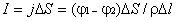 ,
или для плотности тока
,
или для плотности тока 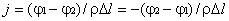 ,
следовательно
,
следовательно
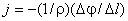 .
.
Перейдем
к пределу при 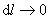 ,
тогда рассматриваемый объем можно
считать цилиндрическим, а поле внутри
него однородным, так что
,
тогда рассматриваемый объем можно
считать цилиндрическим, а поле внутри
него однородным, так что
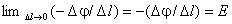 ,
,
где Е — напряженность электрического поля внутри проводника. Учитывая, что j и Есовпадают по направлению, получаем
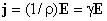 .
.
Это
соотношение является дифференциальной
формой закона Ома для однородного
участка цепи.
Величина 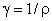 называется
удельной проводимостью. На
неоднородном участке цепи на носители
тока действуют, кроме электростатических
сил
называется
удельной проводимостью. На
неоднородном участке цепи на носители
тока действуют, кроме электростатических
сил 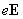 ,
еще и сторонние силы
,
еще и сторонние силы 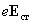 ,
следовательно, плотность тока в этих
участках оказывается пропорциональной
сумме напряженностей. Учет этого приводит
к дифференциальной
форме закон Ома для неоднородного
участка цепи.
,
следовательно, плотность тока в этих
участках оказывается пропорциональной
сумме напряженностей. Учет этого приводит
к дифференциальной
форме закон Ома для неоднородного
участка цепи.
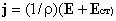 .
.
При прохождении электрического тока в замкнутой цепи на свободные заряды действуют силы со стороны стационарного электрического поля и сторонние силы. При этом на отдельных участках этой цепи ток создается только стационарным электрическим полем. Такие участки цепи называются однородными. На некоторых участках этой цепи, кроме сил стационарного электрического поля, действуют и сторонние силы. Участок цепи, на котором действуют сторонние силы, называют неоднородным участком цепи.
Для того чтобы выяснить, от чего зависит сила тока на этих участках, необходимо уточнить понятие напряжения.

Рис. 1
Рассмотрим вначале однородный участок цепи (рис. 1, а). В этом случае работу по перемещению заряда совершают только силы стационарного электрического поля, и этот участок характеризуют разностью потенциалов Δφ. Разность потенциалов на концах участка Δφ=φ1−φ2=AKq, где AK — работа сил стационарного электрического поля. Неоднородный участок цепи (рис. 1, б) содержит в отличие от однородного участка источник ЭДС, и к работе сил электростатического поля на этом участке добавляется работа сторонних сил. По определению, Aelq=φ1−φ2, где q — положительный заряд, который перемещается между любыми двумя точками цепи; φ1−φ2 — разность потенциалов точек в начале и конце рассматриваемого участка; Astq=ε. Тогда говорят о напряжении для напряженности: Eстац. э. п. = Eэ/стат. п. + Eстор. Напряжение U на участке цепи представляет собой физическую скалярную величину, равную суммарной работе сторонних сил и сил электростатического поля по перемещению единичного положительного заряда на этом участке:
U=AKq+Astorq=φ1−φ2+ε.
Из этой формулы видно, что в общем случае напряжение на данном участке цепи равно алгебраической сумме разности потенциалов и ЭДС на этом участке. Если же на участке действуют только электрические силы (ε = 0), то U=φ1−φ2. Таким образом, только для однородного участка цепи понятия напряжения и разности потенциалов совпадают.
Закон Ома для неоднородного участка цепи имеет вид:
I=UR=φ1−φ2+εR,
где R — общее сопротивление неоднородного участка.
ЭДС ε может быть как положительной, так и отрицательной. Это связано с полярностью включения ЭДС в участок: если направление, создаваемое источником тока, совпадает с направлением тока, проходящего в участке (направление тока на участке совпадает внутри источника с направлением от отрицательного полюса к положительному), т.е. ЭДС способствует движению положительных зарядов в данном направлении, то ε > 0, в противном случае, если ЭДС препятствует движению положительных зарядов в данном направлении, то ε < 0.
Закон Ома для неоднородного участка цепи. Закон Ома для замкнутого контура.
Вернёмся ещё раз к рис. 7.1. Здесь изображена
замкнутая проводящая цепь. На участке
цепи 1-а-2 движение носителей заряда
происходит под действием только
электростатической силы =q
=q .
Такие участки называютсяоднородными.
.
Такие участки называютсяоднородными.
Совсем по-другому обстоят дела на участке
контура 2-b-1. Здесь на
заряды действует не только электростатическая,
но и сторонняя сила. Полную силу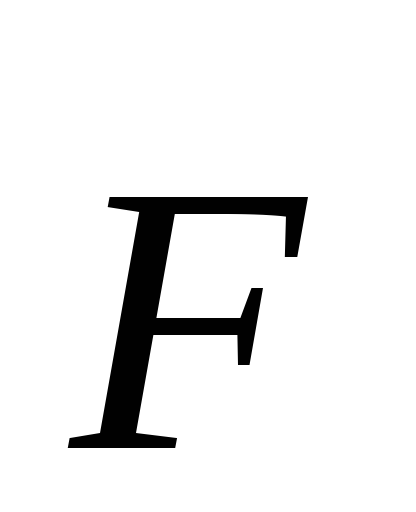 найдем, сложив эти две:
найдем, сложив эти две:
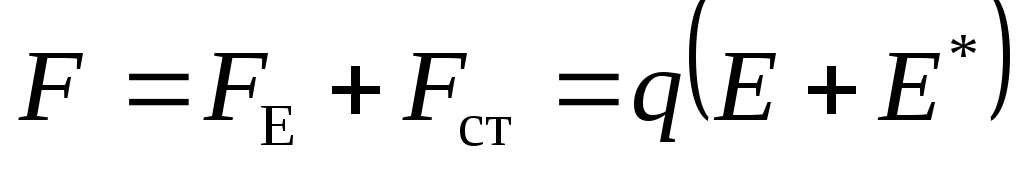 .
.
Участок замкнутого контура, где наряду с электростатической силой действуют и сторонние силы, называют неоднородным.
Можно показать, что на однородном участке
цепи средняя скорость направленного
движения носителей заряда пропорциональна
действующей на них силе. Для этого
достаточно сравнить формулы, полученные
на прошлой лекции:  =
= (6.3) и
(6.3) и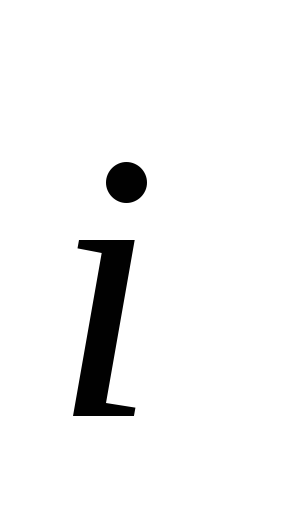 =
= (6.13).
(6.13).
Пропорциональность скорости силе, а
плотности тока — напряжённости сохранится
и в случае неоднородного участка цепи.
Но теперь напряжённость поля равна
сумме напряжённостей электростатического
поля  и поля сторонних сил
и поля сторонних сил :
:
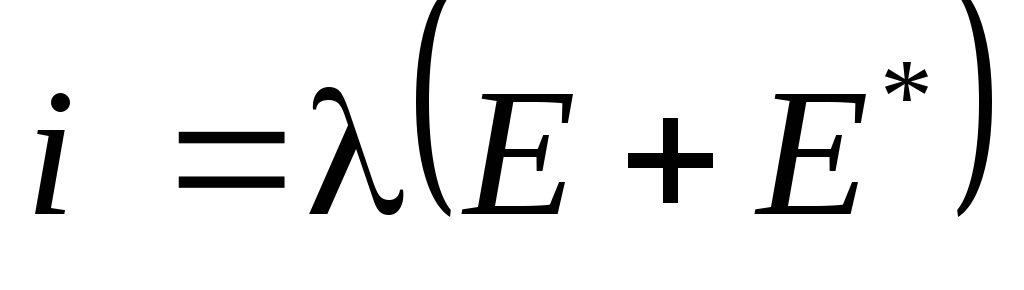 . (7.5)
. (7.5)
Это уравнение закона Ома в локальной дифференциальной форме для неоднородногоучастка цепи.
Теперь перейдём к закону Ома для неоднородного участка цепи в интегральной форме.
Выделим двумя близкими сечениями Sучастокdlтрубки тока (рис. 7.3.). Сопротивление этого участка:
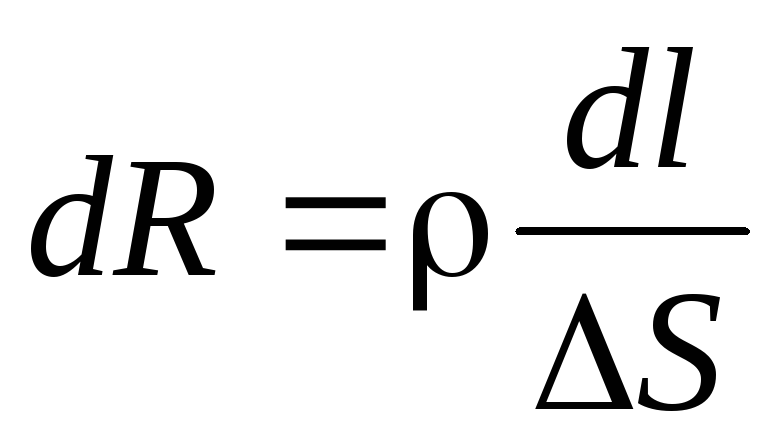 ,
,
а плотность тока можно связать с силой тока:
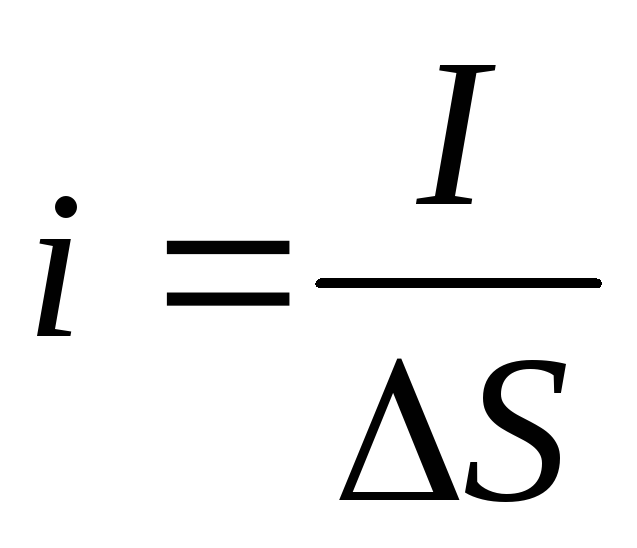 .
.

Рис. 7.3.
Эти два выражения используем в уравнении (7.5), спроецировав его предварительно на линию тока:
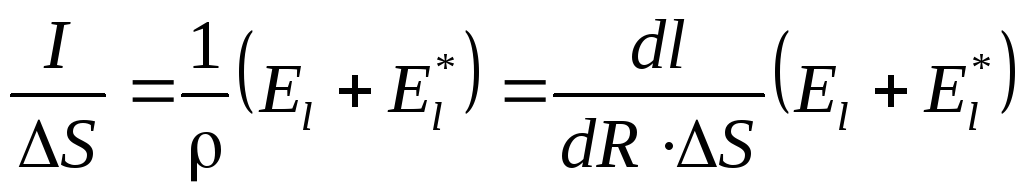
Проинтегрировав последнее уравнение по неоднородному участку 1-2, получим:
 .
.
Произведение IR1-2=U— напряжение на участке 1-2;
первый интеграл справа 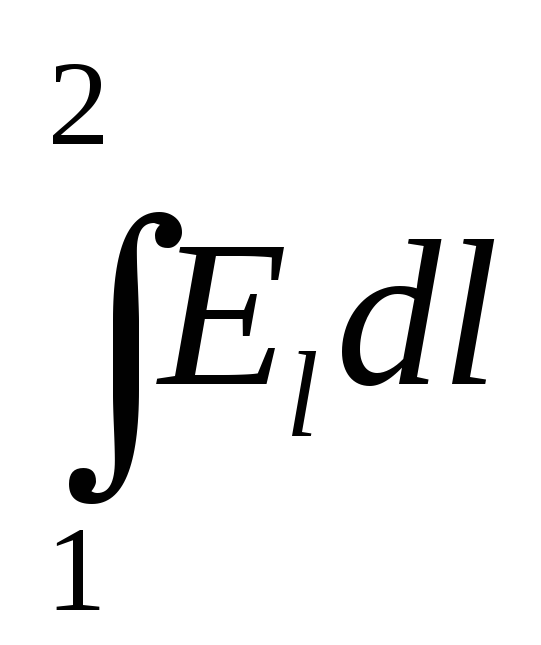 =
=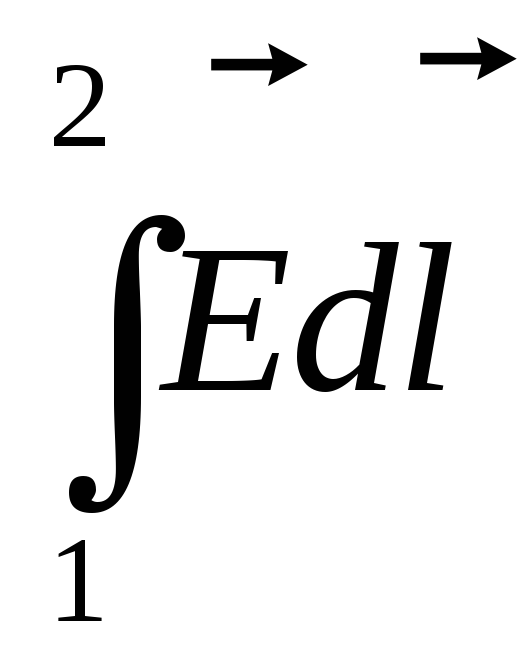 =1–2— разность потенциалов на концах
участка;
=1–2— разность потенциалов на концах
участка;
второй интеграл 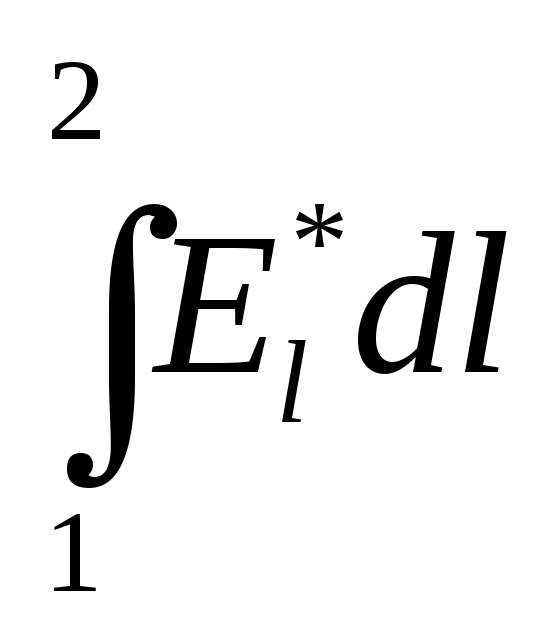 =
=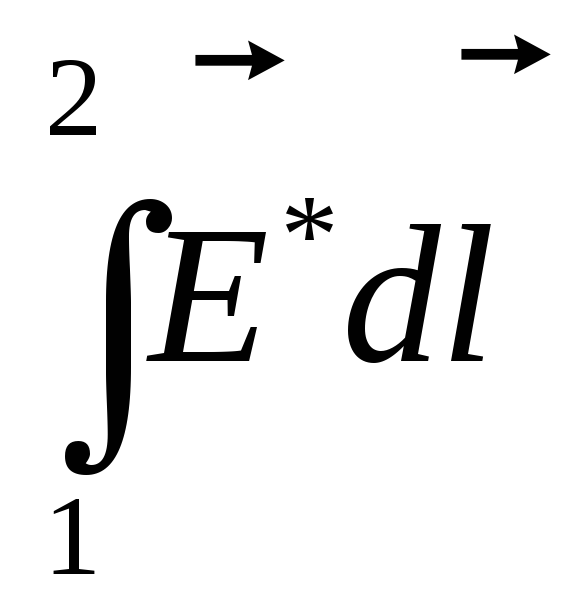 =1-2— э.д.с.
источника тока.
=1-2— э.д.с.
источника тока.
Учтя всё это, конечный результат запишем в виде:
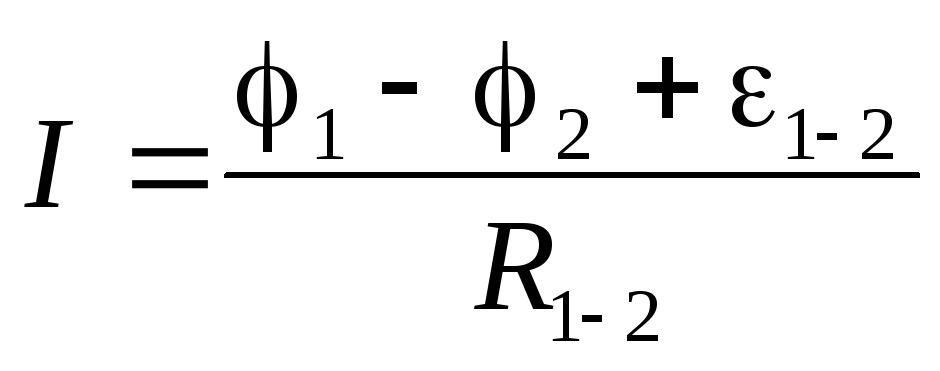 . (7.6)
. (7.6)
Это закон Ома для неоднородного участка цепи в интегральной форме. Обратите внимание, что напряжение на неоднородном участке цепиUне совпадает с разностью потенциалов на его концах (1–2):
IR1-2=U1-2= (1–2) +1-2. (7.7)
Эти две величины равны только в случае однородного участка, где источники тока отсутствуют и 1-2= 0. Тогда:
U1-2=1–2.
Для замкнутого контура уравнение закона Ома (7.6) несколько видоизменяется, так как разность потенциалов в этом случае равна нулю:
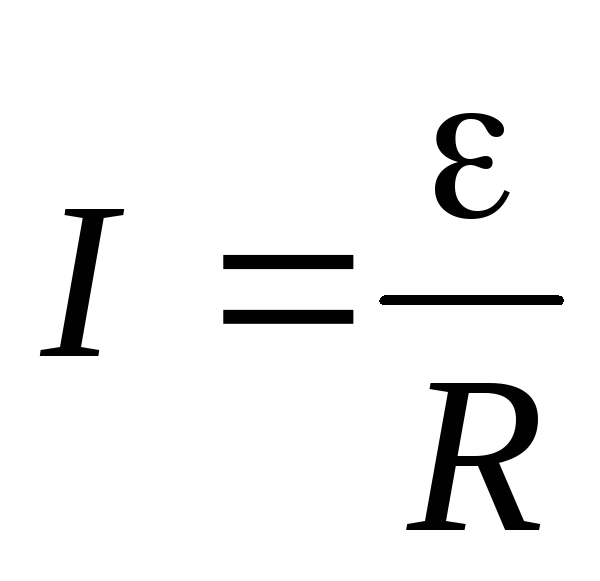 . (7.8)
. (7.8)
В законе Ома для замкнутой цепи (7.8) R — полное сопротивление контура, складывающееся из внешнего сопротивления цепи R0 и внутреннего сопротивления источника r:
R=R0+r.
Правила Кирхгофа
Рассмотренные нами законы постоянного тока позволяют рассчитать токи в сложных разветвлённых электрических цепях. Эти расчёты упрощаются, если пользоваться правилами Кирхгофа.
Правил Кирхгофа два: правило токовиправило напряжений.
Правило токов относится к узлам цепи, то есть, к таким точкам схемы, где сходятся не менее трёх проводников (рис. 7.4.). Правило токов гласит: алгебраическая сумма токов в узле равняется нулю:
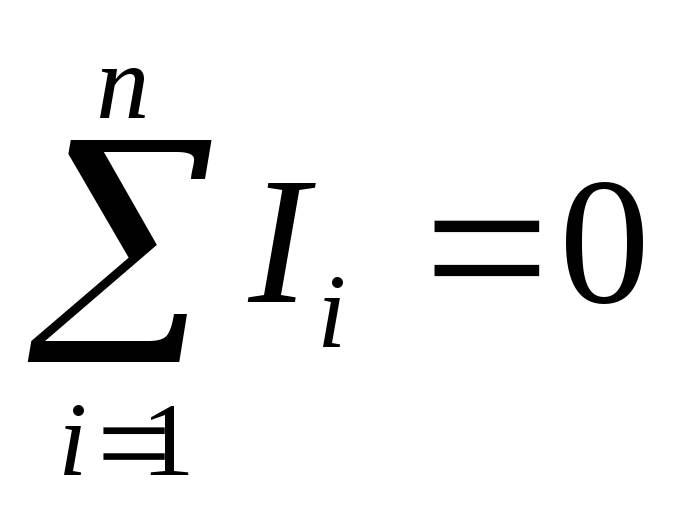 . (7.9)
. (7.9)

Рис. 7.4.
При составлении соответствующего уравнения, токи, втекающие в узел, берутся со знаком плюс, а покидающие его — со знаком минус. Так, для узла А(рис. 7.3.) можно записать:
I1–I2–I3+I4–I5= 0.
Это первое правило Кирхгофа является следствием уравнения непрерывности (см. (6.7)) или закона сохранения электрического заряда.
Правило напряженийотносится к любому замкнутому контуру разветвлённой цепи.
Выделим, например, в разветвлённой сложной цепи замкнутый элемент 1-2-3-1 (рис. 7.5.). Произвольно обозначим в ветвях контура направления токов I1,I2,I3. Для каждой ветви запишем уравнение закона Ома для неоднородного участка цепи:
Участок 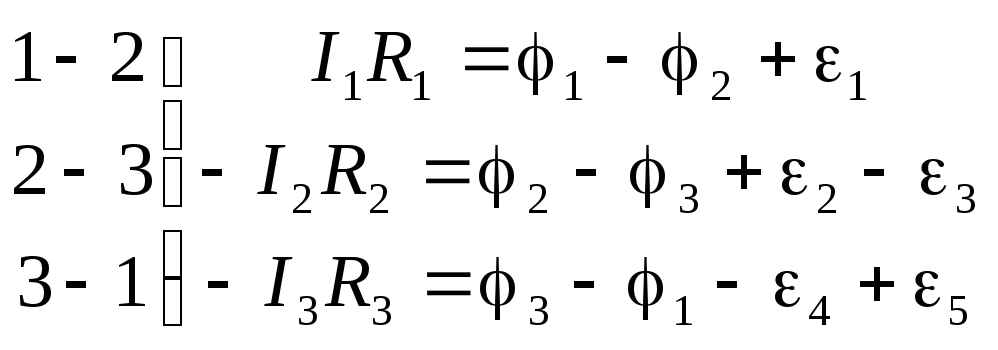 .
.
Здесь R1,R2,R3—полноесопротивление соответствующих ветвей. Сложив эти уравнения, получим формулу второго правила Кирхгофа:
I1R1–I2R2–I3R3=1+2–3–4+5.
Правило напряжений формулируется так: в любом замкнутом контуре алгебраическая сумма падений напряжения равна алгебраической сумме э.д.с., встречающихся в этом контуре:
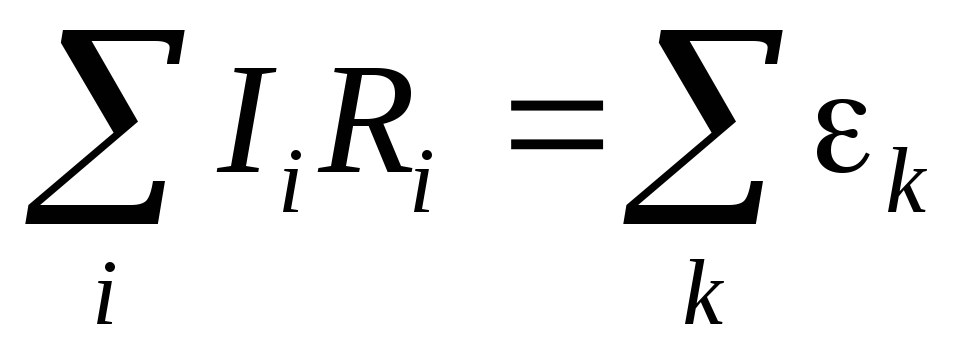 . (7.10)
. (7.10)

Рис. 7.5.
При составлении уравнения (7.10) второго правила Кирхгофа задаются направлением обхода: в нашем примере — по часовой стрелке. Токи, совпадающие с направлением обхода, берутся со знаком плюс (I1), токи противоположного направления — со знаком минус (–I2, –I3).
Э.д.с. источника берётся со знаком плюс, если он создаёт ток, совпадающий с направлением обхода (+1, +2, +5). В противном случае э.д.с. отрицательна (–3, –4).
В качестве примера составим уравнения правил Кирхгофа для конкретной электрической схемы — измерительного моста Уитстона (рис. 7.6.). Мост образуют четыре резистора R1,R2,R3,R4. В точкахAиBк мосту подключен источник питания (,r), а в диагоналиBD — измерительный гальванометр с сопротивлениемRg.
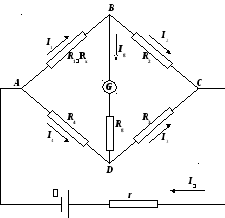
Рис. 7.6.
Во всех ветвях схемы произвольнообозначим направления токовI1,I2, I3, I4, Ig, I.
В схеме четыре узла: точки A,B,C,D. Для трёх из них составим уравнения первого правила Кирхгофа — правила токов:
точка А: I – I1 – I4 = 0; (1)
точка B: I1 – I2 – Ig = 0; (2)
точка D: I4 + Ig – I3 = 0. (3)
Для трёх контуров цепи ABDA,BCDBиADCAсоставим уравнения второго правила Кирхгофа. Во всех контурах направление обхода по часовой стрелке.
ABDA: I1R1 + IgRg – I4R4 = 0; (4)
BCDB: I2R2 – I3R3 – IgRg = 0; (5)
ADCA: I4R4 + I3R3 + Ir = . (6)
Таким образом, мы получили систему шести уравнений, решая которую можно найти все шесть неизвестных токов.
Но чаще мост Уитстона используется для измерения неизвестного сопротивления RxR1. В этом случае резисторыR2,R3иR4— переменные. Меняя их сопротивления, добиваются того, чтобы ток в измерительной диагонали моста оказался равным нулюIg= 0. Это означает, что:
I1=I2см. (1),
I3=I4см.(3),
I1R1 = I4R4 см. (4),
I2R2 = I3R3 см. (5).
Учитывая эти упрощающие обстоятельства, приходим к выводу, что:
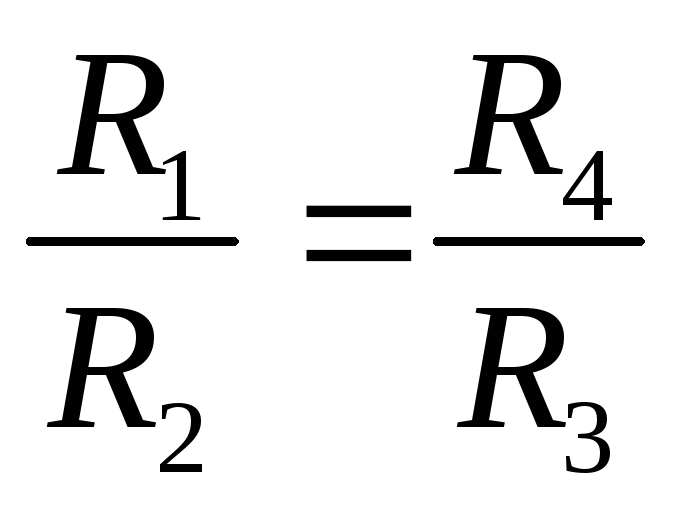 ,
,
или:
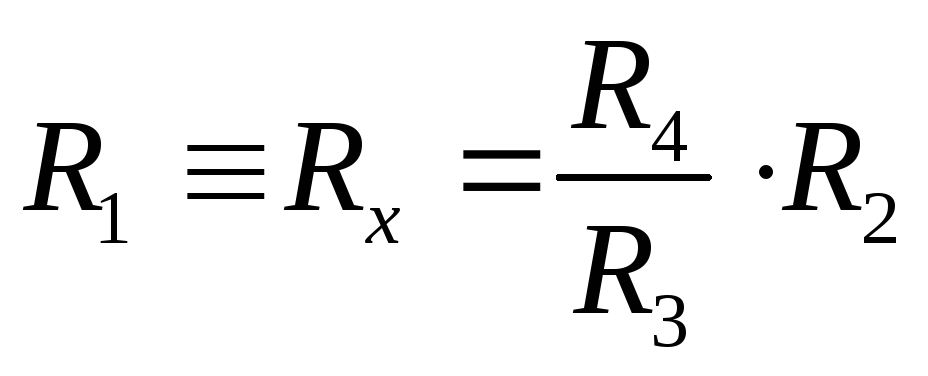 .
.
Замечательно, что для определения неизвестного сопротивления нужно знать лишь сопротивления резисторов моста R2,R3иR4. Э.д.с. источника, его внутреннее сопротивление, как и сопротивление гальванометра при таком измерении не играют никакой роли.
4.5. Закон Ома для неоднородного участка цепи. Электродвижущая сила
Для того, чтобы электрический ток существовал длительное время необходимо наличие замкнутой цепи, свободных носителей зарядов частиц и сторонних сил. В проводнике заряженные частицы движутся под действием кулоновских сил в направлении от точки с большим потенциалом 1 к точке с меньшим потенциалом 2. Сторонние силы (силы не электростатического происхождения) непрерывно отводят заряды от конца проводника с меньшим потенциалом, и подводят их к концу с большим потенциалом (рис.4.6).
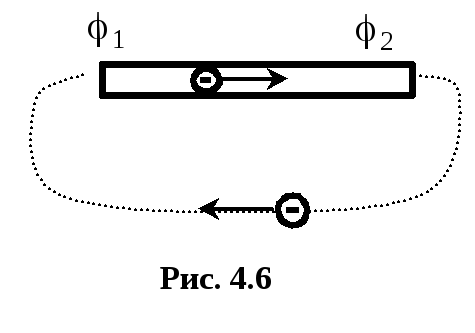
Рассмотрим
участок 1–2 цепи
(рис.4.7), на котором действуют кулоновские
и сторонние силы, поля которых
характеризуется напряженностями 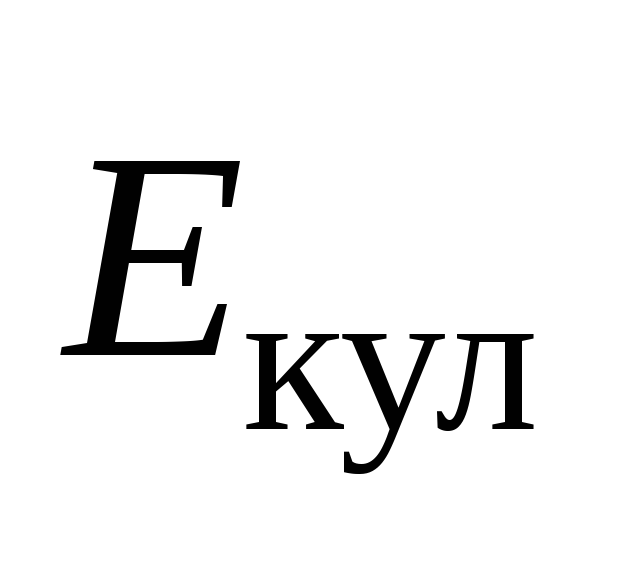 и
и .
Напряженность результирующего поля,
.
Напряженность результирующего поля,
 .
(4.17)
.
(4.17)
Выделим бесконечно малый элемент проводника dl и запишем с учетом (4.17) закон Ома в дифференциальной форме:
. (4.18)
Умножив
левую и правую часть выражения (4.18) на 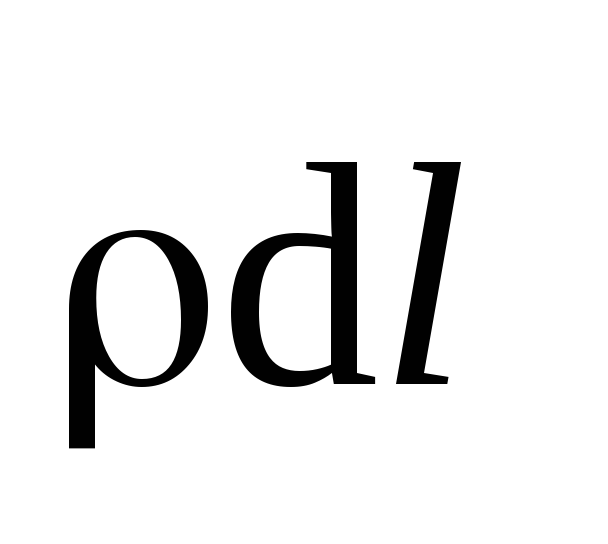 ,
получаем:
,
получаем:
 .
(4.19)
.
(4.19)
Учтем, что все векторы в выражении (4.19) коллинеарны, поскольку являются касательными к линиям тока, а модуль плотности тока j = I /S, где I – сила тока в проводнике; S – площадь поперечного сечения проводника. Тогда выражение (4.19) можно переписать в виде
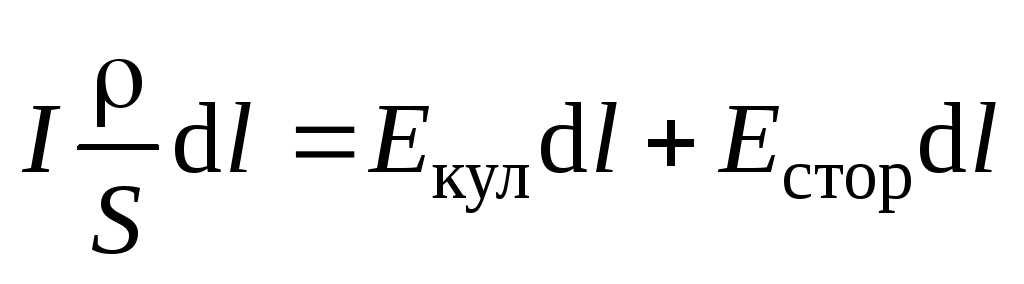 .
(4.20)
.
(4.20)
Проинтегрируем выражение (4.20) по длине участка проводника от сечения 1 до сечения 2 с учетом того, что сила тока в каждом сечении проводника одинакова:
 .
(4.21)
.
(4.21)
Рассмотрим подробнее физический смысл всех слагаемых, входящих в выражение (4.21). Первое численно равно удельной работе кулоновских сил по перемещению заряда из точки 1 в точку 2, т.е. разности потенциалов между этими точками:
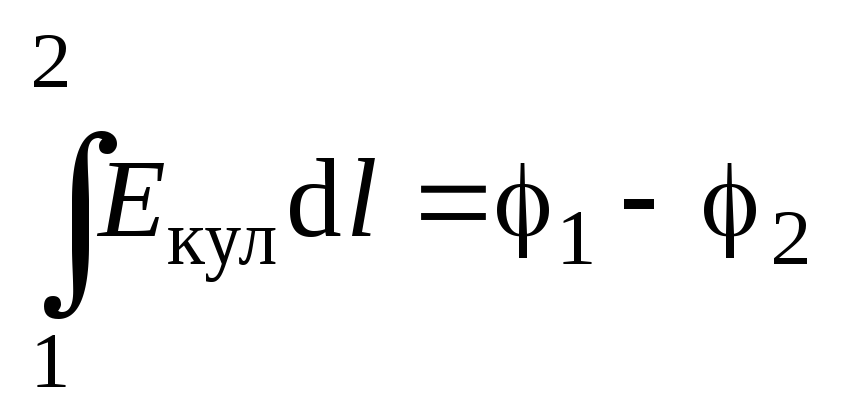 .
(4.22)
.
(4.22)
Второе слагаемое называется электродвижущей силой (ЭДС) Е12, действующей на участке цепи 1–2.
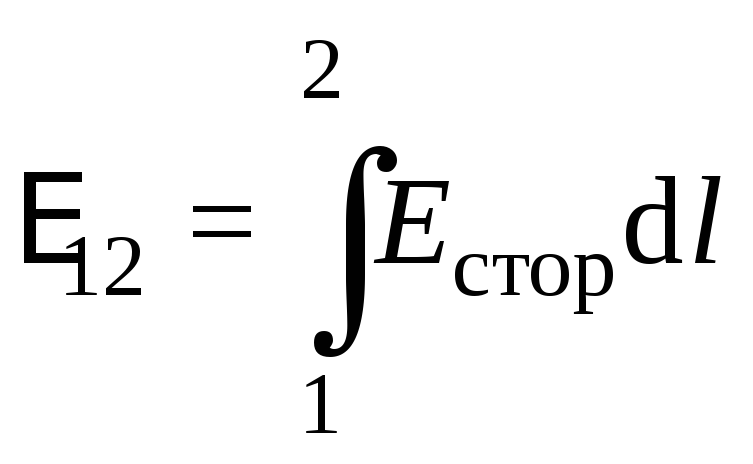 .
(4.23)
.
(4.23)
Электродвижущая сила численно равна удельной работе сторонних сил по перемещению заряда из точки 1 в точку 2. Эта работа производится за счет источника энергии. Поэтому величину Е12 можно назвать электродвижущей силой источника энергии, включенного на участке цепи 1–2.
Напряжением (падением
напряжения) на участке цепи 1–2 называется физическая величина 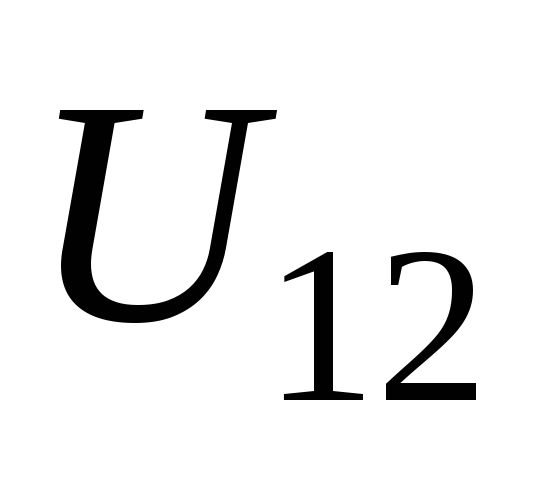 ,
численно равная удельной работе,
совершаемой суммарным полем кулоновских
и сторонних сил при перемещении заряда
из точки1 в
точку 2:
,
численно равная удельной работе,
совершаемой суммарным полем кулоновских
и сторонних сил при перемещении заряда
из точки1 в
точку 2:
, (4.24)
или
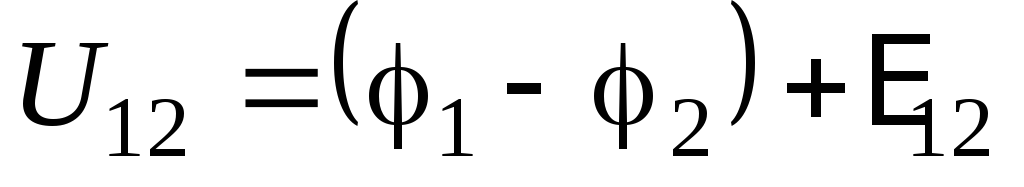 .
(4.25)
.
(4.25)
Введенное нами понятие напряжения не совпадает с тем, которым часто пользуются в электростатике для обозначения разности потенциалов, а является его обобщением. Напряжение на участке цепи равно разности потенциалов только в том случае, если на этом участке не приложены сторонние силы.
Интеграл
 (4.26)
(4.26)
называется сопротивлением участка цепи между сечениями 1 и 2.
С учетом (4.25) и (4.26) выражение (4.21) можно записать так:
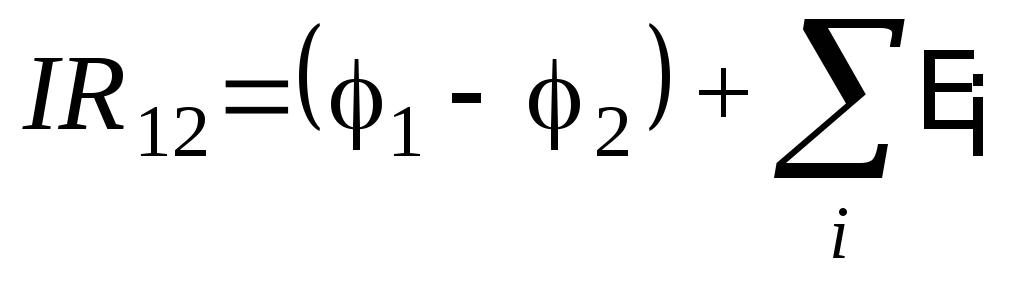 .
(4.27)
.
(4.27)
Это выражение является математической записью обобщенного закона Ома для участка цепи: произведение сопротивления участка цепи на силу тока в нем равно сумме разности потенциалов на этом участке и ЭДС всех источников, включенных на участке.
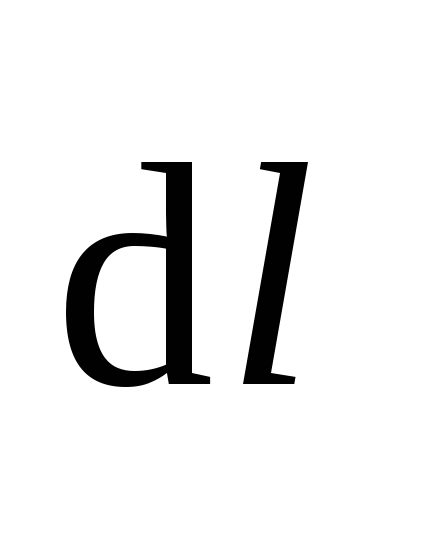 совпадал
с вектором плотности тока
совпадал
с вектором плотности тока ).
Поэтому при определении
).
Поэтому при определении и
ЭДС Ei нужно пользоваться следующим правилом
знаков. Падение напряжения
и
ЭДС Ei нужно пользоваться следующим правилом
знаков. Падение напряжения  считается
положительным, если направление тока
соответствует направлению обхода
участка цепи от точки1 к точке 2.
В противном случае падение напряжения
считается
положительным, если направление тока
соответствует направлению обхода
участка цепи от точки1 к точке 2.
В противном случае падение напряжения  считается
отрицательным. ЭДС Ei считаются положительными, если направление
обхода участка цепи от точки 1 к точке 2 соответствует
перемещению внутри источника Еi от
полюса “–“ к полюсу “+“. В противном
случае Еi следует считать отрицательными.
считается
отрицательным. ЭДС Ei считаются положительными, если направление
обхода участка цепи от точки 1 к точке 2 соответствует
перемещению внутри источника Еi от
полюса “–“ к полюсу “+“. В противном
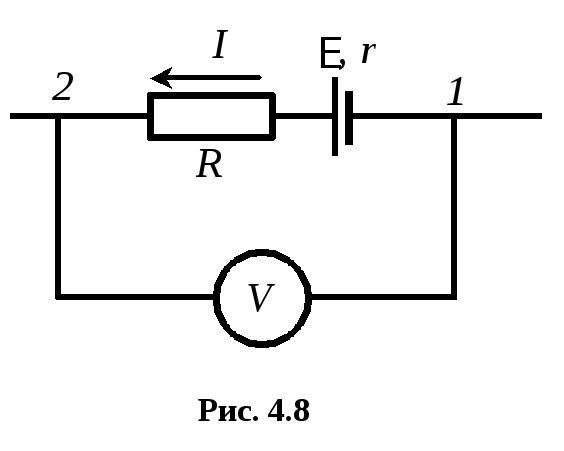
случае Еi следует считать отрицательными.Применим обобщенный закон Ома к участку цепи, изображенному на рис. 4.8. Выберем условно положительное направление тока, как показано на рисунке, и направление обхода от точки 1 к точке 2. Тогда для участка цепи 1 – Е – R – 2 получим
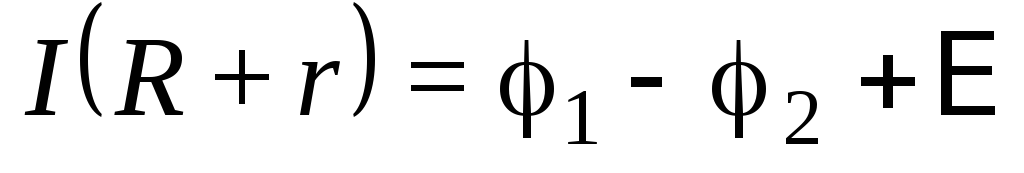 ,
(4.28)
,
(4.28)
где r внутреннее сопротивление источника тока.
Применяя обобщенный закон Ома к участку 1–V–2 (обход через вольтметр), получаем
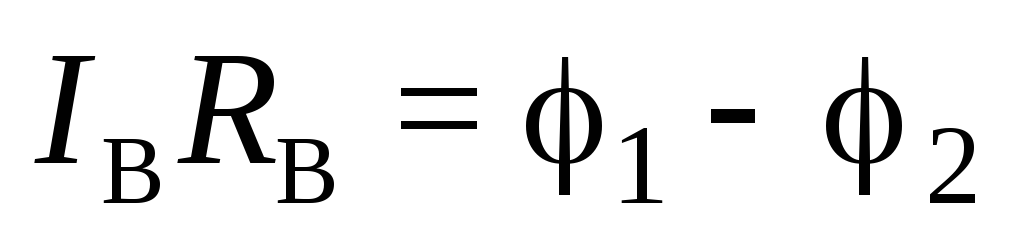 ,
(4.29)
,
(4.29)
где IВ ток, проходящий через вольтметр; RВ сопротивление вольтметра.
Произведение IВ RВ это показания вольтметра. Следовательно, вольтметр показывает разность потенциалов между точками подключения.


 —
является мощностью тепла, выделяемого
в единице объёма;
—
является мощностью тепла, выделяемого
в единице объёма;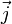 —
плотность электрического тока;
—
плотность электрического тока;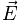 —
это напряжённость электрического поля;
—
это напряжённость электрического поля;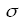 —
проводимость выбранной среды.
—
проводимость выбранной среды.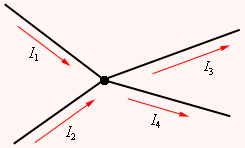

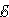 1 +
1 + 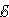 2 = –
2 = –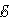 1 –
1 –  2.
2.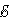 2 +
2 +  3.
3. 1 –
1 –  2,
2, 2 +
2 +  3,
3,