Закон Ома для неоднородного участка цепи
Один из основных законов электродинамики был открыт в 1826 г. немецким учителем физики Георгом Омом. Он установил, что сила тока в проводнике пропорциональна разности потенциалов:
.
| Георг Симон Ом (1787 – 1854) – немецкий физик. В 1826 г. Ом открыл свой основной закон электрической цепи. Этот закон не сразу нашел признание в науке, а лишь после того, как Э. X. Ленц, Б. С. Якоби, К. Гаусс, Г. Кирхгоф и другие ученые положили его в основу своих исследований. В 1881 г. на Международном конгрессе электриков именем Ома была названа единица электрического сопротивления (Ом). Последние годы своей жизни Ом посвятил исследованиям в области акустики. Акустический закон Ома был положен затем немецким ученым Г. Гельмгольцем в основу резонансной теории слуха. Ом вел также исследования и в области оптики и кристаллооптики. |
Рассмотрим неоднородный участок цепи, участок, содержащий источник ЭДС (т.е. участок, где действуют неэлектрические силы). Напряженность поля в любой точке цепи равна векторной сумме поля кулоновских сил и поля сторонних сил, т.е.
Величина, численно равная работе по переносу единичного положительного заряда суммарным полем кулоновских и сторонних сил на участке цепи (1 – 2), называется напряжением на этом участке U12(рис. 7.4).
| . | (7.5.1) |
т.к. , или , тогда
| (7.5.2) |
Напряжение на концах участка цепи совпадает с разностью потенциалов только в случае, если на этом участке нет ЭДС, т.е. на однородном участке цепи. Запишем обобщенный закон Ома для участка цепи содержащей источник ЭДС:
| (7.5.3) |
В электротехнике часто используют термин падение напряжения – изменение напряжения вследствие переноса заряда через сопротивление
| (7.5.4) |
В замкнутой цепи: ;
или
где ; r – внутреннее сопротивление активного участка цепи (рис. 7.5).
Тогда закон Ома для замкнутого участка цепи, содержащего источник ЭДС запишется в виде
| (7.5.5) |
Рис. 7.5
[Физика зачет 33] Электродвижущая сила. Закон Ома для замкнутой цепи и неоднородного участка цепи. Правила Кихгофа. Работа и мощность тока. Тепловое действие тока. Закон Джоуля-Ленца.
Электродвижущая сила.| ЭДС — энергетическая характеристика источника. Это физическая величина, равная отношению работы, совершенной сторонними силами при перемещении электрического заряда по замкнутой цепи, к этому заряду: Измеряется в вольтах (В). |
Закон Ома для замкнутой цепи и неоднородного участка цепи.
Закон ома для замкнутой цепи говорит о том что. Величина тока в замкнутой цепи, которая состоит из источника тока обладающего внутренним сопротивлением, а также внешним нагрузочным сопротивлением. Будет равна отношению электродвижущей силы источника к сумме внешнего и внутреннего сопротивлений.
При прохождении электрического тока в замкнутой цепи на свободные заряды действуют силы со стороны стационарного электрического поля и сторонние силы. При этом на отдельных участках этой цепи ток создается только стационарным электрическим полем. Такие участки цепи называются однородными. На некоторых участках этой цепи, кроме сил стационарного электрического поля, действуют и сторонние силы. Участок цепи, на котором действуют сторонние силы, называют неоднородным участком цепи.
Для того чтобы выяснить, от чего зависит сила тока на этих участках, необходимо уточнить понятие напряжения.
Рис. 1 Рассмотрим вначале однородный участок цепи (рис. 1, а). В этом случае работу по перемещению заряда совершают только силы стационарного электрического поля, и этот участок характеризуют разностью потенциалов Δφ. Разность потенциалов на концах участка , где AK — работа сил стационарного электрического поля. Неоднородный участок цепи (рис. 1, б) содержит в отличие от однородного участка источник ЭДС, и к работе сил электростатического поля на этом участке добавляется работа сторонних сил. По определению, , где q — положительный заряд, который перемещается между любыми двумя точками цепи; — разность потенциалов точек в начале и конце рассматриваемого участка; . Тогда говорят о напряжении для напряженности: Eстац. э. п. = Eэ/стат. п. + Eстор. Напряжение U на участке цепи представляет собой физическую скалярную величину, равную суммарной работе сторонних сил и сил электростатического поля по перемещению единичного положительного заряда на этом участке:
Из этой формулы видно, что в общем случае напряжение на данном участке цепи равно алгебраической сумме разности потенциалов и ЭДС на этом участке. Если же на участке действуют только электрические силы (ε = 0), то . Таким образом, только для однородного участка цепи понятия напряжения и разности потенциалов совпадают.
Закон Ома для неоднородного участка цепи имеет вид:
где R — общее сопротивление неоднородного участка.
ЭДС ε может быть как положительной, так и отрицательной. Это связано с полярностью включения ЭДС в участок: если направление, создаваемое источником тока, совпадает с направлением тока, проходящего в участке (направление тока на участке совпадает внутри источника с направлением от отрицательного полюса к положительному), т.е. ЭДС способствует движению положительных зарядов в данном направлении, то ε > 0, в противном случае, если ЭДС препятствует движению положительных зарядов в данном направлении, то ε < 0.
Правила Кихгофа.
Работа и мощность тока. Тепловое действие тока. Закон Джоуля-Ленца.
При протекании тока по однородному участку цепи электрическое поле совершает работу. За время Δt по цепи протекает заряд Δq = I Δt. Электрическое поле на выделенном учестке совершает работу
| ΔA = (φ1 – φ2) Δq = Δφ12 I Δt = U I Δt, |
Если обе части формулы
| R I2 Δt = U I Δt = ΔA. |
Это соотношение выражает закон сохранения энергии для однородного участка цепи.
Работа ΔA электрического тока I, протекающего по неподвижному проводнику с сопротивлением R, преобразуется в тепло ΔQ, выделяющееся на проводнике.
Мощность электрического тока равна отношению работы тока ΔA к интервалу времени Δt, за которое эта работа была совершена:
| (R + r) I = . |
Умножив обе части этой формулы на Δq = IΔt, мы получим соотношение, выражающее закон сохранения энергии для полной цепи постоянного тока:
| R I2Δt + r I2Δt = IΔt = ΔAст. |
Первый член в левой части ΔQ = R I2Δt – тепло, выделяющееся на внешнем участке цепи за время Δt, второй член ΔQ
При протекании электрического тока по замкнутой цепи работа сторонних сил ΔAст преобразуется в тепло, выделяющееся во внешней цепи (ΔQ) и внутри источника (ΔQист).
|
Следует обратить внимание, что в это соотношение не входит работа электрического поля. При протекании тока по замкнутой цепи электрическое поле работы не совершает; поэтому тепло производится одними только сторонними силами, действующими внутри источника. Роль электрического поля сводится к перераспределению тепла между различными участками цепи.
Внешняя цепь может представлять собой не только проводник с сопротивлением R, но и какое-либо устройство, потребляющее мощность, например, электродвигатель постоянного тока. В этом случае под R нужно понимать эквивалентное сопротивление нагрузки. Энергия, выделяемая во внешней цепи, может частично или полностью преобразовываться не только в тепло, но и в другие виды энергии, например, в механическую работу, совершаемую электродвигателем. Поэтому вопрос об использовании энергии источника тока имеет большое практическое значение.Полная мощность источника, то есть работа, совершаемая сторонними силами за единицу времени, равна
Во внешней цепи выделяется мощность
| Рисунок 1.11.1. Зависимость мощности источника Pист, мощности во внешней цепи P и КПД источника η от силы тока |
Из приведенных графиков видно, что максимальная мощность во внешней цепи Pmax, равная
достигается при R = r. При этом ток в цепи
а КПД источника равен 50 %. Максимальное значение КПД источника достигается при I → 0, т. е. при R → ∞. В случае короткого замыкания полезная мощность P = 0 и вся мощность выделяется внутри источника, что может привести к его перегреву и разрушению. КПД источника при этом обращается в нуль.
Репетитор-онлайн — подготовка к ЦТ
Пример 11. Шесть одинаковых резисторов по 20 Ом каждый и два конденсатора с электроемкостями 15 и 25 мкФ соединены в цепь так, как показано на рисунке. К концам участка подключают источник с ЭДС, равной 0,23 кВ, и внутренним сопротивлением 3,5 Ом. Найти разность потенциалов между обкладками второго конденсатора.
Решение. Между точками A и Б ток не протекает, так как между этими точками в схему включены конденсаторы. Для определения разности потенциалов между указанными точками упростим схему, исключив из рассмотрения участок АБ.
На рис. а показана схема упрощенной цепи.
Ток течет через резисторы R 1, R 2, R 3, R 4 и R 6, соединенные последовательно. Общее сопротивление такой цепи:
R общ = R 1 + R 2 + R 3 + R 4 + R 6 = 5R,
где R 1 = R 2 = R 3 = R 4 = R 6 = R.
Сила тока I определяется законом Ома для полной цепи:
I=ℰRобщ+r=ℰ5R+r,
где ℰ — ЭДС источника тока, ℰ = 0,23 кВ; r — внутреннее сопротивление источника тока, r = 3,5 Ом; R общ — общее сопротивление цепи, R общ = 5R.
Рассчитаем падение напряжения между точками А и Б.
Между точками А и Б находятся резисторы сопротивлениями R 2, R 3 и R 4, соединенные между собой последовательно, как показано на рис. б.
Их общее сопротивление
R общ1 = R 2 + R 3 + R 4 = 3R.
Падение напряжения на указанных резисторах определяется формулой
U АБ = IR общ1,
или в явном виде, —
UАБ=3ℰR5R+r.
Между точками А и Б включена батарея конденсаторов C 1 и C 2, соединенных между собой последовательно, как показано на рис. в.
Их общая электроемкость
Cобщ=C1C2C1+C2,
где C 1 — электроемкость первого конденсатора, C 1 = 15 мкФ; C 2 — электроемкость второго конденсатора, C 2 = 25 мкФ.
Разность потенциалов на обкладках батареи:
Uобщ=qCобщ,
где q — заряд на обкладках каждого из конденсаторов (совпадает с зарядом батареи при последовательном соединении конденсаторов), q = = C 1U 1 = C 2U 2; U 1 — разность потенциалов между обкладками первого конденсатора; U 2 — разность потенциалов между обкладками второго конденсатора (искомая величина).
В явном виде разность потенциалов между обкладками конденсаторов определяется формулой
Uобщ=C2U2Cобщ=(C1+C2)U2C1.
Падение напряжения на резисторах между точками А и Б совпадает с разностью потенциалов на батарее конденсаторов, подключенной к указанным точкам:
U АБ = U общ.
Данное равенство, записанное в явном виде
3ℰR5R+r=(C1+C2)U2C1,
позволяет получить выражение для искомой величины:
U2=3ℰRC1(5R+r)(C1+C2).
Произведем вычисление:
U2=3⋅0,23⋅103⋅20⋅15⋅10−6(5⋅20+3,5)(15+25)⋅10−6=50 В.
Между обкладками второго конденсатора разность потенциалов составляет 50 В.
| Сила тока в замкнутой цепи, состоящей из источника тока с внутренним сопротивление и нагрузки с сопротивлением, равна отношению величины ЭДС источника к сумме внутреннего сопротивления источника и сопротивления нагрузки. |
A. Закон Ома для участка-2 — PhysBook
Закон Ома для неоднородного участка цепи
При прохождении электрического тока в замкнутой цепи на свободные заряды действуют силы со стороны стационарного электрического поля и сторонние силы. При этом на отдельных участках этой цепи ток создается только стационарным электрическим полем. Такие участки цепи называются однородными. На некоторых участках этой цепи, кроме сил стационарного электрического поля, действуют и сторонние силы. Участок цепи, на котором действуют сторонние силы, называют неоднородным участком цепи.
Для того чтобы выяснить, от чего зависит сила тока на этих участках, необходимо уточнить понятие напряжения.
Рис. 1
Рассмотрим вначале однородный участок цепи (рис. 1, а). В этом случае работу по перемещению заряда совершают только силы стационарного электрического поля, и этот участок характеризуют разностью потенциалов Δφ. Разность потенциалов на концах участка \(~\Delta \varphi = \varphi_1 — \varphi_2 = \frac{A_K}{q}\), где AK — работа сил стационарного электрического поля. Неоднородный участок цепи (рис. 1, б) содержит в отличие от однородного участка источник ЭДС, и к работе сил электростатического поля на этом участке добавляется работа сторонних сил. По определению, \(~\frac{A_{el}}{q} = \varphi_1 — \varphi_2\), где q — положительный заряд, который перемещается между любыми двумя точками цепи; \(~\varphi_1 — \varphi_2\) — разность потенциалов точек в начале и конце рассматриваемого участка; \(~\frac{A_{st}}{q} = \varepsilon\). Тогда говорят о напряжении для напряженности: Eстац. э. п. = Eэ/стат. п. + Eстор. Напряжение U на участке цепи представляет собой физическую скалярную величину, равную суммарной работе сторонних сил и сил электростатического поля по перемещению единичного положительного заряда на этом участке:
\(~U = \frac{A_K}{q} + \frac{A_{stor}}{q} = \varphi_1 — \varphi_2 + \varepsilon .\)Из этой формулы видно, что в общем случае напряжение на данном участке цепи равно алгебраической сумме разности потенциалов и ЭДС на этом участке. Если же на участке действуют только электрические силы (ε = 0), то \(~U = \varphi_1 — \varphi_2\). Таким образом, только для однородного участка цепи понятия напряжения и разности потенциалов совпадают.
Закон Ома для неоднородного участка цепи имеет вид:
\(~I = \frac UR = \frac{\varphi_1 — \varphi_2 + \varepsilon}{R} ,\)где R — общее сопротивление неоднородного участка.
ЭДС ε может быть как положительной, так и отрицательной. Это связано с полярностью включения ЭДС в участок: если направление, создаваемое источником тока, совпадает с направлением тока, проходящего в участке (направление тока на участке совпадает внутри источника с направлением от отрицательного полюса к положительному), т.е. ЭДС способствует движению положительных зарядов в данном направлении, то ε > 0, в противном случае, если ЭДС препятствует движению положительных зарядов в данном направлении, то ε < 0.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 261-262.
Закон Ома для неоднородного участка цепи
В простейшем варианте для расчета электрических параметров подразумевают воздействие кулоновских сил, которые обеспечивают перемещение зарядов. Закон Ома для неоднородного участка цепи позволяет учесть дополнительные факторы. Его применение помогает повысить точность вычислений.
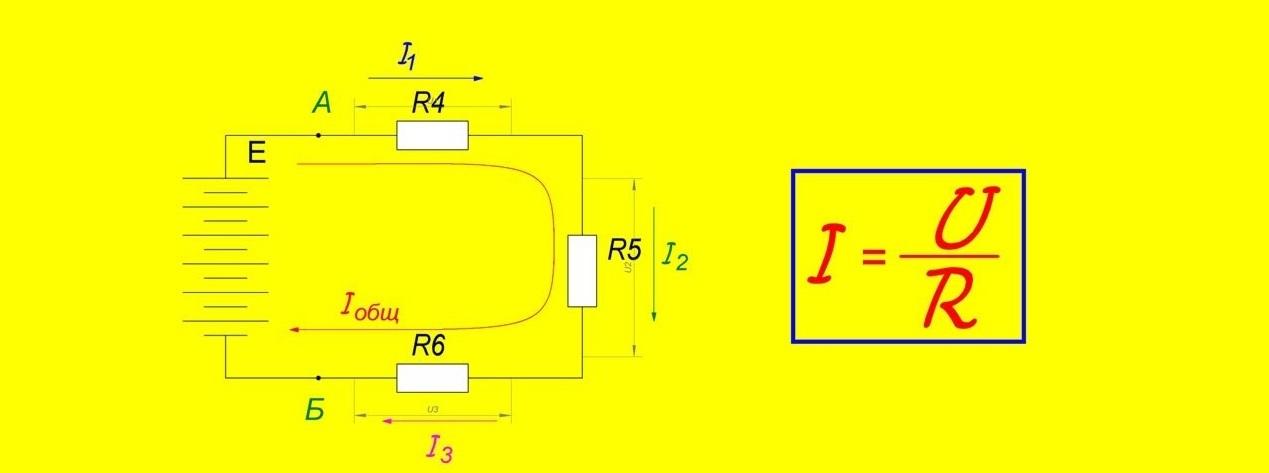
Закон Ома для участка цепи
Неоднородный участок цепи постоянного тока
Определение основных параметров и процессов:
- перемещение зарядов (q) характеризуется плотностью, которая зависит от площади поперечного сечения (S) и силы тока;
- при концентрации (n) можно подсчитать количество единичных зарядов (q0), перемещенных за единицу времени;
- эту величину можно изобразить в виде цилиндрического участка проводника с объемом (V):
q = q0*n*V.
Если подключить клеммы аккумулятора к проводнику, источник питания разрядится. Для длительного поддержания процесса перемещения зарядов можно создать замкнутый в кольцо путь. Однако и в этом случае свободный дрейф электронов ограничивают совместные столкновения, противодействие зарядов молекулярной решетки материала. Чтобы компенсировать сопротивление, необходимо приложение дополнительных «сторонних» сил.
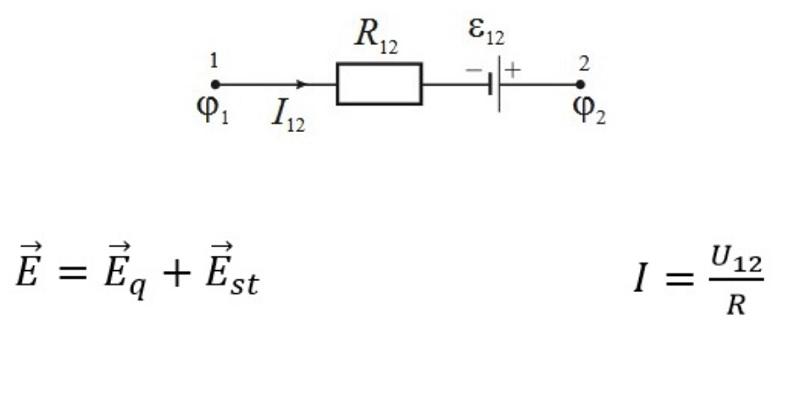
Пример неоднородного участка цепи
Рисунок демонстрирует факторы, которые следует принять во внимание. Для вычисления напряженности в любой точке этой схемы нужно суммировать векторные составляющие Eq и Est (кулоновских и сторонних сил, соответственно). Приведенный закон Ома для неоднородного участка определяет, что сила тока (I12) = напряжение на данном участке (U12) / полное электрическое сопротивление (R).
Чтобы перенести единичный заряд q из точки «1» в точку «2», необходимо выполнить работу A12. Для этого понадобится создание определенной разницы потенциалов (ϕ1- ϕ2). Источник постоянного тока создает электродвижущую силу (ЭДС), которая способна переместить заряд по цепи. Общее напряжение будет содержать сумму перечисленных сил.
Ниже приведены формулы, характеризующие рассмотренный пример:
- A12/q = ϕ1 – ϕ2;
- Ast/q = E12;
- U = A12/q + Ast/q = ϕ1 – ϕ2 + E12;
- I = (ϕ1 – ϕ2 + E12)/ R.
Интегральный вариант представления рассматриваемых процессов даст аналогичный результат.
К сведению. При выполнении расчетов следует учитывать действительную полярность источника постоянного тока. В зависимости от подключения соответствующая ЭДС будет способствовать или препятствовать перемещению заряда.
Следующий пример демонстрирует решение практической задачи. Необходимо рассчитать ток в цепи, которая составлена из источника питания с ЭДС=40V и проводки с электрическим сопротивлением R=5Ом. На выходе измерены потенциалы:
ϕ1= 20V; ϕ2=10V.
Подставив значения в формулу, можно получить нужный результат:
(20-10+40)/5 = +10А.
Знак «плюс» означает, что ток идет по направлению от точки «1» к «2».
Если рассматривать процесс в дифференциальной форме, можно представить «облако», созданное из определенного количества (N) зарядов. Оно перемещается в проводнике с определенной скоростью дрейфа (Vдр). На него действуют три вида сил:
- кулоновские – Fкул;
- сторонние – Fc;
- сопротивления кристаллической решетки – Fсп.
Последний показатель будет зависеть от особенностей материала. Он может выражаться удельной проводимостью. Вектор плотности тока будет равен сумме векторов ЭДС (кулоновской и сторонней природы), деленной на удельное сопротивление.
Закон Ома для замкнутой цепи
В реальной ситуации следует учитывать электрические сопротивления нагрузки (Rн) и самого источника питания (Rи). Классическую формулу дополняют следующим образом:
I = E/(Rн+Rи).
Если в рассмотренный выше пример добавить Rи=1Ом, получится I = (ϕ1 – ϕ2 + E12)/(Rн+Rи) = (20-10+40)/(5+1) = +8,33А. Видно уменьшение силы тока в цепи, обусловленное увеличением общего электрического сопротивления. Чтобы компенсировать потери для подключения более мощной нагрузки, необходимо увеличить ЭДС источника.
Классическая формулировка
Для участка цепи без источника ЭДС достаточно использовать классический закон Ома:
I (сила тока) = U (напряжение) /R (электрическое сопротивление).
Данное соотношение было установлено экспериментальным путем в начале 19 века. В названии сохранена фамилия немецкого ученого, который сделал открытие. Напряжение определяют по разнице потенциалов на концах проводника:
U = ϕ1 – ϕ2.
Элементарные вычисления показывают взаимные зависимости перечисленных параметров:
- I1 = 24/6 = 4А;
- I2 = 60/6 = 10А.
Увеличив разницу потенциалов, при неизменном сопротивлении получают большую силу тока:
I2 > I1.
Чтобы уменьшить ток до нужного уровня, при работе с определенным источником питания изменяют сопротивление:
- I1 = 24/4 = 6А;
- I2 = 24/12 = 2А.
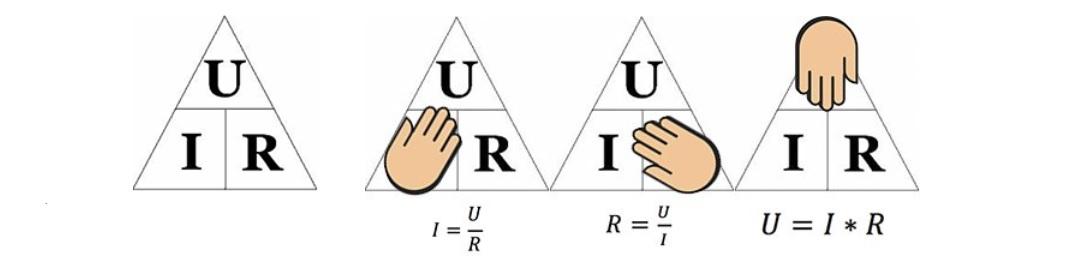
Основные формулы
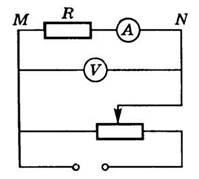
Для запоминания правил пользуются такой картинкой. Чтобы вычислить определенный параметр, закрывают соответствующий сегмент. Взаимное расположение оставшихся компонентов условно изобразит необходимую формулу.
Ток, напряжение и сопротивление
Эта картинка наглядно демонстрирует взаимное влияние тех основных электрических параметров. С ее помощью можно пояснить особенности практического применения на примере типового проекта домашней сети питания.
В современных жилых объектах часто используют кондиционеры, духовые шкафы, другую технику с большой мощностью потребления. Для нормального функционирования требуется увеличивать ток, потому что напряжение ограничено стандартами. Повышающие трансформаторы в данном случае не пригодятся, так как серийные изделия рассчитаны на подключение к сети 220 (380) V.
При увеличении силы тока понадобятся проводники с достаточно большим поперечным сечением. В противном случае концентрация зарядов на единицу объема повысится до критичной величины. Воздействие на кристаллическую решетку повысит температуру металла вплоть до механического разрушения проводки.
Чтобы исключить проблемы, кроме кабельной продукции, тщательно выбирают защитные автоматы. Для создания проекта электроснабжения и перечня подходящих функциональных компонентов пользуются представленными выше формулами.


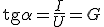 .
.