|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного… Генеалогическое древо Султанов Османской империи: Османские правители, вначале, будучи еще бейлербеями Анатолии, женились на дочерях византийских императоров… Динамика и детерминанты показателей газоанализа юных спортсменов в восстановительном периоде после лабораторных нагрузок до отказа… Интересное: Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным… Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений. Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 10 из 25Следующая ⇒ Рассмотрим магнитную цепь, образованную обмоткой навитой на магнитопровод в виде кольца (тороида). — линейный интеграл от вектора напряженности по замкнутому контуру равен алгебраической сумме токов, охватываемых этим контуром – полному току (Iполн). Для практических целей наибольший интерес представляет частный случай, когда контур интегрирования проходит внутри обмотки с числом витков w и током IВ этом случае полный ток
Сумму токов — wI через поверхность, ограниченную контуром интегрирования, называют магнитодвижущей силой F, F = wI. Если учесть, что угол между векторами Ни dl равен нулю и значение Н в любой точке контура интегрирования одинаково, среднее значение напряженности магнитного поля определится как . Из полученного соотношения следует, что напряженность магнитного поля Н не зависит от магнитных свойств магнитопровода, а прямо пропорциональна току в обмотке. Точнее равна МДС обмотки, приходящейся на единицу длины средней силовой линии магнитопровода. Исходя из соотношений Ф =ВS и В = μa Н получим
Ф = μa НS = μa S(I w / l) = I w / ( l / μa S) = F/Rм.
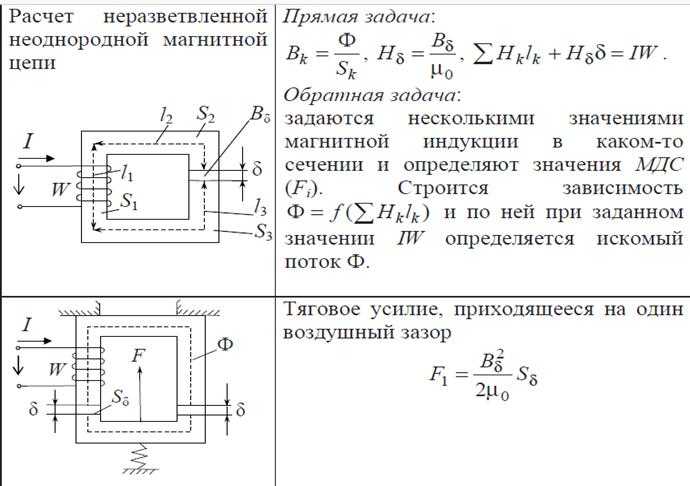
Это выражение называют законом Ома для магнитной цепи. При этом величину Rм = l / μa S принято называть магнитным сопротивлением магнитопровода (по аналогии с электрическим сопротивлением). При анализе магнитных цепей вводят понятие разности магнитных потенциалов между двумя точками магнитной цепи, которая приравнивается к Uм ab = Н l ab . Расчет неразветвленной магнитной цепи постоянного тока Формула, выражающая закон полного тока магнитной цепи, была получена для кольцевого магнитопровода постоянного поперечного сечения и с равномерно распределенной обмоткой. Эту формулу распространяют и на магнитные цепи, где намагничивающая обмотка сосредоточена на ограниченном участке магнитопровода, а отдельные участки цепи выполнены из различных ферромагнитных и неферромагнитных материалов и имеют различное поперечное сечение. В приближенных расчетах магнитных цепей принимают, что магнитный поток на всех участках цепи остается одним и тем же, хотя на самом деле в магнитной цепи образуются также потоки рассеяния Фр, которые замыкаются по воздуху, а не следуют по пути магнитопровода. В расчетах магнитных цепей различают прямую и обратную задачи. Прямая задача Задано: 1) геометрические размеры магнитной цепи; 2) характеристика B = f(H) (кривая намагничивания) ферромагнитных материалов, из которых выполнена магнитная цепь; 3) магнитный поток Ф, который надо создать в магнитной цепи. Требуется найти намагничивающую силу обмотки F = IW. Решение задачи рассматривается применительно к магнитопроводу, представленному на рисунке. Рис. 10. Магнитная цепь 1. Магнитная цепь разбивается на ряд участков с одинаковым поперечным сечением S, выполненном из однородного материала. 2. Намечается путь прохождения средней магнитной линии (на рис. показано пунктиром). 3. Т.к. магнитный поток на всех участках цепи остается постоянным, то магнитная индукция B = Ф / S на каждом из участков и напряженность магнитного поля Н неизменны. Это позволяет сравнительно просто определить значение для контура, образованного средней магнитной линией, а следовательно, найти искомую величину намагничивающей силы, поскольку . Запишем интеграл в виде суммы интегралов с границами интегрирования, совпадающими с началом и концом каждого участка цепи. Тогда . где: L1 и L2 – длины ферромагнитных участков цепи [м]. 4. Значения Н1 и Н2 определяют по известным величинам магнитной индукции В с помощью кривых намагничивания, соответствующих ферромагнитных материалов. А для воздушного зазора А/м. Разделим каждое слагаемое на магнитный поток Ф, получим: (*) Обозначим: — магнитное сопротивление участка 1; — магнитное сопротивление участка 2; — магнитное сопротивление воздушного зазора. С учетом обозначений перепишем выражение (*): или (**) Последнее выражение, т.е. зависимость магнитного потока от магнитодвижущей силы (wI) и магнитных сопротивлений участков магнитной цепи называют основным законом магнитной цепи. Заметна аналогия между уравнением (**) и законом Ома для полной цепи: Составим таблицу аналогий соответствующих величин.
Таблица
Пользуясь аналогиями, можно изобразить схему замещения магнитной цепи, изображенной ранее, в виде.
Обратная задача Задано:
Требуется определить магнитный поток Ф. Непосредственное использование формулы для определения магнитного потока Ф оказывается невозможным, поскольку магнитное сопротивление цепи переменное и само зависит от величины магнитного потока. Такие задачи решаются методом последовательного приближения в следующем порядке. Задаются рядом произвольных значений магнитного потока в цепи и для каждого из этих значений определяют необходимую намагничивающую силу обмотки так, как это делается при решении прямой задачи. По полученным данным строят кривую Ф(F) – вебер-амперную характеристику. Имея эту зависимость, нетрудно для заданного значения намагничивающей силы найти величину магнитного потока. Для оценки необходимого значения Ф можно пренебречь сопротивлением ферромагнитного участка и посчитать поток, который получится под действием намагничивающей силы F при сопротивлении воздушного участка. Это значение Ф заведомо больше расчетного. Остальные значения можно давать меньше. . ⇐ Предыдущая567891011121314Следующая ⇒ Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой. |
Закон полного тока для магнитного поля: физический смысл, формулы
Содержание:
Определение полного тока
Сутью данного закона является определение взаимной связи между электрическим током и образованным его протеканием магнитным полем. Эта особенность выявлена экспериментальным путем в первой половине XIX века. Позднее была создана формулировка, устанавливающая закон полного тока для магнитного поля. Классическое определение приведено ниже. Однако начинать изучение темы следует с базовых принципов.
Схематическое изображение физических параметров
На рисунке отмечены следующие компоненты:
- I∑ – суммарный (полный) ток;
- S – пронизываемая (dS – элементарная) площадка;
- dL – элементарный линейный участок.
- J∑ – плотность распределения токов;
- L – кольцевой замкнутый контур;
- H – напряженность магнитного поля в векторном представлении.
Физический смысл закона
Рассмотрим упрощённый вариант влияния магнитной индукции на электрическое поле. Для этого представим себе два параллельных проводника, по которым циркулируют постоянные токи, например, I1 и I2. Вблизи этих проводников образуется поле, которое мысленно можно ограничить неким контуром L – воображаемой замкнутой фигурой, плоскость которой пересекает потоки движущихся зарядов.
Для этого представим себе два параллельных проводника, по которым циркулируют постоянные токи, например, I1 и I2. Вблизи этих проводников образуется поле, которое мысленно можно ограничить неким контуром L – воображаемой замкнутой фигурой, плоскость которой пересекает потоки движущихся зарядов.
В пределах плоскости, охватываемой контуром L, формируется магнитное поле, напряжённость которого распределена в соответствии с направлениями токов. При этом циркуляция вектора магнитного поля в плоскости замкнутого контура прямо пропорциональна сумме токов, пронзающих данный контур. Полный электрический ток равен векторной сумме его составляющих:
Направления векторов I1 и I2 определяется по правилу буравчика.
Приведённые выше рассуждения можно рассматривать в качестве примера изображающего упрощённую модель частного случая рассматриваемого закона. В действительности же, процессы взаимного влияния магнитных и электрических полей намного сложнее, и они описываются интегральными и дифференциальными уравнениями Максвелла.
Упрощенный подход
Выразить закон в дифференциальном представлении довольно сложно. Потребуется вводить дополнительные компоненты. Необходимо учитывать влияние молекулярных токов. Наличие вихревых токов является причиной образования магнитного вихревого поля в пределах контура.
Вектор электрического смещения сравним с вектором напряжённости присутствующего магнитного поля H. При этом Ориентация вектора смещения зависит от быстроты изменения магнитной индукции.
Для упрощения вычислений на практике часто пользуются формулами закона для магнитного поля полных токов, представленных в виде суммирования предельно малых участков контура, с учётом влияния вихревых полей. При реализации этого метода контур мысленно разбивают на бесконечно малые отрезки. На этих отрезках проводники считаются прямолинейными, а магнитное поле на таких участках контура считают однородным.
На одном дискретном участке вектор напряженности Um определяется по формуле: Um= HL×ΔL, где HL– циркуляция вектора напряжённости на участке ΔL контура L. Тогда суммарная напряжённость UL вдоль всего контура вычисляется по формуле: UL= Σ HL× ΔL.
Тогда суммарная напряжённость UL вдоль всего контура вычисляется по формуле: UL= Σ HL× ΔL.
Суть закона
Рассматриваемый закон, применимый в магнитных цепях, определяет следующую количественную связь между входящими в него составляющими. Циркуляция вектора магнитного поля по замкнутому контуру пропорциональна сумме токов, пронизывающих его. Чтобы понять физический смысл закона полного тока – потребуется ознакомиться с графическим представлением описываемых им процессов.
Из рисунка видно, что около двух проводников с протекающими по ним токами I1 и I2 образуется поле, ограниченное контуром L. Оно вводится как мысленно представляемая замкнутая фигура, плоскость которой пронизывают проводники с движущимися зарядами. Простыми словами этот закон можно выразить так. При наличии нескольких потоков электричества через мысленное представляемую поверхность, охватываемую контуром L, в ее пределах формируется магнитное поле с заданным распределением напряженности.
За положительное направление движения вектора в соответствии с законом для контура магнитной цепи выбирается ход часовой стрелки. Оно также является мысленно представляемым.
Оно также является мысленно представляемым.
Такое определение создаваемого токами вихревого поля предполагает, что направление каждого из токов может быть произвольным.
Для справки! Вводимую полевую структуру и описывающий ее аппарат следует отличать от циркуляции электростатического вектора «Е», который при обходе контура всегда равен нулю. Вследствие этого такое поле относится к потенциальным структурам. Циркуляция же вектора «В» магнитного поля никогда не бывает нулевой. Именно поэтому оно называется «вихревым».
Основные понятия
В соответствии с рассматриваемым законом для расчета магнитных полей применяется следующий упрощенный подход. Полный ток представляется в виде суммы нескольких составляющих, протекающих через поверхность, охватываемую замкнутым контуром L. Теоретические выкладки могут быть представлены следующим образом:
- Полный электрический поток, пронизывающих конур Σ I – это векторная сумма I1 и I2.
- В рассматриваемом примере для его определения используется формула:
ΣI = I1- I2 (минус перед вторым слагаемым означает, что направления токов противоположны).
- Они, в свою очередь, определяются по известному в электротехнике закону (правилу) буравчика.
Напряженность магнитного поля вдоль контура вычисляется на основании полученных выкладок по специальным методикам. Для ее нахождения придется проинтегрировать этот параметр по L, используя уравнение Максвелла, представленное в одной из форм.Оно может быть применено и в дифференциальной форме, но это несколько усложнит выкладки.
Влияние среды
Рассмотренные отношения для закона токов и полей, действующих не в вакууме, а в магнитной среде, приобретают несколько иной вид. В этом случае помимо основных токовых составляющих вводится понятие микроскопических токов, возникающих в магнетике, например, или в любом подобном ему материале.
Нужное соотношение в полном виде выводится из теоремы о векторной циркуляции магнитной индукции B. Простым языком она выражается в следующем виде. Суммарное значение вектора B при интегрировании по выбранному контуру равно сумме охватываемых им макро токов, умноженной на коэффициент магнитной постоянной.
В итоге формула для «В» в веществе определяется выражением:
Интеграл от B по dL = интегралу от Bl по dL= m(I+I1)
где: dL – дискретный элемент контура, направленный вдоль его обхода, Вl– составляющая в направлении касательной в произвольной точке,бI и I1 – ток проводимости и микроскопический (молекулярный) ток.
Если поле действует в среде, состоящей из произвольных материалов – должны учитываться микроскопические токи, характерные именно для этих структур.
Эти выкладки также верны для поля, создаваемого в соленоиде или в любой другой среде, обладающей конечной магнитной проницаемостью.
Практическое применение в расчетах
Закон полного тока является основным законом при расчете магнитных цепей и дает возможность без особых усилий определять напряженность поля.
Примеры магнитных цепей
Магнитная цепь являет собой комплекс физических тел, обладающих сильно выраженными магнитными свойствами, магнитодвижущих сил и других условий, по которым смыкается магнитный поток. Магнитодвижущая сила определяется как произведение количества витков катушки на протекающий в ней электрический ток:
Магнитодвижущая сила определяется как произведение количества витков катушки на протекающий в ней электрический ток:
F=Iω, где:
- F – магнитодвижущая сила;
- ω – количество витков в катушке;
- I – электрический ток.
Подобно тому, как электродвижущая сила электрической цепи провоцирует возникновение тока, так и магнитодвижущая сила магнитной цепи вызывает магнитный поток. Направление магнитодвижущей силы в схемотехнике определяется на основании правила буравчика.
Параметры, описывающие характеристики магнитной или электрической цепи, являются тождественными. Аналогичными являются и мероприятия по расчету цепей. Постоянные токи в электрических цепях возникают благодаря электродвижущей силе. В магнитных цепях эту функцию выполняет магнитодвижущая сила обмоток. Характеристика сопротивления току в электрической цепи имеет свою аналогию в магнитной цепи в виде магнитного сопротивления.
Неразветвленная магнитная цепь
Согласно закону полного тока, выражение, описывающее процессы в магнитной цепи (рис. выше), выглядит так:
выше), выглядит так:
Iω=h2L1+h3L2, где:
- h2 – напряженность поля первого участка;
- h3 – напряженность поля второго участка;
- L1 – длина первого однородного участка;
- L2 – длина второго однородного участка.
Поскольку напряженность магнитного поля и магнитная индукции на первом и втором участках равны:
- h2=B1/µа1, где:
- B1 – магнитная индукция;
- µа1 – магнитная проницаемость первого участка.
- B 1=Φ/S1, где:
- Φ – магнитный поток;
- S1 – площадь поперечного сечения первого участка.
- h3=B2/µа2, где:
- B2 – магнитная индукция второго участка;
- µа2 – магнитная проницаемость второго участка.
- B 2=Φ/S2, где:
- Φ – магнитный поток;
- S2 – площадь поперечного сечения второго участка.
выражение, описывающее закон полного тока, преобразовывается в:
Iω=ΦL1/µа1S1+ ΦL2/µа2S2=ΦRм1+ΦRм2, где:
- Rм1=L1/µа1S1 – магнитное сопротивление первого участка;
- Rм2=L2/µа2S2 – магнитное сопротивление второго участка.

Проводя аналогии с электрической цепью, произведение магнитного потока на магнитное сопротивление является магнитным напряжением:
Uм2=ΦRм2=h3L2.
Если выделить из формулы магнитный поток, получается формула, представляющая собой закон Ома для магнитной цепи:
Φ= Iω/Rм1+Rм2= Iω/∑Rм.
Для магнитной цепи, не имеющей магнитодвижущей силы, выражение будет выглядеть как:
Uм=ΦRм=HL.
Аналогично электрическим цепям на магнитные цепи распространяются постулаты Кирхгофа:
- Сумма магнитных потоков, втекающих в узел, равна сумме магнитных потоков, вытекающих из узла. Выражение выглядит как ∑Φк=0;
- Сумма магнитодвижущих сил, находящихся в контуре, равна сумме падений напряжений на всех отрезках цепи, что соответствует выражению ∑Iω=∑Uм=∑HL.
Закон полного тока для магнитных цепей стоит на одном уровне с основными законами, касающимися электрических цепей. Понимание закона полного тока позволит с легкостью проводить расчет и подбор необходимых устройств, в основе работы которых лежат магнитные потоки.
Магнитное сопротивление и закон Ома для магнитной цепи.
По аналогии с электрической цепью величину
называют магнитным сопротивлением участка магнитной цепи (измеряется в 1/Гн).
Таким образом, магнитное напряжение
Выражение (3) по аналогии с электрической цепью часто называют законом Ома для магнитной цепи Однако вследствие нелинейности цепи, вызванной непостоянством магнитной проницаемости μr ферромагнетиков, оно практически не применяется для расчета магнитных цепей.
Магнитное напряжение вдоль контура
Закон Ома для переменного тока
В представленном примере для изучения берут проводники, через которые пропускают электрический ток. В совокупности они образуют сечение с мнимой площадью (S), которая ограничена неким контуром. Пользуясь классическим правилом «буравчика», несложно установить направление вектора (di или Н). Понятно, что в данном случае рассматривается дискретная величина. Вектор магнитной напряженности и полный ток связаны следующей формулой:
I∑ = ∫L*H*dL.
Магнитодвижущая сила
Представленный закон применяют для расчета рабочих характеристик разных устройств:
- одно,- и трехфазных трансформаторов с подключением к сети 220 (380) V, соответственно;
- электродвигателей постоянного тока;
- катушек с тороидальными сердечниками;
- электрических приводов реле и клапанов;
- аналоговых измерительных приборов и датчиков;
- электромагнитов, которые установлены в подъемных механизмах, системах водоочистки.
Простая магнитная цепь Закон Ома — онлайн калькулятор
Для подробного изучения подойдет несложный пример. В цепи обеспечивается перемещение тока по замкнутому контуру с применением катушки индукции. Созданная магнитодвижущая сила (F) будет зависеть от силы тока (I) в проводнике и количества сделанных витков (W):
F = I * W.
По классическим определениям, ток в цепи появляется при создании разницы потенциалов между точками подключения источника ЭДС. Подобным образом показанная выше сила F провоцирует образование магнитного потока. В данном случае аналогичным образом можно использовать не только правило буравчика, но и технологии расчета цепей. Необходимо только корректно применять отдельные понятия. Так, электрическому сопротивлению соответствует магнитный аналог.
В данном случае аналогичным образом можно использовать не только правило буравчика, но и технологии расчета цепей. Необходимо только корректно применять отдельные понятия. Так, электрическому сопротивлению соответствует магнитный аналог.
При разделении такого контура на два сегмента справедливым будет следующее выражение:
Н1*L1 + h3*L2 = I *W,
где Н1 и h3 (L1 и L2) напряженность (длина) соответствующих частей.
Последовательным преобразованием можно получить удобную для практического применения формулу закона полного тока:
- h2 = B1/ma1;
- B1 = Ф/S1;
- h3 = B2/ma2;
- B2 = Ф/S2;
- I*W = Ф*L1/ma1*S1 + Ф*L1/ma1*S1 = Ф*Rm1 + Ф*Rm2.
Кроме площади поперечного сечения (S), здесь приведены магнитные параметры разных участков (1 и 2):
- Ф – поток;
- В – индукция;
- ma – проницаемость.
Из этого выражения нетрудно получить значение магнитного сопротивления для каждого участка:
Rm = L/ma*S.
По аналогии с формулой Ома для электрических цепей можно вычислить магнитное напряжение:
U = Ф * Rm.
Cучетом частоты питающего сигнала (w) магнитный поток будет зависеть от силы тока и суммарного сопротивления участков цепи:
Ф = (I*w)/(Rm1+Rm2) = (I*w)/∑Rm.
К сведению. По этим же принципам допустимо применение законов Кирхгофа. Так суммарная величина входящих и выходящих магнитных потоков будет равной.
Законы Кирхгофа для магнитной цепи
При расчетах разветвленных магнитных цепей пользуются двумя законами Кирхгофа, аналогичными законам Кирхгофа для электрической цепи.
Первый закон Кирхгофа непосредственно вытекает из непрерывности магнитных линий, т.е. и магнитного потока; алгебраическая сумма магнитных потоков в точке разветвления равна нулю:
Например, для узла а на рис. 6.11,б
— Ф1 — Ф2 + Ф3 = 0
Второй закон Кирхгофа для магнитной цепи основывается на законе полного тока: алгебраическая сумма магнитных напряжений на отдельных участках цепи равна алгебраической сумме МДС:
Например, для левого контура и а рис. 6.11, б
Как следует из закона Ома, для получения наибольшего магнитного потока при наименьшей МДС у магнитной цепи должно быть возможно меньшее магнитное сопротивление. Большая магнитная проницаемость ферромагнитных материалов обеспечивает получение малых магнитных сопротивлений магнитопроводов из этих материалов. Поэтому магнитные цепи электрических машин выполняют преимущественно из ферромагнетиков, а участки цепей из неферромагнитных материалов, то есть неизбежные или необходимые воздушные зазоры, делают, как правило, возможно малыми.
Большая магнитная проницаемость ферромагнитных материалов обеспечивает получение малых магнитных сопротивлений магнитопроводов из этих материалов. Поэтому магнитные цепи электрических машин выполняют преимущественно из ферромагнетиков, а участки цепей из неферромагнитных материалов, то есть неизбежные или необходимые воздушные зазоры, делают, как правило, возможно малыми.
Схема устройства магнитной цепи двухполюсной машины с явно выраженными полюсами показана на рис. 6.12.
Рис. 6.12 Магнитная цепь электрической машины с явно выраженными полюсами
Плоскость 00′, проведенная через середины полюсов N и S и ось машины, делит магнитную цепь на две симметричные части. В каждой из них магнитный поток Ф/2 замыкается через полюсы П, полюсные наконечники ПН, воздушные зазоры, якорь Я и станину машины С. Магнитодвижущая сила создается током в обмотке возбуждения ОВ, расположенной на полюсах N и S. Из северного полюса N магнитные линии выходят и в южный полюс S входят.
Рис, 6. 13. Магнитная цепь электрической машины с неявно выраженными полюсами
13. Магнитная цепь электрической машины с неявно выраженными полюсами
Схема устройства магнитной цепи двухполюсной машины с неявно выраженными полюсами показана на рис. 6.13. Здесь обмотка возбуждения заложена в пазы ротора Р — вращающейся части машины, укрепленной на валу. Как и в предыдущем случае, плоскость 00′, проведенная через середины полюсов N и S, делит магнитную цепь машины на две симметричные части, в каждой из которых магнитный поток Ф/2. Магнитный поток замыкается через ротор машины, воздушные зазоры и станину машины С, представляющую собой неподвижный наружный стальной цилиндр — статор машины.
Торойд
В электротехнике часто приходится иметь дело с катушками разных видов и размеров. Катушка, образованная витками намотанными на сердечник тороидальной формы (в виде бублика), называется тороидом. Важными характеристиками сердечника тора являются его радиусы — внутренний (R1) и внешний (R2).
Поле внутри соленоида на расстоянии r от центра равно:
Предыдущая
РазноеЭлектролизсолей, щелочей, кислот
Следующая
РазноеСхемы подключения трехфазного счетчика. Установка трёхфазного счетчика
Установка трёхфазного счетчика
Ток или поток? Магнитные цепи и их основные характеристики / Хабр
Привет, Хабр! С недавнего времени я стал задумываться об актуальности статей и заметил, что на Хабре нет ни одной обзорной статьи про магнитные цепи. Как так!? Ведь это… а что это такое?
Действительно, наверняка даже самые отстраненные от инженерного дела люди имеют представление о том, что такое электрические цепи, но возможно, что про магнитные цепи не слышали вовсе. Каждый школьник когда-то в учебнике физики наблюдал разные схемы и формулы, описывающие законы Ома. Но магнитные цепи в рамки школьного курса не входят.
Я решил написать данную статью, чтобы показать, насколько удивителен мир физики и заинтересовать школьников в её изучении. В данной статье, однозначно, для полноты вещей будут и выводы формул и использование некоторых математических операций, которые могут быть известны не всем, но такие моменты я постараюсь сгладить. Приступим.
Что нужно вспомнить?
Для более четкого представления сей статьи, неплохо бы вспомнить основные характеристики самого магнитного поля: вектор магнитной индукции, вектор напряженности, поток вектора магнитной индукции — а также нужно вспомнить немного про магнитные вещества, а именно про ферромагнетики.
Полагается, что вам известен обобщенный закон Ома и помнится, что такое ток, напряжение и сопротивление. Если нет, то крайне советую обратиться к сторонним ресурсам, чтобы иметь хотя бы общее представление о том, что последует далее. Крайне советую учебник И.Е. Иродова «Электромагнетизм».
Применение магнитных цепей
Магнитные цепи находят очень большое поле применения, а именно, они используются для надежного пропускания магнитного потока по специальному проводнику с минимальными или, в некоторых случаях, определенными потерями. В электротехнической промышленности широко используется взаимная зависимость магнитной и электрической энергий, переход из одного состояния в другое. На подобном принципе работают, например, трансформаторы, разные электродвигатели, генераторы и другие устройства.
На подобном принципе работают, например, трансформаторы, разные электродвигатели, генераторы и другие устройства.
Конечно, можно продолжительное время говорить об устройствах, разных типах магнитопроводов (про которые речь пойдет далее), но наша первичная цель — рассмотреть выводы основных характеристик магнитных цепей. Продолжаем!
Как устроены магнитные цепи?
Магнитную цепь, на самом деле, не так сложно представить, как может показаться человеку, который о них впервые слышит. Обычно магнитные цепи представляют из себя некоторые фигуры из ферромагнитного сердечника с источником или несколькими источниками ПОтока. Пожалуй, один из самых простых примеров с одним источником, который можно взять на вооружение, проиллюстрирован ниже:
Перед продолжением обусловимся, что среди электротехников сердечник называют магнитопроводом. Часть магнитопровода, на которой отсутствуют обмотки и которая служит для замыкания магнитной цепи, называется «ярмо».
Начнем с тороидального сердечника. Такой тороидальный сердечник может служить формой для катушки, как бы странно это не звучало. Но что за катушка? Ну, первое что приходит в голову — провод, образующий витки. Хорошо, но какого его предназначение? Вернемся к электрическим цепям и вспомним, что существуют источники тока / напряжения, так называемые активные элементы. Так вот, в магнитных цепях роль источника выполняют катушки с током, накрученные на основной элемент магнитной цепи — ферромагнитный магнитопровод.
Вспомним теперь про ферромагнитные материалы. Почему именно они? Дело в том, что благодаря высокому значению магнитной проницаемости, что сигнализирует о хорошей намагниченности ферромагнетика, силовые линии магнитного поля практически не выходят за пределы сердечника, либо не выходят вовсе. Однако это будет справедливо лишь тогда, когда наш сердечник замкнутый, либо имеет небольшие зазоры. То есть, ферромагнетики обладают сильно выраженными магнитными свойствами, когда как у парамагнетиков и диамагнетиков они значительно слабее, что можно наблюдать на следующем графике зависимости намагниченности от напряженности магнитного поля:
Вещества, которые входят в конструкцию магнитопровода, могут обладать не только сильномагнитными свойствами, но также и слабомагнитными. Однако мы рассматриваем сердечник из ферромагнитного материала.
Однако мы рассматриваем сердечник из ферромагнитного материала.
Ещё из школьного курса мы представляем себе картину с линиями магнитной индукции соленоида, мы можем визуально представить его поле и понимаем, что концентрация силовых линий, их насыщенность, наибольшая в центре рассматриваемого соленоида. Тут очень важно вспомнить правило буравчика, чтобы правильно указать направление силовых линий.
Отсюда становится ясно, что катушки-источники порождают магнитное поле, а следовательно и поток линий магнитной индукции. Такие линии будут циркулировать по нашему сердечнику, словно повторяя его форму. Именно поэтому нам важно условие замкнутости сердечника и материал, из которого он сделан. Положим, что наш воображаемый сердечник замкнут. Из этого следует, что и силовые линии замкнуты, а следовательно выполняется теорема Гаусса для магнитного поля, которая гласит: поток линий магнитной индукции через замкнутую поверхность равен нулю. Стоит учесть, что поток адаптируется под площадь сечения. *
*
Ну и в конечном счете ферромагнитный сердечник поток куда-то передает! Аналогичным образом замкнутый проводник позволяет передать электрический ток.
Отлично! Мы разобрались с тем, что такое магнитные цепи и даже вспомнили про теорему Гаусса и ферромагнетики. Теперь поговорим о том, какие следствия вытекают из теоремы Гаусса и возможности пренебрежения полем вне сердечника и в зазорах.
1] Магнитные потоки Ф1 и Ф2 через произвольные сечения будут равны между собой.
2] В узле (разветвлении) сердечника алгебраическая сумма потоков (с учетом их направлений) будет равна нулю… Мне одному это что-то напоминает?
То есть мы окончательно сформулировали, что замкнутая (или почти замкнутая) система из ферромагнитных сердечников может рассматриваться как проводящая цепь. В нашем случае — магнитная.
Расчет магнитных цепей
Теперь внимание. Мы можем провести прямую аналогию и рассматривать магнитный поток в цепи, как характеристику электрической цепи — силу тока. Рассмотренное второе следствие означает, что для магнитной цепи, также как и для электрической, справедливо первое правило Кирхгофа. Отсюда можно лаконично перейти к закону полного тока, который в рамках классического магнетизма будет выглядеть следующим образом (приготовьтесь, немного математики):
Рассмотренное второе следствие означает, что для магнитной цепи, также как и для электрической, справедливо первое правило Кирхгофа. Отсюда можно лаконично перейти к закону полного тока, который в рамках классического магнетизма будет выглядеть следующим образом (приготовьтесь, немного математики):
Криволинейный интеграл по замкнутому контуру от напряженности магнитного поля будет равен алгебраической сумме токов, сцепленных (окруженных) данным контуром.
Также мы помним, что напряженность магнитного поля связана с магнитным потоком следующим образом:
Руководствуясь приведенным законом полного тока и определением напряженности через магнитный поток, мы можем переписать закон полного тока относительно магнитного потока.
Откуда в уравнении появился и что символизирует аргумент l? Все просто. Так как мы рассматриваем контур L, то логично предположить, что на разных его участках наши показатели могут принимать разные значения: площадь сечения может изменяться, как и магнитная проницаемость или магнитный поток.
Полученное уравнение можно рассматривать как второй закон Кирхгофа, который, напомню, звучит следующим образом:
В любой момент времени алгебраическая сумма напряжений на ветвях контура равна нулю.
Для полной ясности, проведем аналогию между электрическими и магнитными цепями, а также их величинами.
Именно проведя аналогичное представление для электрической цепи, мы можем рассчитывать магнитные цепи. Для того, чтобы это сделать, следует:
Мысленно разбить сердечник на отдельные однородные участки (непрерывные, с постоянным сечением) без разветвлений и определить их магнитные сопротивления;
Построить эквивалентную электрическую цепь, последовательно заменяя участки магнитной цепи участками электрической с электрическими сопротивлениями, а также заменяя индуктивности (катушки) на источники ЭДС;
После обозначения заданных сопротивлений и ЭДС, можем вычислить в общем токи в элементах электрической цепи;
Произвести замену полученных величин согласно таблице (токи в потоки, ЭДС в МДС [Магнитодвижущую силу / Ампер-витки], а электрическое сопротивление в магнитное сопротивление).

Именно таким образом, мы можем рассчитать характеристики магнитной цепи. Полученные результаты позволяют, например, вычислить индуктивности.
А примеры расчетов будут?
Здесь — нет. А по ссылке — да! В данном документе Самарского государственного технического университета рассмотрены базовые примеры, которые позволят лучше разобраться в теме, если она вас заинтересовала. Помимо всего прочего, там же приведены теоретические справки. Советую прочитать в надежде, что вы сможете для себя что-то новое подчерпнуть.
Заключение
Во-первых, спасибо, что дочитали статью! Один из способов поддержать меня как автора — подписаться на мой паблик Вконтакте, где иногда выходят «локальные статьи».
Во-вторых, вернемся к началу статьи. Там я задался целью показать, почему физика удивительна. Не хочу быть многословным, поэтому просто попрошу вспомнить все то, что было описано выше. Мы оперировали моделями, которые относятся к разделу физики электричества и перенесли их на физику магнетизма. Наверняка, вы замечали, насколько часто встречаются элементы механики в иных разделах. Это по истине удивительно! Однако главное не поработиться иллюзией, что в мире все законы нам предельно известны…
Наверняка, вы замечали, насколько часто встречаются элементы механики в иных разделах. Это по истине удивительно! Однако главное не поработиться иллюзией, что в мире все законы нам предельно известны…
Задачи расчета магнитных цепей — Электротехника (Физика)
6.4. Задачи расчета магнитных цепей.
Существует два типа задач, а именно:
1. прямая задача – по заданному значению потока Ф определяют МДС w×I обмотки;
2. обратная задача — задается значение МДС w×I и требуется определить поток Ф.
В обоих случаях должны быть известны геометрические размеры магнитопровода (длины l и площади поперечных сечений S всех участков магнитопровода), материалы участков и кривые намагничивания.
Для упрощения расчета пренебрегают магнитными потоками рассеяния Фр (рис. 1.8) и не учитывают выпучивание магнитного поля в воздушных зазорах, считая площадь сечения воздушного зазора S0 (рис. 1.8) равной площади поперечного сечения ферромагнитного магнитопровода.
1.8) и не учитывают выпучивание магнитного поля в воздушных зазорах, считая площадь сечения воздушного зазора S0 (рис. 1.8) равной площади поперечного сечения ферромагнитного магнитопровода.
1.Решение прямой задачи.
1.1Неразветвленная магнитная цепь.
Пример подобной цепи представлен на рис. 1.8.
Эту цепь можно разбить на четыре участка, три из которых выполнены из ферромагнитного материала ( например: электротехническая сталь Э2 ), кривая намагничивания которого известна рис 1.9. Четвёртый участок – воздушный зазор.
Характерный признак неразветвлённой магнитной цепи – магнитный поток Ф на всех участках один и тот же (рис. 1.8). Его значение задано в условии задачи. Магнитный поток Ф называется основным. Этот поток замыкается по магнитопроводу в отличие от потока рассеяния Фр, силовые линии которого замыкаются вокруг витков катушки по воздуху. Обычно Ф значительно больше Фр.
Обычно Ф значительно больше Фр.
Магнитная проницаемость воздуха m0=4p×10-7 Гн/м ничтожно мала по сравнению с проницаемостью ферромагнитного магнитопровода и магнитное сопротивление потоку Фрнесравненно выше, чем для потока Ф (Фр<<Ф).
Чтобы использовать при расчете закон полного тока, выберем контур интегрирования, проходящий внутри катушки с числом витков w и совпадающий со средней линией магнитной индукции. Разобьем магнитную цепь на отдельные участки: участок da – длина средней линии магнитной индукции l1, площадь поперечного сечения S1, на участке ab длина l2, площадь поперечного сечения S2 , на участке cd длина l3 , площадь поперечного сечения S3, на участке воздушного зазора длина l0 , площадь S0=S2.
Пусть S1> S0=S2> S3 , тогда магнитная индукция по участкам:
, , , .
Учитывая соотношения между площадями сечений, получим B1<B2=B0<B3. Далее по кривой намагничивания рис. 1.9, определим напряжённость магнитного поля на ферромагнитных участках Н1,H2, Н3.
Напряженность поля в зазоре рассчитывается по формуле: , где m0=4p×10-7 Гн/м – магнитная постоянная.
Так как напряженность поля на каждом из четырех участков постоянна, интегральная формула закона полного тока принимает следующий вид:
1.8
Из этого уравнения определяется МДС w×I. Отметим, что в уравнении 1.8 слева – сумма падений магнитных напряжений на участках магнитной цепи. Уравнение 1.8 можно представить иначе, если заменить магнитные напряжения в левой части уравнения произведениями потока Ф на магнитные сопротивления участков магнитной цепи (формула 1.6) и общий для всех участков поток Ф вынести за скобки, тогда , откуда
1.9
где , , , .
Абсолютная магнитная проницаемость m1, m2 и m3определяются с помощью кривой намагничивания рис. 1.9
1.9
, , .
Выражение 1.9 как и формулу 1.6 называют законом Ома для магнитной цепи.
1.2.Прямая задача при расчете разветвленных цепей
1.2.1.Симметричная магнитная цепь (рис. 1.10)
В этой цепи l1=l3 и S1=S3. Трехстержневой магнитопровод изготовлен из однородного ферромагнитного материала (кривая намагничивания известна). Магнитные сопротивления стержней 1 и 3 одинаковы. Поток Ф2, возникающий в среднем стержне, разделяется в т. а на две равные части Ф1=Ф3=Ф2 /2.
Пусть задано значение магнитного потока Ф3, требуется определить МДС w×I намагничивающей обмотки.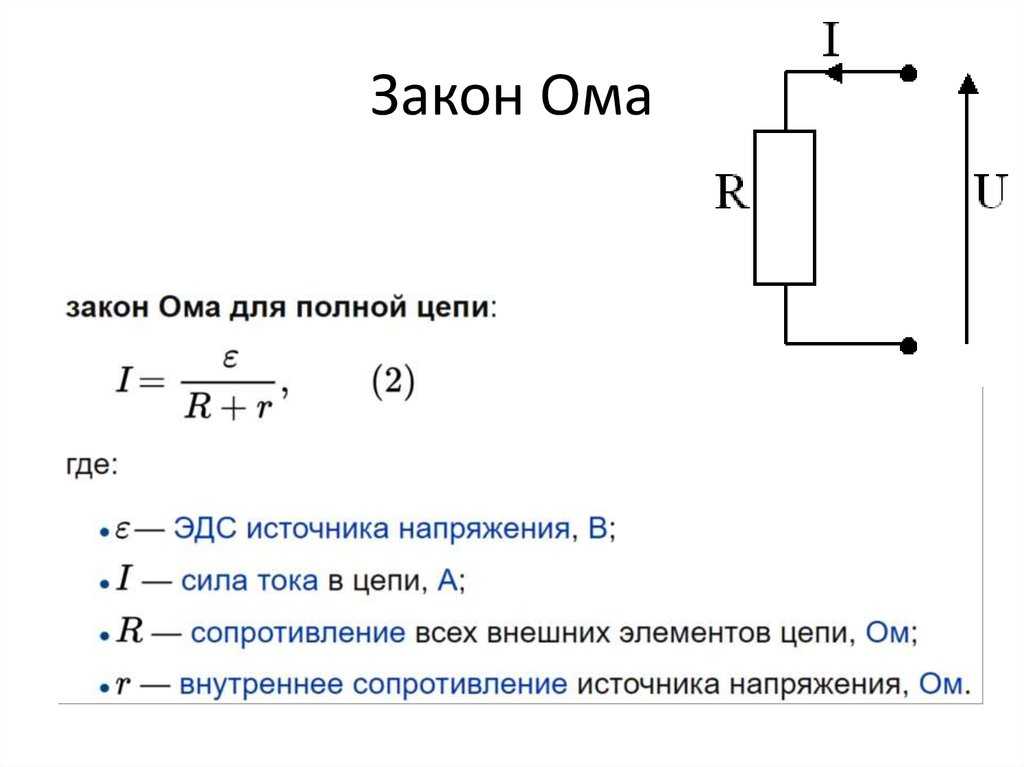
Структуру решения можно представить так: , и Н2 определяют по кривой намагничивания. МДС можно определить из уравнения: wI = H3l3 + H2l2.
1.2.2.Несимметричная магнитная цепь (рис. 1.11).
Здесь S1=S3 и l3=2l1. Задан поток Ф3, определить МДС w×I.
Схема решения:
по кривой намагничивания, тогда магнитное напряжение – по кривой намагничивания, затем Ф1=B1S1 ® Ф2=Ф1+Ф3 ® ® H2 – по кривой намагничивания. МДС w×I определим из уравнения w×I = H3l3 + H2l2=Н1l1 + H2l2 .
МДС w×I определим из уравнения w×I = H3l3 + H2l2=Н1l1 + H2l2 .
1.2.3.Несимметричная магнитная цепь с двумя намагничивающими обмотками (рис. 1.12).
Расчет подобных магнитных цепей производят, используя законы Кирхгофа для магнитных цепей. Перед записью уравнений произвольно намечают направления потоков в стержнях (Ф1, Ф2 и Ф3) и выбирают направления обхода контуров. На рис. 1.12 направления потоков Ф1 и Ф2 приняты совпадающими с МДС w1I1 и w2I2.
Условимся со знаком «+ » записывать потоки, направленные к узлу а, иначе – со знаком «- » .
Со знаком «+ » записывать магнитные напряжения, если направление потока на участке цепи совпадет с направлением обхода контура, иначе – со знаком «- » .
Со знаком «+ » записывать МДС, положительное направление которых совпадает с направлением обхода, иначе – со знаком «- » .
Для цепи (рис.1.12) можно записать следующие уравнения по законам Кирхгофа:
примечание: вместо одного из двух последних уравнений можно записать уравнение для левого контура:
Пусть требуется определить МДС w2I2, чтобы магнитная индукция в воздушном зазоре третьего стержня имела заданное значение В0.
Решение:
1. S0=S3, имеем В3=В0, тогда поток Ф3=В3S3=В0 S0
2. По кривой намагничивания определим напряженность Н3
3. В4=Ф3 / S4 и по кривой намагничивания определим Н4
В4=Ф3 / S4 и по кривой намагничивания определим Н4
4. Напряженность поля в зазоре Н0=В0/m0
5. Из уравнения 1.12 определим напряженность Н2 и по кривой намагничивания находим В2 и поток Ф2=В2S2
6. Из уравнения 1.10 определяется поток Ф1=Ф3 – Ф2
7. Находим индукцию В1=Ф1/ S1 и далее Н1 – по кривой намагничивания
8. Искомое значение w1I1 получаем из уравнения 1.11: .
2.Решение обратной задачи.
2.1 Неразветвленная магнитная цепь (рис. 1.8)
Задано значение МДС w×I, требуется определить магнитный поток Ф. Если известно, что магнитная цепь устройства в рабочих режимах не насыщена и можно считать магнитную проницаемость ферромагнитных участков , то, подсчитав магнитные сопротивления участков цепи можно определить поток Ф из закона Ома для магнитной цепи: .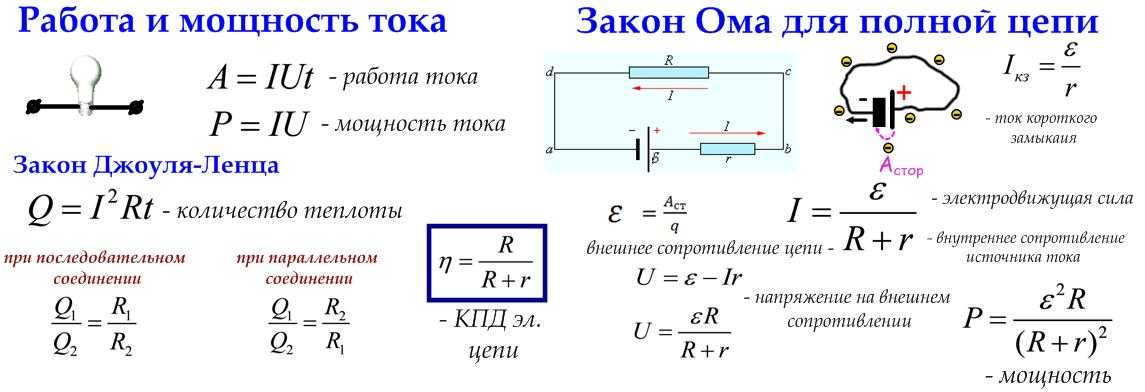 В общем же случае принимается следующий порядок решения:
В общем же случае принимается следующий порядок решения:
2.1.1. Задаются рядом значений потока Ф (Ф’, Ф’’ и т.д.), по которым каждый раз определяется МДС wI (wI’, wI’’ и т.д. ), т.е. несколько раз решается прямая задача.
2.1.2. Строится вспомогательная магнитная характеристика Ф(wI) рис. 1.13.
2.1.3. Используя построенную характеристику, по заданному значению МДС wIзадан. определяем искомое значение потока Фиск.
Примечание: учитывая, что для расчета нужна только часть характеристики в окрестности Фиск, рекомендуется вначале найти приближенное значение Фиск с помощью уравнения (т. к. Н0 >> H1 , Н2 и Н3),
из которого определяется напряженность поля в зазоре Н0 и далее – В0 = m0S0 и приближенное значение потока Фиск=В0S0 , и далее выполняются 2. 1.1 – 2.1.3 пункты расчета.
1.1 – 2.1.3 пункты расчета.
2.2. Разветвленная несимметричная магнитная цепь (рис. 1.14).
По заданному значению МДС w×I определить магнитные потоки Ф1 , Ф3 , Ф2 .
Магнитные сопротивления отдельных участков магнитопровода в общем случае нелинейные из–за нелинейной зависимости между магнитными потоками и током намагничивающей обмотки Ф(I).
При решении задачи удобнее использовать схему замещения (рис. 1.15) магнитной цепи (рис. 1.14), подобную схеме нелинейной электрической цепи постоянного тока с той разницей, что ЭДС заменена на МДС w×I, токи в ветвях электрической цепи – потоками Ф1, Ф2 , Ф3 в ветвях магнитной цепи, нелинейные сопротивления R(I) – магнитными сопротивлениями RM(Ф).
Выделим ветвь с МДС w×I в активный двухполюсник. Второй двухполюсник, в составе которого две параллельные ветви с нелинейными магнитными сопротивлениями RM1 и RM3 – пассивный (рис 1.16).
Задача решается графоаналитическим методом.
Вебер-амперная характеристика активного двухполюсника строится в соответствии с уравнением второго закона Кирхгофа для магнитной цепи:
1.13
Ещё посмотрите лекцию «11 Профессиональная гигиена полости рта» по этой теме.
Для ее построения задаемся рядом значений потока Ф2 , определяем ряд значений индукции , и по кривой намагничивания каждый раз находим напряженность магнитного поля Н2; далее по уравнению 1.13 подсчитываем соответствующие значения магнитных напряжений UabM и строим вебер-амперную характеристику активного двухполюсника Ф2(UabM) рис. 1.17.
1.17.
Чтобы получить вебер-амперную характеристику пассивного двухполюсника, нужно сначала построить характеристики Ф1(UabM) и Ф3(UabM) по описанной выше методике с использованием зависимостей:
Так как ветви с потоками Ф1 , Ф3 соединены между собой параллельно и , то для построения характеристики пассивного двухполюсника Ф1(UabM)+ Ф3(UabM) складываем ординаты характеристик ветвей при одних и тех же значениях UabM.
Поскольку двухполюсники соединены последовательно (рис. 1.16), то точка пересечения их вебер – амперных характеристик определит общий для обоих магнитный поток Ф2 и магнитное напряжение UabM.
Располагая значением UabM и вебер – амперными характеристиками Ф1(UabM) и Ф3(UabM) определяем по рис. 1.17 значения потоков Ф1 и Ф3.
О законе полного тока: формула для магнитных цепей
Содержание
- 1 Суть закона полного тока
- 2 Практическое применение в расчетах
- 3 Видео
В радиоэлектронике применяется ряд законов и постулатов для анализа, как цепей, так и устройств. Сталкиваясь с необходимостью исследования магнитных цепей, применяют закон полного тока для магнитного поля.
Магнитные потоки трансформатора
Суть закона полного тока
Данный постулат характеризует взаимосвязь между током электрической цепи и магнитным полем, появляющимся в связи с протеканием этого тока.
Контур с проводниками под током
Для понимания закона полного тока необходимо представить некоторое число проводников, по которым протекает электрический ток. Множество проводников охватывает некоторый контур, и, соответственно, ограничивает мнимую поверхность S, согласно картинке выше. Направление огибания контура, согласно правилу буравчика, ориентировано по ходу часовой стрелки. Поскольку множество токов является величиной дискретной, то закон полного тока определяется как связь суммарного электрического тока через закольцованный контур L и напряженности магнитного поля, сформированного этим током, и определяется по формуле:
Множество проводников охватывает некоторый контур, и, соответственно, ограничивает мнимую поверхность S, согласно картинке выше. Направление огибания контура, согласно правилу буравчика, ориентировано по ходу часовой стрелки. Поскольку множество токов является величиной дискретной, то закон полного тока определяется как связь суммарного электрического тока через закольцованный контур L и напряженности магнитного поля, сформированного этим током, и определяется по формуле:
∫LHdl=I∑, где:
- H – вектор напряженности магнитного поля;
- dl – направленный элементарный линейный участок, взятый вдоль контура;
- I∑ – суммарная сила тока.
Сущностью закона полного тока является то, что передвижение вектора напряженности магнитного поля по кольцевому контуру приравнивается сумме всех токов, которые находятся в этом контуре. Это выражение является интегральной формой закона полного тока.
Дополнительная информация. Интеграл произведения вектора напряженности магнитного поля и направленного элементарного линейного участка по кольцевому контуру называется циркуляцией вектора Н.
Если заданный контур пронизывает непрерывный пространственный поток движущихся заряженных частиц с плотностью электрического тока J, то общая величина тока, проходящего сквозь площадку, измеряется по выражению:
I∑=∫sJdS, где dS – элементарная площадка контура S.
Произведение JdS характеризует поток вектора плотности тока J, проходящего через поверхность dS.
Помимо интегральной формы, применяется дифференциальная форма закона полного тока. С целью получения дифференциальной формы выражения полного тока следует заменить интеграл по контуру L на интеграл по площади S. Поскольку теорема Стокса в векторном анализе выражается как:
∫LАdl=∫s rotАdS, то ∫LНdl=∫s rotНdS.
Объединив эти выражения с законом полного тока, в интегральной форме получается:
∫s rotНdS =∫s J∑dS.
Поскольку контур L взят произвольным образом, то интегралы в левой и правой частях выражения равны, если равны подынтегральные выражения.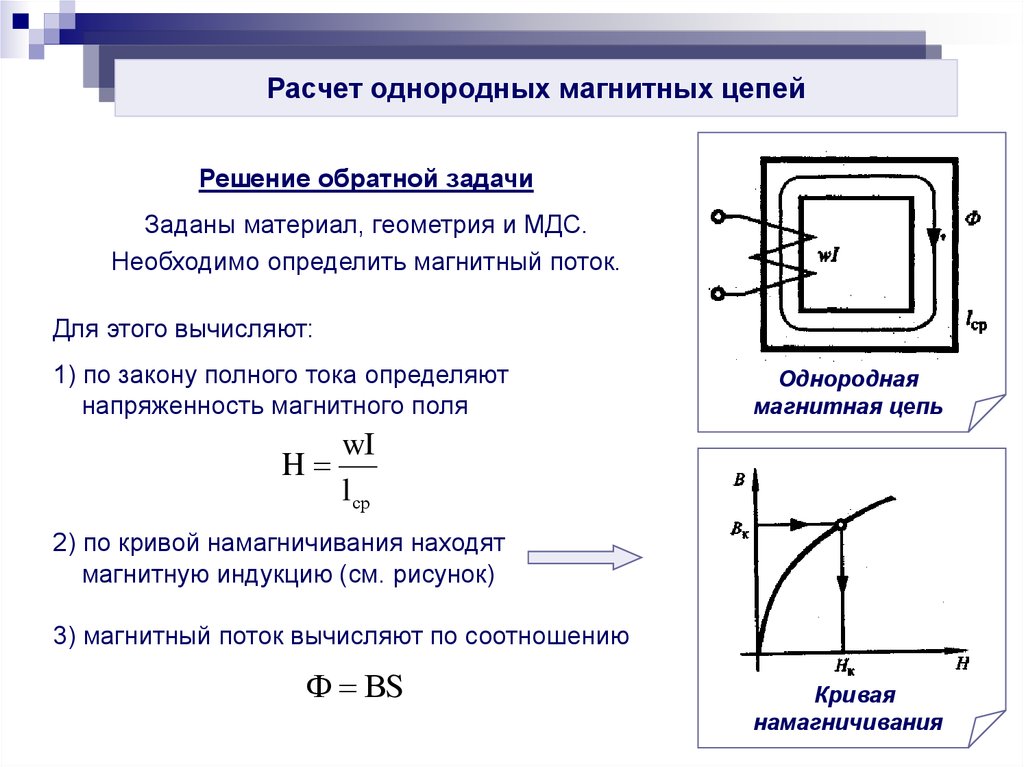 Исходя из этого, выражение преобразовывается в:
Исходя из этого, выражение преобразовывается в:
rotН=J∑.
Данной формулой выражается закон полного тока в дифференциальной форме.
Практическое применение в расчетах
Закон Ома для переменного тока
Закон полного тока является основным законом при расчете магнитных цепей и дает возможность без особых усилий определять напряженность поля.
Примеры магнитных цепей
Магнитная цепь являет собой комплекс физических тел, обладающих сильно выраженными магнитными свойствами, магнитодвижущих сил и других условий, по которым смыкается магнитный поток. Магнитодвижущая сила определяется как произведение количества витков катушки на протекающий в ней электрический ток:
F=Iω, где:
- F – магнитодвижущая сила;
- ω – количество витков в катушке;
- I – электрический ток.
Подобно тому, как электродвижущая сила электрической цепи провоцирует возникновение тока, так и магнитодвижущая сила магнитной цепи вызывает магнитный поток. Направление магнитодвижущей силы в схемотехнике определяется на основании правила буравчика.
Направление магнитодвижущей силы в схемотехнике определяется на основании правила буравчика.
Параметры, описывающие характеристики магнитной или электрической цепи, являются тождественными. Аналогичными являются и мероприятия по расчету цепей. Постоянные токи в электрических цепях возникают благодаря электродвижущей силе. В магнитных цепях эту функцию выполняет магнитодвижущая сила обмоток. Характеристика сопротивления току в электрической цепи имеет свою аналогию в магнитной цепи в виде магнитного сопротивления.
Неразветвленная магнитная цепь
Согласно закону полного тока, выражение, описывающее процессы в магнитной цепи (рис. выше), выглядит так:
Iω=h2L1+h3L2, где:
- h2 – напряженность поля первого участка;
- h3 – напряженность поля второго участка;
- L1 – длина первого однородного участка;
- L2 – длина второго однородного участка.
Поскольку напряженность магнитного поля и магнитная индукции на первом и втором участках равны:
- h2=B1/µа1, где:
- B1 – магнитная индукция;
- µа1 – магнитная проницаемость первого участка.

- B 1=Φ/S1, где:
- Φ – магнитный поток;
- S1 – площадь поперечного сечения первого участка.
- h3=B2/µа2, где:
- B2 – магнитная индукция второго участка;
- µа2 – магнитная проницаемость второго участка.
- B 2=Φ/S2, где:
- Φ – магнитный поток;
- S2 – площадь поперечного сечения второго участка.
выражение, описывающее закон полного тока, преобразовывается в:
Iω=ΦL1/µа1S1+ ΦL2/µа2S2=ΦRм1+ΦRм2, где:
- Rм1=L1/µа1S1 – магнитное сопротивление первого участка;
- Rм2=L2/µа2S2 – магнитное сопротивление второго участка.
Проводя аналогии с электрической цепью, произведение магнитного потока на магнитное сопротивление является магнитным напряжением:
Uм2=ΦRм2=h3L2.
Если выделить из формулы магнитный поток, получается формула, представляющая собой закон Ома для магнитной цепи:
Φ= Iω/Rм1+Rм2= Iω/∑Rм.
Для магнитной цепи, не имеющей магнитодвижущей силы, выражение будет выглядеть как:
Uм=ΦRм=HL.
Аналогично электрическим цепям на магнитные цепи распространяются постулаты Кирхгофа:
- Сумма магнитных потоков, втекающих в узел, равна сумме магнитных потоков, вытекающих из узла. Выражение выглядит как ∑Φк=0;
- Сумма магнитодвижущих сил, находящихся в контуре, равна сумме падений напряжений на всех отрезках цепи, что соответствует выражению ∑Iω=∑Uм=∑HL.
Закон полного тока для магнитных цепей стоит на одном уровне с основными законами, касающимися электрических цепей. Понимание закона полного тока позволит с легкостью проводить расчет и подбор необходимых устройств, в основе работы которых лежат магнитные потоки.
Видео
Оцените статью:
Закон полного тока
Закон в интегральном представлении
Рассмотрим бесконечно прямой проводник, по которому циркулирует электрический ток, образующий поле, ограниченное контуром в виде окружности. Плоскость, пронизывающая проводник, – это круг, очерчённый линией данной окружности (см. рис. 1).
Плоскость, пронизывающая проводник, – это круг, очерчённый линией данной окружности (см. рис. 1).
Рис. 1. Поле бесконечно прямого тока
Воспользуемся методом разбиения контура на мизерные участки dl (элементарные векторы длины контура). Пусть φ – угол между векторами dl и B. В нашем случае, при суммировании отрезков, вектор индукции B поворачивается так, что он очерчивает круг, то есть угол φ → 2π.
Из теоремы Остроградского-Гаусса вытекает формула:
Учитывая, что cos φ = 1,
следовательно:
Данная формула – постулат, подтверждённый экспериментально. Согласно этому постулату, циркуляция вектора B по окружности, то есть по замкнутому контуру, равна μ0I, где μ0 = 1/c2 ε0 – магнитная постоянная.
Ориентация вектора dB определяется путём применения правила буравчика. Это направление всегда перпендикулярно вектору плотности. Если проводников будет несколько (например, N), тогда
Каждый ток, с учётом знака, необходимо учитывать такое количество раз, которое соответствует числу его охватов контуром.
Ток берётся со знаком «+», если он по направлению обхода образует правовинтовую систему. При этом, отрицательным считается ток противоположного направления.
Заметим, что формула справедлива только для вакуума. В обычных условиях необходимо учитывать проницаемость среды.
Если ток распределён в пространстве (произвольный ток), тогда
где S – натянутая на контур поверхность, j – объёмная плотность тока. С учётом последнего выражения, формулу полного тока в вакууме можно записать:
Рис. 2. Иллюстрация закона для вакуума
Отсюда вытекает:
- Закон справедлив не только для бесконечно прямолинейного проводника, но и для контуров, произвольной конфигурации.
- Циркуляция вектора магнитной индукции B сориентированного вдоль магнитных линий, всегда отлична от нуля.
- Ненулевая циркуляция свидетельствует о том, что магнитное поле прямолинейного, бесконечно длинного проводника не потенциально. Такое поле называют вихревым, либо соленоидным.

Для справки
В самой полной и объемлющей системе измерений СГС напряженность магнитного поля представляется в эрстедах (Э). В другой действующей системе (СИ) она выражается в амперах на один метр (А/метр). Сегодня эрстед постепенно вытесняется более удобной в работе единицей – ампером на метр. При переводе результатов измерений или расчетов из СИ в СГС используется следующее соотношение:
1 Э = 1000/(4π) А/м ≈ 79,5775 Ампер/метр.
В заключительной части обзора отметим, что независимо от того, какая используется формулировка закона полных токов – суть его остается неизменной. Своими словами это можно представить так: он выражает отношения между токами, пронизывающими данный контур и создаваемыми в веществе магнитными полями.
Напоследок рекомендуем просмотреть полезное видео по теме статьи:
Материалы по теме:
- Что такое электрическое поле
- Зависимость сопротивления проводника от температуры
- Величайшие открытия Николы Тесла
Опубликовано:
03. 07.2019
07.2019
Обновлено: 03.07.2019
9.1.4. Неразветвленная магнитная цепь
Задачей расчета
неразветвленной магнитной цепи в большинстве случаев является определение МДС F= Iw, необходимой для того, чтобы получить
заданные значения магнитного потока или магнитной индукции в некотором участке магнитопровода (чаще всего в воздушном зазоре).
На рис. 9.9 приведен пример
неразветвленной магнитной цепи — магнитопровод
постоянного поперечного сечения S1 с зазором. На этом же рисунке указаны другие
геометрические размеры обоих участков магнитопровода:
средняя длина l1
магнитной линии первого участка из ферромагнитного материала и длина l2 второго участка — воздушного зазора. Магнитные свойства
ферромагнитного материала заданы основной кривой намагничивания В(Н) (рис. 9.10) и тем самым по (9.4)
зависимостью ma(Н).
По закону полного тока (9.2)
где H1 и H2 — напряженности магнитного поля в первом и втором
участках.
В воздушном зазоре значения
магнитной индукции В2 и
напряженности H2
связаны простым соотношением В2 = mН2, а для участка из ферромагнитного
материала В1 = ma1 Н1.
Кроме того, в неразветвленной
магнитной цепи магнитный поток одинаков в любом поперечном сечении магнитопровода:
Ф
= В1S1 =B2S2, (9.6)
где S1 и S2 — площади поперечного сечения участка из ферромагнитного
материала и воздушного зазора.
Если задан магнитный поток Ф, то по (9. 6) найдем значения индукций B1 и B2. Напряженность поля H1 определим по основной кривой намагничивания (рис. 9.10), а
6) найдем значения индукций B1 и B2. Напряженность поля H1 определим по основной кривой намагничивания (рис. 9.10), а
H2= B2m. Далее по (9.5) вычислим необходимое значение МДС.
Сложнее
обратная задача: расчет магнитного потока при заданной
МДС F.
Заменив в (9.5) напряженности
магнитного поля значениями индукции, получим
,
или с учетом (9.6)
где rMk= lkSkmak — магнитное сопротивление k-гoучастка магнитной цепи, причем магнитное сопротивление k-гo участка нелинейное, если зависимость В(H) для этого участка нелинейная (рис. 9.10), т.е. mak≠ const.
Для участка цепи с нелинейным
магнитным сопротивлением rMможно построить вебер-амперную характеристику — зависимость
магнитного потока Ф от магнитного напряжения UMна этом участке магнитопровода.
Вебер-амперная характеристика участка магнитопровода
рассчитывается по основной кривой намагничивания ферромагнитного материала В(H). Чтобы построить вебер-амперную характеристику, нужно ординаты и
абсциссы всех точек основной кривой намагничивания умножить соответственно на
площадь поперечного сечения участка Sи его среднюю длину l.
На рис. 9.11 приведены
вебер-амперные характеристики Ф(UM1) для ферромагнитного участка с нелинейным магнитным
сопротивлением rM1 и Ф(UM2) для воздушного зазора с постоянным магнитным сопротивлением rM2 = l2 S2m магнитопровода по
рис. 9.9.
Между расчетами нелинейных
электрических цепей постоянного тока и магнитных цепей с
постоянными МДС нетрудно установить аналогию.
Действительно, из уравнения (27. 7) следует, что магнитное напряжение на участке
7) следует, что магнитное напряжение на участке
магнитной цепи равно произведению магнитного сопротивления участка на магнитный
поток UM = rMФ. Эта зависимость аналогична закону Ома
для резистивного элемента электрической цепи постоянного тока U = rI.
Сумма магнитных напряжений в контуре магнитной цепи равна сумме МДС этого
контура SUM = SF, что аналогично второму закону Кирхгофа для электрических цепей
постоянного тока SU = SE.
Продолжая дальше аналогию
между электрическими цепями постоянного тока и магнитными цепями с постоянными МДС, представим неразветвленную
магнитную цепь (рис. 9.9) схемой замещения (рис. 9.12, а).
В качестве иллюстрации
ограничимся применением для анализа неразветвленной магнитной цепи графических
методов: метода сложения вебер-амперных характеристик (рис. 9.11) и метода нагрузочной
характеристики (рис. 9.12, б).
9.12, б).
Согласно первому методу
построим вебер-амперную характеристику всей неразветвленной магнитной цепи Ф(UM1 + UM2), графически складывая по напряжению вебер-амперные
характеристики ее двух участков. При известной МДС F= Iwпо вебер-амперной характеристике всей магнитной цепи
определим рабочую точку А, т. е. магнитный поток Ф,
а по вебер-амперным характеристикам участков магнитопровода
— магнитные напряжения на каждом из них.
Согласно второму методу для
второго (линейного) участка построим нагрузочную характеристику
т. е. прямую, проходящую
через точку Fна оси абсцисс
и точку FrM2на оси ординат. Точка пересечения А нагрузочной
характеристики с вебер-амперной характеристикой ферромагнитного участка цепи Ф(UM1) определяет магнитный поток Ф в цепи и магнитные
напряжения на ферромагнитном участке UM1 и воздушном зазоре UM2. Значение индукции в воздушном зазоре B2 = Ф/S2.
Значение индукции в воздушном зазоре B2 = Ф/S2.
9.1.1. Элементы магнитной цепи
Магнитной цепью (магнитопроводом) называется совокупность различных
ферромагнитных и неферромагнитных частей электротехнических устройств для создания магнитных полей нужных конфигурации и
интенсивности. В зависимости от принципа действия электротехнического
устройства магнитное поле может возбуждаться либо постоянным магнитом, либо
катушкой с током, расположенной в той или иной части магнитной цепи.
К простейшим магнитным цепям
относится тороид из однородного ферромагнитного
материала (рис. 9.1). Такие магнитопроводы
применяются в многообмоточных трансформаторах, магнитных усилителях, в
элементах ЭВМ и других электротехнических устройствах.
На рис. 9.2 показана
более сложная магнитная цепь электромеханического устройства, подвижная часть
которого втягивается в электромагнит при постоянном (или переменном) токе в
катушке. Сила притяжения зависит от положения подвижной части магнитопровода.
Сила притяжения зависит от положения подвижной части магнитопровода.
На рис. 9.3 изображена
магнитная цепь, в которой магнитное поле возбуждается постоянным магнитом. Если
подвижная катушка, расположенная на ферромагнитном цилиндре, включена в цепь
постоянного тока, то на нее действует вращающий момент. Поворот катушки с током
практически не влияет на магнитное поле магнитной цепи. Такая магнитная цепь
есть, например, в измерительных приборах магнитоэлектрической системы.
Рассмотренные магнитные цепи,
как и другие возможные конструкции, можно разделить на неразветвленные
магнитные цепи (рис. 9.1 и 9.3), в которых магнитный поток в любом сечении цепи
одинаков, и разветвленные магнитные цепи (рис. 9.2), в которых магнитные потоки
в различных сечениях цепи различны. В общем случае разветвленные магнитные цепи
могут быть сложной конфигурации, например в электрических двигателях,
генераторах и других устройствах.
В большинстве случаев
магнитную цепь следует считать нелинейной, и лишь при определенных допущениях и
определенных режимах работы магнитную цепь можно считать линейной.
Ом: формула, утверждение, вывод, определение, диаграмма
Содержание
Определение закона Ома
При постоянной температуре Георг Ом обнаружил, что электрический ток, протекающий через заданное линейное сопротивление, пропорционален приложенному к нему напряжению. и обратно пропорциональна сопротивлению. Закон Ома основан на соотношении между напряжением, током и сопротивлением. Или связь между электрическим током и разностью потенциалов описывается законом Ома. В большинстве проводников сила тока точно пропорциональна приложенному к ним напряжению. Георг Симон Ом, немецкий ученый, первым экспериментально проверил закон Ома. В этой статье мы подробно обсудим закон Ома, студенты должны добавить эту страницу в закладки, чтобы получать все обновления.
Подробнее. से बहने व| ओम का नियम वोल्टेज, करंट औा या विद्युत पшить औ औ एक संभावित अंतर के की कड़ी को ओम के नियम द्वारा वर्णित किया गय है।।।।।।।।।।।।।। द द द द।।।।।।।।।।।।।।।।।।।।।।।।।।।।। अधिकांश कंडक्टरों में, करंट उन पर लगाए गए वोल्टेज के बिल्कुल समानुपाती होता है।।।।।। जर्मन वैज्ञानिक जॉर्ज साइमन ओम ने सबसे ओम के नियम को पшить
Формула закона Ома
Ниже мы привели формулу закона Ома. Используя приведенную ниже формулу, учащиеся могут рассчитать значения напряжения, сопротивления и силы тока.
Используя приведенную ниже формулу, учащиеся могут рассчитать значения напряжения, сопротивления и силы тока.
| В = ИК |
Это показывает, что напряжение прямо пропорционально току.
В = напряжение или разность потенциалов проводника
I = ток, протекающий по проводнику
R = сопротивление
| I = V/R |
Мы можем найти ток по приведенной выше формуле, если известны напряжение и сопротивление.
| Р = В/И |
Мы можем найти сопротивление, используя приведенную выше формулу, если мы знаем напряжение и силу тока.
Вывод закона Ома для классов 10 и 12
Согласно закону Ома, если проводимость и другие физические условия (длина, поперечное сечение, материал и т. д.) неизменны, ток, протекающий через проводник, пропорционален потенциалу разница по проводнику.
Пусть АВ — проводник. Потенциал на конце А проводника равен ВА, а потенциал на конце В равен ВВ. Предположим, Va > VB |
Потенциал на конце А проводника равен ВА, а потенциал на конце В равен ВВ. Предположим, Va > VB |
Следовательно, ток будет течь от A к B в проводнике. Если ток равен I, то по закону Ома
(VA – VB ) ∝ I [Если развитие и другие физические условия остаются неизменными]
Или, VA-VB = RI [R = постоянная]
Или, В = RI [Если предполагается VA – VB = V.]
Или, I =V/R
Сопротивление проводника относится к этой константе R. проводник уменьшается при большом токе, а ток увеличивается при уменьшении сопротивления.
Утверждение закона Ома
Если разность потенциалов на проводнике равна V, сила тока в проводнике равна I, а сопротивление проводника равно R, по закону Ома R = V/I
Следовательно, сопротивление = (потенциал разность между двумя концами проводника) / ( ток, протекающий через проводник.)
Таким образом, определение сопротивления по закону Ома представляет собой отношение между разностью потенциалов между двумя концами проводника и током, протекающим через проводник. проводника называется сопротивлением этого проводника.
проводника называется сопротивлением этого проводника.
Единица измерения сопротивления
Единицей измерения сопротивления является Ом (Ом). ампер, то сопротивление этого проводника называется сопротивлением 1 Ом.
1 Ом (Ом) = 1 В / 1 А
Эксперимент с законом Ома
Следующий эксперимент позволяет легко подтвердить закон Ома:
Необходимое оборудование: Резистор, Амперметр, Вольтметр, Батарея. Ключ-вилка, реостат
Схема:Процесс
1. Реостат изначально настроен на получение наименьших показаний амперметра A и вольтметра V, когда ключ K закрыт.
2. Регулируя скользящий контакт реостата, ток в цепи постепенно увеличивается. Процедура включает регистрацию тока, протекающего по цепи, и соответствующей разности потенциалов на проводе сопротивления R.
3. На этой основе получают различные наборы значений напряжения и тока.
4. Отношение V/I вычисляется для каждого набора значений V и I.
5. Вы увидите, что отношение V/I для каждого сценария почти идентично, когда вы его вычислите. Таким образом, V/I равно R, константе.
6. Создайте график, на котором сопоставляются ток и потенциал.
Диаграмма закона Ома
Формула закона Ома с помощью приведенной ниже процедуры учащиеся могут рассчитать значения напряжения, сопротивления и силы тока.
| В = ИК |
Закон Ома в векторной форме
Закон Ома в векторной форме: J=σE
Это закон атома в векторной форме
σ = проводимость
Определение мощности на основании Закона об омах
Электрическая мощность – это скорость преобразования энергии из электрической энергии движущихся зарядов в другие формы энергии, такие как механическая энергия, тепловая энергия, энергия, хранящаяся в магнитных полях, или накопленная энергия. в электрических полях.
в электрических полях.
Единица мощности: ватт.
Используя закон Ома и значения напряжения, тока и сопротивления в качестве замены, можно определить электрическую мощность.
P= VI [Если указаны напряжение и ток]
P= v²/R [Если предоставлены напряжение и сопротивление
P=I² R [[Если предоставлены ток и сопротивление]
Закон Ома: круговая диаграмма
Вот круговая диаграмма, с помощью которой учащиеся могут легко узнать значение различных переменных, таких как ток (I), сопротивление (R), мощность (P) и напряжение (V).
Закон Ома: круговая диаграммаЗакон Ома дает взаимосвязь между током, напряжением и сопротивлением
Здесь мы проверим сопротивление при различных напряжениях и токах, взгляните на таблицу, приведенную ниже.
| Напряжение (В) | Ток(I) | Сопротивление(R) Р = В/И |
| 0,5 | 1 | 0,5 |
| 1 | 2 | 0,5 |
| 2 | 2 | 1 |
| 3 | 1 | 3 |
| 4 | 2 | 2 |
| 6 | 2 | 3 |
| 8 | 2 | 4 |
| 10 | 2 | 5 |
| 12 | 3 | 4 |
| 14 | 7 | 2 |
| 16 | 4 | 4 |
| 18 | 9 | 2 |
| 20 | 10 | 2 |
| 15 | 7 | 2,5 |
| 14 | 2 | 7 |
| 22 | 11 | 2 |
| 13 | 2 | 6,5 |
| 11 | 2 | 5,5 |
| 19 | 2 | 9,5 |
Подробнее: Вермикомпост / Вермикомпостирование: Значение, процесс, цена
Подробнее: Дыхательная система: части, функции, органы и болезни
Закон Ома 10 класса: для магнитной цепи
Закон Ома для магнитных цепей F=ϕS.
Пояснение: Закон Ома для магнитных цепей гласит, что МДС прямо пропорциональна магнитному потоку, тогда как магнитное сопротивление является константой пропорциональности.
Закон Ома применим к
Закон Ома верен для всех металлических проводников при низких температурах . Согласно закону Ома, в металлических проводниках при постоянной температуре и отсутствии магнитных полей ток пропорционален напряжению на концах проводника и обратно пропорционален сопротивлению проводника.
Закон Ома: Ограничения
• Электрические компоненты, допускающие протекание тока только в одном направлении, такие как диоды и транзисторы, не подчиняются закону Ома.
• Закон Ома не распространяется на электронные лампы (диодные лампы, триоды), полупроводники (германий, кремний и т. д.), электролитические материалы и газы под низким давлением, т. е. неомические проводники
Закон Ома: Применение
Закон Ома. право широко используется в различных областях.
• Если мы определяем напряжение, сопротивление или ток в цепи по закону Ома.
• Требуемое падение напряжения на электрических компонентах поддерживается законом Ома.
В амперметрах постоянного тока и других шунтах постоянного тока ток также перенаправляется по закону Ома.
Закон Ома: Решенные вопросы
Ниже мы привели примеры закона Ома. Студенты, готовящиеся к сдаче экзаменов, конкурсных или инженерных вступительных экзаменов, должны знать применение закона Ома. Ниже мы привели несколько примеров, потому что числовые вопросы можно задавать по закону Ома. Следовательно, учащиеся должны решить вопросы, и, прежде чем переходить к вопросам, учащиеся должны знать концепцию закона Ома. В физике все основано на концепциях, и она численно основана на этих концепциях. Таким образом, учащиеся не должны полагаться на теорию в физике, они должны решать вопросы, опираясь на понятия закона Ома.
Q.1 В цепи подключена батарея на 20 вольт, и ток, протекающий через эту цепь, составляет 10 ампер. Найдите сопротивление, включенное в цепь.
Найдите сопротивление, включенное в цепь.
Закон Ома гласит, что
R = V/I
Учитывая, что напряжение цепи составляет 20 вольт.
Ток, протекающий по цепи, равен 10 ампер
Согласно закону Ома, сопротивление цепи (R) = 20/10
Сопротивление цепи (R) = 2 Ом
Таким образом, сопротивление, подключенное в цепи, равно 2 Ом
Ом. В электрической цепи с сопротивлением подключена 12-вольтовая батарея. Величина сопротивления 6 Ом. Найдите силу тока, протекающего по цепи.
Закон Ома гласит, что
I = V/R
Учитывая, что напряжение цепи составляет 12 вольт.
Сопротивление, включенное в электрическую цепь, равно 6 Ом.
Найти: Ток, протекающий по электрической цепи I =?
Используя закон Ома
Ток, протекающий по электрической цепи, I = V/R
Ток, протекающий по электрической цепи, I = 2 ампера
Таким образом, ток, протекающий по электрической цепи, равен 2 ампера.
В. По электрической цепи протекает ток силой 12 ампер, и к цепи подключена батарея напряжением В вольт. Сопротивление 0,5 Ом включено последовательно с аккумулятором. Найдите значение V?
Закон Ома гласит, что
V= IR
Дано, Ток, протекающий по электрической цепи I = 12 ампер
Сопротивление, подключенное последовательно к аккумулятору = 0,5 Ом
Найти: Напряжение V =?
Используя закон Ома
Напряжение батареи В = IR
Напряжение батареи В = 12*0,5
Напряжение батареи В = 6 В Подробнее: Ферментация: процесс, примеры, реакция, диаграмма
Закон Ома: часто задаваемые вопросы
В. Что такое закон Ома?
Закон Ома утверждает, что напряжение на проводнике пропорционально протекающему по нему току, если все физические параметры и температура остаются постоянными.
В. По какой формуле можно рассчитать напряжение по закону Ома?
Формула для расчета напряжения по закону Ома
В = IR
В. Какая формула для расчета тока по закону Ома?
Какая формула для расчета тока по закону Ома?
Формула для расчета тока по закону Ома
I = V/R
В. По какой формуле можно рассчитать сопротивление по закону Ома?
Формула для расчета сопротивления по закону Ома
R = V/I
В. Что такое R в формуле закона Ома?
R — сопротивление в формуле закона Ом.
Делиться заботой!
15
акции
Магнитная цепь Закон Ома Вопросы и ответы
Этот набор вопросов и ответов с несколькими вариантами ответов (MCQ) по основам электротехники посвящен «Закону Ома для магнитной цепи».
1. Закон Ома для магнитных цепей _________
a) F=ϕS
b) F=ϕ/S
c) F=ϕ 2 S
d) F=ϕ/S 2
Посмотреть ответ
Ответ: a
Объяснение: Закон Ома для магнитных цепей утверждает, что МДС прямо пропорциональна магнитному потоку, где сопротивление является константой пропорциональности.
2. Что происходит с МДС при уменьшении магнитного потока?
a) Увеличивается
b) Уменьшается
c) Остается постоянным
d) Становится равным нулю поток уменьшается, МДС также уменьшается.
3. Рассчитайте МДС, если магнитный поток равен 5Вб, а магнитное сопротивление равно 3А/Вб.
а) 10А
б) 10Н
c) 15N
d) 15At
Посмотреть ответ
Ответ: d
Объяснение: Мы знаем, что:
F=ϕS
Подставляя данные из вопроса, получаем MMF = 15At.
реклама
реклама
4. Кольцо площадью поперечного сечения 2 500 мм, окружностью 400 мм и ϕ=800 мкВб имеет катушку из 200 витков, намотанную вокруг него. Рассчитайте плотность потока кольца.
a) 1.6T
b) 2.6T
c) 3.6T
d) 4.6T
Посмотреть ответ
Ответ: a
Объяснение: ϕ=BA => плотность потока B = ϕ/A
Подставляя значения, получаем B=1,6T.
5. Кольцо с площадью поперечного сечения 500 мм 2 , окружностью 400 мм и ϕ=800 мкВб имеет катушку из 200 витков, намотанную вокруг него. Относительная магнитная проницаемость кольца равна 380. Рассчитайте магнитное сопротивление.
Относительная магнитная проницаемость кольца равна 380. Рассчитайте магнитное сопротивление.
а) 1,68 * 10 -4 А/Вб
б) 1,68 * 10 4 А/Вб
в) 1,68 * 10 6 А/Вб
г) 1,68 * 947 — 60458 A/Wb
Посмотреть ответ
Ответ: c
Объяснение: Сопротивление=l/(µ*A) = l/(µ r µ 0 *A)
Подставляя значения, получаем Сопротивление=1,68* 10 6 А/Вб.
6. Кольцо с площадью поперечного сечения 500 мм 2 , окружностью 400 мм и ϕ=800 мкВб имеет катушку из 200 витков, намотанную вокруг него. Относительная магнитная проницаемость кольца равна 380. Рассчитайте магнитодвижущую силу.
а) 1442Ат
б) 1342Ат
в) 1432Ат
г) 1344Ат
Просмотреть Ответ
Ответ: d
Объяснение: Сопротивление=l/(µ*A) = l/(µ r µ 0 *A)
Подставляя значения, получаем Сопротивление S=1,68*106 A/ Вб.
F=ϕS
Подставляя данные значения, получаем F = 1344At.
7. Кольцо с площадью поперечного сечения 500 мм 2 , окружностью 400 мм и ϕ=800 мкВб имеет катушку из 200 витков, намотанную вокруг него. Относительная магнитная проницаемость кольца равна 380. Рассчитайте ток намагничивания.
а) 6.7А
b) 7.7A
c) 7.6
d) 6.1A
Посмотреть ответ
Ответ: a
Объяснение: Сопротивление = l/(µ*A) = l/(µ r µ 0 *A)
Подставляя значения, получаем Сопротивление S=1,68*106 А/Вб.
F=ϕS Подставляя данные значения, получаем F = 1344At.
I=F/N Подставляя значения из вопроса, получаем I=6.7A.
реклама
8. Можно ли применить закон Кирхгофа к магнитным цепям?
а) Да
б) Нет
в) Зависит от контура
d) Недостаточно информации
Просмотреть ответ
Ответ: a
Объяснение: Магнитные цепи имеют эквивалент разности потенциалов электрических цепей. Это разность магнитных потенциалов, которая позволяет нам применять законы Кирхгофа к анализу магнитной цепи.
9. Что такое ММФ?
a) Сила магнитного механизма
b) Магнитодвижущая сила
c) Сила магнитного движения
d) Сила магнитодвижения
View Answer
Ответ: b
Пояснение: МДС обозначает магнитодвижущую силу. На самом деле это не сила. Он аналогичен потенциалу в электрическом поле.
объявление
10. Эквивалент тока I в магнитном законе Ома равен?
a) Поток
b) Сопротивление
c) МДС
d) Сопротивление
Просмотреть ответ
Ответ: a
Объяснение: Эквивалентом тока по закону магнитного Ома является поток, как:
V=IR эквивалентно F=ϕS.
Sanfoundry Global Education & Learning Series – основы электротехники.
Для практики во всех областях базовой электротехники, Вот полный набор из 1000+ вопросов и ответов с множественным выбором .
Следующие шаги:
- Получите бесплатный сертификат о заслугах в области базовой электротехники
- Принять участие в конкурсе по базовой сертификации электротехники
- Станьте лучшим специалистом в области базовой электротехники
- Пройти базовые тесты по электротехнике
- Практические тесты по главам: глава 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
- Пробные тесты по главам: глава 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
реклама
реклама
Подпишитесь на наши информационные бюллетени (тематические). Участвуйте в конкурсе сертификации Sanfoundry, чтобы получить бесплатный Сертификат отличия. Присоединяйтесь к нашим социальным сетям ниже и будьте в курсе последних конкурсов, видео, стажировок и вакансий!
Участвуйте в конкурсе сертификации Sanfoundry, чтобы получить бесплатный Сертификат отличия. Присоединяйтесь к нашим социальным сетям ниже и будьте в курсе последних конкурсов, видео, стажировок и вакансий!
Ютуб | Телеграмма | Линкедин | Инстаграм | Фейсбук | Твиттер | Пинтерест
Маниш Бходжасиа, ветеран технологий с более чем 20-летним стажем работы в Cisco и Wipro, является основателем и техническим директором в 9 лет.0071 Санлитейный завод . Он живет в Бангалоре и занимается разработкой Linux Kernel, SAN Technologies, Advanced C, Data Structures & Alogrithms. Оставайтесь на связи с ним в LinkedIn.
Подпишитесь на его бесплатные мастер-классы на Youtube и технические обсуждения в Telegram SanfoundryClasses.
10.3: Магнитные цепи — Инженерные тексты LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 25023
- Джеймс М.
 Фиоре
Фиоре - Муниципальный колледж Mohawk Valley
Магнитные цепи включают в себя такие приложения, как трансформаторы и реле. Очень простая магнитная цепь показана на рис. 10.3.1. .
Рисунок 10.3.1 : Простая магнитная цепь.
Во-первых, он состоит из магнитного сердечника. Сердцевина может состоять из одного материала, такого как листовая сталь, но также может состоять из нескольких секций и воздушных зазоров. Вокруг сердечника находится по крайней мере один набор витков провода, то есть катушка, сформированная вокруг сердечника. Для трансформаторов используется несколько наборов витков (в простейшем случае один для первичной обмотки, а другой для вторичной). Как мы уже видели, прохождение тока через обмотки создает магнитный поток \(\Phi\) в сердечнике. Поскольку этот поток ограничен площадью поперечного сечения сердечника \(A\), мы можем получить плотность потока \(B\).
\[B = \frac{\Phi}{A} \label{10.4} \]
Где
\(B\) — плотность магнитного потока в теслах,
\(\Phi\) — магнитный поток в веберах,
\(A\) — площадь в квадратных метрах.
Вспомним из главы 9, что один тесла определяется как один вебер на квадратный метр. Альтернативной единицей измерения, которая иногда используется, является гаусс (система единиц cgs), названная в честь Карла Фридриха Гаусса, немецкого математика и ученого.
\[1 \text{ тесла }= 10 000 \text{гаусс} \label{10,5} \] 92} \номер \]
\[B = 0.3T \номер\]
Закон Ома для магнитных цепей (закон Хопкинсона или закон Роуленда)
Между магнитными цепями и электрическими цепями проводится общая параллель, а именно закон Хопкинсона (закон Роуленда). Для электрических цепей закон Ома гласит:
\[V = I R \nonumber \]
Аналогично, для магнитных цепей имеем:
\[\boldsymbol{F} = \Phi \boldsymbol{R} \ метка{10.6} \]
Где
\(\boldsymbol{F}\) — магнитодвижущая сила (или МДС) в ампер-витках,
\(\Phi\) — магнитный поток в веберах,
\(\boldsymbol{R}\) — нежелание материала в ампер-витках/веберах.
Магнитодвижущая сила сравнивается с напряжением источника или электродвижущей силой (ЭДС), магнитный поток уподобляется протеканию тока, а сопротивление заменяет сопротивление (т. е., с одной стороны, мы имеем материал, который сопротивляется потоку тока, а с другой — материал, в котором существует «нежелание» устанавливать магнитный поток). Далее, магнитодвижущая сила есть произведение тока, протекающего через катушку, и количества петель или витков в катушке:
е., с одной стороны, мы имеем материал, который сопротивляется потоку тока, а с другой — материал, в котором существует «нежелание» устанавливать магнитный поток). Далее, магнитодвижущая сила есть произведение тока, протекающего через катушку, и количества петель или витков в катушке:
\[\boldsymbol{F} = N I \label{10.7} \]
Где
\(\boldsymbol{F}\) — магнитодвижущая сила в ампер-витках,
\(Н\) — количество витков или витков в катушке,
\(I\) — ток в катушке в амперах.
Уравнение сопротивления имеет хорошую параллель с уравнением сопротивления (уравнение 2.11 из главы 2):
\[R = \frac{\phi l}{A} \nonumber \]
\[\boldsymbol{ R} = \frac{l}{\mu A} \label{10.8} \]
Где
\(\boldsymbol{R}\) сопротивление в ампер-витках/вебер,
\(l\) длина материала в метрах,
\(A\) крест площадь сечения материала в квадратных метрах,
\(\mu\) — проницаемость материала в генри/метр.
Учитывая характеристики катушки и длину пути магнитной цепи, магнитный поток создает намагничивающую силу \(H\).
\[H = \frac{N I}{l} \label{10.9} \]
Где
\(H\) — намагничивающая сила в ампер-витках/метр,
\(N\) — количество витков или витков в катушке,
\(I\) — ток катушки в амперах,
\(l\) — длина магнитного пути в метрах.
Уравнение \ref{10.8} показывает, что ферромагнитные материалы (т. е. материалы с высокой магнитной проницаемостью, такие как сталь) создают низкое магнитное сопротивление. Практическая проблема здесь заключается в том, что \(\mu\), в отличие от удельного сопротивления \(\rho\) резисторов, не является константой для таких материалов. Он может значительно варьироваться, как видно из общей схемы, представленной на рис. 10.3.2. . В результате нецелесообразно находить нежелание таким же образом, как мы находим сопротивление. Однако не все потеряно.
Рисунок 10.3.2 : Типичная кривая проницаемости для материала с высокой проницаемостью.
Плотность потока и соответствующая сила намагничивания для любого данного материала связаны следующим уравнением: в теслах,
\(\mu\) — проницаемость материала в генри/метр,
\(H\) — намагничивающая сила в ампер-витках/метр.
Еще раз, самое сложное здесь — проницаемость материала сердцевины. Для воздуха мы можем использовать проницаемость свободного пространства \(\mu_0\). 9{-6} H/m \label{10.11} \]
Для других материалов, таких как листовая сталь или литая сталь, мы пойдем другим путем; а именно эмпирически полученная кривая, которая отображает плотность потока \(B\) в зависимости от силы намагничивания \(H\). Такие графики обычно называют «кривыми \(BH\)». Пример показан на рисунке 10.3.3.
. Ясно, что эта кривая не является красивой прямой линией или даже очевидной предсказуемой функцией. Непосредственно очевидными атрибутами являются начальный крутой подъем, за которым следует уплощение кривой. Это уплощение соответствует насыщению магнитного материала. Напротив, график для воздуха показал бы прямую линию с очень пологим уклоном. Как мы увидим, возможность достижения высокой плотности потока для данной силы намагничивания приведет к созданию эффективной и действенной магнитной цепи. Таким образом, несмотря на то, что воздух не насыщает, результирующая плотность потока низкая, что обычно приводит к снижению производительности.
Рисунок 10.3.3 : Общая кривая \(BH\).
Кривая BH
Процесс создания кривой \(BH\) выглядит следующим образом. Сначала мы создаем ядро исследуемого материала. Затем вокруг этого сердечника наматывается катушка проволоки. Пример показан на рисунке 10.3.4. . Здесь у нас есть базовый тороид с катушкой из \(N\) витков.
Рисунок 10.3.4 : Тороидальный сердечник с катушкой.
Начнем с системы в состоянии покоя и без напряжения. К катушке прикладывается небольшой ток \(I\). Это создает намагничивающую силу по уравнению \ref{10.9}. Будет соответствующая плотность потока согласно уравнению \ref{10.10}.
Затем ток увеличивается. Это приводит к увеличению намагничивающей силы и соответствующему изменению плотности потока. Ток увеличивается до тех пор, пока кривая не станет плоской, что указывает на достижение насыщения. Эта траектория показана пунктирной линией на рис. 10.3.5.
, начиная с точки \(\boldsymbol{a}\) с точкой \(\boldsymbol{b}\), указывающей насыщенность. Затем ток уменьшается. Это вызывает уменьшение намагничивающей силы, но, хотя плотность потока уменьшается, он не возвращается точно по исходной траектории. Вместо этого кривая смещается выше оригинала.
Затем ток уменьшается. Это вызывает уменьшение намагничивающей силы, но, хотя плотность потока уменьшается, он не возвращается точно по исходной траектории. Вместо этого кривая смещается выше оригинала.
Рисунок 10.3.5 : Создание кривой BH.
В конце концов ток упадет до нуля. Это соответствует точке \(\boldsymbol{c}\) на графике рис. 10.3.5. . В этот момент, даже если в катушке нет тока, в сердечнике все еще есть поток. Результирующая плотность потока называется сохраняющей способностью и является мерой остаточного магнетизма. Именно это явление позволяет намагничивать материалы.
Если теперь мы изменим направление тока катушки и начнем увеличивать его величину, плотность потока будет продолжать падать. В точке \(\boldsymbol{d}\) он достигнет нуля. Поскольку мы фактически вернули поток к нулю, мы называем намагничивающую силу, необходимую для этого, коэрцитивной силой или коэрцитивной силой.
При увеличении величины тока плотность потока также увеличивается, но с обратным знаком. В конце концов, насыщение снова достигается в точке \(\boldsymbol{e}\). Опять же, если величина тока уменьшится, величина плотности потока также уменьшится, но не будет точно повторять исходную траекторию. На этот раз он пойдет по нижнему пути. Когда ток уменьшается до нуля в точке \(\boldsymbol{f}\), очевидна зеркальная сохраняемость. Дальнейшее положительное увеличение тока показывает зеркальную коэрцитивную силу в точке \(\boldsymbol{g}\). Наконец, когда ток увеличивается до максимума, мы снова достигаем насыщения в точке \(\boldsymbol{b}\).
В конце концов, насыщение снова достигается в точке \(\boldsymbol{e}\). Опять же, если величина тока уменьшится, величина плотности потока также уменьшится, но не будет точно повторять исходную траекторию. На этот раз он пойдет по нижнему пути. Когда ток уменьшается до нуля в точке \(\boldsymbol{f}\), очевидна зеркальная сохраняемость. Дальнейшее положительное увеличение тока показывает зеркальную коэрцитивную силу в точке \(\boldsymbol{g}\). Наконец, когда ток увеличивается до максимума, мы снова достигаем насыщения в точке \(\boldsymbol{b}\).
Если ток повторяется таким же образом, процесс повторяется, и снова используется внешний путь, указанный стрелками. Таким образом, определенное значение намагничивающей силы может привести к различным значениям плотности потока: это зависит от недавней истории материала. Этот эффект известен как гистерезис и встречается и в других областях.
Фактически опубликованные кривые \(BH\) следуют середине петли гистерезиса. Пример кривых \(BH\) для трех различных материалов сердечника показан на рисунке 10. 3.6. 1 . Кривая А относится к листовой стали (обычной для трансформаторов), кривая В — к литой стали, а кривая С — к чугуну. Мы будем использовать их в следующих примерах. Кривые для других материалов также доступны.
3.6. 1 . Кривая А относится к листовой стали (обычной для трансформаторов), кривая В — к литой стали, а кривая С — к чугуну. Мы будем использовать их в следующих примерах. Кривые для других материалов также доступны.
Рисунок 10.3.6 : Кривые BH для: A. Листовой стали B. Литой стали C. Чугуна
Пример 10.3.2
Предположим, что тороид на рис. 10.3.4 изготовлен из литой стали, имеет катушку из 500 витков, сечение 2 см на 2 см и среднюю длину пути 50 см. Определить поток в веберах, если катушку питает ток 0,3 ампер.
Мы будем использовать уравнение \ref{10.9}, чтобы найти силу намагничивания и из кривой \(BH\), чтобы найти плотность потока.
\[H = \frac{N I}{l} \номер\]
\[H = \frac{500 \text{ оборотов} \times 0,3 A}{0,5 м} \nonumber \]
\[H = 300 Ат/м \text{ (ампер-витков на метр)} \nonumber \]
Литая сталь соответствует кривой B (зеленая) на рис. 10.3.5.
. Достойная оценка плотности потока составляет 0,52 тесла. Это соответствующая плотность потока. Чтобы найти поток, нужно найти площадь сердечника. 92 \номер \]
Это соответствующая плотность потока. Чтобы найти поток, нужно найти площадь сердечника. 92 \номер \]
\[\Phi = 2.08E-4Wb \номер\]
КВЛ для магнитных цепей
Беглое изучение уравнений \ref{10.7} и \ref{10.9} показывает, что:
\[\boldsymbol{F} = H l = N I \label{10.12} \]
аналогия с законом Ома, произведение ампер-витков катушки, \(NI\), аналогично повышению напряжения. Далее произведение \(Hl\) аналогично падению напряжения. Если мы затем расширим аналогию, включив в нее понятие закона Кирхгофа о напряжении, то не должно вызывать удивления, что сумма \(NI\) «подъемов» должна равняться сумме \(Hl\) «падений». В схеме рисунка 10.3.4 , есть один «подъем» и один «падение». Таким образом, магнитная цепь аналогична минимальной электрической цепи, показанной на рис. 10.3.7. . \(\boldsymbol{F}\) — магнитодвижущая сила, \(NI\), а \(\boldsymbol{R}\) — сопротивление тороидального сердечника. Это нежелание испытает «падение» \(Hl\).
Рисунок 10. 3.7
: Аналогия электрической цепи для магнитной системы на рис. 10.3.4.
.
3.7
: Аналогия электрической цепи для магнитной системы на рис. 10.3.4.
.
Сердечник может состоять из двух или более различных материалов, создавая эквивалент последовательной цепи. В этом случае таблица, подобная приведенной на рис. 10.3.8. можно использовать для помощи в вычислениях. В этой таблице каждому разделу ядра отведена своя строка. Таблица разделена на две стороны (обратите внимание на толстую разделительную линию в центре). В общем, мы будем решать задачи, где мы знаем данные в левой части и должны найти что-то в правой части, или наоборот. Мост между двумя сторонами (т. е. пересечение толстой линии) представляет собой кривую \(BH\) для материала этого конкретного участка. Исключением из этого правила является, если секция представляет собой воздушный зазор. В этом случае мы можем использовать определение \ref{10.11}, которое показывает, что для воздуха \(H \ приблизительно 7,92\))
Плотность потока
Б (Т)
Сила намагничивания
\(H\) (Ат/м)
Длина
\(л\) (м)
«Капля»
\(Хл\) (Ат)
 3.8
: формат таблицы, используемый для анализа магнитной цепи.
3.8
: формат таблицы, используемый для анализа магнитной цепи.Пришло время привести несколько наглядных примеров. Мы рассмотрим простую систему, подобную той, что изображена на рис. 10.3.4. , двухсекционный сердечник, сердечник с воздушным зазором и сердечник с двумя витками.
Пример 10.3.3
Предположим, ядро на рис. 10.3.9 изготовлен из листовой стали, имеет катушку из 200 витков, сечение 1 см на 1 см и среднюю длину пути 12 см. Определите ток катушки, необходимый для достижения потока 1E−4 Вебера.
Рисунок 10.3.9: Магнитная система для примера 10.3.3 .
Аналогичная схема состоит из одного источника и реактивного сопротивления, как на рис. 10.3.7. . Таким образом,
\[N I = H_{лист} l_{лист} \номер\]
Мы начнем с заполнения тех частей таблицы, к которым можно обращаться напрямую, таких как длина пути, площадь и поток. Не забудьте преобразовать значения сантиметров в метры.
| Раздел | Флюс 92\)) | Плотность потока Б (Т) | Сила намагничивания \(H\) (Ат/м) | Длина \(л\) (м) | «Капля» \(Хл\) (Ат) | Плотность потока Б (Т) | Сила намагничивания \(H\) (Ат/м) | Длина \(л\) (м) | «Капля» \(Хл\) (Ат) |
|---|---|---|---|---|---|---|
| Листовая сталь | 1E−4 | 1E−4 | 1 | 0,12 |
Мы используем кривую \(BH\) на рис. 2\))»> 1E−4
2\))»> 1E−4
На этом этапе мы находим \(Hl\) «каплю» с помощью простого умножения.
| Раздел | Флюс \(\Phi\) (Вб) | 92\))Плотность потока Б (Т) | Сила намагничивания \(H\) (Ат/м) | Длина \(л\) (м) | «Капля» \(Хл\) (Ат) | |
|---|---|---|---|---|---|---|
| Листовая сталь | 1E−4 | 1E−4 | 1 | 190 | 0,12 | 22,8 |
Это «падение» составляет 22,8 ампер-витка, а в катушке 200 витков. Следовательно, требуемый ток:
Следовательно, требуемый ток:
\[I = \frac{H l}{N} \номер\]
\[I = \frac{22.8At}{200 t} \номер\]
\[I = 114 мА \номер\]
Далее рассмотрим ядро с двумя секциями.
Пример 10.3.4
Учитывая магнитную систему, показанную на рис. 10.3.10 Предположим, что секция А изготовлена из листовой стали, а секция В — из литой стали. Каждая часть имеет поперечное сечение 2 см на 2 см. Длина пути А равна 12 см, а длина пути В равна 4 см. Если катушка имеет 50 витков, определите ток катушки, необходимый для достижения потока 2E−4 Вебера.
Рисунок 10.3.10 : Магнитная система для примера 10.3.4 .
Аналоговая схема состоит из одного источника и двух магнитных сопротивлений. Это показано на рисунке 10.3.11. .
Следовательно:
\[N I = H_{лист} l_{лист}+H_{отливка} l_{отливка} \номер\]
Для нашей таблицы будет две строки, одна для листовой стали и вторая для литой стали. В первом ряду потребуется использовать кривую А (листовая сталь) с рис. 2\))»> 4E-4
2\))»> 4E-4
Кривые \(BH\) используются для перехода на правую сторону, и мы получаем: 92\))
Плотность потока
Б (Т)
Сила намагничивания
\(H\) (Ат/м)
Длина
\(л\) (м)
«Капля»
\(Хл\) (Ат)
А теперь заполняем \(Hl\) «капли»: 92\))
Плотность потока
Б (Т)
Сила намагничивания
\(H\) (Ат/м)
Длина
\(л\) (м)
«Капля»
\(Хл\) (Ат)
Используя нашу аналогию с КВЛ, общее «падение» составляет 8,4 А + 11,6 А, или 20 ампер-витков. Катушка была указана как имеющая 50 витков. Следовательно:
Катушка была указана как имеющая 50 витков. Следовательно:
\[I = \frac{H l}{N} \номер\]
\[I = \frac{20 At}{50 t} \nonumber \]
\[I = 400 мА \номер\]
Обратите внимание, что, несмотря на то, что литая стальная секция короче, чем секция из листовой стали, она дает больший «капля»; точно так же, как больший резистор в электрической цепи. Это требует большего тока в катушке, чем если бы весь сердечник был сделан из листовой стали.
Наконец, должно быть очевидно, что потребление тока может быть уменьшено, если катушка имеет больше витков. Здесь есть практический предел, потому что все витки должны соответствовать отверстию сердечника. Как только это пространство заполнено, единственный способ увеличить количество витков — использовать провод более тонкого сечения, но это увеличивает сопротивление провода и потери мощности, а также снижает максимальный ток.
Воздушные зазоры
Некоторые системы включают воздушный зазор в сердечнике. Если для остатка есть только один материал, это создаст систему, подобную той, что изображена на рисунке 10.3.12.
. Основное наблюдение здесь заключается в том, что проницаемость воздуха намного ниже, чем у ферромагнитных материалов, и поэтому зазор будет демонстрировать относительно большое сопротивление по сравнению с длиной его пути. Тогда возникает очевидный вопрос: зачем нам использовать пробел? Одним из возможных вариантов является электромагнитное реле, внутреннее устройство которого показано на рис. 10.3.13.
.
Если для остатка есть только один материал, это создаст систему, подобную той, что изображена на рисунке 10.3.12.
. Основное наблюдение здесь заключается в том, что проницаемость воздуха намного ниже, чем у ферромагнитных материалов, и поэтому зазор будет демонстрировать относительно большое сопротивление по сравнению с длиной его пути. Тогда возникает очевидный вопрос: зачем нам использовать пробел? Одним из возможных вариантов является электромагнитное реле, внутреннее устройство которого показано на рис. 10.3.13.
.
Рисунок 10.3.12 : Аналогичная электрическая схема для системы с воздушным зазором.
Рисунок 10.3.13 : Внутреннее устройство электрического реле.
Чтобы создать реле, мы помещаем одну часть сердечника на шарнир, который можно удерживать в открытом положении с помощью небольшой пружины. Это создает воздушный зазор (слева от сердечника на рисунке). Если подать достаточно большой ток, то результирующего магнитного потока будет достаточно, чтобы преодолеть натяжение пружины и замкнуть второй кусок на первый (т. е. магнитное притяжение). Как только это происходит, зазор исчезает, уменьшая сопротивление вокруг петли. Система будет оставаться закрытой до тех пор, пока не отключится ток катушки и возвратная пружина снова не разъединит две секции. Мы добавляем изолированные металлические контакты в подвижную секцию, и в итоге мы получаем сверхмощный переключатель, который «приводится» в действие управляющим током, а не механическим рычагом, приводимым в движение человеком. 92\). Длина пути основного сердечника составляет 8 см, а длина пути зазора — 1 мм. Сколько витков потребуется катушке, чтобы ток катушки 400 мА достиг потока 1,2E−4 Вебера?
е. магнитное притяжение). Как только это происходит, зазор исчезает, уменьшая сопротивление вокруг петли. Система будет оставаться закрытой до тех пор, пока не отключится ток катушки и возвратная пружина снова не разъединит две секции. Мы добавляем изолированные металлические контакты в подвижную секцию, и в итоге мы получаем сверхмощный переключатель, который «приводится» в действие управляющим током, а не механическим рычагом, приводимым в движение человеком. 92\). Длина пути основного сердечника составляет 8 см, а длина пути зазора — 1 мм. Сколько витков потребуется катушке, чтобы ток катушки 400 мА достиг потока 1,2E−4 Вебера?
Рисунок 10.3.14 : Магнитная система для примера 10.3.5 .
Аналогичная схема состоит из одного источника и двух реактивных резисторов, один для сердечника из листовой стали и второй для воздушного зазора. Это показано на рисунке 10.3.12. . Далее аналогичное отношение КВЛ:
\[N I = H_{лист} l_{лист} +H_{пробел} l_{пробел} \номер\]
В этой таблице будет две строки: одна для сердцевины из листовой стали и одна для воздушного зазора. Как мы видели, поток будет одинаковым в обоих сечениях. Оттуда мы можем заполнить некоторые другие значения в таблице, в результате чего:
Как мы видели, поток будет одинаковым в обоих сечениях. Оттуда мы можем заполнить некоторые другие значения в таблице, в результате чего:
| Раздел | Флюс \(\Phi\) (Вб) | 92\)) | Плотность потока Б (Т) | Сила намагничивания \(H\) (Ат/м) | Длина \(л\) (м) | «Капля» \(Хл\) (Ат) |
|---|---|---|---|---|---|---|
| Листовая сталь | 1.2E-4 | 3E-4 | 0,4 | 63 | 8E-2 | |
| Зазор | 1. 2\))»> 3E-4 2\))»> 3E-4 | 0,4 | 3.183E5 | 1E−3 |
Кривая \(BH\) для листовой стали и определение \ref{10.11} для воздушного зазора используются для перехода на правую сторону, что дает: 92\))
Плотность потока
Б (Т)
Сила намагничивания
\(H\) (Ат/м)
Длина
\(л\) (м)
«Капля»
\(Хл\) (Ат)
 2\))»> 3E-4
2\))»> 3E-4«Капли» \(Hl\) заполнены: 92\))
Плотность потока
Б (Т)
Сила намагничивания
\(H\) (Ат/м)
Длина
\(л\) (м)
«Капля»
\(Хл\) (Ат)
 2\))»> 3E-4
2\))»> 3E-4Используя нашу аналогию с КВЛ, общее «падение» составляет 5,0 Ат + 318,3 А, или 523,3 ампер-витка. Ток катушки был задан равным 400 мА. Следовательно: 92\) и длина стержня 20 см. Первая катушка состоит из 2000 витков, вторая катушка состоит из 500 витков. Если ток 120 мА в катушке 1 достигает потока 2,4E−4 Вебера, определите ток катушки 2.
Рисунок 10.3.15 : Магнитная система для примера 10.3.6 .
Рисунок 10.3.16 : Аналогичная электрическая схема для системы рис. 10.3.15 .
Аналогичная схема состоит из двух источников напряжения и одного сопротивления для сердечника из листовой стали. Это показано на рисунке 10.3.16. .
Аналогичное отношение KVL:
\[N_1 I_1 −N_2 I_2 = H_{лист} l_{лист} \номер\]
Поскольку мы ищем \(I_2\), мы можем преобразовать это уравнение в более удобную форму:
\[N_2 I_2 = N_1 I_1 −H_{лист} l_{лист} \номер\]
Для этой таблицы потребуется только одна строка. 2\))»> 3E-4
2\))»> 3E-4
Кривая \(BH\) для листовой стали используется для перехода на правую сторону:
| Раздел | Флюс \(\Phi\) (Вб) | 92\))Плотность потока Б (Т) | Сила намагничивания \(H\) (Ат/м) | Длина \(л\) (м) | «Капля» \(Хл\) (Ат) |
|---|---|---|---|---|---|
| Листовая сталь | 2. 2\))»> 3E-4 2\))»> 3E-4 | 0,8 | 100 | 0,2 |
\(Hl\) «капля» вычисляется:
| Раздел | Флюс \(\Phi\) (Вб) | Район 92\)) | Плотность потока Б (Т) | Сила намагничивания \(H\) (Ат/м) | Длина \(л\) (м) | «Капля» \(Хл\) (Ат) |
|---|---|---|---|---|---|---|
| Листовая сталь | 2. 2\))»> 3E-4 2\))»> 3E-4 | 0,8 | 100 | 0,2 | 20 |
Используя аналогию с КВЛ, находим:
\[N_2 I_2 = N_1 I_1 −H_{лист} l_{лист} \номер\]
\[N_2 I_2 = 2000 \text{ витков} \times 120mA −20 At \nonumber \]
\[N_2 I_2 = 240At −20 At \номер\]
\[N_2 I_2 = 220At\номер\]
Катушка номер два имеет 500 витков, поэтому ее ток:
\[I_2 = \frac{220 At}{500 витков} \номер\]
\[I_2 = 440 мА \номер\]
Ключевым моментом является то, что в предыдущем примере для работы, как описано, должен использоваться переменный ток. Постоянный ток не даст ожидаемых результатов. Причина этого восходит к определению 10.2.1 и уравнению 10.2.2: если поток не изменяется относительно проводящей катушки, в катушке не будет индуцироваться напряжение. Таким образом, хотя входной постоянный ток будет создавать поток в сердечнике, этот поток будет статичным и неизменным. Следовательно, вторая катушка не будет производить выходной сигнал. Напротив, переменный ток плавно изменяется по амплитуде и полярности. Это создает плавно изменяющийся магнитный поток, который, в свою очередь, позволяет индуцировать напряжение во второй катушке.
Таким образом, хотя входной постоянный ток будет создавать поток в сердечнике, этот поток будет статичным и неизменным. Следовательно, вторая катушка не будет производить выходной сигнал. Напротив, переменный ток плавно изменяется по амплитуде и полярности. Это создает плавно изменяющийся магнитный поток, который, в свою очередь, позволяет индуцировать напряжение во второй катушке.
Предположим на мгновение, что в предыдущем примере использовался переменный ток, обратите внимание, что ток во второй катушке почти в четыре раза выше, чем в первой. Если бы нам удалось свести «падение» сердечника к нулю, возможно, за счет снижения сопротивления сердечника до пренебрежимо малой величины, то ток увеличился бы ровно в четыре раза (до 480 мА против 440 мА). Это то же самое, что отношение количества витков первой катушки к количеству витков второй катушки, и известно как коэффициент витков. Это ключевой параметр, описывающий трансформаторы, который как раз является предметом следующего раздела.
Ссылки
1 Кривые на основе https://en.Wikipedia.org/wiki/Saturation_(magnet); Steinmetz (1917), Теория и расчет электрических цепей; и Бойлестад (2010), Вводный анализ цепей.
Эта страница под названием 10.3: Magnetic Circuits распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Джеймсом М. Фиоре с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами LibreTexts. Платформа; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Джеймс М.
 Фиоре
Фиоре
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4,0
- Показать оглавление
- нет
- Теги
- source@http://www.dissidents.com/resources/DCElectricalCircuitAnalysis.pdf
Закон Ома для магнитных цепей _________
← Предыдущий вопрос Следующий вопрос →
1 ответ
+1 голос
Похожие вопросы
Эквивалент тока I по закону магнитного Ома равен?
спросил 12 сент. 2021 г. в базовой электротехнике по год (88,7 тыс. баллов)
- основы электротехники
- простые магнитопроводы
- закон Ома для магнитной цепи
Можно ли применить закон Кирхгофа к магнитным цепям?
спросил
12 сент. 2021 г.
в базовой электротехнике
по
год
(88,7 тыс. баллов)
2021 г.
в базовой электротехнике
по
год
(88,7 тыс. баллов)
- основы электротехники
- простые магнитопроводы
- закон Ома для магнитной цепи
Рассчитайте МДС, если магнитный поток равен 5Вб, а магнитное сопротивление равно 3А/Вб.
спросил 12 сент. 2021 г. в базовой электротехнике по год (88,7 тыс. баллов)
- основы электротехники
- простые магнитопроводы
- закон Ома для магнитной цепи
Что происходит с МДС при уменьшении магнитного потока? 92, окружностью 400 мм и ϕ=800 мкВб, вокруг него намотана катушка из 200 витков. Относительная магнитная проницаемость кольца равна 380. Рассчитайте магнитное сопротивление.
спросил 12 сент. 2021 г. в базовой электротехнике по год (88,7 тыс. баллов)
- основы электротехники
- простые магнитопроводы
- закон Ома для магнитной цепи
Что такое ММФ?
спросил
12 сент. 2021 г.
в базовой электротехнике
по
год
(88,7 тыс. баллов)
2021 г.
в базовой электротехнике
по
год
(88,7 тыс. баллов)
- основы электротехники
- простые магнитопроводы
- закон Ома для магнитной цепи
Рассчитайте плотность магнитного потока, если напряженность магнитного поля составляет 3 А/м.
спросил 12 сент. 2021 г. в базовой электротехнике по год (88,7 тыс. баллов)
- основы электротехники
- простые магнитопроводы
- проницаемость свободного пространства или магнитная постоянная
В какой из следующих областей существует магнитное поле?
спросил 12 сент. 2021 г. в базовой электротехнике по год (88,7 тыс. баллов)
- основы электротехники
- простые магнитопроводы
- магнитодвижущая сила и напряженность магнитного поля
Рассчитайте напряженность магнитного поля, если плотность магнитного потока равна 4*piT.
спросил
12 сент. 2021 г.
в базовой электротехнике
по
год
(88,7 тыс. баллов)
2021 г.
в базовой электротехнике
по
год
(88,7 тыс. баллов)
- основы электротехники
- простые магнитопроводы
- проницаемость свободного пространства или магнитная постоянная
По мере увеличения напряженности магнитного поля сопротивление?
спросил 12 сент. 2021 г. в базовой электротехнике по год (88,7 тыс. баллов)
- основы электротехники
- простые магнитопроводы
- нежелание
Связь между направлением тока и направлением магнитного поля?
спросил 12 сент. 2021 г. в базовой электротехнике по год (88,7 тыс. баллов)
- основы электротехники
- простые магнитопроводы
- магнитодвижущая сила и напряженность магнитного поля
Рассчитайте плотность магнитного потока, если напряженность магнитного поля составляет 2 А/м.
спросил
12 сент. 2021 г. в базовой электротехнике
по
год
(88,7 тыс. баллов)
в базовой электротехнике
по
год
(88,7 тыс. баллов)
- основы электротехники
- простые магнитопроводы
- проницаемость свободного пространства или магнитная постоянная
Когда из страницы течет электрический ток, каково направление магнитного поля?
спросил 12 сент. 2021 г. в базовой электротехнике по год (88,7 тыс. баллов)
- основы электротехники
- простые магнитопроводы
- магнитодвижущая сила и напряженность магнитного поля
Когда электрический ток течет по странице, каково направление магнитного поля?
спросил 12 сент. 2021 г. в базовой электротехнике по год (88,7 тыс. баллов)
- основы электротехники
- простые магнитопроводы
- магнитодвижущая сила и напряженность магнитного поля
При увеличении плотности магнитного потока сопротивление _____________
спросил
12 сент. 2021 г.
в базовой электротехнике
по
год
(88,7 тыс. баллов)
2021 г.
в базовой электротехнике
по
год
(88,7 тыс. баллов)
- основы электротехники
- простые магнитопроводы
- нежелание
Проницаемость свободного пространства также известна как _________
спросил 12 сент. 2021 г. в базовой электротехнике по год (88,7 тыс. баллов)
- основы электротехники
- простые магнитопроводы
- проницаемость свободного пространства или магнитная постоянная
Отношение B/H непостоянно для ________
спросил 12 сент. 2021 г. в базовой электротехнике по год (88,7 тыс. баллов)
- основы электротехники
- простые магнитопроводы
- определение характеристики b h
Какие из перечисленных обладают отрицательной чувствительностью?
спросил 12 сент. 2021 г. в базовой электротехнике по год (88,7 тыс. баллов)
- основы электротехники
- простые магнитопроводы
- проницаемость свободного пространства или магнитная постоянная
Баллистический гальванометр обычно слегка демпфируют, чтобы ________
спросил
12 сент. 2021 г.
в базовой электротехнике
по
год
(88,7 тыс. баллов)
2021 г.
в базовой электротехнике
по
год
(88,7 тыс. баллов)
- основы электротехники
- простые магнитопроводы
- определение характеристики b h
Диамагнетики обладают относительной магнитной проницаемостью_____________
спросил 12 сент. 2021 г. в базовой электротехнике по год (88,7 тыс. баллов)
- основы электротехники
- простые магнитопроводы
- относительная проницаемость
Приборы PMMC могут использоваться в качестве флюксметров _______
спросил 12 сент. 2021 г. в базовой электротехнике по год (88,7 тыс. баллов)
- основы электротехники
- простые магнитопроводы
- определение характеристики b h
Вещество, относительная проницаемость которого больше, чем проницаемость свободного пространства?
спросил
12 сент. 2021 г.
в базовой электротехнике
по
год
(88,7 тыс. баллов)
баллов)
- основы электротехники
- простые магнитопроводы
- относительная проницаемость
Руководство по проектированию магнитных цепей | Технические примечания | Магниты
1. Основные расчетные формулы
1-1. Полный магнитный поток Φ и электрическая проводимость P
Основная формула расчета для магнитных цепей аналогична закону Ома; а именно, когда полный магнитный поток обозначается через Φ, магнитодвижущей силы через F и магнитного сопротивления через R соотношение между этими тремя элементами выражается следующей формулой:
Однако при расчете магнитной цепи вместо магнитного сопротивления R обычно используется проницаемость P, которая является обратной величиной магнитного сопротивления R. Следовательно, приведенную выше формулу можно заменить следующей формулой:
Когда длина магнитного пути обозначается L, площадь поперечного сечения магнитного пути — A, а магнитная проницаемость магнитного пути — µ, магнитная проводимость P выражается по следующей формуле:
Эта формула показывает, что чем короче длина магнитного пути L и чем больше площадь поперечного сечения А и проницаемость μ, тем больше проницаемость Р (т. е. меньше магнитное сопротивление).
е. меньше магнитное сопротивление).
Кроме того, проницаемость Pt для всей магнитной цепи выражается суммой проницаемости зазора Pg, которая определяется как величина, обратная магнитному сопротивлению в зазоре, а проницаемость рассеяния Pf определяется как величина, обратная магнитному сопротивлению, вызванному магнитным потоком рассеяния ( Pt = Pg + Pf ).
Чтобы понять поток рассеяния для каждого пространства магнитного пути, общая магнитная проницаемость Pt выражается как сумма магнитной проницаемости зазора Pg и магнитной проницаемости каждого пространства магнитного пути (Pf 1 + Pf 2 + Pf 3 + ……. Pf n ).
1-2. Коэффициент потерь магнитодвижущей силы f
Коэффициент потерь магнитодвижущей силы f определяется как отношение полной магнитодвижущей силы F магнитопровод к зазору магнитодвижущая сила Fg.
Общая магнитодвижущая сила F магнитной цепи определяется используемым магнитом, а ее значение является произведением напряженности магнитного поля в точке
рабочая точка магнита Hd и длина магнита Lm.
Кроме того, магнитодвижущая сила зазора Fg является произведением плотности магнитного потока Bg зазора и длины зазора Lg; следовательно, формулу (5) можно расширить до следующей формулы:
1-3. Коэффициент рассеяния σ
Коэффициент рассеяния выражается отношением полного магнитного потока Φt, создаваемого магнитом в магнитопроводе, к сходящемуся в зазоре магнитному потоку Φg.
Полный магнитный поток Φt, создаваемый магнитом, определяется как произведение плотности магнитного потока в рабочей точке Bd и поперечного сечения магнита площадь сечения Am, а магнитный поток, сходящийся в зазоре Φg, определяется как произведение плотности магнитного потока Bg зазора на площадь поперечного сечения зазора Аг; поэтому формулу (7) можно разложить до следующей формулы:
Кроме того, из формулы (2) :Φ = FP формула (7) также может быть выражена следующей формулой:
Поскольку коэффициент потерь магнитодвижущей силы f обычно становится значением, близким к 1, формула (9) примет вид следующую формулу, заменив формулу (5) и формулу (4):
Эта формула также может быть выражена в следующей форме путем деления Pf на каждое пространство магнитного пути рассеяния:
1-4.
 Коэффициент проницаемости Pc
Коэффициент проницаемости PcКоэффициент проницаемости Pc используется для выражения рабочей точки магнита на кривой B-H. Эта величина определяется как отношение плотности магнитного потока Bd к напряженности магнитного поля Hd в рабочей точки и выражается следующей формулой (см. рисунок выше):
1-4-а. Коэффициент магнитной проводимости магнита, включенного в магнитную цепь
Коэффициент магнитной проводимости магнита, включенного в магнитную цепь, можно определить, получив Hd и Bd из формул (6) и формул (8) и подставив их в формулу (11).
И заменив это на
, можно получить следующую формулу:
1-4-б. Коэффициент магнитной проводимости цельного магнита
На коэффициент магнитной проводимости одиночного магнита в значительной степени влияет форма магнита, поэтому очень сложно получить точное значение расчетным путем.
Таким образом, из приведенного ниже рисунка с использованием столбчатого магнита в качестве образца (график, показывающий взаимосвязь между отношением размеров и коэффициентом магнитной проводимости) получена грубая оценка.
Формула приближения будет следующей:
1-5. Методы расчета длины Lm, площади поперечного сечения Am и объема Vm
Длина Lm и площадь поперечного сечения Am, необходимые для магнита: необходимые Lm и Am могут быть получены.
А необходимый Vm равен
, что указывает на то, что необходимый объем магнита обратно пропорционален произведению энергии в рабочей точке.
1-6. Метод определения коэффициента утечки σ и коэффициента потерь магнитодвижущей силы f
1-6-a. Процедуры экспериментального получения σ и f
■ Метод с использованием поисковой катушки
- 1. Намотайте поисковую катушку на магнит и измерьте магнитный поток в зазоре.
- 2. Рассчитайте Bd из полного потока Φg/площадь поперечного сечения магнита Am.
- 3. Получите Hd из кривой B-H (кривая размагничивания).
- 4. Измерьте Bg, Ag, Lg, Am и Lm.
- 5. Рассчитайте f и σ по формуле (6) и формуле (8).
■ Метод без использования поисковой катушки
- 1.
 Предположим, что значение f (обычно между 1,0 и 1,2).
Предположим, что значение f (обычно между 1,0 и 1,2). - 2. Измерьте Lm, Bg и Lg.
- 3. Рассчитайте Hd по формуле (12) на предыдущей странице.
- 4. Получите Bd из кривой B-H (кривая размагничивания).
- 5. Измерьте Am и Ag и рассчитайте σ по формуле (8).
1-6-б. Метод получения σ расчетным путем
Получите Pg и Pf 1 через Pf n по формуле (10),
и рассчитайте σ.
Справочный пример
Пример расчета магнитной проницаемости основных компонентов (Pg, P 1 , P 2 P 3 и P 4 ) пространства пути магнитного рассеяния показан ниже.
1) Проницаемость площади зазора на рисунке
2) Проницаемость полуцилиндрического магнитного пути рассеяния
3) Проницаемость полуцилиндрического (полого) магнитного пути рассеяния
4) Проницаемость четвертьсферического магнитного пути рассеяния
5) Проницаемость Полая четверть сферического магнитного пути рассеяния
Путем объединения проницаемости вышеперечисленных пунктов с 1) по 5) можно получить грубую оценку σ в пространстве магнитного пути рассеяния ( μ 0 : проницаемость вакуума).
2. Формула расчета плотности магнитного потока B(X) на центральной линии магнита
Когда кривая B-H прямая или рабочая точка Bd расположена выше точки перегиба, распределение магнитного поля вне магнита может следует рассматривать так же, как магнитное поле, создаваемое замкнутым током на внешней периферийной поверхности пространства длиной X, имеющего такую же магнитную проницаемость и форму поперечного сечения, что и магнит.
Расчетные формулы для получения этого B(X) для трех типичных форм будут показаны ниже. Эти формулы эффективны в качестве аппроксимационных формул для ферритовых магнитов или неодимовых магнитов.
2-1. Магнит цилиндрической формы
2-2. Магнит в виде квадратной стойки
2-3. Трубчатый магнит
2-4. Когда магнитное тело находится позади магнитного полюса
Подставьте 2L в член L формул 2-1, 2-2 и 2-3.
2-5. Когда магниты одинаковой формы расположены напротив друг друга на расстоянии 2X
, B(X) в центре зазора будет вдвое больше, чем B(X), полученное с использованием формул 2-1, 2-2 и 2-3.
B(X) в точке P внутри пробела будет суммой B(X-P), в которой X-P подставлен в член X предыдущей формулы, и B(X+P), в котором X+P вставлен в член X предыдущей формулы.
2-6. Когда магнитное тело расположено за магнитным полюсом в той же конфигурации, что и в предыдущем разделе
, подставьте 2L в член L формул 2-1, 2-2 и 2-3. B(X) в центре зазора и точка P внутри зазора могут быть получены с помощью тех же процедур, что и 2-5.
3. Расчет эффективного магнитного потока магнитных цепей для двигателей
В магнитных цепях для двигателей условия магнитной цепи сильно различаются в зависимости от элементов, включая количество пазов ротора, форму пазов, и толщина стенки корпуса. Поэтому в этом разделе будут показаны только формулы, которые показывают основные понятия.
1) Площадь поперечного сечения магнита Am
2) Отношение эквивалентных размеров магнита л/д
3) Коэффициент магнитной проводимости одиночного магнита Pi
4) Коэффициент магнитной проводимости одиночного магнита, включая ярмо PL
5) Коэффициент Кертера К c
6) Эффективный коэффициент магнитной проводимости P u
7) Магнитный поток рассеяния σ
8) Магнитный поток насыщения полюсов 00 90 02 О 90 03 03 магнитная цепь
Приведенный выше метод расчета Φg не принимает
с учетом насыщения магнитопровода. Однако в реальных магнитных цепях насыщение может происходить в области корпуса или ротора.
Другими словами, когда Φg, полученное вышеуказанным методом расчета, и Φg в реальном двигателе сравниваются, а g в реальном двигателе меньше расчетного значения, возможно, что магнитная цепь насыщается.
Однако в реальных магнитных цепях насыщение может происходить в области корпуса или ротора.
Другими словами, когда Φg, полученное вышеуказанным методом расчета, и Φg в реальном двигателе сравниваются, а g в реальном двигателе меньше расчетного значения, возможно, что магнитная цепь насыщается.
Таблица преобразования единиц СИ/СГС
Путем умножения характеристического значения в единицах СИ на коэффициент преобразования, указанный слева от ▶, можно получить значение в единицах СГС.
Аналогично, путем умножения характеристического значения в единицах СГС на коэффициент пересчета справа от ◀ можно получить значение в единицах СИ.
| Единица СИ▶ | ◀ Блок CGS | ||||||
|---|---|---|---|---|---|---|---|
| Магнитный терм | Символ изделия | Название устройства | Обозначение блока | Коэффициент пересчета▶ | ◀Коэффициент преобразования | Обозначение блока | Название устройства |
| Магнитный поток | Ф | Вебер | Вб | 10 8 ▶ | ◀10 -8 | Мх | Максвелл |
| Плотность магнитного потока | Б | Тесла | Т | 10 4 ▶ | ◀10 -4 | Г | Гаусс |
| Магнитное поле | Х | Ампер/м | А/м | 4π×10 -3 ▶ | ◀10 3 /4π | Ое | Эрстед |
| Намагничивание | М | Ампер/м | А/м | 10 -3 ▶ | ◀10 3 | Г | Гаусс |
| Магнитная поляризация | Дж | Тесла | Т | 10 4 /4π▶ | ◀4π×10 -4 | Г | Гаусс |
| Магнитодвижущая сила | ФМ | Ампер | А | 4π×10 -1 ▶ | ◀10/4π | Ги | Гилберт |
| Сила магнитного притяжения | Ф | Ньютон | Н | 10 5 ▶ | ◀10 -5 | дин | Дин |
| Проницаемость | мк | Генри/м | В/м | 10 7 /4π▶ | ◀4π×10 -7 | Безразмерный | |
| Проницаемость вакуума | мк 0 | 4π×10 -7 Генри/м | В/м | Безразмерный | 1 | ||
| Магнитное сопротивление | руб. | 1/Генри | Н -1 | 4π×10 -9 ▶ | ◀10 9 /4π | Ги/Мкс | Гилберт/Максвелл |
| Проницаемость | Р | Генри | Х | 10 9 /4π▶ | ◀4π×10 -9 | Мкс/Ги | Максвелл/Гилберт |
| Продукт магнитной энергии | БХ | Дж/м 3 | Дж/м 3 | 4π×10▶ | ◀10 -1 /4π | Г · ОЕ | Гаусс · Эрстед |
| 10▶ | 10 -1 | эрг/см 3 | Эрг/см 3 | ||||
Магнитная цепь
Магнитный поток ф г , протекающий через воздушный зазор в конструкции на рис. 4.2, является частью общего потока, создаваемого током, протекающим в катушке, окружающей материал сердечника.
Этот общий поток ф, протекающий через площадь поперечного сечения катушки, создается током катушки и пропорционален как величине тока катушки i, так и общему числу витков N провода, из которого состоит катушка. катушка. Произведение N и i называется магнитодвижущей силой катушки. Коэффициент пропорциональности в соотношении между полным потоком, создаваемым током катушки, и ммс катушки измеряется в единицах потока (измеряется в веберах) на единицу ммс (измеряется в ампер-витках).
Поскольку общий поток ф пропорционален силовому члену – МДС – можно провести простую аналогию между магнитной цепью и электрической цепью. В электрической цепи постоянного тока ток i протекает под действием электродвижущей силы (ЭДС) E. Закон Ома для электрической цепи гласит, что
, где R — сопротивление цепи протеканию тока. Тогда «магнитный закон Ома» будет равен
, где R — сопротивление магнитной цепи потоку магнитного потока. Этому сопротивлению потоку R было присвоено специальное название, чтобы отличить его от сопротивления потоку тока. Мы называем это сопротивлением магнитной цепи.
Мы называем это сопротивлением магнитной цепи.
Сопротивление магнитной цепи будет примерно постоянным, пока плотность потока в любой части цепи ниже плотности потока насыщения для этой части цепи. Ферромагнитные материалы насыщаются магнитным потоком при уровнях плотности примерно 1-2 Тесла = 1-2 Вебера/(метр) 2 . При уровнях плотности, близких к этому значению насыщения, эффективное сопротивление материала быстро возрастает. На уровнях плотности ниже значения насыщения сопротивление ферромагнитных элементов намного ниже, чем у элементов сопоставимого размера, изготовленных из немагнитных материалов.
Чтобы построить представление простой магнитной цепи с сосредоточенными параметрами для конструкции магнитного выключателя на рис. 4.2, мы должны помнить, что полный поток, создаваемый катушкой, должен состоять из двух компонентов: компонента зазора ф g , который течет через катушку, структуру сердечника, якорь и зазор, и элемент утечки ф ᵜ , протекающий через катушку, часть конструкции сердечника и путь утечки воздуха. На рис. 4.4а показаны два компонента, протекающие по своим физическим путям.
На рис. 4.4а показаны два компонента, протекающие по своим физическим путям.
На рис. 4.4b показан электрический эквивалент «магнитной цепи» устройства. Здесь катушка mmf показана как источник постоянного напряжения величиной Ni, а магнитные сопротивления различных путей потока показаны как эквивалентные сопротивления.
Реактивная часть сердечника, которая несет как поток рассеяния, так и поток зазора, обозначена R c ; сопротивление воздушной части пути потока рассеяния обозначено R ᵜ ; магнитное сопротивление сердечника и якоря части пути потока зазора обозначено R или ; а сопротивление зазора обозначается как R g . Фактические значения магнитных сопротивлений R c , R х , R ca и R g определяются эффективными площадями поперечных сечений соответствующих путей потока, эффективными длинами соответствующих путей потока и магнитные проницаемости соответствующих путей потока. Если материал пути представляет собой ферромагнитный материал, такой как железо, сопротивление пути также будет функцией уровня плотности потока внутри пути, если уровень плотности близок или превышает значение насыщения.
Если материал пути представляет собой ферромагнитный материал, такой как железо, сопротивление пути также будет функцией уровня плотности потока внутри пути, если уровень плотности близок или превышает значение насыщения.
В общем, для любого заданного пути мы имеем для сопротивления пути
, где L p — эффективная длина пути, A p — эффективная площадь поперечного сечения пути, а µ p – магнитная проницаемость среды пути. Если среда пути ферромагнитна, то при высоких уровнях потока пути, ф p , потока мы имеем µ p = µ p (ф p ). Поскольку поток зазора и поток рассеяния являются воздушными путями, проницаемости обоих путей равны проницаемости свободного пространства µ o – это строгая константа, а не функция уровня потока на трассе.
Для зазора мы имеем примерно
, где θ g — это угловое раскрытие зазора, измеренное с якорем в удерживаемом положении.


 При протекании тока I по обмотке в магнитопроводе возбуждается магнитное поле, которое все сосредоточено в объеме кольца (поле рассеяния отсутствует). Выбрав контур интегрирования в виде окружности с радиусом
При протекании тока I по обмотке в магнитопроводе возбуждается магнитное поле, которое все сосредоточено в объеме кольца (поле рассеяния отсутствует). Выбрав контур интегрирования в виде окружности с радиусом 



 измерения
измерения
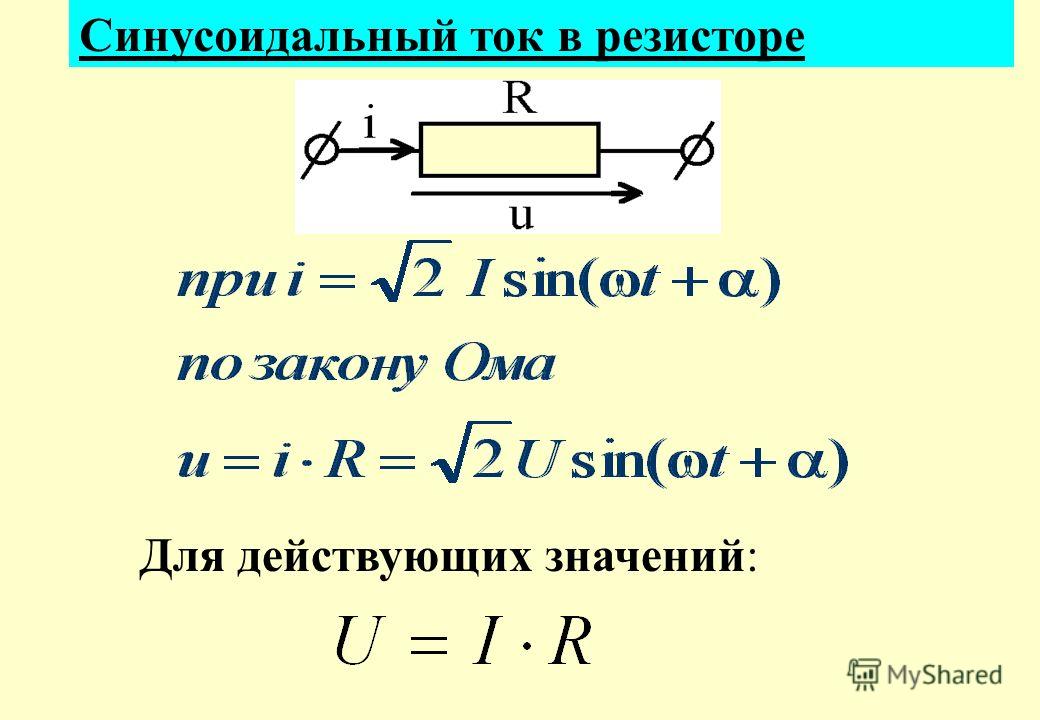

 ..
..